На чтение 4 мин Просмотров 1.2к.
Рассмотрим первый пример. Пусть в плоскости координат задан двумя точками некий отрезок. В данном случае его длину мы можем найти, применяя теорему Пифагора.
Итак, в системе координат начертим отрезок с заданными координатами его концов (x1; y1) и (x2; y2) . На оси X и Y из концов отрезка опустим перпендикуляры. Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.
Вычислим длину данных проекций. Итак, на ось Y длина проекции равна y2-y1, а на ось Х длина проекции равна x2-x1. Применим теорему Пифагора: |AB|² = (y2 – y1)² + (x2 – x1)². В данном случае |AB| является длиной отрезка.
Если использовать данную схему для вычисления длины отрезка, то можно даже отрезок и не строить. Теперь высчитаем, какова длина отрезка с координатами (1;3) и (2;5). Применяя теорему Пифагора, получаем: |AB|² = (2 – 1)² + (5 – 3)² = 1 + 4 = 5. А это значит, что длина нашего отрезка равна 5:1/2.
Рассмотрим следующий способ нахождения длины отрезка. Для этого нам необходимо знать координаты двух точек в какой-либо системе. Рассмотрим данный вариант, применяя двухмерную Декартову систему координат.

Итак, в двухмерной системе координат даны координаты крайних точек отрезка. Если проведем прямые лини через эти точки, они должны быть перпендикулярными к оси координат, то получим прямоугольный треугольник. Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.
Найдем длины проекций (X и Y) исходного отрезка на координатные оси. Их вычислим путем нахождения разницы координат точек по отдельной оси: X = X2-X1, Y = Y2-Y1.
Рассчитаем длину отрезка А, для этого найдем квадратный корень:
Если наш отрезок расположен между точками, координаты которых 2;4 и 4;1, то его длина, соответственно, равна √((4-2)²+(1-4)²) = √13 ≈ 3,61.
Этот онлайн калькулятор рассчитывает длину отрезка и координаты середины отрезка (средней точки) по декартовым координатам концов отрезка. Отрезок и средняя точка отображаются на графике, также на графике показан графический способ нахождения середины отрезка.
Эта страница существует благодаря следующим персонам
![]()
Timur
- Статья : Расчет длины отрезка и координат середины отрезка по двум точкам – Автор, Переводчик en – ru
- Калькулятор : Расчет длины отрезка и координат середины отрезка по двум точкам – Автор, Переводчик en – ru
Этот онлайн калькулятор рассчитывает длину отрезка и координаты середины отрезка по введенным декартовым координатам двух точек – концов отрезка.
Формула вычисления расстояния между двумя точками и это формула длины гипотенузы прямоугольного треугольника . Координаты середины отрезка – среднее арифметическое координат точек .
Отрезок и средняя точка отображаются на графике. Также среднюю точку можно найти построением. Для этого на графике надо построить две дуги с центрами на концах отрезка и с радиусом равным длине отрезка. Затем надо построить прямую линию между точками пересечения дуг. Эта линия пересечет исходный отрезок в середине.
Отрезком обозначают ограниченный двумя точками участок прямой. Точки – концы отрезка.
Общеизвестный факт, что каждая точка А плоскости имеет свои координаты (х, у).
В данном примере вектор AB задан координатами (х2— х1, y2— y1). Квадрат длины вектора будет равен сумме квадратов его координат. Следовательно, расстояние d между точками А и В, или, что то же самое, длина вектора АВ, вычисляется согласно формуле:
Эта формула длины отрезка предоставляет возможность рассчитывать расстояние между двумя произвольными точками плоскости, при условии, что известны координаты этих точек
Вышеуказанную формулу длины отрезка можно доказать и другим способом. В системе координат заданы координаты крайних точек отрезка координатами его концов(х1y1) и (х2,у2).
Прочертим прямые лини через эти точки перпендикулярно к осям координат, в результате имеем прямоугольный треугольник. Первоначальный отрезок является гипотенузой образовавшегося треугольника. Катеты треугольника сформированы отрезками, их длиной будет проекция гипотенузы на оси координат.
Установим длину этих проекций.
На ось у длина проекции равна y2 – y1, а на ось х длина проекции равна х2 – х1. На основании теоремы Пифагора видим, что |AB|² = (y2 – y1)² + (x2 – x1)².
В рассмотренном случае |AB| выступает длиной отрезка.
Вычислим длину отрезка АВ, для этого извлечем квадратный корень. Результатом является все та же формула длины отрезков по известным координатам конца и начала.
Уравнение прямой, которая проходит через две заданные точки: примеры, решения
Данная статья раскрывает получение уравнения прямой, проходящей через две заданные точки в прямоугольной системе координат, расположенной на плоскости. Выведем уравнение прямой, проходящей через две заданные точки в прямоугольной системе координат. Наглядно покажем и решим несколько примеров, касающихся пройденного материала.
Уравнение прямой, проходящей через две заданные точки на плоскости
Перед получением уравнения прямой, проходящей через две заданные точки необходимо обратить внимание на некоторые факты. Существует аксиома, которая говорит о том, что через две несовпадающие точки на плоскости возможно провести прямую и только одну. Иначе говоря, две заданные точки плоскости определяются прямой линией, проходящей через эти точки.
Если плоскость задана прямоугольной системой координат Оху, то любая изображенная в нем прямая будет соответствовать уравнению прямой на плоскости. Также имеется связь с направляющим вектором прямой. Этих данных достаточно для того, чтобы произвести составление уравнения прямой, проходящей через две заданные точки.
Рассмотрим на примере решения подобной задачи. Необходимо составить уравнение прямой a , проходящей через две несовпадающие точки M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) , находящиеся в декартовой системе координат.
В каноническом уравнении прямой на плоскости, имеющего вид x – x 1 a x = y – y 1 a y , задается прямоугольная система координат О х у с прямой, которая пересекается с ней в точке с координатами M 1 ( x 1 , y 1 ) с направляющим вектором a → = ( a x , a y ) .
Необходимо составить каноническое уравнение прямой a , которая пройдет через две точки с координатами M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) .
Прямая а имеет направляющий вектор M 1 M 2 → с координатами ( x 2 – x 1 , y 2 – y 1 ) , так как пересекает точки М 1 и М 2 . Мы получили необходимые данные для того, чтобы преобразовать каноническое уравнение с координатами направляющего вектора M 1 M 2 → = ( x 2 – x 1 , y 2 – y 1 ) и координатами лежащих на них точках M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) . Получим уравнение вида x – x 1 x 2 – x 1 = y – y 1 y 2 – y 1 или x – x 2 x 2 – x 1 = y – y 2 y 2 – y 1 .
Рассмотрим рисунок, приведенный ниже.
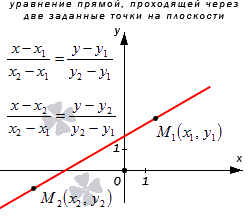
Следуя по вычислениям, запишем параметрические уравнения прямой на плоскости, которое проходит через две точки с координатами M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) . Получим уравнение вида x = x 1 + ( x 2 – x 1 ) · λ y = y 1 + ( y 2 – y 1 ) · λ или x = x 2 + ( x 2 – x 1 ) · λ y = y 2 + ( y 2 – y 1 ) · λ .
Рассмотрим подробней на решении нескольких примеров.
Записать уравнение прямой, проходящей через 2 заданные точки с координатами M 1 – 5 , 2 3 , M 2 1 , – 1 6 .
Каноническим уравнением для прямой, пересекающейся в двух точках с координатами x 1 , y 1 и x 2 , y 2 принимает вид x – x 1 x 2 – x 1 = y – y 1 y 2 – y 1 . По условию задачи имеем, что x 1 = – 5 , y 1 = 2 3 , x 2 = 1 , y 2 = – 1 6 . Необходимо подставить числовые значения в уравнение x – x 1 x 2 – x 1 = y – y 1 y 2 – y 1 . Отсюда получим, что каноническое уравнение примет вид x – ( – 5 ) 1 – ( – 5 ) = y – 2 3 – 1 6 – 2 3 ⇔ x + 5 6 = y – 2 3 – 5 6 .
Ответ: x + 5 6 = y – 2 3 – 5 6 .
При необходимости решения задачи с другим видом уравнения, то для начала можно перейти к каноническому, так как из него проще прийти к любому другому.
Составить общее уравнение прямой, проходящей через точки с координатами M 1 ( 1 , 1 ) и M 2 ( 4 , 2 ) в системе координат О х у .
Для начала необходимо записать каноническое уравнение заданной прямой, которая проходит через заданные две точки. Получим уравнение вида x – 1 4 – 1 = y – 1 2 – 1 ⇔ x – 1 3 = y – 1 1 .
Приведем каноническое уравнение к искомому виду, тогда получим:
x – 1 3 = y – 1 1 ⇔ 1 · x – 1 = 3 · y – 1 ⇔ x – 3 y + 2 = 0
Ответ: x – 3 y + 2 = 0 .
Примеры таких заданий были рассмотрены в школьных учебниках на уроках алгебры. Школьные задачи отличались тем, что известным было уравнение прямой с угловым коэффициентом, имеющее вид y = k x + b . Если необходимо найти значение углового коэффициента k и числа b , при которых уравнение y = k x + b определяет линию в системе О х у , которая проходит через точки M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) , где x 1 ≠ x 2 . Когда x 1 = x 2 , тогда угловой коэффициент принимает значение бесконечности, а прямая М 1 М 2 определена общим неполным уравнением вида x – x 1 = 0 .
Потому как точки М 1 и М 2 находятся на прямой, тогда их координаты удовлетворяют уравнению y 1 = k x 1 + b и y 2 = k x 2 + b . Следует решить систему уравнений y 1 = k x 1 + b y 2 = k x 2 + b относительно k и b .
Для этого найдем k = y 2 – y 1 x 2 – x 1 b = y 1 – y 2 – y 1 x 2 – x 1 · x 1 или k = y 2 – y 1 x 2 – x 1 b = y 2 – y 2 – y 1 x 2 – x 1 · x 2 .
С такими значениями k и b уравнение прямой, проходящее через заданные две точки, принимает следующий вид y = y 2 – y 1 x 2 – x 1 · x + y 2 – y 2 – y 1 x 2 – x 1 · x 1 или y = y 2 – y 1 x 2 – x 1 · x + y 2 – y 2 – y 1 x 2 – x 1 · x 2 .
Запомнить сразу такое огромное количество формул не получится. Для этого необходимо учащать количество повторений в решениях задач.
Записать уравнение прямой с угловым коэффициентом, проходящей через точки с координатами M 2 ( 2 , 1 ) и y = k x + b .
Для решения задачи применяем формулу с угловым коэффициентом, имеющую вид y = k x + b . Коэффициенты k и b должны принимать такое значение, чтобы данное уравнение соответствовало прямой, проходящей через две точки с координатами M 1 ( – 7 , – 5 ) и M 2 ( 2 , 1 ) .
Точки М 1 и М 2 располагаются на прямой, тогда их координаты должны обращать уравнение y = k x + b верное равенство. Отсюда получаем, что – 5 = k · ( – 7 ) + b и 1 = k · 2 + b . Объединим уравнение в систему – 5 = k · – 7 + b 1 = k · 2 + b и решим.
При подстановке получаем, что
– 5 = k · – 7 + b 1 = k · 2 + b ⇔ b = – 5 + 7 k 2 k + b = 1 ⇔ b = – 5 + 7 k 2 k – 5 + 7 k = 1 ⇔ ⇔ b = – 5 + 7 k k = 2 3 ⇔ b = – 5 + 7 · 2 3 k = 2 3 ⇔ b = – 1 3 k = 2 3
Теперь значения k = 2 3 и b = – 1 3 подвергаются подстановке в уравнение y = k x + b . Получаем, что искомым уравнением, проходящим через заданные точки, будет уравнение, имеющее вид y = 2 3 x – 1 3 .
Такой способ решения предопределяет траты большого количества времени. Существует способ, при котором задание решается буквально в два действия.
Запишем каноническое уравнение прямой, проходящей через M 2 ( 2 , 1 ) и M 1 ( – 7 , – 5 ) , имеющее вид x – ( – 7 ) 2 – ( – 7 ) = y – ( – 5 ) 1 – ( – 5 ) ⇔ x + 7 9 = y + 5 6 .
Теперь переходим к уравнению в угловым коэффициентом. Получаем, что: x + 7 9 = y + 5 6 ⇔ 6 · ( x + 7 ) = 9 · ( y + 5 ) ⇔ y = 2 3 x – 1 3 .
Ответ: y = 2 3 x – 1 3 .
Уравнения прямой, которая проходит через две заданные точки в трехмерном пространстве
Если в трехмерном пространстве имеется прямоугольная система координат О х у z с двумя заданными несовпадающими точками с координатами M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , проходящая через них прямая M 1 M 2 , необходимо получить уравнение этой прямой.
Имеем, что канонические уравнения вида x – x 1 a x = y – y 1 a y = z – z 1 a z и параметрические вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ способны задать линию в системе координат О х у z , проходящую через точки, имеющие координаты ( x 1 , y 1 , z 1 ) с направляющим вектором a → = ( a x , a y , a z ) .
Прямая M 1 M 2 имеет направляющий вектор вида M 1 M 2 → = ( x 2 – x 1 , y 2 – y 1 , z 2 – z 1 ) , где прямая проходит через точку M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , отсюда каноническое уравнение может быть вида x – x 1 x 2 – x 1 = y – y 1 y 2 – y 1 = z – z 1 z 2 – z 1 или x – x 2 x 2 – x 1 = y – y 2 y 2 – y 1 = z – z 2 z 2 – z 1 , в свою очередь параметрические x = x 1 + ( x 2 – x 1 ) · λ y = y 1 + ( y 2 – y 1 ) · λ z = z 1 + ( z 2 – z 1 ) · λ или x = x 2 + ( x 2 – x 1 ) · λ y = y 2 + ( y 2 – y 1 ) · λ z = z 2 + ( z 2 – z 1 ) · λ .
Рассмотрим рисунок, на котором изображены 2 заданные точки в пространстве и уравнение прямой.
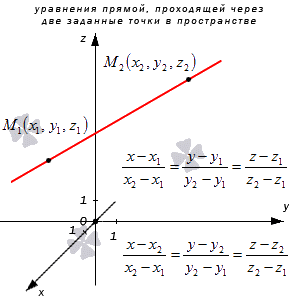
Написать уравнение прямой, определенной в прямоугольной системе координат О х у z трехмерного пространства, проходящей через заданные две точки с координатами M 1 ( 2 , – 3 , 0 ) и M 2 ( 1 , – 3 , – 5 ) .
Необходимо найти каноническое уравнение. Так как речь идет о трехмерном пространстве, значит при прохождении прямой через заданные точки, искомое каноническое уравнение примет вид x – x 1 x 2 – x 1 = y – y 1 y 2 – y 1 = z – z 1 z 2 – z 1 .
По условию имеем, что x 1 = 2 , y 1 = – 3 , z 1 = 0 , x 2 = 1 , y 2 = – 3 , z 2 = – 5 . Отсюда следует, что необходимые уравнения запишутся таким образом:
x – 2 1 – 2 = y – ( – 3 ) – 3 – ( – 3 ) = z – 0 – 5 – 0 ⇔ x – 2 – 1 = y + 3 0 = z – 5
Ответ: x – 2 – 1 = y + 3 0 = z – 5 .
Глава 1. Уравнение прямой (стр. 1 )
 |
Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 |

Глава 1. Уравнение прямой
Геометрия развивается по многим направлениям. Возникновение компьютеров привело к появлению такой области математики как вычислительная геометрия. При создании современных приложений часто требуется разработка эффективных алгоритмов для определения взаиморасположения различных объектов на плоскости, вычисления расстояний между ними, вычисления площадей фигур и др.
В данной главе излагается материал, частично известный вам из курса математики. Мы рассмотрим методы решения геометрических задач, которые эффективно реализуются с помощью компьютера, что позволит вам по другому взглянуть на вопросы, изучаемые в рамках школьного курса геометрии. Для этого придется воспользоваться аналитическим представлением геометрических объектов.
1. 1. Формы записи уравнения прямой
В задачах часто приходится задавать на плоскости различные геометрические объекты. Простейшими геометрическими фигурами на плоскости являются точка и прямая. Точка задается указанием своих координат, например A(15; –5), B(x1; y1). Прямую можно задавать с помощью уравнения прямой. Существуют различные формы записи уравнения прямой. Выбор какой-то конкретной зависит от исходных данных, задающих прямую на плоскости. (Могут быть заданы координаты двух точек, через которые проводится прямая, или коэффициенты при неизвестных в линейном уравнении).
В декартовых координатах каждая прямая определяется уравнением первой степени. Уравнение вида
называется общим уравнением прямой.
Если в общем уравнении прямой коэффициент при y не равен нулю, то уравнение можно разрешить относительно y:

Обозначая k =  и b =
и b =  ,
,
получаем уравнение вида y = kx + b. Если же B = 0, то уравнение имеет вид

Уравнение y = kx + b называется уравнением прямой с угловым коэффициентом; k – угловой коэффициент, b – величина отрезка, который отсекает прямая на оси Oy, считая от начала координат (рис. 1).


Уравнение y – y0 = k(x–x0) – это уравнение прямой с угловым коэффициентом k, которая проходит через точку с координатами (x0; y0).
Рассмотрим две точки с координатами (x1; y1) и (x2; y2), лежащие на прямой y = kx + b. Их координаты удовлетворяют уравнению прямой:
Вычитая из второго равенства первое, имеем y2 – y1 = k(x2 – x1), или
k = 
Пусть точка с координатами (x; y) – произвольная точка на прямой, проходящей через точки с координатами (x1; y1) и (x2; y2) ( рис. 2 ). Тогда, с учетом того факта, что она имеет тот же коэффициент наклона, получаем
k = 
 =
=  или
или  =
= 
 =
= 
является уравнением прямой, которая проходит через точки с координатами (x1; y1) и (x2; y2). Недостатком этой формулы является ее неопределенность при x1 = x2 и (или) y1 = y2. Поэтому ее лучше использовать в виде
Алгоритм для определения значений коэффициентов A, B, C общего уравнения прямой, проходящей через точки (x1; y1) и (x2; y2), будет следующим [1] :
C:= – x1*(y2 – y1)+y1*(x2 – x1)
Рассмотрим пример: x1 = 0, y1 = 0, x2 = 1, y2 = 2. Уравнение прямой, проходящей через точки (x1; y1) и (x2; y2) будет следующим:
C = –x1 * (y2 – y1) + y1 * (x2 – x1) = 0 * 2 + 0 * 1 = 0. ЌСледовательно, уравнение прямой будет иметь вид 2х – у = 0.
1. 2. Положение точек относительно прямой
Множество точек прямой, проходящей через две точки с координатами (x1; y1) и (x2; y2), удовлетворяет уравнению
Это значит, что если имеется точка с координатами (x0; y0) и (x0 – x1) * (y2 – y1) – (y0 – y1) * (x2 – x1) = 0, то эта точка лежит на прямой. B дальнейшем, вместо выражения (x – x1) * (y2 – y1) – (y – y1) * (x2 – x1) мы иногда будем использовать для краткости обозначение Ax + By + C или f(x1, y1, x2, y2, x, y).
Прямая Ax + By + C = 0, проходящая через две заданные точки с координатами (x1; y1) и (x2; y2), разбивает плоскость на две полуплоскости. Рассмотрим возможные значения выражения Ax + By + C.
1) Ax + By + C = 0 – определяет геометрическое место точек, лежащих на прямой.
Запишем алгоритм для определения, лежит ли точка с координатами (x3; y3) на прямой, проходящей через точки (x1; y1) и (x2; y2). Переменная P – переменная логического типа, которая имеет значение “истина”, если точка лежит на прямой и “ложь” в противном случае.
если (x3 – x1)*(y2 – y1) – (y3 – y1)*(x2 – x1)=0
2) Ax + By + C > 0 – определяет геометрическое место точек, лежащих по одну сторону от прямой.
3) Ax + By + C рис. 3 точки (x3; y3) и (x4; y4) лежат по одну сторону от прямой, точки (x3; y3) и (x5; y5) по разные стороны от прямой, а точка (x6; y6) лежит на прямой.

Рассмотрим пример: x1 = 1, y1 = 2, x2 = 5, y2 = 6. Уравнение прямой, проходящей через точки (x1; y1) и (x2; y2), будет следующим:
Следовательно, уравнение прямой будет иметь вид 4х – 4у + 4 = 0 или x – y + 1 = 0. Подставим координаты точек (3; 4), (1; 1), (2; 0), (0; 2) в уравнение прямой. Получим:
1 * 3 – 1 * 4 + 1 = 0, 1 * 2 – 1 * 0 + 1 > 0,
1 * 1 – 1 * 1 + 1 > 0, 1 * 0 – 1 * 2 + 1 L:=”по одну”
Z1:=(x3 – x1)*(y2 – y1) – (y3 – y1)*(x2 – x1)
Z2:=(x4 – x1)*(y2 – y1) – (y4 – y1)*(x2 – x1)
½ то L:=”по разные” (1. 3)
1.3. Взаимное расположение двух отрезков
Пусть нам необходимо определить взаимное расположение двух отрезков. Отрезки на плоскости заданы координатами своих концевых точек. Предположим, что концевые точки одного из отрезков имеют координаты (x1; y1) и (x2; y2), а концевые точки другого – (x3; y3) и (x4; y4). Пусть общее уравнение первой прямой, проходящей через точки (x1;y1) и (x2;y2), имеет вид A1x + B1y + C1 = 0, а второй прямой, проходящей через точки (x3;y3) и (x4;y4), A2x + B2y + C2 = 0.
Определим расположение точек (x3; y3) и (x4; y4) относительно первой прямой. Если они расположены по одну сторону от прямой, то отрезки не могут пересекаться. Аналогично можно определить положение точек (x1; y1) и (x2; y2) относительно другой прямой.
Таким образом, если значения пары выражений Z1 = A1x3 + B1y3 + C1 и Z2 = A1x4 + B1y4 + C1 имеют разные знаки или Z1*Z2 = 0, а также пары Z3 = A2x1 + B2y1 + C2 и Z4 = A2x2 + B2y2 + C2 имеют разные знаки или Z3*Z4 = 0, то отрезки пересекаются. Если же значения пар выражений Z1 и Z2, или Z3 и Z4, имеют одинаковые знаки, то отрезки не пересекаются.
Различные случаи расположения отрезков показаны на рис. 4 .

На этом рисунке отрезки с концами в точках (x1; y1), (x2; y2) и (x4; y4), (x5; y5) пересекаются, отрезки с концами в точках (x1; y1), (x2; y2) и (x3; y3), (x4; y4) не пересекаются, а отрезки с концами в точках (x3; y3), (x4; y4) и (x4; y4) и (x5; y5) имеют общую вершину, что можно считать частным случаем пересечения.
Алгоритм для определения, пересекаются ли два отрезка с концами в точках (x1; y1), (x2; y2) и (x3; y3), (x4; y4) будет следующим:
Z1:=(x3 – x1)*(y2 – y1) – (y3 – y1)*(x2 – x1)
Z2:=(x4 – x1)*(y2 – y1) – (y4 – y1)*(x2 – x1)
Z3:=(x1 – x3)*(y4 – y3) – (y1 – y3)*(x4 – x3)
Z4:=(x2 – x3)*(y4 – y3) – (y2 – y3)*(x4 – x3)
Приведенный фрагмент алгоритма не учитывает крайней ситуации, когда два отрезка лежат на одной прямой. В этом случае (x3 – x1) * (y2 – y1) – (y3 – y1) * (x2 – x1) = 0 и (x4 – x1) * (y2 – y1) – (y4 – y1) * (x2 – x1) = 0.


На рис. 5 отрезки, лежащие на одной прямой не пересекаются, а на рис. 6 – отрезки пересекаются.
Для того, чтобы определить взаимное расположение таких отрезков, поступим следующим образом. Обозначим
Здесь k1 является левой, а k2 – правой точкой проекции первого отрезка (отрезка, заданного координатами (x1; y1), (x2; y2)) на ось Ox. Аналогично k3 является левой, а k4 – правой точкой проекции второго отрезка (отрезка, заданного координатами (x3; y3), (x4; y4)) на ось Ox. Аналогично ищем преокции на ось OY.
Отрезки, лежащие на одной прямой будут пересекаться тогда, когда их проекции на каждую ось пересекаются. (Следует заметить, что если проекции двух произвольных отрезков пересекаются, то это не значит, что и сами отрезки пересекаются, что видно на рис. 7 ).

Для определения взаимного расположения проекций на ось OX воспользуемся следующим фактом (см. рис. 5 и рис. 6 ): координата левой точки пересечения проекций Lx равна max(k1; k3), т. е. максимальной из координат левых точек проекций. Рассуждая аналогично для правых точек проекций, получим, что координата правой точки Rx пересечения равна min(k2; k4). Для того, чтобы отрезки пересекались, необходимо, чтобы левая координата пересечения проекций была не больше правой координаты пересечения отрезков (такой случай имеет место на рис. 5 , когда Lx = х3, а Rx = х2). Поэтому условием пересечения проекций является выполнение неравенства Lx £ Rx. Аналогично можно вычислить величины Lу и Rу, беря соответствующие проекции на ось Оу.
Следует отметить, что длина пересечения проекций в этом случае равна величине Lx– Rx (если Lx– Rx = 0, то проекции имеют только общую точку).
1.4. Точка пересечения отрезков
Для определения места пересечения отрезков (если известно, что они пересекаются), достаточно определить точку пересечения прямых, на которых эти отрезки лежат.
Пусть A1x + B1y + C1 = 0 является уравнением прямой, проходящей через концевые точки первого отрезка, а A2x + B2y + C2 = 0 является уравнением прямой, проходящей через концевые точки второго отрезка.
Тогда для определения точки пересечения отрезков достаточно решить систему уравнений

Домножив первое уравнение на A2, а второе уравнение на A1, получим

Вычитая из первого уравнения второе, можно найти значение y:
y = 
Аналогично можно вычислить значение x:
x = 
Это справедливо в случае, если выражение A2 * B1 – A1 * B2 ¹ 0. Но мы уже знаем, что отрезки пересекаются и не лежат на одной прямой. А это невозможно, если A2 * B1 – A1 * B2 = 0.
2.1 Расстояния между точками. Расстояние от точки до прямой
Расстояние между точками M1(x1; y1) и M2(x2; y2) на плоскости ( рис. 8 ) определяется по формуле
D =  .
.


Расстояние от точки до прямой на плоскости определяется как длина отрезка перпендикуляра, опущенного из точки на прямую. Уравнение вида
 ,
,
где T =  , причем С £ 0 (чего можно достигнуть изменением знака выражения), называется нормальным уравнением прямой. Это уравнение обладает тем свойством, что при подстановке координат произвольной точки в выражение (Ax + By + C)/T получается значение, по абсолютной величине равное расстоянию от точки до прямой ( рис. 9 ).
, причем С £ 0 (чего можно достигнуть изменением знака выражения), называется нормальным уравнением прямой. Это уравнение обладает тем свойством, что при подстановке координат произвольной точки в выражение (Ax + By + C)/T получается значение, по абсолютной величине равное расстоянию от точки до прямой ( рис. 9 ).
Запишем алгоритм для определения расстояния от точки (x3; y3) до прямой, проходящей через точки (x1; y1) и (x2; y2).
C:= – x1*(y2 – y1)+y1*(x2 – x1) (1. 5)
Рассмотрим пример: x1 = 0, y1 = 0, x2 = 3, y2 = 4 x3 = –1, y3 = 7. Уравнение прямой, проходящей через точки (x1; y1) и (x2; y2), будет следующим:
Т =  =
=  =
=  = 5,
= 5,
D =  =
=  = 5.
= 5.
2.2. Расстояние между точкой и отрезком
Для определения расстояния между точкой и отрезком необходимо выяснить, пересекает ли перпендикуляр, опущенный из данной точки на прямую, проходящую через концы отрезка, сам отрезок. Если перпендикуляр пересекает отрезок, то расстояние между точкой и отрезком равно расстоянию между точкой и прямой, проходящей через отрезок. (Эту задачу вы уже умеете решать.)
Если перпендикуляр не пересекает отрезок, то расстояние между точкой и отрезком равно минимальному из расстояний между точкой и одним из концов отрезка.
Для определения взаимного расположения отрезка и перпендикуляра поступим следующим образом.
Рассмотрим треугольник, образованный тремя точками, две из которых (x1; y1) и (x2; y2) являются концами данного отрезка, а третья – данная точка с координатами (x3; y3) (см. рис. 10 , б, в). Конечно, может оказаться, что все точки лежат на одной прямой и такого треугольника не существует. В этом случае, однако, мы будем полагать, что треугольник существует, правда он вырожденный (особый). В вырожденном треугольнике длины сторон могут быть равными 0 (см. рис. 10 , а).
Более того, мы будем полагать, что данный отрезок является основанием рассматриваемого треугольника (см. рис. 10 , б, в).

При таких предположениях для решения исходной задачи нам достаточно определить, является ли один из углов при основании тупым или нет. Действительно, если один из углов при основании является тупым, то перпендикуляр, опущенный из вершины, соответствующей исходной точке, не попадает на основание (отрезок). Иначе перпендикуляр, опущенный из вершины, соответствующей исходной точке, попадает на основание (отрезок).
Для решения последней задачи воспользуемся следующим свойством. Пусть a, b, c – длины сторон треугольника, причем с – длина основания. Тогда треугольник является тупоугольным при основании, если
Поэтому, вычислив значения квадратов длин сторон, нетрудно определить, пересекает ли перпендикуляр, опущенный из точки (x3; y3) на прямую, отрезок с концами в точках (x1; y1) и (x2; y2). И если не пересекает, то расстояние от точки до отрезка равно минимуму из величин a, b. Если же пересекает, то необходимо воспользоваться свойством нормального уравнения прямой .
§ 3. Многоугольники
3.1. Виды многоугольников
Ломаной называется фигура, которая состоит из точек A1, A2, . An и соединяющих их отрезков A1A2, A2A3, . An – 1An ( рис. 11 , а). Точки называются вершинами ломаной, а отрезки – звеньями. Наиболее распространенным способом задания ломаной является использование таблицы, элементы которой соответствуют координатам вершин ломаной в порядке ее обхода из одного конца в другой. Длиной ломаной называется сумма длин ее звеньев.
Многоугольником называется замкнутая ломаная линия без самопересечений (рис. 11, б).
Плоским многоугольником называется конечная часть плоскости, ограниченная многоугольником (рис. 11, в).

Обход плоского многоугольника называется положительным, если при обходе область расположена по левую руку, и отрицательным, если область остается по правую руку.
Расстояние между фигурами на плоскости определяется как длина минимального отрезка, один конец которого принадлежит одной фигуре, а второй конец – другой фигуре.
3.2. Выпуклость многоугольников
Многоугольник является выпуклым, если для каждой прямой, проходящей через любую его сторону, все остальные вершины лежат в одной полуплоскости относительно прямой. Проверим для каждой прямой, проходящей через вершины (x1; y1) и (x2; y2), (x2; y2) и (x3; y3), . (xn – 1; yn – 1) и (xn; yn), (xn; yn) и (x1; y1) взаимное расположение вершин многоугольника. Если они каждый раз расположены в одной полуплоскости относительно проведенной прямой, то многоугольник выпуклый. Если же найдется прямая, проходящая через одну из сторон, и пара вершин многоугольника, лежащих по разные стороны относительно проведенной прямой, то многоугольник не является выпуклым. Случаи выпуклого и невыпуклого многоугольников изображены на рис. 12.

Можно заметить, что для каждой прямой, проходящей через вершины (x1; y1) и (x2; y2), (x2; y2) и (x3; y3), . (xn – 1; yn – 1) и (xn; yn), (xn; yn) и (x1; y1) достаточно ограничится определением взаимного расположения вершин многоугольника (xn; yn) и (x3; y3), (x1; y1) и (x4; y4), . (xn – 2; yn – 2) и (x1; y1), (xn – 1; yn – 1) и (x2; y2), соответственно. Если они каждый раз расположены в одной полуплоскости относительно проведенной прямой, то многоугольник выпуклый. Если же найдется прямая и пара вершин многоугольника, лежащих по разные стороны относительно проведенной прямой, то многоугольник не является выпуклым. Поэтому для определения, является ли многоугольник выпуклым, достаточно воспользоваться алгоритмом
нц для i от 1 до n
½ j:= mod( i, n +1 ) : номер вершины после вершины i
½ k:= mod (j, n +1) : номер вершины после вершины j
½½ то m:=n : номер вершины перед вершиной i
Прямая линия. Уравнение прямой.
Свойства прямой в евклидовой геометрии.
Через любую точку можно провести бесконечно много прямых.
Через любые две несовпадающие точки можно провести единственную прямую.
Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или являются
параллельными (следует из предыдущего).
В трёхмерном пространстве существуют три варианта взаимного расположения двух прямых:
- прямые пересекаются;
- прямые параллельны;
- прямые скрещиваются.
Прямая линия — алгебраическая кривая первого порядка: в декартовой системе координат прямая линия
задается на плоскости уравнением первой степени (линейное уравнение).
Общее уравнение прямой.
Определение. Любая прямая на плоскости может быть задана уравнением первого порядка
причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим
уравнением прямой. В зависимости от значений постоянных А, В и С возможны следующие частные случаи:
• C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат
• А = 0, В ≠0, С ≠0 – прямая параллельна оси Ох
• В = 0, А ≠0, С ≠ 0 – прямая параллельна оси Оу
• В = С = 0, А ≠0 – прямая совпадает с осью Оу
• А = С = 0, В ≠0 – прямая совпадает с осью Ох
Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных
Уравнение прямой по точке и вектору нормали.
Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В)
перпендикулярен прямой , заданной уравнением
Пример. Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору (3, -1).
Решение. Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С
подставим в полученное выражение координаты заданной точки А. Получаем: 3 – 2 + C = 0, следовательно
С = -1. Итого: искомое уравнение: 3х – у – 1 = 0.
Уравнение прямой, проходящей через две точки.
Пусть в пространстве заданы две точки M 1 ( x 1 , y 1 , z 1 ) и M2 ( x 2, y 2 , z 2 ), тогда уравнение прямой,
проходящей через эти точки:
Если какой-либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель. На
плоскости записанное выше уравнение прямой упрощается:
Дробь = k называется угловым коэффициентом прямой.
Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).
Решение. Применяя записанную выше формулу, получаем:
Уравнение прямой по точке и угловому коэффициенту.
Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:
и обозначить , то полученное уравнение называется
уравнением прямой с угловым коэффициентом k.
Уравнение прямой по точке и направляющему вектору.
По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание
прямой через точку и направляющий вектор прямой.
Определение. Каждый ненулевой вектор (α1, α2), компоненты которого удовлетворяют условию
Аα1 + Вα2 = 0 называется направляющим вектором прямой.
Пример. Найти уравнение прямой с направляющим вектором (1, -1) и проходящей через точку А(1, 2).
Решение. Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением,
коэффициенты должны удовлетворять условиям:
1 * A + (-1) * B = 0, т.е. А = В.
Тогда уравнение прямой имеет вид: Ax + Ay + C = 0, или x + y + C / A = 0.
при х = 1, у = 2 получаем С/ A = -3, т.е. искомое уравнение:
Уравнение прямой в отрезках.
Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на –С, получим:
или , где
Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения
прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.
Пример. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках.
С = 1, , а = -1, b = 1.
Нормальное уравнение прямой.
Если обе части уравнения Ах + Ву + С = 0 разделить на число , которое называется
нормирующем множителем, то получим
xcosφ + ysinφ – p = 0 – нормальное уравнение прямой.
[spoiler title=”источники:”]
http://pandia.ru/text/79/489/58441.php
http://www.calc.ru/Uravneniye-Pryamoy.html
[/spoiler]
Содержание:
Декартовы координаты на плоскости:
Изучая материал этой лекции, вы расширите свои знания о координатной плоскости.
Вы научитесь находить длину отрезка и координаты его середины, зная координаты его концов.
Сформируете представление об уравнении фигуры, выведете уравнения прямой и окружности.
Ознакомитесь с методом координат, позволяющим решать геометрические задачи средствами алгебры.
Расстояние между двумя точками с заданными координатами. Координаты середины отрезка
В 6 классе вы ознакомились с координатной плоскостью, то есть с плоскостью, на которой изображены две перпендикулярные координатные прямые (ось абсцисс и ось ординат) с общим началом отсчета (рис. 8.1). Вы умеете отмечать на ней точки по их координатам и наоборот, находить координаты точки, отмеченной на координатной плоскости.
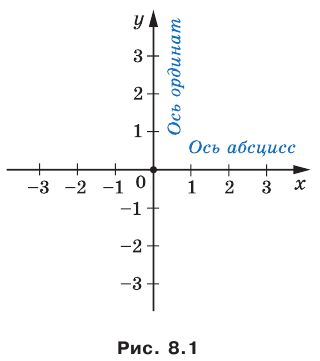
Договорились координатную плоскость с осью 
Координаты точки на плоскости 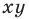 называют декартовыми координатами в честь французского математика Рене Декарта (см. рассказ на с. 103).
называют декартовыми координатами в честь французского математика Рене Декарта (см. рассказ на с. 103).
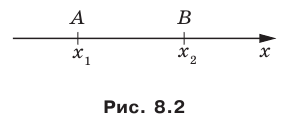
Вы знаете, как находить расстояние в между двумя точками, заданными своими координатами на координатной прямой. Для точек 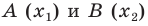 (рис. 8.2) имеем:
(рис. 8.2) имеем:
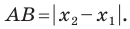
Научимся находить расстояние между точками 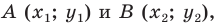 заданными на плоскости
заданными на плоскости 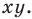
Рассмотрим случай, когда отрезок  не перпендикулярен ни одной из координатных осей (рис. 8.3).
не перпендикулярен ни одной из координатных осей (рис. 8.3).
Через точки  проведем прямые, перпендикулярные координатным осям. Получим прямоугольный треугольник
проведем прямые, перпендикулярные координатным осям. Получим прямоугольный треугольник 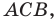 в котором
в котором 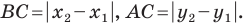 Отсюда
Отсюда 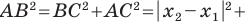
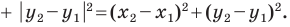
Тогда формулу расстояния между точками 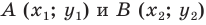 можно записать так:
можно записать так:

Докажите самостоятельно, что эта формула остается верной и для случая, когда отрезок  перпендикулярен одной из осей координат.
перпендикулярен одной из осей координат.
Пусть 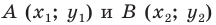 — точки плоскости
— точки плоскости 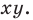 Найдем координаты
Найдем координаты 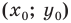 точки
точки 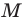 — середины отрезка
— середины отрезка 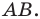
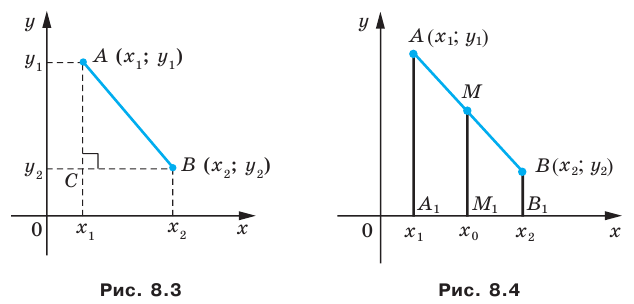
Рассмотрим случай, когда отрезок 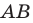 не перпендикулярен ни одной из координатных осей (рис. 8.4). Будем считать, что
не перпендикулярен ни одной из координатных осей (рис. 8.4). Будем считать, что 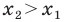 (случай, когда
(случай, когда 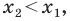 рассматривается аналогично). Через точки
рассматривается аналогично). Через точки 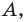
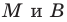 проведем прямые, перпендикулярные оси абсцисс, которые пересекут эту ось соответственно в точках
проведем прямые, перпендикулярные оси абсцисс, которые пересекут эту ось соответственно в точках 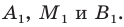 По теореме Фалеса
По теореме Фалеса 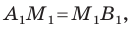 тогда
тогда 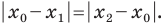 Поскольку
Поскольку 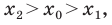 то можем записать:
то можем записать: 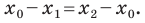 Отсюда
Отсюда  Аналогично можно показать что
Аналогично можно показать что 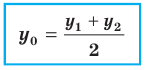
Формулы для нахождения координат середины отрезка остаются верными и для случая, когда отрезок 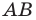 перпендикулярен одной из осей координат. Докажите это самостоятельно.
перпендикулярен одной из осей координат. Докажите это самостоятельно.
Пример №1
Докажите, что треугольник с вершинами в точках 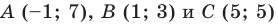 является равнобедренным прямоугольным.
является равнобедренным прямоугольным.
Решение:
Используя формулу расстояния между двумя точками, найдем стороны данного треугольника:
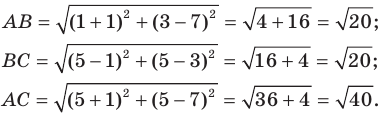
Следовательно, 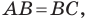 то есть треугольник
то есть треугольник 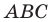 равнобедренный.
равнобедренный.
Поскольку 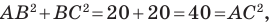 то треугольник
то треугольник 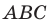 прямоугольный.
прямоугольный. 
Пример №2
Точка 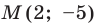 — середина отрезка
— середина отрезка 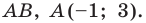 Найдите координаты точки
Найдите координаты точки 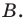
Решение:
Обозначим 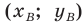 — координаты точки
— координаты точки 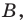
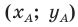 — координаты точки
— координаты точки 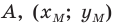 — координаты точки
— координаты точки 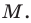
Поскольку 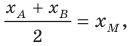 то получаем:
то получаем: 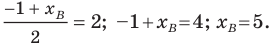
Аналогично 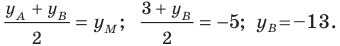
Ответ: 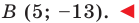
Пример №3
Докажите, что четырехугольник  с вершинами в точках
с вершинами в точках 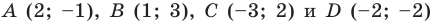 является прямоугольником.
является прямоугольником.
Решение:
Пусть точка 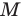 — середина диагонали
— середина диагонали 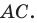 Тогда
Тогда
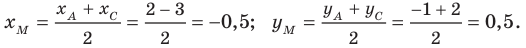
Следовательно, 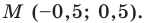
Пусть точка 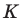 — середина диагонали
— середина диагонали 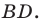 Тогда
Тогда
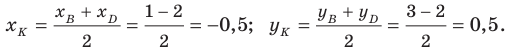
Следовательно, 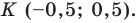
Таким образом, точки 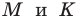 совпадают, то есть диагонали четырехугольника
совпадают, то есть диагонали четырехугольника 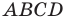 имеют общую середину. Отсюда следует, что четырехугольник
имеют общую середину. Отсюда следует, что четырехугольник 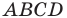 — параллелограмм.
— параллелограмм.
Найдем диагонали параллелограмма:
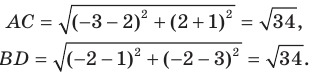
Следовательно, диагонали параллелограмма  равны. Отсюда следует, что этот параллелограмм является прямоугольником.
равны. Отсюда следует, что этот параллелограмм является прямоугольником. 
Уравнение фигуры. Уравнение окружности
Из курса алгебры 7 класса вы знаете, какую фигуру называют графиком уравнения. В этом пункте вы ознакомитесь с понятием уравнения фигуры.
Координаты 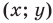 каждой точки параболы, изображенной на рисунке 9.1, являются решением уравнения
каждой точки параболы, изображенной на рисунке 9.1, являются решением уравнения 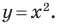 И наоборот, каждое решение уравнения с двумя переменными
И наоборот, каждое решение уравнения с двумя переменными 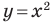 является координатами точки, лежащей на этой параболе. В этом случае говорят, что уравнение параболы, изображенной на рисунке 9.1, имеет вид
является координатами точки, лежащей на этой параболе. В этом случае говорят, что уравнение параболы, изображенной на рисунке 9.1, имеет вид 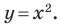
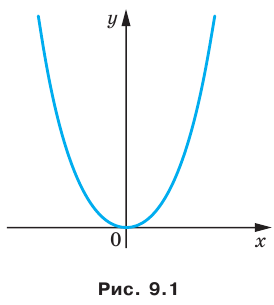
Определение. Уравнением фигуры  заданной на плоскости
заданной на плоскости 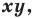 называют уравнение с двумя переменными
называют уравнение с двумя переменными 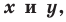 обладающее следующими свойствами:
обладающее следующими свойствами:
- если точка принадлежит фигуре
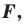 то ее координаты являются решением данного уравнения;
то ее координаты являются решением данного уравнения; - любое решение
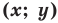 данного уравнения является координатами точки, принадлежащей фигуре
данного уравнения является координатами точки, принадлежащей фигуре 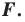
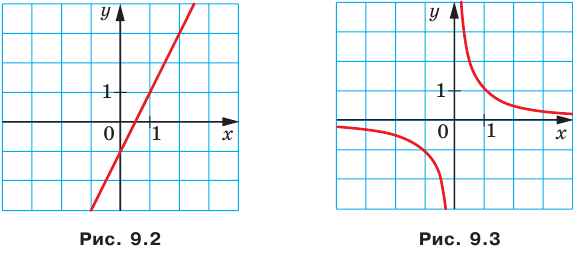
Например, уравнение прямой, изображенной на рисунке 9.2, имеет вид 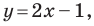 а уравнение гиперболы, изображенной на рисунке 9.3, имеет вид
а уравнение гиперболы, изображенной на рисунке 9.3, имеет вид 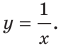 Принято говорить, что, например, уравнения
Принято говорить, что, например, уравнения 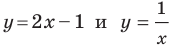 задают прямую и гиперболу соответственно.
задают прямую и гиперболу соответственно.
Если данное уравнение является уравнением фигуры  то эту фигуру можно рассматривать как геометрическое место точек (ГМТ), координаты которых удовлетворяют данному уравнению.
то эту фигуру можно рассматривать как геометрическое место точек (ГМТ), координаты которых удовлетворяют данному уравнению.
Пользуясь этими соображениями, выведем уравнение окружности радиуса 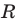 с центром в точке
с центром в точке 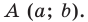
Пусть 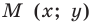 — произвольная точка данной окружности (рис. 9.4). Тогда
— произвольная точка данной окружности (рис. 9.4). Тогда 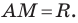 Используя формулу расстояния между точками, получим:
Используя формулу расстояния между точками, получим:
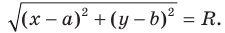
Отсюда
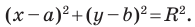
Мы показали, что координаты 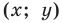 произвольной точки
произвольной точки 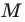 данной окружности являются решением уравнения
данной окружности являются решением уравнения 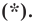 Теперь покажем, что любое решение уравнения
Теперь покажем, что любое решение уравнения 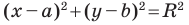 является координатами точки, принадлежащей данной окружности.
является координатами точки, принадлежащей данной окружности.
Пусть пара чисел 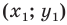 — произвольное решение уравнения
— произвольное решение уравнения 
Тогда 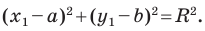 Отсюда
Отсюда 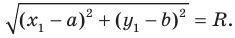
Это равенство показывает, что точка 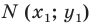 удалена от центра окружности
удалена от центра окружности 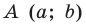 на расстояние, равное радиусу окружности, а следовательно, точка
на расстояние, равное радиусу окружности, а следовательно, точка 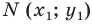 принадлежит данной окружности.
принадлежит данной окружности.
Итак, мы доказали следующую теорему.
Теорема 9.1. Уравнение окружности радиуса 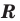 с центром в точке
с центром в точке 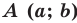 имеет вид
имеет вид
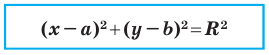
Верно и такое утверждение: любое уравнение вида 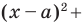 где
где  некоторые числа, причем
некоторые числа, причем  является уравнением окружности радиуса
является уравнением окружности радиуса  с центром в точке с координатами
с центром в точке с координатами 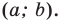
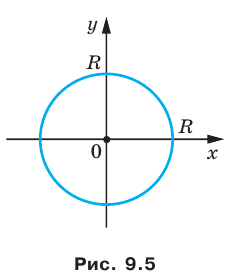
Если центром окружности является начало координат (рис. 9.5), то 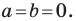 В этом случае уравнение окружности имеет вид
В этом случае уравнение окружности имеет вид 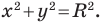
Пример №4
Составьте уравнение окружности, диаметром которой является отрезок 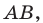 если
если 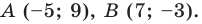
Решение:
Поскольку центр окружности является серединой диаметра, то можем найти координаты 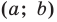 центра
центра  окружности:
окружности:
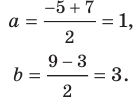
Следовательно, 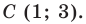
Радиус окружности  равен отрезку
равен отрезку 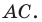 Тогда
Тогда
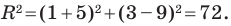
Следовательно, искомое уравнение имеет вид
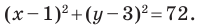
Ответ: 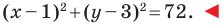
Пример №5
Докажите, что уравнение 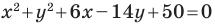 задает окружность. Найдите координаты центра и радиус этой окружности.
задает окружность. Найдите координаты центра и радиус этой окружности.
Решение:
Представим данное уравнение в виде 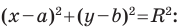
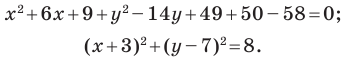
Следовательно, данное уравнение является уравнением окружности с центром в точке 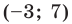 и радиусом
и радиусом 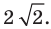
Ответ: 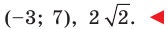
Пример №6
Докажите, что треугольник с вершинами в точках 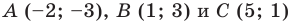 является прямоугольным, и составьте уравнение окружности, описанной около треугольника
является прямоугольным, и составьте уравнение окружности, описанной около треугольника 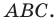
Решение:
Найдем квадраты сторон данного треугольника:
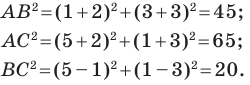
Поскольку 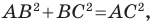 то данный треугольник является прямоугольным с прямым углом при вершине
то данный треугольник является прямоугольным с прямым углом при вершине 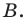 Центром описанной окружности является середина гипотенузы
Центром описанной окружности является середина гипотенузы 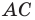 — точка
— точка 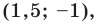 радиус окружности
радиус окружности 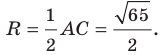 Следовательно, искомое уравнение имеет вид
Следовательно, искомое уравнение имеет вид
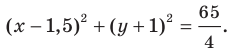
Ответ: 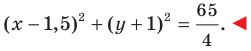
Уравнение прямой
В предыдущем пункте, рассматривая окружность как ГМТ, равноудаленных от данной точки, мы вывели ее уравнение. Для того чтобы вывести уравнение прямой, рассмотрим ее как ГМТ, равноудаленных от двух данных точек.
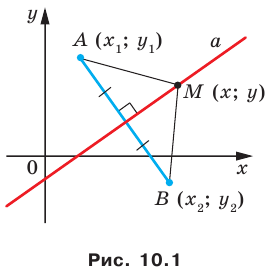
Пусть 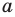 — данная прямая. Выберем две точки
— данная прямая. Выберем две точки 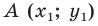 и
и 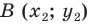 так, чтобы прямая
так, чтобы прямая 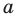 была серединным перпендикуляром отрезка
была серединным перпендикуляром отрезка 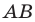 (рис. 10.1).
(рис. 10.1).
Пусть 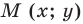 — произвольная точка прямой
— произвольная точка прямой 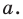 Тогда по свойству серединного перпендикуляра отрезка выполняется равенство
Тогда по свойству серединного перпендикуляра отрезка выполняется равенство 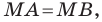 то есть
то есть
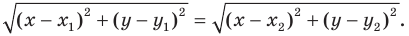
Мы показали, что координаты 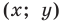 произвольной точки
произвольной точки 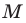 прямой
прямой 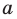 являются решением уравнения
являются решением уравнения 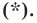
Теперь покажем, что любое решение уравнения 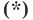 является координатами точки, принадлежащей данной прямой
является координатами точки, принадлежащей данной прямой 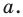
Пусть 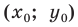 — произвольное решение уравнения
— произвольное решение уравнения 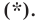 Тогда
Тогда  Это равенство означает, что точка
Это равенство означает, что точка 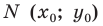 равноудалена от точек
равноудалена от точек  следовательно, точка
следовательно, точка 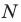 принадлежит серединному перпендикуляру отрезка
принадлежит серединному перпендикуляру отрезка 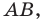 то есть прямой
то есть прямой 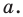
Итак, мы доказали, что уравнение 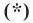 является уравнением данной прямой
является уравнением данной прямой 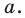
Однако из курса алгебры 7 класса вы знаете, что уравнение прямой выглядит гораздо проще, а именно: 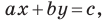 где
где 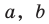 и
и 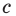 — некоторые числа, причем
— некоторые числа, причем 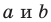 не равны нулю одновременно. Покажем, что уравнение
не равны нулю одновременно. Покажем, что уравнение 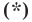 можно преобразовать к такому виду. Возведем обе части уравнения
можно преобразовать к такому виду. Возведем обе части уравнения 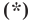 в квадрат. Имеем:
в квадрат. Имеем:
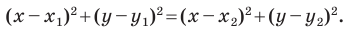
Раскроем скобки и приведем подобные слагаемые. Получим:
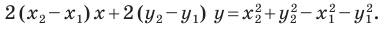
Обозначив 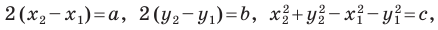 получим уравнение
получим уравнение 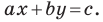
Поскольку точки 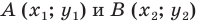 различны, то хотя бы одна из разностей
различны, то хотя бы одна из разностей 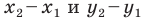 не равна нулю. Следовательно, числа
не равна нулю. Следовательно, числа 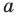 и
и 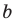 не равны нулю одновременно.
не равны нулю одновременно.
Итак, мы доказали следующую теорему.
Теорема 10.1. Уравнение прямой имеет вид?
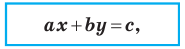
где 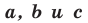 — некоторые числа, причем
— некоторые числа, причем 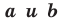 не равны нулю одновременно.
не равны нулю одновременно.
Верно и такое утверждение: любое уравнение вида 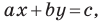 где
где 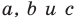 — некоторые числа, причем
— некоторые числа, причем 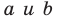 не равны нулю одновременно, является уравнением прямой.
не равны нулю одновременно, является уравнением прямой.
Если 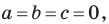 то графиком уравнения
то графиком уравнения 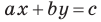 является вся плоскость
является вся плоскость 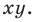 Если
Если 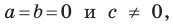 то уравнение не имеет решений.
то уравнение не имеет решений.
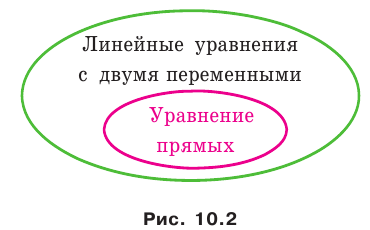
Из курса алгебры 7 класса вы знаете, что уравнение вида 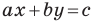 называют линейным уравнением с двумя переменными. Уравнение прямой является частным видом линейного уравнения. Схема, изображенная на рисунке 10.2, иллюстрирует сказанное.
называют линейным уравнением с двумя переменными. Уравнение прямой является частным видом линейного уравнения. Схема, изображенная на рисунке 10.2, иллюстрирует сказанное.
на уроках алгебры в 7 классе мы приняли без доказательства тот факт, что графиком линейной функции 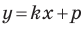 является прямая. Сейчас мы можем это доказать.
является прямая. Сейчас мы можем это доказать.
Перепишем уравнение 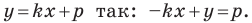 Мы получили уравнение вида
Мы получили уравнение вида 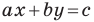 для случая, когда
для случая, когда 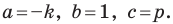 Поскольку в этом уравнении
Поскольку в этом уравнении 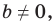 то мы получили уравнение прямой.
то мы получили уравнение прямой.
А любую ли прямую на плоскости можно задать уравнением вида 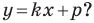 Ответ на этот вопрос отрицательный.
Ответ на этот вопрос отрицательный.
Дело в том, что прямая, перпендикулярная оси абсцисс, не может являться графиком функции, а следовательно, не может быть задана уравнением вида 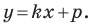
Вместе с тем, если в уравнении прямой 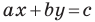 принять
принять 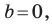 то его можно переписать так:
то его можно переписать так: 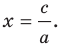 Мы получили частный вид уравнения прямой, все точки которой имеют одинаковые абсциссы. Следовательно, эта прямая перпендикулярна оси абсцисс. Ее называют вертикальной.
Мы получили частный вид уравнения прямой, все точки которой имеют одинаковые абсциссы. Следовательно, эта прямая перпендикулярна оси абсцисс. Ее называют вертикальной.
Если 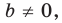 то уравнение прямой
то уравнение прямой 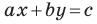 можно записать так:
можно записать так:
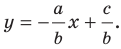 Обозначив
Обозначив 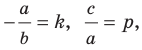 получим уравнение
получим уравнение 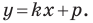
Следовательно, если 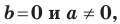 то уравнение прямой
то уравнение прямой 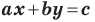 задает вертикальную прямую; если
задает вертикальную прямую; если 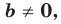 то это уравнение задает невертикальную прямую.
то это уравнение задает невертикальную прямую.
Уравнение невертикальной прямой удобно записывать в виде 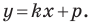
Данная таблица подытоживает материал, рассмотренный в этом пункте.

Пример №7
Составьте уравнение прямой, проходящей через точки:

Решение:
1) Поскольку данные точки имеют равные абсциссы, то прямая 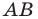 является вертикальной. Ее уравнение имеет вид
является вертикальной. Ее уравнение имеет вид 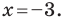
2) Поскольку данные точки имеют разные абсциссы, то прямая 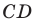 не является вертикальной. Тогда можно воспользоваться уравнением прямой в виде
не является вертикальной. Тогда можно воспользоваться уравнением прямой в виде 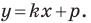
Подставив координаты точек 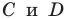 в уравнение
в уравнение  получаем систему уравнений:
получаем систему уравнений:
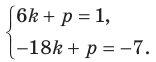
Решив эту систему уравнений, находим, что 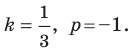
Ответ: 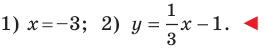
Пример №8
Найдите периметр и площадь треугольника, ограниченного прямой 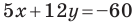 и осями координат.
и осями координат.
Решение:
Найдем точки пересечения данной прямой с осями координат.
С осью абсцисс: при 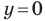 получаем
получаем 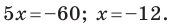
С осью ординат: при 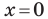 получаем
получаем 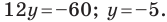
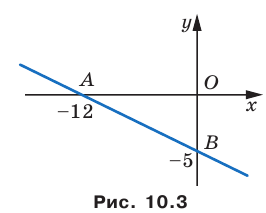
Следовательно, данная прямая и оси координат ограничивают прямоугольный треугольник 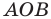 (рис. 10.3) с вершинами
(рис. 10.3) с вершинами 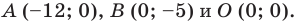 Найдем стороны треугольника:
Найдем стороны треугольника: 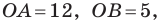
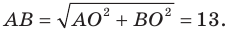 Тогда искомые периметр и площадь соответственно равны
Тогда искомые периметр и площадь соответственно равны 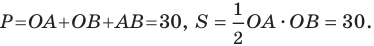
Ответ: 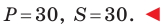
Угловой коэффициент прямой
Рассмотрим уравнение 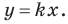 Оно задает невертикальную прямую, проходящую через начало координат.
Оно задает невертикальную прямую, проходящую через начало координат.
Покажем, что прямые 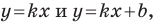 где
где 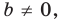 параллельны.
параллельны.
Точки 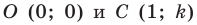 принадлежат прямой
принадлежат прямой 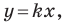 а точки
а точки 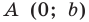 и
и 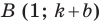 принадлежат прямой
принадлежат прямой 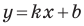 (рис. 11.1). Легко убедиться (сделайте это самостоятельно), что середины диагоналей
(рис. 11.1). Легко убедиться (сделайте это самостоятельно), что середины диагоналей  четырехугольника
четырехугольника 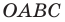 совпадают. Следовательно, четырехугольник
совпадают. Следовательно, четырехугольник 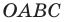 — параллелограмм. Отсюда
— параллелограмм. Отсюда 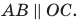
Теперь мы можем сделать такой вывод: если 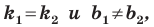 то прямые
то прямые 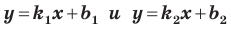 параллельны (1).
параллельны (1).
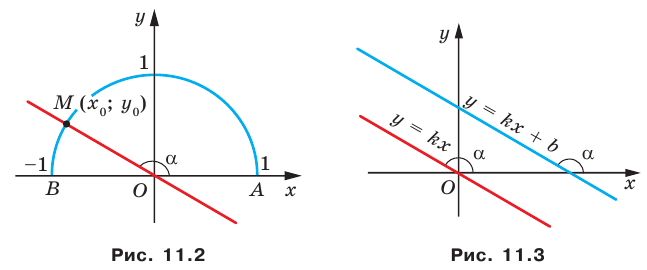
Пусть прямая 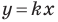 пересекает единичную полуокружность в точке
пересекает единичную полуокружность в точке 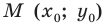 (рис. 11.2). Угол
(рис. 11.2). Угол 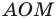 называют углом между данной прямой и положительным направлением оси абсцисс.
называют углом между данной прямой и положительным направлением оси абсцисс.
Если прямая 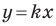 совпадает с осью абсцисс, то угол между этой прямой и положительным направлением оси абсцисс считают равным
совпадает с осью абсцисс, то угол между этой прямой и положительным направлением оси абсцисс считают равным 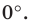
 Если прямая
Если прямая 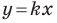 образует с положительным направлением оси абсцисс угол
образует с положительным направлением оси абсцисс угол 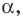 то считают, что и прямая
то считают, что и прямая 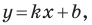 параллельная прямой
параллельная прямой 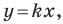 также образует угол
также образует угол 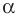 с положительным направлением оси абсцисс (рис. 11.3).
с положительным направлением оси абсцисс (рис. 11.3).
Рассмотрим прямую 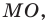 уравнение которой имеет вид
уравнение которой имеет вид 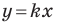 (рис. 11.2). Если
(рис. 11.2). Если 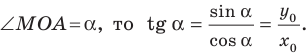 Поскольку точка
Поскольку точка 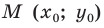 принадлежит прямой
принадлежит прямой 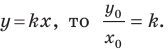 Отсюда
Отсюда 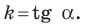 Таким образом, для прямой
Таким образом, для прямой 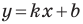 получаем, что
получаем, что
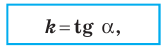
где 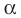 — угол, который образует эта прямая с положительным направлением оси абсцисс. Поэтому коэффициент
— угол, который образует эта прямая с положительным направлением оси абсцисс. Поэтому коэффициент 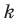 называют угловым коэффициентом этой прямой.
называют угловым коэффициентом этой прямой.
Если невертикальные прямые параллельны, то они образуют равные углы с положительным направлением оси абсцисс. Тогда тангенсы этих углов равны, следовательно, равны и их угловые коэффициенты. Таким образом,
если прямые 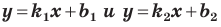 параллельны, то
параллельны, то 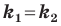 (2).
(2).
Выводы (1) и (2) объединим в одну теорему.
Теорема 11.1. Прямые 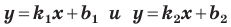 параллельны тогда и только тогда, когда
параллельны тогда и только тогда, когда 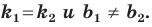
Пример №9
Составьте уравнение прямой, которая проходит через точку 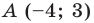 и параллельна прямой
и параллельна прямой 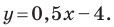
Решение:
Пусть уравнение искомой прямой 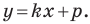 Поскольку эта прямая и прямая
Поскольку эта прямая и прямая 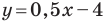 параллельны, то их угловые коэффициенты равны, то есть
параллельны, то их угловые коэффициенты равны, то есть 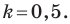
Следовательно, искомое уравнение имеет вид 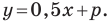 Учитывая, что данная прямая проходит через точку
Учитывая, что данная прямая проходит через точку 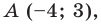 получаем:
получаем: 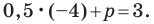 Отсюда
Отсюда 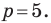
Искомое уравнение имеет вид 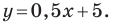
Ответ: 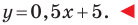
Метод координат
Мы часто говорим: прямая 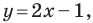 парабола
парабола 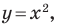 окружность
окружность 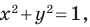 тем самым отождествляя фигуру с ее уравнением. Такой подход позволяет сводить задачу о поиске свойств фигуры к задаче об исследовании ее уравнения. В этом и состоит суть метода координат.
тем самым отождествляя фигуру с ее уравнением. Такой подход позволяет сводить задачу о поиске свойств фигуры к задаче об исследовании ее уравнения. В этом и состоит суть метода координат.
Проиллюстрируем сказанное на таком примере.
Из наглядных соображений очевидно, что прямая и окружность имеют не более двух общих точек. Однако это утверждение не является аксиомой, поэтому его надо доказывать.
Эта задача сводится к исследованию количества решений системы уравнений
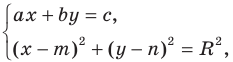
где числа 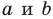 одновременно не равны нулю и
одновременно не равны нулю и 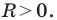
Решая эту систему методом подстановки, мы получим квадратное уравнение, которое может иметь два решения, одно решение или вообще не иметь решений. Следовательно, для данной системы существует три возможных случая:
- система имеет два решения — прямая и окружность пересекаются в двух точках;
- система имеет одно решение — прямая касается окружности;
- система не имеет решений — прямая и окружность не имеют общих точек.
С каждым из этих случаев вы встречались, решая задачи 10.17-10.19.
Метод координат особенно эффективен в тех случаях, когда требуется найти фигуру, все точки которой обладают некоторым свойством, то есть найти геометрическое место точек.
Отметим на плоскости две точки 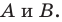 Вы хорошо знаете, какой фигурой является геометрическое место точек
Вы хорошо знаете, какой фигурой является геометрическое место точек 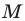 таких, что
таких, что 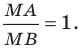
Это серединный перпендикуляр отрезка 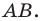 Интересно выяснить, какую фигуру образуют все точки
Интересно выяснить, какую фигуру образуют все точки 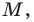 для которых
для которых 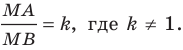 Решим эту задачу для
Решим эту задачу для 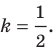
Плоскость, на которой отмечены точки 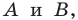 «превратим» в координатную. Сделаем это так: в качестве начала координат выберем точку
«превратим» в координатную. Сделаем это так: в качестве начала координат выберем точку 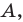 в качестве единичного отрезка — отрезок
в качестве единичного отрезка — отрезок 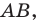 ось абсцисс проведем так, чтобы точка
ось абсцисс проведем так, чтобы точка 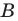 имела координаты
имела координаты 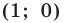 (рис. 11.6).
(рис. 11.6).
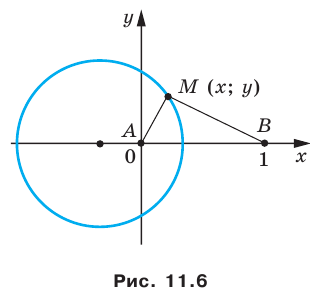
Пусть 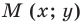 — произвольная точка искомой фигуры
— произвольная точка искомой фигуры 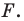 Тогда
Тогда 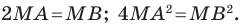 Отсюда
Отсюда
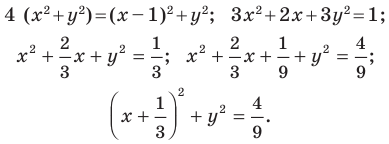
Следовательно, если точка 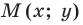 принадлежит фигуре
принадлежит фигуре 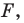 то ее координаты являются решением уравнения
то ее координаты являются решением уравнения 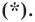
Пусть 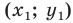 — некоторое решение уравнения
— некоторое решение уравнения 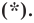 Тогда легко показать, что
Тогда легко показать, что 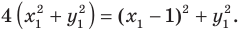 А это означает, что точка
А это означает, что точка 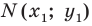 такова, что
такова, что 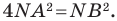 Тогда
Тогда 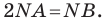 Следовательно, точка
Следовательно, точка 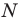 принадлежит фигуре
принадлежит фигуре 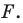
Таким образом, уравнением фигуры 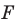 является уравнение
является уравнение 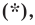 то есть фигура
то есть фигура 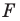 — это окружность с центром в точке
— это окружность с центром в точке 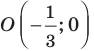 и радиусом
и радиусом 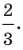
Мы решили задачу для частного случая, когда 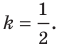 Можно показать, что искомой фигурой для любого положительного
Можно показать, что искомой фигурой для любого положительного 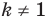 будет окружность. Эту окружность называют окружностью Аполлония
будет окружность. Эту окружность называют окружностью Аполлония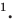
Как строили мост между геометрией и алгеброй
Идея координат зародилась очень давно. Ведь еще в старину люди изучали Землю, наблюдали звезды, а по результатам своих исследований составляли карты, схемы.
Во II в. до н. э. древнегреческий ученый Гиппарх впервые использовал идею координат для определения места расположения объектов на поверхности Земли.
Только в XIV в. французский ученый Николя Орем (ок. 1323-1382) впервые применил в математике идею Гиппарха: он разбил плоскость на клетки (как разбита страница вашей тетради) и стал задавать положение точек широтой и долготой.
Однако огромные возможности применения этой идеи были раскрыты лишь в XVII в. в работах выдающихся французских математиков Пьера Ферма и Рене Декарта. В своих трудах эти ученые показали, как благодаря системе координат можно переходить от точек к числам, от линий к уравнениям, от геометрии к алгебре.
Несмотря на то что П. Ферма опубликовал свою роботу на год раньше Р. Декарта, систему координат, которой мы сегодня пользуемся, называют декартовой. Р. Декарт в своей работе «Рассуждение о методе» предложил новую удобную буквенную символику, которой с незначительными изменениями мы пользуемся и сегодня. Вслед за Декартом мы обозначаем переменные последними буквами латинского алфавита 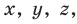 а коэффициенты — первыми:
а коэффициенты — первыми: 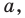
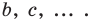 Привычные нам обозначения степеней
Привычные нам обозначения степеней 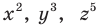 и т. д. также ввел Р. Декарт.
и т. д. также ввел Р. Декарт.

Справочный материал
Расстояние между двумя точками
Расстояние между точками 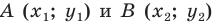 можно найти по формуле
можно найти по формуле 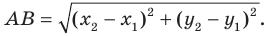
Координаты середины отрезка
Координаты 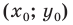 середины отрезка с концами
середины отрезка с концами 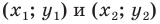 можно найти по формулам:
можно найти по формулам:
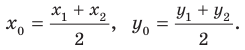
Уравнение фигуры
Уравнением фигуры 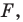 заданной на плоскости
заданной на плоскости 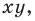 называют уравнение с двумя переменными
называют уравнение с двумя переменными 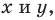 обладающее следующими свойствами:
обладающее следующими свойствами:
1) если точка принадлежит фигуре 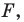 то ее координаты являются решением данного уравнения;
то ее координаты являются решением данного уравнения;
2) любое решение 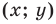 данного уравнения является координатами точки, принадлежащей фигуре
данного уравнения является координатами точки, принадлежащей фигуре 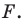
Уравнение окружности
Уравнение окружности радиуса 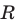 с центром в точке
с центром в точке 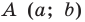 имеет вид
имеет вид 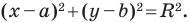
Любое уравнение вида 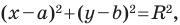 где
где 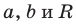 — некоторые числа, причем
— некоторые числа, причем 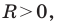 является уравнением окружности радиуса
является уравнением окружности радиуса 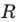 с центром в точке с координатами
с центром в точке с координатами 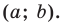
Уравнение прямой
Уравнение прямой имеет вид 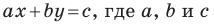 — некоторые числа, причем
— некоторые числа, причем 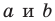 не равны нулю одновременно. Любое уравнение вида
не равны нулю одновременно. Любое уравнение вида 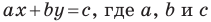 — некоторые числа, причем
— некоторые числа, причем 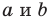 не равны нулю одновременно, является уравнением прямой.
не равны нулю одновременно, является уравнением прямой.
Если 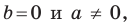 то уравнение прямой
то уравнение прямой 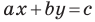 задает вертикальную прямую; если
задает вертикальную прямую; если 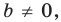 то это уравнение задает невертикальную прямую.
то это уравнение задает невертикальную прямую.
Угловой коэффициент прямой
Коэффициент 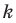 в уравнении прямой
в уравнении прямой 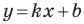 называют угловым коэффициентом прямой, и он равен тангенсу угла, который образует эта прямая с положительным направлением оси абсцисс.
называют угловым коэффициентом прямой, и он равен тангенсу угла, который образует эта прямая с положительным направлением оси абсцисс.
Необходимое и достаточное условие параллельности невертикальных прямых
Прямые 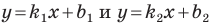 параллельны тогда и только тогда, когда
параллельны тогда и только тогда, когда 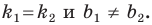
- Декартовы координаты в пространстве
- Геометрические преобразования в геометрии
- Планиметрия – формулы, определение и вычисление
- Стереометрия – формулы, определение и вычисление
- Перпендикулярность прямой и плоскости
- Взаимное расположение прямых в пространстве, прямой и плоскости
- Перпендикулярность прямых и плоскостей в пространстве
- Ортогональное проецирование
План урока:
Взаимосвязь координат векторов и его начала и конца
Определение координат середины отрезка
Вычисление длины вектора и отрезка
Простейшие задачи с использованием координатного метода
Использование признака коллинеарности векторов
Деление отрезка в заданном отношении
Введение прямоугольной системы координат
Взаимосвязь координат векторов и его начала и конца
На координатной плоскости любые две точки можно соединить друг с другом. В результате получается отрезок. Если же дополнительно указано, какая из этих точек – начало отрезка, а какая – конец, то в итоге мы уже имеем вектор. Попробуем определить, есть ли связь между координатами вектора и координатами (можно использовать сокращение коор-ты) его граничных точек.
Пусть в прямоугольной системе координат отмечены точки А (хА;уА) и В(хB;уB).Тогда можно задать вектор АВ. Также построим ещё два вспомогательных вектора ОА и ОВ, начинающиеся в точке О – начале коор-т:

Вектора ОВ и ОА – это радиус-векторы (так как их начало находится в начале координат), поэтому их коор-ты ОВ и ОА совпадают с коор-тами их концов (В и А соответственно):

Итак, зная коор-ты граничных точек вектора, можно найти и координаты данного вектора:

Например, если вектор начинается в точке А (2; 1), а заканчивается в точке В (6; 3), то коор-ты вектора АВ можно определить так:

Задание. Начало вектора находится в точке М, а конец – в точке К. Определите его коор-ты, если:
а) М(2; 7) и К(6; 8);
б) М(5; 1) и К(2; 10);
в) М(0; 8) и К(9; -5).
Решение. Из коор-т К мы просто вычитаем соответствующие коор-ты М, и в итоге определяем коор-ты вектора:

Задание. От точки H (8; 15) отложили вектор m{5; – 6}. Каковы координаты конца этого вектора?
Решение. Обозначим интересующие нас коор-ты как (хк; ук). Для вектора, начинающегося в точке (8; 15) и заканчивающегося в точке (хк; ук), коор-ты можно вычислить так:
x = xk – 8
y = yk – 15
Однако нам даны координаты вектора, то есть величины х и у, поэтому мы можем записать:
5 = xk – 8
-6 = yk – 15
Оба равенства представляет собой уравнения, которые можно решить:
5 = xk – 8
xk = 5 + 8 = 13
-6 = yk – 15
yk = -6 + 15 = 9
В итоге получили, что конец вектора находится в точке (13; 9).
Ответ:(13; 9).
Определение координат середины отрезка
Пусть построен вектор АВ, причем известны коор-ты его начала А (хА; уА) и его конца B (хB; уB). Обозначим буквой С середину отрезка АВ и попытаемся вычислить коор-ты С, которые мы обозначим как (хC; уC):

Рассмотрим вектора АС и СВ. Они имеют одинаковую длину, потому что С разбивает АВ пополам. Также АС и СВ коллинеарны, так как они лежат на одной прямой АВ. При этом они и сонаправлены, а значит, эти вектора равны:

Нам удалось выразить коор-ты С через координаты А и В. В итоге можно сформулировать правило:

Например, пусть необходимо найти координаты середины отрезка HK, при этом известны коор-ты его концов: Н(5; – 2) и К(3; 4). Сначала найдем полусумму коор-т х и получим эту же коор-ту у середины:

Итак, точка середины отрезка имеет коор-ты (4; 1). Для наглядности построим отрезок ОК и продемонстрируем, что его середина действительно находится в точке (4; 1):

Вычисление длины вектора и отрезка
Пусть есть произвольный вектор с коор-тами {x; у}. Отложим его от точки начала координат, после чего из его конца опустим перпендикуляры ОВ и ОС на координатные оси:

Для простоты рассмотрим случай, когда х и у – положительные числа, то есть точка А находится в первой четверти. Тогда длина ОВ будет равна х:
OB = x
Так как ОСАВ – прямоугольник, то стороны ОС и АВ одинаковы, причем ОС имеет длину, равную коор-те у:
AB = OC = y
Теперь изучим ∆ОВА. Он прямоугольный, и ОА в нем – гипотенуза, поэтому можно записать теорему Пифагора:
OA2 = OB2 + AB2
Теперь заменим отрезки ОВ и АВ на х и у:
OA2 = x2 + y2
Осталось извлечь квадратный корень:

Мы вывели формулу для вычисления длины вектора по его координатам. Можно рассмотреть и остальные случаи, когда точка А лежит в другой четверти координатной плоскости или на координатных осях, однако во всех случаях будет получаться одинаковая формула.

Задание. Определите длину вектора с коор-тами:

Решение. Во всех случаях просто возводим каждую коор-ту в квадрат, потом складываем полученные числа и извлекаем из полученной суммы квадратный корень:

Теперь предположим, что имеется две точки с коор-тами (х1; у1) и (х2; у2). Требуется найти длину отрезка, их соединяющего, то есть расстояние между этими двумя точками. Если принять одну из этих точек, например первую, за начало вектора, а вторую за его конец, то задача сведется к вычислению длины этого вектора. Его коор-ты можно будет высчитать так:
x = x2 – x1
y = y2 – y1
Тогда расстояние между точками (обозначим его как d) будет вычисляться по формуле:

Задание. Определите длину отрезка MP, если известны коор-ты его концов:

Простейшие задачи с использованием координатного метода
Выведенные нами формулы являются базовыми для расчетов, связанных с коор-тами. До этого мы решали лишь простейшие задачи на использование этих формул, однако в более сложных задачах надо использовать сразу несколько более сложных формул.
Задание. Известны коор-ты трех вершин параллелограмма АВСD: А(4; 1), В(1; 1), С(3; 5). Определите коор-ты четвертой вершины D.
Решение.

Сначала найдем коор-ты вектора ВС. Мы можем это сделать, так как нам известны коор-ты его начальной и конечной точки:
xBC = xC – xB = 3 – 1 = 2
yBC = yC – yB = 5 – 1 = 4
Так как в параллелограмме противоположные стороны имеют одинаковую длину и при этом параллельны, то вектора ВС и АD равны, то есть имеют одинаковые коор-ты:

Итак, D имеет коор-ты (6; 5).
Ответ (6; 5).
Задание. В – середина отрезка АС. Известны коор-ты точек: А(2; 4) и В(0; 18). Найдите коор-ты С.
Решение.

Для начала будем работать только с коор-той х. Так как В – середина АС, то их абсциссы (напомним, так называют координату х точек) связаны соотношением:

Задание. Отрезок MN имеет длину 13. Даны координаты концов отрезка: M(4; 6) и N (х; 1). Найдите величину переменной х.

Нам по условию известно это расстояние для точек M и N, а также известны 3 и 4 коор-т точек. Поэтому надо просто подставить все известные данные в формулу, получить уравнение и решить его:

Далее извлекаем корень из обеих частей, но при этом появляется два различных корня (так обычно и бывает при решении квадратных уравнений):

Ответ: – 8 или 16.
Задание. Расстояние от точки S(2x; – 2) до точки T (6; 4х) составляет 14. Определите величину х.
Решение. Задача во многом аналогично предыдущей, надо подставить в формулу расстояния между точками данные из условия и решить получившееся уравнение:

Решаем это квадратное уравнение через дискриминант:

Ответ: (– 2,6) или 3.
Задание. Найдите коор-ты точки M на рисунке, если точка А имеет коор-ты (4; 2).

Решение. По рисунку видно, что середина отрезка находится в точке О(0; 0). Коор-ты середины отрезка (то есть точки О) и его граничных точек связаны формулами:

Использование признака коллинеарности векторов
На прошлом уроке мы выяснили, что если вектора коллинеарны, то их коор-ты пропорциональны. Это позволяет определить, лежит ли та или иная точка на указанной прямой.
Задание. Даны точки А(1; 2), В(4; 7) и С (10; 17). Определите, лежит ли точка В на прямой АС.
Решение. Если А, В и С принадлежат одной прямой, то любые два вектора, проведенные через эти точки, окажутся коллинеарными друг другу. Если же они НЕ лежат на одной прямой, то наоборот, любые два таких вектора окажутся неколлинеарными. То есть надо составить два вектора, например, АВ и ВС, и проверить их коллинеарность.
Определим коор-ты АВ:

Напомним, что для проверки векторов на коллинеарность надо поделить их коор-ты друг на друга. Если получится одно и то же число, то вектора коллинеарны:

В обоих случаях получилось одинаковое число, значит, вектора коллинеарны.
Ответ: Да, точка B лежит на прямой AC.
Задание. Проверьте, лежат ли точки А(3; 7), В (8; 12) и С(6; 4) на одной прямой.
Решение. Снова вычисляем коор-ты векторов АВ и ВС:

Получились разные числа, следовательно, вектора АВ и ВС не коллинеарны, а потому точки А, В и С никак не могут лежать на одной прямой.
Ответ: Нет, точки A,B,C не лежат на одной прямой.
Задание. Проверьте, параллельны ли друг другу отрезки АВ и CD, если известны коор-ты: А(1; 1), В(5; 5), С(4; 2), D(6; 4).
Решение. Если отрезки параллельны, то и вектора АВ и CD должны быть коллинеарными. Проверим это также, как мы это делали в двух предыдущих задачах:

Итак, вектора коллинеарны. Означает ли это, что отрезки АВ и CD параллельны? Ещё нет. На самом деле возможно два случая:
1) АВ и CD действительно параллельны;
2) АВ и СD лежат на одной прямой, и тогда их параллельными считать нельзя.

Как же проверить, какой из двух случаев относится к этой задаче? Надо рассмотреть ещё один ВС. Если реализуется второй случай, то он окажется коллинеарен вектору АВ. В первом же случае он будет ему не коллинеарен.

Получили различные числа, значит, АВ и ВС не коллинеарны. Теперь мы можем точно утверждать, что АВ и СD параллельны.
Ответ: Да, отрезки AB и CD параллельны.
Деление отрезка в заданном отношении
Мы уже научились находить коор-ты середины отрезка. Можно сказать, что середина – это точка, которая разбивает отрезок в отношении 1:1, то есть на равные отрезки. А что делать в более сложном случае, если нужно найти точку, разбивающую отрезок в другом отношении, например, в отношении 2:1? Выведем для такого случая формулу.
Пусть точка С разбивает отрезок АВ в некотором отношении так, что отрезок АС в k больше отрезка СВ:

(Примечание. Если отрезок АС меньше СВ, то число k будет меньше единицы.)
Как и обычно, для обозначения коор-т точек используем индексы, совпадающие с обозначением точек: А(xА; уА), В(xВ; уВ) и С(xС; уС).

Нам также потребуются вектора АС{xАС; уАС} и СВ{xСВ; уСВ}. Так как эти вектора сонаправлены, и АС в k раз длиннее, то

Абсолютно аналогичные образования приведут к такому же выражению для коор-ты у:

Рассмотрим на примерах использование этой формулы.
Задание. На отрезке РM отложена точка K так, что она разбивает РM на отрезки РK и KM в отношении РK:KM = 2:1. Даны коор-ты точек: Р(6; 3) и К (18; 12). Вычислите коор-ты K.
Решение.

Отношение РК:КМ = 2:1 означает, что отрезок РК в 2 раза длиннее, чем КМ. Это означает, что в формуле

Задание. Точки B (5; – 16) и H(29; 24) соединены отрезком. Точка M на отрезке ВН отмечена так, что ВМ:МН = 3:5. Определите коор-ты точки М.
Решение. Из отношения ВМ:МН = 3:5 вытекает, что ВМ длиннее МН в
3/5 = 0,6 раз
то есть фактически ВМ короче МН. То есть при использовании формулы

Рассмотрим ещё несколько более усложненных задач с использованием коор-т.
Задание. Точка K лежит на оси Ох, при этом она равноудалена от точек Е(2; 2) и F(6; 10). Найдите коор-ты К.
Решение. У любой точки, лежащей на оси Ох, коор-та у будет равна нулю, в том числе и у точки К:
yk = 0
Будем обозначать неизвестную коор-ту К как х:
xk = x
Напомним расстояние между точками можно рассчитать, используя формулу:

Получили иррациональное уравнение. В данном случае можно просто приравнять подкоренные выражения, однако после получения корней надо проверить, нет ли среди них посторонних:

Проверяем, не является ли корень посторонним. Для этого просто подставляем его в уравнение:

Корень действительно подошел, поэтому коор-та х точки К равна 16.
Ответ: (16; 0).
Введение прямоугольной системы координат
Даже если в формулировке задачи коор-ты и вектора прямо не упоминаются, может быть полезным самостоятельно добавить в нее прямоугольную систему координат. Это позволит использовать формулы, используемые в методе коор-т, для решения задачи.
Задание. Докажите, что если в параллелограмме сложить квадраты всех его сторон, то получится то же число, что и при сложении квадратов диагоналей этого параллелограмма.
Решение. Расположим систему коор-т таким образом, одна из сторон параллелограмма находилась на оси Ох, причем одна ее вершина совпадала с началом коор-т, а другая имела положительную коор-ту х:

Пусть вершина А находится в начале коор-т, и тогда она имеет коор-ты (0; 0). Вершина D лежит на Ох, тогда ее ордината равна нулю, а абсциссу обозначим буквой а. Точка В имеет произвольные коор-ты (b; с), коор-ты же точки С можно рассчитать. Сначала заметим, что вектор коор-ты вектора АВ совпадают с коор-тами точки В, так как он является радиус-вектором:

Вектора АВ и DC равны, потому что они лежат на параллельных прямых и имеют одинаковую длину:

Итак, коор-ты С – это (а + b; с).
Теперь мы должны длину каждой стороны параллелограмма и возвести ее в квадрат. Обратите внимание, что если расстояние между точками рассчитывается по формуле

Равенство доказано.
Задание. В равнобедренном треугольнике длина основания составляет 80 см, а опущенная на нее медиана имеет длину 160 см. Вычислите длины двух других медиан.
Решение. Пусть АВС – рассматриваемый в задаче треугольник, причем АВ – его основание. Расположим систему коор-т так, чтобы ее начало совпадало с точкой, в которой медиана пересекается с основанием:

В этом случае вершина, из которой опущена медиана, будет иметь коор-ты (0; 160), а две другие вершины будут иметь коор-ты (– 40; 0) и (40; 0).
Нам надо найти длину двух других медиан АM и BN. Они одинаковы по длине, поэтому достаточно найти длину только одной из них, например, АМ. Для этого сначала найдем коор-ты М, которая является серединой ВС:

Сегодня мы познакомились с важнейшими формулами, используемыми в методе коор-т, и научились решать некоторые простейшие задачи. В будущем мы узнаем о более сложных задачах, в которых будут фигурировать не только отрезки и многоугольники, но и окружности.
У меня есть отрезок с известными координатами концов. На этом отрезке есть точка. Я знаю расстояние от начала отрезка до этой точки. Мне надо найти координаты этой точки. Как найти эти координаты?
Пример: Есть 2 точки А(3,3) и В(6,4). Длина отрезка примерно 3,16. И есть точка С(?,?) на отрезке. Как найти координаты, если от А до С =1,8 ???
![]()
Dmytro
6,7011 золотой знак20 серебряных знаков55 бронзовых знаков
задан 3 мар 2016 в 20:40
4
Имеется отрезок AB с координатами A(Xa, Ya) и B(Xb, Yb).
Требуется найти координаты точки C(Xc, Yc), лежащей на отрезке AB на расстоянии Rac от точки A.
Rab = sqrt((Xb - Xa) ^ 2 + (Yb - Ya) ^ 2)
k = Rac / Rab
Xc = Xa + (Xb - Xa) * k
Yc = Ya + (Yb - Ya) * k
Обозначения:
f ^ n – возведение f в степень n, в нашем случае (первом) f будет Xb - Xa и n будет 2.
sqrt(f) – квадратный корень из f, в нашем случае f будет (Xb - Xa) ^ 2 + (Yb - Ya) ^ 2.
f / n – деление f на n, в нашем случае f будет Rac и n будет Rab.
f * n – умножение f на n, в нашем случае (первом) f будет Xb - Xa и n будет k.
ответ дан 4 мар 2016 в 6:54
![]()
Konstantin LesKonstantin Les
1,5388 серебряных знаков12 бронзовых знаков
2
Алгоритм без кода (довольно элементарный):
Имеем:
Две точки A, B; len – расстояние от точки А до требуемой точки C
full_len = |B - A| // длина вектора, соединяющего две точки == длина отрезка
C = A + (B - A) * (len / full_len)
Сложение векторов и умножение на число – очевидные операции.
ответ дан 3 мар 2016 в 20:56
int3int3
2,4579 серебряных знаков19 бронзовых знаков
8
nodet – точка конец вектора, в твоем случае точка b
nodef – точка начало вектора, в твоем случае точка a
dx = nodet.x - nodef.x
dy = nodet.y - nodef.y
dz = nodet.z - nodef.z
r = math.sqrt(dx ** 2 + dy ** 2 + dz ** 2)
xx = dx * (step/r)
yy = dy * (step /r)
zz = dz * (step /r)
newnode = node(nodef.x + xx,nodef.y + yy,nodef.z + zz)
newnode – новая точка на заданом расстоянии
ответ дан 12 ноя 2019 в 16:31
qvuer7qvuer7
113 бронзовых знака
