Задача 41513 Даны три последовательные вершины.
Условие
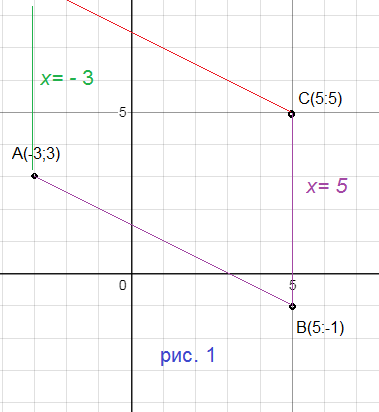
Даны три последовательные вершины параллелограмма А(-3;3), В(5;-1),С(5;5). Не находя координаты вершины D, найти:
1. найти уровень сторон AD
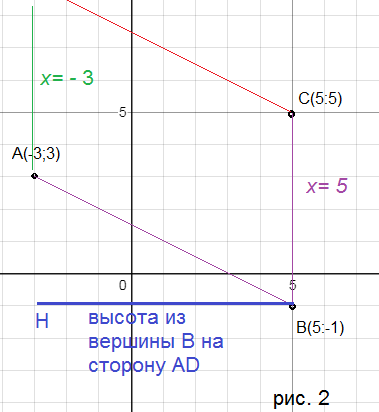
2. уровень высоты опущенной из вершины B на сторону AD
3. найти длину этой высоты
4. уравнение диагонали BD
5. угол между диагоналями параллелограмма
Все решения
Точки В и С имеют одинаковую первую координату, поэтому [i]уравнение прямой[/i] ВС: [red]х=5[/red]
Прямая AD || BC и проходит через точку А, у которой первая координата равна (-3)
Значит, [i]уравнение прямой[/i] АD:[red] x=-3[/red]
Высота ВН перпендикулярна AD и значит параллельна оси Ох.
Уравнение прямой, параллельной оси Ох и проходящей через точку В (5;-1)
y=-1
Точка Н – точка пересечения AD и BH
Значит, координаты точки H (-3;-1)
3)
[green]|BH|[/green]=[green]|x_(H)-x_(B)|[/green]=| -3 – 5|= |-8| = 8
так как это частный случай формулы
при y_(H)=y_(B)
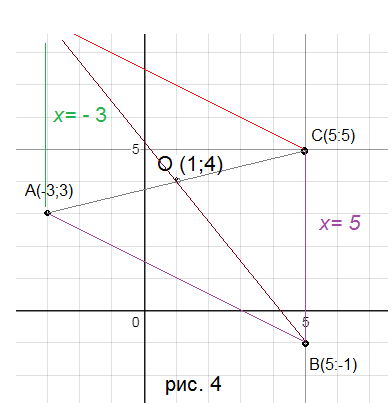
Диагонали параллелограмма в точке пересечения делятся пополам.
Координаты точки О как середины отрезка АС:
x_(O)=[m]frac><2>=frac<-3+5><2>=1[/m]
y_(O)=[m]frac><2>=frac<3+5)><2>=4[/m]
Уравнение диагонали BD – это и уравнение прямой BO.
Составим уравнение применяя общее уравнение прямой, проходящей через две точки
Пропорция, перемножаем крайние и средние члены пропорции
-5*(х-1)=4*(у-4)
-5х+5=4у-16
[b]5х+4у-21=0[/b] -[i] уравнение диагонали[/i] BD
5)
Угол между диагоналями – это меньший из углов, образованных прямыми BO и AC, значит это угол ВОС
Находим его как угол между векторами
vector и vector
Находим координаты векторов
vector=(5-1;-1-4)=(4;-5)
vector=(5-1;5-4))=(4;1)
Находим скалярное произведение векторов vector и vector
vector*vector=4*4+(-5)*1=11
|vector|=sqrt(4^2+(-5)^2)=sqrt(41)
|vector|=sqrt(4^2+1^2)=sqrt(17)
сos ( ∠ vector, vector)=[m]frac<11><sqrt<41>cdot sqrt<17>>=frac<11><sqrt<697>>=frac<11sqrt<697>><697>[/m] 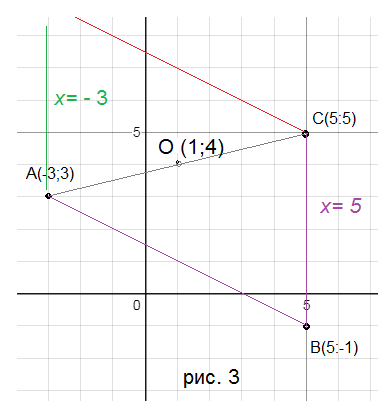
Высота параллелограмма – формулы и свойства. Висота паралелограма – формули і властивості
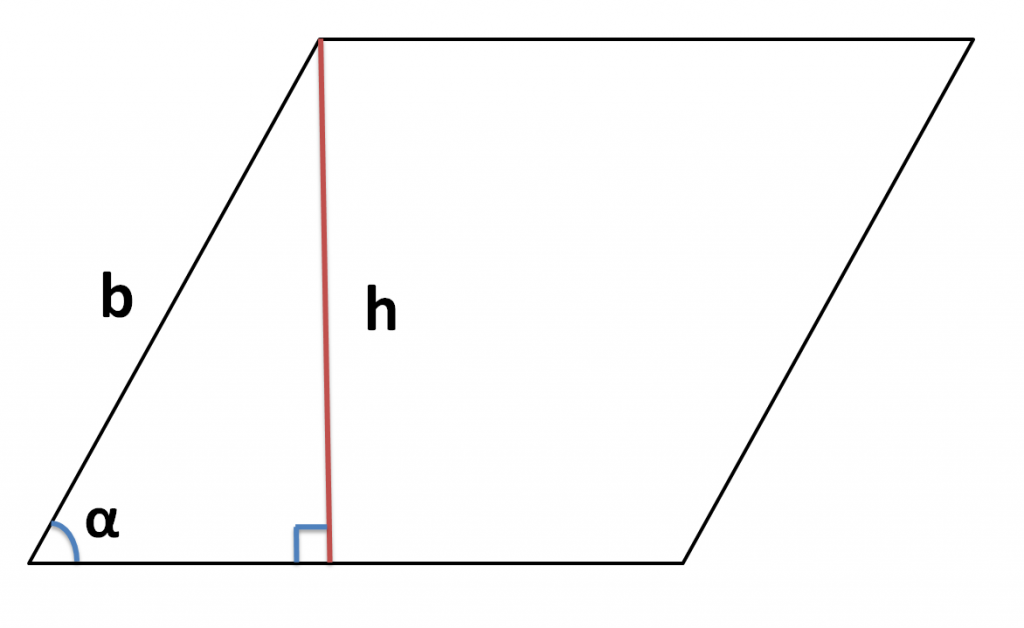
Позначення у формулах еквівалентні позначенням на малюнках, а саме:
а – сторони, паралелограма, паралельні один одному
b – бічні сторони паралелограма
h – висота паралелограма
d – дiагональ паралелограма
S – площа паралелограма
α – гострий кут при основі паралелограма
Висота паралелограма дорівнює співвідношенню площі до підстави (Формула 1)
Висота паралелограма дорівнює твору бічної сторони на синус кута при його основі (Формула 2)
Співвідношення підстав паралелограма дорівнює обернено пропорційному співвідношенню висот, опущених на відповідні сторони (Формула 3)
Висоти паралелограма, опущені з однієї вершини, утворюють кут, рівний куту паралелограма при сусідній вершині (Малюнок 2)
Висота паралелограма рівна, корню з різниці квадрата бічної сторони і квадрата довжини відрізка, створюючого прямокутний трикутник, іншими сторонами якого є бічна сторона і висота (Формула 4)
Висота паралелограма дорівнює корню з різниці квадрата діагоналі, з якої опущена висота і квадрата довжини відрізка між точкою, з якої проведена діагональ і точкою пересічення висоти і основання (Формула 5)
Задача
| Висота паралелограма проведена з вершини тупого кута і дорівнює 5 см. Висота ділить сторону парелелограма навпіл. Гострий кут паралелограма доривнюе 30 градусів. Знайдіть діагональ паралелограма, проведену з вершини тупого кута, и кути, яки вона утворює зі сторонами паралелограма. | Высота параллелограмма проведена из вершины тупого угла и равняется 5 см. Высота делит сторону параллелограмма пополам. Острый угол равняется 30 градусам. Найдите диагональ параллелограмма, проведенную из вершины тупого угла и углы, которые она образует со сторонами параллелограмма. |
Решение.
Поскольку, по условию задачи, AE=ED, то треугольники ABE и DBE равны между собой (по первому признаку равенства треугольников: равны две стороны и угол между ними, AE=ED и BE – общая сторона, а BE образует с AD угол 90 градусов). Таким образом, угол ADB равен 30 градусам. Соответственно, угол DBC также равен 30 градусам как внутренние накрест лежащие при параллельных прямых BC и AD.
Из прямоугольного треугольника ABE определим, что угол ABE равен 180 – 90 – 30 = 60 градусов. Откуда (из равенства треугольников ABE и DBE) угол EBD также равен 60 градусов. Таким образом, диагональ образует со вторым основанием угол ABD = 60 + 60 = 120 градусов. BDC = ABD = 120 градусов как внутренние накрест лежащие.
Найдем длину диагонали.
BE / BD = cos ∠EBD
BE / BD = cos 60
Подставим значение косинуса 60 градусов и получим:
BE / BD = 1/2
По условию задачи BE = 5 см, откуда
5 / BD = 1/2
BD = 10
Ответ: длина диагонали параллелограмма равна 10 см, углы, которые образует диагональ с основаниями равны 30 и 120 градусов.
Даны три последовательные вершины параллелограмма А(1 2) В(-2
Даны три последовательные вершины параллелограмма А(1;2), В(-2;1),С(-4;-5). Не находя координаты вершины D, найти:
уравнение стороны AD;
уравнение высоты BK, опущенной из вершины В на сторону AD;
длину высоты BK;
уравнение диагонали BD;
тангенс угла между диагоналями параллелограмма.
Записать общие уравнения найденных прямых. Построить чертеж.
) Найдем уравнение прямой BC по формуле уравнения прямой, проходящей через две точки А1 и А2:
x-x1x2-x1 = y-y1y2-y1.
x+2-4+2 = y-1-5-1⇒x+22 = y-16⇒3x+6=y-1⇒y=3x+7.
Получили уравнение вида y=kx+b – уравнение с угловым коэффициентом, k=3.
Так как противоположные стороны параллелограмма параллельны, то искомое уравнение прямой AD будем искать как уравнение прямой, проходящей через точку A параллельно прямой BC. Угловые коэффициенты у параллельных прямых одинаковые.
Уравнение прямой, проходящей через данную точку Mx0;y0 в данном направлении, имеет вид:
y-y0=kx-x0.
Тогда уравнение стороны AD имеет вид:
y-2=3x-1⇒3x-y-1=0.
2) Составим уравнение высоты BK, проведенной из вершины B на сторону AD как уравнение прямой, проходящей через точку B перпендикулярно прямой AD.
Из условие перпендикулярности двух прямых: k=-13.
y-1=-13x+2⇒3y-3=-x-2⇒x+3y-1=0.
3) Найдем длину высоты BK по формуле длины перпендикуляра, опущенного из точки B на прямую AD:
d=Ax0+By0+CA2+B2, где A=3, B=-1.
d=3∙-2-1-132+-12=810.
4) Найдем уравнение диагонали BD как уравнение прямой, проходящей через точки B и E, где E – середина отрезка AC.
Если A(x1, y1), C(x2, y2), то координаты точки Ex0;y0 – середины отрезка AC, определяются формулами:
x0=x1+x22; y0=y1+y22.
x0=1-42=-32; y0=2-52=-32.
x+2-32+2 = y-1-32-1⇒x+212 = y-1-52⇒-5x+2=y-1⇒5x+y+9=0.
5) Найдем уравнение диагонали AC как уравнение прямой, проходящей через две данные точки:
x-1-4-1 = y-2-5-2⇒x-15 = y-27⇒7x-7=5y-10⇒7x-5y+3=0,
уравнение с угловым коэффициентом имеет вид y=75x+35, угловой коэффициент k1 прямой AC равен 75.
Уравнение диагонали BD имеет вид 5x+y+9=0, уравнение с угловым коэффициентом имеет вид: y=-5x-9, k2=-5.
Тангенс угла φ между прямыми с угловыми коэффициентами k1 и k2 определяется формулой:
tgφ=k2-k11+k1k2.
Следовательно,
tgφ=-5-751+75∙-5=3256=1615⇒φ≈470.
Построим чертеж:
-3238595250
Ответ. 1) 3x-y-1=0; 2) x+3y-1=0; 3) 810; 4) 5x+y+9=0; 5) 470.
Контрольная работа № 4
Вычислить пределы функций.
а) limx→∞x3-4×2+63×3+10×2+4x=∞∞=limx→∞x31-4x+6x33x31+103x+43×2=limx→∞x33x3=13.
Пределы от функций:-4x, 6×3, 103x и 43×2 равны 0 при x→∞.
б) limx→53×2-14x-5×2-6x+5=00=limx→53x+1x-5x-1x-5=limx→53x+1x-1=164=4;
limx→13×2-14x-5×2-6x+5=limx→13x+1x-1=40=+∞.
в)limx→-23x-6+2×3+8=00=
=limx→-23x-6+23x-62-23x-6+4x+2×2-2x+43x-62-23x-6+4=
=limx→-2x-6+8x+2×2-2x+43x-62-23x-6+4=
=limx→-21×2-2x+43x-62-23x-6+4=
=14+4+4364-23-8+4=112∙4+4+4=1144.
г)limx→01-cos5xxtg2x=limx→02sin25x2xsin2xcos2x=limx→02sin5x25x22∙25×24∙cos2xx∙sin2x2x∙2x=
=limx→02∙25×24∙cos2x2x2=254.
limx→0sin5x25x2=y=5×2=limy→0sinyy=1-первый замечательный предел;
limx→0sin2x2x=y=2x=limy→0sinyy=1-первый замечательный предел.
д)limx→π4tgπ4-xtg2x=0∙∞=y=π4-x⇒x=π4-y;y→0 при x→π4=
=limy→0tgy∙tgπ2-2y=limy→0tgy∙tgπ2-2y=limy→0tgy∙ctg2y=
=limy→0tgytg2y=limy→0tgyy∙ytg2y2y∙2y=limy→0y2y=12.
limx→0tgyy=limx→0tg2y2y=1-следствие из первого замечательного предела.
е) limx→∞13x+213x-15x+7=1∞=limx→∞13x-15+15+213x-15x+7=
=limx→∞1+1713x-15x+7=limx→∞1+1713x-1513x-1517 ∙ 1713x-15 ∙ x+7=
=elimx→∞ 1713x-15 ∙ x+7=e1713;
limx→∞1+1713x-1513x-1517 =y=13x-1517;y→∞ при x→∞=limy→∞1+1yy =e-
второй замечательный предел.
limx→113x+213x-15x+7=15-28=7,58.
Контрольная работа № 5
Производная и дифференциал
1. Найти производные:
а) y=10×5-14×4=10×5-x-44;
y’=10∙5×5-1–4∙x-4-14=50×4+1×5.
б) y=13xsinx=x-13sinx;
y’=-13x-13-1sinx+x-13cosx=-13x3xsinx+13xcosx=
=13xcosx-sinx3x.
в) y=tgxx;
y’=xcos2x-tgx2xx=xcos2x-sinx2xcosxx=2x-sinxcosx2xcos2xx=4x-sin2x4xxcos2x.
г) y=cosx1-sinx;
y’=-sinx1-sinx-cosx∙-cosx1-sinx2=-sinx+sin2x+cos2x1-sinx2=
=1-sinx1-sinx2=11-sinx.
д) y=ln1-ctgx;
y’=1sin2x1-ctgx=1sin2x-sin2x∙cosxsinx=1sin2x-sinx∙cosx=
=22sin2x-sin2x.
е) y=e-x+10lnx
y’=-e-x+10lnxln10x.
ж) y=arctg1+x1-x
y’=11+1+x1-x2∙1-x+1+x1-x2=21+1+x21-x21-x2=
=21-x2+1+x2=21-2x+x2+1+2x+x2=22×2+2=1×2+1.
з) y=sin23xcos32x;
y’=2sin3x∙cos3x∙3cos32x+sin23x3cos22x∙-sin2x∙2=
=3sin6xcos32x-6sin23xcos22x∙sin2x.
и) y=arcsinex+arccos12x=arcsinex+arccos2-x;
y’=11-e2xex-11-2-2×2-xln2∙-1=ex1-e2x+ln22x1-2-2x=
=ex1-e2x+ln222x-1.
к) y=tg3lnx;
y’=1cos23lnx∙3lnxln3x=3lnxln3xcos23lnx.
л) y=xx+1x-2;
y’=x+1x-2+x2x+1x-2∙12xx-2-12xx+1x-22=
=x+1x-2+x-2x+1∙xx-2-x-14x-22=
=x+1x-2-x-2x+1∙3x4x-22.
м) y=arctgx2-lnsinx;
y’=11+x4∙2x-cosxsinx=2×1+x4-ctgx.
2. Найти dydx
а) xy=lnex+y-2-функция выражена неявно.
y+xy’=ex+y∙y’ex+y-2; yex+y-2+xy’ex+y-2=ex+y∙y’;
yex+y-2=ex+y-xex+y-2y’;y’=yex+y-2ex+y-xex+y-2.
dydx=y’=yex+y-2ex+y-xex+y-2.
б) tgy-1=x+y2-функция выражена неявно.
y’cos2y-1=1+2yy’; y’cos2y-1-2yy’=1;
1-2ycos2y-1cos2y-1y’=1;y’=cos2y-11-2ycos2y-1;
dydx=y’=cos2y-11-2ycos2y-1.
в) x=arctgty=t2+1.
Используем формулу:
dydx=y’tx’t=2t2t2+111+t2=tt2+1.
3. Найти d2ydx2:
y=x3x-1.
dydx=y’=3x2x-1-x3x-12=x23x-3-xx-12=2×3-3x2x-12.
d2ydx2=y”=6×2-6xx-12-2x-12×3-3x2x-14=
=x-16xx-12-22×3-3x2x-14=
=6xx2-2x+1-4×3+6x2x-13=6×3-12×2+6x-4×3+6x2x-13=
=2×3-6×2+6xx-13=2xx2-3x+3x-13.
[spoiler title=”источники:”]
http://profmeter.com.ua/communication/learning/course/course7/lesson362/
[/spoiler]
Четырёхугольник, у которого стороны, находящиеся напротив друг друга параллельны и равны друг другу,
называется параллелограммом. Отрезок перпендикулярной прямой, проходящей от любой точки прямой, на
которой лежит одна из сторон параллелограмма через прямую, на которой расположена противоположная
сторона данной фигуры, является высотой параллелограмма. Высот параллелограмма можно провести
бесконечное множество через разные точки, но они неизменно будут перпендикулярны двум сторонам
фигуры.
- Высота параллелограмма через площадь и основание
- Высота параллелограмма через боковую сторону и острый угол
при основании - Высота параллелограмма через длину отрезка, образованного
на основании и боковую сторону - Высота параллелограмма через длину отрезка, образованного
на основании и диагональ
Через площадь и основание
Высота параллелограмма равна отношению площади к основанию.
h = S / a
где h – длина высоты параллелограмма, S – площадь, a – длина основания.
Цифр после
запятой:
Результат в:
Пример. На рисунке представлены пара абсолютно одинаковых параллелограммов. На левом
обозначена длина стороны (основания) в 6 единиц и проходящие через нее в разных точках высоты в 4
единицы.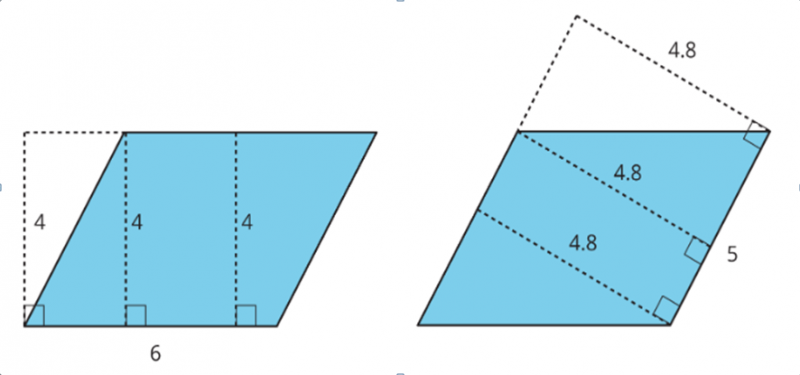
правом обозначена длина стороны (основания) в 5 единиц и проходящие через нее в разных точках высоты
в 4,8 единиц. Площадь параллелограмма можно вычислить умножением длины высоты на длину той стороны
(основания), которой эта высота перпендикулярна. Результат умножения будет одинаков для любой 2 двух
пар высота-основание. В рассматриваемом случае: 4 × 6 = 24; 4,8 × 5 = 24.
Можно визуально убедиться в этом, если разрезать фигуру и переставив части так, как показано на
рисунке.
Исходя из полученного, путем обратного подсчета можно вывести правило для определения высоты из
заданной площади и основания. В приведенном примере расчет будет выглядеть следующим образом: 24 / 6 = 4; 24 / 5 = 4,8.
Через длину отрезка, образованного на основании и диагональ
Вычисление высоты параллелограмма при известных длине отрезка образованного на основании и диагонали
производится также с использованием теоремы Пифагора. Высота в этом случае будет равна квадратному
корню из разницы диагонали и отрезка на основании.
h = √(d² — A2²)
где d — диагональ, A2 — отрезок образованный на основании.
Цифр после
запятой:
Результат в:
Пример. Пусть боковая сторона равна 47 см, отрезок образованный на основании равен
34 см, тогда получим h = √(b² — A1²) = √(47² — 34²) = 32,4 см.
Через боковую сторону и острый угол при основании
Если от тупого угла параллелограмма провести к основанию высоту, то образуется прямоугольный
треугольник, как показано на рисунке ниже. Если нам известна величина острого угла и длина боковой
стороны, то можно вычислить высоту через формулу синуса, который определяется как отношение катета к
гипотенузе. Роль катета здесь играет высота, а боковая сторона является гипотенузой. Соответственно
высота здесь будет равна произведению длины боковой стороны на синус острого угла.
h = b * sinα
где b — боковая сторона, sin α — острый угол при основании.
Цифр после
запятой:
Результат в:
Если известна величина тупого угла параллелограмма, то величину острого можно получить, отняв
величину тупого угла от 180 градусов.
Пример. Пусть боковая сторона b равна 115 см, острый угол при основании α равен 65º,
тогда получим h = b * sinα = 115 * sin 65 = 104 см.
Через длину отрезка, образованного на основании и боковую сторону
Вычисление высоты параллелограмма при известных длине отрезка образованного на основании и боковой
стороне производится с использованием теоремы Пифагора. Высота будет равна квадратному корню из
разницы квадратов боковой стороны и диагонали.
h = √(b² — A1²)
где b — боковая сторона, A1 — отрезок образованный на основании.
Цифр после
запятой:
Результат в:
Пример. Пусть боковая сторона равна 39 см, отрезок образованный на основании равен
16 см, тогда получим h = √(b² — A1²) = √(39² — 16²) = 35,6 см.
Пирамида определяется как трехмерная структура – многогранник, в основе которой лежит многоугольник.
В основании пирамиды находится многоугольник. Углы многоугольника соединены линиями – боковыми
ребрами с одной точкой, которая в пирамиде именуется как вершина. Треугольники, образованные парами
соседних боковых ребер и стороной основания называются боковыми гранями.
В основании правильной пирамиды лежит правильный многоугольник (тот у которого все стороны равны
между собой). У правильной пирамиды длина боковых ребер одинаковая. Соответственно правильная
пирамида образована боковыми гранями, являющимися равными равнобедренными треугольниками,
соединенными с основанием.
Апофемами в пирамиде называют отрезки прямых, проведенных от вершины перпендикулярно к основаниям.
Также, одновременно апофемы являются высотами треугольников – боковых граней.
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на
апофему грани.
Установлено, что умение вычислять длину апофемы, было востребовано с древнейших времен для
строительства сооружений. Предположительно, перед возведением подобных сооружений предварительные
размеры могли быть отрегулированы древними инженерами с помощью натянутых шнуров. Расшифровка
древнеегипетских иероглифов дает перевод значения понятия землемера как «натяжителя веревок».
Умение вычислять высоту параллелограммов, было востребовано с древнейших времен для проверки
правильности измерений земельных участков. Множество древних народов тысячи лет назад воздвигали
пирамиды и курганы для различных целей. Современные измерения позволяют утверждать, что некоторые их
них точно ориентированы – как по сторонам света, так и в трехмерном измерении по созвездиям.
Вероятно, часть из этих сооружений использовалась для определения орбиты Земли относительно звезд.
Эти сведения использовались для определения времени начала различных сельскохозяйственных работ. От
этого зависела урожайность, а значит вопрос выживания народов. Таким образом, вычисление апофемы
позволяло точно ориентировать пирамиду в пространстве и спасало жизни людей.
В параллелограмме могут быть проведены две высоты. Одна из них опускается из верхнего угла на противоположную, длинную сторону, разделяя параллелограмм на прямоугольный треугольник и прямоугольную трапецию. Вторая высота опускается на короткую сторону параллелограмма.
Образованный прямоугольный треугольник внутри параллелограмма дает возможность найти высоту через известную сторону параллелограмма и острый угол, находящийся напротив высоты. Если известен тупой угол, то рассчитать острый можно, отняв известный угол из 180°. Высота будет равна синусу противолежащего угла, умноженному на сторону параллелограмма:
h=a sinα
Как найти высоту параллелограмма
Как определить высоту параллелограмма, зная некоторые из его остальных параметров? Таких, как площадь, длины диагоналей и сторон, величины углов.

Вам понадобится
- калькулятор
Инструкция
В задачах по геометрии, точнее по планиметрии и тригонометрии, иногда требуется найти высоту параллелограмма, исходя из заданных значений сторон, углов, диагоналей и т.п.
Чтобы найти высоту параллелограмма, зная его площадь и длину основания, необходимо воспользоваться правилом определения площади параллелограмма. Площадь параллелограмма, как известно, равняется произведению высоты на длину основания:
S=a*h, где:
S – площадь параллелограмма,
а – длина основания параллелограмма,
h – длина опущенной на сторону а высоты, (или на ее продолжение).
Отсюда получаем, что высота параллелограмма будет равняться площади, разделенной на длину основания:
h=S/a
Например,
дано: площадь параллелограмма равняется 50 кв.см., основание – 10 см.;
найти: высоту параллелограмма.
h=50/10=5 (см).
Так как высота параллелограмма, часть основания и прилежащая к основанию сторона образуют прямоугольный треугольник, то для нахождения высоты параллелограмма можно использовать некоторые соотношения сторон и углов прямоугольных треугольников.
Если известны прилежащая к высоте h (DE) сторона параллелограмма d (AD) и противоположный высоте угол A (BAD), то расчета высоты параллелограмма нужно умножить длину прилежащей стороны на синус противоположного угла:
h=d*sinA,
например, если d=10 см, а угол А=30 градусов, то
H=10*sin(30º)=10*1/2=5 (см).
Если в условиях задачи заданы длина прилежащей к высоте h (DE) стороне параллелограмма d (AD) и длина отсекаемой высотой части основания (АЕ), то высоту параллелограмма можно найти воспользовавшись теоремой Пифагора:
|AE|^2+|ED|^2=|AD|^2, откуда определяем:
h=|ED|=√(|AD|^2-|AE|^2),
т.е. высота параллелограмма равняется корню квадратному из разности квадратов длины прилежащей стороны и отсекаемой высотой части основания.
Например, если длина прилегающей стороны равняется 5 см., а длина отсекаемой части основания равна 3 см, то длина высоты будет:
h=√(5^2-3^2)=4 (см).
Если известны длина прилежащей к высоте диагональ (DВ) параллелограмма и длина отсекаемой высотой части основания (ВЕ), то высоту параллелограмма можно также найти воспользовавшись теоремой Пифагора:
|ВE|^2+|ED|^2=|ВD|^2, откуда определяем:
h=|ED|=√(|ВD|^2-|ВE|^2),
т.е. высота параллелограмма равняется корню квадратному из разности квадратов длины прилежащей диагонали и отсекаемой высотой (и диагональю) части основания.
Например, если длина прилегающей стороны равняется 5 см., а длина отсекаемой части основания равна 4 см, то длина высоты будет:
h=√(5^2-4^2)=3 (см).
Видео по теме
Источники:
- что такое высота параллелограмма
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Height of a parallelogram formula is helpful in calculating height of a parallelogram. The height of a parallelogram is the perpendicular distance between the base side and the parallel side opposite to it.
A parallelogram can be defined as a quadrilateral in which opposite sides are parallel and the length of these opposite sides is also equal. Its opposite angles are also equal.
What is the Height of a Parallelogram Formula?
Height of a parallelogram is calculated using the formula Area is equal to Base multiplied by Height, so if the area of a parallelogram is known its height is calculated by dividing the Area by its Base.
Height of a Parallelogram Formula
The height of a parallelogram formula is derived from the area formula, area of a Parallelogram can be found using the base length and height of the parallelogram.
Area = Base × Height
Height = Area/Base
Perimeter of a parallelogram
Perimeter is defined as the sum of all sides using which a closed figure is been constructed. In the case of a parallelogram, it has 4 sides out of which opposite sides are equal so the perimeter is the sum of all four sides.
Let’s take the measure of opposite sides as X and Y hence
Perimeter of Parallelogram = X + Y + X + Y = 2X + 2Y = 2(X + Y)
Perimeter = 2(X + Y)
Solved Example on Height of Parallelogram
Example 1: Find the height of a parallelogram if its area is 625 cm2 and the length of the base is 25 cm.
Solution:
The height of a parallelogram can be calculated using the height of a parallelogram formula
Height = Area /Base
Height = 625/25
Height = 25 cm.
Hence the height of the parallelogram is 25 cm
Example 2: Find the area of a parallelogram whose base is 20 cm and height is 15 cm.
Solution:
Area of parallelogram = Base × Height
Base and height are given as 20 cm and 15 cm respectively.
Area = 20 × 15
Area = 300 cm.
Example 3: Perimeter of a parallelogram is 226 cm and one side of the parallelogram is of length 12 cm, find the measure of the other side.
Solution:
Perimeter of Parallelogram = 2(X + Y)
Where X is length of one side and Y is length of other side, so let X = 12 cm
226 = 2(X + Y)
2(X + Y) = 226
2(12 + Y) = 226
24 + 2Y =226
2Y = 226 – 24
2Y = 202
Y = 202/2
Y = 101 cm.
Example 4: Find the height of a parallelogram if its area is 800 cm2 and the length of the base is 40 cm.
Solution
The height of a parallelogram can be calculated using the height of a parallelogram formula
Height = Area /Base
Height = 800/40
Height = 20 cm.
Hence the height of the parallelogram is 20 cm
Example 5: Perimeter of a parallelogram is 400 cm and one side of the parallelogram is of length 80 cm, find the measure of another side.
Solution:
Perimeter of Parallelogram = 2(X + Y)
Where X is length of one side and Y is length of other side, so let X = 80 cm
400 = 2(X + Y)
2(X + Y) = 400
2(80 + Y) = 400
160 + 2Y =400
2Y = 400 – 160
2Y = 240
Y = 120 cm.
FAQs on Height of Parallelogram
Question 1: What is the base and height of a parallelogram?
Answer:
“Base” refers to the length of a side and “Height” is the length of a perpendicular between two parallel lines.
Question 2: What is Height of a Parallelogram?
Answer:
Height of a parallelogram is referred to as the perpendicular distance between two parallel lines of a parallelogram.
Question 3: What is area of a parallelogram?
Answer:
Area of parallelogram is referred as the space inside the boundary of a parallelogram.
Related Resources
- Parallel lines
- Area of rectangle
- Perimeter of rectangle
Last Updated :
26 Nov, 2022
Like Article
Save Article