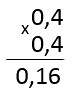Загрузить PDF
Загрузить PDF
До появления калькуляторов студенты и преподаватели вычисляли квадратные корни вручную. Существует несколько способов вычисления квадратного корня числа вручную. Некоторые из них предлагают только приблизительное решение, другие дают точный ответ.
-
1
Разложите подкоренное число на множители, которые являются квадратными числами. В зависимости от подкоренного числа, вы получите приблизительный или точный ответ. Квадратные числа – числа, из которых можно извлечь целый квадратный корень. Множители – числа, которые при перемножении дают исходное число.[1]
Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как √25 = 5, √36 = 6, √49 = 7. Квадратные множители – это множители, которые являются квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.- Например, вычислите квадратный корень из 400 (вручную). Сначала попытайтесь разложить 400 на квадратные множители. 400 кратно 100, то есть делится на 25 – это квадратное число. Разделив 400 на 25, вы получите 16. Число 16 также является квадратным числом. Таким образом, 400 можно разложить на квадратные множители 25 и 16, то есть 25 х 16 = 400.
- Записать это можно следующим образом: √400 = √(25 х 16).
-
2
Квадратные корень из произведения некоторых членов равен произведению квадратных корней из каждого члена, то есть √(а х b) = √a x √b.[2]
Воспользуйтесь этим правилом и извлеките квадратный корень из каждого квадратного множителя и перемножьте полученные результаты, чтобы найти ответ.- В нашем примере извлеките корень из 25 и из 16.
- √(25 х 16)
- √25 х √16
- 5 х 4 = 20
- В нашем примере извлеките корень из 25 и из 16.
-
3
Если подкоренное число не раскладывается на два квадратных множителя (а так происходит в большинстве случаев), вы не сможете найти точный ответ в виде целого числа. Но вы можете упростить задачу, разложив подкоренное число на квадратный множитель и обыкновенный множитель (число, из которого целый квадратный корень извлечь нельзя). Затем вы извлечете квадратный корень из квадратного множителя и будете извлекать корень из обыкновенного множителя.
- Например, вычислите квадратный корень из числа 147. Число 147 нельзя разложить на два квадратных множителя, но его можно разложить на следующие множители: 49 и 3. Решите задачу следующим образом:
- √147
- = √(49 х 3)
- = √49 х √3
- = 7√3
- Например, вычислите квадратный корень из числа 147. Число 147 нельзя разложить на два квадратных множителя, но его можно разложить на следующие множители: 49 и 3. Решите задачу следующим образом:
-
4
Если нужно, оцените значение корня. Теперь можно оценить значение корня (найти приблизительное значение), сравнив его со значениями корней квадратных чисел, находящихся ближе всего (с обеих сторон на числовой прямой) к подкоренному числу. Вы получите значение корня в виде десятичной дроби, которую необходимо умножить на число, стоящее за знаком корня.
- Вернемся к нашему примеру. Подкоренное число 3. Ближайшими к нему квадратными числами будут числа 1 (√1 = 1) и 4 (√4 = 2). Таким образом, значение √3 расположено между 1 и 2. Та как значение √3, вероятно, ближе к 2, чем к 1, то наша оценка: √3 = 1,7. Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу.
- Этот метод также работает с большими числами. Например, рассмотрим √35. Подкоренное число 35. Ближайшими к нему квадратными числами будут числа 25 (√25 = 5) и 36 (√36 = 6). Таким образом, значение √35 расположено между 5 и 6. Так как значение √35 намного ближе к 6, чем к 5 (потому что 35 всего на 1 меньше 36), то можно заявить, что √35 немного меньше 6. Проверка на калькуляторе дает нам ответ 5,92 – мы были правы.
- Вернемся к нашему примеру. Подкоренное число 3. Ближайшими к нему квадратными числами будут числа 1 (√1 = 1) и 4 (√4 = 2). Таким образом, значение √3 расположено между 1 и 2. Та как значение √3, вероятно, ближе к 2, чем к 1, то наша оценка: √3 = 1,7. Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу.
-
5
Еще один способ – разложите подкоренное число на простые множители. Простые множители – числа, которые делятся только на 1 и самих себя. Запишите простые множители в ряд и найдите пары одинаковых множителей. Такие множители можно вынести за знак корня.
- Например, вычислите квадратный корень из 45. Раскладываем подкоренное число на простые множители: 45 = 9 х 5, а 9 = 3 х 3. Таким образом, √45 = √(3 х 3 х 5). 3 можно вынести за знак корня: √45 = 3√5. Теперь можно оценить √5.
- Рассмотрим другой пример: √88.
- √88
- = √(2 х 44)
- = √ (2 х 4 х 11)
- = √ (2 х 2 х 2 х 11). Вы получили три множителя 2; возьмите пару из них и вынесите за знак корня.
- = 2√(2 х 11) = 2√2 х √11. Теперь можно оценить √2 и √11 и найти приблизительный ответ.
Реклама
При помощи деления в столбик
-
1
Этот метод включает процесс, аналогичный делению в столбик, и дает точный ответ. Сначала проведите вертикальную линию, делящую лист на две половины, а затем справа и немного ниже верхнего края листа к вертикальной линии пририсуйте горизонтальную линию. Теперь разделите подкоренное число на пары чисел, начиная с дробной части после запятой. Так, число 79520789182,47897 записывается как “7 95 20 78 91 82, 47 89 70”.
- Для примера вычислим квадратный корень числа 780,14. Нарисуйте две линии (как показано на рисунке) и слева сверху напишите данное число в виде “7 80, 14”. Это нормально, что первая слева цифра является непарной цифрой. Ответ (корень из данного числа) будете записывать справа сверху.
-
2
Для первой слева пары чисел (или одного числа) найдите наибольшее целое число n, квадрат которого меньше или равен рассматриваемой паре чисел (или одного числа). Другими словами, найдите квадратное число, которое расположено ближе всего к первой слева паре чисел (или одному числу), но меньше ее, и извлеките квадратный корень из этого квадратного числа; вы получите число n. Напишите найденное n сверху справа, а квадрат n запишите снизу справа.
- В нашем случае, первым слева числом будет число 7. Далее, 4 < 7, то есть 22 < 7 и n = 2. Напишите 2 сверху справа – это первая цифра в искомом квадратном корне. Напишите 2×2=4 справа снизу; вам понадобится это число для последующих вычислений.
-
3
Вычтите квадрат числа n, которое вы только что нашли, из первой слева пары чисел (или одного числа). Результат вычисления запишите под вычитаемым (квадратом числа n).
- В нашем примере вычтите 4 из 7 и получите 3.
-
4
Снесите вторую пару чисел и запишите ее около значения, полученного в предыдущем шаге. Затем удвойте число сверху справа и запишите полученный результат снизу справа с добавлением “_×_=”.
- В нашем примере второй парой чисел является “80”. Запишите “80” после 3. Затем, удвоенное число сверху справа дает 4. Запишите “4_×_=” снизу справа.
-
5
Заполните прочерки справа. Найдите такое наибольшее число на место прочерков справа (вместо прочерков нужно подставить одно и тоже число), чтобы результат умножения был меньше или равен текущему числу слева.
- В нашем случае, если вместо прочерков поставить число 8, то 48 х 8 = 384, что больше 380. Поэтому 8 – слишком большое число, а вот 7 подойдет. Напишите 7 вместо прочерков и получите: 47 х 7 = 329. Запишите 7 сверху справа – это вторая цифра в искомом квадратном корне числа 780,14.
-
6
Вычтите полученное число из текущего числа слева. Запишите результат из предыдущего шага под текущим числом слева, найдите разницу и запишите ее под вычитаемым.
- В нашем примере, вычтите 329 из 380, что равно 51.
-
7
Повторите шаг 4. Если сносимой парой чисел является дробная часть исходного числа, то поставьте разделитель (запятую) целой и дробной частей в искомом квадратном корне сверху справа. Слева снесите вниз следующую пару чисел. Удвойте число сверху справа и запишите полученный результат снизу справа с добавлением “_×_=”.
- В нашем примере следующей сносимой парой чисел будет дробная часть числа 780.14, поэтому поставьте разделитель целой и дробной частей в искомом квадратном корне сверху справа. Снесите 14 и запишите снизу слева. Удвоенным числом сверху справа (27) будет 54, поэтому напишите “54_×_=” снизу справа.
-
8
Повторите шаги 5 и 6. Найдите такое наибольшее число на место прочерков справа (вместо прочерков нужно подставить одно и тоже число), чтобы результат умножения был меньше или равен текущему числу слева.
- В нашем примере 549 х 9 = 4941, что меньше текущего числа слева (5114). Напишите 9 сверху справа и вычтите результат умножения из текущего числа слева: 5114 – 4941 = 173.
-
9
Если для квадратного корня вам необходимо найти больше знаков после запятой, напишите пару нулей у текущего числа слева и повторяйте шаги 4, 5 и 6. Повторяйте шаги, до тех пор пока не получите нужную вам точность ответа (число знаков после запятой).
Реклама
Понимание процесса
-
1
Для усвоения данного метода представьте число, квадратный корень которого необходимо найти, как площадь квадрата S. В этом случае вы будете искать длину стороны L такого квадрата. Вычисляем такое значение L, при котором L² = S.
-
2
Задайте букву для каждой цифры в ответе. Обозначим через A первую цифру в значении L (искомый квадратный корень). B будет второй цифрой, C – третьей и так далее.
-
3
Задайте букву для каждой пары первых цифр. Обозначим через Sa первую пару цифр в значении S, через Sb – вторую пару цифр и так далее.
-
4
Уясните связь данного метода с делением в столбик. Как и в операции деления, где каждый раз нас интересует только одна следующая цифра делимого числа, при вычислении квадратного корня мы последовательно работаем с парой цифр (для получения одной следующей цифры в значении квадратного корня).
-
5
Рассмотрим первую пару цифр Sa числа S (Sa = 7 в нашем примере) и найдем ее квадратный корень. В этом случае первой цифрой A искомого значения квадратного корня будет такая цифра, квадрат которой меньше или равен Sa (то есть ищем такое A, при котором выполняется неравенство A² ≤ Sa < (A+1)²). В нашем примере, S1 = 7, и 2² ≤ 7 < 3²; таким образом A = 2.
- Допустим, что нужно разделить 88962 на 7; здесь первый шаг будет аналогичным: рассматриваем первую цифру делимого числа 88962 (8) и подбираем такое наибольшее число, которое при умножении на 7 дает значение меньшее или равное 8. То есть ищем такое число d, при котором верно неравенство: 7×d ≤ 8 < 7×(d+1). В этом случае d будет равно 1.
-
6
Мысленно представьте квадрат, площадь которого вам нужно вычислить. Вы ищите L, то есть длину стороны квадрата, площадь которого равна S. A, B, C – цифры в числе L. Записать можно иначе: 10А + B = L (для двузначного числа) или 100А + 10В + С = L (для трехзначного числа) и так далее.
- Пусть (10A+B)² = L² = S = 100A² + 2×10A×B + B². Запомните, что 10A+B – это такое число, у которого цифра B означает единицы, а цифра A – десятки. Например, если A=1 и B=2, то 10A+B равно числу 12.(10A+B)² – это площадь всего квадрата, 100A² – площадь большого внутреннего квадрата, B² – площадь малого внутреннего квадрата, 10A×B – площадь каждого из двух прямоугольников. Сложив площади описанных фигур, вы найдете площадь исходного квадрата.
-
7
Вычтите A² из Sa. Для учета множителя 100 снесите одну пару цифр (Sb) из S: вам нужно, чтобы “SaSb” было равным общей площади квадрата, и из нее вычтите 100A² (площадь большого квадрата). В результате получите число N1, стоящее слева в шаге 4 (N = 380 в нашем примере). N1 = 2×10A×B + B² (площадь двух прямоугольников плюс площадь малого квадрата).
-
8
Выражение N1 = 2×10A×B + B² можно записать как N1 = (2×10A + B) × B. В нашем примере вам известно значение N1 (=380) и A(=2) и необходимо вычислить B. Скорее всего, B не является целым числом, поэтому необходимо найти наибольшее целое B, удовлетворяющее условию: (2×10A + B) × B ≤ N1. При этом B+1 будет слишком большим, поэтому N1 < (2×10A + (B+1)) × (B+1).
-
9
Решите уравнение. Для решения умножьте A на 2, переведите результат в десятки (что эквивалентно умножению на 10), поместите B в положение единиц, и умножьте это число на B. Это число (2×10A + B) × B и это выражение абсолютно идентичны записи “N_×_=” (где N=2×A) сверху справа в шаге 4. А в шаге 5 вы находите наибольшее целое B, которое ставится на место прочерков и соответствует неравенству: (2×10A + B) × B ≤ N1.
-
10
Вычтите площадь (2×10A + B) × B из общей площади (слева в шаге 6). Так вы получите площадь S-(10A+B)², которая еще не учитывалась (и которая поможет вычислить следующие цифры).
-
11
Для вычисления следующей цифры C повторите процесс. Слева снесите следующую пару цифр (Sc) из S для получения N2 и найдите наибольшее C, удовлетворяющее условию (2×10×(10A+B)+C) × C ≤ N2 (что эквивалентно двукратному написанию числа из пары цифр “A B” с соответствующим “_×_=”, и нахождению наибольшего числа, которое можно подставить вместо прочерков).
Реклама
Советы
- Перемещение десятичного разделителя при увеличении числа на 2 цифры (множитель 100), перемещает десятичный разделить на одну цифру в значении квадратного корня этого числа (множитель 10).
- В нашем примере, 1,73 может считаться остатком: 780,14 = 27,9² + 1,73.
- Данный метод верен для любых чисел.
- Записывайте процесс вычисления в том виде, который вам наиболее удобен. Например, некоторые записывают результат над исходным числом.
- Альтернативный метод с использованием непрерывных дробей включает формулу: √z = √(x^2+y) = x + y/(2x + y/(2x + y/(2x + …))). Например, для вычисления квадратного корня из 780,14, целым числом, квадрат которого близок к 780,14 будет число 28, поэтому z=780,14, x=28, y=-3,86. Подставляя эти значения в уравнение и решая его в упрощении до х+у/(2x), уже в младших членах получаем результат 78207/2800 или около 27,931(1), а в следующих членах 4374188/156607 или около 27,930986(5). Решение каждого последующего члена добавляет около 3 цифр к дробной доли по сравнению с предыдущем членом.
Реклама
Предупреждения
- Не забудьте разделить число на пары, начиная с дробной части числа. Например, разделяя 79520789182,47897 как “79 52 07 89 18 2,4 78 97″, вы получите бессмысленное число.
Реклама
Похожие статьи
Источники
Об этой статье
Эту страницу просматривали 926 223 раза.
Была ли эта статья полезной?
В уроке «Степень числа»
мы проходили, что возвести в квадрат число означает умножить число на само себя.
Кратко запись числа в квадрате выглядит следующим образом:
3 · 3 = 32 = 9
Но как быть, если нам нужно получить обратный результат?
Например, узнать, какое число при возведении в квадрат дало бы число «9»?
Запомните!
Нахождение исходного числа, которое в квадрате дало бы требуемое, называется
извлечением квадратного корня.
Извлечение квадратного корня — это действие, обратное возведению в квадрат.
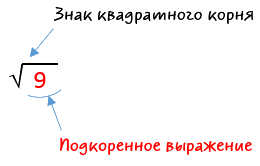
У квадратного корня есть специальный знак.
Исходя из вычислений выше, нетрудно догадаться, что число, которое в квадрате дает «9»,
это число «3». Запись извлечения квадратного корня из числа «9» выглядит так:
√9 = 3
Читаем запись: «Арифметический квадратный корень из девяти». Можно опустить слово «арифметический».
Словосочетания «арифметический квадратный корень» и «квадратный корень» полностью равнозначны.
Число под знаком корня называют подкоренным выражением.
Подкоренное выражение может быть представлено не только одним числом.
Всё, что находится под знаком корня, называют подкоренным выражением. Оно может сожержать как числа, так и буквы.
Запомните!
Извлекать квадратный корень можно только из положительного числа.
-
√−9
= … нельзя извлекать квадратный корень из отрицательного числа; -
√64 = 8
-
√−1,44
= … нельзя извлекать квадратный корень из отрицательного числа; -
√256 = 16
Квадратный корень из нуля
Запомните!
Квадратный корень из нуля равен нулю.
√0 = 0
Квадратный корень из единицы
Запомните!
Квадратный корень из единицы равен единице.
√1 = 1
Как найти квадратный корень из числа
Квадратные корни из целых чисел, чьи квадраты известны, вычислить довольно просто.
Для этого достаточно выучить таблицу квадратов.
Чаще всего в задачах школьного курса математики требуется найти квадратный корень из квадратов чисел от
1 до 20.
Решение примеров с квадратными корнями
Разбор примера
Вычислить арифметический квадратный корень из числа.
- √81 = 9
- √64 = 8
- √100 = 10
Как найти квадратный корень из десятичной дроби
Важно!
При нахождении квадратного корня из десятичной дроби нужно выполнить следующие действия:
- забыть про запятую в исходной десятичной дроби и представить её в виде целого числа;
- вычислить для целого числа квадратный корень;
- полученное целое число заменить на десятичную дробь (поставить запятую исходя из
правила умножения десятичных дробей).
Более подробно разберем на примере ниже.
Разбор примера
Вычислить квадратный корень из десятичной дроби «0,16».
√0,16 =
По первому пункту правила забудем про запятую в десятичной дроби и представим ее в виде целого числа «16».
Нетрудно вспомнить, какое число в квадрате дает «16». Это число
«4».
√16 = 4
√0,16 = …
Вспомним правило умножения десятичных дробей.
Количество знаков после запятой в результате умножения десятичных дробей равняется сумме количества знаков после запятой каждой
дроби.
Т.е., например, при умножении «0,15» на
«0,3» в полученном произведении будет десятичная дробь с тремя знаками после запятой.
0,15 · 0,3 = 0,045
Значит, при вычислении квадратного корня
√0,16
нам нужно найти десятичную дробь, у которой был бы только один знак после запятой.
Мы исходим из того, что в результате умножения десятичной дроби на саму себя в результате должно было получиться
два знака после запятой, как у десятичной дроби «0,16».
Получается, что ответ — десятичная дробь «0,4».
√0,16 = 0,4
Убедимся, что квадрат десятичной дроби
«0,42» дает
«0,16».
Умножим в столбик «0,4» на
«0,4».
Рассмотрим другой пример вычисления квадратного корня из десятичной дроби. Вычислить:
√1,44 =
Представим вместо десятичной дроби «1,44» целое число
«144». Какое число в квадрате даст «144»?
Ответ — число «12».
122 = 144
√144 = 12
√1,44 = …
Так как в десятичной дроби «1,44» — два знака после запятой, значит в десятичной дроби,
которая дала в квадрате «1,44» должен быть один знак после запятой.
√1,44 = 1,2
Убедимся, что «1,22» дает в квадрате «1,44».
1,22 = 1,2 · 1,2 = 1,44
Квадратные корни из чисел
√2,
√3,
√5,
√6,
и т.п.
Не из всех чисел удается легко извлечь квадратный корень. Например, совершенно неочевидно, чему равен
√2
или
√3
и т.п.
В самом деле, какое число в квадрате даст «2»? Или число «3»?
Такое число не будет целым. Более того, оно представляет из себя
непериодическую десятичную дробь
и входит в
множество иррациональных чисел.
Что делать, когда в ответе остаются подобные квадратные корни? Как, например, в примере ниже:
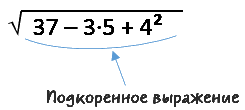
√15 − 2 · 4 =
√15 − 8 =
√7
Нет такого целого числа, которое бы дало в квадрате число «7».
Поэтому, перед завершением задачи внимательно читайте её условие.
Если в задаче дополнительно ничего не сказано об обязательном вычислении всех квадратных корней, тогда ответ можно
оставить с корнем.
√15 − 2 · 4 =
√15 − 8 =
√7
Если в задании сказано, что необходимо вычислить все квадратные корни с помощью микрокалькулятора,
то после вычисления квадратного корня на калькуляторе
округлите результат до необходимого количества знаков.
Текст задания в таком случае может быть написан следующим образом:
«Вычислить. Квадратные корни найти с помощью калькулятора и округлить с точностью до
«0,001».
√15 − 2 · 4 =
√15 − 8 =
√7 ≈ 2,646
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».
Оставить комментарий:
14 июля 2016 в 18:32
Temur Uldashev
Профиль
Благодарили: 0
Сообщений: 2
Temur Uldashev
Профиль
Благодарили: 0
Сообщений: 2
Всем доброго времени суток! Прошу помочь с примером который я не могу решить, по теме «Квадратные корни. Задачи на вычесление» пример выглядит так:
??28-16?3 ( то есть выражение 28-16?3 еще под двумя корнями, не только 28, а все выражение!)
0
Спасибо
Ответить
15 июля 2016 в 0:04
Ответ для Temur Uldashev
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
?(28 ? 16?3) = 4 ? 2?3.
Скобки не знешь?
0
Спасибо
Ответить
15 июля 2016 в 6:53
Ответ для Temur Uldashev
Temur Uldashev
Профиль
Благодарили: 0
Сообщений: 2
Temur Uldashev
Профиль
Благодарили: 0
Сообщений: 2
Затупил. Но и вы не правильно подсказали. Я уже решил ответ ?3-1
0
Спасибо
Ответить
16 июля 2016 в 22:58
Ответ для Temur Uldashev
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Чушь не пори.
Спасибо скажи, что тебе подсказали.
0
Спасибо
Ответить
21 июля 2016 в 13:24
Ответ для Temur Uldashev
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Что не верно у меня, митрофанушка?
0
Спасибо
Ответить
23 ноября 2015 в 15:15
Ксюша Новикова
Профиль
Благодарили: 0
Сообщений: 1
Ксюша Новикова
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
16 сентября 2016 в 14:23
Ответ для Ксюша Новикова
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
1,38 · ?361 = 1,38 · 19 = 26,22
0
Спасибо
Ответить
16 сентября 2015 в 16:11
Макс Простов
Профиль
Благодарили: 0
Сообщений: 4
Макс Простов
Профиль
Благодарили: 0
Сообщений: 4
Расположите в порядке возрастания Корни:3V16, 7V19, 8V13 срочно)))))
0
Спасибо
Ответить
9 сентября 2016 в 9:41
Ответ для Макс Простов
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
?16 = 4
?19 ? 4,35
?13 ? 3,61
3 · 4 = 12
7 · 4,35 = 30,45
8 · 3,61 = 28,88
Ответ: 3?16, 8?13, 7?19
0
Спасибо
Ответить
Из этой статьи вы узнаете:
- что такое «извлечение корня»;
- в каких случаях он извлекается;
- принципы нахождения значения корня;
- основные способы извлечения корня из натуральных и дробных чисел.
Что такое «извлечение корня»
Для начала введем определение «извлечение корня».
Извлечение корня — процесс нахождения значения корня.
При извлечении корня n-ной степени из числа a, мы находим число b, n-ная степень которого равняется a. Если мы нашли такое число b, можно утверждать, что корень извлечен.
Выражения «извлечение корня» и «нахождение значения корня» равнозначны.
В каких случаях извлекается корень?
Корень n-ной степени можно извлечь из числа a точно в случае, если a можно представить в виде n-ной степени некоторого числа b.
4=2×2, следовательно, из числа 4 можно точно извлечь квадратный корень, который равен 2
Когда корень n-ной степени из числа a невозможно представить в виде n-ной степени числа b, то такой корень не извлекается, либо извлекается только приближенное значение корня с точностью до любого десятичного разряда.
2≈1,4142.
Принципы нахождения значения корня и способы их извлечения
- Использование таблицы квадратов, таблицы кубов и т.д.
- Разложение подкоренного выражения (числа) на простые множители
- Извлечение корней из дробных чисел
- Извлечение корня из отрицательного числа
- Поразрядное нахождение значения корня
Необходимо понять, по каким принципам находится значение корней, и каким образом они извлекаются.
Главный принцип нахождения значения корней — основываться на свойствах корней, в том числе на равенстве: bnn=b, которое является справедливым для любого неотрицательного числа b.
Начать следует с наиболее простого и очевидного способа: таблицы квадратов, кубов и т.д.
Когда таблицы под руками нет, вам поможет способ разложения подкоренного числа на простые множители (способ незатейливый).
Стоит уделить внимание извлечению корня из отрицательного числа, что является возможным для корней с нечетными показателями.
Изучим, как извлекать корни из дробных чисел, в том числе из смешанных чисел, обыкновенных и десятичных дробей.
И потихоньку рассмотрим способ поразрядного нахождения значения корня — наиболее сложного и многоступенчатого.
Использование таблицы квадратов, кубов и т.д.
Таблица квадратов включает в себя все числа от 0 до 99 и состоит из 2 зон: в первой зоне можно составить любое число до 99 с помощью вертикального столбца с десятками и горизонтальной строки с единицами, во второй зоне содержатся все квадраты образуемых чисел.
Таблица квадратов
| Таблица квадратов | единицы | ||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| десятки | 0 | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 |
| 1 | 100 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 | |
| 2 | 400 | 441 | 484 | 529 | 576 | 625 | 676 | 729 | 784 | 841 | |
| 3 | 900 | 961 | 1024 | 1089 | 1156 | 1225 | 1296 | 1369 | 1444 | 1521 | |
| 4 | 1600 | 1681 | 1764 | 1849 | 1936 | 2025 | 2116 | 2209 | 2304 | 2041 | |
| 5 | 2500 | 2601 | 2704 | 2809 | 2916 | 3025 | 3136 | 3249 | 3364 | 3481 | |
| 6 | 3600 | 3721 | 3844 | 3969 | 4096 | 4225 | 4356 | 4489 | 4624 | 4761 | |
| 7 | 4900 | 5041 | 5184 | 5329 | 5476 | 5625 | 5776 | 5929 | 6084 | 6241 | |
| 8 | 6400 | 6561 | 6724 | 6889 | 7056 | 7225 | 7396 | 7569 | 7744 | 7921 | |
| 9 | 8100 | 8281 | 8464 | 8649 | 8836 | 9025 | 9216 | 9409 | 9604 | 9801 |
Существуют также таблицы кубов, четвертой степени и т.д., которые созданы по принципу, аналогичному таблице квадратов.
Таблица кубов
| Таблица кубов | единицы | ||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| десятки | 0 | 0 | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 |
| 1 | 1000 | 1 331 | 1 728 | 2 197 | 2 744 | 3 375 | 4 096 | 4 913 | 5 832 | 6 859 | |
| 2 | 8000 | 9 261 | 10 648 | 12 167 | 13 824 | 15 625 | 17 576 | 19 683 | 21 952 | 24 389 | |
| 3 | 27000 | 29 791 | 32 768 | 35 937 | 39 304 | 42 875 | 46 656 | 50 653 | 54 872 | 59 319 | |
| 4 | 64000 | 68 921 | 74 088 | 79 507 | 85 184 | 91 125 | 97 336 | 103 823 | 110 592 | 117 649 | |
| 5 | 125000 | 132 651 | 140 608 | 148 877 | 157 464 | 166 375 | 175 616 | 185 193 | 195 112 | 205 379 | |
| 6 | 216000 | 226 981 | 238 328 | 250 047 | 262 144 | 274 625 | 287 496 | 300 763 | 314 432 | 328 509 | |
| 7 | 343000 | 357 911 | 373 248 | 389 017 | 405 224 | 421 875 | 438 976 | 456 533 | 474 552 | 493 039 | |
| 8 | 512000 | 531 441 | 551 368 | 571 787 | 592 704 | 614 125 | 636 056 | 658 503 | 681 472 | 704 969 | |
| 729000 | 753 571 | 778 688 | 804 357 | 830 584 | 857 375 | 884 736 | 912 673 | 941 192 | 970 299 |
Принцип функционирования таких таблиц прост, однако их часто нет под рукой, что значительно усложняет процесс извлечение корня, поэтому необходимо владеть минимум несколькими способами извлечения корней.
Разложение подкоренного числа на простые множители
Наиболее удобный способ нахождения значения корня после таблицы квадратов и кубов.
Способ разложения подкоренного числа на простые множители подразумевает под собой представление числа в виде степени с необходимым показателем, что дает нам возможность получить значение корня.
Извлечем квадратный корень из 144.
Разложим 144 на простые множители:
Таким образом: 144=2×2×2×2×3×3=(2×2)2×32=(2×2×3)2=122. Следовательно, 144=122=12.
Также при использовании свойств степени и корней можно записать преобразование немного по-другому:
144=2×2×2×2×3×3=24×32=24×32=22×3=12
144=12 – окончательный ответ.
Извлечение корней из дробных чисел
Запоминаем: любое дробное число должно быть записано в виде обыкновенной дроби.
Следуя свойству корня из частного, справедливым является следующее равенство:
pqn=pnqn. Исходя из этого равенства, необходимо воспользоваться правилом извлечения корня из дроби: корень из дроби равен от деления корня числителя на корень знаменателя.
Рассмотрим пример извлечения корня из десятичной дроби, поскольку извлечь корень из обыкновенной дроби можно с помощью таблицы.
Необходимо извлечь кубический корень из 474,552. Первым делом, представим десятичную дробь в виде обыкновенной: 474,552 = 474552/1000. Из этого следует: 47455210003=474552310003. Затем можно приступить к процессу извлечения кубических корней в числителе и знаменателе:
474552=2×2×2×3×3×3×13×13×13=(2×3×13)3=783 и 1000=103, то
4745523=7833=78 и 10003=1033=10.
Завершаем вычисления: 474552310003=7810=7,8.
Извлечение корня из отрицательных чисел
Если знаменатель является нечетным числом, то число под знаком корня может оказаться отрицательным. Из этого следует: для отрицательного числа -a и нечетного показателя корня 2n-1 справедливо равенство:
-a2×n-1=-a2×n-1
Правило извлечения нечетной степени из отрицательных чисел: чтобы извлечь корень из отрицательного числа необходимо извлечь корень из противоположного ему положительного числа и поставить перед ним знак минус.
-122092435. Для начала необходимо преобразовать выражение, чтобы под знаком корня оказалось положительно число:
-122092435=12209243-5
Затем следует заменить смешанное число обыкновенной дробью:
12209243-5=3125243-5
Пользуясь правилом извлечения корней из обыкновенной дроби, извлекаем:
3125243-5=-312552435
Вычисляем корни в числителе и знаменателе:
-312552435=-555355=-53=-123
Краткая запись решения:
-122092435=12209243-5=3125243-5=-312552435=-555355=-53=-123.
Ответ: -122092435=-123.
Поразрядное нахождение значения корня
Бывают случаи, когда под корнем находится число, которое не получается представить в виде n-ной степени некоторого числа. Но необходимо знать значение корня с точностью до некоторого знака.
В таком случае необходимо воспользоваться алгоритмом поразрядного нахождения значения корня, с помощью которого можно получить достаточное количество значений искомого числа.
Как это происходит, разберем на примере извлечения квадратного корня из 5.
Сперва необходимо найти значение разряда единиц. Для этого начнем перебирать значения 0,1,2,…,9, вычисляя при этом 02, 12, …, 92 до необходимого значения, которое больше, чем подкоренное число 5. Все это удобно представить в виде таблицы:
| Возможное значение корня | 0 | 1 | 2 | 3 |
| Это значение в степени | 0 | 1 | 4 | 9 |
Значение ряда единиц равняется 2 (так как 22<5, а 23>5). Переходим в разряду десятых — будем возводить в квадрат числа 2,0, 2,1, 2,2,…,2,9, , сравнивая полученные значения с числом 5.
| Возможное значение корня | 2,0 | 2,1 | 2,2 | 2,3 |
| Это значение в степени | 4 | 4,41 | 4,84 | 5,29 |
Поскольку 2,22<5, а 2,32>5, то значение десятых равняется 2. Переходим к нахождению значения сотых:
| Возможное значение корня | 2.20 | 2,21 | 2,22 | 2,23 | 2,24 |
| Это значение в степени | 4,84 | 4,8841 | 4,8294 | 4,9729 | 5,0176 |
Таким образом, найдено значение корня из пяти — 2,23. Можно находить значения корня дальше:
2,236, 2,2360, 2, 23606, 2,236067,…
Итак, мы изучили несколько наиболее распространенных способов нахождения значения корня, воспользоваться которыми можно в любой ситуации.
Как решать примеры с корнями?
У арифметического квадратного корня есть 3 свойства — их нужно запомнить, чтобы проще решать примеры.
- Корень произведения равен произведению корней
- Извлечь корень из дроби — это извлечь корень из числителя и из знаменателя
- Чтобы возвести корень в степень, нужно возвести в степень значение под корнем
17 дек. 2020 г.
Как просто вычислить квадратный корень?
Разложите подкоренное число на множители, которые являются квадратными числами.
- Например, вычислите квадратный корень из 400 (вручную). Сначала попытайтесь разложить 400 на квадратные множители. 400 кратно 100, то есть делится на 25 – это квадратное число. …
- Записать это можно следующим образом: √400 = √(25 х 16).
Как примерно посчитать корень?
Квадратные корень из произведения некоторых членов равен произведению квадратных корней из каждого члена, то есть √(а х b) = √a x √b. Воспользуйтесь этим правилом и извлеките квадратный корень из каждого квадратного множителя и перемножьте полученные результаты, чтобы найти ответ.
Что значит корни?
radix) — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Как перемножить два одинаковых корня?
Правило умножения . Чтобы умножить один квадратный корень на другой, нужно просто перемножить их подкоренные выражения, а результат записать под общим радикалом: Никаких дополнительных ограничений на числа, стоящие справа или слева, не накладывается: если корни-множители существуют, то и произведение тоже существует.
Сколько будет корень из 169?
Записываем 169 как 132 .
Как извлечь корень из любого числа?
Чтобы извлечь квадратный корень из целого числа, воспользуйтесь делением в столбик. Для этого разделите целое число (делимое) на некоторое число (делитель) так, чтобы результат (частное) совпал с делителем. Например: 16 делить на 4 равно 4; 4 делить на 2 равно 2 и так далее.
Как найти корень с помощью калькулятора?
как на калькуляторе посчитать квадратный корень.. . Если калькулятор «домашний», то вводим число из которого извлечь, затем нажимаем значок корня. Если компьютерный (виндовский) , то там вместо значка корня 4 буквы: Эс_Ку_Ар_Ти. Также можно возвести в степень 1/2 — то же самое.
Как быстро найти корень из числа?
Ответ очевиден: возвести оба числа в квадрат. То, которое в квадрате даст исходное число, и будет корнем. Например, для числа 3364 мы нашли два числа-кандидата: 52 и 58.
Как извлечь корень из 64?
Что такое КОРЕНЬ КУБИЧЕСКИЙ? КОРЕНЬ КУБИЧЕСКИЙ (обозначение 3Ц), число, которое необходимо дважды умножить на само себя для получения заданного числа. Например, кубический корень из 64 равняется 4, поскольку 4x4x4 = 64.
Что такое часть речи корень?
Ко́рень — морфема, несущая лексическое значение слова (или основную часть этого значения); в русском языке корень имеется во всех самостоятельных частях речи и отсутствует во многих служебных частях речи, междометиях и звукоподражательных словах (например, его нет в союзе «и», междометии «ах» и подобных лексических …
Что такое корень слова 3 класс правило?
О.: Корень – это общая часть однокоренных слов, в которой передается их основное значение.
Как умножать корни с одинаковыми основаниями?
Умножение корней с одинаковыми основаниями осуществляется согласно теореме о том, что корень из произведения двух неотрицательных чисел равен произведению квадратных чисел. Это правило применимо как для умножения квадратных корней, так и для перемножения корней с любыми другими одинаковыми основаниями (показателями).
Можно ли умножать корень на корень?
можно ли умножать корень на корень? ЕСЛИ КОРНИ ОДИНАКОВОЙ СТЕПЕНИ, ТО ПЕРЕМНОЖАЮТСЯ ПОДКОРЕННЫЕ ВЫРАЖЕНИЯ, РЕЗУЛЬТАТ ПОД КОРНЕМ ТОЙ ЖЕ СТЕПЕНИ ЕСЛИ КОРНИ РАЗНОЙ СТЕПЕНИ, НО ОДИНАКОВЫЕ ПОДКОРЕННЫЕ ВЫРАЖЕНИЯ, ТО СКЛАДЫВАЮТСЯ СТЕПЕНИ КОРНЕЙ, А ПОДКОРЕННЫЕ ОСТАЮТСЯ ТЕ ЖЕ.
Чему равен √ 1?
Любой корень из 1 равен 1 . Упростим знаменатель.
Чему равняется квадратный корень из 196?
Записываем 196 как 142 .
Как быстро находить корень из числа?
Ответ очевиден: возвести оба числа в квадрат. То, которое в квадрате даст исходное число, и будет корнем. Например, для числа 3364 мы нашли два числа-кандидата: 52 и 58.
Открытый урок по математике на тему “Корень. Решение уравнений”.
план-конспект урока по математике (4 класс) на тему
Открытый урок по математике в 4 классе по теме “Корень. Решение уравнений”. Конспект урока, презинтация, индивидуальные карточки, дополнительные задания, домашнее задание.
Скачать:
| Вложение | Размер |
|---|---|
| otkrytyy_urok_4_kl.docx | 426.01 КБ |
| dopolnitelnye_zadaniya_4_kl.docx | 13.17 КБ |
| kartochka_4_kl.docx | 55.77 КБ |
| domashnee_zadanie_4_kl.docx | 20.02 КБ |
| prezentatsiya_4_kl.pptx | 628.17 КБ |
Предварительный просмотр:
по теме « Корень. Решение составных уравнений»
Учитель первой квалификационной категории
19 марта 2014 года.
Тема урока: Корень. Решение составных уравнений.
Тип урока: усвоение новых знаний.
Познакомить с составными уравнениями, сводящимися к цепочке простых, и построить алгоритм их решения.
Формировать на автоматизированном уровне способность к нахождению неизвестных компонентов действий и умение комментировать выполняемые операции, называя компоненты действий.
Отрабатывать навыки устных и письменных вычислений, повторить и закрепить понятия порядка действий в выражениях, решать задачи, содержащие переменную.
Способствовать развитию грамотной математической речи, способности к выражению в речи действий по алгоритмам.
Развивать навыки самоконтроля
формировать умения решать сложные уравнения, где неизвестное выражено суммой или разностью чисел;
развивать логическое мышление и умение анализировать;
воспитывать коллективизм, взаимопомощь.
Личностные: создание педагогических условий для формирования у обучающихся положительной мотивации к учению, умения преодолевать посильные трудности, чувства коллективизма, взаимовыручки и уважения друг к другу, умения вести диалог, аккуратности.
Регулятивные: формирование умения ставить цели и задачи, планировать и контролировать деятельность, умения классифицировать объекты, создавать, применять и преобразовывать модели, повышать алгоритмическую культуру обучающихся, развивать логическое мышление, познавательную активность и навыки научной речи.
Предметные: формирование умения построения математической модели, решения уравнений, содержащих одно или более одного арифметического действия и задач с помощью уравнений.
Познавательныее: закрепляют навыки и умения применять алгоритм при решении уравнений; систематизируют знания, обобщают и углубляют знания при решении задач на движение
Коммуникативные: умение слушать и вступать в диалог; воспитывать чувство взаимопомощи, уважительное отношение к чужому мнению, требовательное отношение к себе и своей работе
Методы обучения : наглядный, словесный, практический, частично-поисковый, репродуктивный.
Основные этапы урока:
– этап включения учащихся в активную деятельность;
– актуализация опорных знаний, умений и навыков;
– этап закрепления, первичной проверки и коррекции изученного материала;
– этап информации о домашнем задании и инструктаж по его выполнению;
I. Организационный этап
Долгожданный дан звонок –
Ум и сердце в работу вложи,
Каждой секундой в труде дорожи.
– Кто хочет поделиться своим хорошим настроением?
У кого оно такое же? Замечательно! Значит, на уроке у нас всё получится!
II Этап включения учащихся в активную деятельность разминка – устный счёт – на все действия с натуральными числами, проверка теоретического и практического материала при решении уравнений с помощью компонентов
– Цель устного счёта?
28 – И.С. Тургенев
– Что связывает эти фамилии?
– С кем из них на уроке мы встретимся? Почему?
Актуализация опорных знаний СЛАЙД № 2
D + 64 = 92 500 – b = 150 640 : D = 80 (Х + 29) – 48 = 90
Z – 70 = 210 Z : 30 = 600 Z х 2 = 260
Давайте вспомним, что мы знаем об уравнениях.
– Что такое уравнение? (Это математическое равенство с одной или несколькими неизвестными величинами)
– Что значит решить уравнение? (Найти корень)
– Что такое корень уравнения? (Это искомое число, при подстановке которого в уравнение получается верное равенство)
Вспомним название компонентов (ответы)
– Все ли уравнения записанные на доске, одинаковые по сложности? (нет)
– На какие группы можно разделить уравнения? (простые и сложные)
-Как отличить простое уравнение от сложного? (в простом уравнении выполняется одно действие, а в сложном – несколько)
– Какие уравнения уже умеете решать? (простые)
– Вспомним алгоритм решения простых уравнений
– Определить неизвестный компонент действий;
– применить правило его нахождения;
– выполнить действие и получить ответ;
– Решите одно уравнение по выбору, а сосед по парте проверит (работа в парах)
Когда уравненье решаешь дружок,
Ты должен найти у него корешок
Значение буквы проверить не сложно,
Поставь в уравненье его осторожно.
Коль верное равенство выйдет у вас,
То корнем значенье зовите тот час.
– Какие уравнения вы не умеете решать? (составные)
– Какую учебную задачу поставим перед собой на уроке? (научиться решать составные уравнения
III. Постановка учебной задачи
– На какой вопрос предстоит ответить? (как решать сложные уравнения)
– Какова тема урока?
IV «Открытие» учащимися нового знания.
– Давайте решим сложное уравнение
(Х + 29) – 48 = 90 (нужен алгоритм решения этого уравнения)
– Какие есть предположения, как решать это уравнение?
Составление плана решения уравнения:
1. Расставим порядок действий. Если бы это был пример, с чего бы вы начали его решение?
2. Установим название компонентов по последнему действию. Где находится неизвестное число?
3. Вырази чему равен неизвестный компонент?
Х + 29 = 90 + 48 – такое уравнение мы умеем решать?
Х + 29 = 138 – получили простое уравнение.
(109 + 29) – 48 = 90
Повторим алгоритм решения уравнений:
1. Расстановка порядка действий.
2. Установление названия компонентов по последнему действию.
3. Вспомнить правило нахождение неизвестного компонента.
4. Найти корень уравнения.
4. Сделать проверку (порядок действий).
V. Первичное закрепление (у доски с проговариванием)
140 – (75 + 25) = 40
– Работа с индивидуальными карточками (У детей на столах)
VI. Самостоятельная работа с самопроверкой по эталону
Учебник стр. 93, № 304
VII. Динамическая пауза
Цель: смена вида деятельности
«Мозговая гимнастика» (комплекс упражнений, направленный на улучшение мозговой деятельности).
1. «Качания головой». Упражнение стимулирует мыслительные процессы.
У. — Встали, поставили ноги на ширину плеч. Расправим плечи. Дышим глубоко. Вдох-выдох. Голову уроните вперед, позвольте голове медленно качаться из стороны в сторону, пока при помощи дыхания уходит напряжение. Подбородок вычерчивает слегка изогнутую линию на груди по мере расслабления шеи. (30 секунд).
2. «Ленивые восьмёрки». Упражнение активизирует структуры мозга, обеспечивающие запоминание, повышает устойчивость внимания.
У. — Вытянутой правой рукой нарисовать в воздухе в горизонтальной плоскости восьмерки (три раза). Затем левой рукой, а потом обеими руками вместе (руки в замке).
3. «Шапка для размышлений». Улучшает внимание, ясность восприятия и речь.
У. — «Наденьте шапку», т.е. мягко заверните уши от верхней точки до мочки (три раза).
VIII. Включение нового знания в систему знаний . СЛАЙД № 4
– М.Ю.Лермонтова с нашим краем связывало Кропотово.
К югу от Ефремова, в пяти километрах от с. Шипова, расположен поселок Кропотово – Лермонтово Становлянский район Липецкой области, ранее это было с. Любашовка (Каменный Верх)Тульской губернии. Здесь, на левом берегу Любашовки, находились дом и усадьба капитана в отставке Юрия Петровича Лермонтова, отца великого русского поэта. Хоть и немного прожил в Кропотове Михаил Юрьевич, но оно оставило свой след в его душе. Сейчас этот дом не сохранился. Осталась лишь церковь в Шипово. Весной мы совершим поход в это историческое место.
Задача № 1 От Кропотово до Москвы 370 км. От Лобаново до Москвы 362 км. Найдите расстояние от Лобаново до Кроптово. Эта задача для решения её устно, но мы попробуем решить её с помощью уравнения.
Задача №2 (УСТНО) От Лобаново до Кропотого 8 км. Сколько нам потребуется времени, чтобы дойти до Кроптого, если будем идти со скоростью 4 км/ч
– Отправляясь в поход нужно брать с собой продукты.
– Составьте и решите уравнения по рисунку.
(3 х Х) + 5 = 1 + 5 + 5 Х + 2 = 10 + 6
Самоанализ работы учащихся по вопросам: какова цель нашего урока?
— Какие шаги мы делали для достижения поставленной цели?
Д.: — Решали сложные уравнения, используя свойства равенств и взаимосвязь между компонентами действий; решили задачу на движение с помощью уравнения.
– На каком этапе урока вам было легко работать, а когда вы испытывали трудности и какие?
Что такое уравнение и корни уравнения? Как решить уравнение?
Уравнения бывают разные. Вы изучите их многие виды в курсе математике, но все они решаются по одним правилам, эти правила мы сейчас рассмотрим подробно.
Что такое уравнение? Смысл и понятия.
Узнаем сначала все понятия, связанные с уравнением.
Определение:
Уравнение – это равенство, содержащее переменные и числовые значения.
Переменные (аргументы уравнения) или неизвестные уравнения – их обозначают в основном латинскими буквами (x, y, z, f и т.д.). При подстановки числового значения переменной в уравнение получаем верное равенство – это корень уравнения.
Решить уравнение – это значит найти все корни уравнения или доказать, что у данного уравнения нет корней.
Корни уравнения – это значение переменной при котором уравнение превращается в верное равенство.
Рассмотрим теперь, все термины на простом примере:
x+1=3
В данном случае x – переменная или неизвестное значение уравнения.
Можно устно решить данное уравнение. Какое надо число прибавить к 1, чтобы получить 3? Конечно, число 2. То есть наша переменная x =2. Корень уравнения равен 2. Проверим правильно ли мы решили уравнение? Чтобы проверить уравнение, нужно вместо переменной подставить полученный корень уравнения.
Получили верное равенство. Значит, правильно нашли корни уравнения.
Но бывают более сложные уравнения, которые устно не решить. Нужно прибегать к правилам решения уравнений. Рассмотрим правила решения уравнений ниже, которые объяснят нам как решать уравнения.
Правила уменьшения или увеличения уравнения на определенное число.
Чтобы понять правило рассмотрим подробно простой пример:
Решите уравнение x+2=7
Решение:
Чтобы решить данное уравнение нужно левую и правую часть уменьшить на 2. Это нужно сделать для того, чтобы переменная x осталась слева, а известные (т.е. числа) справа. Что значит уменьшить на 2? Это значит отнять от левой части двойку и одновременно от правой части отнять двойку. Если мы делаем какое-то действие, например, вычитание применяя его одновременно к левой части уравнения и к правой, то уравнение не меняет смысл.
Нужно остановиться на этом моменте подробно. Другими словами, мы +2 перенесли с левой части на правую и знак поменяли стало число -2.
Как проверить правильно ли вы нашли корень уравнения? Ведь не все уравнения будут простыми как данное. Чтобы проверить корень уравнения его значение нужно поставить в само уравнение.
Проверка:
Вместо переменной x подставим 5.
x+2=7
5+2=7
Получили верное равенство, значит уравнение решено верно.
Ответ: 5.
Разберем следующий пример:
Решите уравнение x-4=12.
Решение:
Чтобы решить данное уравнение нужно увеличить левую и правую часть уравнения на 4, чтобы переменная x осталось в левой стороне, а известные (т.е. числа) в правой стороне. Прибавим к левой и правой части число 4. Получим:
Другими словами, мы -4 перенесли из левой части уравнения в правую и получили +4. При переносе через равно знаки меняются на противоположные.
Теперь выполним проверку, вместо переменной x подставим в уравнение полученное число 16.
x-4=12
16-4=12
Ответ: 16
Очень важно понять правила переноса частей уравнения через знак равно. Не всегда нужно переносить числа, иногда нужно перенести переменные или даже целые выражения.
Рассмотрим пример:
Решите уравнение 4+3x=2x-5
Решение:
Чтобы решить уравнение необходимо неизвестные перенести в одну сторону, а известные в другую. То есть переменные с x будут в левой части, а числа в правой части.
Сначала перенесем 2x с правой стороны в левую сторону уравнения и получим -2x.
4+3x= 2x -5
4+3x -2x =-5
Далее 4 с левой стороны уравнения перенесем на правую сторону и получим -4
4 +3x-2x=-5
3x-2x=-5 -4
Теперь, когда все неизвестные в левой стороне, а все известные в правой стороне посчитаем их.
(3-2)x=-9
1x=-9 или x=-9
Сделаем проверку, правильно ли решено уравнение? Для этого вместо переменной x в уравнение подставим -9.
4+3x=2x-5
4+3⋅ (-9) =2⋅ (-9) -5
4-27=-18-5
-23=-23
Получилось верное равенство, уравнение решено верно.
Ответ: корень уравнения x=-9.
Правила уменьшения или увеличения уравнения в несколько раз.
Данное правило подходит тогда, когда вы уже посчитали все неизвестные и известные, но какой-то коэффициент остался перед переменной. Чтобы избавится от не нужного коэффициента мы применяем правило уменьшения или увеличения в несколько раз коэффициент уравнения.
Рассмотрим пример:
Решите уравнение 5x=20.
Решение:
В данном уравнение не нужно переносить переменные и числа, все компоненты уравнения стоят на месте. Но нам мешает коэффициент 5 который стоит перед переменной x. Мы не можем его просто взять и перенести в правую сторону уравнения, потому что между число 5 и переменно x стоит умножение 5⋅х. Если бы между переменной и числом стоял знак плюс или минус, мы могли бы 5 перенести вправо. Но мы так поступить не можем. За то мы можем все уравнение уменьшить в 5 раз или поделить на 5. Обязательно делим правую и левую сторону одновременно.
5x=20
5x :5 =20 :5
5:5x=4
1x=4 или x=4
Делаем проверку уравнения. Вместо переменной x подставляем 4.
5x=20
5⋅ 4 =20
20=20 получили верное равенство, корень уравнение найден правильно.
Ответ: x=4.
Рассмотрим следующий пример:
Найдите корни уравнения .
Решение:
Так как перед переменной x стоит коэффициент необходимо от него избавиться. Надо все уравнение увеличить в 3 раза или умножить на 3, обязательно умножаем левую часть уравнения и правую часть.
Сделаем проверку уравнения. Подставим вместо переменной x полученный корень уравнения 21.
7=7 получено верное равенство.
Ответ: корень уравнения равен x=21.
Следующий пример:
Найдите корни уравнения
Решение:
Сначала перенесем -1 в правую сторону уравнения относительно знака равно, а в левую сторону и знаки у них поменяются на противоположные.
Теперь нужно все уравнение умножить на 5, чтобы в коэффициенте перед переменной x убрать из знаменателя 5.
Далее делим все уравнение на 3.
3x :3 =45 :3
(3:3)x=15
Сделаем проверку. Подставим в уравнение найденный корень.
Как решать уравнения? Алгоритм действий.
Подведем итог разобранной теме уравнений, рассмотрим общие правила решения уравнений:
- Перенести неизвестные в одну сторону, а известные в другую сторону уравнения относительно равно.
- Преобразовать и посчитать подобные в уравнении, то есть переменные с переменными, а числа с числами.
- Избавиться от коэффициента при переменной если нужно.
- В итоге всех действий получаем корень уравнение. Выполняем проверку.
Эти правила действуют на любой вид уравнения (линейный, квадратный, логарифмический, тригонометрический, рациональные, иррациональные, показательные и другие виды). Поэтому важно понять эти простые правила и научиться ими пользоваться.
Математика. 4 класс
Конспект урока
Математика, 4 класс
Урок 21. Решение уравнений
Перечень вопросов, рассматриваемых в теме:
- Что такое уравнение?
- Как решить уравнение, где в ответе не число, а числовое выражение.
- Что такое корень уравнения?
- Как найти неизвестное вычитаемое?
Глоссарий по теме:
Уравнение – это равенство с неизвестным числом. Неизвестное число обозначают латинской буквой.
Решить уравнение – это значит найти значение неизвестного, при котором равенство будет верным.
Корень уравнения – это значение неизвестного, обозначенного латинской буквой в уравнении.
Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
Обязательная и дополнительная литература по теме урока:
1. Моро М. И. Учебник для 4 класса четырехлетней начальной школы. М. «Просвещение» — 2017.С. 62,63
2. Волкова Е. В. математика Всероссийская проверочная работа за курс начальной школы. Издательство «Экзамен» 2018.С.27
3. Петерсон Л. Г. математика 3 класс. Часть 2. Ювента, 2015.-96с.: ил. С.77-78
Теоретический материал для самостоятельного изучения:
376 + 282; (х – у) : 3
Являются ли эти записи уравнениями?
Это не уравнения, так как в уравнении должен быть знак «=». Это выражения.
Уравнение – это равенство с неизвестным числом. Неизвестное число обозначают латинской буквой.
Рассмотрите другие записи:
24 + х = 49; 24 + х = 79 – 30
Это уравнения, так как это равенства, содержащие переменную.
Попробуем их решить.
Что значит решить уравнение?
Решить уравнение – это значит найти значение неизвестного, при котором равенство будет верным.
Вспомните алгоритм решения уравнений.
- Вспомнить компоненты действия данного уравнения.
- Определить неизвестный компонент.
- Вспомнить правило нахождения неизвестного компонента.
- Применить правило и найти неизвестный компонент.
- Записать ответ.
- Сделать проверку
Используя алгоритм, решите первое уравнение
Значение неизвестного х = 25. Это корень уравнения.
Корень уравнения – это значение неизвестного, обозначенного латинской буквой в уравнении. В данном случае – это х.
Можно ли решить второе уравнение, используя этот же алгоритм?
Такие уравнения не рассматривались. Какова же цель нашего урока?
Цель урока: научиться решать уравнения, в которых в ответе не число, а числовое выражение.
Такие уравнения мы будем называть составные. Поэтому тема урока: «Решение составных уравнений»
Чтобы решить это уравнение, нужно упростить правую часть.
24 + х = 79 – 30, после чего получаем уравнение известного вам вида
Ответ: корень уравнения 25
Составим алгоритм решения составных уравнений.
Алгоритм решения составных уравнений
1. Найти значение числового выражения.
2. Вспомнить компоненты действия данного уравнения.
3. Определить неизвестный компонент.
4. Вспомнить правило нахождения неизвестного компонента.
5. Применить правило и найти неизвестный компонент.
6. Записать ответ.
7. Сделать проверку.
Решим еще одно уравнение:
Применяем алгоритм решения составных уравнений:
- Найти значение числового выражения: 75 – х = 9 ∙ 7
- Вспомнить компоненты действия данного уравнения: 75 – х = 63
3. Определить неизвестный компонент.
4. Вспомнить правило нахождения неизвестного компонента.
5. Применить правило и найти неизвестный компонент.
6. Записать ответ.
7. Сделать проверку.
Ответ: корень уравнения 12
Вывод: чтобы решить составное уравнение, в которых в ответе не число, а числовое выражение, необходимо упростить правую часть ( т.е решить выражение), после чего получаем уравнение известного вам вида и решаем его, используя алгоритм решения уравнений.
Решим задачу, составив уравнение:
Сумма неизвестного числа и числа 390 равна произведению чисел 70 и 6. Найди это число.
1. Сумма неизвестного числа и числа 390 – обозначим неизвестное число переменной х, тогда получим х + 390
2. Произведение чисел 70 и 6: 70 ∙ 6
3. Получаем уравнение: х + 390 = 70 ∙ 6
Применяя алгоритм решения составных уравнений, решим его:
[spoiler title=”источники:”]
http://tutomath.ru/6-klass/chto-takoe-uravnenie-i-korni-uravneniya-kak-reshit-uravnenie.html
http://resh.edu.ru/subject/lesson/4580/conspect/
[/spoiler]
