
Классическая задача математики: найти квадратный корень уравнения является одной из основных в алгебре и является темой, которую изучают студенты везде по миру, начиная с младших классов средней школы. Вычисление корней уравнения нередко отражает наши навыки и знания в математике.
Однако, на пути к решению математических задач встречаются различные сложности и ситуации, которые требуют от нас внимания и аккуратности. Одна из этих задач: найти корень дискриминантом 0, и понятие дискриминанта ведет к лучшему пониманию этого вопроса.
Дискриминант является ключевым компонентом, который определяет количество корней у уравнения и типы возможных решений. Когда дискриминант равен нулю, ситуация немного отличается от других случаев, и в данной статье мы исследуем, какие изменения наступают и как найти корень в подобных ситуациях.
Давайте погрузимся в мир дискриминанта 0 и узнаем, как успешно преодолеть эти сложности, подробно обсудив через примеры и практические задачи.
Основные понятия для понимания дискриминанта 0
Для понимания термина “дискриминант 0” необходимо знать основные понятия, связанные с квадратным уравнением и его корнями. В данном разделе мы объясним ключевые термины и их значения, а также рассмотреем случаи, когда дискриминант равен нулю.
Квадратичное уравнение
Квадратичное уравнение – это алгебраическое уравнение второй степени, имеющее вид: Ax² + Bx + C = 0, где A, B и C – числа (коэффициенты), а x – неизвестная величина (переменная), которую мы ищем. Числа А, В и С могут быть целыми, рациональными, иррациональными, вещественными или комплексными.
Корни квадратичного уравнения

Корнями квадратичного уравнения являются значения x, при которых уравнение принимает значение 0 (то есть квадратичное уравнение обращается в true). Например, для уравнения 2x² – 3x + 5 = 0, корнями будут такие значения x, при которых 2x² – 3x + 5 = 0. Количество корней квадратичного уравнения зависит от значения дискриминанта.
Дискриминант квадратичного уравнения
Дискриминант квадратичного уравнения – это величина, задающая количество корней квадратичного уравнения. Дискриминант определяется по формуле: D = B² – 4AC. Уравнение будет иметь два корня, если D > 0, один корень, когда D = 0 и не одного корня – когда D < 0.
- Два действительных корня: если D > 0, уравнение имеет два различных корня.
- Один двойно́й корень: если D = 0, уравнение имеет один корень, который повторяется дважды.
- Нет действительных корней: если D < 0, уравнение не имеет действительных корней и имеет два комплексных корня.
В данном разделе рассмотрим случай, когда дискриминант равен нулю (D = 0).
Пример уравнения для работы с дискриминантом
Для удобства работы с дискриминантом и понимания процесса нахождения корней квадратного уравнения, рассмотрим пример следующего уравнения:
x2 – 5x + 6 = 0
Мы будем рассматривать дискриминант как величину, которая позволяет нам определить число решений уравнения и их тип. В данном уравнении, дискриминант D будет рассчитываться следующим образом:
D = b2 – 4ac
где a, b и c являются коэффициентами уравнения. В нашем примере:
a = 1, b = -5, c = 6
Теперь, когда у нас есть a, b и c, найдем дискриминант для этого уравнения:
D = (-5)2 – 4 * 1 * 6 = 25 – 24 = 1
У нас получилось D = 1, что означает, что квадратное уравнение имеет ровно один корень, рекомендуемое уравнение для решения:
x = (-b ± √D) / (2a)
В нашем примере следующим образом:
x = (-(-5) ± √1) / (2 * 1)
Упростив выражение, получим:
x = (5 ± 1) / 2
Тут у нас два случая, когда мы плюсуем или минусуем квадратный корень из дискриминанта:
-
если вы берете менее или равное, то x = (5 + 1) / 2 = 6 / 2 = 3
-
если вы берете более или равное, то x = (5 – 1) / 2 = 4 / 2 = 2
Таким образом, у этого квадратного уравнения есть корень 2 и 3. Это важно для понимания того, что в ситуации, когда дискриминант равен нулю, у вас всегда один корень.
Особенности решения квадратного уравнения
Решение квадратного уравнения связано с определенными характеристиками, которые позволяют понять как находить корни данной проблемы.
Значение дискриминанта – одним из важных факторов, который определяет наличие корней функции.
Дискриминант рассчитывается через формулу b^2 – 4ac.
При дискриминанте 0, корни в квадратном уравнении являются действительными, но равными между собой. В этом случае легко найти корень используя формулу D = 0, после явного упрощения уравнения решить квадратное уравнение.
Решение уравнения когда дискриминант равен 0:
D = b^2 – 4ac = 0, упростим уравнение и получим корень.
x = -b / 2a
Учитывая все данные особенности квадратного уравнения, можно находить нужные корни и решать задачи согласно своим потребностям.
Что делать, если нужно решить другой тип уравнения?

В случае в котором решения будет уходить за данные “равландские” границы, стоит обратиться к более сложным вариантам решений, с использованием комплексной математики.
При этом, требует обширный обзор данных математических проблем, а также применение дополнительных математических понятий для возможности предоставления более детального описания ситуации и поисков решения.
Совет: для всех возможных вариантов решений квадратного уравнения, пройти проверку данных значений дискриминанта и продолжить обработку, в зависимости от полученных результатов.
Теория и практика решения проблемы дискриминанта
Теория дискриминанта
Дискриминантом называется величина, определяющая вид корней квадратного уравнения. Если имеем квадратное уравнение вида ax^2 + bx + c = 0, где a ≠ 0, то дискриминант можно найти по формуле D = b^2 – 4ac. Результат вычисления дискриминанта позволяет нам определить тип корней:
- Если D > 0, имеем 2 различных действительных корня.
- Если D = 0, имеем единственный действительный корень.
- Если D < 0, корней нет.
Решение уравнений с дискриминантом 0

Если дискриминант равен 0, у нас есть единственный корень уравнения. Его можно найти по формуле x = -b/(2a). В этом разделе мы рассмотрим, как на практике найти корень, если дискриминант равен 0, и какие различные случаи могут возникнуть при решениях задач.
| Уравнение | Дискриминант D | Корень x |
|---|---|---|
| (x + 5)(x – 3) = 0 | 0 | x = -5 |
| 2x^2 – 2x – 12 = 0 | 0 | x = 1 |
Для того чтобы проверить, является ли дискриминант 0, нужно посчитать значение дискриминанта для каждого отдельного уравнения, а затем сравнить с нулём. Если он равен нулю, корень уравнения можно однозначно определить по формуле x = -b/(2a).
В заключении стоит отметить, что при интерпретации значения дискриминанта, следует внимательно обрабатывать случаи, когда D = 0. Это важная деталь моделей, основанных на дискриминанте, таких как дифференциальные эquations и квазилинейные уравнения.
Процесс вычисления кореня квадратного уравнения
Алгебраические методы
Существует множество методов, которые могут использоваться для вычисления кореня квадратного уравнения. Один из наиболее известных и используемых методов – формула извлечения квадратного корня. Она имеет следующий вид: x = (-b ± √(b2 – 4ac)) / (2a).
Формула извлечения квадратного корня основана на свойстве квадратного уравнения и обнаружении своих корней, как результат корня из второго степени. Общий вид корня задается знаком ±, что позволяет найти два корня: один положительный и один отрицательный.
Процесс вычисления кореня квадратного уравнения
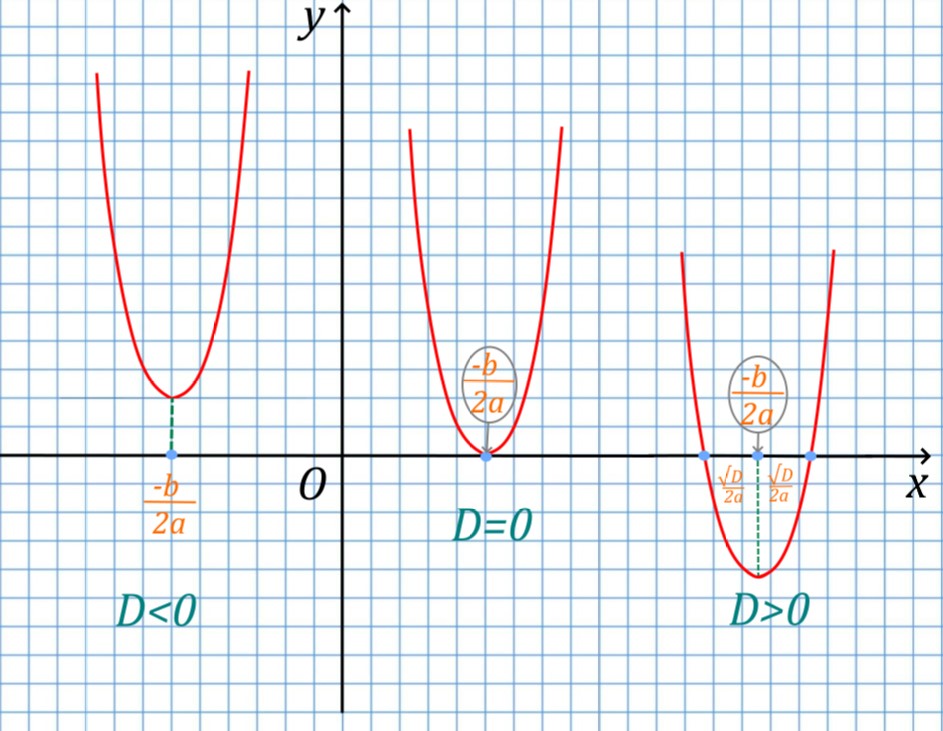
Для того, чтобы найти корень квадратного уравнения:
- Находим дискриминант. Определяем его по формуле b2 – 4ac, где a, b, c – это коэффициенты уравнения, входящие в квадратное уравнение (ax2 + bx + c).
- Определяем тип корней. Если дискриминант > 0, уравнение имеет два вещественных корня разных значений. Если дискриминант = 0, уравнение имеет два одинаковых вещественных корня. Если дискриминант < 0, уравнение имеет два комплексных корня.
- Вычисляем корень из дискриминанта. Если уравнение имеет нетривиальные корень и реальный дискриминант, вычисляйте его корень.
- Применяем формулу извлечения квадратного корня, к искомому корню единицы, используя найденный дискриминант.
- – При положительном дискриминанте уравнение находит два корня: x1 = ( -b + √(b2 – 4ac)) / 2a и x2 = ( -b – √(b2 – 4ac)) / 2a.
- – Если дискриминант равен нулю, то уравнение имеет один корень: x = -b / 2a.
- – Если дискриминант меньше нуля, то уравнение имеет два комплексных корня с одинаковыми действительными частями и мнимыми частями: x1 = -b / 2a + Ln1 и x2 = -b / 2a + Ln2.
Когда вы найдете свои корены, убедитесь, что они представляют реальные решения нашего исходного квадратного уравнения.
Практические упражнения для понимания дискриминанта 0
Чтобы лучше разобраться с дискриминантом и понять как из него образуется корень, предложены следующие упражнения. Обратите внимание, что случаи, когда дискриминант равен нулю, связаны с наличием единственного действительного корня у квадратного уравнения.
Упражнение 1: Найдите дискриминант для квадратного уравнения с заданными коэффициентами
Уравнение: ax² + bx + c = 0, где a ≠ 0
| № | a | b | c | Δ = b² – 4ac |
|---|---|---|---|---|
| 1 | 1 | 5 | 6 | 25 – 4*1*6 = -1 |
| 2 | 1 | 4 | 4 | 16 – 4*1*4 = 0 |
| 3 | 2 | 10 | 14 | 100 – 4*2*14 = -16 |
В упражнении 1 решаем квадратное уравнение для трех разных случаев, когда дискриминант может быть отрицательным, нулевым и положительным. Проанализируйте различные результаты для каждого случая.
Упражнение 2: Записи сводных и полных квадратных уравнений на основе дискриминанта
| № | Δ = b² – 4ac | Записи квадратных уравнений |
|---|---|---|
| 1 | 0 | (x – h)² = k, где h = -b/2a, k = c – h²/4a² |
| 2 | Отрицательное значение | Демонстрация процесса перехода от уравнения с отрицательным дискриминантом к консолидированному модулю |
| 3 | Положительное значение | Демонстрация процесса перехода от уравнения с положительным дискриминантом к полному квадратному |
Заполните вышеуказанные таблицы, добавив теоремы и иллюстрировав на практике, как записывать квадратные уравнения для любого дискриминанта. В задании 1 привести аналитический путь, на котором решение проходит через сокращенный и полный квадратный формат.
Упражнение 3: Решение квадратных уравнений для различных дискриминантов и вычисление корней.
| № | Уравнение | Корни (x1, x2) |
|---|---|---|
| 1 | x² – 36 = 0 | 6, -6 |
| 2 | x² + 6x + 9 = 0 | x = -3, x = -3 |
Во втором упражнении решим две квадратных уравнения, указанные в таблице, с различными дискриминантами и вычислим их корни.
Завершайте упражнения, проверяйте решения и сравнивайте свою продуктивность на использование теоремы разложения значений дискриминанатов.
Вопрос-ответ:
Что делать, если у меня дискриминант равен 0?
Если дискриминант вашего квадратного уравнения равен 0, то это означает, что у вас есть ровно один корень. Чтобы найти этот корень, добавьте результат деления числительного проиводятся обеих частей квадратного уравнения на знаменатель (последнее число в квадратном уравнении). Вы получите ответ.
Почему дискриминант равен 0, если у меня есть ровно один корень?
Дискриминант – это число, определяющее количество решений квадратного уравнения. Если дискриминант равен 0, это означает, что у квадратного уравнения ровно один корень. Чтобы понять связь между числом кореней и дискриминантом, представь, что дискриминант – это площадь квадрата с длиной стороны, равный сумме квадратов коэффициентов. Если площадь квадрата ровна 0, длина стороны (то есть корень уравнения) тоже равна 0.
Можно ли найти корень при помощи формулы для квадратных уравнений, если дискриминант равен 0?
Да, вы можете найти корень при помощи формулы для квадратных уравнений, даже если дискриминант равен 0. Здесь формула для квадратного уравнения: x = (-b ± √(b² – 4ac))/2a. Если дискриминант равен 0, то предпоследний элемент формулы станет 0, что приведет к тому, что ваш ответ – это (-b / 2a). Просто выполните расчет и получишь корень вашего квадратного уравнения.
Если дискриминант равен 0, что будет с четирихчатным решением квадратного уравнения?
Если дискриминант равен 0, тебе не нужет пользоваться корнем квадратного уравнения, чтобы решить вопрос. В этом случае, можно найти корень квадратного уравнения умножением последнего числа двечника уравнения на числитель обеих частей квадратного уравнения деления последнего числа на знаменатель квадратного уравнения. То есть, корень квадратного уравнения (-b / 2a). Помните, что получится только один результат.
Что такое дискриминант?
Дискриминант является одним из ключевых понятий в алгебре и необходим для решения квадратных уравнений. Он определяется как разница между квадратом коэффициента при x^2 и четырехмы раз помноженным на коэффициент при x на коэффициент при свободном члене.