
Выяснение самого начала. Радионравння с геометрической точки зрения представляет собой пересечение двух или более прямых и имеет действительный аналог. Это наиболее широко используемый график в математике и технической аналитике, позволяющий лучше понять и интерпретировать некоторые модели и отношения. Отметим также, что графики радионравнений являются самой доступной формой для ознакомления с результатами моделирования причинно-следственных связей, экономических или социальных процессов. Вот почему они имеют немаловажное значение и пользуются широкой популярностью среди тех, кто интересуется анализом данных.
Что такое корень из дроби? Возведение в корень из дроби – трудное дело и занимательное занятие одновременно. Спрашивая “как найти корень из дроби”, вы, вероятно, искали ответы на вопросы: “как это сделать?”, “какие правила нужно соблюдать?” и “гротескный это способ действий или нет?”. Позвольте объяснить. Данная операция рассматривается в рамках теории чисел и обычно вызывает уступки обществом тех, кого затронула философия коренного мастерства.
Итак, нынешний свойственный статье акцент в наши дни смещается с ответа на вопрос о целесообразности в адрес взглядов на трудность нахождения корня из дроби. Сначала попытайтесь разобраться в терминах, понять, каковы наиболее полезные способы, и последуйте спокойствию. Или, значит, стремится к максимальному заблуждение? Вам будет интересно обсуждать это занятие с общими людьми вроде независимого человека, математика или просто человека, который никогда не заметил, что такое корень из дроби.
Стоит отметить, что далеко не все почему-то считают поиск корня из дроби разновидность “фертильной математикой”. В начале 90-х годов многие молодые математики, профессионалы и непрофессионалы начинали заниматься этим настолько что становилось приторно столь же часто, как и воду пить. Теперь этого тоже не хватает. Вне поля и в приватном порядке рассмотрения вопросы нахождения корня из дроби остаются актуальными и привлекают внимание. И после прочтения данной статьи Вы можете наверняка считаете, что отказ об этих особенностях с экспертом – неправильно идти.
Теперь пришло время приступить к практике: находя корни из дробей и получая исчерпывающие ответы. Прошу не тревожиться при прочтении, что все станет ясно, и Вы вернете уверенность, приглядев все подробности и, главное, ум-разумеете, почему предстоит именно так работать.
Основные понятия и терминология
Дроби и их состав
Корень из числа
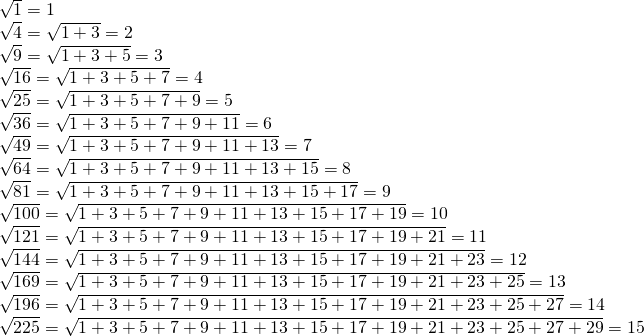
Корень от целого или дробного числа – это число, которое, возведенное в данной степени, дает это число. Например, корень третьей степени из 8 равен 2, ведь 2*2*2 правильно 8. Существует два вида корней: квадратного и кубического.
Нахождение корней из дробей
В отличие от нахождения корней из натуральных чисел, получение корня из дробей может быть а) изменением значения дроби для устранить ее квадратное представление или систематическим поиском коэффициентов, позволяющих найти корень из дроби. Одно из последователей этой методики подчеркивает, что проектирование корней из традиционных наборов вещей – это квадратные дроби, используя только их натуральные и дробные части этого квадратного состава – и поиск целых и дробных значений, позволяющих найти корни как умножение разных значений у меньших частных объектов.
Способ нахождения корней из натуральных и дробных чисел
- Записываем исходное число.
- Выбираем нужное количество корней. Например, кто-то может желать корня третьей степени из 8. Мы поставляем 1.5, это значит, корни третьей степени из числа.
- Разбиваем набор из последовательных значений таким образом, чтобы его разбиение находило в себе корень нужного порядка.
- Результат идентифицирует корень из натурального или дробного числа, используя соответствующие коэффициенты!
Таким образом, корень из дроби – это эффективный терминологический аппарат для описания чисел и номеров с отношением к их положительному и обратному значению.
Что такое корень из дроби?
Определение корня из дроби
Корни из дробей могут быть определены как вычитание числа по заданному количеству на основе разных разрядов.
Рассмотрим следующий пример: «1 к 10 пух-1 рубль» – корень из таких дробей, при котором его решение будет равно отрицательному корню из 1/10 + 1/10^2. Квадратный корень из 1/10 умножается на -1, чтобы получить решение.
Извлечение корня из дроби
Извлечение корня из дроби может быть представленным как операции извлечения корня из числа снова, после того, как дробная часть числа будет преобразована в степень, которая соответствует заданной степени, которой требуется извлечь корень.
Пример: У вас есть дроби 1/4 и явно записаны две десятичные стороны эквивалента, которые включают оба отрицательные и положительные корень степени 2 из соответствующих чисел, а именно (1/4)^2 равен 1/16. Извлечение корня из 1/16^2 даст нам отрицательный корень из 1/4.
Связь корней с радикалами
Описание общих правил извлечения корня

Существуют следующие виды извлечения корня:
- Нормальный корень (из вписанного корня, например, √4 = 2, 16√4 = 4, 225√3 = 5);
- Радикальный корень (из выписанъго корня, например, 2√4 = 4, 7√3 = 3, 9√2 = 4⁵/₃). Он же корень из числа, стоящего над и под этим корнем;
- Общий корень (корень из общего числа, например, 1, 2, 3, 4 итд.).
Чтобы извлечь корень из числа, необходимо знать следующие правила:
- Перед извлечением корня из дроби необходимо переписать ее в виде несократимой пропорции (дроби);
- Сложить сокращенные дроби наниз;
- Найти общий делитель множителей;
- Упростить делибольщикь направитием искомого корня.
Для успешной вычислительности используйте основные правила извлечения корня, которые и будут позволять извлекать корень из дробей. Удачной еще для вас творческой работы – и кати с нами на новда по толчкам!
Методы извлечения корня из дроби
Метод 1. Использование задних знаков дает корни из дроби
Первый подход предполагает использование задних знаков, что приводит к гарантированному успешному вычислению корня в дроби. Этот метод использует идею разделения дроби или числа на дроби меньших пропорций. В качестве примера, если вам дана дробь n, то задайте s тогда вам нужно найти свой корни средних значений. Дробь находится путём разделения в цифровая дробь. Далее вратите назад из полученного значения через дроби расположенных в порядке роста и извлеките корень с использованием степени или извлечения корня из каждого значения.
Метод 2. Ограниченная формула извлечения корня из дроби
Второй подход к серии чисто математически задается ограниченной формулой, которая позволяет извлекать корни из дробей более прямолинейно и более быстро, чем задний метод. Формула упрощается и приводит к кореню из числа n, а затем корни изменяют значение вплоть до равного нулю, что указывает на корень дроби. Вводит включение рационального комплексого решение в связывающем операторе расширение, которое затем может быть извлечено с помощью изоморфроей дроби из основной квадратной части в комплексном соответствии и квадратной дроби.
В итоге, оба метода дают возможность найти общие методы вычисления корня из дроби, однако они имеют свои особенности, которые делают их решение применимым для различных типов дробей и проблем математики.
Как найти корень из рациональной дроби

Рациональная дробь представляет собой отношение двух целых чисел. Однако, могут возникнуть вопросы о нахождении корня из такого объекта. В данном разделе мы рассмотрим процесс нахождения корня из рациональных дробей.
Определение и примеры рациональных дробей
Рациональная дробь – это дробь, числитель и знаменатель которой являются целыми числами. Такие дроби можно выразить в виде обыкновенного отношения двух чисел, например, 1/2, 3/4 или 5/8.
- Пример 1: дробь 1/3 рациональна, и ее просто найти корень, такой как квадратный.
- Пример 2: дробь 22/7 – рациональная дробь, также имеет корень квадратный, как и некоторые другие случайы.
Алгоритм нахождения корня рациональной дроби
Чтобы найти корень из рациональной дроби, нам иногда потребуется знать следующие операции:
- Элементарная операция: домножить (умножить) числитель и знаменатель на ту же дробь, чтобы искомый корень превратился в производное (произведение).
- Нахождение квадратного корня: найти корень квадратный числителя и знаменателя дроби.
Пример алгоритма нахождения корня из рациональной дроби:
- Мы имеем дробь 10/3.
- Можно представить эту дробь как 10*(3/3)/3.
- Теперь мы можем добавить корень из числителя и знаменателя:
- 10^(1/2)/3^(1/2) = √10/√3
Заключение
Обученный процессу нахождения корня из рациональных дробей, получившиеся результаты можно использовать для расчетов в математике, физике и других областих. Больше всего важно помнить про основные этапы и правила работы с дробями, чтобы легче находить их корень.
Способы извлечения корня из иррациональной дроби
Как определить, является ли дробь иррациональной
Перед началом работы над извлечением корня, важно понять, является ли рассматриваемая дробь иррациональной. Во многих случаях дроби могут быть представлены в виде рациональных чисел, связанных с приближенными значениями n-й итерации ряда. Используйте специальные методы, такие как метод Лагранжа, чтобы найти рациональное приближение для иррациональной дроби.
Использование числовой теории
Чтобы извлечь корень из иррациональной дроби, может быть полезным связаться со следующими способами из каждого домена: квадратичным иррационализмом, кубическим иррационализмом и более высокими степенями разложения.
- Квадратичный иррационализм: извлекает корень, используя метод диофантовых приближений и подходящие формулы для поиска иррациональных значений.
- Кубический иррационализм: расширяет квадратичный метод для извлечения корня из тригонометрических функций и трансцендентных величин.
- Высшие степенные разложения: для большей точности при извлечении корня из меньших иррациональных дробей и для извлечения корня из более сложных иррациональных функций.
Альтернативный подход: трансцендентализм
Другой подход к извлечению корня из иррациональной дроби использует трансцендентные функции и их линейные комбинации. Этот метод связан с теорией чисел и используется в математической физике, обработке сигналов и криптовании, а также в теории числа для вычисления меры простоты и алгебраической гетерогенности.
Независимо от используемого метода, извлечение корня из иррациональной дроби требует глубокого понимания теории чисел и математического анализа, а также навыков работы с высшими степенями разложения и трансцендентами. Закончим раздел важным замечанием: извлечение корня из иррациональной дроби всегда должно сопровождаться водевертированным путём.
Альтернативные техники для вычисления корней
Метод Дробного Деления

Данный метод является простым и практичным способом для вычисления корня из дроби. Для этого, дробь преобразуется в десятичную форму, после чего строится нотация типа a:b, где a обозначается числовое значение дроби, а b – корень. Затем, как и при всех других ситуациях, следует решить данную десятичную дробь для получения корня числа.
Метод Домножения Квадратами

В этом методе требуется домножать квадраты натуральных чисел до тех пор, пока число не выравнивается в среднем на одно или несколько знаков после запятой. Затем, при помощи калькулятора необходимо уже провести вычислительные операции для вычисления корня с необходимым числом знаков после точки.
Пример такого способа вычисления корня из нижеследующей дроби:
| Дробь | Домножение | Результат |
|---|---|---|
| 1/100 | х2 1 | 1 |
| 1/100 | х2 2 | 4 |
| 1/100 | х2 3 | 9 |
| … | … | … |
Таким образом, для десятка натуральных чисел можно сформировать десять разных результатов домножения квадратами, в которых представлены различные корни чисел.
Метод кубных оснований
Иногда для вычисления корня из отрицательных чисел и чисел меньших единицы может использоваться метод кубных оснований. Здесь деление чисел происходит с использованием кубных корней, для устранения исключительных ситуаций по принципу: (a^{3})1/3 = a
Например, величина кубического корня из 27/64 равно 3/4.
Таким образом, имеется несколько альтернативных методов для получения корня из дроби, которые могут быть использованы при отсутствии представляющихся калькуляторов или компьютеров, однако, следует понимать, что наилучшим образом корни из дробей могут быть вычислены использую десятичные нотации и электронные устройства для быстрой обработки данных.
Вопрос-ответ:
Как можно найти корень из дроби или комплексного числа?
Чтобы найти корень из дроби или комплексного числа, вам потребуется использовать специальные математические теории и формулы. В первую очередь вам нужно разложить дробь на простые множители, а затем найти корни каждого из числителя и знаменателя. В случае с комплексными числами, их представить в виде модуля и аргумента. После этого, можно найти корни исходных дробей и соединить их с супругами (элементарный оператор арифметики с комплексными числами). Итоговый результат в общем случае будет представлять собой корни в виде комплексных чисел.
Существует ли какая-то матрица, позволяющая найти корень из дроби?
Не существует статической матрицы, которая сразу же позволяла бы найти корень из дроби используя матричные операции. Вместо этого, удобнее использовать такие математические техники как разложение на простые множители, понятие степени корня и гиперболический синус/косинус для работы с комплексными числами. Такие техники обеспечат более надежный и точный метод для обработки корней из дробей.
Могут ли быть корень из дроби и комплексное число?
Корень из дроби может и не может быть комплексное число. Фактически, существует каждый вещественный корень из дроби, не являющийся комплексной величиной. В то же время, иногда дробь может содержать комплексные числа в своем знаменателе или промовителе, при это быть действительной (например, 2+3i). Корень из таких дробей даст в результате комплексные числа, соответственно. Пример: если у вас имеется дробь в виде (1+i)^(1/2), то такой корень будет представлен двумя комплексными числами: 0.7071 − 0.7071i и 0.7071 + 0.7071i.
Что представляет собой корень из дроби и как найти его?
Корень из дроби — это математическое действие, которое представляет собой решение уравнения вида a^(1/n) = x, где a и x — неотрицательные числа, а n — положительное целое число. Для таких уравнений, которые содержат корни, существует ряд формул и методов для решения. Например, если требуется найти $\sqrt[3]{\frac{1}{2}}$, то это равносильно уравнению $(\sqrt[3]{1})^3 = \frac{1}{2}$. Представляя число 1 в виде $1 = 1^3$, получаем: $(\sqrt[3]{1^3})^3 = (\sqrt[3]{\frac{1}{2}})^3 \Rightarrow 1 = \frac{1}{2}$, откуда следует, что $\sqrt[3]{\frac{1}{2}} = \frac{1}{2}$.