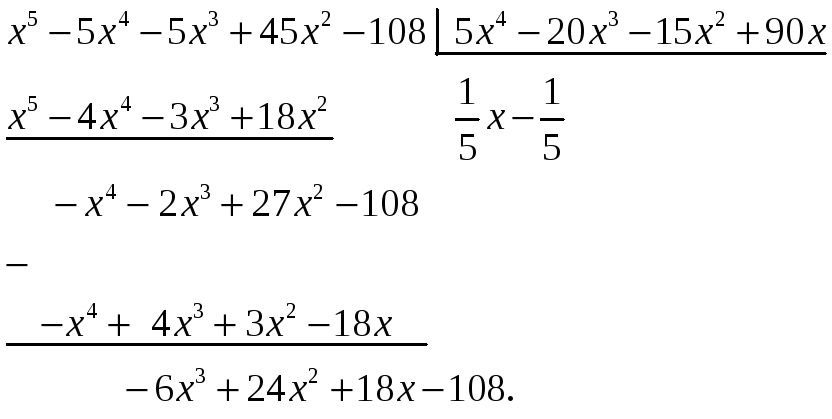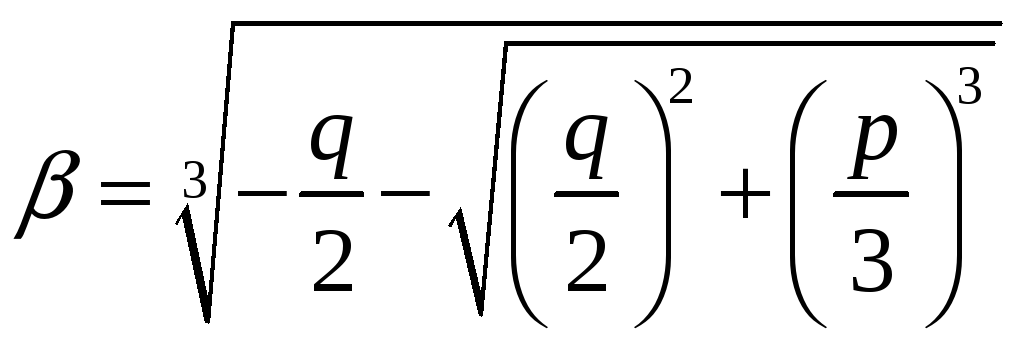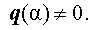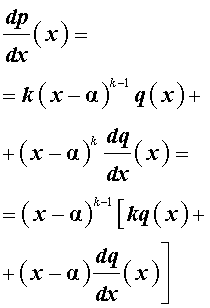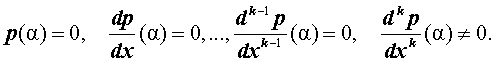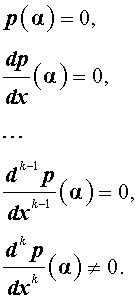Как найти корень кратности многочлена

Если при значении

многочлен

принимает значение
,
то число

называется корнем этого многочлена.

Число

является корнем многочлена тогда и
только тогда, когда

делится на
,
т.е.
.
Если при этом

делится на
,
но уже не делится на
,
то

называется
-кратным
корнем многочлена
.
Корни кратности

называются простыми корнями многочлена.

Чтобы проверить, будет ли число

корнем многочлена

и какой кратности, можно воспользоваться
схемой Горнера. Сначала

делится на
,
затем, если остаток равен нулю, полученное
частное делится снова на

и т.д. до получения ненулевого остатка.

Пример 1. Проверить, является ли
число

корнем многочлена

и найти кратность.

Решение. Деление на

осуществляем по схеме Горнера

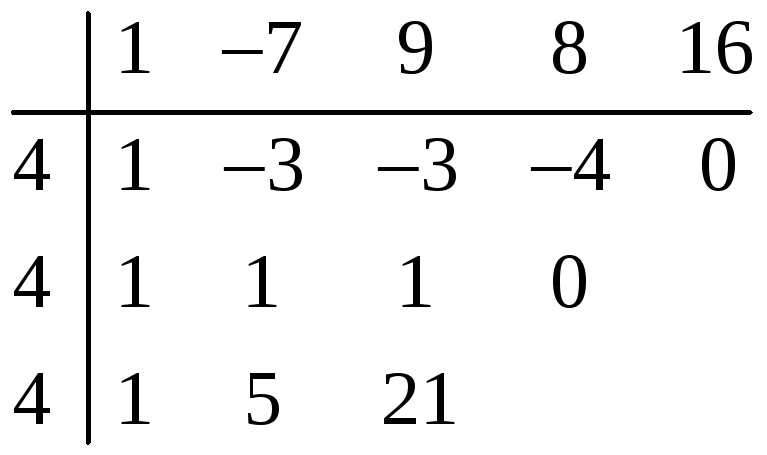
— корень кратности 2.

Пусть

— все различные корни многочлена

с кратностями, равными соответственно

— старший коэффициент
.
Тогда
.Корень
многочлена кратности

является корнем кратности

для его производной. Поэтому
,
где

— многочлен, уже не имеющий

своими корнями. Отсюда н.о.д. многочленов

и

равен
.

Следовательно, многочлен

имеет числа

простыми корнями.

Теперь для отыскания всех корней
многочлена

достаточно найти все корни многочлена
.
Это бывает сделать проще, так как степень

меньше степени
,
когда
.
Построение многочлена

называется отделением кратных корней
многочлена
.

Пример 2. Отделить кратные корни
многочлена
.

Решение.
.
Находим
.
Для этого делим с остатком

на
:

делится на остаток
.
Поэтому
.
Искомый многочлен, отделяющий кратные
корни
,
равен
.

Заметим, что в примере 2 все корни

легко вычислить.

Литература:
— § 22,
— § 9.4;

— № 555-559, 563-566, 569, 570, 585.

§ 3. Вычисление корней многочлена.

Задача вычисления корней некоторого
многочлена часто возникает в практике.
Согласно основной теореме алгебры, все
корни произвольного многочлена

с коэффициентами из числового поля

содержатся в поле комплексных чисел
.
Однако не существует какого-либо
универсального метода вычисления этих
корней. Метод решения этой задачи зависит
от степени многочлена и числового поля
.
Мы перечислим лишь самые основные методы
решения задачи вычисления корней
многочлена.

1. Корни многочленов 3-й и 4-й степени.

Если
,
то для отыскания всех корней многочлена

необходимо решить уравнение

(1)

Разделим обе части (1) на
.
В результате получим уравнение

(2)

имеющее те же корни, что и уравнение
(1). Сделаем теперь замену неизвестного
.
Эту замену проще всего осуществить,
представляя многочлен

по степеням

с помощью схемы Горнера (§
1) и делая затем замену
.
В результате замены получим уравнение

(3)

Корни уравнения (3) находятся по формуле
Кардано

где,
,

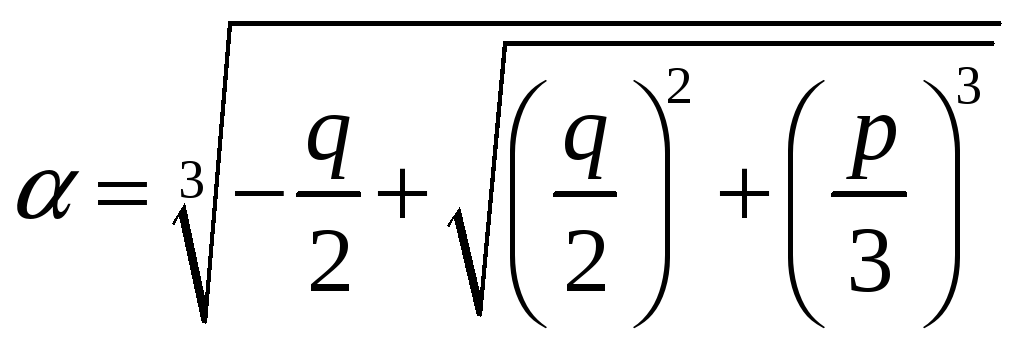
(корни извлекаются в поле комплексных
чисел
).
Применяя эту формулу, нужно для каждого
их трех значений

брать то значение
,
для которого выполняется условие

(такое значение всегда существует).

Если

— все корни уравнения (3), то

— все корни уравнения (1) и многочлена
.

Пример 1. Найти корни многочлена
.

Решение. Разложим многочлен

по степеням
.
Полагая
,
получим уравнение
.
Его корни находятся по формуле
,
где

или
.
Значениями корня

являются числа
.
Соответствующие им значения второго
корня

Отсюда
.
Корни многочлена
,
.

Если

— многочлен 4-й степени, то для вычисления
его корней достаточно иметь способ
вычисления всех корней уравнения вида

(4)

Способ Феррари решения уравнения (4)
состоит в следующем.

Левую часть (4) представляют в виде

, (5)

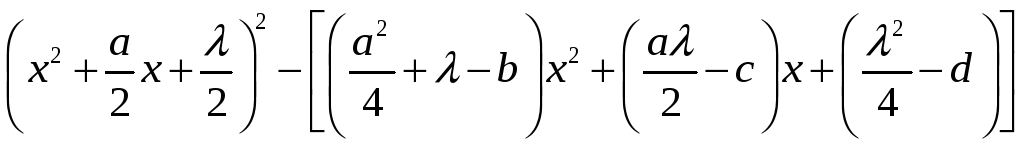
а затем подбирают

так, чтобы выражение в квадратных скобках
стало квадратом двучлена первой степени.
Для этого необходимо и достаточно
выполнение условия

, (6)

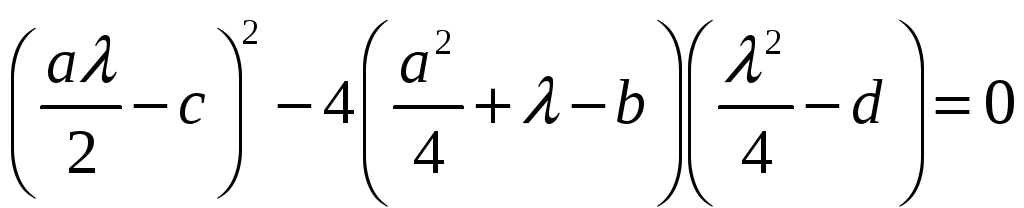
из которого следует, что

является корнем вспомогательного
кубического уравнения (6). Теперь находим
какой-нибудь один корень

и, подставляя его значение в (5), разлагаем
левую часть (4) как разность квадратов
на множители. Задача вычисления корней
сведена теперь к решению двух квадратных
уравнений.

Пример 2. Найти корни многочлена
.

Решение. Составим уравнение

(7)

Представим левую часть (7) в виде

(8)

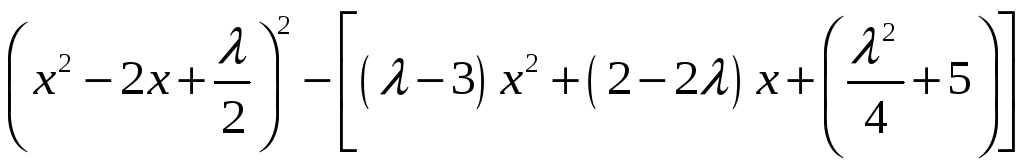
Подберем

так, чтобы дискриминант квадратного
трехчлена в квадратных скобках был
равен нулю:

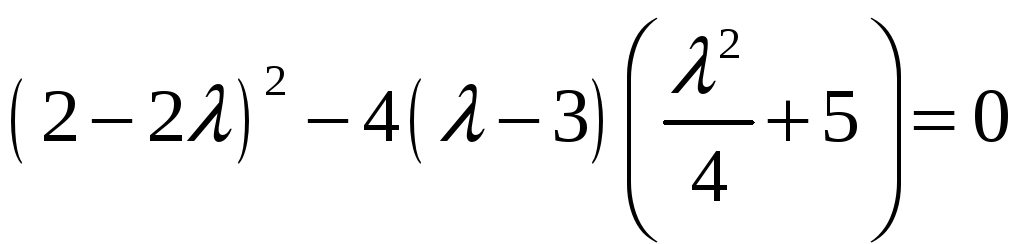
или

.

Можно заметить, что 4 — один из корней
этого уравнения. Тогда подставим

в (8) и уравнение (7) примет вид:

или

.

Отсюда, решая уравнения

и
,
получим корни нашего многочлена

Литература:

— § 38,

— № 167, 173, 174.

2. Рациональные корни
многочленов с рациональными коэффициентами.

Многочлен

имеет те же корни, что и многочлен

с целыми коэффициентами, полученный из

умножением на общее кратное знаменателей
всех коэффициентов
.

Если несократимая дробь

является корнем многочлена

с целыми коэффициентами, то выполняются
следующие условия:

1)

— делитель числа
;

2)

— делитель числа
;

3) для любого целого числа

число

является делителем числа
.

Поэтому все рациональные корни многочлена

(если они существуют) нужно искать среди
несократимых дробей, удовлетворяющих
условиям 1, 2, 3.

Если
,
то все рациональные корни

являются целыми числами.

Пример. Найти рациональные корни
многочлена

и определить их кратность.

Решение. Если

— несократимая дробь, является корнем
,
то

делит 12, а

делит 2. Все делители 12:
,
а делители 2: 1,2.

Зафиксируем
.
Тогда по (3) условию
.
В качестве

возьмем

и
.
Тогда

и
.
.
.
Числа 1 и -1 не являются корнями. Если
число

— корень, то

и
.
Такому условию удовлетворяют -2, 4. С
помощью схемы Горнера выясняем, что
число -2 является корнем кратности 2.

Далее, зафиксируем
.
Тогда

и

().
Проверять надо лишь

взаимно простые с
,
т.е.,
.
Среди этих чисел условию ()
удовлетворяют -1, 3. Проверяя по схеме
Горнера дроби

и

выясняем, что корнем является
.
Итак,

— простой корень,

— корень кратности 2.

Литература:

— § 57,

— § 11, 3,

— № 649-651.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Кратные корни многочленов

Пусть p(x) – многочлен степени n , а q(x) – многочлен степени n – k , где n и k – натуральные числа, удовлетворяющие неравенству .

Определение . Число α называют корнем кратности k многочлена p(x) , если справедливо равенство

p(x) = (x – α) k q (x) ,

(1)

Утверждение 1 . Число α является корнем кратности k многочлена p(x) тогда и тогда, когда оно является корнем производной этого многочлена кратности k – 1 .

Доказательство . Взяв производную от обеих частей формулы (1), получаем

Поскольку выражение, стоящее в квадратных скобках, при x = α не обращается в нуль, то утверждение 1 доказано.

Из утверждения 1 вытекает следующее

Утверждение 2 . Число α является корнем кратности k многочлена p(x) тогда и тогда, когда выполнены равенства:

Определить кратность корня x0 многочлена f(x).

Третья производная:
f”'(x) = 60x 2 — 120x + 42
f”'(2) = 60*2 2 — 120*2 + 42 = 240 — 240 + 42 = 42, не равно нулю => кратность равна количеству найденных производных.

Ответ: 3

Метод второй: схема Горнера:

1	-5	7	-2	4	-8
2	1	-3	1	0	4	0
2	1	-1	-1	-2	0
2	1	1	1	0
2	1	3	7
2	1

Как видно из схемы Горнера количество нулей равно 3, следовательно и кратность равна 3. Схема Горнера метод намного удобнее, если x₀ — число больше 2, производными считать труднее.

Кратные корни многочлена

При рассмотрении вопроса о корнях многочлена, особо выделяют понятие кратных корней.

Определение. Пусть задан многочлен $fleft(xright) in Pleft[xright]$ ($Pleft[xright]$ — множество всех многочленов от буквы $x$ над полем $P$) и $alpha$, где $alpha$ — корень многочлена $fleft(xright)$. Элемент $alpha$ назовем $k$-кратным ($k in mathbb $, $k>1$) корнем многочлена, если имеет место следующее представление: $$fleft(xright)=left(x-alpharight)^k f_left(xright),, f_left(alpharight) ne 0.$$

Принято рассматривать понятие кратного корня для $k>1$. Если же $fleft(xright)$ можно представить следующим образом: $$fleft(xright)=left(x-alpharight) f_left(xright),, f_left(alpharight) ne 0,$$ то $alpha$ называется простым (однократным) корнем многочлена$fleft(xright)$. Если для $fleft(xright)$ имеет место следующее равенство: $$fleft(xright)=left(x-alpharight)^2 f_left(xright),, f_left(alpharight) ne 0,$$ то $alpha$ называется двукратным корнем многочлена $fleft(xright)$. Аналогично, существуют корни трехкратные, четырехкратные и так далее.

Часто условие $f_left(alpharight) ne 0$ заменяют на $f_left(xright),barvdots,(x-alpha)$. Эквивалентность этих условий вытекает из следствий теоремы Безу. Тогда, набор условий, что $f(x),vdots,left(x-alpharight)^k$, но $f(x),barvdots,left(x-alpharight)^$ эквивалентен тому, что $alpha$ — $k$-кратный корень многочлена $f(x)$.

Процесс нахождения кратности корня

Пусть задан многочлен $fleft(xright) in Pleft[xright]$ и его корень $alpha$ ( $deg fleft(xright) > 0$). Рассмотрим задачу о нахождении кратности корня $alpha$.

Так как $alpha$ — корень $fleft(xright)$, то имеет место следующее представление: $$fleft(xright)=left(x-alpharight)f_left(xright).$$ Тогда, если $alpha$ не является корнем $f_left(xright)$ ($f_left(alpharight) ne 0$), то, по определению, $alpha$ — простой корень многочлена $fleft(xright)$. В противном случае, $alpha$ — $k$-кратный ($k in mathbb $, $k > 1 $) корень $fleft(xright)$. Задача сводится к нахождению $k-1$, то есть к нахождению кратности корня $f_left(xright)$, где $deg f_left(xright) = deg fleft(xright) — 1$. Учитывая, что $deg fleft(xright) > 0$, то повторение такого алгоритма решает задачу. Для этого используется алгоритм Горнера.

Стоит упомянуть, что иногда удобней пользоваться критерием кратности корня.

Примеры решения задач

1. Пусть задан многочлен $fleft(xright)=x^3-3x^2+4$. Определить, является ли $2$ корнем многочлена $f(x)$. В случае положительного ответа найти его кратность.

Для решении задачи воспользуемся алгоритмом Горнера. Стоит обратить внимание на то, что хоть и слагаемое вида $a_x^1$ отсутствует в записи, но нулевой коэффициент необходимо не забыть занести в таблицу.

$1$	$-3$	$0$	$4$
$2$	$1$	$-1$	$-2$	$0$
$2$	$1$	$1$	$0$
$2$	$1$	$3$

Из таблицы видно, что многочлен $f(x)$ поделился на $left(x-2right)^2$ без остатка, а на $left(x-2right)^3$ — нет. Получаем, что $2$ — двукратный корень многочлена $f(x)$.

Так как $alpha$ — двукратный корень многочлена $f(x)$, то $f(x)$ представим в следующем виде: $$fleft(xright)=left(x-alpharight)^2 f_left(xright),$$где $f_(alpha) ne 0$. Аналогично, $g(x)$ можно представить следующим образом: $$gleft(xright)=left(x-alpharight) g_left(xright),$$где $g_(alpha) ne 0$. Тогда, $$f(x)g(x)=left(x-alpharight)^2f_(x)(x-alpha)g_(x)=left(x-alpharight)^3f_(x)g_(x).$$Так как $f_(alpha) ne 0$ и $g_(alpha) ne 0$, то $f_(alpha)g_(alpha)ne0$. Обозначим $f(x)g(x)=h(x)$, $f_(x)g_(x)=h_(x)$, тогда перепишем выражение многочлена $f(x)g(x)$ следующим образом: $$h(x)=left(x-alpharight)^3h_(x),$$ где $h_(alpha)ne0$. Тогда по определению $alpha$ — корень $f(x)g(x)$ третьей кратности.

Для решении задачи воспользуемся алгоритмом Горнера.

$1$	$5$	$10$	$10$	$5$	$1$
$-1$	$1$	$4$	$6$	$4$	$1$	$0$
$-1$	$1$	$3$	$3$	$1$	$0$
$-1$	$1$	$2$	$1$	$0$
$-1$	$1$	$1$	$0$
$-1$	$1$	$0$

Из таблицы видно, что многочлен пятой степени $f(x)$ поделился на $left(x+1right)^5$ без остатка. Получаем, что $-1$ — корень пятой кратности.

По определению, для того, что бы $2$ была корнем второй кратности, необходимо что бы имело место следующее представление: $$f(x)=left(x-2right)^2f_(x),, f_(2) ne 0.$$С другой стороны, в нашем случае: $$f_(x)=x^2+x-6=(x-2)(x+3),, f_(2)=0.$$ Получаем, что $2$ не корень второй кратности. Тогда найдем его кратность. Выразим $f(x)$ подставив $f_(x)=(x-2)(x+3)$:$$f(x)=left(x-2right)^3(x+3)=left(x-2right)^3f_(x),$$ $f_(2)=(2+3)=5ne0$. Значит, по определению, $2$ — корень многочлена $f(x)$ третьей кратности.

Представим исходный многочлен следующим образом: $$f(x)=x^4(x^4-8x^3+10x^2-1).$$
Обозначим $f_(x)=x^4-8x^3+10x^2-1$. Легко убедиться, что $f_(0)=-1ne0$. Получаем, что, по определению кратного корня, $0$ — корень многочлена $f(x)$ четвертой кратности.

Макеты страниц

Задание:

Определить кратность корня x₀ многочлена f(x)

f(x) = x⁵ – 5x⁴ + 7x³ – 2x² + 4x – 8, x₀ = 2;

Решение:

Метод первый: производными

f(2) = 2⁵ – 5*2⁴ + 7*2³ – 2*2² + 4*2 – 8 = 32 – 80 + 56 – 8 + 8 – 8 = 88 – 80 – 8 = 0

Первая производная:
f'(x) = 5x⁴ – 20x³ + 21x² – 4x + 4
f'(2) = 5 * 2⁴ – 20*2³ + 21*2² – 4*2 + 4 = 80 – 160 + 84 – 8 + 4 = 164 – 160 – 8 + 4 = 0

Вторая производная: 
f”(x) = 20x³ – 60x² + 42x – 4
f”(2) = 20 * 2³ – 60*2² + 42*2 – 4 = 160 – 240 + 84 – 4 = 244 – 244 = 0

Третья производная:
f”'(x) = 60x² – 120x + 42
f”'(2) = 60*2² – 120*2 + 42 = 240 – 240 + 42 = 42, не равно нулю => кратность равна количеству найденных производных.

Ответ: 3

---

Метод второй: схема Горнера:

---

	1	-5	7	-2	4	-8
2	1	-3	1	0	4	0
2	1	-1	-1	-2	0
2	1	1	1	0
2	1	3	7
2	1

Как видно из схемы Горнера количество нулей равно 3, следовательно и кратность равна 3. Схема Горнера метод намного удобнее, если x₀ – число больше 2, производными считать труднее. 

Ответ: 3

Кратные корни многочленов

Пусть p(x) – многочлен степени n , а q(x) – многочлен степени n – k , где n и k – натуральные числа, удовлетворяющие неравенству .

Определение . Число α называют корнем кратности k многочлена p(x) , если справедливо равенство

p(x) = (x – α) k q (x) ,

(1)

Утверждение 1 . Число α является корнем кратности k многочлена p(x) тогда и тогда, когда оно является корнем производной этого многочлена кратности k – 1 .

Доказательство . Взяв производную от обеих частей формулы (1), получаем

Поскольку выражение, стоящее в квадратных скобках, при x = α не обращается в нуль, то утверждение 1 доказано.

Из утверждения 1 вытекает следующее

Утверждение 2 . Число α является корнем кратности k многочлена p(x) тогда и тогда, когда выполнены равенства:

Задача . Найти все значения параметра m , при которых многочлен

имеет корень кратности 2 .

Решение . Воспользовавшись утверждением 2, получаем

Источник

Критерий кратности корня

Теорема. Корень $alpha$ многочлена $f(x)$ является его $k$-кратным корнем тогда и только тогда, когда он является корнем кратности $k-1$ его первой производной.

Так как мы работаем с критерием, то доказательство будет проведено в обе стороны.

Необходимость. Пусть $alpha$ — $k$-кратный корень многочлена $f(x)$. Необходимо доказать, что $alpha$ — корень кратности $k-1$ многочлена $f'(x)$. По определению кратного корня можно записать следующее:$$f(x)=left(x-alpharight)^kf_<1>(x),, f_<1>(x) barvdots (x-alpha).$$

Стоит отметить, что условия $f_<1>(x) barvdots(x-alpha)$ и $f(alpha)ne0$ являются эквивалентными по следствию теоремы Безу.

Дифференцируя $f(x)$, получаем: $$f'(x)=kleft(x-alpharight)^f_<1>(x)+left(x-alpharight)^kf’_<1>(x).$$Вынося $left(x-alpharight)^$ из первого и второго слагаемого, получаем: $$f'(x)=left(x-alpharight)^(kf_<1>(x)+(x-alpha)f’_<1>(x)),$$ при этом слагаемое $(kf_<1>(x)+(x-alpha)f’_<1>(x)) barvdots (x-alpha)$, так как в противном случае выполнялось бы условие $f_<1>(x) ,vdots, (x-alpha)$, что противоречит тому, что $alpha$ — $k$-кратный корень многочлена $f(x)$.

Следовательно, $alpha$ — корень кратности $k-1$ многочлена $f'(x)$ по определению кратного корня.

Достаточность. Теперь пусть $alpha$ — корень многочлена $f(x)$ и корень кратности $k-1$ многочлена $f'(x)$. Тогда можно записать следующее: $$f(x)=(x-alpha)f_<1>(x),$$ $$f'(x)=left(x-alpharight)^g(x),, g(x)barvdots(x-alpha).$$

Пусть $kgeqslant2$. Тогда продифференцируем $f(x)$ и получим: $$f'(x)=f_<1>(x)+(x-alpha)f’_<1>(x).$$Учитывая, что $f'(x),vdots,(x-alpha)$, то и $f_<1>(x),vdots,(x-alpha)$, иными словами, многочлен $f_<1>(x)$ можно представить так: $$f_<1>(x)=(x-alpha)f_<2>(x).$$ Тогда $f(x)$ представляется в следующем виде: $$f(x)=left(x-alpharight)^2f_<2>(x).$$ Теперь продифференцируем $f(x)$ в очередной раз, получим: $$f'(x)=2(x-alpha)f_<2>(x)+left(x-alpharight)^2f’_<2>(x).$$

Если $k=2$, тогда $alpha$ — простой корень $f'(x)$, значит $f'(x)barvdotsleft(x-alpharight)^2$. Получаем, что $f_<2>(x)barvdots(x-alpha)$, потому $alpha$ — двукратный корень $f(x)$.

Если же $kgeqslant3$, то $f'(x),vdots,left(x-alpharight)^2$, тогда из текущего представления $f'(x)$ видно, что $f_<2>(x),vdots,(x-alpha)$, значит $f_<2>(x)$ можно представить в следующем виде: $$f_<2>(x)=(x-alpha)f_<3>(x).$$ Откуда $f(x)$ представляется как: $$f(x)=left(x-alpharight)^3f_<3>(x).$$

Продолжая такой процесс, получим: $$f(x)=left(x-alpharight)^f_(x).$$ Дифференцируя $f(x)$, получаем: $$f'(x)=(k-1)left(x-alpharight)^f_(x)+left(x-alpharight)^f’_(x).$$ По аналогии получаем, что $f_(x),vdots,(x-alpha)$, откуда $$f_(x)=(x-alpha)f_(x).$$ Тогда $f(x)$ представляется так: $$f(x)=left(x-alpharight)^kf_(x).$$Дифференцируя $f(x)$ ещё раз, получаем следующее: $$f'(x)=kleft(x-alpharight)^f_(x)+left(x-alpharight)^kf’_(x).$$Теперь, если $f_(x),vdots,(x-alpha)$, то $alpha$ — корень $f'(x)$ кратности больше чем $k-1$, что противоречит условию. Значит $f_(x) barvdots(x-alpha)$, тогда $alpha$ — корень $f(x)$ кратности $k$, что и требовалось доказать.

Примеры решения задач

1. Используя критерий кратности корня, найти кратность корня $-1$ многочлена $f(x)=x^3-3x-2$.

Продифференцируем $f(x)$, получим: $$f'(x)=3x^2-3=3(x^2-1)=3(x-1)(x+1).$$
Учитывая, что $-1$ — простой корень $f'(x)$ и $f(-1)=0$, тогда, по критерию кратности корня, $-1$ — корень второй кратности многочлена $f(x)$.

Продифференцируем $f(x)$, получим: $$f'(x)=3x^2-14x+15.$$ Легко проверить, что $f'(3)=27-42+15=0$. Теперь продифференцируем $f'(x)$, получим: $$f^<primeprime>(x)=6x-14.$$ Подставляя $3$ имеем $f^<primeprime>(3)=4ne0$. Значит $3$ — простой корень $f'(x)$. Так как $3$ — корень $f(x)$ и простой корень $f'(x)$, то, пользуясь критерием, получаем, что $3$ — корень второй кратности многочлена $f(x)$.

Продифференцируем $f(x)$, получим: $$f'(x)=4x^3-12x^2+12x-4.$$Значит $g(x)=f'(x)$, тогда, пользуясь критерием кратности корня, если $1$ — корень четвертой кратности многочлена $f(x)$, то $1$ — корень третьей кратности многочлена $f'(x)$.

Пользуясь критерием кратности корня, $alpha$ — корень второй кратности многочлена $f'(x)$. Тогда имеют место следующие равенства: $$f'(x)=left(x-alpharight)^2h_<1>(x),, h_<1>(alpha)ne0,$$ $$g(x)=left(x-alpharight)^2h_<2>(x),, h_<2>(alpha)ne0.$$Тогда $l(x)$ можно представить в следующем виде: $$l(x)=left(x-alpharight)^4h_<1>(x)h_<2>(x)=left(x-alpharight)^4h(x),, h(alpha)ne0.$$Получаем, что $alpha$ — корень четвертой кратности многочлена $l(x)$.

По критерию кратности корня, $alpha$ — корень шестой кратности многочлена $f'(x)$. Рассуждая аналогично, можем применить критерий кратности корня ещё раз и получить, что $alpha$ — корень пятой кратности многочлена $f^<primeprime>(x)$. Применяя критерий в очередной раз, получаем результат, что $alpha$ — корень четвертой кратности многочлена $f^<primeprimeprime>(x)$.

Источник

Кратные корни многочлена

При рассмотрении вопроса о корнях многочлена, особо выделяют понятие кратных корней.

Определение. Пусть задан многочлен $fleft(xright) in Pleft[xright]$ ($Pleft[xright]$ — множество всех многочленов от буквы $x$ над полем $P$) и $alpha$, где $alpha$ — корень многочлена $fleft(xright)$. Элемент $alpha$ назовем $k$-кратным ($k in mathbb $, $k>1$) корнем многочлена, если имеет место следующее представление: $$fleft(xright)=left(x-alpharight)^k f_<1>left(xright),, f_<1>left(alpharight) ne 0.$$

Принято рассматривать понятие кратного корня для $k>1$. Если же $fleft(xright)$ можно представить следующим образом: $$fleft(xright)=left(x-alpharight) f_<1>left(xright),, f_<1>left(alpharight) ne 0,$$ то $alpha$ называется простым (однократным) корнем многочлена$fleft(xright)$. Если для $fleft(xright)$ имеет место следующее равенство: $$fleft(xright)=left(x-alpharight)^2 f_<1>left(xright),, f_<1>left(alpharight) ne 0,$$ то $alpha$ называется двукратным корнем многочлена $fleft(xright)$. Аналогично, существуют корни трехкратные, четырехкратные и так далее.

Часто условие $f_<1>left(alpharight) ne 0$ заменяют на $f_<1>left(xright),barvdots,(x-alpha)$. Эквивалентность этих условий вытекает из следствий теоремы Безу. Тогда, набор условий, что $f(x),vdots,left(x-alpharight)^k$, но $f(x),barvdots,left(x-alpharight)^$ эквивалентен тому, что $alpha$ — $k$-кратный корень многочлена $f(x)$.

Процесс нахождения кратности корня

Пусть задан многочлен $fleft(xright) in Pleft[xright]$ и его корень $alpha$ ( $deg fleft(xright) > 0$). Рассмотрим задачу о нахождении кратности корня $alpha$.

Так как $alpha$ — корень $fleft(xright)$, то имеет место следующее представление: $$fleft(xright)=left(x-alpharight)f_<1>left(xright).$$ Тогда, если $alpha$ не является корнем $f_<1>left(xright)$ ($f_<1>left(alpharight) ne 0$), то, по определению, $alpha$ — простой корень многочлена $fleft(xright)$. В противном случае, $alpha$ — $k$-кратный ($k in mathbb $, $k > 1 $) корень $fleft(xright)$. Задача сводится к нахождению $k-1$, то есть к нахождению кратности корня $f_<1>left(xright)$, где $deg f_<1>left(xright) = deg fleft(xright) — 1$. Учитывая, что $deg fleft(xright) > 0$, то повторение такого алгоритма решает задачу. Для этого используется алгоритм Горнера.

Стоит упомянуть, что иногда удобней пользоваться критерием кратности корня.

Примеры решения задач

1. Пусть задан многочлен $fleft(xright)=x^3-3x^2+4$. Определить, является ли $2$ корнем многочлена $f(x)$. В случае положительного ответа найти его кратность.

Для решении задачи воспользуемся алгоритмом Горнера. Стоит обратить внимание на то, что хоть и слагаемое вида $a_<1>x^1$ отсутствует в записи, но нулевой коэффициент необходимо не забыть занести в таблицу.

$1$	$-3$	$0$	$4$
$2$	$1$	$-1$	$-2$	$0$
$2$	$1$	$1$	$0$
$2$	$1$	$3$

Из таблицы видно, что многочлен $f(x)$ поделился на $left(x-2right)^2$ без остатка, а на $left(x-2right)^3$ — нет. Получаем, что $2$ — двукратный корень многочлена $f(x)$.

Так как $alpha$ — двукратный корень многочлена $f(x)$, то $f(x)$ представим в следующем виде: $$fleft(xright)=left(x-alpharight)^2 f_<1>left(xright),$$где $f_<1>(alpha) ne 0$. Аналогично, $g(x)$ можно представить следующим образом: $$gleft(xright)=left(x-alpharight) g_<1>left(xright),$$где $g_<1>(alpha) ne 0$. Тогда, $$f(x)g(x)=left(x-alpharight)^2f_<1>(x)(x-alpha)g_<1>(x)=left(x-alpharight)^3f_<1>(x)g_<1>(x).$$Так как $f_<1>(alpha) ne 0$ и $g_<1>(alpha) ne 0$, то $f_<1>(alpha)g_<1>(alpha)ne0$. Обозначим $f(x)g(x)=h(x)$, $f_<1>(x)g_<1>(x)=h_<1>(x)$, тогда перепишем выражение многочлена $f(x)g(x)$ следующим образом: $$h(x)=left(x-alpharight)^3h_<1>(x),$$ где $h_<1>(alpha)ne0$. Тогда по определению $alpha$ — корень $f(x)g(x)$ третьей кратности.

Для решении задачи воспользуемся алгоритмом Горнера.

$1$	$5$	$10$	$10$	$5$	$1$
$-1$	$1$	$4$	$6$	$4$	$1$	$0$
$-1$	$1$	$3$	$3$	$1$	$0$
$-1$	$1$	$2$	$1$	$0$
$-1$	$1$	$1$	$0$
$-1$	$1$	$0$

Из таблицы видно, что многочлен пятой степени $f(x)$ поделился на $left(x+1right)^5$ без остатка. Получаем, что $-1$ — корень пятой кратности.

По определению, для того, что бы $2$ была корнем второй кратности, необходимо что бы имело место следующее представление: $$f(x)=left(x-2right)^2f_<1>(x),, f_<1>(2) ne 0.$$С другой стороны, в нашем случае: $$f_<1>(x)=x^2+x-6=(x-2)(x+3),, f_<1>(2)=0.$$ Получаем, что $2$ не корень второй кратности. Тогда найдем его кратность. Выразим $f(x)$ подставив $f_<1>(x)=(x-2)(x+3)$:$$f(x)=left(x-2right)^3(x+3)=left(x-2right)^3f_<2>(x),$$ $f_<2>(2)=(2+3)=5ne0$. Значит, по определению, $2$ — корень многочлена $f(x)$ третьей кратности.

Представим исходный многочлен следующим образом: $$f(x)=x^4(x^4-8x^3+10x^2-1).$$
Обозначим $f_<1>(x)=x^4-8x^3+10x^2-1$. Легко убедиться, что $f_<1>(0)=-1ne0$. Получаем, что, по определению кратного корня, $0$ — корень многочлена $f(x)$ четвертой кратности.

Источник

Разложение полинома на множители. Кратные корни. Теорема о необходимом и достаточном условии существовании кратного корня

Любой многочлен степени n вида представляется произведением постоянного множителя при старшей степени и n линейных множителей , i=1, 2, …, n, то есть , причем , i=1, 2, …, n являются корнями многочлена.

Эта теорема сформулирована для комплексных корней , i=1, 2, …, n и комплексных коэффициентов , k=0, 1, 2, …, n. Она является основой для разложения любого многочлена на множители.

Если коэффициенты , k=0, 1, 2, …, n – действительные числа, то комплексные корни многочлена ОБЯЗАТЕЛЬНО будут встречаться комплексно сопряженными парами.

К примеру, если корни и многочлена являются комплексно сопряженными, а остальные корни действительные, то многочлен представится в виде , где

Замечание.

Среди корней многочлена могут быть повторяющиеся.

Доказательство теоремы проводится с использованием основной теоремы алгебры и следствия из теоремы Безу.

Определение. Число называется корнем полинома , если .

В силу теоремы Безу это равносильно тому, что .

Определение. Число называется корнем кратности полинома , если и . Корни кратности 1 называются простыми корнями, корни кратности больше 1 называются кратными корнями.

Теорема. Если — корень кратности полинома , то — корень кратности полинома . Если — общий корень , то — кратный корень .

Доказательство. Пусть — корень кратности полинома .

1. Если , то — корень кратности многочлена .

2. Если корень , то и, значит, — кратный корень многочлена .

Наибольший общий делитель. Алгоритм Евклида

Общим делителем нескольких чисел называется число, которое является делите-лем каждого из них. Например, числа 36, 60, 42 имеют общие делители 2, 3 и 6. Среди всех общих делителей всегда есть наибольший, в данном случае это 6. Это и есть наибольший общий делитель (НОД).

Чтобы найти наибольший общий делитель (НОД) нескольких чисел надо:

1) представить каждое число как произведение его простых множителей, например:

360 = 2 · 2 · 2 · 3 · 3 · 5 ,

2) записать степени всех простых множителей:

360 = 2 · 2 · 2 · 3 · 3 · 5 = 2 3 · 3 2 · 5 1 ,

3) выписать все общие делители (множители) этих чисел;

4) выбрать наименьшую степень каждого из них, встретившуюся во всех произведениях;

5) перемножить эти степени.

Алгоритм Евклида для целых чисел

Пусть и — целые числа, не равные одновременно нулю, и последовательность чисел

определена тем, что каждое — это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть

Тогда НОД(a,b), наибольший общий делитель и , равен , последнему ненулевому члену этой последовательности.

Существование таких , то есть возможность деления с остатком на для любого целого и целого , доказывается индукцией по m.

Корректность этого алгоритма вытекает из следующих двух утверждений:

Пусть , тогда НОД (a, b) = НОД (b, r).

Операция освобождения полинома от кратных корней

Вещественные полиномы. Разложение полинома на множители первой и второй степени.

Выражения вида 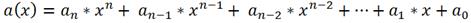называются многочленами от x степени n (a_n ≠ 0) с действительными коэффициентами, если a_i, i = 0,1,2. n — действительные числа.

Как известно, если комплексное число – корень многочлена, то обязательно и комплексно сопряженное ему число является корнем многочлена. Поэтому их произведение

представляет собой квадратичное выражение.

Таким образом, любой многочлен с действительными коэффициентами всегда можно представить в виде произведения линейных и квадратичных множителей

где , а x₁, . x_s — действительные корни многочлена. То есть, если известны все корни многочлена с действительными коэффициентами, то можно сразу написать его разложение на множители.

Подбор корней многочлена.

В общем случае найти корни многочлена степени n довольно сложная задача, но можно попытаться найти хотя бы один корень x₀. Разделив исходный многочлен на одночлен x-x₀, мы получим многочлен степени n-1. Тем самым мы упростили исходную задачу, так как раскладывать на множители теперь надо многочлен степени n-1. Например, для многочлена третьей степени после деления на x₀ мы получим многочлен второй степени, корни которого найдем, просто решив квадратное уравнение. Существенную помощь в подборе рациональных корней многочлена может оказать следующая теорема.

Теорема. Если многочлен a(x)= a_n*x n + a_n-1*x n-1 + a_n-2*x n-2 + . + a₁*x + a₀, a_n ≠ 0 c целыми коэффициентами имеет рациональный корень x₀ =

(причем эта дробь несократима), то p – делитель свободного члена a₀, а q – делитель старшего коэффициента a_n. Из этой теоремы следует, что если старший коэффициент равен единице, то целые корни многочлена следует искать только среди делителей свободного члена.

Источник