Как найти корень квадратного трехчлена 8 класс - Сайт, где вы сможете решить свои вопросы

Квадратным трехчленом называется многочлен вида (ax^2 + bx + c), где (x) – переменная, (a, b, c) – некоторые числа, причем (a ≠ 0).

Числа (a,b,c) называются коэффициентами. Число (a) называется старшим коэффициентом, число (b) – коэффициентом при (x), а число (c) называют свободным членом.

Корнем квадратного трехчлена (ax^2 +bx+c) называют любое значение переменной (x), такое, что квадратный трехчлен (ax^2 +bx+c) обращается в нуль.

Для того чтобы найти корни квадратного трехчлена, необходимо решить квадратное уравнение вида (ax^2 +bx+c =0).

Нахождение корней квадратного трехчлена

1 способ. Нахождение корней квадратного трехчлена по формуле.

Найти значение дискриминанта по формуле (D =b^2-4ac).
В зависимости от значения дискриминанта вычислить корни по формулам:

a) если (D>0), то квадратный трехчлен имеет два корня: (x_1=frac{-b-sqrt{D}}{2a}; x_2=frac{-b+sqrt{D}}{2a};)

b) если (D=0), то квадратный трехчлен имеет один корень: (x=-frac{b}{2a};)

c) если (D<0), то квадратный трехчлен не имеет корней.

2 способ. Нахождение корней квадратного трехчлена выделением полного квадрата.

Рассмотрим на примере приведенного квадратного трехчлена. Приведенное квадратное уравнение – уравнение, у которого на старший коэффициент равен единице.

Найдем корни квадратного трехчлена (x^2-4x-60). Для этого решим следующее квадратное уравнение: (x^2-4x-60=0).

Выделим полный квадрат из трехчлена, стоящего в левой части уравнения:

((x^2-2cdot xcdot2+2^2)-2^2-60=0 \(x-2)^2-64=0 \(x-2)^2-8^2=0.)

Левую часть уравнения разложим на множители по формуле разности квадратов:

((x-2-8)(x-2+8)=0 \(x-10)(x+6)=0.)

Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый из множителей:

(x-10=0; x+6=0 \x=10; x=-6)

Ответ: –6; 10.

Источник

Тема 3.

Квадратный трёхчлен и его корни. Разложение квадратного трехчлена на множители.

Квадратный трёхчлен — это многочлен вида ax² + bx + c, где x — переменная, a, b, c — некоторые числа, причем a ≠ 0.

Если x = 2, то 2x² – 5x – 3 = 2 ∙ 2² – 5 ∙ 2 – 3 = -5

Если x = -5, то 2x² – 5x – 3 = 2 ∙ (-5)² – 5 ∙ (-5) – 3 = 72

Если x = 3, то 2x² – 5x – 3 = 2 ∙ 3² – 5 ∙ 3 – 3 = 0

Корень квадратного трёхчлена – это значение переменной, при котором значение квадратного трёхчлена равно 0.

Чтобы найти корни квадратного трёхчлена ax² + bx + c, необходимо решить квадратное уравнение ax² + bx + c = 0.

2x² – 5x – 3 = 0

D = 25 – 4 ∙ 2 ∙ -3 = 49

x1=5+74=3

x1=5-74=-0,5

Ответ: -0,5; 3

Количество корней зависит от дискриминанта.

Если D > 0, то квадратный трехчлен имеет 2 корня;

Если D = 0, то квадратный трехчлен имеет 1 корень;

Если же D < 0, то квадратный трехчлен не имеет корней.

При решении задач иногда удобно выделить квадрат двучлена из квадратного трехчлена.

Например, выделим квадрат двучлена из квадратного трехчлена x² – 6x – 2.

Вспомним формулы сокращенного умножения:

a+b2=a2+2ab+b2
a-b2=a2-2ab+b2

x2-6x-2=x2-6x+9-9-2=x-32-11

При решении уравнений, неравенств удобно, когда квадратный трёхчлен представлен в виде произведения множителей, например

-2×2+14x-20=-2×2-7x+10=-2×2-2x-5x+10=-2xx-2-5x-2=-2x-2x-5

х = 2 и х = 5 – корни квадратного трехчлена.

Таким образом, ax2+bx+c=ax-x1x-x2,

где x₁, x₂– корни квадратного трехчлена ax² + bx + c.

Разложить на множители 3×2+5x-2

3×2+5x-2=0

D=52-4∙3∙-2=49

x1=-5+76=26=13

x2=-5-76=-126=-2

3×2+5x-2=3x-13x–2

3×2+5x-2=3x-1x+2

Источник

Квадратный трехчлен – это многочлен вида (ax^2+bx+c) ((a≠0)).

Пример:

(x^2-2x+1)
(3x^2-5x+6)

Почему его называют именно так? Потому что, наибольшая степень у него – квадрат, а состоит он из трех слагаемых (одночленов). Вот и получается – квадратный трехчлен.

Примеры не квадратных трехчленов:

(x^3-3x^2-5x+6) – кубический четырёхчлен
(2x+1) – линейный двучлен

Корень квадратного трехчлена:

Значение переменной (x), при котором квадратный трехчлен обращается в ноль, называют его корнем.

Пример:
У трехчлена (x^2-2x+1) корень (1), потому что (1^2-2·1+1=0)
У трехчлена (x^2+2x-3) корни (1) и (-3), потому что (1^2+2-3=0) и ((-3)^2-6-3=9-9=0)

Например: если нужно найти корни для квадратного трехчлена (x^2-2x+1), приравняем его к нулю и решим уравнение (x^2-2x+1=0).

(D=4-4cdot1=0)
(x=frac{2-0}{2}=frac{2}{2}=1)

Готово. Корень равен (1).

Разложение квадратного трёхчлена на множители:

Квадратный трехчлен (ax^2+bx+c) можно разложить как (a(x-x_1 )(x-x_2)), если дискриминант уравнения (ax^2+bx+c=0) больше нуля (x_1) и (x_2) – корни того же уравнения).

Например, рассмотрим трехчлен (3x^2+13x-10).
У квадратного уравнения (3x^2+13x-10=0) дискриминант равен 289 (больше нуля), а корни равны (-5) и (frac{2}{3}). Поэтому (3x^2+13x-10=3(x+5)(x-frac{2}{3})). В верности этого утверждения легко убедится – если мы раскроем скобки, то получим исходный трехчлен.

Квадратный трехчлен (ax^2+bx+c) можно представить как (a(x-x_1)^2), если дискриминант уравнения (ax^2+bx+c=0) равен нулю.

Например, рассмотрим трехчлен (x^2+6x+9).
У квадратного уравнения (x^2+6x+9=0) дискриминант равен (0), а единственный корень равен (-3). Значит, (x^2+6x+9=(x+3)^2) (здесь коэффициент (a=1), поэтому перед скобкой не пишется – незачем). Обратите внимание, что тоже самое преобразование можно сделать и по формулам сокращенного умножения.

Квадратный трехчлен (ax^2+bx+c) не раскладывается на множители, если дискриминант уравнения (ax^2+bx+c=0) меньше нуля.

Например, у трехчленов (x^2+x+4) и (-5x^2+2x-1) – дискриминант меньше нуля. Поэтому разложить их на множители невозможно.

Пример. Разложите на множители (2x^2-11x+12).
Решение:
Найдем корни квадратного уравнения (2x^2-11x+12=0)

(D=11^2-4 cdot 2 cdot 12=121-96=25>0)
(x_1=frac{11-5}{4}=1,5;) (x_2=frac{11+5}{4}=4.)

Значит, (2x^2-11x+12=2(x-1,5)(x-4))
Ответ: (2(x-1,5)(x-4))

Полученный ответ, может быть, записать по-другому: ((2x-3)(x-4)).

Пример. (Задание из ОГЭ) Квадратный трехчлен разложен на множители (5x^2+33x+40=5(x++ 5)(x-a)). Найдите (a).
Решение:
(5x^2+33x+40=0)
(D=33^2-4 cdot 5 cdot 40=1089-800=289=17^2)
(x_1=frac{-33-17}{10}=-5)
(x_2=frac{-33+17}{10}=-1,6)
(5x^2+33x+40=5(x+5)(x+1,6))
Ответ: (-1,6)

Смотрите также:
Квадратный трехчлен (шпаргалка)

Источник

Квадра́тное уравне́ние — алгебраическое уравнение второй степени с общим видом

${displaystyle ax^{2}+bx+c=0,;aneq 0,}$

в котором — неизвестное, а коэффициенты , и — вещественные или комплексные числа.

Корень уравнения $ax^{2}+bx+c=0$ — это значение неизвестного , обращающее квадратный трёхчлен ${displaystyle ax^{2}+bx+c}$ в ноль, а квадратное уравнение в верное числовое равенство. Также это значение называется корнем самого многочлена ${displaystyle ax^{2}+bx+c.}$

Элементы квадратного уравнения имеют собственные названия^[1]:

Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице^[1]. Такое уравнение может быть получено делением всего выражения на старший коэффициент :

${displaystyle x^{2}+px+q=0,quad p={dfrac {b}{a}},quad q={dfrac {c}{a}}.}$

Полным называют такое квадратное уравнение, все коэффициенты которого отличны от нуля.

Неполным называется такое квадратное уравнение, в котором хотя бы один из коэффициентов, кроме старшего (либо второй коэффициент, либо свободный член), равен нулю.

Квадратное уравнение является разрешимым в радикалах, то есть его корни могут быть выражены через коэффициенты в общем виде.

Исторические сведения о квадратных уравнениях[править | править код]

Древний Вавилон[править | править код]

Уже во втором тысячелетии до нашей эры вавилоняне знали, как решать квадратные уравнения^[1]. Решение их в Древнем Вавилоне было тесно связано с практическими задачами, в основном такими, как измерение площади земельных участков, земельные работы, связанные с военными нуждами; наличие этих познаний также обусловлено развитием математики и астрономии вообще. Были известны способы решения как полных, так и неполных квадратных уравнений. Приведём примеры квадратных уравнений, решавшихся в Древнем Вавилоне, используя современную алгебраическую запись:

$x^{2}+x={frac {3}{4}}; x^{2}-x=14{frac {1}{2}}.$

Правила решения квадратных уравнений во многом аналогичны современным, однако в вавилонских текстах не зафиксированы рассуждения, путём которых эти правила были получены.

Индия[править | править код]

Задачи, решаемые с помощью квадратных уравнений, встречаются в трактате по астрономии «Ариабхаттиам», написанным индийским астрономом и математиком Ариабхатой в 499 году нашей эры. Один из первых известных выводов формулы корней квадратного уравнения принадлежит индийскому учёному Брахмагупте (около 598 г.)^[1]; Брахмагупта изложил универсальное правило решения квадратного уравнения, приведённого к каноническому виду: ${displaystyle ax^{2}+bx=c;}$ притом предполагалось, что в нём все коэффициенты, кроме могут быть отрицательными. Сформулированное учёным правило по своему существу совпадает с современным.

Корни квадратного уравнения на множестве действительных чисел[править | править код]

I способ. Общая формула для вычисления корней с помощью дискриминанта[править | править код]

Дискриминантом квадратного уравнения ${displaystyle ax^{2}+bx+c=0}$ называется величина ${displaystyle {mathcal {D}}=b^{2}-4ac}$ .

Условие
Количество корней	Два корня	Один корень кратности 2 (другими словами, два равных корня)	Действительных корней нет
Формула	${displaystyle x_{1,2}={frac {-bpm {sqrt {mathcal {D}}}}{2a}}}$ (1)	${displaystyle x=-{frac {b}{2a}}}$	—

Данный метод универсальный, однако не единственный.

II способ. Корни квадратного уравнения при чётном коэффициенте b[править | править код]

Для уравнений вида $ax^{2}+2kx+c=0$ , то есть при чётном , где

$k={frac {1}{2}}b,$

вместо формулы (1) для нахождения корней существует возможность использования более простых выражений^[1].

Примечание: данные ниже формулы можно получить, подставив в стандартные формулы выражение b = 2k, через несложные преобразования.

Дискриминант	Корни
неприведённое	приведённое	D > 0	неприведённое	приведённое
удобнее вычислять значение четверти дискриминанта: ${frac {D}{4}}=k^{2}-ac$ Все необходимые свойства при этом сохраняются.	${frac {D}{4}}=k^{2}-c$ .	$x_{1,2}={frac {-kpm {sqrt {k^{2}-ac}}}{a}}.$	$x_{1,2}=-kpm {sqrt {k^{2}-c}}$
D = 0	$x={frac {-k}{a}}$

III способ. Решение неполных квадратных уравнений[править | править код]

К решению неполных квадратных уравнений практикуется особый подход. Рассматриваются три возможных ситуации.

IV способ. Использование частных соотношений коэффициентов[править | править код]

Существуют частные случаи квадратных уравнений, в которых коэффициенты находятся в соотношениях между собой, позволяющих решать их гораздо проще.

Корни квадратного уравнения, в котором сумма старшего коэффициента и свободного члена равна второму коэффициенту[править | править код]

Если в квадратном уравнении $ax^{2}+bx+c=0$ сумма первого коэффициента и свободного члена равна второму коэффициенту: a+c=b , то его корнями являются и число, противоположное отношению свободного члена к старшему коэффициенту ( $-{frac {c}{a}}$ ).

Доказательство

Способ 1. Сначала выясним, действительно ли такое уравнение имеет два корня (в том числе, два совпадающих):

${displaystyle {mathcal {D}}=b^{2}-4ac=(a+c)^{2}-4ac=a^{2}+2ac+c^{2}-4ac=a^{2}-2ac+c^{2}=(a-c)^{2}}$

Да, это так, ведь при любых действительных значениях коэффициентов $(a-c)^{2}geqslant 0$ , а значит и дискриминант неотрицателен. Таким образом, если anot =c , то уравнение имеет два корня, если же a=c , то оно имеет только один корень.
Найдём эти корни:

${displaystyle x_{1,2}={frac {-bpm {sqrt {mathcal {D}}}}{2a}}={frac {-(a+c)pm {sqrt {(a-c)^{2}}}}{2a}}={frac {-a-cpm |a-c|}{2a}}={frac {-a-cpm amp c}{2a}}}$

$x_{1}={frac {-a-c-a+c}{2a}}={frac {-2a}{2a}}=-1;$

$x_{2}={frac {-a-c+a-c}{2a}}={frac {-2c}{2a}}=-{frac {c}{a}}.$

В частности, если a=c , то корень будет один: -1.

Способ 2.

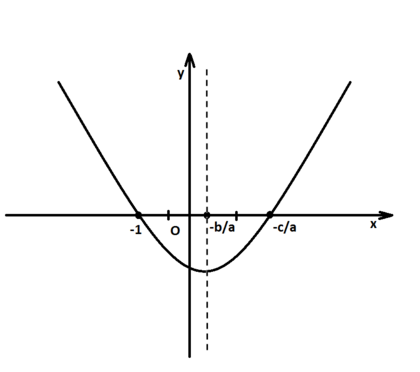
Геометрическая интерпретация: парабола, заданная аналитически указанной формулой, пересекает ось x в двух точках, абсциссами которых и являются корни, хотя бы один из которых равен -1

Используем геометрическую модель корней квадратного уравнения: их мы будем рассматривать как точки пересечения параболы $y=ax^{2}+bx+c$ с осью абсцисс. Всякая парабола вне зависимости от задающего её выражения является фигурой, симметричной относительно прямой $x=-{frac {b}{2a}}$ . Это означает, что отрезок всякой перпендикулярной к ней прямой, отсекаемый на ней параболой, делится осью симметрии пополам. Сказанное, в частности, верно и для оси абсцисс. Таким образом, для всякой параболы справедливо одно из следующих равенств: $-{frac {b}{2a}}+rho (x_{1};-{frac {b}{2a}})=x_{2}$ (если $x_{1}<x_{2}$ ) или $-{frac {b}{2a}}-rho (-{frac {b}{2a}};x_{1})=x_{2}$ (если верно неравенство противоположного смысла). Используя тождество , выражающее геометрический смысл модуля, а также принимая, что $x_{1}=-1$ (это можно доказать, подставив равенство в квадратный трёхчлен: $acdot (-1)^{2}+bcdot (-1)+c=(a+c)-b=0$ , поэтому -1 – корень такого уравнения) , приходим к следующему равенству: $-{frac {b}{2a}}pm |-{frac {b}{2a}}-(-1)|=x_{2}.$ Если учитывать, что разность в том случае, когда мы прибавляем модуль, всегда положительна, а в том, когда отнимаем – отрицательна, что говорит о тождественности этих случаев, и, к тому же, помня о равенстве b-a=c , раскрываем модуль: $x_{2}=-{frac {b}{2a}}-{frac {b}{2a}}+1=-{frac {2b-2a}{2a}}=-{frac {b-a}{a}}=-{frac {c}{a}}$ . Во втором случае,совершив аналогичные преобразования, придём к тому же результату, ч.т.д.

Отсюда следует, что перед решением какого-либо квадратного уравнения целесообразна проверка возможности применения к нему этой теоремы: сравнить сумму старшего коэффициента и свободного члена со вторым коэффициентом.

Корни квадратного уравнения, сумма всех коэффициентов которого равна нулю[править | править код]

Если в квадратном уравнении сумма всех его коэффициентов равна нулю ( a+b+c=0 ), то корнями такого уравнения являются и отношение свободного члена к старшему коэффициенту ( ${frac {c}{a}}$ ).

Доказательство

Способ 1. Прежде всего заметим, что из равенства a+b+c=0 следует, что
Установим количество корней:

${displaystyle {mathcal {D}}=b^{2}-4ac=(-(a+c))^{2}-4ac=a^{2}+2ac+c^{2}-4ac=a^{2}-2ac+c^{2}=(a-c)^{2}.}$

При любых значениях коэффициентов уравнение имеет хотя бы один корень: действительно, ведь при любых значениях коэффициентов $(a-c)^{2}geqslant 0$ , а значит и дискриминант неотрицателен. Обратите внимание, что если anot =c , то уравнение имеет два корня, если же a=c , то только один.
Найдём эти корни:

${displaystyle x_{1,2}={frac {-bpm {sqrt {mathcal {D}}}}{2a}}={frac {a+cpm {sqrt {(a-c)^{2}}}}{2a}}={frac {a+cpm |a-c|}{2a}}={frac {a+cpm amp c}{2a}};}$

$x_{1}={frac {a+c+a-c}{2a}}={frac {2a}{2a}}=1;$

$x_{2}={frac {a+c-a+c}{2a}}={frac {2c}{2a}}={frac {c}{a}},$

что и требовалось доказать.

В частности, если a=c

, то уравнение имеет только один корень, которым является число

Способ 2. Пользуясь данным выше определением корня квадратного уравнения, обнаруживаем путём подстановки, что число 1 является таковым в рассматриваемом случае: $acdot 1^{2}+bcdot 1+c=0$ – верное равенство, следовательно, единица – корень такого вида квадратных уравнений. Далее, по теореме Виета находим второй корень: согласно этой теореме, произведение корней уравнения равно числу, равному отношению свободного члена к старшему коэффициенту – $x_{1}x_{2}={frac {c}{a}}Rightarrow x_{2}={frac {c}{ax_{1}}}={frac {c}{acdot 1}}={frac {c}{a}}$ , ч.т.д.

Отсюда следует, что перед решением уравнения стандартными методами целесообразна проверка применимости к нему этой теоремы, а именно сложение всех коэффициентов данного уравнения и установление, не равна ли нулю эта сумма.

V способ. Разложение квадратного трёхчлена на линейные множители[править | править код]

Если трёхчлен вида ${displaystyle ax^{2}+bx+c~(anot =0)}$ удастся каким-либо образом представить в качестве произведения линейных множителей , то можно найти корни уравнения $ax^{2}+bx+c=0$ — ими будут $-{frac {m}{k}}$ и $-{frac {n}{l}}$ , действительно, ведь ${displaystyle (kx+m)(lx+n)=0Longleftrightarrow {biggl [}{begin{array}{lcl}kx+m=0,\lx+n=0,end{array}}}$ а решив указанные линейные уравнения, получим вышеописанное. Квадратный трёхчлен не всегда раскладывается на линейные множители с действительными коэффициентами: это возможно, если соответствующее ему уравнение имеет действительные корни.

Рассматриваются некоторые частные случаи.

Использование формулы квадрата суммы (разности)[править | править код]

Если квадратный трёхчлен имеет вид $(ax)^{2}+2abx+b^{2}$ , то применив к нему названную формулу, можно разложить его на линейные множители и, значит, найти корни:

${displaystyle (ax)^{2}+2abx+b^{2}=(ax+b)^{2},}$

${displaystyle (ax+b)^{2}=0,}$

$x=-{frac {b}{a}}.$

Выделение полного квадрата суммы (разности)[править | править код]

Также названную формулу применяют, пользуясь методом, получившим названия «выделение полного квадрата суммы (разности)». Применительно к приведённому квадратному уравнению с введёнными ранее обозначениями, это означает следующее:

прибавляют и отнимают одно и то же число:
$x^{2}+px+({frac {p}{2}})^{2}-({frac {p}{2}})^{2}+q=0;$ .
применяют формулу к полученному выражению, переносят вычитаемое и свободный член в правую часть:
${displaystyle (x^{2}+2{frac {p}{2}}x+({frac {p}{2}})^{2})+(-({frac {p}{2}})^{2}+q)=0,}$
$(x+{frac {p}{2}})^{2}={frac {p^{2}}{4}}-q;$
извлекают из левой и правой частей уравнения квадратный корень и выражают переменную:
${displaystyle x+{frac {p}{2}}=pm {sqrt {{frac {p^{2}}{4}}-q}},}$
$x_{1,2}=-{frac {p}{2}}pm {sqrt {{frac {p^{2}}{4}}-q}}.$

Примечание: данная формула совпадает с предлагаемой в разделе «Корни приведённого квадратного уравнения», которую, в свою очередь, можно получить из общей формулы (1) путём подстановки равенства a = 1. Этот факт не просто совпадение: описанным методом, произведя, правда, некоторые дополнительные рассуждения, можно вывести и общую формулу, а также доказать свойства дискриминанта.

VI способ. Использование прямой и обратной теоремы Виета[править | править код]

Прямая теорема Виета (см. ниже) и обратная ей теорема позволяют решать приведённые квадратные уравнения устно, не прибегая к вычислениям по формуле (1).

Согласно обратной теореме, всякая пара чисел (число) $x_{1},x_{2}$ , будучи решением системы уравнений

${displaystyle {begin{cases}x_{1}+x_{2}=-p,\x_{1}x_{2}=q,end{cases}}}$

являются корнями уравнения $x^{2}+px+q=0$

Подобрать устно числа, удовлетворяющие этим уравнениям, поможет прямая теорема. С её помощью можно определить знаки корней, не зная сами корни. Для этого следует руководствоваться правилом:

1) если свободный член отрицателен, то корни имеют различный знак, и наибольший по модулю из корней — знак, противоположный знаку второго коэффициента уравнения;

2) если свободный член положителен, то оба корня обладают одинаковым знаком, и это — знак, противоположный знаку второго коэффициента.

VII способ. Метод «переброски»[править | править код]

По своей сущности метод «переброски» является просто модификацией теоремы Виета.

Метод «переброски» — это сведение уравнения, которое нельзя привести так, чтобы все коэффициенты остались целыми, к приведённому уравнению с целыми коэффициентами:

1) умножаем обе части на старший коэффициент:

${displaystyle ax^{2}+bx+c=0quad mid ;cdot a,}$

${displaystyle (ax)^{2}+b(ax)+ac=0;}$

2) заменяем

${displaystyle y^{2}+by+ac=0.}$

Далее решаем уравнение относительно y по методу, описанному выше, и находим x = y/a.

Как можно заметить, в методе «переброски» старший коэффициент как раз «перебрасывается» к свободному члену.

Графическое решение квадратного уравнения[править | править код]

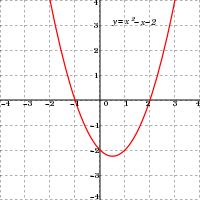
Графиком квадратичной функции является парабола. Решениями (корнями) квадратного уравнения называют абсциссы точек пересечения параболы с осью абсцисс. Если парабола, описываемая квадратичной функцией, не пересекается с осью абсцисс, уравнение не имеет вещественных корней. Если парабола пересекается с осью абсцисс в одной точке (в вершине параболы), уравнение имеет один вещественный корень (также говорят, что уравнение имеет два совпадающих корня). Если парабола пересекает ось абсцисс в двух точках, уравнение имеет два вещественных корня (см. изображение справа.)

Если коэффициент положительный, ветви параболы направлены вверх и наоборот. Если коэффициент положительный (при положительном , при отрицательном наоборот), то вершина параболы лежит в левой полуплоскости и наоборот.

Графический способ решения квадратных уравнений[править | править код]

Помимо универсального способа, описанного выше, существует так называемый графический способ. В общем виде этот способ решения рационального уравнения вида заключается в следующем: в одной системе координат строят графики функций y=f(x) и y=g(x) и находят абсциссы общих точек этих графиков; найденные числа и будут корнями уравнения.

Есть всего пять основных способов графического решения квадратных уравнений.

Приём I[править | править код]

Для решения квадратного уравнения $ax^{2}+bx+c=0$ строится график функции $y=ax^{2}+bx+c$
и отыскиваются абсциссы точек пересечения такого графика с осью .

Приём II[править | править код]

Для решения того же уравнения этим приёмом уравнение преобразуют к виду $ax^{2}=-bx-c$
и строят в одной системе координат графики квадратичной функции $y=ax^{2}$ и линейной функции y=-bx-c , затем находят абсциссу точек их пересечения.

Приём III[править | править код]

Данный приём подразумевает преобразование исходного уравнения к виду $a(x+l)^{2}+m=0$ , используя метод выделения полного квадрата суммы (разности) и затем в $a(x+l)^{2}=-m$ . После этого строятся график функции $y=a(x+l)^{2}$ (им является график функции $y=ax^{2}$ , смещённый на |l| единиц масштаба вправо или влево в зависимости от знака) и прямую y=-m , параллельную оси абсцисс. Корнями уравнения будут абсциссы точек пересечения параболы и прямой.

Приём IV[править | править код]

Квадратное уравнение преобразуют к виду $ax^{2}+c=-bx$ , строят график функции $y=ax^{2}+c$ (им является график функции $y=ax^{2}$ , смещённый на единиц масштаба вверх, если этот коэффициент положителен, либо вниз, если он отрицателен), и y=-bx , находят абсциссы их общих точек.

Приём V[править | править код]

Квадратное уравнение преобразуют к особому виду:

${displaystyle {dfrac {ax^{2}}{x}}+{dfrac {bx}{x}}+{dfrac {c}{x}}={dfrac {0}{x}};}$

${displaystyle ax+b+{dfrac {c}{x}}=0;}$

затем

${displaystyle ax+b=-{dfrac {c}{x}}.}$

Совершив преобразования, строят графики линейной функции y=ax+b и обратной пропорциональности $y=-{frac {c}{x}}; (cnot =0)$ , отыскивают абсциссы точек пересечения этих графиков. Этот приём имеет границу применимости: если c=0 , то приём не используется.

Решение квадратных уравнений с помощью циркуля и линейки[править | править код]

Описанные выше приёмы графического решения имеют существенные недостатки: они достаточно трудоёмки, при этом точность построения кривых — парабол и гипербол — низка. Указанные проблемы не присущи предлагаемому ниже методу, предполагающему относительно более точные построения циркулем и линейкой.

Чтобы произвести такое решение, нужно выполнить нижеследующую последовательность действий.

Построить в системе координат окружность с центром в точке ${displaystyle Sleft(-{dfrac {b}{2a}};{dfrac {a+c}{2a}}right)}$ , пересекающую ось в точке .
Далее возможны три случая:

Доказательство

Иллюстрация к доказательству.

Рассматриваемый способ предполагает построение окружности, пересекающей ось ординат в точках (точке), абсциссы которых являются корнями (или корнем) решаемого уравнения. Как нужно строить такую окружность? Предположим, что она уже построена. Окружность определяется однозначно заданием трёх своих точек. Пусть в случае, если корня два, это будут точки $A(x_{1};0),B(x_{2};0),C(0;1)$ , где $x_{1},x_{2}$ , естественно, действительные корни квадратного уравнения (подчёркиваем: если они имеются). Найдём координаты центра такой окружности. Для этого докажем, что эта окружность проходит через точку $D(0;{frac {c}{a}})$ . Действительно, согласно теореме о секущих, в принятых обозначениях выполняется равенство (см рисунок). Преобразовывая это выражение, получаем величину отрезка OD, которой и определяется искомая ордината точки D: ${displaystyle OD={dfrac {OAcdot OB}{OC}}={frac {x_{1}x_{2}}{1}}={frac {c}{a}}}$ (в последнем преобразовании использована теорема Виета (см. ниже в одноимённом разделе)). Если же корень один, то есть ось абсцисс будет касательной к такой окружности, и окружность пересекает ось y в точке с ординатой 1, то она обязательно пересечёт её и в точке с указанной выше ординатой (в частности, если 1=c/a, это могут быть совпадающие точки), что доказывается аналогично с использованием уже теоремы о секущей и касательной, являющаяся частным случаем теоремы о секущих. В первом случае ( ${displaystyle {dfrac {c}{a}}not =1}$ ), определяющими будут точка касания, точка оси y с ординатой 1, и её же точка с ординатой ${displaystyle {dfrac {c}{a}}}$ . Если c/a и 1 – совпадающие точки, а корня два, определяющими будут эта точка и точки пересечения с осью абсцисс. В случае, когда (1=c/a) и корень один, указанных сведений достаточно для доказательства, так как такая окружность может быть только одна – её центром будет вершина квадрата, образуемого отрезками касательных и перпендикулярами, а радиус – стороне этого квадрата, составляющей 1. Пускай S – центр окружности, имеющей с осью абсцисс две общие точки. Найдём его координаты: для этого опустим от этой точки перпендикуляры к координатным осям. Концы этих перпендикуляров будут серединами отрезков AB и CD – ведь треугольники ASB и CSD равнобедренные, так как в них AS=BS=CS=DS как радиусы одной окружности, следовательно, высоты в них, проведённые к основаниям, также являются и медианами. Найдём координаты середин названных отрезков. Так как парабола симметрична относительно прямой ${displaystyle x=-{dfrac {b}{2a}}}$ , то точка этой прямой с такой же абсциссой будет являться серединой отрезка AB. Следовательно, абсцисса точки S равна этому числу. В случае же, если уравнение имеет один корень, то ось x является касательной по отношению к окружности,поэтому, согласно её свойству, её радиус перпендикулярен оси, следовательно, и в этом случае указанное число – абсцисса центра. Её ординату найдём так: ${displaystyle {dfrac {CD}{2}}={dfrac {OC+(OC+CD)}{2}}={dfrac {OC+OD}{2}}={dfrac {1+{dfrac {c}{a}}}{2}}={dfrac {a+c}{2a}}}$ . В третьем из возможных случаев, когда ca=1 (и, значит, a=c), то ${displaystyle {dfrac {c}{a}}=1={dfrac {2a}{2a}}={dfrac {a+c}{2a}}}$ .

Итак, нами найдены необходимые для построения данные. Действительно, если мы построим окружность с центром в точке ${displaystyle S(-{dfrac {b}{2a}};{dfrac {c+a}{2a}})}$ , проходящую через точку C(0;1) , то она, в случаях, когда уравнение имеет действительные корни, пересечёт ось x в точках, абсциссы которых есть эти корни. Причём, если длина радиуса больше длины перпендикуляра к оси Ox, то уравнение имеет два корня (предположив обратное, мы бы получили противоречие с доказанным выше), если длины равны, то один (по той же причине), если же длина радиуса меньше длины перпендикуляра, то окружность не имеет общих точек с осью x, следовательно, и действительных корней у уравнения нет (доказывается тоже от противного: если корни есть, то окружность, проходящая через A, B, C совпадает с данной, и поэтому пересекает ось, однако она не должна пересекать ось абсцисс по условию, значит, предположение неверно).

Корни квадратного уравнения на множестве комплексных чисел[править | править код]

Уравнение с действительными коэффициентами[править | править код]

Квадратное уравнение с вещественными коэффициентами a,~b,~c всегда имеет с учётом кратности два комплексных корня, о чём гласит основная теорема алгебры. При этом, в случае неотрицательного дискриминанта корни будут вещественными, а в случае отрицательного — комплексно-сопряжёнными:

Уравнение с комплексными коэффициентами[править | править код]

В комплексном случае квадратное уравнение решается по той же формуле (1) и указанным выше её вариантам, но различимыми являются только два случая: нулевого дискриминанта (один двукратный корень) и ненулевого (два корня единичной кратности).

Корни приведённого квадратного уравнения[править | править код]

Квадратное уравнение вида $x^{2}+px+q=0,$ в котором старший коэффициент равен единице, называют приведённым. В этом случае формула для корней (1) упрощается до

$x_{1,2}=-{frac {p}{2}}pm {sqrt {left({frac {p}{2}}right)^{2}-q}}.$

Мнемонические правила:

Из «Радионяни»:

«Минус» напишем сначала,
Рядом с ним p пополам,
«Плюс-минус» знак радикала,
С детства знакомого нам.
Ну, а под корнем, приятель,
Сводится всё к пустяку:
p пополам и в квадрате
Минус прекрасное^[2] q.

Из «Радионяни» (второй вариант):

p, со знаком взяв обратным,
На два мы его разделим,
И от корня аккуратно
Знаком «минус-плюс» отделим.
А под корнем очень кстати
Половина p в квадрате
Минус q — и вот решенья,
То есть корни уравненья.

Из «Радионяни» (третий вариант на мотив Подмосковных вечеров):

Чтобы x найти к половине p,

Взятой с минусом не забудь,
Радикал приставь с плюсом минусом,
Аккуратно, не как-нибудь.
А под ним квадрат половины p,

Ты, убавь на q и конец,
Будет формула приведенная,
Рассуждений твоих венец.
Будет формула приведенная,
Рассуждений твоих венец.

Теорема Виета ^[3][править | править код]

Формулировка для приведённого квадратного уравнения[править | править код]

Сумма корней приведённого квадратного уравнения $x^{2}+px+q=0$ (вещественных или комплексных) равна второму коэффициенту , взятому с противоположным знаком, а произведение этих корней — свободному члену :

$x_{1}+x_{2}=-p,quad x_{1}x_{2}=q.$

С его помощью приведённые уравнения можно решать устно:

Для неприведённого квадратного уравнения[править | править код]

В общем случае, то есть для неприведённого квадратного уравнения ${displaystyle ax^{2}+bx+c=0colon }$

${displaystyle {begin{cases}x_{1}+x_{2}=-b/a,\x_{1}x_{2}=c/a.end{cases}}}$

На практике (следуя методу «переброски») для вычисления корней применяется модификация теорема Виета:

${displaystyle {begin{cases}x_{1}+x_{2}=-b/a&mid cdot a,\x_{1}x_{2}=c/a&mid cdot a^{2};end{cases}}}$

${displaystyle {begin{cases}(ax_{1})+(ax_{2})=-b,\(ax_{1})(ax_{2})=ac,end{cases}}}$

по которой можно устно находить ax₁, ax₂, а оттуда — сами корни:

Но у некоторых неприведённых уравнений корни можно устно угадать даже по стандартной теореме Виета:

Разложение квадратного трёхчлена на множители и теоремы, следующие из этого[править | править код]

Если известны оба корня квадратного трёхчлена, его можно разложить по формуле

${displaystyle ax^{2}+bx+c=a(x-x_{1})(x-x_{2})}$

(2)

Доказательство[править | править код]

Для доказательства этого утверждения воспользуемся теоремой Виета. Согласно этой теореме, корни $x_{1}$ и $x_{2}$ квадратного уравнения $ax^{2}+bx+c=0$ образуют соотношения с его коэффициентами: ${displaystyle x_{1}+x_{2}=-{frac {b}{a}}, x_{1}x_{2}={frac {c}{a}}}$ . Подставим эти соотношения в квадратный трёхчлен:

${displaystyle {begin{alignedat}{2}ax^{2}+bx+c&=a(x^{2}+{frac {b}{a}}x+{frac {c}{a}})=a(x^{2}-(x_{1}+x_{2})x+x_{1}x_{2})=\&=a(x^{2}-x_{1}x-x_{2}x+x_{1}x_{2})=a(x(x-x_{1})-x_{2}(x-x_{1}))\&=a(x-x_{1})(x-x_{2}).end{alignedat}}}$

В случае нулевого дискриминанта это соотношение становится одним из вариантов формулы квадрата суммы или разности.

Из формулы (2) имеются два важных следствия:

Следствие 1[править | править код]

Если квадратный трёхчлен раскладывается на линейные множители с вещественными коэффициентами, то он имеет вещественные корни.

Доказательство[править | править код]

Пусть $ax^{2}+bx+c=(kx+m)(nx+l)$ . Тогда, переписав это разложение, получим:

$(kx+m)(nx+l)=k(x+{frac {m}{k}})n(x+{frac {l}{n}})=kn(x-(-{frac {m}{k}}))(x-(-{frac {l}{n}}))$

Сопоставив полученное выражение с формулой (2), находим, что корнями такого трёхчлена являются $-{frac {m}{k}}$ и $-{frac {l}{n}}$ . Так как коэффициенты вещественны, то и числа, противоположные их отношениям также являются элементами множества .

Следствие 2[править | править код]

Если квадратный трёхчлен не имеет вещественных корней, то он не раскладывается на линейные множители с вещественными коэффициентами.

Доказательство[править | править код]

Действительно, если мы предположим противное (что такой трёхчлен раскладывается на линейные множители), то, согласно следствию 1, он имеет корни в множестве , что противоречит условию, а потому наше предположение неверно, и такой трёхчлен не раскладывается на линейные множители.

Для квадратичной функции:
f (x) = x² − x − 2 = (x + 1)(x − 2) действительной переменной x, x — координаты точки, где график пересекает ось абсцисс, x = −1 и x = 2, являются решениями квадратного уравнения: x² − x − 2 = 0.

Уравнения, сводящиеся к квадратным[править | править код]

Алгебраические[править | править код]

Уравнение вида $acdot f^{2}(x)+bcdot f(x)+c=0$ является уравнением, сводящимся к квадратному.

В общем случае оно решается методом введения новой переменной, то есть заменой где — множество значений функции , c последующим решением квадратного уравнения $acdot t^{2}+bcdot t+c=0$ .

Также при решении можно обойтись без замены, решив совокупность двух уравнений:

$f(x)={frac {-b-{sqrt {b^{2}-4cdot acdot c}}}{2a}}$

$f(x)={frac {-b+{sqrt {b^{2}-4cdot acdot c}}}{2a}}$

К примеру, если $f(x)=x^{2}$ , то уравнение принимает вид:

${displaystyle ax^{4}+bx^{2}+c=0.}$

Такое уравнение 4-й степени называется биквадратным^[4]^[1].

С помощью замены

$y=x+{dfrac {k}{x}}$

к квадратному уравнению сводится уравнение

$ax^{4}+bx^{3}+cx^{2}+kbx+k^{2}a=0,$

известное как возвратное или обобщённо-симметрическое уравнение^[1].

Дифференциальные[править | править код]

Линейное однородное дифференциальное уравнение с постоянными коэффициентами второго порядка

подстановкой $y=e^{kx}$ сводится к характеристическому квадратному уравнению:

$k^{2}+pk+q=0$

Если решения этого уравнения $k_{1}$ и $k_{2}$ не равны друг другу, то общее решение имеет вид:

$y=Ae^{k_{1}x}+Be^{k_{2}x}$

, где

— произвольные постоянные.

Для комплексных корней $k_{1,2}=k_{r}pm k_{i}i$ можно переписать общее решение, используя формулу Эйлера:

${displaystyle y=e^{k_{r}x}left(Acos {k_{i}x}+Bsin {k_{i}x}right)=Ce^{k_{r}x}cos(k_{i}x+varphi ),}$

где A, B, C, φ — любые постоянные. Если решения характеристического уравнения совпадают $k_{1}=k_{2}=k$ , общее решение записывается в виде:

$y=Axe^{kx}+Be^{kx}$

Уравнения такого типа часто встречаются в самых разнообразных задачах математики и физики, например, в теории колебаний или теории цепей переменного тока.

Примечания[править | править код]

Литература[править | править код]

Квадратное уравнение; Квадратный трёхчлен // Энциклопедический словарь юного математика / Сост. А. П. Савин. — М.: Педагогика, 1985. — С. 133-136. — 352 с.

Ссылки[править | править код]

Weisstein, Eric W. Quadratic Equation (англ.) на сайте Wolfram MathWorld.
Вывод формулы корней полного квадратного уравнения. Решение приведённых квадратных уравнений и уравнений с чётным вторым коэффициентом Архивная копия от 28 января 2016 на Wayback Machine / Фестиваль педагогических идей «Открытый урок».
Математические методы

Источник

Квадратный трехчлен. Корень квадратного трехчлена

Квадратным трехчленом называют трехчлен вида ax² +bx+c, где a,b,c некоторые произвольные вещественные (действительные) числа, а x – переменная. Причем a ≠ 0

Числа a,b,c называются коэффициентами. Число а – называется старшим коэффициентом, число b коэффициентом при х, а число с называют свободным членом.

Корнем квадратного трехчлена ax² +bx+c называют любое значение переменной х, такое, что квадратный трехчлен ax² +bx+c обращается в нуль.

Для того, чтобы найти корни квадратного трехчлена необходимо решить квадратное уравнение вида ax² +bx+c =0.

Как найти корни квадратного трехчлена

1 способ.

Нахождение корней квадратного трехчлена по формуле.

1. Найти значение дискриминанта по формуле D =b²-4ac.

2. В зависимости от значения дискриминанта вычислить корни по формулам:

Если D > 0, то квадратный трехчлен имеет два корня:

$begin mathsize 12px style x subscript 1 equals fraction numerator negative b minus square root of D over denominator 2 a end fraction semicolon space space space x subscript 2 equals fraction numerator negative b plus square root of D over denominator 2 a end fraction end style$

Если D<0, то квадратный трехчлен имеет один корень:

$begin mathsize 12px style x equals fraction numerator negative b over denominator 2 a end fraction end style$

Если дискриминант отрицателен, то квадратный трехчлен не имеет корней.

2 способ.

Нахождение корней квадратного трехчлена выделением полного квадрата. Рассмотрим на примере приведенного квадратного трехчлена. Приведенное квадратное уравнение, уравнение у которого на старший коэффициент равен единице.

Найдем корни квадратного трехчлена x²+2x-3. Для этого решим следующее квадратное уравнение: x²+2x-3=0;

Преобразуем это уравнение:

x²+2x=3;

В левой части уравнения стоит многочлен x²+2x, для того чтобы представить его в виде квадрата суммы нам необходимо чтобы там был еще один коэффициент равный 1. Добавим и вычтем из этого выражения 1, получим:

(x²+2x+1) -1=3

То, что в скобках можно представить в виде квадрата двучлена

(x+1)² -1=3;

(x+1)² = 4;

Данное уравнение распадается на два случая либо x+1=2 , либо х+1=-2.

В первом случае получаем ответ х=1, а во втором, х=-3.

Ответ: х=1, х=-3.

В результате преобразований нам необходимо получить в левой части квадрат двучлена, а в правой части некоторое число. В правой части не должна содержаться переменная.

Вопросы к конспектам

Найдите сумму квадратов уравнения: 4х = 3x²+ 1.

Найти корень уравнения: (x – 5)²– x²= 3.

Найти корень уравнения: 2x³ + 8х = x²+ 4.

Найти корни квадратного трехчлена 3х²–2x–5.

Найти корни квадратного трехчлена 3x²+2x-8.

Найти корни квадратного трехчлена x²-13x+12.

Найти корни уравнения: (3х – 1)(х + 4) = 0.

Не решая уравнений, укажите какие из них, имеют корни с противоположными знаками.
1) x² – 4,5x + 2 = 0;
2) 3x² + 8x – 3 = 0;
3) 3x² + 7x – 3 = 0;
4) x² – 7x + 10 = 0;
5) x² – 3x – 18 = 0.

Решите уравнение x²– 4x+3 = 0.

Указать промежуток, содержащий все корни квадратного уравнения x² + 1,5 x – 1 = 0.

Источник

Квадратный трехчлен – это многочлен вида (ax^2+bx+c) ((a≠0)).

Корень квадратного трехчлена:

Значение переменной (x), при котором квадратный трехчлен обращается в ноль, называют его корнем.

Разложение квадратного трёхчлена на множители:

Квадратный трехчлен (ax^2+bx+c) можно разложить как (a(x-x_1 )(x-x_2)), если дискриминант уравнения (ax^2+bx+c=0) больше нуля (x_1) и (x_2) – корни того же уравнения).

Квадратный трехчлен (ax^2+bx+c) можно представить как (a(x-x_1)^2), если дискриминант уравнения (ax^2+bx+c=0) равен нулю.

Квадратный трехчлен (ax^2+bx+c) не раскладывается на множители, если дискриминант уравнения (ax^2+bx+c=0) меньше нуля.

Исторические сведения о квадратных уравнениях[править | править код]

Древний Вавилон[править | править код]

Индия[править | править код]

Корни квадратного уравнения на множестве действительных чисел[править | править код]

I способ. Общая формула для вычисления корней с помощью дискриминанта[править | править код]

II способ. Корни квадратного уравнения при чётном коэффициенте b[править | править код]

III способ. Решение неполных квадратных уравнений[править | править код]

IV способ. Использование частных соотношений коэффициентов[править | править код]

Корни квадратного уравнения, в котором сумма старшего коэффициента и свободного члена равна второму коэффициенту[править | править код]

Корни квадратного уравнения, сумма всех коэффициентов которого равна нулю[править | править код]

V способ. Разложение квадратного трёхчлена на линейные множители[править | править код]

Использование формулы квадрата суммы (разности)[править | править код]

Выделение полного квадрата суммы (разности)[править | править код]

VI способ. Использование прямой и обратной теоремы Виета[править | править код]

VII способ. Метод «переброски»[править | править код]

Графическое решение квадратного уравнения[править | править код]

Графический способ решения квадратных уравнений[править | править код]

Приём I[править | править код]

Приём II[править | править код]

Приём III[править | править код]

Приём IV[править | править код]

Приём V[править | править код]

Решение квадратных уравнений с помощью циркуля и линейки[править | править код]

Корни квадратного уравнения на множестве комплексных чисел[править | править код]

Уравнение с действительными коэффициентами[править | править код]

Уравнение с комплексными коэффициентами[править | править код]

Корни приведённого квадратного уравнения[править | править код]

Теорема Виета [3][править | править код]

Формулировка для приведённого квадратного уравнения[править | править код]

Для неприведённого квадратного уравнения[править | править код]

Разложение квадратного трёхчлена на множители и теоремы, следующие из этого[править | править код]

Доказательство[править | править код]

Следствие 1[править | править код]

Доказательство[править | править код]

Следствие 2[править | править код]

Доказательство[править | править код]

Уравнения, сводящиеся к квадратным[править | править код]

Алгебраические[править | править код]

Дифференциальные[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Квадратный трехчлен. Корень квадратного трехчлена

Вам также может понравиться

Остаточное изображение на телевизоре samsung как исправить

Как найти ккт в сети

Ютуб как найти человека по номеру телефона

Добавить комментарий Отменить ответ

Теорема Виета ^[3][править | править код]