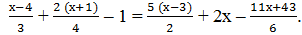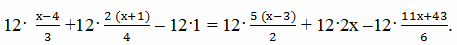Как найти корень линейного уравнения с корнем

Линейные уравнения

Линейные уравнения – уравнения, которые можно представить в виде (ax+b=0), где (a) и (b) – какие-либо числа.

Проще говоря, это такие уравнения , в которых переменные (обычно иксы) в первой степени . При этом не должно быть переменных в знаменателях дробей .

А тут (a=0, b=5) (пояснение: данное уравнение может быть представлено в виде (0cdot x+5=0))

Здесь (a) и (b) изначально не определены, но преобразовав уравнение, мы сможем их найти.

Тоже самое, (a) и (b) пока что неизвестны.

Решение линейных уравнений

При решении линейных уравнений, мы стремимся найти корень, то есть такое значение для переменной, которое превратит уравнение в правильное равенство.

В простых уравнениях корень очевиден сразу или легко находиться подбором. Например, понятно, что корнем уравнения (x+3=5) будет число (2), ведь именно двойка при подстановке ее вместо икса даст (5=5) – верное равенство.

Однако в более сложных случаях ответ сразу не виден. И тогда на помощь приходят равносильные преобразования .

Чтобы найти корень уравнения нужно равносильными преобразования привести данное нам уравнение к виду

Это число и будет корнем.

То есть, мы преобразовываем уравнение, делая его с каждым шагом все проще, до тех пор, пока не сведем к совсем примитивному уравнению «икс = число», где корень – очевиден. Наиболее часто применяемыми при решении линейных уравнений являются следующие преобразования:

1. Прибавление или вычитание из обеих частей уравнения одинакового числа или выражения.

Например: прибавим (5) к обеим частям уравнения (6x-5=1)

Обратите внимание, что тот же результат мы могли бы получить быстрее – просто записав пятерку с другой стороны уравнения и поменяв при этом ее знак. Собственно, именно так и делается школьный «перенос через равно со сменой знака на противоположный».

2. Умножение или деление обеих частей уравнения на одинаковое число или выражение.

Например: разделим уравнение (-2x=8) на минус два

Обычно данный шаг выполняется в самом конце, когда уравнение уже приведено к виду (ax=b), и мы делим на (a), чтобы убрать его слева.

3. Использование свойств и законов математики: раскрытие скобок, приведение подобных слагаемых, сокращение дробей и т.д.

Чаще всего при решении линейного уравнения приходиться делать несколько разных преобразований.

Пример. Решить линейное уравнение (6(4-x)+x=3-2x)

Прибавляем (2x) слева и справа

Вычитаем (24) из обеих частей уравнения

Опять приводим подобные слагаемые

Теперь делим уравнение на (-3), тем самым убирая коэффициент перед иксом в левой части.

Ответ найден. Однако давайте его проверим. Если семерка действительно корень, то при подстановке ее вместо икса в первоначальное уравнение должно получиться верное равенство – одинаковые числа слева и справа. Пробуем.

Сошлось. Значит, семерка и в самом деле является корнем исходного линейного уравнения.

Не ленитесь проверять подстановкой найденные вами ответы, особенно если вы решаете уравнение на контрольной или экзамене.

Остается вопрос – а как определить, что делать с уравнением на очередном шаге? Как именно его преобразовывать? Делить на что-то? Или вычитать? И что конкретно вычитать? На что делить?

Ваша цель – привести уравнение к виду (x=[число]), то есть, слева икс без коэффициентов и чисел, а справа – только число без переменных. Поэтому смотрите, что вам мешает и делайте действие, обратное тому, что делает мешающий компонент.

Чтобы лучше это понять, разберем по шагам решение линейного уравнения (x+3=13-4x).

Давайте подумаем: чем данное уравнение отличается от (x=[число])? Что нам мешает? Что не так?

Ну, во-первых, мешает тройка, так как слева должен быть только одинокий икс, без чисел. А что «делает» тройка? Прибавляется к иксу. Значит, чтобы ее убрать – вычтем такую же тройку. Но если мы вычитаем тройку слева, то должны вычесть ее и справа, чтобы равенство не было нарушено.

Хорошо. Теперь что мешает? (4x) справа, ведь там должны быть только числа. (4x) вычитается – убираем прибавлением.

Теперь приводим подобные слагаемые слева и справа.

Уже почти готово. Осталось убрать пятерку слева. Что она «делает»? Умножается на икс. Поэтому убираем ее делением.

Решение завершено, корень уравнения – двойка. Можете проверить подстановкой.

Заметим, что чаще всего корень в линейных уравнениях только один. Однако могут встретиться два особых случая.

6.5.1. Линейное уравнение с одной переменной

У очень многих школьников возникает вопрос — как решить уравнение с x. Что значит решить уравнение и как найти корень уравнения. Давайте рассмотрим основную схему решения обычного уравнения, называемого линейным, с одной переменной.

Правила и определения

Основные правила и определения для линейного уравнения с одной переменной.

• Равенство с переменной называют уравнением.
• Решить уравнение – значит найти множество его корней. Уравнение может иметь один, два, несколько, множество корней или не иметь их вовсе.
• Каждое значение переменной, при котором данное уравнение превращается в верное равенство, называется корнем уравнения.
• Уравнения, имеющие одни и те же корни, называются равносильными уравнениями.
• Любое слагаемое уравнения можно перенести из одной части равенства в другую, изменив при этом знак слагаемого на противоположный.
• Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному уравнению.

Примеры. Решить уравнение.

Уравнение 1

1. 1,5х-0,3х = -2-4. Собрали слагаемые, содержащие переменную, в левой части равенства, а свободные члены – в правой части равенства. При этом применяли свойство: любое слагаемое уравнения можно перенести из одной части равенства в другую, изменив при этом знак слагаемого на противоположный.
2. 1,2х = -6. Привели подобные слагаемые по правилу: чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на их общую буквенную часть (т.е. к полученному результату приписать их общую буквенную часть).
3. х = -6 : 1,2. Обе части равенства разделили на коэффициент при переменной, так как если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному уравнению.
4. х = -5. Делили по правилу деления десятичной дроби на десятичную дробь:
5. чтобы разделить число на десятичную дробь, нужно перенести запятые в делимом и делителе на столько цифр вправо, сколько их стоит после запятой в делителе, а затем выполнить деление на натуральное число: 6 : 1,2 = 60 : 12 = 5.

Ответ: 5.

Уравнение 2

3∙(2х-9) = 4∙(х-4).

1. 6х-27 = 4х-16. Раскрыли скобки, используя распределительный закон умножения относительно вычитания: чтобы разность двух чисел умножить на третье число, можно отдельно уменьшаемое и отдельно вычитаемое умножить на третье число, а затем из первого результата вычесть второй результат, т.е. (a-b) ∙ c = a ∙ c-b ∙ c.
2. 6х-4х = -16+27. Собрали слагаемые, содержащие переменную, в левой части равенства, а свободные члены – в правой части равенства. При этом применяли свойство: любое слагаемое уравнения можно перенести из одной части равенства в другую, изменив при этом знак слагаемого на противоположный.
3. 2х = 11. Привели подобные слагаемые по правилу: чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на их общую буквенную часть (т.е. к полученному результату приписать их общую буквенную часть).
4. х = 11 : 2. Обе части равенства разделили на коэффициент при переменной, так как если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному уравнению.

Ответ: 5,5.

Уравнение 3

1. 7х-3-2х = х-9. Раскрыли скобки по правилу раскрытия скобок, перед которыми стоит знак «-»: если перед скобками стоит знак «-», то убираем скобки, знак «-» и записываем слагаемые, стоявшие в скобках, с противоположными знаками.
2. 7х-2х-х = -9+3. Собрали слагаемые, содержащие переменную, в левой части равенства, а свободные члены – в правой части равенства. При этом применяли свойство: любое слагаемое уравнения можно перенести из одной части равенства в другую, изменив при этом знак слагаемого на противоположный.
3. 4х = -6. Привели подобные слагаемые по правилу: чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на их общую буквенную часть (т.е. к полученному результату приписать их общую буквенную часть).
4. х = -6 : 4. Обе части равенства разделили на коэффициент при переменной, так как если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному уравнению.

Ответ: -1,5.

Уравнение 4

1. 3 ∙ (х-5) = 7 ∙ 12 — 4 ∙ (2х-11). Умножили обе части равенства на 12 – наименьший общий знаменатель для знаменателей данных дробей.
2. 3х-15 = 84-8х+44. Раскрыли скобки, используя распределительный закон умножения относительно вычитания: чтобы разность двух чисел умножить на третье число, можно отдельно уменьшаемое и отдельно вычитаемое умножить на третье число, а затем из первого результата вычесть второй результат, т.е. (a-b) ∙ c = a ∙ c-b ∙ c.
3. 3х+8х = 84+44+15. Собрали слагаемые, содержащие переменную, в левой части равенства, а свободные члены – в правой части равенства. При этом применяли свойство: любое слагаемое уравнения можно перенести из одной части равенства в другую, изменив при этом знак слагаемого на противоположный.
4. 11х = 143. Привели подобные слагаемые по правилу: чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на их общую буквенную часть (т.е. к полученному результату приписать их общую буквенную часть).
5. х = 143 : 11. Обе части равенства разделили на коэффициент при переменной, так как если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному уравнению.

Ответ: 13.

Уравнения для самостоятельного решения

Решить самостоятельно уравнения:

а) 3-2,6х = 5х+1,48;

б) 1,6 · (х+5) = 4 · (4,5-0,6х);

в) 9х- (6х+2,5) = — (х-5,5);

5а) 0,2; 5б) 2,5; 5в) 2; 5г) -1.

Важные выводы

Итак, для того, чтобы решить уравнение — надо определить его переменную, перенести неизвестную переменную в левую часть уравнения, а известные — в праву. При необходимости упростить левую и правую части и затем найти корень уравнения.

Решение простых линейных уравнений

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.

Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.

Решить уравнение значит найти все возможные корни или убедиться, что их нет.

Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Какие бывают виды уравнений

Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.

Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.

Линейное уравнение выглядит так	ах + b = 0, где a и b — действительные числа. Что поможет в решении: если а не равно нулю, то у уравнения единственный корень: х = -b : а; если а равно нулю — у уравнения нет корней; если а и b равны нулю, то корень уравнения — любое число.
Квадратное уравнение выглядит так:	ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Числовой коэффициент — число, которое стоит при неизвестной переменной.

Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:

Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.

Как решать простые уравнения

Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.

1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.

Для примера рассмотрим простейшее уравнение: x+3=5

Начнем с того, что в каждом уравнении есть левая и правая часть.

Перенесем 3 из левой части в правую и меняем знак на противоположный.

Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.

Решим еще один пример: 6x = 5x + 10.

Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.

Приведем подобные и завершим решение.

2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.

Применим правило при решении примера: 4x=8.

При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.

Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.

Разделим каждую часть на 4. Как это выглядит:

Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:

Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12

Разделим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.

−4x = 12 | : (−4)
x = −3

Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.

Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.

Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.

Алгоритм решения простого линейного уравнения
Раскрываем скобки, если они есть. Группируем члены, которые содержат неизвестную переменную в одну часть уравнения, остальные члены — в другую. Приводим подобные члены в каждой части уравнения. Решаем уравнение, которое получилось: aх = b. Делим обе части на коэффициент при неизвестном.

Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.

Примеры линейных уравнений

Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!

Пример 1. Как правильно решить уравнение: 6х + 1 = 19.

Перенести 1 из левой части в правую со знаком минус.

Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.

Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3 (х − 4) + 2х − 1.

5х − 15 + 2 = 3х − 12 + 2х − 1

Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.

5х − 3х − 2х = −12 − 1 + 15 − 2

Приведем подобные члены.

Ответ: х — любое число.

Пример 3. Решить: 4х = 1/8.

Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.

Пример 4. Решить: 4(х + 2) = 6 − 7х.

1. 4х + 8 = 6 − 7х
2. 4х + 7х = 6 − 8
3. 11х = −2
4. х = −2 : 11
5. х = −2/11

Ответ: −2/11 или −(0,18). О десятичных дробях можно почитать в другой нашей статье.

Пример 5. Решить:

2. 3(3х — 4) = 4 · 7х + 24
3. 9х — 12 = 28х + 24
4. 9х — 28х = 24 + 12
5. -19х = 36
6. х = 36 : (-19)
7. х = – 36/19

Пример 6. Как решить линейное уравнение: х + 7 = х + 4.

5х — 15 + 2 = 3х — 2 + 2х — 1

Сгруппировать в левой части неизвестные члены, в правой — свободные члены:

Приведем подобные члены.

Ответ: нет решений.

Пример 7. Решить: 2(х + 3) = 5 − 7х.

[spoiler title=”источники:”]

http://mathematics-repetition.com/reshit-uravnenie-kak-nayti-koren-uravneniya/

http://skysmart.ru/articles/mathematic/reshenie-prostyh-linejnyh-uravnenij

[/spoiler]

Уравнение с одним неизвестным, которое после раскрытия скобок и приведения подобных членов принимает вид  

aх + b = 0, где a и b произвольные числа, называется линейным уравнением с одним неизвестным. Cегодня разберёмся, как эти линейные уравнения решать.

Например, все уравнения:

2х + 3= 7 – 0,5х;  0,3х = 0;  x/2 + 3 = 1/2 (х – 2) – линейные.

Значение неизвестного, обращающее уравнение в верное равенство называется решением или корнем уравнения.

Например, если в уравнении 3х + 7 = 13 вместо неизвестного х подставить число 2 , то получим верное равенство 3· 2 +7 = 13. Значит, значение х = 2 есть решение или корень уравнения.

А значение х = 3 не обращает  уравнение  3х + 7 = 13 в верное равенство, так  как  3· 2 +7 ≠ 13. Значит, значение х = 3 не является решением или корнем уравнения.

Решение любых линейных уравнений сводится к решению уравнений вида

aх + b = 0.

Перенесем свободный член из левой части уравнения в правую, изменив при этом знак перед b на противоположный, получим

aх = ‒ b.

Если a ≠ 0, то х = ‒ b/a .

Пример 1. Решите уравнение 3х + 2 =11.

Перенесем 2 из левой части уравнения в правую, изменив при этом знак перед 2 на противоположный, получим 
3х = 11 – 2.

Выполним вычитание, тогда
3х = 9.

Чтобы найти х надо разделить произведение на известный множитель, то есть     
х = 9 : 3.

Значит, значение х = 3 является  решением или корнем уравнения.

Ответ: х = 3.

Если а = 0 и b = 0, то получим уравнение  0х = 0. Это уравнение имеет бесконечно много  решений, так как при умножении любого числа на 0 мы получаем 0,но b тоже равно 0. Решением этого уравнения  является любое число.

Пример 2. Решите уравнение 5(х – 3) + 2 = 3 (х – 4) + 2х ‒ 1.

Раскроем скобки:
5х – 15 + 2 = 3х – 12 + 2х ‒ 1.

Сгруппируем  в левой части члены, содержащие неизвестные, а в правой ‒ свободные члены:
5х – 3х ‒ 2х =  – 12  ‒ 1 + 15 ‒ 2.

Приведем подобные члены:
0х = 0.

Ответ: х –  любое число.

Если а = 0 и b ≠ 0, то получим уравнение  0х = – b. Это уравнение решений не имеет, так как при умножении любого числа на 0 мы получаем 0, но  b ≠ 0 .

Пример 3. Решите уравнение х + 8 = х + 5.

Сгруппируем  в левой части члены, содержащие неизвестные, а в правой ‒ свободные члены:
х – х = 5 ‒ 8.

Приведем подобные члены: 
0х = ‒ 3.

Ответ: нет решений.

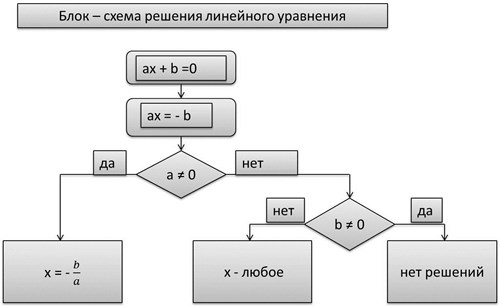
На рисунке 1 изображена схема решения линейного уравнения

Составим общую схему решения уравнений с одной переменной. Рассмотрим решение примера 4.

Пример 4. Пусть надо решить уравнение 

1) Умножим все члены уравнения на наименьшее общее кратное знаменателей, равное 12.

2) После сокращения получим
4 (х – 4) + 3·2 (х + 1) ‒ 12 = 6·5 (х – 3) + 24х – 2 (11х + 43)

3) Чтобы отделить члены, содержащие неизвестные и свободные члены, раскроем скобки:
4х – 16 + 6х + 6 – 12 = 30х – 90 + 24х – 22х – 86 .

4) Сгруппируем в одной части члены, содержащие неизвестные, а в другой – свободные члены:
4х + 6х – 30х – 24х + 22х = ‒ 90 – 86 + 16 – 6 + 12.

5) Приведем подобные члены:
‒ 22х = ‒ 154.

6) Разделим на  – 22 , Получим
х = 7.

Как видим, корень уравнения равен семи.

Вообще такие уравнения можно решать по следующей схеме:

а) привести уравнение к целому виду;

б) раскрыть скобки;

в) сгруппировать члены, содержащие неизвестное, в одной части уравнения, а свободные члены ‒ в другой;

г) привести подобные члены;

д) решить уравнение вида aх = b,которое получили после приведения подобных членов.

Однако эта схема не обязательна для всякого уравнения. При решении многих более простых уравнений приходится начинать не с первого, а со второго (Пример. 2),  третьего (Пример. 1, 3) и даже с пятого этапа, как в примере 5.

СЛОЖНА-А-А 🙀 Ты же знаешь, что если не разобраться в теме сейчас, то потом придется исправлять оценки. Беги на бесплатное онлайн-занятие с репетитором (подробности тут + 🎁).

Пример 5. Решите уравнение 2х = 1/4.

Находим неизвестное  х = 1/4 : 2,
х = 1/8 .

Рассмотрим решение некоторых линейных уравнений, встречающихся на основном государственном экзамене.

Пример 6. Решите уравнение 2 (х + 3) = 5 – 6х.

Решение

2х + 6 = 5 – 6х

2х + 6х = 5 – 6

8х = ‒1

х = ‒1 : 8

х = ‒ 0, 125

Ответ: ‒ 0, 125

Пример 7. Решите уравнение – 6 (5 – 3х) = 8х – 7.

Решение

– 30 + 18х = 8х – 7

18х  – 8х =  – 7 +30

10х = 23

х = 23 : 10

х = 2,3

Ответ: 2,3

Пример 8. Решите уравнение

 

Решение:

3(3х – 4) = 4 · 7х + 24

9х – 12 = 28х + 24

9х – 28х = 24 + 12

-19х = 36

х = 36 : (-19)

х = – 36/19

Ответ: – .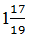 

Пример 9. Найдите f(6), если f (x + 2) = 3^7-х

Решение

Так как надо найти f(6), а нам известно f (x + 2),
то х + 2 = 6.

Решаем линейное уравнение х + 2 = 6,
получаем х = 6 – 2, х = 4.

Если х = 4, тогда
f(6) = 3^7-4 = 3³ = 27

Ответ: 27.

Молодец! Раз ты дочитал это до конца, вероятно, ты все отлично усвоил.  Но если вдруг что-то еще непонятно – попробуй онлайн-занятие с репетитором (подробности тут + 🎁).

Если у Вас остались вопросы, есть желание разобраться с решением уравнений более основательно, записывайтесь на мои уроки в РАСПИСАНИИ. Буду рада Вам помочь!

Также TutorOnline советует посмотреть новый видеоурок от нашего репетитора Ольги Александровны, который поможет разобраться как с линейными уравнениями, так и с другими.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

В данной статье рассмотрим принцип решения таких уравнений как линейные уравнения. Запишем определение этих уравнений, зададим общий вид. Разберем все условия нахождения решений линейных уравнений, используя, в том числе, практические примеры.

Обратим внимание, что материал ниже содержит информацию по линейным уравнениям с одной переменной. Линейные уравнения с двумя переменными рассматриваются в отдельной статье.

Что такое линейное уравнение

Линейное уравнение – это уравнение, запись которого такова:
a·x=b, где x – переменная, a и b – некоторые числа.

Такая формулировка использована в учебнике алгебры (7 класс) Ю.Н.Макарычева.

В различных учебных материалах могут встречаться разные определения. К примеру, Виленкин Н.Я. к линейным относит также те уравнения, которые возможно преобразовать в вид a·x=b при помощи переноса слагаемых из одной части в другую со сменой знака и приведения подобных слагаемых. Если следовать такой трактовке, уравнение 5·x=2·x+6 – также линейное.

А вот учебник алгебры (7 класс) Мордковича А.Г. задает такое описание:

Линейное уравнение с одной переменной x – это уравнение вида a·x+b=0, где a и b – некоторые числа, называемые коэффициентами линейного уравнения.

Мы сразу условимся, что в данной статье под линейным уравнением с одной переменной мы будем понимать уравнение записи a·x+b=0, где x – переменная; a, b – коэффициенты. Подобная форма линейного уравнения нам видится наиболее оправданной, поскольку линейные уравнения – это алгебраические уравнения первой степени. А прочие уравнения, указанные выше, и уравнения, приведенные равносильными преобразованиями в вид a·x+b=0, определим, как уравнения, сводящиеся к линейным уравнениям.

При таком подходе уравнение 5·x+8=0 – линейное, а 5·x=−8 –  уравнение, сводящееся к линейному.

Принцип решения линейных уравнений

Рассмотрим, как определить, будет ли заданное линейное уравнение иметь корни и, если да, то сколько и как их определить.

Дадим пояснение. Нам известно, что в процессе решения уравнения возможно осуществлять преобразование заданного уравнения в равносильное ему, а значит имеющее те же корни, что исходное уравнение, или также не имеющее корней. Мы можем производить следующие равносильные преобразования:

• перенести слагаемое из одной части в другую, сменив знак на противоположный;
• умножить или разделить обе части уравнения на одно и то же число, не равное нулю.

Таким образом, преобразуем линейное уравнение a·x+b=0, перенеся слагаемое b из левой части в правую часть со сменой знака. Получим: a·x=−b.

Далее мы разделим обе части равенства на число а, при этом условившись, что это число отлично от нуля, иначе деление станет невозможным. Случай, когда а=0, рассмотрим позже.

Итак, производим деление обеих частей уравнения на не равное нулю число а, получив в итоге равенство вида x=-ba. Т.е., когда a≠0, исходное уравнение a·x+b=0 равносильно равенству x=-ba, в котором очевиден корень -ba.

Методом от противного возможно продемонстрировать, что найденный корень – единственный. Зададим обозначение найденного корня -ba как x1. Выскажем предположение, что имеется еще один корень линейного уравнения с обозначением x2. И конечно: x2≠x1, а это, в свою очередь, опираясь на определение равных чисел через разность, равносильно условию x1−x2≠0. С учетом вышесказанного мы можем составить следующие равенства, подставив корни:
a·x1+b=0 и a·x2+b=0.
Свойство числовых равенств дает возможность произвести почленное вычитание частей равенств:

a·x1+b−(a·x2+b)=0−0, отсюда: a·(x1−x2)+(b−b)=0 и далее a·(x1−x2)=0. Равенство a·(x1−x2)=0 является неверным, поскольку ранее условием было задано, что a≠0 и x1−x2≠0. Полученное противоречие и служит доказательством того, что при a≠0 линейное уравнение a·x+b=0 имеет лишь один корень.

Обоснуем еще два пункта условий, содержащие a=0.

Когда a=0 линейное уравнение a·x+b=0 запишется как 0·x+b=0. Свойство умножения числа на нуль дает нам право утверждать, что какое бы число не было взято в качестве x, подставив его в равенство 0·x+b=0, получим b=0. Равенство справедливо при  b=0; в прочих случаях, когда b≠0, равенство становится неверным.

Таким образом, когда a=0 и  b=0, любое число может стать корнем линейного уравнения a·x+b=0, поскольку при выполнении этих условий, подставляя вместо x любое число, получаем верное числовое равенство 0=0. Когда же a=0 и b≠0 линейное уравнение a·x+b=0 вовсе не будет иметь корней, поскольку при выполнении указанных условий, подставляя вместо x любое число, получаем неверное числовое равенство b=0.

Все приведенные рассуждения дают нам возможность записать алгоритм, дающий возможность найти решение любого линейного уравнения:

• по виду записи определяем значения коэффициентов a и b и анализируем их;
• при a=0 и b=0 уравнение будет иметь бесконечно много корней, т.е. любое число станет корнем заданного уравнения;
• при a=0 и b≠0 заданное уравнение не будет иметь корней;
• при a, отличном от нуля, начинаем поиск единственного корня исходного линейного уравнения:

1. перенесем коэффициент b в правую часть со сменой знака на противоположный, приводя линейное уравнение к виду a·x=−b;
2. обе части полученного равенства делим на число a, что даст нам искомый корень заданного уравнения: x=-ba.

Собственно, описанная последовательность действий и есть ответ на вопрос, как находить решение линейного уравнения.

Напоследок уточним, что уравнения вида a·x=b решаются по похожему алгоритму с единственным отличием, что число b в такой записи уже перенесено в нужную часть уравнения, и при a≠0 можно сразу выполнять деление частей уравнения на число a.

Таким образом, чтобы найти решение уравнения a·x=b, используем такой алгоритм:

• при a=0 и b=0 уравнение будет иметь бесконечно много корней, т.е. любое число может стать его корнем;
• при a=0 и b≠0 заданное уравнение не будет иметь корней;
• при a, не равном нулю, обе части уравнения делятся на число a, что дает возможность найти единственный корень, который равен ba.

Примеры решения линейных уравнений

Для наглядности приведем решение уравнения записи a·x=b. 

Проще говоря, это такие уравнения, в которых переменные (обычно иксы) в первой степени. При этом не должно быть переменных в знаменателях дробей.

Например:		(2x+7=0)		Здесь (a=2, b=7)
		(5=0)		А тут (a=0, b=5) (пояснение: данное уравнение может быть представлено в виде (0cdot x+5=0))
		(-7(5-3y)=91)		Здесь (a) и (b) изначально не определены, но преобразовав уравнение, мы сможем их найти.
		(frac{x+2}{3})(+x=1-)(frac{3}{4})(x)		Тоже самое, (a) и (b) пока что неизвестны.

Решение линейных уравнений

В простых уравнениях корень очевиден сразу или легко находиться подбором. Например, понятно, что корнем уравнения (x+3=5) будет число (2), ведь именно двойка при подстановке ее вместо икса даст (5=5) – верное равенство.

Однако в более сложных случаях ответ сразу не виден. И тогда на помощь приходят равносильные преобразования.

То есть, мы преобразовываем уравнение, делая его с каждым шагом все проще, до тех пор, пока не сведем к совсем примитивному уравнению «икс = число», где корень – очевиден. Наиболее часто применяемыми при решении линейных уравнений являются следующие преобразования:

Например: прибавим (5) к обеим частям уравнения (6x-5=1)

                  (6x-5=1)         (|+5)
(6x-5+5=1+5)
(6x=6)

Обратите внимание, что тот же результат мы могли бы получить быстрее – просто записав пятерку с другой стороны уравнения и поменяв при этом ее знак. Собственно, именно так и делается школьный «перенос через равно со сменой знака на противоположный».

Например: разделим уравнение (-2x=8) на минус два

                  (-2x=8)         (|:(-2))
(x=-4)

Обычно данный шаг выполняется в самом конце, когда уравнение уже приведено к виду (ax=b), и мы делим на (a), чтобы убрать его слева.

Например: раскроем скобки в уравнении (2(3+x)=4(3x-2)-5)

                  (6+2x=12x-8-5)

Чаще всего при решении линейного уравнения приходиться делать несколько разных преобразований.

Пример. Решить линейное уравнение (6(4-x)+x=3-2x)

Решение:

(6(4-x)+x=3-2x)		Раскрываем скобки
(24-6x+x=3-2x)		Приводим подобные слагаемые
(24-5x=3-2x)		Прибавляем (2x) слева и справа
(24-5x+2x=3)		Вычитаем (24) из обеих частей уравнения
(-5x+2x=3-24)		Опять приводим подобные слагаемые
(-3x=-21)		Теперь делим уравнение на (-3), тем самым убирая коэффициент перед иксом в левой части.
(x=7)

Ответ: (7)

Ответ найден. Однако давайте его проверим. Если семерка действительно корень, то при подстановке ее вместо икса в первоначальное уравнение должно получиться верное равенство – одинаковые числа слева и справа. Пробуем.

                   Проверка:
         (6(4-7)+7=3-2cdot7)
           (6cdot(-3)+7=3-14)
                (-18+7=-11)
                  (-11=-11)

Сошлось. Значит, семерка и в самом деле является корнем исходного линейного уравнения.

Остается вопрос – а как определить, что делать с уравнением на очередном шаге? Как именно его преобразовывать? Делить на что-то? Или вычитать? И что конкретно вычитать? На что делить?

Ответ прост:

Чтобы лучше это понять, разберем по шагам решение линейного уравнения (x+3=13-4x).

Давайте подумаем: чем данное уравнение отличается от (x=[число])? Что нам мешает? Что не так?

Ну, во-первых, мешает тройка, так как слева должен быть только одинокий икс, без чисел. А что «делает» тройка? Прибавляется к иксу. Значит, чтобы ее убрать – вычтем такую же тройку. Но если мы вычитаем тройку слева, то должны вычесть ее и справа, чтобы равенство не было нарушено.

                  (x+3=13-4x)         (|-3)
(x+3-3=13-4x-3)
(x=10-4x)

Хорошо. Теперь что мешает? (4x) справа, ведь там должны быть только числа. (4x) вычитается – убираем прибавлением.

                  (x=10-4x)         (|+4x)
(x+4x=10-4x+4x)

Теперь приводим подобные слагаемые слева и справа.

(5x=10)

Уже почти готово. Осталось убрать пятерку слева. Что она «делает»? Умножается на икс. Поэтому убираем ее делением.

                  (5x=10)         (|:5)
(frac{5x}{5})(=)(frac{10}{5})
(x=2)

Решение завершено, корень уравнения – двойка. Можете проверить подстановкой.

Заметим, что чаще всего корень в линейных уравнениях только один. Однако могут встретиться два особых случая.

Особый случай 1 – в линейном уравнении нет корней.

Пример. Решить уравнение (3x-1=2(x+3)+x)

Решение:

(3x-1=2(x+3)+x)		Раскроем скобки
(3x-1=2x+6+x)		Приведем подобные слагаемые
(3x-1=3x+6)		Перенесем члены с переменной влево, а просто числа – вправо, меняя при этом знаки
(3x-3x=6+1)		Опять приведем подобные слагаемые
(0=7)		Ну и при каком иксе ноль станет равен (7)? Ни при каком, тут икс вообще никак не влияет и не может «исправить» неверность получившегося равенства. Поэтому ответ – в этом линейном уравнении нет корней.

Ответ: нет корней.

На самом деле, то, что мы придем к такому результату было видно раньше, еще когда мы получили (3x-1=3x+6). Вдумайтесь: как могут быть равны (3x) из которых вычли (1), и (3x) к которым прибавили (6)? Очевидно, что никак, ведь с одним и тем же выражением сделали разные действия! Понятно, что результаты будут отличаться.

Особый случай 2 – в линейном уравнении бесконечное количество корней.

Пример. Решить линейное уравнение (8(x+2)-4=12x-4(x-3))

Решение:

(8(x+2)-4=12x-4(x-3))		Начинаем преобразовывать – раскрываем скобки
(8x+16-4=12x-4x+12)		Приводим подобные слагаемые
(8x+12=8x+12)		Переносом через равно собираем иксы справа, а числа слева
(8x-8x=12-12)		И вновь приводим подобные
(0=0)		Очевидно, что тут “подойдет” любое значение для икса, ведь он никак не влияет на полученное уравнение. И значит равенство всегда будет верным.

Ответ: любое число.

Это, кстати, было заметно еще раньше, на этапе: (8x+12=8x+12). Действительно, слева и справа – одинаковые выражения. Какой икс ни подставь – будет одно и то же число и там, и там.

Более сложные линейные уравнения.

Исходное уравнение не всегда сразу выглядит как линейное, иногда оно «маскируется» под другие, более сложные уравнения. Однако в процессе преобразований маскировка спадает.

Пример. Найдите корень уравнения (2x^{2}-(x-4)^{2}=(3+x)^{2}-15)

Решение:

(2x^{2}-(x-4)^{2}=(3+x)^{2}-15)		Казалось бы, здесь есть икс в квадрате – это не линейное уравнение! Но не спешите. Давайте применим формулы сокращенного умножения
(2x^{2}-(x^{2}-8x+16)=9+6x+x^{2}-15)		Почему результат раскрытия ((x-4)^{2}) стоит в скобке, а результат ((3+x)^{2}) нет? Потому что перед первым квадратом стоит минус, который изменит все знаки. И чтобы не забыть об этом – берем результат в скобки, которую теперь раскрываем.
(2x^{2}-x^{2}+8x-16=9+6x+x^{2}-15)		Приводим подобные слагаемые
(x^{2}+8x-16=x^{2}+6x-6)		Далее как обычно: «иксы – влево, числа – вправо», не забывая менять знаки.
(x^{2}-x^{2}+8x-6x=-6+16)		Опять приводим подобные.
(2x=10)		Вот так. Оказывается, исходное уравнение – вполне себе линейное, а иксы в квадрате не более чем ширма, чтоб нас запутать. 🙂 Дорешиваем, деля уравнение на (2), и получаем ответ.

Ответ: (x=5)

Пример. Решить линейное уравнение (frac{x+2}{2}) (-) (frac{1}{3}) (=) (frac{9+7x}{6})

Решение:

(frac{x+2}{2}) (-) (frac{1}{3}) (=) (frac{9+7x}{6})		Уравнение не похоже на линейное, дроби какие-то… Однако давайте избавимся от знаменателей, умножив обе части уравнения на общий знаменатель всех дробей – шестерку
(6cdot)((frac{x+2}{2}) (-) (frac{1}{3})) (=) (frac{9+7x}{6})(cdot 6)		Раскрываем скобку слева
(6cdot)(frac{x+2}{2}) (-) (6cdot)(frac{1}{3}) (=) (frac{9+7x}{6})(cdot 6)		Теперь сокращаем знаменатели
(3(x+2)-2=9+7x)		Вот теперь похоже на обычное линейное! Дорешиваем его. Раскрываем скобки
(3x+6-2=9+7x)		Переносом через равно собираем иксы справа, а числа слева
(3x-7x=9-6+2)		Приводим подобные слагаемые
(-4x=5)		Ну и поделив на (-4) правую и левую часть, получаем ответ

Ответ: (x=-1,25)

Смотрите также:
Линейная функция

Скачать статью