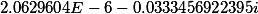Вычисление корней многочлена любой степени
Вычисляет вещественные корни полинома любой степени численным методом или аналитически, если аналитическое решение существует
Статьи, описывающие этот калькулятор
- Вычисление корней полинома
Вычисление корней многочлена любой степени
Коэффициенты многочлена, разделенные пробелом.
Точность вычисления
Знаков после запятой: 5
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
График
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Этот калькулятор использует следующие калькуляторы
- Деление многочленов
- Изоляция корней многочлена методом VAS-CF
- Кубическое уравнение
- Наибольший общий делитель (НОД) двух многочленов
- Разложение многочлена на свободные от квадратов множители
- Решение квадратного уравнения
- Сдвиг многочлена
- Уравнение 4-й степени
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Изоляция корней многочлена
- • Вычисление корней полинома
- • Метод выделения полного квадрата
- • Интерполяционный многочлен Ньютона (полином Ньютона)
- • Интерполяционный многочлен Лагранжа (полином Лагранжа)
- • Раздел: Алгебра ( 46 калькуляторов )
PLANETCALC, Вычисление корней многочлена любой степени
| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Подпишитесь, чтобы подтвердить свой ответ
Подписаться
Войдите, чтобы сохранять заметки
Войти
Номер Строки
Примеры
-
рациональные:корни:x^3-7x+6
-
рациональные:корни:3x^3-5x^2+5x-2
-
рациональные:корни:6x^4-11x^3+8x^2-33x-30
-
рациональные:корни:2x^{2}+4x-6
- Показать больше
Описание
Найдите корни многочленов, используя теорему о рациональных корнях шаг за шагом
rational-roots-calculator
ru
Блог-сообщения, имеющие отношение к Symbolab
High School Math Solutions – Quadratic Equations Calculator, Part 1
A quadratic equation is a second degree polynomial having the general form ax^2 + bx + c = 0, where a, b, and c…
Read More
Введите Задачу
Сохранить в блокнот!
Войти
Онлайн калькулятор решает произвольное полиномиальное уравнение до 10 степени . Вычисляет действительные и комплексные корни на заданном промежутке (итерационный-дифференциальный алгоритм).
Инструкция
– Введите полиномиальное уравнение.
– Задайте промежуток.
– Нажмите “Вычислить”.
* Калькулятор вычисляет только действительные корни.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

| Коэффициенты полинома 4 степени |
| Исходный многочлен |
| Кубическая резольвента |
| Корни кубической резольвенты |
| Корни заданного многочлена 4 степени |
| Вспомогательные коэффициенты |
| F2= |
| F1= |
| T= |
Данный калькулятор позволяет высчитывать корни произвольного полинома четвертой степени. Коэффициенты могут быть как вещественными так и комплексными числами.
Использовалась определенная методика, которая нигде не описана и не разобрана.
Формулами Феррари не стал пользоваться – не интересно.
Несмотря на свой собственный путь, все равно утыкаешься в задачу решения вспомогательного уравнения третьей степени, так называемой кубической резольвенты.
И по всей видимости избежать её никак не получится.
Но дальше все идет по другому.
По любому значения корня резольвенты, мы высчитываем три вспомогательный параметра.
Зная эти три параметра, мы можем легко найти все четыре корня исходного уравнения.
Есть только один нюанс с которым сталкивались предшественники, мне тоже надо иногда каким то определять знак + или – для одного вспомогательного параметра.
Теперь в виде формул
Заменой 
Решение данного уравнения ищем в виде сумм двух функций
Три вспомогательных параметра связаны к коэффициентами приведенного полинома через следующие соотношения
Выражая любой из вспомогательных параметров мы получаем, в том или ином виде кубическую резольвенту
Например, если выразим F2
Это кубическое уравнение которое подстановкой 
Теперь о нюансе о котором говорил раньше. Какой же знак брать когда высчитываем корни?
Критерий оказывается очень простой. Берем любой корень резольвенты и сравниваем его
если это условие верное то ставится +(плюс), если условие неверное то -(минус)
Дальше все эти параметры подставляются в формулу
+F(T,F_2))
Еще хотелось бы поговорить про критерий. Вдумчивый читатель спросит: “А что если любой корень резольвенты является комплексным числом? Какой в этом случае критерий?”
Лучшим способом, я посчитал для подстановка корня в исходное уравнение. Для этого есть простой алогритический способ описанный в статье Значение производной многочлена по методу Горнера. Если выражение обращается в ноль, то есть является верным, то знак не меняется. Если иначе то знак ставим минус.
Решать комплексные уравнения 4 степени теперь можно достаточно легко и быстро. В онлайн сервисах Вы такого не найдете.
Попробуйте решить уравнение 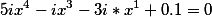
Один из корней равен
Кто считает что действительной частью можно принебречь и отбросить как “почти ноль” глубоко ошибается. Отбросив его у нас значение функции будет 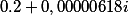
И только с учетом “такой маленькой” действительной части уравнение становиться тождественным.
Поэтому точность в вычислениях очень важны.
Если Вы вдруг заметили ошибку в расчетах ( а вдруг?) , просьба сообщить. Но я надеюсь, что такого не произойдет.
Несколько примеров:
| Исходный многочлен |
*x^3+(-9i)*x^2+(-4)*x^1+(-10i)) |
| Кубическая резольвента |
*x^2+(2620+2464i)*x^1+(-18432-34560i)) |
| Корни кубической резольвенты |
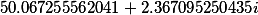 |
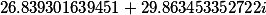 |
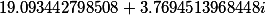 |
| Корни заданного многочлена 4 степени |
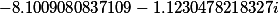 |
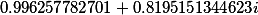 |
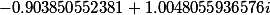 |
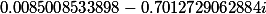 |
| Вспомогательные коэффициенты |
F2=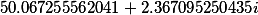 |
F1=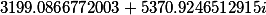 |
T=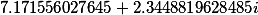 |
| Исходный многочлен |
*x^3+(-4)*x^2+(-20)*x^1+(-5)) |
| Кубическая резольвента |
*x^2+(272)*x^1+(-128)) |
| Корни кубической резольвенты |
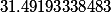 |
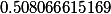 |
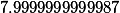 |
| Корни заданного многочлена 4 степени |
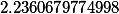 |
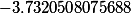 |
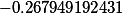 |
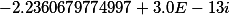 |
| Вспомогательные коэффициенты |
F2=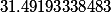 |
F1=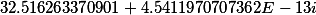 |
T=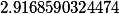 |
корни многочлена онлайн
Вы искали корни многочлена онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и найти корни многочлена онлайн, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели – у нас уже есть решение.
Например, «корни многочлена онлайн».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как корни многочлена онлайн,найти корни многочлена онлайн,онлайн решить уравнение алгебраическое,решение уравнений высших степеней онлайн,решение уравнений онлайн высших степеней,решить алгебраическое уравнение онлайн,х 3 4 х 0. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и корни многочлена онлайн. Просто введите задачу в окошко и нажмите
«решить» здесь (например, онлайн решить уравнение алгебраическое).
Где можно решить любую задачу по математике, а так же корни многочлена онлайн Онлайн?
Решить задачу корни многочлена онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать – это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.


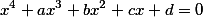
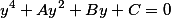
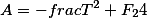
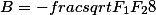
^2-frac{F_1}{2}}{64})
=8B^2)
)