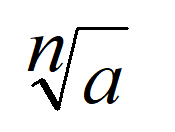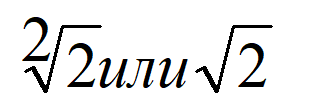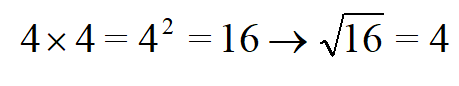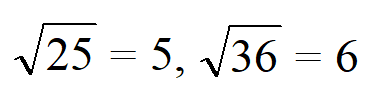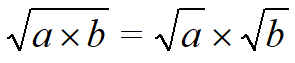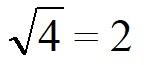Как вычислить корень на калькуляторе
Если у вас есть возможность пользоваться компьютером, наверняка есть и доступ к программе-калькулятору. Такие приложения включают все возможности обычного гаджета, добавляя к ним удобство использования, свойственное современному программному обеспечению. Например, вычисление корней в программном калькуляторе Windows возможно четырьмя способами.

Вам понадобится
- ОС Windows.
Инструкция
Запустите программу-калькулятор. Соответствующую ссылку можно найти в главном меню ОС, но проще нажать клавишу Win, набрать «ка» и нажать клавишу Enter – система поймет вас с двух букв и откроет программный калькулятор. Для более ранних версий Windows – например, XP – этот метод можно заменить нажатием сочетания клавиш Win + R и вводом команды calc с последующим нажатием клавиши Enter.
Если показатель степени корня, который требуется вычислить, равен двойке, сразу поле запуска приложения начинайте вводить подкоренное значение. Это можно делать как с клавиатуры, так и щелкая по кнопкам в интерфейсе программы. Закончив, кликните по кнопке с изображением радикала – второй сверху в правой колонке. Программа извлечет корень и отобразит результат.
Для расчета значения кубического корня возможностей запускаемого по умолчанию интерфейса недостаточно, поэтому активируйте более продвинутый – «инженерный». Для этого нажмите сочетание клавиш Ctrl + 2 или выберите соответствующий пункт в разделе «Вид» меню приложения. Затем введите число, корень которого следует рассчитать, и кликните по кнопке интерфейса, помеченной символами ³√x, и задача будет выполнена.
При извлечении корня с более высоким показателем степени операция ввода будет состоять из двух шагов. Сначала наберите подкоренное число, затем кликните по кнопке с символами ʸ√x, введите показатель степени и нажмите клавишу Enter. Результат появится в соответствующем поле интерфейса приложения.
Есть еще один способ извлечения корня произвольной степени, при котором используется операция возведения в степень с дробным показателем. Вы же знаете, что извлечение корня, например, четвертой степени равносильно возведению в степень 1/4. Поэтому введите сначала число, из которого надо извлечь корень, затем кликните по кнопке возведения в произвольную степень xʸ и наберите десятичную дробь, соответствующую единице, поделенной на показатель степени. Для корня четвертой степени это будет число 1/4=0,25. Нажмите Enter, и корень будет извлечен.
Источники:
- как посчитать корень на калькуляторе
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
как на калькуляторе посчитать квадратный корень.. .
Если калькулятор «домашний», то вводим число из которого извлечь, затем нажимаем значок корня.
Если компьютерный (виндовский) , то там вместо значка корня 4 буквы: Эс_Ку_Ар_Ти.
Также можно возвести в степень 1/2 — то же самое.
если нет функции — считай численно.
замечательный алгоритм извлечения корня из А:
V1 = чему угодно, например — самому А, или значению корня на глазок
а дальше последовательно считаешь:
Вычислить квадратный корень из числа
Необходимо произвести сложные расчеты, а электронного вычислительного устройства под рукой не оказалось? Воспользуйтесь онлайн программой — калькулятором корней. Она поможет:
- найти квадратные или кубические корни из заданных чисел;
- выполнить математическое действие с дробными степенями.
| Число знаков после запятой: |
| √ |
Что такое квадратный корень
Корень n степени натурального числа a — число, n степень которого равна a (подкоренное число). Обозначается корень символом √. Его называют радикалом.
Каждое математическое действие имеет противодействие: сложение→вычитание, умножение→деление, возведение в степень→извлечение корня.
Квадратным корнем из числа a будет число, квадрат которого равен a. Из этого следует ответ на вопрос, как вычислить корень из числа? Нужно подобрать число, которое во второй степени будет равно значению под корнем.
Обычно 2 не пишут над знаком корня. Поскольку это самая маленькая степень, а соответственно если нет числа, то подразумевается показатель 2. Решаем: чтобы вычислить корень квадратный из 16, нужно найти число, при возведении которого во вторую степень получиться 16.
Проводим расчеты вручную
Вычисления методом разложения на простые множители выполняется двумя способами, в зависимости от того, какое подкоренное число:
1.Целое, которое можно разложить на квадратные множители и получить точный ответ.
Квадратные числа — числа, из которых можно извлечь корень без остатка. А множители — числа, которые при перемножении дают исходное число.
25, 36, 49 — квадратные числа, поскольку:
Получается, что квадратные множители — множители, которые являются квадратными числами.
Возьмем 784 и извлечем из него корень.
2.Неделимое. Его нельзя разложить на квадратные множители.
Такие примеры встречаются чаще, чем с целыми числами. Их решение не будет точным, другими словами целым. Оно будет дробным и приблизительным. Упростить задачу поможет разложение подкоренного числа на квадратный множитель и число, из которого извлечь квадратный корень нельзя.
2,7 x 2,7 = 7,2. Не подходит, так как 7,2>7, берем меньшее 2,6 x 2,6 = 6,76. Оставляем, ведь 6,76
Как вычислить корень из сложного числа? Тоже методом оценивая значения корня.
При делении в столбик получается максимально точный ответ при извлечении корня.
— целую часть справа налево;
Извлеките из этого числа корень — √n. Запишите полученный результат сверху справа, а квадрат этого числа — снизу справа.
А верхнее число справа удвойте и запишите справа выражение 4_х_=_.
Как думаете сколько времени вы потратите на такие расчеты? Сложно, долго, запутанно. Тогда почему бы не упростить себе задачу? Воспользуйтесь нашей программой, которая поможет произвести быстрые и точные расчеты.
Загрузить PDF
Загрузить PDF
Научный калькулятор выполняет более высокие математические функции, что делает его полезным для студентов, изучающих алгебру, тригонометрию, и другие дополнительные занятия по математике. Следующие шаги объясняют, как выбрать и использовать научный калькулятор для алгебры в более продвинутых математических классах.
Шаги
-
1
Изучите типы научных калькуляторов. Научные калькуляторы бывают в нескольких вариантах, как описано ниже:
- Калькулятор с числовым-дисплеем. Это базовый уровень научного калькулятора, а также самый недорогой. В старых версиях используются светоизлучающие диоды (LED) для отображения цифр, но большинство научных калькуляторов теперь используют жидкокристаллический дисплей (LCD). Этот тип калькулятора подходит для большинства средних школ по алгебре и тригонометрии, а также начального уровня алгебры и тригонометрии в колледже.
- Графический калькулятор. Калькулятор имеет большую ЖК-панель для графы результатов на координатной сетке. Они полезны для отображения функций, таких как у = ах + Ь, но они стоят дороже, чем калькулятор с цифровым дисплеем и лучше подходят для высших математических классов, которые являются частью колледжа инженерного учебного плана.
- Программируемый калькулятор. Программируемый калькулятор разработан, чтобы помочь со сложными уравнениями, которые включают в себя много повторяющихся шагов. Этот тип калькулятора используется на работе ученых и инженеров и лучше подходит для тех, кто изучает эти дисциплины. Это самый дорогостоящий калькулятор и на нем наиболее трудно научиться эффективно работать. Одной из форм программируемого калькулятора является компьютерная алгебраическая система (КАС).
- Калькулятор с числовым-дисплеем. Это базовый уровень научного калькулятора, а также самый недорогой. В старых версиях используются светоизлучающие диоды (LED) для отображения цифр, но большинство научных калькуляторов теперь используют жидкокристаллический дисплей (LCD). Этот тип калькулятора подходит для большинства средних школ по алгебре и тригонометрии, а также начального уровня алгебры и тригонометрии в колледже.
-
2
Ознакомьтесь с тем, как можно вводить уравнение в научный калькулятор. Есть также несколько способов ввода данных в один калькулятор.
- Алгебраические скобки обозначения. Этот тип калькулятора следует правилам алгебры для порядка операций при вводе уравнений в него: элементы в скобках, скобки или фигурные скобки; затем показатели (возведение числа в степень), умножение, деление, сложение, и вычитание.
- Улучшенная система прямой подачи алгебраической логики. Этот формат является собственностью научных калькуляторов, сделанных Sharp. Это позволяет пользователям вводить элементы уравнения в том же порядке, как они в учебнике.
- Обратная польская нотация. Обычно встречаются в научных калькуляторах, сделанных Hewlett-Packard, в обратной польской нотации вводятся значения уравнения. Этот тип калькулятора заменяет клавишу “Ввод” для знака равенства (=), а также имеет особенности дисплея, он двухстрочный. Многие программируемые калькуляторы используют обратную польскую нотацию.
- Алгебраические скобки обозначения. Этот тип калькулятора следует правилам алгебры для порядка операций при вводе уравнений в него: элементы в скобках, скобки или фигурные скобки; затем показатели (возведение числа в степень), умножение, деление, сложение, и вычитание.
-
3
Узнайте, как включается калькулятор и выключается. Некоторые научные калькуляторы имеют отдельную кнопку включения / выключения, а другие интегрировали все в клавишу “AC”. Солнечные калькуляторы отключаются автоматически после определенного периода неиспользования сохранения батареи.
- Солнечные калькуляторы часто не имеют включения / выключения, а автоматически включаются, когда свет попадает на фотоэлектрические панели сверху и выключается, когда свет уже не действует на панель.
- Солнечные калькуляторы часто не имеют включения / выключения, а автоматически включаются, когда свет попадает на фотоэлектрические панели сверху и выключается, когда свет уже не действует на панель.
-
4
Обратите внимание на клавиши для очистки значения. В стандартных калькуляторах, научных калькуляторах можно использовать “C”, чтобы удалять текущую запись с экрана и “AC”, чтобы очистить весь расчет или использовать “C”, чтобы удалить последний расчет, и “CE”, чтобы удалить только текущую запись.
-
5
Рассмотрим научный калькулятор с возможностью памяти. Существует функция памяти, которая позволяет хранить цифры для последующего использования в расчете. Это можно использовать для хранения результатов частичных расчетов или длинных чисел, которые будут использоваться более одного раза.
- Калькуляторы с памятью могут иметь одну ячейку памяти или больше, две или три.
- Клавиши памяти включаются “STO” и “RCL” для “вызова” или “MR” для “вызова памяти”, а также “MC” для “памяти четкой.” В некоторых калькуляторах есть “M +” клавиша, чтобы вы могли добавить к значению в памяти и клавиша “М-“, чтобы вы могли вычесть из значения. Еще можно поменять значение в памяти для отображения значений и обратно.
-
6
Будьте в курсе других функциональных клавиш калькулятора. В научных калькуляторах есть другие функциональные клавиши, которых нет на обычном калькуляторе. Некоторые научные калькуляторы могут вызвать несколько функций одной и той же клавишей; нужно нажать другую клавишу, с надписью “2-й,” для того, чтобы активизировать вторичные функции клавиши.
- Открытие и закрытие скобки. Эти клавиши позволяют вводит уравнение. Используйте скобки на клавише ([]) и скобки ({}), а также обычные скобки, и всегда обязательно вводите столько закрывающих скобок, сколько открытых.
- Экспонент функции. Используйте эту клавишу, она позволит возвести ряд в степень. Основная клавиша экспоненты обычно отмечается “х”, за которой следует “у” индекс. В некоторых научных калькуляторах может быть клавиша для возведения в квадрат, маркируя “х”, затем следует верхний индекс “2” .Калькулятор Microsoft Windows также имеет функцию Cubing (“X последующим верхним индексом” 3 “) и 10 функции (” 10 “, а затем с помощью верхнего индекса” х “), что дает силу 10 возвести в степень. Некоторые калькуляторы оснащены “AB / С”, которые позволяют поднять ряд (а) дробным показателем степени (б / с).
- Корень расчета функции. Большинство научных калькуляторов имеют клавишу для извлечения квадратных корней, с надписью либо “SQRT” или с корнем над «х». Некоторые калькуляторы предлагают клавишу для извлечения других числовых корней, они обозначаются с корнем, показывая “Y” в корне. Другие калькуляторы позволяют извлечь эти корни с дробной клавишей экспонента; например, ввод показателя степени 1/3 такой же, как извлечение кубического корня.
- Показательная функция. Это позволяет ввести число в экспоненциальном (научном) формате обозначения. (Этот формат начинается с десятичного числа от 1 до 9,999, за которым следует буква “Е”, и целое число, представляющее показатель, который вы вводите.) Клавиша для этого может быть помечена “EXP”, “EE”, или “ENG”.
- Логарифмические функции. Научные калькуляторы могут вычислить логарифм по основанию 10 или натуральный логарифм (экспонента) отображаемого числа. Клавиша для базового логарифма 10 называется “lg”, в то время как клавиша натурального логарифма называется “ln”
- Взаимная функция. Обычно надпись “1 / х” это тоже самое что “х” с “-1” индексом.
- Клавиша Пи. Эта клавиша представляет значение пи, отношение диаметра окружности к ее длине. Нажатие клавиши отображает значение пи.
- Тригонометрические функции. Большинство научных калькуляторов имеют клавиши для наиболее распространенных тригонометрических функций: синус («sin»), косинус (“cos”), и тангенс (“Tan”). Некоторые калькуляторы также оснащены клавишами таких функций как гиперболические эквиваленты: “sinh”, “cosh”, и “tanh”.
- Управление клавишами рад / град. Это позволяет преобразовать значение угла в тригонометрии из градусов в радианы или наоборот, когда это необходимо. (Радиан равен чуть более 57 градусов; 1 радиан умноженное на пи равняется 9/10 градуса на 180 градусов)
- Клавиша факториал. Маркировка “n” или аналогично, эта клавиша находит произведение последовательности числа от 1 до значения, указанного; ввод 5 последовательности 1 х 2 х 3 х 4 х 5 = 120. Факториал, понятие часто используемое при выяснении вероятности и шансов в статистике, но не в алгебре.
- Обратная клавиша. Эта клавиша, с надписью “Inv” используется с тригонометрическими функциональными клавишами, чтобы найти меру угла, для которых синус, косинус, или тангенс известен. Он также используется с логарифмической функцией клавиш, когда значение логарифма известно, чтобы найти значение базового числа.
Реклама
- Открытие и закрытие скобки. Эти клавиши позволяют вводит уравнение. Используйте скобки на клавише ([]) и скобки ({}), а также обычные скобки, и всегда обязательно вводите столько закрывающих скобок, сколько открытых.
Советы
- При выборе научного калькулятора, выясните, для каких подсчетов вы будете его использовать. Вы должны выбрать калькулятор, который пригодится вам в математических классах.
- После того, как вы купите научный калькулятор, найдите время, чтобы ознакомиться с его функциями, прежде чем использовать его в классе. Чем больше времени вы потратите на изучение калькулятора, тем лучше вы сможете его использовать.
- Взгляните на несколько калькуляторов, прежде чем купить, ознакомьтесь с их макетами. Вы можете работать с калькулятором, с приложениями доступными вашей операционной системе, или онлайн-калькулятором, чтобы ознакомиться с некоторыми из функций автономного научного калькулятора, прежде чем купить его.
Реклама
Предупреждения
- Знайте, что некоторые научные калькуляторы не допускаются при приеме в некоторых колледжах на подготовительных тестах. Программируемые калькуляторы, такие как Texas Instruments ‘TI-89 Titanium и TI-Nspire CX CAS не допускаются при сдачи экзамена, но разрешены для приема SAT. ACT позволяет пользоваться научными калькуляторами, такими как TI-83 Plus или TI-Inspire CX .
Реклама
Об этой статье
Эту страницу просматривали 18 099 раз.
Была ли эта статья полезной?
Как калькулятор находит корень заданного числа?
Дима Гричанюк
12 августа 2016 · 82,1 K
аналитик в Fuzzy Logic Labs, преподаватель департамента Механики и мехатроники РУДН · 12 авг 2016
Реалистичнее всего в условиях крайне ограниченного объема вычислительной мощности калькулятора – использование метода Ньютона. Для квадратного корня он, если коротко и просто, заключается в следующем.
Пусть, например, ищется корень числа 13. Берем в качестве ответа любое число. Например, единицу. Считаем полусумму значений этого возможного ответа и исходного числа, делённого на этот «ответ»:
(1 + 13/1) / 2 = 7
Теперь вероятным ответом будет 7. Повторяем приём ещё несколько раз:
(7 + 13/7) / 2 = 4,4286
(4,4286 + 13/4,4286) / 2 = 3,682
(3,682 + 13/3,682) / 2 = 3,606
И так далее. Уже сейчас ошибка очень маленькая: если проверить и возвести 3,606 в квадрат, получится 13,0057. Калькулятору очень легко делать сложения и чуть сложнее деления, но цепочку таких операций он может провести довольно быстро.
12,5 K
Увы, но этот вариант нахождения корня не будет действовать для единицы
Комментировать ответ…Комментировать…
Привет.
После лекций по мат.анализу я помню такую интересную штуку: компьютер наш владеет лишь операциями сложения (вычитания), умножения и деления. Соответственно, может решать многочлены. Но вот наши замечательные функции вроде корня из X, SinX, CosX, e^X (и т.д.) многочленами не являются (для каждого случая есть доказательство, мол, почему не являются. Ну, например… Читать далее
1,6 K
Компьютер умеет только складывать. Все остальное так же делается через сложение )
Комментировать ответ…Комментировать…
910
Комментировать ответ…Комментировать…
|
Два способа. Во-первых, квадратный корень – это число в степени 1/2. Так что можно воспользоваться функцией “x^y” (доступна при выборе режима “Инженерный”): набрать число, нажать эту кнопочку, набрать 0,5 и нажать Enter. Во-вторых, извлечение корня есть операция, обратная возведению в квадрат. А в калькуляторе (опять же в режиме “Инженерный”) есть специальный флажок инверсной функции Inv. Так что наберите число, отметьте этот флажок (или нажмите кнопочку Inv) и нажмите кнопочку “х квадрат”. Отмазка: в калькуляторе из Windows 7 этот способ почему-то не работает. модератор выбрал этот ответ лучшим CyBear более года назад Извлечение корня из числаИзвлечение квадратного корня из числа подразумевает нахождение такого числа, которое будучи возведенным в квадрат (умноженное самое на себя) даст при этом первоначальное число. Так например, квадратным корнем из 36 будет являться число 6, так как 6*6 = 6^6 = 36. Для обозначения операции извлечения корня в математике используют специальный символ – “√”. А в программировании функция извлечения квадратного корня чаще всего называется “sqrt” сокращенное от английского “SQuare RooT”, что дословно и переводится как “квадратный корень”. Ради примера поищем квадратный корень числа 12. Чтобы найти квадратный корень можно: 1. Воспользоваться калькулятором, ввести 12 и найти символ “√”. Получим число 3,4641016151377545870548926830117 ~ 3,464 2. Воспользоваться таблицей Брадиса для извлечения квадратных корней в диапазоне 0-99 и найти на пересечении соответствующей строки (десятки) и столбца (единицы) искомое значение 3,4641 3. Еще одним вариантом может быть использование универсального алгоритма, который называют “вавилонский”. Он описывается формулой √c= √(a^2+b)=a+b/2a и дает приблизительное вычисления корня с точностью, которая часто бывает достаточной. Для числа 12 вычисление по этой формуле будет выглядеть так: √12 = √(3^2+3)=3+3/(2*3) = 3+1/2 = 3,5. И это достаточно точное вычисление! В калькуляторе Windows ничего сложного нет извлечь квадратный корень – эта функция заложена в классической форме калькулятора – достаточно ввести число и нажать на значок корня. Чтобы извлечь корень кубический или произвольный степени следует воспользоваться уже инженерным калькулятором. Для этого в меню Вид выбираем вкладку Инженерный. Получаем такую картинку: Кубический корень уже есть по умолчанию на панели калькулятора и просто вводим число и нажимаем нужную кнопку, а корень произвольной степени находится так: Сперва вводим радикал, то есть подкоренное выражение, например 64, нажимаем кнопку корень у из х (смотри в пятом столбике) и далее нажимаем нужную нам степень корня, например 4. Жмем на равно и получаем ответ – 2. Вот мы и посчитали, что корень четвертой степени из 64 равен 2. Galina7v7 7 лет назад Многие корни можно извлечь устно.Для этого необходимо знать хоть немного ряд квадратов чисел:1,4,9,16,25,36,49,64,81,121,144,169,196,225,256,,,и по возможности квадраты двузначных чисел,если часто решаете такие задачи.При извлечении квадратов помогает разложение на множители подкоренного числа,и извлечь сомножители,если там будут квадраты чисел.Если и этого не окажется,то постараться проанализировать-между какими квадратами расположено подкоренное число,чтобы определить уровни.Эти анализы подходят для квадратов целых чисел,и для устного вычисления корня.Вычисление неточных корней подходит извлечение по калькулятору,или по таблице корней. Корень из числа можно извлечь в MS Excel задав, =число^(1/n), где n – корень n-й степени. Например, корень 4-й степени из 81 будет задаваться =81^(1/4) и ответ будет 3. Или выбрав среди математических функций в Эксель СТЕПЕНЬ(число; степень) и записав =СТЕПЕНЬ(81; 1/4) Быстрый Стриж 7 лет назад Корень из числа можно вычислить умножив исходное число на степень 1/2 или произвести вычисление на любом калькуляторе, используя математический значок корня. Корень числа редко бывает целым значением и чаще всего округляется. Знаете ответ? |