На этапе подготовки к заключительному тестированию учащимся старших классов необходимо подтянуть знания по теме «Показательные уравнения». Опыт прошлых лет свидетельствует о том, что подобные задания вызывают у школьников определенные затруднения. Поэтому старшеклассникам, независимо от уровня их подготовки, необходимо тщательно усвоить теорию, запомнить формулы и понять принцип решения таких уравнений. Научившись справляться с данным видом задач, выпускники смогут рассчитывать на высокие баллы при сдаче ЕГЭ по математике.
Готовьтесь к экзаменационному тестированию вместе со «Школково»!
При повторении пройденных материалов многие учащиеся сталкиваются с проблемой поиска нужных для решения уравнений формул. Школьный учебник не всегда находится под рукой, а отбор необходимой информации по теме в Интернете занимает долгое время.
Образовательный портал «Школково» предлагает ученикам воспользоваться нашей базой знаний. Мы реализуем совершенно новый метод подготовки к итоговому тестированию. Занимаясь на нашем сайте, вы сможете выявить пробелы в знаниях и уделить внимание именно тем заданиям, которые вызывают наибольшие затруднения.
Преподаватели «Школково» собрали, систематизировали и изложили весь необходимый для успешной сдачи ЕГЭ материал в максимально простой и доступной форме.
Основные определения и формулы представлены в разделе «Теоретическая справка».
Для лучшего усвоения материала рекомендуем попрактиковаться в выполнении заданий. Внимательно просмотрите представленные на данной странице примеры показательных уравнений с решением, чтобы понять алгоритм вычисления. После этого приступайте к выполнению задач в разделе «Каталоги». Вы можете начать с самых легких заданий или сразу перейти к решению сложных показательных уравнений с несколькими неизвестными или иррациональным уравнениям со знаком корня. База упражнений на нашем сайте постоянно дополняется и обновляется.
Те примеры с показателями, которые вызвали у вас затруднения, можно добавить в «Избранное». Так вы можете быстро найти их и обсудить решение с преподавателем.
Чтобы успешно сдать ЕГЭ, занимайтесь на портале «Школково» каждый день!
Корни и степени
-
Степень с натуральным показателем
-
Степень с целым показателем
-
Кубический корень
-
Корень -ной степени
-
Сравнение арифметических корней
-
Как избавиться от иррациональности в знаменателе
-
Как упрощать иррациональные выражения, пользуясь формулами сокращенного умножения
Степенью называется выражение вида .
Здесь — основание степени,
— показатель степени.
к оглавлению ▴
Степень с натуральным показателем
Проще всего определяется степень с натуральным (то есть целым положительным) показателем.
По определению, .
Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы.
Возвести число в квадрат — значит умножить его само на себя.
.
Возвести число в куб — значит умножить его само на себя три раза.
.
Возвести число в натуральную степень — значит умножить его само на себя
раз:
к оглавлению ▴
Степень с целым показателем
Показатель степени может быть не только натуральным (то есть целым положительным), но и равным нулю, а также целым отрицательным.
По определению,
.
Это верно для . Выражение 00 не определено.
Определим также, что такое степень с целым отрицательным показателем.
Конечно, все это верно для , поскольку на ноль делить нельзя.
Например,
Заметим, что при возведении в минус первую степень дробь переворачивается.
Показатель степени может быть не только целым, но и дробным, то есть рациональным числом. В статье «Числовые множества» мы говорили, что такое рациональные числа. Это числа, которые можно записать в виде дроби , где
— целое,
— натуральное.
Здесь нам понадобится новое понятие — корень -степени. Корни и степени — две взаимосвязанные темы. Начнем с уже знакомого вам арифметического квадратного корня.
Определение.
Арифметический квадратный корень из числа — это такое неотрицательное число, квадрат которого равен
.
Согласно определению,
В школьной математике мы извлекаем корень только из неотрицательных чисел. Выражение для нас сейчас имеет смысл только при
.
Выражение всегда неотрицательно, т.е.
. Например,
.
Свойства арифметического квадратного корня:
Запомним важное правило:
По определению,  .
.
к оглавлению ▴
Кубический корень
Аналогично, кубический корень из — это такое число, которое при возведении в третью степень дает число
.
Например, , так как
;
, так как
;
, так как
.
Обратите внимание, что корень третьей степени можно извлекать как из положительных, так и из отрицательных чисел.
Теперь мы можем дать определение корня -ной степени для любого целого
.
к оглавлению ▴
Корень  -ной степени
-ной степени
Корень -ной степени из числа
— это такое число, при возведении которого в
-ную степень получается число
.
Например,
Заметим, что корень третьей, пятой, девятой — словом, любой нечетной степени, — можно извлекать как из положительных, так и из отрицательных чисел.
Квадратный корень, а также корень четвертой, десятой, в общем, любой четной степени можно извлекать только из неотрицательных чисел.
Итак, — такое число, что
. Оказывается, корни можно записывать в виде степеней с рациональным показателем. Это удобно.
По определению,
в общем случае .
Сразу договоримся, что основание степени больше 0.
Например,
Выражение по определению равно
.
При этом также выполняется условие, что больше 0.
Например,
Запомним правила действий со степенями:
— при перемножении степеней показатели складываются;
— при делении степени на степень показатели вычитаются;
— при возведении степени в степень показатели перемножаются;
Покажем, как применяются эти формулы в заданиях ЕГЭ по математике:
1.
Внесли все под общий корень, разложили на множители, сократили дробь и извлекли корень.
2.
3.
Здесь мы записали корни в виде степеней и использовали формулы действий со степенями.
4. Найдите значение выражения при
Решение:
При получим
Ответ: -0,5.
5. Найдите значение выражения при
Решение:
При a = 12 получим
Мы воспользовались свойствами степеней.
Ответ: 144.
6. Найдите значение выражения при b = – 5.
Решение:
При b = – 5 получим:
Ответ: -125.
7. Расположите в порядке возрастания:
Решение:
Запишем выражения как степени с положительным показателем и сравним.
Так как
то
Так как
то
Сравним и
для этого оценим их разность:
значит
Получим : поэтому
Ответ:
8. Представьте выражение в виде степени:
Решение:
Вынесем за скобку степень с меньшим показателем:
Ответ:
9. Упростите выражение:
Решение:
Приведем основания 6 и 12 к основаниям 2 и 3:
(выполним деление степеней с одинаковыми основаниями)
Ответ: 0,25.
10. Чему равно значение выражения при
?
Решение:
При получим
Ответ: 9.
к оглавлению ▴
Сравнение арифметических корней
11. Какое из чисел больше: или
?
Решение:
Возведем в квадрат оба числа (числа положительные):
Найдем разность полученных результатов:
так как
Значит, первое число больше второго.
Ответ:
к оглавлению ▴
Как избавиться от иррациональности в знаменателе
Если дана дробь вида то нужно умножить числитель и знаменатель дроби на
:
Тогда знаменатель станет рациональным.
Если дана дробь вида или
то нужно умножить числитель и знаменатель дроби на сопряженное выражение, чтобы получить в знаменателе разность квадратов.
Сопряженные выражения – это выражения, отличающиеся только знаками. Например,
и
и
– сопряженные выражения.
Пример:
12. Вот несколько примеров – как избавиться от иррациональности в знаменателе:
Пример 1.
Пример 2.
Пример 3.
Пример 4.
Совет. Если в знаменателе дана сумма двух корней, то в разности первым числом пишите то, которое больше, и тогда разность квадратов корней будет положительным числом.
Пример 5.
13. Сравните и
1)
2) Сравним и 14.
то и
а значит,
Ответ: меньше.
к оглавлению ▴
Как упрощать иррациональные выражения, пользуясь формулами сокращенного умножения
Покажем несколько примеров.
14. Упростите: выражения:
Пример 5.
т.к.
Пример 6.
Пример 7.
так как
Следующие несколько задач решаются с помощью формулы:
Решение:
Получим уравнение
Ответ:
19. Вычислите значение выражения:
Решение:
Ответ: 1.
20. Вычислите значение выражения:
Решение:
Ответ: 1.
21. Вычислите значение выражения: если
Решение.
Если то
следовательно
Ответ: – 1.
22. Вычислите:
Решение:
Ответ: 1.
Рассмотрим уравнение вида где
Это равенство выполняется, только если
Подробно об таких уравнениях – в статье «Показательные уравнения».
При решении уравнений такого вида мы пользуемся монотонностью показательной функции.
23. Решите уравнение:
а)
б)
в)
Решение.
23. Решите уравнение:
Решение:
тогда
Ответ: -1.
24. Решите уравнение:
Решение:
Ответ: 4.
25. Решите уравнение:
Решение:
Значит,
Ответ: -0,2.
Если вы хотите разобрать большее количество примеров – записывайтесь на курсы подготовки к ЕГЭ по математике онлайн
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Корни и степени» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Что такое корень n-й степени из действительного числа
Чтобы научиться работать с корнями степени (n), необходимо знать, что такое арифметический КВАДРАТНЫЙ корень и его свойства.
Корнем n-й степени ((n=2, 3, 4, 5, 6… )) некоторого числа (a) называют такое неотрицательное число (b), которое при возведении в степень (n in N) дает (a). Корень n-ой степени обозначается при помощи знака радикала (sqrt[n]{a}):
$$ sqrt[n]{a}=b; $$
$$ b^{n}=underbrace{b*b*b*…*b}_{n ; раз}=a. $$
Число (n in N) при этом называют показателем корня, а число (a) покоренным выражением.
Если (n=2), то перед вами корень 2-й степени или обычный арифметический квадратный корень, который все проходили в 8-м классе.
Если (n=3), то это корень 3-й степени, (sqrt[3]{a}). Его обычно называют кубическим корнем. Чтобы его вычислить, нужно найти такое число, которое умноженное на само себя три раза, даст подкоренное выражение.
Если (n=4), то корень 4-й степени, (sqrt[4]{a}) и т.д.
Операция извлечения корня n-й степени является обратной к операции возведения в n-ю степень. Для того, чтобы вычислить корень n-й степени от (a), нужно сообразить какое число в степени (n) будет давать (a).
Пример 1
$$ sqrt[3]{27}=3 $$
Кубический корень из числа 27 равняется 3. Действительно, если число 3 возвести в 3-ю степень, то мы получим 27.
Пример 2
$$ sqrt[4]{16}=2 $$
Корень 4-й степени из 16-и равен 2. Двойка в 4-й степени равна 16.
Пример 3
$$ sqrt[n]{0}=0 $$
Если извлечь корень n-й степени из 0, всегда будет 0.
Пример 4
$$ sqrt[n]{1}=1 $$
Если извлечь корень n-й степени из 1, всегда будет 1.
Пример 5
$$ sqrt[3]{19}= ? $$
Мы не можем в уме подобрать такое число, которое при возведении в 3-ю степень даст 19. Если посчитать на калькуляторе, то получим (2,668…) – иррациональное число с бесконечным количеством знаков после запятой.
Обычно, в математике, когда у вас получается иррациональное число, корень не считают и оставляют так как есть (sqrt[3]{19}).
Что же делать, если под рукой нет калькулятора, а нужно оценить, чему равен такой корень. В этом случае нужно подобрать справа и слева ближайшие числа, корень из которых посчитать можно:
$$ sqrt[3]{8} le sqrt[3]{19} le sqrt[3]{27} $$
$$ 2 le sqrt[3]{19} le 3 $$
Получается, что наш корень лежит между числами 2 и 3.
Пример 6
Оценить значение (sqrt[4]{15}= ?)
$$ sqrt[4]{1} le sqrt[4]{15} le sqrt[4]{16}; $$
$$ 1 le sqrt[4]{15} le 2; $$
Корень четной и нечетной степеней
Надо четко различать правила работы c четными и нечетными степенями. Дело в том, что корень четной степени можно взять только из неотрицательного числа. Из отрицательных чисел корень четной степени не существует.
Корень нечетной степени можно посчитать из любых действительных чисел. Иногда в школьной программе встречаются задания, в которых требуется определить имеет ли смысл выражение:
Пример 7
$$ sqrt[3]{-27}=-3 $$
Данное выражение имеет смысл, так как корень нечетной степени можно посчитать из любого числа, даже отрицательного. Напоминаю, что извлечь корень 3-й степени, значит найти такое число, которое при возведении в 3-ю степень даст покоренное выражение. Если ((-3)) умножить на само себя три раза, то мы получим покоренное выражение (-27=(-3)*(-3)*(-3)).
Пример 8
$$ sqrt[4]{-27} $$
Так как корень четной степени, а под корнем стоит отрицательное число, то выражение не имеет смысла. Невозможно найти число, которое при умножении на само себя четыре раза, даст отрицательное значение.
Из-под знака нечетного показателя корня можно выносить минус. Это упрощает процесс подсчета.
$$sqrt[5]{-32}=-sqrt[5]{32}=-2;$$
Свойства корня n-й степени
Пусть есть два числа a и b, для них будут выполняться следующие свойства:
$$ (sqrt[n]{a})^n=a $$
$$ sqrt[n]{a^n}=a $$
$$ sqrt[n]{a*b}=sqrt[n]{a}*sqrt[n]{b} $$
$$ sqrt[n]{frac{a}{b}}=frac{sqrt[n]{a}}{sqrt[n]{b}}, b neq 0 $$
$$ (sqrt[n]{a})^k=sqrt[n]{a^k} $$
$$sqrt[n] {sqrt[k]{a}}=sqrt[n*k]{a} $$
$$ sqrt[n*p]{a^{k*p}}=sqrt[n]{a^k} $$
При использовании вышеперечисленных свойств важно помнить: корень четной степени не существует из отрицательных чисел, и сам корень четной степени всегда положителен. Надо быть внимательным и следить, чтобы в ходе преобразований эти ограничения не нарушались.
Рассмотрим примеры на свойства корня степени (n).
Пример 9
$$(sqrt[5]{7})^5=7;$$
При возведении корня с показателем (n) в степень (n) остается просто подкоренное выражение, так как возведение в степень и извлечение корня это взаимно обратные операции.
Обратите внимание, что неважно, где стоит степень – над корнем или под корнем, результат будет одинаковым.
$$sqrt[5]{7^5}=7$$
Из рассмотренного выше примера следует свойство ((sqrt[n]{a})^k=sqrt[n]{a^k}). Не имеет значения, извлекаете ли вы сначала корень, а потом возводите в степень, или наоборот, сначала возводите в степень подкоренное выражение, и только потом извлекаете корень.
Пример 10
$$sqrt[3]{8^2}=(sqrt[3]{8})^2=2^{2}=4;$$
$$sqrt[3]{8^2}=sqrt[3]{64}=4;$$
Получается одно и тоже.
Более того, показатель корня и степень подкоренного выражения можно домножить на одно и тоже число (p), результат от этого не изменится. Может пригодиться в различных преобразованиях и при сравнении корней между собой.
$$ sqrt[n]{a^k}=sqrt[n*p]{a^{k*p}};$$
Пример 11
$$ sqrt[3]{10^2}=sqrt[3*2]{10^{2*2}}=sqrt[6]{10^{4}}=sqrt[6]{1000};$$
Эту же формулу можно использовать наоборот:
$$ sqrt[n*p]{a^{k*p}}=sqrt[n]{a^k} $$
То есть можно сокращать показатель корня и степень подкоренного выражения, что существенно упрощает вычисления в некоторых случаях.
Пример 12
$$ sqrt[6]{16}=sqrt[6]{2^4}=sqrt[3]{2^2}=sqrt[3]{4};$$
Рассмотрим применение формул корня от произведения и частного, без которых невозможно решить ни один приличный пример.
Корень степени (n) от произведения равен произведению корней степени (n) от этих множителей.
$$ sqrt[n]{a*b}=sqrt[n]{a}*sqrt[n]{b} $$
И аналогично корень степени (n) от частного равен частному корней n-й степени.
$$ sqrt[n]{frac{a}{b}}=frac{sqrt[n]{a}}{sqrt[n]{b}}, b neq 0 $$
Пример 13
$$sqrt[3]{125*8}=sqrt[3]{125}*sqrt[3]{8}=5*2=10;$$
$$sqrt[3]{-frac{27}{8}}=frac{-sqrt[3]{27}}{sqrt[3]{8}}=frac{-3}{2};$$
Формулы справедливы не только для двух множителей:
Пример 14
$$sqrt[3]{125*8*27}=sqrt[3]{125}*sqrt[3]{8}*sqrt{27}=5*2*3=30;$$
Пример 15
$$sqrt[4]{frac{16*81}{625}}=frac{sqrt[4]{16*81}}{sqrt[4]{625}}=frac{sqrt[4]{16}*sqrt[4]{81}}{sqrt[4]{625}}=frac{2*3}{5}=frac{6}{5};$$
Обратите внимание! Формулы произведения и частного корней справедливы только для корней с одинаковыми показателями. Нельзя перемножить корни с разными показателями.
$$sqrt[3]{6}*sqrt[4]{7}=?$$
Ничего здесь сделать мы не можем!
И следите за отрицательными числами при использовании корней четной степени. Произведение двух отрицательных чисел может существовать под одним корнем, так как они при умножении дают знак плюс. Но разбивать такое произведение на два корня четной степени ни в коем случае нельзя: выражение теряет всякий смысл.
$$sqrt[4]{-15*(-7)} neq sqrt[4]{-15}*sqrt[4]{-7};$$
$$sqrt[4]{-15*(-7)} = sqrt[4]{15*7}=sqrt[4]{15}*sqrt[4]{7};$$
Корнем n-ой степени из действительного числа (a) называют такое число (b), (n)-ая степень которого равна (a).
(sqrt[n]{a}=b), если (b^n=a)
Примеры:
(sqrt[4]{16}=2), так как (2^4=16)
(sqrt[3]{-frac{1}{125}})(=) (-frac{1}{5}),так как ((-frac{1}{5})^3) (=) (-frac{1}{125})
Как вычислить корень n-ой степени?
Чтобы вычислить корень (n)-ой степени, надо задать себе вопрос: какое число в (n)-ой степени, даст выражение под корнем?
Например. Вычислите корень (n)-ой степени: а)(sqrt[4]{16}); б) (sqrt[3]{-64}); в) (sqrt[5]{0,00001}); г)(sqrt[3]{8000}); д) (sqrt[4]{frac{1}{81}}).
а) Какое число в (4)-ой степени, даст (16)? Очевидно, (2). Поэтому:
(sqrt[4]{16}=2)
б) Какое число в (3)-ей степени, даст (-64)?
(sqrt[3]{-64}=-4)
в) Какое число в (5)-ой степени, даст (0,00001)?
(sqrt[5]{0,00001}=0,1)
г) Какое число в (3)-ей степени, даст (8000)?
(sqrt[3]{8000}=20)
д) Какое число в (4)-ой степени, даст (frac{1}{81})?
(sqrt[4]{frac{1}{81}}=frac{1}{3})
Мы рассмотрели самые простые примеры с корнем (n)-ой степени. Для решения более сложных задач с корнями (n)-ой степени – жизненно необходимо знать их свойства.
Пример. Вычислите:
|
(sqrt 3cdot sqrt[3]{-3} cdot sqrt{27} cdot sqrt[3]{9} -) (frac{sqrt[5]{-64}}{sqrt[5]{2}})(=) |
В данный момент ни один из корней нельзя вычислить. Поэтому применим свойства корня (n)-ой степени и преобразуем выражение. |
|
|
(=sqrt{3}cdot sqrt[3]{-3}cdot sqrt{27}cdot sqrt[3]{9}-sqrt[5]{-32}=) |
Переставим множители в первом слагаемом так, что бы квадратный корень и корень (n)-ой степени стояли рядом. Так легче будет применять свойства т.к. большинство свойств корней (n)-ой степени работают только с корнями одинаковой степени. |
|
|
(=sqrt{3} cdot sqrt{27} cdot sqrt[3]{-3}cdot sqrt[3]{9}-(-5)=) |
Применим свойство (sqrt[n]{a}cdot sqrt[n]{b}=sqrt[n]{acdot b}) и раскроем скобку |
|
|
(=sqrt{81}cdot sqrt[3]{-27}+5=) |
Вычисли (sqrt{81}) и (sqrt[3]{-27}) |
|
|
(=9cdot(-3)+5 =-27+5=-22) |
Корень n-ой степени и квадратный корень связаны?
Да, арифметический квадратный корень является как раз корнем (n)-ой степени, у которого (n=2). Математики договорились для упрощения записи эту двойку над корнем не писать, то есть (sqrt[2]{a}) записывать просто (sqrt{a}). Суть при этом осталась той же.

Заметим, что также как и в квадратном корне, корнем (n)-ой степени из (a) называют число (b), а не запись (sqrt[n]{a}). То есть, корень третьей степени из (8), это именно (2), а не (sqrt[3]{8}). Но если корень «неизвлекаем» – его проще записать как (sqrt[n]{a}) (например, (sqrt[3]{23}). Такие числа называются иррациональными.
В любом случае, любой корень любой степени – это просто число, пусть и записанное в непривычном вам виде.
Особенность корня n-ой степени
Корень (n)-ой степени с нечетными (n) может извлекаться из любого числа, даже отрицательного (см. примеры в начале). Но если (n) – четное ((sqrt[4]{a}), (sqrt[6]{a}),(sqrt[8]{a})… ), то такой корень извлекается только если (a ≥ 0) (кстати, у квадратного корня так же). Это связано с тем, что извлечение корня – действие, обратное возведению в степень.

А возведение в четную степень делает даже отрицательное число положительным. Действительно, ((-2)^6=(-2) cdot (-2) cdot (-2) cdot (-2) cdot (-2) cdot (-2)=64). Поэтому мы не можем получить под корнем четной степени отрицательного числа. А значит, и извлечь такой корень из отрицательного числа – не можем.

Нечетная же степень таких ограничений не имеет – отрицательное число, возведенное в нечетную степень останется отрицательным: ((-2)^5=(-2) cdot (-2) cdot (-2) cdot (-2) cdot (-2)=-32). Поэтому под корнем нечетной степени можно получить отрицательное число. А значит и извлечь его из отрицательного числа – тоже можно.

Определение. Корнем n-ой степени из комплексного числа z называется комплексное число, n-ая степень которого равна z.
 , если
, если  .
.
Получим правило извлечения корня n-ой степени из комплексного числа, записанного в тригонометрической форме, пользуясь определением. Итак, пусть  . Найдем
. Найдем 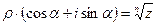 . Имеем по определению
. Имеем по определению 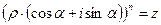 , откуда по формуле Муавра получим
, откуда по формуле Муавра получим 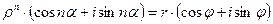 . Так модуль комплексного числа определяется однозначно, а аргумент – с точностью до слагаемого, кратного
. Так модуль комплексного числа определяется однозначно, а аргумент – с точностью до слагаемого, кратного  , то
, то 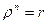 и
и 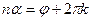 . Таким образом,
. Таким образом, 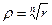 , а
, а  .
.
Итак,  .
.
Пример. Найти  . Запишем число в тригонометрической форме
. Запишем число в тригонометрической форме  . Теперь применим формулу
. Теперь применим формулу  .
.
Если k=0, то  . Если k=1, то
. Если k=1, то  .
.
Если k=2, то 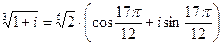 . Если k=3, то
. Если k=3, то  .
.
Заметим, что при извлечении корня третьей степени получили три различных комплексных числа. Справедлива следующая теорема.
Лемма. Существует ровно n различных корней n-ой степени из комплексного числа. Для получения этих значений достаточно применить формулу для вычисления корня при  .
.
Интересным свойством обладают комплексные корни n-ой степени из единицы. Попробуем получить это свойство, рассматривая пример  . Запишем единицу в тригонометрической форме и применим формулу для вычисления корней:
. Запишем единицу в тригонометрической форме и применим формулу для вычисления корней:
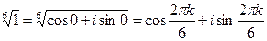 . Получим шесть различных значений. Изобразим их на комплексной плоскости.
. Получим шесть различных значений. Изобразим их на комплексной плоскости.
Итак, полученные значения оказались вершинами правильного шестиугольника, вписанного в единичную окружность, причем одна из вершин – в точке (1,0).
Это утверждение можно обобщить. Попробуйте сделать это самостоятельно .
Определение. Корень n-ой степени из единицы называется первообразным корнем, если все корни представимы в виде его степени.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8447 —  | 7339 —
| 7339 —  или читать все.
или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Степень
Степенью называется выражение вида: , где:
- — основание степени;
- — показатель степени.
Степень с натуральным показателем
Определем понятие степени, показатель которой — натуральное число (т.е. целое и положительное).
- По определению: .
- Возвести число в квадрат — значит умножить его само на себя:
- Возвести число в куб — значит умножить его само на себя три раза: .
Возвести число в натуральную степень — значит умножить число само на себя раз:

Степень с целым показателем
Если показателем степени является целое положительное число:
, n > 0
Возведение в нулевую степень:
, a ≠ 0
Если показателем степени является целое отрицательное число:
 , a ≠ 0
, a ≠ 0
Прим: выражение не определено, в случае n ≤ 0. Если n > 0, то

Степень с рациональным показателем
- a > 0;
- n — натуральное число;
- m — целое число;


Свойства степеней

Корень
Арифметический квадратный корень
Уравнение имеет два решения: x=2 и x=-2. Это числа, квадрат которых равен 4.
Рассмотрим уравнение . Нарисуем график функции и увидим, что и у этого уравнения два решения, одно положительное, другое отрицательное.

Но в данному случае решения не являются целыми числами. Более того, они не являются рациональными. Для того, чтобы записать эти иррациональные решения, мы вводим специальный символ квадратного корня.
Арифметический квадратный корень — это неотрицательное число, квадрат которого равен , a ≥ 0. При a Корень из квадрата

Например, . А решения уравнения соответственно и
Кубический корень
Кубический корень из числа — это число, куб которого равен . Кубический корень определен для всех . Его можно извлечь из любого числа: .
Корень n-ой степени
Корень -й степени из числа — это число, -я степень которого равна .
Поздравляю: сегодня мы будем разбирать корни — одну из самых мозговыносящих тем 8-го класса.:)
 У вас тоже так? Читайте дальше — и всё поймёте
У вас тоже так? Читайте дальше — и всё поймёте
Многие путаются в корнях не потому, что они сложные (чего там сложного-то — пара определений и ещё пара свойств), а потому что в большинстве школьных учебников корни определяются через такие дебри, что разобраться в этой писанине могут разве что сами авторы учебников. Да и то лишь с бутылкой хорошего виски.:)
Поэтому сейчас я дам самое правильное и самое грамотное определение корня — единственное, которое вам действительно следует запомнить. А уже затем объясню: зачем всё это нужно и как это применять на практике.
Но сначала запомните один важный момент, про который многие составители учебников почему-то «забывают»:
Вот в этом грёбаном «несколько отличается» скрыто, наверное, 95% всех ошибок и недопонимания, связанного с корнями. Поэтому давайте раз и навсегда разберёмся с терминологией:
Определение. из числа $a$ — это любое неотрицательное число $b$ такое, что $<^>=a$. А из того же числа $a$ — это вообще любое число $b$, для которого выполняется всё то же равенство: $<^>=a$.
В любом случае корень обозначается вот так:
Число $n$ в такой записи называется , а число $a$ — . В частности, при $n=2$ получим наш «любимый» квадратный корень (кстати, это корень чётной степени), а при $n=3$ — кубический (степень нечётная), который тоже часто встречается в задачах и уравнениях.
Примеры. Классические примеры квадратных корней:
Кстати, $sqrt<0>=0$, а $sqrt<1>=1$. Это вполне логично, поскольку $<<0>^<2>>=0$ и $<<1>^<2>>=1$.
Кубические корни тоже часто встречаются — не надо их бояться:
Ну, и парочка «экзотических примеров»:
Если вы не поняли, в чём разница между чётной и нечётной степенью — перечитайте определение ещё раз. Это очень важно!
А мы тем временем рассмотрим одну неприятную особенность корней, из-за которой нам и потребовалось вводить раздельное определение для чётных и нечётных показателей.
Зачем вообще нужны корни?
Прочитав определение, многие ученики спросят: «Что курили математики, когда это придумывали?» И вправду: зачем вообще нужны все эти корни?
Чтобы ответить на этот вопрос, вернёмся на минутку в начальные классы. Вспомните: в те далёкие времена, когда деревья были зеленее, а пельмени вкуснее, основная наша забота была в том, чтобы правильно умножать числа. Ну, что-нибудь в духе «пять на пять — двадцать пять», вот это вот всё. Но ведь можно умножать числа не парами, а тройками, четвёрками и вообще целыми комплектами:
Ну и так далее. Ладно, ладно: последние две строчки я считал на калькуляторе.:)
Однако суть не в этом. Фишка в другом: математики — людишки ленивые, поэтому им было в лом записывать умножение десяти пятёрок вот так:
[5cdot 5cdot 5cdot 5cdot 5cdot 5=15 625]
Поэтому они придумали степени. Почему бы вместо длинной строки не записать количество множителей в виде верхнего индекса? Типа вот такого:
[5cdot 5cdot 5cdot 5cdot 5cdot 5=<<5>^<6>>=15 625]
Это же очень удобно! Все вычисления сокращаются в разы, и можно не тратить кучу листов пергамента блокнотиков на запись какого-нибудь 5 183 . Такую запись назвали степенью числа, у неё нашли кучу свойств, но счастье оказалось недолгим.
После грандиозной пьянки, которую организовали как раз по поводу «открытия» степеней, какой-то особо упоротый математик вдруг спросил: «А что, если нам известна степень числа, но неизвестно само число?» Вот, действительно, если нам известно, что некое число $b$, допустим, в 5-й степени даёт 243, то как нам догадаться, чему равно само число $b$?
Проблема эта оказалась гораздо более глобальной, чем может показаться на первый взгляд. Потому что выяснилось, что для большинства «готовых» степеней таких «исходных» чисел нет. Судите сами:
А, что если $<^<3>>=50$? Получается, что нужно найти некое число, которое будучи трижды умноженное само на себя даст нам 50. Но что это за число? Оно явно больше 3, поскольку 3 3 = 27 3 = 64 > 50. Т.е. это число лежит где-то между тройкой и четвёркой, но чему оно равно — фиг поймёшь.
Именно для этого математики и придумали корни $n$-й степени. Именно для этого ввели значок радикала $sqrt<*>$. Чтобы обозначить то самое число $b$, которое в указанной степени даст нам заранее известную величину
Не спорю: зачастую эти корни легко считаются — мы видели несколько таких примеров выше. Но всё-таки в большинстве случаев, если вы загадаете произвольное число, а затем попробуете извлечь из него корень произвольной степени, вас ждёт жестокий облом.
Да что там! Даже самый простой и всем знакомый $sqrt<2>$ нельзя представить в привычном нам виде — как целое число или дробушка. А если вы вобьёте это число в калькулятор, то увидите вот это:
Как видите, после запятой идёт бесконечная последовательность цифр, которые не подчиняются никакой логике. Можно, конечно, округлить это число, чтобы быстро сравнить с другими числами. Например:
[sqrt<2>=1,4142. approx 1,4 lt 1,5]
Или вот ещё пример:
[sqrt<3>=1,73205. approx 1,7 gt 1,5]
Но все эти округления, во-первых, довольно грубые; а во-вторых, работать с примерными значениями тоже надо уметь, иначе можно словить кучу неочевидных ошибок (кстати, навык сравнения и округления в обязательном порядке проверяют на профильном ЕГЭ).
Поэтому в серьёзной математике без корней не обойтись — они являются такими же равноправными представителями множества всех действительных чисел $mathbb$, как и давно знакомые нам дроби и целые числа.
Невозможность представить корень в виде дроби вида $frac
$ означает, что данный корень не является рациональным числом. Такие числа называются иррациональными, и их нельзя точно представить иначе как с помощью радикала, либо других специально предназначенных для этого конструкций (логарифмов, степеней, пределов и т.д.). Но об этом — в другой раз.
Рассмотрим несколько примеров, где после всех вычислений иррациональные числа всё же останутся в ответе.
Естественно, по внешнему виду корня практически невозможно догадаться о том, какие числа будут идти после запятой. Впрочем, можно, посчитать на калькуляторе, но даже самый совершенный калькулятор дат нам лишь несколько первых цифр иррационального числа. Поэтому гораздо правильнее записать ответы в виде $sqrt<5>$ и $sqrt[3]<-2>$.
Именно для этого их и придумали. Чтобы удобно записывать ответы.
Почему нужны два определения?
Внимательный читатель уже наверняка заметил, что все квадратные корни, приведённые в примерах, извлекаются из положительных чисел. Ну, в крайнем случае из нуля. А вот кубические корни невозмутимо извлекаются абсолютно из любого числа — хоть положительного, хоть отрицательного.
Почему так происходит? Взгляните на график функции $y=<^<2>>$:
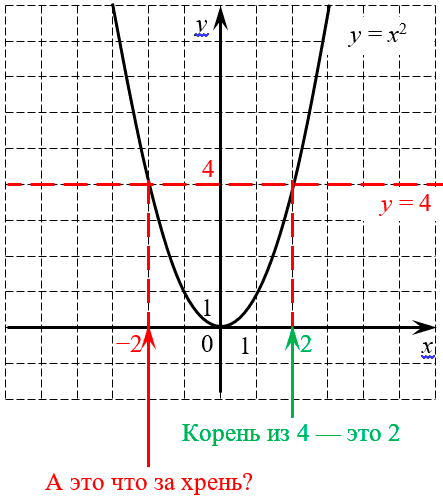 График квадратичной функции даёт два корня: положительный и отрицательный
График квадратичной функции даёт два корня: положительный и отрицательный
Попробуем с помощью этого графика посчитать $sqrt<4>$. Для этого на графике проведена горизонтальная линия $y=4$ (отмечена красным цветом), которая пересекается с параболой в двух точках:$<_<1>>=2$ и $<_<2>>=-2$. Это вполне логично, поскольку
С первым числом всё понятно — оно положительное, поэтому оно и есть корень:
Но что тогда делать со второй точкой? Типа у четвёрки сразу два корня? Ведь если возвести в квадрат число −2, мы тоже получим 4. Почему бы тогда не записать$sqrt<4>=-2$? И почему учителя смотрят на подобные записи так, как будто хотят вас сожрать?:)
В том-то и беда, что если не накладывать никаких дополнительных условий, то квадратных корней у четвёрки будет два — положительный и отрицательный. И у любого положительного числа их тоже будет два. А вот у отрицательных чисел корней вообще не будет — это видно всё по тому же графику, поскольку парабола нигде не опускается ниже оси y, т.е. не принимает отрицательных значений.
Подобная проблема возникает у всех корней с чётным показателем:
- Строго говоря, корней с чётным показателем $n$ у каждого положительного числа будет сразу две штуки;
- Из отрицательных чисел корень с чётным $n$ вообще не извлекается.
Именно поэтому в определении корня чётной степени $n$ специально оговаривается, что ответ должен быть неотрицательным числом. Так мы избавляемся от неоднозначности.
Зато для нечётных $n$ такой проблемы нет. Чтобы убедиться в этом, давайте взглянем на график функции $y=<^<3>>$:
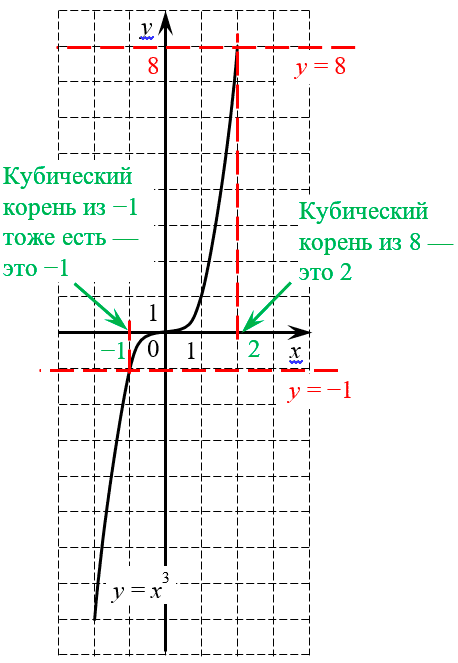 Кубическая парабола принимает любые значения, поэтому кубический корень извлекается из любого числа
Кубическая парабола принимает любые значения, поэтому кубический корень извлекается из любого числа
Из этого графика можно сделать два вывода:
- Ветви кубической параболы, в отличие от обычной, уходят на бесконечность в обе стороны — и вверх, и вниз. Поэтому на какой бы высоте мы ни проводили горизонтальную прямую, эта прямая обязательно пересечётся с нашим графиком. Следовательно, кубический корень можно извлечь всегда, абсолютно из любого числа;
- Кроме того, такое пересечение всегда будет единственным, поэтому не нужно думать, какое число считать «правильным» корнем, а на какое — забить. Именно поэтому определение корней для нечётной степени проще, чем для чётной (отсутствует требование неотрицательности).
Жаль, что эти простые вещи не объясняют в большинстве учебников. Вместо этого нам начинают парить мозг всякими арифметическими корнями и их свойствами.
Да, я не спорю: что такое арифметический корень — тоже надо знать. И я подробно расскажу об этом в отдельном уроке. Сегодня мы тоже поговорим о нём, поскольку без него все размышления о корнях $n$-й кратности были бы неполными.
Но сначала надо чётко усвоить то определение, которое я дал выше. Иначе из-за обилия терминов в голове начнётся такая каша, что в итоге вообще ничего не поймёте.
А всего-то и нужно понять разницу между чётными и нечётными показателями. Поэтому ещё раз соберём всё, что действительно нужно знать о корнях:
- Корень чётной степени существует лишь из неотрицательного числа и сам всегда является неотрицательным числом. Для отрицательных чисел такой корень неопределён.
- А вот корень нечётной степени существует из любого числа и сам может быть любым числом: для положительных чисел он положителен, а для отрицательных — как намекает кэп, отрицательный.
Разве это сложно? Нет, не сложно. Понятно? Да вообще очевидно! Поэтому сейчас мы немного потренируемся с вычислениями.
Основные свойства и ограничения
У корней много странных свойств и ограничений — об этом будет отдельный урок. Поэтому сейчас мы рассмотрим лишь самую важную «фишку», которая относится лишь к корням с чётным показателем. Запишем это свойство в виде формулы:
Другими словами, если возвести число в чётную степень, а затем из этого извлечь корень той же степени, мы получим не исходное число, а его модуль. Это простая теорема, которая легко доказывается (достаточно отдельно рассмотреть неотрицательные $x$, а затем отдельно — отрицательные). О ней постоянно талдычат учителя, её дают в каждом школьном учебнике. Но как только дело доходит до решения иррациональных уравнений (т.е. уравнений, содержащих знак радикала), ученики дружно забывают эту формулу.
Чтобы детально разобраться в вопросе, давайте на минуту забудем все формулы и попробуем посчитать два числа напролом:
Это очень простые примеры. Первый пример решит большинство людишек, а вот на втором многие залипают. Чтобы без проблем решить любую подобную хрень, всегда учитывайте порядок действий:
- Сначала число возводится в четвёртую степень. Ну, это как бы несложно. Получится новое число, которое даже в таблице умножения можно найти;
- И вот уже из этого нового числа необходимо извлечь корень четвёртой степени. Т.е. никакого «сокращения» корней и степеней не происходит — это последовательные действия.
Раберёмся с первым выражением: $sqrt[4]<<<3>^<4>>>$. Очевидно, что сначала надо посчитать выражение, стоящее под корнем:
Затем извлекаем корень четвёртой степени из числа 81:
Теперь сделаем то же самое со вторым выражением. Сначала возводим число −3 в четвёртую степени, для чего потребуется умножить его само на себя 4 раза:
[<<left( -3
ight)>^<4>>=left( -3
ight)cdot left( -3
ight)cdot left( -3
ight)cdot left( -3
ight)=81]
Получили положительное число, поскольку общее количество минусов в произведении — 4 штуки, и они все взаимно уничтожится (ведь минус на минус даёт плюс). Дальше вновь извлекаем корень:
В принципе, эту строчку можно было не писать, поскольку и ежу понятно, что ответ получится один и тот же. Т.е. чётный корень из той же чётной степени «сжигает» минусы, и в этом смысле результат неотличим от обычного модуля:
Эти вычисления хорошо согласуются с определением корня чётной степени: результат всегда неотрицателен, да и под знаком радикала тоже всегда стоит неотрицательное число. В противном случае корень не определён.
Замечание по поводу порядка действий
Таким образом, ни в коем случае нельзя бездумно сокращать корни и степени, тем самым якобы «упрощая» исходное выражение. Потому что если под корнем стоит отрицательное число, а его показатель является чётным, мы получим кучу проблем.
Впрочем, все эти проблемы актуальны лишь для чётных показателей.
Вынесение минуса из-под знака корня
Естественно, у корней с нечётными показателями тоже есть своя фишка, которой в принципе не бывает у чётных. А именно:
Короче говоря, можно выносить минус из-под знака корней нечётной степени. Это очень полезное свойство, которое позволяет «вышвырнуть» все минусы наружу:
Это простое свойство значительно упрощает многие вычисления. Теперь не нужно переживать: вдруг под корнем затесалось отрицательное выражение, а степень у корня оказалась чётной? Достаточно лишь «вышвырнуть» все минусы за пределы корней, после чего их можно будет умножать друг на друга, делить и вообще делать многие подозрительные вещи, которые в случае с «классическими» корнями гарантированно приведут нас к ошибке.
И вот тут на сцену выходит ещё одно определение — то самое, с которого в большинстве школ и начинают изучение иррациональных выражений. И без которого наши рассуждения были бы неполными. Встречайте!
Арифметический корень
Давайте предположим на минутку, что под знаком корня могут находиться лишь положительные числа или в крайнем случае ноль. Забьём на чётные/нечётные показатели, забьём на все определения, приведённые выше — будем работать только с неотрицательными числами. Что тогда?
А тогда мы получим арифметический корень — он частично пересекается с нашими «стандартными» определениями, но всё же отличается от них.
Определение. из неотрицательного числа $a$ называется такое неотрицательное число $b$, что $<^>=a$.
Как видим, нас больше не интересует чётность. Взамен неё появилось новое ограничение: подкоренное выражение теперь всегда неотрицательно, да и сам корень тоже неотрицателен.
Чтобы лучше понять, чем арифметический корень отличается от обычного, взгляните на уже знакомые нам графики квадратной и кубической параболы:
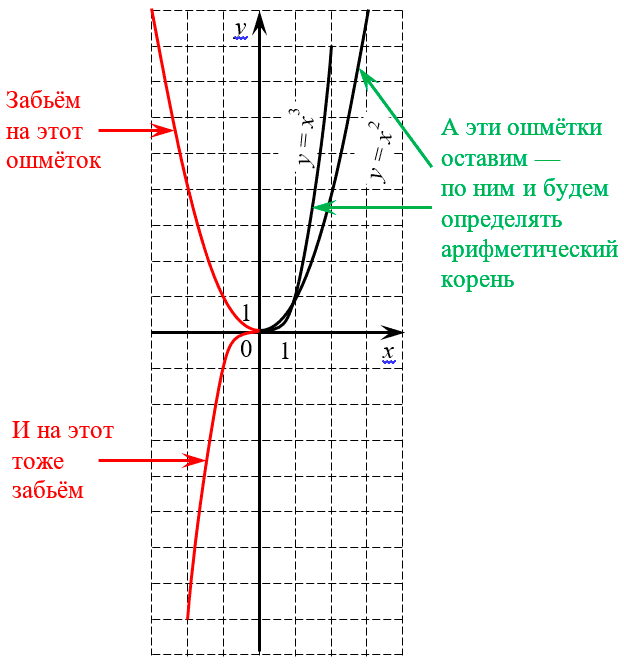 Область поиска арифметического корня — неотрицательные числа
Область поиска арифметического корня — неотрицательные числа
Как видите, отныне нас интересуют лишь те куски графиков, которые расположены в первой координатной четверти — там, где координаты $x$ и $y$ положительны (или хотя бы ноль). Больше не нужно смотреть на показатель, чтобы понять: имеем мы право ставить под корень отрицательное число или нет. Потому что отрицательные числа больше в принципе не рассматриваются.
Возможно, вы спросите: «Ну и зачем нам такое кастрированное определение?» Или: «Почему нельзя обойтись стандартным определением, данным выше?»
Что ж, приведу всего одно свойство, из-за которого новое определение становится целесообразным. Например, правило возведения в степень:
Обратите внимание: мы можем возвести подкоренное выражение в любую степень и одновременно умножить на эту же степень показатель корня — и в результате получится то же самое число! Вот примеры:
Ну и что в этом такого? Почему мы не могли сделать это раньше? А вот почему. Рассмотрим простое выражение: $sqrt[3]<-2>$ — это число вполне нормальное в нашем классическом понимании, но абсолютно недопустимо с точки зрения арифметического корня. Попробуем преобразовать его:
Как видите, в первом случае мы вынесли минус из-под радикала (имеем полное право, т.к. показатель нечётный), а во втором — воспользовались указанной выше формулой. Т.е. с точки зрения математики всё сделано по правилам.
WTF?! Как одно и то же число может быть и положительным, и отрицательным? Никак. Просто формула возведения в степень, которая прекрасно работает для положительных чисел и нуля, начинает выдавать полную ересь в случае с отрицательными числами.
Вот для того, чтобы избавиться от подобной неоднозначности, и придумали арифметические корни. Им посвящён отдельный большой урок, где мы подробно рассматриваем все их свойства. Так что сейчас не будем на них останавливаться — урок и так получился слишком затянутым.
Алгебраический корень: для тех, кто хочет знать больше
Долго думал: выносить эту тему в отдельный параграф или нет. В итоге решил оставить здесь. Данный материал предназначен для тех, кто хочет понять корни ещё лучше — уже не на среднем «школьном» уровне, а на приближенном к олимпиадному.
Так вот: помимо «классического» определения корня $n$-й степени из числа и связанного с ним разделения на чётные и нечётные показатели есть более «взрослое» определение, которое вообще не зависит от чётности и прочих тонкостей. Это называется алгебраическим корнем.
Определение. из числа любого $a$ — это множество всех чисел $b$ таких, что $<^>=a$. Для таких корней нет устоявшегося обозначения, поэтому просто поставим чёрточку сверху:
Принципиальное отличие от стандартного определения, приведённого в начале урока, состоит в том, что алгебраический корень — это не конкретное число, а множество. А поскольку мы работаем с действительными числами, это множество бывает лишь трёх типов:
- Пустое множество. Возникает в случае, когда требуется найти алгебраический корень чётной степени из отрицательного числа;
- Множество, состоящее из одного-единственного элемента. Все корни нечётных степеней, а также корни чётных степеней из нуля попадают в эту категорию;
- Наконец, множество может включать два числа — те самые $<_<1>>$ и $<_<2>>=-<_<1>>$, которое мы видели на графике квадратичной функции. Соответственно, такой расклад возможен лишь при извлечении корня чётной степени из положительного числа.
Последний случай заслуживает более подробного рассмотрения. Посчитаем парочку примеров, чтобы понять разницу.
Решение. С первым выражением всё просто:
Именно два числа входят в состав множества. Потому что каждое из них в квадрате даёт четвёрку.
Тут мы видим множество, состоящее лишь из одного числа. Это вполне логично, поскольку показатель корня — нечётный.
Наконец, последнее выражение:
Получили пустое множество. Потому что нет ни одного действительного числа, которое при возведении в четвёртую (т.е. чётную!) степень даст нам отрицательное число −16.
Финальное замечание. Обратите внимание: я не случайно везде отмечал, что мы работаем с действительными числами. Потому что есть ещё комплексные числа — там вполне можно посчитать и $sqrt[4]<-16>$, и многие другие странные вещи.
Однако в современном школьном курсе математики комплексные числа почти не встречаются. Их вычеркнули из большинства учебников, поскольку наши чиновники считают эту тему «слишком сложной для понимания».
На этом всё. В следующем уроке мы рассмотрим все ключевые свойства корней и научимся, наконец, упрощать иррациональные выражения.:)
