Квадратный корень из числа — это значение, которое при умножении само на себя дает исходное число. Каждое положительное число имеет два квадратных корня (то же значение с положительным и отрицательным знаками). Ниже приводится запись квадратного корня:√25 = ±5
Для отрицательного числа результат извлечения квадратного корня включает комплексные числа, обсуждение которых выходит за рамки данной статьи.
Математическое представление квадрата числа
Все мы в детстве узнали, что, когда число умножается само на себя, мы получаем его квадрат. Также квадрат числа можно представить как многократное умножение этого числа. Попробуем разобраться в этом на примере.
Предположим, мы хотим получить квадрат 5. Если мы умножим число (в данном случае 5) на 5, мы получим квадрат этого числа. Для обозначения квадрата числа используется следующая запись:
52 = 25
При программировании на Python довольно часто возникает необходимость использовать функцию извлечения квадратного корня. Есть несколько способов найти квадратный корень числа в Python.
1. Используя оператор возведения в степень
num = 25 sqrt = num ** (0.5) print("Квадратный корень из числа "+str(num)+" это "+str(sqrt))
Вывод:
Квадратный корень из числа 25 это 5.0Объяснение: Мы можем использовать оператор «**» в Python, чтобы получить квадратный корень. Любое число, возведенное в степень 0.5, дает нам квадратный корень из этого числа.
2. Использование math.sqrt()
Квадратный корень из числа можно получить с помощью функции sqrt() из модуля math, как показано ниже. Далее мы увидим три сценария, в которых передадим положительный, нулевой и отрицательный числовые аргументы в sqrt().
a. Использование положительного числа в качестве аргумента.
import math num = 25 sqrt = math.sqrt(num) print("Квадратный корень из числа " + str(num) + " это " + str(sqrt))
Вывод: Квадратный корень из числа 25 это 5.0.
b. Использование ноля в качестве аргумента.
import math num = 0 sqrt = math.sqrt(num) print("Квадратный корень из числа " + str(num) + " это " + str(sqrt))
Вывод: Квадратный корень из числа 0 это 0.0.
c. Использование отрицательного числа в качестве аргумента.
import math num = -25 sqrt = math.sqrt(num) print("Квадратный корень из числа " + str(num) + " это " + str(sqrt))
Вывод:
Traceback (most recent call last):
File "C:wb.py", line 3, in
sqrt = math.sqrt(num)
ValueError: math domain errorОбъяснение: Когда мы передаем отрицательное число в качестве аргумента, мы получаем следующую ошибку «math domain error». Из чего следует, что аргумент должен быть больше 0. Итак, чтобы решить эту проблему, мы должны использовать функцию sqrt() из модуля cmath.
3. Использование cmath.sqrt()
Ниже приведены примеры применения cmath.sqrt().
а. Использование отрицательного числа в качестве аргумента.
import cmath num = -25 sqrt = cmath.sqrt(num) print("Квадратный корень из числа " + str(num) + " это " + str(sqrt))
Вывод: Квадратный корень из числа -25 это 5j.
Объяснение: Для отрицательных чисел мы должны использовать функцию sqrt() модуля cmath, которая занимается математическими вычислениями над комплексными числами.
b. Использование комплексного числа в качестве аргумента.
import cmath num = 4 + 9j sqrt = cmath.sqrt(num) print("Квадратный корень из числа " + str(num) + " это " + str(sqrt))
Вывод: Квадратный корень из числа (4+9j) это (2.6314309606938298+1.7100961671491028j).
Объяснение: Для нахождения квадратного корня из комплексного числа мы также можем использовать функцию cmath.sqrt().
4. Использование np.sqrt()
import numpy as np num = -25 sqrt = np.sqrt(num) print("Квадратный корень из числа " + str(num) + " это " + str(sqrt))
Вывод:
...
RuntimeWarning: invalid value encountered in sqrt
Квадратный корень из числа -25 это nan5. Использование scipy.sqrt()
import scipy as sc num = 25 sqrt = sc.sqrt(num) print("Квадратный корень из числа " + str(num) + " это " + str(sqrt))
Вывод: Квадратный корень из числа 25 это 5.0.
Объяснение: Как и функция sqrt() модуля numpy, в scipy квадратный корень из положительных, нулевых и комплексных чисел может быть успешно вычислен, но для отрицательных возвращается nan с RunTimeWarning.
6. Использование sympy.sqrt()
import sympy as smp num = 25 sqrt = smp.sqrt(num) print("Квадратный корень из числа "+str(num)+" это "+str(sqrt))
Вывод: Квадратный корень из числа 25 это 5.
Объяснение: sympy — это модуль Python для символьных вычислений. С помощью функции sympy.sqrt() мы можем получить квадратный корень из положительных, нулевых, отрицательных и комплексных чисел. Единственная разница между этим и другими методами заключается в том, что, если при использовании sympy.sqrt() аргумент является целым числом, то результат также является целым числом, в отличие от других способов, в которых возвращаемое значение всегда число с плавающей точкой, независимо от типа данных аргумента.
Заключение
Наконец, мы подошли к завершению этой статьи. В начале мы кратко затронули использование квадратного корня в математике. Затем мы обсудили принципы внутреннего устройства функции извлечения квадратного корня и ее возможную реализацию. В завершении мы рассмотрели различные методы применения этой функции в Python.
Если коротко, то разница в реализации. И очевидно в скорости выполнения, входных и выходных параметрах. А вообще-то интересно заглянуть, что там во встроенных функциях.
pow(x, n)
@overload
def pow(base: int, exp: int, mod: None = ...) -> Any: ... # returns int or float depending on whether exp is non-negative
@overload
def pow(base: int, exp: int, mod: int) -> int: ...
@overload
def pow(base: float, exp: float, mod: None = ...) -> float: ...
@overload
def pow(base: _SupportsPow2[_E, _T_co], exp: _E) -> _T_co: ...
@overload
def pow(base: _SupportsPow3[_E, _M, _T_co], exp: _E, mod: _M) -> _T_co: ...
math.sqrt()
def sqrt(__x: SupportsFloat) -> float: ...
math.pow()
def pow(__x: SupportsFloat, __y: SupportsFloat) -> float: ...
И немного документации math.pow(). Здесь хотелось бы перевести одно заключение из документации:
В отличие от встроенного оператора **, math.pow () преобразует оба своих аргумента в тип float. Используйте ** или встроенную функцию pow () для вычисления точных целочисленных степеней.
А так же можно пользоваться и cmath модулем, для комплексных чисел и не только. Он возращает комплексное число, но при получении квадратного корня из 4, например, мнимая часть будет равняться 0j.
def sqrt(__z: _C) -> complex: ...
Можно сделать вывод, что под каждую конкретную задачу может быть подобран оптимальная функция для вычислений. Думаю, что тема достаточно обширна и можно исследовать, например, скорости для вычисления в том или ином случае.
Все вышеописанное для версии python 3.х.x.
upd
И все таки я решил посмотреть глубже. Не уверен в верности моей попытки, но все же (скажите, где я ошибся). Я решил исследовать две built-in функции: pow() и math.pow(). Найти их исходный код можно pow и math.pow.
Для pow() были найдены данные строки
/*[clinic input]
pow as builtin_pow
base: object
exp: object
mod: object = None
Equivalent to base**exp with 2 arguments or base**exp % mod with 3 arguments
Some types, such as ints, are able to use a more efficient algorithm when
invoked using the three argument form.
[clinic start generated code]*/
static PyObject *
builtin_pow_impl(PyObject *module, PyObject *base, PyObject *exp,
PyObject *mod)
/*[clinic end generated code: output=3ca1538221bbf15f input=435dbd48a12efb23]*/
{
return PyNumber_Power(base, exp, mod);
}
Что это может означать? В данной документации можно найти, как это работает. А конкретно в документации написано, что используется препроцессор для CPython и в данной конструкции “магическим образом преобразуются в переменные С с типом данных, которые нам нужны”(вольный перевод.). Функция PyNumber_Power() импортируется из DLL библиотеки (могу ошибаться, т.к. нашел только вызов в python3dll.c-файле, строка 409, EXPORT_FUNC(PyNumber_Power)). Вот в принципе и все.
Для math.pow() реализация немного интересней:
/*[clinic input]
math.pow
x: double
y: double
/
Return x**y (x to the power of y).
[clinic start generated code]*/
static PyObject *
math_pow_impl(PyObject *module, double x, double y)
/*[clinic end generated code: output=fff93e65abccd6b0 input=c26f1f6075088bfd]*/
{
double r;
int odd_y;
/* deal directly with IEEE specials, to cope with problems on various
platforms whose semantics don't exactly match C99 */
r = 0.; /* silence compiler warning */
if (!Py_IS_FINITE(x) || !Py_IS_FINITE(y)) {
errno = 0;
if (Py_IS_NAN(x))
r = y == 0. ? 1. : x; /* NaN**0 = 1 */
else if (Py_IS_NAN(y))
r = x == 1. ? 1. : y; /* 1**NaN = 1 */
else if (Py_IS_INFINITY(x)) {
odd_y = Py_IS_FINITE(y) && fmod(fabs(y), 2.0) == 1.0;
if (y > 0.)
r = odd_y ? x : fabs(x);
else if (y == 0.)
r = 1.;
else /* y < 0. */
r = odd_y ? copysign(0., x) : 0.;
}
else if (Py_IS_INFINITY(y)) {
if (fabs(x) == 1.0)
r = 1.;
else if (y > 0. && fabs(x) > 1.0)
r = y;
else if (y < 0. && fabs(x) < 1.0) {
r = -y; /* result is +inf */
}
else
r = 0.;
}
}
else {
/* let libm handle finite**finite */
errno = 0;
r = pow(x, y);
/* a NaN result should arise only from (-ve)**(finite
non-integer); in this case we want to raise ValueError. */
if (!Py_IS_FINITE(r)) {
if (Py_IS_NAN(r)) {
errno = EDOM;
}
/*
an infinite result here arises either from:
(A) (+/-0.)**negative (-> divide-by-zero)
(B) overflow of x**y with x and y finite
*/
else if (Py_IS_INFINITY(r)) {
if (x == 0.)
errno = EDOM;
else
errno = ERANGE;
}
}
}
if (errno && is_error(r))
return NULL;
else
return PyFloat_FromDouble(r);
}
Можно увидеть не только использования Argument Clinic-препроцессора, но и обработку некоторых крайних значений (бесконечность ** бесконечность, например) и обработку ошибок.
Можно копать дальше, не уверен есть ли необходимость. Но инетересно же) можно так же увидеть еще одну интересную реализацию для long_pow() здесь
Как извлечь корень в Python (sqrt)
Содержание:развернуть
- Что такое квадратный корень
- Квадратный корень
-
Положительное число
-
Отрицательное число
-
Ноль
- Кубический корень
- Корень n-степени
- Решение реальной задачи с использованием sqrt
Если вам нужно найти сторону квадрата, когда известна одна лишь его площадь, или вы намерены рассчитать расстояние между двумя точками в декартовых координатах, то без особого инструмента не обойтись. Математики прошлого придумали для этих вычислений квадратный корень, а разработчики Python воплотили его в функции sqrt().
Но обо всём по порядку.
Что такое квадратный корень
Корнем квадратным из числа “X” называется такое число “Y”, которое при возведении его во вторую степень даст в результате то самое число “X”.
Операция нахождения числа “Y” называется извлечением квадратного корня из “X”. В математике для её записи применяют знак радикала:
Нотация питона отличается в обоих случаях, и возведение в степень записывается при помощи оператора “**“:
a = 2
b = a ** 2
print(b)
> 4
А квадратный корень в питоне представлен в виде функции sqrt(), которая существует в рамках модуля math. Поэтому, чтобы начать работу с корнями, модуль math нужно предварительно импортировать:
import math
Функция sqrt() принимает один параметр — то число, из которого требуется извлечь квадратный корень. Тип данных возвращаемого значения — float.
import math
import random
# пример использования функции sqrt()
# отыщем корень случайного числа и выведем его на экран
rand_num = random.randint(1, 100)
sqrt_rand_num = math.sqrt(rand_num)
print('Случайное число = ', rand_num)
> Случайное число = 49
print('Корень = ', sqrt_rand_num)
> Корень = 7.0
Квадратный корень
Положительное число
Именно на работу с неотрицательными числами “заточена” функция sqrt(). Если число больше или равно нулю, то неважно, какой у него тип. Вы можете извлекать корень из целых чисел:
import math
print(math.sqrt(100))
> 10.0
А можете — из вещественных:
import math
print(math.sqrt(111.5))
> 10.559356040971437
Легко проверить корректность полученных результатов с помощью обратной операции возведения в степень:
print(math.sqrt(70.5))
> 8.396427811873332
# возвести в степень можно так
print(8.396427811873332 ** 2)
> 70.5
# а можно с помощью функции pow()
print(pow(8.396427811873332, 2))
> 70.5
Отрицательное число
Функция sqrt() не принимает отрицательных аргументов. Только положительные целые числа, вещественные числа и ноль.
Такая работа функции идёт вразрез с математическим определением. В математике корень спокойно извлекается из чисел меньше 0. Вот только результат получается комплексным, а таким он нужен для относительно узкого круга реальных задач, вроде расчетов в сфере электроэнергетики или физики волновых явлений.
Поэтому, если передадите отрицательное число в sqrt(), то получите ошибку:
print(math.sqrt(-1))
> ValueError: math domain error
Ноль
Функция sqrt() корректно отрабатывает с нулём на входе. Результат тривиален и ожидаем:
print(math.sqrt(0))
> 0.0
Кубический корень
Само название функции sqrt() намекает нам на то, что она не подходит для извлечения корня степени отличной от двойки. Поэтому для извлечения кубических корней, сначала необходимо вспомнить связь между степенями и корнями, которую продемонстрируем на корне квадратном:
Вышеуказанное соотношение несложно доказать и для других степеней вида 1/n.
# Квадратный корень можно извлечь с помощью операции возведения в степень "**"
a = 4
b = a ** 0.5
print(b)
> 2.0
В случае с квадратным или кубическим корнем эти операции действительно эквивалентны, но, вообще говоря, в математике извлечение корня и возведение в дробную степень имеют существенные отличия при рациональных степенях вида m/n, где m != 1. Формально, в дробно-рациональную степень можно возводить только положительные вещественные числа. В противном случае возникают проблемы:

print(pow(8, 1/3))
> 2.0
Или же:
print(8 ** (1/3))
> 2.0
То, что справедливо для корня третьей степени, справедливо и для корней произвольной степени.
# извлечём корень 17-й степени из числа 5600
x = 5600
y = 17
z = pow(x, (1/y))
print(z)
> 1.6614284717080507
# проверяем корректность результата
print(pow(z, y))
> 5600.0
Но раз уж мы разбираемся с математической темой, то попытаемся мыслить более обобщённо. С помощью генератора случайных чисел с заданной точностью будем вычислять корень случайной степени из случайного числа:
import random
# точность можно задать на ваше усмотрение
x = random.randint(1, 10000)
y = random.randint(1, 100)
z = pow(x, (1 / y))
print('Корень степени', y, 'из числа', x, 'равен', z)
# при проверке вероятны незначительные расхождения из-за погрешности вычислений
print('Проверка', pow(z, y))
# но специально для вас автор накликал целочисленный результат
> Корень степени 17 из числа 6620 равен 1.6778624404513571
> Проверка 6620.0
Решение реальной задачи с использованием sqrt
Корень — дитя геометрии. Когда Пифагор доказал свою знаменитую теорему, людям тут же захотелось вычислять стороны треугольников, проверять прямоту внешних углов и сооружать лестницы нужной длины.
Соотношение a2 + b2 = c2, где “a” и “b” — катеты, а “c” — гипотенуза — естественным образом требует извлекать корни при поиске неизвестной стороны. Python-а под рукой у древних греков и вавилонян не было, поэтому считать приходилось методом приближений. Жизнь стала проще, но расчет теоремы Пифагора никто не отменял и в XXI веке.

- Ваше местоположение;
- Центр Земли;
- Пиковая высота вышки.
Модель готова, приступаем к написанию кода:
import math
# расстояние от вас до вышки
from_you_to_base_station = 23
# радиус земли
earth_radius = 6371
# расчет расстояния от центра земли до пика сооружения по теореме Пифагора
height = math.sqrt(from_you_to_base_station ** 2 + earth_radius ** 2)
# расчет высоты вышки(км)
base_station_height = height - earth_radius
print('Требуемая высота(м): ', round(base_station_height * 1000))
> Требуемая высота(м): 42
Расчёт выполнен, результат заказчику предоставлен. Можно идти пить чай и радоваться тому, что теперь ещё больше людей смогут звонить родным и сидеть в интернете.
В этой статье мы рассмотрим, как извлечь корень в Python, а также какой модуль и функция для этого используется. Но давайте обо всем по порядку.
Если мы знаем только общую площадь квадрата и хотим узнать размер одной его стороны либо же собираемся рассчитать расстояние между 2-мя точками в декартовых координатах, нам потребуется квадратный корень. Это не проблема, если речь идет о математике. Но что делать, когда речь идет о языке программирования? К нашему счастью разработчики Python предусмотрели для решения вышеописанной задачи специальную функцию. Но прежде чем продолжить, давайте немного вспомним теорию.
Квадратный корень — что это?
Квадратным корнем, полученным из числа «A», называют число «B», которое при возведении во 2-ю степень даст в итоге то самое изначальное число «A».
B2 = A
Непосредственную операцию, позволяющую найти значение «B», называют извлечением корня из «A». Математики применяют для обозначения этой операции специальный знак (его еще называют знаком радикала):
B = √A
Когда речь идет о корне в «Питоне», ситуация обстоит иначе, причем в обоих случаях. К примеру, само возведение числа в степень записывают посредством оператора «**«:
X = 2
Y = X ** 2
print(Y)
Ответ в консоли «Пайтона» будет равняться четырем.
Касаемо квадратного корня, то он в Python представлен функцией sqrt(). Однако она существует не сама по себе, а в рамках соответствующего математического модуля math. Таким образом, перед началом работы этот модуль надо будет импортировать, но это абсолютно не сложно сделать на практике:
import math
Идем дальше. Наша функция sqrt() принимает лишь один параметр – значение, из которого нам надо извлечь √. Давайте напишем простенький код и задействуем float в качестве типа данных возвращаемого значения.
import math
import random
# попробуем функцию sqrt() на практике
# найдем корень случайного числа с последующим выводом его на экран
rand_num = random.randint(5, 55)
sqrt_rand_num = math.sqrt(rand_num)
print('Наше случайное число = ', rand_num)
print('Искомое значение корня = ', sqrt_rand_num)
Вы можете попробовать работу этого кода у себя на компьютере или на любом онлайн-компиляторе. Вот, к примеру, компилятор для Python 3.
Результат может быть таким:
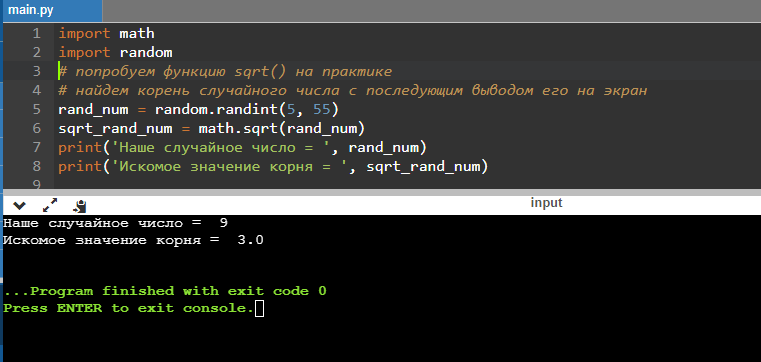
Или таким:
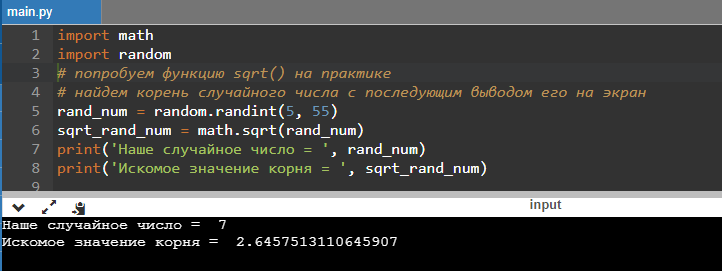
Так как мы используем модуль random, результат будет различаться при каждом выполнении кода.
Но никто не мешает сделать все намного проще:
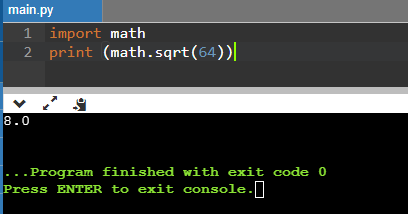
print (math.sqrt(64))
Ответ очевиден:
Положительные числа
Функция sqrt() предназначена для работы с положительными значениями. Если число больше либо равно нулю, то неважно, какой тип данных у него, ведь извлечение корня возможно как из целых, так и из вещественных чисел.
Из целых:
import math
print(math.sqrt(81))
> 9.0
Из вещественных:
print(math.sqrt(81.5))
> 9.027735042633894
Сомневаетесь в корректности итоговых результатов предыдущего примера? Просто выполните обратное возведение в степень:
print(9.027735042633894 ** 2)
> 81.5
Также не забывайте, что сделать это можно и посредством специальной функции pow:
print(pow(9.027735042633894, 2))
> 81.5
Отрицательные значения и ноль
Функция sqrt в «Питоне» — вещь полезная и знать ее нужно, однако она не принимает отрицательного числа — лишь положительные (целые и вещественные), а также ноль.
Такая ограниченная возможность использования не соответствует математическим канонам, ведь в реальной жизни специалисты по математике без проблем извлекают √ и из отрицательных значений. Да, результат будет комплексным и пригодится лишь для решения довольно узкого спектра задач, типа расчетов волновых явлений в физике либо вычислений в энергетической сфере.
Учитывайте вышесказанное, если пытаетесь извлекать корни в Python посредством этой функции. Передав отрицательное значение, вы получите error:
import math
print(math.sqrt(-1))
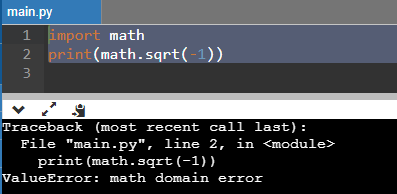
А вот если говорить про ноль, то ошибки не будет, так как код отработает корректно. Однако результат тут очевиден, поэтому практическая ценность данной возможности весьма условна:
import math
print(math.sqrt(0))
> 0.0
Хотите знать о «Питоне» намного больше? Добро пожаловать на специализированный курс в «Отус»!

По материалам:
- http://python-teach.ru/python-dlya-nachinayushhih/vychislenie-kvadratnogo-kornya-chisla-v-python/.
В Python есть предопределенная функция sqrt(), которая возвращает квадратный корень числа. Она определяет квадратный корень из значения, которое умножается на само себя и дает число. Функция sqrt() не используется напрямую для нахождения квадратного корня из заданного числа, поэтому нам нужно использовать математический модуль для вызова функции sqrt() в Python.
Например, квадратный корень из 144 равен 12.

Использование метода math.sqrt()
Функция sqrt() – это встроенная функция, которая возвращает квадратный корень из любого числа. Ниже приведены шаги, чтобы найти квадратный корень из числа.
- Запустите программу.
- Определите любое число, квадратный корень которого нужно найти.
- Вызовите функцию sqrt() и передайте значение, которое вы определили на шаге 2, сохраните результат в переменной.
- Выведите квадратный корень.
- Завершите программу.
Давайте напишем программу на Python.
SqrRoot.py
import math # import math module
N = 25 # define the value to the variable N
result = math.sqrt(N) # use math.sqrt() function and pass the variable.
print(" Square root of 25 is :", result) # prints the square root of a given number
M = 625 # define the value
result = math.sqrt(M) # use math.sqrt() function and pass the variable
print(" Square root of 625 is :", result) # prints the square root of a given number
P = 144 # define the value
result = math.sqrt(P) # use math.sqrt() function and pass the variable
print(" Square root of 144 is :", result) # prints the square root of a given number
S = 64 # define the value
result = math.sqrt(S) # use math.sqrt() function and pass the variable
print(" Square root of 64 is :", result) # prints the square root of a given number
Выход:

Давайте создадим программу на Python, которая находит квадратный корень десятичных чисел.
SqrRoot.py
import math
print(" The Square root of 4.5 is", math.sqrt(4.5)) # Pass the decimal number
print(" The Square root of 627 is", math.sqrt(627)) # Pass the decimal number
print(" The Square root of 6.25 is", math.sqrt(6.25)) # Pass the decimal number
print(" The Square root of 0 is", math.sqrt(0)) # Pass number as 0
Выход:

В следующей программе мы прочитали число от пользователя и нашли квадратный корень.
SqRoot_Usr.py
import math # import math module
a = int(input("Enter a number to get the Square root")) # take an input
res = math.sqrt(a) # Use math.sqrt() function and pass the variable a.
print("Square root of the number is", res) # print the Square Root
Выход:

Использование функции math.pow()
Pow() – это встроенная функция, которая используется в Python для возврата степени числа. У него два параметра. Первый параметр определяет число, а второй параметр определяет увеличение мощности до этого числа.
Pow_Sqrt.py
import math # import the math module
num = float(input("Enter the number :")) # take an input
SquareRoot = math.pow(num, 0.5) # Use the math.pow() function and pass the value and 0.5(which is equal to √) as an parameters
print(" The Square Root of the given number {0} = {1}" .format(num, SquareRoot)) # print the Square Root.
Выход:

Использование оператора **
Мы также можем использовать оператор экспоненты, чтобы найти квадратный корень из числа. Оператор может применяться между двумя операндами. Например, x ** y. Это означает, что левый операнд возведен в степень правого.
Ниже приведены шаги, чтобы найти квадратный корень из числа.
- Шаг 1. Определите функцию и передайте значение в качестве аргумента.
- Шаг 2. Если заданное число меньше 0 или отрицательное, оно ничего не возвращает.
- Шаг 3. Используйте экспоненциальный знак **, чтобы найти степень числа.
- Шаг 4. Возьмите числовое значение у пользователя.
- Шаг 5. Вызовите функцию и сохраните ее вывод в переменной.
- Шаг 6. Отобразите квадратный корень числа в Python.
- Шаг 7. Выход из программы.
Давайте реализуем вышеуказанные шаги.
SqrtFun.py
import math # import the math package or module
def sqrt_fun(num): # define the sqrt_fun() and pass the num as an argument
if num < 0: # if num is less than 0 or negative, it returns nothing
return
else:
return num ** 0.5 # Use the exponent operator
num = int(input(" Enter a numeric value: ") ) # take an input from the user
res = sqrt_fun(num) # call the sqrt_fun() to find the result
print(" Square Root of the {0} = {1}".format(num, res)) # print the Square Root of the variable
Выход:

Как мы видим в приведенном выше примере, сначала мы берем ввод(число) от пользователя, а затем используем оператор степени **, чтобы узнать степень числа. Где 0,5 равно √(символ корня), чтобы увеличить степень данного числа.
Давайте создадим программу Python, которая находит квадратный корень из указанного диапазона, в следующей программе вычисление из всех чисел от 0 до 50.
Sqrloop.py
import math
for i in range(50):
print("Square root of a number {0} = {1}".format(i,math.sqrt(i)))
Выход:



Изучаю Python вместе с вами, читаю, собираю и записываю информацию опытных программистов.
