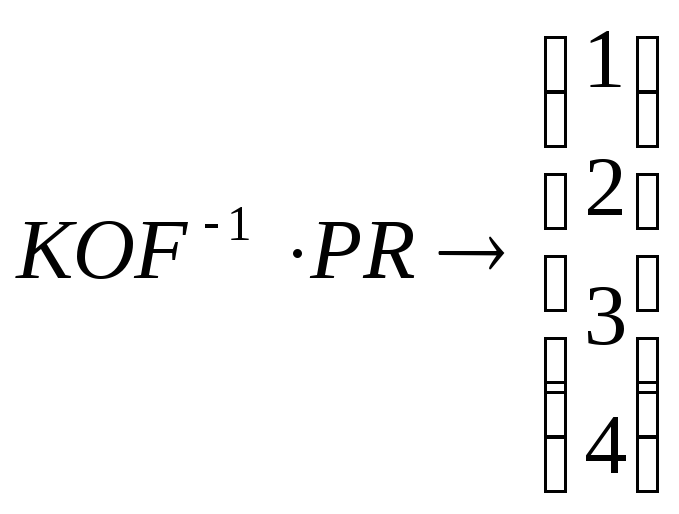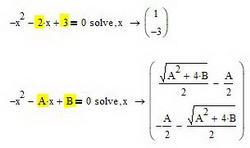Тема
7.
Решение
уравнений и их систем.
-
Аналитическое
решение уравнений.
Для
аналитического решения уравнений в
Mathcad
существует специальный оператор solve
(решить). Чтобы с его помощью найти корни
уравнения нужно выполнить следующую
последовательность действий:
-
ввести
оператор solve
(решить) при помощи одноименной команды
панели symbolie; -
в
левом маркере задать вид решаемого
уравнения (в качестве знака равенства
следует использовать логическое
равенство на панели Boolean); -
в
правый маркер ввести переменную,
относительно которой должно быть решено
уравнение.
Ответ
оператора solve
представляет в виде выражения (численного
или буквального). Если решений несколько,
то они представляются в виде вектора
(матрицы – столбца).
Лучше
всего Mathcad
справляется с поиском корней алгебраических
полиномов. При этом находится все корни
– как действительные, так и мнимые. Их
общее число, как известно (исходя из
знаменитой теоремы Гаусса), равно n
,где n-
степень полинома.
Пример:
Поиск всех решений уравнения
Решаемое
уравнение можно задавать и со знаком
равенства. Однако в качестве знака
равенства следует использовать логическое
равенство (на панели Boolean).
Весьма
неплохо справляется символьный процессор
Mathcad
с показателями и логарифмическими
уравнениями. При решении логарифмических
уравнений нужно помнить, что натуральный
логарифм задается функцией ln,
десятичный – функцией log.
Для задания логарифма при основании x
также служит функция log,
однако в этом случае она принимает два
параметра: первый соответствует величине,
от которой ищется логарифм, второй –
основанию логарифма. Решая логарифмическое
или показательное уравнение, ответ
оператор solve
дает обычно в виде сложного выражения
из чисел и логарифмов от чисел. Чтобы
привести его к более простому виду,
следует использовать оператор simplify.
Пример:
Решение логарифмических и показательных
уравнений.
Хуже
всего символьный процессор Mathcad
решает тригонометрические уравнения.
Большинство таких уравнений, как
известно, имеет бесконечное множество
корней. Так, например, решение уравнения
sin(x)=0
запишется в виде
,
(R
– множество цельных чисел). Однако
Mathcad
находит корни только на промежутке
одного периода заданной в уравнении
тригонометрической функции.
Пример:
Решение тригонометрических уравнений.
-
Численное
решение уравнений.
Далеко
не все уравнения можно решать аналитически.
Чаще их приходится решать численными
методами.
Для
численного поиска решений алгебраических
уравнений с одним неизвестным в Mathcad
существует специальная встроенная
функция root
(корень). Функция эта может использоваться
в двух различных формах, при этом
реализуются разные численные алгоритмы.
Так, если определена только одна точка
приближения к корню, поиск решений будет
осуществляться так называемым методом
секущих.
Если же задан интервал, на котором
предположительно локализовано решение,
то поиск его будет осуществлен с
применением метода деления пополам
(метод Больцано).
Если
необходимо найти корень некоторого
уравнения, причем известен интервал, в
котором он локализован, проще всего
использовать функцию root
с четырьмя аргументами: root(f(x),x,a,b),
где f(x)
– функция, определяющая уравнение, x
– переменная, a
и b
– границы интервала локализации.
Обязательным
условием является то, что значения
функции на концах интервала должны быть
противоположных знаков. Если это условие
нарушается, система выдает сообщение
об ошибке. Кроме того, функция f(x)
должна быть ограниченной и непрерывной
на промежутке [a,b].
Очень
важной характеристикой решения является
его точность. В Mathcad
можно регулировать величину погрешности
решения, изменяя значение специальной
системной переменной TOL
(от англ. «tolerance»
– точность). Изменить величину этой
системной переменной можно либо при
помощи панели, открываемой командой
Math
► Options
(Инструменты ►Опции документа), либо
выполнив соответствующее присваивание
непосредственно слева или сверху функции
численного решения. По умолчанию TOL
равняется 10-3.
Величина
TOL
должна задаваться исходя из того, сколько
знаков в мантии ее решения являются
значимыми. Например, если решение нужно
получить с точностью до пятого знака
после запятой, то TOL
должен быть равен 10-5.
Пример:
Найти первый положительный корен
уравнения
Задаем
функцию
Значение
первого положительного корня очевидно.
TOL:=0,1.
Ответ точен до первого знака после
запятой:
TOL:=0,0001.
Ответ точен до 4-го знака после запятой:
TOL:=0,0000000001.
Ответ точен до 10-го знака:
Пример:
Решение уравнений методом секущих.
Задаем
функцию, описывающую уравнение:
Точное
значение первого положительного корня:
Задаем
начальное приближение:
x:=0.2
Ищем
корень при различных значениях TOL:
TOL:=10-4
root(f(x),x)=0.240805743114691
TOL:=10-4
root(f(x),x)=0.28518778874873
Одним
из основных недостатков функции root
является то, что одновременно она
способна найти только один корень
уравнения. Чтобы найти остальные корни,
придется проделать те же операции, но
для других приближений.
Однако,
если уравнение представлено алгебраическим
полиномом в Mathcad
существует специальная функция поиска
всех корней – функция polyroots
(v),
где v
– вектор, составленный из коэффициентов
полинома.
Важной
особенностью задания v
является то, что коэффициенты располагаются
в векторе сверху вниз соответственно
увеличению степеней членов полинома,
к которым они относятся.
Пример:
Поиск корней полинома численным методом
x4+x3+x-10=0
Переписывать
коэффициенты из выражения в вектор не
очень интересное и приятное занятие. К
тому же довольно легко либо допустить
ошибку в самом числе, либо просто
перепутать знаки. Для решения этой
проблемы нужно использовать специальный
оператор coeffs,
расположенный на панели symbolic.
Причем, полином может быть представлен
и в неразвернутой форме: к стандартному
виду оператор coeffs
приведет его автоматически.
Пример:
Использование оператора coeffs.
(x2+x-3)2+(x-10)3=0
f(x):=(x2+x-3)2+(x-10)3
-
Решение
систем линейных уравнений.
Все
методы решения систем линейных
алгебраических уравнений можно разделить
на две основные группы. К первой относятся
так называемые прямые
(или матричные) методы: Крамера и Гаусса.
Во вторую группу входят довольно
специфичные итерационные
методы.
В
системе Mathcad
реализованы в виде специальных функций
методы обеих групп, однако ниже остановимся
только на прямых методах.
Ниже
следующий пример демонстрирует
аналитическое решение системы уравнений
методом Крамера.
Пример:
Решить систему линейных уравнений
методом Крамера:
x+y+z+p=10
x-y-z-p=-8
x+y-z+p=4
-x-y+z+p=4
Прежде
всего следует переписать систему в
матричном виде
Если
такой метод решения систем линейных
уравнений не очень нравится, то можно
воспользоваться специальной встроенной
функцией lsolve(M,V),
где M
– матрица коэффициентов, V-
вектор правых частей. Функция эта также
использует метод Крамера.
Пример:
Решение системы линейных уравнений при
помощи функции lsolve
Особенностью
функции lsolve
является то, что она может найти решение
системы уравнений не только численно,
но и аналитически.
В
Mathcad
метод Крамера считается основным при
решении систем линейных алгебраических
уравнений. Однако, есть возможность
решения такой системы уравнений и
методом Гаусса. Для этого служит функция
rref(M),
где M
– матрица, полученная слиянием матрицы
коэффициентов и вектора правых частей.
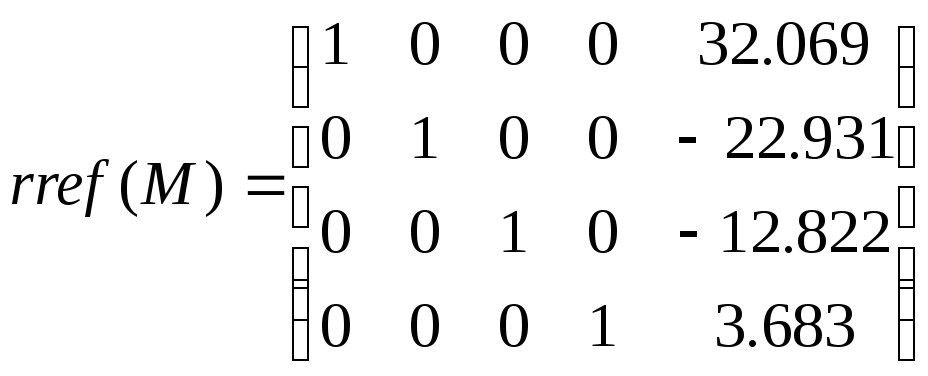
Пример:
Решить систему линейных алгебраических
уравнений методом Гаусса.
3x+2y-z+10k=100
x-4y+5z-k=56
23x+56y-43z+12k=49
x+y+z+k=0
Составляем
матрицу коэффициентов и вектор правых
частей:
Объединяем
матрицу коэффициентов и вектор правых
частей в одну матрицу:
M:=augment(KOF,PR)
Находим
корни системы
Для решения уравнений в Mathcad можно воспользоваться двумя способами:
- Метод Given – Find
- Метод Solve
Использование метода Given – Find:
Это наиболее распространенный способ решения обычных алгебраических уравнений. Он достаточно прост. В рабочем поле записываем слово Given. Это служебное слово. Оно подключает определенные программные модули mathcad для обработки исходных данных, необходимых для решения уравнения численными методами.
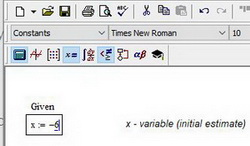
Затем указывается начальное приближение для искомой переменной. Это нужно для увеличения скорости и точности решения уравнения. Если начальное приближение не задать, то mathcad по умолчанию примет его равным нулю
Рис. 1. Ввод данных в поле mathcad
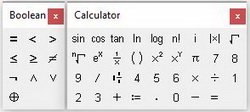
Далее вводится уравнение. Его можно записать в явном или неявном виде. Само уравнение набирается с клавиатуры вручную с использованием панели Calculator. Из этой панели можно взять основные математические операции: дроби, тригонометрию, факториалы и прочее. Уравнение нужно записывать с использованием логического символа “ровно”. На панели Boolean он выделен жирным шрифтом (см. рис. 2)
Рис. 2. Панели Boolean и Calculator
После уравнения вводится функция Find(x) (где х – переменная). Это функция, которая возвращает результат. Значение функции Find(x) можно присвоить какой-либо переменной с помощью символа “:=” и использовать ее далее в расчетах
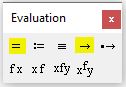
Для получения результата, после Find(x) следует поставить символ “→” либо “=” из панели Evaluation (см. рис. 3). Причем, если вы используете символ “→“, то mathcad определит все корни уравнения и сформирует матрицу результатов. Но если вы используете символ “=“, то mathcad выведет единственный корень, который был наиболее близок к начальному приближению. Так что, если вы не знаете сколько корней имеет уравнение, то лучше использовать стрелочку
Рис. 3. Панель “Evaluation”
В зависимости от сложности уравнения через определенное время MathCad выведет результат. На рис.4 можно рассмотреть синтаксис и различие результатов выводимых mathcad. Обратите внимание, что выводимые результаты одного и того же уравнения различны
Рис. 4. Результат численного решения уравнения
Mathcad позволяет решать уравния в символьном виде. Например, если мы заменим все числовые константы на неизвестные параметры и решим уравнение относительно x, то результат выведется в символьном виде (см. рис. 5). Причем, обратите внимание, что в данном случае нам не нужно вводить начальное приближение и мы должны использовать символ “→” для вывода результата
Рис. 5. Результат символьного решения уравнения
Использование метода Solve:
Этот метод отличается от выше рассмотренного синтаксисом. На свободном поле вводим уравнение с использованием логического символа “ровно” из панели Boolean. После ввода уравнения, не смещая курсор ввода, на панели Symbolic нажимаем кнопку solve (см. рис. 6)
Рис. 6. Панель Symbolic
Затем ставим запятую и вводим переменную, относительно которой нужно решить уравнение (в нашем случае это x). Нажимаем Enter на клавиатуре и смотрим результат (см. рис. 7)
Рис. 7. Результат решения уравнения методом Solve
Обратите внимание, что метод подходит как для численного так и для символьного представления результатов
Как показывает моя личная инженерная практика, иногда не удается решить уравнения с помощью Given – Find, но получается в Solve. При этом, к сожалению, метод Solve не очень удобен для далнейшего использования результатов решения уравнения
Математика,
вопрос задал marvelsmarvels007,
1 месяц назад
Ответы на вопрос
Ответил oleksandralemisko
1
Ответ:
m=595/124
m= -479/185
c=3,7
k=2,3
marvelsmarvels007:
Можно полный ответ
Предыдущий вопрос
Следующий вопрос
Новые вопросы
Русский язык,
24 дня назад
10 предложений на тему я и мама…
Геометрия,
24 дня назад
ПОМОГИТЕ ПОЖАЛУЙСТА!!!!! СРОЧНО!!! Дана окружность. OL-32 ; найти – LM…
Українська мова,
1 месяц назад
6. НЕ потребує редагування словосполучення А подорожуюча молодь Б хвилюючі слова В оточуюче середовище Г поширена думка д початкуючий поет…
Қазақ тiлi,
1 месяц назад
Мәтінде қарамен белгіленген сөз қандай көңіл- күйді білдіреді? – Данияр, сен Ұлы Жібек жолы туралы білесің бе? – Мен Ұлы Жібек жолы туралы көп ақпарат білемін. Қажет болса, сенімен бөлісе аламын.
Математика,
5 лет назад
Обчисліть значення виразу (√8+2√7-√8-2√7)². Просто решите…
Математика,
5 лет назад
За один час самолёт пролетает 720 км. Сколько км он полетит за 7/12 часа…
5-е
занятие по
MATLAB
ЛАБОРАТОРНАЯ
РАБОТА №5
Применение функций операционного исчисления
для исследования линейных
динамических систем
в системе
MATLAB.
Преобразование Лапласа в
MATLAB — функция
laplace.
1.1. syms
x y t; % задание символьных переменных
f1
= t; % зададим
функцию-оригинал;
L1
= laplace(f1) %
определение изображения по Лапласу от линейной функции;
f2
= sym(’10’); % функцию
f2 = 10 выражаем в символьном виде;
L2
= laplace(f2) %
определение изображения от постоянной;
f3
= sym(‘3’)*t +
sym(‘7’); % оригинал линейной функции;
L3
= laplace(f3)
% изображение линейной функции;
f4
= exp(-t); %
оригинал экспоненциальной функции (со знаком минус);
L4
= laplace(f4) %
изображение экспоненциальной функции ;
f5
= exp(t); %
оригинал экспоненциальной функции (со знаком плюс);
L5
= laplace(f5) %
изображение экспоненциальной функции ;
L6 =
laplace(exp(t))
f6 =
sin(x);
L6
= laplace(f6) %
изображение тригонометрической функции sin(x);
L7
= laplace(cos(x))
% изображение тригонометрической функции cos(x);
Передаточные функции.
Определение. Передаточной функцией линейной динамической системы называется
отношение изображения по Лапласу выходного сигнала к изображению по Лапласу
входного сигнала при нулевых начальных условиях.
Передаточная функция в общем случае является дробно рациональной функцией
относительно оператора преобразования Лапласа:

(1)
Условие
m £
n отвечает условию реализуемости систем.
Создание передаточных функций —
tf. % См. help tf;
2.1.
Сформируем следующую передаточную функцию W1:

(2)
2.2. В командной строке
MATLAB набираем (или создаем М-сценарий):
W1=tf(12,[1 2 3 1])
% Результат
возвращается в виде:
Transfer
function:
12
———————
s^3 + 2
s^2 + 3 s + 1
2.3. . Сформируем следующую
передаточную функцию W2:

(3)
В командной строке
MATLAB набираем:
W2=tf([3 5 4],[1 2 3 1])
% Результат
возвращается в виде:
Transfer
function:
3 s^2
+ 5 s + 4
———————
s^3 + 2 s^2 + 3 s + 1
Формирование передаточных функций с разложением на
множители числителя и знаменателя с заданным коэффициентом передачи —
zpk
(zero–pole–gain),
символ k
отображает gain.
Нули передаточной функции — это корни числителя, полюса —
корни знаменателя.
2.4. Сформируем передаточную функцию со статическим
коэффициентом, равным 7.7, и с полюсами
.
Назовем ее передаточной функцией с выделенными нулями и полюсами.
В командной строке
MATLAB набираем:
W3=zpk([],[-3.3,-0.25,-12.7],7.7)
% Результат возвращается в
виде:
Zero/pole/gain:
7.7
————————-
(s+3.3)
(s+12.7) (s+0.25)
%
Символ []означает, что в
числителе передаточной функции характеристический полином
%нулевой
2.5. Сформируем передаточную функцию со статическим
коэффициентом, равным 7.7, с полюсами
и
с нулями .
В командной строке
MATLAB набираем:
W4=zpk([4,-5],[-3.3,-0.25,-12.7],7.7)
% Результат
возвращается в виде:
Zero/pole/gain:
7.7
(s-4) (s+5)
————————-
(s+3.3)
(s+12.7) (s+0.25)
2.6. Взаимное преобразование форм передаточных функций.
2.6.1. Преобразуем полученную передаточную функцию
W4 в рациональную форму:
% В командной строке MATLAB
набираем:
» w44=tf(W4)
% Результат
возвращается в виде:
Transfer function:
7.7 s^2 +
7.7 s – 154
———————————
s^3 + 16.25 s^2 +
45.91 s + 10.48
2.6.2. Преобразуем рациональную
передаточную функцию в форму с выделенными нулями и полюсами:
% В командной строке MATLAB сформируем
простую передаточную функцию вида:
.
W5=tf(10,[1,3,2])
% Результат
возвращается в виде:
Transfer
function:
10
————-
s^2 + 3 s + 2
% Полученная передаточная функция соответствует описанию
объекта, состоящего из двух последовательно соединенных инерционных звеньев с
результирующим коэффициентом передачи, равным 10, и постоянными времени
.
% Передаточная функция с выделенными нулями и полюсами
w55:
w55=zpk(W5) % Формат
преобразования
% Результат преобразования
Zero/pole/gain:
10
———
(s+2)(s+1)
% Преобразуем рациональную передаточную функцию
W2 в форму с выделенными нулями и полюсами:
w22=zpk(W2) % Формат
преобразования
% Результат преобразования
Zero/pole/gain:
3 (s^2 +
1.667s + 1.333)
——————————–
(s+0.4302) (s^2 +
1.57s + 2.325)
%
Рассмотренные передаточные функции типа (1) описывают объекты управления с одним
входом и одним выходом — системы
SISO (single input single output).
2.7.
Оценка динамики объекта управления по заданной передаточной функции.
Динамика объекта управления определяется знаменателем
передаточной функции, точнее корнями характеристического уравнения,
составленного из знаменателя. Если корни характеристического уравнения “левые”,
то соответствующий переходный процесс будет установившимся, если же корни
“правые”, то переходный процесс будет неустановившимся, т.е. стремиться к
бесконечности (по выходной координате объекта или по всем возможным
координатам).
Для расчета корней характеристического уравнения
можно использовать функцию
eig.
2.7.1. Определим корни
характеристического уравнения для объекта с передаточной функцией W5
и
w55.
» eig(W5)
% W5
— рациональная передаточная функция
ans =
-2
-1
» eig(w55)
% w55
— передаточная функция с выделенными нулями и полюсами
ans =
-2
-1
%
Результат получен один и тот же. Форма
w55
позволяет сразу определить корни, если
%
они простые
2.7.2.
Определим корни характеристического
уравнения для объекта с передаточной функцией W2
и
w22.
»eig(W2)
% W2 — рациональная передаточная функция
ans =
-0.7849 +
1.3071i
-0.7849 –
1.3071i
-0.4302
»eig(w22)
%w22
— передаточная функция с выделенными нулями и полюсами, получена из
W2
ans =
-0.7849 + 1.3071i
-0.7849 – 1.3071i
-0.4302
%
Получены два комплексных корня и один простой. Простой корень легко может быть
определен из передаточной функции
w22.
2.7.3. Передаточные функции с кратными корнями.
Зададим простой корень, равный 6.78 тройной кратности и с помощью
zpk сформируем следующую передаточную
функцию w66:
»
w66=zpk([],[-6.78,-6.78,-6.78],7)
% Рассчитаем корни соответствующего
характеристического уравнения
» eig(w66)
ans =
-6.7800
-6.7800
-6.7800
%
Получены три простых одинаковых корня
2.7.4. Передаточные функции
с комплекными корнями.
Комплексные корни входят сопряженными
парами.
Зададим один простой корень и два
комплесно-сопряженных с помощью zpk.
»
w77=zpk([],[-5+2.3*i,-5-2.3*i,-5.7],6)
Zero/pole/gain:
6
—————————
(s+5.7) (s^2 + 10s + 30.29)
% Имеем один простой корень, равный -5.7, и
два комплесно-сопряженных: –5+2.3i;
-5-2.3i, где
% i
— символ мнимой единицы (можно использовать и
j
одновременно или совместно).
Рациональная передаточная функция, соответствующая
w77,
будет иметь вид:
» W77=tf(w77)
Transfer function:
6
——————————–
s^3 + 15.7 s^2 + 87.29 s +
172.7
Передаточные функции многомерных систем.
Формирование передаточных функций для многомерных
систем (MIMO
—
multiple input multiple output) основано на
представлении числителя и знаменателя в виде передаточных функций одномерных
систем.
1-й способ формирования
передаточной функции системы
MIMO с помощью
tf.
—
формирование массива ячеек, содержащих многочлены числителя — N;
—
формирование массива
ячеек, содержащих многочлены знаменателя — D.
Массивы числителя и знаменателя содержат
векторы-строки, которые заключаются в фигурные скобки.
3.1. Формирование многомерной передаточной функции,
которая описывает объект управления с двумя входами (два управляющих
воздействия) для объекта третьего порядка.
% Формируем массив ячеек числителя
N
» N={[1,- 2.3];[2,3.4]};
% Формируем массив знаменателя
D
» D={[1 3.6
];[2 3 5]};
% Формируем передаточную функцию многомерной системы
М
» M1=tf(N,D)
% Результат возвращается в виде
Transfer function from
input to output…
s – 2.3
#1: ——-
% По первому входу
s + 3.6
2 s + 3.4
#2: —————
% По второму входу
2 s^2 + 3 s + 5
2-й способ формирования
передаточной функции системы
MIMO с помощью
tf.
Заключается в объединении
предаточных функций одномерных систем.
3.2. Сформируем передаточную функцию
системы MIMO по известным передаточным функциям систем SISO.
% Первая система
SISO имеет передаточную функцию S11
» S11=tf([1
2],[1 3 2]) %
Последовательное соединение двух инерционных звеньев
Transfer
function:
s + 2
————-
s^2 + 3 s + 2
% Вторая система
SISO имеет передаточную функцию S21
»
S21=tf([7],[2 1]) %
Передаточная функция одного инерционного звена
Transfer
function:
7
—–
2s + 1
% Передаточная функция многомерной
системы М2
» M2=[S11;S21]
Transfer
function from input to output…
s +
2
#1:
————-
s^2 + 3
s + 2
7
#2: ——-
2 s + 1
3-й способ формирования
передаточной функции системы
MIMO с помощью
zpk.
3.3.
Формирование передаточной функции системы
MIMO по массиву ячеек.
% Формируем массив ячеек числителя
передаточной функции MIMO
»
Z={[1],5;[-1],[-2 -4]};
% Формируем массив ячеек знаменателя
передаточной функции MIMO
» P={[-1
-2],[-3 -6];[-1 -2],[-4 -5]};
% Формируем массив ячеек статического
коэффициента передачи MIMO
» K=[3 5;7 9];
% Формируем передаточную функцию М3 системы
MIMO
» M3=zpk(Z1,P1,K)
% Результат формирования М3 по заданным ячейкам
выдается по каждому управлению (которых два) к каждой выходной координате
(которых две)
Zero/pole/gain from input 1
to output…
3 (s-1)
#1: ———–
(s+1) (s+2)
7 (s+1)
#2: ———–
(s+1) (s+2)
Zero/pole/gain from input 2
to output…
5 (s-5)
#1: ———–
(s+3) (s+6)
9 (s+2) (s+4)
#2: ————-
(s+4) (s+5)
4-й
способ формирования передаточной функции системы
MIMO с помощью
zpk.
Основан на предварительном формировании с помощью
zpk
передаточных функций одномерных систем.
3.4. Формирование передаточной функции
MIMO
по заданным передаточным функциям
SISO.
%
Формируем первую передаточную функцию
SISO
» z1=zpk([1],[-1 -2],2)
% Для массива числителя MIMO
Zero/pole/gain:
2 (s-1)
———–
(s+1) (s+2)
%
Формируем вторую передаточную функцию
SISO
» z2=zpk([],[-3 -4],4)
% Для массива числителя
MIMO
Zero/pole/gain:
4
———–
(s+3) (s+4)
%
Формируем третью передаточную функцию
SISO
» p1=zpk(2,[-1.2 -2.3],5)
% Для массива знаменателя
MIMO
Zero/pole/gain:
5 (s-2)
—————
(s+1.2) (s+2.3)
%
Формируем четвертую передаточную функцию
SISO
»
p2=zpk([],[-3 -5],6) % Для массива
знаменателя MIMO
Zero/pole/gain:
6
———–
(s+3) (s+5)
% Формируем передаточную функцию
MIMO с
двумя входами и двумя выходами
» M4=[z1 z2;p1 p2;[]]
Zero/pole/gain from input 1
to output…
2 (s-1)
#1: ———–
(s+1) (s+2)
5 (s-2)
#2: —————
(s+1.2) (s+2.3)
Zero/pole/gain from input 2
to output…
4
#1: ———–
(s+3) (s+4)
6
#2: ———–
(s+3) (s+5)
% Знак пустого множества
[]
относится к статическому коэффициенту
K
передачи системы MIMO.
Заполнение коэффициента K
должно происходить с учетом количества входов и ли количества входных
воздействий. В рассматриваемо случае число столбцов
K
должно равняться двум.
3.5. Определение корней характеристического уравнения
многомерной системы —
eig,
pole.
Для системы
MIMO с
заданной передаточной функцией М4 корни соответствующего характеристического
уравнения можно определять с помощью функций
eig,pole.
% Найдем корни в формате вывода в виде строки (путем
транспонирования)
» eig(M4)’
% или
можно определить как pole(M4)
ans =
-2.0000 -1.0000
-2.3000 -1.2000 -4.0000 -5.0000 -3.0000
3.6. Определение нулей передаточной функции
многомерной системы —
tzero.
% Найдем нули в формате вывода в виде строки (путем
транспонирования)
» tzero(M4)’
ans =
3.3998 -1.9076
-0.8795 -5.8627
Задание:
—
Сформировать передаточную функцию 4-х последовательно соединенных
инерционных звеньев и одного дифференцирующего звена на входе системы.
—
Сформировать передаточную функцию 2-х последовательно соединенных
колебательных звеньев.
—
Сформировать передаточную функцию с последовательным соединением 2-х
инерционных и 2-х колебательных звеньев.
—
Сформировать передаточную функцию с последовательным соединением трех
инерционных звеньев с тремя управлениями, приложенными в различных точках
системы.
—
Формирование провести с помощью
tf,zpk
и с произвольными числовыми параметрами звеньев (чтобы они были устойчивыми).
Построение переходных и
импульсных характеристик систем, заданных передаточными функциями.
4.1. Переходные
характеристики —
step.
Определение. Переходной
характеристикой (функцией) объекта (системы) управления называется его реакция
во времени при воздействии на него единичной функции (единичного скачка) при
нулевых начальных условиях.
%Форматы записи
step
рассмотрим на примерах с передаточными функциями.
W1=tf(12,[1 2 3
1]); % Рациональная передаточная функция
» step(W1),grid
% С автоматическим установлением временного интервала
»
step(W1,25),grid % С задаваемым установлением временного
интервала от 0 до 25
» Z=zpk([],[-1 -2],4);
% Функция с выделенными нулями и полюсами
» step(Z),grid
% С автоматическим установлением временного
интервала
» step(Z,13),grid
% С задаваемым временным интервалом от 0 до 13
» step(Z,13,’r*’),grid,hold
on,step(W1,’g*’)% Совмещение двух
графиков— 1сп.
»
step(Z,13,’r*’,W1,’g*’),grid %
Совмещение двух графиков — 2-й способ
Задание.
—
Построить переходные характеристики для
всех ранее рассмотренных передаточных функций, как систем
SISO,
так и MIMO/
—
Для систем
MIMO
построить переходные характеристики по каждой выходной координате с
соответствующим управлением. Совместить отдельные характеристики в одной системе
координат.
4.2.
Импульсные характеристики —
impulse.
Определение. Импульсной
характеристикой (функцией) системы называется реакция системы во времени при
воздействии на нее функции Дирака
(с бесконечно большой амплитудой и бесконечной малой длительности).
%Форматы
записи
impulse рассмотрим на примерах с передаточными функциями.
W1=tf(12,[1 2 3 1]); %
Рациональная передаточная функция
»
impulse(W1),grid
% С автоматическим установлением временного интервала
»
impulse(W1,25),grid
% С задаваемым установлением временного интервала от 0 до 25
» Z=zpk([],[-1 -2],4);
% Функция с выделенными нулями и полюсами
»
impulse(Z),grid
% С автоматическим установлением
временного интервала
»
impulse(Z,13),grid
% С задаваемым временным интервалом от 0
до 13
»
impulse(Z,13,’r*’),grid,hold
on,step(W1,’g*’)% Совмещение графиков—
1сп.
»
impulse(Z,13,’r*’,W1,’g*’),grid
%
Совмещение графиков — 2-й способ
Задание.
—
Построить импульсные характеристики для
всех ранее рассмотренных передаточных функций, как систем
SISO,
так и MIMO/
—
Для систем
MIMO
построить импульсные характеристики по каждой выходной координате с
соответствующим управлением. Совместить отдельные характеристики в одной системе
координат.
—
Совместить графики соответствующих
импульсных и переходных функций.
Найти корни уравнения маткад прайм
Уравнение и системы уравнений в математическом пакете Mathcad в символьном виде решаются с использованием специального оператора символьного решения solve в сочетании со знаком символьного равенства, который может быть также введен с рабочей панели “Символика”. Например:
Аналогичные действия при решении уравнений в Mathcad можно выполнить, используя меню “Символика”. Для этого необходимо записать вычисляемое выражение. Затем выделить переменную, относительно которой решается уравнение, войти в меню Символика, Переменная, Разрешить. Например:
В случае, если необходимо упростить полученный результат, используется знак равенства [=]. Например:
При решении некоторых уравнений, результат включает большое количество символов. Mathcad сохраняет его в буфере, а на дисплей выводитcя сообщение: “This array has more elements than can be displayed at one time. Try using the “submatrix” function” – “Этот массив содержит больше элементов, чем может быть отображено одновременно. Попытайтесь использовать функцию “submatrix””. В этом случае рекомендуется использовать численное решение. Или, в случае необходимости, символьное решение может быть выведено и отображено на дисплее.
Символьное решение может быть получено с использованием блока given … find. В этом случае при записи уравнения для связи его левой и правой части использует символ логического равенства “=” с панели инструментов Boolean, например:
Аналогичным способом решаются системы уравнений в символьном виде. Ниже приводятся примеры решения систем уравнений в символьном виде различными способами. При использовании оператора символьного решения solve в сочетании со знаком символьного равенства 
Пример использования блока given…find для решения системы уравнений:
Нахождение корней уравнения в MathCad
Дата добавления: 2015-07-23 ; просмотров: 18087 ; Нарушение авторских прав
Цель работы:нахождение корней уравнения в программе MathCad с использованием встроенных функций root,polyroots, символьного решения.
Указания к выполнению лабораторной работы:
IНахождение корней уравнения в программе MathCad с использованием встроенной функции root
1. Запустить программу MathCad .
2. Записать на рабочем листе MathCad вид функции f(х), для которой необходимо найти на заданном интервале корни.
3. Создать цикл из точек интервала, на котором определяются корни, и вычислить в этих точках функцию f(х). Построить график функции f(х) и график функции х0=0 (т.е. ось х).
4. Определить точки пересечения двух кривых f(х) и х0, которые будут приближением к корням уравнения.
4.1. Использовать для определения на графике значений корней в контекстном меню (рис.17, a) опцию Trace (рис. 17,б), установить флажок в окне Track Data Poіnt.
4.2. Подвести курсор мыши к точкам пересечения кривых, координаты точек пересечения кривых, т.е. корни, будут представлены в окнах Х-Value и У- Value, а на графике отобразится вертикальная прямая.
5. Задать для независимой переменной х начальное приближение, которое выбирается как значение точки пересечения кривых f(х) и х0. Обратиться ко встроенной в MathCad функции root(f(x), x) (функция root возвращает значение независимой переменной х, для которой f(х) равняется 0) и найти корень х1.
6. Найти второй (х2) и третий (х3) корни уравнения f(х)=0 (уравнение третьей степени имеет не больше трех действительных корней), задав для них соответственно их начальные значения как координаты точек пересечения кривых f(х) и х0 и использовав функцию root.
Рисунок 17 – Диалоговые окна для определения координат точек пересечения кривых
ІІ Нахождение корней уравнения в программе MathCad с использованием встроенной функции polyroots, которая возвращает вектор, имеющий все корни уравнения, коэффициенты уравнения при этом задаются вектором.
1. Записать на рабочем листе MathCad вид функции f(х), для которой необходимо найти на заданном интервале корни.
2. Записать как вектор v все коэффициенты уравнения, расположить их в порядке увеличения степеней.
3. Найти корни, обратившись ко встроенной функции r:=polyroots(v), результат будет получено относительно трансформированного вектора r T .
4. Для интервала нахождения корня и количества элементов вектора r T создать соответствующие циклы и вычислить значение функции в точках цикла.
5. Построить график функции в точках цикла, а также в найденных точках корней, в которых функция будет иметь значения, равные нулю.
ІІІ Нахождение корней уравнения в программе MathCad с использованием символьных решений уравнений.
1. Ввести левую часть уравнения.
2. Ввести знак равенства с использованием панели управления Evaluatіon (Выражения) или с помощью нажатия клавиш Ctrl + =.
3. За знаком равенства ввести правую часть уравнения.
4. Выделить переменную, относительно которой решается уравнение.
5. Выбрать команду Symbolіc/Varіable/Solve.
По окончанию решения корни уравнения выводятся в виде вектора.
ІV Найти приближенное решение с использованием функции mіnerr(x1. ).
1. Задать приближение последовательно для первого корня х:=1.
2. Ввести ключевое слово gіven (дано), из которого начинается блок решений.
3. Записать уравнение, используя знак логического равенства между правой и левой частями уравнения.
4. Обратиться к функции mіnerr( x). Корень будет найдено.
Таблица 1.1 – Варианты заданий к лабораторной работе № 1
| № варианта | Интервал нахождения корней | Уравнение |
| [-1; 3] | x 3 -2,92x 2 +1,4355x+0,791=0 | |
| [-2; 3] | x 3 -2,56x 2 -1,325x+4,395=0 | |
| [-3,5; 2,5] | x 3 +2,84x 2 -5,606x-14,766=0 | |
| [-2,5; 2,5] | x 3 +1,41x 2 -5,472x-7,38=0 |
| [-1,6; 1,1] | x 3 +0,85x 2 -0,432x+0,044=0 |
| [-1,6; 1,6] | x 3 -0,12x 2 -1,478x+0,192=0 |
| [-1,6; 0,8] | x 3 +0,77x 2 -0,251x-0,017=0 |
| [-1,4; 1] | x 3 +0,88x 2 -0,3999x-0,0376=0 |
| [-1,4; 2,5] | x 3 +0,78x 2 -0,827x-0,1467=0 |
| [-2,6; 1,4] | x 3 +2,28x 2 -1,9347x-3,90757=0 |
| [-2,6; 3,2] | x 3 -0,805x 2 -7x+2,77=0 |
| [-3; 3] | x 3 -0,345x 2 -5,569x+3,15=0 |
| [-2; 3,4] | x 3 -3,335x 2 -1,679x+8,05=0 |
| [-1; 2,8] | x 3 -2,5x 2 +0,0099x+0,517=0 |
| [-1,2; 3] | x 3 -3x 2 +0,569x+1,599=0 |
| [-2,5; 2,5] | x 3 -2,2x 2 +0,82x+0,23=0 |
| [-1,2; 4,6] | x 3 -5x 2 +0,903x+6,77=0 |
| [-1; 7,4] | x 3 -7,5x 2 +0,499x+4,12=0 |
| [-1.6; 9] | x 3 -7,8x 2 +0,899x+8,1=0 |
| [-3,4; 2] | x 3 +2x 2 -4,9x-3,22=0 |
| [-3,4; 1,2] | x 3 +3x 2 -0,939x-1,801=0 |
| [-4,6; 3,0] | x 3 +5,3x 2 +0,6799x-13,17=0 |
| [-2,4; 8,2] | x 3 -6,2x 2 -12,999x+11,1=0 |
| [-3,2; 2,7] | x 3 -0,34x 2 -4,339x-0,09=0 |
| [-1; 3] | x 3 -1,5x 2 +0,129x+0,07=0 |
| [-1; 3] | x 3 -5,5x 2 +2,79x+0,11=0 |
| [-1; 3] | x 3 -5,7x 2 -6,219x-2,03=0 |
| [-1; 3] | x 3 -3,78x 2 -7,459x-4,13=0 |
| [-1; 3] | x 3 -5x 2 -9,9119x+0,01=0 |
| [-1; 3] | x 3 -7x 2 -1,339x-7,55=0 |
Пример
І Для уравнения найти корни на интервале [-1, 1], шаг изменения переменной х равен 0.1.
1 Записать цикл из точек интервала х:=-1, -0.9..1.
2 Записать функции и х0=0.
3 Построить графики для этих функций.
4 Определить на графике точки пересечения кривых и х0=0.
5 Задать как приближение значения точек пересечения х1, х2, х3. В примере х1=-0.9, х2=0.2, х3= 0.7.
6 Вычислить значение корней с помощью формул: root (f(x1),x1), root (f(x2),x2), root (f(x3),x3). Полученные значения корней такие: х1=-0.92, х2=0.21, х3= 0.721 (рис. 18).
Рисунок 18 – Результат нахождения корней с использованием функции root
II Для уравнения найти корни на интервале [-1.1, 7.1] , шаг изменения переменной х равен 0.1.
1. Создать вектор из коэффициентов уравнения, используя панель управления Matrix (Матрица) (рис.19) и задав один столбец и четыре строки для коэффициентов уравнения.
Рисунок 19 – Диалоговое окно для определения вектора из коэффициентов уравнения
Вектор из коэффициентов уравнения будет иметь следующий вид
2. С помощью встроенной функции r:=polyroots(v) найти корни уравнения и представить их в виде вектора r T , транспонированного по отношению к r, то есть преобразованного из столбца в строку.
3. Создать циклы для переменной х и количества найденных корней:
4. Построить графики для функции и определить функцию в точках корней. В точках корней значения функции равны нулю.
5. Определить значения корней на графике (рис. 20).
Рисунок 20 – Результат нахождения корней с использованием функции polyroots
III Для уравнения найти корни с использованием символьных решений уравнений.
1. Записать левую часть уравнения
.
2. Поставить логический знак «=» и в правой части записать 0.
3. Выделить переменную х.
4. Обратиться в главном меню MathCad к команде Symbolic/Variable/ Solve.
Найдены корни уравнения запишутся в виде вектора:
IV Найти приближенное решение вышеприведенного уравнения с использованием функции minerr( x1,…).
1. Задать приближение последовательно для первого корня х:=1.
2. Ввести ключевое слово given (дано), с которого начинается блок решений.
3. Записать уравнение, используя знак логического равенства между правой и левой частью уравнения.
4. Обратиться к функции minerr( x). Корень будет найдено.
5. Аналогические действия выполнить для двух других корней уравнения, поскольку уравнения третьей степени имеет не больше трех корней.
Контрольные вопросы
1 Какие встроенные функции позволяют находить корни уравнения?
2 Как выполняется символьное нахождение корней уравнений?
Лабораторная работа №3
Действия с матрицами в MathCad
Цель работы:выполнение действий с матрицами в программе MathCad .
Указания к выполнению лабораторной работы:
1. Запустить программу MathCad .
2. Создать матрицы , , , , , из коэффициентов a, b, c, m, k, n в соответствии с вариантом задания.
3. Выполнить действия с матрицами в соответствии с вариантом задания.
4. Найти ранг матрицы А.
5. В символьном виде выполнить транспонирование матрицы В, инвертирование матрицы А.
6. Найти обратную матрицу К. Найти детерминант матрицы А.
Таблица 2.1 – Варианты заданий к лабораторной работе № 2
| Номер варианта | Значение элементов матриц | Действия с матрицами |
| a=1; b=0.5; c=-1; m=2; k=-2.1;n=-0.8 | 1) A+A×M; 2) B×C; 3) M 3 ; 4)D+m×K; 5)A×D+D×M; 6)K -2 | |
| a=-2; b=1; c=1.5; m=-3; k=-0.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 | |
| a=-1; b=5; c=1.3; m=0.9; k=0.1;n=-0.5 | 1) A-M; 2) B-a×C 3) M 2 -B; 4)D-×K; 5)A+7×D; 6)A -2 | |
| a=1; b=0.5; c=1; m=0.2; k=0.27 ;n=0.7 | 1) A 2 ; 2) B×C+M; 3) n×M 2 ; 4)D-K; 5)A×B-D×C; 6)D -2 | |
| a=3; b=2.1; c=0.91; m=1.2; k=1; n=3 | 1) A 2 +M; 2) B-M; 3) b×C -3 ; 4)D+3K; 5)A×K-D; 6)M -2 | |
| a=4; b=-0.5; c=-1; m=3.2; k=1.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 | |
| a=1; b=2.5; c=0.3; m=1; k=-2.1;n=-0.8 | 1) A-M; 2) B-a×C 3) M 2 -B; 4)D-×K; 5)A+7×D; 6)A -2 | |
| a=2; b=0.5; c=-1.1; m=2; k=1.9 ;n=-3.8 | 1) A 2 ; 2) B×C+M; 3) n×M 2 ; 4)D-K; 5)A×B-D×C; 6)D -2 | |
| a=3; b=-2.5; c=4; m=3; k=-2.1;n=0.8 | 1) A 2 +M; 2) B-M; 3) b×C -3 ; 4)D+3K; 5)A×K-D; 6)M -2 | |
| a=3.1; b=1.5; c=2.1; m=3.2; k=1.1;n=-1.6 | 1) A+A×M; 2) B×C; 3) M 3 ; 4)D+m×K; 5)A×D+D×M; 6)K -2 | |
| a=-2; b=1; c=1.5; m=-3; k=-0.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 | |
| a=-1; b=5; c=1.3; m=0.9; k=0.1;n=-0.5 | 1) A-M; 2) B-a×C 3) M 2 -B; 4)D-×K; 5)A+7×D; 6)A -2 | |
| a=1; b=0.5; c=1; m=0.2; k=0.27 ;n=0.7 | 1) A 2 ; 2) B×C+M; 3) n×M 2 ; 4)D-K; 5)A×B-D×C; 6)D -2 | |
| a=3; b=2.1; c=0.91; m=1.2; k=1; n=3 | 1) A 2 +M; 2) B-M; 3) b×C -3 ; 4)D+3K; 5)A×K-D; 6)M -2 | |
| a=4; b=-0.5; c=-1; m=3.2; k=1.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 | |
| a=1; b=2.5; c=0.3; m=1; k=-2.1;n=-0.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 |
Продолжение табл. 2.1
| a=2; b=0.5; c=-1.1; m=2; k=1.9 ;n=-3.8 | 1) A-M; 2) B-a×C 3) M 2 -B; 4)D-×K; 5)A+7×D; 6)A -2 |
| a=3; b=-2.5; c=4; m=3; k=-2.1;n=0.8 | 1) A 2 ; 2) B×C+M; 3) n×M 2 ; 4)D-K; 5)A×B-D×C; 6)D -2 |
| a=3.1; b=1.5; c=2.1; m=3.2; k=1.1;n=-1.6 | 1) A 2 +M; 2) B-M; 3) b×C -3 ; 4)D+3K; 5)A×K-D; 6)M -2 |
| a=1; b=0.5; c=-1; m=2; k=-2.1;n=-0.8 | 1) A+A×M; 2) B×C; 3) M 3 ; 4)D+m×K; 5)A×D+D×M; 6)K -2 |
| a=-2; b=1; c=1.5; m=-3; k=-0.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 |
| a=-1; b=5; c=1.3; m=0.9; k=0.1;n=-0.5 | 1) A-M; 2) B-a×C 3) M 2 -B; 4)D-×K; 5)A+7×D; 6)A -2 |
| a=1; b=0.5; c=1; m=0.2; k=0.27 ;n=0.7 | 1) A 2 ; 2) B×C+M; 3) n×M 2 ; 4)D-K; 5)A×B-D×C; 6)D -2 |
| a=3; b=2.1; c=0.91; m=1.2; k=1; n=3 | 1) A 2 +M; 2) B-M; 3) b×C -3 ; 4)D+3K; 5)A×K-D; 6)M -2 |
| a=4; b=-0.5; c=-1; m=3.2; k=1.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 |
| a=1; b=2.5; c=0.3; m=1; k=-2.1;n=-0.8 | 1) A+A×M; 2) B×C; 3) M 3 ; 4)D+m×K; 5)A×D+D×M; 6)K -2 |
| a=2; b=0.5; c=-1.1; m=2; k=1.9 ;n=-3.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 |
| a=3; b=-2.5; c=4; m=3; k=-2.1;n=0.8 | 1) A-M; 2) B-a×C 3) M 2 -B; 4)D-×K; 5)A+7×D; 6)A -2 |
| a=3.1; b=1.5; c=2.1; m=3.2; k=1.1;n=-1.6 | 1) A 2 ; 2) B×C+M; 3) n×M 2 ; 4)D-K; 5)A×B-D×C; 6)D -2 |
| a=-2; b=1; c=1.5; m=-3; k=-0.1;n=1.8 | 1) A 2 +M; 2) B-M; 3) b×C -3 ; 4)D+3K; 5)A×K-D; 6)M -2 |
Пример
Выполнить действия с матрицами, создав их из заданных коэффициентов a=1, b=2, c= 3, m=4, k=5, n=6. Матрицы имеют следующий вид:
1. Создать матрицы.
1.1. Выбрать панель управления Matrіx (Матрица).
1.2. Определить число строк и столбцов для каждой матрицы (рис.21).
Рисунок 21 – Диалоговое окно для определения размера матрицы
1.3. Матрицы в примере имеют такие размеры: А – (3´3), В – (3´2), С(2´2), М(1´2), К(3´3).
1.4. Заполнить матрицы соответствующими параметрами (рис. 29).
2 Выполнить следующие действия с матрицами:
1) А+n·K; 2)A·B; 3) A 2 ; 4) A·D; 5)D·M; 6) D-1.
3 Найти ранг матрицы А (ранг матрицы -наибольший порядок минора этой матрицы, который отличный от нуля): rank(A).
4 В символьном виде выполнить транспонирование матрицы В, т.е. заменить местами строки и столбцы матрицы В.
4.1 Выделить матрицу В.
4.2 Обратиться в главном меню к команде Symbolіc / Matrіx/Transpose (рис. 28).
5 В символьном виде выполнить инвертирование матрицы А (т.е. найти матрицу, которая будет обратной к матрице А) .
5.1 Выделить матрицу A.
5.2 Обратиться в главном меню к команде Symbolіc/Matrіx/Іnvert (рис.28).
6 В символьном виде найти обратную матрицу К.
6.1 Выделить матрицу К.
6.2 Обратиться в главном меню к команде Symbolіc / Matrіx/Іnvert (рис.28).
7 В символьном виде найти детерминант (определитель) матрицы А.
7.1 Выделить матрицу A.
7.2 Обратиться в главном меню к команде Symbolіc/Matrіx/Determіnant (рис.22).
Рисунок 22 – Меню Symbolic для работы с матрицами в символьном виде
Рисунок 23 – Результаты вычисления матриц
Контрольные вопросы
1 Як можно создать матрицу и вектор?
2 Какие действия выполняются с матрицами?
3 Как определяются элементы матрицы?
Лабораторная работа №4
Нахождение решений системы линейных уравнений в MathCad
Цель работы:нахождение решений системы линейных уравнений в программе MathCad .
Указания к выполнению лабораторной работы:
I Найти решение системы линейных уравнений с использованием функции soln.
1 Запустить программу MathCad.
2 Создать матрицу А из коэффициентов при неизвестных.
3 Создать вектор b из свободных членов.
4 Обратиться к встроенной программе решения линейных уравнений soln и записать soln1:=А -1 ×b.
5 Получить решение линейного уравнения у векторному виде
.
IIНайти решение системы линейных уравнений с использованием так званого «блоку решений».
1 Задать начальные значения переменным, которые есть в уравнении.
2 Ввести ключевое слово given (дано), с которого начинается блок решений.
3 Записать уравнение, используя знак логического равенства между правой и левой частью уравнения из панели управления Evaluation (Выражения).
4 Ввести ключевое слово find (найти), которым заканчивается блок решений.
IIIНайти решение вышеприведенной системы уравнений с использованием функции lsolve.
1Создать матрицу А из коэффициентов при неизвестных.
2 Создать вектор b из свободных членов.
4 Обратиться к встроенной программе решения линейных уравнений lsolve и записать lsolve(А,b).
5 Получить результат решения линейного уравнения в векторном виде
.
IVНайти приближенное решение с использованием функции minerr(x1,…).
1 Задать приближение последовательно для значений переменной х1, х2,… хn.
2 Ввести ключевое слово given (дано), с которого начинается блок решений.
3 Записать систему уравнений, используя знак логического равенства между правой и левой частями каждого уравнения.
4 Обратиться к функции minerr( x1,x2. ). Значения неизвестных будут найдены.
Таблица 3.1 – Варианты заданий к лабораторной работе № 3
| № варианта | Коэффициенты при неизвестных | Свободные члени | ||
| a11 а21 а31 а41 | а12 а22 а23 а24 | а13 а23 а33 а34 | а14 а24 а34 а44 | в1 в2 в3 в4 |
| 0,12 | -0,43 | 0,14 | 0,64 | -0,17 |
| -0,07 | 0,34 | -0,72 | 0,32 | 0,62 |
| 1,18 | -0,08 | -0,25 | 0,43 | 1,12 |
| 1,17 | 0,53 | -0,84 | -0,53 | 1,15 |
| 0,12 | -0,43 | 0,14 | 0,64 | -0,17 |
| -0,07 | 0,34 | -0,72 | 0,32 | 0,62 |
| 1,18 | -0,08 | -0,25 | 0,43 | 1,12 |
| 1,17 | 0,53 | -0,84 | -0,53 | 1,15 |
| 3,7 | 5,6 | 9,5 | ||
| 3,36 | 31,1 | 1,5 | ||
| 7,93 | 4,2 | 6,3 | 4,4 | |
| 42,7 | 3,7 | 6,2 | ||
| 1,3 | 1,6 | 2,2 | ||
| 4,4 | 6,7 | 2,5 | ||
| 2,8 | 0,73 | 67,8 | ||
| 3,4 | ||||
| 5,3 | 1,6 | 5,5 | 3,3 | |
| 4,1 | 6,4 | 3,9 | ||
| 2,1 | 3,3 | 2,04 | 4,9 | |
| 3,1 | ||||
| 0,2 | ||||
| 8,3 | 5,3 | |||
| 2,6 | 6,1 | 4,1 | ||
| 0,93 | 3,8 | |||
| 34,7 | ||||
| 3,6 | ||||
| 3,4 | 4,2 | |||
| 44,7 | ||||
| 5,1 | 0,2 | |||
| 3,4 | 5,34 | |||
| 2,7 | 6,7 | |||
| 3,3 | ||||
| 2,5 | 1,3 | |||
| 5,2 | 0,78 | |||
| 6,11 | 4,2 | |||
| 6,78 | 3,76 | |||
| 2,3 | ||||
| 3,4 | 2,5 | |||
| 0,2 | ||||
| 1,25 | ||||
| 3,3 | 8,2 | |||
| 1,2 | ||||
| 1,3 | ||||
| 5,9 | ||||
| 6,6 | ||||
| 3,3 | 2,1 | |||
| 4,8 | ||||
| 0,4 | ||||
| 0,2 | ||||
| 1,3 | 1,5 | 2,22 | 3,2 | |
| 3,4 | 5,55 | 1,3 | ||
| 3,3 | 2,2 | 6,77 | ||
| 4,9 | 3,6 | 6,88 | ||
| 0,4 | ||||
| 0,3 | ||||
| 3,3 | 7,6 | 5,5 | ||
| 5,4 | ||||
| 9,2 | ||||
| 3,2 | ||||
| 0,44 | ||||
| 0,67 |
| 3,35 | 5,3 | |||
| 4,22 | 6,7 | 3,5 | ||
| 2,8 | 3,8 | 2,9 | ||
| 2,34 | 3,44 | |||
| 5,23 | ||||
| 13,4 | 6,33 | 5,1 | 2,11 | 3,33 |
| 4,66 | 6,1 | 3,33 | 5,44 | 0,11 |
| 2,22 | 2,55 | 6,33 | 4,44 | |
| 2,98 | 3,78 | 6,11 | 3,33 |
Пример
I Найти решение системы уравнений с использованием функции soln
1 Создать матрицу А
А:= .
2 Создать вектор b
b:= .
3 Найти решение системы, используя функцию soln
.
4 Результат решения
II Найти решение вышеприведенной системы уравнений с использованием так званого «блоку решений»
1 Задать начальные значения переменным, которые присутствуют в уравнении
2 Ввести ключевое слово given (дано), с которого начинается блок решений.
3 Записать уравнение, используя знак логического равенства между правой и левой частями уравнения из панели управления Evaluation (Выражения).
4 Ввести ключевое слово find (найти), которым заканчивается блок решений.
5 Результат решения
IIIНайти решение вышеприведенной системы уравнений с использованием функции lsolve.
1 Создать матрицу А
.
2 Создать вектор b
.
3 Найти решение системы, используя функцию lsolve:
IVНайти решение вышеприведенной системы уравнений с использованием функции minerr (x,у,z).
1 Задать начальные условия для неизвестных, например, x=1,у=1,z=1.
2 Ввести ключевое слово given (дано), с которого начинается блок решений.
3 Записать уравнения, используя знак логического равенства между правой и левой частью уравнения из панели.
4 Обратиться к функции minerr (x,у,z). Решение системы уравнений будет найдено.
Контрольные вопросы
1 Какие встроенные функции позволяют найти решение системы линейных уравнений?
2 В каком виде представляются результаты решения системы линейных уравнений?
Лабораторная работа №5
Нахождение решений системы нелинейных уравнений в MathCad
Цель работы: нахождение решений системы нелинейных уравнений в программе MathCad .
Указания к выполнению лабораторной работы:
І Найти решение системы нелинейных уравнений с использованием так называемого “блока решений”.
1 Задать начальные значения переменным, которые есть в уравнении.
2 Ввести ключевое слово gіven (дано), из которого начинается блок решений.
3 Записать уравнение, используя знак логического равенства между правой и левой частями уравнения из панели управления.
4 Ввести ключевое слово fіnd (найти), которым заканчивается блок решений.
ІІ. Найти приближенное решение с использованием функции mіnerr(x1. ).
1 Задать приближение последовательно для значений переменной х1, х2. хn.
2 Ввести ключевое слово gіven (дано), из которого начинается блок решений.
3 Записать систему уравнений, используя знак логического равенства между правой и левой частями каждого уравнения.
4 Обратиться к функции mіnerr( x1,x2. ). Значение неизвестных будет найдено.
Таблица 4.1 – Варианты задания к лабораторной работе №4
| № варианта | Система уравнений | № варианта | Система уравнений |
Пример
Найти решение системы нелинейных уравнений с использованием так называемого «блока решений».
1 Задать начальные значения переменным, которые есть в уравнении
2 Ввести ключевое слово given (дано), с которого начинается блок решений.
3 Записать уравнения, используя знак логического равенства между правой и левой частью уравнения из панели управления
4 Ввести ключевое слово find (найти), которым заканчивается блок решений.
5 Результат решения
IIНайти приближенное решение с использованием функции minerr(x1,…).
1 Задать приближения последовательно для значений переменной х=1, y=1.
2 Ввести ключевое слово given (дано), с которого начинается блок решений.
3 Записать систему уравнений, используя знак логического равенства между правой и лево частью каждого уравнения.
4 Обратится к функции minerr( x,y.). Значение неизвестных будет найдено.
Контрольные вопросы
1 Какие встроенные функции позволяют найти решение системы нелинейных уравнений?
2 В каком виде представляются результаты решения системы нелинейных уравнений?
3 Нужно ли задавать начальные приближения при решении системы нелинейных уравнений?
Лабораторная работа № 6
Символьные действия математического анализа в MathCad
Цель работы:определение неопределенных и определенных интегралов и производных в программе MathCad с использованием символьных операций.
Указания к выполнению лабораторной работы:
1 Запустить программу MathCad.
2 Записать на рабочем листе в соответствии с номером варианта формулы для определения неопределенных интегралов, определенных интегралов, производных первого порядка. От производных первого порядка определить производные второго, третьего порядков.
3 Применить последовательно к каждой функции команды меню Symbolic/Simplify, отметив последовательно каждую из функций.
Таблица 5.1 – Варианты задания к лабораторной работе №5
| Номер варианта | Неопределенные интегралы | Определенные интегралы | Производные |
Продолжение табл. 5.1
Продолжение табл. 5.1
Примеры
1 Найти неопределенный интеграл .
Результат :
2 Найти определенный интеграл .
Результат .
3 Найти производные первого порядка .
Результат .
4 Найти производные высокого порядка .
Результат
Контрольные вопросы
1 Как найти в символьном виде определенные и неопределенные интегралы?
2 Можно ли применять символьные операции к интегралам по области, к трехмерным интегралам, к контурным интегралам?
3 Можно ли в символьному виде найти производные высоких порядков?
| | | следующая лекция ==> | |
| Задание 3. | | | Лабораторная работа № 1 |
Не нашли то, что искали? Google вам в помощь!
Найти корни уравнения маткад прайм
Глава 4. Решение уравнений
4.1 Функция root
Функция root используется для решения одного уравнения с одним неизвестным. Перед началом решения желательно построить график функции, чтобы проверить, есть ли корни, то есть пересекает ли график ось абсцисс. Начальное приближение лучше всего выбрать по графику поближе к корню, так как итерационные методы весьма чувствительны к выбору начального приближения.
Обращение к функции осуществляется следующим образом:
root ( f ( x ), x ), где f ( x ) – выражение, равное нулю; x – аргумент, варьируя который, система ищет значение, обращающее в нуль ( рис. 4.1 ).
Уравнение
начальное приближение
решение
или
другие корни
Задан интервал поиска корней
Рис. 4. 1 Использование функции root
Функция f ( x ) и аргумент x должны быть скалярами, то есть результат вычисления функции – число, а не вектор или матрица. Функция root использует метод секущих. Корень уравнения – ближайшее к начальному приближению значение x , обращающее функцию f ( x ) в нуль. Если корней несколько, то для отыскания каждого корня необходимо задавать свое начальное приближение.
Mathcad позволяет вместо начального приближения задавать диапазон значений аргумента, в котором лежит значение искомого корня. В этом случае обращение к функции root должно иметь четыре параметра:
root ( f ( x ), x , а, b ),
где a и b – границы интервала, в котором лежит один корень уравнения. Внутри интервала не должно быть больше одного корня, так как Mathcad выводит на экран лишь один корень, лежащий внутри интервала.
Значение функции на границах интервала должно быть разного знака, иначе, возможно, корень не будет найден.
Если уравнение не имеет действительных корней, то есть на графике функция f ( x ) нигде не равна нулю, то для вывода комплексных корней надо ввести начальное приближение в комплексной форме (рис. 4.2) .
Если функция имеет мнимый корень,
то начальное приближение задается комплексным числом
– начальное приближение
Рис. 4. 2 Решение уравнения с комплексными корнями
Для ввода мнимой единицы надо ввести с клавиатуры 1 i или 1 j .
Если уравнение имеет несколько корней, то для их нахождения можно использовать разложение функции f ( x ) на простые множители:
где x 1, x 2 , , xn – корни уравнения. Начальное приближение можно задать только для первого корня. В качестве функции f ( x ) нужно взять
,
где ,
и т. д. (рис. 4.3)
у этой функции 3 корня
диапазон значений х для вывода графика
Рис. 4. 3 Определение трех корней уравнения
Если функция f ( x ) имеет малый наклон вблизи искомого корня, то функция root ( f ( x ), x ) может сходиться к значению, довольно далеко отстоящему от корня. В таком случае для уточнения корня необходимо уменьшить значение погрешности вычислений, задаваемое встроенной переменной TOL . Для этого:
1) в стандартном меню Mathcad выберите команду Tools → Worksheet Options → Built – In Variables (Инструменты → Параметры документов → Встроенные переменные);
2) в открывшемся окне поменяйте значение Convergence Tolerance ( TOL ) (Погрешность сходимости).
Чем меньше константа TOL , тем ближе к нулю будет значение функции при найденном корне уравнения, но тем больше будет время вычисления корня.
Для повышения точности расчета корня можно заменить f ( x ) на
.
Корень можно найти и по графику, увеличив масштаб. Для этого необходимо:
1) выделить график, щелкнув левой кнопкой мыши внутри графика;
2)в главном меню Mathcad выбрать команду Format → Graph → Zoom (Формат→График→Масштаб);
3) при нажатии левой кнопки мыши обвести пунктирной линией область графика вблизи искомого корня, которую надо увеличить;
4) в открытом окне X – Y Zoom (Масштаб по осям X – Y ) нажать кнопку Zoom .
Прямо с графика можно передать в буфер обмена численное значение корня. Для этого выполните следующие действия:
1) Выделите график, щелкнув левой кнопкой мыши внутри графика,
2) в главном меню Mathcad выберите команду Format → Graph → Trace (Формат→График→Трассировка),
3) щелкните левой кнопкой мыши внутри графика – появится перекрестье осей,
4) двигая мышь при нажатой левой кнопке, установите перекрестье на пересечении графика с осью абсцисс. При этом численные значения координат перекрестья появляются в открытом окне X – Y Trace (Трассировка X и Y ).
5) правильно выбрав положение перекрестья, нажмите кнопки Copy X и Copy Y – численные значения будут помещены в буфер
6) вне поля графика запишите имя, которое хотите дать корню, и оператор присваивания :=. Нажмите кнопку Paste (Вставить) в стандартном меню Mathcad или в контекстном меню, открывающемся при нажатии правой кнопки мыши.
Рис. 4. 4 Определение корня уравнения по графику
В окне X – Y Trace есть пункт Track Data Points (Отмечать расчетные точки). Если установить этот флажок, при перемещении мыши пунктирное перекрестье на графике будет перемещаться скачками, отмечая расчетные значения функции. Если флажок снять, движение перекрестья становится плавным.
При работе с Mathcad постоянно пользуйтесь правой кнопкой мыши (в контекстном меню каждый раз появляются новые, наиболее нужные в данный момент функции). Щелкните правой кнопкой мыши на графике: в открывшемся контекстном меню есть пункты Zoom и Trace .
[spoiler title=”источники:”]
http://life-prog.ru/2_59715_nahozhdenie-korney-uravneniya-v-mathcad.html
http://www.math.mrsu.ru/text/courses/mcad/4.1.htm
[/spoiler]