Здравствуйте.
В этой и следующей статье рассмотрим задание №9 из ОГЭ по математике – УРАВНЕНИЯ.
Уравнения могут встретиться линейные или квадратные (полные и неполные).
В данной статье рассмотрим линейные уравнения.
Уравнение №1.
Уравнение №2.
Уравнение №3.
Уравнение №4.
Уравнение №5.
Уравнение №6.
И всё)
Знаете, как проще решить? Пишите решение в комментариях!
Ставьте ЛАЙК) и ПОДПИСЫВАЙТЕСЬ!
#огэ 2022 #математика #огэ по математике 2022 #логика #линейные уравнения #уравнения огэ #задание 9 #задание 9 огэ 2022 #огэ
Задание №9 ОГЭ по математике
В девятом задании модуля алгебра ОГЭ по математике нам предлагают решить уравнения. Это могут быть как линейные уравнения, которые решаются переносом всех известных членов в одну сторону, а неизвестных (x) в другую, так и квадратные уравнения, которые в свою очередь могут быть полными и неполными. Судя по материалам ОГЭ и практике проведения экзамена, наиболее вероятным заданием может быть решение линейного или квадратного уравнения. Тем не менее мы рассмотрим задания по всей этой тематике. Сложность заданий как всегда возрастает от задания к заданию. Ответом в задании №9 является целое число или конечная десятичная дробь.
Теория к заданию №9
Ниже я привел теорию по решениям линейных и квадратных уравнений:
Схема решения, правила и алгоритм действий при решении линейного уравнения:

Схема решения, правила и порядок действий при решении квадратного уравнения:

В трех типовых вариантах я разобрал данные случаи – в первом варианте вы найдете подробные указания по решению линейных уравнений, во втором разобран пример решения неполного квадратного уравнения, а в третьем – решение полного квадратного уравнения с вычислением дискриминанта.
Найдите корень уравнения:
Данное уравнение представляет собой обыкновенное уравнение первой степени и решается переносом всех известных частей в правую часть, оставив x слева.
Для начала следует раскрыть скобки: 10x – 90 = 7
Затем переносим 90 в правую часть (не забываем поменять знак):
Затем делим обе части на 10:
pазбирался: Даниил Романович | обсудить разбор | оценить
Это неполное квадратное уравнение, в котором не обязательно вычислять дискриминант, а достаточно вынести x за скобку:
Произведение множителей тогда равно нулю, когда один из множителей равен нолю:
Так как в ответе просят указать наименьший корень, то это -4.
pазбирался: Даниил Романович | обсудить разбор | оценить
Уравнение является полным квадратным уравнением, поэтому классическим вариантом решения является вычисление дискриминанта. Но в данном случае можно заметить, что все множители кратны двум, поэтому можно все уравнение разделить на 2 для удобства вычисления:
Далее вычисляем дискриминант:
x = (- b — √D) / 2a = (5 — 3 )/ 2 •4 = 0,25
x = (- b + √D) / 2a = (5 + 3 )/ 2 •4 = 1
Так как нам нужно выбрать меньший из корней по условию, то выбираем 0,25
pазбирался: Даниил Романович | обсудить разбор | оценить
В данной задаче нам предстоит решить линейное уравнение. Подход к решению таких уравнений достаточно простой – всё, что известно переносим в правую часть, всё, что неизвестно – оставляем в левой. Далее выполняем необходимое арифметическое действие.
Переносим 9 в правую часть (не забываем про смену знака):
7х = 40 + 9, что эквивалентно
х в нашем случае – это неизвестный множитель, следовательно, чтобы его найти, делим произведение на известный множитель:
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите корень уравнения: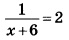
режде всего, исключим
Корень – осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Далее решаем уравнение. Представляем число 2 в уравнении справа в виде дроби 2/1. Уравнение получает
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Выполним умножение в левой части уравнения и раскроем скобки справа:
Поменяем местами левую и правую части уравнения, чтобы оно приняло привычный вид:
Переносим 12 из левой части в правую:
ОДЗ это значение не исключает, поэтому оно является искомым результатом.Ответ: -5,5
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите корень уравнения: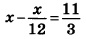
Обе части уравнения приводим к единому знаменателю 12: 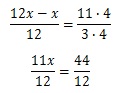 Т.к. знаменатели в левой и правой частях уравнения одинаковы, не равны нулю и не содержат переменных, то их можно сократить (т.е. ими можно пренебречь). Тогда получаем: 11х=44 х=44:11 х=4
Т.к. знаменатели в левой и правой частях уравнения одинаковы, не равны нулю и не содержат переменных, то их можно сократить (т.е. ими можно пренебречь). Тогда получаем: 11х=44 х=44:11 х=4
pазбирался: Даниил Романович | обсудить разбор | оценить
Имеем линейное уравнение:
Следовательно, начинаем решение с переноса слагаемых (с переменной влево, без переменной – вправо): 3х + 7х= – 5 – 2, не забывая изменять знак у слагаемых, которые переносим. Теперь приводим подобные в каждой части, получаем 10х= –7.
Находим неизвестный множитель делением произведения –7 на известный множитель 10, получаем –0,7.
Запись решения выглядит так:
pазбирался: Даниил Романович | обсудить разбор | оценить
Алгебра. Урок 4. Уравнения, системы уравнений
Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Уравнения”.

Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Линейные уравнения
Линейные уравнения
Линейное уравнение – уравнение вида a x = b , где x – переменная, a и b некоторые числа, причем a ≠ 0 .
Примеры линейных уравнений:
- 3 x = 2
- 2 7 x = − 5
Линейными уравнениями называют не только уравнения вида a x = b , но и любые уравнения, которые при помощи преобразований и упрощений сводятся к этому виду.
Как же решать уравнения, которые приведены к виду a x = b ? Достаточно поделить левую и правую часть уравнения на величину a . В результате получим ответ: x = b a .
Как распознать, является ли произвольное уравнение линейным или нет? Надо обратить внимание на переменную, которая присутствует в нем. Если старшая степень, в которой стоит переменная, равна единице, то такое уравнение является линейным уравнением.
Для того, чтобы решить линейное уравнение , необходимо раскрыть скобки (если они есть), перенести «иксы» в левую часть, числа – в правую, привести подобные слагаемые. Получится уравнение вида a x = b . Решение данного линейного уравнения: x = b a .
Примеры решения линейных уравнений:
- 2 x + 1 = 2 ( x − 3 ) + 8
Это линейное уравнение, так как переменная стоит в первое степени.
Попробуем преобразовать его к виду a x = b :
Для начала раскроем скобки:
2 x + 1 = 4 x − 6 + 8
В левую часть переносятся все слагаемые с x , в правую – числа:
Теперь поделим левую и правую часть на число ( -2 ) :
− 2 x − 2 = 1 − 2 = − 1 2 = − 0,5
Это уравнение не является линейным уравнением, так как старшая степень, в которой стоит переменная x равна двум.
Это уравнение выглядит линейным на первый взгляд, но после раскрытия скобок старшая степень становится равна двум:
x 2 + 3 x − 8 = x − 1
Это уравнение не является линейным уравнением.
Особые случаи (в 4 задании ОГЭ они не встречались, но знать их полезно)
- 2 x − 4 = 2 ( x − 2 )
Это линейное уравнение. Раскроем скобки, перенесем иксы влево, числа вправо:
2 x − 2 x = − 4 + 4
И как же здесь искать x , если его нет? После выполнения преобразований мы получили верное равенство (тождество), которое не зависит от значения переменной x . Какое бы значение x мы ни подставляли бы в исходное уравнение, в результате всегда получается верное равенство (тождество). Значит x может быть любым числом. Запишем ответ к данном линейному уравнению.
Это линейное уравнение. Раскроем скобки, перенесем иксы влево, числа вправо:
2 x − 4 = 2 x − 16
2 x − 2 x = − 16 + 4
В результате преобразований x сократился, но в итоге получилось неверное равенство, так как . Какое бы значение x мы ни подставляли бы в исходное уравнение, в результате всегда будет неверное равенство. А это означает, что нет таких значений x , при которых равенство становилось бы верным. Запишем ответ к данному линейному уравнению.
Квадратные уравнения
Квадратное уравнение – уравнение вида a x 2 + b x + c = 0, где x – переменная, a , b и c – некоторые числа, причем a ≠ 0 .
Алгоритм решения квадратного уравнения:
- Раскрыть скобки, перенести все слагаемые в левую часть, чтобы уравнение приобрело вид: a x 2 + b x + c = 0
- Выписать, чему равны в числах коэффициенты: a = … b = … c = …
- Вычислить дискриминант по формуле: D = b 2 − 4 a c
- Если D > 0 , будет два различных корня, которые находятся по формуле: x 1,2 = − b ± D 2 a
- Если D = 0, будет один корень, который находится по формуле: x = − b 2 a
- Если D 0, решений нет: x ∈ ∅
Примеры решения квадратного уравнения:
- − x 2 + 6 x + 7 = 0
a = − 1, b = 6, c = 7
D = b 2 − 4 a c = 6 2 − 4 ⋅ ( − 1 ) ⋅ 7 = 36 + 28 = 64
D > 0 – будет два различных корня:
x 1,2 = − b ± D 2 a = − 6 ± 64 2 ⋅ ( − 1 ) = − 6 ± 8 − 2 = [ − 6 + 8 − 2 = 2 − 2 = − 1 − 6 − 8 − 2 = − 14 − 2 = 7
Ответ: x 1 = − 1, x 2 = 7
a = − 1, b = 4, c = − 4
D = b 2 − 4 a c = 4 2 − 4 ⋅ ( − 1 ) ⋅ ( − 4 ) = 16 − 16 = 0
D = 0 – будет один корень:
x = − b 2 a = − 4 2 ⋅ ( − 1 ) = − 4 − 2 = 2
a = 2, b = − 7, c = 10
D = b 2 − 4 a c = ( − 7 ) 2 − 4 ⋅ 2 ⋅ 10 = 49 − 80 = − 31
D 0 – решений нет.
Также существуют неполные квадратные уравнения (это квадратные уравнения, у которых либо b = 0, либо с = 0, либо b = с = 0 ). Смотрите видео, как решать такие квадратные уравнения!
Разложение квадратного трехчлена на множители
Квадратный трехчлен можно разложить на множители следующим образом:
a x 2 + b x + c = a ⋅ ( x − x 1 ) ⋅ ( x − x 2 )
где a – число, коэффициент перед старшим коэффициентом,
x – переменная (то есть буква),
x 1 и x 2 – числа, корни квадратного уравнения a x 2 + b x + c = 0 , которые найдены через дискриминант.
Если квадратное уравнение имеет только один корень , то разложение выглядит так:
a x 2 + b x + c = a ⋅ ( x − x 0 ) 2
Примеры разложения квадратного трехчлена на множители:
- − x 2 + 6 x + 7 = 0 ⇒ x 1 = − 1, x 2 = 7
− x 2 + 6 x + 7 = ( − 1 ) ⋅ ( x − ( − 1 ) ) ( x − 7 ) = − ( x + 1 ) ( x − 7 ) = ( x + 1 ) ( 7 − x )
- − x 2 + 4 x − 4 = 0 ; ⇒ x 0 = 2
− x 2 + 4 x − 4 = ( − 1 ) ⋅ ( x − 2 ) 2 = − ( x − 2 ) 2
Если квадратный трехчлен является неполным, ( ( b = 0 или c = 0 ) то его можно разложить на множители следующими способами:
- c = 0 ⇒ a x 2 + b x = x ( a x + b )
- b = 0 ⇒ применить формулу сокращенного умножения для разности квадратов.
Дробно рациональные уравнения
Пусть f ( x ) и g ( x ) – некоторые функции, зависящие от переменной x .
Дробно рациональное уравнение – это уравнение вида f ( x ) g ( x ) = 0 .
Для того, чтобы решить дробно рациональное уравнение, надо вспомнить, что такое ОДЗ и когда оно возникает.
ОДЗ – область допустимых значений переменной.
В выражении вида f ( x ) g ( x ) = 0
ОДЗ: g ( x ) ≠ 0 (знаменатель дроби не может быть равен нулю).
Алгоритм решения дробно рационального уравнения:
- Привести выражение к виду f ( x ) g ( x ) = 0 .
- Выписать ОДЗ: g ( x ) ≠ 0.
- Приравнять числитель дроби к нулю f ( x ) = 0 и найти корни.
- Указать в ответе корни из числителя, исключив те корни, которые попали в ОДЗ.
Пример решения дробного рационального уравнения:
Решить дробно рациональное уравнение x 2 − 4 2 − x = 1.
Решение:
Будем действовать в соответствии с алгоритмом.
- Привести выражение к виду f ( x ) g ( x ) = 0 .
Переносим единичку в левую часть, записываем к ней дополнительный множитель, чтобы привести оба слагаемых к одному общему знаменателю:
x 2 − 4 2 − x − 1 2 − x = 0
x 2 − 4 2 − x − 2 − x 2 − x = 0
x 2 − 4 − ( 2 − x ) 2 − x = 0
x 2 − 4 − 2 + x 2 − x = 0
x 2 + x − 6 2 − x = 0
Первый шаг алгоритма выполнен успешно.
Обводим в рамочку ОДЗ, не забываем про него: x ≠ 2
- Приравнять числитель дроби к нулю f ( x ) = 0 и найти корни:
x 2 + x − 6 = 0 – Квадратное уравнение. Решаем через дискриминант.
a = 1, b = 1, c = − 6
D = b 2 − 4 a c = 1 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 1 + 24 = 25
D > 0 – будет два различных корня.
x 1,2 = − b ± D 2 a = − 1 ± 25 2 ⋅ 1 = − 1 ± 5 2 = [ − 1 + 5 2 = 4 2 = 2 − 1 − 5 2 = − 6 2 = − 3
- Указать в ответе корни из числителя, исключив те корни, которые попали в ОДЗ.
Корни, полученные на предыдущем шаге:
Значит, в ответ идет только один корень, x = − 3.
Системы уравнений
Системой уравнений называют два уравнения с двумя неизвестными (как правило, неизвестные обозначаются x и y ) , которые объединены в общую систему фигурной скобкой.
Пример системы уравнений
Решить систему уравнений – найти пару чисел x и y , которые при подстановке в систему уравнений образуют верное равенство в обоих уравнениях системы.
Существует два метода решений систем линейных уравнений:
- Метод подстановки.
- Метод сложения.
Алгоритм решения системы уравнений методом подстановки:
- Выразить из любого уравнения одну переменную через другую.
- Подставить в другое уравнение вместо выраженной переменной полученное значение.
- Решить уравнение с одной неизвестной.
- Найти оставшуюся неизвестную.
Решить систему уравнений методом подстановки
Решение:
- Выразить из любого уравнения одну переменную через другую.
- Подставить в другое уравнение вместо выраженной переменной полученное значение.
- Решить уравнение с одной неизвестной.
3 ( 8 − 2 y ) − y = − 4
y = − 28 − 7 = 28 7 = 4
- Найти оставшуюся неизвестную.
x = 8 − 2 y = 8 − 2 ⋅ 4 = 8 − 8 = 0
Ответ можно записать одним из трех способов:
Решение системы уравнений методом сложения.
Метод сложения основывается на следующем свойстве:
Идея метода сложения состоит в том, чтобы избавиться от одной из переменных, сложив уравнения.
Решить систему уравнений методом сложения
Давайте избавимся в данном примере от переменной x . Суть метода состоит в том, чтобы в первом и во втором уравнении перед переменной x стояли противоположные коэффициенты. Во втором уравнении перед x стоит коэффициент 3 . Для того, чтобы метод сложения сработал, надо чтобы перед переменной x оказался коэффициент ( − 3 ) . Для этого домножим левую и правую часть первого уравнения на ( − 3 ) .
Теперь, когда перед переменной в обоих уравнениях стоят противоположные коэффициенты, при сложении левых частей уравнений переменная x исчезнет.
( − 3 x − 6 y ) + ( 3 x − y ) = ( − 24 ) + ( − 4 )
− 3 x − 6 y + 3 x − y = − 24 − 4
y = − 28 − 7 = 28 7 = 4
Осталось найти переменную x . Для этого подставим y = 4 в любое из двух уравнений системы. Например, в первое.
Ответ можно записать одним из трех способов:
Задание №9 из ОГЭ 2020. Типовые задачи и принцип их решения.
Урок алгебры в 9 классе на тему “Решение уравнений, подготовка к ОГЭ”
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Алгебра 9 класс.
Тема: Подготовка к ОГЭ. Решение уравнений.
Образовательные: отработать применение способов решения уравнений;
продолжить работу по совершенствованию практических навыков и вычислительной культуры при выполнении тренировочных заданий ОГЭ.
Развивающие: развитие логического мышления, памяти, внимания; развитие общеучебных умений, умения сравнивать и обобщать.
Воспитательные: воспитание трудолюбия, взаимопомощи, математической культуры.
Тип урока: совершенствование знаний, умений и навыков.
Оборудование: интерактивная доска, компьютер, проектор, дидактический материал, презентация.
«Математику нельзя изучать, наблюдая, как это делает сосед» Л. Нивен.
1. Организационный момент. (3 мин)
2. Повторение (фронтальный опрос).(7 мин)
Ответить на вопросы:
– сколько модулей в тесте ОГЭ? Какие это модули?
– сколько баллов нужно набрать для успешного прохождения экзамена?
– какие задания в тесте расположены под номерами 4, 8, 21? (уравнения, системы уравнений)
уравнением называется …. (Математическое равенство с одной или несколькими неизвестными величинами).
Корнем уравнения называется……. (такое значение переменной, при котором уравнение превращается в верное равенство.)
Решить устно (слайд 1):
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5)  ;
;
6)  ;
;
7)  .
.
3. Актуализация знаний.(12 мин)
Повторим коротко виды уравнений и способы их решения (слайд 2):
Алгоритмы решения уравнений














 ,
,



Решить у доски (слайд 3):
1)  ;
;
2)  ;
;
3)  .
.
Какие уравнения называются дробно-рациональными? Какой алгоритм решения таких уравнений? (1. Находим ОДЗ; 2. Приводим к общему знаменателю; 3. Решаем уравнение в числителе.)
4)  ;
;
5) .
.
4. Физкультминутка для глаз(слайд 4). (2 мин)

5. Работа в группах(слайд 5). (15 мин)
Разноуровневые задания. В группе необходимо решить не менее одного уравнения каждого вида.
Линейные: 1)  ;
;
2)  ;
;
3)  .
.
Квадратные: 1)  ;
;
2)  ;
;
3)  .
.
Дробно-рациональные: 1)  ;
;
2)  ;
;
3)  .
.
6. Отчет о работе каждой группы. Оценивание учащихся командирами групп (фронтально).
7. Рефлексия.(2 мин)
Каждый учащийся наклеивает на свою самостоятельную работу стикер одного из цветов:
Красный – «я не понял эту тему»
Желтый – «нужно решить еще несколько примеров»
Зеленый – «я понял эту тему».
8. Домашнее задание.
Тест №34 («математика 9 класс ГИА 2015» под редакцией Д.А. Мальцева)
1) «Алгебра» 9 класс под ред. А.Г. Мордковича;
2) «Математика» 9 класс ГИА 2015 под ред. Д.А.Мальцева;
3) «ГИА математика» под ред. И.В. Третьяка;
4) материалы сайта alexlarin . net , mathgia . ru .
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 932 человека из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 682 человека из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 308 человек из 69 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»
Свидетельство и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 575 969 материалов в базе
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Другие материалы
- 25.09.2015
- 1516
- 0
- 25.09.2015
- 559
- 0
- 25.09.2015
- 414
- 0
- 25.09.2015
- 1283
- 0
- 25.09.2015
- 561
- 2
- 25.09.2015
- 497
- 0
- 25.09.2015
- 494
- 0
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 25.09.2015 7630
- DOCX 68.7 кбайт
- 3 скачивания
- Рейтинг: 4 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Дубовская Александра Анатольевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала

- На сайте: 7 лет и 5 месяцев
- Подписчики: 0
- Всего просмотров: 9876
- Всего материалов: 3
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Объявлен конкурс дизайн-проектов для школьных пространств
Время чтения: 2 минуты
Тринадцатилетняя школьница из Индии разработала приложение против буллинга
Время чтения: 1 минута
Приемная кампания в вузах начнется 20 июня
Время чтения: 1 минута
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
Профессия педагога на третьем месте по популярности среди абитуриентов
Время чтения: 1 минута
Минпросвещения подключит студотряды к обновлению школьной инфраструктуры
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
[spoiler title=”источники:”]
http://infourok.ru/urok-algebri-v-klasse-na-temu-reshenie-uravneniy-podgotovka-k-oge-434952.html
[/spoiler]
Для решения данного номера ученику потребуется знание и умение работать с:
1. Линейными уравнениями. Напомним, что целью преобразований линейного уравнения является получение выражения “неизвестная = число”.
2. Квадратными уравнениями. Напомним, что квадратным называется уравнение вида ах2+bx+c=0, корни уравнения находим по формуле
x1,2 =(-b+-(D)1//2) / 2a, где a, b, c –коэффициенты, D=b2-4ac – дискриминант.
Корни квадратного уравнения можно вычислить и по теореме Виета. Кому что нравится, на вкус и на цвет – товарища нет!Рассмотрим характерные примеры.
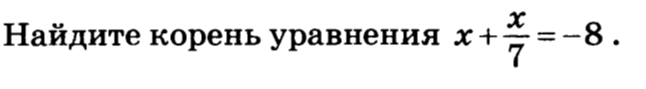
Решение:
1. Данное уравнение линейное, имеет один корень. Найдем его.
2. Избавимся от 7 в знаменателе. Для этого левую и правую части уравнения умножим на 7. Имеем, 7х+х=-8*7 или 8х=-56
3. х=-7
Ответ: -7.
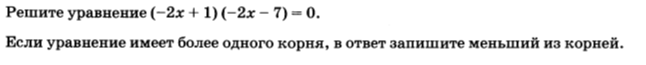
Решение:
1. Преобразуем данное уравнение к стандартной записи квадратного уравнения, для этого перемножим два многочлена. Имеем
4x2+14x-2x-7=0 или 4x2+12x-7=0
2. Дальше решаем по известным формулам
D=122-4*4*(-7)=144+112=256 дискриминант больше нуля, имеем 2 корня.
3. x1=(-12+16)/2*4=4/8=1/2=0,5 x2==(-12-16)/2*4=28/8=3,5
4. Выбираем меньший из корней 0,5.
Ответ: 0,5.

Решение:
1. Данное уравнение не надо преобразовывать, поэтому корни уравнения находим по известным формулам.
2. D=(-15)2-4*4*9=225-144=81
3. x1 =(-(-15)+9)/2*4=24/8=3 x2==(-(-15)-9)/2*4=6/8=3/4=0,75
4. Выбираем меньший из корней 0,75.
Ответ: 0,75.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Джамиля Агишева
При выполнении задания 9 ОГЭ по математике необходимо:
уметь решать линейные и квадратные уравнения, системы уравнений и неравенств.
Пример 1. Решите уравнение .
Решение. Уравнение линейное. Раскрываем скобки, приводим подобные слагаемые, все «иксы» переносим в левую часть равенства, всё без «иксов» – вправо:
Ответ: – 2.
Пример 2. Решите уравнение . Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Решение. Уравнение является квадратным ,
,
. Вычисляем дискриминант и корни:
Ответ: .
Пример 3. Решите уравнение . Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Решение. В левой части данного уравнения произведение двух множителей-скобок, и это произведение равно нулю. Это возможно тогда и только тогда, когда хотя бы один из множителей равен нулю. Значит, получаем два уравнения:

Тогда меньший из корней уравнения равен -0,75.
Ответ: -0,75.
Пример 4. Решите систему уравнений
В ответе запишите значение .
Решение. Используем метод подстановки: из второго уравнения можно выразить y и подставить в первое уравнение.
Таким образом, .
Пример 5. На рисунке изображены графики функций и
. Вычислите ординату точки B.

Решение. Для нахождения координат точек пересечения графиков заданных функций необходимо решить систему уравнений.
Найдём корни первого уравнения системы.
̶ абсцисса точка B.
Тогда ордината точки В:
Ответ: -5.
Пример 6. Найдите наибольшее значение x, удовлетворяющее системе неравенств:
Решение. Выразим из каждого неравенства переменную x. Не забываем, что при делении обеих частей неравенства на положительное число знак неравенства не меняется, при делении на отрицательное число ̶ знак неравенства меняется на противоположный.
Используем числовую прямую. Решение первого неравенства отметим штриховкой («ёлочкой») с наклоном вправо, второго неравенства ̶ штриховкой с наклоном влево. При этом точка -2 будет «закрашенной», т.к. знак первого неравенства нестрогий, а точка -5,5 будет «выколотой», т.к. знак второго неравенства строгий.

Решением системы неравенств является тот промежуток, на котором пересеклись две «ёлочки», то есть две штриховки. Это промежуток . «Выколотой» точке соответствует круглая скобка, «закрашенной» ̶ квадратная.
Ответим на вопрос задачи. Наибольшее значение
Ответ: .
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 9 ОГЭ по математике. Уравнения, неравенства, системы уравнений и неравенств» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
07.05.2023
Каталог заданий.
Уравнения
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 20 № 311546 

i
Один из корней уравнения равен −1. Найдите второй корень.
Аналоги к заданию № 311546: 311552 Все
Источник: ГИА-2013. Математика. Диагностическая работа № 1. (вар. 1) 02.10.2012г.
Решение
·
Критерии
·
Помощь
2
Тип 20 № 311587 

i
Решите уравнение:
Аналоги к заданию № 311587: 311857 316240 316267 … Все
Источник: ГИА-2012. Математика. Диагностическая работа № 1 (1 вар)
Решение
·
Критерии
·
Помощь
3
Тип 20 № 311589 

i
Решите уравнение:
Аналоги к заданию № 311589: 311586 311594 311595 … Все
Источник: ГИА-2012. Математика. Диагностическая работа № 1 (3вар)
Решение
·
Критерии
·
Помощь
4
Тип 20 № 311591 

i
Решите уравнение:
Источник: ГИА-2012. Математика. Диагностическая работа №1 (4 вар)
Решение
·
Критерии
·
Помощь
5
Тип 20 № 311618 

i
Решите уравнение
Аналоги к заданию № 311618: 338137 338228 338236 … Все
Источник: ГИА-2012. Математика. Диагностическая работа №2 (9 вар.)
Решение
·
Критерии
·
Помощь
Пройти тестирование по этим заданиям
