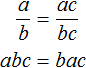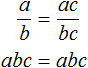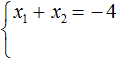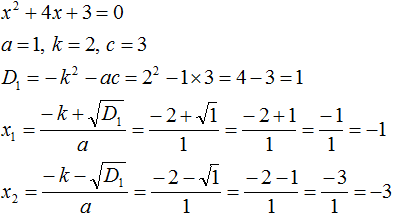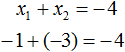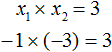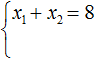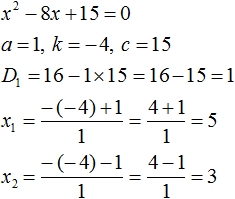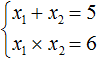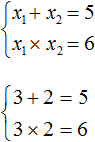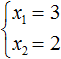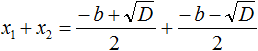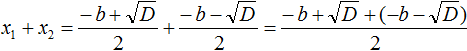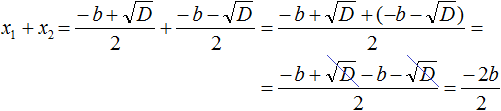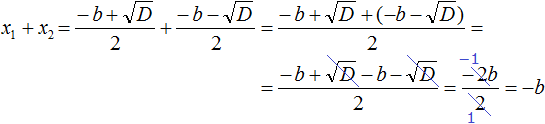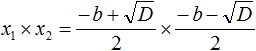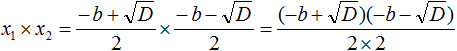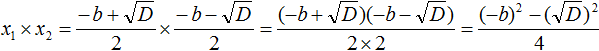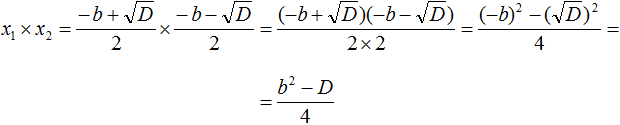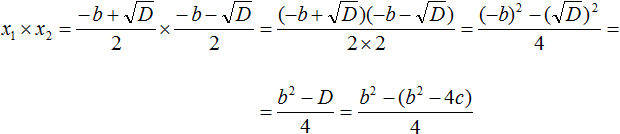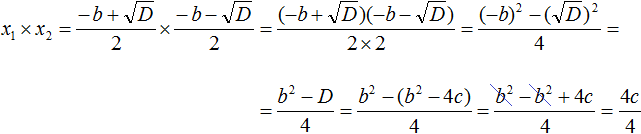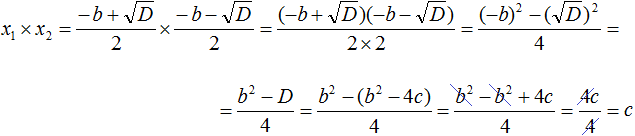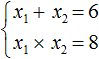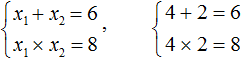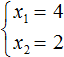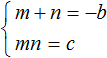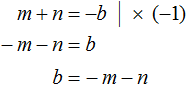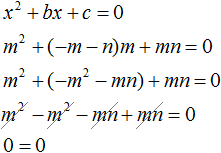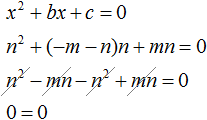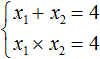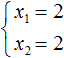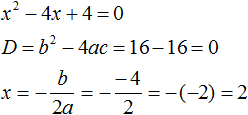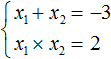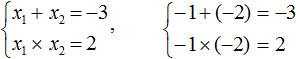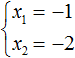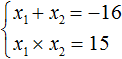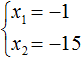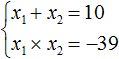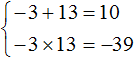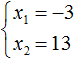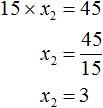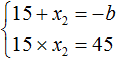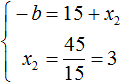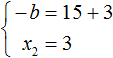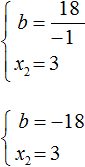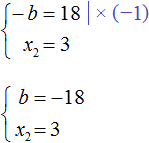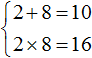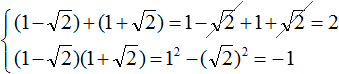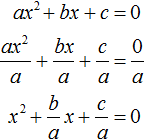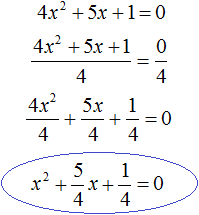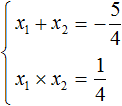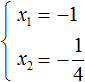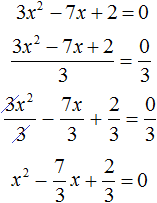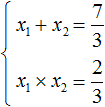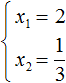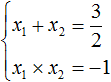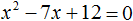Как найти корень уравнения через теорему виета - Сайт, где вы сможете решить свои вопросы

После того, как вы внимательно изучите, как решать квадратные уравнения обычным образом с помощью
формулы для корней
можно рассмотреть другой способ решения квадратных уравнений — с помощью теоремы Виета.

Перед тем, как изучить теорему Виета, хорошо потренируйтесь в
определении коэффициентов
«a», «b» и «с» в квадратных уравнениях.
Без этого вам будет трудно применить теорему Виета.

Когда можно применить теорему Виета

Не ко всем квадратным уравнениям имеет смысл использовать эту теорему.
Применять теорему Виета имеет смысл только к приведённым квадратным уравнениям.

Запомните!

Приведенное квадратное уравнение — это уравнение, в котором старший
коэффициент «a = 1».
В общем виде приведенное квадратное уравнение выглядит следующим образом:

x² + px + q = 0

Обратите внимание, что разница с обычным общим видом
квадратного уравнения «ax² + bx + c = 0» в том, что в
приведённом уравнении «x² + px + q = 0» коэффициент
«а = 1».

Если сравнить приведенное квадратное уравнение «x² + px + q = 0» с обычным общим видом квадратного
уравнения «ax² + bx + c = 0», то становится видно,
что
«p = b», а «q = c».

Теперь давайте на примерах разберем, к каким уравнениям можно применять теорему Виета, а где это не целесообразно.

Уравнение	Коэффициенты	Вывод
x² − 7x + 1 = 0	a = 1 p = −7 q = 1	Так как «a = 1» можно использовать теорему Виета.
3x² − 1 + x = 0 Приведем уравнение к общему виду: 3x² + x − 1 = 0	a = 3 p = 1 q = −1	Так как «a = 3» не следует использовать теорему Виета.
−x² = −3 + 2x Приведем уравнение к общему виду: −x² + 3 − 2x = 0 −x² − 2x + 3 = 0	a = −1 p = −2 q = 3	Так как «a = −1» не следует использовать теорему Виета.

Уравнение

Коэффициенты

Вывод

x² − 7x + 1 = 0

a = 1
p = −7
q = 1

Так как «a = 1» можно использовать теорему Виета.

3x² − 1 + x = 0

Приведем уравнение к общему виду:

3x² + x − 1 = 0

a = 3
p = 1
q = −1

Так как «a = 3» не следует использовать теорему Виета.

−x² = −3 + 2x

Приведем уравнение к общему виду:

−x² + 3 − 2x = 0
−x² − 2x + 3 = 0

a = −1
p = −2
q = 3

Так как «a = −1» не следует использовать теорему Виета.

Как использовать теорему Виета

Теперь мы готовы перейти к самому методу Виета для решения квадратных уравнений.

Запомните!

Теорема Виета для приведённых квадратных уравнений «x² + px + q = 0» гласит
что справедливо следующее:

, где «x₁» и «x₂» — корни этого уравнения.

Чтобы было проще запомнить формулу Виета, следует запомнить:
«Коэффициент «p» —
значит плохой, поэтому он берется со знаком минус».

Рассмотрим пример.

x² + 4x − 5 = 0

Так как в этом уравнении «a = 1», квадратное уравнение
считается приведённым, значит, можно
использовать метод Виета.
Выпишем коэффициенты «p» и «q».

p = 4
q = −5

Запишем теорему Виета для квадратного уравнения.

	x₁ + x₂ = −4
x₁ · x₂ = −5

Методом подбора мы приходим к тому, что корни уравнения
«x₁ = −5» и «x₂ = 1». Запишем ответ.

Ответ: x₁ = −5; x₂ = 1

Рассмотрим другой пример.

x² + x − 6 = 0

Старший коэффициент «a = 1» поэтому можно применять теорему Виета.

	x₁ + x₂ = −1
x₁ · x₂ = −6

Методом подбора получим, что корни уравнения
«x₁ = −3» и «x₂ = 2». Запишем ответ.

Ответ: x₁ = −3; x₂ = 2

Важно!

Если у вас не получается решить уравнение с помощью теоремы Виета, не отчаивайтесь.
Вы всегда можете решить любое квадратное уравнение, используя
формулу для нахождения корней.

Деление уравнение на первый коэффициент

Рассмотрим уравнение, которое по заданию требуется решить, используя теорему Виета.

2x² − 16x − 18 = 0

Сейчас в уравнении «a = 2»,
поэтому перед тем, как использовать теорему Виета нужно сделать так, чтобы «a = 1».

Для этого достаточно разделить все уравнение на «2».
Таким образом, мы сделаем квадратное уравнение приведённым.

2x² − 16x − 18 = 0 | (:2)
2x²(:2) − 16x(:2) − 18(:2) = 0
x² − 8x − 9 = 0

Теперь «a = 1» и можно смело записывать формулу Виета и находить корни методом подбора.

	x₁ + x₂ = −(−8)
x₁ · x₂ = −9

Методом подбора получим, что корни уравнения
«x₁ = 9» и «x₂ = −1». Запишем ответ.

Ответ: x₁ = 9; x₂ = −1

Бывают задачи, где требуется найти не только корни уравнения, но и коэффициенты самого уравнения. Например, как в такой задаче.

Корни «x₁» и
«x₂» квадратного уравнения
«x² + px + 3 = 0» удовлетворяют
условию «x₂ = 3x₁».
Найти «p», «x₁»,
«x₂».

Запишем теорему Виета для этого уравнения.

По условию дано, что
«x₂ = 3x₁».
Подставим это выражение в систему вместо «x₂».

	x₁ + 3x₁ = −p
x₁ · 3x₁ = 3

Решим полученное квадратное уравнение «x₁² = 1»
методом подбора и найдем «x₁».

x₁² = 1

(Первый корень) x₁ = 1
(Второй корень) x₁ = −1

Мы получили два значения «x₁».
Для каждого из полученных значений найдем «p» и запишем все полученные результаты в ответ.

(Первый корень) x₁ = 1

Найдем
«x₂»

x₁ · x₂ = 3
1 · x₂ = 3
x₂ = 3

Найдем «p»

x₁ + x₂ = −p
1 + 3 = −p
4 = −p
p = −4;
(Второй корень) x₁ = −1

Найдем «x₂»

x₁ · x₂ = 3
−1 · x₂ = 3
−x₂ = 3 | ·(−1)
x₂ = −3

Найдем «p»

x₁ + x₂ = −p
−1 + −3 = −p
−4 = −p
p = 4

Ответ: (x₁ = 1; x₂ = 3; p = −4) и
(x₁ = −1; x₂ = −3; p = 4)

Теорема Виета в общем виде

В школьном курсе математики теорему Виета используют только для приведённых уравнений,
где старший коэффициент «a = 1», но, на самом деле, теорему Виета можно применить к любому квадратному уравнению.

В общем виде теорема Виета для квадратного уравнения выглядит так:

Убедимся в правильности этой теоремы на примере. Рассмотрим неприведённое квадратное уравнение.

3x² + 3x − 18 = 0

Используем для него теорему Виета в общем виде.

	x₁ + x₂ = −1
x₁ · x₂ = −6

Методом подбора получим, что корни уравнения
«x₁ = −3» и «x₂ = 2». Запишем ответ.

Ответ: x₁ = −3; x₂ = 2

В заданиях школьной математики мы не рекомендуем использовать теорему Виета в общем виде.

Другими словами, реальную пользу теорема Виета приносит только для приведённых квадратных уравнений, в
которых «a = 1».
Именно в таких случаях она не усложняет жизнь, а позволят без дополнительных расчетов быстро найти корни.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

Источник

Что называют теоремой?

Если человек обнаружил в математике какую-нибудь закономерность, позволяющую быстро решить ту или иную задачу, то ему не следует говорить о том, что он сделал открытие. Потому что может случиться так, что эта закономерность работает только для определённых случаев, а для других не работает или вовсе решает задачу неправильно.

Чтобы поделиться своим открытием с другими людьми, найденную закономерность следует сформулировать в виде утверждения, а затем доказать это утверждение, приводя неоспоримые факты.

Сформулированное утверждение называют теоремой. А доказательство теоремы состоит из фактов, логических рассуждений и вычислений, которые не оспариваются.

Например, теоремой можно назвать следующее утверждение:

«Если числитель и знаменатель обыкновенной дроби умнóжить на какое-нибудь число, то значение данной дроби не измéнится».

А затем привести такое доказательство:

Пусть, имеется дробь . Умнóжим числитель и знаменатель этой дроби на число с. Тогда полýчится дробь . Докáжем, что дроби и равны. То есть докажем, что равенство является верным.

Для доказательства этого равенства воспользуемся основным свойством пропорции:

От перестановки мест сомножителей произведение не меняется. Поэтому в получившемся равенстве можно упорядочить правую часть по алфавиту:

Поскольку равенство является пропорцией, а пропорция это равенство двух отношений, то дроби и равны. Теорема доказана.

Теорема Виета

Французский математик Франсуа Виет выявил интересную взаимосвязь между коэффициентами приведённого квадратного уравнения и корнями этого же уравнения. Эта взаимосвязь представлена в виде теоремы и формулируется так:

Сумма корней приведённого квадратного уравнения x²+ bx + c = 0 равна второму коэффициенту, взятому с противоположным знáком, а произведение корней равно свободному члену.

То есть, если имеется приведённое квадратное уравнение x²+ bx + c = 0, а его корнями являются числа x₁ и x₂, то справедливы следующие два равенства:

Знак системы (фигурная скобка) говорит о том, что значения x₁ и x₂удовлетворяют обоим равенствам.

Покажем теорему Виета на примере приведённого квадратного уравнения x²+ 4x + 3 = 0.

Мы пока не знаем какие корни имеет уравнение x²+ 4x + 3 = 0. Но по теореме Виета можно записать, что сумма этих корней равна второму коэффициенту 4, взятому с противоположным знáком. Если коэффициент 4 взять с противоположным знáком, то получим −4. Тогда:

А произведение корней по теореме Виета будет равно свободному члену. В уравнении x²+ 4x + 3 = 0 свободным членом является 3. Тогда:

Теперь проверим действительно ли сумма корней равна −4, и равно ли произведение 3. Для этого найдём корни уравнения x²+ 4x + 3 = 0. А для удобства воспользуемся формулами для чётного второго коэффициента:

Корнями уравнения являются числа −1 и −3. По теореме Виета их сумма должна была равняться второму коэффициенту уравнения x²+ 4x + 3 = 0, взятому с противоположным знаком. Действительно, так оно и есть. Вторым коэффициентов в уравнении x²+ 4x + 3 = 0 является 4. Если взять его с противоположным знаком и приравнять сумму корней x₁+ x₂ к этому коэффициенту, то получается верное равенство:

А произведение корней −1 и −3 по теореме Виета должно было равняться свободному члену уравнения x²+ 4x + 3 = 0, то есть числу 3. Видим, что это условие тоже выполняется:

Значит выражение 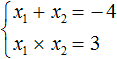является справедливым.

Рассмотрим квадратное уравнение x²− 8x + 15 = 0. По теореме Виета сумма корней этого уравнения равна второму коэффициенту, взятому с противоположным знаком. Второй коэффициент равен −8. Если взять его с противоположным знаком, то получим 8. Тогда:

А произведение корней равно свободному члену. В уравнении x²− 8x + 15 = 0 свободным членом является 15. Тогда:

Теперь проверим действительно ли сумма корней равна 8, и равно ли произведение 15. Для этого найдём корни данного уравнения. А для удобства воспользуемся формулами для чётного второго коэффициента. В этот раз пропустим нéкоторые подробные записи:

Видим, что корнями уравнения x²− 8x + 15 = 0 являются числа 5 и 3. Их сумма равна 8. То есть сумма корней равна второму коэффициенту уравнения x²− 8x + 15 = 0, взятому с противоположным знаком.

А произведение чисел 5 и 3 равно 15. То есть равно свободному члену уравнения x²− 8x + 15 = 0.

Значит выражение 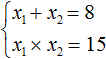является справедливым.

Замечание. Чтобы теорема Виета выполнялась, квадратное уравнение обязательно должно быть приведённым и иметь корни.

Например, рассмотрим квадратное уравнение x²− 2x + 4 = 0. Напишем сумму и произведение корней этого уравнения:

Но уравнение x²− 2x + 4 = 0 не имеет корней, сумма которых равна 2, а произведение которых равно 4. Убедиться в этом можно, вычислив дискриминант:

D₁ = k²− ac = (−1)²− 1 × 4 = −3

А значит записывать выражение 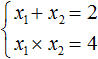не имеет смысла.

Теорема Виета полезна тем, что позволяет до начала решения узнать знаки корней уравнения.

Например, запишем для уравнения x²− 5x + 6 = 0 сумму и произведение его корней. Сумма корней равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:

Посмотрев на эти два равенства можно сразу понять, что оба корня должны быть положительными. Потому что произведение x₁× x₂= 6 будет выполняться только в двух случаях: если значения x₁ и x₂ положительны либо они оба отрицательны. Если эти значения будут отрицательными, то не будет выполняться равенство x₁+ x₂= 5, поскольку его правая часть равна положительному числу. А значения x₁ и x₂ должны удовлетворять как равенству x₁+ x₂= 5, так и равенству x₁× x₂= 6.

Ещё одна польза от теоремы Виета в том, что корни можно найти методом подбора. В данном примере корни должны быть такими, чтобы они удовлетворяли как равенству x₁+ x₂= 5 так и равенству x₁× x₂= 6. Очевидно, что таковыми являются корни 3 и 2

Значит, x₁= 3, x₂= 2

Доказательство теоремы Виета

Пусть дано приведённое квадратное уравнение x²+ bx + c = 0. Если его дискриминант больше нуля, то оно имеет два корня, сумма которых равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:

Докажем, что равенства x₁+ x₂= −b и x₁× x₂= c имеют место быть.

Вспомним формулы корней квадратного уравнения:

Найдём сумму корней x₁ и x₂. Для этого подставим в выражение x₁+ x₂ вместо x₁ и x₂ соответствующие выражения из правой части формул корней квадратного уравнения. Не забываем, что в приведённом квадратном уравнении x²+ bx + c = 0 старший коэффициент a равен единице. Тогда в процессе подстановки знаменатель станет равен просто 2

Запишем правую часть в виде дроби с одним знаменателем:

Раскроем скобки в числителе и приведём подобные члены:

Сократим дробь на 2, тогда получим −b

Значит x₁+ x₂ действительно равно −b

x₁+ x₂= −b

Теперь аналогично докажем, что произведение x₁× x₂ равно свободному члену c.

Подставим вместо x₁ и x₂ соответствующие выражения из формул корней квадратного уравнения. Не забываем, что коэффициент a всё ещё равен единице:

Чтобы перемнóжить дроби, нужно перемнóжить их числители и знаменатели:

В числителе теперь содержится произведение суммы двух выражений и разности этих же выражений. Воспользуемся тождеством (a + b)(a − b) = a²− b². Тогда в числителе полýчится А знаменатель будет равен 4

Теперь в числителе выражение (−b)² станет равно b², а выражение станет равно просто D

Но D равно b²− 4ac. Подстáвим это выражение вместо D, не забывая что a = 1. То есть вместо b²− 4ac надо подставить b²− 4c

В получившемся выражении раскроем скобки в числителе и приведём подобные члены:

Сократим получившуюся дробь на 4

Значит x₁× x₂ действительно равно c.

x₁× x₂= c

Таким образом, сумма корней приведённого квадратного уравнения x²+ bx + c = 0 равна второму коэффициенту, взятому с противоположным знáком (x₁+ x₂= −b), а произведение корней равно свободному члену (x₁× x₂= c). Теорема доказана.

Теорема, обратная теореме Виета

Когда записана сумма и произведение корней приведённого квадратного уравнения, обычно начинается подбор подходящих корней к этому уравнению. В этот момент в работу включается так называемая теорема, обратная теореме Виета. Она формулируется так:

Если числа x₁ и x₂ таковы, что их сумма равна второму коэффициенту уравнения x²+ bx + c = 0, взятому с противоположным знáком, а произведение чисел x₁ и x₂ равно свободному члену уравнения x²+ bx + c = 0, то числа x₁ и x₂ являются корнями уравнения x²+ bx + c = 0.

Обратные теоремы бывают поставлены так, что их утверждением является заключение первой теоремы.

Так, доказывая теорему Виета мы пришли к заключению, что сумма x₁ и x₂ равна −b, а произведение x₁ и x₂ равно c. В обратной же теореме это заключение служит утверждением.

Ранее мы решили уравнение x²− 5x + 6 = 0 и написали для него такую сумму и произведение корней:

А затем подобрали корни 3 и 2. По сути мы применили теорему, обратную теореме Виета. Числа 3 и 2 таковы, что их сумма равна второму коэффициенту уравнения x²− 5x + 6 = 0, взятому с противоположным знаком (числу 5), а произведение чисел 3 и 2 равно свободному члену (числу 6). Значит числа 3 и 2 являются корнями уравнения x²− 5x + 6 = 0.

Пример 2. Решить квадратное уравнение x²− 6x + 8 = 0 по теореме, обратной теореме Виета.

В данном уравнении a = 1. Значит квадратное уравнение является приведённым. Его можно решить по теореме, обратной теореме Виета.

Сначала запишем сумму и произведение корней уравнения. Сумма корней будет равна 6, поскольку второй коэффициент исходного уравнения равен −6. А произведение корней будет равно 8

Теперь имея эти два равенства можно подобрать подходящие корни. Они должны удовлетворять как равенству x₁+ x₂= 6, так и равенству x₁× x₂= 8

Подбор корней удобнее выполнять с помощью их произведения. Используя равенство x₁× x₂= 8 нужно найти такие x₁ и x₂, произведение которых равно 8.

Число 8 можно получить если перемножить числа 4 и 2 либо 1 и 8.

4 × 2 = 8
1 × 8 = 8

Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли не только равенству x₁× x₂= 8, но и равенству x₁+ x₂= 6.

Сразу делаем вывод, что значения 1 и 8 не годятся, поскольку они хоть и удовлетворяют равенству x₁× x₂= 8, но не удовлетворяют равенству x₁+ x₂= 6.

Зато значения 4 и 2 подходят как равенству x₁× x₂= 8, так и равенству x₁+ x₂= 6, поскольку эти значения удовлетворяют обоим равенствам:

Значит корнями уравнения x²− 6x + 8 = 0 являются числа 4 и 2.

Обратная теорема, как и любая теорема нуждается в доказательстве. Докажем теорему, обратную теореме Виета. Для удобства корни x₁ и x₂ обозначим как m и n. Тогда утверждение теоремы, обратной теореме Виета примет следующий вид:

Если числа m и n таковы, что их сумма равна второму коэффициенту уравнения x²+ bx + c = 0, взятому с противоположным знáком, а произведение чисел m и n равно свободному члену уравнения x²+ bx + c = 0, то числа m и n являются корнями уравнения x²+ bx + c = 0

Для начала запишем, что сумма m и n равна −b, а произведение mn равно c

Чтобы доказать, что числа m и n являются корнями уравнения x²+ bx + c = 0, нужно поочередно подстáвить буквы m и n в это уравнение вместо x, затем выполнить возможные тождественные преобразования. Если в результате преобразований левая часть станет равна нулю, то это будет означать, что числа m и n являются корнями уравнения x²+ bx + c = 0.

Помимо букв m и n нам нужно знать чему равен параметр b. Выразим его из равенства m + n = −b. Легче всего это сделать, умножив обе части этого равенства на −1

Теперь всё готово для подстановок. Подстáвим m в уравнение x²+ bx + c = 0 вместо x, а выражение −m − n подставим вместо b

Видим, что при x = m получается верное равенство. Значит число m является корнем уравнения x²+ bx + c = 0.

Аналогично докажем, что число n является корнем уравнения x²+ bx + c = 0. Подставим вместо x букву n, а вместо c подставим mn, поскольку c = mn.

Видим, что при x = n тоже получается верное равенство. Значит число n является корнем уравнения.

Следовательно, числа m и n являются корнями уравнения x²+ bx + c = 0.

Примеры решения уравнений по теореме, обратной теореме Виета

Пример 1. Решить квадратное уравнение x²− 4x + 4 = 0 по теореме, обратной теореме Виета.

Запишем сумму корней x₁ и x₂ и приравняем её к второму коэффициенту, взятому с противоположным знаком. Также запишем произведение корней x₁ и x₂ и приравняем его к свободному члену:

В данном примере очевидно, что корнями являются числа 2 и 2. Потому что их сумма равна 4 и произведение равно 4

Значение x₁ совпадает с x₂. Это тот случай, когда квадратное уравнение имеет только один корень. Если мы попробуем решить данное уравнение с помощью формул корней квадратного уравнения, то обнаружим что дискриминант равен нулю, и корень вычисляется по формуле

Данный пример показывает, что теорема обратная теореме Виета, работает и для уравнений, имеющих только один корень. Признаком того, что квадратное уравнение имеет только один корень является то, что значения x₁ и x₂ совпадают.

Пример 2. Решить уравнение x²+ 3x + 2 = 0 по теореме, обратной теореме Виета.

Запишем сумму и произведение корней данного уравнения:

Теперь подберём значения x₁ и x₂. Здесь начинается самое интересное. Произведение корней равно 2. Число 2 можно получить перемножив 1 и 2. Но сумма корней x₁+ x₂ равна отрицательному числу −3. Значит значения 1 и 2 не подходят.

Сумма бывает отрицательной если оба слагаемых отрицательны либо отрицательным является одно слагаемое, модуль которого больше.

Если подберём корни с разными знаками, то не будет выполняться равенство x₁× x₂= 2.

Если подберем положительные корни, то будет выполняться равенство x₁× x₂= 2, но не будет выполняться равенство x₁+ x₂= −3.

Очевидно, что корнями являются два отрицательных числа. Произведение отрицательных чисел есть положительное число. А сумма отрицательных чисел есть отрицательное число.

Тогда равенствам будут удовлетворять числа −1 и −2.

Итак, корнями являются числа −1 и −2

Пример 3. Решить уравнение x²+ 16x + 15 = 0 по теореме, обратной теореме Виета.

Запишем сумму и произведение корней данного уравнения:

Как и в прошлом примере сумма корней равна отрицательному числу, а произведение корней — положительному числу.

Произведение бывает положительным если оба сомножителя положительны либо оба сомножителя отрицательны. Первый вариант отпадает сразу, поскольку сумма корней равна отрицательному числу. Тогда получается, что оба корня будут отрицательными. Попробуем подобрать их.

Число 15 можно получить, если перемножить числа −1 и −15 или (−3) и (−5). В данном случае подходит первый вариант, поскольку сумма чисел −1 и −15 равна −16, а их произведение равно 15. Значит корнями уравнения x²+ 16x + 15 = 0 являются числа −1 и −15

Пример 4. Решить уравнение x²− 10x − 39 = 0 по теореме, обратной теореме Виета.

Запишем сумму и произведение корней данного уравнения:

Произведение корней равно отрицательному числу. Значит один из корней является отрицательным. Число −39 можно получить если перемножить числа −3 и 13 либо −13 и 3. Из этих комбинаций больше годится комбинация −3 и 13, поскольку при перемножении этих чисел получается −39, а при сложении 10

Значит корнями уравнения x²− 10x − 39 = 0 являются числа −3 и 13

Пример 5. Первый корень уравнения x²+ bx + 45 = 0 равен 15. Найти второй корень этого уравнения, а также значение коэффициента b.

По теореме Виета произведение корней приведённого квадратного уравнения равно свободному члену. В данном случае это произведение равно 45

x₁ × x₂ = 45

При этом один из корней уже известен — это корень 15.

15 × x₂ = 45

Тогда второй корень будет равен 3, потому что число 45 получается, если 15 умножить на 3

15 × 3 = 45

Значит x₂ = 3

Этот второй корень также можно было бы получить, выразив из равенства 15 × x₂ = 45 переменную x₂

Теперь определим значение коэффициента b. Для этого напишем сумму корней уравнения:

15 + 3 = 18

По теореме Виета сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком. Если сумма корней равна 18, а 18 это положительное число, то в самóм уравнении этот коэффициент будет отрицательным:

x²− 18x + 45 = 0

Значит b = −18.

Обычно решение к такой задаче записывают так. Сначала записывают основную теорему Виета в виде суммы и произведения корней:

Затем в это выражение подставляют имеющиеся известные значения. В нашем случае известно, что первый корень равен 15, а свободный член уравнения x²+ bx + 45 = 0 равен 45

Из этой системы следует найти x₂ и b. Выразим эти параметры:

Из этой системы мы видим, что x₂ равно 3. Подставим его в первое равенство:

Теперь из первого равенства мы видим, что −b равно 18

Но нас интересует b, а не −b. Следует помнить, что −b это −1b. Чтобы найти b нужно 18 разделить на −1. Тогда b станет равно −18

Этот же результат можно получить если в выражении 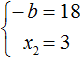умножить первое равенство на −1

Теперь возвращаемся к исходному уравнению x²+ bx + 45 = 0 и подставляем найденное значение b

Выполним умножение −18 на x. Получим −18x

Раскроем скобки:

Пример 6. Используя теорему Виета, написать приведённое квадратное уравнение, корнями которых являются числа 2 и 8.

В этом задании корни уже известны. То есть x₁= 2, x₂= 8. По ним надо составить квадратное уравнение вида x²+ bx + c = 0.

Запишем сумму и произведение корней:

По теореме Виета сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком. Если сумма корней 2 и 8 равна 10, то в самóм уравнении число 10 должно быть с противоположным знаком. Значит b = −10.

Произведение корней по теореме Виета равно свободному члену. У нас это произведение равно 16.

Значит b = −10, c = 16. Отсюда:

x²− 10x + 16 = 0

Пример 7. Используя теорему Виета, написать приведённое квадратное уравнение, корнями которых являются числа и .

Запишем сумму и произведение корней:

Сумма корней равна 2. Тогда в уравнении второй коэффициент будет равен −2. А произведение корней равно −1. Значит свободный член будет равен −1. Тогда:

x²− 2x − 1 = 0

Когда квадратное уравнение неприведённое

Теорема Виета выполняется только тогда, когда квадратное уравнение является приведённым.

Если квадратное уравнение не является приведённым, но всё равно возникла необходимость применить теорему Виета, то обе части неприведённого квадратного уравнения следует разделить на коэффициент, который располагается перед x².

Если к примеру в квадратном уравнении ax²+ bx + c = 0 коэффициент a не равен единице, то данное уравнение является неприведённым. Чтобы сделать его приведённым, надо разделить обе его части на коэффициент, который располагается перед x², то есть на a

Получилось уравнение , которое является приведённым. В нём второй коэффициент равен , а свободный член равен . Тогда сумма и произведение корней будут выглядеть так:

Например, решим квадратное уравнение 4x²+ 5x + 1 = 0. Это уравнение не является приведённым. Приведённым оно станет, если разделить обе его части на коэффициент, который располагается перед x², то есть на 4

Получили приведённое квадратное уравнение. В нём второй коэффициент равен , а свободный член . Тогда по теореме Виета имеем:

Отсюда методом подбора находим корни −1 и

Возможно этот метод вы редко будете использовать при решении квадратных уравнений. Но знать о нём не помешает.

Пример 2. Решить квадратное уравнение 3x²− 7x + 2 = 0

Данное уравнение не является приведённым, а значит его пока нельзя решить по теореме, обратной теореме Виета.

Сделаем данное уравнение приведенным. Разделим обе части на коэффициент, который располагается перед x²

Получили уравнение . Запишем сумму и произведение корней этого уравнения:

Отсюда методом подбора находим корни 2 и

Пример 3. Решить квадратное уравнение 2x²− 3x − 2 = 0

Это неприведённое квадратное уравнение. Чтобы сделать его приведённым, нужно разделить обе его части на 2. Сделать это можно в уме. Если 2x² разделить на 2, то полýчится x²

Далее если −3x разделить на 2, то полýчится . Чтобы видеть где коэффициент, а где переменная, такое выражение записывают в виде

Далее если −2 разделить на 2, то полýчится −1

Прирáвниваем получившееся выражение к нулю:

Теперь применяем теорему Виета. Сумма корней будет равна второму коэффициенту, взятому с противоположным знáком, а произведение корней свободному члену:

Отсюда методом подбора находим корни 2 и

Задания для самостоятельного решения

Задание 1. Написать сумму и произведение корней для квадратного уравнения:

Решение:

Задание 2. Написать сумму и произведение корней для квадратного уравнения:

Решение:

Задание 3. Написать сумму и произведение корней для квадратного уравнения:

Решение:

Задание 4. Решить квадратное уравнение по теореме, обратной теореме Виета:

Решение:

Задание 5. Решить квадратное уравнение по теореме, обратной теореме Виета:

Решение:

Задание 6. Решить квадратное уравнение по теореме, обратной теореме Виета:

Решение:

Задание 7. Решить квадратное уравнение по теореме, обратной теореме Виета:

Решение:

Задание 8. Решить квадратное уравнение по теореме, обратной теореме Виета:

Решение:

Задание 9. Решить квадратное уравнение по теореме, обратной теореме Виета:

Решение:

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Источник

В квадратных уравнениях существует целый ряд соотношений. Основными являются отношения между корнями и коэффициентами. Также в квадратных уравнениях работает ряд соотношений, которые задаются теоремой Виета.

В этой теме мы приведем саму теорему Виета и ее доказательство для квадратного уравнения, теорему, обратную теореме Виета, разберем ряд примеров решения задач. Особое внимание в материале мы уделим рассмотрению формул Виета, которые задают связь между действительными корнями алгебраического уравнения степени n и его коэффициентами.

Формулировка и доказательство теоремы Виета

Формула корней квадратного уравнения a·x2+b·x+c=0 вида x1=-b+D2·a, x2=-b-D2·a, где D=b2−4·a·c, устанавливает соотношения x1+x2=-ba, x1·x2=ca. Это подтверждает и теорема Виета.

Теорема 1

В квадратном уравнении a·x2+b·x+c=0, где x1 и x2 – корни, сумма корней будет равна соотношению коэффициентов b и a, которое было взято с противоположным знаком, а произведение корней будет равно отношению коэффициентов c и a, т. е. x1+x2=-ba, x1·x2=ca.

Доказательство 1

Предлагаем вам следующую схему проведения доказательства: возьмем формулу корней, составим суму и произведение корней квадратного уравнения и затем преобразуем полученные выражения для того, чтобы убедиться, что они равны -ba и ca соответственно.

Составим сумму корней x1+x2=-b+D2·a+-b-D2·a. Приведем дроби к общему знаменателю -b+D2·a+-b-D2·a=-b+D+-b-D2·a. Раскроем скобки в числителе полученной дроби и приведем подобные слагаемые: -b+D+-b-D2·a=-b+D-b-D2·a=-2·b2·a. Сократим дробь на: 2-ba=-ba.

Так мы доказали первое соотношение теоремы Виета, которое относится к сумме корней квадратного уравнения.

Теперь давайте перейдем ко второму соотношению.

Для этого нам необходимо составить произведение корней квадратного уравнения: x1·x2=-b+D2·a·-b-D2·a.

Вспомним правило умножения дробей и запишем последнее произведение следующим образом: -b+D·-b-D4·a2.

Проведем в числителе дроби умножение скобки на скобку или же воспользуемся формулой разности квадратов для того, чтобы преобразовать это произведение быстрее: -b+D·-b-D4·a2=-b2-D24·a2.

Воспользуемся определением квадратного корня для того, чтобы осуществить следующий переход: -b2-D24·a2=b2-D4·a2. Формула D=b2−4·a·c отвечает дискриминанту квадратного уравнения, следовательно, в дробь вместо D можно подставить b2−4·a·c:

b2-D4·a2=b2-(b2-4·a·c)4·a2

Раскроем скобки, приведем подобные слагаемые и получим: 4·a·c4·a2. Если сократить ее на 4·a, то остается ca. Так мы доказали второе соотношение теоремы Виета для произведения корней.

Запись доказательства теоремы Виета может иметь весьма лаконичный вид, если опустить пояснения:

x1+x2=-b+D2·a+-b-D2·a=-b+D+-b-D2·a=-2·b2·a=-ba,x1·x2=-b+D2·a·-b-D2·a=-b+D·-b-D4·a2=-b2-D24·a2=b2-D4·a2==D=b2-4·a·c=b2-b2-4·a·c4·a2=4·a·c4·a2=ca.

При дискриминанте квадратного уравнения равном нулю уравнение будет иметь только один корень. Чтобы иметь возможность применить к такому уравнению теорему Виета, мы можем предположить, что уравнение при дискриминанте, равном нулю, имеет два одинаковых корня. Действительно, при D=0 корень квадратного уравнения равен: -b2·a, тогда x1+x2=-b2·a+-b2·a=-b+(-b)2·a=-2·b2·a=-ba и x1·x2=-b2·a·-b2·a=-b·-b4·a2=b24·a2, а так как D=0, то есть, b2-4·a·c=0, откуда b2=4·a·c, то b24·a2=4·a·c4·a2=ca.

Чаще всего на практике теорема Виета применяется по отношению к приведенному квадратному уравнению вида x2+p·x+q=0, где старший коэффициент a равен 1. В связи с этим и формулируют теорему Виета именно для уравнений такого вида. Это не ограничивает общности в связи с тем, что любое квадратное уравнение может быть заменено равносильным уравнением. Для этого необходимо поделить обе его части на число a, отличное от нуля.

Приведем еще одну формулировку теоремы Виета.

Теорема 2

Сумма корней в приведенном квадратном уравнении x2+p·x+q=0 будет равна коэффициенту при x, который взят с противоположным знаком, произведение корней будет равно свободному члену, т.е. x1+x2=−p, x1·x2=q.

Теорема, обратная теореме Виета

Если внимательно посмотреть на вторую формулировку теоремы Виета, то можно увидеть, что для корней x1 и x2 приведенного квадратного уравнения x2+p·x+q=0 будут справедливы соотношения x1+x2=−p, x1·x2=q. Из этих соотношений x1+x2=−p, x1·x2=q следует, что x1 и x2 – это корни квадратного уравнения x2+p·x+q=0. Так мы приходим к утверждению, которое является обратным теореме Виета.

Предлагаем теперь оформить это утверждение как теорему и провести ее доказательство.

Теорема 3

Если числа x1 и x2 таковы, что x1+x2=−p и x1·x2=q, то x1 и x2 являются корнями приведенного квадратного уравнения x2+p·x+q=0.

Доказательство 2

Замена коэффициентов p и q на их выражение через x1 и x2 позволяет преобразовать уравнение x2+p·x+q=0 в равносильное ему x2−(x1+x2)·x+x1·x2=0.

Если в полученное уравнение подставить число x1 вместо x, то мы получим равенство x12−(x1+x2)·x1+x1·x2=0. Это равенство при любых x1 и x2 превращается в верное числовое равенство 0=0, так как x12−(x1+x2)·x1+x1·x2=x12−x12−x2·x1+x1·x2=0. Это значит, что x1 – корень уравнения x2−(x1+x2)·x+x1·x2=0, и что x1 также является корнем равносильного ему уравнения x2+p·x+q=0.

Подстановка в уравнение x2−(x1+x2)·x+x1·x2=0 числа x2вместо x позволяет получить равенство x22−(x1+x2)·x2+x1·x2=0. Это равенство можно считать верным, так как x22−(x1+x2)·x2+x1·x2=x22−x1·x2−x22+x1·x2=0. Получается, что x2 является корнем уравнения x2−(x1+x2)·x+x1·x2=0, а значит, и уравнения x2+p·x+q=0.

Теорема, обратная теореме Виета, доказана.

Примеры использования теоремы Виета

Давайте теперь приступим к разбору наиболее типичных примеров по теме. Начнем с разбора задач, которые требуют применения теоремы, обратной теореме Виета. Ее можно применять для проверки чисел, полученных в ходе вычислений, на предмет того, являются ли они корнями заданного квадратного уравнения. Для этого необходимо вычислить их сумму и разность, а затем проверить справедливость соотношений x1+x2=-ba, x1·x2=ac.

Выполнение обоих соотношений свидетельствует о том, что числа, полученные в ходе вычислений, являются корнями уравнения. Если же мы видим, что хотя бы одно из условий не выполняется, то данные числа не могут быть корнями квадратного уравнения, данного в условии задачи.

Пример 1

Какая из пар чисел 1) x1=−5, x2=3, или 2) x1=1-3, x2=3+3, или 3) x1=2+72, x2=2-72 является парой корней квадратного уравнения 4·x2−16·x+9=0?

Решение

Найдем коэффициенты квадратного уравнения 4·x2−16·x+9=0. Это a=4, b=−16, c=9. В соответствии с теоремой Виета сумма корней квадратного уравнения должна быть равна -ba, то есть, 164=4, а произведение корней должно быть равно ca, то есть, 94.

Проверим полученные числа, вычислив сумму и произведение чисел из трех заданных пар и сравнив их с полученными значениями.

В первом случае x1+x2=−5+3=−2. Это значение отлично от 4, следовательно, проверку можно не продолжать. Согласно теореме, обратной теореме Виета, можно сразу сделать вывод о том, что первая пара чисел не является корнями данного квадратного уравнения.

Во втором случае x1+x2=1-3+3+3=4. Мы видим, что первое условие выполняется. А вот второе условие нет: x1·x2=1-3·3+3=3+3-3·3-3=-2·3. Значение, которое мы получили, отлично от 94. Это значит, что вторая пара чисел не является корнями квадратного уравнения.

Перейдем к рассмотрению третьей пары. Здесь x1+x2=2+72+2-72=4 и x1·x2=2+72·2-72=22-722=4-74=164-74=94. Выполняются оба условия, а это значит, что x1 и x2 являются корнями заданного квадратного уравнения.

Ответ: x1=2+72, x2=2-72

Мы также можем использовать теорему, обратную теореме Виета, для подбора корней квадратного уравнения. Наиболее простой способ – это подбор целых корней приведенных квадратных уравнений с целыми коэффициентами. Можно рассматривать и другие варианты. Но это может существенно затруднить проведение вычислений.

Для подбора корней мы используем тот факт, что если сумма двух чисел равна второму коэффициенту квадратного уравнения, взятому со знаком минус, а произведение этих чисел равно свободному члену, то эти числа являются корнями данного квадратного уравнения.

Пример 2

В качестве примера используем квадратное уравнение x2−5·x+6=0. Числа x1 и x2 могут быть корнями этого уравнения в том случае, если выполняются два равенства x1+x2=5 и x1·x2=6. Подберем такие числа. Это числа 2 и 3, так как 2+3=5 и 2·3=6. Получается, что 2 и 3 – корни данного квадратного уравнения.

Теорему, обратную теореме Виета, можно использовать для нахождения второго корня, когда первый известен или очевиден. Для этого мы можем использовать соотношения x1+x2=-ba, x1·x2=ca.

Пример 3

Рассмотрим квадратное уравнение 512·x2−509·x−3=0. Необходимо найти корни данного уравнения.

Решение

Первым корнем уравнения является 1, так как сумма коэффициентов этого квадратного уравнения равна нулю. Получается, что x1=1.

Теперь найдем второй корень. Для этого можно использовать соотношение x1·x2=ca. Получается, что 1·x2=−3512, откуда x2=-3512.

Ответ: корни заданного в условии задачи квадратного уравнения 1 и -3512.

Подбирать корни, используя теорему, обратную теореме Виета, можно лишь в простых случаях. В остальных случаях лучше проводить поиск с использованием формулы корней квадратного уравнения через дискриминант.

Благодаря теореме, обратной теореме Виета, мы также можем составлять квадратные уравнения по имеющимся корням x1 и x2. Для этого нам необходимо вычислить сумму корней, которая дает коэффициент при x с противоположным знаком приведенного квадратного уравнения, и произведение корней, которое дает свободный член.

Пример 4

Напишите квадратное уравнение, корнями которого являются числа −11 и 23.

Решение

Примем, что x1=−11 и x2=23. Сумма и произведение данных чисел будут равны: x1+x2=12 и x1·x2=−253. Это значит, что второй коэффициент -12, свободный член −253.

Составляем уравнение: x2−12·x−253=0.

Ответ: x2−12·x−253=0.

Мы можем использовать теорему Виета для решения заданий, которые связаны со знаками корней квадратных уравнений. Связь между теоремой Виета связана со знаками корней приведенного квадратного уравнения x2+p·x+q=0 следующим образом:

если квадратное уравнение имеет действительные корни и если свободный член q является положительным числом, то эти корни будут иметь одинаковый знак «+» или «-»;
если квадратное уравнение имеет корни и если свободный член q является отрицательным числом, то один корень будет «+», а второй «-».

Оба этих утверждения являются следствием формулы x1·x2=q и правила умножения положительных и отрицательных чисел, а также чисел с разными знаками.

Пример 5

Являются ли корни квадратного уравнения x2−64·x−21=0 положительными?

Решение

По теореме Виета корни данного уравнения не могут быть оба положительными, так как для них должно выполняться равенство x1·x2=−21. Это невозможно при положительных x1 и x2.

Ответ: Нет

Пример 6

При каких значениях параметра r квадратное уравнение x2+(r+2)·x+r−1=0 будет иметь два действительных корня с разными знаками.

Решение

Начнем с того, что найдем значения каких r, при которых в уравнении будет два корня. Найдем дискриминант и посмотрим, при каких r он будет принимать положительные значения. D=(r+2)2−4·1·(r−1)=r2+4·r+4−4·r+4=r2+8. Значение выражения r2+8 положительно при любых действительных r, следовательно, дискриминант будет больше нуля при любых действительных r. Это значит, что исходное квадратное уравнение будет иметь два корня при любых действительных значениях параметра r.

Теперь посмотрим, когда корни будут иметь разные знаки. Это возможно в том случае, если их произведение будет отрицательным. Согласно теореме Виета произведение корней приведенного квадратного уравнения равно свободному члену. Значит, правильным решением будут те значения r, при которых свободный член r−1 отрицателен. Решим линейное неравенство r−1<0, получаем r<1.

Ответ: при r<1.

Формулы Виета

Существует ряд формул, которые применимы для осуществления действий с корнями и коэффициентами не только квадратных, но также кубических и других видов уравнений. Их называют формулами Виета.

Для алгебраического уравнения степени n вида a0·xn+a1·xn-1+…+an-1·x+an=0 считается, что уравнение имеет n действительных корней x1, x2, …, xn , среди которых могут быть совпадающие:
x1+x2+x3+…+xn=-a1a0,x1·x2+x1·x3+…+xn-1·xn=a2a0,x1·x2·x3+x1·x2·x4+…+xn-2·xn-1·xn=-a3a0,…x1·x2·x3·…·xn=(-1)n·ana0

Определение 1

Получить формулы Виета нам помогают:

теорема о разложении многочлена на линейные множители;
определение равных многочленов через равенство всех их соответствующих коэффициентов.

Так, многочлен a0·xn+a1·xn-1+…+an-1·x+an и его разложение на линейные множители вида a0·(x-x1)·(x-x2)·…·(x-xn) равны.

Если мы раскрываем скобки в последнем произведении и приравниваем соответствующие коэффициенты, то получаем формулы Виета. Приняв n=2, мы можем получить формулу Виета для квадратного уравнения: x1+x2=-a1a0, x1·x2=a2a0.

Определение 2

Формула Виета для кубического уравнения:
x1+x2+x3=-a1a0,x1·x2+x1·x3+x2·x3=a2a0,x1·x2·x3=-a3a0

Левая часть записи формул Виета содержит так называемые элементарные симметрические многочлены.

Источник

Теорема Виета помогает решать квадратные уравнения путём подбора. В этой статье даны определения, доказательства, формулы и примеры решений квадратных уравнений для чайников.

Что такое теорема Виета

Франсуа Виет (1540-1603 гг) – математика, создатель знаменитых формул Виета

Теорема Виета нужна для быстрого решения квадратных уравнений (простыми словами).

Если более подробно, то теорема Виета – это сумма корней данного квадратного уравнения равняется второму коэффициенту, который взят с противоположным знаком, а произведение равно свободному члену. Это свойство обладает любым приведённым квадратным уравнением, у которого есть корни.

При помощи теоремы Виета можно легко решать квадратные уравнения путём подбора, поэтому скажем “спасибо” этому математику с мечем в руках за наш счастливый 7 класс.

Нужна помощь в написании работы?

Мы – биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Заказать работу

Доказательство теоремы Виета

Чтобы доказать теорему, можно воспользоваться известными формулами корней, благодаря которым составим сумму и произведение корней квадратного уравнения. Только после этого мы сможем убедиться, что они равны и, соответственно, .

Допустим у нас есть уравнение: . У этого уравнения есть такие корни: и . Докажем, что , .

По формулам корней квадратного уравнения:

${x_1} = {-p + sqrt{D}over{2a}}$ , ${x_2} = {p - sqrt{D}over{2a}}$ .

1. Найдём сумму корней:

${x_1 + x_2} = {-p + sqrt{D}over{2a}} + {-p - sqrt{D}over{2a}} = {-p + sqrt{D} - p - sqrt{D}over{2a}} = -p$ .

Разберём это уравнение, как оно у нас получилось именно таким:

= .

Шаг 1. Приводим дроби к общему знаменателю, получается:

= = .

Шаг 2. У нас получилась дробь, где нужно раскрыть скобки:

= = . Сокращаем дробь на 2 и получаем:

Мы доказали соотношение для суммы корней квадратного уравнения по теореме Виета.

2. Найдём произведение корней:

${x_1 * x_2} = {-p + sqrt{D}over{2}} * {-p - sqrt{D}over{2}} = {(-p + sqrt{D}) * (-p - sqrt{D})over{4}}$ =

= = ${p^2 - D}over{4}}$ = ${{p^2 - (p^2 - 4q)}over{4}}$ = ${p^2 - p^2 + 4q}over{4}}$ = .

Докажем это уравнение:

${x_1 * x_2} = {-p + sqrt{D}over{2a}} * {-p - sqrt{D}over{2a}}$ .

Шаг 1. Есть правило умножение дробей, по которому мы и умножаем данное уравнение:

${(-p + sqrt{D}) * (-p - sqrt{D})over{4a^2}}$ .

Шаг 2. Далее выполняется умножение скобку на скобку (в числителе). Можно воспользоваться формулой сокращённого умножения (ФСУ) – формула разности, откуда получается:

${(-p + sqrt{D} * (-p - sqrt{D})over{4a^2}} = {{(-p)^2 - (sqrt{D})^2}over{4a^2}}$ .

Теперь вспоминаем определение квадратного корня и считаем:

${{(-p){^2} - (sqrt{D})^2}over{4a^2}}$ = ${p^2 - Dover{4a^2}}$ .

Шаг 3. Вспоминаем дискриминант квадратного уравнения: . Поэтому в последнюю дробь вместо D (дискриминанта) мы подставляем , тогда получается:

${b^2 - D}over{4a^2}$ = ${b^2 - (b^2 - 4 * a * c)}over{4a^2}$ .

Шаг 4. Раскрываем скобки и приводим подобные слагаемые к дроби:

${4 * a * cover{4 * a^2}}$ .

Шаг 5. Сокращаем «4a» и получаем .

Вот мы и доказали соотношение для произведения корней по теореме Виета.

ВАЖНО! Если дискриминант равняется нулю, тогда у квадратного уравнения всего один корень.

Теорема, обратная теореме Виета

По теореме, обратной теореме Виета можно проверять, правильно ли решено наше уравнение. Чтобы понять саму теорему, нужно более подробно её рассмотреть.

Если числа и такие:

и , тогда они и есть корнями квадратного уравнения .

Доказательство обратной теоремы Виета

Шаг 1. Подставим в уравнение выражения для его коэффициентов:

$x^2 - (x_1 + x_2)x + x_{1} * x_{2} = 0$

Шаг 2. Преобразуем левую часть уравнения:

$x^2 - x_1 * x - x_2 * x + x_{1} * x_{2} = 0$ ;

Шаг 3. Найдём Корни уравнения , а для этого используем свойство о равенстве произведения нулю:

или . Откуда и получается: или .

Примеры с решениями по теореме Виета

Задание

Найдите сумму, произведение и сумму квадратов корней квадратного уравнения , не находя корней уравнения.

Решение

Шаг 1. Вспомним формулу дискриминанта . Подставляем наши цифры под буквы. То есть, , – это заменяет , а . Отсюда следует:

. Получается:

. Если дискриминант больше нуля, тогда у уравнения есть корни. По теореме Виета их сумма , а произведение .

Выразим сумму квадратов корней через их сумму и произведение:

Ответ

7; 12; 25.

Задание

Решите уравнение . При этом не применяйте формулы квадратного уравнения.

Решение

У данного уравнения есть корни, которые по дискриминанту (D) больше нуля. Соответственно, по теореме Виета сумма корней этого уравнения равна 4, а произведение – 5. Сначала определяем делители числа , сумма которых равняется 4. Это числа «5» и «-1». Их произведение равно – 5, а сумма – 4. Значит, по теореме, обратной теореме Виета, они являются корнями данного уравнения.

Ответ

Задание

Найдите, если это возможно, сумму и произведение корней уравнения:

Решение

. Так как дискриминант меньше нуля, значит у уравнения нет корней.

Ответ

Нет корней.

Задание

Составьте уравнение, каждый корень которого в два раза больше соответствующего корня уравнения:

Решение

По теореме Виета сумма корней данного уравнения равна 12, а произведение = 7. Значит, два корня положительны.

Сумма корней нового уравнения будет равна:

, а произведение .

По теореме, обратной теореме Виета, новое уравнение имеет вид:

Ответ

Получилось уравнение, каждый корень которого в два раза больше:

Итак, мы рассмотрели, как решать уравнение при помощи теоремы Виета. Очень удобно пользоваться данной теоремой, если решаются задания, которые связаны со знаками корней квадратных уравнений. То есть, если в формуле свободный член – число положительное, и если в квадратном уравнении имеются действительные корни, тогда они оба могут быть либо отрицательными, либо положительными.

А если свободный член – отрицательное число, и если в квадратном уравнении есть действительные корни, тогда оба знака будут разными. То есть, если один корень положительный, тогда другой корень будет только отрицательный.

Полезные источники:

Дорофеев Г. В., Суворова С. Б., Бунимович Е. А. Алгебра 8 класс: Москва “Просвещение”, 2016 – 318 с.
Рубин А. Г., Чулков П. В. – учебник Алгебра 8 класс:Москва “Баласс”, 2015 – 237 с.
Никольский С. М., Потопав М. К., Решетников Н. Н., Шевкин А. В. – Алгебра 8 класс: Москва “Просвещение”, 2014 – 300

Источник

В восьмом классе, учащиеся знакомятся с
квадратными уравнениями и способами их решения.
При этом, как показывает опыт, большинство
учащихся при решении полных квадратных
уравнений применяют только один способ –
формулу корней квадратного уравнения. Для
учеников, хорошо владеющих навыками устного
счета, этот способ явно нерационален. Решать
квадратные уравнения учащимся приходится часто
и в старших классах, а там тратить время на расчет
дискриминанта просто жалко. На мой взгляд, при
изучении квадратных уравнений, следует уделить
больше времени и внимания применению теоремы
Виета (по программе А.Г. Мордковича Алгебра-8, на
изучение темы “Теорема Виета. Разложение
квадратного трехчлена на линейные множители”
запланировано только два часа).

В большинстве учебников алгебры эта теорема
формулируется для приведенного квадратного
уравнения и гласит, что если уравнение имеет корни и , то для них выполняются
равенства , . Затем
формулируется утверждение, обратное к теореме
Виета, и предлагается ряд примеров для отработки
этой темы.

Возьмем конкретные примеры и проследим на них
логику решения с помощью теоремы Виета.

Пример 1. Решить уравнение .

Решение.

Допустим, это уравнение имеет корни, а именно, и . Тогда по теореме Виета
одновременно должны выполняться равенства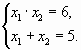

Обратим внимание, что произведение корней –
положительное число. А значит, корни уравнения
одного знака. А так как сумма корней также
является положительным числом, делаем вывод, что
оба корня уравнения – положительные. Вернемся
снова к произведению корней. Допустим, что корни
уравнения – целые положительные числа. Тогда
получить верное первое равенство можно только
двумя способами (с точностью до порядка
множителей):
или . Проверим
для предложенных пар чисел выполнимость второго
утверждения теоремы Виета: . Таким образом, числа 2 и 3
удовлетворяют обоим равенствам, а значит, и
являются корнями заданного уравнения.

Ответ: 2; 3.

Выделим основные этапы рассуждений при решении
приведенного квадратного уравнения с помощью теоремы Виета:

записать утверждение теоремы Виета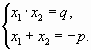

(*)

(первым равенством рекомендуется записывать
произведение корней);

определить знаки корней уравнения (Если
произведение и сумма корней – положительные, то
оба корня – положительные числа. Если
произведение корней – положительное число, а
сумма корней – отрицательное, то оба корня –
отрицательные числа. Если произведение корней –
отрицательное число, то корни имеют разные знаки.
При этом, если сумма корней – положительная, то
больший по модулю корень является положительным
числом, а если сумма корней меньше нуля, то
больший по модулю корень – отрицательное число);
подобрать пары целых чисел, произведение
которых дает верное первое равенство в записи (*);
из найденных пар чисел выбрать ту пару, которая
при подстановке во второе равенство в записи (*)
даст верное равенство;
указать в ответе найденные корни уравнения.

Приведем еще примеры.

Пример 2. Решите уравнение .

Решение.

Пусть и – корни
заданного уравнения. Тогда по теореме Виета 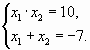Заметим, что
произведение – положительное, а сумма –
отрицательное число. Значит, оба корня –
отрицательные числа. Подбираем пары множителей,
дающих произведение 10 (-1 и -10; -2 и -5). Вторая пара
чисел в сумме дает -7. Значит, числа -2 и -5 являются
корнями данного уравнения.

Ответ: -2; -5.

Пример 3. Решите уравнение .

Решение.

Пусть и – корни
заданного уравнения. Тогда по теореме Виета 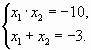Заметим, что
произведение – отрицательное. Значит, корни –
разного знака. Сумма корней – также
отрицательное число. Значит, больший по модулю
корень – отрицательный. Подбираем пары
множителей, дающих произведение -10 (1 и -10; 2 и -5).
Вторая пара чисел в сумме дает -3. Значит, числа 2 и
-5 являются корнями данного уравнения.

Ответ: 2; -5.

Заметим, что теорему Виета в принципе можно
сформулировать и для полного квадратного
уравнения: если квадратное уравнение имеет корни и , то для них выполняются
равенства , . Однако
применение этой теоремы довольно проблематично,
так как в полном квадратном уравнении по крайней
мере один из корней (при их наличии, конечно)
является дробным числом. А работать с подбором
дробей долго и трудно. Но все-таки выход есть.

Рассмотрим полное квадратное уравнение . Умножим обе
части уравнения на первый коэффициент а и
запишем уравнение в виде . Введем новую переменную и получим
приведенное квадратное уравнение , корни которого и (при их наличии) могут быть
найдены по теореме Виета. Тогда корни исходного
уравнения будут . Обратим внимание, что составить
вспомогательное приведенное уравнение очень просто:
второй коэффициент сохраняется, а третий
коэффициент равен произведению ас. При
определенном навыке учащиеся сразу составляют
вспомогательное уравнение, находят его корни по
теореме Виета и указывают корни заданного
полного уравнения. Приведем примеры.

Пример 4. Решите уравнение .

Решение

Составим вспомогательное уравнение и по теореме
Виета найдем его корни . А значит, корни исходного уравнения .

Ответ: .

Пример 5. Решите уравнение .

Решение

Вспомогательное уравнение имеет вид . По теореме
Виета его корни . Находим корни исходного уравнения .

Ответ: .

И еще один случай, когда применение теоремы
Виета позволяет устно найти корни полного
квадратного уравнения. Нетрудно доказать, что число
1 является корнем уравнения , тогда и только тогда, когда . Второй
корень уравнения находится по теореме Виета и
равен . Еще
одно утверждение: чтобы число –1 являлось
корнем уравнения необходимо и достаточно, чтобы . Тогда второй
корень уравнения по теореме Виета равен . Аналогичные
утверждения можно сформулировать и для
приведенного квадратного уравнения.