Как найти корень уравнения егэ 2014 - Сайт, где вы сможете решить свои вопросы

Задания по теме «Простейшие уравнения»

Открытый банк заданий по теме простейшие уравнения. Задания B5 из ЕГЭ по математике (профильный уровень)

Задание №887

Условие

Найдите корень уравнения 5^<log_<25>(10x-8)>=8.

Решение

Найдем ОДЗ: 10x-8>0.

10x-8=64, значит, условие 10x-8>0 выполняется.

Ответ

Задание №886

Условие

Найдите корни уравнения cosfrac<pi(x+5)><6>=0,5. В ответе напишите наибольший отрицательный корень.

Решение

а) frac<pi(x+5)><6>=frac<pi><3>+2pi k, frac<6>=frac13+2k, x+5=2+12k, x=-3+12k.

Наибольший отрицательный корень данного вида x=-3.

б) frac<pi(x+5)><6>=-frac<pi><3>+2pi k , frac<6>=-frac13+2k, x+5=-2+12k, x=-7+12k.

Наибольший отрицательный корень данного вида x=-7.

Значит, наибольший отрицательный корень уравнения x=-3.

Задание №1. Простейшие уравнения. Профильный ЕГЭ по математике

В задании №1 варианта ЕГЭ вам встретятся всевозможные уравнения: квадратные и сводящиеся к квадратным, дробно-рациональные, иррациональные, степенные, показательные и логарифмические и даже тригонометрические. Видите, как много нужно знать, чтобы справиться с заданием! И еще ловушки и «подводные камни», которые ждут вас в самом неожиданном месте.

Вот список тем, которые стоит повторить:

Уравнения, сводящиеся к квадратным

1. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Кажется, что уравнение очень простое. Но иногда здесь ошибаются даже отличники. А вот шестиклассник бы не ошибся.

С левой частью уравнения все понятно. Дробь умножается на А в правой части — смешанное число Его целая часть равна 19, а дробная часть равна Запишем это число в виде неправильной дроби:

Выбираем меньший корень.

Ответ: – 6,5.

2. Решите уравнение

Возведем в квадрат левую часть уравнения. Получим:

Дробно-рациональные уравнения

3. Найдите корень уравнения

Перенесем единицу в левую часть уравнения. Представим 1 как и приведем дроби к общему знаменателю:

Это довольно простой тип уравнений. Главное – внимательность.

Иррациональные уравнения

Так называются уравнения, содержащие знак корня – квадратного, кубического или n-ной степени.

4. Решите уравнение:

Выражение под корнем должно быть неотрицательно, а знаменатель дроби не равен нулю.

Значит, .

Возведём обе части уравнения в квадрат:

Условие при этом выполняется.

5. Решите уравнение Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

А в этом уравнении есть ловушка. Решите его самостоятельно и после этого читайте дальше.

Выражение под корнем должно быть неотрицательно. И сам корень — величина неотрицательная. Значит, и правая часть должна быть больше или равна нуля. Следовательно, уравнение равносильно системе:

Решение таких уравнений лучше всего записывать в виде цепочки равносильных переходов:

Мы получили, что . Это единственный корень уравнения.

Типичная ошибка в решении этого уравнения такая. Учащиеся честно пишут ОДЗ, помня, что выражение под корнем должно быть неотрицательно:

Возводят обе части уравнения в квадрат. Получают квадратное уравнение: Находят его корни: или Пишут в ответ: -9 (как меньший из корней). В итоге ноль баллов.

Теперь вы знаете, в чем дело. Конечно же, число -9 корнем этого уравнения быть не может.

6. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Запишем решение как цепочку равносильных переходов.

Показательные уравнения

При решении показательных уравнений мы пользуемся свойством монотонности показательной функции.

7. Решите уравнение

Вспомним, что Уравнение приобретает вид: Функция монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.

8. Решите уравнение

Функция монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.

9. Решите уравнение

Представим в виде степени с основанием 3 и воспользуемся тем, что

Логарифмические уравнения

Решая логарифмические уравнения, мы также пользуемся монотонностью логарифмической функции: каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, значит, равны и сами числа.

И конечно, помним про область допустимых значений логарифма:

Логарифмы определены только для положительных чисел;

Основание логарифма должно быть положительно и не равно единице.

10. Решите уравнение:

Область допустимых значений: . Значит,

Представим 2 в правой части уравнения как – чтобы слева и справа в уравнении были логарифмы по основанию 5.

Функция монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом

11. Решите уравнение:

Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:

12. Решите уравнение:

Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:

Записываем решение как цепочку равносильных переходов.

13. Решите уравнение. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

В этом уравнении тоже есть ловушка. Мы помним, что основание логарифма должно быть положительно и не равно единице.

Первое уравнение мы получили просто из определения логарифма.

Квадратное уравнение имеет два корня: и

Очевидно, корень является посторонним, поскольку основание логарифма должно быть положительным. Значит, единственный корень уравнения:

Тригонометрические уравнения (Часть 1 ЕГЭ по математике)

Тригонометрические уравнения? В первой части вариантов ЕГЭ? – Да. Причем это задание не проще, чем задача 13 из второй части варианта Профильного ЕГЭ.

14. Найдите корень уравнения: В ответе запишите наибольший отрицательный корень.

Типичная ошибка — решать это уравнение в уме. Мы не будем так делать! Несмотря на то, что это задание включено в первую части варианта ЕГЭ, оно является полноценным тригонометрическим уравнением, причем с отбором решений.

Сделаем замену Получим:

Получаем решения: Вернемся к переменной x.

Поделим обе части уравнения на и умножим на 4.

Первой серии принадлежат решения

Вторая серия включает решения

Наибольший отрицательный корень — тот из отрицательных, который ближе всех к нулю. Это

15. Решите уравнение В ответе напишите наименьший положительный корень.

Сделаем замену Получим: Решения этого уравнения:

Вернемся к переменной х:

Умножим обе части уравнения на 4 и разделим на

Выпишем несколько решений уравнения и выберем наименьший положительный корень:

Наименьший положительный корень

Мы разобрали основные типы уравнений, встречающихся в задании №1 Профильного ЕГЭ по математике. Конечно, это не все, и видов уравнений в этой задаче существует намного больше. Именно поэтому мы рекомендуем начинать подготовку к ЕГЭ по математике не с задания 1, а с текстовых задач на проценты, движение и работу и основ теории вероятностей.
Успеха вам в подготовке к ЕГЭ!

1. Прототипы темы: «Простейшие уравнения»

Все прототипы заданий темы «Простейшие уравнения», которые могут выпасть на ЕГЭ по математике (профильный уровень). Источники заданий: fipi.ru, os.fipi.ru, реальные ЕГЭ прошлых лет, mathege.ru.
Условия прототипов взяты у Евгения Пифагора из его видеокурса: «1–11 задания ЕГЭ профиль (первая часть с нуля)». Содержание курса:
▶ 14 часов теоретических видео (про все правила и формулы);
▶ 73,5 часа разборов задач прототипов и ДЗ.

Решение №1806 Найдите корень уравнения tg(π(x+6)/3)=√3.

Найдите корень уравнения tg(π(x+6)/3)=√3. В ответе запишите наименьший положительный корень.

Запись опубликована: 06.07.2021
Рубрика записи1. Прототипы темы: «Простейшие уравнения»
Комментарии к записи:0 комментариев

Решение №1805 Найдите корень уравнения tg(π(x+2)/3)=−√3.

Найдите корень уравнения tg(π(x+2)/3)=−√3. В ответе запишите наибольший отрицательный корень.

Запись опубликована: 06.07.2021
Рубрика записи1. Прототипы темы: «Простейшие уравнения»
Комментарии к записи:0 комментариев

Решение №1804 Найдите корень уравнения cos(π(x−7)/3)=1/2.

Найдите корень уравнения cos(π(x−7)/3)=1/2. В ответе запишите наименьший положительный корень.

Запись опубликована: 06.07.2021
Рубрика записи1. Прототипы темы: «Простейшие уравнения»
Комментарии к записи:0 комментариев

Решение №1803 Найдите корень уравнения cos(π(x−7)/3)=1/2.

Найдите корень уравнения cos(π(x−7)/3)=1/2. В ответе запишите наибольший отрицательный корень.

Запись опубликована: 06.07.2021
Рубрика записи1. Прототипы темы: «Простейшие уравнения»
Комментарии к записи:0 комментариев

Решение №1802 Найдите корень уравнения sin(π(x−3)/4)=√2/2.

Найдите корень уравнения sin(π(x−3)/4)=√2/2. В ответе запишите наименьший положительный корень.

Запись опубликована: 06.07.2021
Рубрика записи1. Прототипы темы: «Простейшие уравнения»
Комментарии к записи:0 комментариев

Решение №1801 Найдите корень уравнения sin(π(4х−3)/4)=1.

Найдите корень уравнения sin(π(4х−3)/4)=1. В ответе запишите наибольший отрицательный корень.

Запись опубликована: 06.07.2021
Рубрика записи1. Прототипы темы: «Простейшие уравнения»
Комментарии к записи:0 комментариев

Решение №1800 Найдите корень уравнения 9^(2+5x)=1,8∙5^(2+5x).

Найдите корень уравнения 9^(2+5x)=1,8∙5^(2+5x).

[spoiler title=”источники:”]

http://ege-study.ru/ru/ege/materialy/matematika/zadanie-1-prostejshie-uravneniya/

http://ege314.ru/5-prostejshie-uravneniya-ege/

[/spoiler]

Источник

ЕГЭ-2014 по математике для «чайников»: советы репетитора

www.EGEprosto.ru

ВВЕДЕНИЕ

Вниманию учащихся, сдающих ЕГЭ в 2014 году, предлагается учебное пособие для самостоятельной подготовки

«ЕГЭ-2014 ПО МАТЕМАТИКЕ ДЛЯ «ЧАЙНИКОВ»: СОВЕТЫ РЕПЕТИТОРА»

Пособие состоит из 5 тематических разделов–шагов, в соответствии с которыми, как мне представляется, довольно удобно готовиться к этому экзамену.

А именно:
 Шаг №1: «Начни с простого…»	(задания В1 – В4)
 Шаг №2: «Геометрия»	(задания В5, В8, В10 и B13)
 Шаг №3: «Простейшие уравнения и преобразования»	(задания В7 и В11)
 Шаг №4: «Производная функции»	(задание В9 и B15)
 Шаг №5: «Текстовые задачи»	(задания В6, В12 и В14)

Свои отзывы и пожелания (если они вдруг неожиданно обнаружатся 🙂 вы можете отправить мне, перейдя по этой ссылке: http://egeprosto.ru/kontakty

ЛЕНИВО ГОТОВИТЬСЯ ПО КНИЖКЕ САМОСТОЯТЕЛЬНО?

Запишись на дистанционный курс здесь: http://egeprosto.ru/besplatnyj-material/#reg

ЖЕЛАЮ УСПЕХОВ В РАБОТЕ!

АВТОР

ЕГЭ-2014 по математике для «чайников»: советы репетитора	www.EGEprosto.ru
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ ……………………………………………………………………………………………………………………..	2
ГЛАВА 3: «УРАВНЕНИЯ И ВЫРАЖЕНИЯ» …………………………………………………………..	4
ЗАДАНИЕ В7………………………………………………………………………………………………………………….	5
7.1. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ …………………………………………………………………………………..	6
ОТСТУПЛЕНИЕ: «СТЕПЕНИ ЧИСЕЛ» ………………………………………………………………………………..	6
ПРИМЕРЫ РЕШЕНИЯ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ …………………………………………………….	8
7.2. УРАВНЕНИЯ, СОДЕРЖАЩИЕ КОРЕНЬ ………………………………………………………………………	11
7.3. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ ……………………………………………………………………………	15
ОТСТУПЛЕНИЕ: «НЕМНОГО О ЛОГАРИФМАХ»……………………………………………………………..	16
ЛОГАРИФМЫ – ЧТО ЭТО? …………………………………………………………………………………………	16
ЛОГАРИФМЫ: «ИНСТРУКЦИЯ ПО ПРИМЕНЕНИЮ»…………………………………………………..	18
И ЕЩЕ ОДНА ОСОБЕННОСТЬ ЛОГАРИФМОВ…………………………………………………………….	18
ПРИМЕРЫ РЕШЕНИЯ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ ……………………………………………..	19
ЗАДАНИЕ B11 ……………………………………………………………………………………………………………..	22
11.1. ТРИГОНОМЕТРИЧЕСКИЕ ВЫРАЖЕНИЯ …………………………………………………………………..	23
ОТСТУПЛЕНИЕ: «ФОРМУЛЫ ПРИВЕДЕНИЯ»…………………………………………………………………	24
ПРИМЕРЫ ВЫЧИСЛЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ ………………………………..	26
11.2. ЛОГАРИФМИЧЕСКИЕ И СТЕПЕННЫЕ ВЫРАЖЕНИЯ ………………………………………………..	34

ЕГЭ-2014 по математике для «чайников»: советы репетитора

www.EGEprosto.ru

ГЛАВА 3: «УРАВНЕНИЯ И ВЫРАЖЕНИЯ»

После насыщенной различной информацией и относительно сложной предыдущей главы, в которой было показано решение геометрических заданий В5, 8, 10 и В13, эта глава может показаться отдыхом. Хотя, понятное дело, кому-то хорошо отдыхалось и на геометрии, да и вообще на просматривании (или разглядывании) любого текста .

Итак, Глава 3 состоит всего лишь из двух заданий ЕГЭ: В7 и В11. Задание В7 предлагает решить несложное уравнение (как правило, логарифмическое или «с корнем»), а задание В11 – найти значение выражения (как правило, тригонометрического).

Рассмотрим наиболее распространенные примеры обоих заданий.

ЕГЭ-2014 по математике для «чайников»: советы репетитора

www.EGEprosto.ru

ЗАДАНИЕ В7

Еще одна возможность заработать весьма легкий балл – решить уравнение, которое предлагает задание В7 («найдите корень уравнения»).

Предлагаемое на ЕГЭ уравнение, судя по всему, будет относиться к одному из 3-х типов:

1	−12		1
1) Показательное уравнение. Например, ( )		=	9	.
3

Вэтих уравнениях находится в показателе степени, то есть «наверху»;

2)Уравнение, содержащее корень. Например, √2 + 7 = 5.

Вэтих уравнениях находится «под знаком корня»;

3)Логарифмическое уравнение. Например, log2(8 − ) = 4.

Эти уравнения, как следует из названия, содержат так называемые «логарифмы», и находится «под знаком логарифма».

Раздел, посвященный заданию В7, получится довольно большим, так как придется рассматривать решение уравнений всех 3-х типов. Но придется потерпеть – не отказываться же из-за этого от возможности заработать балл на столь раннем этапе ЕГЭ!

Для того чтобы вспомнить (или узнать) сведения, необходимые для успешного выполнения заданий В7, сделаем на протяжении этой главы еще два Тематических Отступления, посвященных степеням чисел и логарифмам.

Поскольку это Пособие предназначено, в первую очередь, для категории «чайников», то все объяснения написаны соответствующим языком. В этих Отступлениях, для «облегчения понимания» (как говорится в известной рекламе), порой специально искажается и огрубляется суть разбираемой темы, а некоторые вещи не объясняются вообще.

Ипричина этого проста – иногда проще и правильнее «просто сделать», имея лишь общее и приблизительное понимание, чем тратить время и силы на изучение всех деталей. К тому же – часто ненужное. Подобно тому, как многие люди вполне успешно работают на компьютере, не зная принципов его работы. А тем более – не зная компьютерного «железа».

Ивот – для поддержания умственного тонуса – первое Тематическое Отступление этой главы, посвященное степеням чисел.

ЕГЭ-2014 по математике для «чайников»: советы репетитора

www.EGEprosto.ru

7.1. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ

ОТСТУПЛЕНИЕ: «СТЕПЕНИ ЧИСЕЛ»

Освежим память когда-то знакомыми сведениями.

Как известно, степени чисел могут быть целыми и дробными, положительными и отрицательными. Кратко напомним об этом конкретными примерами.

1)Целая положительная степень (то есть 1,2,3 … и так далее).

22 = 2 ∙ 2 = 4 25 = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 = 32,

53 = 5 ∙ 5 ∙ 5 = 125 101 = 10

2)Целая отрицательная степень (то есть −1, −2, −3 … и так далее).

2−2 = 212 = 14

2−5 = 215 = 321

5−3 = 513 = 1251

10−1 =	1	=	1
1	10
	10
В общем случае,	− =		.

3) Дробная положительная степень.

1	2
42		= √4 = 2
= √4
1	3
83		= 2
= √8

811 = 4 81 = 3

4 √

В числителе дроби не обязательно должна стоять 1. В этом случае число нужно понимать так:

3
=	√ 3
2
4		4
2		3		3
			2
3
=	√	= √64 = 4
8		8

815 = 4√815

ЕГЭ-2014 по математике для «чайников»: советы репетитора

www.EGEprosto.ru

4) Дробная отрицательная степень. Здесь получается комбинация пунктов 2) и 3).

4−2

= 1

= 1 = 1

√4

= 1

= 1 = 1

4−2

= 1

√43

√64 8

Вместе с тем, многие числа, возведенные в дробную степень, не могут быть выражены в

виде целых чисел (и даже простых дробей).

Например, 52 = √5, 203 = √20.

В этих случаях их именно так и записывают, без дальнейшего вычисления.

5)Любое число в нулевой степени равно 1.

Например, 40 = 1, 100 = 1.

6)1 в любой степени равно 1.

Например, 15 = 1, 1−2 = 1, 199 = 1.

Следующий набор правил показывает, какие действия можно выполнять с двумя и более числами, имеющими степени (то есть любыми числами, указанными в предыдущих пунктах). Обратите внимание, что умножать и делить друг на друга можно только числа с одинаковыми основаниями!

Этот набор правил, позволяющий «собирать и разбирать» выражения, содержащие степень, я

называю «Показательным конструктором». Итак, вот эти формулы:

1) ∙ = +

Например, 32 ∙ 33 = 32+3 = 35

2) = −

Например, 3332 = 33−2 = 31 = 3

3) ( ∙ ) = ∙

Например, (2 ∙ 3)4 = 24 ∙ 34

4)( ) =

Например, (23)4 = 2344

5)( ) = ∙

Например, (23)4 = 23∙4 = 212

Вот такое получилось первое Отступление этой главы – занимательное и бодрящее .

ЕГЭ-2014 по математике для «чайников»: советы репетитора

www.EGEprosto.ru

ПРИМЕРЫ РЕШЕНИЯ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ

В7.1.1. НАЙДИТЕ КОРЕНЬ УРАВНЕНИЯ

	−
(		)	=

Показательные уравнения удобно решать по следующей простой схеме.

1-Й ЭТАП: ПРИВЕСТИ ОБЕ ЧАСТИ УРАВНЕНИЯ К ОДИНАКОВЫМ ОСНОВАНИЯМ.

В принципе, можно приводить левое основание к правому, правое к левому или оба основания к какому-либо третьему. А выбирать нужно тот вариант приведения, который проще с точки зрения вычислений. Зачем создавать себе лишние трудности? Здесь удобнее поработать с правой частью:

1		1		12	1	2
	=		=		= (		)
9	2	2
	3		3	3
							1	−12	1	2
Тогда уравнение будет выглядеть так: ( )		= ( )
							3		3

2-Й ЭТАП: ПРИРАВНЯТЬ «ВЕРХУШКИ», ТО ЕСТЬ СТЕПЕНИ.

− 12 = 2; = 2 + 12 = 14

3-ЭТАП: ПРОВЕРИТЬ ПОЛУЧЕННЫЙ КОРЕНЬ.

Подставляем = 14 в исходное уравнение и проверяем, будут ли равны обе части уравнения

1	14−12	1	2	1
(		)	= (	)	=
3	3	9

Действительно, при = 14, левая часть уравнения равна правой.

4-Й ЭТАП: ВНИМАТЕЛЬНО (!) ЗАПИСАТЬ ОТВЕТ.

1 4

ЕГЭ-2014 по математике для «чайников»: советы репетитора	www.EGEprosto.ru
В7.1.2. НАЙДИТЕ КОРЕНЬ УРАВНЕНИЯ − =		.


1-Й ЭТАП: ПРИВЕСТИ ОБЕ ЧАСТИ УРАВНЕНИЯ К ОДИНАКОВЫМ ОСНОВАНИЯМ.
Проще преобразовать правую часть уравнения к основанию 4:
1	=		1	= 4−3
	3
64	4
Тогда уравнение будет выглядеть так:
45 −13 = 4−3
2-Й ЭТАП: ПРИРАВНЯТЬ «ВЕРХУШКИ», ТО ЕСТЬ СТЕПЕНИ.
5 − 13 = − 3
5 = − 3 + 13 = 10
		10
=		= 2
5
3-ЭТАП: ПРОВЕРИТЬ ПОЛУЧЕННЫЙ КОРЕНЬ.
45∙2−13 = 410−13 = 4−3 =	1	=	1
3
		4	64

Проверка показала, что корень = 2 найден правильно.

4-Й ЭТАП: ВНИМАТЕЛЬНО (!) ЗАПИСАТЬ ОТВЕТ.

ЕГЭ-2014 по математике для «чайников»: советы репетитора	www.EGEprosto.ru
В7.1.3. НАЙДИТЕ КОРЕНЬ УРАВНЕНИЯ
											−
									(	)	=

1	-Й ЭТАП: ПРИВЕСТИ ОБЕ ЧАСТИ УРАВНЕНИЯ К ОДИНАКОВЫМ ОСНОВАНИЯМ.
В этом примере лучше преобразовать обе части уравнения к основанию 8.
С учетом того, что 1	= 8−1, а 64 = 82, получим такое уравнение:
					8
(8−1) −12 = 82
8− +12 = 82
2	-Й ЭТАП: ПРИРАВНЯТЬ «ВЕРХУШКИ», ТО ЕСТЬ СТЕПЕНИ.
− + 12 = 2
= 12 − 2 = 10
3	-ЭТАП: ПРОВЕРИТЬ ПОЛУЧЕННЫЙ КОРЕНЬ.
	1	10−12		1	−2	1
(	)			= (	) =		= 82 = 64
			2
8				8		⁄ 1
								(8)
Уравнение решено правильно.
4	-Й ЭТАП: ВНИМАТЕЛЬНО (!) ЗАПИСАТЬ ОТВЕТ.

1		0

А теперь перейдем ко второму типу уравнений, ожидаемых в задании B5.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
20.05.2015144.9 Кб133.doc
#
#
#
20.05.2015493.06 Кб8bu.doc
#
#
#
#
#
#
#

Источник

28
Янв 2014

Категория: 12 (С1) УравненияЕГЭ (диагностич. работы)Тригонометрические выражения, уравнения и неравенства

С1 (№15) Тренировочной работы от 28 января 2014 г.

2014-01-28
2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №13»

Разбор заданий части В Тренировочной работы в формате ЕГЭ по математике смотрите здесь. А также есть разбор C2(№16), С3(№17), С4(№18).

С1.

a) Решите уравнение $frac{2sin^2x-sqrt3sinx}{2cosx+1}=0.$

б) Найдите все корни этого уравнения, принадлежащие отрезку $[2pi;frac{7pi}{2}].$

Решение:

а) Исходное уравнение равносильно следующей системе:

$begin{cases} 2sin^2x-sqrt3sinx=0,& &2cosx+1neq 0; end{cases}$

$begin{cases} sinx(2sinx-sqrt3)=0,& &cosxneq -frac{1}{2}; end{cases}$

$begin{cases}left[begin{gathered} sinx=0,& sinx=frac{sqrt3}{2}; end{gathered}right& &cosxneq -frac{1}{2}; end{cases}$

Наносим на тригонометрический круг решения уравнений и $sinx=frac{sqrt3}{2}$ и видим, что условие $cosxneq -frac{1}{2}$ «уничтожает» одну серию корней ( $frac{2pi}{3}+2pi m,;min Z$ ).

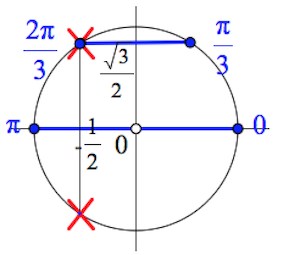
Итак, решение данного уравнения: $pi n,;nin Z;;frac{pi}{3}+2pi k,;kin Z.$

б) Произведем отбор корней уравнения из отрезка $[2pi;frac{7pi}{2}]$ при помощи тригонометрического круга.

В отрезок $[2pi;frac{7pi}{2}]$ попадают три точки: $2pi,;frac{7pi}{3},;3pi.$

Ответ: а) $pi n,;nin Z;;frac{pi}{3}+2pi k,;kin Z ;$ б) $2pi,;frac{7pi}{3},;3pi.$

Аналогичное задание для самопроверки:

a) Решите уравнение $frac{2sin^2x-sinx}{2cosx-sqrt3}=0.$

б) Найдите все корни этого уравнения, принадлежащие отрезку $[frac{3pi}{2};3pi].$

Ответ: + показать

Автор: egeMax |

комментариев 9

Источник

В задании №5 варианта ЕГЭ вам встретятся всевозможные уравнения: квадратные и сводящиеся к квадратным, дробно-рациональные, иррациональные, степенные, показательные и логарифмические и даже тригонометрические. Видите, как много нужно знать, чтобы справиться с заданием! И еще ловушки и «подводные камни», которые ждут вас в самом неожиданном месте.

Вот список тем, которые стоит повторить:

Квадратные уравнения

Арифметический квадратный корень

Корни и степени

Показательная функция

Показательные уравнения

Логарифмическая функция

Логарифмические уравнения

Тригонометрический круг

Формулы приведения

Формулы тригонометрии

Простейшие тригонометрические уравнения 1

Уравнения, сводящиеся к квадратным

1. Решите уравнение $frac{6}{13}x^2=19frac{1}{2}$ . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

С левой частью уравнения все понятно. Дробь $frac{6}{13}$ умножается на x^2. А в правой части — смешанное число $19frac{1}{2}.$ Его целая часть равна 19, а дробная часть равна $frac{1}{2}.$ Запишем это число в виде неправильной дроби:

$19frac{1}{2}= frac{19cdot 2+1}{2} = frac{39}{2}.$

Получим:

$frac{6}{13}x^2=frac{39}{2};$

$x^2=frac{39cdot 13}{2cdot 6}=frac{13cdot 3cdot 13}{2cdot 6}=frac{{13}^2}{4};$

$x=pm frac{13}{2};$

или

Выбираем меньший корень.

Ответ: -6,5.

2. Решите уравнение

Возведем в квадрат левую часть уравнения. Получим:

Ответ: -6.

Дробно-рациональные уравнения

3. Найдите корень уравнения

Перенесем единицу в левую часть уравнения. Представим 1 как $frac{4x-5}{4x-5}$ и приведем дроби к общему знаменателю:

$frac{5x-3}{4x-5}-frac{4x-5}{4x-5}=0;$

$frac{x+2}{4x-5}=0;$

x= - 2.

Ответ: -2.

Это довольно простой тип уравнений. Главное – внимательность.

Иррациональные уравнения

Так называются уравнения, содержащие знак корня – квадратного, кубического или n-ной степени.

4. Решите уравнение:

$sqrt{frac{6}{4{x}-54} } =frac{1}{7}.$

Выражение под корнем должно быть неотрицательно, а знаменатель дроби не равен нулю.

Значит, .

Возведём обе части уравнения в квадрат:

$frac{6}{4{x}-{ 54}} =frac{1}{49}.$

Решим пропорцию:

Условие при этом выполняется.

Ответ: 87.

5. Решите уравнение Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

А в этом уравнении есть ловушка. Решите его самостоятельно и после этого читайте дальше.

$left{begin{matrix} 72-x=x^2\72-xgeq 0 hfill \xgeq 0 hfill end{matrix}right.$ .

Решение таких уравнений лучше всего записывать в виде цепочки равносильных переходов:

$sqrt{72-x}=x Leftrightarrow left{begin{matrix} 72-x=x^2\72-x geq 0 \x geq 0 end{matrix}right. Leftrightarrow$

Мы получили, что x=8 . Это единственный корень уравнения.

Возводят обе части уравнения в квадрат. Получают квадратное уравнение: Находят его корни: x=8 или x=-9. Пишут в ответ: -9 (как меньший из корней). В итоге ноль баллов.

Теперь вы знаете, в чем дело. Конечно же, число -9 корнем этого уравнения быть не может.

Ответ: 8.

6. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Запишем решение как цепочку равносильных переходов:

Ответ: 9.

Показательные уравнения

При решении показательных уравнений мы пользуемся свойством монотонности показательной функции.

7. Решите уравнение $5^{x-7}=frac{1}{125}.$

Вспомним, что $125 = 5{}^{3}.$ Уравнение приобретает вид: $5{}^{x}{}^{-}{}^{7 }= 5{}^{-}{}^{3}.$ Функция y = 5^x монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.

откуда x = 4.

Ответ: 4.

8. Решите уравнение ${left(frac{1}{49}right)}^{x-8}=7.$

Представим ${left(frac{1}{49}right)}^{ }$ как $7^{-2};$

${left(7^{-2}right)}^{x-8}=7;$

$7^{-2x+16}=7.$

Функция y = 7^x монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.

x=7,5.

Ответ: 7,5.

9. Решите уравнение $left(frac{1}{9} right)^{{ x}-13} =3.$

Представим ${textstylefrac{1}{9}}$ в виде степени с основанием 3 и воспользуемся тем, что $left({ a}^{{ m}} right)^{{ n}} ={ a}^{{ mn}}.$

$left(3^{-2} right)^{{ x}-{ 13}} =3;$
$3^{-2{ x}+{ 26}} =3^{1} ;$

Ответ: 12,5.

Логарифмические уравнения

И конечно, помним про область допустимых значений логарифма:

Логарифмы определены только для положительных чисел.

Основание логарифма должно быть положительно и не равно единице.

10. Решите уравнение:

${{log}_5 left(4+xright)=2 }.$

Область допустимых значений: . Значит,

Представим 2 в правой части уравнения как ${{log}_5 25 }$ , чтобы слева и справа в уравнении были логарифмы по основанию 5.

${{log}_5 left(4+xright)={{log}_5 25 } }.$

Функция $y = {{log}_5 x }$ монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом

4+x=25;
x=21.

Ответ: 21.

11. Решите уравнение: ${{log}_8 left(x^2+xright)={{log}_8 left(x^2-4right) } }.$

Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:

Ответ: -4.

12. Решите уравнение: $2^{{{log}_4 left(4x+5right) }}=9.$

${{log}_4 b }=frac{{{log}_2 b }}{{{log}_2 4 }}=frac{{{log}_2 b }}{2}.$

Записываем решение как цепочку равносильных переходов.

Ответ: 19.

13. Решите уравнение. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

${{log}_{x-5} 49=2 }.$

Получим систему:

$small left{begin{matrix} left ( x-5 right )^2=49\x-50 \x-5 neq 1 end{matrix}right..$

Первое уравнение мы получили просто из определения логарифма.

Квадратное уравнение имеет два корня: x=12 и x=-2.

Очевидно, корень x=-2 является посторонним, поскольку основание логарифма должно быть положительным. Значит, единственный корень уравнения: x=12.

Ответ: 12.

Тригонометрические уравнения (Часть 1 ЕГЭ по математике)

14. Найдите корень уравнения: $cos frac{pi (x+1)}{4}=frac{sqrt{2}}{2}.$ В ответе запишите наибольший отрицательный корень.

Сделаем замену $frac{pi left(x+1right)}{4}=t.$ Получим: $cos t=frac{sqrt{2}}{2}.$

Получаем решения: $t=pm frac{pi }{4}+2pi n, nin Z.$ Вернемся к переменной x.

$frac{pi (x+1)}{4}=pm frac{pi }{4}+2pi n, nin Z.$ Поделим обе части уравнения на и умножим на 4.

$left[ begin{array}{c}x=8n, nin Z \x=-2+8n end{array}right..$

Первой серии принадлежат решения

Вторая серия включает решения

Наибольший отрицательный корень — тот из отрицательных, который ближе всех к нулю. Это x = -2.

Ответ: -2.

15. Решите уравнение: $tg frac{pi left( x+1right)}{4}= -1.$ В ответе напишите наименьший положительный корень.

Решение:

Сделаем замену $frac{pi left(x+1right)}{4}=t.$ Получим: tgt=-1. Решения этого уравнения:

$t=-frac{pi }{4}+pi n, nin Z.$ Вернемся к переменной х:

$frac{pi left(x+1right)}{4}=-frac{pi }{4}+pi n, n in Z.$ Умножим обе части уравнения на 4 и разделим на .

Выпишем несколько решений уравнения и выберем наименьший положительный корень:

Наименьший положительный корень x = 2.

Ответ: 2.

Мы разобрали основные типы уравнений, встречающихся в задании №5 Профильного ЕГЭ по математике. Конечно, это не все, и видов уравнений в этой задаче существует намного больше. Именно поэтому мы рекомендуем начинать подготовку к ЕГЭ по математике не с задания 1, а с текстовых задач на проценты, движение и работу и основ теории вероятностей.
Успеха вам в подготовке к ЕГЭ!

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задание №5. Простейшие уравнения. Профильный ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Всем привет! Сегодня я решил рассказать Вам про решение уравнение из ЕГЭ по базовой математике. Мы разберём с Вами в этой статье все возможные виды уравнений на ЕГЭ по математике, и убедимся на примере, что уравнения из ЕГЭ — не проблема, а халявный балл!

Автор статьи: Артемий Ульянов

Дата выпуска: 07.05.2022

Уравнения со степенями

1-е уравнение.

Начать решение наших уравнений я решил с уравнений, в которых приходится работать со степенями. Рассмотрим следующее уравнение, и попробуем его решить.

1-е уравнение.

На самом деле, уравнение довольно лёгкое. Стоит лишь вспомнить, какая степень «5-ки» может дать нам дробь «1/125». Ну конечно же, это степень «-3». Разложим на степень правую часть нашего уравнения, и получим следующий результат:

Раскладываем на степень правую часть уравнения.

Как мы видим, уравнение стало выглядеть значительно проще. Многие из Вас подумают, что стоит перебросить правую часть выражения за знак «равно» со знаком «минус», но тогда нам станет неудобно работать с уравнением. Но вот если приглядеться, то мы можем заметить, что в правой и левой части у каждого члена уравнения одно и то же основание — «5». В таких случаях, мы можем хитро избавиться от наших оснований, и записать уравнение вот в таком виде:

Избавляемся от наших оснований и находим корень уравнения.

Всё! Теперь нам стало сразу легче решать уравнение, и мы быстро нашли наш единственный корень x = -10. Давайте попробуем решить ещё пару таких уравнений.

2-е уравнение.

Рассмотрим следующее уравнение, и попробуем найти все его возможные корни:

2-е уравнениe.

Здесь ситуация уже чуть-чуть легче. Можно заметить, что число 81 — это «3» в «4-й степени». Тогда, мы разложим на степень правую часть нашего уравнения, и получим следующее:

Раскладываем на степень правую часть уравнения.

Всё! Как мы видим, ситуация та же. У каждого члена уравнения одинаковое основание, поэтому мы можем от них избавиться, и сразу найти корни нашего уравнения.

Находим корни 2-го уравнения.

И вот таким, простым способом, мы смогли с Вами решить первые два уравнения. Но вот не каждый сейчас понимает, почему когда одинаковые основания у каждого члена нашего уравнения, то мы можем просто от них избавиться? Давайте попробуем разобраться, составив небольшую схему таких уравнений.

Схема предыдущих двух уравнений.

Прологарифмируем обе части нашего уравнения, взяв за основание логарифма «a». Тогда, мы получим следующее уравнение:

Прологарифмируем обе части нашего уравнения.

Теперь в обеих частях нашего уравнения, вынесем по формуле степени «b» и «c» за знак логарифма, и получим следующее выражение:

Выносим степени за знак логарифма.

А теперь, зная из основной формулы логарифмов, что логарифм «a» по основанию «a» равен «1», упростим наше выражение:

Избавляемся от логарифмов.

Всё! Теперь мы с Вами доказали, что в уравнениях такого типа можно безболезненно избавляться от оснований, просто прологарифмировав обе части уравнения.

Логарифмические уравнения

1-е уравнение

Раз уж мы с Вами заговорили про логарифмы, давайте попробуем решить различные типы логарифмических уравнений. Рассмотрим следующее уравнение:

1-е уравнение.

Это — один из самых простых видов таких уравнений. Для решения такого уравнения, следует просто избавиться от логарифма по формуле, и таким образом мы без труда сможем найти все корни уравнения. Давайте же этим и займёмся!

Находим корни уравнения.

Всё! Это было не так уж и сложно, мы с Вами легко справились с таким уравнением. Давайте рассмотрим пример чуть сложнее.

2-е уравнение

Рассмотрим более сложный тип логарифмический уравнений:

2-е уравнение.

Данное уравнение можно решить единственным способом. Для этого, мы разложим логарифм левой части уравнения, и получим следующее выражение:

Раскладываем логарифм левой части уравнения.

В левой части уравнения мы можем наблюдать произведение степеней. Воспользуемся этой формулой в обратную сторону, и получим следующее уравнение:

Воспользуемся формулой произведения степеней в обратную сторону.

Всё, теперь мы смогли с вами упростить уравнение до вот такого вида. Далее, я предлагаю воспользоваться одной из формулой логарифмов и поменять значение нашего логарифма в левой части уравнения:

Формула замены значения логарифма.

Пользуемся нашей формулой, приведённой выше.

И теперь, мы спокойно можем избавиться от нашего логарифма в показатели степени левой части уравнения, ведь «25» — это «5» во «2-й степени». Тогда, мы получим следующее уравнение:

Избавляемся от логарифма в показатели степени и находим единственный корень уравнения.

Всё! Уравнение решено, и у нас получился корень x = -4. Согласитесь, это было не так уж и сложно. А теперь давайте рассмотрим с вами самый тяжёлый случай логарифмических уравнений.

3-е уравнение

Напоследок я решил разобрать одно из самых сложных уравнений, до решения которого не так уж и легко догадаться. Рассмотрим следующее уравнение:

3-е уравнение.

Да, это уравнение выглядит уже сложнее, чем два предыдущих… А всё из-за разных оснований логарифмов… Попробуем воспользоваться формулой перехода от одного основания к другому в правой части уравнения в обратную сторону, тогда мы получим следующее выражение:

Формула перехода от одного основания логарифма к другому

Раскрываем формулу перехода от одного основания к другому в правой части уравнения.

Теперь мы имеем дело с одинаковыми основаниями, и нам не составит особого труда решить это уравнение. Для начала, умножим обе части уравнения на знаменатель дроби в правой части уравнения и перенесём со знаком «минус» логарифм в правой части уравнения, тогда мы получим следующее выражение:

Умножаем обе части уравнения на знаменатель дроби в правой части уравнения.

А теперь попробуем вынести общий множитель за скобки, тогда мы получаем следующее уравнение:

Выносим общий множитель за скобки.

Всё, теперь мы максимально упростили наше уравнение. Из курса «7-го» класса мы с Вами знаем, что произведение множителей равно нулю, когда один из множителей равен нулю. Случай с правой скобкой нет смысла затрагивать, так как там нет неизвестных, а вот случай с левой скобкой — вполне. Тогда, мы можем смело записать наше уравнение в следующем виде:

Переписываем уравнение, уже без второго множителя.

И теперь, у нас с Вами получилось максимально упростить наше выражение и мы вернулись к самому первому виду логарифмических уравнений, обсуждаемый нами ранее. Решим же его!

Находим корни уравнения.

Всё! Мы нашли единственный корень нашего уравнения, x = -2. Это было не так уж и сложно, как мы с Вами думали.

Квадратные уравнения

1-е уравнение

Зачастую, в ЕГЭ по базовой математике вы можете встретить задание, где необходимо решить квадратное уравнение, поэтому это ещё один из самых важных типов уравнений, которые стоит научиться решать. Рассмотрим следующее уравнение:

1-е уравнение.

Опытные ученические взгляды уже смогли разглядеть в этом уравнении формулу «разности квадратов». Давайте же раскроем эту формулу! Получаем следующее произведение скобок, равное нулю:

Раскрываем формулу разности квадратов.

Произведение множителей равно нулю, когда один из множителей равен нулю. Наш множитель «5» точно не может быть равен нулю, а вот множитель «(2x + 5)» вполне может стать отличным множителем, равным нулю. Запишем наше видоизменённое уравнение:

Видоизменяем наше уравнение, и находим его корни.

Всё! Мы нашли с Вами наш единственный корень уравнения, x = —2.5. Это было не так уж и сложно.

2-е уравнение

Грех не рассмотреть самый стандартный вид квадратных уравнений. Запишем следующее уравнение и попытаемся его решить:

2-е уравнение.

Решать такое уравнение можно по-разному, мы же воспользуемся дискриминантом, делённым на «4». Давайте же найдём корни нашего уравнения!

Находим все корни уравнения.

Всё! Мы с вами нашли все корни этого уравнения — [-3; 9]. Это было проще простого.

Уравнения с квадратным корнем

1-е уравнение

Последний тип уравнений, который мы сегодня с вами рассмотрим, так это типа уравнений с квадратным корнем. Запишем следующее уравнение:

1-e уравнение.

Выглядит всё не так уж и страшно. Умножим обе части нашего уравнение на произведение наших знаменателей, чтобы полностью избавиться от них. Получаем следующее уравнение:

Умножаем обе части нашего уравнения на произведение знаменателей.

Всё, мы упростили наше уравнение до самого обыкновенного вида уравнений с квадратным корнем. Для того, чтобы найти наш «x» — достаточно просто возвести обе части уравнения в квадрат. Так мы и сделаем!

Возводим обе части уравнения в квадрат.

И теперь, мы с Вами получили наш единственный корень уравнения, x = 49. Это было элементарней элементарного.

2-е уравнение

Рассмотрим ещё один вид таких уравнений. Запишем следующее уравнение:

2-е уравнение.

Здесь все ещё проще. Возведём обе части нашего уравнения в квадрат, и получим следующее:

Возводим обе части уравнения в квадрат и находим корни уравнения.

Всё, мы сразу с Вами нашли единственный корень нашего уравнения, x = 3. И эта задача тоже не вызвала у нас никаких трудностей, как и все предыдущие. Вот мы с Вами и доказали, что уравнения из ЕГЭ по базовой математике — не такая уж и страшная вещь.

Итог занятия

Сегодня мы с Вами разобрали все основные типы уравнений, которые могут Вам встретиться на ЕГЭ по базовой математике, и мы убедились на личном опыте, что решать такие задания элементарно, если знать:

— Формулы сокращённого умножения

— Формулы по работе с логарифмами

— Формулы для нахождения корней квадратного уравнения

— Основные свойства степеней

А на этом у меня всё, спасибо Всем за сегодняшний урок, следите за нашими новостями в Telegram и на платформе Яндекс Дзен, пока-пока!

Источник

Задания по теме «Простейшие уравнения»

Задание №887

Условие

Решение

Ответ

Задание №886

Условие

Решение

Задание №1. Простейшие уравнения. Профильный ЕГЭ по математике

1. Прототипы темы: «Простейшие уравнения»

Решение №1806 Найдите корень уравнения tg(π(x+6)/3)=√3.

Решение №1805 Найдите корень уравнения tg(π(x+2)/3)=−√3.

Решение №1804 Найдите корень уравнения cos(π(x−7)/3)=1/2.

Решение №1803 Найдите корень уравнения cos(π(x−7)/3)=1/2.

Решение №1802 Найдите корень уравнения sin(π(x−3)/4)=√2/2.

Решение №1801 Найдите корень уравнения sin(π(4х−3)/4)=1.

Решение №1800 Найдите корень уравнения 9^(2+5x)=1,8∙5^(2+5x).

С1 (№15) Тренировочной работы от 28 января 2014 г.

В новом формате ЕГЭ по математике задание значится как «Задание №13»

Уравнения со степенями

1-е уравнение.

2-е уравнение.

Логарифмические уравнения

1-е уравнение

2-е уравнение

3-е уравнение

Квадратные уравнения

1-е уравнение

2-е уравнение

Уравнения с квадратным корнем

1-е уравнение

2-е уравнение

Итог занятия

Вам также может понравиться

Как составить бизнес план детям

Как найти подходящие коньки

Как правильно составить на расчетный счет

Добавить комментарий Отменить ответ