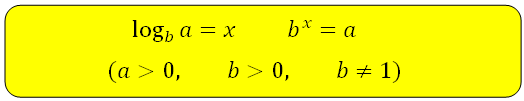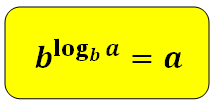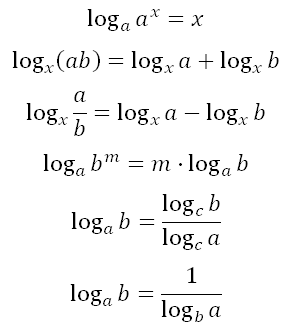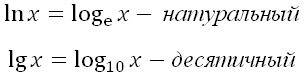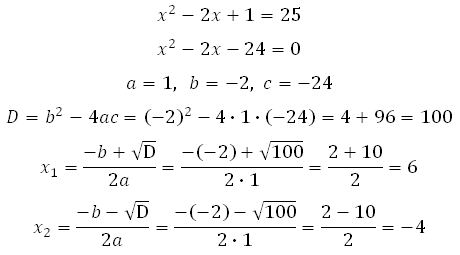Данный калькулятор позволяет найти решение логарифмических уравнений.
Логарифмическое уравнение – это уравнения, в которых переменная величина находится под знаком логарифма. Логарифмическая функция всегда монотонна и может принимать любые значения. Кроме того, переменный аргумент логарифма должен быть больше нуля и переменное основание логарифма должно быть положительным и не равным единице.
При решении логарифмических уравнений зачастую необходимо логарифмировать или потенцировать обе части уравнения. Логарифмировать алгебраическое выражение – выразить его логарифм через логарифмы отдельных чисел, входящих в это выражение. Потенцирование – нахождение выражения, от которого получен результат логарифмирования.
Для того чтобы найти корни логарифмического уравнения, нужно ввести это уравнение в ячейку и нажать на кнопку «Вычислить». В ответе отображаются корни уравнения и график логарифмической функции.
Калькулятор поможет найти решение логарифмических уравнений онлайн.
Для получения полного хода решения нажимаем в ответе Step-by-step.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Логарифмические уравнения. Продолжаем рассматривать задачи из части В ЕГЭ по математике. Мы с вами уже рассмотрели решения некоторых уравнений в статьях «Тригонометрические уравнения», «Решение рациональных уравнений». В этой статье рассмотрим логарифмические уравнения. Сразу скажу, что никаких сложных преобразований при решении таких уравнений на ЕГЭ не будет. Они просты.
Достаточно знать и понимать основное логарифмическое тождество, знать свойства логарифма. Обратите внимание на то, то после решения ОБЯЗАТЕЛЬНО нужно сделать проверку — подставить полученное значение в исходное уравнение и вычислить, в итоге должно получиться верное равенство.
Определение:
Логарифмом числа a по основанию b называется показатель степени, в который нужно возвести b, чтобы получить a.
Основное логарифмическое тождество:
Например:
log39 = 2, так как 32 = 9
Свойства логарифмов:
Частные случаи логарифмов:
Решим задачи. В первом примере мы сделаем проверку. В последующих проверку сделайте самостоятельно.
Найдите корень уравнения: log3(4–x) = 4
Используем основное логарифмическое тождество.
Так как logba = x bx = a, то
34 = 4 – x
x = 4 – 81
x = – 77
Проверка:
log3(4–(–77)) = 4
log381 = 4
34 = 81 Верно.
Ответ: – 77
Решите самостоятельно:
Найдите корень уравнения: log2 (4 – x) = 7
Посмотреть решение
Найдите корень уравнения log5 (4 + x) = 2
Используем основное логарифмическое тождество.
Так как logab = x bx = a, то
52 = 4 + x
x =52 – 4
x = 21
Проверка:
log5(4 + 21) = 2
log525 = 2
52 = 25 Верно.
Ответ: 21
Найдите корень уравнения log3(14 – x) = log35.
Имеет место следующее свойство, смысл его таков: если в левой и правой частях уравнения имеем логарифмы с одинаковым основанием, то можем приравнять выражения, стоящие под знаками логарифмов.
Если logca = logcb, то a = b
14 – x = 5
x = 9
Сделайте проверку.
Ответ: 9
Решите самостоятельно:
Найдите корень уравнения log5(5 – x) = log53.
Посмотреть решение
Найдите корень уравнения: log4(x + 3) = log4(4x – 15).
Если logca = logcb, то a = b
x + 3 = 4x – 15
3x = 18
x = 6
Сделайте проверку.
Ответ: 6
Найдите корень уравнения log1/8(13 – x) = – 2.
(1/8)–2 = 13 – x
82 = 13 – x
x = 13 – 64
x = – 51
Сделайте проверку.
Небольшое дополнение – здесь используется свойство
степени (отрицательная степень дроби).
Ответ: – 51
Решите самостоятельно:
Найдите корень уравнения: log1/7(7 – x) = – 2
Посмотреть решение
Найдите корень уравнения log2 (4 – x) = 2 log2 5.
Преобразуем правую часть. воспользуемся свойством:
logabm = m∙logab
log2(4 – x) = log252
Если logca = logcb, то a = b
4 – x = 52
4 – x = 25
x = – 21
Сделайте проверку.
Ответ: – 21
Решите самостоятельно:
Найдите корень уравнения: log5(5 – x) = 2 log5 3
Посмотреть решение
Решите уравнение log5(x2 + 4x) = log5(x2 + 11)
Если logca = logcb, то a = b
x2 + 4x = x2 + 11
4x = 11
x = 2,75
Сделайте проверку.
Ответ: 2,75
Решите самостоятельно:
Найдите корень уравнения log5(x2 + x) = log5(x2 + 10).
Посмотреть решение
Решите уравнение log2(2 – x) = log2(2 – 3x) +1.
Необходимо с правой стороны уравнения получить выражение вида:
log2 (……)
Представляем 1 как логарифм с основанием 2:
1 = log2 2
Далее применяем свойство:
logс(ab) = logсa + logсb
log2(2 – x) = log2(2 – 3x) + log22
Получаем:
log2(2 – x) = log2 2 (2 – 3x)
Если logca = logcb, то a = b, значит
2 – x = 4 – 6x
5x = 2
x = 0,4
Сделайте проверку.
Ответ: 0,4
Решите самостоятельно:
Найдите корень уравнения log5(7 – x) = log5(3 – x) +1
Посмотреть решение
Решите уравнение logх–125 = 2. Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Воспользуемся основным логарифмическим тождеством:
(x – 1)2= 25
Далее необходимо решить квадратное уравнение. Кстати, квадратное уравнение, как вы поняли, это очень важная «буковка» в математической азбуке. К нему сводятся очень многие решения совершенно различных задач. Помнить формулы дискриминанта и корней нужно обязательно, и уметь решать такое уравнение вы должны очень быстро, периодически практикуйтесь.
Конечно же, опытный глаз сразу увидит, что в нашем примере выражение, стоящее под знаком квадрата равно 5 или – 5, так как только эти два числа при возведении в квадрат дают 25, устно можно посчитать:
корни равны 6 и – 4.
Корень “–4″ не является решением, так как основание логарифма должно быть больше нуля, а при “– 4″ оно равно «–5». Решением является корень 6. Сделайте проверку.
Ответ: 6.
Решите самостоятельно:
Решите уравнение logx–5 49 = 2. Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Посмотреть решение
Как вы убедились, никаких сложных преобразований с логарифмическими уравнениями нет. Достаточно знать свойства логарифма и уметь применять их. В задачах ЕГЭ, связанных с преобразованием логарифмических выражений, выполняются более серьёзные преобразования и требуются более глубокие навыки в решении. Такие примеры мы рассмотрим, не пропустите! Успехов вам!!!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Калькулятор онлайн.
Решение логарифмических уравнений.
Этот математический калькулятор онлайн поможет вам решить логарифмическое уравнение.
Программа для решения логарифмического уравнения не просто даёт ответ задачи, она приводит подробное
решение с пояснениями, т.е. отображает процесс получения ответа.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.
Вы можете посмотреть теорию о логарифмической функции и логарифмах и
некоторые методы решения логарифмических уравнений.
Примеры подробного решения >>
ln(b) или log(b) или log(e,b)– натуральный логарифм числа b
log(10,b) – десятичный логарифм числа b
log(a,b) – логарифм b по основанию a
Введите логарифмическое уравнение
Наши игры, головоломки, эмуляторы:
Немного теории.
Логарифмическая функция. Логарифмы
Задача 1. Найти положительный корень уравнения x4 = 81
По определению арифметического корня имеем ( x = sqrt[4]{81} = 3 )
Задача 2. Решить уравнение 3x = 81
Запишем данное уравнение так: 3x = 34, откуда x = 4
В задаче 1 неизвестным является основание степени, а в задаче 2 — показатель степени. Способ решения задачи 2 состоял в том,
что левую и правую части уравнения удалось представить в виде степени с одним и тем же основанием 3.
Но уже, например, уравнение 3x = 80 таким способом решить не удаётся. Однако это уравнение имеет корень.
Чтобы уметь решать такие уравнения, вводится понятие логарифма числа.
Уравнение ax = b, где a > 0, ( a neq 1 ), b > 0, имеет единственный корень. Этот корень называют
логарифмом числа b no основанию a и обозначают logab
Например, корнем уравнения 3x = 81 является число 4, т.е. log381 = 4.
Определение. Логарифмом положительного числа b по основанию a, где a > 0, ( a neq 1 ), называется показатель степени,
в которую надо возвести число a, чтобы получить b
Например:
log28 = 3, так как 23 = 8
( log_3 frac{1}{9} = -2 ), так как ( 3^{-2} = frac{1}{9} )
log77 = 1, так как 71 = 7
Определение логарифма можно записать так:
$$ a^{log_a b} = b $$
Это равенство справедливо при b > 0, b > 0, ( a neq 1 ). Его обычно называют основным логарифмическим тождеством.
Действие нахождения логарифма числа называют логарифмированием.
Действие нахождения числа по его логарифму называют потенцированием.
Вычислить log64128
Обозначим log64128 = х. По определению логарифма 64x = 128. Так как 64 = 26, 128 = 27,
то 2 6x = 27, откуда 6x = 7, х = 7/6.
Ответ log64128 = 7/6
Вычислить ( 3^{-2log_3 5} )
Используя свойства степени и основное логарифмическое тождество, находим
$$ 3^{-2log_3 5} = left( 3^{log_3 5} right)^{-2} = 5^{-2} = frac{1}{25}$$
Решить уравнение log3(1-x) = 2
По определению логарифма 32 = 1 – x, откуда x = -8
Свойства логарифмов
При выполнении преобразований выражений, содержащих логарифмы, при вычислениях и при решении уравнений часто используются
различные свойства логарифмов. Рассмотрим основные из них.
Пусть а > 0, ( a neq 1 ), b > 0, c > 0, r — любое действительное число. Тогда справедливы формулы:
1) loga(bc) = logab + logac
2) ( log_a frac{b}{c} = log_a b – log_a c )
3) logabr = r logab
Десятичные и натуральные логарифмы
Для логарифмов чисел составлены специальные таблицы (таблицы логарифмов). Логарифмы вычисляют также с помощью микрокалькулятора.
И в том и в другом случае находятся только десятичные или натуральные логарифмы.
Определение. Десятичным логарифмом числа называют логарифм этого числа по основанию 10 и пишут
lg b вместо log10b
Определение. Натуральным логарифмом числа называют логарифм этого числа по основанию e, где e — иррациональное число,
приближённо равное 2,7. При этом пишут ln b вместо logeb
Иррациональное число e играет важную роль в математике и её приложениях. Число e можно представить как сумму:
$$ e = 1 + frac{1}{1} + frac{1}{1 cdot 2} + frac{1}{1 cdot 2 cdot 3} + dots + frac{1}{1 cdot 2 cdot 3 cdot dots cdot n} + dots $$
или
$$ e = sum_{n=0}^{infty} frac{1}{n!} $$
$$ e approx 2,7182818284 $$
Оказывается, что достаточно знать значения только десятичных или только натуральных логарифмов чисел, чтобы находить логарифмы
чисел по любому основанию.
Для этого используется формула замены основания логарифма:
$$ log_a b = frac{log_c b}{log_c a} $$
где b > 0, a > 0, ( a neq 1 ), c > 0, ( c neq 1 )
Следствия из формулы замены основания логарифма.
При c = 10 и c = e получаются формулы перехода к десятичным и натуральным логарифмам:
$$ log_a b = frac{lg b}{lg a} , ;; log_a b = frac{ln b}{ln a} $$
Логарифмическая функция, её свойства и график
В математике и её приложениях часто встречается логарифмическая функция
y = logax
где а — заданное число, a > 0, ( a neq 1 )
Логарифмическая функция обладает свойствами:
1) Область определения логарифмической функции — множество всех положительных чисел.
2) Множество значений логарифмической функции — множество всех действительных чисел.
3) Логарифмическая функция не является ограниченной.
4) Логарифмическая функция y = logax является возрастающей на промежутке ( (0; +infty) ), если a > 1,
и убывающей, если 0 < a < 1.
5) Если a > 1, то функция y = logax принимает положительные значения при х > 1,
отрицательные при 0 < x < 1.
Если 0 < a < 1, то функция y = logax принимает положительные значения при 0 < х < 1,
отрицательные при х > 1.
Ось Oy является вертикальной асимптотой графика функции y = logax

Отметим, что график любой логарифмической функции y = logax проходит через точку (1; 0).
При решении уравнений часто используется следующая теорема:
Теорема. Если logax1 = logax2 где a > 0, ( a neq 1 ),
x1 > 0, x2 > 0, то x1 = x2
Логарифмическая функция y = logax и показательная функция y = ax, где a > 0, ( a neq 1 ), взаимно обратны.
Логарифмические уравнения
Решить уравнение log2(x+1) + log2(x+3) = 3
Предположим, что х — такое число, при котором равенство является верным, т.е. х — корень уравнения. Тогда по свойству логарифма
верно равенство
log2((x+1)(x+3)) = 3
Из этого равенства по определению логарифма получаем
(x+1)(x+3) = 8
х2 + 4х + 3 = 8, т.е. х2 + 4x – 5 = 0, откуда x1 = 1, х2 = -5
Так как квадратное уравнение является следствием исходного уравнения, то необходима проверка.
Проверим, являются ли числа 1 и -5 корнями исходного уравнения.
Подставляя в левую часть исходного уравнения х = 1, получаем
log2(1+1) + log2(1+3) = log22 + log24 = 1 + 2 = 3, т.е. х = 1 — корень уравнения.
При х = -5 числа х + 1 и х + 3 отрицательны, и поэтому левая часть уравнения не имеет смысла, т.е. х = -5 не является корнем этого
уравнения.
Ответ x = 1
Решить уравнение lg(2x2 – 4x + 12) = lg x + lg(x+3)
По свойству логарифмов
lg(2x2 – 4x + 12) = lg(x2 + 3x)
откуда
2x2 – 4x + 12 = x2 + 3x
x2 – 7x + 12 = 0
x1 = 3, х2 = 4
Проверка показывает, что оба значения х являются корнями исходного уравнения.
Ответ x1 = 3, х2 = 4
Решить уравнение log4(2x – 1) • log4x = 2 log4(2x – 1)
Преобразуем данное уравнение:
log4(2x – 1) • log4x – 2 log4(2x – 1) = 0
log4(2х – 1) • (log4 x – 2) = 0
Приравнивая каждый из множителей левой части уравнения к нулю, получаем:
1) log4 (2х – 1) = 0, откуда 2х – 1 = 1, х1 = 1
2) log4 х – 2 = 0, откуда log4 = 2, х2 = 16
Проверка показывает, что оба значения х являются корнями исходного уравнения.
Ответ x1 = 1, х2 = 16
Задать свой вопрос
*более 50 000 пользователей получили ответ на «Решим всё»
Задача 5231 log3(4-x)=2 найдите корень уравнения…
Условие
slava191
14.11.2015
log3(4-x)=2 найдите корень уравнения
математика 10-11 класс
17865
Решение
4-x = 9
-x = 5
x=-5
Ответ: -5
Вопросы к решению (1)
Написать комментарий
Меню
- Решим всё
- Найти задачу
- Категории
- Статьи
- Тесты
- Архив задач
Присоединяйся в ВК
Как решать логарифмические уравнения – подробный разбор
Опубликовано 12.01.2018
Чтобы ответить на вопрос как решать логарифмические уравнения давайте вспомним, что такое логарифм. Логарифм – это показатель степени, в которую нужно возвести основание логарифма, чтобы получить число.
Например,
или число 3 (показатель степени) мы можем записать так
, таким образом
Основание логарифма всегда положительное число, не равное 1. Число под знаком логарифма – строго больше нуля.
Теперь переходим непосредственно к вопросу – как решать логарифмические уравнения из профильного и из базового ЕГЭ.
Пример 1 Найдите корень уравнения.
согласно определению логарифма:
Все неизвестные переносим в левую часть уравнения (слева от =), а известные – переносим в правую сторону.
Получим:
Делаем проверку:
Ответ:
Пример 2. Найдите корень уравнения.
Здесь для решения данного логарифмического уравнения будем использовать свойство логарифма:
То есть внесем число 3 справа под знак логарифма.
или
Если показатели степени равны, основания степени равны, то равны числа, получаемые в результате, то есть получим
Делаем проверку:
Получаем:
Ответ:
Пример 3. Найдите корень уравнения
Используем следующее свойство логарифма:
Тогда получим:
Делаем проверку:
Ответ:
Пример 4. Найдите корень уравнения.
Используя определение логарифма, получим:
Проверим:
Ответ: .
Таким образом, теперь вы можете составить четкую инструкцию, как решать логарифмические уравнения. Она заключается в следующих шагах:
- Сделать справа и слева от знака равенства (=) логарифмы по одному основанию, избавившись от коэффициентов перед логарифмами, используя свойства логарифмов.
- Избавляемся от логарифмов, используя правило потенцирования. Остаются только числа, которые были под знаком логарифма.
- Решаем получившееся обычное уравнение – как найти корень уравнения смотрите здесь.
- Делаем проверку
- Записываем ответ.
( 4 оценки, среднее 5 из 5 )