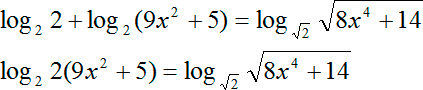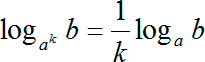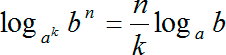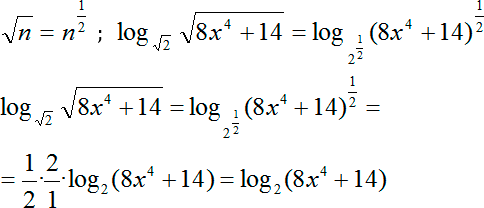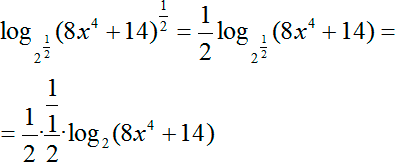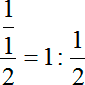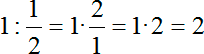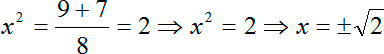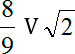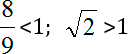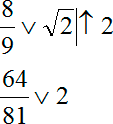Как найти корень уравнения при логарифмах

Как решать логарифмические уравнения

Уравнения, содержащие в том или ином виде логарифмы от некоторого выражения, зависящего от (х), называются логарифмическими.

Давайте сразу же рассмотрим пример, так будет легче всего разобраться.

Пример 1
$$ log_{2}(x)=log_{2}(5)$$

Мы видим слева и справа логарифмы с одинаковыми основаниями, равными (2). Вполне логично предположить, что логарифмы будут равны, если будут равны выражения, стоящие под логарифмом (их называют аргументами) – то есть (х=5). Мы только что решили логарифмическое уравнение!

На самом деле, абсолютно такая же логика применима при решении почти всех логарифмических уравнений – если у нас сравниваются два логарифма с одинаковыми основаниями, то мы можем избавиться от логарифмов, приравнять их аргументы и решить получившееся уравнение.

Пример 2
$$ log_{3}(2x+5)=log_{3}(11) $$

Опять имеем два логарифма с одинаковым основанием (3). Избавляемся от логарифмов, приравнивая аргументы:

$$ 2x+5=11,$$
$$ 2x=6,$$
$$ x=3.$$

Кажется, что все очень просто. Но есть несколько непростых нюансов, которые необходимо обсудить. Давайте посмотрим еще один пример:

Пример 3
$$ log_{2}(1+3x)=log_{2}(2x-3) $$

Смотрим на основания – они одинаковые, значит убираем логарифмы и решаем уравнение:

$$1+3x=2x-3,$$
$$3x-2x=-3-1,$$
$$x=-4.$$

Мы решили уравнение, но я хочу позанудствовать и проверить, действительно ли получившийся корень является корнем исходного уравнения. Для этого подставим его в логарифмическое уравнение:

$$ log_{2}(1+3*(-4))=log_{2}(2*(-4)-3),$$
$$log_{2}(-11)=log_{2}(-11).$$

Мы получили слева и справа два одинаковых логарифма, вот только эти логарифмы НЕ СУЩЕСТВУЮТ, потому что нельзя взять логарифм от отрицательного числа.

Действительно, давайте вспомним определение логарифма (log_{a}b) – это в какую степень нужно возвести (a), чтобы получить (b). При этом определение справедливо не для всех (a) и (b), а только для (a>0), (b>0), (a neq 1). Подробнее про логарифм и его свойства можно почитать здесь.

Значит, с нашим решением что-то не так – мы нашли корень, подставили его в уравнение, но получили логарифм от отрицательного числа, который не существует!

Тут самое время вспомнить про область допустимых значений (ОДЗ). В логарифмах нужно всегда внимательно следить за тем, чтобы не нарушались ограничения, которые вытекают из определения логарифма. Рассмотрим логарифм от некоторой функции:

$$log_{a}f(x)$$

Область допустимых значений (ОДЗ) для него будет задаваться системой неравенств:

$$ begin{cases}
f(x)>0, \
a>0, \
a neq 1.
end{cases}$$

И при решении любых логарифмических уравнений или неравенств всегда первым делом записываем ОДЗ для каждого логарифма в уравнении.
В нашем примере 3, ОДЗ будет выглядеть вот так:

$$ begin{cases}
1+3x>0, \
2x-3>0. \
end{cases}$$

Решаем получившуюся систему

$$ begin{cases}
x>-frac{1}{3}, \
x>frac{3}{2}. \
end{cases}$$

Находим (х), удовлетворяющие одновременно обоим неравенствам, и получаем в итоге ОДЗ:
$$x>frac{3}{2}.$$

Вспоминаем, что решая это уравнение мы получили корень (x=-4), который нашему ОДЗ не удовлетворяет. Поэтому в примере 3 корней нет.

И так, всегда пишем ОДЗ!

Следующая трудность при решении логарифмических уравнений возникает, когда у нас сравниваются логарифмы с разными основаниями:

Пример 4
$$ log_{2}(x)=log_{4}(9).$$

Запишем ОДЗ: (x>0).

У логарифма слева основание (2), а у логарифма справа основание (4). Чтобы воспользоваться способом решения, аналогичным первым трем примерам, необходимо привести логарифмы к одинаковому основанию.

$$ log_{2}(x)=log_{2}(3).$$

Ого, как я такое получил?
Просто воспользовался формулой возведения в степень основания и аргумента логарифма – если возвести в одинаковую степень, то логарифм от этого не поменяется:

$$ log_{a}(b)=log_{a^n}(b^n).$$

В нашем примере возведем основание и аргумент в степень (frac{1}{2}):

$$ log_{4}(9)=log_{4^{frac{1}{2}}}(9^{frac{1}{2}})=log_{2}(3).$$

$$ log_{2}(x)=log_{2}(3).$$

Ну теперь основании у логарифмов одинаковые и можно с чистым сердцем приравнять аргументы, как мы делали до этого.
$$x=3.$$

Кстати, решить уравнение (log_{2}(x)=log_{4}(9))
можно было и по-другому – привести к основанию (4) логарифм, стоящий слева в уравнении:

Опять воспользуемся свойством логарифма:
$$ log_{a}(b)=log_{a^n}(b^n);$$
$$log_{2}(x)=log_{2^2}(x^2)=log_{4}(x^2);$$
Подставим в исходное уравнение наши преобразования:
$$ log_{4}(x^2)=log_{4}(9);$$
Ура, у нас слева и справа логарифмы с одинаковым основанием – вычеркиваем логарифмы:
$$x^2=9;$$
Решаем аккуратно простейшее квадратное уравнение. Не забываем, что у него будет 2 корня!
$$x=pm3;$$

Опа, у нас получилось два корня. А когда мы решали первым способом был один корень! Что за дела?

Вспоминаем, что в самом начале к уравнению мы записывали ОДЗ (х>0). Тогда корень (x=-3) не удовлетворяет ОДЗ. Обратите внимание, что без учета ОДЗ в этом случае, мы бы получили неправильный ответ.

Ответ: (x=3.)

Подробнее про свойства логарифмов можно посмотреть тут. Логарифмические уравнения с разными основаниями встречаются в ЕГЭ регулярно, поэтому важно уметь применять все свойства логарифмов.

Рассмотрим еще один пример.

Пример 5
$$log_{5}(x)=2$$

Как видим, в примере есть только логарифм в левой части равенства, а справа стоит просто число 2. Давайте постараемся привести к такому же виду, как и в прошлых примерах. То есть сделаем так, чтобы справа появился логарифм с основанием 5.

Оказывается, любое число (a) можно представить в виде логарифма с нужным вам основанием (b) по формуле:
$$a=log_{b}(b^a);$$
Эту формулу можно просто запомнить. А въедливым читателям, я бы рекомендовал посидеть и подумать откуда берется данное выражение. Подсказка – оно напрямую вытекает из определения логарифма. Задайте себе вопрос – «В какую степень нужно возвести основание, чтобы получить аргумент?»

И так, воспользуемся формулой и распишем 2-ку:
$$2=log_{5}(5^2);$$
Подставим в уравнение:
$$log_{5}(x)=log_{5}(5^2);$$
Ура, у нас два логарифма с одинаковыми основаниями, теперь можно приравнять подлогарифмические выражения.
$$x=5^2;$$
$$x=25.$$

Пример 6
$$log_{3}(x+2)=0$$

Начинаем с ОДЗ:
$$x+2>0;$$
$$x>-2.$$

Приступаем к решению уравнения. Что делать в случае, когда справа стоит (0)? Ничего страшного в этом нет, действуем по прежнему плану – представим (0) в виде логарифма по нашей формуле:
$$a=log_{b}(b^a);$$
$$log_{3}(x+2)=log_{3}(3^0);$$
Вспоминаем, что любое число в нулевой степени это единица.
$$log_{3}(x+2)=log_{3}(1);$$
$$x+2=1;$$
$$x=-1.$$
Корень удовлетворяет ОДЗ – записываем ответ.
Ответ: (x=-1).

Подведем итоги. В большинстве случаев, для того, чтобы решить простейшее логарифмическое уравнение, необходимо привести логарифмы слева и справа к одинаковому основанию. Затем приравнять подлогарифмические выражения и решить получившееся уравнения. При этом ни в коем случае не забываем про ОДЗ. На ЕГЭ, если вы вдруг запишите в ответ хотя бы один корень, не удовлетворяющий ОДЗ, то вам поставят за это задание 0 баллов.

В общем виде формула для решения логарифмов выглядит так:
$$ log_{a}(f(x))=log_{a}(g(x)) qquad (*)$$
где (a>0) – основание логарифмов, а (f(x)) и (g(x)) – какие-то выражения, зависящие от (x).
$$ begin{cases}
f(x)>0, или \
g(x)>0. \
end{cases}$$
$$f(x)=g(x).$$

Обратите внимание на «или» в ОДЗ. Оказывается можно накладывать условие больше нуля только на одную функцию: либо на f(x), либо на g(x) – смотря какое неравенство вам кажется легче для решения. Дело в том, что если одна из функций будет больше нуля, то и другая автоматически тоже будет будет больше, ведь мы ищем корни, при которых (f(x)=g(x)).

Для того, чтобы закрепить материал, решим еще одно логарифмическое уравнение:

Пример 7
$$2*log_{4}(4+x)=4-log_{2}(x-2);$$

Здесь все несколько сложнее, чем в предыдущих примерах. Для того чтобы представить наше уравнение в виде (*), нужно избавиться от множителя (2) перед первым логарифмом, кроме этого, нам мешается отдельное слагаемое (4), и в придачу ко всем этим неприятностям у логарифмов разные основания!

Но перед тем как решать, запишем ОДЗ:
$$ begin{cases}
4+x>0, \
x-2>0. \
end{cases}$$

$$ begin{cases}
x>-4, \
x>2. \
end{cases}$$

Находим пересечение и в итоге ОДЗ получается:
$$ x>2.$$

Приступаем непосредственно к решению уравнения. Самое главное, нам необходимо привести все логарифмы к одинаковому основанию, и, по возможности, привести к виду (log_{a}f(x)=log_{a}g(x)).
Здесь не обойтись без свойств логарифмов.
Воспользуемся формулой вынесения степени из основания логарифма:
$$log_{a^n}(b)=frac{1}{n}*log_{a}(b)$$
$$log_{4}(4+x)=log_{2^2}(4+x)=frac{1}{2}*log_{2}(4+x)$$

Подставим в уравнение
$$2*frac{1}{2}*log_{2}(4+x)=4-log_{2}(x-2);$$
$$log_{2}(4+x)=4-log_{2}(x-2);$$
Теперь у нас хотя бы логарифмы с одинаковым основанием. Далее преобразуем левую часть уравнения, воспользовавшись формулами:
$$ a=log_{b}(b^a);$$
$$log_{a}(b)-log_{a}(c)=log_{a}(frac{b}{c})$$
$$4-log_{2}(x-2)=log_{2}(2^4)-log_{2}(2-x)=log_{2}(16)-log_{2}(2-x)=log_{2}(frac{16}{2-x});$$
Подставим получившееся выражение в уравнение:
$$log_{2}(4+x)=log_{2}(frac{16}{2-x});$$

Ура, теперь у нас слева и справа в уравнении логарифмы с одинаковым основанием (2).
Избавляемся от логарифмов и решаем:
$$4+x=frac{16}{x-2};$$
Перекинем все налево и приведем к общему знаменателю
$$4+x-frac{16}{x-2}=0;$$
$$frac{(4+x)(x-2)}{x-2}—frac{16}{x-2}=0;$$
$$frac{4x-8+x^2-2x–16}{x-2}=0;$$
$$frac{x^2+2x-24}{x-2}=0;$$
Дробь равна 0, когда числитель равен 0
$$x^2+2x-24=0;$$
$$D=(2^2-4*(-24)=4+96=100;$$
$${x}_{1,2}=frac{-2pm 10}{2};$$
$${x}_{1}=4;$$
$${x}_{2}=-6;$$
Мы получили два корня. Но не забываем про ОДЗ. Выше мы его посчитали и получилось, что (x>2). Значит второй корень не подходит.
Ответ: (x=4).

Логарифмические уравнения с переменным основанием

Рассмотри теперь уравнение, в котором есть, так называемый, логарифм с переменным основанием. То есть логарифм, у которого в основании стоит какое-то выражение, зависящее от (х).

Пример 8
$$log_{1-x}(x^2+3x+1)=1;$$

В основании логарифма стоит ((1-х)), это переменное основание, потому что я могу подставлять различные значения (х) и каждый раз основание логарифма будет разным. Ничего страшного в этом нет, начинаем решать, руководствуясь тем же принципом, что и в предыдущих примерах – стараемся привести обе части уравнения к виду двух логарифмов с одинаковым основанием. Для этого нужно представить (1) справа в виде логарифма с основанием ((1-х)).

Но первым делом выпишем ОДЗ, не забывая накладывать условия и на основание логарифма, так как оно зависит от (х):
$$ begin{cases}
x^2+3x+1>0, \
1-x>0, \
1-xneq1.\
end{cases} qquad (**)$$

Теперь приступаем к решению самого уравнения. Выпишем еще раз формулу, по которой преобразуем правую часть:

$$a=log_{b}(b^a);$$
Где (а=1), а (b=1-x):
$$1=log_{1-x}(1-x)^1=log_{1-x}(1-x);$$
Подставим в уравнение
$$log_{1-x}(x^2+3x+1)=log_{1-x}(1-x);$$

Два логарифма с одинаковым основанием – можем приравнять аргументы:
$$x^2+3x+1=1-x;$$
$$x^2+4x=0;$$
$$x(x+4)=0;$$
$$x=0;$$
$$x=-4.$$
Получили два корня, проверим удовлетворяют ли они ОДЗ, подставив их в (**). Корень (0) не удовлетворяет последнему неравенству в ОДЗ, а ((-4)) удовлетворяет всем условиям.
Ответ: x=-4.

Замена переменной в уравнениях с логарифмами

Разберем еще один частый тип логарифмических уравнений – это уравнения с заменой переменной. Общий принцип заключается в том, чтобы привести все логарифмы в уравнении к одинаковому основанию и одинаковому аргументу, а потом сделать замену.

Проще разобрать на примерах:

Пример 9

$$log^2_{2}(x)+6=5*log_{2}(x)$$

Как и любой пример на логарифмы, начинаем с ОДЗ:

$$x>0.$$

В уравнении один из логарифмов в квадрате, поэтому представить в виде равенства двух логарифмов, как мы делали в предыдущих примерах, не получится. Кроме этого, замечаем, что у нас оба логарифма абсолютно одинаковые (у них одинаковые основания, и одинаковые аргументы).

Попробуем сделать замену:
$$t=log_{2}(x)$$
Тогда наше уравнение после замены примет вид:
$$t^2-5t+6=0;$$
$$D=25-24=1;$$
$$t_{1}=frac{5+1}{2}=3;$$
$$t_{2}=frac{5-1}{2}=1;$$
И сделаем обратную замену, получив два простых логарифмических уравнения:
$$t_{1}=log_{2}(x)=3;$$
$$log_{2}(x)=log_{2}(2^3);$$
$$x=8.$$
$$t_{2}=log_{2}(x)=1;$$
$$log_{2}(x)=log_{2}(2^1);$$
$$x=2.$$
Обязательно, не забываем проверить, удовлетворяют ли корни ОДЗ ((x>0)). Оба корня подходят, записываем ответ.
Ответ: (x=8; , x=2.)

Пример 10
$$ log_{2}left(frac{8}{x}right)-frac{10}{log_{2}(16x)} = 0;$$

Как обычно, начинаем с ОДЗ:
$$ begin{cases}
frac{8}{x}>0, \
log_{2}(16x)neq0,\
16x>0.\
end{cases}$$

Решаем каждое из получившихся неравенств в системе:
$$ begin{cases}
x>0, \
xneqfrac{1}{16},\
x>0.\
end{cases}$$
В итоге ОДЗ будет: (xin(0;frac{1}{16})cup(frac{1}{16};infty)).

Посмотрим теперь на сам пример. Видим два логарифма, у них одинаковые основания, что хорошо. Но функции, стоящие под логарифмами, разные. Постараемся при помощи свойств логарифма сделать одинаковые аргументы, чтобы потом сделать замену.

Воспользуемся формулами суммы и разности логарифмов с одинаковыми основаниями:
$$log_{a}(b*c)=log_{a}(b)+log_{a}(c);$$
$$log_{a}(frac{b}{c})=log_{a}(b)-log_{a}(c);$$
$$log_{2}left(frac{8}{x}right)=log_{2}(8)-log_{2}(x)=3-log_{2}(x);$$
$$log_{2}(16x)=log_{2}(16)+log_{2}(x)=4+log_{2}(x);$$
Подставим наши преобразования в исходное уравнение
$$3-log_{2}(x)-frac{10}{4+log_{2}(x)}=0;$$
Теперь в уравнении все логарифмы одинаковые, модем сделать замену. Пусть (t=log_{2}(x)).
$$3-t-frac{10}{4+t}=0;$$
Приводим к общему знаменателю
$$frac{(3-t)(4+t)-10}{4+t}=0;$$
$$frac{-t^2-t+2}{4+t}=0;$$
Дробь равна нулю, когда числитель равен нулю:
$$-t^2-t+2=0;$$
$$t_{1}=1;$$
$$t_{2}=-2;$$
Делаем обратную замену:
$$t_{1}=log_{2}(x)=1;$$
$$log_{2}(x)=log_{2}(2^1);$$
$$x=2.$$
$$t_{2}=log_{2}(x)=-2;$$
$$log_{2}(x)=log_{2}({2}^{-2});$$
$$x=frac{1}{4}.$$
Сверяем с ОДЗ, видим, что оба корня подходят, записываем ответ.
Ответ: (x=2; , x=frac{1}{4}.)

Пример 11
$$log_{2}(x^2+4x)+log_{0,5}(frac{x}{4})+2=log_{2}(x^2+3x-4)$$

Область допустимых значений:
$$ begin{cases}
x^2+4x>0, \
x^2+3x-4>0,\
x>0.\
end{cases}$$

$$ begin{cases}
x(x+4)>0, \
x>0,\
(x-1)(x+4)>0.\
end{cases}$$

Зеденым цветом показано решение первого неравенства в системе, синим – второго и фиолетовым третьего. Область, которая находится на пересечении сразу всех трех промежутков заштрихована бордовым.

Решаем методом интервалов, и находим пересечение решений всех неравенств в системе:

В итоге получаем ОДЗ: (x>1).

Приступаем к решению самого уравнения. Первым делом приведем все логарифмы к одинаковому основанию (2). Для этого нужно преобразовать только второе слагаемое в уравнении:
$$0,5=frac{1}{2}=2^{-1};$$
$$log_{2}(x^2+4x)+log_{2^{-1}}(frac{x}{4})+2=log_{2}(x^2+3x-4);$$
Вынесем степень из основания, воспользовавшись формулой (log_{a^n}(b)=frac{1}{n}log_{a}(b)).
$$log_{2}(x^2+4x)-log_{2}(frac{x}{4})+2=log_{2}(x^2+3x-4);$$
В первом слагаемом под логарифмом вынесем общий множитель (х). А квадратный многочлен под логарифмом справа разложим на множители при помощи дискриминанта:
$$log_{2}(x(x+4))-log_{2}(frac{x}{4})+2=log_{2}((x-1)(x+4));$$
И опять воспользуемся формулами суммыразности логарифмов:

$$log_{a}(b*c)=log_{a}(b)+log_{a}(c);$$
$$log_{a}left(frac{b}{c}right)=log_{a}(b)-log_{a}(c);$$
$$log_{2}(x)+log_{2}(x+4)-log_{2}(x)+log_{2}(4)+2=log_{2}(x-1)+log_{2}(x+4);$$
Сократим подобные слагаемые и посчитаем (log_{2}(4)=2):
$$4=log_{2}(x-1);$$
$$log_{2}(x-1)=4;$$
$$log_{2}(x-1)=log_{2}(2^4);$$
$$x-1=16;$$
$$x=17.$$
Сверяем корень с ОДЗ – подходит. Записываем ответ.
Ответ: (x=17).

Как решать логарифмические уравнения – подробный разбор

Опубликовано 12.01.2018

Чтобы ответить на вопрос как решать логарифмические уравнения давайте вспомним, что такое логарифм. Логарифм – это показатель степени, в которую нужно возвести основание логарифма, чтобы получить число.

Например,

или число 3 (показатель степени) мы можем записать так  , таким образом 

Основание логарифма всегда положительное число, не равное 1. Число под знаком логарифма – строго больше нуля.

Теперь переходим непосредственно к вопросу – как решать логарифмические уравнения из профильного и из базового ЕГЭ.

Пример 1 Найдите корень уравнения.

согласно определению логарифма:

Все неизвестные переносим в левую часть уравнения (слева от =), а известные – переносим в правую сторону.

Получим:

Делаем проверку:

Ответ:

Пример 2. Найдите корень уравнения.

Здесь для решения данного логарифмического уравнения будем использовать свойство логарифма:

То есть внесем число 3 справа под знак логарифма.

или

Если показатели степени равны, основания степени равны, то равны числа, получаемые в результате, то есть получим

Делаем проверку:

Получаем:

Ответ:

Пример 3. Найдите корень уравнения

Используем следующее свойство логарифма:

Тогда получим:

Делаем проверку:

Ответ:

Пример 4. Найдите корень уравнения.

Используя определение логарифма, получим:

Проверим:

Ответ: .

Таким образом, теперь вы можете составить четкую инструкцию, как решать логарифмические уравнения. Она заключается в следующих шагах:

1. Сделать справа и слева от знака равенства (=) логарифмы по одному основанию, избавившись от коэффициентов перед логарифмами, используя свойства логарифмов.
2. Избавляемся от логарифмов, используя правило потенцирования. Остаются только числа, которые были под знаком логарифма.
3. Решаем получившееся обычное уравнение – как найти корень уравнения смотрите здесь.
4. Делаем проверку
5. Записываем ответ.

( 4 оценки, среднее 5 из 5 )

18 февраля 2014

В этом видеоуроке мы рассмотрим решение довольно серьезного логарифмического уравнения, в котором не просто требуется найти корни, но и отобрать те из них, которые лежат на заданном отрезке.

Задача C1. Решите уравнение. Найдите все корни этого уравнения, принадлежащие промежутку.

Замечание по поводу логарифмический уравнений

Перед тем как переходить непосредственно к уравнению, хочу поделиться небольшой исторической справкой. Дело в том, что ЕГЭ по математике в том виде, котором нам предстоит его сдавать, существует в России уже не первый год. И то уравнение, которое вы сейчас видите на своих экранах, появилось в контрольно-измерительных материалах уже давно.

Однако из года в год ко мне приходят ученики которые пытаются решать вот такие, прямо скажем, непростые уравнения, но при этом не могут понять: с чего им вообще начинать и как подступиться к логарифмам? Такая проблема может возникнуть даже у сильных, хорошо подготовленных учеников.

В результате многие начинают опасаться этой темы, а то и вовсе считать себя тупыми. Так вот, запомните: если у вас не получается решить такое уравнение, это совершенно не значит, что вы — тупые. Потому что, например, вот с таким уравнением вы справитесь практически устно:

log₂ x = 4

А если это не так, вы сейчас не читали бы этот текст, поскольку были заняты более простыми и приземленными задачами. Конечно, кто-то сейчас возразит: «А какое отношение это простейшее уравнение имеет к нашей здоровой конструкции?» Отвечаю: любое логарифмическое уравнение, каким бы сложным оно ни было, в итоге сводится вот к таким простейшим, устно решаемым конструкциям.

Разумеется, переходить от сложных логарифмических уравнений к более простым нужно не с помощью подбора или танцев с бубном, а по четким, давно определенным правилам, которые так и называются — правила преобразования логарифмических выражений. Зная их, вы без труда разберетесь даже с самыми навороченными уравнениями в ЕГЭ по математике.

И именно об этих правилах мы будем говорить в сегодняшнем уроке. Поехали!

Решение логарифмического уравнения в задаче C1

Итак, решаем уравнение:

В первую очередь, когда речь заходит о логарифмических уравнениях, вспоминаем основную тактику — если можно выразиться, основное правило решения логарифмических уравнений. Заключается оно в следующем:

Теорема о канонической форме. Любое логарифмическое уравнение, что бы в него не входило, какие бы логарифмы, по какому бы основанию, и что бы в себе не cодержали, обязательно нужно привести к уравнению вида:

log_a f (x) = log_a g(x)

Если мы посмотрим на наше уравнение, то заметим сразу две проблемы:

1. Слева у нас стоит сумма двух чисел, одно из которых вообще не является логарифмом.
2. Справа стоит вполне себе логарифм, однако в его основании стоит корень. А у логарифма слева — просто 2, т.е. основания логарифмов слева и справа различаются.

Итак, мы составили этакий список проблем, которые отделяют наше уравнение от того канонического уравнения, к которому нужно привести любое логарифмическое уравнение в процессе решения. Таким образом, решение нашего уравнения на данном этапе сводится к тому, чтобы устранить описанные выше две проблемы.

Любое логарифмическое уравнение решается быстро и легко, если свести его к канонической форме.

Сумма логарифмов и логарифм произведения

Давайте действовать по порядку. Сначала разберемся с конструкцией, которая стоит слева. Что мы можем сказать про сумму двух логарифмов? Давайте вспомним замечательную формулу:

log_a f (x) + log_a g(x) = log_a f (x) · g(x)

Но стоить учесть, что в нашем случае первое слагаемо вообще не является логарифмом. Значит, нужно представить единицу в виде логарифма по основанию 2 (именно 2, потому что слева стоит логарифм по основанию 2). Как это сделать? Опять вспоминаем замечательную формулу:

a = log_b b^a

Здесь нужно понимать: когда мы говорим «Любое основание b», то подразумеваем, что b все-таки не может быть произвольным числом. Если мы вставляем какое-то число в логарифм, на него сразу накладываются определенные ограничения, а именно: основание логарифма должно быть больше 0 и не должно быть равно 1. Иначе логарифм просто не имеет смысла. Запишем это:

0 < b ≠ 1

Давайте посмотрим, что происходит в нашем случае:

1 = log₂ 2¹ = log₂ 2

Теперь перепишем все наше уравнение с учетом этого факта. И сразу же применяем другое правило: сумма логарифмов равна логарифму произведения аргументов. В итоге получим:

Мы получили новое уравнение. Как видим, оно уже гораздо ближе к тому каноническому равнению, к которому мы стремимся. Но есть одна проблема, мы записали ее в виде второго пункта: у наших логарифмов, которые стоят слева и справа, разные основания. Переходим к следующему шагу.

Правила вынесения степеней из логарифма

Итак у логарифма, который стоит слева, основание просто 2, а у логарифма, который стоит справа, в основании присутствует корень. Но и это не является проблемой, если вспомнить, что из оснований из аргументов логарифма можно выносить в степень. Давайте запишем одно из этих правил:

log_a bⁿ = n · log_a b

Переведя на человеческий язык: можно выносить степень из основания логарифма и ставить ее спереди в качестве множителя. Число n «мигрировало» из логарифма наружу и стало коэффициентом спереди.

С тем же успехом мы можем вынести степень из основания логарифма. Выглядеть это будет так:

Другими словами, если вынести степень из аргумента логарифма, эта степень также пишется в качестве множителя перед логарифмом, но уже не в виде числа, а в виде обратного числа 1/k.

Однако и это еще не все! Мы можем объединить две данные формулы и почить следующую формулу:

Когда степень стоит и в основании, и в аргументе логарифма, мы можем сэкономить время и упростить вычисления, если сразу же вынести степени и из основания, и из аргумента. При этом то, что стояло в аргументе (в нашем случае это коэффициент n), окажется в числителе. А то, что было степенью у основания, a^k, отправится в знаменатель.

И именно эти формулы мы сейчас будем применять для того, чтобы свести наши логарифмы к одному и тому же основанию.

Вынесение степени из основания логарифма

Прежде всего, выберем более-менее красивое основание. Очевидно, что с двойкой в основании намного приятней работать, чем с корнем. Таким образом, давайте попробуем привести второй логарифм к основанию 2. Давайте выпишем этот логарифм отдельно:

Что мы можем здесь сделать? Вспомним формулу степени с рациональным показателем. Другими словами, мы можем записать в корни в качестве степени с рациональным показателем. А затем выносим степень 1/2 и из аргумента, и из основания логарифма. Сокращаем двойки в коэффициентах в числителе и знаменателе, стоящих перед логарифмом:

Наконец, перепишем исходное уравнение с учетом новых коэффициентов:

log₂ 2(9x² + 5) = log₂ (8x⁴ + 14)

Мы получили каноническое логарифмическое уравнение. И слева, и справа у нас стоит логарифм по одному и тому же основанию 2. Помимо этих логарифмов никаких коэффициентов, никаких слагаемых ни слева, ни справа нет.

Следственно, мы можем избавиться от знака логарифма. Разумеется, с учетом области определения. Но прежде, чем это сделать, давайте вернемся назад и сделаем небольшое уточнение по поводу дробей.

Деление дроби на дробь: дополнительные соображения

Далеко не всем ученикам понятно, откуда берутся и куда деваются множители перед правым логарифмом. Запишем еще раз:

Давайте разберемся, что такое дробь. Запишем:

А теперь вспоминаем правило деления дробей: чтобы разделить на 1/2 нужно умножить на перевернутую дробь:

Разумеется, для удобства дальнейших вычислений мы можем записать двойку как 2/1 — и именно это мы наблюдаем в качестве второго коэффициента в процессе решения.

Надеюсь, теперь всем понятно, откуда берется второй коэффициент, поэтому переходим непосредственно к решению нашего канонического логарифмического уравнения.

Избавление от знака логарифма

Напоминаю, что сейчас мы можем избавиться от логарифмов и оставить следующее выражение:

2(9x² + 5) = 8x⁴ + 14

Давайте раскроем скобки слева. Получим:

18x² + 10 = 8x⁴ + 14

Перенесем все из левой части в правую:

8x⁴ + 14 − 18x² − 10 = 0

Приведем подобные и получим:

8x⁴ − 18x² + 4 = 0

Можем разделить обе части этого уравнения на 2, чтобы упростить коэффициенты, и получим:

4x⁴ − 9x² + 2 = 0

Перед нами обычное биквадратное уравнение, и его корни легко считаются через дискриминант. Итак, запишем дискриминант:

D = 81 − 4 · 4 · 2 = 81 − 32 = 49

Прекрасно, Дискриминант «красивый», корень из него равен 7. Все, считаем сами иксы. Но в данном случае корни получатся не x, а x², потому что у нас биквадратное уравнение. Итак, наши варианты:

Обратите внимание: мы извлекали корни, поэтому ответов будет два, т.к. квадрат — функция четная. И если мы напишем лишь корень из двух, то второй корень мы просто потеряем.

Теперь расписываем второй корень нашего биквадратного уравнения:

Опять же, мы извлекаем арифметический квадратный корень из обеих частей нашего уравнения и получаем два корня. Однако помните:

Недостаточно просто приравнять аргументы логарифмов в канонической форме. Помните об области определения!

Итого мы получили четыре корня. Все они действительно являются решениями нашего исходного уравнения. Взгляните: в нашем исходном логарифмическом уравнении внутри логарифмов стоит либо 9x² + 5 (эта функция всегда положительна), либо 8x⁴ + 14 — она тоже всегда положительна. Следовательно, область определения логарифмов выполняется в любом случае, какой бы корень мы не получили, а это значит, что все четыре корня являются решениями нашего уравнения.

Прекрасно, теперь переходим ко второй части задачи.

Отбор корней логарифмического уравнения на отрезке

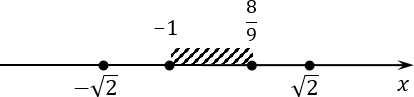
Отбираем из наших четырех корней те, которые лежат на отрезке [−1; 8/9]. Возвращаемся к нашим корням, и сейчас будем выполнять их отбор. Для начала предлагаю начертить координатную ось и отметить на ней концы отрезка:

Обе точки будут закрашенные. Т.е. по условию задачи нас интересует заштрихованный отрезок. Теперь давайте разбираться с корнями.

Иррациональные корни

Начнем с иррациональных корней. Заметим, что 8/9 < 9/9 = 1. С другой стороны, корень из двух явно больше единицы. Следовательно, наши корни будут находиться на отрезке в таком положении:

Из этого следует, что корень из двух не попадает в интересующий нас отрезок. Аналогично мы получим и с отрицательным корнем: он меньше, чем −1, т. е. лежит левее интересующего нас отрезка.

Рациональные корни

Остается два корня: x = 1/2 и x = −1/2. Давайте заметим, что левый конец отрезка (−1) — отрицательный, а правый (8/9) — положительный. Следовательно, где-то между этими концами лежит число 0. Корень x = −1/2 будет находиться между −1 и 0, т.е. попадет в окончательный ответ. Аналогично поступаем с корнем x = 1/2. Этот корень также лежит на рассматриваемом отрезке.

Убедиться, что число 8/9 больше, чем 1/2, можно очень просто. Давайте вычтем эти числа друг из друга:

Получили дробь 7/18 > 0, а это по определению означает, что 8/9 > 1/2.

Давайте отметим подходящие корни на оси координат:

Окончательным ответом будут два корня: 1/2 и −1/2.

Сравнение иррациональный чисел: универсальный алгоритм

В заключении хотел бы еще раз вернуться к иррациональным числам. На их примере мы сейчас посмотрим, как сравнивать рациональные и иррациональные величины в математике. Для начала по между ними вот такую галочку V — знак «больше» или «меньше», но мы пока не знаем, в какую сторону он направлен. Запишем:

Зачем вообще нужны какие-то алгоритмы сравнения? Дело в том, что в данной задаче нам очень повезло: в процессе решения возникло разделяющее число 1, про которое мы точно можем сказать:

Однако далеко не всегда вы с ходу увидите такое число. Поэтому давайте попробуем сравнить наши числа «в лоб», напрямую.

Как это делается? Делаем то же самое, что и с обычными неравенствами:

1. Сначала, если бы у нас где-то были отрицательные коэффициенты, то мы умножили бы обе части неравенства на −1. Разумеется, поменяв при этом знак. Вот такая галочка V изменилась бы на такую — Λ.
2. Но в нашем случае обе стороны уже положительны, поэтому ничего менять не надо. Что действительно нужно, так это возвести обе части в квадрат, чтобы избавится от радикала.

Если при сравнении иррациональных чисел не удается с ходу подобрать разделяющий элемент, рекомендую выполнять такое сравнение «в лоб» — расписывая как обычное неравенство.

При решении это оформляется вот таким образом:

Теперь это все легко сравнивается. Дело в том, что 64/81 < 81/81 = 1 < 2. На основании той цепочки преобразований мы заключаем, что 64/81 < 2 и, следовательно, корень больше 8/9.

Все, мы получили строгое доказательство, что все числа отмечены на числовой прямой х правильно и именно в той последовательности, в которой они должны быть на самом деле. Вот к такому решению никто не придерется, поэтому запомните: если вы сразу не видите разделяющее число (в нашем случае это 1), то смело выписывайте приведенную выше конструкцию, умножайте, возводите в квадрат — и в итоге вы получите красивое неравенство. Из этого неравенства точно будет понятно, какое число больше, а какое — меньше.

Возвращаясь к нашей задаче, хотелось бы еще раз обратить ваше внимание на то, что мы делали в самом начале при решении нашего уравнения. А именно: мы внимательно посмотрели на наше исходное логарифмическое уравнение и попытались свести его к каноническому логарифмическому уравнению. Где слева и справа стоят только логарифмы — без всяких дополнительных слагаемых, коэффициентов спереди и т. д. Нам нужны не два логарифма по основанию a или b, именно логарифм, равный другому логарифму.

Кроме того, основания логарифмов также должны быть равны. При этом если уравнение составлено грамотно, то с помощью элементарных логарифмических преобразований (сумма логарифмов, преобразование числа в логарифм и т.д.) мы сведем это уравнение именно к каноническому.

Поэтому впредь, когда вы видите логарифмическое равнение, которое не решается сразу «в лоб», не стоит теряться или пробовать подобрать ответ. Достаточно выполнить следующие шаги:

1. Привести все свободные элементы к логарифму;
2. Затем эти логарифмы сложить;
3. В полученной конструкции все логарифмы привести к одному и тому же основанию.

В результате вы получите простое уравнение, которое решается элементарными средствами алгебры из материалов 8—9 класса. В общем, заходите на мой сайт, тренируйтесь решать логарифмы, решайте логарифмические уравнения как я, решайте их лучше меня. А у меня на этом все. С Вами был Павел Бердов. До новых встреч!

Смотрите также:

1. Задача C1: логарифмы и тригонометрия в одном уравнении
2. Задача C1: еще одно показательное уравнение
3. Тест к уроку «Что такое логарифм» (средний)
4. Решение задач B12: №448—455
5. Как решать задачу 18: графический подход
6. Задача B15: частный случай при работе с квадратичной функцией

В продолжении темы.

Для начала сразу обозначим, что способов решения логарифмических уравнений есть несколько. Я опишу два. Если у вас есть свой способ, поделитесь в комментариях.

Уже несколько лет, мне перестали попадаться дети, которые понимают, что такое логарифм. Поэтому решение логарифмических уравнений даётся им с трудом. Приходится идти на всякие хитрости и ухищрения, чтобы ребенок при решении написал всё, что нужно, не понимая зачем. Впрочем, не будем слишком сильно растягивать вступление.

Итак, для начала обозначим два типа логарифмических уравнений, про которые будем говорить.

То есть, уравнение с которым мы работаем мы должны привести к одному из данных типов, используя свойства логарифма. Если не приводится, можно использовать метод замены переменной или еще что-нибудь нашаманить. Принципиальной разницы между этими двумя типами нет: из первого можно сделать второй, из второго первый. Но на практике удобней их разграничивать.

Теперь вспомним, что логарифмическая функция определена не на всём множестве значений переменной, а только на положительных значениях. Это значит, что при решении логарифмического уравнения, нам придется затрагивать тему отбора корней. Это может быть ОДЗ, может быть проверка или что-то еще.

Рассмотрим решение первого типа уравнений, которое часто называют простейшее логарифмическое уравнение. Если основание логарифма положительное и не равно единицы (в противном случае уравнение не решается), то данное уравнение имеет один корень.

Оговоримся, что нахождение ОДЗ или ограничение на выражение под логарифмом, в данном случае, излишне, потому что степень всегда положительна, при положительном основании. Но, когда вы работаете с детьми, вы должны оценить риски. Если вы скажете им, что нахождение ОДЗ в уравнениях подобного типа не нужно, они могут запомнить, что ОДЗ не нужно вообще и возникнут проблемы. Всё зависит от того с какими детьми мы разговариваем.

Теперь рассмотрим схему решений уравнения второго типа. Здесь без ОДЗ мы уже не обойдемся. Используя второй способ, мы тоже находим область допустимых значений, но в неявном виде.

В первом способе при нахождении ОДЗ достаточно только одного какого-то неравенства, потому что затем мы приравниваем функции и вторая также автоматически станет положительной. Но опять же нельзя отбросить второе условие сразу же, есть риск, что дети останутся без осознания почему мы это делаем. Возникнет много вопросов, а при решении неравенств эти вопросы опять вылезут.

И наконец, самое интересное, какой способ лучше. Буду повторять это стопятьсот тысяч раз. Учителю необходимо учитывать конкретную ситуацию и, исходя из нее, решать, что говорить детям. Я категорически против того, чтобы выбрать один способ и везде и всюду использовать только его. Это ужасная узость мышления, которая опасна в жизни и ужасно неуместна в математике. Детей необходимо учить оценивать трудоемкость каждого способа и давать им возможность выбирать.

Я хочу привести несколько примеров, иллюстрирующих необходимость ОДЗ, для всех кто сомневается, что это важное понятие.

По-моему, в уравнениях подобного типа ОДЗ стоит находить всегда в начале решения. Потому что, когда мы начнем его решать, можно забыть, что оно имело какие-то ограничения и, получив ответ с облегчением записать все полученные числа. В данном случае ОДЗ – множество положительных чисел.

Дальше преобразуем наше уравнение, чтобы свести его к одному из типов.

Теперь посмотрим, что будет, если мы не станем искать ОДЗ, а будем использовать переход к равносильной системе.

Надеюсь проблема видна всем. И подобное “расширение” ОДЗ будет происходить всегда, при решении уравнения с преобразованиями.

Думаю, на этом мы пока остановимся, спасибо всем кто дочитал до этого момента. Еще несколько примеров рассмотрим в следующей статье. Не переключайтесь!

Логарифмические уравнения — коротко о главном

Определение логарифмических уравнений

Логарифмическое уравнение — уравнение, в котором неизвестные переменные находятся внутри логарифмов.

Простейшим логарифмическим уравнением является уравнение вида ( displaystyle lo{{g}_{a}}~x~=~b).

Процесс решения любого логарифмического уравнения сводится к приведению логарифмического уравнения к виду ( displaystyle lo{{g}_{a}}left( fleft( x right) right)~=~lo{{g}_{a}}left( gleft( x right) right)), и переходе от уравнения с логарифмами к уравнению без них: ( displaystyle fleft( x right)=gleft( x right)).

ОДЗ (Область допустимых значений) для логарифмического уравнения:

( displaystyle left{ begin{align}& f(x)>0,\ & a>0,text{}\& ane 1.\end{align}right.)

5 основных методов решения логарифмических уравнений:

1 метод. Использование определения логарифма:

( displaystyle lo{{g}_{a}}~f(x)=b Leftrightarrow ~f(x)={{a}^{b}}, a>0, ane 1).

2 метод. Использование свойств логарифма:

• ( displaystyle lo{{g}_{{{a}^{c}}}}b=frac{1}{c}lo{{g}_{a}}b)
• ( displaystyle ccdot lo{{g}_{a}}b=lo{{g}_{a}}{{b}^{c}})
• ( displaystyle lo{{g}_{a}}b+lo{{g}_{a}}c=lo{{g}_{a}}left( bc right))
• ( displaystyle lo{{g}_{a}}b-lo{{g}_{a}}c=lo{{g}_{a}}left( frac{b}{c} right))
• ( displaystyle {{log }_{{{a}^{n}}}}b=frac{1}{n}cdot {{log }_{a}}b)
• ( displaystyle {{log }_{{{a}^{n}}}}{{b}^{m}}=frac{m}{n}cdot {{log }_{a}}b)
• ( displaystyle lo{{g}_{a}}1=0,~a>0,ane 1)
• ( displaystyle lo{{g}_{a}}a=1~(a>0,ane 1))

3 метод. Введение новой переменной (замена):

Замена ( displaystyle lo{{g}_{a}}x~=~t)позволяетсвести логарифмическое уравнение к более простому алгебраическому уравнению относительно t.

4 метод. Переход к новому основанию:

( displaystyle {{log }_{a}}b=frac{{{log }_{c}}b}{{{log }_{c}}a}text{ }left( c>0;text{ }ne text{1} right)).

( displaystyle {{log }_{a}}b=frac{1}{{{log }_{b}}a},text{ }left( bne 1 right)).

5 метод. Логарифмирование:

Берется логарифм от правой и левой частей уравнения.

Теорема: Если ( displaystyle a>1), то функция ( displaystyle f(x)=lo{{g}_{a}}x) является монотонно возрастающей, если ( displaystyle 0<a<1), то функция( displaystyle f(x)=lo{{g}_{a}}x) является монотонно убывающей.

( displaystyle left{ begin{array}{l}fleft( x right)=gleft( x right)\fleft( x right)ge A\gleft( x right)le Aend{array} right.Leftrightarrow left{ begin{array}{l}fleft( x right)=A\gleft( x right)=Aend{array} right.).

Метод введения новой переменной

Я начну с рассмотрения первого метода. Как ты уже понял из названия, суть этого метода – ввести такую замену переменной, что твое логарифмическое уравнение чудесным образом преобразится в такое, которое ты уже с легкостью можешь решить.

Все что тебе останется после решения этого самого «упрощенного уравнения» — это сделать «обратную замену» : то есть вернуться от замененного к заменяемому. Давай проиллюстрируем только что сказанное на очень простом примере:

Упрощая полученное выражение, мы окончательно получим:

Теперь, как и раньше, пришла очередь проверки:

Пусть вначале ( displaystyle x=10), так как ( displaystyle lg 10=1), то ( displaystyle frac{1}{4-1}+frac{2}{2+1}=frac{1}{3}+frac{2}{3}=1), верно!

Теперь ( displaystyle x=100,lg 100=2), тогда ( displaystyle frac{1}{4-2}+frac{2}{2+2}=frac{1}{2}+frac{2}{4}=1), все верно!

Таким образом, числа ( displaystyle 10) и ( displaystyle 100) являются корнями нашего исходного уравнения.

Ответ: ( displaystyle 10,100).

Мне кажется, что основную идею ты уловил. Она не нова и распространяется не только на логарифмические уравнения. 

Другое дело, что иногда довольно сложно сразу «увидеть» замену. Здесь требуется некоторый опыт, который придет к тебе после некоторых усилий с твоей стороны.

А пока что потренируйся в решении следующих примеров:

2. ( displaystyle frac{{{log }_{2}}frac{x}{2}}{{{log }_{2}}x}-frac{{{log }_{2}}{{x}^{2}}}{{{log }_{2}}x-1}=1)

3. ( displaystyle 0.1{{lg }^{4}}x-{{lg }^{2}}x+0,9=0.)

Готов? Давай проверим, что у тебя получилось:

Вначале решим второй пример.

Он как раз демонстрирует тебе, что не всегда замену удается сделать, что говорится, «в лоб». Прежде нам нужно немного преобразовать наше уравнение: применить формулу разности логарифмов в числителе первой дроби, и вынести степень в числителе второй.

Сделав это, ты получишь:

Давай сделаем ее: ( displaystyle t=lo{{g}_{2}}x). Теперь приведем дроби к общему знаменателю и упростим. Тогда мы получим:

Самостоятельно сделай проверку и удостоверься в том, что ( displaystyle {{x}_{1}}) и ( displaystyle {{x}_{2}}) в самом деле являются корнями нашего первоначального уравнения.

Теперь давай попробуем решить третье уравнение

4. ( displaystyle 1+{{log }_{x}}frac{4-x}{10}=left( lg {{x}^{2}}-1 right){{log }_{x}}10)

Этот примерчик позаковырестее, однако, я постараюсь решить его вообще не прибегая к замене переменной!

Давай опять, будем делать, что можно: а можно для начала разложить логарифм слева по формуле для логарифма отношения, а также вынести двойку вперед у логарифма в скобках. В итоге у меня получится:

Ну вот, теперь ты, как я надеюсь, научился решать достаточно сложные задачи, которые « в лоб» не одолеешь! Но логарифмические уравнения бывают еще более коварными! Вот например такие:

Дальнейшие упрощения, увы, нам уже недоступны.

Давай сделаем проверку вместе:

Если ( displaystyle {{x}_{1}}), ( displaystyle {{x}_{2}})– корни уравнения ( displaystyle a{{x}^{2}}+bx+c=0), то:

Так как ( displaystyle {{log }_{2x+3}}~left( 3x+7 right)=1/{{log }_{3x+7}}~left( 2x+3 right)), то введем замену ( displaystyle t={{log }_{3x+7}}~left( 2x+3 right)).

Тогда мое исходное уравнение примет вот такой простой вид: ( displaystyle frac{2}{t}+t-3=0)

Его корни равны: ( displaystyle {{t}_{1}}=2,{{t}_{2}}=1), тогда

Тебе осталось сделать проверку!

Следующее уравнение попробуй решить самостоятельно. Не торопись и будь внимателен, тогда удача будет на твоей стороне!

На самом деле, пример решается в два действия:

1. Преобразуем ( displaystyle {{log }_{5}}3=frac{1}{{{log }_{3}}5})

2. Теперь справа у меня стоит выражение ( displaystyle frac{{{log }_{3}}left( 2x+10 right)}{{{log }_{3}}5}), которое равно ( displaystyle {{log }_{5}}left( 2x+10 right))

Таким образом, исходное уравнение свелось к простейшему:

Опишем непосредственно сам мини-максный метод

Я думаю, что ты понимаешь, от каких слов произошло такое название? Верно, от слов минимум и максимум. Кратко метод можно представить в виде:

Теперь давай рассмотрим конкретные примеры:

• ( displaystyle {{log }_{frac{1}{3}}}left( 1+{{left( {{x}^{2}}-3x+2 right)}^{2}} right)=sqrt{{{x}^{2}}-6x+8})
• ( displaystyle {{left( 4{{x}^{2}}-7{x} -2 right)}^{2}}+log _{5}^{5}left( 2{{x}^{2}}-11x+15 right)=0)
• ( displaystyle {{log }_{3}}left( {{x}^{2}}+6x+18 right)=2{{sin }^{2}}frac{pi x}{6})

Ответ: ( displaystyle 2)

2. ( displaystyle {{left( 4{{x}^{2}}-7{x} -2 right)}^{2}}+log _{5}^{2}left( 2{{x}^{2}}-11x+15 right)=0)

Давай сразу задумаемся, что здесь написано? Я имею в виду общую структуру. Здесь сказано, что сумма двух квадратов равна нулю. Когда это возможно? Только тогда, когда оба этих числа по отдельности равны нулю. Тогда перейдем к следующей системе:

Ответ: нет решений.

3. ( displaystyle {{log }_{3}}left( {{x}^{2}}+6x+18 right)=2{{sin }^{2}}frac{pi x}{6})

Давай вначале рассмотрим правую часть – она попроще. По определению синуса:

Таким образом, ( displaystyle {{log }_{3}}left( {{left( x+3 right)}^{2}}+9 right)ge 2)

Тогда наше исходное уравнение равносильно следующей системе:

Теперь я подставлю его во второе уравнение:

Ответ: ( displaystyle x=-3)

Ну как, теперь тебе стала ясна техника применения мини-максного метода? Тогда постарайся решить следующий пример самостоятельно.

Левая часть – сумма двух неотрицательных величин (единицы и модуля) а потому, левая часть не меньше единицы, причем она равна единице только тогда, когда

Тогда исходное уравнение также не имеет корней.

Ответ: решений нет.