Как найти корень уравнения с дробями калькулятор

Рациональные уравнения

В рациональных уравнениях обе части уравнения представляют собой рациональные выражения вида: s(x) =
0 или расширено: s(x) = b(x), где s(x), b(x) – рациональные выражения.

Рациональное выражение является алгебраическим выражением, которое состоит из рациональных чисел и
переменной величины, соединенных с помощью сложения, вычитания, умножения, деления и возведения в
степень с натуральным показателем. Таким образом, это целые и дробные выражения без радикалов.

Действия с рациональными числами обладают свойствами действий с целыми числами.

К примеру, при умножении рациональных чисел есть дополнительное свойство – умножение взаимно обратных
чисел. Для того чтобы умножить два рациональных числа, необходимо умножить модули этих чисел, а
перед ответом поставить «плюс», если у множителей одинаковые знаки и «минус», если знаки разные.

Умножение рационального числа на ноль. Когда в рациональном уравнении хоть один множитель – ноль, то
и произведение будет равняться нолю.

Умножение рациональных чисел с разными знаками. При умножении нескольких чисел с разными знаками,
необходимо умножить модули каждого из этих чисел. Если количество множителей с отрицательными
знаками – четное, то произведение всегда будет со знаком «плюс», если количество множителей с
отрицательными знаками – нечетное, то и произведение будет со знаком «минус».

Делить на ноль в рациональных уравнениях, как и в обычных нельзя.

Чтобы решить рациональное уравнение, необходимо определить тип этого уравнения и применить некоторые
математические хитрости, созданные для этого типа. Если Вы не помните этих хитростей, то можете
воспользоваться калькулятором для решения рациональных уравнений, который быстро подберёт все корни
данного уравнений.

Решением рационального уравнения будут являться корень – конкретное число, при постановке которого в
уравнение даст верное равенство. Корней рационального уравнения может быть много и важно в решении не
упустить ни один корень.

Также читайте нашу статью “Калькулятор
иррациональных урвнений онлайн”

Бесплатный онлайн калькулятор

Наш бесплатный решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все,
что вам необходимо
сделать – это просто ввести свои данные в калькуляторе. Так же вы можете посмотреть
видео
инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то
вы
можете задать их в нашей группе ВКонтакте: pocketteacher.
Вступайте
в нашу группу, мы всегда рады помочь вам.

bold{mathrm{Basic}}	bold{alphabetagamma}	bold{mathrm{ABGamma}}	bold{sincos}	bold{gedivrightarrow}	bold{overline{x}spacemathbb{C}forall}	bold{sumspaceintspaceproduct}	bold{begin{pmatrix}square&square\square&squareend{pmatrix}}	bold{H_{2}O}
square^{2} x^{square} sqrt{square} nthroot[msquare]{square} frac{msquare}{msquare} log_{msquare} pi theta infty int frac{d}{dx} ge le cdot div x^{circ} (square) |square| (f:circ:g) f(x) ln e^{square} left(squareright)^{‘} frac{partial}{partial x} int_{msquare}^{msquare} lim sum sin cos tan cot csc sec alpha beta gamma delta zeta eta theta iota kappa lambda mu nu xi pi rho sigma tau upsilon phi chi psi omega A B Gamma Delta E Z H Theta K Lambda M N Xi Pi P Sigma T Upsilon Phi X Psi Omega sin cos tan cot sec csc sinh cosh tanh coth sech arcsin arccos arctan arccot arcsec arccsc arcsinh arccosh arctanh arccoth arcsech begin{cases}square\squareend{cases} begin{cases}square\square\squareend{cases} = ne div cdot times < > le ge (square) [square] ▭:longdivision{▭} times twostack{▭}{▭} + twostack{▭}{▭} – twostack{▭}{▭} square! x^{circ} rightarrow lfloorsquarerfloor lceilsquarerceil overline{square} vec{square} in forall notin exist mathbb{R} mathbb{C} mathbb{N} mathbb{Z} emptyset vee wedge neg oplus cap cup square^{c} subset subsete superset supersete int intint intintint int_{square}^{square} int_{square}^{square}int_{square}^{square} int_{square}^{square}int_{square}^{square}int_{square}^{square} sum prod lim lim _{xto infty } lim _{xto 0+} lim _{xto 0-} frac{d}{dx} frac{d^2}{dx^2} left(squareright)^{‘} left(squareright)^{”} frac{partial}{partial x} (2times2) (2times3) (3times3) (3times2) (4times2) (4times3) (4times4) (3times4) (2times4) (5times5) (1times2) (1times3) (1times4) (1times5) (1times6) (2times1) (3times1) (4times1) (5times1) (6times1) (7times1) mathrm{Радианы} mathrm{Степени} square! ( ) % mathrm{очистить} arcsin sin sqrt{square} 7 8 9 div arccos cos ln 4 5 6 times arctan tan log 1 2 3 – pi e x^{square} 0 . bold{=} +

Подпишитесь, чтобы подтвердить свой ответ

Подписаться

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

• frac{5}{x-7}=frac{2}{x-2}
  

• frac{7x+5}{x-4}-frac{6x-1}{x-3}-frac{1}{x^{2}-7x+12}=1
  

• frac{7}{x-3}-frac{10}{x-2}-frac{6}{x-1}=0
  

• frac{x-3}{3-x}=2
  

• Показать больше

Описание

Решайте рациональные уравнения шаг за шагом

rational-equation-calculator

ru

Блог-сообщения, имеющие отношение к Symbolab

High School Math Solutions – Quadratic Equations Calculator, Part 1

A quadratic equation is a second degree polynomial having the general form ax^2 + bx + c = 0, where a, b, and c…

Read More

Введите Задачу

Сохранить в блокнот!

Войти

Решение уравнений с дробями

По-шагово решать уравнения с дробями с помощью калькулятора онлайн, но есть дилемма у учеников 5, 6, 7, 8 классов школы, как вводить дробь в форму калькулятора. Анимированная картинка поможет

Примеры уравнений с дробью

Указанные выше примеры содержат также:

• модуль или абсолютное значение: absolute(x) или |x|
• квадратные корни sqrt(x),
  кубические корни cbrt(x)
• тригонометрические функции:
  синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x)
• показательные функции и экспоненты exp(x)
• обратные тригонометрические функции:
  арксинус asin(x), арккосинус acos(x), арктангенс atan(x),
  арккотангенс acot(x)
• натуральные логарифмы ln(x),
  десятичные логарифмы log(x)
• гиперболические функции:
  гиперболический синус sh(x), гиперболический косинус ch(x),
  гиперболический тангенс и котангенс tanh(x), ctanh(x)
• обратные гиперболические функции:
  гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x),
  гиперболический арктангенс atanh(x), гиперболический арккотангенс acoth(x)
• другие тригонометрические и гиперболические функции:
  секанс sec(x), косеканс csc(x), арксеканс asec(x),
  арккосеканс acsc(x), гиперболический секанс sech(x),
  гиперболический косеканс csch(x), гиперболический арксеканс asech(x),
  гиперболический арккосеканс acsch(x)
• функции округления:
  в меньшую сторону floor(x), в большую сторону ceiling(x)
• знак числа:
  sign(x)
• для теории вероятности:
  функция ошибок erf(x) (интеграл вероятности),
  функция Лапласа laplace(x)
• Факториал от x:
  x! или factorial(x)
• Гамма-функция gamma(x)
• Функция Ламберта LambertW(x)
• Тригонометрические интегралы: Si(x),
  Ci(x),
  Shi(x),
  Chi(x)

Правила ввода

Можно делать следующие операции

2*x

– умножение

3/x

– деление

x^2

– возведение в квадрат

x^3

– возведение в куб

x^5

– возведение в степень

x + 7

– сложение

x – 6

– вычитание

Действительные числа

вводить в виде 7.5, не 7,5

Постоянные

pi

– число Пи

e

– основание натурального логарифма

i

– комплексное число

oo

– символ бесконечности

Универсальный математический калькулятор

Онлайн-калькулятор позволяет решать математические выражения любой сложности с выводом подробного результата решения по шагам.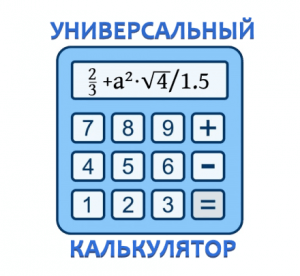

Также универсальный калькулятор умеет производить действия со скобками, дробями, тригонометрическими функциями, возведение в любую степень и многое другое (смотрите примеры ниже).

Онлайн калькулятор уравнений, интегралов, производных, пределов, дробей и пр.

Разделитель системы уравнений

Натуральный логарифм и предел:

Пояснения к калькулятору

1. Для решения математического выражения необходимо набрать его в поле ввода с помощью предложенной виртуальной клавиатуры и нажать кнопку ↵ .
2. Управлять курсором можно кликами в нужное местоположение в поле ввода или с помощью клавиш со стрелками ← и → .
3. ⌫ – удалить в поле ввода символ слева от курсора.
4. C – очистить поле ввода.
5. При использовании скобок ( ) в выражении в целях упрощения может производится автоматическое закрытие, ранее открытых скобок.
6. Для того чтобы ввести смешанное число или дробь необходимо нажать кнопку ½ , ввести сначала значение числителя, затем нажать кнопку со стрелкой вправо → и внести значение знаменателя дроби. Для ввода целой части смешанного числа необходимо установить курсор перед дробью с помощью клавиши ← и ввести число.
7. Ввод числа в n-ой степени и квадратного корня прозводится кнопками a b и √ соответственно. Завершить ввод значения в степени или в корне можно клавишей → .

Упрощение выражений, раскрытие скобок, разложение многочленов на множители

Калькулятор позволяет произвести некоторые алгебраические преобразования с выражениями. Результат выводится в нескольких вариантах упрощения/разложения/раскрытия скобок и пр.

Решение уравнений и неравенств

Математический калькулятор может решать уравнения и неравентства относительно переменной “x”. Если есть необходимость найти другую переменную, например “y”, то следует просто поменять их местами в выражении. Ввод переменных “x”,”y”,”z” производится в группе xyz нажатием соответствующих кнопок x , y , z .

Примеры решений уравнений и неравенств:

Решение систем уравнений и неравенств

Системы уравнений и неравенств также решаются с помощью онлайн калькулятора. Чтобы задать систему необходимо ввести уравнения/неравенства, разделяя их точкой с запятой с помощью кнопки ; .

Примеры вычислений систем уравнений и неравенств:

Вычисление выражений с логарифмами

В калькуляторе кнопкой log_e(x) возможно задать натуральный логарифм, т.е логарифм с основанием “e”: log_e(x) – это ln(x). Для того чтобы ввести логарифм с другим основанием нужно преобразовать логарифм по следующей формуле: $$log_a left(bright) = frac<log left(bright)><log left(aright)>$$ Например, $$log_ <3>left(5x-1right) = frac<log left(5x-1right)><log left(3right)>$$

Примеры решений выражений с логарифмами:

Вычисление пределов функций

Предел функции задается последовательным нажатием групповой кнопки f(x) и функциональной кнопки lim .

Примеры решений пределов:

Решение интегралов

Онлайн калькулятор предоставляет инструменты для интегрирования функций. Вычисления производятся как с неопределенными, так и с определенными интегралами. Ввод интегралов в поле калькулятора осуществляется вызовом групповой кнопки f(x) и далее:
∫ f(x) – для неопределенного интеграла;
b a∫ f(x) – для определенного интеграла.

В определенном интеграле кроме самой функции необходимо задать нижний и верхний пределы.

Примеры вычислений интегралов:

Вычисление производных

Математический калькулятор может дифференцировать функции (нахождение производной) произвольного порядка в точке “x”. Ввод производной в поле калькулятора осуществляется вызовом групповой кнопки f(x) и далее:
f'(x) – производная первого порядка;
f”(x) – производная второго порядка;
f”'(x) – производная третьего порядка.
f n (x) – производная любого n-о порядка.

Действия над комплексными числами

Онлайн калькулятор имеет функционал для работы с комплексными числами (операции сложения, вычитания, умножения, деления, возведения в степень и пр.). Комплексное число обзначается символом “i” и вводится с помощью групповой кнопки xyz и кнопки i

Решить уравнение с дробями онлайн

При помощи калькулятора можно решать уравнение с дробями. Для этого просто введите заданные дроби и быстро получите результат. Калькулятор простой в использовании и выдаёт только точный ответ.

Калькулятор

Инструкция

Примечание: π записывается как pi; корень квадратный как sqrt().

Шаг 1. Введите заданный пример, состоящий из дробей.

Шаг 2. Нажмите кнопку “Решить”.

Шаг 3. Получите подробный результат.

Чтобы калькулятор посчитал дроби правильно, вводите дробь через знак: “/”. Например: . Калькулятор посчитает уравнение и даже покажет на графике, почему получился такой результат.

Что такое уравнение с дробями

Уравнение с дробями – это уравнение, в котором коэффициенты являются дробными числами. Линейные уравнения с дробями решается по стандартной схеме: неизвестные переносятся в одну сторону, а известные – в другую.

Рассмотрим на примере:

Дроби с неизвестными переносятся влево, а остальные дроби – вправо. Когда переносятся числа за знак равенства, тогда у чисел знак меняется на противоположный:

Теперь нужно выполнить только действия обеих частей равенства:

.

Получилось обыкновенное линейное уравнение. Теперь нужно поделить левую и правую части на коэффициент при переменной.

Средняя оценка 2.5 / 5. Количество оценок: 66

Калькулятор дробей: решение уравнений с дробями

Онлайн калькулятор дробей позволяет производить простейшие арифметические операции с дробями: сложение дробей, вычитание дробей, умножение дробей, деление дробей. Чтобы произвести вычисления, заполните поля соответствующие числителям и знаменателям двух дробей.

Онлайн калькулятор уравнений с дробями

Дробью в математике называется число, представляющее часть единицы или несколько её частей.

Обыкновенная дробь записывается в виде двух чисел, разделенных обычно горизонтальной чертой, обозначающей знак деления. Число, располагающееся над чертой, называется числителем. Число, располагающееся под чертой, называется знаменателем. Знаменатель дроби показывает количество равных частей, на которое разделено целое, а числитель дроби – количество взятых этих частей целого.

Дроби бывают правильными и неправильными.

• Правильной называется дробь, у которой числитель меньше знаменателя.
• Неправильная дробь – если у дроби числитель больше знаменателя.

Смешанной называется дробь, записанная в виде целого числа и правильной дроби, и понимается как сумма этого числа и дробной части. Соответственно, дробь, не имеющая целую часть, называется простой дробью. Любая смешанная дробь может быть преобразована в неправильную простую дробь.

Как перевести смешанную дробь в обыкновенную

Для того, чтобы перевести смешанную дробь в обыкновенную, необходимо к числителю дроби прибавить произведение целой части и знаменателя: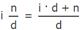

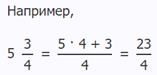
Как перевести обыкновенную дробь в смешанную

Для того, чтобы перевести обыкновенную дробь в смешанную, необходимо:

1. Поделить числитель дроби на её знаменатель
2. Результат от деления будет являться целой частью
3. Остаток отделения будет являться числителем

Как перевести обыкновенную дробь в десятичную

Для того, чтобы перевести обыкновенную дробь в десятичную, нужно разделить её числитель на знаменатель.

Как перевести десятичную дробь в обыкновенную

Для того, чтобы перевести десятичную дробь в обыкновенную, необходимо:

1. Записать дробь в виде десятичная
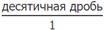
2. Умножать числитель и знаменатель на 10 до тех пор, пока числитель не станет целым числом.
3. Найти наибольший общий делитель и сократить дробь.

Как перевести дробь в проценты

Для того, чтобы перевести обыкновенную или смешанную дробь в проценты, необходимо перевести её в десятичную дробь и умножить на 100.

Как перевести проценты в дробь

Для того, чтобы перевести проценты в дробь, необходимо получить из процентов десятичную дробь (разделив на 100), затем полученную десятичную дробь перевести в обыкновенную.

Сложение дробей

Алгоритм действий при сложении двух дробей такой:

1. Перевести смешанные дроби в обыкновенные (избавиться от целой части).
2. Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
3. Выполнить сложение дробей путем сложения их числителей.
4. Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
5. Если числитель итоговой дроби больше знаменателя, то выделить целую часть.

Вычитание дробей

Алгоритм действий при вычитании двух дробей:

1. Перевести смешанные дроби в обыкновенные (избавиться от целой части).
2. Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
3. Вычесть одну дробь из другой, путем вычитания числителя второй дроби из числителя первой.
4. Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
5. Если числитель итоговой дроби больше знаменателя, то выделить целую часть.

Умножение дробей

Алгоритм действий при умножении двух дробей:

1. Перевести смешанные дроби в обыкновенные (избавиться от целой части).
2. Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
3. Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
4. Если числитель итоговой дроби больше знаменателя, то выделить целую часть.

Деление дробей

Алгоритм действий при делении двух дробей:

1. Перевести смешанные дроби в обыкновенные (избавиться от целой части).
2. Чтобы произвести деление дробей, нужно преобразовать вторую дробь, поменяв местами её числитель и знаменатель, а затем произвести умножение дробей.
3. Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
4. Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
5. Если числитель итоговой дроби больше знаменателя, то выделить целую часть.

[spoiler title=”источники:”]

http://nauchniestati.ru/kalkulatory/reshit-uravnenie-s-drobjami-onlajn/

[/spoiler]