План урока:
Целое уравнение и его степень
Решение уравнений методом подбора корня
Решение уравнений с помощью разложения многочлена на множители
Графический метод решения уравнений
Решение дробно-рациональных уравнений
Целое уравнение и его степень
Ранее мы уже изучали понятие целого выражения. Так называют любое выражение с переменной, в котором могут использоваться любые арифметические операции, а также возведение в степень. Однако есть важное ограничение – в целом выражении переменная НЕ может находиться в знаменателе какой-нибудь дроби или быть частью делителя. Также переменная не может находиться под знаком корня. Для наглядности приведем примеры целых выражений:
х – 5;
(а3 + 6а)(а – 5а2);
(n3 + 7)/5 (в знаменателе находится только число, без переменной);
А вот примеры нецелых выражений:
Отличительной особенностью целых выражений является то, что в них переменная может принимать любое значение. В нецелых же выражениях возникают ограничения на значения переменной, ведь знаменатель дроби не должен равняться нулю, в выражение под знаком корня не должно быть отрицательным.
Введем понятие целого уравнения.
Приведем примеры целых ур-ний:
0,75х7 + 0,53х6 – 45х = 18
Напомним, что в математике существует понятие равносильных уравнений.
Когда мы решаем ур-ния, мы в каждой новой строчке записываем ур-ние, равносильное предыдущему. Для этого используются равносильные преобразования (перенос слагаемых через знак «=» с противоположным знаком, деление обоих частей равенства на одинаковые числа и т. д.).
Можно доказать (мы этого делать не будем), что любое целое ур-ние можно возможно преобразовать так, чтобы получилось иное, равносильное ему ур-ние, где в левой части будет находиться многочлен, а справа – ноль. Для этого надо лишь раскрыть скобки и умножить ур-ние на какое-нибудь число, чтобы избавиться от дробей.
Пример. Преобразуйте целое ур-ние
так, чтобы слева стоял многочлен, а справа – ноль.
Решение. В ур-нии есть дроби со знаменателями 5 и 4. Если умножить обе части на 20 (это наименьшее общее кратное чисел 5 и 4), то дроби исчезнут:
Теперь раскроем скобки:
4(5х3 – 3х4 + 45х – 27х2) – 40 = 10х2 + 5х + 35
20х3 – 12х4 + 180х – 108х2 – 40 = 10х2 + 5х + 35
Осталось перенести все слагаемые влево и привести подобные слагаемые:
20х3 – 12х4 + 180х – 108х2 – 40 – 10х2 – 5х – 35 = 0
– 12х4 + 20х3 – 118х2 + 175х – 75 = 0
Получили ур-ние в той форме, которую и надо было найти по условию.
Ответ:– 12х4 + 20х3 – 118х2 + 175х – 75 = 0
В математике любой полином можно обозначить как Р(х). Если ур-ние привели к тому виду, когда в одной части многочлен, а в другой ноль, то говорят, что получили ур-ние вида Р(х) = 0.
Получается, что решение целого уравнения всегда можно свести к решению равносильного ему ур-ния Р(х) = 0. Именно поэтому многочлены играют такую большую роль в математике
Напомним, что степенью многочлена называется максимальная степень входящего в его состав одночлена. Это же число является и степенью целого уравнения Р(х) = 0, а также степенью любого равносильного ему целого ур-ния.
Пример. Определите степень ур-ния
(х3 – 5)(2х + 7) = 2х4 + 9
Решение. Приведем ур-ние к виду Р(х) = 0. Для этого раскроем скобки:
(х3 – 5)(2х + 7) = 2х4 + 9
2х4 + 7х3 – 10х – 35 = 2х4 + 9
Перенесем все слагаемые влево и приведем подобные слагаемые:
2х4 + 7х3 – 10х – 35 – 2х4 – 9 = 0
7х3 – 10х – 44 = 0
Получили в левой части многочлен 3-ей степени. Следовательно, и исходное ур-ние имело такую же степень
Ответ: 3
Приведем примеры ур-ний первой степени:
5х + 8 = 0
9z– 6 = 0
5,4568у + 0,0002145 = 0
Все они являются линейными ур-ниями, метод их решения изучался ранее. Они имеют 1 корень.
Приведем примеры ур-ний второй степени:
6t2 + 98t – 52 = 0
54у + 23у = 0
12x2– 65 = 0
Это квадратные ур-ния. У них не более двух действительных корней. Для их нахождения в общем случае надо вычислить дискриминант и использовать формулу
Квадратные и линейные ур-ния умели решать ещё в Древнем Вавилоне 4 тысячи лет назад! А вот с ур-ния 3-ей степени (их ещё называют кубическими уравнениями) оказались значительно сложнее. Приведем их примеры:
2х3 + 4х2 – 19х + 17 = 0
у3 – 5у + 7 = 0
Лишь в 1545 году итальянец Джералимо Кардано опубликовал книгу, в которой описывался общий алгоритм решения кубических ур-ний. Он достаточно сложный и не входит в школьный курс математики. Его ученик, Лодовико Феррари, предложил метод решения ур-ний четвертой степени. В качестве примера такого ур-ния можно привести:
5х4 + 6х3 – 2х2 – 10х + 1 = 0
Лишь в XIX веке было доказано, что для ур-ний более высоких степеней (5-ой, 6-ой и т. д.) не существует универсальных формул, с помощью которых можно было бы найти их корни.
Отметим, что если степень целого ур-ния равна n, то у него не более n корней (но их число может быть и меньше). Так, количество корней кубического уравнения не превышает трех, а у ур-ния 4-ой степени их не более 4.
Чтобы доказать это утверждение, сначала покажем способ составления уравнения Р(х) = 0, имеющего заранее заданные корни. Пусть требуется составить ур-ние, имеющее корни k1, k2,k3,…kn. Приравняем к нулю следующее произведение скобок:
(х – k1)(х – k2)(х – k3)…(х – kn) = 0
Составленное ур-ние имеет все требуемые корни и никаких других корней. Действительно, произведение множителей может равняться нулю только в случае, если хотя бы один из множителей нулевой. Поэтому для решения ур-ния
(х – k1)(х – k2)(х – k3)…(х – kn) = 0
надо каждую скобку приравнять к нулю:
х – k1 = 0 или х – k2 = 0 или х – k3 = 0 или…х – kn = 0
Перенесем второе слагаемое вправо в каждом равенстве и получим:
х = k1 или х = k2 или х = k3 или…х = kn
Чтобы вместо произведения скобок слева стоял многочлен, надо просто раскрыть скобки.
Пример. Составьте уравнение в виде Р(х) = 0, имеющее корни 1, 2, 3 и 4.
Запишем целое ур-ние, имеющее требуемые корни:
(х – 1)(х – 2)(х – 3)(х – 4) = 0
Будем поочередно раскрывать скобки, умножая 1-ую скобку на 2-ую, полученный результат на 3-ю и т.д.:
(х2 – 3х + 2)(х – 3)(х – 4) = 0
(х3 – 6х2 + 11х – 6)(х – 4) = 0
х4 – 10х3 + 35х2 – 50х +24 = 0
Получили ур-ние вида Р(х) = 0. Для проверки вычислений можно подставить в него числа 1, 2, 3 и 4 и убедиться, что они обращают ур-ние в верное равенство.
Ответ: х4 – 10х3 + 35х2 – 50х +24 = 0
Заметим, что в рассмотренном примере, когда мы перемножали многочлены, мы получали новый полином, чья степень увеличивалась на единицу. Мы перемножили 4 скобки (х – k1), а потому получили полином 4 степени. Если бы мы перемножали, скажем, 10 таких скобок, то и многочлен бы получился 10-ой степени. Именно поэтому ур-ние n-ой степени не более n корней.
Действительно, предположим, что какое-то ур-ние n-ой степени имеет хотя бы (n + 1) корень. Обозначим эти корни как k1, k2,k3,…kn, kn+1 и запишем уравнение:
(х – k1)(х – k2)(х – k3)…(х – kn)(х – kn+1) = 0
Оно, по определению, равносильно исходному ур-нию, ведь оно имеет тот же набор корней. Слева записаны (n + 1) скобок, поэтому при их раскрытии мы получим полином степени (n + 1). Значит, и исходное ур-ние на самом деле имеет степень n + 1, а не n. Получили противоречие, которое означает, что на самом деле у уравнения n-ой степени не более n корней.
Особо акцентируем внимание на том факте, что если корнями уравнения являются некоторые числа k1, k2,k3,…kn, то этому ур-нию равносильна запись (х – k1)(х – k2)(х – k3)…(х – kn) = 0
Этот факт будет использован далее при решении ур-ний.
Решение уравнений методом подбора корня
Необязательно преобразовывать ур-ние, чтобы найти его корни. Одним из приемов решения целых уравнений является метод подбора корня. Ведь если надо доказать, что какое-то число – это корень ур-ния, достаточно просто подставить это число в ур-ние и получить справедливое равенство!
Пример. Докажите, что корнями ур-ния
х3 – 2х2 – х + 2 = 0
являются только числа (– 1), 1 и 2.
Решение. Подставим в ур-ние каждую из предполагаемых корней и получим справедливое равенство. При х = – 1 имеем:
(– 1)3 – 2(– 1)2 – (– 1) + 2 = 0
–1 – 2 + 1 + 2 = 0
0 = 0
При х = 1 получаем:
13 – 2•12 – 1 + 2 = 0
1 – 2 – 1 + 2 = 0
0 = 0
Наконец, рассмотрим случай, когда х = 2
23 – 2•22 – 2 + 2 = 0
8 – 8 – 2 + 2 = 0
0 = 0
Исходное ур-ние имеет 3-ю степень, поэтому у него не более 3 корней. То есть других корней, кроме (– 1), 1 и 2 , у него нет.
Конечно, просто так подобрать корни довольно тяжело. Однако есть некоторые правила, которые помогают в этом. Для начала введем понятие коэффициентов уравнения.
Понятно, что ур-ние Р(х) = 0 в общем виде можно записать так:
а0xn + a1xn–1 + … + аn–1х + аn = 0
Числа а0, а1, а2,…аnи называют коэффициентами уравнений.
Например, для уравнения
5х4 – 7х3 + 9х2 – х + 12 = 0
коэффициенты равны
а0 = 5
а1 = – 7
а2 = 9
а3 = – 1
а4 = + 12
Если одна из слагаемых «пропущено» в уравнении, то считают, что коэффициент перед ним равен нулю. Например, в ур-нии
х3 + 2х – 15 = 0
нет слагаемого с буквенной частью х2. Можно считать, что ур-ние равносильно записи
х3 + 0х2 + 2х – 15 = 0
где слагаемое х2 есть, но перед ним стоит ноль. Тогда коэффициент а1 = 0.
Для обозначения первого коэффициента а0 может использоваться термин старший коэффициент, а для последнего коэффициента аn – термин «свободный член» или «свободный коэффициент».
Изучение коэффициентов ур-ния помогает быстрее подобрать корень. Существует следующая теорема:
Докажем это утверждение. Пусть m – это целый корень уравнения с целыми коэффициентами
а0xn + a1xn–1 + … + аn–1х + аn = 0
Тогда можно подставить туда число m и получить верное равенство:
а0mn + a1mn–1 + … + аn–1m + аn = 0
Поделим обе его части на m и получим
а0mn–1 + a1mn–2 + … + аn–1 + аn/m = 0
Справа – целое число (ноль), значит, и сумма чисел слева также целая. Все числа а0mn–1, a1mn–2, аn–1, очевидно, целые (так как и целыми являются и m, и все коэффициенты). Значит, и число аn/m должно быть целым. Но это возможно лишь в том случае, если m является делителем числа аn.
Из доказанной теоремы следует, что при подборе корней ур-ния достаточно рассматривать только те из них, которые являются делителями свободного члена. При этом следует учитывать и отрицательные делители.
Пример. Найдите целые корни уравнения
2х4 – х3 – 9х2 + 4х + 4 = 0
Решение. Все коэффициенты ур-ния – целые, а потому целый корень должен быть делителем свободного члена, то есть числа 4. Делителями четверки являются 1 и (– 1), 2 и (– 2), 4 и (– 4). Подставляя каждое из этих чисел в ур-ние, получим верные равенства только для чисел 1, 2 и (– 2):
2•14 – 13 – 9•12 + 4•1 + 4 = 2 – 1 – 9 + 4 + 4 = 0
2•24 – 23 – 9•22 + 4•2 + 4 = 32 – 8 – 36 + 8 + 4 = 0
2•(– 2)4 – (– 2)3 – 9•(– 2)2 + 4(– 2) + 4 = 32 + 8 – 36 – 8 + 4 = 0
Таким образом, только эти числа и могут быть целыми корнями ур-ния. Так как мы рассматриваем ур-ние 4 степени, то, возможно, у него помимо 3 целых корней есть ещё один дробный.
Ответ: 1; 2; (– 2).
Пример. Решите ур-ние
0,5х3 + 0,5х + 5 = 0
Решение. У ур-ния дробные коэффициенты. Умножим обе части равенства на 2 и получим ур-ние с целыми коэффициентами:
0,5х3 + 0,5х + 5 = 0
(0,5х3 + 0,5х + 5)•2 = 0•2
х3 + х + 10 = 0
Попытаемся подобрать целый корень ур-ния. Он должен быть делителем свободного члена, то есть десятки. Возможными кандидатами являются числа 1 и (– 1), 2 и (– 2), 5 и (– 5), 10 и (– 10). Подходит только корень х = – 2:
(– 2)3 + (– 2) + 10 = – 8 – 2 + 10 = 0
Обратим внимание, что в левой части ур-ния стоит сумма функций, возрастающих на всей числовой прямой: у = х3 и у = х + 10. Значит, и вся левая часть х3 + х + 10 монотонно возрастает. Это значит, что у ур-ния есть только один корень, и мы его нашли ранее подбором.
Ответ: – 2
Ещё быстрее можно узнать, является ли единица корнем уравнения.
Докажем это. Подставим в ур-ние
а0xn + a1xn–1 + … + аn–1х + аn = 0
значение х = 1. Так как единица в любой степени равна самой единице, то получим:
а01n + a11n–1 + … + аn–11 + аn = 0
а0 + a1 + … + аn–1 + аn = 0
Получили равенство, в котором слева стоит сумма коэффициентов, в справа – ноль. Если сумма коэффициентов действительно равна нулю, то равенство верное, а, значит, единица является корнем ур-ния.
Пример. Укажите хотя бы 1 корень ур-ния
499х10 – 9990х7 + 501х6 – 10х5 + 10000х4 – 1000 = 0
Решение. Заметим, что при сложении коэффициентов ур-ния получается 0:
499 – 9990 + 501 – 10 + 10000 – 1000 = (499 + 501 – 1000) + (10000 – 9990 – 10) = 0 + 0 = 0
Следовательно, единица является его корнем.
Ответ: 1.
Решение уравнений с помощью разложения многочлена на множители
Если в уравнении вида P(x) = 0в левой части удается выполнить разложение многочлена на множители, то дальше каждый из множителей можно отдельно приравнять к нулю.
Пример. Решите ур-ние
х4 – 16 = 0
Решение. Степень х4 можно представить как (х2)2, а 16 – как 42. Получается, что слева стоит разность квадратов, которую можно разложить на множители по известной формуле:
х4 – 16 = 0
(х2 – 4)(х2 + 4) = 0
Приравняем каждую скобку к нулю и получим два квадратных ур-ния:
х2 – 4 = 0 или х2 + 4 = 0
х2 = 4 или х2 = – 4
Первое ур-ние имеет два противоположных корня: 2 и (– 2). Второе ур-ние корней не имеет.
Ответ: 2 и (– 2).
Предположим, что у ур-ния 3-ей степени есть 3 корня, и подбором мы нашли один из них. Как найти оставшиеся корни? Здесь помогает процедура, известная как «деление многочленов в столбик». Продемонстрируем ее на примере. Пусть надо решить ур-ние
100х3 – 210х2 + 134х – 24 = 0
Можно заметить, сумма всех коэффициентов ур-ния равна нулю:
100 – 210 + 134 – 24 = 0
Следовательно, первый корень – это 1.
Предположим, что у исходного ур-нияР(х) = 0 есть 3 корня, k1, k2и k3. Тогда ему равносильно другое ур-ние
(х – k1)(х – k2)(х – k3) = 0
Мы нашли, что первый корень k1 = 1, то есть
(х – 1)(х – k2)(х – k3) = 0
Обозначим как P1(x) = 0 ещё одно ур-ние, корнями которого будут только числа k2 и k3. Очевидно, что корнями ур-ния
(х – 1)•P1(x) = 0
Будут числа 1, k2 и k3. Его корни совпадают с корнями исходного ур-ния, а потому запишем
(х – 1)•P1(x) = 100х3 – 210х2 + 134х – 24
Поделим обе части на (х – 1):
Итак, если «поделить» исходное ур-ние на х – 1, то получим какой-то многочлен Р1(х), причем решением уравнения P1(x) = 0 будут оставшиеся два корня, k2и k3. Деление можно выполнить в столбик. Для этого сначала запишем «делимое» и «делитель», как и при делении чисел:
Смотрим на первое слагаемое делимого. Это 100х3. На какой одночлен нужно умножить делитель (х – 1), чтобы получился полином со слагаемым 100х3? Это 100х2. Действительно, (х – 1)100х2 = 100х3 – 100х2. Запишем слагаемое 100х2 в результат деления, а результат его умножения на делитель, то есть 100х3 – 100х2, вычтем из делимого:
Теперь вычтем из делимого то выражение, которое мы записали под ним. Слагаемые 100х3, естественно, сократятся:
(100х3 – 210х2) – (100х3 – 100х2) = 100х3 – 210х2 – 100х3 + 100х2 = – 110х2
Далее снесем слагаемое 134х вниз:
На какое слагаемое нужно умножить (х – 1), что получился полином со слагаемым (– 110х2). Очевидно, на (– 110х):
(х – 1)(– 110х2) = –110х2 + 110х
Запишем в поле «ответа» слагаемое (– 110х2), а под делимый многочлен – результат его умножения на (х – 1):
При вычитании из (–110х2 + 134х) полинома (–110х2 + 110х) остается 24х. Далее сносим последнее слагаемое делимого многочлена вниз:
Выражение х – 1 нужно умножить на 24, чтобы получить 24х – 24. Запишем в поле «ответа» число 24, а в столбике произведение 24(х –1) = 24х – 24:
В результате в остатке получился ноль. Значит, всё сделано правильно. С помощью деления столбиком мы смогли разложить полином 100х3 – 210х2 + 134х – 24 на множители:
100х3 – 210х2 + 134х – 24 = (х – 1)(100х2 – 110х + 24)
Теперь перепишем исходное ур-ние с учетом этого разложения:
100х3 – 210х2 + 134х – 24 = 0
(х – 1)(100х2 – 110х + 24) = 0
Теперь каждую отдельную скобку можно приравнять нулю. Получим ур-ние х – 1 = 0, корень которого, равный единице, мы уже нашли подбором. Приравняв к нулю вторую скобку, получим квадратное ур-ние:
100х2 – 110х + 24 = 0
D =b2 – 4ас = (– 110)2 – 4•100•24 = 12100 – 9600 = 2500
Итак, мы нашли три корня ур-ния: 1; 0,3 и 0,8.
В данном случае мы воспользовались следующим правилом:
Пример. Решите уравнение
2х3 – 8х2 + 16 = 0
Решение. Все коэффициенты целые, а потому, если у уравнения есть целый корень, то он должен быть делителем 16. Перечислим эти делители: 1, – 1, 2, – 2, 4, – 4, 8, – 8, 16, – 16. Из всех них подходит только двойка:
2•23 – 8•22 + 16 = 16 – 32 + 16 = 0
Итак, первый корень равен 2. Это значит, что исходный многочлен можно разложить на множители, один из которых – это (х – 2). Второй множитель найдем делением в столбик. Так как в многочлене 2х3 – 8х2 + 16 нет слагаемого с буквенной часть х, то искусственно добавим её:
2х3 – 8х2 + 16 = 2х3 – 8х2 + 0х + 16
Теперь возможно деление:
Получили, что 2х3 – 8х2 + 16 = (х – 2)(2х – 4х – 8)
С учетом этого перепишем исходное ур-ние:
2х3 – 8х2 + 16 = 0
(х – 2)(2х – 4х – 8) = 0
х – 2 = 0 или 2х – 4х – 8 = 0
Решим квадратное ур-ние
D =b2 – 4ас = (– 4)2 – 4•2•(– 8) = 16 + 64 = 80
В 8 классе мы узнали, что если у квадратного ур-ния ах2 + bx + c = 0 есть два корня, то многочлен ах2 + bx + c можно разложить на множители по формуле
ах2 + bx + c = а(х – k1)(х – k2)
где k1 и k2– корни квадратного ур-ния. Оказывается, такое же действие можно выполнять с многочленами и более высоких степеней. В частности, если у кубического ур-ния есть 3 корня k1, k2 и k3, то его можно разложить на множители по формуле
ах3 +bx2 + cx + d = a(х – k1)(х – k2)(х – k3)
Пример. Разложите на множители многочлен 2х3 – 4х2 – 2х + 4.
Решение. Целые корни этого многочлена (если они есть), должны быть делителем четверки. Из всех таких делителей подходят три: 1, (– 1) и 2:
2•13 – 4•12 – 2•1 + 4 = 2 – 4 – 2 + 4 = 0
2•(– 1)3 – 4•(– 1)2 – 2•(– 1) + 4 = – 2 – 4 + 2 + 4 = 0
2•23 – 4•22 – 2•2 + 4 = 16 – 16 – 4 + 4 = 0
Значит, многочлен можно разложить на множители:
2х3 – 4х2 – 2х + 4 = 2(х + 1)(х – 1)(х – 2)
Возникает вопрос – почему перед скобками нужна двойка? Попробуем сначала перемножить скобки без ее использования:
(х + 1)(х – 1)(х – 2) = (х2 – 1)(х – 2) = х3 – 2х2 – х + 2
Получили не тот многочлен, который стоит в условии. Однако ур-ние
х3 – 2х2 – х + 2 = 0
имеет те же корни (1, 2 и (– 1)), что и ур-ние
2х3 – 4х2 – 2х + 4 = 0
Дело в том, что это равносильные ур-ния, причем второе получено умножением первого на два:
2•(х3 – 2х2 – х + 2) = 2х3 – 4х2 – 2х + 4
Надо понимать, что хотя ур-ния 2х3 – 4х2 – 2х + 4 = 0 и х3 – 2х2 – х + 2 = 0, по сути, одинаковы, многочлены в их левой части различны. Заметим, что при перемножении скобок (х – k1), (х – k2), (х – k3) и т.д. всегда будет получаться полином, у которого старший коэффициент равен единице. Поэтому, чтобы учесть этот самый коэффициент, надо домножить произведение скобок на него:
2х3 – 4х2 – 2х + 4= 2•(х3 – 2х2 – х + 2) = 2(х + 1)(х – 1)(х – 2)
Ответ: 2(х + 1)(х – 1)(х – 2).
Графический метод решения уравнений
Любое ур-ние с одной переменной можно представить в виде равенства
у(х) = g(x)
где у(х) и g(x) – некоторые функции от аргумента х.
Построив графики этих функций, можно примерно найти точки их пересечений. Они и будут соответствовать корням уравнения.
Пример. Решите графически уравнение
х3 – х2 – 1 = 0
Решение. Строить график уравнения х3 – х2 – 1 = 0 довольно сложно, поэтому перенесем слагаемое (– х2 – 1) вправо:
х3 – х2 – 1 = 0
х3 = х2 + 1
Построим графики у = х3 и у = х2 + 1 (второй можно получить переносом параболы у = х2 на единицу вверх):
Видно, они пересекаются в точке, примерно соответствующей значению х ≈ 1,4. Если построить графики уравнения более точно (с помощью компьютера), то можно найти, что х ≈ 1,46557.
Ответ: х ≈ 1,46557
Конечно, графический метод решения уравнений не является абсолютно точным, однако он помогает быстро найти примерное положение корня. Также с его помощью можно определить количество корней уравнения. В рассмотренном примере был только 1 корень.
Пример. Определите количество корней уравнений
а)х3 – х – 3 = 0
б) х3 – 2х + 0,5 = 0
Решение. Перенесем два последних слагаемых вправо в каждом ур-нии:
а) х3 = х + 3
б) х3 = 2х – 0,5
Построим графики функций у = х3, у = х + 3 и у = 2х – 0,5:
Видно, что прямая у = х + 3 пересекает график у = х3 в одной точке, поэтому у первого ур-ния будет 1 решение.Прямая у = 2х – 0,5 пересекает кубическую параболу в трех точках, а потому у второго ур-ния 3 корня.
Ответ: а) один корень; б) три корня.
Решение дробно-рациональных уравнений
До этого мы рассматривали только целые ур-ния, где переменная НЕ находится в знаменателе какого-нибудь выражения. Однако, если в ур-нии есть выр-ние, содержащее переменную в знаменателе, или присутствует деление на выр-ние с переменной, то его называют дробно-рациональным уравнением.
Приведем несколько примеров ур-ний, считающихся дробно-рациональными:
С помощью равносильных преобразований любое дробно-рациональное ур-ние возможно записать в виде отношения двух полиномов:
Дробь равна нулю лишь тогда, когда ее числитель равен нулю, а знаменатель – не равен. Таким образом, нужно сначала решить ур-ние Р(х) = 0 и потом проверить, что полученные корни не обращают полином Q(x) в ноль.
Обычно для решения дробно-рациональных уравнений используют такой алгоритм:
1) Приводят все дроби к единому знаменателю, умножают на него ур-ние и получают целое ур-ние.
2) Решают полученное целое ур-ние.
3) Исключают из числа корней те, которые обращают знаменатель хотя бы одной из дробей в ноль.
Пример. Решите ур-ние
Решение.
Умножим обе части равенства на знаменатель 1-ой дроби:
2х2 – 3х – 2 = х2(х – 2)
Раскроем скобки и перенесем все слагаемые в одну сторону:
2х2 – 3х – 2 = х3– 2х2
х3 – 2х2 – 2х2 + 3х + 2 = 0
х3 – 4х2 + 3х + 2 = 0
У ур-ния могут быть только те целые корни, которые являются делителями двойки. Из кандидатов 1, – 1, 2 и – 2 подходит только двойка:
23 – 4•22 + 3•2 + 2 = 8 – 16 + 6 + 2 = 0
Нашли один корень, а потому исходный многочлен можно поделить в столбик на (х – 2):
Получили, что х3 – 4х2 + 3х + 2 = (х – 2)(х2 – 2х – 1)
Тогда ур-ние примет вид:
(х – 2)(х2 – 2х – 1) = 0
х – 2 = 0 или х2 – 2х – 1 = 0
Решим квадратное ур-ние:
D =b2 – 4ас = (– 2)2 – 4•1•(– 1) = 4 + 4 = 8
Мы нашли все 3 корня кубического ур-ния. Теперь надо проверить, не обращают ли какие-нибудь из них знаменатели дроби в исходном ур-нии
в ноль. Очевидно, что при х = 2 знаменатель (х – 2) превратится в ноль:
х – 2 = 2 – 2 = 0
Это значит, что этот корень надо исключить из списка решений. Такой корень называют посторонним корнем ур-ния.
Также ясно, что два остальных корня не обращают знаменатель в ноль, а потому они НЕ должны быть исключены из ответа:
Пример. Найдите все корни ур-ния
Решение. Если сразу привести выражение слева к общему знаменателю 4(х2 + х – 2)(х2 + х – 20), то получится очень длинное и неудобное выражение. Однако знаменатели довольно схожи, поэтому можно провести замену. Обозначим х2 + х как у:
у = х2 + х
Тогда уравнение примет вид
Приведем дроби к общему знаменателю 4(у – 2)(у – 20):
Знаменатель должен равняться нулю:
4(у – 20) + 28(у – 2) + (у – 2)(у – 20) = 0
4у – 80 + 28у – 56 + у2 – 20у – 2у + 40 = 0
у2 + 10у – 96 = 0
Решаем квадратное ур-ние:
D =b2 – 4ас = (10)2 – 4•1•(– 96) = 100 + 384 = 484
Получили, что у1 = – 16, а у2 = 6. Произведем обратную замену:
у = х2 + х
х2 + х = – 16 или х2 + х = 6
х2 + х + 16 = 0 или х2 + х – 6 = 0
Дискриминант 1-ого ур-ния отрицателен:
D =b2 – 4ас = (1)2 – 4•1•(16) = 1– 64 = – 63
А потому оно не имеет решений. Решим 2-ое ур-ние:
D = b2 – 4ас = (1)2 – 4•1•(– 6) = 1+ 24 = 25
Нашли два корня: 2 и (– 3). Осталось проверить, не обращают ли они знаменатели дробей в ур-нии
в ноль. Подстановкой можно убедиться, что не обращают.
Ответ: – 3 и 2.
При решении дробно-рациональных ур-ний может использоваться и графический метод.
Пример. Сколько корней имеет уравнение
Решение. Построим графики функций у = х2 – 4 и у = 2/х:
Видно, что графики пересекаются в 3 точках, поэтому ур-ние имеет 3 корня.
Ответ: 3 корня.
Математика, 2 класс
Урок №26. Уравнение. Решение уравнений подбором неизвестного числа
Перечень вопросов, рассматриваемых в теме:
– Что такое уравнение, корень уравнения?
– Как решить уравнение?
Глоссарий по теме:
Уравнение – равенство, содержащее неизвестное число, которое надо найти.
Корень уравнения – это значение буквы, при котором из уравнения получается верное равенство.
Решить уравнение, значит найти его корни.
Основная и дополнительная литература по теме урока
1. Моро М. И., Бантова М. А., Бельтюкова Г. В. и др. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1.– 8-е изд. – М.: Просвещение, 2017. – С. 80-81.
2. Моро М. И., Бантова М. А. Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций. В 2 ч. Ч.1. – 6-е изд., дораб. – М.: Просвещение, 2016. – С. 60.
3. Моро М. И., Волкова С. И. Для тех, кто любит математику. Пособие для учащихся общеобразовательных организаций. 9-е изд. – М.: Просвещение, 2014. – С. 60.
Теоретический материал для самостоятельного изучения
Вы умеете читать буквенные выражения. Например:
Вы уже знаете, что равенства бывают верные и неверные.
Рассмотрим верное равенство с окошком: 
Запишем вместо окошка маленькую латинскую букву 
Это число 8. Получили верное равенство: сумма чисел 8 и 4 равна 12.
х + 4 = 12
х = 8
8 + 4 = 12
Равенство с буквой 
Неизвестное число обозначается маленькими латинскими буквами, как и в буквенном выражении.
Решить уравнение – значит найти все такие значения х (если они есть), при которых равенство будет верным. Значение буквы, при котором из уравнения получается верное равенство, называется корень уравнения.
Решим уравнение 10 – d = 6 способом подбора.
Возьмём число 5. Сейчас проверим, верно ли подобрали число. Заменим d в уравнении числом 5. Получим равенство: 10 – 5 = 6. Оно неверно. Значит, число подобрали неверно.
Попробуем взять другое число. Например, 4. При подстановке его вместо d получили верное равенство: 10 – 4 = 6. Значит, число четыре – корень уравнения, его решение.
Сейчас мы с вами рассмотрим, как по схеме составить уравнение. Перед нами такая схема. Изучим, что обозначает каждое число в схеме. Число 27 обозначает «целое». Оно состоит из двух частей. Первая «часть» – это число 20, вторая «часть» – это число х.
20 х
27
Воспользуемся правилом,
ЧАСТЬ + ЧАСТЬ = ЦЕЛОЕ
Запишем равенства:
20 + x = 27
27 – x = 20
Рассмотрим другой пример. Перед вами другая схема. Изучим, где на схеме целое, а где части: х – это «целое», а 30 и 6 – это части.
30 6
х
Воспользуемся правилом,
Вывод: Уравнение – это равенство, содержащее неизвестное число, которое надо найти. Когда решение уравнения находится легко, пользуются способом подбора. Нужно подобрать такое число, чтобы получилось верное равенство.
Тренировочные задания.
- Соедините уравнение с его решением.
Правильные ответы:
2. Выберите и подчеркните среди математических записей уравнения.
15 + 6 = 21
17 – d
b + 3 = 12
3 + 5 > 6
48 – a = 8
9 + e < 39
k – 4 = 10
Правильные ответы:
15 + 6 = 21
17 – d
b + 3 = 12
3 + 5 > 6
48 – a = 8
9 + e < 39
k – 4 = 10
Здравствуйте, уважаемые читатели!
Мы собрались снова на этом канале для того, чтобы продолжить изучение одного из интереснейших разделов алгебры. В двух предыдущих статьях (ссылки я прикреплю в конце) было рассмотрено 8 видов уравнений. В этой публикации я расскажу только об одном уравнении, к сожалению, не очень любимом учениками за продолжительность его решения.
Но сначала обратимся к теории.
9. Рациональные уравнения, решаемые методом подбора рациональных корней
Алгоритм метода подбора рациональных корней
Рассмотрим на следующих примерах, как решаются уравнения методом подбора рациональных корней.
Ещё один пример, иллюстрирующий метод подбора.
Ура! Мы справились. Как видно, решение рациональных уравнений методом подбора рациональных корней – это достаточно трудоёмкая процедура. Надо быть предельно внимательными и, главное, не забывать о корнях, найденных с помощью теорем 3 и 4.
А сейчас я предлагаю Вам прорешать подготовленные мною уравнения по этой теме. Ответы, как обычно, я прикреплю в комментариях.
Привожу названия и ссылки на статьи, в которых положено начало цикла: 1) “Рациональные уравнения с одним неизвестным: простейшие, решаемые методами разложения на множители и замены (не специальной)”; 2) “Рациональные уравнения с одним неизвестным: специальные замены”.
Если Вы обратили внимание, то для того, чтобы легко находить материалы для 10-11 класса, я нарисовала соответствующую картинку и подписала её словом “Эпизод”. Нумерация эпизодов идёт по порядку, начиная с первого.
Все материалы, публикуемые на канале Дружелюбный философ, разработаны мною и могут быть полезными не только для подготовки к экзаменам, но и для читателей, увлекающихся математикой, а также для родителей, которые хотят помочь своих детям в подготовке по предмету “Математика” в школе.
Спасибо, что интересуетесь математикой. Следите за выходом новых публикаций.
Вы находитесь на дружелюбном канале.
Уважайте себя. С уважением, автор.
Автор проекта:
Шелкова Полина,
Класс: 10Руководитель:
Злобова Людмила Викторовна,
учитель математики
ВВЕДЕНИЕ
Слово «тригонометрия» греческое, оно переводится как «измерение треугольников» (τρίγονον – «тригон» – треугольник и μετρειν – «метрео» – измеряю).
Тригонометрия, как и всякая другая наука, выросла из практической деятельности человека. Потребности развивающегося мореплавания, для которого требовалось умение правильно определять курс корабля в открытом море по положению небесных светил, оказали большое влияние на развитие астрономии и тесно связанной с ней тригонометрией. Предполагают, что основополагающее значение для развития тригонометрии в эпоху ее зарождения, имели работы древнегреческого астронома Гиппарха Никейского (180-125 лет до н. э.) (прил. №3). Систематическое использование полной окружности в 360° установилось в основном благодаря Гиппарху и его таблице хорд (прил. №2). Т.е. таблицы, которые выражают длину хорды для различных центральных углов в круге постоянного радиуса, что является аналогом современных таблиц тригонометрических функций. Впрочем, до нас не дошли оригинальные таблицы Гиппарха, как и почти все, что им написано. И мы, можем составить себе о них представление главным образом по сочинению «Великое построение» или «Альмагесту» знаменитого астронома Клавдия Птолемея, жившего в середине II века н.э.
Несмотря на то, что в работах ученых древности нет «тригонометрии» в строгом смысле этого слова, но по существу они, пользуясь известными им средствами элементарной геометрии, решали те задачи, которыми занимается тригонометрия. Например, задачи на решение треугольников (определение всех сторон и углов треугольника по трем его известным элементам), теоремы Евклида и Архимеда представленные в геометрическом виде, эквивалентны специфическим тригонометрическим формулам. Главным достижением средневековой Индии стала замена хорд синусами. Это позволило вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии, как учению о тригонометрических величинах.
Учёные стран Ближнего и Среднего Востока с VIII века развили тригонометрию своих предшественников. Уже в середине IX века среднеазиатский учёный аль-Хорезми написал сочинение «Об индийском счёте». После того, как трактаты мусульманских ученых были переведены на латынь, многие идеи греческих, индийских и мусульманских математиков стали достоянием европейской, а затем и мировой науки. В дальнейшем потребности географии, геодезии, военного дела, способствовали развитию тригонометрии. Особенно усиленно шло ее развитие в средневековое время. Большая заслуга в формировании тригонометрии как отдельной науки принадлежит азербайджанскому ученому Насир ад-Дину ат-Туси (1201-1274), написавшему «Трактат о полном четырехстороннике». Творения ученых этого периода привели к выделению тригонометрии как нового самостоятельного раздела науки. Однако в их трудах еще не была введена необходимая символика. Современный вид тригонометрия получила в трудах Леонарда Эйлера (1707-1783). На основании трудов Эйлера были составлены учебники тригонометрии, излагавшие ее в строгой научной последовательности (прил. №4). Тригонометрические вычисления применяются во многих областях человеческой деятельности: в геометрии, в физике, в астрономии, в архитектуре, в геодезии, инженерном деле, в акустике, в электронике и т.д.
I РАЗДЕЛ (теоретический)
Тема проекта и её актуальность: почему я выбрала тему «Способы отбора корней в тригонометрических уравнениях»?
- Расширить и углубить свои знания, полученные в курсе геометрии 8-9 класса.
- Тригонометрические уравнения рассматриваются в курсе алгебры и начал математического анализа 10-11 класса.
- Тригонометрические уравнения включены в КИМы ЕГЭ по математике.
Решение тригонометрических уравнений и отбор корней, принадлежащих заданному промежутку – это одна из сложнейших тем математики, которая выносится на Единый Государственный Экзамен. По результатам анкетирования многие учащиеся затрудняются или вообще не умеют решать тригонометрические уравнения и особенно затрудняются в отборе корней, принадлежащих промежутку. Немаловажно также знать, тригонометрические формулы, табличные значения тригонометрических функций для решения целого ряда заданий Единого Государственного Экзамена по математике.
Цель проекта: изучить способы отбора корней в тригонометрических уравнениях и выбрать для себя наиболее рациональные подходы для качественной подготовки к ЕГЭ.
Задачи:
- познакомиться с историческими сведениями о возникновении тригонометрии, как науки;
- изучить соответствующую литературу;
- научиться решать тригонометрические уравнения;
- найти теоретический материал и изучить методы отбора корней в тригонометрических уравнениях;
- научиться отбирать корни в тригонометрических уравнениях, принадлежащим заданному промежутку;
- подготовиться к ЕГЭ по математике.
Приёмы отбора корней тригонометрического уравнения на заданном промежутке.
При решении тригонометрических уравнений предлагается провести отбор корней из множества значений неизвестного. В тригонометрическом уравнении отбор корней можно осуществлять следующими способами: арифметическим, алгебраическим, геометрическим и функционально-графическим.
Арифметический способ отбора корней состоит в непосредственной подстановке полученных корней в уравнение, учитывая имеющиеся ограничения, при переборе значений целочисленного параметра.
Алгебраический способ предполагает составление неравенств, соответствующих дополнительным условиям, и их решение относительно целочисленного параметра.
Геометрический способ предполагает использование при отборе корней двух вариантов: тригонометрической окружности или числовой прямой. Тригонометрическая окружность более удобна, когда речь идет об отборе корней на промежутке или в случае, когда значение обратных тригонометрических функций, входящих в решения, не являются табличными. В остальных случаях предпочтительнее модель числовой прямой. Числовую прямую удобно использовать при отборе корней на промежутке, длина которого не превосходит 2 или требуется найти наибольший отрицательный или наименьший положительный корень уравнения.
Функционально-графический способ предполагает отбор корней осуществлять с использование графиков тригонометрических функций. Чтобы использовать данный способ отбора корней, требуется умение схематичного построения графиков тригонометрических функций.
II РАЗДЕЛ (практический)
Покажу практически три наиболее эффективных и рациональных, с моей точки зрения, метода отбора корней на примере решения следующего тригонометрического уравнения:
sinx=cos2x;
sinx−cos2x=0; [применили формулу двойного угла: cos2x = cos2x−sin2x]
sinx−(cos2x−sin2x)=0;
sinx−(1−sin2x−sin2x)=0;
sinx−(1−2sin2x)=0;
2sin2x+sinx−1=0.
Введем новую переменную: sinx = t, -1 ≤ t ≤1, получим
2t2+t-1=0
D=b2-4ac, т.е. D=9
t1 = -1, t2 = ½.
Вернемся к замене:
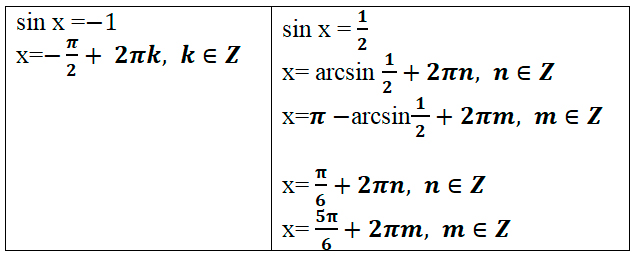
б) Рассмотрим три способа отбора корней, попадающих в отрезок 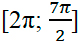
1 способ: обратимся к единичной окружности. Отметим на ней дугу, соответствующую указанному отрезку, т.е. выполним отбор корней арифметическим способом и с помощью тригонометрической окружности:
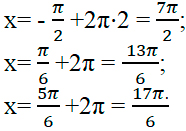
2 способ: указанный отрезок соответствует неравенству: Подставим в него полученные корни: 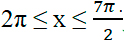

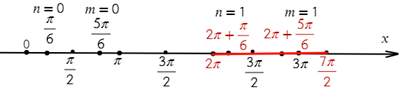
3 способ: разместим корни уравнения на числовой прямой. Сначала отметим корни, подставив вместо n, и нуль (0), а потом добавим к каждому корню периоды.
Нам останется только выбрать корни, которые попали в нужный нам отрезок.
Ответ:
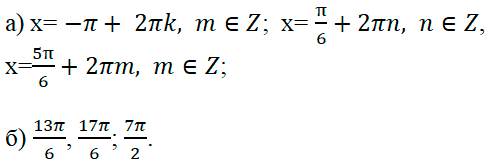
(Более подробный пример в приложении №1)
ЗАКЛЮЧЕНИЕ
При работе над моим проектом я изучила методы решения тригонометрических уравнений и способы отбора корней тригонометрических уравнений. Выяснила для себя положительные и отрицательные моменты. При апробации этих подходов в отборе корней тригонометрического уравнения, понимаешь, что каждый из этих способов удобен по-своему в том или ином случае. Например, алгебраический способ (решение неравенством) наиболее эффективен, когда промежуток для отбора корней достаточно большой, в тоже время он дает практически стопроцентное нахождение целочисленного параметра для вычисления корней, а применение арифметического способа приводит к громоздким вычислениям. При отборе корней уравнения, удовлетворяющих дополнительным условиям, т.е. когда корни уравнения принадлежат заданному промежутку, мне проще и нагляднее получить корни с помощью тригонометрической окружности, а проверить себя можно арифметическим способом. Замечу, что при решении тригонометрических уравнений трудности, связанные с отбором корней, возрастают, если в уравнении приходится учитывать ОДЗ. Как показывает практика и анкетирование моих одноклассников, из четырёх возможных методов отбора корней тригонометрического уравнения по дополнительным условиям, наиболее предпочтительным является отбор корней по окружности. Анкетирование проходили 12 респондентов, изучающих тригонометрию (прил. №5). Большинство из них отвечали, что этот раздел математики достаточно сложный: большой объем информации, очень много формул, табличных значений, которые нужно знать и уметь применять на практике. Еще как одна из проблем – небольшое количество времени, отведенное на изучение этого сложного раздела математики. И я разделяю их мнение. При такой сложности, многие считают, что тригонометрия важный раздел математики, который находит применение в других науках и практической деятельности человека.
СПИСОК ЛИТЕРАТУРЫ
- Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс: учеб для общеобразоват. организаций: базовый и углубленный уровни/ [С.М.Никольский, М.К.Потапов, Н.Н.Решетников и др.]-3 -е изд.- М.: Просвещение, 2016.
- Алгебра и начала математического анализа: Учеб для 10-11 кл.общеобразоват. организаций / А.Н.Колмогоров, А.М.Абрамов, Ю.П.Дудницин и др. под редакцией А.Н.Колмогорова – М. Просвещение, 2017.
- С.В Кравцев и др. Методы решения задач по алгебре: от простых до самых сложных – М: Издательство: «Экзамен», 2005.
- Корянов А.Г., Прокофьев А.А. – Тригонометрические уравнения: методы решения и отбор корней. – М.: Математика ЕГЭ, 2012.
Электронные ресурсы
- https://ru.wikipedia.org/wiki/Тригонометрия
- https://www.yaklass.ru/p/ege/matematika/podgotovka-k-ege-po-matematike-profilnyi-uroven-10744/trigonometricheskie-uravneniia-s-ogranicheniiami-zadacha-13-536475/re-a4b9cc95-fe96-40c2-b70c-f46548b726a0
- https://mat.1sept.ru/1999/no19.htm
- https://math-ege.sdamgia.ru/
- https://alexlarin.net/ege21.html
- https://www.academia.edu/10962821/МАТЕМАТИКА_ЕГЭ_2012_Тригонометрические_уравнения_методы_решений_и_отбор_корней_типовые_задания_С1
- http://teacher-andreeva.ru/wp-content/uploads/2016/03/тригоном-ур-я.pdf
- https://reshimvse.com/article.php?id=100
Пример:
а) реши уравнение
sinx=cos2x
.
б) Найди все корни этого уравнения, принадлежащие отрезку
2π;7π2
.
a) Уравнение прежде всего иррациональное, поэтому решается возведением обеих частей в квадрат. С учётом области определения получаем:
sinx=cos2x;sinx≥0,cos2x≥0.
Стоит заметить, что рассматривать оба неравенства в системе нам не нужно, так как мы будем решать уравнение. Поэтому можно оставить только одно — более простое неравенство:
sinx=cos2x;(1)sinx≥0.
Решим уравнение системы ((1)). Прежде всего избавимся от двойного угла в уравнении:
sinx=cos2x;sinx−cos2x=0;sinx−(cos2x−sin2x)=0;sinx−(1−sin2x−sin2x)=0;sinx−(1−2sin2x)=0;2sin2x+sinx−1=0;sinx=−1,sinx=12.
(sin x= -1) исключаем, так как это значение не входит в область определения, а решения второго уравнения обозначим на тригонометрической окружности.
Рис. (1). Решения уравнения на единичной окружности
Эти решения можно записать в виде:
x=π6+2πn,n∈ℤ,x=5π6+2πm,m∈ℤ.
б) Рассмотрим три способа отбора корней, попадающих в отрезок
2π;7π2
.
(1) способ:
вернёмся к единичной окружности. Отметим на ней дугу, соответствующую указанному промежутку, подпишем начало и конец, отметим точки окружности, представляющие серии решений и принадлежащие дуге, укажем их значения, принадлежащие промежутку.
2π+π6=13π6,2π+5π6=17π6.
Рис. (2). Отбор корней с помощью единичной окружности
Обрати внимание!
Нельзя отмечать и подписывать посторонние точки на окружности!
(2) способ:
указанный отрезок соответствует неравенству
2π≤x≤7π2
. Подставим в него полученные корни:
| 2π≤π6+2πn≤7π2,n∈ℤ:π;2≤16+2n≤72,n∈ℤ−16;2−16≤2n≤72−16,n∈ℤ;116≤2n≤206,n∈ℤ:2;1112≤n≤2012,n∈ℤ;1112≤n≤1812,n∈ℤ;n=1;π6+2π⋅1=13π6 | 2π≤5π6+2πm≤7π2,m∈ℤ:π;2≤56+2m≤72,m∈ℤ−56;2−56≤2m≤72−56,m∈ℤ;76≤2m≤166,m∈ℤ:2;712≤m≤1612,m∈ℤ;712≤m≤1412,m∈ℤ;m=1;5π6+2π⋅1=17π6 |
Обрати внимание!
Обязательно выдели целые части дробей для оценки значений (n) и (m)!
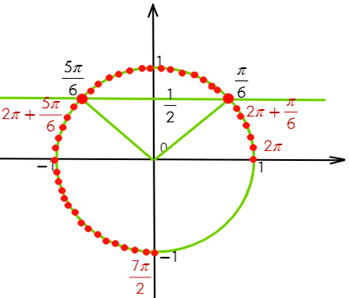
(3) способ:
разместим корни уравнения на числовой прямой. Сначала отметим корни, подставив вместо (n) и (m) (0), а потом добавим к каждому корню периоды. На числовой прямой должен быть выделен заданный отрезок, обозначены его концы, отмечены все последовательные значения серий корней, начиная с точек, расположенных левее промежутка, и заканчивая точками, расположенными правее промежутка.
Рис. (3). Отбор корней с помощью координатной прямой
Нам останется только выбрать корни, которые попали в нужный нам отрезок.
Ответ: а)
π6+2πn,n∈ℤ;5π6+2πm,m∈ℤ
; б)
13π6,17π6.
Рекомендуем при решении тригонометрических уравнений использовать несколько разных способов отбора. Это поможет тебе убедиться в правильности отбора корней и выработать навык выбора наиболее удобного способа.
Источники:
Рис. 1. Решения уравнения на единичной окружности. © ЯКласс.
Рис. 2. Отбор корней с помощью единичной окружности. © ЯКласс.
Рис. 3. Отбор корней с помощью координатной прямой. © ЯКласс.




























































