Содержание:
Квадратные корни
Уравнение х2 = 9 имеет два решения: 3 и -3. Говорят, что 3 и -3 — квадратные корни из числа 9.
Квадратным корнем из числа а называют число, I квадрат которого равен а.
Примеры:
Квадратными корнями из числа:
- а) 1600 являются 40 и – 40, поскольку 402 = 1600 и (-40)2 = 1600;
- б) 0,49 являются 0,7 и 0,7, поскольку 0,72 = 0,49 и (-0,7)2 = 0,49.
Среди известных вам чисел нет такого, квадрат которого был бы равен отрицательному числу, поэтому квадратного корня из отрицательного числа не существует.
Квадратный корень из числа 0 равен нулю. Квадратный корень из положительного числа имеет два значения: одно из них положительное, другое — противоположное ему отрицательное число.
Неотрицательное значение квадратного корня называют арифметическим значением этого корня.
Арифметическое значение квадратного корня из числа a обозначают символом 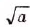
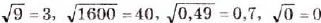
Примечание. Символом 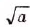 обозначают только арифметическое значение квадратного корня из числа а, хотя читается оно короче: «квадратный корень из числа а».
обозначают только арифметическое значение квадратного корня из числа а, хотя читается оно короче: «квадратный корень из числа а».
Вычисление арифметического значения квадратного корня называют извлечением квадратного корня.
Из небольших чисел, являющихся точными квадратами чисел, извлекать квадратные корни желательно устно.
| а | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | 144 |
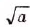 |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Квадратные корни из больших натуральных чисел можно находить, пользуясь таблицей квадратов.
Например, 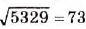 ,
, 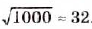 .
.
С помощью калькулятора можно извлекать квадратные корни с большей точностью. Например, чтобы извлечь квадратный корень из 1000, набираем это число, затем нажимаем клавишу 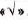 . На экране высвечивается число 31,622776.
. На экране высвечивается число 31,622776.
Следовательно, 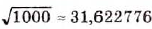 .
.
Если таким способом найти значение 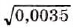 , то на некоторых калькуляторах высвечиваются два числа: 5,9160797 и -2. Число -2 здесь показывает порядок искомого значения, записанного в стандартном виде. Следовательно,
, то на некоторых калькуляторах высвечиваются два числа: 5,9160797 и -2. Число -2 здесь показывает порядок искомого значения, записанного в стандартном виде. Следовательно,
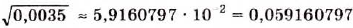 .
.
Хотите знать ещё больше?
Извлекать квадратные корни из натуральных чисел вавилонские учёные умели ещё 4 тыс. лет тому назад Они составили таблицу квадратов многих натуральных чисел и, пользуясь ею, находили квадратные корни. Если число m не было точным квадратом натурального числа, то они искали ближайшее приближённое значение а квадратного корня из m, представляли число m в виде m = а2 + b и применяли правило, которое сейчас можно записать в виде формулы 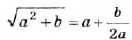 Например, если m = 108, то
Например, если m = 108, то 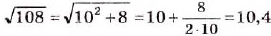 .
.
Проверка. 10,42 = 108,16.
Это правило извлечения квадратных корней было известно и учёным Древней Греции.
Известны и другие алгоритмы извлечения квадратных корней, но теперь это удобнее делать с помощью калькулятора.
Квадратный корень из произведения, дроби, степени
Арифметический корень из а — неотрицательное значение квадратного корня из неотрицательного числа а. Поэтому для любого неотрицательного числа а выполняется тождество 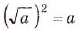 .
.
Примеры:
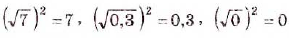
Верны и такие тождества:
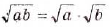 — для неотрицательных значений а и b;
— для неотрицательных значений а и b;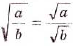 — для неотрицательного а и положительного b;
— для неотрицательного а и положительного b;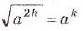 – для неотрицательного а и натурального к.
– для неотрицательного а и натурального к.
Докажем эти тождества:
1. Если а и b — произвольные неотрицательные числа, то числа 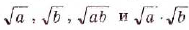 также неотрицательные. Кроме того,
также неотрицательные. Кроме того, 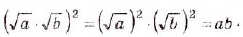
Следовательно, 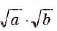 — неотрицательное число, квадрат которого равен ab, то есть
— неотрицательное число, квадрат которого равен ab, то есть 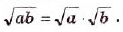
2. Если 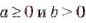 , то числа
, то числа 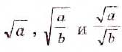 неотрицательные, a
неотрицательные, a 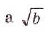 — положительное. Кроме того,
— положительное. Кроме того,
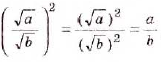
Следовательно, 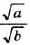 неотрицательное число, квадрат которого равен
неотрицательное число, квадрат которого равен 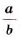 , то есть
, то есть 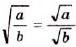
3. Если число а — неотрицательное, a k — натуральное, то числа 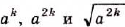 — неотрицательные. Кроме того,
— неотрицательные. Кроме того,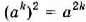 . Следовательно,
. Следовательно, 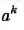 — неотрицательный квадратный корень из
— неотрицательный квадратный корень из 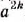 , то есть
, то есть
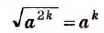
Доказанные три теоремы кратко можно сформулировать так.
- Корень из произведения двух неотрицательных чисел равен произведению корней из этих чисел (теорема о корне из произведения).
- Корень из дроби, числитель которой неотрицательный, а знаменатель положительный, равен корню из числителя, делённому на корень из знаменателя (теорема о корне из дроби).
- Корень из степени a , в котором числа а — неотрицательное и k — натуральное, равен ст (теорема о корне из степени)
Примечание. Здесь под «корнем» понимают только квадратный арифметический корень.
Теорему о корне из произведения можно распространить на три множителя и более. Действительно, если числа а, b и с — неотрицательные, то 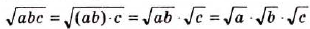 Если в доказанных тождествах поменять местами их левые и правые части, то получим:
Если в доказанных тождествах поменять местами их левые и правые части, то получим:
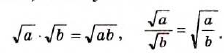 Эти тождества показывают, как можно умножать и делить корни. Например,
Эти тождества показывают, как можно умножать и делить корни. Например,
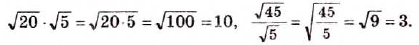
Из теоремы о корне из степени следует, что 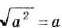 , если
, если 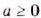 . Если а < 0, то равенство
. Если а < 0, то равенство 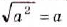 – а неверное, поскольку число
– а неверное, поскольку число 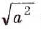 неотрицательное и не может быть равным отрицательному числу а.
неотрицательное и не может быть равным отрицательному числу а.
Равенство 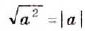 верное при каждом значении а, поскольку число
верное при каждом значении а, поскольку число 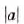 — неотрицательное и его квадрат равен а2.
— неотрицательное и его квадрат равен а2.
Примеры: 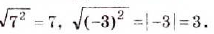
Хотите знать ещё больше?
В сформулированных выше теоремах представлены только простейшие случаи преобразования арифметических значений квадратных корней: если все числа под корнями положительные или неотрицательные Но бывают и такие выражения, в которых под знаком корня — произведение либо частное двух отрицательных чисел. В этом случае можно использовать определения квадратного корня, арифметического значения квадратного корня и т. д.
Например, 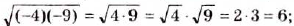
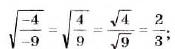 .
.
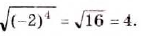
Из теоремы 3 несложно получить такое следствие.
Если натуральное число 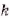 — чётное, то для любых значений а выполняется тождество
— чётное, то для любых значений а выполняется тождество 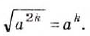
Ведь обе части этого равенства — числа неотрицательные, их квадраты – равны.
Выполним вместе!
Пример:
Найдите значение выражения: а) 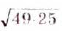 ; б)
; б) 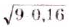 ; в)
; в) 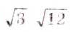 ; г)
; г) 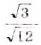 .
.
Решение:
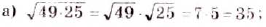
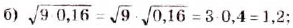
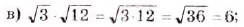
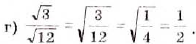
О т в е т. а) 35; б) 1,2; в) 6; г) 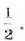
Преобразование выражений с корнями
Выражения с квадратными корнями можно складывать, вычитать, умножать, возводить в степень и делить (на делитель, отличный от нуля).
Примеры:
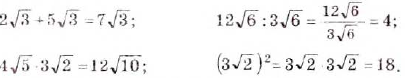
Рассмотрим и другие преобразования выражений с корнями.
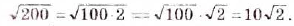
Подобное преобразование называют вынесением множителя за знак корня. В последнем примере за знак корня вынесен множитель 10.
Преобразование, обратное вынесению множителя за знак корня, называют внесением множителя под знак корня. 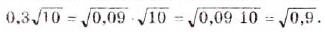
В атом примере под знак корня вносим множитель 0,3. Рассмотренные преобразования осуществляются на основании теоремы о корне из произведения.
Если знак корня находится в знаменателе дроби, то такую дробь можно заменить тождественной, знаменатель которой не имеет корней. Достаточно умножить члены дроби на соответствующее выражение. Например, 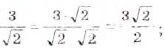
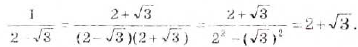
Такие преобразования называют освобождением дроби от иррациональности в знаменателе.
Эти преобразования можно выполнять также с выражениями, содержащими переменные. Например,
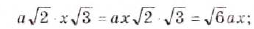
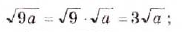
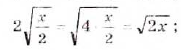
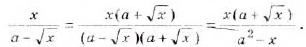
Примечание. При вынесении переменной за знак корня необходимо помнить, что равенство 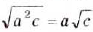 верно только при неотрицательных значениях а и с. Если
верно только при неотрицательных значениях а и с. Если 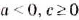 , то
, то 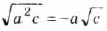 . При любых действительных значениях а и неотрицательных с верно тождество:
. При любых действительных значениях а и неотрицательных с верно тождество: 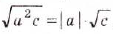 .
.
Пример:
Вынесите множитель за знак корня: a) 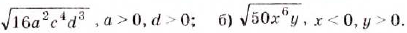
Решение:
а) 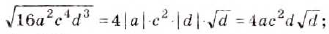 б)
б) 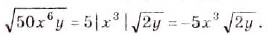 Ответ. a)
Ответ. a) 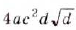 ; б)
; б) 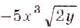 .
.
При внесении переменной под знак корня следует помнить, что под корень можно вносить лишь положительные числа.
Пример:
Внесите множитель под знак корня: а) 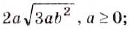 ; б)
; б) 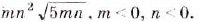
Решение:
а) 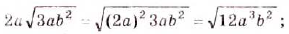 ; б)
; б) 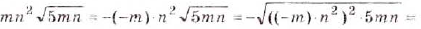
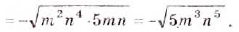 О т в е т. a)
О т в е т. a) 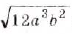 ; б)
; б) 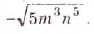
Используя словосочетание «выражения с корнями», в этой главе мы будем говорить только о «выражениях с арифметическими квадратными корнями». Но в математике выражения с корнями имеют более широкий смысл поскольку корни бывают не только квадратные, но и кубические четвёртой, пятой …. n-й степеней. Корни из числа а таких степеней обозначают символами:
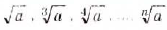
Выражения, содержащие любые из таких корней, называют выражениями с корнями, или иррациональными выражениями. Выражения с арифметическими квадратными корнями – это только часть иррациональных выражений (рис 45) .

Рис. 45 Раньше знаки корней 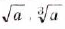 …,
…, 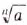 называли радикалами, поэтому в некоторых публикациях иррациональные выражения до сих пор называют выражениями с радикалами.
называли радикалами, поэтому в некоторых публикациях иррациональные выражения до сих пор называют выражениями с радикалами.
Выполним вместе!
Пример:
Упростите выражение: а) 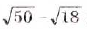 ; б)
; б) 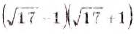 ; в)
; в)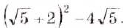 .
.
Решение:
a) 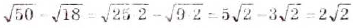 . б)
. б) 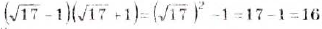 ;
;
в) 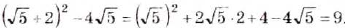 . О т в е т. a)
. О т в е т. a) 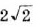 ; б)16; в) 9.
; б)16; в) 9.
Пример:
Разложите на множители выражение: a) 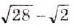 ; б)
; б) 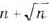 ; в)
; в) 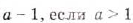 .
.
Решение:
а) 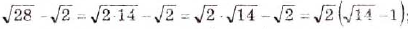 ; б)
; б) 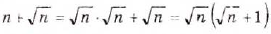 ; в) если а — число положительное, то
; в) если а — число положительное, то 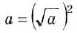 . Поэтому
. Поэтому
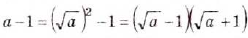
Ответ, a) 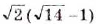 ; б)
; б) 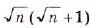 ; в)
; в) 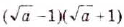 .
.
Пример:
Освободитесь от иррациональности в знаменателе дроби:
а) 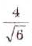 ; б)
; б) 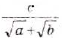 ;
;
Решение:
а) 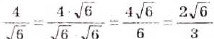 ; б)
; б) 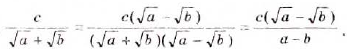
Ответ. а)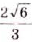 ; б)
; б) 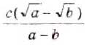 .
.
ИСТОРИЧЕСКИЕ СВЕДЕНИЯ
Квадратные корни из чисел вавилонские математики умели вычислять ещё 4 тыс. лет тому назад. Находили даже приближённые значения квадратных корней, пользуясь правилом, которое теперь можно записать (при небольших значениях с) в виде приближённого равенства:
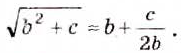 В XIII в. европейские математики предложили сокращённое обозначение корня. Вместо нынешнего
В XIII в. европейские математики предложили сокращённое обозначение корня. Вместо нынешнего 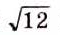 писали R12 (от латинского Radix — корень). Позднее вместо R стали писать знак V, например V7, V(a + b). Затем над многочленом за корнем добавили черту:
писали R12 (от латинского Radix — корень). Позднее вместо R стали писать знак V, например V7, V(a + b). Затем над многочленом за корнем добавили черту: 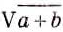 . Р. Декарт (1596 -1650) соединил знак корня с чертой, после чего запись приобрела современный вид:
. Р. Декарт (1596 -1650) соединил знак корня с чертой, после чего запись приобрела современный вид: 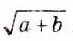 . Действительные числа входили в математику непросто. Учёные античного мира не предполагали, что кроме целых и дробных могут быть и другие числа. Хотя Пифагор (VI в. до и. э.) и его ученики доказали: если длина стороны квадрата равна 1, то длину его диагонали нельзя выразить ни одним рациональным числом. Таким образом, они выяснили, что существуют отрезки, длины которых не выражаются рациональными числами, но при этом иррациональных чисел не ввели. Математики Индии и Среднего Востока пользовались иррациональными числами, но считали их ненастоящими, неправильными, «глухими». И только когда Р. Декарт предложил каждой точке координатной прямой поставить в соответствие число, иррациональные числа объединили с рациональными во множество действительных чисел. Строгая теория действительных чисел появилась лишь в XIX в. В 8 классе изучают не все действительные числа. Кроме квадратных существуют корни третьей, четвёртой и высших степеней, например
. Действительные числа входили в математику непросто. Учёные античного мира не предполагали, что кроме целых и дробных могут быть и другие числа. Хотя Пифагор (VI в. до и. э.) и его ученики доказали: если длина стороны квадрата равна 1, то длину его диагонали нельзя выразить ни одним рациональным числом. Таким образом, они выяснили, что существуют отрезки, длины которых не выражаются рациональными числами, но при этом иррациональных чисел не ввели. Математики Индии и Среднего Востока пользовались иррациональными числами, но считали их ненастоящими, неправильными, «глухими». И только когда Р. Декарт предложил каждой точке координатной прямой поставить в соответствие число, иррациональные числа объединили с рациональными во множество действительных чисел. Строгая теория действительных чисел появилась лишь в XIX в. В 8 классе изучают не все действительные числа. Кроме квадратных существуют корни третьей, четвёртой и высших степеней, например 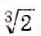 ,
, 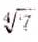 ,
, 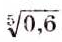 . С такими действительными числами вы ознакомитесь в старших классах.
. С такими действительными числами вы ознакомитесь в старших классах.
ОСНОВНОЕ В ГЛАВЕ
Квадратным корнем из числа а называют число, квадрат которого равен а. Например, число 16 имеет два квадратных корня: 4 и -4. Неотрицательное значение квадратного корня из числа а называют арифметическим значением корня я обозначают символом 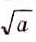 . Свойства квадратных корней. Если а > 0 и b > 0, то
. Свойства квадратных корней. Если а > 0 и b > 0, то
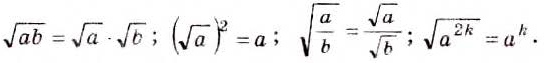
Для любого действительного 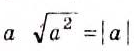 . Значения многих квадратных корней — числа не рациональные, а иррациональные. Числа целые и дробные, положительные, отрицательные и нуль вместе составляют множество рациональных чисел. Каждое рациональное число можно записать в виде дроби
. Значения многих квадратных корней — числа не рациональные, а иррациональные. Числа целые и дробные, положительные, отрицательные и нуль вместе составляют множество рациональных чисел. Каждое рациональное число можно записать в виде дроби 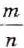 , где
, где 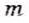 — число целое, а n— натуральное. Любое рациональное число можно представить в виде бесконечной периодической десятичной дроби. А любая бесконечная периодическая десятичная дробь изображает некоторое рациональное число. Примеры:
— число целое, а n— натуральное. Любое рациональное число можно представить в виде бесконечной периодической десятичной дроби. А любая бесконечная периодическая десятичная дробь изображает некоторое рациональное число. Примеры: 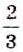 = 0,6666…,
= 0,6666…, 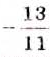 =1,181818…. Числа, которые можно представить в виде бесконечных непериодических десятичных дробей, называют иррациональными. Примеры иррациональных чисел:
=1,181818…. Числа, которые можно представить в виде бесконечных непериодических десятичных дробей, называют иррациональными. Примеры иррациональных чисел: 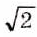 = 1,4142136…,
= 1,4142136…, 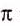 = 3,1415927… . Иррациональные числа вместе с рациональными образуют множество действительных чисел. Множества натуральных, целых, рациональных и действительных чисел обозначают соответственно буквами N, Z, Q, R (см. рис. 41). Действительные числа можно складывать, вычитать, умножать, возводить в степень и делить (на числа, отличные от нуля). Для сложения и умножения произвольных действительных чисел верны переместительный, сочетательный и распределительный законы: а + b = b + а, ab=ba, a + (b + c) = (a + b) + c, a . (bc) = (ab) . c, (a + b) с = ас +bс.
= 3,1415927… . Иррациональные числа вместе с рациональными образуют множество действительных чисел. Множества натуральных, целых, рациональных и действительных чисел обозначают соответственно буквами N, Z, Q, R (см. рис. 41). Действительные числа можно складывать, вычитать, умножать, возводить в степень и делить (на числа, отличные от нуля). Для сложения и умножения произвольных действительных чисел верны переместительный, сочетательный и распределительный законы: а + b = b + а, ab=ba, a + (b + c) = (a + b) + c, a . (bc) = (ab) . c, (a + b) с = ас +bс.
Квадратные корни. Арифметический квадратный корень
Рассмотрим квадрат, площадь которого равна 49 квадратным единицам. Пусть длина его стороны составляет 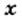 единиц. Тогда уравнение
единиц. Тогда уравнение 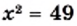 можно рассматривать как математическую модель задачи о нахождении стороны квадрата, площадь которого равна 49 квадратным единицам.
можно рассматривать как математическую модель задачи о нахождении стороны квадрата, площадь которого равна 49 квадратным единицам.
Корнями этого уравнения являются числа 7 и —7. Говорят, что числа 7 и —7 являются квадратными корнями из числа 49.
Определение: Квадратным корнем из числа 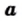 называют число, квадрат которого равен
называют число, квадрат которого равен 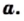
Приведем несколько примеров.
Квадратными корнями из числа 9 являются числа 3 и —3. Действительно, 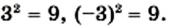
Квадратными корнями из числа 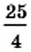 являются числа
являются числа 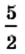 и
и 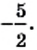
Действительно, 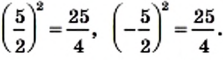
Квадратным корнем из числа 0 является только число 0. Действительно, существует лишь одно число, квадрат которого равен нулю, — это число 0.
Поскольку не существует числа, квадрат которого равен отрицательному числу, то квадратного корня из отрицательного числа не существует.
Положительный корень уравнения 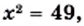 число 7, является ответом в задаче о нахождении стороны квадрата, площадь которого равна 49 квадратным единицам. Это число называют арифметическим квадратным корнем из числа 49.
число 7, является ответом в задаче о нахождении стороны квадрата, площадь которого равна 49 квадратным единицам. Это число называют арифметическим квадратным корнем из числа 49.
Определение: Арифметическим квадратным корнем из числа 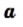 называют неотрицательное число, квадрат которого равен
называют неотрицательное число, квадрат которого равен 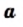 .
.
Арифметический квадратный корень из числа 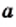 обозначают
обозначают 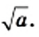 Знак
Знак 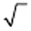 называют знаком квадратного корня или радикалом (от лат. radix — корень).
называют знаком квадратного корня или радикалом (от лат. radix — корень).
Запись 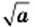 читают: «квадратный корень из
читают: «квадратный корень из 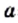 », опуская при чтении слово «арифметический».
», опуская при чтении слово «арифметический».
Выражение, стоящее под радикалом, называют подкоренным выражением. Например, в записи 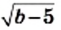 двучлен
двучлен 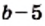 является подкоренным выражением. Из определения арифметического квадратного корня следует, что подкоренное выражение может принимать только неотрицательные значения.
является подкоренным выражением. Из определения арифметического квадратного корня следует, что подкоренное выражение может принимать только неотрицательные значения.
Действие нахождения арифметического квадратного корня из числа называют извлечением квадратного корня.
Рассмотрим несколько примеров:
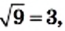 так как
так как 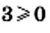 и
и 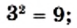
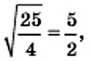 так как
так как 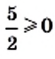 и
и 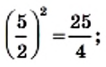
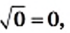 так как
так как 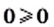 и
и 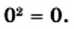
Вообще, равенство 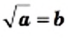 выполняется при условии, что
выполняется при условии, что  и
и 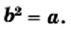
Этот вывод можно представить в другой форме: для любого неотрицательного числа 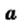 справедливо, что
справедливо, что 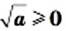 а
а 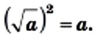
Например, 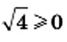 и
и 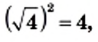
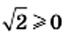 и
и 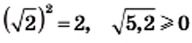 и
и 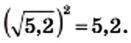
Подчеркнем, что к понятию квадратного корня мы пришли, решая уравнение вида 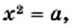 где
где 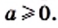 Корни этого уравнения — числа, каждое из которых является квадратным корнем из числа
Корни этого уравнения — числа, каждое из которых является квадратным корнем из числа 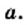
Поиск корней уравнения 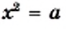 проиллюстрируем, решив графически уравнение
проиллюстрируем, решив графически уравнение 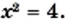
В одной системе координат построим графики функций 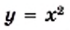 и
и 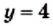 (рис. 17). Точки пересечения этих графиков имеют абсциссы 2 и —2, которые и являются корнями данного уравнения.
(рис. 17). Точки пересечения этих графиков имеют абсциссы 2 и —2, которые и являются корнями данного уравнения.
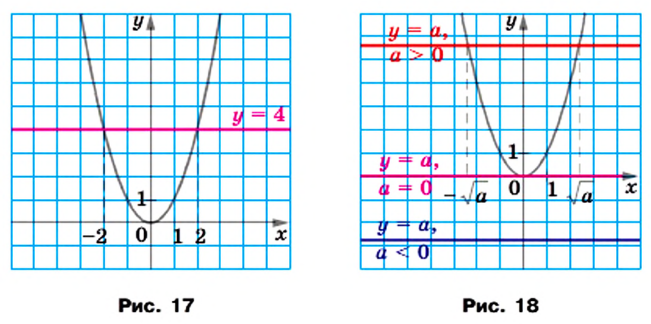
Уравнение 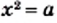 при
при 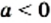 не имеет корней, что подтверждается графически: графики функций
не имеет корней, что подтверждается графически: графики функций 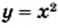 и
и 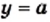 при
при 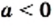 общих точек не имеют (рис. 18).
общих точек не имеют (рис. 18).
При 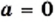 уравнение
уравнение 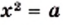 имеет единственный корень
имеет единственный корень 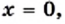 что также подтверждается графически: графики функций
что также подтверждается графически: графики функций 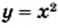 и
и 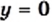 имеют только одну общую точку (рис. 18).
имеют только одну общую точку (рис. 18).
Графический метод также позволяет сделать следующий вывод: если 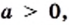 то уравнение
то уравнение 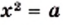 имеет два корня. Действительно, парабола
имеет два корня. Действительно, парабола 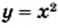 и прямая
и прямая 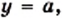 где
где 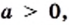 имеют две общие точки (рис. 18). При этом корнями уравнения
имеют две общие точки (рис. 18). При этом корнями уравнения 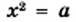 являются числа
являются числа 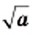 и
и 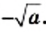 Действительно,
Действительно, 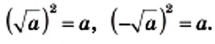
Например, уравнение 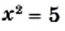 имеет два корня:
имеет два корня: 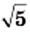 и
и 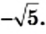
Пример:
Найдите значение выражения 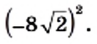
Решение:
Применив правило возведения произведения в степень и тождество 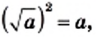 получим:
получим:
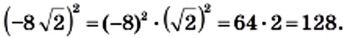
Пример:
Решите уравнение: 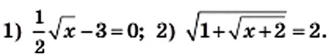
Решение:
1) Имеем: 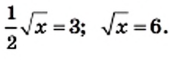 Тогда
Тогда 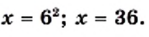
Ответ: 36.
2) 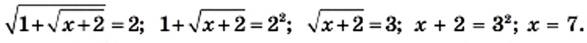
Ответ: 7.
Пример:
Решите уравнение 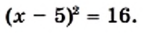
Решение:
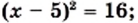
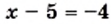 или
или 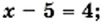
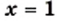 или
или 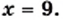
Ответ: 1; 9. ▲
Пример:
Решите уравнение 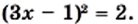
Решение:
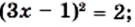
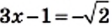 или
или 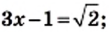
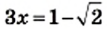 или
или 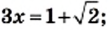
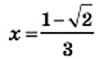 или
или 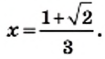
Ответ: 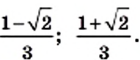
Пример:
При каких значениях 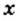 имеет смысл выражение:
имеет смысл выражение: 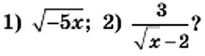
Решение:
1) Выражение 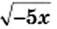 имеет смысл, если подкоренное выражение
имеет смысл, если подкоренное выражение 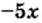 принимает неотрицательные значения. Подкоренное выражение является произведением двух множителей, один из которых — отрицательное число. Следовательно, это произведение будет принимать неотрицательные значения, если другой множитель
принимает неотрицательные значения. Подкоренное выражение является произведением двух множителей, один из которых — отрицательное число. Следовательно, это произведение будет принимать неотрицательные значения, если другой множитель 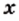 будет принимать неположительные значения.
будет принимать неположительные значения.
Ответ: при 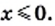
2) Данное выражение имеет смысл, если выполняются два условия: имеет смысл выражение 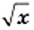 и знаменатель
и знаменатель 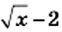 отличен от нуля. Следовательно, должны одновременно выполняться два условия:
отличен от нуля. Следовательно, должны одновременно выполняться два условия: 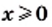 и
и 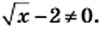 Отсюда
Отсюда 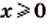 и
и 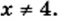
Ответ: при 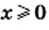 и
и 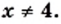
Пример:
Решите уравнение: 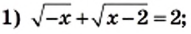
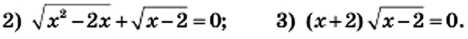
Решение:
1) Левая часть данного уравнения имеет смысл, если подкоренные выражения 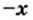 и
и 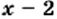 одновременно принимают неотрицательные значения. Из того, что первое подкоренное выражение должно быть неотрицательным, получаем:
одновременно принимают неотрицательные значения. Из того, что первое подкоренное выражение должно быть неотрицательным, получаем: 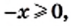 тогда
тогда  Однако если
Однако если 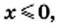 то второе подкоренное выражение,
то второе подкоренное выражение, 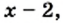 принимает только отрицательные значения. Следовательно, левая часть данного уравнения не имеет смысла.
принимает только отрицательные значения. Следовательно, левая часть данного уравнения не имеет смысла.
Ответ: корней нет.
2) Левая часть данного уравнения является суммой двух слагаемых, каждое из которых может принимать только неотрицательные значения. Тогда их сумма будет равна нулю, если каждое из слагаемых равно нулю. Следовательно, одновременно должны выполняться два условия: 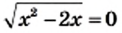 и
и 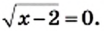 Это означает, что надо найти общие корни полученных уравнений, то есть решить систему уравнений
Это означает, что надо найти общие корни полученных уравнений, то есть решить систему уравнений
Имеем, 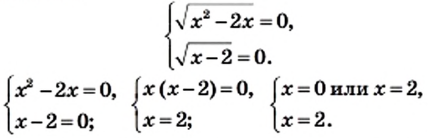
Решением последней системы, а значит, и исходного уравнения, является число 2.
Ответ: 2.
3) Используя условие равенства произведения нулю, получаем:
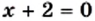 или
или 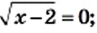
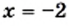 или
или 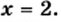
Однако при 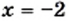 выражение
выражение 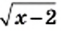 не имеет смысла. Следовательно, данное уравнение имеет единственный корень — число 2.
не имеет смысла. Следовательно, данное уравнение имеет единственный корень — число 2.
Ответ: 2.
Свойства арифметического квадратного корня
Легко проверить, что 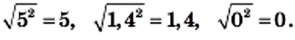 Может показаться, что при любом значении а выполняется равенство
Может показаться, что при любом значении а выполняется равенство 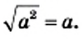 Однако это не так. Например, равенство
Однако это не так. Например, равенство 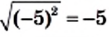 является ошибочным, поскольку
является ошибочным, поскольку 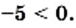 На самом деле
На самом деле 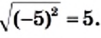 Также можно убедиться, что, например,
Также можно убедиться, что, например,
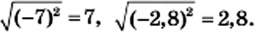
Вообще, справедлива следующая теорема.
Теорема: Для любого действительного числа а выполняется равенство
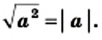
Доказательство: Для того чтобы доказать равенство 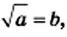 надо показать, что
надо показать, что 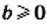 и
и 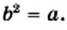
Имеем: 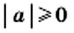 при любом
при любом 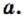
Также из определения модуля следует, что 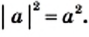
Следующая теорема обобщает доказанный факт.
Теорема: (арифметический квадратный корень из степени). Для любого действительного числа 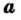 и любого натурального числа
и любого натурального числа 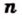 выполняется равенство
выполняется равенство
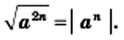
Доказательство этой теоремы аналогично доказательству теоремы 15.1. Проведите это доказательство самостоятельно.
Теорема: (арифметический квадратный корень из произведения). Для любых действительных чисел 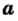 и
и 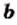 таких, что
таких, что 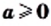 и
и 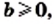 выполняется равенство
выполняется равенство
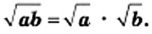
Доказательство: Имеем: 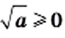 и
и 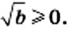 Тогда
Тогда 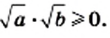 Кроме того,
Кроме того, 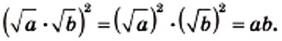
Следовательно, выражение 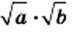 принимает только неотрицательные значения, и его квадрат равен
принимает только неотрицательные значения, и его квадрат равен 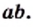
Эту теорему можно обобщить для произведения трех и более множителей. Например, если 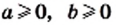 и
и 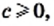 то
то
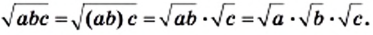
Теорема: (арифметический квадратный корень из дроби). Для любых действительных чисел 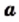 и
и 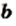 таких, что
таких, что 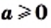 и
и 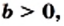 выполняется равенство
выполняется равенство
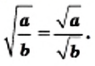
Доказательство этой теоремы аналогично доказательству теоремы 15.3. Проведите это доказательство самостоятельно.
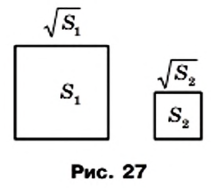
Понятно, что из двух квадратов с площадями 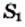 и
и 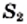 (рис. 27) большую сторону имеет тот, у которого площадь больше, то есть если
(рис. 27) большую сторону имеет тот, у которого площадь больше, то есть если 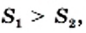 то
то 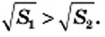 Это очевидное соображение иллюстрирует такое свойство арифметического квадратного корня: для любых неотрицательных чисел
Это очевидное соображение иллюстрирует такое свойство арифметического квадратного корня: для любых неотрицательных чисел 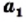 и
и 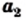 таких, что
таких, что 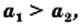 выполняется неравенство
выполняется неравенство 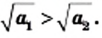
Пример:
Найдите значение выражения: 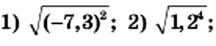
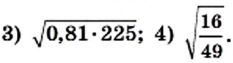
Решение:
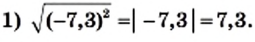
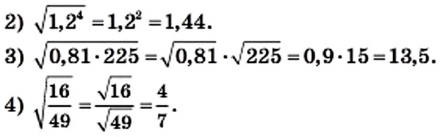
Пример:
Найдите значение выражения: 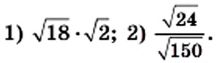
Решение:
1) Заменив произведение корней корнем из произведения, получим:
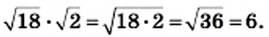
2) Заменив частное корней корнем из частного (дроби), получим:
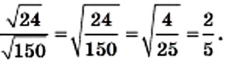
Пример:
Упростите выражение: 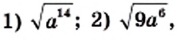 если
если 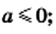
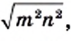 если
если 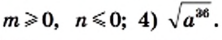
Решение:
1) По теореме об арифметическом квадратном корне из степени имеем:
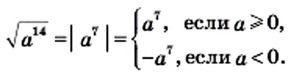
2) Имеем: 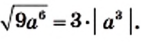 Поскольку по условию
Поскольку по условию 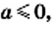 то
то 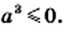 Тогда
Тогда
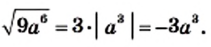
3) Имеем: 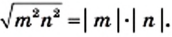 Поскольку по условию
Поскольку по условию 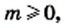 то
то 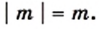 Поскольку
Поскольку 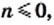 то
то 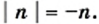 Следовательно,
Следовательно,
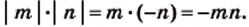
4) Имеем: 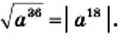 Поскольку
Поскольку 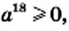 то
то 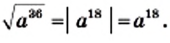
Пример:
Найдите значение выражения: 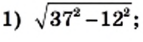
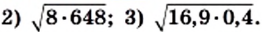
Решение:
1) Преобразовав подкоренное выражение по формуле разности квадратов, получаем:
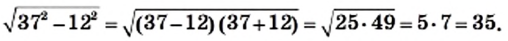
Пример:
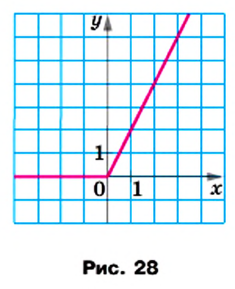
Постройте график функции 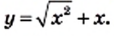
Решение:
Поскольку 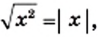 то
то 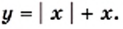
Если 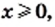 то
то 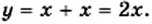
Если 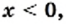 то
то 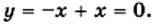
Следовательно, 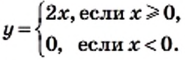
График функции изображен на рисунке 28.
Тождественные преобразования выражений, содержащих квадратные корни
Пользуясь теоремой об арифметическом квадратном корне из произведения, преобразуем выражение 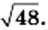 Имеем:
Имеем: 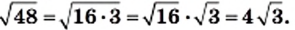 Выражение
Выражение 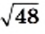 мы представили в виде произведения рационального числа 4 и иррационального числа
мы представили в виде произведения рационального числа 4 и иррационального числа 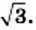 Такое преобразование называют вынесением множителя из-под знака корня. В данном случае был вынесен из-под знака корня множитель 4. Рассмотрим выполненное преобразование в обратном порядке:
Такое преобразование называют вынесением множителя из-под знака корня. В данном случае был вынесен из-под знака корня множитель 4. Рассмотрим выполненное преобразование в обратном порядке:
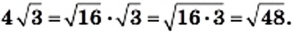
Такое преобразование называют внесением множителя под знак корня. В данном случае был внесен под знак корня множитель 4.
Пример:
Вынесите множитель из-под знака корня: 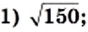
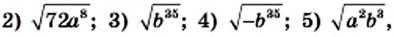 если
если 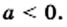
Решение:
1) Представим число, стоящее под знаком корня, в виде произведения двух чисел, одно из которых является квадратом рационального числа:
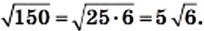
2) 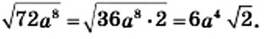
3) Поскольку подкоренное выражение должно быть неотрицательным, то из условия следует, что 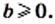 Тогда
Тогда
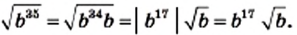
4) Из условия следует, что 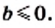 Тогда
Тогда
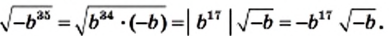
5) Из условия следует, что 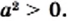 Поскольку подкоренное выражение должно быть неотрицательным, то получаем, что
Поскольку подкоренное выражение должно быть неотрицательным, то получаем, что 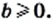 Тогда
Тогда
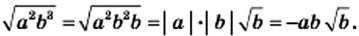
Пример:
Внесите множитель под знак корня: 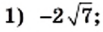
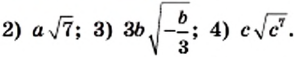
Решение:
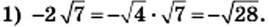
2) Если 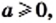 то
то 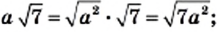 если
если 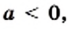 то
то 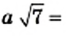
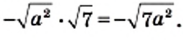
3) Из условия следует, что 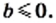 Тогда
Тогда 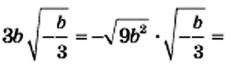
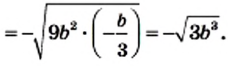
4) Из условия следует, что 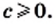 Тогда
Тогда 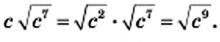
Пример:
Упростите выражение:
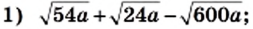
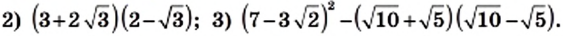
Решение:
1) Имеем:
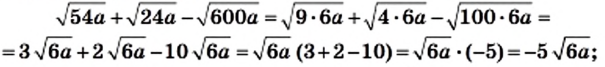
2) 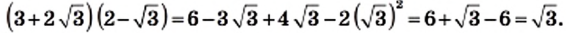
3) Применяя формулы сокращенного умножения (квадрат двучлена и произведение разности и суммы двух выражений), получим:
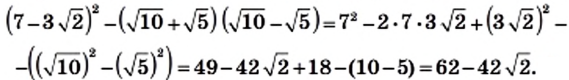
Пример:
Разложите на множители выражение: 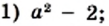
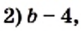 если
если 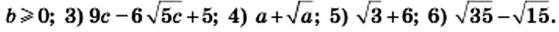
Решение:
1) Представив данное выражение в виде разности квадратов, получим:
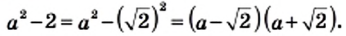
2) Поскольку по условию 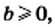 то
то 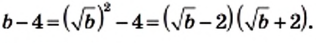
3) Применим формулу квадрата разности:
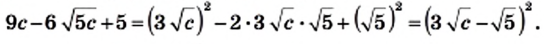
4) Имеем: 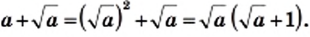
5) 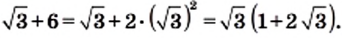
6) 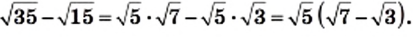
Пример:
Сократите дробь: 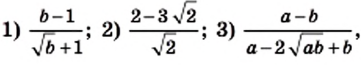
если 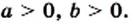
Решение:
1) Разложив числитель данной дроби на множители, получаем:
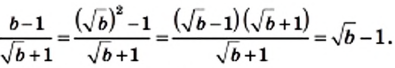
2) 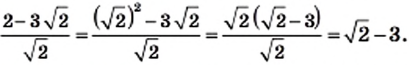
3) Поскольку по условию 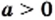 и
и 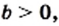 то числитель и знаменатель данной дроби можно разложить на множители и полученную дробь сократить:
то числитель и знаменатель данной дроби можно разложить на множители и полученную дробь сократить:
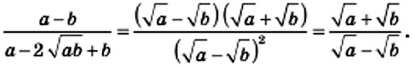
Освободиться от иррациональности в знаменателе дроби означает преобразовать дробь так, чтобы ее знаменатель не содержал квадратного корня.
Пример:
Освободитесь от иррациональности в знаменателе дроби: 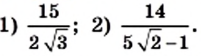
Решение:
1) Умножив числитель и знаменатель данной дроби на 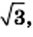 получаем:
получаем:
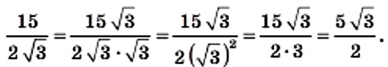
2) Умножив числитель и знаменатель данной дроби на выражение 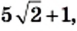 получаем:
получаем:
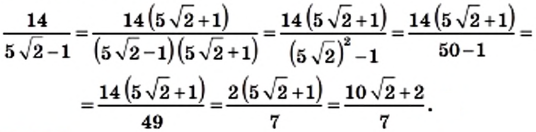
Пример:
Докажите тождество
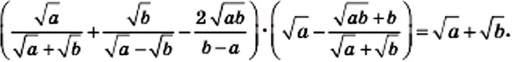
Решение:
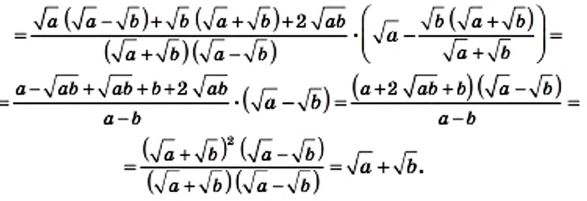
Пример:
Упростите выражение 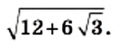
Решение:
Представив подкоренное выражение в виде квадрата суммы, получаем:
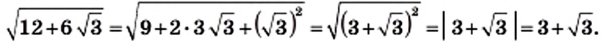
Растут ли в огороде радикалы?
В Древней Греции действие извлечения корня отождествляли с поиском стороны квадрата по его площади, а сам квадратный корень называли «стороной».
В Древней Индии слово «мула» означало «начало», «основание», «корень дерева». Это же слово стали употреблять и по отношению к стороне квадрата, возможно, исходя из такой ассоциации: из стороны квадрата, как из корня, вырастает сам квадрат. Вероятно, поэтому в латинском языке понятия «сторона» и «корень» выражаются одним и тем же словом — radix. От этого слова произошел термин «радикал».
Слово radix можно также перевести как «редис», то есть корнеплод — часть растения — видоизмененный корень, который может являться съедобным.
В XIII-XV вв. европейские математики, сокращая слово radix, обозначали квадратный корень знаками 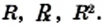 Например, запись
Например, запись 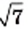 имела следующий вид:
имела следующий вид: 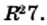 .
.
В XVI в. стали использовать знак 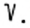 Происхождение этого символа, по-видимому, связано с рукописным начертанием латинской буквы
Происхождение этого символа, по-видимому, связано с рукописным начертанием латинской буквы 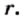
В XVII в. выдающийся французский математик Рене Декарт, соединив знак 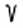 с горизонтальной черточкой, получил символ Рене Декарт
с горизонтальной черточкой, получил символ Рене Декарт  который мы и используем сегодня. (1596-1650)
который мы и используем сегодня. (1596-1650)
Множество и его элементы. Подмножество
Мы часто говорим: стадо баранов, букет цветов, коллекция марок, косяк рыб, стая птиц, рой пчел, собрание картин, набор ручек, компания друзей.
Если в этих парах перемешать первые слова, то может получиться смешно: букет баранов, косяк картин, стадо друзей. В то же время такие словосочетания, как коллекция рыб, коллекция птиц, коллекция картин, коллекция ручек и т. д., вполне приемлемы. Дело в том, что слово «коллекция» достаточно универсальное. Однако в математике есть термин, которым можно заменить любое из первых слов в данных парах. Это слово множество.
Приведем еще несколько примеров множеств:
Отдельным важнейшим множествам присвоены общепринятые названия и обозначения:
Как правило, множества обозначают прописными буквами латинского алфавита: 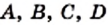 и т. д.
и т. д.
Объекты, составляющие данное множество, называют элементами этого множества. Обычно элементы обозначают строчными буквами латинского алфавита: 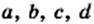 и т. д.
и т. д.
Если 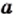 — элемент множества
— элемент множества 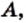 то пишут:
то пишут: 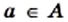 (читают: «
(читают: «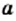 принадлежит множеству
принадлежит множеству 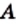 »). Если
»). Если 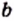 не является элементом множества
не является элементом множества 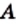 , то пишут:
, то пишут: 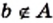 (читают: «
(читают: «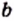 не принадлежит множеству
не принадлежит множеству 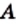 »).
»).
Если множество 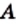 состоит из трех элементов
состоит из трех элементов 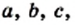 то пишут:
то пишут: 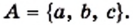
Если 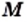 — множество натуральных делителей числа 6, то пишут:
— множество натуральных делителей числа 6, то пишут: 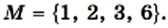 Множество делителей числа 6, являющихся составными числами, имеет следующий вид: {6}. Это пример одноэлементного множества.
Множество делителей числа 6, являющихся составными числами, имеет следующий вид: {6}. Это пример одноэлементного множества.
Задавать множество с помощью фигурных скобок, в которых указан список его элементов, удобно в тех случаях, когда множество состоит из небольшого количества элементов.
Определение: Два множества 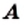 и
и 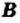 называют равными, если они состоят из одних и тех же элементов, то есть каждый элемент множества
называют равными, если они состоят из одних и тех же элементов, то есть каждый элемент множества  принадлежит множеству
принадлежит множеству  и, наоборот, каждый элемент множества В принадлежит множеству
и, наоборот, каждый элемент множества В принадлежит множеству  .
.
Если множества  и
и 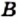 равны, то пишут:
равны, то пишут: 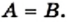
Из определения следует, что множество однозначно определяется своими элементами. Если множество записано с помощью фигурных скобок, то порядок, в котором выписаны его элементы, не имеет значения. Так, для множества, состоящего из трех элементов 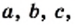 существует шесть вариантов его записи:
существует шесть вариантов его записи:
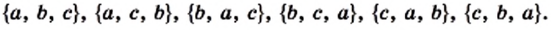
Поскольку из определения равных множеств следует, что, например, 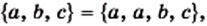 то в дальнейшем будем рассматривать множества, состоящие из разных элементов. Так, множество букв слова «космодром» имеет вид {к, о, с, м, д, р}.
то в дальнейшем будем рассматривать множества, состоящие из разных элементов. Так, множество букв слова «космодром» имеет вид {к, о, с, м, д, р}.
Заметим, что 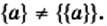 Действительно, множество
Действительно, множество 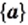 состоит из одного элемента и; множество
состоит из одного элемента и; множество 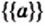 состоит из одного элемента — множества
состоит из одного элемента — множества 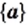 .
.
Чаще всего множество задают одним из следующих двух способов.
Первый способ состоит в том, что множество задают указанием (перечислением) всех его элементов. Мы уже использовали этот способ, записывая множество с помощью фигурных скобок, в которых указывали список его элементов. Ясно, что не всякое множество можно задать таким способом. Например, множество четных чисел так задать невозможно.
Второй способ состоит в том, что указывают характеристическое свойство элементов множества, то есть свойство, которым обладают все элементы данного множества и только они. Например, свойство «натуральное число при делении на 2 дает в остатке 1» задает множество нечетных чисел.
Если задавать множество характеристическим свойством его элементов, то может оказаться, что ни один объект этим свойством не обладает.
Обратимся к примерам.
Приведенные примеры указывают на то, что удобно к совокупности множеств отнести еще одно особенное множество, не содержащее ни одного элемента. Его называют пустым множеством и обозначают символом 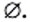
Заметим, что множество 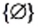 не является пустым. Оно содержит один элемент — пустое множество.
не является пустым. Оно содержит один элемент — пустое множество.
Рассмотрим множество цифр десятичной системы счисления: 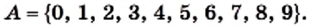 Выделим из множества его элементы, являющиеся четными цифрами. Получим множество
Выделим из множества его элементы, являющиеся четными цифрами. Получим множество 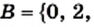
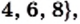 все элементы которого являются элементами множества
все элементы которого являются элементами множества 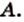
Определение: Множество 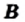 называют подмножеством множества
называют подмножеством множества 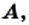 если каждый элемент множества
если каждый элемент множества 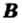 является элементом множества
является элементом множества 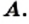
Это записывают так: 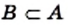 или
или 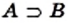 (читают: «множество
(читают: «множество 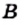 является подмножеством множества
является подмножеством множества 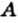 » или «множество
» или «множество 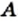 содержит множество
содержит множество 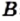 »).
»).
Рассмотрим примеры:
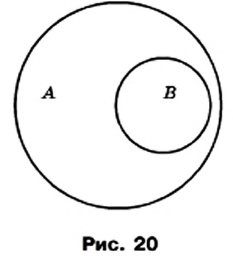
Для иллюстрации соотношений между множествами пользуются схемами, которые называют диаграммами Эйлера.
На рисунке 20 изображены множество 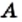 (больший круг) и множество
(больший круг) и множество 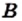 (меньший круг, содержащийся в большем). Эта схема означает, что
(меньший круг, содержащийся в большем). Эта схема означает, что 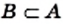 (или
(или 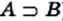 ).
).
Из определений подмножества и равенства множеств следует, что если 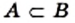 и
и 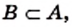 то
то 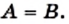
Если в множестве 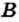 нет элемента, не принадлежащего множеству А, то множество
нет элемента, не принадлежащего множеству А, то множество 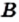 является подмножеством множества
является подмножеством множества 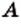 . В силу этих соображений пустое множество считают подмножеством любого множества. Действительно, пустое множество не содержит ни одного элемента, следовательно, в нем нет элемента, который не принадлежит данному множеству
. В силу этих соображений пустое множество считают подмножеством любого множества. Действительно, пустое множество не содержит ни одного элемента, следовательно, в нем нет элемента, который не принадлежит данному множеству 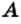 . Поэтому для любого множества
. Поэтому для любого множества 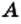 справедливо утверждение:
справедливо утверждение: 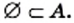
Любое множество 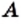 является подмножеством самого себя, то есть
является подмножеством самого себя, то есть 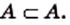
- Заказать решение задач по высшей математике
Пример:
Выпишите все подмножества множества 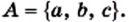
Решение:
Имеем: 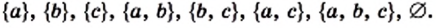
Числовые множества
Натуральные числа — это первые числа, которыми начали пользоваться люди. С ними вы ознакомились в детстве, когда учились считать предметы. Все натуральные числа образуют множество натуральных чисел, которое обозначают буквой 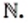
Практические потребности людей привели к возникновению дробных чисел. Позже появилась необходимость рассматривать величины, для характеристики которых положительных чисел оказалось недостаточно. Так возникли отрицательные числа.
Все натуральные числа, противоположные им числа и число нуль образуют множество целых чисел, которое обозначают буквой 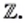
Например, 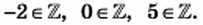
Множество натуральных чисел является подмножеством множества целых чисел, то есть 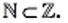
Целые и дробные (как положительные, так и отрицательные) числа образуют множество рациональных чисел, которое обозначают буквой 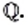 Например,
Например, 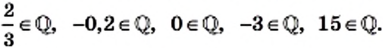
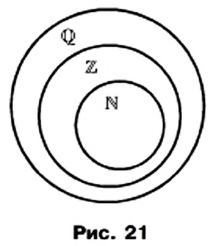
Понятно, что 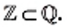 Схема, изображенная на рисунке 21, показывает, как соотносятся множества
Схема, изображенная на рисунке 21, показывает, как соотносятся множества 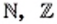 и
и 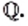
Каждое рациональное число можно представить в виде отношения 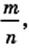 где
где 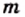 — целое число, а
— целое число, а 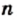 — натуральное. Например,
— натуральное. Например,
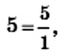
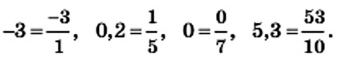
С возможностью такого представления связано название «рациональное число»: одним из значений латинского слова ratio является «отношение».
В 6 классе вы узнали, что каждое рациональное число можно представить в виде конечной десятичной дроби или в виде бесконечной периодической десятичной дроби. Для дроби 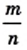 такое представление можно получить, выполнив деление числа
такое представление можно получить, выполнив деление числа 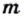 на число
на число 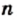 уголком.
уголком.
Например, 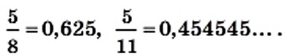
Число 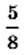 записано в виде конечной десятичной дроби, а число
записано в виде конечной десятичной дроби, а число 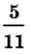 в виде бесконечной периодической десятичной дроби. В записи 0,454545… цифры 4 и 5 периодически повторяются. Повторяющуюся группу цифр называют периодом дроби и записывают в круглых скобках. В данном случае период дроби составляет 45, а дробь
в виде бесконечной периодической десятичной дроби. В записи 0,454545… цифры 4 и 5 периодически повторяются. Повторяющуюся группу цифр называют периодом дроби и записывают в круглых скобках. В данном случае период дроби составляет 45, а дробь 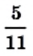 записывают так:
записывают так: 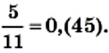
Заметим, что любую конечную десятичную дробь и любое целое число можно представить в виде бесконечной периодической десятичной дроби. Например,
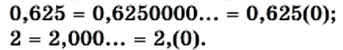
Следовательно, каждое рациональное число можно представить в виде бесконечной периодической десятичной дроби.
Справедливо и такое утверждение: каждая бесконечная периодическая десятичная дробь является записью некоторого рационального числа.
В 9 классе вы научитесь записывать бесконечную периодическую десятичную дробь в виде обыкновенной дроби.
Сумма и произведение двух натуральных чисел являются натуральными числами. Однако разность натуральных чисел не всегда обладает таким свойством. Например, 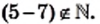
Сумма, разность, произведение двух целых чисел являются целыми числами. Однако частное целых чисел не всегда обладает таким свойством. Например, 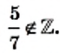
Сумма, разность, произведение и частное (кроме деления на нуль) двух рациональных чисел являются рациональными числами.
Итак, действие вычитания натуральных чисел может вывести результат за пределы множества 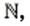 действие деления целых чисел — за пределы множества
действие деления целых чисел — за пределы множества 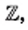 однако выполнение любого из четырех арифметических действий с рациональными числами не выводит результат за пределы множества
однако выполнение любого из четырех арифметических действий с рациональными числами не выводит результат за пределы множества 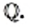
Вы ознакомились с новым действием — извлечением квадратного корня. Возникает естественный вопрос: всегда ли квадратный корень из неотрицательного рационального числа является рациональным числом? Иными словами, может ли действие извлечения квадратного корня из рационального числа вывести результат за пределы множества 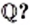
Рассмотрим уравнение 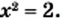 Поскольку
Поскольку 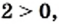 то это уравнение имеет два корня:
то это уравнение имеет два корня: 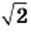 и
и 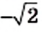 (рис. 22). Однако не существует рационального числа, квадрат которого равен 2 (доказательство этого факта вы можете найти в рубрике «Когда сделаны уроки» в рассказе «Открытие иррациональности»), то есть числа
(рис. 22). Однако не существует рационального числа, квадрат которого равен 2 (доказательство этого факта вы можете найти в рубрике «Когда сделаны уроки» в рассказе «Открытие иррациональности»), то есть числа 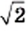 и
и 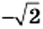 не являются рациональными. Эти числа — примеры иррациональных чисел (приставка «ир» означает отрицание).
не являются рациональными. Эти числа — примеры иррациональных чисел (приставка «ир» означает отрицание).
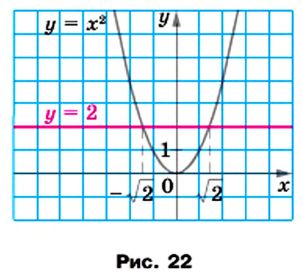
Следовательно, действие извлечения корня из рационального числа может вывести результат за пределы множества 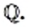
Ни одно иррациональное число не может быть представлено в виде дроби 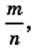 где
где 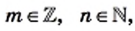 а следовательно, и в виде бесконечной периодической десятичной дроби.
а следовательно, и в виде бесконечной периодической десятичной дроби.
Иррациональные числа могут быть представлены в виде бесконечных непериодических десятичных дробей.
Например, с помощью специальной компьютерной программы можно установить, что
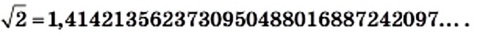
Числа 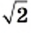 и
и 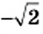 — это не первые иррациональные числа, с которыми вы встречаетесь. Число
— это не первые иррациональные числа, с которыми вы встречаетесь. Число 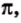 равное отношению длины окружности к диаметру, также является иррациональным:
равное отношению длины окружности к диаметру, также является иррациональным:
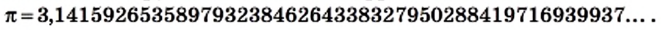
Иррациональные числа возникают не только в результате извлечения квадратных корней. Их можно конструировать, строя бесконечные непериодические десятичные дроби.
Например, число 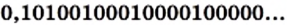 (после запятой записаны последовательно степени числа 10) является иррациональным. Действительно, если предположить, что у рассматриваемой десятичной дроби есть период, состоящий из
(после запятой записаны последовательно степени числа 10) является иррациональным. Действительно, если предположить, что у рассматриваемой десятичной дроби есть период, состоящий из 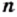 цифр, то с некоторого места этот период будет полностью состоять из нулей. Иными словами, начиная с этого места в записи не должна встретиться ни одна единица, что противоречит конструкции числа.
цифр, то с некоторого места этот период будет полностью состоять из нулей. Иными словами, начиная с этого места в записи не должна встретиться ни одна единица, что противоречит конструкции числа.
Вместе множества иррациональных и рациональных чисел образуют множество действительных чисел. Его обозначают буквой 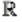 (первой буквой латинского слова realis — «реальный», «существующий в действительности»).
(первой буквой латинского слова realis — «реальный», «существующий в действительности»).
Теперь «цепочку» 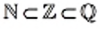 можно продолжить:
можно продолжить: 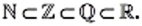
Связь между числовыми множествами, рассмотренными в этом пункте, иллюстрирует схема, изображенная на рисунке 23.
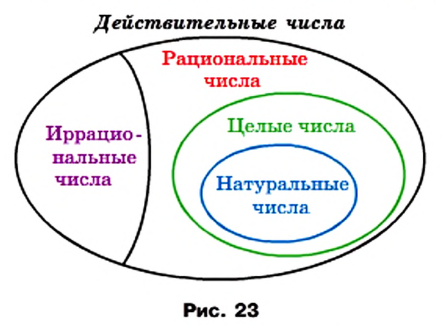
Длину любого отрезка можно выразить действительным числом. Eh-от факт позволяет установить связь между множеством 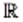 и множеством точек координатной прямой. Точке
и множеством точек координатной прямой. Точке 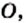 началу отсчета, поставим в соответствие число 0. Каждой точке
началу отсчета, поставим в соответствие число 0. Каждой точке  координатной прямой, отличной от точки
координатной прямой, отличной от точки  поставим в соответствие единственное число, равное длине отрезка
поставим в соответствие единственное число, равное длине отрезка 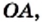 если точка А расположена справа от точки
если точка А расположена справа от точки  и число, противоположное длине отрезка
и число, противоположное длине отрезка 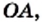 если точка
если точка 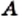 расположена слева от точки
расположена слева от точки 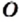 . Также понятно, что каждое действительное число является соответствующим единственной точке координатной прямой.
. Также понятно, что каждое действительное число является соответствующим единственной точке координатной прямой.
Над действительными числами можно выполнять четыре арифметических действия: сложение, вычитание, умножение, деление (кроме деления на ноль), в результате будем получать действительное число. Эти действия обладают известными вам свойствами:
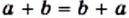 Переместительное свойство сложения
Переместительное свойство сложения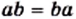 Переместительное свойство умножения
Переместительное свойство умножения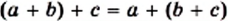 Сочетательное свойство сложения
Сочетательное свойство сложения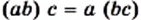 Сочетательное свойство умножения
Сочетательное свойство умножения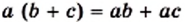 Распределительное свойство умножения относительно сложения
Распределительное свойство умножения относительно сложения
Действительные числа можно сравнивать, используя правила сравнения десятичных дробей, то есть сравнивая цифры в соответствующих разрядах. Например, 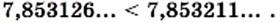
Любое положительное действительное число больше нуля и любого отрицательного действительного числа. Любое отрицательное действительное число меньше нуля. Из двух отрицательных действительных чисел больше то, у которого модуль меньше.
Если отметить на координатной прямой два действительных числа, то меньшее из них будет расположено слева от большего.
Находя длину окружности и площадь круга, вы пользовались приближенным значением числа 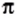 (например,
(например, 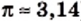 ). Аналогично при решении практических задач, где нужно выполнить действия с действительными числами, при необходимости эти числа заменяют их приближенными значениями. Например, для числа
). Аналогично при решении практических задач, где нужно выполнить действия с действительными числами, при необходимости эти числа заменяют их приближенными значениями. Например, для числа 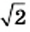 можно воспользоваться такими приближенными равенствами:
можно воспользоваться такими приближенными равенствами: 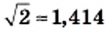 или
или 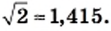 Первое из них называют приближенным значением числа
Первое из них называют приближенным значением числа 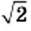 по недостатку с точностью до 0,001, второе — приближенным значением числа
по недостатку с точностью до 0,001, второе — приближенным значением числа 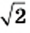 по избытку с точностью до 0,001. Более подробно о приближенных значениях вы узнаете в 9 классе.
по избытку с точностью до 0,001. Более подробно о приближенных значениях вы узнаете в 9 классе.
В заключение подчеркнем, что из любого неотрицательного действительного числа можно извлечь квадратный корень и в результате этого действия получить действительное число. Следовательно, действие извлечения квадратного корня из неотрицательного действительного числа не выводит результат за пределы множества 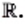
Открытие иррациональности
Решая графически уравнение 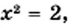 мы установили, что длина каждого из отрезков
мы установили, что длина каждого из отрезков 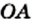 и
и 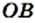 равна
равна 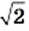 (рис. 24). Покажем, что число
(рис. 24). Покажем, что число 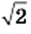 иррациональное. Предположим, что число
иррациональное. Предположим, что число 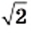 рациональное. Тогда его можно
рациональное. Тогда его можно
представить в виде несократимой дроби 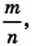 где
где 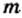 и
и 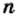 — натуральные числа. Имеем:
— натуральные числа. Имеем:
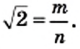
Тогда 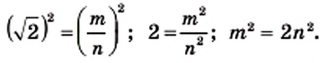
Из последнего равенства следует, что число 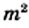 четное. А это значит, что четным является и число
четное. А это значит, что четным является и число 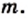 Тогда
Тогда 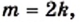 где
где 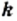 — некоторое натуральное число. Имеем:
— некоторое натуральное число. Имеем: 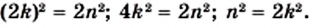 Отсюда следует, что число
Отсюда следует, что число 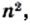 а следовательно, и число
а следовательно, и число 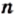 четные.
четные.
Таким образом, числитель и знаменатель дроби 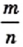 — четные числа. Следовательно, эта дробь является сократимой. Получили противоречие.
— четные числа. Следовательно, эта дробь является сократимой. Получили противоречие.
Приведенный пример показывает, что существуют отрезки (в нашем случае это отрезки 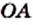 и
и 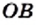 на рисунке 24), длины которых нельзя выразить рациональными числами, то есть для измерения отрезков рациональных чисел недостаточно.
на рисунке 24), длины которых нельзя выразить рациональными числами, то есть для измерения отрезков рациональных чисел недостаточно.
Этот факт был открыт в школе великого древнегреческого ученого Пифагора.
Сначала пифагорейцы считали, что для любых отрезков 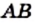 и
и 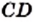 всегда можно найти такой отрезок
всегда можно найти такой отрезок 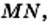 который в каждом из них укладывается целое число раз. Отсюда следовало, что отношение длин любых двух отрезков выражается отношением целых чисел, то есть рациональным числом.
который в каждом из них укладывается целое число раз. Отсюда следовало, что отношение длин любых двух отрезков выражается отношением целых чисел, то есть рациональным числом.
Например, на рисунке 25 имеем: 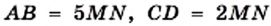
и 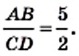 . Отрезок
. Отрезок 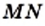 называют общей мерой отрезков
называют общей мерой отрезков 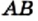 и
и 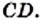
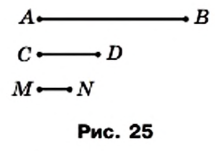
Если для отрезков существует общая мера, то их называют соизмеримыми. Например, отрезки  и
и  (рис. 25) являются соизмеримыми.
(рис. 25) являются соизмеримыми.
Итак, древнегреческие ученые считали, что любые два отрезка соизмеримы. А из этого следовало, что длину любого отрезка можно выразить рациональным числом.
Действительно, пусть некоторый отрезок  выбран в качестве единичного. Тогда для отрезка
выбран в качестве единичного. Тогда для отрезка  и любого другого отрезка
и любого другого отрезка 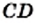 существует отрезок длиной
существует отрезок длиной 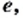 являющийся их общей мерой. Получаем:
являющийся их общей мерой. Получаем: 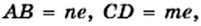 где
где 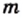 и — некоторые натуральные числа. Отсюда
и — некоторые натуральные числа. Отсюда 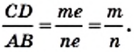 Поскольку
Поскольку 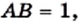 то
то 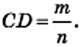
Однако сами же пифагорейцы сделали выдающееся открытие. Они доказали, что диагональ и сторона квадрата несоизмеримы, то есть если сторону квадрата принять за единицу, то длину диагонали квадрата выразить рациональным числом нельзя.
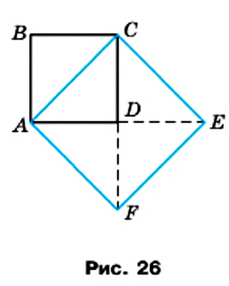
Для доказательства рассмотрим произвольный квадрат 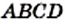 и примем его сторону за единицу длины. Тогда его площадь равна
и примем его сторону за единицу длины. Тогда его площадь равна 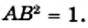 На диагонали
На диагонали 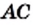 построим квадрат
построим квадрат 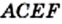 (рис. 26). Понятно, что площадь квадрата
(рис. 26). Понятно, что площадь квадрата 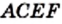 в 2 раза больше площади квадрата
в 2 раза больше площади квадрата 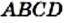 . Отсюда
. Отсюда 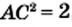 , то есть
, то есть 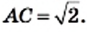 Следовательно, длина диагонали
Следовательно, длина диагонали 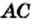 не может быть выражена рациональным числом.
не может быть выражена рациональным числом.
Это открытие изменило один из фундаментальных постулатов древнегреческих ученых, заключавшийся в том, что отношение любых двух величин выражается отношением целых чисел.
Существует легенда о том, что пифагорейцы держали открытие иррациональных чисел в строжайшей тайне, а человека, разгласившего этот факт, покарали боги: он погиб при кораблекрушении.
ГЛАВНОЕ В ПАРАГРАФЕ 2
Свойства функции 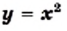
Область определения: 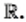
Область значений: множество неотрицательных чисел.
График: парабола.
Нуль функции: 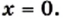
Свойство графика: если точка 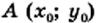 принадлежит графику функции, то точка
принадлежит графику функции, то точка 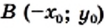 также принадлежит графику.
также принадлежит графику.
Квадратный корень
Квадратным корнем из числа 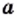 называют число, квадрат которого равен
называют число, квадрат которого равен 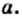
Арифметический квадратный корень
Арифметическим квадратным корнем из числа 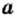 называют неотрицательное число, квадрат которого равен
называют неотрицательное число, квадрат которого равен 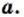
Равные множества
Два множества 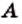 и
и 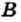 называют равными, если они состоят из одних и тех же элементов, то есть каждый элемент множества
называют равными, если они состоят из одних и тех же элементов, то есть каждый элемент множества 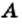 принадлежит множеству
принадлежит множеству 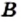 и, наоборот, каждый элемент множества
и, наоборот, каждый элемент множества 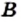 принадлежит множеству
принадлежит множеству 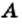 .
.
Подмножество
Множество 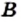 называют подмножеством множества
называют подмножеством множества 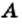 , если каждый элемент множества
, если каждый элемент множества 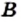 является элементом множества
является элементом множества 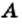 .
.
Обозначения числовых множеств
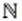 — множество натуральных чисел;
— множество натуральных чисел;
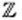 — множество целых чисел;
— множество целых чисел;
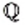 — множество рациональных чисел;
— множество рациональных чисел;
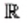 — множество действительных чисел.
— множество действительных чисел.
Связь между числовыми множествами
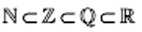
Свойства арифметического квадратного корня
Для любого действительного числа 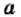 выполняется равенство
выполняется равенство
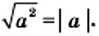
Для любого действительного числа 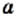 и любого натурального числа
и любого натурального числа 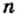 выполняется равенство
выполняется равенство 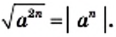
Для любых действительных чисел 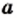 и
и 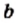 таких, что
таких, что 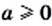 и
и 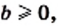 выполняется равенство
выполняется равенство 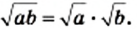
Для любых действительных чисел 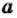 и
и 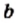 таких, что
таких, что  и
и 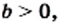
выполняется равенство 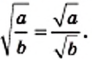
Для любых неотрицательных чисел 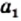 и
и 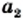 таких, что
таких, что 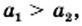 выполняется неравенство
выполняется неравенство 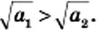
Свойства функции 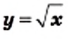
Область определения: множество неотрицательных чисел.
Область значений: множество неотрицательных чисел.
График: ветвь параболы.
Нуль функции: 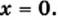
Большему значению аргумента соответствует большее значение функции.
———
Квадратные корни
Функция y=x2 её график и свойства
Функция 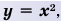 её график и свойства
её график и свойства
Пример №223
Пусть сторона квадрата равна 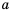 см. Тогда его площадь (в
см. Тогда его площадь (в 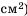 можно найти но формуле
можно найти но формуле 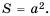 В этой формуле каждому положительному значению переменной
В этой формуле каждому положительному значению переменной 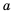 соответствует единственное значение переменной
соответствует единственное значение переменной 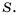
Если обозначить независимую переменную через 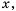 а зависимую – через
а зависимую – через 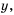 то получим функцию, которую задают формулой
то получим функцию, которую задают формулой 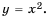 В этой формуле переменная
В этой формуле переменная 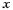 может принимать любые значения (положительные, отрицательные, значение нуль).
может принимать любые значения (положительные, отрицательные, значение нуль).
Составим таблицу значений функции 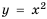 для нескольких значений аргумента:
для нескольких значений аргумента: 
Отметим на координатной плоскости точки 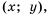 координаты которых записаны в таблице (рис. 8). Если на этой плоскости отметить больше точек, координаты которых удовлетворяют формуле
координаты которых записаны в таблице (рис. 8). Если на этой плоскости отметить больше точек, координаты которых удовлетворяют формуле 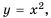 а потом соединить их плавной линией, то получим график функции
а потом соединить их плавной линией, то получим график функции 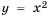 (рис. 9). График этой функции называют параболой, точку (0; 0) – вершиной параболы. Вершина делит параболу на две части, каждую из которых называют ветвью параболы.
(рис. 9). График этой функции называют параболой, точку (0; 0) – вершиной параболы. Вершина делит параболу на две части, каждую из которых называют ветвью параболы.
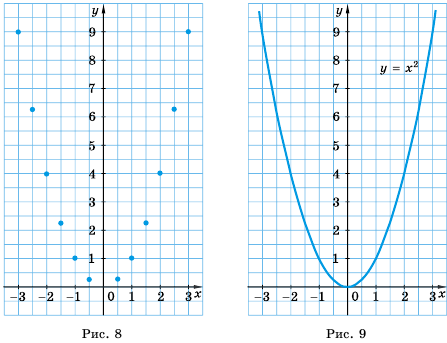
Сформулируем некоторые свойства функции 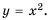
1. Область определения функции состоит из всех чисел.
2. Область значений функции состоит из всех неотрицательных чисел, то есть 
Действительно, так как 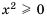 для любого
для любого 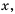 то
то 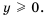
3. Графиком функции является парабола с вершиной в точке 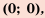 ветви которой направлены вверх. Все точки параболы, за исключением вершины, лежат выше оси абсцисс.
ветви которой направлены вверх. Все точки параболы, за исключением вершины, лежат выше оси абсцисс.
4. Противоположным значениям аргумента соответствует одно и то же значение функции.
Действительно, это следует из того, что 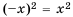 при любом значении
при любом значении 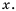
Пример №224
Решите графически уравнение 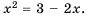
Решение:
График функции 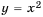 – парабола, а функции
– парабола, а функции 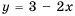 – прямая, проходящая через точки (0; 3) и (2; -1).
– прямая, проходящая через точки (0; 3) и (2; -1).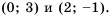 Построим эти графики в одной системе координат ( рис.10). Они пересекутся в двух точках с абсциссами
Построим эти графики в одной системе координат ( рис.10). Они пересекутся в двух точках с абсциссами 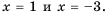
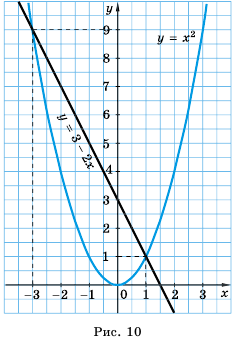
Убедимся, что числа 1 и -3 являются корнями уравнения:
1) для 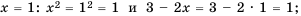
2) для 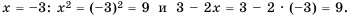
Следовательно, 3 и -1 – корни уравнения 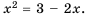
Ответ. -3; 1.
Пример №225
Между какими последовательными целыми числами лежит корень уравнения 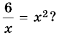
Решение:
Решим уравнение графически, построив графики функций 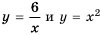 в одной системе координат. Так как
в одной системе координат. Так как 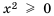 для любого
для любого 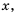 то в данном уравнении и
то в данном уравнении и 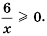
Откуда 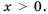 Поэтому рассмотрим графики функций только для
Поэтому рассмотрим графики функций только для 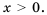 Это ветвь гиперболы и ветвь параболы, лежащие в первой координатной четверти (рис. 11).
Это ветвь гиперболы и ветвь параболы, лежащие в первой координатной четверти (рис. 11).
Графики пересекаются в одной точке, абсцисса которой является корнем уравнения и заключена между числами 1 и 2.
Таким образом, корень уравнения 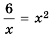 лежит между числами 1 и 2.
лежит между числами 1 и 2.
Ответ. Между числами 1 и 2. 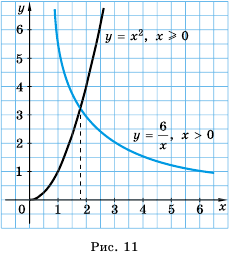
Арифметический квадратный корень
Если известна сторона квадрата, можно легко найти его площадь. Но часто приходится решать и обратную задачу: по известной площади квадрата находить его сторону.
Пример №226
Площадь квадрата равна 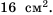 Чему равна длина его стороны?
Чему равна длина его стороны?
Решение:
Пусть длина стороны квадрата равна 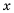 см, тогда его площадь будет
см, тогда его площадь будет 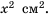 Имеем уравнение:
Имеем уравнение: 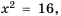 корнями которого являются числа 4 и -4. Действительно,
корнями которого являются числа 4 и -4. Действительно, 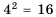 и
и 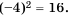 Длина не может выражаться отрицательным числом, поэтому условию задачи удовлетворяет только один из корней уравнения – число 4. Следовательно, длина стороны квадрата равна 4 см.
Длина не может выражаться отрицательным числом, поэтому условию задачи удовлетворяет только один из корней уравнения – число 4. Следовательно, длина стороны квадрата равна 4 см.
Корни уравнения 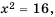 то есть числа, квадраты которых равны 16, называют квадратными корнями из числа 16.
то есть числа, квадраты которых равны 16, называют квадратными корнями из числа 16.
Квадратным корнем из числа  называют число, квадрат которого равен
называют число, квадрат которого равен  .
.
Например, квадратными корнями из числа 100 являются числа 10 и -10, потому что 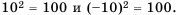 Квадратным корнем из числа 0 является число 0, потому что
Квадратным корнем из числа 0 является число 0, потому что 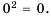 Квадратного корня из числа -16 мы не найдем, ведь среди известных нам чисел не существует числа, квадрат которого равнялся бы -16.
Квадратного корня из числа -16 мы не найдем, ведь среди известных нам чисел не существует числа, квадрат которого равнялся бы -16.
Число 4, являющееся неотрицательным корнем уравнения . 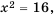 называют арифметическим квадратным корнем из числа 16.
называют арифметическим квадратным корнем из числа 16.
Арифметическим квадратным корнем из числа а называют неотрицательное число, квадрат которого равен 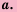
Арифметический квадратный корень из числа 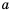 обозначают
обозначают 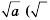 знак арифметического квадратного корня, или радикал). Выражение, стоящее под знаком корня, называют подкоренным выражением. Запись
знак арифметического квадратного корня, или радикал). Выражение, стоящее под знаком корня, называют подкоренным выражением. Запись 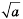 читают следующим образом: квадратный корень из
читают следующим образом: квадратный корень из 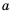 (слово арифметический при чтении принято опускать, поскольку в школе рассматривают только арифметические корни).
(слово арифметический при чтении принято опускать, поскольку в школе рассматривают только арифметические корни).
Пример №227
1) 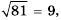 так как
так как 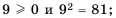
2) 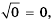 так как
так как 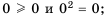
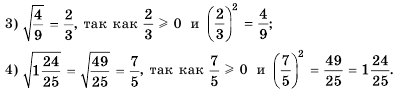
Вообще равенство 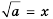 является верным, если выполняются два условия:
является верным, если выполняются два условия: 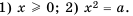
Так как 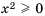 для всех значений переменной
для всех значений переменной 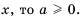
Выражение 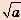 не имеет смысла, если
не имеет смысла, если 
Например, не имеют смысла выражения 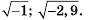
Действие нахождения значения арифметического квадратного корня называют извлечением квадратного корня. Из небольших чисел квадратный корень желательно извлекать устно. Извлекать квадратный корень из больших чисел поможет таблица квадратов двузначных натуральных чисел на форзаце или калькулятор.
Пример №228
Найдите значение корня 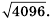
Решение:
По таблице квадратов двузначных натуральных чисел имеем: 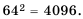 Поэтому
Поэтому 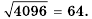
Пример №229
Вычислите 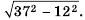
Решение:
Сначала нужно найти значение выражения 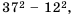 а потом извлечь из него корень:
а потом извлечь из него корень:
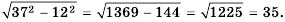
Ответ. 35.
Рассмотрим уравнение 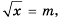 где
где 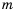 – некоторое число. Если
– некоторое число. Если 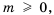 то по определению квадратного корня следует, что
то по определению квадратного корня следует, что 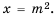 Если же
Если же 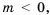 то уравнение не имеет решений, так как по определению число
то уравнение не имеет решений, так как по определению число 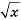 – неотрицательное.
– неотрицательное.
Систематизируем данные о решениях уравнения 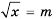 в виде схемы:
в виде схемы:
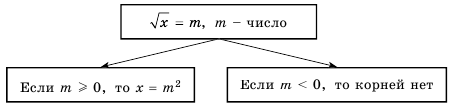
Пример №230
Решите уравнение:
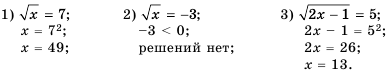
Ответ. 1) 49; 2) решений нет; 3) 13.
Множество. Подмножество. Числовые множества. Рациональные числа. Иррациональные числа. Действительные числа
Понятие множества является одним из основных понятий математики. Под множеством будем понимать совокупность объектов, имеющих общую природу (или объединенных по общему признаку), сами объекты при этом будем называть элементами множества.
Как правило, множества обозначают большими латинскими буквами. Если, например, множество 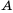 состоит из чисел 1, 2, 3, а множество
состоит из чисел 1, 2, 3, а множество 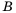 – из знаков
– из знаков 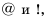 то это записывают так:
то это записывают так: 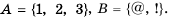 Числа 1, 2, 3 – элементы множества
Числа 1, 2, 3 – элементы множества 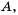 а знаки
а знаки 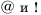 – элементы множества
– элементы множества 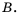 Тот факт, что число 1 принадлежит множеству
Тот факт, что число 1 принадлежит множеству 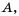 записывают с помощью уже известного нам символа
записывают с помощью уже известного нам символа 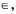 а именно:
а именно: 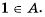 Тот факт, что число 1 не принадлежит множеству
Тот факт, что число 1 не принадлежит множеству 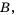 записывают так:
записывают так: 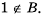
Множества, количество элементов которых можно выразить натуральным числом, называют конечными.
Множество, не содержащее ни одного элемента, называют пустым множеством. Его обозначают символом 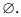 Так, например, пустым множеством является множество корней уравнения
Так, например, пустым множеством является множество корней уравнения 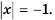
Множества, количество элементов которых нельзя выразить натуральным числом и которые не являются пустыми, называют бесконечными.
Если каждый элемент множества 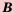 является элементом множества
является элементом множества 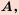 то говорят, что множество
то говорят, что множество 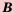 является подмножеством множества
является подмножеством множества 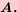
Записывают это следующим образом: 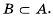 Схематическая иллюстрация этого факта представлена на рисунке 12.
Схематическая иллюстрация этого факта представлена на рисунке 12.
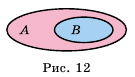
Пример №231
Пусть 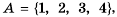
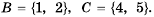 Тогда множество
Тогда множество 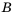 является подмножеством множества
является подмножеством множества 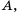 то есть
то есть 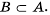 Множество
Множество 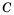 не является подмножеством множества
не является подмножеством множества 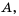 так как множество
так как множество 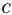 содержит элемент – число 5, которое не является элементом множества
содержит элемент – число 5, которое не является элементом множества 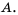
Считают, что пустое множество является подмножеством любого множества, то есть 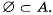
Целые числа и дробные числа образуют множество рациональных чисел.
Множество натуральных чисел обозначают буквой 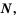 множество целых чисел – буквой
множество целых чисел – буквой 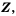 множество рациональных чисел -буквой
множество рациональных чисел -буквой 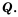 Они являются бесконечными множествами.
Они являются бесконечными множествами.
Можно утверждать, что 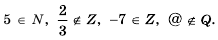
Любое рациональное число можно представить в виде 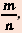 где
где 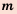 – целое число,
– целое число, 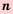 – натуральное число.
– натуральное число.
Например 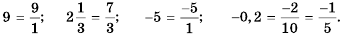
Рациональное число можно также представить и в виде десятичной дроби. Для этого достаточно числитель дроби разделить на ее знаменатель. Например,
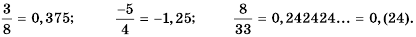
В последнем случае мы получили бесконечную десятичную периодическую дробь. Дроби 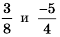 также можно представить в виде бесконечных десятичных периодических дробей, дописав справа в десятичной части бесконечное много нулей:
также можно представить в виде бесконечных десятичных периодических дробей, дописав справа в десятичной части бесконечное много нулей:

Таким образом, каждое рациональное число можно представить в виде бесконечной десятичной периодической дроби.
Справедливо и обратное утверждение:
Каждая бесконечная периодическая десятичная дробь является записью некоторого рационального числа.
Например,
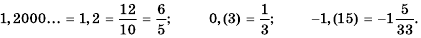
В правильности этих равенств легко убедиться, выполнив соответствующее деление.
Но в математике существуют числа, которые нельзя записать в виде 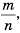 где
где 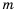 – целое число, а
– целое число, а 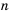 – натуральное.
– натуральное.
Числа, которые нельзя записать в виде 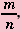 где
где 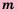 – целое число, a
– целое число, a 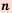 — натуральное, называют иррациональными числами.
— натуральное, называют иррациональными числами.
Префикс «иp» означает отрицание, иррациональные значит не рациональные.
Например, иррациональными являются числа 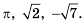 Приближенные значения таких чисел можно находить с определенной точностью (то есть округленными до определенного разряда) с помощью микрокалькулятора или компьютера:
Приближенные значения таких чисел можно находить с определенной точностью (то есть округленными до определенного разряда) с помощью микрокалькулятора или компьютера:
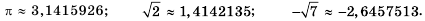
Каждое иррациональное число можно представить в виде бесконечной десятичной непериодической дроби.
Рациональные числа вместе с иррациональными числами образуют множество действительных чисел.
Множество действительных чисел обозначают буквой 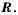
Так как каждое натуральное число является целым числом, то множество 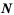 является подмножеством множества
является подмножеством множества 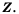 Аналогично, множество
Аналогично, множество 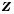 является подмножеством множества
является подмножеством множества 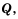 а множество
а множество 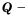 подмножеством множества
подмножеством множества 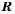 (рис. 13).
(рис. 13).
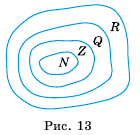
Действительные числа, записанные в виде бесконечных десятичных непериодических дробей, можно сравнивать по тем же правилам, что и конечные десятичные дроби. Например,
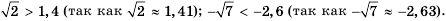
В задачах с практическим содержанием действительные числа (для выполнения арифметических действий) заменяют на их приближенные значения, округленные до определенного разряда.
Пример №232
Вычислите 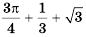 с точностью до тысячных.
с точностью до тысячных.
Решение:
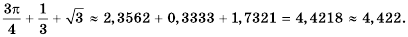
Заметим, что при сложении, вычитании, умножении, делении и возведении в степень действительных чисел справедливы те же свойства и ограничения, что и при действиях с рациональными числами.
Понятие числа появилось очень давно.
А еще раньше Оно является одним из самых общих понятий математики. Потребность в измерениях и подсчетах обусловила появление положительных рациональных чисел. Именно тогда возникли и использовались натуральные числа и дробные числа, которые рассматривались как отношение натуральных чисел.
Следующим этапом развития понятия числа является введение в практику отрицательных чисел. В Древнем Китае эти числа появились во II в. до н. э. Там умели складывать и вычитать отрицательные числа. Отрицательные числа толковали как долг, а положительные – как имущество. В Индии в VII в. эти числа воспринимали так же, но еще и умели их умножать и делить.
Уже древние вавилоняне около 4 тыс. лет назад знали ответ на вопрос: «Какова должна быть длина стороны квадрата, чтобы его площадь равнялась 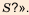 Ими были составлены таблицы квадратов чисел и квадратных корней. Вавилоняне использовали и метод нахождения приближенного значения квадратного корня из числа
Ими были составлены таблицы квадратов чисел и квадратных корней. Вавилоняне использовали и метод нахождения приближенного значения квадратного корня из числа 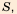 не являющегося квадратом натурального числа. Суть метода заключалась в том, что число
не являющегося квадратом натурального числа. Суть метода заключалась в том, что число 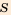 записывали в виде
записывали в виде 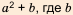 было достаточно малым в сравнении с
было достаточно малым в сравнении с 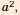 и применяли формулу
и применяли формулу
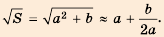
Например, с помощью этого метода:
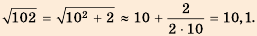
Проверим точность результата: 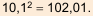
Такой метод вычисления приближенного значения квадратного корня использовался и в Древней Греции. Его детально описал Герон Александрийский (I в. н. э.).
В эпоху Возрождения (XV – нач. XVII в.) европейские математики обозначали корень латинским словом Radix (корень), потом – сокращенно – буквой 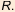 Так появился термин «радикал», которым называют знак корня. Впоследствии для обозначения корня стали использовать точку, а потом ромбик. Спустя некоторое время – уже знак
Так появился термин «радикал», которым называют знак корня. Впоследствии для обозначения корня стали использовать точку, а потом ромбик. Спустя некоторое время – уже знак  и горизонтальную черточку над подкоренным выражением. Затем знак
и горизонтальную черточку над подкоренным выражением. Затем знак  и черточка были объединены, и современные математики стали использовать знак квадратного корня в привычном нам виде:
и черточка были объединены, и современные математики стали использовать знак квадратного корня в привычном нам виде: 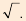
Тождество (√a)2=a, a⩾0 уравнение  x2=a
x2=a
Тождество 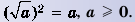 уравнение
уравнение 
Напомним, что для любых значений 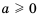 равенство
равенство 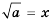 является верным, если выполняются два условия:
является верным, если выполняются два условия: 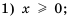
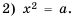 Подставив в последнее равенство вместо
Подставив в последнее равенство вместо 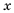 его запись в виде
его запись в виде 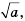 получим тождество
получим тождество 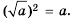
Для любого  справедливо тождество
справедливо тождество
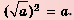
Пример №233
Вычислите:
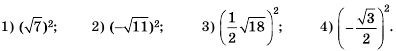
Решение:
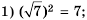
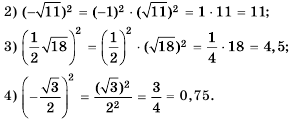 Ответ:
Ответ: 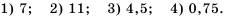
Рассмотрим уравнение 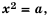 где
где 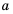 – некоторое число.
– некоторое число.
Так как квадрат числа не может быть отрицательным, то при 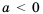 уравнение
уравнение 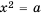 не имеет решений, что можно записать следующим образом:
не имеет решений, что можно записать следующим образом: 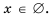
Если 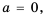 то единственным корнем уравнения
то единственным корнем уравнения 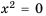 является число 0.
является число 0.
Если 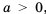 то корни уравнения
то корни уравнения 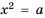 – числа
– числа 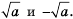 Действительно,
Действительно, 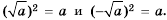 Для того чтобы убедиться, что уравнение
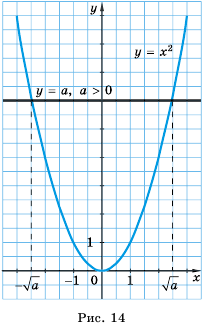
Для того чтобы убедиться, что уравнение 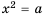 при
при 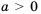 других корней не имеет, обратимся к графическому методу решения уравнения. Построим графики функций
других корней не имеет, обратимся к графическому методу решения уравнения. Построим графики функций 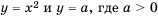 (рис. 14). Эти графики пересекутся дважды: в точках с абсциссами
(рис. 14). Эти графики пересекутся дважды: в точках с абсциссами 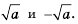 Систематизируем данные о решениях уравнения
Систематизируем данные о решениях уравнения 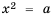 в виде схемы:
в виде схемы:
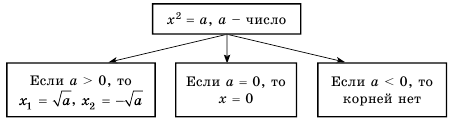
Пример №234
Решите уравнение:
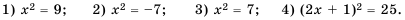
Решение:
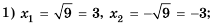
2) уравнение корней не имеет, то есть 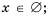
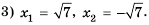 Эти корни являются иррациональными числами;
Эти корни являются иррациональными числами;
4) Имеем:
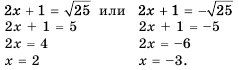
Таким образом, получим два корня: 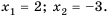
Ответ. 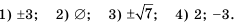
Свойства арифметического квадратного корня
Сравним значения выражений 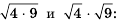
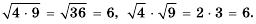
Имеем: 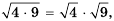 то есть корень из произведения двух чисел равен произведению их корней. Это свойство справедливо для произведения любых двух неотрицательных чисел.
то есть корень из произведения двух чисел равен произведению их корней. Это свойство справедливо для произведения любых двух неотрицательных чисел.
Теорема (о корне из произведения). Корень из произведения двух неотрицательных чисел равен произведению корней из этих чисел, то есть при  и
и 
Доказательство: Так как 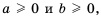 то выражения
то выражения 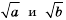 имеют смысл, причем
имеют смысл, причем 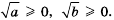 Поэтому
Поэтому 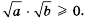 Кроме того,
Кроме того, 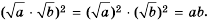
Имеем: 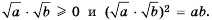 Тогда по определению арифметического квадратного корня:
Тогда по определению арифметического квадратного корня: 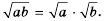
Доказанная теорема распространяется и на случай, когда множителей под знаком корня три и больше.
Следствие. Корень из произведения неотрицательных множителей равен произведению корней из этих множителей.
Доказательство: Докажем это следствие, например, для трех чисел 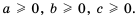
Имеем: 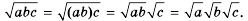
Пример №235
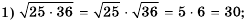
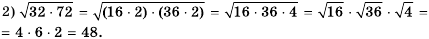
Замечание 1. Очевидно, что выражение 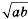 имеет смысл при условии
имеет смысл при условии 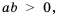 то есть когда переменные
то есть когда переменные 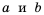 – одного знака, а значит и тогда, когда переменные
– одного знака, а значит и тогда, когда переменные 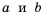 одновременно отрицательны. В таком случае тождество, рассмотренное выше, принимает вид
одновременно отрицательны. В таком случае тождество, рассмотренное выше, принимает вид 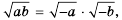 где
где 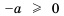 и
и 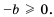 Учитывая оба случая, можно записать, что
Учитывая оба случая, можно записать, что
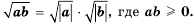
Если в равенстве 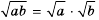 поменять местами левую и правую части, получим тождество:
поменять местами левую и правую части, получим тождество:
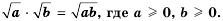
Произведение корней из неотрицательных чисел равно корню из произведения этих чисел.
Пример №236
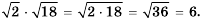
Рассмотрим квадратный корень из дроби.
Теорема (о корне из дроби). Корень из дроби, числитель которой неотрицателен, а знаменатель -положителен, равен корню из числителя, деленному на корень из знаменателя, то есть при 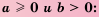
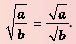
Доказательство: Так как 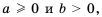 то выражения
то выражения 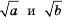 имеют смысл и
имеют смысл и 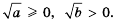 Поэтому
Поэтому 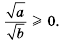
Кроме того,
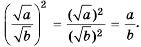
Имеем: 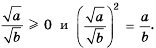 Тогда по определению квадратного корня:
Тогда по определению квадратного корня: 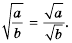
Пример №237
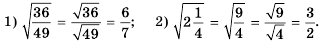
Замечание 2. По аналогии с замечанием 1, тождество, только что рассмотренное нами, можно записать и так:
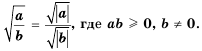
Если в равенстве 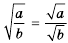 поменять местами левую и правую части, получим тождество:
поменять местами левую и правую части, получим тождество:
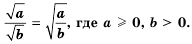
Частное, числитель которого является корнем из неотрицательного числа, а знаменатель — корнем из положительного числа, равно корню из частного этих чисел.
Пример №238
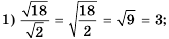
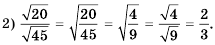
Рассмотрим, как извлечь квадратный корень из квадрата.
Теорема (о корне из квадрата). Для любого значения справедливо равенство
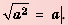
Доказательство: Так как 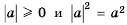 для любого
для любого 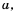 то по определению квадратного корня:
то по определению квадратного корня: 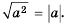
Пример №239
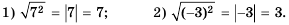
Рассмотрим квадратный корень из степени.
Теорема (о корне из степени). Для любого значения  и натурального числа
и натурального числа 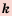 справедливо равенство
справедливо равенство
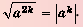
Доказательство: 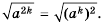 По теореме о корне из квадрата имеем
По теореме о корне из квадрата имеем 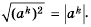 Следовательно,
Следовательно, 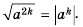
Пример №240
Вычислите: 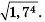
Решение:
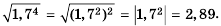
Пример №241
Упростите выражение: 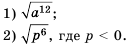
Решение:
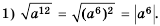 Так как
Так как 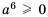 для любого
для любого 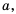 то
то 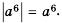 Следовательно,
Следовательно, 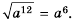
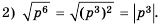 Так как
Так как 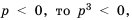 поэтому
поэтому 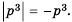 Следовательно, если
Следовательно, если 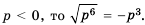
Ответ. 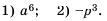
Тождественные преобразования выражений, содержащих квадратные корни
Рассмотрим тождественные преобразования выражений, содержащих квадратные корни.
Вынесение множителя из-под знака корня
Воспользуемся теоремой о корне из произведения для преобразования выражения 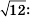
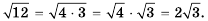
Говорят, что множитель вынесли из-под знака корня. В данном случае из-под знака корня вынесли множитель 2.
Пример №242
Вынесите множитель из-под знака корня в выражении 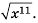
Решение:
Выражение 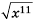 имеет смысл при
имеет смысл при 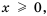 поскольку
поскольку 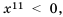 если
если 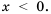 Представим выражение
Представим выражение 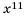 в виде произведения
в виде произведения 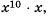 в котором
в котором 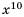 является степенью с четным показателем. Тогда
является степенью с четным показателем. Тогда
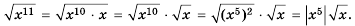
Так как 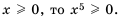 Поэтому
Поэтому 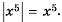
Следовательно, 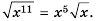
Ответ. 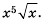
Внесение множителя под знак корня
Рассмотрим тождественное преобразование, обратное к предыдущему. Воспользуемся правилом умножения корней:
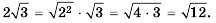
Говорят, что множитель внесли под знак корня. В данном случае под знак корня внесли множитель 2.
Отметим, что под знак корня можно вносить только положительный множитель.
Пример №243
Внести множитель под знак корня:

Решение:
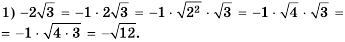
2) Множитель 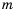 может принимать любые значения (быть положительным, нулем или отрицательным). Поэтому рассмотрим два случая:
может принимать любые значения (быть положительным, нулем или отрицательным). Поэтому рассмотрим два случая:
– если 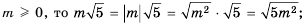
– если 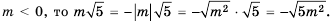
Ответ. 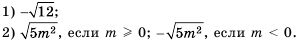
Сложение, вычитание, умножение, деление и возведение в степень выражений, содержащих квадратные корни
Используя свойства умножения и деления корней, можно выполнять арифметические действия с выражениями, содержащими квадратные корни.
Пример №244
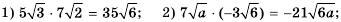
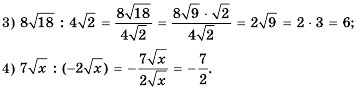
Используя тождество 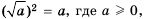 можно возводить в степень выражения, содержащие квадратные корни.
можно возводить в степень выражения, содержащие квадратные корни.
Пример №245
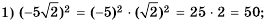
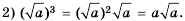
Рассмотрим примеры, где квадратные корни можно складывать.
Пример №246
Упростите выражение 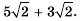
Решение:
Слагаемые содержат общий множитель 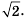 Вынесем его за скобки и выполним действие в скобках:
Вынесем его за скобки и выполним действие в скобках: 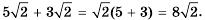
Обычно решение записывают короче: 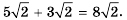
Заметим, что выражения 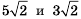 в данном примере называют подобными радикалами (по аналогии с подобными слагаемыми), мы их сложили по правилу приведения подобных слагаемых.
в данном примере называют подобными радикалами (по аналогии с подобными слагаемыми), мы их сложили по правилу приведения подобных слагаемых.
Пример №247
Упростите выражение 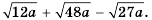
Решение:
В каждом из слагаемых можно вынести множитель из-под знака корня, в результате получим подобные радикалы и приведем их: 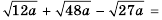
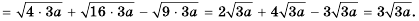
Ответ. 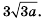
Пример №248
Упростите выражение:

Решение:
Применим формулы сокращенного умножения.
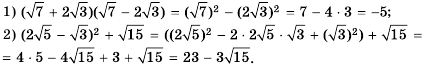
Ответ. 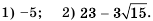
Сокращение дробей
Пример №249
Сократите дробь: 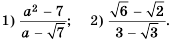
Решение:
1) Учитывая, что 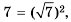 числитель дроби представим в виде разности квадратов, получим:
числитель дроби представим в виде разности квадратов, получим:
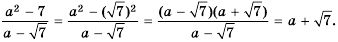
2) Учитывая, что 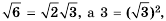 в числителе и знаменателе вынесем за скобки общий множитель, получим:
в числителе и знаменателе вынесем за скобки общий множитель, получим:
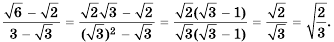
Ответ. 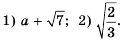
Избавление от иррациональности в знаменателе дроби
Пример №250
Преобразуйте дробь 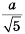 так, чтобы она не содержала корня в знаменателе.
так, чтобы она не содержала корня в знаменателе.
Решение:
Учитывая, что 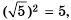 достаточно числитель и знаменатель дроби умножить на
достаточно числитель и знаменатель дроби умножить на 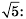
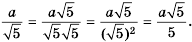
Ответ. 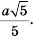
В таких случаях говорят, что избавились от иррациональности в знаменателе дроби.
Пример №251
Избавьтесь от иррациональности в знаменателе дроби 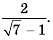
Решение:
Умножим числитель и знаменатель дроби на 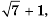 чтобы в знаменателе получить формулу сокращенного умножения разности двух выражений на их сумму:
чтобы в знаменателе получить формулу сокращенного умножения разности двух выражений на их сумму:
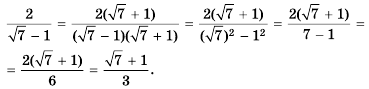
Ответ. 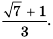
Заметим, что выражение 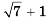 называют сопряженным выражению
называют сопряженным выражению 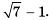 Вообще-то, если в формулах сокращенного умножения в результате умножения скобок, содержащих радикалы, получается рациональное выражение, то выражения в скобках называют взаимно сопряженными. Так,
Вообще-то, если в формулах сокращенного умножения в результате умножения скобок, содержащих радикалы, получается рациональное выражение, то выражения в скобках называют взаимно сопряженными. Так, 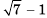 и
и 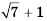 взаимно сопряженные выражения.
взаимно сопряженные выражения.
Взаимно сопряженными также являются выражения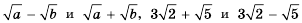 и им подобные.
и им подобные.
Функция y= √x её график и свойства
Функция 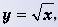 её график и свойства
её график и свойства
Пример №252
Пусть 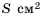 – площадь квадрата, а см – длина его стороны. Так как
– площадь квадрата, а см – длина его стороны. Так как 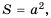 то зависимость длины стороны
то зависимость длины стороны 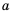 квадрата от его площади
квадрата от его площади 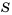 можно задать формулой
можно задать формулой
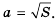
Рассмотрим функцию 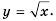 Очевидно, что переменная
Очевидно, что переменная 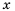 принимает только неотрицательные значения, то есть
принимает только неотрицательные значения, то есть 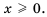
Составим таблицу значений функции 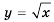 для нескольких значений аргумента:
для нескольких значений аргумента: 
Отметим эти точки на координатной плоскости (рис. 15). Если бы мы отметили на этой плоскости больше точек, координаты которых удовлетворяют уравнению 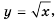 а потом соединили их плавной линией, то получили бы график функции
а потом соединили их плавной линией, то получили бы график функции 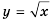 (рис. 16).
(рис. 16).
Графиком этой функции является ветвь параболы. 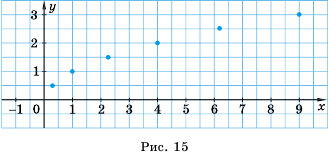
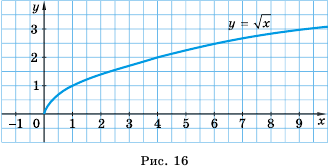
Обобщим свойства функции 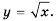
1. Областью определения функции является множество всех неотрицательных чисел: 
2. Областью значений функции является множество всех неотрицательных чисел: 
3. График функции – ветвь параболы, выходящая из точки 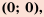 все другие точки графика лежат в первой координатной четверти.
все другие точки графика лежат в первой координатной четверти.
Большему значению аргумента соответствует большее значение функции
Последнее свойство дает возможность сравнивать значения выражении, содержащих корни.
Пример №253
Сравните числа:
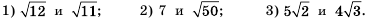
Решение:
1) Так как 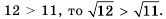
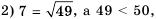 поэтому
поэтому 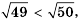 значит,
значит, 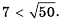
3) Внесем множитель в обоих выражениях под знак корня:
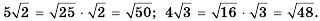
Так как 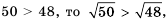 поэтому
поэтому 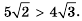
Пример №254
Решите графически уравнение 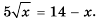
Решение:
Поскольку мы пока не умеем строить график функции 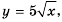 разделим обе части уравнения на число 5. Получим уравнение:
разделим обе части уравнения на число 5. Получим уравнение: 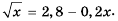
Построим графики функций 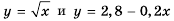 в одной системе координат (рис. 17). Они пересекаются в точке с абсциссой 4. Проверкой убеждаемся, что число 4 – корень уравнения. Действительно,
в одной системе координат (рис. 17). Они пересекаются в точке с абсциссой 4. Проверкой убеждаемся, что число 4 – корень уравнения. Действительно, 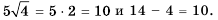
Ответ. 4. 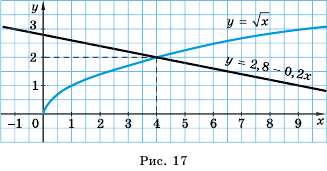
Пример №255
Постройте график функции
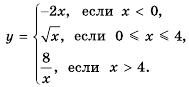
Ответ. График изображен на рисунке 18.
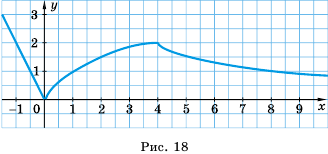
- Квадратные уравнения
- Неравенства
- Числовые последовательности
- Предел числовой последовательности
- Формулы сокращенного умножения
- Разложение многочленов на множители
- Системы линейных уравнений с двумя переменными
- Рациональные выражения
Вы зашли на проект “Решаем вместе математику, 8-9 классы”. В седьмой статье мы продолжаем изучать тему “Квадратные корни” и начинаем рассматривать подобные треугольники.
Формулы сокращённого умножения
Рассмотрим, как применяются формулы сокращённого умножения в вычислениях с квадратными корнями.
Задание 8. Квадратные корни в формулах сокращённого умножения
Подобие треугольников общего вида
А теперь рассмотрим, какие задания по теме “Подобие треугольников общего вида” могут встретиться на экзамене.
Задание под номером 8 привело нас к замечательному выводу: отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Домашнее задание Дана 7
Ответы к заданиям Вы найдёте в разделе “Комментарии”.
Бонус для тружеников.
Ссылки на предыдущие статьи проекта:
Дан 1
Дан 2
Дан 3
Дан 4
Дан 5
Дан 6
Вы находитесь на дружелюбном канале.
Уважайте себя. С уважением, автор.
#математика #проект по математике для 9 класса #огэ по математике #школьное образование #репетитор по математике #обучение математике
Поиск значений выражений — основное математическое действие. Им сопровождается каждый пример, задача. Поэтому чтобы вам было проще работать с различными математическими выражениями, подробно разберем способы и правила их решения в данной статье. Правила представлены в порядке увеличения сложности: от простейших выражений до выражений с функциями. Для лучшего понимания каждый пункт сопровождается подробным пояснением и расписанными примерами.
Поиск значения числовых выражений
Числовые выражения представляют собой математические задачи, состоящие, преимущественно, из чисел. Они подразделяются на несколько групп в зависимости от своей сложности: простейшие, со скобками, корнями, дробями и т.д. Каждый тип выражений подразумевает свои правила нахождения значения, порядок действий. Рассмотрим каждый случай подробнее.
Простейшие числовые выражения. К простейшим числовым выражениям относятся примеры, состоящие из двух элементов:
- Числа (целые, дробные и т.д.);
- Знаки: «+», «—», «•» и «÷».
Чтобы найти значение выражения в данном случае, необходимо выполнить все арифметические действия (которые подразумевают конкретные знаки). В случае отсутствия скобок решение примера производится слева направо. Первыми выполняются действия деления и умножения. Вторыми — сложение и вычитание.
Пример 1. Решение числового выражения
Задача. Решить:
20 — 2 • 10 ÷ 5 — 4 = ?
Решение. Чтобы решить выражение, нам необходимо выполнить все арифметические действия в соответствии с установленными правилами. Поиск значения начинается с решения деления и умножения. В первую очередь находим произведение цифр 2 и 10 (если рассматривать с левой стороны, данное действие является первым по значимости). Получаем 20. Теперь это число делим на 5. Итог — 4. Когда известно значение основных действий, можем подставить его в наш пример:
20 — 4 — 4 = ?
Упрощенный пример также решаем слева направо: 20 — 4 = 16. Второе действие: 16 — 4 = 12. Ответ 12.
Решение без пояснений. 20 — 2 • 10 ÷ 5 — 4 = 20 — (2 • 10 ÷ 5) — 4 = 20 — 4 — 4 = 12.
Ответ. 12
Пример 2. Решение числового выражения
Задача. Решить:
0,2 — 5 • (— 4) + 1/2 • 5 • 4 = ?
Решение. Начинаем решение с умножения и деления. Умножая 5 на (— 4) получаем (— 20), т.к. производное сохраняет знак множителя. Далее умножаем 1/2 на 5. Для этого преобразуем дробь: 1/2 = 5/10 = 0,5. 0,5 умножаем на 5. Ответ — 2,5. Далее умножаем полученное число на 4. 2,5 • 4 = 10. Получаем следующее выражение:
0,2 — (— 20) + 10
Теперь нам остается решить сложение и вычитание. В первую очередь раскрываем скобку и получаем:
0,2 + 20 + 10 = 30,2
Решение без пояснений. 0,2 — 5 • (— 4) + 1/2 • 5 • 4 = 0,2 — (— 20) + 10 = 0,2 + 20 + 10 = 30,2
Ответ. 30,2
Находим значение выражения со скобками
Скобки определяют порядок действий при решении примера. Выражения, находящиеся внутри скобок «()» имеют первостепенную значимость, независимо от того, какое математическое действие в них выполняется.
Пример 3. Значение числового выражения со скобками
Задача. Решить:
5 + (7 — 2 • 3) • (6 — 4) ÷ 2 = ?
Решение. Начинаем нахождение значения выражения с решения скобок. Порядок действий определяется слева направо. При этом не забываем, что после раскрытия скобок в первую очередь решаем умножение и деление и лишь потом — вычитание и сложение:
- 7 — 2 • 3 = 7 — 6 = 1
- 6 — 4 = 2
Когда скобки решены, подставляем полученные значения в наш пример:
5 + 1 • 2 ÷ 2
Снова решаем все по порядку, не забывая о том, что деление и умножение выполняется в первую очередь:
- 1 • 2 = 2
- 2 ÷ 2 = 1
Упрощенное выражение выглядит следующим образом:
5 + 1 = 6
Решение без пояснений. 5 + (7 — 2 • 3) • (6 — 4) ÷ 2 = 5 + (7 — 6) • 2 ÷ 2 = 5+ 1 • 2 ÷ 2 = 5 + 1 = 6
Ответ. 6
Значение числового выражения со скобками
Задача. Решить:
4 + (3 + 1 + 4 • (2+3)) = ?
Решение. Подобные примеры решаются поэтапно. Помним, что поиск выражения со скобками начинается с решения скобок. Поэтому в первую очередь решаем:
3 + 1 + 4 • (2+3)
В уже упрощенном примере снова встречаются скобки. Их будем решать в первую очередь:
2 + 3 = 5
Теперь можем подставить определенное значение в общую скобку:
3 + 1 + 4 • 5
Начинаем решение с умножения и далее слева направо:
- 4 • 5 = 20
- 3 + 1 = 4
- 4 + 20 = 24
Далее подставляем полученный ответ вместо большой скобки и получаем:
4 + 24 = 28
Решение без пояснений. 4 + (3 + 1 + 4 • (2+3)) = 4 + (3 + 1 + 4 • 5) = 4 + (3 + 1 + 20) = 4 + 24 = 28
Ответ. 28
Важно: Чтобы правильно определить значение числового выражения с множественными скобками, необходимо выполнять все действия постепенно. Скобки читаются слева направо. Приоритет в решении внутри скобок остается за делением и умножением.
Поиск значения выражения с корнями
Часто алгебраические задания основываются на нахождении значений из-под корня. И если определить √4 несложно (напомним, это будет 2), то с примерами, которые полностью расположены под корнем, возникает ряд вопросов. На самом деле в таких заданиях нет ничего сложного. В данном случае порядок действий следующий:
- Решаем все выражение, которое находится под корнем (не забываем о правильной последовательности: сперва скобки, деление и умножение, а лишь потом — сложение и вычитание);
- Извлекаем корень из числа, которое получили в результате решения обычного примера.
Если же и под корнем имеется корень (например: √ 4 + 8 — √4), то начинаем решение примера с его извлечения (в нашем примере это будет: √ 4 + 8 — 2). Если подкоренные числа возведены во вторую степень, то их квадратный корень будет равняться модулю подкоренного выражения.
Значение числового выражения с корнями
Задача. Решить:
√ 2² • 2² • 3² = ?
Решение. Все действия под корнем одинаковы — умножение. Это дает нам право разделить выражение на множители. Получаем:
√2² • √2² • √3² = ?
Т.к. под квадратным корнем у нас числа, возведенные во вторую степень, получаем:
2 • 2 • 3 = 12
Решение без пояснений. √ 2² • 2² • 3² = √2² • √2² • √3² = 2 • 2 • 3 = 12
Ответ. 12
Нет времени решать самому?
Наши эксперты помогут!
Находим значение числовых выражений со степенями
Следующий математический знак, который имеет приоритет в процессе решения, — степени. Они представляют собой результат многократного умножения числа на себя. Само число является основанием степени. А количество операций умножения — ее показателем. Причем выражен он может быть не только целым числом, но и дробью, полноценным числовым выражением.
Начинается решение выражения со степенями с вычисления самих степеней. Если они представляют собой полноценное выражение (например: [3^{3 cdot 4-10}]), то его необходимо решить в нашем примере это будет: [3^{12-10}=3^{2}=9].
Задача. Решите:
[ 3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=? ]
Решение. Чтобы решить это выражение со степенями, воспользуемся равенством:
[(a cdot b)^{r}=a^{r} cdot b^{r}]
Рассматривая пример слева направо, видим, что у первых двух множителей одинаковые степени. Это позволяет нам упростить выражение:
[ (3 cdot 7)^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3} cdot 21^{2 / 3} ]
Зная, что при умножении степени с одинаковыми показателями складываются, получаем следующее выражение:
[ 21^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3+2 / 3}=21^{1}=21 ]
Решение без пояснений: [3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=(3 cdot 7)^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3+2 / 3}=21^{1}=21]
Ответ. 21
Интересно: Этот же пример можно решить и другим способом, преобразовав число 21 в степени ⅔ в два множителя. В данном случае решение будет выглядеть следующим образом:
[3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=3^{1 / 3} cdot 7^{1 / 3} cdot(3 cdot 7)^{2 / 3}=3^{1 / 3} cdot 7^{1 / 3} cdot 3^{2 / 3} cdot 7^{2 / 3}=3^{1 / 3+2 / 3} cdot 7^{1 / 3+2 / 3}=3^{1}+7^{1}=21]
Ответ. 21
Задача. Решить:
[ 2^{-2 sqrt{5}} cdot 4^{sqrt{5}-1}+left((sqrt{3})^{1 / 3}right)^{6} ]
Решение. В данном случает получить точные числовые значения показателей степеней не удастся. Поэтому искать значение выражения с дробями в виде степени будем снова через упрощение:

Ответ. 3,25
Выражения с дробями
Поиск значения выражения дробей начинается с их приведения к общему виду. В большинстве случаев проще представить все значения в виде обыкновенной дроби с числителем и знаменателем. После преобразования всех чисел необходимо привести все дроби к общему знаменателю.
Важно: Прежде чем найти выражение дробей, необходимо провести вычисления в их знаменателе и числителе отдельно. В данном случае действуют стандартные правила решения.
Когда дроби приведены к единому знаменателю можно переходить к решению. Вычисление значений верхней строки (числителя) и нижней (знаменателя) производятся параллельно.
Задача. Решить:
[ 6 frac{2}{13}+4 frac{1}{13}=? ]
Решение. Действуя по главному правилу, прежде чем найти значение числового выражения, преобразуем всего его части в простую дробь. Получаем:
[ frac{6 cdot 13+2}{13}+frac{4 cdot 13+1}{13} ]
Теперь выполняем вычисления в знаменателе и числителе и находим ответ:
[ frac{6 cdot 13+2}{13}+frac{4 cdot 13+1}{13}=frac{80}{13}+frac{53}{13}=frac{133}{13}=10 frac{3}{13} ]
Ответ. [10 frac{3}{13}]
Примеры(2):

Задача. Решить:
[ frac{2}{sqrt{5}-1}-frac{2 sqrt{5}-7}{4}-3=? ]
Решение. В данном примере мы не можем извлечь корень из пятерки. Но мы можем воспользоваться формулой разложения корней:
[ frac{2}{sqrt{5}-1}=frac{2(sqrt{5}+1)}{(sqrt{5}-1)(sqrt{5}+1)}=frac{2(sqrt{5}+1)}{5-1}=frac{2 sqrt{5}+2}{4} ]
Теперь можем придать нашему первоначальному выражению следующий вид:
[ frac{2 sqrt{5}+2}{4} frac{2 sqrt{5}-7}{4}-3=frac{2 sqrt{5}+2-2 sqrt{5}+7}{4}-3=frac{9}{4} 3=-frac{3}{4} ]
Ответ. [-frac{3}{4}].
Выражения с логарифмами
Как и степени, логарифмы (log), имеющиеся в выражении, вычисляются (если это возможно) в первую очередь. К примеру, зная, что [log _{2} 4=2] мы можем сразу упростить выражение [log _{2} 4+5 cdot 6] до простого и понятного 2 + 5*6 = 32.
Со степенями логарифмы объединяет и порядок выполнения действий. Прежде чем искать значение выражения логарифмов, необходимо вычислить его основание (если оно представлено математическим выражением).
В случаях, когда полное вычисление логарифма невозможно, производится упрощение примера.
Задача. Решить:
[log _{27} 81+log _{27} 9=?]
Решение. Чтобы найти логарифм выражения, воспользуемся свойствами логарифмов и представим значение логарифмов со степенями:
![]()
Это позволит нам решить пример следующим образом:

Ответ. 2
Решаем выражения с тригонометрической функцией
Часто в выражениях встречаются тригонометрические функции. Всего их в математике шесть:
- Синус;
- Косинус;
- Котангенс;
- Тангенс;
- Секанс;
- Косеканс.
Изучение тригонометрии начинается в 9-м классе, когда ученики уже подготовлены к сложным задачам. Большинство заданий представляются с sin и cos. Остальные функции встречаются значительно реже.
В математических примерах, которые содержат sin, cos, tg и др. функции, вычисление тригонометрической функции производится в первую очередь. Если это невозможно — осуществляется упрощение выражения до получения краткой формулы.
Задача. Решить:
[ frac{24}{sin ^{2} 127+1+sin ^{2} 217} ]
Решение. Разложим 217 на 90 и 127. Т.к. по формуле приведения sin(90 + a) = cosa, получаем:
sin217 — sin (90 + 127) = cos127
Теперь заменяем полученной формулой наше слагаемое в знаменателе дроби:
[ frac{24}{sin ^{2} 127+cos ^{2} 127+1} ]
Вспоминаем, что по тригонометрическому тождеству sin2a+ cos2 a= 1 (независимо от значения угла a). Поэтому одну часть слагаемого знаменателя (sin2127+ cos2127) преобразуем в единицу и получаем:
[ frac{24}{sin ^{2} 127+cos ^{2} 127+1}=frac{24}{1+1}=frac{24}{2}=2 ]
Ответ. 2

Важно: Не стоит бояться буквенных тригонометрических значений. Большинство примеров построено таким образом, чтобы функции можно было заменить более удобной для вычисления формулой. Поэтому вместо того, чтобы пытаться сразу решить пример, стоит обратить внимание на особенности функций и возможность их приведения к подходящей формуле.
Задача. Решить:
[ sqrt{4} 8-sqrt{1} 92 sin ^{2} frac{19 pi}{12}=? ]
Решение. Начинаем решение с разбора второй дроби. Обращаем внимание, что 192 = 48 • 2. А значит, корень этого числа можно представить в виде 2√48. Зная это и используя формулу косинуса двойного угла, преобразим наше выражение:

Теперь по формуле приведения решаем наш пример:
[ sqrt{4} 8 cos left(3 pi+frac{pi}{6}right)=sqrt{4} 8left(-cos frac{pi}{6}right)=-sqrt{4} 8 cdot frac{sqrt{3}}{2}=-4 sqrt{3} cdot frac{sqrt{3}}{2}=-6 ]
Ответ. — 6.
Общий случай: находим значения выражений с дробями, функциями, степенями и не только
Самым сложным считается поиск числовых выражений общих случаев. Они представляют собой тригонометрические примеры, которые могут содержать:
- Степени;
- Скобки;
- Корни;
- Функции и т.д.
Общие числовые выражения сложны только длительностью решения. В остальном же они ничуть не сложнее, чем решение каждого примера (со скобкой, степенями, функциями и т.д.) по отдельности.
Чтобы найти значение выражения с логарифмами, тригонометрическими функциями, скобками и/или другими действиями, необходимо помнить три основных правила:
- Упрощение. Прежде чем приступать к решению внимательно изучите выражение. Особенно — его степени, корни, логарифмы, функции. В большинстве случаев их можно сократить или заменить простым числовым значением еще до решения.
- Скобки. Независимо от типа выражения, действий, начинать решение всегда необходимо со скобок. Часто именно игнорирование этого правила приводит к получению неверного ответа или отсутствию решения в принципе.
- Общий вид. Старайтесь привести выражение к общему виду. Особенно это касается дробей. Смешанные и десятичные дроби преобразуйте в обычные.
- Последовательность. Действия в скобках и действия после их решения выполняются слева направо. В первую очередь необходимо совершать умножение и деление. Когда все произведения и частные найдены, можно переходить к сложению и вычитанию.
Для удобства решения и устранения возможных ошибок рекомендуем расставлять порядок действий непосредственно над математическими знаками.
Задача. Решить:
[ -frac{sqrt{2} sin left(frac{pi}{6}+2left(frac{2 pi}{5}+frac{3 pi}{5}right)right)+3}{operatorname{Ln} e^{2}}+left(1+3^{sqrt{9}}right)=? ]
Решение. Чтобы решить этот пример, сначала найдем значение выражения числителя дроби, а точнее — подкоренного выражения. Для этого необходимо вычислить значение sin и общего выражения. Начинаем с раскрытия скобок в числителе:

Полученное значение можем подставить в подкоренное выражение для вычисления числителя дроби:
[ sqrt{2} sin cdotleft(frac{pi}{6}+2left(frac{2 pi}{5}+frac{3 pi}{5}right)+3=sqrt{4}=2right. ]
Со знаменателем дела обстоят куда проще:
[ ln e^{2}=2 ]
Числитель и знаменатель у нас одинаковые, что позволяет нам их сократить:

Теперь остается решить следующее выражение:

Ответ. 27
Как видите, при последовательном решении примеров с большим количеством действий нет ничего сложного. Главное — верно обозначить последовательность шагов и четко ей следовать.
Как найти значение выражения числителя дроби, подкорневого значения рационально?
Независимо от типа выражения решать его необходимо последовательно, руководствуясь стандартными правилами (описаны ранее). Но не стоит забывать, что во многих случаях поиск ответа может быть значительно упрощен за счет рационального подхода к решению. Основывается он на нескольких правилах.
Правило 1. Когда произведение равно нулю
Производное равно нулю в том случае, если хотя бы один из его сомножителей равен нулю. Если вы решаете пример из нескольких сомножителей, одним из которых является «0», то проводить многочисленные вычислительные действия не стоит.
Например, выражение [3 cdotleft(451+4+frac{18}{3}right)left(1-sin left(frac{3 pi}{4}right)right) cdot 0] будет равняться нулю.
Правило 2. Группировка и вынесение чисел
Ускорить процесс поиска ответа можно за счет группировки множителей, слагаемых или вынесения единого множителя за скобки. Также не стоит забывать о возможности сокращения дроби.
Например, выражение [frac{left(451+4+frac{18}{3}right)}{4left(451+4+frac{18}{3}right)}] решать не надо. Достаточно сократить скобки, чтобы получить ответ [=frac{1}{4}]
Решение примеров с переменными
Примеры с переменными отличаются от числовых только формой предоставления. В данном случае значения предоставляются дополнительно к выражению.
Пример задания: Найдите значение выражения 2x — y, если x = 2,5, а y = 2. В данном случае решение будет выглядеть следующим образом:
2x — y = 2 • 2,5 — 2 = 3
При этом в таких примерах сохраняются все описанные выше правила. Касается это и советов по рациональному решению примеров. Так, решать дробь [frac{sqrt{y}}{sqrt{y}}] бессмысленно, т.к. при любых значениях «y» ответ будет одинаковым — 1.
Факт 1.
(bullet) Возьмем некоторое неотрицательное число (a) (то есть (ageqslant 0)). Тогда (арифметическим) квадратным корнем из числа (a) называется такое неотрицательное число (b), при возведении которого в квадрат мы получим число (a): [sqrt a=bquad text{то же самое, что }quad a=b^2] Из определения следует, что (ageqslant 0, bgeqslant 0). Эти ограничения являются важным условием существования квадратного корня и их следует запомнить!
Вспомним, что любое число при возведении в квадрат дает неотрицательный результат. То есть (100^2=10000geqslant 0) и ((-100)^2=10000geqslant 0).
(bullet) Чему равен (sqrt{25})? Мы знаем, что (5^2=25) и ((-5)^2=25). Так как по определению мы должны найти неотрицательное число, то (-5) не подходит, следовательно, (sqrt{25}=5) (так как (25=5^2)).
Нахождение значения (sqrt a) называется извлечением квадратного корня из числа (a), а число (a) называется подкоренным выражением.
(bullet) Исходя из определения, выражения (sqrt{-25}), (sqrt{-4}) и т.п. не имеют смысла.
Факт 2.
Для быстрых вычислений полезно будет выучить таблицу квадратов натуральных чисел от (1) до (20): [begin{array}{|ll|}
hline
1^2=1 & quad11^2=121 \
2^2=4 & quad12^2=144\
3^2=9 & quad13^2=169\
4^2=16 & quad14^2=196\
5^2=25 & quad15^2=225\
6^2=36 & quad16^2=256\
7^2=49 & quad17^2=289\
8^2=64 & quad18^2=324\
9^2=81 & quad19^2=361\
10^2=100& quad20^2=400\
hline end{array}]
Факт 3.
Какие действия можно выполнять с квадратными корнями?
(bullet) Сумма или разность квадратных корней НЕ РАВНА квадратному корню из суммы или разности, то есть [sqrt apmsqrt bne sqrt{apm b}] Таким образом, если вам нужно вычислить, например, (sqrt{25}+sqrt{49}), то первоначально вы должны найти значения (sqrt{25}) и (sqrt{49}), а затем их сложить. Следовательно, [sqrt{25}+sqrt{49}=5+7=12] Если значения (sqrt a) или (sqrt b) при сложении (sqrt
a+sqrt b) найти не удается, то такое выражение дальше не преобразуется и остается таким, как есть. Например, в сумме (sqrt
2+ sqrt {49}) мы можем найти (sqrt{49}) – это (7), а вот (sqrt
2) никак преобразовать нельзя, поэтому (sqrt 2+sqrt{49}=sqrt
2+7). Дальше это выражение, к сожалению, упростить никак нельзя
(bullet) Произведение/частное квадратных корней равно квадратному корню из произведения/частного, то есть [sqrt acdot sqrt b=sqrt{ab}quad text{и}quad
sqrt a:sqrt b=sqrt{a:b}] (при условии, что обе части равенств имеют смысл)
Пример: (sqrt{32}cdot sqrt 2=sqrt{32cdot
2}=sqrt{64}=8);
(sqrt{768}:sqrt3=sqrt{768:3}=sqrt{256}=16);
(sqrt{(-25)cdot (-64)}=sqrt{25cdot 64}=sqrt{25}cdot sqrt{64}=
5cdot 8=40).
(bullet) Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
Рассмотрим пример. Найдем (sqrt{44100}). Так как (44100:100=441), то (44100=100cdot 441). По признаку делимости число (441) делится на (9) (так как сумма его цифр равна 9 и делится на 9), следовательно, (441:9=49), то есть (441=9cdot 49).
Таким образом, мы получили: [sqrt{44100}=sqrt{9cdot 49cdot 100}=
sqrt9cdot sqrt{49}cdot sqrt{100}=3cdot 7cdot 10=210] Рассмотрим еще один пример: [sqrt{dfrac{32cdot 294}{27}}=
sqrt{dfrac{16cdot 2cdot 3cdot 49cdot 2}{9cdot 3}}= sqrt{
dfrac{16cdot4cdot49}{9}}=dfrac{sqrt{16}cdot sqrt4 cdot
sqrt{49}}{sqrt9}=dfrac{4cdot 2cdot 7}3=dfrac{56}3]
(bullet) Покажем, как вносить числа под знак квадратного корня на примере выражения (5sqrt2) (сокращенная запись от выражения (5cdot
sqrt2)). Так как (5=sqrt{25}), то [5sqrt2=sqrt{25}cdot sqrt2=sqrt{25cdot 2}=sqrt{50}] Заметим также, что, например,
1) (sqrt2+3sqrt2=4sqrt2),
2) (5sqrt3-sqrt3=4sqrt3)
3) (sqrt a+sqrt a=2sqrt a).
Почему так? Объясним на примере 1). Как вы уже поняли, как-то преобразовать число (sqrt2) мы не можем. Представим, что (sqrt2) – это некоторое число (a). Соответственно, выражение (sqrt2+3sqrt2) есть не что иное, как (a+3a) (одно число (a) плюс еще три таких же числа (a)). А мы знаем, что это равно четырем таким числам (a), то есть (4sqrt2).
Факт 4.
(bullet) Часто говорят “нельзя извлечь корень”, когда не удается избавиться от знака (sqrt {} ) корня (радикала) при нахождении значения какого-то числа. Например, извлечь корень из числа (16) можно, потому что (16=4^2), поэтому (sqrt{16}=4). А вот извлечь корень из числа (3), то есть найти (sqrt3), нельзя, потому что нет такого числа, которое в квадрате даст (3).
Такие числа (или выражения с такими числами) являются иррациональными. Например, числа (sqrt3, 1+sqrt2, sqrt{15}) и т.п. являются иррациональными.
Также иррациональными являются числа (pi) (число “пи”, приблизительно равное (3,14)), (e) (это число называют числом Эйлера, приблизительно оно равно (2,7)) и т.д.
(bullet) Обращаем ваше внимание на то, что любое число будет либо рациональным, либо иррациональным. А вместе все рациональные и все иррациональные числа образуют множество, называющееся множеством действительных (вещественных) чисел. Обозначается это множество буквой (mathbb{R}).
Значит, все числа, которые на данный момент мы знаем, называются вещественными числами.
Факт 5.
(bullet) Модуль вещественного числа (a) – это неотрицательное число (|a|), равное расстоянию от точки (a) до (0) на вещественной прямой. Например, (|3|) и (|-3|) равны 3, так как расстояния от точек (3) и (-3) до (0) одинаковы и равны (3). 
(bullet) Если (a) – неотрицательное число, то (|a|=a).
Пример: (|5|=5); (qquad |sqrt2|=sqrt2).
(bullet) Если (a) – отрицательное число, то (|a|=-a).
Пример: (|-5|=-(-5)=5); (qquad |-sqrt3|=-(-sqrt3)=sqrt3).
Говорят, что у отрицательных чисел модуль “съедает” минус, а положительные числа, а также число (0), модуль оставляет без изменений.
НО такое правило годится только для чисел. Если у вас под знаком модуля находится неизвестная (x) (или какая-то другая неизвестная), например, (|x|), про которую мы не знаем, положительная она, равна нулю или отрицательная, то избавиться от модуля мы не можем. В этом случае это выражение таким и остается: (|x|).
(bullet) Имеют место следующие формулы: [{large{sqrt{a^2}=|a|}}] [{large{(sqrt{a})^2=a}},
text{ при условии } ageqslant 0] Очень часто допускается такая ошибка: говорят, что (sqrt{a^2}) и ((sqrt a)^2) – одно и то же. Это верно только в том случае, когда (a) – положительное число или ноль. А вот если (a) – отрицательное число, то это неверно. Достаточно рассмотреть такой пример. Возьмем вместо (a) число (-1). Тогда (sqrt{(-1)^2}=sqrt{1}=1), а вот выражение ((sqrt {-1})^2) вообще не существует (ведь нельзя под знак корня помещать отрицательные числа!).
Поэтому обращаем ваше внимание на то, что (sqrt{a^2}) не равен ((sqrt a)^2)!
Пример: 1) (sqrt{left(-sqrt2right)^2}=|-sqrt2|=sqrt2), т.к. (-sqrt2<0);
(phantom{00000}) 2) ((sqrt{2})^2=2).
(bullet) Так как (sqrt{a^2}=|a|), то [sqrt{a^{2n}}=|a^n|] (выражение (2n) обозначает четное число)
То есть при извлечении корня из числа, находящегося в какой-то степени, эта степень уменьшается в два раза.
Пример:
1) (sqrt{4^6}=|4^3|=4^3=64)
2) (sqrt{(-25)^2}=|-25|=25) (заметим, что если модуль не поставить, то получится, что корень из числа равен (-25); но мы помним, что по определению корня такого быть не может: у нас всегда при извлечении корня должно получаться положительное число или ноль)
3) (sqrt{x^{16}}=|x^8|=x^8) (так как любое число в четной степени неотрицательно)
Факт 6.
Как сравнить два квадратных корня?
(bullet) Для квадратных корней верно: если (sqrt a<sqrt b), то (a<b); если (sqrt a=sqrt b), то (a=b).
Пример:
1) сравним (sqrt{50}) и (6sqrt2). Для начала преобразуем второе выражение в (sqrt{36}cdot sqrt2=sqrt{36cdot 2}=sqrt{72}). Таким образом, так как (50<72), то и (sqrt{50}<sqrt{72}). Следовательно, (sqrt{50}<6sqrt2).
2) Между какими целыми числами находится (sqrt{50})?
Так как (sqrt{49}=7), (sqrt{64}=8), а (49<50<64), то (7<sqrt{50}<8), то есть число (sqrt{50}) находится между числами (7) и (8).
3) Сравним (sqrt 2-1) и (0,5). Предположим, что (sqrt2-1>0,5): [begin{aligned}
&sqrt 2-1>0,5 big| +1quad text{(прибавим единицу к обеим
частям)}\[1ex]
&sqrt2>0,5+1 big| ^2 quadtext{(возведем обе части в
квадрат)}\[1ex]
&2>1,5^2\
&2>2,25 end{aligned}] Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и (sqrt 2-1<0,5).
Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!
Возводить обе части уравнения/неравенства в квадрат можно ТОЛЬКО ТОГДА, когда обе части неотрицательные. Например, в неравенстве из предыдущего примера возводить обе части в квадрат можно, в неравенстве (-3<sqrt2) нельзя (убедитесь в этом сами)!
(bullet) Следует запомнить, что [begin{aligned}
&sqrt 2approx 1,4\[1ex]
&sqrt 3approx 1,7 end{aligned}] Знание приблизительного значения данных чисел поможет вам при сравнении чисел!
(bullet) Для того, чтобы извлечь корень (если он извлекается) из какого-то большого числа, которого нет в таблице квадратов, нужно сначала определить, между какими “сотнями” оно находится, затем – между какими “десятками”, а потом уже определить последнюю цифру этого числа. Покажем, как это работает, на примере.
Возьмем (sqrt{28224}). Мы знаем, что (100^2=10,000), (200^2=40,000) и т.д. Заметим, что (28224) находится между (10,000) и (40,000). Следовательно, (sqrt{28224}) находится между (100) и (200).
Теперь определим, между какими “десятками” находится наше число (то есть, например, между (120) и (130)). Также из таблицы квадратов знаем, что (11^2=121), (12^2=144) и т.д., тогда (110^2=12100), (120^2=14400), (130^2=16900), (140^2=19600), (150^2=22500), (160^2=25600), (170^2=28900). Таким образом, мы видим, что (28224) находится между (160^2) и (170^2). Следовательно, число (sqrt{28224}) находится между (160) и (170).
Попробуем определить последнюю цифру. Давайте вспомним, какие однозначные числа при возведении в квадрат дают на конце (4)? Это (2^2) и (8^2). Следовательно, (sqrt{28224}) будет заканчиваться либо на 2, либо на 8. Проверим это. Найдем (162^2) и (168^2):
(162^2=162cdot 162=26224)
(168^2=168cdot 168=28224).
Следовательно, (sqrt{28224}=168). Вуаля!
Корни и степени
-
Степень с натуральным показателем
-
Степень с целым показателем
-
Кубический корень
-
Корень -ной степени
-
Сравнение арифметических корней
-
Как избавиться от иррациональности в знаменателе
-
Как упрощать иррациональные выражения, пользуясь формулами сокращенного умножения
Степенью называется выражение вида .
Здесь — основание степени,
— показатель степени.
к оглавлению ▴
Степень с натуральным показателем
Проще всего определяется степень с натуральным (то есть целым положительным) показателем.
По определению, .
Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы.
Возвести число в квадрат — значит умножить его само на себя.
.
Возвести число в куб — значит умножить его само на себя три раза.
.
Возвести число в натуральную степень — значит умножить его само на себя
раз:
к оглавлению ▴
Степень с целым показателем
Показатель степени может быть не только натуральным (то есть целым положительным), но и равным нулю, а также целым отрицательным.
По определению,
.
Это верно для . Выражение 00 не определено.
Определим также, что такое степень с целым отрицательным показателем.
Конечно, все это верно для , поскольку на ноль делить нельзя.
Например,
Заметим, что при возведении в минус первую степень дробь переворачивается.
Показатель степени может быть не только целым, но и дробным, то есть рациональным числом. В статье «Числовые множества» мы говорили, что такое рациональные числа. Это числа, которые можно записать в виде дроби , где
— целое,
— натуральное.
Здесь нам понадобится новое понятие — корень -степени. Корни и степени — две взаимосвязанные темы. Начнем с уже знакомого вам арифметического квадратного корня.
Определение.
Арифметический квадратный корень из числа — это такое неотрицательное число, квадрат которого равен
.
Согласно определению,
В школьной математике мы извлекаем корень только из неотрицательных чисел. Выражение для нас сейчас имеет смысл только при
.
Выражение всегда неотрицательно, т.е.
. Например,
.
Свойства арифметического квадратного корня:
Запомним важное правило:
По определению,  .
.
к оглавлению ▴
Кубический корень
Аналогично, кубический корень из — это такое число, которое при возведении в третью степень дает число
.
Например, , так как
;
, так как
;
, так как
.
Обратите внимание, что корень третьей степени можно извлекать как из положительных, так и из отрицательных чисел.
Теперь мы можем дать определение корня -ной степени для любого целого
.
к оглавлению ▴
Корень  -ной степени
-ной степени
Корень -ной степени из числа
— это такое число, при возведении которого в
-ную степень получается число
.
Например,
Заметим, что корень третьей, пятой, девятой — словом, любой нечетной степени, — можно извлекать как из положительных, так и из отрицательных чисел.
Квадратный корень, а также корень четвертой, десятой, в общем, любой четной степени можно извлекать только из неотрицательных чисел.
Итак, — такое число, что
. Оказывается, корни можно записывать в виде степеней с рациональным показателем. Это удобно.
По определению,
в общем случае .
Сразу договоримся, что основание степени больше 0.
Например,
Выражение по определению равно
.
При этом также выполняется условие, что больше 0.
Например,
Запомним правила действий со степенями:
— при перемножении степеней показатели складываются;
— при делении степени на степень показатели вычитаются;
— при возведении степени в степень показатели перемножаются;
Покажем, как применяются эти формулы в заданиях ЕГЭ по математике:
1.
Внесли все под общий корень, разложили на множители, сократили дробь и извлекли корень.
2.
3.
Здесь мы записали корни в виде степеней и использовали формулы действий со степенями.
4. Найдите значение выражения при
Решение:
При получим
Ответ: -0,5.
5. Найдите значение выражения при
Решение:
При a = 12 получим
Мы воспользовались свойствами степеней.
Ответ: 144.
6. Найдите значение выражения при b = – 5.
Решение:
При b = – 5 получим:
Ответ: -125.
7. Расположите в порядке возрастания:
Решение:
Запишем выражения как степени с положительным показателем и сравним.
Так как
то
Так как
то
Сравним и
для этого оценим их разность:
значит
Получим : поэтому
Ответ:
8. Представьте выражение в виде степени:
Решение:
Вынесем за скобку степень с меньшим показателем:
Ответ:
9. Упростите выражение:
Решение:
Приведем основания 6 и 12 к основаниям 2 и 3:
(выполним деление степеней с одинаковыми основаниями)
Ответ: 0,25.
10. Чему равно значение выражения при
?
Решение:
При получим
Ответ: 9.
к оглавлению ▴
Сравнение арифметических корней
11. Какое из чисел больше: или
?
Решение:
Возведем в квадрат оба числа (числа положительные):
Найдем разность полученных результатов:
так как
Значит, первое число больше второго.
Ответ:
к оглавлению ▴
Как избавиться от иррациональности в знаменателе
Если дана дробь вида то нужно умножить числитель и знаменатель дроби на
:
Тогда знаменатель станет рациональным.
Если дана дробь вида или
то нужно умножить числитель и знаменатель дроби на сопряженное выражение, чтобы получить в знаменателе разность квадратов.
Сопряженные выражения – это выражения, отличающиеся только знаками. Например,
и
и
– сопряженные выражения.
Пример:
12. Вот несколько примеров – как избавиться от иррациональности в знаменателе:
Пример 1.
Пример 2.
Пример 3.
Пример 4.
Совет. Если в знаменателе дана сумма двух корней, то в разности первым числом пишите то, которое больше, и тогда разность квадратов корней будет положительным числом.
Пример 5.
13. Сравните и
1)
2) Сравним и 14.
то и
а значит,
Ответ: меньше.
к оглавлению ▴
Как упрощать иррациональные выражения, пользуясь формулами сокращенного умножения
Покажем несколько примеров.
14. Упростите: выражения:
Пример 5.
т.к.
Пример 6.
Пример 7.
так как
Следующие несколько задач решаются с помощью формулы:
Решение:
Получим уравнение
Ответ:
19. Вычислите значение выражения:
Решение:
Ответ: 1.
20. Вычислите значение выражения:
Решение:
Ответ: 1.
21. Вычислите значение выражения: если
Решение.
Если то
следовательно
Ответ: – 1.
22. Вычислите:
Решение:
Ответ: 1.
Рассмотрим уравнение вида где
Это равенство выполняется, только если
Подробно об таких уравнениях – в статье «Показательные уравнения».
При решении уравнений такого вида мы пользуемся монотонностью показательной функции.
23. Решите уравнение:
а)
б)
в)
Решение.
23. Решите уравнение:
Решение:
тогда
Ответ: -1.
24. Решите уравнение:
Решение:
Ответ: 4.
25. Решите уравнение:
Решение:
Значит,
Ответ: -0,2.
Если вы хотите разобрать большее количество примеров – записывайтесь на курсы подготовки к ЕГЭ по математике онлайн
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Корни и степени» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023

