Как найти коридор ошибок

1. Расчет и статистическая оценка параметров градуировочного графика

В
большинстве инструментальных методов
анализа непосредственному измерению
подвергается некоторая физическая
величина, функционально связанная с
содержанием (концентрацией или
количеством) определяемого вещества.
В качестве примера можно назвать
потенциал электрода в ионометрии,
оптическую плотность в фотометрии,
площадь пика в газовой хроматографии
и т.п.

Зависимость
аналитического сигнала от содержания
определяемого вещества (градуировочная
функция) устанавливается опытным или
расчетным путем и выражается в виде
таблиц, графиков или формул. Иногда
градуировочный график может представлять
собой зависимость между преобразованными
величинами аналитического сигнала и
определяемого содержания для того,
чтобы получить линейную зависимость
вида:

y = bx + a,

где y
– измеряемая величина; x
– концентрация (количество) определяемого
вещества или элемента; b
– угловой коэффициент линейной зависимости;
a
– свободный член.

Для
использования приведенной функции в
целях количественного анализа, т.е. для
определения конкретной величины x
по измеренному значению y,
необходимо заранее найти числовые
значения констант b
и a,
т.е. провести калибровку. Если калибровка
проведена и значения констант установлены,
величину x_i
находят по измеренному значению y_i:

x_i
= 1/b y_i
–
a/b.

Числовые
значения коэффициентов, входящих в
уравнения (). Графический метод вычисления
коэффициентов более прост и во многих
случаях дает вполне удовлетворительные
результаты, но он менее точен. Наилучшие
результаты дает использование метода
наименьших квадратов и элементов
математической статистики.

Коэффициенты
b
и a
рассчитывают по экспериментально
измеренным значениям переменной y
для заданных значений аргумента x
с использованием следующих формул:

,

,

Коэффициенты
рассчитываются на основании измерений,
проведенных в m экспериментальных точках
(m>2).

Если
полученные значения коэффициентов a
и b
использовать для вычисления значений
y
по заданным значениям аргумента x,
то вычисленные значения y, обозначаемые
Y₁,
Y₂,
… Y_n,
будут отличаться от измеренных. Разброс
значений y_i
относительно Y_i
характеризует величина дисперсии
адекватности s₀²,
которую вычисляют по формуле:

Дисперсии
s_a²
и s_b²,
связанные с вычислением коэффициентов
a и b, вычисляют по формулам

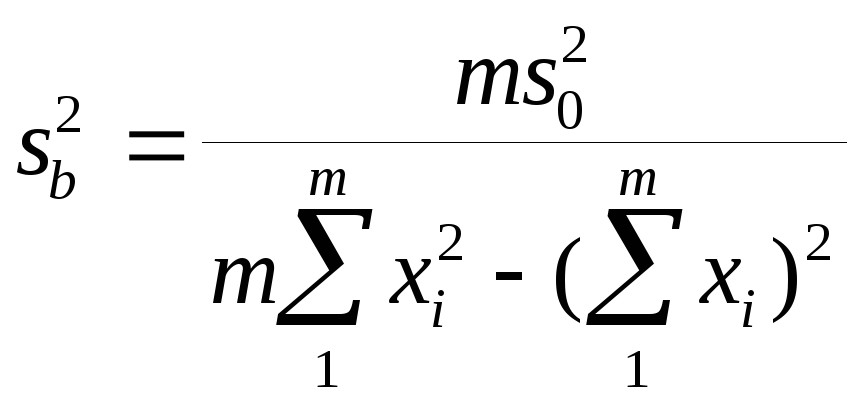
при числе степеней
свободы f = m-2.

Стандартные
отклонения s_b
и s_a
и величины b
и a,
необходимые для оценки доверительных
интервалов констант, рассчитываются
по уравнениям

s_b=s_b²;
s_a=s_a²

b =
t(P;F)s_b
и a
= t(P;F)s_a.

1. Коридор ошибок

Значимость
отклонений экспериментальных точек
можно оценить, построив доверительные
границы y
рассеяния величины y. Если известно
уравнение теоретической прямой y
= bx+a,
то 95% границы y
можно
определить, проведя две линии, параллельные
прямой, на расстоянии от нее по оси
ординат, равном 1.96s_y.
На практике прямую проводят согласно
статистическим оценкам коэффициентов
a и b. В этом случае области допустимых
значений (так называемые коридоры
ошибок) строят по МНК на основании
расчетов по следующей формуле:

n_j
– число вариант, использованных для
определения y_j.

Формула
() – уравнение двух гипербол, внутри
которых находится область допустимых
значений y. Размер этой области определяется
не только, числом точек m, значением
дисперсии адекватности и доверительной
вероятностью (через коэффициент Стьюдента
t), но зависит от того, насколько исследуемое
значение аргумента x удалено от среднего
значения x. Вблизи значений x_i
=
x мы имеем наиболее узкие доверительные
интервалы рассеяния точек, а именно
y=
t(P;F)s₀/m.
Наоборот,
крайние точки на прямой при одном и том
же значении доверительной вероятности
будут испытывать в эксперименте
наибольшее случайное рассеяние. Поэтому
для градуировки методов измерений,
удовлетворяющих условиям линейности,
экспериментальным точкам, расположенным
на концах рабочего интервала следует
придавать больший статистический вес,
т.е. число параллельных измерений в
крайних точках должно быть больше, чем
в точках, лежащих ближе к центру графика.
При возможности проведения достаточного
числа параллельных измерений в каждой
из экспериментальных точек следует
уменьшать число измерений вблизи центра
прямой и увеличивать его на концах
прямой.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Проверка адекватности регрессионной модели и значимости показателей тесноты корреляционной связи

Информация, содержащаяся в эмпирических данных, извлекается с большей полнотой, чем полученная традиционными методами описательной статистики, и, что самое важное, может быть представлена с разных точек зрения. Тем самым перед исследователем открывается обширная область для теоретических выводов, формирования новых представлений и гипотез.

Особое внимание необходимо обратить на интерпретацию и оценку параметров уравнения. Параметры уравнения регрессии следует проверить на их значимость.

Для того чтобы получить оценку значимости коэффициентов регрессии при линейной зависимости у от х, и х₂, используют t-кри- терий Стьюдента.

Значимость коэффициентов линейного уравнения регрессии а₀ и а_х оценивается с помощью ^-критерия Стьюдента (п /_табл с уровнем значимости 0,05 и числом степеней свободы (п-т- 1).

Уравнение признают окончательным и применяют в качестве модели изучаемого показателя для последующего анализа в том случае, если в данном уравнении все коэффициенты регрессии значимы.

Показатели множественной регрессии и корреляции могут оказаться подверженными действию случайных факторов, поэтому только после проверки адекватности уравнения оно может быть пригодно.

Прежде всего, следует установить, соответствуют ли полученные данные тем гипотетическим представлениям, которые сложились в результате анализа, и показывают ли они причинно-следственные связи, которые ожидались. Для оценки адекватности модели можно вычислить отклонение теоретических данных от эмпирических, остаточную дисперсию, а также ошибку аппроксимации, которая определяется по формуле:

1) для однофакторной регрессионной модели:

2) для многофакторной регрессионной модели:

Общая оценка адекватности уравнения может быть получена с помощью дисперсионного F-критерия Фишера, на основании которого проводят проверку значимости регрессии:

1) для однофакторной регрессионной модели:

где т — число параметров в уравнении регрессии; п — число единиц наблюдения;

2) для многофакторной регрессионной модели:

Распределение Фишера [Рональд Фишер (1890—1968) — английский ученый] — двухпараметрическое распределение неотрицательной случайной величины, являющейся в частном случае, при т= 1, квадратом случайной величины, распределенной по Стьюденту. Для распределения Фишера имеются таблицы критических значений, зависящих от чисел степеней свободы т и п- т — I, при различных уровнях значимости.

Считается, что влияние факторного признака статистически существенно, для принятого уровня значимости 0,05 или 0,01, если F_p (расчетное) > F_T (табличное), то влияние факторного признака считается существенным и данное уравнение регрессии будет статистически значимым.

F_T зависит от трех параметров:

• 1) определяет достоверность выводов (называется уровнем значимости). Для социологических и экономических задач F_T — 0,05 — определяет вероятность отвергнуть правильную гипотезу в 5 случаях из 100;
• 2) определяется количеством значений факторного признака
• (т-1);
• 3) определяется объемом выборки, уменьшенным на количество значений факторного признака (п — т).

F_T определяется по таблице критических значений критерия Фишера.

Вернемся к примеру 10.1.

Проведем оценку адекватности регрессионной модели:

выражающей зависимость между производительностью труда и выполнением плана реализации, с помощью F-критерия Фишера:

Эмпирическое значение Fбольше табличного, следовательно, уравнение регрессии можно признать адекватным.

Оценим значимость параметров уравнения регрессии с помощью /-критерия Стьюдента:

Табличное значение /-критерия с уровнем значимости 0,05 и числом степеней свободы (п — 2) равно 2,307. Так как /_эмп > /_табл, то параметры уравнения регрессии признаются значимыми.

Значимость коэффициента корреляции оценим с помощью /-критерия Стьюдента по формуле

Эмпирическое значение / больше табличного, следовательно, коэффициент корреляции можно признать значимым.

Вычислим ошибку аппроксимации по формуле

На основании данных расчетов можно сделать заключение, что построенная регрессионная модель зависимости производительности труда от выполнения плана реализации может быть использована для анализа и прогноза.

Итак, в общем виде многообразие видов регрессионных моделей порождается формой связи изучаемых признаков (линейной или нелинейной) и представлениями о распределении остатков (ошибки, шума) модели. Кроме того, модели более высокого уровня включают не одно, а систему регрессионных уравнений. Поиск решений для множества моделей приводит исследователя к задаче преобразования этих моделей и получения форм с хорошо известными и реализуемыми алгоритмами оценивания, как, например, в описанном выше случае с нелинейными моделями. Реформирование моделей производится при помощи трансформационных изменений переменных (отклика предикторов) или введением особых ограничений на признаковые или параметрические значения.

Благодаря своей разработанности и гибкости метод регрессионного анализа в настоящее время широко распространен в аналитической практике. Он становится также неотъемлемой частью или обычным логическим дополнением многих методов многомерной статистики в факторном, дискриминантном анализе, методе канонических корреляций, многомерном шкалировании, кластерном анализе и т. д.

Дальнейшее развитие теории регрессионного анализа, прежде всего, видится в разработке новых нелинейных форм, позволяющих с высокой степенью адекватности описывать реальные процессы, расклассификации многочисленных регрессионных моделей и методов их решения, ориентированной на конкретные группы исследовательских задач, определении перспектив использования регрессионного анализа в сочетании с другими методами статистического анализа.

Пример 10.3. По территории регионов имеются следующие данные:

Прожиточный min в день одного трудоспособного, руб.

Среднедневная заработная плата, руб.

Простая линейная регрессия в EXCEL

history 26 января 2019 г.

Группы статей
• Статистический анализ

Регрессия позволяет прогнозировать зависимую переменную на основании значений фактора. В MS EXCEL имеется множество функций, которые возвращают не только наклон и сдвиг линии регрессии, характеризующей линейную взаимосвязь между факторами, но и регрессионную статистику. Здесь рассмотрим простую линейную регрессию, т.е. прогнозирование на основе одного фактора.

Disclaimer : Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей Регрессионного анализа. Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения Регрессии – плохая идея.

Статья про Регрессионный анализ получилась большая, поэтому ниже для удобства приведены ее разделы:

Примечание : Если прогнозирование переменной осуществляется на основе нескольких факторов, то имеет место множественная регрессия .

Чтобы разобраться, чем может помочь MS EXCEL при проведении регрессионного анализа, напомним вкратце теорию, введем термины и обозначения, которые могут отличаться в зависимости от различных источников.

Примечание : Для тех, кому некогда, незачем или просто не хочется разбираться в теоретических выкладках предлагается сразу перейти к вычислительной части — оценке неизвестных параметров линейной модели .

Немного теории и основные понятия

Пусть у нас есть массив данных, представляющий собой значения двух переменных Х и Y. Причем значения переменной Х мы можем произвольно задавать (контролировать) и использовать эту переменную для предсказания значений зависимой переменной Y. Таким образом, случайной величиной является только переменная Y.

Примером такой задачи может быть производственный процесс изготовления некого волокна, причем прочность этого волокна (Y) зависит только от рабочей температуры процесса в реакторе (Х), которая задается оператором.

Построим диаграмму рассеяния (см. файл примера лист Линейный ), созданию которой посвящена отдельная статья . Вообще, построение диаграммы рассеяния для целей регрессионного анализа де-факто является стандартом.

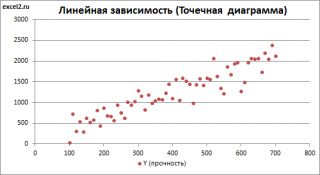
СОВЕТ : Подробнее о построении различных типов диаграмм см. статьи Основы построения диаграмм и Основные типы диаграмм .

Приведенная выше диаграмма рассеяния свидетельствует о возможной линейной взаимосвязи между Y от Х: очевидно, что точки данных в основном располагаются вдоль прямой линии.

Примечание : Наличие даже такой очевидной линейной взаимосвязи не может являться доказательством о наличии причинной взаимосвязи переменных. Наличие причинной взаимосвязи не может быть доказано на основании только анализа имеющихся измерений, а должно быть обосновано с помощью других исследований, например теоретических выкладок.

Примечание : Как известно, уравнение прямой линии имеет вид Y = m * X + k , где коэффициент m отвечает за наклон линии ( slope ), k – за сдвиг линии по вертикали ( intercept ), k равно значению Y при Х=0.

Предположим, что мы можем зафиксировать переменную Х ( рабочую температуру процесса ) при некотором значении Х _i и произвести несколько наблюдений переменной Y ( прочность нити ). Очевидно, что при одном и том же значении Хi мы получим различные значения Y. Это обусловлено влиянием других факторов на Y. Например, локальные колебания давления в реакторе, концентрации раствора, наличие ошибок измерения и др. Предполагается, что воздействие этих факторов имеет случайную природу и для каждого измерения имеются одинаковые условия проведения эксперимента (т.е. другие факторы не изменяются).

Полученные значения Y, при заданном Хi, будут колебаться вокруг некого значения . При увеличении количества измерений, среднее этих измерений, будет стремиться к математическому ожиданию случайной величины Y (при Х _i ) равному μy(i)=Е(Y _i ).

Подобные рассуждения можно привести для любого значения Хi.

Чтобы двинуться дальше, воспользуемся материалом из раздела Проверка статистических гипотез . В статье о проверке гипотезы о среднем значении генеральной совокупности в качестве нулевой гипотезы предполагалось равенство неизвестного значения μ заданному μ0.

В нашем случае простой линейной регрессии в качестве нулевой гипотезы предположим, что между переменными μy(i) и Хi существует линейная взаимосвязь μ _y(i) =α* Х _i +β. Уравнение μ _y(i) =α* Х _i +β можно переписать в обобщенном виде (для всех Х и μ _y ) как μ _y =α* Х +β.

Для наглядности проведем прямую линию соединяющую все μy(i).

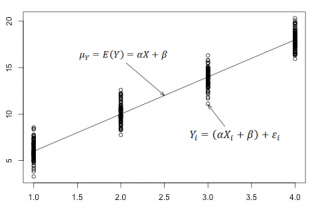
Данная линия называется регрессионной линией генеральной совокупности (population regression line), параметры которой ( наклон a и сдвиг β ) нам не известны (по аналогии с гипотезой о среднем значении генеральной совокупности , где нам было неизвестно истинное значение μ).

Теперь сделаем переход от нашего предположения, что μy=a* Х + β , к предсказанию значения случайной переменной Y в зависимости от значения контролируемой переменной Х. Для этого уравнение связи двух переменных запишем в виде Y=a*X+β+ε, где ε — случайная ошибка, которая отражает суммарный эффект влияния других факторов на Y (эти «другие» факторы не участвуют в нашей модели). Напомним, что т.к. переменная Х фиксирована, то ошибка ε определяется только свойствами переменной Y.

Уравнение Y=a*X+b+ε называют линейной регрессионной моделью . Часто Х еще называют независимой переменной (еще предиктором и регрессором , английский термин predictor , regressor ), а Y – зависимой (или объясняемой , response variable ). Так как регрессор у нас один, то такая модель называется простой линейной регрессионной моделью ( simple linear regression model ). α часто называют коэффициентом регрессии.

Предположения линейной регрессионной модели перечислены в следующем разделе.

Предположения линейной регрессионной модели

Чтобы модель линейной регрессии Yi=a*Xi+β+ε _i была адекватной — требуется:

• Ошибки ε _i должны быть независимыми переменными;
• При каждом значении Xi ошибки ε _i должны быть иметь нормальное распределение (также предполагается равенство нулю математического ожидания, т.е. Е[ε _i ]=0);
• При каждом значении Xi ошибки ε _i должны иметь равные дисперсии (обозначим ее σ 2 ).

Примечание : Последнее условие называется гомоскедастичность — стабильность, гомогенность дисперсии случайной ошибки e. Т.е. дисперсия ошибки σ 2 не должна зависеть от значения Xi.

Используя предположение о равенстве математического ожидания Е[ε _i ]=0 покажем, что μy(i)=Е[Yi]:

Е[Yi]= Е[a*Xi+β+ε _i ]= Е[a*Xi+β]+ Е[ε _i ]= a*Xi+β= μy(i), т.к. a, Xi и β постоянные значения.

Дисперсия случайной переменной Y равна дисперсии ошибки ε, т.е. VAR(Y)= VAR(ε)=σ 2 . Это является следствием, что все значения переменной Х являются const, а VAR(ε)=VAR(ε _i ).

Задачи регрессионного анализа

Для проверки гипотезы о линейной взаимосвязи переменной Y от X делают выборку из генеральной совокупности (этой совокупности соответствует регрессионная линия генеральной совокупности , т.е. μy=a* Х +β). Выборка будет состоять из n точек, т.е. из n пар значений .

На основании этой выборки мы можем вычислить оценки наклона a и сдвига β, которые обозначим соответственно a и b . Также часто используются обозначения â и b̂.

Далее, используя эти оценки, мы также можем проверить гипотезу: имеется ли линейная связь между X и Y статистически значимой?

Первая задача регрессионного анализа – оценка неизвестных параметров ( estimation of the unknown parameters ). Подробнее см. раздел Оценки неизвестных параметров модели .

Вторая задача регрессионного анализа – Проверка адекватности модели ( model adequacy checking ).

Примечание : Оценки параметров модели обычно вычисляются методом наименьших квадратов (МНК), которому посвящена отдельная статья .

Оценка неизвестных параметров линейной модели (используя функции MS EXCEL)

Неизвестные параметры простой линейной регрессионной модели Y=a*X+β+ε оценим с помощью метода наименьших квадратов (в статье про МНК подробно описано этот метод ).

Для вычисления параметров линейной модели методом МНК получены следующие выражения:

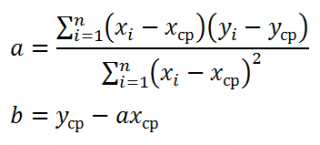
Таким образом, мы получим уравнение прямой линии Y= a *X+ b , которая наилучшим образом аппроксимирует имеющиеся данные.

Примечание : В статье про метод наименьших квадратов рассмотрены случаи аппроксимации линейной и квадратичной функцией , а также степенной , логарифмической и экспоненциальной функцией .

Оценку параметров в MS EXCEL можно выполнить различными способами:

Сначала рассмотрим функции НАКЛОН() , ОТРЕЗОК() и ЛИНЕЙН() .

Пусть значения Х и Y находятся соответственно в диапазонах C 23: C 83 и B 23: B 83 (см. файл примера внизу статьи).

Примечание : Значения двух переменных Х и Y можно сгенерировать, задав тренд и величину случайного разброса (см. статью Генерация данных для линейной регрессии в MS EXCEL ).

В MS EXCEL наклон прямой линии а ( оценку коэффициента регрессии ), можно найти по методу МНК с помощью функции НАКЛОН() , а сдвиг b ( оценку постоянного члена или константы регрессии ), с помощью функции ОТРЕЗОК() . В английской версии это функции SLOPE и INTERCEPT соответственно.

Аналогичный результат можно получить с помощью функции ЛИНЕЙН() , английская версия LINEST (см. статью об этой функции ).

Формула =ЛИНЕЙН(C23:C83;B23:B83) вернет наклон а . А формула = ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2) — сдвиг b . Здесь требуются пояснения.

Функция ЛИНЕЙН() имеет 4 аргумента и возвращает целый массив значений:

ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])

Если 4-й аргумент статистика имеет значение ЛОЖЬ или опущен, то функция ЛИНЕЙН() возвращает только оценки параметров модели: a и b .

Примечание : Остальные значения, возвращаемые функцией ЛИНЕЙН() , нам потребуются при вычислении стандартных ошибок и для проверки значимости регрессии . В этом случае аргумент статистика должен иметь значение ИСТИНА.

Чтобы вывести сразу обе оценки:

• в одной строке необходимо выделить 2 ячейки,
• ввести формулу в Строке формул
• нажать CTRL+SHIFT+ENTER (см. статью про формулы массива ).

Если в Строке формул выделить формулу = ЛИНЕЙН(C23:C83;B23:B83) и нажать клавишу F9 , то мы увидим что-то типа <3,01279389265416;154,240057900613>. Это как раз значения a и b . Как видно, оба значения разделены точкой с запятой «;», что свидетельствует, что функция вернула значения «в нескольких ячейках одной строки».

Если требуется вывести параметры линии не в одной строке, а одном столбце (ячейки друг под другом), то используйте формулу = ТРАНСП(ЛИНЕЙН(C23:C83;B23:B83)) . При этом выделять нужно 2 ячейки в одном столбце. Если теперь выделить новую формулу и нажать клавишу F9, то мы увидим что 2 значения разделены двоеточием «:», что означает, что значения выведены в столбец (функция ТРАНСП() транспонировала строку в столбец ).

Чтобы разобраться в этом подробнее необходимо ознакомиться с формулами массива .

Чтобы не связываться с вводом формул массива , можно использовать функцию ИНДЕКС() . Формула = ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);1) или просто ЛИНЕЙН(C23:C83;B23:B83) вернет параметр, отвечающий за наклон линии, т.е. а . Формула =ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2) вернет параметр b .

Оценка неизвестных параметров линейной модели (через статистики выборок)

Наклон линии, т.е. коэффициент а , можно также вычислить через коэффициент корреляции и стандартные отклонения выборок :

= КОРРЕЛ(B23:B83;C23:C83) *(СТАНДОТКЛОН.В(C23:C83)/ СТАНДОТКЛОН.В(B23:B83))

Вышеуказанная формула математически эквивалентна отношению ковариации выборок Х и Y и дисперсии выборки Х:

И, наконец, запишем еще одну формулу для нахождения сдвига b . Воспользуемся тем фактом, что линия регрессии проходит через точку средних значений переменных Х и Y.

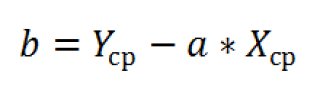
Вычислив средние значения и подставив в формулу ранее найденный наклон а , получим сдвиг b .

Оценка неизвестных параметров линейной модели (матричная форма)

Также параметры линии регрессии можно найти в матричной форме (см. файл примера лист Матричная форма ).

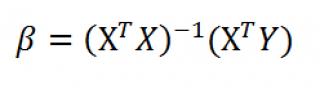
В формуле символом β обозначен столбец с искомыми параметрами модели: β0 (сдвиг b ), β1 (наклон a ).

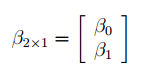
Матрица Х равна:

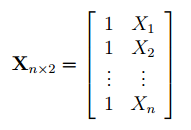
Матрица Х называется регрессионной матрицей или матрицей плана . Она состоит из 2-х столбцов и n строк, где n – количество точек данных. Первый столбец — столбец единиц, второй – значения переменной Х.

Матрица Х T – это транспонированная матрица Х . Она состоит соответственно из n столбцов и 2-х строк.

В формуле символом Y обозначен столбец значений переменной Y.

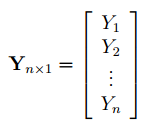
Чтобы перемножить матрицы используйте функцию МУМНОЖ() . Чтобы найти обратную матрицу используйте функцию МОБР() .

Пусть дан массив значений переменных Х и Y (n=10, т.е.10 точек).

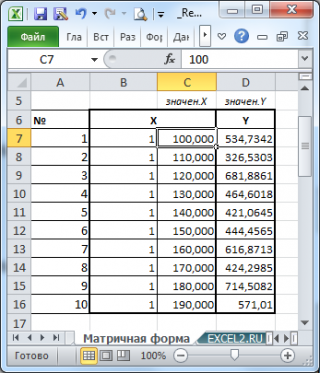
Слева от него достроим столбец с 1 для матрицы Х.

и введя ее как формулу массива в 2 ячейки, получим оценку параметров модели.

Красота применения матричной формы полностью раскрывается в случае множественной регрессии .

Построение линии регрессии

Для отображения линии регрессии построим сначала диаграмму рассеяния , на которой отобразим все точки (см. начало статьи ).

Для построения прямой линии используйте вычисленные выше оценки параметров модели a и b (т.е. вычислите у по формуле y = a * x + b ) или функцию ТЕНДЕНЦИЯ() .

Формула = ТЕНДЕНЦИЯ($C$23:$C$83;$B$23:$B$83;B23) возвращает расчетные (прогнозные) значения ŷi для заданного значения Хi из столбца В2 .

Примечание : Линию регрессии можно также построить с помощью функции ПРЕДСКАЗ() . Эта функция возвращает прогнозные значения ŷi, но, в отличие от функции ТЕНДЕНЦИЯ() работает только в случае одного регрессора. Функция ТЕНДЕНЦИЯ() может быть использована и в случае множественной регрессии (в этом случае 3-й аргумент функции должен быть ссылкой на диапазон, содержащий все значения Хi для выбранного наблюдения i).

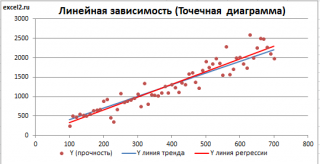
Как видно из диаграммы выше линия тренда и линия регрессии не обязательно совпадают: отклонения точек от линии тренда случайны, а МНК лишь подбирает линию наиболее точно аппроксимирующую случайные точки данных.

Линию регрессии можно построить и с помощью встроенных средств диаграммы, т.е. с помощью инструмента Линия тренда. Для этого выделите диаграмму, в меню выберите вкладку Макет , в группе Анализ нажмите Линия тренда , затем Линейное приближение. В диалоговом окне установите галочку Показывать уравнение на диаграмме (подробнее см. в статье про МНК ).

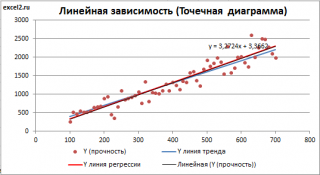
Построенная таким образом линия, разумеется, должна совпасть с ранее построенной нами линией регрессии, а параметры уравнения a и b должны совпасть с параметрами уравнения отображенными на диаграмме.

Примечание: Для того, чтобы вычисленные параметры уравнения a и b совпадали с параметрами уравнения на диаграмме, необходимо, чтобы тип у диаграммы был Точечная, а не График , т.к. тип диаграммы График не использует значения Х, а вместо значений Х используется последовательность 1; 2; 3; . Именно эти значения и берутся при расчете параметров линии тренда . Убедиться в этом можно если построить диаграмму График (см. файл примера ), а значения Хнач и Хшаг установить равным 1. Только в этом случае параметры уравнения на диаграмме совпадут с a и b .

Коэффициент детерминации R 2

Коэффициент детерминации R 2 показывает насколько полезна построенная нами линейная регрессионная модель .

Предположим, что у нас есть n значений переменной Y и мы хотим предсказать значение yi, но без использования значений переменной Х (т.е. без построения регрессионной модели ). Очевидно, что лучшей оценкой для yi будет среднее значение ȳ. Соответственно, ошибка предсказания будет равна (yi — ȳ).

Примечание : Далее будет использована терминология и обозначения дисперсионного анализа .

После построения регрессионной модели для предсказания значения yi мы будем использовать значение ŷi=a*xi+b. Ошибка предсказания теперь будет равна (yi — ŷi).

Теперь с помощью диаграммы сравним ошибки предсказания полученные без построения модели и с помощью модели.

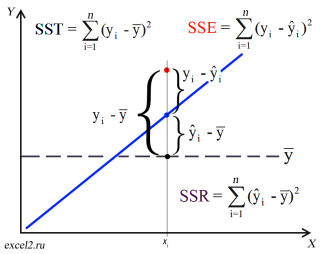
Очевидно, что используя регрессионную модель мы уменьшили первоначальную (полную) ошибку (yi — ȳ) на значение (ŷi — ȳ) до величины (yi — ŷi).

(yi — ŷi) – это оставшаяся, необъясненная ошибка.

Очевидно, что все три ошибки связаны выражением:

(yi — ȳ)= (ŷi — ȳ) + (yi — ŷi)

Можно показать, что в общем виде справедливо следующее выражение:

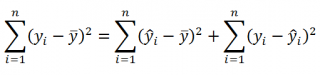
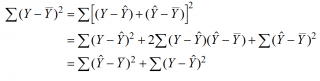
или в других, общепринятых в зарубежной литературе, обозначениях:

Total Sum of Squares = Regression Sum of Squares + Error Sum of Squares

Примечание : SS — Sum of Squares — Сумма Квадратов.

Как видно из формулы величины SST, SSR, SSE имеют размерность дисперсии (вариации) и соответственно описывают разброс (изменчивость): Общую изменчивость (Total variation), Изменчивость объясненную моделью (Explained variation) и Необъясненную изменчивость (Unexplained variation).

По определению коэффициент детерминации R 2 равен:

R 2 = Изменчивость объясненная моделью / Общая изменчивость.

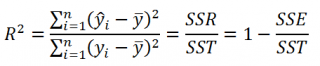
Этот показатель равен квадрату коэффициента корреляции и в MS EXCEL его можно вычислить с помощью функции КВПИРСОН() или ЛИНЕЙН() :

R ₂ принимает значения от 0 до 1 (1 соответствует идеальной линейной зависимости Y от Х). Однако, на практике малые значения R2 вовсе не обязательно указывают, что переменную Х нельзя использовать для прогнозирования переменной Y. Малые значения R2 могут указывать на нелинейность связи или на то, что поведение переменной Y объясняется не только Х, но и другими факторами.

Стандартная ошибка регрессии

Стандартная ошибка регрессии ( Standard Error of a regression ) показывает насколько велика ошибка предсказания значений переменной Y на основании значений Х. Отдельные значения Yi мы можем предсказывать лишь с точностью +/- несколько значений (обычно 2-3, в зависимости от формы распределения ошибки ε).

Теперь вспомним уравнение линейной регрессионной модели Y=a*X+β+ε. Ошибка ε имеет случайную природу, т.е. является случайной величиной и поэтому имеет свою функцию распределения со средним значением μ и дисперсией σ 2 .

Оценив значение дисперсии σ 2 и вычислив из нее квадратный корень – получим Стандартную ошибку регрессии. Чем точки наблюдений на диаграмме рассеяния ближе находятся к прямой линии, тем меньше Стандартная ошибка.

Примечание : Вспомним , что при построении модели предполагается, что среднее значение ошибки ε равно 0, т.е. E[ε]=0.

Оценим дисперсию σ 2 . Помимо вычисления Стандартной ошибки регрессии эта оценка нам потребуется в дальнейшем еще и при построении доверительных интервалов для оценки параметров регрессии a и b .

Для оценки дисперсии ошибки ε используем остатки регрессии — разности между имеющимися значениями yi и значениями, предсказанными регрессионной моделью ŷ. Чем лучше регрессионная модель согласуется с данными (точки располагается близко к прямой линии), тем меньше величина остатков.

Для оценки дисперсии σ 2 используют следующую формулу:

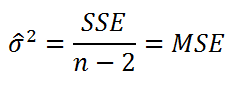
где SSE – сумма квадратов значений ошибок модели ε _i =yi — ŷi ( Sum of Squared Errors ).

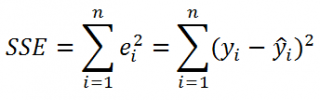
SSE часто обозначают и как SSres – сумма квадратов остатков ( Sum of Squared residuals ).

Оценка дисперсии s 2 также имеет общепринятое обозначение MSE (Mean Square of Errors), т.е. среднее квадратов ошибок или MSRES (Mean Square of Residuals), т.е. среднее квадратов остатков . Хотя правильнее говорить сумме квадратов остатков, т.к. ошибка чаще ассоциируется с ошибкой модели ε, которая является непрерывной случайной величиной. Но, здесь мы будем использовать термины SSE и MSE, предполагая, что речь идет об остатках.

Примечание : Напомним, что когда мы использовали МНК для нахождения параметров модели, то критерием оптимизации была минимизация именно SSE (SSres). Это выражение представляет собой сумму квадратов расстояний между наблюденными значениями yi и предсказанными моделью значениями ŷi, которые лежат на линии регрессии.

Математическое ожидание случайной величины MSE равно дисперсии ошибки ε, т.е. σ 2 .

Чтобы понять почему SSE выбрана в качестве основы для оценки дисперсии ошибки ε, вспомним, что σ 2 является также дисперсией случайной величины Y (относительно среднего значения μy, при заданном значении Хi). А т.к. оценкой μy является значение ŷi = a * Хi + b (значение уравнения регрессии при Х= Хi), то логично использовать именно SSE в качестве основы для оценки дисперсии σ 2 . Затем SSE усредняется на количество точек данных n за вычетом числа 2. Величина n-2 – это количество степеней свободы ( df – degrees of freedom ), т.е. число параметров системы, которые могут изменяться независимо (вспомним, что у нас в этом примере есть n независимых наблюдений переменной Y). В случае простой линейной регрессии число степеней свободы равно n-2, т.к. при построении линии регрессии было оценено 2 параметра модели (на это было «потрачено» 2 степени свободы ).

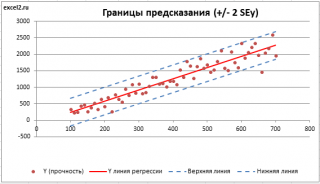
Итак, как сказано было выше, квадратный корень из s 2 имеет специальное название Стандартная ошибка регрессии ( Standard Error of a regression ) и обозначается SEy. SEy показывает насколько велика ошибка предсказания. Отдельные значения Y мы можем предсказывать с точностью +/- несколько значений SEy (см. этот раздел ). Если ошибки предсказания ε имеют нормальное распределение , то примерно 2/3 всех предсказанных значений будут на расстоянии не больше SEy от линии регрессии . SEy имеет размерность переменной Y и откладывается по вертикали. Часто на диаграмме рассеяния строят границы предсказания соответствующие +/- 2 SEy (т.е. 95% точек данных будут располагаться в пределах этих границ).

В MS EXCEL стандартную ошибку SEy можно вычислить непосредственно по формуле:

= КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))

или с помощью функции ЛИНЕЙН() :

Примечание : Подробнее о функции ЛИНЕЙН() см. эту статью .

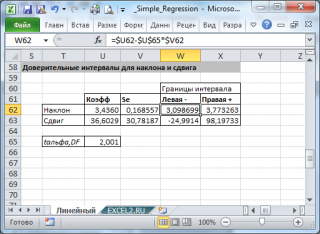
Стандартные ошибки и доверительные интервалы для наклона и сдвига

В разделе Оценка неизвестных параметров линейной модели мы получили точечные оценки наклона а и сдвига b . Так как эти оценки получены на основе случайных величин (значений переменных Х и Y), то эти оценки сами являются случайными величинами и соответственно имеют функцию распределения со средним значением и дисперсией . Но, чтобы перейти от точечных оценок к интервальным , необходимо вычислить соответствующие стандартные ошибки (т.е. стандартные отклонения ).

Стандартная ошибка коэффициента регрессии a вычисляется на основании стандартной ошибки регрессии по следующей формуле:

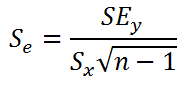
где Sx – стандартное отклонение величины х, вычисляемое по формуле:

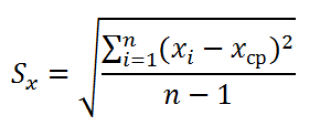
где Sey – стандартная ошибка регрессии, т.е. ошибка предсказания значения переменой Y ( см. выше ).

В MS EXCEL стандартную ошибку коэффициента регрессии Se можно вычислить впрямую по вышеуказанной формуле:

= КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))/ СТАНДОТКЛОН.В(B23:B83) /КОРЕНЬ(СЧЁТ(B23:B83) -1)

или с помощью функции ЛИНЕЙН() :

Формулы приведены в файле примера на листе Линейный в разделе Регрессионная статистика .

Примечание : Подробнее о функции ЛИНЕЙН() см. эту статью .

При построении двухстороннего доверительного интервала для коэффициента регрессии его границы определяются следующим образом:

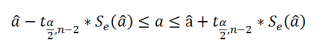
где — квантиль распределения Стьюдента с n-2 степенями свободы. Величина а с «крышкой» является другим обозначением наклона а .

Например для уровня значимости альфа=0,05, можно вычислить с помощью формулы =СТЬЮДЕНТ.ОБР.2Х(0,05;n-2)

Вышеуказанная формула следует из того факта, что если ошибки регрессии распределены нормально и независимо, то выборочное распределение случайной величины

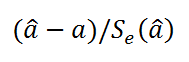
является t-распределением Стьюдента с n-2 степенью свободы (то же справедливо и для наклона b ).

Примечание : Подробнее о построении доверительных интервалов в MS EXCEL можно прочитать в этой статье Доверительные интервалы в MS EXCEL .

В результате получим, что найденный доверительный интервал с вероятностью 95% (1-0,05) накроет истинное значение коэффициента регрессии. Здесь мы считаем, что коэффициент регрессии a имеет распределение Стьюдента с n-2 степенями свободы (n – количество наблюдений, т.е. пар Х и Y).

Примечание : Подробнее о построении доверительных интервалов с использованием t-распределения см. статью про построение доверительных интервалов для среднего .

Стандартная ошибка сдвига b вычисляется по следующей формуле:

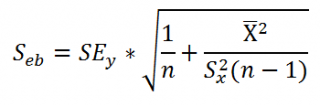
В MS EXCEL стандартную ошибку сдвига Seb можно вычислить с помощью функции ЛИНЕЙН() :

При построении двухстороннего доверительного интервала для сдвига его границы определяются аналогичным образом как для наклона : b +/- t*Seb.

Проверка значимости взаимосвязи переменных

Когда мы строим модель Y=αX+β+ε мы предполагаем, что между Y и X существует линейная взаимосвязь. Однако, как это иногда бывает в статистике, можно вычислять параметры связи даже тогда, когда в действительности она не существует, и обусловлена лишь случайностью.

Единственный вариант, когда Y не зависит X (в рамках модели Y=αX+β+ε), возможен, когда коэффициент регрессии a равен 0.

Чтобы убедиться, что вычисленная нами оценка наклона прямой линии не обусловлена лишь случайностью (не случайно отлична от 0), используют проверку гипотез . В качестве нулевой гипотезы Н ₀ принимают, что связи нет, т.е. a=0. В качестве альтернативной гипотезы Н ₁ принимают, что a <>0.

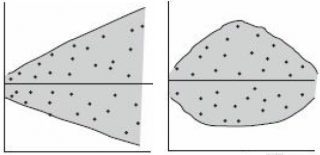
Ниже на рисунках показаны 2 ситуации, когда нулевую гипотезу Н ₀ не удается отвергнуть.

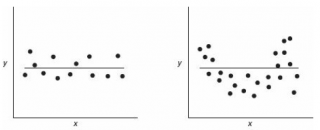
На левой картинке отсутствует любая зависимость между переменными, на правой – связь между ними нелинейная, но при этом коэффициент линейной корреляции равен 0.

Ниже — 2 ситуации, когда нулевая гипотеза Н ₀ отвергается.

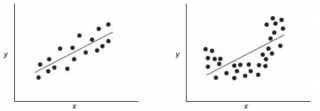
На левой картинке очевидна линейная зависимость, на правой — зависимость нелинейная, но коэффициент корреляции не равен 0 (метод МНК вычисляет показатели наклона и сдвига просто на основании значений выборки).

Для проверки гипотезы нам потребуется:

• Установить уровень значимости , пусть альфа=0,05;
• Рассчитать с помощью функции ЛИНЕЙН() стандартное отклонение Se для коэффициента регрессии (см. предыдущий раздел );
• Рассчитать число степеней свободы: DF=n-2 или по формуле = ИНДЕКС(ЛИНЕЙН(C24:C84;B24:B84;;ИСТИНА);4;2)
• Вычислить значение тестовой статистики t ₀ =a/S _e , которая имеет распределение Стьюдента с числом степеней свободы DF=n-2;
• Сравнить значение тестовой статистики |t0| с пороговым значением t _альфа ,n-2. Если значение тестовой статистики больше порогового значения, то нулевая гипотеза отвергается ( наклон не может быть объяснен лишь случайностью при заданном уровне альфа) либо
• вычислить p-значение и сравнить его с уровнем значимости .

В файле примера приведен пример проверки гипотезы:

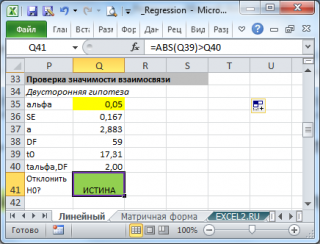
Изменяя наклон тренда k (ячейка В8 ) можно убедиться, что при малых углах тренда (например, 0,05) тест часто показывает, что связь между переменными случайна. При больших углах (k>1), тест практически всегда подтверждает значимость линейной связи между переменными.

Примечание : Проверка значимости взаимосвязи эквивалентна проверке статистической значимости коэффициента корреляции . В файле примера показана эквивалентность обоих подходов. Также проверку значимости можно провести с помощью процедуры F-тест .

Доверительные интервалы для нового наблюдения Y и среднего значения

Вычислив параметры простой линейной регрессионной модели Y=aX+β+ε мы получили точечную оценку значения нового наблюдения Y при заданном значении Хi, а именно: Ŷ= a * Хi + b

Ŷ также является точечной оценкой для среднего значения Yi при заданном Хi. Но, при построении доверительных интервалов используются различные стандартные ошибки .

Стандартная ошибка нового наблюдения Y при заданном Хi учитывает 2 источника неопределенности:

• неопределенность связанную со случайностью оценок параметров модели a и b ;
• случайность ошибки модели ε.

Учет этих неопределенностей приводит к стандартной ошибке S(Y|Xi), которая рассчитывается с учетом известного значения Xi.

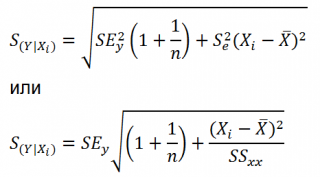
где SS _xx – сумма квадратов отклонений от среднего значений переменной Х:

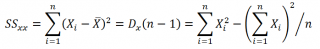
В MS EXCEL 2010 нет функции, которая бы рассчитывала эту стандартную ошибку , поэтому ее необходимо рассчитывать по вышеуказанным формулам.

Доверительный интервал или Интервал предсказания для нового наблюдения (Prediction Interval for a New Observation) построим по схеме показанной в разделе Проверка значимости взаимосвязи переменных (см. файл примера лист Интервалы ). Т.к. границы интервала зависят от значения Хi (точнее от расстояния Хi до среднего значения Х _ср ), то интервал будет постепенно расширяться при удалении от Х _ср .

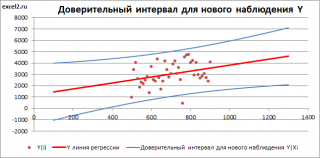
Границы доверительного интервала для нового наблюдения рассчитываются по формуле:

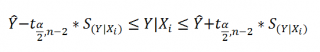
Аналогичным образом построим доверительный интервал для среднего значения Y при заданном Хi (Confidence Interval for the Mean of Y). В этом случае доверительный интервал будет уже, т.к. средние значения имеют меньшую изменчивость по сравнению с отдельными наблюдениями ( средние значения, в рамках нашей линейной модели Y=aX+β+ε, не включают ошибку ε).

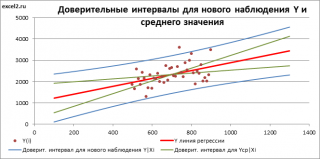
Стандартная ошибка S(Yср|Xi) вычисляется по практически аналогичным формулам как и стандартная ошибка для нового наблюдения:

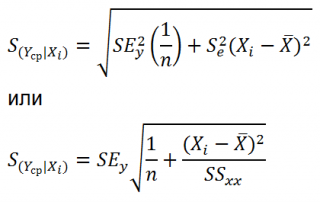
Как видно из формул, стандартная ошибка S(Yср|Xi) меньше стандартной ошибки S(Y|Xi) для индивидуального значения .

Границы доверительного интервала для среднего значения рассчитываются по формуле:

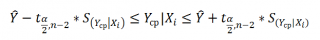
Проверка адекватности линейной регрессионной модели

Модель адекватна, когда все предположения, лежащие в ее основе, выполнены (см. раздел Предположения линейной регрессионной модели ).

Проверка адекватности модели в основном основана на исследовании остатков модели (model residuals), т.е. значений ei=yi – ŷi для каждого Хi. В рамках простой линейной модели n остатков имеют только n-2 связанных с ними степеней свободы . Следовательно, хотя, остатки не являются независимыми величинами, но при достаточно большом n это не оказывает какого-либо влияния на проверку адекватности модели.

Чтобы проверить предположение о нормальности распределения ошибок строят график проверки на нормальность (Normal probability Plot).

В файле примера на листе Адекватность построен график проверки на нормальность . В случае нормального распределения значения остатков должны быть близки к прямой линии.

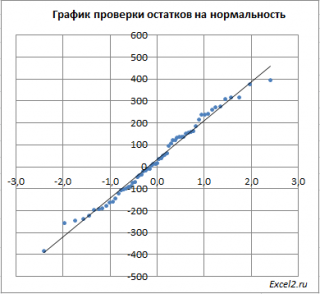
Так как значения переменной Y мы генерировали с помощью тренда , вокруг которого значения имели нормальный разброс, то ожидать сюрпризов не приходится – значения остатков располагаются вблизи прямой.

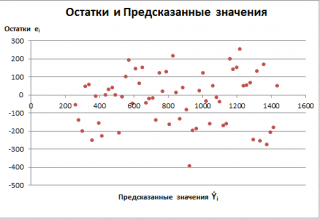
Также при проверке модели на адекватность часто строят график зависимости остатков от предсказанных значений Y. Если точки не демонстрируют характерных, так называемых «паттернов» (шаблонов) типа вор о нок или другого неравномерного распределения, в зависимости от значений Y, то у нас нет очевидных доказательств неадекватности модели.

В нашем случае точки располагаются примерно равномерно.

Часто при проверке адекватности модели вместо остатков используют нормированные остатки. Как показано в разделе Стандартная ошибка регрессии оценкой стандартного отклонения ошибок является величина SEy равная квадратному корню из величины MSE. Поэтому логично нормирование остатков проводить именно на эту величину.

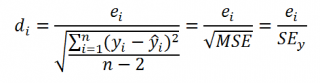
SEy можно вычислить с помощью функции ЛИНЕЙН() :

Иногда нормирование остатков производится на величину стандартного отклонения остатков (это мы увидим в статье об инструменте Регрессия , доступного в надстройке MS EXCEL Пакет анализа ), т.е. по формуле:

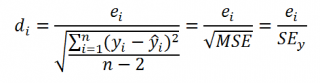
Вышеуказанное равенство приблизительное, т.к. среднее значение остатков близко, но не обязательно точно равно 0.

Что такое регрессионный анализ?

Регрессионный анализ — это набор статистических методов оценки отношений между переменными. Его можно использовать для оценки степени взаимосвязи между переменными и для моделирования будущей зависимости. По сути, регрессионные методы показывают, как по изменениям «независимых переменных» можно зафиксировать изменение «зависимой переменной».

Зависимую переменную в бизнесе называют предиктором (характеристика, за изменением которой наблюдают). Это может быть уровень продаж, риски, ценообразование, производительность и так далее. Независимые переменные — те, которые могут объяснять поведение выше приведенных факторов (время года, покупательная способность населения, место продаж и многое другое).Регрессионный анализ включает несколько моделей. Наиболее распространенные из них: линейная, мультилинейная (или множественная линейная) и нелинейная.

Как видно из названий, модели отличаются типом зависимости переменных: линейная описывается линейной функцией; мультилинейная также представляет линейную функцию, но в нее входит больше параметров (независимых переменных); нелинейная модель — та, в которой экспериментальные данные характеризуются функцией, являющейся нелинейной (показательной, логарифмической, тригонометрической и так далее).

Чаще всего используются простые линейные и мультилинейные модели.

Регрессионный анализ предлагает множество приложений в различных дисциплинах, включая финансы.

Рассмотрим поподробнее принципы построения и адаптации результатов метода.

Линейный регрессионный анализ основан на шести фундаментальных предположениях:

• Переменные показывают линейную зависимость;
• Независимая переменная не случайна;
• Значение невязки (ошибки) равно нулю;
• Значение невязки постоянно для всех наблюдений;
• Значение невязки не коррелирует по всем наблюдениям;
• Остаточные значения подчиняются нормальному распределению.

Простая линейная модель выражается с помощью следующего уравнения:

Основы линейной регрессии

Что такое регрессия?

Разместим точки на двумерном графике рассеяния и скажем, что мы имеем линейное соотношение, если данные аппроксимируются прямой линией.

Если мы полагаем, что y зависит от x, причём изменения в y вызываются именно изменениями в x, мы можем определить линию регрессии (регрессия y на x), которая лучше всего описывает прямолинейное соотношение между этими двумя переменными.

Статистическое использование слова «регрессия» исходит из явления, известного как регрессия к среднему, приписываемого сэру Френсису Гальтону (1889).

Он показал, что, хотя высокие отцы имеют тенденцию иметь высоких сыновей, средний рост сыновей меньше, чем у их высоких отцов. Средний рост сыновей «регрессировал» и «двигался вспять» к среднему росту всех отцов в популяции. Таким образом, в среднем высокие отцы имеют более низких (но всё-таки высоких) сыновей, а низкие отцы имеют сыновей более высоких (но всё-таки довольно низких).

Линия регрессии

Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:

x называется независимой переменной или предиктором.

Y – зависимая переменная или переменная отклика. Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y»

• a – свободный член (пересечение) линии оценки; это значение Y, когда x=0 (Рис.1).
• b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу.
• a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b.

Парную линейную регрессию можно расширить, включив в нее более одной независимой переменной; в этом случае она известна как множественная регрессия.

Рис.1. Линия линейной регрессии, показывающая пересечение a и угловой коэффициент b (величину возрастания Y при увеличении x на одну единицу)

Метод наименьших квадратов

Мы выполняем регрессионный анализ, используя выборку наблюдений, где a и b – выборочные оценки истинных (генеральных) параметров, α и β , которые определяют линию линейной регрессии в популяции (генеральной совокупности).

Наиболее простым методом определения коэффициентов a и b является метод наименьших квадратов (МНК).

Подгонка оценивается, рассматривая остатки (вертикальное расстояние каждой точки от линии, например, остаток = наблюдаемому y – предсказанный y, Рис. 2).

Линию лучшей подгонки выбирают так, чтобы сумма квадратов остатков была минимальной.

Рис. 2. Линия линейной регрессии с изображенными остатками (вертикальные пунктирные линии) для каждой точки.

Предположения линейной регрессии

Итак, для каждой наблюдаемой величины остаток равен разнице и соответствующего предсказанного Каждый остаток может быть положительным или отрицательным.

Можно использовать остатки для проверки следующих предположений, лежащих в основе линейной регрессии:

• Остатки нормально распределены с нулевым средним значением;

Если допущения линейности, нормальности и/или постоянной дисперсии сомнительны, мы можем преобразовать или и рассчитать новую линию регрессии, для которой эти допущения удовлетворяются (например, использовать логарифмическое преобразование или др.).

Аномальные значения (выбросы) и точки влияния

«Влиятельное» наблюдение, если оно опущено, изменяет одну или больше оценок параметров модели (т.е. угловой коэффициент или свободный член).

Выброс (наблюдение, которое противоречит большинству значений в наборе данных) может быть «влиятельным» наблюдением и может хорошо обнаруживаться визуально, при осмотре двумерной диаграммы рассеяния или графика остатков.

И для выбросов, и для «влиятельных» наблюдений (точек) используют модели, как с их включением, так и без них, обращают внимание на изменение оценки (коэффициентов регрессии).

При проведении анализа не стоит отбрасывать выбросы или точки влияния автоматически, поскольку простое игнорирование может повлиять на полученные результаты. Всегда изучайте причины появления этих выбросов и анализируйте их.

Гипотеза линейной регрессии

При построении линейной регрессии проверяется нулевая гипотеза о том, что генеральный угловой коэффициент линии регрессии β равен нулю.

Если угловой коэффициент линии равен нулю, между и нет линейного соотношения: изменение не влияет на

Для тестирования нулевой гипотезы о том, что истинный угловой коэффициент равен нулю можно воспользоваться следующим алгоритмом:

Вычислить статистику критерия, равную отношению , которая подчиняется распределению с степенями свободы, где стандартная ошибка коэффициента

,

— оценка дисперсии остатков.

Обычно если достигнутый уровень значимости нулевая гипотеза отклоняется.

Можно рассчитать 95% доверительный интервал для генерального углового коэффициента :

где процентная точка распределения со степенями свободы что дает вероятность двустороннего критерия

Это тот интервал, который содержит генеральный угловой коэффициент с вероятностью 95%.

Для больших выборок, скажем, мы можем аппроксимировать значением 1,96 (то есть статистика критерия будет стремиться к нормальному распределению)

Оценка качества линейной регрессии: коэффициент детерминации R 2

Из-за линейного соотношения и мы ожидаем, что изменяется, по мере того как изменяется , и называем это вариацией, которая обусловлена или объясняется регрессией. Остаточная вариация должна быть как можно меньше.

Если это так, то большая часть вариации будет объясняться регрессией, а точки будут лежать близко к линии регрессии, т.е. линия хорошо соответствует данным.

Долю общей дисперсии , которая объясняется регрессией называют коэффициентом детерминации, обычно выражают через процентное соотношение и обозначают R 2 (в парной линейной регрессии это величина r 2 , квадрат коэффициента корреляции), позволяет субъективно оценить качество уравнения регрессии.

Разность представляет собой процент дисперсии который нельзя объяснить регрессией.

Нет формального теста для оценки мы вынуждены положиться на субъективное суждение, чтобы определить качество подгонки линии регрессии.

Применение линии регрессии для прогноза

Можно применять регрессионную линию для прогнозирования значения по значению в пределе наблюдаемого диапазона (никогда не экстраполируйте вне этих пределов).

Мы предсказываем среднюю величину для наблюдаемых, которые имеют определенное значение путем подстановки этого значения в уравнение линии регрессии.

Итак, если прогнозируем как Используем эту предсказанную величину и ее стандартную ошибку, чтобы оценить доверительный интервал для истинной средней величины в популяции.

Повторение этой процедуры для различных величин позволяет построить доверительные границы для этой линии. Это полоса или область, которая содержит истинную линию, например, с 95% доверительной вероятностью.

Подобным образом можно рассчитать более широкую область, внутри которой, как мы ожидаем, лежит наибольшее число (обычно 95%) наблюдений.

Простые регрессионные планы

Простые регрессионные планы содержат один непрерывный предиктор. Если существует 3 наблюдения со значениями предиктора P , например, 7, 4 и 9, а план включает эффект первого порядка P , то матрица плана X будет иметь вид

а регрессионное уравнение с использованием P для X1 выглядит как

Если простой регрессионный план содержит эффект высшего порядка для P , например квадратичный эффект, то значения в столбце X1 в матрице плана будут возведены во вторую степень:

а уравнение примет вид

Y = b 0 + b 1 P 2

Сигма -ограниченные и сверхпараметризованные методы кодирования не применяются по отношению к простым регрессионным планам и другим планам, содержащим только непрерывные предикторы (поскольку, просто не существует категориальных предикторов). Независимо от выбранного метода кодирования, значения непрерывных переменных увеличиваются в соответствующей степени и используются как значения для переменных X . При этом перекодировка не выполняется. Кроме того, при описании регрессионных планов можно опустить рассмотрение матрицы плана X , а работать только с регрессионным уравнением.

Пример: простой регрессионный анализ

Этот пример использует данные, представленные в таблице:

Рис. 3. Таблица исходных данных.

Данные составлены на основе сравнения переписей 1960 и 1970 в произвольно выбранных 30 округах. Названия округов представлены в виде имен наблюдений. Информация относительно каждой переменной представлена ниже:

Рис. 4. Таблица спецификаций переменных.

Задача исследования

Для этого примера будут анализироваться корреляция уровня бедности и степень, которая предсказывает процент семей, которые находятся за чертой бедности. Следовательно мы будем трактовать переменную 3 ( Pt_Poor ) как зависимую переменную.

Можно выдвинуть гипотезу: изменение численности населения и процент семей, которые находятся за чертой бедности, связаны между собой. Кажется разумным ожидать, что бедность ведет к оттоку населения, следовательно, здесь будет отрицательная корреляция между процентом людей за чертой бедности и изменением численности населения. Следовательно мы будем трактовать переменную 1 ( Pop_Chng ) как переменную-предиктор.

Просмотр результатов

Коэффициенты регрессии

Рис. 5. Коэффициенты регрессии Pt_Poor на Pop_Chng.

На пересечении строки Pop_Chng и столбца Парам. не стандартизованный коэффициент для регрессии Pt_Poor на Pop_Chng равен -0.40374 . Это означает, что для каждого уменьшения численности населения на единицу, имеется увеличение уровня бедности на .40374. Верхний и нижний (по умолчанию) 95% доверительные пределы для этого не стандартизованного коэффициента не включают ноль, так что коэффициент регрессии значим на уровне p . Обратите внимание на не стандартизованный коэффициент, который также является коэффициентом корреляции Пирсона для простых регрессионных планов, равен -.65, который означает, что для каждого уменьшения стандартного отклонения численности населения происходит увеличение стандартного отклонения уровня бедности на .65.

Распределение переменных

Коэффициенты корреляции могут стать существенно завышены или занижены, если в данных присутствуют большие выбросы. Изучим распределение зависимой переменной Pt_Poor по округам. Для этого построим гистограмму переменной Pt_Poor .

Рис. 6. Гистограмма переменной Pt_Poor.

Как вы можете заметить, распределение этой переменной заметно отличается от нормального распределения. Тем не менее, хотя даже два округа (два правых столбца) имеют высокий процент семей, которые находятся за чертой бедности, чем ожидалось в случае нормального распределения, кажется, что они находятся «внутри диапазона.»

Рис. 7. Гистограмма переменной Pt_Poor.

Это суждение в некоторой степени субъективно. Эмпирическое правило гласит, что выбросы необходимо учитывать, если наблюдение (или наблюдения) не попадают в интервал (среднее ± 3 умноженное на стандартное отклонение). В этом случае стоит повторить анализ с выбросами и без, чтобы убедиться, что они не оказывают серьезного эффекта на корреляцию между членами совокупности.

Диаграмма рассеяния

Если одна из гипотез априори о взаимосвязи между заданными переменными, то ее полезно проверить на графике соответствующей диаграммы рассеяния.

Рис. 8. Диаграмма рассеяния.

Диаграмма рассеяния показывает явную отрицательную корреляцию ( -.65 ) между двумя переменными. На ней также показан 95% доверительный интервал для линии регрессии, т.е., с 95% вероятностью линия регрессии проходит между двумя пунктирными кривыми.

Критерии значимости

Рис. 9. Таблица, содержащая критерии значимости.

Критерий для коэффициента регрессии Pop_Chng подтверждает, что Pop_Chng сильно связано с Pt_Poor , p .

На этом примере было показано, как проанализировать простой регрессионный план. Была также представлена интерпретация не стандартизованных и стандартизованных коэффициентов регрессии. Обсуждена важность изучения распределения откликов зависимой переменной, продемонстрирована техника определения направления и силы взаимосвязи между предиктором и зависимой переменной.

Основы линейной регрессии

Что такое регрессия? 

Линия регрессии 

Метод наименьших квадратов

Предположения линейной регрессии

Аномальные значения (выбросы) и точки влияния

Гипотеза линейной регрессии

Оценка качества линейной регрессии: коэффициент детерминации R²

Применение линии регрессии для прогноза

Простые регрессионные планы

Пример: простой регрессионный анализ

Рассмотрим две непрерывные переменные x=(x₁, x₂, .., x_n), y=(y₁, y₂, …, y_n).

Разместим точки на двумерном графике рассеяния и скажем, что мы имеем линейное соотношение, если данные аппроксимируются  прямой линией.

Если мы полагаем, что y зависит от x, причём изменения в y вызываются именно изменениями в x, мы можем определить линию регрессии (регрессия y на x), которая лучше всего описывает прямолинейное соотношение между этими двумя переменными.

Статистическое использование слова «регрессия» исходит из явления, известного как регрессия к среднему, приписываемого сэру Френсису Гальтону (1889).

Он показал, что, хотя высокие отцы имеют тенденцию иметь высоких сыновей, средний рост сыновей меньше, чем у их высоких отцов. Средний рост сыновей «регрессировал» и «двигался вспять» к среднему росту всех отцов в популяции. Таким образом, в среднем высокие отцы имеют более низких (но всё-таки высоких) сыновей, а низкие отцы имеют сыновей более высоких (но всё-таки довольно низких).

Линия регрессии

Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:

Y=a+bx.

x называется независимой переменной или предиктором.

Y – зависимая переменная или переменная отклика. Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y»

• a – свободный член (пересечение) линии оценки; это значение Y, когда x=0 (Рис.1).
• b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу.
• a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b.

Парную линейную регрессию можно расширить, включив в нее более одной независимой переменной; в этом случае она известна как множественная регрессия.

Рис.1. Линия линейной регрессии, показывающая пересечение a и угловой коэффициент b (величину возрастания Y при увеличении x на одну единицу)

Метод наименьших квадратов

Мы выполняем регрессионный анализ, используя выборку наблюдений, где a и b – выборочные оценки истинных (генеральных) параметров, α и β , которые определяют линию линейной регрессии в популяции (генеральной совокупности).

Наиболее простым методом определения коэффициентов a и b является метод наименьших квадратов (МНК).

Подгонка оценивается, рассматривая остатки (вертикальное расстояние каждой точки от линии, например, остаток = наблюдаемому y – предсказанный y, Рис. 2).

Линию лучшей подгонки выбирают так, чтобы сумма квадратов остатков была минимальной.

Рис. 2. Линия линейной регрессии с изображенными остатками (вертикальные пунктирные линии) для каждой точки.

Предположения линейной регрессии

Итак, для каждой наблюдаемой величины остаток равен разнице и соответствующего предсказанного Каждый остаток может быть положительным или отрицательным.

Можно использовать остатки для проверки следующих предположений, лежащих в основе линейной регрессии:

• Остатки нормально распределены с нулевым средним значением;

Если допущения линейности, нормальности и/или постоянной дисперсии сомнительны, мы можем преобразовать или и рассчитать новую линию регрессии, для которой эти допущения удовлетворяются (например, использовать логарифмическое преобразование или др.).

Аномальные значения (выбросы) и точки влияния

«Влиятельное» наблюдение, если оно опущено, изменяет одну или больше оценок параметров модели (т.е. угловой коэффициент или свободный член). 

Выброс (наблюдение, которое противоречит большинству значений в наборе данных) может быть «влиятельным» наблюдением и может хорошо обнаруживаться визуально, при осмотре двумерной диаграммы рассеяния или графика остатков.

И для выбросов, и для «влиятельных» наблюдений (точек) используют модели, как с их включением, так и без них, обращают внимание на изменение оценки (коэффициентов регрессии).

При проведении анализа не стоит отбрасывать выбросы или точки влияния автоматически, поскольку простое игнорирование может повлиять на полученные результаты. Всегда изучайте причины появления этих выбросов и анализируйте их.

Гипотеза линейной регрессии

При построении линейной регрессии проверяется нулевая гипотеза о том, что генеральный угловой коэффициент линии регрессии β равен нулю.

Если угловой коэффициент линии равен нулю, между и нет линейного соотношения: изменение не влияет на

Для тестирования нулевой гипотезы о том, что истинный угловой коэффициент равен нулю можно воспользоваться следующим алгоритмом:

Вычислить статистику критерия, равную отношению , которая подчиняется распределению с степенями свободы, где стандартная ошибка коэффициента

,

— оценка дисперсии остатков.

Обычно если достигнутый уровень значимости нулевая гипотеза отклоняется.

Можно рассчитать 95% доверительный интервал для генерального углового коэффициента :

где процентная точка распределения со степенями свободы что дает вероятность двустороннего критерия

Это тот интервал, который содержит генеральный угловой коэффициент с вероятностью 95%.

Для больших выборок, скажем, мы можем аппроксимировать значением 1,96 (то есть статистика критерия будет стремиться к нормальному распределению)

Оценка качества линейной регрессии: коэффициент детерминации R²

Из-за линейного соотношения  и мы ожидаем, что  изменяется, по мере того как изменяется , и называем это вариацией, которая обусловлена или объясняется регрессией. Остаточная вариация должна быть как можно меньше.

Если это так, то большая часть вариации  будет объясняться регрессией, а точки будут лежать близко к линии регрессии, т.е. линия хорошо соответствует данным.

Долю общей дисперсии , которая объясняется регрессией называют коэффициентом детерминации, обычно выражают через процентное соотношение и обозначают R² (в парной линейной регрессии это величина r², квадрат коэффициента корреляции), позволяет субъективно оценить качество уравнения регрессии.

Разность представляет собой процент дисперсии который нельзя объяснить регрессией.

Нет формального теста для оценки мы вынуждены положиться на субъективное суждение, чтобы определить качество подгонки линии регрессии.

Применение линии регрессии для прогноза

Можно применять регрессионную линию для прогнозирования значения по значению в пределе наблюдаемого диапазона (никогда не экстраполируйте вне этих пределов).

Мы предсказываем среднюю величину для наблюдаемых, которые имеют определенное значение путем подстановки этого значения в уравнение линии регрессии.

Итак, если прогнозируем как Используем эту предсказанную величину и ее стандартную ошибку, чтобы оценить доверительный интервал для истинной средней величины в популяции.

Повторение этой процедуры для различных величин позволяет построить доверительные границы для этой линии. Это полоса или область, которая содержит истинную линию, например, с 95% доверительной вероятностью.

Подобным образом можно рассчитать более широкую область, внутри которой, как мы ожидаем, лежит наибольшее число (обычно 95%) наблюдений.

Простые регрессионные планы

Простые регрессионные планы содержат один непрерывный предиктор. Если существует 3 наблюдения со значениями предиктора P, например, 7, 4 и 9, а план включает эффект первого порядка P, то матрица плана X будет иметь вид

а регрессионное уравнение с использованием P для X1 выглядит как

Y = b0 + b1P

Если простой регрессионный план содержит эффект высшего порядка для P, например квадратичный эффект, то значения в столбце X1 в матрице плана будут возведены во вторую степень:

а уравнение примет вид

Y = b0 + b1P2

Сигма-ограниченные и сверхпараметризованные методы кодирования не применяются по отношению к простым регрессионным планам и другим планам, содержащим только непрерывные предикторы (поскольку, просто не существует категориальных предикторов). Независимо от выбранного метода кодирования, значения непрерывных переменных увеличиваются в соответствующей степени и используются как значения для переменных X. При этом перекодировка не выполняется. Кроме того, при описании регрессионных планов можно опустить рассмотрение матрицы плана X, а работать только с регрессионным уравнением.

Пример: простой регрессионный анализ

Этот пример использует данные, представленные в таблице:

Рис. 3. Таблица исходных данных.

Данные составлены на основе сравнения переписей 1960 и 1970 в произвольно выбранных 30 округах. Названия округов представлены в виде имен наблюдений. Информация относительно каждой переменной представлена ниже:

Рис. 4. Таблица спецификаций переменных.

Задача исследования

Для этого примера будут анализироваться корреляция уровня бедности и степень, которая предсказывает процент семей, которые находятся за чертой бедности. Следовательно мы будем трактовать переменную 3 (Pt_Poor) как зависимую переменную.

Можно выдвинуть гипотезу: изменение численности населения и процент семей, которые находятся за чертой бедности, связаны между собой. Кажется разумным ожидать, что бедность ведет к оттоку населения, следовательно, здесь будет отрицательная корреляция между процентом людей за чертой бедности и изменением численности населения. Следовательно мы будем трактовать переменную 1 (Pop_Chng) как переменную-предиктор.

Просмотр результатов

Коэффициенты регрессии

Рис. 5. Коэффициенты регрессии Pt_Poor на Pop_Chng.

На пересечении строки Pop_Chng и столбца Парам. не стандартизованный коэффициент для регрессии Pt_Poor на Pop_Chng равен -0.40374. Это означает, что для каждого уменьшения численности населения на единицу, имеется увеличение уровня бедности на .40374. Верхний и нижний (по умолчанию) 95% доверительные пределы для этого не стандартизованного коэффициента не включают ноль, так что коэффициент регрессии значим на уровне p<.05. Обратите внимание на не стандартизованный коэффициент, который также является коэффициентом корреляции Пирсона для простых регрессионных планов, равен -.65, который означает, что для каждого уменьшения стандартного отклонения численности населения происходит увеличение стандартного отклонения уровня бедности на .65.

Распределение переменных

Коэффициенты корреляции могут стать существенно завышены или занижены, если в данных присутствуют большие выбросы. Изучим распределение зависимой переменной Pt_Poor по округам. Для этого построим гистограмму переменной Pt_Poor.

Рис. 6. Гистограмма переменной Pt_Poor.

Как вы можете заметить, распределение этой переменной заметно отличается от нормального распределения. Тем не менее, хотя даже два округа (два правых столбца) имеют высокий процент семей, которые находятся за чертой бедности, чем ожидалось в случае нормального распределения, кажется, что они находятся «внутри диапазона.»

Рис. 7. Гистограмма переменной Pt_Poor.

Это суждение в некоторой степени субъективно. Эмпирическое правило гласит, что выбросы необходимо учитывать, если наблюдение (или наблюдения) не попадают в интервал (среднее ± 3 умноженное на стандартное отклонение). В этом случае стоит повторить анализ с выбросами и без, чтобы убедиться, что они не оказывают серьезного эффекта на корреляцию между членами совокупности.

Диаграмма рассеяния

Если одна из гипотез априори о взаимосвязи между заданными переменными, то ее полезно проверить на графике соответствующей диаграммы рассеяния.

Рис. 8. Диаграмма рассеяния.

Диаграмма рассеяния показывает явную отрицательную корреляцию (-.65) между двумя переменными. На ней также показан 95% доверительный интервал для линии регрессии, т.е., с 95% вероятностью линия регрессии проходит между двумя пунктирными кривыми.

Критерии значимости

Рис. 9. Таблица, содержащая критерии значимости.

Критерий для коэффициента регрессии Pop_Chng подтверждает, что Pop_Chng сильно связано с Pt_Poor, p<.001.

Итог

На этом примере было показано, как проанализировать простой регрессионный план. Была также представлена интерпретация не стандартизованных и стандартизованных коэффициентов регрессии. Обсуждена важность изучения распределения откликов зависимой переменной, продемонстрирована техника определения направления и силы взаимосвязи между предиктором и зависимой переменной.

Связанные определения:
Линейная регрессия
Матрица плана
Общая линейная модель
Регрессия

В начало

Содержание портала

Известия Института математики и информатики Удмуртского государственного университета

2021. Том 58. С. 3-17

УДК 519.64, 51.72

© Т.М. Банникова, В. М. Немцов, Н. А. Баранова, Г. Н. Коныгин, О. М. Немцова

МЕТОД ОЦЕНКИ СТАТИСТИЧЕСКОЙ ПОГРЕШНОСТИ РЕШЕНИЯ В ОБРАТНОЙ ЗАДАЧЕ СПЕКТРОСКОПИИ

Предложен метод получения коридора статистической погрешности решения обратной задачи спектроскопии, для оценки статистической ошибки экспериментальных данных которой может быть применим нормальный закон распределения. С помощью математического моделирования статистической ошибки парциальных спектральных составляющих, полученных по численному устойчивому решению обратной задачи, стало возможным указать погрешность соответствующего решения. Проблема получения коридора погрешности решения обратных задач является актуальной, поскольку существующие способы оценки погрешности решения построены на анализе гладких функциональных зависимостей при наложении жестких ограничений на область допустимых решений (компактность, монотонность и т.п.). Их использование при компьютерной обработке реальных экспериментальных данных крайне затруднительно и поэтому, как правило, не применяется. В работе, на основе выделения парциальных спектральных составляющих и оценки их погрешности, предложен способ получения коридора статистической погрешности решения обратных задач спектроскопии. На примерах обработки мёссбауэровских спектров продемонстрирована необходимость и значимость нахождения коридора погрешности решения для обеспечения достоверных результатов.

Ключевые слова: коридор погрешности решения, обратная задача, нормальный закон распределения, мёссбауэровская спектроскопия, среднеквадратичная ошибка, парциальные составляющие.

Б01: 10.35634/2226-3594-2021-58-01 Введение

Очевидно, что при решении обратных некорректных задач вопрос погрешности получаемого решения является принципиально важным [1,2]. Такое свойство некорректных задач, как неустойчивость к погрешностям входных данных является существенным препятствием к нахождению истинного решения задачи и его погрешности. На сегодняшний день разработано большое количество математических методов решения некорректных задач [3-7], которые обеспечивают получение устойчивого решения. Однако, их развитие и усовершенствование продолжается, и связано это с повышением требований к свойствам получаемых решений (гладкость высокого порядка, неотрицательность, разрешимость линий и т.п.) [8-10]. В них, как правило, предлагаются оценки ошибки решения по норме пространства, в котором решение ищется [11-14], что не всегда доступно в реальном эксперименте. Например, в обратных задачах спектроскопии [15] истинное решение далеко не всегда является нормальным, т. е. минимальным по норме, как предполагается в методе регуляризации [16]. Для получения физически значимого решения и корректной интерпретации результатов обработки данных в этих задачах необходимо привлекать априорную информацию об искомом решении [17,18] и уметь находить коридор ошибки получаемого решения [19]. Иногда, для уменьшения влияния погрешности экспериментальных данных на устойчивость решения, применяют специальные фильтровочные функции [20], или выполняют предварительную обработку спектральных данных с помощью машин с экстремальным обучением [21]. Несмотря на сложность и трудоемкость решения обратных задач, актуальность развития методов их решения постоянно возрастает. Последние исследования при установлении диагноза и рассмотрении возможности раннего лечения пациентов,

переболевших СОУГО-19, показали необходимость своевременного проведение магнитно-резонансной томографии больных [22]. В проблеме снижения воздействия на окружающую среду при добыче нефти и газа путем преобразования метана и других газообразных углеводородов в СО2 огромную роль имеет потенциальное использование спектрометров с преобразованием Фурье изображения [23]. Применение высокочувствительного экспериментального метода исследования локальной атомной структуры с разрешением 1-2 А по глубине в многослойных малоконтрастных тонких пленках [2] также является актуальной задачей.

К сожалению, в большинстве научных публикаций, посвященных решению обратных задач предлагаются способы оценки погрешности решения, построенные на анализе модельных гладких функциональных зависимостей при наложении жестких ограничений на оператор задачи [3,5,14,24] и/или область допустимых решений (компактность, монотонность и т. п.) [18]. Их применение при обработке экспериментальных данных со статистической ошибкой и неизвестной гладкостью решения чрезвычайно затруднительно. Существуют единичные работы с указанием коридора ошибки решения, полученного либо прямым моделированием ошибок входных параметров [25,26], либо без описания способа его получения [27].

§ 1. Постановка задачи

В мёссбауэровском эксперименте исследуется зависимость интенсивности N(V) прошедшего через образец излучения от относительной скорости источника излучения V. Как правило, для расшифровки мёссбауэровских спектров используется нормированный сигнал:

= , (1)

N (то)

где N (V) — количество импульсов при значении скорости V, N (то) — количество импульсов в отсутствии резонансного поглощения. Реальный спектр снимается в дискретном поканальном режиме, когда каждому каналу спектра г соответствует скорость V;, поэтому реальный нормированный сигнал (1) является дискретным:

= ^М-^), (2)

N (то)

где г = 1,…, п — количество каналов регистрации, N — количество зарегистрированных импульсов в г-ом канале. Известно, что вероятность наблюдения 7-квантов за время измерения в мёссбауэровском эксперименте определяется закономерностями распада и задается распределением Пуассона:

N N

Р^) = -N0^ ехр(—N0),

которое при N ^ то стремится к нормальному распределению с математическим ожиданием М^) = N0 и дисперсией а2 = N0:

1 ( ^ — ^)2 Р(к ‘ = тт, ехр(—Чг1) ■

9.9 • 105

9.3 • 105

Nк

20 40 60 Каналы

а)

80 100

0.09 Ук

0.07

И

Н

О

^

0.02 0.01 0.00

-6.5 -6.0 -5.5 -5.0 -4.5 -4.0 -3.5 V, мм/с

б)

Рис. 1. Модель экспериментального спектра (точки) с четырьмя парциальными составляющими (штриховые линии): а) исходный спектр с интенсивностями парциальных составляющих 1к лоренцовской формы; б) нормированный спектр

0

В мёссбауэровском эксперименте обычно количество импульсов в каждом канале N > > 105, поэтому для оценки статистической погрешности эксперимента можно использовать нормальный закон распределения. Тем самым погрешность или среднеквадратичное отклонение экспериментального сигнала в каждой точке равно а2 = N.

Резонансная линия поглощения мёссбауэровского спектра является функцией Лоренца, и выделенный из эксперимента нормированный сигнал описывается суперпозицией элементарных функций Лоренца вида:

ьг(У) = – 1

4

1 + р (V – V)2

где Г — ширина элементарной линии Лоренца. В формировании мёссбауэровских спектров принимают участие поглощающие ядра атомов, в общем случае не являющиеся химически и кристаллографически эквивалентными. Каждой неэквивалентной позиции (локальной конфигурации) резонансных ядер соответствует отдельная элементарная функция Лоренца в мёссбауэровском спектре. Таким образом, математическая модель мёссбауэровского спектра представляет собой сумму парциальных Лоренцовских линий (рис. 1), интенсивности которых пропорциональны вероятностям отдельных позиций р;:

к = Е—т25-. (3)

к 1 + р (V – V; )2

При наличии большого числа неэквивалентных позиций к для описания мёссбауэровских спектров используют непрерывное представление линейной суперпозиции (3):

У СРн ^н . (4)

у =/ -4-, г =1,…,п, (4)

1 + Г2 (V – Ун)2

где рн — функция плотности вероятности распределения локальных конфигураций. Интегральное уравнение Фредгольма первого рода (4) описывает обратную задачу мёссбауэ-ровской спектроскопии по определению функции рн € Ь2[Нт;п, Нтах], соответствующей вектору экспериментальных данных Уг, г = 1,…, п. В данной работе, на примере мёсс-бауэровской спектроскопии, предлагается оригинальная методика получения коридора статистической ошибки решения обратных задач, для оценки статистической погрешности экспериментальных данных которых применим нормальный закон распределения.

§ 2. Методика оценки погрешности решения

Каждая точка нормированного мёссбауэровского спектра уг описывается суммой парциальных лоренцовских линий, заданных на всем интервале съемки экспериментального спектра. В точке г в интенсивность уг дает вклад каждая парциальная линия лоренцовской зависимости. Таким образом, можно записать

Уг = У; + ^Р]¿(V – V]), где У; = Р;¿(V – Н^г). (5)

3=г

При к = г вклад У; равен вероятности р;, так как ¿(V – Vk=i) = 1. При ] = г вклады от остальных составляющих учитываются в сумме (5), например при ] = к + 1 вклад равен выражению ¿(V; – (рис. 1, б). Поскольку при к = г вклад У; равен вероятности р;, то, используя У; вместо у;, в формуле (2) всегда можно найти , соответствующее парциальному вкладу в реальный ненормированный экспериментальный спектр, и вычислить погрешность Д^; = пользуясь формулой (2),

—^

= – Ук), (6)

и величину погрешности парциальной линии

ДУ = Д^к = >/(Т-У)

к ^ ‘

Тогда в точке I = к погрешность решения определяется как Дрк = ДУк.

В случае непрерывного представления линейной суперпозиции (4) погрешность парциальной линии связана с погрешностью решения следующим уравнением:

гУя=к+1

ДУн = Дрн=к / т – Ун)йУп, (7)

¿Уи=к

где рн — функция плотности вероятности распределения локальных конфигураций, которая определена на интервале [Ят;п, Нтах], и существует взаимно однозначное соответствие

[Утт) Утах] ^^ [Нтт) Нтах] •

Таким образом, чтобы найти погрешность решения достаточно смоделировать интенсивности парциальных лоренцовских линий Ук, дающих вклад в каждую точку нормированного мёссбауэровского спектра уг. Поскольку интенсивности Ук пропорциональны вероятностям отдельных позиций рк, то на первом шаге следует найти решение обратной задачи (3) (или, для непрерывного случая, задачи (4)).

Для определения решения обратной задачи следует использовать методы, обеспечивающие восстановление экспериментальных данных и гарантирующие пропорциональность погрешности решения статистической ошибке измерений. Критерием достоверности решения и восстановления экспериментальных данных является критерий х2 ~ 1 Пирсона [28]:

2 = (yi — Yi)

л п • а2-

i=1

2

Здесь относительная среднеквадратичная ошибка экспериментальных данных в точке i определяется аналогично выражению (6) заменой k на i, то есть Ni = N^(1 — y^):

2 = 1 — yi

°yi n ‘

Для оценки погрешности решения pH используется восстановленное значение среднеквад-

1 _ Уи

ратичной ошибки парциальной интенсивности аИ = —ту-в точке H и критерий х2 [29].

Покажем на примере классического и самого успешного метода решения обратных задач — метода регуляризации Тихонова, развитию которого посвящено в последнее время много работ [30-33], методику определения функции распределения ри из обратной задачи мёссбауэровской спектроскопии. Уравнение, связывающее экспериментальный сигнал y(V) с функцией плотности вероятности распределения параметра H (сверхтонкое магнитное поле), имеет вид:

Г И max

Ap = L(H,V)p(H)dH = y(V), V E [Vmin,Vmax], (8)

J Hmin

где y(V) — мёссбауэровский спектр; p(H) — искомая функция распределения параметра; L(H, V) — функции Лоренца, задающие форму элементарных или парциальных составляющих; [Hmin, Hmax] — интервал существования непрерывного распределения p(H).

Уравнение (8) представляет собой интегральное уравнение Фредгольма первого рода с вполне непрерывным оператором А: ¿2[Ит;п, Итах] ^ ^[^тт, ^тах], где ¿(И, V) — действительная функция непрерывная в прямоугольнике (Ит;п ^ И ^ Итах, Ут;п ^ V ^ Vmax}. Вместо точной правой части уравнения у°^) известно приближенное значение у^): \у — У°11ь2 ^ На искомую функцию накладываются дополнительные ограничения:

(1) р(И) — непрерывно дифференцируемая функция, р(И) € ^г21[Ит;п, Итах] и

-тах 2(И)^И , />ЯтахА^Р2–Л1/2

” р(И’= 1 и р2(И)йиЧ

(2) р(Итт) = 0 или р'(Ит1п) = 0, р(Итах) = 0 или р'(Итах) = 0, — граничные условия;

(3) р(И) ^ 0 на [Ит;п, Итах] — условие неотрицательности. Введем в рассмотрение функционал ^[р(И)]:

д[р(И)] = { I Ар — у \|2 +а I р 11^1} , или (9)

-^тах

У Ь(И, V)р(И)ЙИ — y(V)

– тт

2— тах

¿V + а у (р2(И) +

–

ф п 2

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

йИ

ЙИ V ,

где а — параметр регуляризации, контролирующий гладкость решения.

Для построения конечно-разностной аппроксимации функционала (9) на отрезках [Ит;п, Итах] и [Ут;п,Утах] выбираются сетки (И,}к=1 и (V}™=1 с шагами ДИ и ДV соответственно. Выполняется дискретная аппроксимация функций р(И), у^) векторами р,, ] = 1,…, к, уг, г = 1,…, п, а интегрального оператора — матрицей А = (а,} с помощью метода коллокаций [34]:

Г

а, = Ь(И,^)ЙИ

В результате аппроксимации непрерывного пространства Ь2 дискретным пространством /2 на равномерных сетках, а производной й/йИ разностным отношением, имеем дискретную аппроксимацию функционала (9):

, п к 2 к / 2 Л

^ы= — у) + а^(р2 + ()ДИ!,

^ г=1 ,=1 .7=1^ ‘ ‘

Известно, что достаточным условием минимума функционала является обращение в ноль его первой вариации (уравнение Эйлера), которая определяется соотношением

д[Рк + Др] — д[рк ] = д^[Рк, Др]Др + о(Др),

где Др — малое приращение вектора рк. Таким образом, задача сводится к решению системы линейных алгебраических уравнений:

(А*А + В )рк = А*уп, (10)

где А* — сопряженная матрица, В — матрица вида:

в

а +

2а АН2

а

а

АН2

а +

АН2

2а

а

АН2 АН2

V

0

0

0

а

АН2

а +

2а

АН2/

(11)

В результате вместо некорректного уравнения первого рода (8) решается система линейных уравнений (10) с параметром регуляризации а. При построении матрицы В учитывается тип граничных условий, например, при р(Нт;п) = 0 и р'(Нтах) = 0 матрица В имеет вид (11). Параметр а выбирается из условия минимума невязки ||Лр — у|| ^ 6 и априорных ограничений на искомое решение — условие (1). Матрица Л*Л является симметричной и положительно определенной, и, следовательно, матрица (Л*Л + В) не вырождена.

В методе регуляризации Тихонова показано, что система линейных алгебраических уравнений (10) разрешима при а > 0 и ее решение сходится к решению непрерывной задачи по норме соболевского пространства ЭД^1. Полученное решение ра является приближенным, но оно принадлежит к тому классу решений, элементом которого является точное решение р0 уравнения (8). Если уровень погрешности исходных данных стремится к нулю (6 ^ 0), то можно найти такое а (6), при котором приближенное решение сходится к точному решению ||ра — р°||^ 1 ^ 0 при 6 ^ 0.

Следующий этап регуляризованного алгоритма заключается в удовлетворении требованию неотрицательности решения на всей области определения параметра Н. Для этого применяется итерационный алгоритм сужения области определения решения [35]:

Ра+1 = ((АЙ+1)*(АЙ+1) + В)-1(ЛЙ+1)* у,

в котором на первом шаге й = 1 в качестве начального интервала задается вся область определения решения [Нт;п, Нтах], а следующий интервал определяется правилом обнуления элементов основной матрицы системы:

П]

Я], р(Н]) ^ 0, 0, р(Н]) < 0,

3

1,…, п.

Таким образом, область поиска решения уточняется на каждом шаге итерации. Одновременно с отрицательными осцилляциями исчезают и ложные положительные, а истинные локальные максимумы остаются. Как правило, после нескольких итераций получается полностью неотрицательное решение.

Следовательно, для определения коридора статистической погрешности решения обратной задачи спектроскопии выполняется последовательность действий:

(1) нахождение решения обратной задачи рк, обеспечивающее восстановление экспериментального спектра в рамках критерия х2;

(2) построение парциальных спектральных составляющих Ук, соответствующих рк;

(3) моделирование экспериментальной интенсивности парциальной составляющей спектра;

0

0

0

(4) вычисление статистической погрешности Д^к парциальной составляющей;

(5) вычисление статистической погрешности нормированной ДУк парциальной составляющей и, соответственно, Дрк = ДУ”к.

Таким образом, решается проблема построения коридора погрешности решения обратной задачи спектроскопии методом выделения парциальных спектральных составляющих. Достоинство метода заключается в том, что он использует принцип разложения спектрального сигнала на парциальные составляющие, который является основой спектроскопических исследований и успешно реализован в многочисленных методах обработки спектров [15,23,25].

§ 3. Демонстрационные примеры

Эффективность предложенной методики проиллюстрирована на примерах обработки двух мёссбауэровских спектров: использованный в работе [36] модельный спектр с хорошо разрешенными парциальными спектральными линиями (рис. 2, а), и полученный на спектрометре ЯГРС-4М спектр разупорядоченного сплава Бе75Ое25 (рис. 2, б). Статистический набор составлял соответственно = 106 и = 8 • 105 импульсов. Для обработки спектров была записана обратная задача мёссбауэровской спектроскопии в виде уравнения (8), из которого определялась функция распределения плотности вероятности р— методами регуляризации [36, 37] и погрешность решения по формуле (7). Для спектра с хорошо разрешенными парциальными спектральными линиями восстановление экспериментальных данных произошло с выполнением критерия х2 < 1. Из рис. 2, а видно, что величина ошибки решения существенно меньше значений вероятностей в точках локальных максимумов на кривой распределения р- . Тем самым, полученное решение можно считать достоверным. В спектре разупорядоченного сплава Бе75Ое25, в отличие от смоделированного спектра, указать количество парциальных составляющих и их интенсивности без качественной математической обработки невозможно. В этой ситуации для оценки достоверности результатов обработки огромное значение имеет коридор погрешности решения. На рис. 2, б видно, что в области И > 170 кЭ количество локальных максимумов на кривой распределения р— с учетом полученного коридора погрешности определяется однозначно. А в области И < 170 кЭ без указания коридора погрешности решения полученные на распределении р— два локальных максимума могли быть отнесены к ошибке метода обработки. Несмотря на то, что коридор ошибки был построен с учетом полученного при восстановлении экспериментальных данных значения х2 = 1.6, два локальных максимума в области И < 170 кЭ оказались статистически достоверны [29].

Полученные результаты показывают, что когда количество парциальных составляющих к относительно невелико и их относительные интенсивности Ук значительно превышают величину ДУ (спектр на рис. 2, а), для экономии трудовых затрат и энергетических ресурсов можно уменьшить величину статистического набора эксперимента с 106 до 105. Если ДУ сравнима с относительной интенсивностью парциальных составляющих (рис. 2, б), то для уменьшения относительной погрешности и увеличения точности количественных оценок необходимо увеличение статистического набора спектра.

Заключение

Предложенный способ получения коридора статистической погрешности решения обратной задачи спектроскопии в условиях нормального закона распределения статистической ошибки экспериментальных данных основан на выделении парциальных спектральных составляющих и оценки их погрешности. С помощью математического моделирования статистической ошибки парциальных спектральных составляющих стало возможным

<D

sd н о

(U

sd н о

-6 -4 -2 0 2 4 6 100 150 200 250 300 350

V, мм / с

H, кЭ

-6 -4 -2 0 2 4 6 100 150 200 250 300 350

V, мм/с

H, кЭ

б)

(U

sd н о

op

(U

и н о

Рис. 2. Мёссбауэровские спектры (слева) и решения обратной задачи мёссбауэровской спектроскопии с указанием коридора погрешности (справа): а) модельный спектр с хорошо разрешенными парциальными спектральными линиями; б) спектр разупорядоченного сплава Ре75ве25

указать погрешность численного решения. К достоинству метода следует отнести тот момент, что разложение спектрального сигнала на парциальные составляющие является основой спектроскопических исследований. Определение коридора погрешности позволяет корректно интерпретировать результаты экспериментальных исследований и обеспечивает достоверность результатов.

СПИСОК ЛИТЕРАТУРЫ

1. Огородников И. Н. Введение в обратные задачи физической диагностики. Екатеринбург: Изд-во Урал. ун-та, 2017. https://www.elibrary.ru/item.asp?id=29050248

2. Babanov Yu. A., Vasin V.V., Ponomarev D. A., Devyaterikov D. I., Romashev L.N., Ustinov V. V. A subnanometric resolution method for studying local atomic structure of interface and surface of multilayered nanoheterostructure thin films // Thin Solid Films. 2018. Vol. 656. P. 44-52. https://doi.org/10.1016/j.tsf.2018.04.024

3. Lee J. W., Prenter P. M. An analysis of the numerical solution of Fredholm integral equations of the first kind //Numerische Mathematik. 1978. Vol. 30. No. 1. P. 1-23. https://doi.org/10.1007/BF01403903

4. Hansen P. C. The Backus-Gilbert method: SVD analysis and fast implementation // Inverse Problems. 1994. Vol. 10. No. 4. P. 895-904. https://doi.Org/10.1088/0266-5611/10/4/009

5. Kabanikhin S. I. Definitions and examples of inverse and ill-posed problems // Journal of Inverse and Ill-posed Problems. 2008. Vol. 16. No. 4. P. 317-357. https://doi.org/10.1515/JIIP.2008.019

6. Razavy M. An introduction to inverse problems in physics. Singapore: World Scientific, 2020. https://doi.org/10.1142/11860

7. Wells J. W., Birkinshaw K. A matrix approach to resolution enhancement of XPS spectra by a modified maximum entropy method // Journal of Electron Spectroscopy and Related Phenomena. 2006. Vol. 152. No. 1-2. P. 37-43. https://doi.org/10.1016/j.elspec.2006.03.003

8. Xu P. A new look at Akaike’s Bayesian information criterion for inverse ill-posed problems // Journal of the Franklin Institute. 2021. Vol. 358. No. 7. P. 4077-4102. https://doi.org/10.1016/j.jfranklin.2021.03.003

9. Zheng S., Ding C., Nie F. Regularized singular value decomposition and application to recommender system // arXiv:1804.05090 [cs.LG]. 2018. https://arxiv.org/abs/1804.05090v1

10. Xiong X., Xue X. A fractional Tikhonov regularization method for identifying a space-dependent source in the time-fractional diffusion equation // Applied Mathematics and Computation. 2019. Vol. 349. P. 292-303. https://doi.org/10.1016/j.amc.2018.12.063

11. Mohammadian-Behbahani M.-R., Saramad S. Integral-equation based methods for parameter estimation in output pulses of radiation detectors: Application in nuclear medicine and spectroscopy // Nuclear Instruments and Methods in Physics Research. Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 2018. Vol. 887. P. 7-12. https://doi.org/10.1016/j.nima.2017.12.073

12. Vasin V. V. Irregular nonlinear operator equations: Tikhonov’s regularization and iterative approximation // Journal of Inverse and Ill-posed Problems. 2013. Vol. 21. No. 1. P. 109-123. https://doi.org/10.1515/jip-2012-0084

13. Qiao B., Liu J., Liu J., Yang Z., Chen X. An enhanced sparse regularization method for impact force identification // Mechanical Systems and Signal Processing. 2019. Vol. 126. P. 341-367. https://doi.org/10.1016/j.ymssp.2019.02.039

14. Леонов А. С. Для каких обратных задач априорная оценка точности приближенного решения может иметь порядок ошибки данных // Сибирский журнал вычислительной математики. 2014. Т. 17. № 4. С. 339-348. http://mi.mathnet.ru/sjvm554

15. Верлань А. Ф., Сизиков В. С. Интегральные уравнения: методы, алгоритмы, программы. Киев: Наукова думка, 1986.

16. Морозов В. А. О восстановлении зашумленных сигналов методом регуляризации // Вычислительные методы и программирование. 2012. Т. 13. Вып. 1. С. 247-252. http://mi.mathnet.ru/vmp26

17. Васин В. В., Агеев А. Л. Некорректные задачи с априорной информацией. Екатеринбург: УИФ «Наука», 1993.

18. Ягола А. Г. Некорректные задачи с априорной информацией // Сибирские электронные математические известия. 2010. Т. 7. С. 343-361. http://mi.mathnet.ru/semr292

19. Nemtsova O. M., Ageev A. L., Voronina E. V. The estimation of the error of the hyperfine interaction parameter distribution from Mossbauer spectra // Nuclear Instruments and Methods in Physics Research. Section B: Beam Interactions with Materials and Atoms. 2002. Vol. 187. Issue 1. P. 132-136. https://doi.org/10.1016/S0168-583X(01)00830-8

20. Sussman M. S. Linear signal combination T2 spectroscopy // Magnetic Resonance Imaging. 2020. Vol. 66. P. 257-266. https://doi.org/10.1016/j.mri.2019.11.016

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

21. Henríquez P. A., Ruz G. A. Noise reduction for near-infrared spectroscopy data using extreme learning machines // Engineering Applications of Artificial Intelligence. 2019. Vol. 79. P. 13-22. https://doi.org/10.1016/j.engappai.2018.12.005

22. Zelada-Ríos L., Pacheco-Barrios K., Galecio-Castillo M., Yamunaque-Chunga C., Alvarez-Toledo K., Otiniano-Sifuentes R. Acute disseminated encephalomyelitis and COVID-19: A systematic synthesis of worldwide cases // Journal of Neuroimmunology. 2021. Vol. 359. 577674. https://doi.org/10.1016/jjneuroim.202L577674

23. Miguel R.B., Talebi-Moghaddam S., Zamani M., Turcotte C., Daun K.J. Assessing flare combustion efficiency using imaging Fourier transform spectroscopy // Journal of Quantitative Spectroscopy and Radiative Transfer. 2021. Vol. 273. 107835. https://doi.org/10.1016/j.jqsrt.2021.107835

24. Calvetti D., Lewis B., Reichel L., Sgallari F. Tikhonov regularization with nonnegativity constraint // Electronic Transactions on Numerical Analysis. 2004. Vol. 18. No. 1. P. 153-173.

25. Lekhtmakher S., Shapiro M. On the paper “Inverse methods for analyzing aerosol spectrometer measurements: A critical review” // Journal of Aerosol Science. 2000. Vol. 31. No. 7. P. 867-873. https://doi.org/10.1016/S0021-8502(99)00561-3

26. Samaras S., Nicolae D., Bockmann Ch., Vasilescu J., Binietoglou I., Labzovskii L., Toanca F., Papayannis A. Using Raman-lidar-based regularized microphysical retrievals and Aerosol Mass Spectrometer measurements for the characterization of biomass burning aerosols // Journal of Computational Physics. 2015. Vol. 299. P. 156-174. https://doi.org/10.1016/j.jcp.2015.06.045

27. Чуев М. А. Эффективный метод анализа сверхтонкой структуры гамма резонансных спектров с использованием профиля Фойта // Доклады Академии наук. 2011. Т. 438. № 6. С. 747-751. https://www.elibrary.ru/item.asp?id=16525971

28. Pearson K. On the criterion that a given system of deviations from the probable in the case of a correlated system of variables in such that it can be reasonably supposed to have arisen from random sampling // The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. Series 5. 1900. Vol. 50. No. 302. P. 157-175. https://doi.org/10.1080/14786440009463897

29. Тейлор Дж. Введение в теорию ошибок. М.: Мир, 1985.

30. Prakash J., Sanny D., Kalva S. K., Pramanik M., Yalavarthy P. K. Fractional regularization to improve photoacoustic tomographic image reconstruction // IEEE Transactions on Medical Imaging. 2019. Vol. 38. No. 8. P. 1935-1947. https://doi.org/10.1109/TMI.2018.2889314

31. Reddy G. D. A class of parameter choice rules for stationary iterated weighted Tikhonov regularization scheme // Applied Mathematics and Computation. 2019. Vol. 347. P. 464-476. https://doi.org/10.1016/j.amc.2018.11.015

32. Mohammady S., Eslahchi M. R. Extension of Tikhonov regularization method using linear fractional programming // Journal of Computational and Applied Mathematics. 2020. Vol. 371. 112677. https://doi.org/10.1016/j.cam.2019.112677

33. Gao Y., Xiao L., Wu B. TSVD and Tikhonov methods and influence factor analysis for NMR data in shale rock // Journal of Petroleum Science and Engineering. 2020. Vol. 194. 107508. https://doi.org/10.1016/j.petrol.2020.107508

34. Ким И. Г., Латыпова Н. В., Моторина О. Л. Численные методы: учеб.-метод. пособие. Ч. 2. Ижевск: Изд-во «Удмуртский университет», 2013.

35. Немцова О. М., Коныгин Г. Н. Повышение разрешающей способности метода регуляризации Тихонова при решении обратной задачи мёссбауэровской спектроскопии // Журнал прикладной спектроскопии. 2018. Т. 85. № 5. С. 830-835. https://www.elibrary.ru/item.asp?id=36962286

36. Немцова О. М., Коныгин Г. Н., Порсев В. Е. Разрешение перекрывающихся спектральных составляющих методом взвешенной регуляризации Тихонова // Журнал прикладной спектроскопии. 2021. Т. 88. № 2. С. 315-324. https://www.elibrary.ru/item.asp?id=44889288

37. Коныгин Г. Н., Немцова О. М., Порсев В. Е. Обработка мёссбауэровских спектров твердых растворов с применением функции Фойгта // Журнал прикладной спектроскопии. 2019. Т. 86. № 3. С. 374-381. https://www.elibrary.ru/item.asp?id=37522491

Поступила в редакцию 02.10.2021

Банникова Татьяна Михайловна, к. пед. н., доцент, Удмуртский государственный университет, 426034, Россия, г. Ижевск, ул. Университетская, 1. ORCID: https://orcid.org/0000-0003-4211-8421 E-mail: t.bannikova2011 @yandex.ru

Немцов Виктор Михайлович, младший научный сотрудник, Физико-технический институт Удмуртского федерального исследовательского центра УрО РАН, 426067, Россия, г. Ижевск, ул. Т. Барамзи-ной, 34.

ORCID: https://orcid.org/0000-0003-2551-7041 E-mail: viktorn93@gmail.com

Баранова Наталья Анатольевна, к. пед. н., доцент, Удмуртский государственный университет, 426034, Россия, г. Ижевск, ул. Университетская, 1. ORCID: https://orcid.org/0000-0002-4410-3613 E-mail: natik-231@yandex.ru

Коныгин Григорий Николаевич, к. ф.-м. н., старший научный сотрудник, Физико-технический институт Удмуртского федерального исследовательского центра УрО РАН, 426067, Россия, г. Ижевск, ул. Т. Барамзиной, 34.

ORCID: https://orcid.org/0000-0002-6202-9509 E-mail: gnkon@mail.ru

Немцова Ольга Михайловна, к. ф.-м. н., старший научный сотрудник, Физико-технический институт Удмуртского федерального исследовательского центра УрО РАН, 426067, Россия, г. Ижевск, ул. Т. Барамзиной, 34.

ORCID: https://orcid.org/0000-0002-5676-9578 E-mail: olganemtsova1968@gmail.com

Цитирование: Т. М. Банникова, В. М. Немцов, Н. А. Баранова, Г. Н. Коныгин, О. М. Немцова. Метод оценки статистической погрешности решения в обратной задаче спектроскопии // Известия Института математики и информатики Удмуртского государственного университета. 2021. Т. 58. С. 3-17.

T.M. Bannikova, V.M. Nemtsov, N.A. Baranova, G.N. Konygin, O.M. Nemtsova A method for estimating the statistical error of the solution in the inverse spectroscopy problem

Keywords: solution error interval, inverse problem, normal distribution law, Mossbauer spectroscopy, mean squared error, partial components.

MSC2020: 65F22, 47A52

DOI: 10.35634/2226-3594-2021-58-01

A method for obtaining the interval of statistical error of the solution of the inverse spectroscopy problem, for the estimation of the statistical error of experimental data of which the normal distribution law can be applied, has been proposed. With the help of mathematical modeling of the statistical error of partial spectral components obtained from the numerically stable solution of the inverse problem, it has become possible to specify the error of the corresponding solution. The problem of getting the inverse solution error interval is actual because the existing methods of solution error evaluation are based on the analysis of smooth functional dependences under rigid restrictions on the region of acceptable solutions (compactness, monotonicity, etc.). Their use in computer processing of real experimental data is extremely difficult and therefore, as a rule, is not applied. Based on the extraction of partial spectral components and the estimation of their error, a method for obtaining an interval of statistical error for the solution of inverse spectroscopy problems has been proposed in this work. The necessity and importance of finding the solution error interval to provide reliable results is demonstrated using examples of processing Mossbauer spectra.

REFERENCES

1. Ogorodnikov I.N. Vvedenie v obratnye zadachi fizicheskoi diagnostiki (Introduction to inverse problems of physical diagnostics), Yekaterinburg: Ural Federal University, 2017. https://www.elibrary.ru/item.asp?id=29050248

2. Babanov Yu. A., Vasin V. V., Ponomarev D.A., Devyaterikov D. I., Romashev L.N., Ustinov V. V. A subnanometric resolution method for studying local atomic structure of interface and surface of multilayered nanoheterostructure thin films, Thin Solid Films, 2018, vol. 656, pp. 44-52. https://doi.org/10.1016/j.tsf.2018.04.024

3. Lee J. W., Prenter P. M. An analysis of the numerical solution of Fredholm integral equations of the first kind, Numerische Mathematik, 1978, vol. 30, no. 1, pp. 1-23. https://doi.org/10.1007/BF01403903

4. Hansen P. C. The Backus-Gilbert method: SVD analysis and fast implementation, Inverse Problems, 1994, vol. 10, no. 4, pp. 895-904. https://doi.org/10.1088/0266-5611/10/4/009

5. Kabanikhin S. I. Definitions and examples of inverse and ill-posed problems, Journal of Inverse and Ill-posed Problems, 2008, vol. 16, no. 4, pp. 317-357. https://doi.org/10.1515/JIIP.2008.019

6. Razavy M. An introduction to inverse problems in physics, Singapore: World Scientific, 2020. https://doi.org/10.1142/11860

7. Wells J. W., Birkinshaw K. A matrix approach to resolution enhancement of XPS spectra by a modified maximum entropy method, Journal of Electron Spectroscopy and Related Phenomena, 2006, vol. 152, no. 1-2, pp. 37-43. https://doi.org/10.1016/j.elspec.2006.03.003

8. Xu P. A new look at Akaike’s Bayesian information criterion for inverse ill-posed problems, Journal of the Franklin Institute, 2021, vol. 358, no. 7, pp. 4077-4102. https://doi.org/10.1016/j.jfranklin.2021.03.003

9. Zheng S., Ding C., Nie F. Regularized singular value decomposition and application to recommender system, arXiv:1804.05090 [cs.LG], 2018. https://arxiv.org/abs/1804.05090v1

10. Xiong X., Xue X. A fractional Tikhonov regularization method for identifying a space-dependent source in the time-fractional diffusion equation, Applied Mathematics and Computation, 2019, vol. 349, pp. 292-303. https://doi.org/10.1016/j.amc.2018.12.063

11. Mohammadian-Behbahani M.-R., Saramad S. Integral-equation based methods for parameter estimation in output pulses of radiation detectors: Application in nuclear medicine and spectroscopy, Nuclear Instruments and Methods in Physics Research. Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2018, vol. 887, pp. 7-12. https://doi.org/10.1016/j.nima.2017.12.073

12. Vasin V. V. Irregular nonlinear operator equations: Tikhonov’s regularization and iterative approximation, Journal of Inverse and Ill-posed Problems, 2013, vol. 21, no. 1, pp. 109-123. https://doi.org/10.1515/jip-2012-0084

13. Qiao B., Liu J., Liu J., Yang Z., Chen X. An enhanced sparse regularization method for impact force identification, Mechanical Systems and Signal Processing, 2019, vol. 126, pp. 341-367. https://doi.org/10.1016/j.ymssp.2019.02.039

14. Leonov A. S. Which of inverse problems can have a priori approximate solution accuracy estimates comparable in order with the data accuracy, Numerical Analysis and Applications, 2014, vol. 7, no. 4, pp. 284-292. https://doi.org/10.1134/S199542391404003X

15. Verlan’ A. F., Sizikov V. S. Integral’nye uravneniya: metody, algoritmy, programmy (Integral equations: methods, algorithms, programs), Kiev: Naukova Dumka, 1986.

16. Morozov V. A. On restoration of noisy signals by a regularization method, Vychislitel’nye Metody i Programmirovanie, 2012, vol. 13, issue 1, pp. 247-252 (in Russian). http://mi.mathnet.ru/eng/vmp26

17. Vasin V. V., Ageev A. L. Ill-posed problems with a priori information, Berlin: De Gruyter, 2013. https://doi.org/10.1515/9783110900118

18. Yagola A. G. Ill-posed problems with apriori information, Sibirskie Elektronnye Matematicheskie Izvestiya, 2010, vol. 7, pp. 343-361 (in Russian). http://mi.mathnet.ru/eng/semr292

19. Nemtsova O. M. Ageev A. L., Voronina E. V. The estimation of the error of the hyperfine interaction parameter distribution from Mossbauer spectra, Nuclear Instruments and Methods in Physics Research. Section B: Beam Interactions with Materials and Atoms, 2002, vol. 187, issue 1, pp. 132-136. https://doi.org/10.1016/S0168-583X(01)00830-8

20. Sussman M. S. Linear signal combination T2 spectroscopy, Magnetic Resonance Imaging, 2020, vol. 66, pp. 257-266. https://doi.org/10.1016/j.mri.2019.11.016

21. Henríquez P. A., Ruz G. A. Noise reduction for near-infrared spectroscopy data using extreme learning machines, Engineering Applications of Artificial Intelligence, 2019, vol. 79, pp. 13-22. https://doi.org/10.10167j.engappai.2018.12.005

22. Zelada-Ríos L., Pacheco-Barrios K., Galecio-Castillo M., Yamunaque-Chunga C., Alvarez-Toledo K., Otiniano-Sifuentes R. Acute disseminated encephalomyelitis and COVID-19: A systematic synthesis of worldwide cases, Journal of Neuroimmunology, 2021, vol. 359, 577674. https://doi.org/10.10167j.jneuroim.2021.577674

23. Miguel R. B., Talebi-Moghaddam S., Zamani M., Turcotte C., Daun K.J. Assessing flare combustion efficiency using imaging Fourier transform spectroscopy, Journal of Quantitative Spectroscopy and Radiative Transfer, 2021, vol. 273, 107835. https://doi.org/10.1016/j.jqsrt.2021.107835

24. Calvetti D., Lewis B., Reichel L., Sgallari F. Tikhonov regularization with nonnegativity constraint, Electronic Transactions on Numerical Analysis, 2004, vol. 18, no. 1, pp. 153-173.

25. Lekhtmakher S., Shapiro M. On the paper “Inverse methods for analyzing aerosol spectrometer measurements: A critical review”, Journal of Aerosol Science, 2000, vol. 31, no. 7, pp. 867-873. https://doi.org/10.1016/S0021-8502(99)00561-3

26. Samaras S., Nicolae D., Bockmann Ch., Vasilescu J., Binietoglou I., Labzovskii L., Toanca F., Papayannis A. Using Raman-lidar-based regularized microphysical retrievals and Aerosol Mass Spectrometer measurements for the characterization of biomass burning aerosols, Journal of Computational Physics, 2015, vol. 299, pp. 156-174. https://doi.org/10.1016/jjcp.2015.06.045

27. Chuev M. A. An effective method for analyzing the hyperfine structure of gamma resonance spectra using the Voith profile, Doklady Akademii Nauk, 2011, vol. 438, no. 6, pp. 747-751 (in Russian). https://www.elibrary.ru/item.asp?id=16525971

28. Pearson K. On the criterion that a given system of deviations from the probable in the case of a correlated system of variables in such that it can be reasonably supposed to have arisen from random sampling, The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. Series 5, 1900, vol. 50, no. 302, pp. 157-175. https://doi.org/10.1080/14786440009463897

29. Taylor J. R. An introduction to error analysis: The study of uncertainties in physical measurements, University Science Books, 1982.

30. Prakash J., Sanny D., Kalva S. K., Pramanik M., Yalavarthy P. K. Fractional regularization to improve photoacoustic tomographic image reconstruction, IEEE Transactions on Medical Imaging, 2019, vol. 38, no. 8, pp. 1935-1947. https://doi.org/10.1109/TMI.2018.2889314

31. Reddy G. D. A class of parameter choice rules for stationary iterated weighted Tikhonov regularization scheme, Applied Mathematics and Computation, 2019, vol. 347, pp. 464-476. https://doi.org/10.1016/j.amc.2018.11.015

32. Mohammady S., Eslahchi M. R. Extension of Tikhonov regularization method using linear fractional programming, Journal of Computational and Applied Mathematics, 2020, vol. 371, 112677. https://doi.org/10.1016Zj.cam.2019.112677

33. Gao Y., Xiao L., Wu B. TSVD and Tikhonov methods and influence factor analysis for NMR data in shale rock, Journal of Petroleum Science and Engineering, 2020, vol. 194, 107508. https://doi.org/10.1016/j.petrol.2020.107508

34. Kim I. G., Latypova N. V., Motorina O. L. Chislennye metody: uchebno-metodicheskoe posobie. Chast’ 2 (Numerical methods: study guide. Part 2), Izhevsk: Udmurt State University, 2013.

35. Nemtsova O. M., Konygin G. N. Improvement of the Tikhonov regularization method for solving the inverse problem of Mossbauer spectroscopy, Journal of Applied Spectroscopy, 2018, vol. 85, no. 5, pp. 931-935. https://doi.org/10.1007/s10812-018-0741-2

36. Nemtsova O. M., Konygin G. N., Porsev V. E. Separation of overlapping spectral lines using the Tikhonov regularization method, Journal of Applied Spectroscopy, 2021, vol. 88, no. 2, pp. 373-381. https://doi.org/10.1007/s10812-021-01185-5

37. Konygin G. N., Nemtsova O. M., Porsev V. E. Mossbauer spectra of solid solutions processed using the Voigt function, Journal of Applied Spectroscopy, 2019, vol. 86, no. 3, pp. 409-415. https://doi.org/10.1007/s10812-019-00834-0

Received 02.10.2021

Tat’yana Mikhailovna Bannikova, Candidate of Pedagogics, Associate Professor, Udmurt State University, ul. Universitetskaya, 1, Izhevsk, 426034, Russia. ORCID: https://orcid.org/0000-0003-4211-8421 E-mail: t.bannikova2011@yandex.ru

Viktor Mikhailovich Nemtsov, Junior Researcher, Udmurt Federal Research Center, Ural Branch of the Russian Academy of Sciences, ul. T. Baramzinoi, 34, Izhevsk, 426067, Russia. ORCID: https://orcid.org/0000-0003-2551-7041 E-mail: viktorn93@gmail.com

Natal’ya Anatol’evna Baranova, Candidate of Pedagogics, Associate Professor, Udmurt State University, ul. Universitetskaya, 1, Izhevsk, 426034, Russia. ORCID: https://orcid.org/0000-0002-4410-3613 E-mail: natik-231@yandex.ru

Grigorii Nikolaevich Konygin, Candidate of Physics and Mathematics, Senior Researcher, Udmurt Federal Research Center, Ural Branch of the Russian Academy of Sciences, ul. T. Baramzinoi, 34, Izhevsk, 426067, Russia.

ORCID: https://orcid.org/0000-0002-6202-9509 E-mail: gnkon@mail.ru

Ol’ga Mikhailovna Nemtsova, Candidate of Physics and Mathematics, Senior Researcher, Udmurt Federal Research Center, Ural Branch of the Russian Academy of Sciences, ul. T. Baramzinoi, 34, Izhevsk, 426067, Russia.

ORCID: https://orcid.org/0000-0002-5676-9578 E-mail: olganemtsova1968@gmail.com

Citation: T. M. Bannikova, V. M. Nemtsov, N. A. Baranova, G. N. Konygin, O. M. Nemtsova. A method for estimating the statistical error of the solution in the inverse spectroscopy problem, Izvestiya Instituta Matematiki i Informatiki Udmurtskogo Gosudarstvennogo Universiteta, 2021, vol. 58, pp. 3-17.