Как найти корни функции алгоритм - Сайт, где вы сможете решить свои вопросы

У этого термина существуют и другие значения, см. Метод (значения).

Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Модификацией метода является метод хорд и касательных. Также метод Ньютона может быть использован для решения задач оптимизации, в которых требуется определить ноль первой производной либо градиента в случае многомерного пространства.

Описание метода[править | править код]

Обоснование[править | править код]

Чтобы численно решить уравнение f(x)=0 методом простой итерации, его необходимо привести к эквивалентному уравнению: , где varphi — сжимающее отображение.

Для наилучшей сходимости метода в точке очередного приближения $x^{*}$ должно выполняться условие ${displaystyle varphi '(x^{*})=0}$ . Решение данного уравнения ищут в виде , тогда:

${displaystyle varphi '(x^{*})=1+alpha '(x^{*})f(x^{*})+alpha (x^{*})f'(x^{*})=0.}$

В предположении, что точка приближения «достаточно близка» к корню и что заданная функция непрерывна ${displaystyle (f(x^{*})approx f({tilde {x}})=0)}$ , окончательная формула для такова:

${displaystyle alpha (x)=-{frac {1}{f'(x)}}.}$

С учётом этого функция определяется:

${displaystyle varphi (x)=x-{frac {f(x)}{f'(x)}}.}$

При некоторых условиях эта функция в окрестности корня осуществляет сжимающее отображение.

В этом случае алгоритм нахождения численного решения уравнения f(x)=0 сводится к итерационной процедуре вычисления:

${displaystyle x_{n+1}=x_{n}-{frac {f(x_{n})}{f'(x_{n})}}.}$

По теореме Банаха последовательность приближений стремится к корню уравнения f(x)=0 .

Иллюстрация метода Ньютона (синим изображена функция , ноль которой необходимо найти, красным — касательная в точке очередного приближения $scriptstyle {x_{n}}$ ). Здесь мы можем увидеть, что последующее приближение $scriptstyle {x_{{n+1}}}$ лучше предыдущего $scriptstyle {x_{n}}$ .

Геометрическая интерпретация[править | править код]

Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к графику исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка берётся в качестве следующего приближения. И так далее, пока не будет достигнута необходимая точность.

Пусть 1) вещественнозначная функция непрерывно дифференцируема на интервале ;
2) существует искомая точка ${displaystyle x^{*}in (a,,b)}$ : ${displaystyle f(x^{*})=0}$ ;
3) существуют C > 0 и такие, что

для ${displaystyle xin (a,,x^{*}-delta ]cup [x^{*}+delta ,,b)}$
и
для ${displaystyle xin (x^{*}-delta ,,x^{*})cup (x^{*},,x^{*}+delta )}$ ;
4) точка ${displaystyle x_{n}in (a,,b)}$ такова, что ${displaystyle f(x_{n})neq 0}$ .
Тогда формула итеративного приближения $x_{n}$ к $x^{{*}}$
может быть выведена из геометрического смысла касательной следующим образом:

${displaystyle f'(x_{n})=mathrm {tg} ,alpha _{n}={frac {Delta y}{Delta x}}={frac {f(x_{n})-0}{x_{n}-x_{n+1}}}={frac {0-f(x_{n})}{x_{n+1}-x_{n}}},}$

где ${displaystyle alpha _{n}}$ — угол наклона касательной прямой
${displaystyle y(x)=f(x_{n})+(x-x_{n})cdot mathrm {tg} ,alpha _{n}}$
к графику
в точке ${displaystyle (x_{n};f(x_{n}))}$ .

Следовательно (в уравнении касательной прямой полагаем ${displaystyle y(x_{n+1})=0}$ ) искомое выражение для $x_{{n+1}}$ имеет вид :

${displaystyle x_{n+1}=x_{n}-{frac {f(x_{n})}{f'(x_{n})}}.}$

Если ${displaystyle x_{n+1}in (a,,b)}$ , то это значение можно использовать в качестве следующего приближения к
$x^{{*}}$ .

Если ${displaystyle x_{n+1}notin (a,,b)}$ , то имеет место «перелёт» (корень $x^{{*}}$ лежит рядом с границей ). В этом случае надо (воспользовавшись идеей метода половинного деления) заменять
$x_{{n+1}}$ на
${displaystyle {frac {x_{n}+x_{n+1}}{2}}}$
до тех пор, пока точка «не вернётся» в область поиска
.

Замечания. 1) Наличие непрерывной производной даёт возможность строить непрерывно меняющуюся касательную на всей области поиска решения .
2) Случаи граничного (в точке или в точке ) расположения искомого решения $x^{{*}}$ рассматриваются аналогичным образом.
3) С геометрической точки зрения равенство
${displaystyle f'(x_{n})=0}$
означает, что касательная прямая к графику

в точке
${displaystyle (x_{n};f(x_{n}))}$ –
параллельна оси

и при
${displaystyle f(x_{n})neq 0}$
не пересекается с ней в конечной части.
4) Чем больше константа C > 0 и чем меньше константа из пункта 3 условий,
тем для ${displaystyle x_{n}in (a,,x^{*}-delta ]cup [x^{*}+delta ,,b)}$
пересечение касательной к графику и оси ближе к точке ${displaystyle (x^{*};;0)}$ ,
то есть тем ближе значение $x_{{n+1}}$ к искомой ${displaystyle x^{*}in (a,,b)}$ .

Итерационный процесс начинается с некоторого начального приближения
${displaystyle x_{0}in (a,,b)}$ ,
причём между
${displaystyle x_{0}in (a,,b)}$
и искомой точкой
${displaystyle x^{*}in (a,,b)}$
не должно быть других нулей функции
,
то есть «чем ближе $x_{0}$
к искомому корню $x^{{*}}$ ,
тем лучше». Если предположения о нахождении $x^{{*}}$ отсутствуют, методом проб и ошибок можно сузить область возможных значений, применив теорему о промежуточных значениях.

Для предварительно заданных ${displaystyle varepsilon _{x}>0}$ , ${displaystyle varepsilon _{f}>0}$
итерационный процесс завершается если
${displaystyle leftvert {frac {f(x_{n})}{f'(x_{n})}}rightvert approx vert x_{n+1}-x_{n}vert <varepsilon _{x}}$ и
${displaystyle vert f(x_{n+1})vert <varepsilon _{f}}$ .
В частности, для матрицы дисплея ${displaystyle varepsilon _{x}}$ и ${displaystyle varepsilon _{f}}$ могут быть рассчитаны,
исходя из масштаба отображения графика ,
то есть если $x_{n}$ и $x_{{n+1}}$ попадают в один вертикальный, а ${displaystyle f(x_{n})}$ и ${displaystyle f(x_{n+1})}$ в один горизонтальный ряд.

Алгоритм[править | править код]

Задается начальное приближение $x_{0}$ .
Пока не выполнено условие остановки, в качестве которого можно взять ${displaystyle |x_{n+1}-x_{n}|<varepsilon }$ или ${displaystyle |f(x_{n+1})|<varepsilon }$ (то есть погрешность в нужных пределах), вычисляют новое приближение: ${displaystyle x_{n+1}=x_{n}-{frac {f(x_{n})}{f'(x_{n})}}}$ .

Пример[править | править код]

Иллюстрация применения метода Ньютона к функции $f(x)=cos x-x^{3}$ с начальным приближением в точке $x_{0}=0{,}5$ .
График последовательных приближений.	График сходимости.
Согласно способу практического определения скорость сходимости может быть оценена как тангенс угла наклона графика сходимости, то есть в данном случае равна двум.

Рассмотрим задачу о нахождении положительных , для которых $cos x=x^{3}$ . Эта задача может быть представлена как задача нахождения нуля функции $f(x)=cos x-x^{3}$ . Имеем выражение для производной $f'(x)=-sin x-3x^{2}$ . Так как для всех и $x^{3}>1$ для x>1 , очевидно, что решение лежит между 0 и 1. Возьмём в качестве начального приближения значение $x_{0}=0{,}5$ , тогда:

${begin{matrix}x_{1}&=&x_{0}-{dfrac {f(x_{0})}{f'(x_{0})}}&=&1{,}112;141;637;097,\x_{2}&=&x_{1}-{dfrac {f(x_{1})}{f'(x_{1})}}&=&underline {0{,}}909;672;693;736,\x_{3}&=&x_{2}-{dfrac {f(x_{2})}{f'(x_{2})}}&=&underline {0{,}86}7;263;818;209,\x_{4}&=&x_{3}-{dfrac {f(x_{3})}{f'(x_{3})}}&=&underline {0{,}865;47}7;135;298,\x_{5}&=&x_{4}-{dfrac {f(x_{4})}{f'(x_{4})}}&=&underline {0{,}865;474;033;1}11,\x_{6}&=&x_{5}-{dfrac {f(x_{5})}{f'(x_{5})}}&=&underline {0{,}865;474;033;102}.end{matrix}}$

Подчёркиванием отмечены верные значащие цифры. Видно, что их количество от шага к шагу растёт (приблизительно удваиваясь с каждым шагом): от 1 к 2, от 2 к 5, от 5 к 10, иллюстрируя квадратичную скорость сходимости.

Условия применения[править | править код]

Иллюстрация расхождения метода Ньютона, применённого к функции $scriptstyle {f(x)=x^{3}-2x+2}$ с начальным приближением в точке $scriptstyle {x_{0}=0}$ .

Рассмотрим ряд примеров, указывающих на недостатки метода.

Контрпримеры[править | править код]

Если начальное приближение недостаточно близко к решению, то метод может не сойтись.

Пусть

${displaystyle f(x)=x^{3}-2x+2.}$

Тогда

$x_{{n+1}}=x_{{n}}-{frac {x_{n}^{3}-2x_{n}+2}{3x_{n}^{2}-2}}.$

Возьмём ноль в качестве начального приближения. Первая итерация даст в качестве приближения единицу. В свою очередь, вторая снова даст ноль. Метод зациклится и решение не будет найдено. В общем случае построение последовательности приближений может быть очень запутанным.

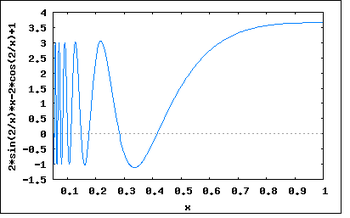
График производной функции $scriptstyle {f(x)=x+x^{2}sin(2/x)}$ при приближении к нулю справа.

Если производная не непрерывна в точке корня, то метод может расходиться в любой окрестности корня.

Рассмотрим функцию:

${displaystyle f(x)={begin{cases}0,&x=0,\x+x^{2}sin left({dfrac {2}{x}}right),&xneq 0.end{cases}}}$

Тогда и всюду, кроме 0.

В окрестности корня производная меняет знак при приближении к нулю справа или слева. В то время, как ${displaystyle f(x)geqslant x-x^{2}>0}$ для .

Таким образом не ограничено вблизи корня, и метод будет расходиться, хотя функция всюду дифференцируема, её производная не равна нулю в корне, бесконечно дифференцируема везде, кроме как в корне, а её производная ограничена в окрестности корня.

Если не существует вторая производная в точке корня, то скорость сходимости метода может быть заметно снижена.

Рассмотрим пример:

${displaystyle f(x)=x+x^{4/3}.}$

Тогда ${displaystyle f'(x)=1+(4/3)x^{1/3}}$ и ${displaystyle f''(x)=(4/9)x^{-2/3}}$ за исключением x=0 , где она не определена.

На очередном шаге имеем $x_{n}$ :

${displaystyle x_{n+1}=x_{n}-{frac {f(x_{n})}{f'(x_{n})}}={frac {(1/3)x_{n}^{4/3}}{(1+(4/3)x_{n}^{1/3})}}.}$

Скорость сходимости полученной последовательности составляет приблизительно 4/3. Это существенно меньше, нежели 2, необходимое для квадратичной сходимости, поэтому в данном случае можно говорить лишь о линейной сходимости, хотя функция всюду непрерывно дифференцируема, производная в корне не равна нулю, и бесконечно дифференцируема везде, кроме как в корне.

Если производная в точке корня равна нулю, то скорость сходимости не будет квадратичной, а сам метод может преждевременно прекратить поиск, и дать неверное для заданной точности приближение.

Пусть

${displaystyle f(x)=x^{2}.}$

Тогда и следовательно . Таким образом сходимость метода не квадратичная, а линейная, хотя функция всюду бесконечно дифференцируема.

Ограничения[править | править код]

Пусть задано уравнение f(x)=0 , где и надо найти его решение.

Ниже приведена формулировка основной теоремы, которая позволяет дать чёткие условия применимости. Она носит имя советского математика и экономиста Леонида Витальевича Канторовича (1912—1986).

Теорема Канторовича.

Если существуют такие константы , что:

${displaystyle {frac {1}{|f'(x)|}}<A}$ на , то есть сут и не равна нулю;
${displaystyle left|{frac {f(x)}{f'(x)}}right|<B}$ на , то есть ограничена;
на , и ${displaystyle |f''(x)|leqslant Cleqslant {frac {1}{2AB}}}$ ;

Причём длина рассматриваемого отрезка ${displaystyle |a-b|<{frac {1}{AB}}left(1-{sqrt {1-2ABC}}right)}$ . Тогда справедливы следующие утверждения:

на существует корень $x^{*}$ уравнения ${displaystyle f(x)=0colon exists x^{*}in [a,;b]colon f(x^{*})=0}$ ;
если ${displaystyle x_{0}={frac {a+b}{2}}}$ , то итерационная последовательность сходится к этому корню: ${displaystyle left{x_{n+1}=x_{n}-{frac {f(x_{n})}{f'(x_{n})}}right}to x^{*}}$ ;
погрешность может быть оценена по формуле ${displaystyle |x^{*}-x_{n}|leqslant {frac {B}{2^{n-1}}}(2ABC)^{2^{n-1}}}$ .

Из последнего из утверждений теоремы в частности следует квадратичная сходимость метода:

${displaystyle |x^{*}-x_{n}|leqslant {frac {B}{2^{n-1}}}(2ABC)^{2^{n-1}}={frac {1}{2}}{frac {B}{2^{n-2}}}left((2ABC)^{2^{n-2}}right)^{2}=alpha |x^{*}-x_{n-1}|^{2}.}$

Тогда ограничения на исходную функцию f(x) будут выглядеть так:

функция должна быть ограничена;
функция должна быть гладкой, дважды дифференцируемой;
её первая производная равномерно отделена от нуля;
её вторая производная должна быть равномерно ограничена.

Историческая справка[править | править код]

Метод был описан Исааком Ньютоном в рукописи «Об анализе уравнениями бесконечных рядов» (лат. «De analysi per aequationes numero terminorum infinitas»), адресованной в 1669 году Барроу, и в работе «Метод флюксий и бесконечные ряды» (лат. «De metodis fluxionum et serierum infinitarum») или «Аналитическая геометрия» (лат. «Geometria analytica») в собраниях трудов Ньютона, которая была написана в 1671 году. В своих работах Ньютон вводит такие понятия, как разложение функции в ряд, бесконечно малые и флюксии (производные в нынешнем понимании). Указанные работы были изданы значительно позднее: первая вышла в свет в 1711 году благодаря Уильяму Джонсону, вторая была издана Джоном Кользоном в 1736 году уже после смерти создателя. Однако описание метода существенно отличалось от его нынешнего изложения: Ньютон применял свой метод исключительно к полиномам. Он вычислял не последовательные приближения $x_{n}$ , а последовательность полиномов и в результате получал приближённое решение .

Впервые метод был опубликован в трактате «Алгебра» Джона Валлиса в 1685 году, по просьбе которого он был кратко описан самим Ньютоном. В 1690 году Джозеф Рафсон опубликовал упрощённое описание в работе «Общий анализ уравнений» (лат. «Analysis aequationum universalis»). Рафсон рассматривал метод Ньютона как чисто алгебраический и ограничил его применение полиномами, однако при этом он описал метод на основе последовательных приближений $x_{n}$ вместо более трудной для понимания последовательности полиномов, использованной Ньютоном. Наконец, в 1740 году метод Ньютона был описан Томасом Симпсоном как итеративный метод первого порядка решения нелинейных уравнений с использованием производной в том виде, в котором он излагается здесь. В той же публикации Симпсон обобщил метод на случай системы из двух уравнений и отметил, что метод Ньютона также может быть применён для решения задач оптимизации путём нахождения нуля производной или градиента.

В 1879 году Артур Кэли в работе «Проблема комплексных чисел Ньютона — Фурье» (англ. «The Newton-Fourier imaginary problem») был первым, кто отметил трудности в обобщении метода Ньютона на случай мнимых корней полиномов степени выше второй и комплексных начальных приближений. Эта работа открыла путь к изучению теории фракталов.

Обобщения и модификации[править | править код]

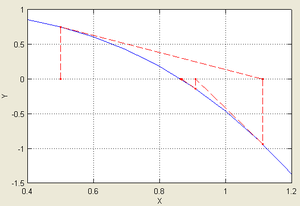
Иллюстрация последовательных приближений метода одной касательной, применённого к функции $scriptstyle {f(x)=e^{x}-2}$ с начальным приближением в точке $scriptstyle {x_{0}=1{,}8}$ .

Метод секущих[править | править код]

Родственный метод секущих является «приближённым» методом Ньютона и позволяет не вычислять производную. Значение производной в итерационной формуле заменяется её оценкой по двум предыдущим точкам итераций:

${displaystyle f'(x_{n})approx {frac {f(x_{n})-f(x_{n-1})}{x_{n}-x_{n-1}}}}$ .

Таким образом, основная формула имеет вид

${displaystyle x_{n+1}=x_{n}-f(x_{n})cdot {frac {x_{n}-x_{n-1}}{f(x_{n})-f(x_{n-1})}}.}$

Этот метод схож с методом Ньютона, но имеет немного меньшую скорость сходимости. Порядок сходимости метода равен золотому сечению — 1,618…

Замечания. 1) Для начала итерационного процесса требуются два различных значения
$x_{0}$ и
$x_{1}$ .
2) В отличие от «настоящего метода Ньютона» (метода касательных), требующего хранить только ${displaystyle x_{n}}$
(и в ходе вычислений — временно ${displaystyle f(x_{n})}$ и ${displaystyle f'(x_{n})}$ ),
для метода секущих требуется сохранение
${displaystyle x_{n-1}}$ ,
${displaystyle x_{n}}$ ,
${displaystyle f(x_{n-1})}$ ,
${displaystyle f(x_{n})}$ .
3) Применяется, если вычисление f'(x) затруднено
(например, требует большого количества машинных ресурсов: времени и/или памяти).

Метод одной касательной[править | править код]

В целях уменьшения числа обращений к значениям производной функции применяют так называемый метод одной касательной.

Формула итераций этого метода имеет вид:

${displaystyle x_{n+1}=x_{n}-{frac {1}{f'(x_{0})}}f(x_{n}).}$

Суть метода заключается в том, чтобы вычислять производную лишь один раз, в точке начального приближения $x_{0}$ , а затем использовать это значение на каждой последующей итерации:

${displaystyle alpha (x)=alpha _{0}=-{dfrac {1}{f'(x_{0})}}.}$

При таком выборе $alpha _{0}$ в точке $x_{0}$ выполнено равенство:

${displaystyle varphi '(x_{0})=1+alpha _{0}f'(x_{0})=0,}$

и если отрезок, на котором предполагается наличие корня $x^{*}$ и выбрано начальное приближение $x_{0}$ , достаточно мал, а производная непрерывна, то значение ${displaystyle varphi '(x^{*})}$ будет не сильно отличаться от ${displaystyle varphi '(x_{0})=0}$ и, следовательно, график пройдёт почти горизонтально, пересекая прямую y=x , что в свою очередь обеспечит быструю сходимость последовательности точек приближений к корню.

Этот метод является частным случаем метода простой итерации. Он имеет линейный порядок сходимости.

Метод Ньютона-Фурье[править | править код]

Метод Ньютона-Фурье – это расширение метода Ньютона, выведенное Жозефом Фурье для получения оценок на абсолютную ошибку аппроксимации корня, в то же время обеспечивая квадратичную сходимость с обеих сторон.

Предположим, что f(x) дважды непрерывно дифференцируема на отрезке [a, b] и что f имеет корень на этом интервале. Дополнительно положим, что f′(x), f″(x) ≠ 0 на этом отрезке (например, это верно, если f(a) < 0, f(b) > 0, и f″(x) > 0 на этом отрезке). Это гарантирует наличие единственного корня на этом отрезке, обозначим его α. Эти рассуждения относятся к вогнутой вверх функции. Если она вогнута вниз, то заменим f(x) на −f(x), поскольку они имеют одни и те же корни.

Пусть x₀ = b будет правым концом отрезка, на котором мы ищем корень, а z₀ = a – левым концом того же отрезка. Если x_n найдено, определим

${displaystyle x_{n+1}=x_{n}-{frac {f(x_{n})}{f'(x_{n})}},}$

которое выражает обычный метод Ньютона, как описано выше. Затем определим

${displaystyle z_{n+1}=z_{n}-{frac {f(z_{n})}{f'(x_{n})}},}$

где знаменатель равен f′(x_n), а не f′(z_n). Итерации x_n будут строго убывающими к корню, а итерации z_n – строго возрастающими к корню. Также выполняется следующее соотношение:

${displaystyle lim _{nto infty }{frac {x_{n+1}-z_{n+1}}{(x_{n}-z_{n})^{2}}}={frac {f''(alpha )}{2f'(alpha )}}}$

таким образом, расстояние между x_n и z_n уменьшается квадратичным образом.

Многомерный случай[править | править код]

Обобщим полученный результат на многомерный случай.

Пусть необходимо найти решение системы:

${displaystyle left{{begin{array}{lcr}f_{1}(x_{1},;x_{2},;ldots ,;x_{n})&=&0,\ldots &&\f_{m}(x_{1},;x_{2},;ldots ,;x_{n})&=&0.end{array}}right.}$

Выбирая некоторое начальное значение ${displaystyle {vec {x}}^{[0]}}$ , последовательные приближения ${displaystyle {vec {x}}^{[j+1]}}$ находят путём решения систем уравнений:

${displaystyle f_{i}+sum _{k=1}^{n}{frac {partial f_{i}}{partial x_{k}}}(x_{k}^{[j+1]}-x_{k}^{[j]})=0,qquad i=1,;2,;ldots ,;m,}$

где ${displaystyle {vec {x}}^{[j]}=(x_{1}^{[j]},;x_{2}^{[j]},;ldots ,;x_{n}^{[j]}),quad j=0,;1,;2,;ldots }$ .

Применительно к задачам оптимизации[править | править код]

Пусть необходимо найти минимум функции многих переменных ${displaystyle f({vec {x}})colon mathbb {R} ^{n}to mathbb {R} }$ . Эта задача равносильна задаче нахождения нуля градиента . Применим изложенный выше метод Ньютона:

${displaystyle nabla f({vec {x}}^{[j]})+H({vec {x}}^{[j]})({vec {x}}^{[j+1]}-{vec {x}}^{[j]})=0,quad j=1,;2,;ldots ,;n,}$

где — гессиан функции .

В более удобном итеративном виде это выражение выглядит так:

${displaystyle {vec {x}}^{[j+1]}={vec {x}}^{[j]}-H^{-1}({vec {x}}^{[j]})nabla f({vec {x}}^{[j]}).}$

В случае квадратичной функции метод Ньютона находит экстремум за одну итерацию.

Нахождение матрицы Гессе связано с большими вычислительными затратами, и зачастую не представляется возможным. В таких случаях альтернативой могут служить квазиньютоновские методы, в которых приближение матрицы Гессе строится в процессе накопления информации о кривизне функции.

Метод Ньютона — Рафсона[править | править код]

Метод Ньютона — Рафсона является улучшением метода Ньютона нахождения экстремума, описанного выше. Основное отличие заключается в том, что на очередной итерации каким-либо из методов одномерной оптимизации выбирается оптимальный шаг:

${displaystyle {vec {x}}^{[j+1]}={vec {x}}^{[j]}-lambda _{j}H^{-1}({vec {x}}^{[j]})nabla f({vec {x}}^{[j]}),}$

где ${displaystyle lambda _{j}=arg min _{lambda }f({vec {x}}^{[j]}-lambda H^{-1}({vec {x}}^{[j]})nabla f({vec {x}}^{[j]})).}$
Для оптимизации вычислений применяют следующее улучшение: вместо того, чтобы на каждой итерации заново вычислять гессиан целевой функции, ограничиваются начальным приближением ${displaystyle H(f({vec {x}}^{[0]}))}$ и обновляют его лишь раз в шагов, либо не обновляют вовсе.

Применительно к задачам о наименьших квадратах[править | править код]

На практике часто встречаются задачи, в которых требуется произвести настройку свободных параметров объекта или подогнать математическую модель под реальные данные. В этих случаях появляются задачи о наименьших квадратах:

$F({vec {x}})=|{vec {f}}({vec {x}})|=sum _{{i=1}}^{m}f_{i}^{2}({vec {x}})=sum _{{i=1}}^{m}(varphi _{i}({vec {x}})-{mathcal {F}}_{i})^{2}to min .$

Эти задачи отличаются особым видом градиента и матрицы Гессе:

$nabla F({vec {x}})=2J^{T}({vec {x}}){vec {f}}({vec {x}}),$

$H({vec {x}})=2J^{T}({vec {x}})J({vec {x}})+2Q({vec {x}}),qquad Q({vec {x}})=sum _{{i=1}}^{m}f_{i}({vec {x}})H_{i}({vec {x}}),$

где — матрица Якоби вектор-функции , $H_{i}({vec {x}})$ — матрица Гессе для её компоненты $f_{i}({vec {x}})$ .

Тогда очередной шаг определяется из системы:

$left[J^{T}({vec {x}})J({vec {x}})+sum _{{i=1}}^{m}f_{i}({vec {x}})H_{i}({vec {x}})right]{vec {p}}=-J^{T}({vec {x}}){vec {f}}({vec {x}}).$

Метод Гаусса — Ньютона[править | править код]

Метод Гаусса — Ньютона строится на предположении о том, что слагаемое $J^{T}({vec {x}})J({vec {x}})$ доминирует над . Это требование не соблюдается, если минимальные невязки велики, то есть если норма сравнима с максимальным собственным значением матрицы $J^{T}({vec {x}})J({vec {x}})$ . В противном случае можно записать:

$J^{T}({vec {x}})J({vec {x}}){vec {p}}=-J^{T}({vec {x}}){vec {f}}({vec {x}}).$

Таким образом, когда норма близка к нулю, а матрица имеет полный столбцевой ранг, шаг мало отличается от ньютоновского (с учётом ), и метод может достигать квадратичной скорости сходимости, хотя вторые производные и не учитываются. Улучшением метода является алгоритм Левенберга — Марквардта, основанный на эвристических соображениях.

Обобщение на комплексную плоскость[править | править код]

Бассейны Ньютона для полинома пятой степени $scriptstyle {p(x)=x^{5}-1}$ . Разными цветами закрашены области притяжения для разных корней. Более тёмные области соответствуют большему числу итераций.

До сих пор в описании метода использовались функции, осуществляющие отображения в пределах множества вещественных значений. Однако метод может быть применён и для нахождения нуля функции комплексной переменной. При этом процедура остаётся неизменной:

${displaystyle z_{n+1}=z_{n}-{frac {f(z_{n})}{f'(z_{n})}}.}$

Особый интерес представляет выбор начального приближения $z_{0}$ . Ввиду того, что функция может иметь несколько нулей, в различных случаях метод может сходиться к различным значениям, и вполне естественно возникает желание выяснить, какие области обеспечат сходимость к тому или иному корню. Этот вопрос заинтересовал Артура Кэли ещё в 1879 году, однако разрешить его смогли лишь в 70-х годах двадцатого столетия с появлением вычислительной техники. Оказалось, что на пересечениях этих областей (их принято называть областями притяжения) образуются так называемые фракталы — бесконечные самоподобные геометрические фигуры.

Ввиду того, что Ньютон применял свой метод исключительно к полиномам, фракталы, образованные в результате такого применения, обрели название фракталов Ньютона или бассейнов Ньютона.

Реализация[править | править код]

Scala[править | править код]

object NewtonMethod {

  val accuracy = 1e-6

  @tailrec
  def method(x0: Double, f: Double => Double, dfdx: Double => Double, e: Double): Double = {
    val x1 = x0 - f(x0) / dfdx(x0)
    if (abs(x1 - x0) < e) x1
    else method(x1, f, dfdx, e)
  }

  def g(C: Double) = (x: Double) => x*x - C

  def dgdx(x: Double) = 2*x

  def sqrt(x: Double) = x match {
    case 0 => 0
    case x if (x < 0) => Double.NaN
    case x if (x > 0) => method(x/2, g(x), dgdx, accuracy) 
  }
}

Python[править | править код]

from math import sin, cos
from typing import Callable
import unittest


def newton(f: Callable[[float], float], f_prime: Callable[[float], float], x0: float, 
	eps: float=1e-7, kmax: int=1e3) -> float:
	"""
	solves f(x) = 0 by Newton's method with precision eps
	:param f: f
	:param f_prime: f'
	:param x0: starting point
	:param eps: precision wanted
	:return: root of f(x) = 0
	"""
	x, x_prev, i = x0, x0 + 2 * eps, 0
	
	while abs(x - x_prev) >= eps and i < kmax:
		x, x_prev, i = x - f(x) / f_prime(x), x, i + 1

	return x


class TestNewton(unittest.TestCase):
	def test_0(self):
		def f(x: float) -> float:
			return x**2 - 20 * sin(x)


		def f_prime(x: float) -> float:
			return 2 * x - 20 * cos(x)


		x0, x_star = 2, 2.7529466338187049383

		self.assertAlmostEqual(newton(f, f_prime, x0), x_star)


if __name__ == '__main__':
	unittest.main()

PHP[править | править код]

<?php
// PHP 5.4
function newtons_method(
	$a = -1, $b = 1, 
	$f = function($x) {
	
		return pow($x, 4) - 1;
	
	},
	$derivative_f = function($x) {

		return 4 * pow($x, 3);
	
	}, $eps = 1E-3) {

        $xa = $a;
        $xb = $b;

        $iteration = 0;

        while (abs($xb) > $eps) {

            $p1 = $f($xa);
            $q1 = $derivative_f($xa);
            $xa -= $p1 / $q1;
            $xb = $p1;
            ++$iteration;

        }

        return $xa;

}

Octave[править | править код]

function res = nt()
  eps = 1e-7;
  x0_1 = [-0.5,0.5];
  max_iter = 500;
  xopt = new(@resh, eps, max_iter);   
  xopt
endfunction
function a = new(f, eps, max_iter)
  x=-1;
  p0=1;
  i=0;
 while (abs(p0)>=eps)
    [p1,q1]=f(x);
    x=x-p1/q1;
   p0=p1;
   i=i+1;
 end
 i
 a=x;
endfunction
function[p,q]= resh(x)   % p= -5*x.^5+4*x.^4-12*x.^3+11*x.^2-2*x+1;
   p=-25*x.^4+16*x.^3-36*x.^2+22*x-2;
   q=-100*x.^3+48*x.^2-72*x+22;
endfunction

Delphi[править | править код]

// вычисляемая функция
function fx(x: Double): Double;
begin
  Result := x * x - 17;
end;

// производная функция от f(x)
function dfx(x: Double): Double;
begin
  Result := 2 * x;
end;

function solve(fx, dfx: TFunc<Double, Double>; x0: Double): Double;
const
  eps = 0.000001;
var
  x1: Double;
begin
  x1 := x0 - fx(x0) / dfx(x0); // первое приближение
  while (Abs(x1-x0) > eps) do begin // пока не достигнута точность 0.000001
    x0 := x1;
    x1 := x1 - fx(x1) / dfx(x1); // последующие приближения
  end;
  Result := x1;
end;

// Вызов
solve(fx, dfx,4));

C++[править | править код]

#include <stdio.h>
#include <math.h>

#define eps 0.000001
double fx(double x) { return x * x - 17;} // вычисляемая функция
double dfx(double x) { return 2 * x;} // производная функции

typedef double(*function)(double x); // задание типа function

double solve(function fx, function dfx, double x0) {
  double x1  = x0 - fx(x0) / dfx(x0); // первое приближение
  while (fabs(x1 - x0) > eps) { // пока не достигнута точность 0.000001
    x0 = x1;
    x1 = x0 - fx(x0) / dfx(x0); // последующие приближения
  }
  return x1;
}

int main () {
  printf("%fn", solve(fx, dfx, 4)); // вывод на экран
  return 0;
}

C[править | править код]

typedef double (*function)(double x);

double TangentsMethod(function f, function df, double xn, double eps) {
   double x1  = xn - f(xn)/df(xn);
   double x0 = xn;
   while(abs(x0-x1) > eps) {
      x0 = x1;
      x1 = x1 - f(x1)/df(x1);
   }
   return x1;
}

//Выбор начального приближения
xn = MyFunction(A)*My2Derivative(A) > 0 ? B : A;

double MyFunction(double x) { return (pow(x, 5) - x - 0.2); } //Ваша функция
double MyDerivative(double x) { return (5*pow(x, 4) - 1); } //Первая производная
double My2Derivative(double x) { return (20*pow(x, 3)); } //Вторая производная

//Пример вызова функции
double x = TangentsMethod(MyFunction, MyDerivative, xn, 0.1)

Haskell[править | править код]

import Data.List ( iterate' )

main :: IO ()
main = print $ solve ( x -> x * x - 17) ( * 2) 4

-- Функция solve универсальна для всех вещественных типов значения которых можно сравнивать.
solve = esolve 0.000001

esolve epsilon func deriv x0 = fst . head $ dropWhile pred pairs
  where
    pred (xn, xn1) = (abs $ xn - xn1) > epsilon -- Функция pred определяет достигнута ли необходимая точность.
    next xn = xn - func xn / deriv xn -- Функция next вычисляет новое приближение.
    iters   = iterate' next x0        -- Бесконечный список итераций.
    pairs   = zip iters (tail iters)  -- Бесконечный список пар итераций вида: [(x0, x1), (x1, x2) ..].

Литература[править | править код]

Акулич И. Л. Математическое программирование в примерах и задачах : Учеб. пособие для студентов эконом. спец. вузов. — М. : Высшая школа, 1986. — 319 с. : ил. — ББК 22.1 А44. — УДК 517.8^(G).
Амосов А. А., Дубинский Ю. А., Копченова Н. П. Вычислительные методы для инженеров : Учеб. пособие. — М. : Высшая школа, 1994. — 544 с. : ил. — ББК 32.97 А62. — УДК 683.1^(G). — ISBN 5-06-000625-5.
Бахвалов Н. С., Жидков Н. П., Кобельков Г. Г. Численные методы. — 8-е изд. — М. : Лаборатория Базовых Знаний, 2000.
Вавилов С. И. Исаак Ньютон. — М. : Изд. АН СССР, 1945.
Волков Е. А. Численные методы. — М. : Физматлит, 2003.
Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. — М. : Мир, 1985.
Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М. : Наука, 1970. — С. 575—576.
Коршунов Ю. М., Коршунов Ю. М. Математические основы кибернетики. — Энергоатомиздат, 1972.
Максимов Ю. А.,Филлиповская Е. А. Алгоритмы решения задач нелинейного программирования. — М. : МИФИ, 1982.
Морозов А. Д. Введение в теорию фракталов. — МИФИ, 2002.

См. также[править | править код]

Метод простой итерации
Двоичный поиск
Метод дихотомии
Метод секущих
Метод Мюллера
Метод хорд
Метод бисекции
Фрактал
Численное решение уравнений
Целочисленный квадратный корень
Быстрый обратный квадратный корень

Ссылки[править | править код]

«Бассейны Ньютона» на сайте fractalworld.xaoc.ru
«Исаак Ньютон» на сайте www.scottish-wetlands.org
«Математические работы Канторовича» на сайте Института математики СО РАН
Hazewinkel, Michiel, ed. (2001), Newton method, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Weisstein, Eric W. Newton’s Method (англ.) на сайте Wolfram MathWorld.
Newton’s method, Citizendium.
Mathews, J., The Accelerated and Modified Newton Methods, Course notes.
Wu, X., Roots of Equations, Course notes.

Источник

From Wikipedia, the free encyclopedia

In mathematics and computing, a root-finding algorithm is an algorithm for finding zeros, also called “roots”, of continuous functions. A zero of a function f, from the real numbers to real numbers or from the complex numbers to the complex numbers, is a number x such that f(x) = 0. As, generally, the zeros of a function cannot be computed exactly nor expressed in closed form, root-finding algorithms provide approximations to zeros, expressed either as floating-point numbers or as small isolating intervals, or disks for complex roots (an interval or disk output being equivalent to an approximate output together with an error bound).^[1]

Solving an equation f(x) = g(x) is the same as finding the roots of the function h(x) = f(x) – g(x). Thus root-finding algorithms allow solving any equation defined by continuous functions. However, most root-finding algorithms do not guarantee that they will find all the roots; in particular, if such an algorithm does not find any root, that does not mean that no root exists.

Most numerical root-finding methods use iteration, producing a sequence of numbers that hopefully converges towards the root as its limit. They require one or more initial guesses of the root as starting values, then each iteration of the algorithm produces a successively more accurate approximation to the root. Since the iteration must be stopped at some point, these methods produce an approximation to the root, not an exact solution. Many methods compute subsequent values by evaluating an auxiliary function on the preceding values. The limit is thus a fixed point of the auxiliary function, which is chosen for having the roots of the original equation as fixed points, and for converging rapidly to these fixed points.

The behavior of general root-finding algorithms is studied in numerical analysis. However, for polynomials, root-finding study belongs generally to computer algebra, since algebraic properties of polynomials are fundamental for the most efficient algorithms. The efficiency of an algorithm may depend dramatically on the characteristics of the given functions. For example, many algorithms use the derivative of the input function, while others work on every continuous function. In general, numerical algorithms are not guaranteed to find all the roots of a function, so failing to find a root does not prove that there is no root. However, for polynomials, there are specific algorithms that use algebraic properties for certifying that no root is missed, and locating the roots in separate intervals (or disks for complex roots) that are small enough to ensure the convergence of numerical methods (typically Newton’s method) to the unique root so located.

Bracketing methods[edit]

Bracketing methods determine successively smaller intervals (brackets) that contain a root. When the interval is small enough, then a root has been found. They generally use the intermediate value theorem, which asserts that if a continuous function has values of opposite signs at the end points of an interval, then the function has at least one root in the interval. Therefore, they require to start with an interval such that the function takes opposite signs at the end points of the interval. However, in the case of polynomials there are other methods (Descartes’ rule of signs, Budan’s theorem and Sturm’s theorem) for getting information on the number of roots in an interval. They lead to efficient algorithms for real-root isolation of polynomials, which ensure finding all real roots with a guaranteed accuracy.

Bisection method[edit]

The simplest root-finding algorithm is the bisection method. Let f be a continuous function, for which one knows an interval [a, b] such that f(a) and f(b) have opposite signs (a bracket). Let c = (a +b)/2 be the middle of the interval (the midpoint or the point that bisects the interval). Then either f(a) and f(c), or f(c) and f(b) have opposite signs, and one has divided by two the size of the interval. Although the bisection method is robust, it gains one and only one bit of accuracy with each iteration. Therefore, the number of function evaluations required for finding an ε-approximate root is ${displaystyle log _{2}{frac {b-a}{varepsilon }}}$ . Other methods, under appropriate conditions, can gain accuracy faster.

False position (regula falsi)[edit]

The false position method, also called the regula falsi method, is similar to the bisection method, but instead of using bisection search’s middle of the interval it uses the x-intercept of the line that connects the plotted function values at the endpoints of the interval, that is

${displaystyle c={frac {af(b)-bf(a)}{f(b)-f(a)}}.}$

False position is similar to the secant method, except that, instead of retaining the last two points, it makes sure to keep one point on either side of the root. The false position method can be faster than the bisection method and will never diverge like the secant method; however, it may fail to converge in some naive implementations due to roundoff errors that may lead to a wrong sign for f(c); typically, this may occur if the rate of variation of f is large in the neighborhood of the root.

ITP method[edit]

The ITP method is the only known method to bracket the root with the same worst case guarantees of the bisection method while guaranteeing a superlinear convergence to the root of smooth functions as the secant method. It is also the only known method guaranteed to outperform the bisection method on the average for any continuous distribution on the location of the root (see ITP Method#Analysis). It does so by keeping track of both the bracketing interval as well as the minmax interval in which any point therein converges as fast as the bisection method. The construction of the queried point c follows three steps: interpolation (similar to the regula falsi), truncation (adjusting the regula falsi similar to Regula falsi § Improvements in regula falsi) and then projection onto the minmax interval. The combination of these steps produces a simultaneously minmax optimal method with guarantees similar to interpolation based methods for smooth functions, and, in practice will outperform both the bisection method and interpolation based methods under both smooth and non-smooth functions.

Interpolation[edit]

Many root-finding processes work by interpolation. This consists in using the last computed approximate values of the root for approximating the function by a polynomial of low degree, which takes the same values at these approximate roots. Then the root of the polynomial is computed and used as a new approximate value of the root of the function, and the process is iterated.

Two values allow interpolating a function by a polynomial of degree one (that is approximating the graph of the function by a line). This is the basis of the secant method. Three values define a quadratic function, which approximates the graph of the function by a parabola. This is Muller’s method.

Regula falsi is also an interpolation method, which differs from the secant method by using, for interpolating by a line, two points that are not necessarily the last two computed points.

Iterative methods[edit]

Although all root-finding algorithms proceed by iteration, an iterative root-finding method generally uses a specific type of iteration, consisting of defining an auxiliary function, which is applied to the last computed approximations of a root for getting a new approximation. The iteration stops when a fixed point (up to the desired precision) of the auxiliary function is reached, that is when the new computed value is sufficiently close to the preceding ones.

Newton’s method (and similar derivative-based methods)[edit]

Newton’s method assumes the function f to have a continuous derivative. Newton’s method may not converge if started too far away from a root. However, when it does converge, it is faster than the bisection method, and is usually quadratic. Newton’s method is also important because it readily generalizes to higher-dimensional problems. Newton-like methods with higher orders of convergence are the Householder’s methods. The first one after Newton’s method is Halley’s method with cubic order of convergence.

Secant method[edit]

Replacing the derivative in Newton’s method with a finite difference, we get the secant method. This method does not require the computation (nor the existence) of a derivative, but the price is slower convergence (the order is approximately 1.6 (golden ratio)). A generalization of the secant method in higher dimensions is Broyden’s method.

Steffensen’s method[edit]

If we use a polynomial fit to remove the quadratic part of the finite difference used in the Secant method, so that it better approximates the derivative, we obtain Steffensen’s method, which has quadratic convergence, and whose behavior (both good and bad) is essentially the same as Newton’s method but does not require a derivative.

Fixed point iteration method[edit]

We can use the fixed-point iteration to find the root of a function. Given a function f(x) which we have set to zero to find the root (), we rewrite the equation in terms of so that becomes (note, there are often many g(x) functions for each function). Next, we relabel each side of the equation as ${displaystyle x_{n+1}=g(x_{n})}$ so that we can perform the iteration. Next, we pick a value for ${displaystyle x_{1}}$ and perform the iteration until it converges towards a root of the function. If the iteration converges, it will converge to a root. The iteration will only converge if .

As an example of converting to , if given the function ${displaystyle f(x)=x^{2}+x-1}$ , we will rewrite it as one of the following equations.

${displaystyle x_{n+1}=(1/x_{n})-1}$

${displaystyle x_{n+1}=1/(x_{n}+1)}$

${displaystyle x_{n+1}=1-x_{n}^{2}}$

${displaystyle x_{n+1}=x_{n}^{2}+2x_{n}-1}$

, or

${displaystyle x_{n+1}=pm {sqrt {1-x_{n}}}}$

Inverse interpolation[edit]

The appearance of complex values in interpolation methods can be avoided by interpolating the inverse of f, resulting in the inverse quadratic interpolation method. Again, convergence is asymptotically faster than the secant method, but inverse quadratic interpolation often behaves poorly when the iterates are not close to the root.

Combinations of methods[edit]

Brent’s method[edit]

Brent’s method is a combination of the bisection method, the secant method and inverse quadratic interpolation. At every iteration, Brent’s method decides which method out of these three is likely to do best, and proceeds by doing a step according to that method. This gives a robust and fast method, which therefore enjoys considerable popularity.

Ridders’ method[edit]

Ridders’ method is a hybrid method that uses the value of function at the midpoint of the interval to perform an exponential interpolation to the root. This gives a fast convergence with a guaranteed convergence of at most twice the number of iterations as the bisection method.

Roots of polynomials [edit]

Finding roots in higher dimensions[edit]

The bisection method has been generalized to higher dimensions; these methods are called generalized bisection methods.^[2]^[3] At each iteration, the domain is partitioned into two parts, and the algorithm decides – based on a small number of function evaluations – which of these two parts must contain a root. In one dimension, the criterion for decision is that the function has opposite signs. The main challenge in extending the method to multiple dimensions is to find a criterion that can be computed easily, and guarantees the existence of a root.

The Poincaré–Miranda theorem gives a criterion for the existence of a root in a rectangle, but it is hard to verify, since it requires to evaluate the function on the entire boundary of the triangle.

Another criterion is given by a theorem of Kronecker.^[4] It says that, if the topological degree of a function f on a rectangle is non-zero, then the rectangle must contain at least one root of f. This criterion is the basis for several root-finding methods, such as by Stenger^[5] and Kearfott.^[6] However, computing the topological degree can be time-consuming.

A third criterion is based on a characteristic polyhedron. This criterion is used by a method called Characteristic Bisection.^[2]^: 19– It does not require to compute the topological degree – it only requires to compute the signs of function values. The number of required evaluations is at least ${displaystyle log _{2}(D/epsilon )}$ , where D is the length of the longest edge of the characteristic polyhedron.^[7]^{: 11, Lemma.4.7} Note that ^[7] prove a lower bound on the number of evaluations, and not an upper bound.

A fourth method uses an intermediate-value theorem on simplices.^[8] Again, no upper bound on the number of queries is given.

References[edit]

^ Press, W. H.; Teukolsky, S. A.; Vetterling, W. T.; Flannery, B. P. (2007). “Chapter 9. Root Finding and Nonlinear Sets of Equations”. Numerical Recipes: The Art of Scientific Computing (3rd ed.). New York: Cambridge University Press. ISBN 978-0-521-88068-8.
^ ^a ^b Mourrain, B.; Vrahatis, M. N.; Yakoubsohn, J. C. (2002-06-01). “On the Complexity of Isolating Real Roots and Computing with Certainty the Topological Degree”. Journal of Complexity. 18 (2): 612–640. doi:10.1006/jcom.2001.0636. ISSN 0885-064X.
^ Vrahatis, Michael N. (2020). Sergeyev, Yaroslav D.; Kvasov, Dmitri E. (eds.). “Generalizations of the Intermediate Value Theorem for Approximating Fixed Points and Zeros of Continuous Functions”. Numerical Computations: Theory and Algorithms. Lecture Notes in Computer Science. Cham: Springer International Publishing. 11974: 223–238. doi:10.1007/978-3-030-40616-5_17. ISBN 978-3-030-40616-5. S2CID 211160947.
^ “Iterative solution of nonlinear equations in several variables”. Guide books. Retrieved 2023-04-16.
^ Stenger, Frank (1975-03-01). “Computing the topological degree of a mapping inRn”. Numerische Mathematik. 25 (1): 23–38. doi:10.1007/BF01419526. ISSN 0945-3245. S2CID 122196773.
^ Kearfott, Baker (1979-06-01). “An efficient degree-computation method for a generalized method of bisection”. Numerische Mathematik. 32 (2): 109–127. doi:10.1007/BF01404868. ISSN 0029-599X. S2CID 122058552.
^ ^a ^b Vrahatis, M. N.; Iordanidis, K. I. (1986-03-01). “A rapid Generalized Method of Bisection for solving Systems of Non-linear Equations”. Numerische Mathematik. 49 (2): 123–138. doi:10.1007/BF01389620. ISSN 0945-3245.
^ Vrahatis, Michael N. (2020-04-15). “Intermediate value theorem for simplices for simplicial approximation of fixed points and zeros”. Topology and its Applications. 275: 107036. doi:10.1016/j.topol.2019.107036. ISSN 0166-8641.

Этапы приближенного решения нелинейных уравнений

Приближенное решение уравнения состоит из двух этапов:

Отделение корней, то есть нахождение интервалов из области определения функции f(x), в каждом из которых содержится только один корень уравнения f(x)=0.
Уточнение корней до заданной точности.

Отделение корней

Отделение корней можно проводить графически и аналитически.
Для того чтобы графически отделить корни уравнения, необходимо построить график функции f(x). Абсциссы точек его пересечения с осью Ox являются действительными корнями уравнения.

Для примера рассмотрим задачу решения уравнения

где угол x задан в градусах. Указанное уравнение можно переписать в виде
f(x)=0
Для графического отсечения корней достаточно построить график функции

Из рисунка видно, что корень уравнения лежит в промежутке x∈(6;8).

Аналитическое отделение корней

Аналитическое отделение корней основано на следующих теоремах.
Теорема 1. Если непрерывная функция f(x) принимает на концах отрезка [a; b] значения разных знаков, т.е.

то на этом отрезке содержится по крайней мере один корень уравнения.
Теорема 2. Если непрерывная на отрезке [a; b] функция f(x) принимает на концах отрезка значения разных знаков, а производная f'(x) сохраняет знак внутри указанного отрезка, то внутри отрезка существует единственный корень уравнения f(x) = 0.

Уточнение корней

Для уточнения корней может использоваться один из следующих методов:

Метод последовательных приближений (метод итераций)
Метод Ньютона (метод касательных)
Метод секущих (метод хорд)
Метод половинного деления (метод дихотомии)

Метод последовательных приближений (метод итераций)

Метод итерации — численный метод решения математических задач, используемый для приближённого решения алгебраических уравнений и систем. Суть метода заключается в нахождении по приближённому значению величины следующего приближения (являющегося более точным). Метод позволяет получить решение с заданной точностью в виде предела последовательности итераций. Характер сходимости и сам факт сходимости метода зависит от выбора начального приближения решения.
Функциональное уравнение может быть записано в виде
x=f(x)
Функцию f(x) называют сжимающим отображением.

Последовательность чисел x₀, x₁ ,…, x_n называется итерационной, если для любого номера n>0 элемент x_n выражается через элемент x_n-1 по рекуррентной формуле

а в качестве x₀ взято любое число из области задания функции f(x).

Реализация на C++ для рассмотренного выше примера

Уравнение может быть записано в форме

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

#define _USE_MATH_DEFINES
#include <iostream>
#include <cmath>
using namespace std;
double find(double x, double eps)
{
  double rez; int iter = 0;
  cout << “x0= ” << x << ” “;
  do {
    rez = x;
    x = 1 / (sin(M_PI*x / 180));
    iter++;
  } while (fabs(rez – x) > eps && iter<20000);
  cout << iter << ” iterations” << endl;
  return x;
}
int main()
{
  cout << find(7, 0.00001);
  cin.get();
  return 0;
}

Результат выполнения

Метод Ньютона (метод касательных)

Если известно начальное приближение x₀ корня уравнения f(x)=0, то последовательные приближения находят по формуле

Графическая интерпретация метода касательных имеет вид

Реализация на C++
Для заданного уравнения

производная будет иметь вид f'(x)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

#define _USE_MATH_DEFINES
#include <iostream>
#include <cmath>
using namespace std;
double find(double x, double eps)
{
  double f, df; int iter = 0;
  cout << “x0= ” << x << ” “;
  do {
    f = sin(M_PI*x / 180) – 1 / x;
    df = M_PI / 180 * cos(M_PI*x / 180) + 1 / (x*x);
    x = x – f / df;
    iter++;
  } while (fabs(f) > eps && iter<20000);
  cout << iter << ” iterations” << endl;
  return x;
}
int main()
{
  cout << find(1, 0.00001);
  cin.get(); return 0;
}

Результат выполнения

Метод секущих (метод хорд)

Если x₀, x₁ – приближенные значения корня уравнения f(x) = 0 и выполняется условие

то последующие приближения находят по формуле

Методом хорд называют также метод, при котором один из концов отрезка закреплен, т.е. вычисление приближения корня уравнения f(x) = 0 производят по формулам:

Геометрическая интерпретация метода хорд:

Реализация на C++
В отличие от двух рассмотренных выше методов, метод хорд предполагает наличие двух начальных приближений, представляющих собой концы отрезка, внутри которого располагается искомый корень.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

#define _USE_MATH_DEFINES
#include <iostream>
#include <cmath>
using namespace std;
double find(double x0, double x1, double eps)
{
  double rez = x1, f0, f;
  int iter = 0;
  cout << “x0= ” << x0 << ” x1= ” << x1 << ” “;
  do {
    f = sin(M_PI*rez / 180) – 1 / rez;
    f0 = sin(M_PI*x0 / 180) – 1 / x0;
    rez = rez – f / (f – f0)*(rez – x0);
    iter++;
  } while (fabs(f) > eps && iter<20000);
  cout << iter << ” iterations” << endl;
  return rez;
}
int main()
{
  cout << find(1.0, 10.0, 0.000001);
  cin.get(); return 0;
}

Результат выполнения

Метод половинного деления (метод дихотомии)

Если x₀, x₁ – приближенные значения корня уравнения f(x) = 0 и выполняется условие

то последующие приближения находятся по формуле

и вычисляется f(x_i). Если f(x_i)=0, то корень найден. В противном случае из отрезков выбирается тот, на концах которого f(x) принимает значения разных знаков, и проделывается аналогичная операция. Процесс продолжается до получения требуемой точности.

Геометрическая интерпретация метода дихотомии

Реализация на C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

#define _USE_MATH_DEFINES
#include <iostream>
#include <cmath>
using namespace std;
double func(double x)
{
  return (sin(M_PI*x / 180) – 1 / x);
}
double find(double x0, double x1, double eps)
{
  double left = x0, right = x1, x, fl, fr, f;
  int iter = 0;
  cout << “x0= ” << x0 << ” x1= ” << x1 << ” “;
  do {
    x = (left + right) / 2;
    f = func(x);
    if (f > 0) right = x;
    else left = x;
    iter++;
  } while (fabs(f) > eps && iter<20000);
  cout << iter << ” iterations” << endl;
  return x;
}
int main()
{
  cout << find(1.0, 10.0, 0.000001);
  cin.get(); return 0;
}

Результат выполнения

Для численного поиска решения также можно использовать генетические алгоритмы.

Назад: Алгоритмизация

Источник

Алгоритмы поиска корней непрерывных функций

В математике и вычисляя, алгоритм поиска корня является алгоритмом для поиска нулей, также называемых «корнями», непрерывных функций. Ноль функции f, от действительных чисел до действительных чисел или от комплексных чисел до комплексных чисел, является числом x таким, что f ( x) = 0. Поскольку, как правило, нули функции не могут быть точно вычислены или выражены в закрытой форме, алгоритмы поиска корня обеспечивают приближение к нулям, выраженное либо как с плавающей запятой числа или как небольшие изолирующие интервалы, или диски для комплексных корней (интервал или вывод диска эквивалентен приблизительному выводу вместе с границей ошибки).

Решение уравнения f (x) = g (x) аналогично нахождению корней функции h (x) = f (x) – g (x). Таким образом, алгоритмы поиска корней позволяют решить любое уравнение, заданное непрерывными функциями. Однако большинство алгоритмов поиска корней не гарантируют, что они найдут все корни; в частности, если такой алгоритм не находит корня, это не означает, что корня не существует.

Большинство численных методов поиска корня используют итерацию, создавая последовательность чисел, которые, надеюсь, сходятся к корню как предел. Для них требуется одно или несколько начальных предположений о корне в качестве начальных значений, затем каждая итерация алгоритма дает более точное приближение к корню. Поскольку в какой-то момент итерация должна быть остановлена, эти методы дают приближение к корню, а не точное решение. Многие методы вычисляют последующие значения, оценивая вспомогательную функцию для предыдущих значений. Таким образом, предел представляет собой фиксированную точку вспомогательной функции, которая выбрана для того, чтобы корни исходного уравнения были фиксированными точками, и для быстрого схода с этими фиксированными точками.

Поведение общих алгоритмов поиска корней изучается в численном анализе. Однако для многочленов поиск корней обычно относится к компьютерной алгебре, поскольку алгебраические свойства многочленов являются фундаментальными для наиболее эффективных алгоритмов. Эффективность алгоритма может сильно зависеть от характеристик данных функций. Например, многие алгоритмы используют производную входной функции, в то время как другие работают с каждой непрерывной функцией. В общем, численные алгоритмы не гарантируют нахождение всех корней функции, поэтому невозможность найти корень не доказывает, что корня нет. Однако для многочленов существуют определенные алгоритмы, которые используют алгебраические свойства для подтверждения того, что корень не пропущен, и поиска корней в отдельных интервалах (или дисков для сложных корней), которые малы достаточно, чтобы обеспечить сходимость численных методов (обычно метод Ньютона ) к уникальному корню, расположенному таким образом.

Содержание

1 Методы брекетинга
- 1.1 Метод деления пополам
- 1.2 Ложное положение (regula falsi)
2 Интерполяция
3 Итерационные методы
- 3.1 Метод Ньютона (и аналогичные методы, основанные на производных)
- 3.2 Метод секущих
- 3.3 Метод Стеффенсена
- 3.4 Обратная интерполяция
4 Комбинации методов
- 4.1 Метод Брента
5 Корни многочленов
- 5.1 Нахождение одного корня
- 5.2 Поиск корней в парах
- 5.3 Поиск всех корней одновременно
- 5.4 Методы исключения и включения
- 5.5 Изоляция действительного корня
- 5.6 Поиск нескольких корней многочленов
6 См. Также
7 Ссылки

Методы скобок

Методы скобок определяют последовательно меньшие интервалы (скобки), содержащие корень. Когда интервал достаточно мал, значит, корень найден. Обычно они используют теорему о промежуточном значении, которая утверждает, что если непрерывная функция имеет значения противоположных знаков в конечных точках интервала, то функция имеет по крайней мере один корень в интервале. Следовательно, они требуют начинать с интервала, так что функция принимает противоположные знаки в конечных точках интервала. Однако в случае многочленов существуют другие методы (правило знаков Декарта, теорема Будана и теорема Штурма ) для получения информация о количестве корней в интервале. Они приводят к эффективным алгоритмам изоляции действительных корней многочленов, которые обеспечивают нахождение всех действительных корней с гарантированной точностью.

Метод деления пополам

Простейшим алгоритмом поиска корня является метод деления пополам. Пусть f – непрерывная функция, для которой известен интервал [a, b] такой, что f (a) и f (b) имеют противоположные знаки (скобка). Пусть c = (a + b) / 2 – середина интервала (середина или точка, которая делит интервал пополам). Тогда либо f (a) и f (c), либо f (c) и f (b) имеют противоположные знаки, и один разделил размер интервала на два. Хотя метод деления пополам является надежным, он дает один и только один бит точности с каждой итерацией. Другие методы, при соответствующих условиях, могут быстрее повысить точность.

Ложное положение (regula falsi)

Метод ложного положения, также называемый методом regula falsi, аналогичен методу деления пополам, но вместо использования середины поиска пополам интервала он использует x-точку пересечения линии, которая соединяет построенные значения функции в конечных точках интервала, то есть

c = af (b) – bf (a) f (b) – f (а). { displaystyle c = { frac {af (b) -bf (a)} {f (b) -f (a)}}.} ${ displaystyle c = { frac {af (b) -bf (a)} {f (b) -f (a)}}.}$

Ложное положение аналогично методу секущей, за исключением того, что вместо сохранения двух последних точек он сохраняет по одной точке по обе стороны от корня. Метод ложного положения может быть быстрее, чем метод деления пополам, и никогда не будет расходиться, как метод секущей; однако он может не сойтись в некоторых наивных реализациях из-за ошибок округления, которые могут привести к неправильному знаку для f (c); обычно это может происходить, если скорость изменения f велика в окрестности корня.

Метод Риддерса – вариант метода ложного положения, который использует значение функции в середине интервала для получения функции с тем же корнем, к которой применяется метод ложного положения. Это дает более быструю сходимость с аналогичной надежностью.

Интерполяция

Многие процессы поиска корней работают с помощью интерполяции. Это заключается в использовании последних вычисленных приближенных значений корня для аппроксимации функции полиномом низкой степени, который принимает те же значения в этих приближенных корнях. Затем вычисляется корень полинома и используется как новое приближенное значение корня функции, и процесс повторяется.

Два значения позволяют интерполировать функцию полиномом первой степени (то есть аппроксимировать график функции линией). Это основа метода секущих. Три значения определяют квадратичную функцию, которая аппроксимирует график функции параболой . Это метод Мюллера..

Regula falsi – это также метод интерполяции, который отличается от метода секущей за счет использования для интерполяции по линии двух точек, которые не обязательно являются двумя последними вычисленными точками.

Итерационные методы

Хотя все алгоритмы поиска корней выполняются с помощью итерации, итеративный метод поиска корней обычно использует определенный тип итерации, состоящий из определения вспомогательной функции, которая применяется к последним вычисленным приближениям корня для получения нового приближения. Итерация останавливается, когда фиксированная точка (от до желаемая точность) вспомогательной функции достигается, то есть когда новое вычисленное значение достаточно близко к предыдущим.

Метод Ньютона (и аналогичные методы, основанные на производной)

Метод Ньютона предполагает, что функция f имеет непрерывную производную. Метод Ньютона может не сходиться, если начат слишком далеко от корня. Однако когда он сходится, он быстрее, чем метод деления пополам, и обычно является квадратичным. Метод Ньютона важен еще и потому, что он легко обобщается на многомерные проблемы. Ньютоноподобные методы с более высокими порядками сходимости – это методы Хаусхолдера. Первым после метода Ньютона является метод Галлея с кубическим порядком сходимости.

Метод секущих

Заменяя производную в методе Ньютона на конечную разность, мы получаем метод секанса. Этот метод не требует вычисления (или наличия) производной, но цена сходимости медленнее (порядок равен примерно 1,6 (золотое сечение )). Обобщением метода секущих в более высоких измерениях является метод Бройдена.

метод Стеффенсена

Если мы используем полиномиальную аппроксимацию для удаления квадратичной части конечной разности, используемой в методе секанса, чтобы она лучше аппроксимирует производную, мы получаем метод Стеффенсена, который имеет квадратичную сходимость и поведение которого (как хорошее, так и плохое) по существу совпадает с методом Ньютона, но не требует производной.

Обратная интерполяция

Появления комплексных значений в методах интерполяции можно избежать путем интерполяции обратного f, что приводит к обратной квадратичной интерполяции метод. Опять же, сходимость асимптотически быстрее, чем метод секущей, но обратная квадратичная интерполяция часто ведет себя плохо, когда итерации не близки к корню.

Комбинации методов

Метод Брента

Метод Брента представляет собой комбинацию метода деления пополам, метода секущей и обратной квадратичной интерполяции. На каждой итерации метод Брента решает, какой из этих трех методов с наибольшей вероятностью будет работать лучше, и продолжает выполнение шага в соответствии с этим методом. Это дает надежный и быстрый метод, который поэтому пользуется большой популярностью.

Корни многочленов

Нахождение корней многочлена – давняя проблема, которая на протяжении всей истории была объектом многих исследований. Свидетельством этого является то, что до 19 века алгебра по существу означала теорию полиномиальных уравнений.

Найти корень линейного многочлена (первая степень) легко и нужно только одно деление. Для квадратичных многочленов (степень два) квадратная формула дает решение, но ее численная оценка может потребовать некоторой осторожности для обеспечения числовой стабильности. Для степеней третьей и четвертой существуют решения в замкнутой форме в терминах радикалов, которые, как правило, неудобны для числовой оценки, так как являются слишком сложными и включают вычисление нескольких корней n-й степени вычисление которого не проще, чем прямое вычисление корней многочлена (например, выражение вещественных корней кубического многочлена может включать нереальные кубические корни ). Для многочленов пятой степени и выше теорема Абеля – Руффини утверждает, что, как правило, не существует радикального выражения корней.

Итак, за исключением очень низких степеней, поиск корней многочленов заключается в нахождении приближений корней. По основной теореме алгебры известно, что многочлен степени n имеет не более n действительных или комплексных корней, и это число достигается почти для всех многочленов.

Отсюда следует, что задачу нахождения корня для многочленов можно разделить на три разные подзадачи;

Нахождение одного корня
Нахождение всех корней
Нахождение корней в определенной области комплексной плоскости, как правило, настоящие корни или действительные корни в заданном интервале (например, когда корни представляют физическую величину, интересны только действительные положительные).

Для поиска одного корня, метод Ньютона и другие общие итерационные методы обычно работают хорошо.

Самый старый метод поиска всех корней – это, когда корень r был найден, разделить многочлен на x – r и итеративно перезапустить поиск корня частного многочлена. Однако, за исключением низких степеней, это не работает из-за числовой нестабильности : многочлен Уилкинсона показывает, что очень небольшое изменение одного коэффициента может резко изменить не только значение корни, но также и их природа (реальная или сложная). Кроме того, даже с хорошим приближением, когда кто-то оценивает многочлен с приближенным корнем, он может получить результат, который далеко не будет близким к нулю. Например, если полином степени 20 (степень многочлена Уилкинсона) имеет корень, близкий к 10, производная полинома в корне может иметь порядок 10 20; { displaystyle 10 ^ {20};} ${ displaystyle 10 ^ {20};}$ это означает, что ошибка 10–10 { displaystyle 10 ^ {- 10}} $10 ^ {{- 10}}$ в значении корня может дать значение полинома в приближенном корне, которое имеет порядок 10 10. { displaystyle 10 ^ {10}.} ${ displaystyle 10 ^ {10}.}$

Чтобы избежать этих проблем, были разработаны методы, которые вычисляют все корни одновременно с любой желаемой точностью. В настоящее время наиболее эффективным методом является метод Аберта. Бесплатная реализация доступна под названием MPSolve. Это эталонная реализация, которая может регулярно находить корни многочленов степени более 1000 с более чем 1000 значащими десятичными знаками.

Методы вычисления всех корней могут использоваться для вычисления действительных корней. Однако может быть сложно решить, является ли корень с небольшой мнимой частью реальным или нет. Более того, поскольку количество реальных корней в среднем является логарифмом степени, вычисление нереальных корней является пустой тратой компьютерных ресурсов, когда кто-то интересуется реальными корнями.

Самый старый метод вычисления количества действительных корней и количества корней в интервале является результатом теоремы Штурма, но методы, основанные на правиле знаков Декарта и его расширения – теоремы Будана и Винсента – обычно более эффективны. Для нахождения корней все действуют путем уменьшения размера интервалов, в которых ищутся корни, до получения интервалов, содержащих ноль или один корень. Затем интервалы, содержащие один корень, могут быть дополнительно сокращены для получения квадратичной сходимости метода Ньютона к изолированным корням. Основные системы компьютерной алгебры (Maple, Mathematica, SageMath, PARI / GP ) имеют каждый вариант этого метода в качестве алгоритма по умолчанию для действительных корней многочлена.

Нахождение одного корня

Наиболее широко используемым методом вычисления корня является метод Ньютона, который состоит из итераций вычисления

xn + 1 = xn – е (xn) f ′ (xn), { displaystyle x_ {n + 1} = x_ {n} – { frac {f (x_ {n})} {f ‘(x_ {n})}},} ${displaystyle x_{n+1}=x_{n}-{frac {f(x_{n})}{f'(x_{n})}},}$

, начиная с правильно выбранного значения x 0. { displaystyle x_ {0}.} $x_ {0}.$ Если f является многочленом, вычисления выполняются быстрее при использовании правила Хорнера для вычисления многочлена и его производной.

Сходимость обычно квадратичная, она может сходиться очень медленно или даже не сходиться вообще. В частности, если многочлен не имеет действительного корня и x 0 { displaystyle x_ {0}} $x_ {0}$ реально, то метод Ньютона не может сходиться. Однако, если у многочлена есть действительный корень, который больше, чем больший действительный корень его производной, то метод Ньютона квадратично сходится к этому наибольшему корню, если x 0 { displaystyle x_ {0}} $x_ {0}$ больше, чем этот больший корень (есть простые способы вычисления верхней границы корней, см. Свойства полиномиальных корней ). Это отправная точка метода Хорнера для вычисления корней.

Когда был найден один корень r, можно использовать евклидово деление для удаления множителя x – r из полинома. Вычисление корня из полученного частного и повторение процесса в принципе обеспечивают способ вычисления всех корней. Однако эта итерационная схема численно нестабильна; ошибки аппроксимации накапливаются во время последовательных факторизаций, так что последние корни определяются с помощью полинома, который сильно отличается от множителя исходного полинома. Чтобы уменьшить эту ошибку, для каждого найденного корня можно перезапустить метод Ньютона с исходным полиномом и этим приблизительным корнем в качестве начального значения.

Однако нет гарантии, что это позволит найти все корни. Фактически, проблема нахождения корней многочлена по его коэффициентам в целом очень плохо обусловлена . Это иллюстрируется многочленом Уилкинсона : корни этого многочлена степени 20 – это 20 первых положительных целых чисел; изменение последнего бита 32-битного представления одного из его коэффициентов (равного –210) дает полином только с 10 действительными корнями и 10 комплексными корнями с мнимой частью больше 0,6.

Тесно связаны с методом Ньютона методом Галлея и методом Лагерра. Оба используют полином и его два первых вывода для итерационного процесса, который имеет кубическую сходимость. Объединяя два последовательных шага этих методов в один тест, мы получаем коэффициент сходимости , равный 9, за счет 6 полиномиальных вычислений (с правилом Хорнера). С другой стороны, объединение трех шагов метода Ньютона дает скорость сходимости 8 за счет того же количества полиномиальных вычислений. Это дает небольшое преимущество этим методам (менее ясно для метода Лагерра, поскольку квадратный корень должен вычисляться на каждом шаге).

При применении этих методов к многочленам с действительными коэффициентами и действительными начальными точками методы Ньютона и Галлея остаются внутри линии действительных чисел. Чтобы найти сложные корни, нужно выбрать сложные отправные точки. Напротив, метод Лагерра с квадратным корнем в оценке сам по себе оставляет действительную ось.

Другой класс методов основан на преобразовании задачи поиска корней полинома в задачу поиска собственных значений сопутствующей матрицы полинома. В принципе, можно использовать любой алгоритм собственных значений , чтобы найти корни полинома. Однако из соображений эффективности предпочтение отдается методам, использующим структуру матрицы, т.е. которые могут быть реализованы в безматричной форме. Среди этих методов – метод степени , применение которого для транспонирования сопутствующей матрицы является классическим методом нахождения корня из наибольшего модуля. Метод обратной мощности со сдвигами, который сначала находит какой-то наименьший корень, – это то, что управляет сложным (cpoly) вариантом алгоритма Дженкинса – Трауба и придает ему численную стабильность. Кроме того, он нечувствителен к множественным корням и имеет быструю сходимость с порядком 1 + φ ≈ 2.6 { displaystyle 1+ varphi приблизительно 2.6}(где φ { displaystyle varphi } varphi – это золотое сечение ) даже при наличии кластерных корней. Эта быстрая сходимость требует трех вычислений полинома на шаг, что приводит к невязке O (| f (x) |), что является более медленной сходимостью, чем с тремя шагами метода Ньютона.

Поиск корней в парах

Если данный полином имеет только действительные коэффициенты, можно избежать вычислений с комплексными числами. Для этого нужно найти квадратичные множители для пар сопряженных комплексных корней. Применение многомерного метода Ньютона к этой задаче приводит к методу Бэрстоу.

Реальный вариант алгоритма Дженкинса – Трауба является усовершенствованием этого метода.

Поиск всех корней одновременно

Простой Дюран-Кернер и немного более сложный метод Аберта одновременно находят все корни, используя только простые комплексное число арифметика. Ускоренные алгоритмы для многоточечной оценки и интерполяции, подобные быстрому преобразованию Фурье, могут помочь ускорить их для больших степеней полинома. Желательно выбирать асимметричный, но равномерно распределенный набор начальных точек. Реализация этого метода в бесплатном программном обеспечении MPSolve является эталоном его эффективности и точности.

Другой метод с этим стилем – это метод Данделина – Греффе (иногда также приписываемый Лобачевскому ), который использует полиномиальные преобразования для многократного и неявно возводить корни в квадрат. Это значительно увеличивает отклонения в корнях. Применяя формулы Виэта, можно получить простые приближения для модуля корней и, с некоторыми дополнительными усилиями, для самих корней.

Методы исключения и включения

Существует несколько быстрых тестов, которые определяют, не содержит ли сегмент реальной линии или область комплексной плоскости корней. Ограничивая модуль корней и рекурсивно разделяя начальную область, указанную этими границами, можно выделить небольшие области, которые могут содержать корни, а затем применить другие методы для их точного определения.

Все эти методы включают нахождение коэффициентов сдвинутых и масштабированных версий полинома. Для больших степеней становятся возможными ускоренные методы на основе БПФ.

Реальные корни см. В следующих разделах.

Алгоритм Лемера – Шура использует тест Шура – Кона для кругов; в качестве варианта алгоритм глобального деления пополам Уилфа использует вычисление числа витков для прямоугольных областей в комплексной плоскости.

В методе разбиения круга используются полиномиальные преобразования на основе БПФ для поиска факторов большой степени, соответствующих кластерам корней. Точность факторизации максимизируется с помощью итерации типа Ньютона. Этот метод полезен для поиска корней многочленов высокой степени с произвольной точностью; в этой настройке он имеет почти оптимальную сложность.

Изоляция действительного корня

Нахождение действительных корней многочлена с действительными коэффициентами – проблема, которой уделялось много внимания с начала 19 века, и до сих пор является активной областью исследований. Большинство алгоритмов поиска корней могут найти некоторые настоящие корни, но не могут подтвердить, что нашли все корни. Методы поиска всех сложных корней, такие как метод Аберта, могут предоставить реальные корни. Однако из-за числовой нестабильности многочленов (см. многочлен Уилкинсона ) им может потребоваться арифметика произвольной точности для определения того, какие корни являются действительными. Более того, они вычисляют все комплексные корни, хотя лишь немногие из них настоящие.

Отсюда следует, что стандартный способ вычисления действительных корней заключается в вычислении первых непересекающихся интервалов, называемых изолирующими интервалами, так что каждый из них содержит ровно один действительный корень, а вместе они содержат все корни. Это вычисление называется изоляцией реального корня. Имея разделительный интервал, можно использовать быстрые численные методы, такие как метод Ньютона для повышения точности результата.

Самый старый полный алгоритм изоляции действительного корня является результатом теоремы Штурма. Однако он оказывается намного менее эффективным, чем методы, основанные на правиле знаков Декарта и теореме Винсента. Эти методы делятся на два основных класса: один использует непрерывные дроби, а другой – деление пополам. Оба метода были значительно усовершенствованы с начала 21 века. Благодаря этим усовершенствованиям они достигают вычислительной сложности, которая аналогична сложности лучших алгоритмов для вычисления всех корней (даже если все корни действительны).

Эти алгоритмы реализованы и доступны в Mathematica (метод непрерывных дробей) и Maple (метод деления пополам). Обе реализации могут регулярно находить действительные корни многочленов степени выше 1000.

Нахождение множественных корней многочленов

Большинство алгоритмов поиска корней плохо себя ведут при множественных корнях или очень близких корнях. Однако для многочленов, коэффициенты которых точно заданы как целые числа или рациональные числа, существует эффективный метод разложения их на множители, которые имеют только простые корни и коэффициенты которых также точно заданы. Этот метод, называемый факторизация без квадратов, основан на том, что кратные корни многочлена являются корнями наибольшего общего делителя многочлена и его производной..

Факторизация многочлена p без квадратов является факторизацией p = p 1 p 2 2 ⋯ pkk { displaystyle p = p_ {1} p_ {2} ^ {2} cdots p_ {k} ^ {k}} $p = p_ {1} p_ {2} ^ {2} cdots p_ {k} ^ {k}$ , где каждый pi { displaystyle p_ {i}} $p_{i}$ равен 1 или многочлену без нескольких корней и двум различным pi { displaystyle p_ {i}} $p_{i}$ не имеют общего корня.

Эффективным методом вычисления этой факторизации является алгоритм Юна.

См. Также

Список алгоритмов поиска корня
метод Бройдена – квазиньютоновский метод поиска корня для многопараметрический случай
Криптографически безопасный генератор псевдослучайных чисел – Тип функций, неразрешимых с помощью алгоритмов поиска корней
Научная библиотека GNU
Метод Греффе – Алгоритм нахождения полиномиальных корней
Лилля метод – Графический метод для вещественных корней многочлена
MPSolve – Программное обеспечение для приближения корней многочлена с произвольно высокой точностью
Кратность (математика) – Количество раз, когда объект необходимо учитывать для выполнения общей формулы
алгоритм n-го корня
Система полиномиальных уравнений – Алгоритмы нахождения корней для общих корней нескольких многомерных многочленов
Теорема Канторовича – Начальные условия, обеспечивающие сходимость метода Ньютона

Литература

Источник

Решение уравнений с помощью графиков

Решение линейных уравнений

Как ты уже знаешь, графиком линейного уравнения является прямая линия, отсюда и название данного вида.

Линейные уравнения достаточно легко решать алгебраическим путем – все неизвестные переносим в одну сторону уравнения, все, что нам известно – в другую и вуаля! Мы нашли корень.

Сейчас же я покажу тебе, как это сделать графическим способом.

Итак, у тебя есть уравнение: ( displaystyle 2{x} -10=2)

Как его решить?

Вариант 1, и самый распространенный – перенести неизвестные в одну сторону, а известные в другую, получаем:

( displaystyle 2x=2+10)

( displaystyle 2x=12)

Обычно дальше мы делим правую часть на левую, и получаем искомый корень, но мы с тобой попробуем построить левую и правую части как две различные функции в одной системе координат.

Иными словами, у нас будет:

( displaystyle {{y}_{1}}=2x)

( displaystyle {{y}_{2}}=12)

А теперь строим. Что у тебя получилось?

reshenie uravnenij s pomoshyu grafikov funktsij 1

Как ты думаешь, что является корнем нашего уравнения? Правильно, координата ( displaystyle x) точки пересечения графиков:

reshenie uravnenij s pomoshyu grafikov funktsij 2

Наш ответ: ( displaystyle x=6)

Вот и вся премудрость графического решения. Как ты с легкостью можешь проверить, корнем нашего уравнения является число ( displaystyle 6)!

Вариант 1. Напрямую

Просто строим параболу по данному уравнению: ( displaystyle {{x}^{2}}+2{x} -8=0)

Чтобы сделать это быстро, дам тебе одну маленькую подсказку: удобно начать построение с определения вершины параболы. Определить координаты вершины параболы помогут следующие формулы:

( displaystyle x=-frac{b}{2a})

( displaystyle y=-frac{{{b}^{2}}-4ac}{4a})

Ты скажешь «Стоп! Формула для ( displaystyle y) очень похожа на формулу нахождения дискриминанта» да, так оно и есть, и это является огромным минусом «прямого» построения параболы, чтобы найти ее корни.

Тем не менее, давай досчитаем до конца, а потом я покажу, как это сделать намного (намного!) проще!

Посчитал? Какие координаты вершины параболы у тебя получились? Давай разбираться вместе:

( displaystyle x=frac{-2}{2}=-1)

( displaystyle y=-frac{{{2}^{2}}-4cdot left( -8 right)}{4}=-frac{4+32}{4}=-9)

Точно такой же ответ? Молодец!

И вот мы знаем уже координаты вершины, а для построения параболы нам нужно еще … точек. Как ты думаешь, сколько минимум точек нам необходимо? Правильно, ( displaystyle 3).

Ты знаешь, что парабола симметрична относительно своей вершины, например:

reshenie kvadratnyh uravnenij s pomoshyu grafikov funktsij 1

Соответственно, нам необходимо еще две точки по левой или правой ветви параболы, а в дальнейшем мы эти точки симметрично отразим на противоположную сторону:

reshenie kvadratnyh uravnenij s pomoshyu grafikov funktsij 2

Возвращаемся к нашей параболе.

Для нашего случая точка ( displaystyle Aleft( -1;-9 right)). Нам необходимо еще две точки, соответственно, ( displaystyle x) можно взять положительные, а можно взять отрицательные? Какие точки тебе удобней?

Мне удобней работать с положительными, поэтому я рассчитаю при ( displaystyle x=0) и ( displaystyle x=2).

При ( displaystyle x=0):

( displaystyle y={{0}^{2}}+0-8=-8)

При ( displaystyle x=2):

( displaystyle y={{2}^{2}}+2cdot 2-8=0)

Теперь у нас есть три точки, и мы спокойно можем построить нашу параболу, отразив две последние точки относительно ее вершины:

reshenie kvadratnyh uravnenij s pomoshyu grafikov funktsij 3

Как ты думаешь, что является решением уравнения?

Правильно, точки, в которых ( displaystyle y=0), то есть ( displaystyle x=2) и ( displaystyle x=-4). Потому что ( displaystyle {{x}^{2}}+2{x} -8=0).

И если мы говорим, что ( displaystyle y={{x}^{2}}+2{x} -8), то значит, что ( displaystyle y) тоже должен быть равен ( displaystyle 0), или ( displaystyle y={{x}^{2}}+2{x} -8=0).

Просто? Это мы закончили с тобой решение уравнения сложным графическим способом, то ли еще будет!

Конечно, ты можешь проверить наш ответ алгебраическим путем – посчитаешь корни через теорему Виета или Дискриминант.

Что у тебя получилось? То же самое?

Вот видишь! Теперь посмотрим совсем простое графическое решение, уверена, оно тебе очень понравится!

Решение смешанных неравенств

Теперь перейдем к более сложным неравенствам!

Как тебе такое:

( displaystyle 4x<{{x}^{3}})?

Жуть, правда? Честно говоря, я понятия не имею, как решить такое алгебраически… Но, оно и не надо. Графически ничего сложного в этом нет! Глаза боятся, а руки делают!

Первое, с чего мы начнем, – это с построения двух графиков:

( displaystyle {{y}_{1}}=4x)

( displaystyle {{y}_{2}}={{x}^{3}})

Я не буду расписывать для каждого таблицу – уверена, ты отлично справишься с этим самостоятельно (еще бы, столько прорешать примеров!).

Расписал? Теперь строй два графика.

Сравним наши рисунки?

У тебя так же? Отлично!

Теперь расставим точки пересечения и цветом определим, какой график у нас по идее должен быть больше, то есть ( displaystyle {{y}_{2}}={{x}^{3}}).

Смотри, что получилось в итоге:

А теперь просто смотрим, в каком месте у нас выделенный график находится выше, чем график ( displaystyle {{y}_{1}}=4x)? Смело бери карандаш и закрашивай данную область! Она и будет решением нашего сложного неравенства!

На каких промежутках по оси ( displaystyle Ox) у нас ( displaystyle {{y}_{2}}={{x}^{3}}) находится выше, чем ( displaystyle {{y}_{1}}=4x)? Верно, ( displaystyle xin left( -2;0 right)cup left( 2;+infty right)).

Это и есть ответ!

Ну вот, теперь тебе по плечу и любое уравнение, и любая система, и уж тем более любое неравенство!

Источник

Описание метода[править | править код]

Обоснование[править | править код]

Геометрическая интерпретация[править | править код]

Алгоритм[править | править код]

Пример[править | править код]

Условия применения[править | править код]

Контрпримеры[править | править код]

Ограничения[править | править код]

Историческая справка[править | править код]

Обобщения и модификации[править | править код]

Метод секущих[править | править код]

Метод одной касательной[править | править код]

Метод Ньютона-Фурье[править | править код]

Многомерный случай[править | править код]

Применительно к задачам оптимизации[править | править код]

Метод Ньютона — Рафсона[править | править код]

Применительно к задачам о наименьших квадратах[править | править код]

Метод Гаусса — Ньютона[править | править код]

Обобщение на комплексную плоскость[править | править код]

Реализация[править | править код]

Scala[править | править код]

Python[править | править код]

PHP[править | править код]

Octave[править | править код]

Delphi[править | править код]

C++[править | править код]

C[править | править код]

Haskell[править | править код]

Литература[править | править код]

См. также[править | править код]

Ссылки[править | править код]

Bracketing methods[edit]

Bisection method[edit]

False position (regula falsi)[edit]

ITP method[edit]

Interpolation[edit]

Iterative methods[edit]

Newton’s method (and similar derivative-based methods)[edit]

Secant method[edit]

Steffensen’s method[edit]

Fixed point iteration method[edit]

Inverse interpolation[edit]

Combinations of methods[edit]

Brent’s method[edit]

Ridders’ method[edit]

Roots of polynomials [edit]

Finding roots in higher dimensions[edit]

See also[edit]

References[edit]

Further reading[edit]

Этапы приближенного решения нелинейных уравнений

Отделение корней

Аналитическое отделение корней

Уточнение корней

Метод последовательных приближений (метод итераций)

Метод Ньютона (метод касательных)

Метод секущих (метод хорд)

Метод половинного деления (метод дихотомии)

Содержание

Методы скобок

Метод деления пополам

Ложное положение (regula falsi)

Интерполяция

Итерационные методы

Метод Ньютона (и аналогичные методы, основанные на производной)

Метод секущих

метод Стеффенсена

Обратная интерполяция

Комбинации методов

Метод Брента

Корни многочленов

Нахождение одного корня

Поиск корней в парах

Поиск всех корней одновременно

Методы исключения и включения

Изоляция действительного корня

Нахождение множественных корней многочленов

См. Также

Литература

Решение уравнений с помощью графиков