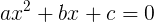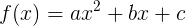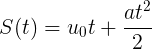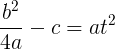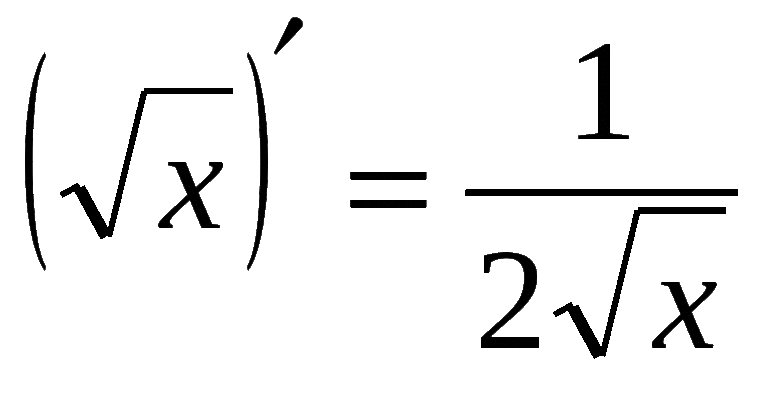Решение квадратных уравнений через производные
Время на прочтение
3 мин
Количество просмотров 43K
Здравствуйте, уважаемые читатели. После прочтения статьи у вас, вероятно, возникнет закономерный вопрос: «А зачем, собственно, это надо?». В силу этого сперва считаю необходимым заблаговременно сообщить, что искомый метод решения квадратных уравнений представлен скорее с морально-эстетической стороны математики, нежели со стороны практического сухого применения. Также заранее извиняюсь перед теми читателями, которые посчитают мои дилетантские изречения неприемлемыми. Итак, начнем
забивать гвозди микроскопом
.
Имеем алгебраическое уравнение второй степени (оно же квадратное) в общем виде:
Перейдем от квадратного уравнения к квадратичной функции:
Где, очевидно, необходимо найти такие значения аргумента 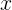
Кажется, нужно просто решить квадратное уравнение с помощью теоремы Виета или через дискриминант. Но мы ведь собрались здесь не для этого. Давайте-ка лучше возьмем производную!
Исходя из определения физического смысла производной первого порядка ясно, что подставляя аргумент 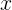
Что же дальше делать? Непонятно. А в любом непонятном случае нужно брать производную ещё раз:
На этот раз мы получили «скорость скорости» изменения функции (то бишь ускорение) в конкретной точке. Немного проанализировав полученное, можно сделать вывод, что «ускорением» является константа, которая не зависит от аргумента функции — запомним это.
Сейчас вспомним немного физику и равноускоренное движение (РУД). Что у нас есть в арсенале? Верно, имеется формула для определения координаты перемещения по оси 
Где 
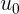
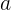
Нетрудно заметить, что наша изначальная функция как раз представляет из себя РУД.
Разве формула перемещения для РУД не является следствием решения квадратного уравнения?
Нет. Формула для РУД выше по факту есть результат взятия интеграла от формулы скорости при ПРУД. Или из графика 
Формула перемещения при РУД не вытекает из решения каких-либо квадратных уравнений. Это очень важно, иначе не было бы смысла статьи.
Теперь осталось разобраться что есть что, и чего нам не хватает.
«Ускорение» 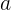
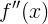
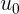
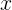
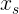

В таком случае возникает вопрос, какой же 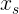
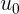
В таком случае составим уравнение для поиска 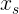
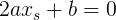
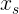

Корнем такого уравнения относительно 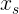
А значением исходной функции 
Вспомним, какой целью мы задались в самом начале: «необходимо найти такие значения аргумента 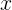

Так как теперь нам известна начальная скорость, ускорение и какой путь необходимо пройти, то настало время отметить следующее:
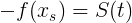
Тогда, подставив все известные величины, получим:
Поделим все на 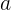
Теперь становится очевидно, что:
Соединим все «детали пазла» воедино:
Вот мы и получили окончательное решение поставленной задачи. Вообще Америку мы не открыли — мы просто пришли к формуле решения квадратного уравнения через дискриминант окольными путями. Практического смысла это не несет (примерно таким же образом можно решать уравнения первой/второй степени любого (не обязательно общего) вида).
Целью этой статьи является, в частности, подогрев интереса к анализу мат. функций и вообще к математике.
С вами был Петр, спасибо за внимание!
Применение производной для решения нелинейных уравнений и неравенств
- Количество корней кубического уравнения
- Количество корней произвольного уравнения
- Решение неравенств с построением графиков
п.1. Количество корней кубического уравнения
Кубическое уравнение $$ ax^3+bx^2+cx+d=0 $$ на множестве действительных чисел может иметь один, два или три корня.
С помощью производной можно быстро ответить на вопрос, сколько корней имеет данное уравнение. begin{gather*} f(x)=ax^3+bx^2+cx+d\ f'(x)=3ax^2+bx+c end{gather*} Если в уравнении (f'(x)=0) дискриминант (D=4b^2-12ac=4(b^2-3ac)gt 0), кубическая парабола имеет две точки экстремума: (x_{1,2}=frac{-2bpmsqrt{D}}{6a}). Если при этом значения функции в точках экстремума (f(x_1)cdot f(x_2)lt 0), т.е. расположены по разные стороны от оси OX, парабола имеет три точки пересечения с этой осью. Исходное уравнение имеет три корня.
Если две точки экстремума найдены, но (f(x_1)cdot f(x_2)=0), уравнение имеет два корня.
Во всех остальных случаях – у исходного уравнения 1 корень.
Уравнение (ax^3+bx^2+cx+d=0)
Имеет три корня, если ( begin{cases} b^2-3acgt 0\ f(x_1)cdot f(x_2)lt 0 end{cases} )
Имеет два корня, если ( begin{cases} b^2-3acgt 0\ f(x_1)cdot f(x_2)= 0 end{cases} )
В противном случае – один корень.
Пример 1. Сколько корней имеют уравнения:
п.2. Количество корней произвольного уравнения
Задачи на подсчет количества корней решаются с помощью построения графиков при полном или частичном исследовании функций.
Пример 2. а) Найдите число корней уравнения (frac 1x+frac{1}{x-1}+frac{1}{x-3})
б) Найдите число корней уравнения (frac 1x+frac{1}{x-1}+frac{1}{x-3}=k)
Построим график функции слева, а затем найдем для него количество точек пересечения с горизонталью (y=1). Это и будет ответом на вопрос задачи (а).
Исследуем функцию: $$ f(x)=frac1x+frac{1}{x-1}+frac{1}{x-3} $$ Алгоритм исследования и построения графика – см. §49 данного справочника.
1) ОДЗ: (xneleft{0;1;3right})
Все три точки – точки разрыва 2-го рода. begin{gather*} lim_{xrightarrow -0}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=-infty-1-frac13=-infty\ lim_{xrightarrow +0}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=+infty-1-frac13=+infty\ lim_{xrightarrow 1-0}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=1-infty-frac12=-infty\ lim_{xrightarrow 1+0}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=1+infty-frac12=+infty\ lim_{xrightarrow 3-0}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=frac13+frac12-infty=-infty\ lim_{xrightarrow 3+0}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=frac13+frac12+infty=+infty end{gather*} 2) Функция ни четная, ни нечетная.
Функция непериодическая.
3) Асимптоты
1. Вертикальные (x=0, x=1, x=3) – точки разрыва 2-го рода
2. Горизонтальные: begin{gather*} lim_{xrightarrow -infty}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=-0-0-0=-0\ lim_{xrightarrow +infty}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=+0+0+0=+0\ end{gather*} Горизонтальная асимптота (y=0)
На минус бесконечности функция стремится к 0 снизу, на плюс бесконечности – сверху.
3. Наклонные: (k=0), нет.
4) Первая производная $$ f'(x)=-frac{1}{x^2}-frac{1}{(x-1)^2}-frac{1}{(x-3)^2}lt 0 $$ Производная отрицательная на всей ОДЗ.
Функция убывает.
5) Вторую производную не исследуем, т.к. перегибы не влияют на количество точек пересечения с горизонталью.
6) Точки пересечения с OY – нет, т.к. (x=0) – асимптота
Точки пересечения с OX – две, (0lt x_1lt 1,1lt x_2lt 3)
7) График
Получаем ответ для задачи (а) 3 корня.
Решаем более общую задачу (б). Передвигаем горизонталь (y=k) снизу вверх и считаем количество точек пересечения с графиком функции. Последовательно, получаем:
При (klt 0) – три корня
При (k=0) – два корня
При (kgt 0) – три корня
Ответ: а) 3 корня; б) при (k=0) два корня, при (kne 0) три корня.
Пример 3. Найдите все значения параметра a, при каждом из которых уравнение $$ sqrt{x-1}+sqrt{10-2x}=a $$ имеет по крайней мере одно решение.
Исследуем функцию (f(x)=sqrt{x-1}+sqrt{10-2x})
ОДЗ: ( begin{cases} x-1geq 0\ 10-2xgeq 0 end{cases} Rightarrow begin{cases} xgeq 1\ xleq 5 end{cases} Rightarrow 1leq xleq 5 )
Функция определена на конечном интервале.
Поэтому используем сокращенный алгоритм для построения графика.
Значения функции на концах интервала: (f(1)=0+sqrt{8}=2sqrt{2}, f(5)=sqrt{4}+0=2)
Первая производная: begin{gather*} f'(x)=frac{1}{2sqrt{x-1}}+frac{-2}{2sqrt{10-2x}}=frac{1}{2sqrt{x-1}}-frac{1}{sqrt{10-2x}}\ f'(x)=0 text{при} 2sqrt{x-1}=sqrt{10-2x}Rightarrow 4(x-1)=10-2xRightarrow 6x=14Rightarrow x=frac73\ fleft(frac73right)=sqrt{frac73-1}+sqrt{10-2cdot frac73}=sqrt{frac43}+sqrt{frac{16}{3}}=frac{6}{sqrt{3}}=2sqrt{3} end{gather*} Промежутки монотонности:
| (x) | 1 | (1; 7/3) | 7/3 | (7/3; 5) | 5 |
| (f'(x)) | ∅ | + | 0 | – | ∅ |
| (f(x)) | (2sqrt{2}) | (nearrow ) | max (2sqrt{3}) |
(searrow ) | 2 |
Можем строить график:
(y=a) – горизонтальная прямая.
Количество точек пересечения (f(x)) и (y) равно количеству решений.
Получаем:
| $$ alt 2 $$ | нет решений |
| $$ 2leq alt 2sqrt{2} $$ | 1 решение |
| $$ 2sqrt{2}leq alt 2sqrt{3} $$ | 2 решения |
| $$ a=2sqrt{3} $$ | 1 решение |
| $$ agt 2sqrt{3} $$ | нет решений |
По крайней мере одно решение будет в интервале (2leq aleq 2sqrt{3}).
Ответ: (ainleft[2;2sqrt{3}right])
п.3. Решение неравенств с построением графиков
Пример 4. Решите неравенство (frac{2+log_3 x}{x-1}gt frac{6}{2x-1})
Разобьем неравенство на совокупность двух систем.
Если (xgt 1), то (x-1gt 0), на него можно умножить слева и справа и не менять знак.
Если (xlt 1), то (x-1lt 0), умножить также можно, только знак нужно поменять.
Сразу учтем требование ОДЗ для логарифма: (xgt 0)
Получаем совокупность: begin{gather*} left[ begin{array}{l} begin{cases} xgt 1\ 2+log_3 xgtfrac{6(x-1)}{2x-1} end{cases} \ begin{cases} 0lt xlt 1\ 2+log_3 xltfrac{6(x-1)}{2x-1} end{cases} end{array} right. \ 2+log_3 xgt frac{6(x-1)}{2x-1}Rightarrow log_3 xgt frac{6(x-1)-2(2x-1)}{2x-1}Rightarrow log_3 xgt frac{2x-4}{2x-1}\ left[ begin{array}{l} begin{cases} xgt 1\ log_3 xgtfrac{2x-4}{2x-1} end{cases} \ begin{cases} 0lt xlt 1\ log_3 xltfrac{2x-4}{2x-1} end{cases} end{array} right. end{gather*} Исследуем функцию (f(x)=frac{2x-4}{2x-1}=frac{2x-1-3}{2x-1}=1-frac{3}{2x-1})
Точка разрыва: (x=frac12) – вертикальная асимптота
Односторонние пределы: begin{gather*} lim_{xrightarrow frac12 -0}left(1-frac{3}{2x-1}right)=1-frac{3}{-0}=+infty\ lim_{xrightarrow frac12 +0}left(1-frac{3}{2x-1}right)=1-frac{3}{+0}=-infty end{gather*} Второе слагаемое стремится к 0 на бесконечности, и это дает горизонтальную асимптоту: (y=1) begin{gather*} lim_{xrightarrow -infty}left(1-frac{3}{2x-1}right)=1-frac{3}{-infty}=1+0\ lim_{xrightarrow +infty}left(1-frac{3}{2x-1}right)=1-frac{3}{+infty}=1-0 end{gather*} На минус бесконечности кривая стремится к (y=1) сверху, а на плюс бесконечности – снизу.
Первая производная: $$ f'(x)=left(1-frac{3}{2x-1}right)’=frac{3}{(2x-1)^2}gt 0 $$ Производная положительная на всей ОДЗ, функция возрастает.
Вторая производная: $$ f”(x)=-frac{6}{(2x-1)^3} $$ Одна критическая точка 2-го порядка (x=frac12)
| (x) | (left(0;frac12right)) | (frac12) | (left(frac12;+inftyright)) |
| (f”(x)) | >0 | ∅ | <0 |
| (f(x)) | (cup) | ∅ | (cap) |
Пересечения с осью OY: (f(0)=1-frac{3}{0-1}=4), точка (0;4)
Пересечение с осью OX: (1-frac{3}{2x-1}=0Rightarrow 2x-1=3 Rightarrow x=2), точка (2;0)
Строим графики (f(x)=frac{2x-4}{2x-1}) и (g(x)=log_3 x)
Первая система из совокупности ( begin{cases} xgt 1\ log_3 xgt frac{2x-4}{2x-1} end{cases} )
Логарифм при (xgt 1) все время выше, чем правая ветка гиперболы, т.е. система справедлива для всех (xgt 1).
Вторая система из совокупности ( begin{cases} 0lt xlt 1\ log_3 xlt frac{2x-4}{2x-1} end{cases} )
Логарифм попадает под левую ветку гиперболы на интервале (0lt xltfrac12), т.е. $$ begin{cases} 0lt xlt 1\ 0lt xltfrac12 end{cases} Rightarrow 0lt xltfrac12 $$ Решение совокупности – это объединение полученных решений систем: $$ 0lt xltfrac12cup xgt 1 $$ Ответ: (xinleft(0;frac12right)cup (1;+infty))
Как определить количество корней уравнения через производную
Определение 1. Пусть функция определена в некоторой окрестности точки . Придавая независимой переменной приращение х , невыводящее за пределы окрестности, получим новое значение + х , также принадлежащее окрестности . Тогда значение функции заменится новым значением , то есть получит приращение
Если существует предел отношения приращении функции у к вызвавшему его приращению независимой переменной х при стремлении х к 0, т.е. , то он называется производной функции в точке х и обозначается .
Операция вычисления производной называется операцией дифференцирования.
Образно говоря, равенство означает, что производная функции в точке х равна скорости изменения переменной у относительно переменой в указанной точке.
Определение 2. Функция , заданная в некоторой окрестности точки R называется дифференцируемой в этой точке, если ее приращение , представимо в этой окрестности в виде , где – постоянная, О( х) – бесконечно малая более высокого порядка, чем х.
Линейная функция (аргумента х ) называется дифференциалом функции в точке х и обозначается df(x или dy .
Таким образом, у = dy + О( х) , .
Можно доказать следующую теорему:
Теорема 1. Функция дифференцируема в некоторой точке в том и только том случае, когда в этой точке имеет конечную производную.
Учитывая определение 2 и утверждение теоремы, в качестве определения дифференцируемой функции может быть принято следующее:
Определение 3. Если функция у имеет производную в точке , то говорят, что при данном значении функция дифференцируема.
То есть существование производной функции в точке х равносильно ее дифференцируемости в этой точке.
Теорема 2 . Если функция дифференцируема в некоторой точке, то она непрерывна в этой точке.
Обратная теорема не верна: существуют функции, непрерывные в некоторой точке, но не дифференцируемые в этой точке.
Если функция определена в некоторой окрестности точки , принимает в этой точке наибольшее (наименьшее) в рассматриваемой окрестности значение и имеет в точке х производную, то эта производная равна нулю.
1) непрерывна на отрезке [ ]
2) имеет в каждой точке интервала конечную производную,
3) принимает равные значения на концах отрезка [ ], то есть f(a) = f(b) , то существует, по крайней мере, одна такая точка , что .
Если функция непрерывна на отрезке [ ] и в каждой точке интервала имеет конечную или определенного знака бесконечную производную, то существует такая точка , что f(b) – f(a) = f ( (b – a).
Используя теорему Лагранжа, можно доказать следующие теоремы:
Условие постоянства функции
Теорема 3. (Условие постоянства функции) Пусть функция определена и непрерывна на промежутке Х и во всех его внутренних точках имеет конечную производную . Для того, чтобы была на указанном отрезке постоянной, необходимое и достаточное условие внутри Х.
Если две функции и определены и непрерывны в промежутке Х и внутри него имеют конечные производные и , причем (внутри Х), то эти функции на всем промежутке Х отличаются лишь на постоянную: (C = const).
Теорема 4. (Признак монотонности функций)
Для того чтобы дифференцируемая на интервале функция возрастала (убывала) на этом интервале, необходимо и достаточно, чтобы ее производная была во всех точках интервала неотрицательна (неположительна).
Если производная функция во всех точках интервала положительна (отрицательна), то функция строго возрастает (строго убывает) на этом интервале.
Если функции и непрерывны на отрезке [ ] и в каждой точке интервала имеют конечные производные , , причем для , а f(а) g(а) , тогда для любой точки выполняется неравенство .
На основании утверждения теоремы 5 для того, чтобы доказать неравенство f(x) 0 при х 0 , достаточно доказать, что f(0) 0 и (х) 0 при х 0 . А для того, чтобы доказать неравенство при , можно воспользоваться второй производной и при и т.д.
С помощью производной можно также определить число корней того или иного уравнения. Один из возможных приемов основан на следующей теореме:
Если функция определена и непрерывна на отрезке и во всех его внутренних точках имеет конечную производную, то между любыми двумя корнями этой функции, расположенными на отрезке, имеется хотя бы 1 корень ее производной.
Рассмотренные теоретические положения используются при решении задач.
Задача 1. Докажите тождество 3 arcsin x – arccos( 3 4 ) = , если .
Решение. Рассмотрим функцию 3 arcsinx – arccos( 3 4 на отрезке [ ]. Докажем, что f(х) = с, с = const. Для этого достаточно доказать, что (т.3)
Если , то следовательно, и . Для определения значения вычислим значение функции в произвольной точке интервала . Пусть , тогда и .
Вычислим значение функции на концах заданного отрезка.
Таким образом, тождество верно при любом .
Задача 2. Найдите сумму .
Решение. Представив искомую сумму в виде , заметим, что .
Используя формулу суммы членов геометрической прогрессии, получим,
Итак, искомая сумма имеет вид .
Используя полученную формулу, можно, например, вычислить
Задача 3. Найдите сумму:
Решение. Используя результат, полученный в примере 2, заметим, что
Задача 4. Решите уравнение:
Решение. Очевидно, что – корень уравнения. Докажем, что уравнение других корней не имеет. Рассмотрим функцию
Для функции точка является точкой минимума, в которой функция принимает наименьшее значение. Значит, для всех , отличных от нуля, > .
Задача 5. Решите уравнение:
Преобразуем уравнение к виду:
Рассмотрим функции и при .
Сравним множества значений этих функций. Очевидно, что .
Найдем с использованием производной.
Функция непрерывна на промежутке и имеет на нем единственную критическую точку , в которой достигает своего наибольшего значения.
Следовательно, решение уравнения находим из решения системы:
Рассмотрим функцию , при .
Функция непрерывна на промежутке и является возрастающей, . – является точкой минимума функции , в которой функция принимает наименьшее значение, ровное нулю. Следовательно, для всех > .
Таким образом, исходное уравнение имеет единственный корень .
Задача 6. Докажите, что уравнение может иметь не более трех различных корней.
Решение. Рассмотрим функцию . Функция является дифференцируемой на R . Предположим, что функция имеет более трех различных корней, например, четыре. Тогда должна иметь не более трех различных корней (т.6), то есть обращается в нуль не менее трех раз.
Функция дифференцируема на R . Ее производная обращается в нуль не менее двух раз. Тогда имеет не менее двух нулей, а ее производная не менее одного нуля. Но функция нулей не имеет. Получили противоречие. Значит, сделанное предположение неверно, функция более трех различных корней иметь не может. Таким образом, заданное уравнение может иметь не более трех различных корней.
Производную можно использовать при доказательстве и решении неравенств.
Задача 7. Доказать, что при 0$”>.
Доказательство. Докажем справедливость следующих неравенств:
0. end –>
Для доказательства неравенства (2) рассмотрим функцию
Применение производной для решения нелинейных уравнений и неравенств
п.1. Количество корней кубического уравнения
Кубическое уравнение $$ ax^3+bx^2+cx+d=0 $$ на множестве действительных чисел может иметь один, два или три корня.
С помощью производной можно быстро ответить на вопрос, сколько корней имеет данное уравнение. begin f(x)=ax^3+bx^2+cx+d\ f'(x)=3ax^2+bx+c end Если в уравнении (f'(x)=0) дискриминант (D=4b^2-12ac=4(b^2-3ac)gt 0), кубическая парабола имеет две точки экстремума: (x_<1,2>=frac<-2bpmsqrt><6a>). Если при этом значения функции в точках экстремума (f(x_1)cdot f(x_2)lt 0), т.е. расположены по разные стороны от оси OX, парабола имеет три точки пересечения с этой осью. Исходное уравнение имеет три корня.
Если две точки экстремума найдены, но (f(x_1)cdot f(x_2)=0), уравнение имеет два корня.
Во всех остальных случаях – у исходного уравнения 1 корень.
Пример 1. Сколько корней имеют уравнения:
п.2. Количество корней произвольного уравнения
Задачи на подсчет количества корней решаются с помощью построения графиков при полном или частичном исследовании функций.
Пример 2. а) Найдите число корней уравнения (frac 1x+frac<1>+frac<1>)
б) Найдите число корней уравнения (frac 1x+frac<1>+frac<1>=k)
Построим график функции слева, а затем найдем для него количество точек пересечения с горизонталью (y=1). Это и будет ответом на вопрос задачи (а).
Исследуем функцию: $$ f(x)=frac1x+frac<1>+frac<1> $$ Алгоритм исследования и построения графика – см. §49 данного справочника.
1) ОДЗ: (xneleft<0;1;3right>)
Все три точки – точки разрыва 2-го рода. begin lim_left(frac1x+frac<1>+frac<1>right)=-infty-1-frac13=-infty\ lim_left(frac1x+frac<1>+frac<1>right)=+infty-1-frac13=+infty\ lim_left(frac1x+frac<1>+frac<1>right)=1-infty-frac12=-infty\ lim_left(frac1x+frac<1>+frac<1>right)=1+infty-frac12=+infty\ lim_left(frac1x+frac<1>+frac<1>right)=frac13+frac12-infty=-infty\ lim_left(frac1x+frac<1>+frac<1>right)=frac13+frac12+infty=+infty end 2) Функция ни четная, ни нечетная.
Функция непериодическая.
3) Асимптоты
1. Вертикальные (x=0, x=1, x=3) – точки разрыва 2-го рода
2. Горизонтальные: begin lim_left(frac1x+frac<1>+frac<1>right)=-0-0-0=-0\ lim_left(frac1x+frac<1>+frac<1>right)=+0+0+0=+0\ end Горизонтальная асимптота (y=0)
На минус бесконечности функция стремится к 0 снизу, на плюс бесконечности – сверху.
3. Наклонные: (k=0), нет.
4) Первая производная $$ f'(x)=-frac<1>-frac<1><(x-1)^2>-frac<1><(x-3)^2>lt 0 $$ Производная отрицательная на всей ОДЗ.
Функция убывает.
5) Вторую производную не исследуем, т.к. перегибы не влияют на количество точек пересечения с горизонталью.
6) Точки пересечения с OY – нет, т.к. (x=0) – асимптота
Точки пересечения с OX – две, (0lt x_1lt 1,1lt x_2lt 3)
7) График
Получаем ответ для задачи (а) 3 корня.
Решаем более общую задачу (б). Передвигаем горизонталь (y=k) снизу вверх и считаем количество точек пересечения с графиком функции. Последовательно, получаем:
При (klt 0) – три корня
При (k=0) – два корня
При (kgt 0) – три корня
Ответ: а) 3 корня; б) при (k=0) два корня, при (kne 0) три корня.
Пример 3. Найдите все значения параметра a, при каждом из которых уравнение $$ sqrt+sqrt<10-2x>=a $$ имеет по крайней мере одно решение.
Исследуем функцию (f(x)=sqrt+sqrt<10-2x>)
ОДЗ: ( begin x-1geq 0\ 10-2xgeq 0 end Rightarrow begin xgeq 1\ xleq 5 end Rightarrow 1leq xleq 5 )
Функция определена на конечном интервале.
Поэтому используем сокращенный алгоритм для построения графика.
Значения функции на концах интервала: (f(1)=0+sqrt<8>=2sqrt<2>, f(5)=sqrt<4>+0=2)
Первая производная: begin f'(x)=frac<1><2sqrt>+frac<-2><2sqrt<10-2x>>=frac<1><2sqrt>-frac<1><sqrt<10-2x>>\ f'(x)=0 text<при> 2sqrt=sqrt<10-2x>Rightarrow 4(x-1)=10-2xRightarrow 6x=14Rightarrow x=frac73\ fleft(frac73right)=sqrt<frac73-1>+sqrt<10-2cdot frac73>=sqrt<frac43>+sqrt<frac<16><3>>=frac<6><sqrt<3>>=2sqrt <3>end Промежутки монотонности:
| (x) | 1 | (1; 7/3) | 7/3 | (7/3; 5) | 5 |
| (f'(x)) | ∅ | + | 0 | – | ∅ |
| (f(x)) | (2sqrt<2>) | (nearrow ) | max (2sqrt<3>) |
(searrow ) | 2 |
Можем строить график:
(y=a) – горизонтальная прямая.
Количество точек пересечения (f(x)) и (y) равно количеству решений.
Получаем:
| $$ alt 2 $$ | нет решений |
| $$ 2leq alt 2sqrt <2>$$ | 1 решение |
| $$ 2sqrt<2>leq alt 2sqrt <3>$$ | 2 решения |
| $$ a=2sqrt <3>$$ | 1 решение |
| $$ agt 2sqrt <3>$$ | нет решений |
По крайней мере одно решение будет в интервале (2leq aleq 2sqrt<3>).
п.3. Решение неравенств с построением графиков
Пример 4. Решите неравенство (frac<2+log_3 x>gt frac<6><2x-1>)
Разобьем неравенство на совокупность двух систем.
Если (xgt 1), то (x-1gt 0), на него можно умножить слева и справа и не менять знак.
Если (xlt 1), то (x-1lt 0), умножить также можно, только знак нужно поменять.
Сразу учтем требование ОДЗ для логарифма: (xgt 0)
Получаем совокупность: begin left[ begin begin xgt 1\ 2+log_3 xgtfrac<6(x-1)> <2x-1>end \ begin 0lt xlt 1\ 2+log_3 xltfrac<6(x-1)> <2x-1>end end right. \ 2+log_3 xgt frac<6(x-1)><2x-1>Rightarrow log_3 xgt frac<6(x-1)-2(2x-1)><2x-1>Rightarrow log_3 xgt frac<2x-4><2x-1>\ left[ begin begin xgt 1\ log_3 xgtfrac<2x-4> <2x-1>end \ begin 0lt xlt 1\ log_3 xltfrac<2x-4> <2x-1>end end right. end Исследуем функцию (f(x)=frac<2x-4><2x-1>=frac<2x-1-3><2x-1>=1-frac<3><2x-1>)
Точка разрыва: (x=frac12) – вертикальная асимптота
Односторонние пределы: begin lim_left(1-frac<3><2x-1>right)=1-frac<3><-0>=+infty\ lim_left(1-frac<3><2x-1>right)=1-frac<3><+0>=-infty end Второе слагаемое стремится к 0 на бесконечности, и это дает горизонтальную асимптоту: (y=1) begin lim_left(1-frac<3><2x-1>right)=1-frac<3><-infty>=1+0\ lim_left(1-frac<3><2x-1>right)=1-frac<3><+infty>=1-0 end На минус бесконечности кривая стремится к (y=1) сверху, а на плюс бесконечности – снизу.
Первая производная: $$ f'(x)=left(1-frac<3><2x-1>right)’=frac<3><(2x-1)^2>gt 0 $$ Производная положительная на всей ОДЗ, функция возрастает.
Вторая производная: $$ f”(x)=-frac<6> <(2x-1)^3>$$ Одна критическая точка 2-го порядка (x=frac12)
“Решаем с помощью производной”
Разделы: Математика
Производная широко применяется при решении ряда задач элементарной математики. Из всего круга таких задач выделим те, при решении которых используется теорема Лагранжа и ее следствия. К ним относятся задачи на доказательство тождеств, неравенств, вывод формул тригонометрии, разложение алгебраических выражений на множители, решение уравнений, неравенств, систем уравнений, уравнений с параметрами. При этом можно указать общие методы решения и некоторые частные приемы.
Теорема Лагранжа. Пусть функция f непрерывна на отрезке [a;b] и дифференцируема во внутренних точках этого отрезка. Тогда существует внутренняя точка с этого отрезка, такая, что .
Следствие 1 (условие постоянства). Если функция f непрерывна на отрезке [a;b], а ее производная равна нулю внутри этого отрезка, то функция f постоянна на [a;b].
Следствие 2. Если функции 

Условие монотонности функции также является следствием теоремы Лагранжа. В школьном учебнике оно устанавливается отдельно в виде теоремы.
Следствие 3 (условие монотонности). Если функция f непрерывна на промежутке I и ее производная положительна (соответственно отрицательна) во внутренних точках этого промежутка, то функция f возрастает (соответственно убывает) на I.
Теорему Лагранжа можно применять:
– при доказательстве неравенств, в частности – числовых неравенств;
– при исследовании вопроса о корнях многочлена или уравнения;
– при решении уравнений.
В процессе решения таких задач вводится в рассмотрение функция f(x) на отрезке [a;b], удовлетворяющая условиям теоремы Лагранжа, для нее записывается формула Лагранжа , c 
Пример 1. Доказать, что .
Решение. Функция f(x)=arccosx на отрезке [0,6;0,8] непрерывна и дифференцируема на интервале (0,6;0,8), . Следовательно, для функции f(x) на данном отрезке выполняются условия теоремы Лагранжа и , где 0,6 , т.е. . Оценим число . Так как 0,6 2 . Тогда и окончательно .
Пример 2. Доказать, что e x >=ex.
Решение. Неравенство справедливо при х=1. Рассмотрим функцию f(x)=e x -ex. Тогда для любого числа b (b>1) для данной функции выполняются условия теоремы Лагранжа на отрезке [1;b], а для b , т.е. . Так как c>1 при b>1, то e c >e и, следовательно, e c -e>0. Тогда , а значит e b -eb>0, т.е. e b >eb для любого b>1. Таким образом доказано, что e x >=ex при x>=1.
Если b , т.е. с c c -e , следует, что e b -eb>0, т.е. e b >eb.
Итак, доказано, что неравенство e x >=ex верно при любом действительном х. В частности, при x=c+1 получим e c+1 >=e(c+1), т.е. e c >=c+1, где с – любое действительное число.
Пример 3. Доказать, что уравнение не имеет действительных положительных корней.
Решение. Пусть b – любое положительное число. Рассмотрим функцию f(x)= , непрерывную на отрезке [a;b] и имеющую производную на интервале (0;b). По теореме Лагранжа имеем , 0 . А так как при любом с>0 e c >c+1 (доказано в примере 2), то e c -c>1 и, следовательно, . Отсюда получим , а значит для любого b>0. Таким образом, при x>0, т.е. , следовательно, равенство не выполняется ни при каком x>0. А, значит, уравнение не имеет действительных положительных корней.
Пример 4. Доказать, что на промежутке (0, 2
Решение. Предположим, что уравнение имеет не менее трех различных действительных корней х1, х2, х3, принадлежащих промежутку (0,2

Найдем производную f’(x):
. Так как для любых х, то уравнение f’(x)=0 имеет единственный корень x=



Пример 5. Решить уравнение x 9 -9x 5 +63x-55=0.
Решение. Легко заметить, что число х1=1 является корнем данного уравнения. Предположим, что существует еще хотя бы один действительный корень х2, отличный от х1. Числа х1 и х2 являются нулями функции f(x)=x 9 -9x 5 +63x-55 и, следовательно, f(x1)=f(x2)=0. Применим терему Лагранжа к функции f(x) на отрезке [x1;x2], если x1 x2. Следовательно, найдется такая внутренняя точка с этого отрезка, что будет выполняться . Учитывая, что f(x1)=f(x2)=0, получим f’(с)=0, т.е. число с – корень уравнения f’(x)=0. Но производная f’(x)=9x 8 -45x 4 +63, т.е. f’(x)=9(x 4 -2,5) 2 +6,75 положительна для любых х, а значит уравнение f’(x)=0 не имеет корней. Полученное противоречие доказывает, что найденный корень х1=1 является единственным корнем уравнения x 9 -9x 5 +63x-55=0.
Определить число критических точек функции y=(x 2 -1)(x 2 -8х)(x-9).
Решение. Так как степень многочлена f(x)= (x 2 -1)(x 2 -8х)(x-9) равна 5, то его производная f’(x) является многочленом четвертой степени и имеет не более четырех действительных корней. Применим теорему Лагранжа к функции f(x)=(x+1)(x-1)х(x-8)(x-9) на отрезках [-1;0], [0;1], [1;8], [8;9] и при этом учтем, что f(-1)=f(0)=f(1)=f(8)=f(9)=0. На каждом таком отрезке найдутся внутренние точки х1, х2, х3, х4 соответственно, такие, что , , , , т.е. f’(x1)=0, f’(x2)=0, f’(x3)=0, f’(x4)=0. А учитывая, что x1, х2, х3, х4 – различные корни многочлена f’(x) четвертой степени, делаем вывод, что других корней, отличных от полученных, нет и, следовательно, функция y=(x 2 -1)(x 2 -8х)(x-9) имеет четыре критические точки.
Условие монотонности функции можно применять:
– при решении неравенств;
– при доказательстве неравенств с переменной;
– при доказательстве числовых неравенств;
– при исследовании вопроса о количестве корней уравнения;
– в некоторых случаях при решении уравнений, уравнений с параметрами, систем уравнений.
Решение задач с использованием условия монотонности основано на связи между возрастанием или убыванием функции и знаком ее производной на некотором промежутке. При этом, сравнивая различные значения аргумента из этого промежутка рассматриваемой монотонной функции, делается вывод о соответствующих значениях данной функции.
Пример 7. Доказать, что 3xcosx .
Решение. Докажем, что, если 0 , то sinx+sin2x-3xcosx>0, т.е. cosx(tgx+2sinx-3x)>0. Рассмотрим непрерывную на промежутке функцию f(x)=tgx-3x+2sinx. Ее производная при принимает положительные значения, следовательно, функция f(x) возрастает на промежутке и на нем f(x)>f(0).
Учитывая, что f(0)=0, будем иметь tgx-3x+2sinx>0. А так как на промежутке cosx>0, то и cosx(tgx+2sinx-3x)>0. Таким образом доказано, что sinx+sin2x-3xcosx>0, то есть, что 3xcosx .
Пример 8. Доказать, что
1) и , если 0 и , если e . Так как ее производная равна нулю при х=е, а при 0 0 и f’(x) e, то на промежутке (0;e] функция f(x) возрастает, а на промежутке [e;+
Если же e f(x2), то есть , откуда и получим и .
Доказанными в примере 8 неравенствами можно воспользоваться при сравнении чисел и при доказательстве числовых неравенств.
Пример 9. Сравнить (сtg48°) tg48° и (сtg50°) tg50° .
Решение. Заметим, что сtg48°=сtg , tg48°=tg , ctg50°=ctg , tg50°=tg , а также, что . Взяв , и учитывая, что , если 0 , т.е. (сtg48°) tg48° > (сtg50°) tg50° .
Пример 10. Доказать, что 2006 2007 >2007 2006 .
Решение. Воспользуемся неравенством x1 x2 >x2 x1 , если e 2007 >2007 2006 .
Определить число действительных корней уравнения 2х 3 -24х-19=0.
Решение. Функция f(x)= 2х 3 -24х-19 непрерывна на всей числовой прямой и имеет производную f’(x)=6x 2 -24=6(x-2)(x+2).
При x 2 f’(x)>0, а при –2 0, f(2)=-51 0. Так как функция f(x) на концах отрезков [-3;-2], [-2;2], [2;5] принимает значения разных знаков, то на каждом из них имеется только один корень уравнения. Таким образом, уравнение 2х 3 -24х-19=0 имеет три действительных корня, которые находятся на промежутках (-3;-2), (-2;2), (2;5).
Остальные следствия теоремы Лагранжа можно применять:
– при доказательстве тождеств, в частности при выводе формул элементарной математики;
– при упрощении выражений;
– при разложении алгебраических выражений на множители.
При решении ряда таких задач на некотором промежутке рассматривается либо одна функция f(x), такая, что ее производная f’(x)=0 и, следовательно, функция постоянна, т.е. имеет вид f(x)=c, либо две функции f(x) и g(x), такие, что f’(x)=g’(x), и делается вывод, что f(x)=g(x)+c (c – постоянная). Эту постоянную находят, положив х равным некоторому значению х1.
Пример 12. Вывести формулу .
Решение. Функция f(x)= непрерывна на всей числовой прямой. Найдем производную этой функции f’(x)=2sinxcosx-sin2x=sin2x-sin2x. f’(x)=0 для любого действительного значения х, следовательно, на основании условия постоянства функции можно сделать вывод, что функция f(x) постоянна, т.е. f(x)=c. Для определения постоянной c положим х=0 и получим f(0)=c, т.е. sin 2 0-0,5+0,5cos0=c. Таким образом, с=0 и значит f(x)=0, откуда и получим =0, или .
Пример 13. Доказать, что arctgx=arcsin при x , тогда они непрерывны на любом отрезке [b;0]. Найдем производные этих функций.
, . Так как при x и тогда f’(x)=g’(x) внутри отрезка [b;0]. На основании следствия 2 имеем f(x)=g(x)+c, где с – постоянная. Для определения с положим, например, х=-1, что дает arctg(-1)=arcsin , то есть Итак, получим arctgx=arcsin при x
Решение. Заметим, что , для любого действительного х и функции , непрерывны на всей числовой прямой. Имеем ,
1) Рассмотрим функцию F(x)=f(x)+g(x), x 


F(x)= , а F’(x)=f’(x)+g’(x)= . Если x 


, cледовательно, с=
, следовательно, с=0. Имеем: при x 


2) Рассмотрим функцию G(x)=f(x)-g(x), x 


Если x 
Если x 


Имеем: при x 


3) Вычислим значения f(x) и g(x) при х=± 1 и х=0.
f(-1)=arccos(-1)=

Таким образом, данное тождество доказано для всех действительных х.
Пример 15. Разложить на множители выражение
y 2 (x-z)+x 2 (z-y)+z 2 (y-x).
Решение. На данное выражение будем смотреть как на функцию от переменной х: f(x)=y 2 (x-z)+x 2 (z-y)+z 2 (y-x).
f’(x)=y 2 +2x(z-y)-z 2 =y 2 -z 2 -2x(y-z)=(y-z)(y+z)-2x(y-z)=(y-z)(y+z-2x).
Будем считать, что (y-z)(y+z-2x) есть производная некоторой другой функции g(x), при этом множитель (y-z) будем рассматривать как постоянную, вынесенную при дифференцировании за знак производной, т.е.
g’(x)=(y-z)((y+z)-2x). В качестве функции g(x) можно взять g(x)=(y-z)((y-z)x-x 2 ).
Так как функции f(x) и g(x) непрерывны и дифференцируемы на всей числовой прямой и f’(x)=g’(x), то по следствию 2 f(x)=g(x)+c, где с не зависит от х, но, возможно, зависит от y и z. Имеем y 2 (x-z)+x 2 (z-y)+z 2 (y-x)=(y-z)((y+z)x-x 2 )+c. Найдем с, полагая в этом равенстве, например, х=0. Имеем yz 2 -zy 2 =c. Тогда f(x)=g(x)+yz 2 -zy 2 , то есть
f(x)=(y-z)((y+z)x-x 2 )+yz 2 -zy 2 =(y-z)(xy+xz-x 2 )-yz(y-z)=(y-z)(xy-x 2 +xz-yz)=(y-z)(x(y-x)-z(y-x))=(y-z)(y-x)(x-z).
Итак, y 2 (x-z)+x 2 (z-y)+z 2 (y-x)=(y-z)(y-x)(x-z).
[spoiler title=”источники:”]
http://reshator.com/sprav/algebra/10-11-klass/primenenie-proizvodnoj-dlya-resheniya-nelinejnyh-uravnenij-i-neravenstv/
http://urok.1sept.ru/articles/417890
[/spoiler]
Понятие производной
Смысл производной основан на понятии предела функции. Состоит запись выражения из трёх частей, в одной из которых указывается, к чему стремится неизвестное. Оно может достигать как нуля, так и бесконечности. Таким образом, предел представляет собой динамическую величину. Например, пусть имеется некая функция f (x) = (1 + x)1/x.
При иксе, который равен нулю, функция будет не определена, но можно исследовать, как она будет себя вести при приближении переменной к нулю. Для этого можно взять какое-либо значение икса и, подставив его в уравнение, вычислить функцию. Затем в формулу подставить иное произвольное число, но такое, чтобы оно было меньше предыдущего, то есть приближалось к нулю.
Выполнив несколько таких вычислений, можно увидеть, что значение функции начнёт приближаться к некой величине. Это значение и считается пределом рассматриваемого выражения при иксе, стремящемся к нулю.
Следует рассмотреть другую функцию: f (x) = 1 / x. Подставляя вместо икса различные числа, можно будет отметить, что при уменьшении исходной величины переменной числовое значение в ответе увеличивается, то есть результат функции ничем не ограничивается. Это означает, что при иксе, который стремится к нулю, предел будет равняться бесконечности.
Понятие предела помогает дать определение непрерывности. Функция f (x) непрерывна в точке x = c только тогда, когда знак предела и выражения можно поменять друг с другом местами: lim f (x) = f (lim x) = f с. Используя это свойство, можно определить точки разрыва и непрерывность. Зная определения можно понять, что представляет собой производная.
Пусть имеется линейная функция y = k * x + b, графиком которой будет прямая. При изменении икса на дельту по игреку будет происходить прирост на Δy = k * Δx. Получается, что величина k является скоростью роста функции: k = (f (x + Δx) — f (x)) / Δx. В этом случае график прямой имеет постоянный наклон, поэтому коэффициент k — константа.
Если же функция имеет произвольный вид, например, она состоит из сложного многочлена с дробями и квадратами, то, как вычислить постоянную k, непонятно. Вот тут на помощь и приходит понятие производной. Можно взять отношение дельта-икс на дельта-игрек и посмотреть, какой предел будет у функции: f'(x) = lim (f (x + Δx) — f (x)) / Δx. По сути, это действие и является нахождением производной.
Свойства корня
Находить производные подкоренных выражений невозможно без знания свойств степеней и корней. По определению, корнем квадратным из произвольного числа, которое больше нуля, называется такое неотрицательное число, которое при возведении в квадрат равняется этому числу.
То есть выражение √a = b тождественно равенству: b2 = a. Например, √16 = 4, так как 42 = 16. Таким образом, можно утверждать, что корнем энной степени числа а будет такое выражение, которое при возведении в эту степень будет равняться а. Степень корня указывается в верхнем регистре значка, а основание записывается под знаком корня и называется подкоренным выражением.
Выделяют следующие свойства корней:
- Если подкоренное выражение представляет умножение неотрицательных чисел, то корень квадратный будет равняться произведению корней членов выражения: √ a * b * … * n = √ a * √ b * … * √ n.
- Когда под корнем находится отношение двух положительных чисел, то для решения выражения нужно извлечь корень из числителя и знаменателя, а после выполнить деление: √ a / b = √ a / b = √ a / √ b.
- В случае когда а больше или равняется нулю и при этом n является натуральным, то корень из подкоренного выражения будет равняться а в степени n: √ a2n = an.
- При действительном числе и чётном значении показателей подкоренного выражения будет справедливым равенство: 2*m√ a2*m = | a |. Если же показатель нечётный, то в ответе действительное число будет всегда положительное.
- При извлечении корня из корня n√ m√ действие можно заменить произведением показателей при неизменном подкоренном выражении.
- Сложение и вычитание корней возможно только в том случае, когда количественные или буквенные значения подкоренных выражений совпадают: n √ m + k √ m = (n + k) √ m.
- Умножить корни с одинаковыми показателями возможно лишь тогда, когда показатель у всех перемножаемых членов одинаков: √ n * √ m = √ n * m.
Для любой степени существует основная формула, по которой может быть найдена производная.
Выглядит она как (xn)’ = n * xn -1. Эта формула используется и для дифференцирования корней. Кроме этого, для успешного решения задач на нахождение производной квадратного корня из х необходимо знать и свойства степеней.
Нахождение выражения из Х
В общем случае формула производной корня из х равна дроби, в числителе которой стоит единица, а в знаменателе произведение степени корня на корень той же степени в подкоренном выражении, где находится неизвестное, уменьшенное на единицу, в степени. Математически это теорема записывается следующей формулой: (n√x)’ = 1 / (n * n√ xn-1).
Эта формула имеет название первообразной. Она подходит для использования в выражениях любой кратности. В качестве примера можно рассмотреть взятие производной квадратного и кубического корня.
Так, для квадратного степенного уравнения справедливо выражение: (n√x)’ = 1 / 2 * √x. То есть производная квадратного корня х является дробью, делимое которой равняется единице, а делитель состоит из двойки, умножаемой на квадратный корень из неизвестного.
Аналогично можно сформулировать теорему и для нахождения производной кубического корня из x. Для этого случая решением задания на вычисление производной будет дробь, в числителе которой находится единица, а в знаменателе произведение тройки на корень кубический из икса в степени два. Формула для вычисления выглядит следующим образом: (3√x)’ = 1 / (3 3 √x2).
Можно обратить внимание, что, по сути, операция сводится к таким же действиям, как и при возведении дробей в степень, когда делитель равняется тому же показателю.
Иными словами, вычисление производной коренного выражения сводится к использованию формул для нахождения функции дроби.
Для доказательства формул используют следующие рассуждения. Производная переменной под квадратным корнем это то же, что и нахождение функции при возведении многочлена в степень одна вторая: (√x)’ = (х ½)’. Поэтому можно воспользоваться формулой для расчёта производной неизвестного числа в степени эн. А значит, запись вида (х½)’ = ½ х-½ = 1 / (2√х) будет верной.
Формула производной третьей степени доказывается по такому же принципу. Используя правило дифференцирования и переписав кубический корень как тройную степень, можно записать: (3√x)’ = (х 1/3 )’ = 1 / 3 * (x-2/3) = 1 / 3 * (3√х2). Тут следует отметить, что степень -2/3 образовывается путём вычитания единицы из дроби, в числителе которой стоит два, а в знаменателе три.
Примеры заданий
При взятии производной функции f (x) = n√хm необходимо привести корень к степенному виду: f (x)’ = (n√х m)’ = xm/n.
Так как из производных степени известно, что (xm)’ = m * xm-1, то и алгоритм решения для нахождения ответа коренного выражения сводится к преобразованию исходного уравнения путём перехода к степени: f (x)’ = (n√хm)’ = (xm/n)’ = m/n * x (m/n) -1 = (m/n * n√хm-n).
Этот подход позволяет не запоминать сложную формулу, что часто и используется на практике.
Для закрепления теории следует решить несколько типовых примеров:
- Определить, чему будет равна производная от корня квадратного, кратного разности три минус икс в квадрате. Запись условия задачи выглядит так: (√ 3 — x 2)’. Мысленно можно обозначить выражение в скобках буквой S. Получается, что задача будет состоять в поиске производной (√ S)’. Используя знание формулы, можно утверждать, что (√ S)’ = S’ / (2 * √ S). Ту же самую формулу можно будет получить, воспользовавшись преобразованием задания в степенную функцию: (√ S)’ = (S½)‘ = (½) * S(½ — 1 ) * S’ = S-½ * S’ / 2 = S’ / (2 * √ S). Таким образом, (√ 3 — x 2)’ = (3 — x2)’ / (2 * √ 3 — x2) = – 2* x / 2 * √ 3 — x2 = – x / √ 3 — x2.
- Рассчитать, чему будет равна производная функции 1 / (2 * 3√ x7). Исходное выражение нужно преобразовать так, чтобы неизвестная оказалась в числителе, а затем уже воспользоваться стандартным алгоритмом: (1 / 2 * 3√ x7)’ = 1 / 2 * (x-7/3)’. Теперь нужно взять производную от степенной функции. В итоге получится выражение: 1 / 2 * (-7 / 3) * x (-7/3) — 1 = -(7 / 6) * x-10/3 = (-7 / 6) * (1 / 3√ x10).
- Необходимо найти производную суммы многочленов: p (x) = 3 + 4 √ x+3. По теореме дифференцирования ответ будет равняться сумме производных каждого члена равенства: p (x)’ = (3)’ + (4 √ x+3)’. Первое слагаемое равняется нулю, поэтому останется только найти производную корня. Используя снова правило производной, выражение можно переписать как 4 * (√ x+3)’. На следующем этапе многочлен в скобках нужно представить в виде степенной функции: (√x + 3)’ = 1 / ((2√x + 2)) * (x + 2)’ = 2 * (x +2)’ / √x+2. Так как производная суммы, это то же самое, что сумма производных, то будет верным записать: (4 √ x+2)’ = (2 / √x+2) *({(x)’ + (2)’}). Производная для двойки равна нулю, поэтому плюсовать её смысла нет. В итоге получится: p (x)’ = (3 + 4 √ x+3)’ = 2/ √x +2 = 2 / √x +2.
Расчёт на онлайн-калькуляторе
Попрактиковавшись в решении различных примеров, найти производную корня простых выражений будет довольно просто. Но если в заданиях будут стоять двойные корни или сама функция будет содержать большой многочлен, могут возникнуть проблемы. Связаны они обычно не с алгоритмом решения, а с трудностью вычисления и преобразования.
Такого рода задачи требуют повышенного внимания и скрупулёзности в расчётах. При этом поиску ответа понадобится уделить довольно много времени. Поэтому для помощи в нахождении производных коренных функций и существуют в интернете математические онлайн-калькуляторы.
Это сервисы, предлагающие бесплатно услуги по автоматическому расчёту производной любой сложности. Воспользоваться ими может каждый желающий, имеющий доступ к интернету. Для нахождения ответа не нужно обладать какими-то особыми знаниями. Всё что требуется от пользователя — ввести в предложенную форму условие и нажать кнопку «Вычислить». Весь процесс расчёта займёт одну-две секунды.
При этом большинство сервисов, кроме предоставления ответа на своих страницах, дает возможность ознакомиться с теоретическим материалом и предлагает рассмотреть решения заданий различной сложности. Поэтому вопроса, каким образом получился тот или иной ответ, возникнуть не должно.
Из различных онлайн-калькуляторов, считающих производные, можно выделить следующие:
- Webmath.
- Kontrolnaya-rabota
- Onlinemschool.
- Сalc.
- Nauchniestati.
Сайты, используемые для вычислений, характеризуются интуитивно понятным интерфейсом, не содержащим нагромождения ненужной информации. На их страницах нет рекламного и вирусного кода.
Примечательно и то, что, выполнив пару вычислений, пользователь научится самостоятельно вычислять производную. А всё дело в том, что особенностью таких ресурсов является возможность обучения. Кроме непосредственно ответа, программа-расчётчик выдаст пошаговое вычисление с комментариями.
Кроме учащихся, онлайн-калькуляторы будут полезны и инженерам. Даже незначительная ошибка, допущенная в расчёте, приведёт к неверному ответу. В то же время при автоматических вычислениях появление ошибки исключено.
Производная корень из Х — формулы и примеры вычислений
Понятие производной
Смысл производной основан на понятии предела функции. Состоит запись выражения из трёх частей, в одной из которых указывается, к чему стремится неизвестное. Оно может достигать как нуля, так и бесконечности. Таким образом, предел представляет собой динамическую величину. Например, пусть имеется некая функция f (x) = (1 + x) 1/x .
При иксе, который равен нулю, функция будет не определена, но можно исследовать, как она будет себя вести при приближении переменной к нулю. Для этого можно взять какое-либо значение икса и, подставив его в уравнение, вычислить функцию. Затем в формулу подставить иное произвольное число, но такое, чтобы оно было меньше предыдущего, то есть приближалось к нулю.
Выполнив несколько таких вычислений, можно увидеть, что значение функции начнёт приближаться к некой величине. Это значение и считается пределом рассматриваемого выражения при иксе, стремящемся к нулю.
Следует рассмотреть другую функцию: f (x) = 1 / x. Подставляя вместо икса различные числа, можно будет отметить, что при уменьшении исходной величины переменной числовое значение в ответе увеличивается, то есть результат функции ничем не ограничивается. Это означает, что при иксе, который стремится к нулю, предел будет равняться бесконечности.
Понятие предела помогает дать определение непрерывности. Функция f (x) непрерывна в точке x = c только тогда, когда знак предела и выражения можно поменять друг с другом местами: lim f (x) = f (lim x) = f с. Используя это свойство, можно определить точки разрыва и непрерывность. Зная определения можно понять, что представляет собой производная.
Пусть имеется линейная функция y = k * x + b, графиком которой будет прямая. При изменении икса на дельту по игреку будет происходить прирост на Δy = k * Δx. Получается, что величина k является скоростью роста функции: k = (f (x + Δx) — f (x)) / Δx. В этом случае график прямой имеет постоянный наклон, поэтому коэффициент k — константа.
Если же функция имеет произвольный вид, например, она состоит из сложного многочлена с дробями и квадратами, то, как вычислить постоянную k, непонятно. Вот тут на помощь и приходит понятие производной. Можно взять отношение дельта-икс на дельта-игрек и посмотреть, какой предел будет у функции: f'(x) = lim (f (x + Δx) — f (x)) / Δx. По сути, это действие и является нахождением производной.
Свойства корня
Находить производные подкоренных выражений невозможно без знания свойств степеней и корней. По определению, корнем квадратным из произвольного числа, которое больше нуля, называется такое неотрицательное число, которое при возведении в квадрат равняется этому числу.
То есть выражение √a = b тождественно равенству: b 2 = a. Например, √16 = 4, так как 4 2 = 16. Таким образом, можно утверждать, что корнем энной степени числа а будет такое выражение, которое при возведении в эту степень будет равняться а. Степень корня указывается в верхнем регистре значка, а основание записывается под знаком корня и называется подкоренным выражением.
Выделяют следующие свойства корней:
- Если подкоренное выражение представляет умножение неотрицательных чисел, то корень квадратный будет равняться произведению корней членов выражения: √ a * b * … * n = √ a * √ b * … * √ n.
- Когда под корнем находится отношение двух положительных чисел, то для решения выражения нужно извлечь корень из числителя и знаменателя, а после выполнить деление: √ a / b = √ a / b = √ a / √ b.
- В случае когда а больше или равняется нулю и при этом n является натуральным, то корень из подкоренного выражения будет равняться а в степени n: √ a 2 n = a n .
- При действительном числе и чётном значении показателей подкоренного выражения будет справедливым равенство: 2*m √ a 2*m = | a |. Если же показатель нечётный, то в ответе действительное число будет всегда положительное.
- При извлечении корня из корня n √ m √ действие можно заменить произведением показателей при неизменном подкоренном выражении.
- Сложение и вычитание корней возможно только в том случае, когда количественные или буквенные значения подкоренных выражений совпадают: n √ m + k √ m = (n + k) √ m.
- Умножить корни с одинаковыми показателями возможно лишь тогда, когда показатель у всех перемножаемых членов одинаков: √ n * √ m = √ n * m.
Для любой степени существует основная формула, по которой может быть найдена производная.
Выглядит она как (x n )’ = n * x n -1 . Эта формула используется и для дифференцирования корней. Кроме этого, для успешного решения задач на нахождение производной квадратного корня из х необходимо знать и свойства степеней.
Нахождение выражения из Х
В общем случае формула производной корня из х равна дроби, в числителе которой стоит единица, а в знаменателе произведение степени корня на корень той же степени в подкоренном выражении, где находится неизвестное, уменьшенное на единицу, в степени. Математически это теорема записывается следующей формулой: ( n √x)’ = 1 / (n * n √ x n -1 ).
Эта формула имеет название первообразной. Она подходит для использования в выражениях любой кратности. В качестве примера можно рассмотреть взятие производной квадратного и кубического корня.
Так, для квадратного степенного уравнения справедливо выражение: (n√x)’ = 1 / 2 * √x. То есть производная квадратного корня х является дробью, делимое которой равняется единице, а делитель состоит из двойки, умножаемой на квадратный корень из неизвестного.
Аналогично можно сформулировать теорему и для нахождения производной кубического корня из x. Для этого случая решением задания на вычисление производной будет дробь, в числителе которой находится единица, а в знаменателе произведение тройки на корень кубический из икса в степени два. Формула для вычисления выглядит следующим образом: ( 3 √x)’ = 1 / (3 3 √x 2 ).
Можно обратить внимание, что, по сути, операция сводится к таким же действиям, как и при возведении дробей в степень, когда делитель равняется тому же показателю.
Иными словами, вычисление производной коренного выражения сводится к использованию формул для нахождения функции дроби.
Для доказательства формул используют следующие рассуждения. Производная переменной под квадратным корнем это то же, что и нахождение функции при возведении многочлена в степень одна вторая: (√x)’ = (х ½ )’. Поэтому можно воспользоваться формулой для расчёта производной неизвестного числа в степени эн. А значит, запись вида (х ½ )’ = ½ х -½ = 1 / (2√х) будет верной.
Формула производной третьей степени доказывается по такому же принципу. Используя правило дифференцирования и переписав кубический корень как тройную степень, можно записать: ( 3 √x)’ = (х 1/3 )’ = 1 / 3 * (x- 2/3 ) = 1 / 3 * ( 3 √х 2 ). Тут следует отметить, что степень -2/3 образовывается путём вычитания единицы из дроби, в числителе которой стоит два, а в знаменателе три.
Примеры заданий
При взятии производной функции f (x) = n √х m необходимо привести корень к степенному виду: f (x)’ = ( n √х m )’ = x m/n .
Так как из производных степени известно, что (x m )’ = m * x m-1 , то и алгоритм решения для нахождения ответа коренного выражения сводится к преобразованию исходного уравнения путём перехода к степени: f (x)’ = ( n √х m )’ = (x m/n )’ = m/n * x ( m/n) -1 = (m/n * n √х m-n ).
Этот подход позволяет не запоминать сложную формулу, что часто и используется на практике.
Для закрепления теории следует решить несколько типовых примеров:
- Определить, чему будет равна производная от корня квадратного, кратного разности три минус икс в квадрате. Запись условия задачи выглядит так: (√ 3 — x 2 )’. Мысленно можно обозначить выражение в скобках буквой S. Получается, что задача будет состоять в поиске производной (√ S)’. Используя знание формулы, можно утверждать, что (√ S)’ = S’ / (2 * √ S). Ту же самую формулу можно будет получить, воспользовавшись преобразованием задания в степенную функцию: (√ S)’ = (S ½ ) ‘ = (½) * S (½ — 1 ) * S’ = S -½ * S’ / 2 = S’ / (2 * √ S). Таким образом, (√ 3 — x 2 )’ = (3 — x 2 )’ / (2 * √ 3 — x 2 ) = — 2* x / 2 * √ 3 — x 2 = — x / √ 3 — x 2 .
- Рассчитать, чему будет равна производная функции 1 / (2 * 3√ x7). Исходное выражение нужно преобразовать так, чтобы неизвестная оказалась в числителе, а затем уже воспользоваться стандартным алгоритмом: (1 / 2 * 3√ x7)’ = 1 / 2 * (x-7/3)’. Теперь нужно взять производную от степенной функции. В итоге получится выражение: 1 / 2 * (-7 / 3) * x (-7/3) — 1 = -(7 / 6) * x-10/3 = (-7 / 6) * (1 / 3√ x10).
- Необходимо найти производную суммы многочленов: p (x) = 3 + 4 √ x+3. По теореме дифференцирования ответ будет равняться сумме производных каждого члена равенства: p (x)’ = (3)’ + (4 √ x+3)’. Первое слагаемое равняется нулю, поэтому останется только найти производную корня. Используя снова правило производной, выражение можно переписать как 4 * (√ x+3)’. На следующем этапе многочлен в скобках нужно представить в виде степенной функции: (√x + 3)’ = 1 / ((2√x + 2)) * (x + 2)’ = 2 * (x +2)’ / √x+2. Так как производная суммы, это то же самое, что сумма производных, то будет верным записать: (4 √ x+2)’ = (2 / √x+2) *(<(x)’ + (2)’>). Производная для двойки равна нулю, поэтому плюсовать её смысла нет. В итоге получится: p (x)’ = (3 + 4 √ x+3)’ = 2/ √x +2 = 2 / √x +2.
Расчёт на онлайн-калькуляторе
Попрактиковавшись в решении различных примеров, найти производную корня простых выражений будет довольно просто. Но если в заданиях будут стоять двойные корни или сама функция будет содержать большой многочлен, могут возникнуть проблемы. Связаны они обычно не с алгоритмом решения, а с трудностью вычисления и преобразования.
Такого рода задачи требуют повышенного внимания и скрупулёзности в расчётах. При этом поиску ответа понадобится уделить довольно много времени. Поэтому для помощи в нахождении производных коренных функций и существуют в интернете математические онлайн-калькуляторы.
Это сервисы, предлагающие бесплатно услуги по автоматическому расчёту производной любой сложности. Воспользоваться ими может каждый желающий, имеющий доступ к интернету. Для нахождения ответа не нужно обладать какими-то особыми знаниями. Всё что требуется от пользователя — ввести в предложенную форму условие и нажать кнопку «Вычислить». Весь процесс расчёта займёт одну-две секунды.
При этом большинство сервисов, кроме предоставления ответа на своих страницах, дает возможность ознакомиться с теоретическим материалом и предлагает рассмотреть решения заданий различной сложности. Поэтому вопроса, каким образом получился тот или иной ответ, возникнуть не должно.
Из различных онлайн-калькуляторов, считающих производные, можно выделить следующие:
- Webmath.
- Kontrolnaya-rabota
- Onlinemschool.
- Сalc.
- Nauchniestati.
Сайты, используемые для вычислений, характеризуются интуитивно понятным интерфейсом, не содержащим нагромождения ненужной информации. На их страницах нет рекламного и вирусного кода.
Примечательно и то, что, выполнив пару вычислений, пользователь научится самостоятельно вычислять производную. А всё дело в том, что особенностью таких ресурсов является возможность обучения. Кроме непосредственно ответа, программа-расчётчик выдаст пошаговое вычисление с комментариями.
Кроме учащихся, онлайн-калькуляторы будут полезны и инженерам. Даже незначительная ошибка, допущенная в расчёте, приведёт к неверному ответу. В то же время при автоматических вычислениях появление ошибки исключено.
Производная корня икс
Формула
Производная от корня равна единице, деленной на два таких же корня.
Если под корнем находится сложная функция $u=u(x)$, то производная от корня этой функции будет равна: единице, деленной на два таких же корня и умноженной на производную подкоренного выражения, то есть
Примеры вычисления производной корня
Задание. Найти производную функции $y(x)=2 sqrt$
Решение. Искомая производная равна:
Согласно правилам дифференцирования, вынесем константу 2 за знак производной, в итоге будем иметь:
Производная от корня квадратного х. Производная сложной функции. Примеры вычисления производных
Ниже приведены преобразования, поясняющие, почему формулы нахождения производной квадратного и кубического корня именно такие, как приведены на рисунке.
Разумеется, данные формулы можно вообще не запоминать, если принять во внимание, что извлечение корня производной степени — это то же самое, что возведение в степень дроби, знаменатель которой равен той же степени. Тогда нахождение производной корня сводится к применению формулы нахождения производной степени соответствующей дроби .
Производная переменной под квадратным корнем
Квадратный корень — это точно то же самое действие, что и возведение в степень 1/2, значит для нахождения производной корня можно применить формулу из правила нахождения производной от переменной в произвольной степени:
(х 1/2 )» = 1/2 х -1/2 = 1 / (2√х)
Производная кубического корня (производная корня третьей степени)
Представим себе кубический корень как степень 1/3 и найдем производную по общим правилам дифференцирования. Краткую формулу можно посмотреть на картинке выше, а ниже расписано пояснение, почему именно так.
Степень -2/3 получается в следствие вычитания единицы из 1/3
Вывод формулы производной степенной функции (x в степени a). Рассмотрены производные от корней из x. Формула производной степенной функции высшего порядка. Примеры вычисления производных.
См. также: Степенная функция и корни, формулы и график
Графики степенной функции
Основные формулы
Производная от x в степени a равна a , умноженному на x в степени a минус один:
(1) .
Производная от корня степени n из x в степени m равна:
(2) .
Вывод формулы производной степенной функции
Случай x > 0
Рассмотрим степенную функцию от переменной x с показателем степени a :
(3) .
Здесь a является произвольным действительным числом. Сначала рассмотрим случай .
Чтобы найти производную функции (3), воспользуемся свойствами степенной функции и преобразуем ее к следующему виду:
.
Теперь находим производную, применяя :
;
.
Здесь .
Формула (1) доказана.
Вывод формулы производной от корня степени n из x в степени m
Теперь рассмотрим функцию, являющуюся корнем следующего вида:
(4) .
Чтобы найти производную, преобразуем корень к степенной функции:
.
Сравнивая с формулой (3) мы видим, что
.
Тогда
.
На практике нет необходимости запоминать формулу (2). Гораздо удобнее сначала преобразовать корни к степенным функциям, а затем находить их производные, применяя формулу (1) (см. примеры в конце страницы).
Случай x = 0
Если , то степенная функция определена и при значении переменной x = 0 . Найдем производную функции (3) при x = 0 . Для этого воспользуемся определением производной:
.
Подставим x = 0 :
.
При этом под производной мы понимаем правосторонний предел, для которого .
Итак, мы нашли:
.
Отсюда видно, что при , .
При , .
При , .
Этот результат получается и по формуле (1):
(1) .
Поэтому формула (1) справедлива и при x = 0 .
Случай x 3 и m = 1 мы имеем кубический корень из x :
.
Он определен и при отрицательных значениях переменной x .
Найдем производную степенной функции (3) при и при рациональных значениях постоянной a , для которых она определена. Для этого представим x в следующем виде:
.
Тогда ,
.
Находим производную, вынося постоянную за знак производной и применяя правило дифференцирования сложной функции :
.
Здесь . Но
.
Поскольку , то
.
Тогда
.
То есть формула (1) справедлива и при :
(1) .
Производные высших порядков
Теперь найдем производные высших порядков от степенной функции
(3) .
Производную первого порядка мы уже нашли:
.
Вынося постоянную a за знак производной, находим производную второго порядка:
.
Аналогичным образом находим производные третьего и четвертого порядков:
;
Отсюда видно, что производная произвольного n-го порядка имеет следующий вид:
.
Заметим, что если a является натуральным числом , , то n -я производная является постоянной:
.
Тогда все последующие производные равны нулю:
,
при .
Примеры вычисления производных
Пример
Найдите производную функции:
.
Преобразуем корни к степеням:
;
.
Тогда исходная функция приобретает вид:
.
Находим производные степеней:
;
.
Производная постоянной равна нулю:
.
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.
Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного — в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.
Пример 1. Найти производную функции
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
Пример 2. Найти производную функции
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило, проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.
Таблица производных простых функций
| 1. Производная константы (числа). Любого числа (1, 2, 5, 200. ), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто | |
| 2. Производная независимой переменной. Чаще всего «икса». Всегда равна единице. Это тоже важно запомнить надолго | |
| 3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни. | |
| 4. Производная переменной в степени -1 | |
| 5. Производная квадратного корня | |
| 6. Производная синуса | |
| 7. Производная косинуса |  |
| 8. Производная тангенса |  |
| 9. Производная котангенса |  |
| 10. Производная арксинуса |  |
| 11. Производная арккосинуса |  |
| 12. Производная арктангенса |  |
| 13. Производная арккотангенса |  |
| 14. Производная натурального логарифма | |
| 15. Производная логарифмической функции |  |
| 16. Производная экспоненты | |
| 17. Производная показательной функции |
Правила дифференцирования
| 1. Производная суммы или разности |  |
| 2. Производная произведения |  |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного |  |
| 4. Производная сложной функции |  |
Правило 1. Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.
Правило 2. Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной :
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3. Если функции
дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём
т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье «Производная произведения и частного функций « .
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u «v , в котором u — число, например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка — механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде 
Если же перед Вами задача вроде 
Пошаговые примеры — как найти производную
Пример 3. Найти производную функции
Решение. Определяем части выражения функции: всё выражение представляет произведение, а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль. Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как производную «икса». Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
А проверить решение задачи на производную можно на .
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного: производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, 
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде 
Пример 5. Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Проверить решение задачи на производную можно на калькуляторе производных онлайн .
Пример 6. Найти производную функции
Решение. В данной функции видим частное, делимое которого — квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .
Функции сложного вида не всегда подходят под определение сложной функции. Если имеется функция вида y = sin x — (2 — 3) · a r c t g x x 5 7 x 10 — 17 x 3 + x — 11 , то ее нельзя считать сложной в отличие от y = sin 2 x .
Данная статья покажет понятие сложной функции и ее выявление. Поработаем с формулами нахождения производной с примерами решений в заключении. Применение таблицы производных и правила дифференцирования заметно уменьшают время для нахождения производной.
Основные определения
Сложной функцией считается такая функция, у которой аргумент также является функцией.
Обозначается это таким образом: f (g (x)) . Имеем, что функция g (x) считается аргументом f (g (x)) .
Если есть функция f и является функцией котангенса, тогда g (x) = ln x – это функция натурального логарифма. Получаем, что сложная функция f (g (x)) запишется как arctg(lnx). Или функция f , являющаяся функцией возведенной в 4 степень, где g (x) = x 2 + 2 x — 3 считается целой рациональной функцией, получаем, что f (g (x)) = (x 2 + 2 x — 3) 4 .
Очевидно, что g (x) может быть сложной. Из примера y = sin 2 x + 1 x 3 — 5 видно, что значение g имеет кубический корень с дробью. Данное выражение разрешено обозначать как y = f (f 1 (f 2 (x))) . Откуда имеем, что f – это функция синуса, а f 1 — функция, располагаемая под квадратным корнем, f 2 (x) = 2 x + 1 x 3 — 5 — дробная рациональная функция.
Степень вложенности определено любым натуральным числом и записывается как y = f (f 1 (f 2 (f 3 (. . . (f n (x)))))) .
Понятие композиция функции относится к количеству вложенных функций по условию задачи. Для решения используется формула нахождения производной сложной функции вида
(f (g (x))) » = f » (g (x)) · g » (x)
Примеры
Найти производную сложной функции вида y = (2 x + 1) 2 .
По условию видно, что f является функцией возведения в квадрат, а g (x) = 2 x + 1 считается линейной функцией.
Применим формулу производной для сложной функции и запишем:
f » (g (x)) = ((g (x)) 2) » = 2 · (g (x)) 2 — 1 = 2 · g (x) = 2 · (2 x + 1) ; g » (x) = (2 x + 1) » = (2 x) » + 1 » = 2 · x » + 0 = 2 · 1 · x 1 — 1 = 2 ⇒ (f (g (x))) » = f » (g (x)) · g » (x) = 2 · (2 x + 1) · 2 = 8 x + 4
Необходимо найти производную с упрощенным исходным видом функции. Получаем:
y = (2 x + 1) 2 = 4 x 2 + 4 x + 1
Отсюда имеем, что
y » = (4 x 2 + 4 x + 1) » = (4 x 2) » + (4 x) » + 1 » = 4 · (x 2) » + 4 · (x) » + 0 = = 4 · 2 · x 2 — 1 + 4 · 1 · x 1 — 1 = 8 x + 4
При решении задач такого вида важно понимать, где будет располагаться функция вида f и g (x) .
Следует найти производные сложных функций вида y = sin 2 x и y = sin x 2 .
Первая запись функции говорит о том, что f является функцией возведения в квадрат, а g (x) – функцией синуса. Тогда получим, что
y » = (sin 2 x) » = 2 · sin 2 — 1 x · (sin x) » = 2 · sin x · cos x
Вторая запись показывает, что f является функцией синуса, а g (x) = x 2 обозначаем степенную функцию. Отсюда следует, что произведение сложной функции запишем как
y » = (sin x 2) » = cos (x 2) · (x 2) » = cos (x 2) · 2 · x 2 — 1 = 2 · x · cos (x 2)
Формула для производной y = f (f 1 (f 2 (f 3 (. . . (f n (x)))))) запишется как y » = f » (f 1 (f 2 (f 3 (. . . (f n (x)))))) · f 1 » (f 2 (f 3 (. . . (f n (x))))) · · f 2 » (f 3 (. . . (f n (x)))) · . . . · f n » (x)
Найти производную функции y = sin (ln 3 a r c t g (2 x)) .
Данный пример показывает сложность записи и определения расположения функций. Тогда y = f (f 1 (f 2 (f 3 (f 4 (x))))) обозначим, где f , f 1 , f 2 , f 3 , f 4 (x) является функцией синуса, функцией возведения в 3 степень, функцией с логарифмом и основанием е, функцией арктангенса и линейной.
Из формулы определения сложной функции имеем, что
y » = f » (f 1 (f 2 (f 3 (f 4 (x))))) · f 1 » (f 2 (f 3 (f 4 (x)))) · · f 2 » (f 3 (f 4 (x))) · f 3 » (f 4 (x)) · f 4 » (x)
Получаем, что следует найти
- f » (f 1 (f 2 (f 3 (f 4 (x))))) в качестве производной синуса по таблице производных, тогда f » (f 1 (f 2 (f 3 (f 4 (x))))) = cos (ln 3 a r c t g (2 x)) .
- f 1 » (f 2 (f 3 (f 4 (x)))) в качестве производной степенной функции, тогда f 1 » (f 2 (f 3 (f 4 (x)))) = 3 · ln 3 — 1 a r c t g (2 x) = 3 · ln 2 a r c t g (2 x) .
- f 2 » (f 3 (f 4 (x))) в качестве производной логарифмической, тогда f 2 » (f 3 (f 4 (x))) = 1 a r c t g (2 x) .
- f 3 » (f 4 (x)) в качестве производной арктангенса, тогда f 3 » (f 4 (x)) = 1 1 + (2 x) 2 = 1 1 + 4 x 2 .
- При нахождении производной f 4 (x) = 2 x произвести вынесение 2 за знак производной с применением формулы производной степенной функции с показателем, который равняется 1 , тогда f 4 » (x) = (2 x) » = 2 · x » = 2 · 1 · x 1 — 1 = 2 .
Производим объединение промежуточных результатов и получаем, что
y » = f » (f 1 (f 2 (f 3 (f 4 (x))))) · f 1 » (f 2 (f 3 (f 4 (x)))) · · f 2 » (f 3 (f 4 (x))) · f 3 » (f 4 (x)) · f 4 » (x) = = cos (ln 3 a r c t g (2 x)) · 3 · ln 2 a r c t g (2 x) · 1 a r c t g (2 x) · 1 1 + 4 x 2 · 2 = = 6 · cos (ln 3 a r c t g (2 x)) · ln 2 a r c t g (2 x) a r c t g (2 x) · (1 + 4 x 2)
Разбор таких функций напоминает матрешки. Правила дифференцирования не всегда могут быть применены в явном виде при помощи таблицы производных. Зачастую нужно применять формулу нахождения производных сложных функций.
Существуют некоторые различия сложного вида от сложных функций. При явном умении это различать, нахождение производных будет давать особенно легко.
Необходимо рассмотреть на приведении подобного примера. Если имеется функция вида y = t g 2 x + 3 t g x + 1 , тогда ее можно рассмотреть в качестве сложной вида g (x) = t g x , f (g) = g 2 + 3 g + 1 . Очевидно, что необходимо применение формулы для сложной производной:
f » (g (x)) = (g 2 (x) + 3 g (x) + 1) » = (g 2 (x)) » + (3 g (x)) » + 1 » = = 2 · g 2 — 1 (x) + 3 · g » (x) + 0 = 2 g (x) + 3 · 1 · g 1 — 1 (x) = = 2 g (x) + 3 = 2 t g x + 3 ; g » (x) = (t g x) » = 1 cos 2 x ⇒ y » = (f (g (x))) » = f » (g (x)) · g » (x) = (2 t g x + 3) · 1 cos 2 x = 2 t g x + 3 cos 2 x
Функция вида y = t g x 2 + 3 t g x + 1 не считается сложной, так как имеет сумму t g x 2 , 3 t g x и 1 . Однако, t g x 2 считается сложной функцией, то получаем степенную функцию вида g (x) = x 2 и f , являющуюся функцией тангенса. Для этого следует продифференцировать по сумме. Получаем, что
y » = (t g x 2 + 3 t g x + 1) » = (t g x 2) » + (3 t g x) » + 1 » = = (t g x 2) » + 3 · (t g x) » + 0 = (t g x 2) » + 3 cos 2 x
Переходим к нахождению производной сложной функции (t g x 2) » :
f » (g (x)) = (t g (g (x))) » = 1 cos 2 g (x) = 1 cos 2 (x 2) g » (x) = (x 2) » = 2 · x 2 — 1 = 2 x ⇒ (t g x 2) » = f » (g (x)) · g » (x) = 2 x cos 2 (x 2)
Получаем, что y » = (t g x 2 + 3 t g x + 1) » = (t g x 2) » + 3 cos 2 x = 2 x cos 2 (x 2) + 3 cos 2 x
Функции сложного вида могут быть включены в состав сложных функций, причем сами сложные функции могут являться составными функции сложного вида.
Для примера рассмотрим сложную функцию вида y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x · (x 2 + 1)
Данная функция может быть представлена в виде y = f (g (x)) , где значение f является функцией логарифма по основанию 3 , а g (x) считается суммой двух функций вида h (x) = x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 и k (x) = ln 2 x · (x 2 + 1) . Очевидно, что y = f (h (x) + k (x)) .
Рассмотрим функцию h (x) . Это отношение l (x) = x 2 + 3 cos 3 (2 x + 1) + 7 к m (x) = e x 2 + 3 3
Имеем, что l (x) = x 2 + 3 cos 2 (2 x + 1) + 7 = n (x) + p (x) является суммой двух функций n (x) = x 2 + 7 и p (x) = 3 cos 3 (2 x + 1) , где p (x) = 3 · p 1 (p 2 (p 3 (x))) является сложной функцией с числовым коэффициентом 3 , а p 1 — функцией возведения в куб, p 2 функцией косинуса, p 3 (x) = 2 x + 1 — линейной функцией.
Получили, что m (x) = e x 2 + 3 3 = q (x) + r (x) является суммой двух функций q (x) = e x 2 и r (x) = 3 3 , где q (x) = q 1 (q 2 (x)) — сложная функция, q 1 — функция с экспонентой, q 2 (x) = x 2 — степенная функция.
Отсюда видно, что h (x) = l (x) m (x) = n (x) + p (x) q (x) + r (x) = n (x) + 3 · p 1 (p 2 (p 3 (x))) q 1 (q 2 (x)) + r (x)
При переходе к выражению вида k (x) = ln 2 x · (x 2 + 1) = s (x) · t (x) видно, что функция представлена в виде сложной s (x) = ln 2 x = s 1 (s 2 (x)) с целой рациональной t (x) = x 2 + 1 , где s 1 является функцией возведения в квадрат, а s 2 (x) = ln x — логарифмической с основанием е.
Отсюда следует, что выражение примет вид k (x) = s (x) · t (x) = s 1 (s 2 (x)) · t (x) .
Тогда получим, что
y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x · (x 2 + 1) = = f n (x) + 3 · p 1 (p 2 (p 3 (x))) q 1 (q 2 (x)) = r (x) + s 1 (s 2 (x)) · t (x)
По структурам функции стало явно, как и какие формулы необходимо применять для упрощения выражения при его дифференцировании. Для ознакомления подобных задач и и для понятия их решения необходимо обратиться к пункту дифференцирования функции, то есть нахождения ее производной.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Перед тем как находить производную корня, обратите внимание на остальные функции, присутствующие в решаемом примере. Если в задаче имеется много подкоренных выражений, то воспользуйтесь следующим правилом нахождения производной квадратного корня:
А для нахождения производной кубического корня примените формулу:
где через ³√х обозначен кубический корень из х.
Если , предназначенном для дифференцирования, встречается переменная в дробных , то переведите корня в степенную функцию с соответствующим показателем. Для квадратного корня это будет степень ½, а для кубического корня – ⅓:
где ^ обозначает возведение в степень.
Для нахождения производной степенной функции вообще и х^½, x^⅓, в частности, воспользуйтесь следующим правилом:
Для производной корня из этого соотношения вытекает:
Продифференцировав все , внимательно посмотрите на остальные части примера. Если в ответе у вас получилось очень громоздкое выражение, то наверняка его можно упростить. Большинство школьных примеров составлено таким образом, чтобы в итоге получилось небольшое число или компактное выражение.
Во многих задачах на нахождение производной, корни (квадратные и кубические) встречаются вместе с другими функциями. Чтобы найти производную корня в этом случае, применяйте следующие правила:
производная константы (постоянного числа, C) равняется нулю: C» = 0;
постоянный множитель выносится за знак производной: (k*f)» = k * (f)» (f – произвольная функция) ;
производная суммы нескольких функций равняется сумме производных: (f + g)» = (f)» + (g)»;
производная произведения двух функций равняется… нет, не произведению производных, а следующему выражению: (fg)» = (f)»g + f (g)»;
производная частного также равняется не частному производных, а находится согласно следующего правила: (f/g)» = ((f)»g – f(g)») / g².
На этой странице вы сможете вычислять производную функции онлайн с получением подробного решения задачи. Решение производных функции производится с использованием тех правил дифференцирования, которые студенты изучают в курсе математического анализа в институте. Для того, чтобы найти производную функции нужно в поле «Функция» ввести функцию для дифференцирования согласно правил ввода данных.
Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю: Математический смысл этого определения понять не очень просто, поскольку в школьном курсе алгебры понятие предела функции либо не изучают совсем, либо изучают очень поверхностно. Но для того, чтобы научиться находить производные различных функций, это и не обязательно.
- производная корень из икс
источники:
http://www.webmath.ru/poleznoe/formules_10_6.php
http://mkmorozov.ru/dictionary/proizvodnaya-ot-kornya-kvadratnogo-h-proizvodnaya-slozhnoi-funkcii-primery/