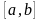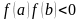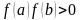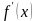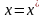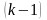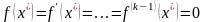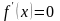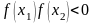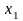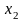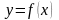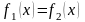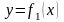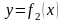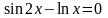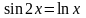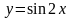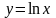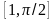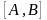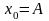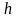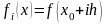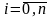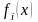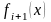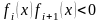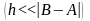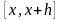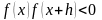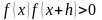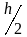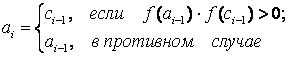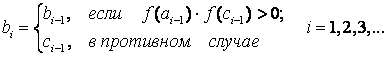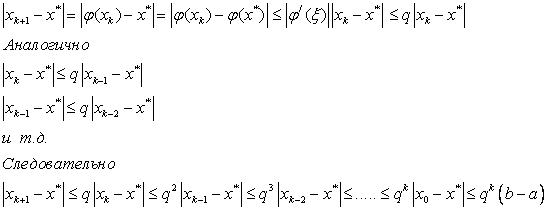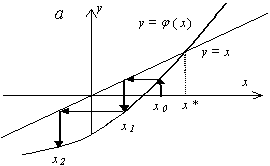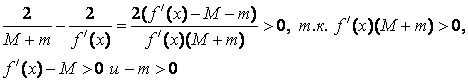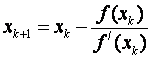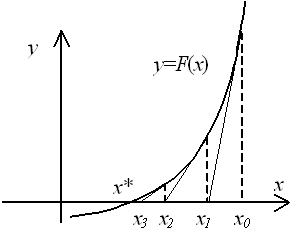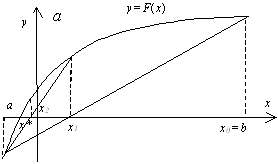- 10•x•e 2x = 10*x*exp(2*x)
- x•e -x +cos(3x) = x*exp(-x)+cos(3*x)
- x 3 -x 2 +3 = x^3-x^2+3
- Выражение 0.9*x=sin(x)+1 необходимо преобразовать к виду: sin(x)+1-0.9*x . Аналогично, x^2-7=5-3x к виду x^2+3x-12 .
Пусть дано уравнение f(x)=0 , где f(x) определено и непрерывно в некотором конечном или бесконечном интервале a ≤ x ≤ b . Всякое значение ξ, обращающее функцию f(x) в нуль, то есть такое, что f(ξ)=0 называется корнем уравнения или нулем функции f(x) . Число ξ называется корнем k -ой кратности, если при x = ξ вместе с функцией f(x) обращаются в нуль ее производные до (k-1) порядка включительно: f(ξ)=f’(ξ)= … =f k-1 (ξ) = 0 . Однократный корень называется простым.
Приближенное нахождение корней уравнения складывается из двух этапов:
- Отделение корней, то есть установление интервалов [αi,βi] , в которых содержится один корень уравнения.
- f(a)•f(b) , т.е. значения функции на его концах имеют противоположные знаки.
- f’(x) сохраняет постоянный знак, т.е. функция монотонна (эти два условия достаточны, но НЕ необходимы) для единственности корня на искомом отрезке).
- f”(x) сохраняет постоянный знак, т.е. функция выпукла вверх, либо – вниз.
- Уточнение приближенных корней, то есть доведение их до заданной точности.
Геометрическая интерпретация метода Ньютона (метод касательных)
Критерий завершения итерационного процесса имеет вид
Численные методы: решение нелинейных уравнений
Задачи решения уравнений постоянно возникают на практике, например, в экономике, развивая бизнес, вы хотите узнать, когда прибыль достигнет определенного значения, в медицине при исследовании действия лекарственных препаратов, важно знать, когда концентрация вещества достигнет заданного уровня и т.д.
В задачах оптимизации часто необходимо определять точки, в которых производная функции обращается в 0, что является необходимым условием локального экстремума.
В статистике при построении оценок методом наименьших квадратов или методом максимального правдоподобия также приходится решать нелинейные уравнения и системы уравнений.
Итак, возникает целый класс задач, связанных с нахождением решений нелинейных уравнений, например, уравнения или уравнения и т.д.
В простейшем случае у нас имеется функция , заданная на отрезке ( a , b ) и принимающая определенные значения.
Каждому значению x из этого отрезка мы можем сопоставить число , это и есть функциональная зависимость, ключевое понятие математики.
Нам нужно найти такое значение при котором такие называются корнями функции
Визуально нам нужно определить точку пересечения графика функции с осью абсцисс.
Метод деления пополам
Простейшим методом нахождения корней уравнения является метод деления пополам или дихотомия.
Этот метод является интуитивно ясным и каждый действовал бы при решении задачи подобным образом.
Алгоритм состоит в следующем.
Предположим, мы нашли две точки и , такие что и имеют разные знаки, тогда между этими точками находится хотя бы один корень функции .
Поделим отрезок пополам и введем среднюю точку .
Тогда либо , либо .
Оставим ту половину отрезка, для которой значения на концах имеют разные знаки. Теперь этот отрезок снова делим пополам и оставляем ту его часть, на границах которой функция имеет разные знаки, и так далее, достижения требуемой точности.
Очевидно, постепенно мы сузим область, где находится корень функции, а, следовательно, с определенной степенью точности определим его.
Заметьте, описанный алгоритм применим для любой непрерывной функции.
К достоинствам метода деления пополам следует отнести его высокую надежность и простоту.
Недостатком метода является тот факт, что прежде чем начать его применение, необходимо найти две точки, значения функции в которых имеют разные знаки. Очевидно, что метод неприменим для корней четной кратности и также не может быть обобщен на случай комплексных корней и на системы уравнений.
Порядок сходимости метода линейный, на каждом шаге точность возрастает вдвое, чем больше сделано итераций, тем точнее определен корень.
Метод Ньютона: теоретические основы
Классический метод Ньютона или касательных заключается в том, что если — некоторое приближение к корню уравнения , то следующее приближение определяется как корень касательной к функции , проведенной в точке .
Уравнение касательной к функции в точке имеет вид:
В уравнении касательной положим и .
Тогда алгоритм последовательных вычислений в методе Ньютона состоит в следующем:
Сходимость метода касательных квадратичная, порядок сходимости равен 2.
Таким образом, сходимость метода касательных Ньютона очень быстрая.
Запомните этот замечательный факт!
Без всяких изменений метод обобщается на комплексный случай.
Если корень является корнем второй кратности и выше, то порядок сходимости падает и становится линейным.
Упражнение 1. Найти с помощью метода касательных решение уравнения на отрезке (0, 2).
Упражнение 2. Найти с помощью метода касательных решение уравнения на отрезке (1, 3).
К недостаткам метода Ньютона следует отнести его локальность, поскольку он гарантированно сходится при произвольном стартовом приближении только, если везде выполнено условие , в противной ситуации сходимость есть лишь в некоторой окрестности корня.
Недостатком метода Ньютона является необходимость вычисления производных на каждом шаге.
Визуализация метода Ньютона
Метод Ньютона (метод касательных) применяется в том случае, если уравнение f(x) = 0 имеет корень , и выполняются условия:
1) функция y= f(x) определена и непрерывна при ;
2) f(a)·f(b) 0. Таким образом, выбирается точка с абсциссой x0, в которой касательная к кривой y=f(x) на отрезке [a;b] пересекает ось Ox. За точку x0 сначала удобно выбирать один из концов отрезка.
Рассмотрим метод Ньютона на конкретном примере.
Пусть нам дана возрастающая функция y = f(x) =x 2 -2, непрерывная на отрезке (0;2), и имеющая f ‘(x) = 2x > 0 и f ”(x) = 2 > 0.
Уравнение касательной в общем виде имеет представление:
В нашем случае: y-y0=2x0·(x-x0). В качестве точки x0 выбираем точку B1(b; f(b)) = (2,2). Проводим касательную к функции y = f(x) в точке B1, и обозначаем точку пересечения касательной и оси Ox точкой x1. Получаем уравнение первой касательной:y-2=2·2(x-2), y=4x-6.
Точка пересечения касательной и оси Ox: x1 =
Рисунок 2. Результат первой итерации
Затем находим точку пересечения функции y=f(x) и перпендикуляра, проведенного к оси Ox через точку x1, получаем точку В2 =(1.5; 0.25). Снова проводим касательную к функции y = f(x) в точке В2, и обозначаем точку пересечения касательной и оси Ox точкой x2.
Точка пересечения касательной и оси Ox: x2 = .
Рисунок 3. Вторая итерация метода Ньютона
Затем находим точку пересечения функции y=f(x) и перпендикуляра, проведенного к оси Ox через точку x2, получаем точку В3 и так далее.
В3 = ()
Рисунок 4. Третий шаг метода касательных
Первое приближение корня определяется по формуле:
= 1.5.
Второе приближение корня определяется по формуле:
=
Третье приближение корня определяется по формуле:
Таким образом, i-ое приближение корня определяется по формуле:
Вычисления ведутся до тех пор, пока не будет достигнуто совпадение десятичных знаков, которые необходимы в ответе, или заданной точности e – до выполнения неравенства |xi–xi-1|
using namespace std;
float f(double x) //возвращает значение функции f(x) = x^2-2
float df(float x) //возвращает значение производной
float d2f(float x) // значение второй производной
int _tmain(int argc, _TCHAR* argv[])
int exit = 0, i=0;//переменные для выхода и цикла
double x0,xn;// вычисляемые приближения для корня
double a, b, eps;// границы отрезка и необходимая точность
cin>>a>>b; // вводим границы отрезка, на котором будем искать корень
cin>>eps; // вводим нужную точность вычислений
if (a > b) // если пользователь перепутал границы отрезка, меняем их местами
if (f(a)*f(b)>0) // если знаки функции на краях отрезка одинаковые, то здесь нет корня
cout 0) x0 = a; // для выбора начальной точки проверяем f(x0)*d2f(x0)>0 ?
xn = x0-f(x0)/df(x0); // считаем первое приближение
cout eps) // пока не достигнем необходимой точности, будет продолжать вычислять
xn = x0-f(x0)/df(x0); // непосредственно формула Ньютона
> while (exit!=1); // пока пользователь не ввел exit = 1
Посмотрим, как это работает. Нажмем на зеленый треугольник в верхнем левом углу экрана, или же клавишу F5.
Если происходит ошибка компиляции «Ошибка error LNK1123: сбой при преобразовании в COFF: файл недопустим или поврежден», то это лечится либо установкой первого Service pack 1, либо в настройках проекта Свойства -> Компоновщик отключаем инкрементную компоновку.
Рис. 4. Решение ошибки компиляции проекта
Мы будем искать корни у функции f(x) = x2-2.
Сначала проверим работу приложения на «неправильных» входных данных. На отрезке [3; 5] нет корней, наша программа должна выдать сообщение об ошибке.
У нас появилось окно приложения:
Рис. 5. Ввод входных данных
Введем границы отрезка 3 и 5, и точность 0.05. Программа, как и надо, выдала сообщение об ошибке, что на данном отрезке корней нет.
Рис. 6. Ошибка «На этом отрезке корней нет!»
Выходить мы пока не собираемся, так что на сообщение «Exit?» вводим «0».
Теперь проверим работу приложения на корректных входных данных. Введем отрезок [0; 2] и точность 0.0001.
Рис. 7. Вычисление корня с необходимой точностью
Как мы видим, необходимая точность была достигнута уже на 4-ой итерации.
Чтобы выйти из приложения, введем «Exit?» => 1.
Метод секущих
Чтобы избежать вычисления производной, метод Ньютона можно упростить, заменив производную на приближенное значение, вычисленное по двум предыдущим точкам:
/
Итерационный процесс имеет вид:
где .
Это двухшаговый итерационный процесс, поскольку использует для нахождения последующего приближения два предыдущих.
Порядок сходимости метода секущих ниже, чем у метода касательных и равен в случае однократного корня .
Эта замечательная величина называется золотым сечением:
Убедимся в этом, считая для удобства, что .
Таким образом, с точностью до бесконечно малых более высокого порядка
Отбрасывая остаточный член, получаем рекуррентное соотношение, решение которого естественно искать в виде .
После подстановки имеем: и
Для сходимости необходимо, чтобы было положительным, поэтому .
Поскольку знание производной не требуется, то при том же объёме вычислений в методе секущих (несмотря на меньший порядок сходимости) можно добиться большей точности, чем в методе касательных.
Отметим, что вблизи корня приходится делить на малое число, и это приводит к потере точности (особенно в случае кратных корней), поэтому, выбрав относительно малое , выполняют вычисления до выполнения и продолжают их пока модуль разности соседних приближений убывает.
Как только начнется рост, вычисления прекращают и последнюю итерацию не используют.
Такая процедура определения момента окончания итераций называется приемом Гарвика.
Метод парабол
Рассмотрим трехшаговый метод, в котором приближение определяется по трем предыдущим точкам , и .
Для этого заменим, аналогично методу секущих, функцию интерполяционной параболой проходящей через точки , и .
В форме Ньютона она имеет вид:
Точка определяется как тот из корней этого полинома, который ближе по модулю к точке .
Порядок сходимости метода парабол выше, чем у метода секущих, но ниже, чем у метода Ньютона.
Важным отличием от ранее рассмотренных методов, является то обстоятельство, что даже если вещественна при вещественных и стартовые приближения выбраны вещественными, метод парабол может привести к комплексному корню исходной задачи.
Этот метод очень удобен для поиска корней многочленов высокой степени.
Метод простых итераций
Задачу нахождения решений уравнений можно формулировать как задачу нахождения корней: , или как задачу нахождения неподвижной точки.
Пусть и — сжатие: (в частности, тот факт, что — сжатие, как легко видеть, означает, что).
По теореме Банаха существует и единственна неподвижная точка
Она может быть найдена как предел простой итерационной процедуры
где начальное приближение — произвольная точка промежутка .
Если функция дифференцируема, то удобным критерием сжатия является число . Действительно, по теореме Лагранжа
Таким образом, если производная меньше единицы, то является сжатием.
Условие существенно, ибо если, например, на [0,1] , то неподвижная точка отсутствует, хотя производная равна нулю. Скорость сходимости зависит от величины . Чем меньше , тем быстрее сходимость.
Рассмотрим уравнение: .
Если в качестве взять функцию , то соответствующая итерационная процедура будет иметь вид: . Как нетрудно убедиться, метод итераций в данном случае расходится при любой начальной точке , не совпадающей с собственно неподвижной точкой .
Однако можно в качестве можно взять, например, функцию . Соответствующая итерационная процедура имеет вид: .
Эти итерации сходятся к неподвижной точке для любого начального приближения :
Действительно, в первом случае , т.е. для выполнения условия необходимо чтобы , но тогда . Таким образом, отображение сжатием не является.
Рассмотрим , неподвижная точка та же самая, ситуация другая. Здесь, хотя формально производная может быть довольно большой (при малых ж), однако уже на следующем шаге она будет меньше 1.
т.е. такой итерационный процесс всегда сходится.
Метод Ньютона представляет собой частный случай метода простых итераций.
Здесь нетрудно убедиться, что при существует окрестность корня, в которой .
то если корень кратности , то в его окрестности и, следовательно,.
Если — простой корень, то сходимость метода касательных квадратичная (то есть порядок сходимости равен 2).
Поскольку , то
Таким образом, сходимость метода Ньютона очень быстрая.
Нахождение всех корней уравнения
Недостатком почти всех итерационных методов нахождения корней является то, что они при однократном применении позволяют найти лишь один корень функции, к тому же, мы не знаем какой именно.
Чтобы найти другие корни, можно было бы брать новые стартовые точки и применять метод вновь, но нет гарантии, что при этом итерации сойдутся к новому корню, а не к уже найденному, если вообще сойдутся.
Для поиска других корней используется метод удаления корней.
Пусть — корень функции , рассмотрим функцию. Точка будет являться корнем функции на единицу меньшей кратности, чем, при этом все остальные корни у функций и совпадают с учетом кратности.
Применяя тот или иной метод нахождения корней к функции , мы найдем новый корень (который может в случае кратных корней и совпадать с ). Далее можно рассмотреть функцию и искать корни у неё.
Повторяя указанную процедуру, можно найти все корни с учетом кратности.
Заметим, что когда мы производим деление на тот или иной корень , то в действительности мы делим лишь на найденное приближение , и, тем самым, несколько сдвигаем корни вспомогательной функции относительно истинных корней функции . Это может привести к значительным погрешностям, если процедура отделения применялась уже достаточное число раз.
Чтобы избежать этого, с помощью вспомогательных функций вычисляются лишь первые итерации, а окончательные проводятся по исходной функции , используя в качестве стартового приближения, последнюю итерацию, полученную по вспомогательной функции.
Мы рассмотрели решение уравнений только в одномерном случае, нахождение решений многомерных уравнений существенно более трудная задача.
Метод Ньютона онлайн
Данный онлайн калькулятор находит корень уравнения приближённо. В основе алгоритма его работы лежит метод Ньютона. Чтобы начать работу, необходимо ввести исходные данные своей задачи.
Методом Ньютона, найти корень (
максимальное кол-во итераций:
критерий останова вычислений:
Метод Ньютона является численным, т.е. корень уравнения находится приближенно. При этом можно заранее задать точность его нахождения.
Пусть нам дано уравнение
Формула для поиска корня уравнения выглядит следующим образом:
и – приближённые значения корня уравнения на -ой и ( )-ой итерациях соответственно, – значение функции в точке , – значение производной функции в точке .
Как видно, для того чтобы начать работу необходимо задать точку – начальное приближение для корня уравнения . От выбора точки зависит сойдётся ли алгоритм к решению или нет. Сходимость метода квадратичная, но она резко ухудшается если мы ищем кратный корень уравнения, т.е. если и одновременно , где – кратный корень уравнения .
Вычисления по приведённой выше формуле можно продолжать до бесконечности, соответственно на практике необходим некоторый критерий, который будет определять нужно ли нам продолжать вычисления или нет. Как правило, используется критерий останова вычислений на основе приращения или же на основе близости функции к нулю в некоторой точке .
Критерий останова вычислений на основе приращения задаётся следующей формулой:
т.е. различие (по модулю) между двумя последовательными приближениями к корню уравнения ( и ) должны быть меньше, некоторой наперёд заданной величины .
Критерий останова вычислений на основе близости функции к нулю определяется следующей формулой:
т.е. отличие (по модулю) между функцией в некоторой точке и нулём меньше .
В тоже время, если последовательность к корню не сходится, то критерии останова не сработают и процесс поиска корня будет продолжаться бесконечно. Чтобы предотвратить такую ситуацию, на практике вычисления прекращают после некоторого, заданного количества итераций.
На рисунке ниже приведена геометрическая интерпретация процесса поиска корня уравнения методом Ньютона.
В точке мы строим касательную к графику функции . Уравнение касательной в этой точке имеет вид:
Находим точку пересечения полученной касательной с осью абсцисс, т.е. рассматриваем точку с координатами . Подставляя координаты указанной точки в уравнение касательной, получаем следующее соотношение:
Из данного уравнения находим :
Продолжая данный процесс, получим формулу метода Ньютона, приведенную выше. Из-за того, что на каждой итерации фактически происходит построение касательной, метод Ньютона также иногда называют методом касательных.
Другие полезные разделы:
Оставить свой комментарий:
Мы в социальных сетях:
Группа ВКонтакте | Бот в Телеграмме
[spoiler title=”источники:”]
http://statistica.ru/branches-maths/chislennye-metody-resheniya-uravneniy/
http://mathforyou.net/online/numerical/newton/
[/spoiler]
Локализация корней
– это процедура нахождения в области
определения функции
таких отрезков, на которых уравнение
(2.1) имеет только один корень (одно
решение). Для локализации корней уравнения
(2.1) необходимо иметь критерий, позволяющий
убедиться, что, во-первых, на некотором
рассматриваемом отрезке
числовой оси
имеется корень, а, во-вторых, что этот
корень единственный на указанном
отрезке. Если функция
непрерывна на отрезке
,
а на концах отрезка её значения имеют
разные знаки (не равны нулю), то есть
,
то на этом отрезке расположен по крайней
мере один корень (нечетное число корней).
Если
,
то на отрезке
либо нет корней, либо их четное число,
данный случай рассматриваться не будет.
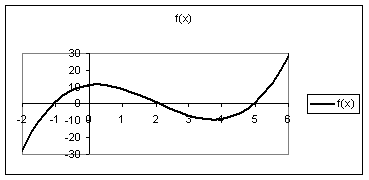
Как видно из рис.
2.1, условие
не обеспечивает единственности корня,
но является необходимым условием его
наличия. Достаточным условием,
обеспечивающим единственность корня
на отрезке
,
является требование монотонности
функции на данном отрезке. В качестве
признака монотонности функции
можно воспользоваться условием
знакопостоянства ее производной
.
Заметим, что если на области определения
функции отсутствуют точки, в которых
ее производная равна нулю или не
существует, то функция монотонна на
всей области определения.
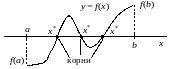
Рис.
2.1. Локализация корней. Функция
не монотонна на отрезке
.
Таким образом,
если на отрезке
функция
непрерывна и монотонна, а ее значения
на концах отрезка имеют разные знаки
(не равны нулю), то на рассматриваемом
отрезке существует один и только один
корень соответствующего уравнения
.
Число
называется корнем кратности
уравнения (2.1), если при
вместе с функцией
равны нулю ее производные до порядка
:
.
Корень кратности один называется
простым.
Воспользовавшись
рассмотренным критерием, составим общий
алгоритм аналитической локализации
корней нелинейного уравнения с одной
переменной:
-
Вычисление первой
производнойфункции
.
-
Выявление на
области определения функции интервалов
монотонности, определяемых точками, в
которых
или не существует.
-
Выбор среди
интервалов монотонности тех, на концах
которых значения функции имеют разные
знаки,
,
где
и
– границы интервалов.
Локализацию корней
можно выполнить графически, если удается
построить график функции
и определить отрезки, на которых она
имеет только одну точку пересечения с
осью абсцисс.
В ряде случаев бывает удобно заменить
уравнение
эквивалентным уравнением вида
,
корни которого определяются абсциссами
точек пересечения графиков функций
и
.
В качестве примера рассмотрим уравнение
.
Перейдем к эквивалентному уравнению
и построим графики функций
и
(рис. 2.2).
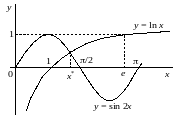
Рис.
2.2. Графическая локализация корней
уравнения
.
Из графиков,
представленных на рис. 2.2, видно, что
уравнение
содержит один
корень
,
расположенный в интервале
.
Локализация корней
может быть также выполнена табличным
способом. Допустим, что корни уравнения
(2.1) находятся на отрезке
оси
.
Выбор данного отрезка (интервала поиска
корней) может быть сделан, например, на
основе анализа конкретной задачи. Будем
вычислять значения
,
начиная с точки
,
двигаясь вправо с некоторым шагом
(рис. 2.3). Получим набор значений функции
,
.
При обнаружении
пары соседних значений
и
,
имеющих разные знаки (
),
соответствующие значения аргумента
можно считать границами отрезка,
содержащего корень.
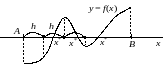
Рис.
2.3. Табличный подход к локализации
корней.
Надежность
табличного подхода к локализации корней
уравнений зависит как от характера
функции
,
так и от выбранной величины шага
.
Действительно, если при достаточно
малом значении
на границах текущего отрезка
функция
принимает
значения одного знака, то естественно
ожидать, что уравнение
корней на этом
отрезке не имеет. Однако, это не всегда
так. При несоблюдении условия монотонности
функции
на отрезке
в его пределах могут оказаться корни
уравнения (рис.2.4.а). Также на отрезке
может располагаться несколько корней
и при выполнении условия
(рис. 2.4.б).
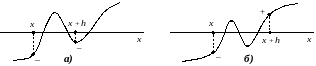
Рис 2.4. Наличие нескольких корней при
несоблюдении условия монотонности
функции: а)
;
б)
.
Предвидя подобные
ситуации, следует выбирать достаточно
малые значения
,
учитывая характер функции
,
например, с учетом значений
.
Поскольку
табличный способ предполагает выполнение
лишь элементарных арифметических и
логических операций, количество которых
может быть велико при малых значениях
,
то его целесообразно реализовывать на
компьютере, но не рационально использовать
при ручном счете. Локализуя корни, мы,
по сути, получаем их приближенные
значения с точностью до выбранного
шага. Так, например, если в качестве
приближенного значения корня взять
середину отрезка локализации, то
абсолютная погрешность данного значения
не будет превосходить половины шага
.
Уменьшая шаг в окрестности каждого
корня, можно, в принципе, повысить
точность локализации корней до любого
наперед заданного значения, однако
данный способ требует большого объема
вычислений. Поэтому при проведении
численных экспериментов с варьированием
параметров задачи, когда приходится
многократно осуществлять поиск корней,
подобный метод не целесообразен для
уточнения корней и используется только
для их локализации. Уточнение корней
проводится с помощью других методов,
более экономичных в плане вычислительных
ресурсов.
В общем случае в
связи с отсутствием гарантий надежности
(рис. 2.4) табличный способ локализации
корней практически не применяется на
практике.
Соседние файлы в папке 3-й семестр
- #
- #
1. Приближенное решение нелинейных алгебраических уравнений
Метод деления отрезка пополам (дихотомии)
Метод простой итерации
Метод Ньютона (метод касательных)
Метод хорд
Постановка задачи
Дано
нелинейное алгебраическое уравнение
f(x)=0 (1)
Нелинейность уравнения означает,
что график функции не есть прямая линия, т.е. в f(x) входит x в
некоторой степени или под знаком функции.
Решить
уравнение – это найти такое x* ∈ R: f(x*)=0. Значение x*
называют корнем уравнения. Нелинейное уравнение может иметь
несколько корней. Геометрическая интерпретация корней уравнения представлена на
рис. 1. Корнями уравнения (1) являются точки x1*, x2*,
x3*, в которых функция f(x) пересекает ось x.
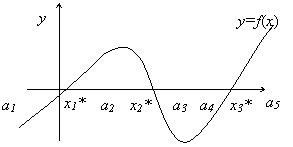
нелинейного уравнения (1) можно разделить на точные
(аналитические) и приближенные (итерационные). В точных методах
корень представляется некоторой алгебраической формулой. Например, решение
квадратных уравнений, некоторых тригонометрических уравнений и т. д.
В приближенных
методах процесс нахождения решения, вообще говоря, бесконечен. Решение
получается в виде бесконечной последовательности {xn},
такой, что . По
определению предела, для любого (сколь угодно малого) ε,
найдется такое N, что при n>N,
|xn – x*|<
ε. Члены этой последовательности xn называются последовательными приближениями
к решению, или итерациями. Наперёд заданное число
ε называют точностью метода, а N – это количество
итераций, которое необходимо выполнить, чтобы получить решение с точностью ε.
Существует
различные методы нахождения приближенного решения, т.е. способы построения
последовательности итераций {xn}, однако все они имеют общие
этапы, изображенные на рисунке.
Наиболее часто используется следующий критерий остановки итерационного
процесса: |xn+1–xn|<ε, т.е. разница между соседними итерациями
становится малой. Также для окончания итерационного процесса используется условие
|f(xn)|<ε , где f(xn)
– невязка метода.
Прежде чем использовать приближенный метод, уравнение надо исследовать
его на наличие корней и уточнить, где эти корни находятся, т.е. найти
интервалы изоляции корней. Интервалом изоляции корня
называется отрезок, на котором корень уравнения существует и единственен.
Необходимое условие существования корня уравнения
на отрезке [a,b]: Пусть
f(x) непрерывна и f(a)f(b)<0
(т.е., на концах интервала функция имеет разные знаки). Тогда внутри отрезка [a, b]
существует хотя бы один корень уравнения f(x)=0.
Достаточное
условие единственности корня на отрезке [a,b]:
Корень будет
единственным, если f(a)f(b)<0 и
f /(x) не меняет знак на
отрезке [a, b], т.е. f(x) –
монотонная функция, в этом случае отрезок [a,b]
будет интервалом изоляции.
Если корней несколько, то для каждого нужно найти интервал изоляции.
Существуют различные способы исследования функции: аналитический,
табличный, графический.
Аналитический способ состоит в нахождении экстремумов
функции f(x),
исследование ее поведения при и нахождение участков возрастания и убывания
функции.
Графический способ – это построение графика функции f(x) и определение числа
корней по количеству пересечений графика с осью x.
Табличный способ – это построение таблицы,
состоящей из столбца аргумента x и столбца
значений функции f(x).
О наличии корней свидетельствуют перемены знака функции. Чтобы не произошла потеря
корней, шаг изменения аргумента должен быть достаточно мелким, а интервал
изменения достаточно широким.
Пример.
Решить
уравнение x3‑ 6x2+3x+11=0, т.е. f(x)= x3‑ 6x2+3x+11.
Найдем
производную f/(x)=3x2-12x+3.
Найдем нули
производной f/(x)=3x2-12x+3=0; D=144-4*3*3=108;
X1== 0.268;
X2== 3.732;
Так как f/()>0, то f/(x)>0 при
, f/(x)<0 при
и f/(x)>0 при
. Кроме того, f(
)=
<0, f(
)=
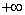
интервале
возрастает от до f(x1)= 3x12-12x1+3=11.39;
на интервале –
убывает до f(x2)= 3x22-12x2+3=-9.39 и на интервале 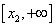
, т.е. уравнение
имеет три корня.
Найдем интервалы изоляции для каждого из корней.
Рассмотрим для первого корня отрезок [-2, -1]:
f(-2)= -27<0, f(-1)= 1>0, f/(x)>0 при т.е. этот отрезок является интервалом изоляции
корня.
Рассмотрим для второго корня отрезок [1, 3]:
f(1)= 9>0, f(3)= -7<0, f/(x)<0 при т.е. этот отрезок является интервалом
изоляции корня.
Рассмотрим для третьего корня отрезок [4, 5]:
f(4)= -9<0, f(5)=1>0, f/(x)>0 при т.е. этот отрезок является интервалом
изоляции корня.
Табличный
способ:
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
f(x) |
-79 |
-27 |
1 |
11 |
9 |
1 |
-7 |
-9 |
1 |
29 |
81 |
Графический
способ
Приближенные (Итерационные) методы.
Пусть интервалы изоляции
корней известны. Познакомимся с несколькими итерационными методами,
позволяющими найти корень на известном интервале изоляции [a, b].
Метод деления отрезка пополам (дихотомии)
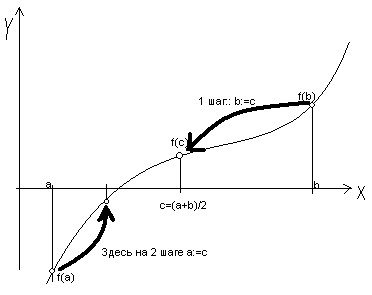
Идея метода:
Найдем середину отрезка [a, b]:
c=(a+b)/2. Корень остался на одной из частей:
[a, c] или [c, b]. Если f(a) * f(с)<0,
то корень попал на отрезок [a, c], тогда деление отрезка можно повторить, приняв в
качестве нового правого конца точку c, т.е. b=c. В противном
случае корень попал на половину [c, b], и необходимо изменить значение левого конца
отрезка: a=c. Поскольку корень всегда заключен внутри отрезка,
итерационный процесс можно останавливать, если длина отрезка станет меньше
заданной точности: |b – a|< ε
Найдем первый корень уравнения f(x)=x3 –
6x2+3x+11=0 с точностью
Вычисления оформляются в виде
таблицы
|
k |
a |
b |
c |
f(a) |
f(c) |
|b-a| |
|
0 |
-2 |
-1 |
-1.5 |
-27 |
-10.375 |
1 |
|
1 |
-1.5 |
-1 |
-1.25 |
-10.375 |
-4.07813 |
0.5 |
|
2 |
-1.25 |
-1 |
-1.125 |
-4.07813 |
-1.39258 |
0.25 |
|
3 |
-1.125 |
-1 |
-1.0625 |
-1.39258 |
-0.1604 |
0.125 |
|
4 |
-1.0625 |
-1 |
-1.03125 |
-0.1604 |
0.42868 |
0.0625 |
|
5 |
-1.0625 |
-1.03125 |
-1.04688 |
-0.1604 |
0.136372 |
0.03125 |
|
6 |
………. |
|||||
|
7 |
||||||
|
8 |
||||||
|
9 |
||||||
|
10 |
-1.05469 |
-1.05371 |
-1.0542 |
-0.01146 |
-0.00218 |
0.000977 |
где a0 , b0 – начальные границы
интервала изоляции корня;
В результате
расчета приближенное значение первого корня: при точности
и х=-1.0542 при точности
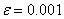
Графическая иллюстрация метода:
Этот пример в Excel: dich.xls (20 Кб)
Метод простой итерации
С помощью эквивалентных преобразований приведем исходное уравнение f(x) к виду, удобному для применения
метода простой итерации: x=φ(x).
Выберем начальное приближение x0∈[a, b]. Следующие
итерации находим по формуле: xk+1=φ(xk),
т.е. x1=φ(x0),
x2=φ(x1)
и т.д.. Итерационный процесс заканчивается, если |xk+1–xk|<ε. Представить
исходное уравнение в эквивалентном виде x=φ(x)
можно бесконечным числом способов. Из всевозможных таких представлений выбирают
тот, который дает сходящуюся к корню последовательность вычислений. Очевидно,
что .
Достаточное условие сходимости: пусть φ(x)
имеет производную на отрезке
[a,b], 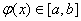
для всех x из отрезка
[a,b], тогда итерационный
процесс сходится к корню уравнения т.е. .
Доказательство
следует из следующих оценок:
Первое неравенство следует из теоремы Лагранжа о среднем и того, что .
Остальные по
инерции.
Так как .
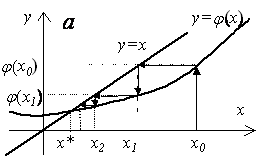
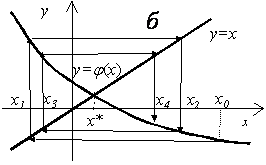
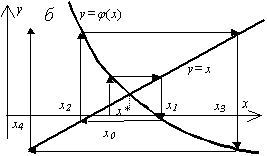
Геометрический смысл метода простой итерации.
|
|
|
|
|
|
|
Сходящийся метод |
|
|
|
|
|
|
|
Расходящийся |
В качестве
начального приближения обычно берут середину отрезка [a,b]: .
На практике часто в качестве берут функцию
, где с – некоторая постоянная.
Постоянную c выбирают таким образом, чтобы для всех x∈[a, b].
При таком выборе функции метод простой итерации называют методом
релаксации.
Получим
условия на выбор с:
Таким образом, если f/(x)<0, то 2/f/(x)<c<0. Если же f/(x)>0, то 2/f/(x)>c>0.
Видно, что знак у с совпадает со знаком f/(x).
Часто с берут в виде: .
Убедимся, что
такое c удовлетворяет условию сходимости:
Пусть f/(x)>0. Тогда M>0 и m>0 -> c>0 и
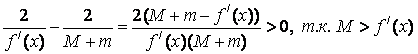
Пусть f/(x)<0. Тогда M<0 и m<0-> c<0 и
Следовательно,
2/f/(x)<c<0.
Найдем, второй корень нашего исходного уравнения x3‑
6x2+3x+11=0, который лежит на интервале [1, 3] с точностью .
Сначала
найдем функцию .
В нашем случае f(x)= x3‑
6x2+3x+11.
Для нахождения c необходимо найти максимальное
и минимальное значения f/(x)
на отрезке [1, 3]. Для этого необходимо найти значения f/(x) на концах интервала и в точках, где f//(x)=0, т.е. в точках экстремума, если такие точки для
рассматриваемого интервала существуют. И выбрать среди этих значений f/(x) максимальное и
минимальное значения.
f/(1)=3x2-12x+3=-6, f/(3)=-6, f//(x)=6x-12=0
при x=2 , f/(2)=-8.
Следовательно,
Таким
образом, .
Вычисления
оформим в виде таблицы:
|
k |
x |
|xk+1-xk| |
|f(xk)| |
|
0 |
2 |
– |
1 |
|
1 |
2.142857 |
0.142857 |
0.282799 |
|
2 |
2.102457 |
0.0404 |
0.07896 |
|
3 |
2.113737 |
0.01128 |
0.022164 |
|
4 |
2.110571 |
0.003166 |
0.006213 |
|
5 |
2.111459 |
0.000888 |
0.001742 |
|
6 |
2.11121 |
0.000249 |
0.000489 |
Здесь x0=(1+3)/2=2, ,
и т.д.
Условием
окончания итерационного процесса является условие: |xk+1–xk|<ε или |f(xk)|<ε.
Метод Ньютона (метод касательных)
Напомним, что
мы решаем уравнение f(x)=0.
Метод
определяется формулой
Геометрическая интерпретация такова:
участок кривой y=f(x) при 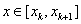
, или
, если
, заменяется отрезком касательной, проведённой
из точки xk.
Уравнение касательной имеет вид . Найдем точку пересечения, которую обозначим xk+1, касательной с осью y=0:
.
Откуда .
Можно
показать, что |xk+1– x*| < q * |xk – x*|2,
т.е. метод сходится со вторым порядком.
Метод Ньютона можно трактовать как метод простой итерации при .
Замечание. Если известен интервал изоляции корня уравнения, в котором f//(x) не меняет знак, то
в качестве начального приближения берут тот конец интервала изоляции, для
которого знаки f(x) и f//(x) совпадают.
Найдем, третий корень методом Ньютона нашего исходного уравнения x3‑
6x2+3x+11=0, который лежит на интервале [4, 5] с точностью . Сначала убедимся, что f//(x) не меняет знака на
этом отрезке.
f//(x)=6x-12.
f//(x)>0 при x>2, т.е. f//(x)>0 на интервале [4,5]. Так как f(5)=1>0,
то x0=5.
Вычисления
оформим в виде таблицы:
|
k |
xk |
|xk+1-xk| |
f(xk) |
f/(xk) |
|
0 |
5 |
– |
1 |
18 |
|
1 |
4.944444 |
0.055556 |
0.027606 |
17.00926 |
|
2 |
4.942821 |
0.001623 |
2.33E-05 |
16.98059 |
|
3 |
4.94282 |
1.37E-06 |
1.66E-11 |
16.98057 |
Здесь f(xk)=xk3‑ 6xk2+3xk+11, f/(xk)=3xk-12xk+3, .
В качестве корня можно взять
значение: x=4.943. Видно, что процесс сошелся уже на
второй итерации.
Для сравнения найдем
первый корень нашего уравнения x3‑ 6x2+3x+11=0 на
отрезке [-2,-1] методом Ньютона:
Так как f//(x)=6x-12,
то f//(x)<0 на
интервале [-2,-1], а так как f(-2)=-27>0, то x0=-2.
|
k |
xk |
|xk+1-xk| |
f(xk) |
f/(xk) |
|
0 |
-2 |
-27 |
39 |
|
|
1 |
-1.30769 |
0.692308 |
-5.41966 |
23.82249 |
|
2 |
-1.08019 |
0.227502 |
-0.50182 |
19.46272 |
|
3 |
-1.05441 |
0.025783 |
-0.00613 |
18.9882 |
|
4 |
-1.05408 |
0.000323 |
-9.5E-07 |
18.98229 |
|
5 |
-1.05408 |
5.02E-08 |
-2.3E-14 |
18.98229 |
Напомним, что методом дихотомии
мы достигли данной точности 0.001 на 10-ой итерации.
Вычислим второй корень нашего
уравнения на отрезке [1,3]. Заметим, что f//(x)=6x-12 меняет знак на отрезке при
х=2. Уменьшим интервал изоляции так, чтобы f//(x) не меняла знака. Рассмотрим интервал [2.1; 3]. f//(2.1)=6*2.1-12=0.6>0 b f(2.1)=0.101>0.
Следовательно, x0=2.1.
|
k |
xk |
|xk+1-xk| |
f(xk) |
f/(xk) |
|
0 |
2.1 |
0.101 |
-8.97 |
|
|
1 |
2.11126 |
0.01126 |
3.95E-05 |
-8.96286 |
|
2 |
2.111264 |
4.4E-06 |
6.47E-12 |
-8.96286 |
|
3 |
2.111264 |
7.22E-13 |
0 |
-8.96286 |
Если сравнивать с методом
простой итерации, то значение этого корня мы получили за две итерации вместо
шести.
Эти примеры показывают, что
метод Ньютона является более быстросходящимся. Но для его использования
необходимо брать начальное приближение достаточно близким к корню.
Упрощенный
метод Ньютона. Эта модификация метода Ньютона используется, если
производная f /(x) представляет
собой сложную функцию, и для ее вычисления на каждой итерации используется
много времени. Зададим x0 – начальное
приближение и вычислим производную z=f /(x0). На следующих итерациях
используется вычисленное значение производной: . Это упрощение
несколько замедляет процесс сходимости к решению, однако сокращает время
каждого итерационного цикла.
Метод хорд
В этом методе
кривая f(x) заменяется прямой линией – хордой, стягивающей точки (a, f(a)) и (b,
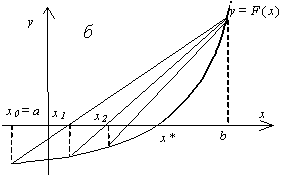
f(b)). В зависимости от знака выражения f(a) f //(a)
метод хорд имеет два варианта, изображенных на рис. 2 а, б.
|
|
|
|
Рис. 2. Метод хорд |
Пусть f(a)f //(a)>0 (рис. 2 а). Тогда x0=b,
точка a будет оставаться неподвижной. Следующее приближение x1
находим как точку пересечения хорды, соединяющей точки (a, f(a)) и (x0, f(x0))
с осью x. Уравнение хорды: . Тогда точка пересечения
хорды с осью x: .
Пусть теперь f(a)f //(a)<0 (рис. 2). Тогда x0=a,
точка b неподвижна. Проведем хорду, соединяющую точки (b, f(b)) и (x0, f(x0)):. Вычисляем точку пересечения
хорды с осью x: .
На следующей
итерации в качестве x0 надо взять вычисленное значение x1.
Таким образом,
имеем следующую последовательность вычислений:
Если f(a) f //(a)>0, то x0=b и .
Если же f(a) f //(a)<0, то x0=a и .
Окончание
итерационного цикла в этом методе происходит по условию малости невязки
уравнения: |f(x1)| < ε или .
Задание. Найти первый и третий
корень уравнения x3‑ 6x2+3x+11=0 методом хорд.
Для первого
корня a=-2, b=-1. , тогда расчет ведется по
первым формулам: x0=b
и .
|
k |
xk |
|xk+1-xk| |
f(xk) |
|
0 |
-1 |
1 |
|
|
1 |
-1.03571 |
0.035714 |
0.345618 |
|
2 |
-1.0479 |
0.012187 |
0.117007 |
|
3 |
-1.05201 |
0.004108 |
0.039334 |
|
4 |
-1.05339 |
0.001379 |
0.013192 |
|
5 |
-1.05385 |
0.000462 |
0.004421 |
Для последнего корня: a=4, b=5, 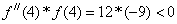
формулам: x0=a и .
|
k |
xk |
|xk+1-xk| |
f(xk) |
|
0 |
4 |
-9 |
|
|
1 |
4.9 |
0.9 |
-0.711 |
|
2 |
4.941555 |
0.041555 |
-0.02147 |
|
3 |
4.942783 |
0.001229 |
-0.00062 |
|
4 |
4.942819 |
3.57E-05 |
-1.8E-05 |
Аналогичные рассуждения, если функция убывает: значение функции в следующей точке будет меньше, чем в предыдущей, значит производная будет отрицательной.
Итак, если производная положительна на промежутке, то это значит, что функция на этом промежутке возрастает. На рисунке 1 такие участки показаны зеленым. А если производная отрицательна, то функция убывает, на рисунке 1 участки показаны синим:
$$f^{/}(x)>0 leftrightarrow f(x) Uparrow ;$$
$$f^{/}(x)<0 leftrightarrow f(x) Downarrow ;$$
Кроме этого, производная от функции может быть равна нулю. Функция в той точке, где производная равна нулю, будет принимать наибольшее или наименьшее значение в окрестности этой точки. На графике нашей функции (Рис. 1) эти точки выглядят как «холмы» и «впадины».
Обратите внимание, что «холмов» и «впадин» на графике может быть бесконечно много, какие-то из этих «холмов» будут выше, какие-то ниже. Производная равна нулю во всех таких точках. И значения функции во всех таких точках я называю наибольшими и наименьшими, хотя на самом деле это локальные наибольшие и наименьшие значения.
Кстати, ТОЧКАМИ минимума или максимума называют координаты «холмов» и «впадин» по оси (x). Еще их называют точками экстремума функции: это общее название для минимумов и максимумов. Поэтому, когда вас просят найти точки экстремума, это значит найти координаты по оси (x) и минимумов, и максимумов.
В точке (x=-2) будет минимум функции. Точка (x=-3) из знаменателя, поэтому на рисунке она выколотая: ее мы не рассматриваем.
Чтобы определить наименьшее значение, подставим в исходную функцию найденную точку минимума и концы отрезка (xin[-2,5;0]):
$$y(-2)=3x—ln(x+3)^3=3*(-2)-ln(-2+3)^3=-6-0=-6;$$
$$y(-2,5)=3x—ln(x+3)^3=3*(-2,5)-ln(-2,5+3)^3=-7,5-ln(0,5)^3;$$
$$y(0)=3x—ln(x+3)^3=3*0-ln(0+3)^3=ln(3)^3;$$
Обратите внимание, что значение функции в точках ((-2,5)) и ((0)) получились “плохие”: мы не можем посчитать значения таких логарифмов без калькулятора. Поэтому, если возникает такая ситуация, то мы просто отбрасываем эти значения, ведь в заданиях ЕГЭ в первой части не может быть иррациональных значений. Такая маленькая хитрость. Но будьте внимательны, может быть, иррациональные значения у вас получаются, потому что где-то ошибка.
Кстати, подставлять в этом примере границы отрезка необязательно еще и по другой причине: на промежутке ([-2,5;-2)) функция убывает, а на промежутке ((-2;0]] возрастает. Минимальное значение на указанном промежутке может быть только в точке минимума.
Ответ: (-6.)
Пример 21
Найдите наименьшее значение функции (y=x*sqrt{x}-9x+25) на интервале ([1;50].)
Производную от данной функции можно посчитать, воспользовавшись формулой производной от произведения ((f(x)*g(x))^{/}=(f(x))^{/}*g(x)+f(x)*(g(x))^{/}:)
$$y^{/}=(x*sqrt{x}-9x+25)^{/}=(xsqrt{x})^{/}-(9x)^{/}+25^{/}=x^{/}*sqrt{x}+x*(sqrt{x})^{/}-9=$$
$$=1*sqrt{x}+x*frac{1}{2sqrt{x}}-9=sqrt{x}+frac{sqrt{x}*sqrt{x}}{2sqrt{x}}-9=sqrt{x}+frac{1}{2}*sqrt{x}-9=frac{3}{2}*sqrt{x}-9;$$
Есть другой вариант взятия производной, на мой взгляд, он легче. Для это мы представим квадратный корень в виде степени:
$$sqrt{x}=x^{frac{1}{2}};$$
$$y^{/}=(x*sqrt{x}-9x+25)^{/}=(x*x^{frac{1}{2}}-9x+25)^{/}=(x^{frac{3}{2}-9x+25)^{/}=frac{3}[2}*x^{frac{1}{2}}-9=frac{3}{2}*sqrt{x}-9;$$
Приравниваем производную к нулю и находим корни уравнения на указанном интервале:
$$frac{3}{2}*sqrt{x}-9=0;$$
$$sqrt{x}=9*frac{2}{3};$$
$$sqrt{x}=6;$$
$$x=36;$$
На числовой прямой определяем знаки производной и промежутки возрастания и убывания функции: