Microsoft Excel представляет собой приложение для работы с электронными таблицами. Одно из самых значительных его преимуществ – это возможность осуществления различных расчетов с использованием встроенных формул и функций.

Вам понадобится
- – MS Excel.
Инструкция
Выполните решение нелинейного уравнения в Excel на примере следующего задания. Найти корни полинома x3 – 0,01×2 – 0,7044x + 0,139104 = 0. Для этого сначала выполните графическое решение уравнения. Известно, что для решения такого уравнения нужно найти точку пересечения графика функции f(x) и оси абсцисс, то есть необходимо узнать такое значение x, при котором функция обратится в ноль.
Проведите табулирование полинома на интервале, к примеру, от –1 до 1, возьмите для этого шаг 0,2. Введите в первую ячейку –1, в следующую –0,8, затем выделите обе, наведите курсор мыши на правый нижний угол, чтобы появился значок плюса, и протяните до тех пор, пока не появится значение 1.
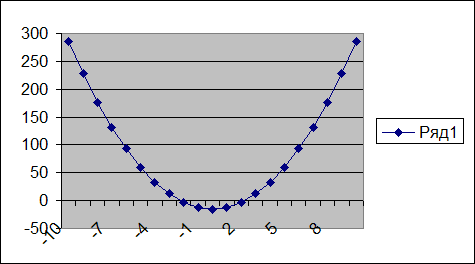
Затем в ячейке справа от –1 введите формулу = A2^3 – 0,01*A2^2 – 0,7044*A2 + 0,139104. С помощью автозаполнения найдите y для всех значений x. Выполните построение графика функции по полученным расчетам. На графике найдите пересечения оси абсцисс и определите интервалы, на которых находятся корни полинома. В нашем случае это [-1,-0.8] и [0.2,0.4], а также [0.6,0.8].
Найдите корни уравнения с помощью последовательного приближения. Установите погрешность вычисления корней, а также предельное число с помощью меню «Сервис» и вкладки «Параметры». Введите начальные приближения и значения функции, затем вызовите меню «Сервис», пункт «Подбор параметра».
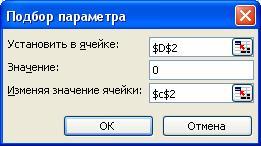
Заполните появившееся диалоговое окно таким образом: в поле «Установить в ячейке» введите B14 (ссылка на ячейку, которая отводится под искомую переменную), в поле «Значение» установите 0 (правая часть уравнения), а в поле «Изменяя значение ячейки» введите абсолютную ссылку на ячейку A14 (ячейка с формулой, по которой вычисляется значение левой половины уравнения). Удобнее вводить ссылки не вручную, а выбирая нужные ячейки левой кнопкой мыши. Щелкните «ОК». На экране отобразится результат подбора. Поиск двух оставшихся корней произведите аналогично.
Источники:
- как в excel найти корень
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Содержание | Назад
Рассмотрим пример нахождения всех корней уравнения
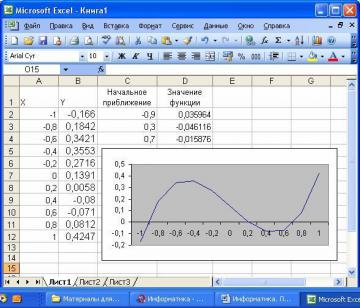
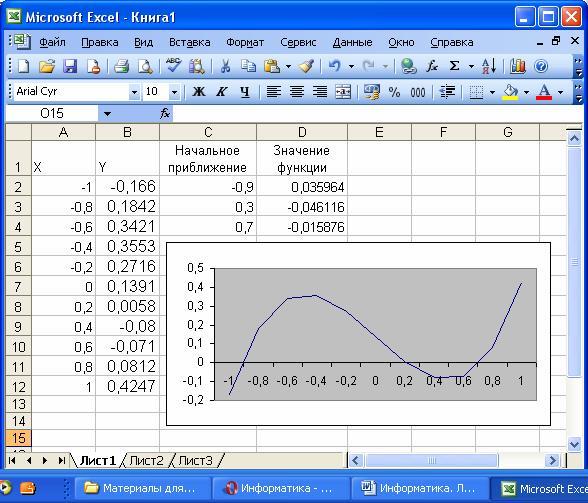
Отметим, что у полинома третьей степени имеется не более трех вещественных корней. Для нахождения корней их предварительно надо локализовать. С этой целью необходимо полином протабулировать. Построим таблицу значений полинома на отрезке [—1,1] с шагом 0,2 и график полинома. Результат приведен на рис. 29, где в ячейку В2 введена формула
=A2^3 — 0,01*A2^2 — 0,7044*A2 + 0,139104.
На рис. 29 видно, что полином меняет знак на интервалах [—1,—0,8], [0,2, 0,4] и [0,6, 0,8]. Это означает, что на каждом из них имеется корень данного полинома. Поскольку полином третьей степени имеет не более трех действительных корней, мы локализовали все его корни.
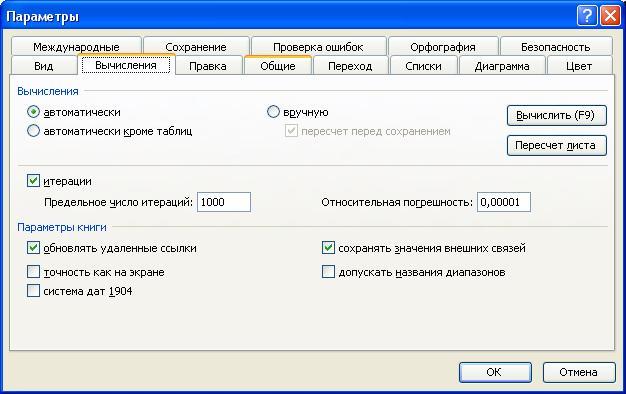
Найдем корни полинома методом последовательных приближений с помощью команды Сервис / Подбор параметров. Относительная погрешность вычислений и предельное число итераций задаются на вкладке Вычисления диалогового окна Параметры, открываемого командой Сервис / Параметры (рис. 30).
Зададим относительную погрешность и предельное число итераций равными 0,00001 и 1000 соответственно. В качестве начальных приближений к корням можно взять любые точки из отрезков локализации корней. Возьмем в качестве начальных приближений их средние точки: —0.9, 0.3, 0,7 и введем их в диапазон ячеек С2:С4. В ячейку D2 введем формулу
=C2^3 — 0,01*C2^2 — 0,7044*C2 + 0,139104.
Выделим эту ячейку и с помощью маркера заполнения протащим введенную в нее формулу на диапазон D2:D4. В ячейках D2:D4 будут вычислены значения полинома при значениях аргумента, введенных в ячейки C2:C4.
Теперь выберем команду Сервис / Подбор параметров и заполним диалоговое окно Подбор параметров следующим образом (рис. 31).
В поле Установить в ячейке введем D2. В этом поле дается ссылка на ячейку, в которую введена формула, вычисляющая значение левой части уравнения. В поле Значение введем 0 (в этом поле указывается правая часть уравнения). В поле Изменяя значение ячейки введем С2 (в этом поле дается ссылка на ячейку, отведенную под переменную).
Вводить ссылки на ячейки в поля диалогового окна Подбор параметров удобнее не с клавиатуры, а щелчком на соответствующей ячейке. При этом Excel автоматически будет превращать их в абсолютные ссылки (в нашем примере в $D$2 и $C$2).
После нажатия кнопки ОК средство подбора параметров находит приближенное значение корня, которое помещается в ячейку С2. В данном случае оно равно —0,920. Аналогично в ячейках С3 и С4 находим два оставшихся корня. Они равны 0,210 и 0,720.
Содержание | Назад
В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.
Рассмотрим на примерах некоторые варианты решений.
Решение уравнений методом подбора параметров Excel
Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» – «Работа с данными» – «Анализ «что-если»» – «Подбор параметра».
Рассмотрим на примере решение квадратного уравнения х2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
- Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
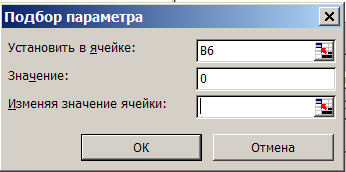
- Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» – ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» – В1. Здесь должен отобразиться отобранный параметр.
- После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».
Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».
Как решить систему уравнений матричным методом в Excel
Дана система уравнений:
- Значения элементов введем в ячейки Excel в виде таблицы.
- Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
- Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
- Умножим обратную матрицу Ах-1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
- Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.
Получены корни уравнений.
Решение системы уравнений методом Крамера в Excel
Возьмем систему уравнений из предыдущего примера:
Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.
Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.
Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).
Определитель системы больше 0 – решение можно найти по формуле Крамера (Dx / |A|).
Для расчета Х1: =U2/$U$1, где U2 – D1. Для расчета Х2: =U3/$U$1. И т.д. Получим корни уравнений:
Решение систем уравнений методом Гаусса в Excel
Для примера возьмем простейшую систему уравнений:
3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9
Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.
Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.
- Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
- Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
- Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
- Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: {=B12:E12/D12}.
- В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки ({=(B11:E11-B16:E16*D11)/C11}). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты ({=(B10:E10-B15:E15*C10-B16:E16*D10)/B10}). В последнем столбце новой матрицы получаем корни уравнения.
Примеры решения уравнений методом итераций в Excel
Вычисления в книге должны быть настроены следующим образом:
Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:
Хn+1 = Xn– F (Xn) / M, n = 0, 1, 2, … .
M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:
f’ (1) = -2 * f’ (2) = -11.
Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х3 – 1. М = 11.
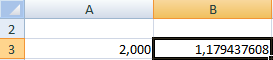
В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.
Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:
Скачать решения уравнений в Excel
Корень на заданном промежутке один.
Содержание | Назад
Рассмотрим пример нахождения всех корней уравнения
Отметим, что у полинома третьей степени имеется не более трех вещественных корней. Для нахождения корней их предварительно надо локализовать. С этой целью необходимо полином протабулировать. Построим таблицу значений полинома на отрезке [—1,1] с шагом 0,2 и график полинома. Результат приведен на рис. 29, где в ячейку В2 введена формула
=A2^3 — 0,01*A2^2 — 0,7044*A2 + 0,139104.
На рис. 29 видно, что полином меняет знак на интервалах [—1,—0,8], [0,2, 0,4] и [0,6, 0,8]. Это означает, что на каждом из них имеется корень данного полинома. Поскольку полином третьей степени имеет не более трех действительных корней, мы локализовали все его корни.
Найдем корни полинома методом последовательных приближений с помощью команды Сервис / Подбор параметров. Относительная погрешность вычислений и предельное число итераций задаются на вкладке Вычисления диалогового окна Параметры, открываемого командой Сервис / Параметры (рис. 30).
Зададим относительную погрешность и предельное число итераций равными 0,00001 и 1000 соответственно. В качестве начальных приближений к корням можно взять любые точки из отрезков локализации корней. Возьмем в качестве начальных приближений их средние точки: —0.9, 0.3, 0,7 и введем их в диапазон ячеек С2:С4. В ячейку D2 введем формулу
=C2^3 — 0,01*C2^2 — 0,7044*C2 + 0,139104.
Выделим эту ячейку и с помощью маркера заполнения протащим введенную в нее формулу на диапазон D2:D4. В ячейках D2:D4 будут вычислены значения полинома при значениях аргумента, введенных в ячейки C2:C4.
Теперь выберем команду Сервис / Подбор параметров и заполним диалоговое окно Подбор параметров следующим образом (рис. 31).
В поле Установить в ячейке введем D2. В этом поле дается ссылка на ячейку, в которую введена формула, вычисляющая значение левой части уравнения. В поле Значение введем 0 (в этом поле указывается правая часть уравнения). В поле Изменяя значение ячейки введем С2 (в этом поле дается ссылка на ячейку, отведенную под переменную).
Вводить ссылки на ячейки в поля диалогового окна Подбор параметров удобнее не с клавиатуры, а щелчком на соответствующей ячейке. При этом Excel автоматически будет превращать их в абсолютные ссылки (в нашем примере в $D$2 и $C$2).
После нажатия кнопки ОК средство подбора параметров находит приближенное значение корня, которое помещается в ячейку С2. В данном случае оно равно —0,920. Аналогично в ячейках С3 и С4 находим два оставшихся корня. Они равны 0,210 и 0,720.
Содержание | Назад
11
Р

уравнений в Excel
Функция Подбор
параметра может быть использована в
следующих случаях:
А) нахождение
значения аргумента (параметра) функции,
соответствующего определённому значению
функции (в том числе 0);
Б) нахождение
значений аргумента (параметра) функции
при изменении вида её графика.
А.
Использование функции Подбор параметра
для нахождения значения аргумента
функции, соответствующего заданному
значению функции
Первый случай
использования иначе может быть представлен
таким образом: поиск определенного
результата для ячейки с помощью подбора
значения другой ячейки.
Например, одна
ячейка содержит формулу, в которой есть
ссылки на другую ячейку.
Значение в ячейке
С1 представляет собой среднее арифметическое
значение в ячейках А1 и В1:
Допустим, что для
целей исследования необходимо найти
значение, которое должна принять ячейка
А1, для того чтобы ячейка С1 приняла
значение 855.
Безусловно, можно
самостоятельно путём перебора значений
в ячейке А1 достичь необходимый результат.
Однако, в целях минимизации затрат
времени следует воспользоваться функцией
Подбор параметра.
Для этого необходимо:
-
выполнить команду
Подбор параметра из меню Сервис.
В результате
появится запрос Подбор параметра :
-
в поле Установить
в ячейке ввести ссылку или имя ячейки,
содержащую формулу, для которой следует
подобрать параметр. Автоматически в
поле Установить в ячейке отображается
имя ячейки, которая была активной на
момент выполнения команды Подбор
параметра из меню Сервис. Кнопка
свёртывания окна диалога
,
расположенная справа от поля, позволяет
временно убрать диалоговое окно с
экрана, чтобы было удобнее выделить
диапазон на листе. Выделив диапазон,
следует нажать кнопку
для вывода на экран диалогового окна. -
в поле Значение
ввести число, которое должно возвращать
формула с искомым значением параметра.
Например, 855. -
в поле Изменяя
значение ячейки указать ссылку на
ячейку, содержащую параметр, значение
которого требуется подобрать для
получения требуемого результата. На
эту ячейку прямо или косвенно должна
ссылаться формула, содержащаяся в
ячейке, адрес которой указан в поле
Установить в ячейке. В нашем случае
это А1.
В итоге диалоговое
окно примет следующий вид:
-
нажать кнопку ОК
для закрытия диалогового окна. После
выполнения этого действия появляется
запрос Результат подбора параметра,
а искомое значение параметра
отображается в ячейке А1:
Б.
Использование функции Подбор параметра
для нахождения значения аргумента
функции при изменении вида ее графика.
Допустим, что для
решения поставленной задачи нам предстоит
проанализировать построенный в Ms
Excel график функции y
= 2*x-2 в диапазоне аргумента
от –3 до 6.
Для этого следует:
1) в ячейки А1-А10
ввести значения от –3 до 6 с шагом 1; в
ячейку В1 – ввести формулу 2*А1-2 и путём
перетаскивания маркера заполнения

эту формулу на ячейки В2-В10. В результате
соответствующий участок листа примет
следующий вид:
-
выделив диапазон
В1-В10, нажать кнопку Мастер диаграмм
на Стандартной панели инструментов.
-
на первом шаге
работы Мастера диаграмм выбрать
тип диаграммы График; -
на втором шаге
работы Мастера диаграмм на вкладке
Ряд в поле Подписи по оси Х задать
диапазон А1-А10; -
последовательными
нажатиями кнопки Далее и Готово
закончите работу Мастера.
В результате должен
быть построен график функции:
Далее предположим,
что необходимо узнать значение аргумента
данной функции, при котором значение
самой функции будет равно 0.
Чтобы решить эту
задачу с помощью построенного графика
и функции Подбор параметра необходимо:
-
щелчком левой
кнопки мыши на графике выделить ряд
данных, содержащий маркер данных,
который нужно изменить,
а затем выделить
щелчком сам маркер
-
перетащить маркер
до уровня, соответствующего требуемому
значению функции:
-
если значение
маркера данных получено из формулы,
появится диалоговое окно Подбор
параметра:
в поле Установить
в ячейке отображается ссылка на
ячейку, содержащую формулу, в поле
Значение — требуемая величина
-
в поле Изменяя
значение ячейки выбрать ячейку,
значение которой нужно изменить (А6) и
нажать кнопку ОК.
При подборе можно
изменять только одну ячейку.
При этом исходное
значение аргумента в ряде данных сменится
на значение, полученное в результате
подбора параметра
Решение уравнений
Функция Подбор параметра позволяет
находить одно значение аргумента,
соответствующее заданному значению
функции (например, 0). Однако часто функция
может принимать одно значение при
нескольких значениях аргументов. То
есть уравнение может иметь несколько
корней.
Например, функция у=3*х2 -15 может
принимать значение 0 при двух значениях
аргументов.
Однако, функция Подбор параметра
найдет только один корень уравнения
– самый близкий к значению в ячейке,
указанной в поле Изменяя значение
ячейки.
Так, если попытаться решить указанное
выше уравнение с помощью Ms
Excel и встроенной в него
функции Подбор параметра, то исходные
данные можно представить в следующем
виде:
Выполнив команду
Подбор параметра из меню Сервис,
необходимо заполнить поля диалогового
окна следующим образом:
В результате
найденным корнем уравнения будет
значение 2,2360797 в ячейке А4
Однако, это не
единственный корень. В этом можно
убедиться, решив уравнение или построив
график функции у=3*х2-15
Для построения
графика следует:
1) в ячейки С4-С24
ввести значения от –10 до 10 с шагом 1; в
ячейку D1 – ввести формулу
3*C4*C4-15 и
путём перетаскивания маркера заполнения
заполнить этой формулой ячейки D5-D24;
-
выделив диапазон
D4-D24, нажать
кнопку Мастер диаграмм на Стандартной
панели инструментов; -
на первом шаге
работы Мастера диаграмм выбрать
тип диаграммы График; -
на втором шаге
работы Мастера диаграмм в закладке
Ряд в поле Подписи по оси Х указать
диапазон С4-С24; -
последовательными
нажатиями кнопки Далее и Готово
закончить работу Мастера.
В результате должен
быть построен график функции:
Из графика видно,
что уравнение 3*x2-15=0
имеет 2 корня, к тому же эти корни примерно
равны –2 и 2. Одни корень 2,2360797 нам уже
известен.
Для поиска второго
корня можно поступить двояко, используя
пункт А или Б:
А. Изменим значение,
например, в ячейке С4 на –2 (более близкое
к ожидаемому корню). Выделим ячейку D4
и выполним команду Подбор параметра
из меню Сервис. Заполним поля
запроса:
и после щелчка по
кнопке ОК в ячейке С4 получим значение
второго корня -2,23606503:
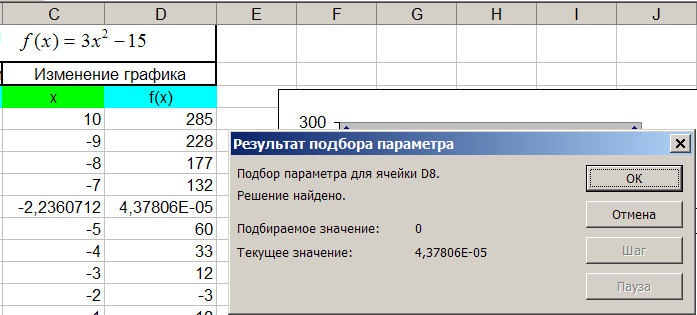
Б. Построим график
функции в интервале от -10 до 10:
Щелчком левой
кнопки мыши на графике выделим ряд
данных, содержащий маркер данных, близкий
ко второму корню:
Выделим щелчком
этот маркер:
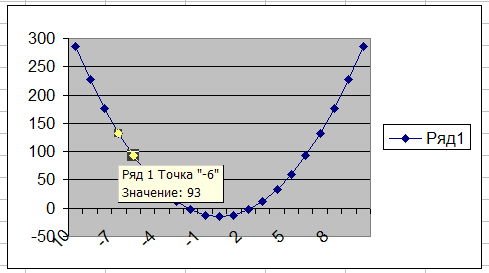
Перетащим маркер
до уровня, соответствующего требуемому
значению функции (а именно вниз до 0):
Заполним поле
Изменяя значение ячейки запроса:
И щелкнув по кнопке
ОК, в ячейке С8 получим значение второго
корня:
Вы могли обратить
внимание, что значения корня, полученные
в п.А и п.Б имеют несущественное отличие.
Это вызвано следующим обстоятельством.
По умолчанию команда Подбор параметра
прекращает итерационные вычисления,
когда выполняется 100 итераций, либо при
получении результата, который находится
в пределах 0,001 от заданного целевого
значения. Если нужна большая точность,
можно изменить используемые по умолчанию
параметры командой Параметры меню
Сервис. Затем на вкладке Вычисления
в поле Предельное число итераций
введите значение больше 100, а в поле
Относительная погрешность – значение
меньше 0,001.
Если Ms
Excel выполняет сложную
задачу подбора параметра, можно нажать
кнопку Пауза в окне запроса Результат
подбора параметра и прервать вычисления,
а затем нажать кнопку Шаг, чтобы
просмотреть результаты каждой
последовательной итерации. Когда Вы
решаете задачу в пошаговом режиме, в
этом окне запроса появляется кнопка
Продолжить. Нажмите ее, когда решите
вернуться в обычный режим подбора
параметра.