Как найти корни кубической параболы

Как найти корни кубической параболы

Куби́ческое уравне́ние — алгебраическое уравнение третьей степени, общий вид которого следующий:

ax^{3}+bx^{2}+cx+d=0,;aneq 0.

Здесь коэффициенты a,b,c,d — вещественные или комплексные числа.

Для анализа и решения кубического уравнения можно в декартовой системе координат начертить график левой части, полученная кривая называется кубической параболой (см. рисунки).

Кубическое уравнение общего вида может быть приведено к каноническому виду путём деления на a и замены переменной x=y-{tfrac {b}{3a}}. В результате получается упрощённый вид уравнения:

{displaystyle y^{3}+py+q=0,}

где

p={frac {c}{a}}-{frac {b^{2}}{3a^{2}}}={frac {3ac-b^{2}}{3a^{2}}},
{displaystyle q={frac {d}{a}}-{frac {bc}{3a^{2}}}+{frac {2b^{3}}{27a^{3}}}={frac {27a^{2}d-9abc+2b^{3}}{27a^{3}}}.}

Кубическое уравнение разрешимо в радикалах, см. Формула Кардано.

История[править | править код]

Древний период[править | править код]

Кубические уравнения были известны ещё древним египтянам, вавилонянам, древним грекам, китайцам и индийцам[1][2]. Были найдены клинописные таблички Старовавилонского периода (XX—XVI век до н. э.), содержащие таблицы значений кубов и кубических корней[3][4]. Вавилоняне могли использовать эти таблицы для решения кубических уравнений, но не существует никаких свидетельств, что они это делали[5].

Задача удвоения куба использует простейшее и наиболее старое из кубических уравнений, и древние египтяне не верили, что решение его существует[6]. В пятом веке до нашей эры Гиппократ свёл эту задачу к нахождению двух средних пропорциональных между одним отрезком и другим, вдвое большим его, но не смог решить её с помощью циркуля и линейки[7], что, как теперь известно, невозможно сделать.

В III веке нашей эры древнегреческий математик Диофант нашёл целые и рациональные решения для некоторых кубических уравнений с двумя неизвестными (диофантовых уравнений)[2][8]. Считается, что Гиппократ, Менехм и Архимед подошли ближе к решению задачи об удвоении куба с помощью конических сечений[7], хотя некоторые историки, такие как Ревиэль Нетц (Reviel Netz), говорят о том, что неизвестно, думали ли греки о кубических уравнениях, или просто о задачах, которые могут привести к кубическим уравнениям. Другие, как, например, Томас Хит, переводчик и комментатор всех дошедших до нас трудов Архимеда, не соглашаются, указывая на свидетельства, что Архимед действительно решал кубические уравнения с помощью пересечения двух конусов[9].

Численные методы решения кубических уравнений появляются в китайском математическом тексте Математика в девяти книгах, составленном около второго столетия до нашей эры и прокомментированном китайским математиком Лю Хуэем в третьем столетии[1].

В VII веке во времена династии Тан астроном и математик Ван Сяотун[en] в своём математическом трактате, озаглавленном Цзигу Суаньцзин, изложил и решил 25 кубических уравнений вида x^{3}+px^{2}+qx=N, в 23 из которых p,qneq 0, и в двух уравнениях q=0[10].

Средневековье[править | править код]

В XI веке персидский поэт и математик Омар Хайям (1048—1131) сделал существенный прогресс в теории кубических уравнений. В ранних работах, посвящённых кубическим уравнениям, он обнаружил, что кубическое уравнение может иметь два решения (случай трёх корней остался им незамеченным[11]), и утверждал, что уравнение не может быть решено с помощью циркуля и линейки. Он также нашёл геометрическое решение[12][13]. В его более позднем труде, Трактат о демонстрации задач алгебры, он описал полную классификацию кубических уравнений с их общими геометрическими решениями, использующими пересечения конических сечений[14][15].

В XII столетии индийский математик Бхаскара II пытался решать кубические уравнения без особых успехов. Однако он привёл один пример решения кубического уравнения[16]:

{displaystyle x^{3}+12x=6x^{2}+35.}

В том же XII столетии персидский математик Шараф ад-Дин написал Al-Mu’adalat (Трактат об уравнениях), в котором говорится о восьми типах кубических уравнений с положительными решениями и о пяти типах, не имеющих положительных решений. Он использовал подход, который позднее стал известен как метод «Руффини — Горнера» для численной аппроксимации корня кубического уравнения. Он разработал также концепцию производной функции и экстремумов кривой для решения кубических уравнений, которые могут не иметь положительных значений[17]. Он понял важность дискриминанта кубического уравнения для нахождения алгебраического решения некоторых специальных видов кубических уравнений[18].

В средневековой Европе до XVI века успехов в решении кубических уравнений не было. Леонардо Пизанский, известный также как Фибоначчи (1170—1250), умел находить положительные решения кубического уравнения x^{3}+2x^{2}+10x=20 с помощью вавилонских цифр. Он указал решение {displaystyle 1,22,7,42,33,4,40,} что равно {displaystyle 1+22/60+7/60^{2}+42/60^{3}+33/60^{4}+4/60^{5}+40/60^{6}} в стандартной записи и отличается от точного решения только на три триллионных[19].

Лука Пачоли в своём трактате «Сумма арифметики, геометрии, отношений и пропорций» (1494 год) писал, что общее решение кубических уравнений «столь же невозможно при современном состоянии науки, как и решение квадратуры круга циркулем и линейкой»[20].

Открытие дель Ферро — Тартальи[править | править код]

В начале XVI века итальянский математик Сципион дель Ферро нашёл общий метод решения важного класса кубических уравнений, а именно, уравнений вида {displaystyle x^{3}+mx=n} с неотрицательными n и m. Фактически все кубические уравнения можно свести к такому виду, если допустить возможность для m и n быть отрицательными, но отрицательные числа в то время ещё не считались допустимыми. Дель Ферро держал своё открытие в секрете, пока не рассказал о нём перед своей смертью своему ученику Антонио Фиоре (Antonio Fiore).

Никколо Фонтана Тарталья.

В 1535 году Никколо Тарталья получил две задачи в виде кубических уравнений от Дзуанне да Кои (Zuanne da Coi) и объявил, что он их может решить. Он вскоре получил вызов от Фиоре на математическое соревнование, которое после его завершения стало знаменитым. Каждый из них должен был предложить определённое число задач сопернику для решения. Оказалось, что все задачи, полученные Тартальей, сводились к кубическим уравнениям типа {displaystyle x^{3}+mx=n}. Незадолго до истечения срока Тарталье удалось разработать общий метод решения кубических уравнений этого типа (переоткрыв метод дель Ферро), а также обобщить его на два других типа ({displaystyle x^{3}=mx+n} и {displaystyle x^{3}+n=mx}). После этого он быстро решил все предложенные ему задачи. Фиоре же получил от Тартальи задачи из различных разделов математики, многие из которых оказались ему не под силу; в результате Тарталья выиграл соревнование.

Позднее Джероламо Кардано (1501—1576) неоднократно пытался убедить Тарталья раскрыть секрет решения кубических уравнений. В 1539 году ему это удалось: Тарталья сообщил свой метод, но при условии, что Кардано никому его не откроет до выхода книги самого Тартальи о кубических уравнениях, над которой он работал и где собирался опубликовать метод. Спустя шесть лет Тарталья так и не опубликовал свою книгу, а Кардано, узнав к тому времени о работах Ферро, счёл возможным опубликовать метод дель Ферро (с упоминанием имени Тартальи, как независимо его открывшего) в своей книге «Ars Magna» в 1545 году. Кардано оправдывался тем, что обещал не сообщать никому результаты Тартальи, а не дель Ферро. Тем не менее, Тарталья считал, что Кардано нарушил обещание и послал тому вызов на соревнование, который Кардано не принял. Вызов, в конце концов, принял ученик Кардано Лодовико Феррари (1522—1565), и оказался победителем[21].

Кардано заметил, что метод Тарталья иногда (а именно — при наличии трех действительных корней) требует извлечения квадратного корня из отрицательного числа. Он даже включил вычисления с этими комплексными числами в Ars Magna, но, на самом деле, до конца проблему не понял. Рафаэль Бомбелли изучал эту проблему детально, а потому считается первооткрывателем комплексных чисел.

Франсуа Виет (1540—1603) независимо вывел решение кубического уравнения с тремя действительными корнями.
Его решение было основано на тригонометрической формуле

(2{cdot}cos phi)^3-3{cdot}(2{cdot}cos phi)=2{cdot}cos(3{cdot}phi).

В частности, подстановка x=2{cdot}a{cdot}cos phi приводит уравнение

{displaystyle x^{3}-3{cdot }a^{2}{cdot }x=a^{2}cdot b.}

к виду

2{cdot}a{cdot}cos (3{cdot}phi)= b.

Позднее Рене Декарт (1596—1650) углубил работу Виета
[22].

Корни уравнения[править | править код]

Число x, обращающее уравнение в тождество, называется корнем или решением уравнения. Оно является также корнем многочлена третьей степени, стоящего в левой части канонической записи.

Над полем комплексных чисел, согласно основной теореме алгебры, кубическое уравнение

ax^3 + bx^2 + cx + d = 0

всегда имеет 3 корня x_{1},x_{2},x_{3} (с учётом кратности).

Так как каждый вещественный многочлен нечётной степени имеет хотя бы один вещественный корень, все возможные случаи состава корней кубического уравнения исчерпываются тремя, описанными ниже.

Эти случаи различаются с помощью знака дискриминанта:

{displaystyle Delta =a^{4}{cdot }(x_{1}-x_{2})^{2}{cdot }(x_{1}-x_{3})^{2}{cdot }(x_{2}-x_{3})^{2}=}

{displaystyle =-4{cdot }b^{3}cdot d+b^{2}{cdot }c^{2}-4{cdot }a{cdot }c^{3}+18{cdot }a{cdot }b{cdot }c{cdot }d-27{cdot }a^{2}{cdot }d^{2}.}

Возможны три случая:

По теореме Виета корни кубического уравнения x_{1},,x_{2},,x_{3} связаны с коэффициентами a,,b,,c,,d следующими соотношениями[23]:

x_{1}+x_{2}+x_{3}=-{frac {b}{a}},
x_{1}x_{2}+x_{2}x_{3}+x_{1}x_{3}={frac {c}{a}},
x_{1},x_{2},x_{3}=-{frac {d}{a}}.

Делением указанных соотношений друг на друга можно получить ещё несколько соотношений:

{frac {1}{x_{1}}}+{frac {1}{x_{2}}}+{frac {1}{x_{3}}}=-{frac {c}{d}},quad dneq 0,
{displaystyle {frac {1}{x_{1}x_{2}}}+{frac {1}{x_{2}x_{3}}}+{frac {1}{x_{1}x_{3}}}={frac {b}{d}},quad dneq 0,}
{displaystyle {frac {1}{x_{1}x_{2}x_{3}}}=-{frac {a}{d}},quad dneq 0.}

Методы решения[править | править код]

Общие точные методы решения:

  • Формула Кардано
  • Тригонометрическая формула Виета
  • Преобразование Чирнгауза

Для некоторых особых типов кубических уравнений существуют специальные методы решения. См., например:

  • Возвратное уравнение
  • Теорема Безу

Также можно применять численные методы решения уравнений.

Подстановка Виета[править | править код]

Как указывалось выше, любое кубическое уравнение можно привести к виду:

t^{3}+pt+q=0,

Сделаем подстановку, известную как подстановка Виета:

t=w-{frac {p}{3w}}

В результате получим уравнение:

w^{3}+q-{frac {p^{3}}{27w^{3}}}=0.

Умножив на {displaystyle w^{3}}, получим уравнение шестой степени от w, которое, на самом деле, является квадратным уравнением от {displaystyle w^{3}}:

w^{6}+qw^{3}-{frac {p^{3}}{27}}=0

Геометрическое решение Омара Хайяма кубического уравнения для случая {displaystyle a=2,b=16}, дающее корень 2. То, что вертикальная прямая пересекает ось x в центре круга, — специфично для данного конкретного примера.

Решая это уравнение, получим {displaystyle w^{3}}. Если w_{1}, {displaystyle w_{2}} и {displaystyle w_{3}} являются тремя кубическими корнями {displaystyle w^{3}}, то корни исходного уравнения можно получить по формулам

t_{1}=w_{1}-{frac {p}{3w_{1}}},quad t_{2}=w_{2}-{frac {p}{3w_{2}}}quad и quad t_{3}=w_{3}-{frac {p}{3w_{3}}}.

Решение Омара Хайяма[править | править код]

Как показано на графике, для решения уравнения третьей степени x^{3}+a^{2}x=b, где b>0, Омар Хайям построил параболу {displaystyle y={frac {x^{2}}{a}},} окружность, диаметром которой является отрезок {displaystyle left[0,{frac {b}{a^{2}}}right]} положительной полуоси x, и вертикальную прямую, проходящую через пересечение параболы и окружности. Решение определяется длиной горизонтального отрезка от начала координат до пересечения вертикальной прямой с осью x.

Простое современное доказательство построения: умножаем на x уравнение и группируем члены

{frac {x^{4}}{a^{2}}}=x,left({frac {b}{a^{2}}}-xright),.

Левая часть — это значение y^{2} на параболе. Уравнение окружности, y^{2}+x,left(x-{frac {b}{a^{2}}}right)=0, совпадает с правой частью уравнения и даёт значение y^{2} на окружности.

См. также[править | править код]

  • Корень Бринга
  • Кубика

Примечания[править | править код]

  1. ↑ 1 2 John Crossley, Anthony W.-C. Lun. The Nine Chapters on the Mathematical Art: Companion and Commentary. — Oxford University Press, 1999. — С. 176. — ISBN 978-0-19-853936-0.
  2. ↑ 1 2 Van der Waerden. Geometry and Algebra of Ancient Civilizations. — Zurich, 1983. — С. chapter 4. — ISBN 0-387-12159-5.
  3. ↑ Roger Cooke. The History of Mathematics. — John Wiley & Sons, 2012. — P. 63. — ISBN 978-1-118-46029-0.
  4. ↑ Karen Rhea Nemet-Nejat. Daily Life in Ancient Mesopotamia. — Greenwood Publishing Group, 1998. — P. 306. — ISBN 978-0-313-29497-6.
  5. ↑ Roger Cooke. Classical Algebra: Its Nature, Origins, and Uses. — John Wiley & Sons, 2008. — P. 64. — ISBN 978-0-470-27797-3.
  6. ↑ Guilbeau, 1930 утверждает, что «египтяне полагали, что решение невозможно, но греки подошли к решению ближе.»
  7. ↑ 1 2 Guilbeau, 1930
  8. ↑ Thomas L. Heath. Diophantus of Alexandria: A Study in the History of Greek Algebra. — Martino Pub, 2009. — ISBN 978-1578987542.
  9. ↑ Archimedes (translation by T. L. Heath). The works of Archimedes. — Rough Draft Printing, 2007. — ISBN 978-1603860512.
  10. ↑ Yoshio Mikami. The Development of Mathematics in China and Japan. — 2nd ed. — New York: Chelsea Publishing Co., 1974. — С. 53—56. — ISBN 978-0-8284-0149-4.
  11. ↑ История математики, том I, 1970, с. 225.
  12. ↑ Работа Омара Хайама, Scripta Math. 26 (1963), стр. 323—337
  13. ↑ в книге О’Коннора и Робертсона «Omar Khayyam», MacTutor History of Mathematics archive, University of St Andrews, можно прочитать Эта задача привела Хайама к кубическому уравнению x3 + 200x = 20x2 + 2000, и он нашёл положительный корень этого уравнения как пересечение равнобочной гиперболы и окружности. Приближённое численное решение было затем найдено путём интерполяции тригонометрических таблиц.
  14. ↑ J. J. O’Connor и E. F. Robertson (1999), Omar Khayyam Архивная копия от 1 марта 2012 на Wayback Machine, в архиве истории математики MacTutor[en], утверждают, «Хайям, похоже, был первым, кто задумался об общей теории кубических уравнений.»
  15. ↑ Guilbeau, 1930 утверждает, «Омар Аль Хей Хорасан около 1079 года сделал много по пути продвижения методов решения алгебраических уравнений с помощью пересекающихся конических сечений.»
  16. ↑ Datta, Singh. History of Hindu Mathematics. — Delhi, India, 2004. — С. 76,. — ISBN 81-86050-86-8. стр. 76, Equation of Higher Degree; Bharattya Kala Prakashan
  17. ↑ O’Connor, John J.; Robertson, Edmund F., «Sharaf al-Din al-Muzaffar al-Tusi», MacTutor History of Mathematics archive, University of St Andrews.
  18. ↑ J. L. Berggren. Innovation and Tradition in Sharaf al-Din al-Tusi’s Muadalat // Journal of the American Oriental Society. — 1990. — Vol. 110. — Вып. 2. — P. 304—309. — doi:10.2307/604533.
  19. ↑ R. N. Knott and the Plus Team. The life and numbers of Fibonacci // Plus Magazine. — 2013.
  20. ↑ Андронов И. К. Математика действительных и комплексных чисел. — Просвещение, 1975. — С. 91—92. — 158 с.
  21. ↑ Victor Katz. A History of Mathematics. — Boston: Addison Wesley, 2004. — С. 220. — ISBN 9780321016188.
  22. ↑ R. W. D. Nickalls. Viète, Descartes and the cubic equation // Mathematical Gazette. — July 2006. — Т. 90. — P. 203—208.
  23. ↑ Бронштейн И. Н., Семендяев К. А. Справочник по математике. — Изд. 7-е, стереотипное. — М.: Государственное издательство технико-теоретической литературы, 1967. — С. 139.

Литература[править | править код]

  • Бронштейн И. Н., Семендяев К. А. Справочник по математике. — Изд. 7-е, стереотипное. — М.: Государственное издательство технико-теоретической литературы, 1967. — С. 138—139.
  • История математики. С древнейших времен до начала Нового времени // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I. — 352 с.
  • Лекция 4 в Табачников С.Л.. Фукс Д.Б. Математический дивертисмент. — МЦНМО, 2011. — 512 с. — 2000 экз. — ISBN 978-5-94057-731-7.
  • Guilbeau, Lucye (1930), The History of the Solution of the Cubic Equation, Mathematics News Letter Т. 5 (4): 8–12, DOI 10.2307/3027812

Ссылки[править | править код]

  • Подробное онлайн решение кубического уравнения
Источник

Кубическая функция

Кубическая функция — это функция вида y=ax³, где a — число ( a≠0).

График кубической функции называется кубической параболой.

Для начала рассмотрим свойства и график кубической функции y=x³ (при a=1).

Свойства функция y=x³:

1) Область определения — множество действительных чисел:

2) Область значений — все действительные числа:

3) Функция имеет один нуль:

4) Точка O (0;0) делит кубическую параболу на две равные части, каждая из которых называется ветвью кубической параболы. Ветви кубической параболы симметричны относительно точки O — начала координат.

Отсюда следует, что противоположным значениям x соответствуют противоположные значения y: (- x)³= — x³ .

5) Функция возрастает на всей числовой прямой.

6) Промежутки знакопостоянства: функция принимает положительные значения при x∈(0;∞) (или y>0 при x>0);

функция принимает отрицательные значения при x∈(-∞;0) (или y

Эти точки отмечаем на координатной плоскости и строим кубическую параболу:

График функции y=ax³ при a≠1 ( a≠0) получают из графика функции y=x³ при помощи геометрических преобразований.

Функция y=x³ — один из частных случаев степенной функции

где α — любое действительное число.

В курсе алгебры из частных случаев степенной функции мы уже встречались с квадратичной функцией y=x² и функцией обратной пропорциональности

Применение производной для решения нелинейных уравнений и неравенств

п.1. Количество корней кубического уравнения

Кубическое уравнение $$ ax^3+bx^2+cx+d=0 $$ на множестве действительных чисел может иметь один, два или три корня.
С помощью производной можно быстро ответить на вопрос, сколько корней имеет данное уравнение. begin f(x)=ax^3+bx^2+cx+d\ f'(x)=3ax^2+bx+c end Если в уравнении (f'(x)=0) дискриминант (D=4b^2-12ac=4(b^2-3ac)gt 0), кубическая парабола имеет две точки экстремума: (x_<1,2>=frac<-2bpmsqrt><6a>). Если при этом значения функции в точках экстремума (f(x_1)cdot f(x_2)lt 0), т.е. расположены по разные стороны от оси OX, парабола имеет три точки пересечения с этой осью. Исходное уравнение имеет три корня.
Если две точки экстремума найдены, но (f(x_1)cdot f(x_2)=0), уравнение имеет два корня.
Во всех остальных случаях – у исходного уравнения 1 корень.

Пример 1. Сколько корней имеют уравнения:

п.2. Количество корней произвольного уравнения

Задачи на подсчет количества корней решаются с помощью построения графиков при полном или частичном исследовании функций.

Пример 2. а) Найдите число корней уравнения (frac 1x+frac<1>+frac<1>)
б) Найдите число корней уравнения (frac 1x+frac<1>+frac<1>=k)

Построим график функции слева, а затем найдем для него количество точек пересечения с горизонталью (y=1). Это и будет ответом на вопрос задачи (а).
Исследуем функцию: $$ f(x)=frac1x+frac<1>+frac<1> $$ Алгоритм исследования и построения графика – см. §49 данного справочника.
1) ОДЗ: (xneleft<0;1;3right>)
Все три точки – точки разрыва 2-го рода. begin lim_left(frac1x+frac<1>+frac<1>right)=-infty-1-frac13=-infty\ lim_left(frac1x+frac<1>+frac<1>right)=+infty-1-frac13=+infty\ lim_left(frac1x+frac<1>+frac<1>right)=1-infty-frac12=-infty\ lim_left(frac1x+frac<1>+frac<1>right)=1+infty-frac12=+infty\ lim_left(frac1x+frac<1>+frac<1>right)=frac13+frac12-infty=-infty\ lim_left(frac1x+frac<1>+frac<1>right)=frac13+frac12+infty=+infty end 2) Функция ни четная, ни нечетная.
Функция непериодическая.
3) Асимптоты
1. Вертикальные (x=0, x=1, x=3) – точки разрыва 2-го рода
2. Горизонтальные: begin lim_left(frac1x+frac<1>+frac<1>right)=-0-0-0=-0\ lim_left(frac1x+frac<1>+frac<1>right)=+0+0+0=+0\ end Горизонтальная асимптота (y=0)
На минус бесконечности функция стремится к 0 снизу, на плюс бесконечности – сверху.
3. Наклонные: (k=0), нет.
4) Первая производная $$ f'(x)=-frac<1>-frac<1><(x-1)^2>-frac<1><(x-3)^2>lt 0 $$ Производная отрицательная на всей ОДЗ.
Функция убывает.

5) Вторую производную не исследуем, т.к. перегибы не влияют на количество точек пересечения с горизонталью.

6) Точки пересечения с OY – нет, т.к. (x=0) – асимптота
Точки пересечения с OX – две, (0lt x_1lt 1,1lt x_2lt 3)

7) График

Получаем ответ для задачи (а) 3 корня.

Решаем более общую задачу (б). Передвигаем горизонталь (y=k) снизу вверх и считаем количество точек пересечения с графиком функции. Последовательно, получаем:
При (klt 0) – три корня
При (k=0) – два корня
При (kgt 0) – три корня

Ответ: а) 3 корня; б) при (k=0) два корня, при (kne 0) три корня.

Пример 3. Найдите все значения параметра a, при каждом из которых уравнение $$ sqrt+sqrt<10-2x>=a $$ имеет по крайней мере одно решение.

Исследуем функцию (f(x)=sqrt+sqrt<10-2x>)
ОДЗ: ( begin x-1geq 0\ 10-2xgeq 0 end Rightarrow begin xgeq 1\ xleq 5 end Rightarrow 1leq xleq 5 )
Функция определена на конечном интервале.
Поэтому используем сокращенный алгоритм для построения графика.
Значения функции на концах интервала: (f(1)=0+sqrt<8>=2sqrt<2>, f(5)=sqrt<4>+0=2)
Первая производная: begin f'(x)=frac<1><2sqrt>+frac<-2><2sqrt<10-2x>>=frac<1><2sqrt>-frac<1><sqrt<10-2x>>\ f'(x)=0 text<при> 2sqrt=sqrt<10-2x>Rightarrow 4(x-1)=10-2xRightarrow 6x=14Rightarrow x=frac73\ fleft(frac73right)=sqrt<frac73-1>+sqrt<10-2cdot frac73>=sqrt<frac43>+sqrt<frac<16><3>>=frac<6><sqrt<3>>=2sqrt <3>end Промежутки монотонности:

(x) 1 (1; 7/3) 7/3 (7/3; 5) 5
(f'(x)) ∅ + 0 – ∅
(f(x)) (2sqrt<2>) (nearrow ) max
(2sqrt<3>)		 (searrow ) 2

Можем строить график:

(y=a) – горизонтальная прямая.
Количество точек пересечения (f(x)) и (y) равно количеству решений.
Получаем:

$$ alt 2 $$ нет решений
$$ 2leq alt 2sqrt <2>$$ 1 решение
$$ 2sqrt<2>leq alt 2sqrt <3>$$ 2 решения
$$ a=2sqrt <3>$$ 1 решение
$$ agt 2sqrt <3>$$ нет решений

По крайней мере одно решение будет в интервале (2leq aleq 2sqrt<3>).

п.3. Решение неравенств с построением графиков

Пример 4. Решите неравенство (frac<2+log_3 x>gt frac<6><2x-1>)

Разобьем неравенство на совокупность двух систем.
Если (xgt 1), то (x-1gt 0), на него можно умножить слева и справа и не менять знак.
Если (xlt 1), то (x-1lt 0), умножить также можно, только знак нужно поменять.
Сразу учтем требование ОДЗ для логарифма: (xgt 0)

Получаем совокупность: begin left[ begin begin xgt 1\ 2+log_3 xgtfrac<6(x-1)> <2x-1>end \ begin 0lt xlt 1\ 2+log_3 xltfrac<6(x-1)> <2x-1>end end right. \ 2+log_3 xgt frac<6(x-1)><2x-1>Rightarrow log_3 xgt frac<6(x-1)-2(2x-1)><2x-1>Rightarrow log_3 xgt frac<2x-4><2x-1>\ left[ begin begin xgt 1\ log_3 xgtfrac<2x-4> <2x-1>end \ begin 0lt xlt 1\ log_3 xltfrac<2x-4> <2x-1>end end right. end Исследуем функцию (f(x)=frac<2x-4><2x-1>=frac<2x-1-3><2x-1>=1-frac<3><2x-1>)
Точка разрыва: (x=frac12) – вертикальная асимптота
Односторонние пределы: begin lim_left(1-frac<3><2x-1>right)=1-frac<3><-0>=+infty\ lim_left(1-frac<3><2x-1>right)=1-frac<3><+0>=-infty end Второе слагаемое стремится к 0 на бесконечности, и это дает горизонтальную асимптоту: (y=1) begin lim_left(1-frac<3><2x-1>right)=1-frac<3><-infty>=1+0\ lim_left(1-frac<3><2x-1>right)=1-frac<3><+infty>=1-0 end На минус бесконечности кривая стремится к (y=1) сверху, а на плюс бесконечности – снизу.
Первая производная: $$ f'(x)=left(1-frac<3><2x-1>right)’=frac<3><(2x-1)^2>gt 0 $$ Производная положительная на всей ОДЗ, функция возрастает.
Вторая производная: $$ f”(x)=-frac<6> <(2x-1)^3>$$ Одна критическая точка 2-го порядка (x=frac12)

Построить график функции кубического уравнения

Мы уже говорили, что уже арабские математики средневековья владели всей теорией решения квадратных уравнений. Другое дело – уравнения кубические. Если решение квадратных уравнений может быть найдено с помощью определенных построений циркулем и линейкой (эти построения, так называемые «приложения площадей», были известны уже древним грекам), то корень кубического уравнения, вообще говоря, невозможно построить циркулем и линейкой. Поэтому для их решений были нужны другие методы. Во-первых, существовали приближенные методы вычисления корней, с помощью которых можно было найти корень с любой заданной точностью. А во-вторых, для анализа разрешимости уравнения, числа его корней и примерной их оценки применялись графические методы.

Под графическим решением уравнения мы сейчас обычно понимаем (в простейшем случае) построение графиков функций и и нахождение абсцисс точек их пересечения. В более общем случае уравнение может быть сведено к системе каких-либо двух уравнений с двумя неизвестными – не обязательно эти уравнения должны иметь форму и . Каждое из уравнений трактуется как уравнение некоторой кривой на координатной плоскости; координаты точек их пересечения этих кривых удовлетворяют обоим уравнениям, и, следовательно, являются решением системы, по ним можно получить и корень исходного уравнения. Разумеется, с помощью графического решения, как правило, невозможно найти значение корней уравнения точно. Тем не менее, оно часто бывает полезным для того, чтобы приблизительно определить их значение или получить общее представление о числе положительных и отрицательных корней и т. п.

Хотя у древних греков не было идеи графиков функций в современном смысле, они владели определенной техникой, которую мы бы, в переводе на современный язык, сочли именно графическим решением уравнений. Задача, которую было необходимо решить, формулировалась в виде некоторого соотношения (уравнения), которое затем переводилось в форму двух соотношений между двумя неизвестными величинами (система двух уравнений с двумя неизвестными). Эти две величины трактовались как расстояния от точки до двух перпендикулярных прямых (фактически, осей координат): строились две кривые, соответствующие двум данным соотношениям между этими расстояниями (координатами), и находились точки пересечения этих кривых.

С помощью этой техники греки, а затем и арабы, находили, в частности, решения кубических уравнений. Уже говорилось, что с помощью точек пересечения гиперболы и параболы или двух парабол Менехм строил решение знаменитой задачи об удвоении куба, то есть решал уравнение вида 3 = . Греки сталкивались и с другими типами кубических уравнений. Так, Архимед рассматривал задачу о делении шара плоскостью на два сегмента, объемы которых находятся в данном отношении (1 : 2 = ). Эта задача сводится к решению кубического уравнения вида 3 + = 2 . Дело в том, что объем шарового сегмента (как это открыл тот же Архимед) является кубической функцией его высоты (да еще без линейного члена):

Это довольно приятное обстоятельство: скажем, площадь кругового сектора зависит от его высоты существенно более сложным образом.

Архимед построил корень полученного кубического уравнения как координату точки пересечения параболы и гиперболы и произвел тщательный анализ задачи.

Выведите уравнение, соответствующее задаче Архимеда (приняв за высоту одного из сегментов).

Если радиус шара , а высота одного из сегментов , то высота другого – . Объем первого сегмента ,

а объем второго (в сумме, нетрудно видеть, они составляют – известная формула объема шара, доказанная также Архимедом).

Т. к. отношение объемов равно ,

4 3 – 3 2 + 3 = (3 2 – 3 ) ,

3 ( + 1) + 4 3 = 3 ( + 1) 2 ,

3 + 4 3 / ( + 1) = 3 2 .

Другой вариант – положить обратное отношение равным . Тогда:

[spoiler title=”источники:”]

http://reshator.com/sprav/algebra/10-11-klass/primenenie-proizvodnoj-dlya-resheniya-nelinejnyh-uravnenij-i-neravenstv/

http://files.school-collection.edu.ru/dlrstore/747e2c5b-94cd-2790-c830-53d7b87da0a0/00145619916288759.htm

[/spoiler]

Источник

Как решать графические уравнения кубическая парабола

Мы уже говорили, что уже арабские математики средневековья владели всей теорией решения квадратных уравнений. Другое дело – уравнения кубические. Если решение квадратных уравнений может быть найдено с помощью определенных построений циркулем и линейкой (эти построения, так называемые «приложения площадей», были известны уже древним грекам), то корень кубического уравнения, вообще говоря, невозможно построить циркулем и линейкой. Поэтому для их решений были нужны другие методы. Во-первых, существовали приближенные методы вычисления корней, с помощью которых можно было найти корень с любой заданной точностью. А во-вторых, для анализа разрешимости уравнения, числа его корней и примерной их оценки применялись графические методы.

Под графическим решением уравнения мы сейчас обычно понимаем (в простейшем случае) построение графиков функций и и нахождение абсцисс точек их пересечения. В более общем случае уравнение может быть сведено к системе каких-либо двух уравнений с двумя неизвестными – не обязательно эти уравнения должны иметь форму и . Каждое из уравнений трактуется как уравнение некоторой кривой на координатной плоскости; координаты точек их пересечения этих кривых удовлетворяют обоим уравнениям, и, следовательно, являются решением системы, по ним можно получить и корень исходного уравнения. Разумеется, с помощью графического решения, как правило, невозможно найти значение корней уравнения точно. Тем не менее, оно часто бывает полезным для того, чтобы приблизительно определить их значение или получить общее представление о числе положительных и отрицательных корней и т. п.

Хотя у древних греков не было идеи графиков функций в современном смысле, они владели определенной техникой, которую мы бы, в переводе на современный язык, сочли именно графическим решением уравнений. Задача, которую было необходимо решить, формулировалась в виде некоторого соотношения (уравнения), которое затем переводилось в форму двух соотношений между двумя неизвестными величинами (система двух уравнений с двумя неизвестными). Эти две величины трактовались как расстояния от точки до двух перпендикулярных прямых (фактически, осей координат): строились две кривые, соответствующие двум данным соотношениям между этими расстояниями (координатами), и находились точки пересечения этих кривых.

С помощью этой техники греки, а затем и арабы, находили, в частности, решения кубических уравнений. Уже говорилось, что с помощью точек пересечения гиперболы и параболы или двух парабол Менехм строил решение знаменитой задачи об удвоении куба, то есть решал уравнение вида 3 = . Греки сталкивались и с другими типами кубических уравнений. Так, Архимед рассматривал задачу о делении шара плоскостью на два сегмента, объемы которых находятся в данном отношении (1 : 2 = ). Эта задача сводится к решению кубического уравнения вида 3 + = 2 . Дело в том, что объем шарового сегмента (как это открыл тот же Архимед) является кубической функцией его высоты (да еще без линейного члена):

Это довольно приятное обстоятельство: скажем, площадь кругового сектора зависит от его высоты существенно более сложным образом.

Архимед построил корень полученного кубического уравнения как координату точки пересечения параболы и гиперболы и произвел тщательный анализ задачи.

Выведите уравнение, соответствующее задаче Архимеда (приняв за высоту одного из сегментов).

Если радиус шара , а высота одного из сегментов , то высота другого – . Объем первого сегмента ,

а объем второго (в сумме, нетрудно видеть, они составляют – известная формула объема шара, доказанная также Архимедом).

Т. к. отношение объемов равно ,

4 3 – 3 2 + 3 = (3 2 – 3 ) ,

3 ( + 1) + 4 3 = 3 ( + 1) 2 ,

3 + 4 3 / ( + 1) = 3 2 .

Другой вариант – положить обратное отношение равным . Тогда:

Кубическая парабола

Вы будете перенаправлены на Автор24

Кубическая парабола – это парабола, задаваемая уравнением вида $y=ax^3$, где $a ≠ 0$. Также в литературе можно встретить и другие формулы для кубической параболы, все они эквивалентны.

Рисунок 1. График кубической параболы

Свойства функции кубической параболы

  1. График кубической параболы определён на всём пространстве действительных чисел.
  2. Функция, задаваемая графиком кубической параболы, является нечётной, то есть: $f(-x) =(-x)^3= — x^3 = f(x)$.
  3. Из этого следует, что обратная функция кубической параболы, заданная уравнением $y = -x^3$ будет располагаться II и IV четвертях графика, тогда как для $y = x^3$ график располагается в I и III четвертях.
  4. График кубической параболы центрально-симметричен относительно начала координат или точки перегиба, если он сдвинут относительно начала координат. То есть форма кривой справа до точки перегиба полностью идентична форме кривой слева. График кубической параболы хотя бы 1 раз пересекает ось абсцисс.
  5. График кубической параболы возрастает на всей области определения.

Анализ графика функции кубической параболы

  1. Найдя производную $f'(x)$ кубической функции первого порядка и приравняв полученное выражение к нулю, вы получите критические точки для кубической параболы, называемые также локальными минимумами и максимумами.
  2. Вторая производная $f»(x)$ параболы определяет точку перегиба функции.
  3. Области значения и определения кубической параболы — все действительные числа.

Найдите точку перегиба для кубической параболы, заданной уравнением $y = 2x^3 + 6x^2 – x +2$.

  1. Сначала найдём первую производную функции, она равна: $y’ = 6x^2 + 12x – 1$.
  2. Теперь найдём вторую производную, $y» = 12x + 12$. Чтобы найти значение по оси абсцисс точки перегиба, приравняем вторую производную к нулю и решим уравнение: $12x + 12 = 0$, $x = -1$.
  3. Найдём значение по оси ординат, для этого в исходную функцию подставим значение найденного $x$: $y = -2 + 6 + 1 +2 = 7$. Точка перегиба кубической параболы, заданной уравнением $y = 2x^3 + 6x^2 – x +2$ находится по координатам $(-1; 7)$.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 09 12 2021

Кубическая функция

Кубическая функция — это функция вида y=ax³, где a — число ( a≠0).

График кубической функции называется кубической параболой.

Для начала рассмотрим свойства и график кубической функции y=x³ (при a=1).

Свойства функция y=x³:

1) Область определения — множество действительных чисел:

2) Область значений — все действительные числа:

3) Функция имеет один нуль:

4) Точка O (0;0) делит кубическую параболу на две равные части, каждая из которых называется ветвью кубической параболы. Ветви кубической параболы симметричны относительно точки O — начала координат.

Отсюда следует, что противоположным значениям x соответствуют противоположные значения y: (- x)³= — x³ .

5) Функция возрастает на всей числовой прямой.

6) Промежутки знакопостоянства: функция принимает положительные значения при x∈(0;∞) (или y>0 при x>0);

функция принимает отрицательные значения при x∈(-∞;0) (или y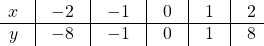

Эти точки отмечаем на координатной плоскости и строим кубическую параболу:

График функции y=ax³ при a≠1 ( a≠0) получают из графика функции y=x³ при помощи геометрических преобразований.

Функция y=x³ — один из частных случаев степенной функции

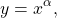
где α — любое действительное число.

В курсе алгебры из частных случаев степенной функции мы уже встречались с квадратичной функцией y=x² и функцией обратной пропорциональности

источники:

http://spravochnick.ru/matematika/parabola/kubicheskaya_parabola/

http://www.algebraclass.ru/kubicheskaya-funkciya/

Источник

Содержание

Кубическое уравнение

Куби́ческое уравне́ние — алгебраическое уравнение третьей степени, общий вид которого следующий:

$$ax^{3}+bx^{2}+cx+d=0,; aneq 0.$$

Кубическое уравнение разрешимо в радикалах.

Для графического анализа кубического уравнения в декартовой системе координат используется кубическая парабола.

Кубические уравнения были известны ещё в древнем Вавилоне, древним грекам, китайцам, индийцам и египтянам[1][2][3]. Были найдены клинописные таблички Старовавилонского периода (20—16 век до нашей эры), содержащие таблицы вычисления кубов и кубических корней[4][5]. Вавилоняне могли использовать эти таблицы для решения кубических уравнений, но не существует никаких свидетельств, что они это делали[6].

Над полем комплексных чисел, согласно основной теореме алгебры, кубическое уравнение
всегда имеет 3 корня $x_{1},x_{2},x_{3}$ (с учётом кратности).

Так как каждый вещественный многочлен нечётной степени имеет хотя бы один вещественный корень, все возможные случаи состава корней кубического уравнения исчерпываются тремя, описанными ниже. Эти случаи легко различаются с помощью дискриминанта

$$ Delta =a^{4}{cdot }(x_{1}-x_{2})^{2}{cdot }(x_{1}-x_{3})^{2}{cdot }(x_{2}-x_{3})^{2}=-4{cdot }b^{3}cdot d+b^{2}{cdot }c^{2}-4{cdot }a{cdot }c^{3}+18{cdot }a{cdot }b{cdot }c{cdot }d-27{cdot }a^{2}{cdot }d^{2}.$$

Итак, возможны только три случая:

  • Если Δ > 0, тогда уравнение имеет три различных вещественных корня.

  • Если Δ < 0, то уравнение имеет один вещественный и пару комплексно сопряжённых корней.

  • Если Δ = 0, тогда хотя бы два корня совпадают. Это может быть, когда уравнение имеет двойной вещественный корень и ещё один отличный от них вещественный корень; либо все три корня совпадают, образуя корень кратности 3. Разделить эти два случая помогает результант кубического уравнения и его второй производной: у многочлена есть корень кратности 3 тогда и только тогда, когда указанный результант также равен нулю.

Результант — Википедия

Discriminant – Wikipedia

Теорема Виета

По теореме Виета корни кубического уравнения $ x_{1},,x_{2},,x_{3}$ связаны с коэффициентами $a,,b,,c,,d$ следующими соотношениями[22]:

$$ x_{1}+x_{2}+x_{3}=-{frac {b}{a}},$$

$$x_{1}x_{2}+x_{2}x_{3}+x_{1}x_{3}={frac {c}{a}},$$

$$x_{1},x_{2},x_{3}=-{frac {d}{a}}.$$

Кубическая парабола

desmos – Это функция $f(x) = (x^3 + 3x^2 – 6x – 8)/4$

График кубической функции с 3-мя действительными корнями (корни там где кривая пересекает горизонтальную ось при y = 0). В данном случае есть две критические точки.

Если все коэффициенты a, b, c и d кубического уравнения вещественные числа, то оно имеет по крайней мере один вещественный корень (это верно для всех полиномиальных функций нечетной степени).

Методы решения

Общие точные методы решения:

  • Формула Кардано (см ниже)

  • Тригонометрическая формула Виета (используется тригонометрическое тождество $ cos 3varphi =4cos ^{3}varphi -3cos varphi $)

  • Преобразование Чирнгауза

Для некоторых особых типов кубических уравнений существуют специальные методы решения. См., например:

  • Возвратное уравнение

  • Теорема Безу

Также можно применять численные методы решения уравнений.

Канонический вид

Кубическое уравнение общего вида может быть приведено к каноническому виду путём деления на a и замены переменной $x=y-{tfrac {b}{3a}},$ приводящей уравнение к виду:

$$ y^{3}+py+q=0,$$

где

$$q={frac {2b^{3}}{27a^{3}}}-{frac {bc}{3a^{2}}}+{frac {d}{a}}={frac {2b^{3}-9abc+27a^{2}d}{27a^{3}}},$$

$$ p={frac {c}{a}}-{frac {b^{2}}{3a^{2}}}={frac {3ac-b^{2}}{3a^{2}}}.$$

Формула Кардано

Формула Кардано — Википедия

формула для нахождения корней канонической формы кубического уравнения над полем комплексных чисел. Названа в честь итальянского математика Джероламо Кардано, опубликовавшего её в 1545 году[1].

Определим величину:

$$ Q=left({frac {p}{3}}right)^{3}+left({frac {q}{2}}right)^{2}.$$

Если все коэффициенты кубического уравнения вещественны, то и Q вещественно, и по его знаку можно определить тип корней:

Q > 0 — один вещественный корень и два сопряжённых комплексных корня.

Q = 0 — один однократный вещественный корень и один двукратный, или, если p = q = 0, то один трёхкратный вещественный корень.

Q < 0 — три вещественных корня. Это так называемый «неприводимый» случай, и именно при анализе этой ситуации впервые исторически возникло понятие комплексного числа, потому что вещественный результат получается по формуле с помощью комплексных чисел.

По формуле Кардано, корни кубического уравнения в канонической форме равны:

$ y_{1}=alpha +beta ,$

$y_{2,3}=-{frac {alpha +beta }{2}}pm i{frac {alpha -beta }{2}}{sqrt {3}},$

где

$ alpha ={sqrt[{3}]{-{frac {q}{2}}+{sqrt {Q}}}},$

$ beta ={sqrt[{3}]{-{frac {q}{2}}-{sqrt {Q}}}},$

Дискриминант многочлена $y^{3}+py+q$ при этом равен $Delta =-108Q$.

Применяя данные формулы, для каждого из трёх значений $alpha$ необходимо брать такое $beta $, для которого выполняется условие $ alpha beta =-p/3$ (такое значение $ beta $ всегда существует).

Если кубическое уравнение вещественное, то рекомендуется по возможности выбирать вещественные значения $ alpha ,beta $.

Источник

Кубическая парабола

Автор статьи

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Определение 1

Кубическая парабола – это парабола, задаваемая уравнением вида $y=ax^3$, где $a ≠ 0$. Также в литературе можно встретить и другие формулы для кубической параболы, все они эквивалентны.

График кубической параболы

Рисунок 1. График кубической параболы

Свойства функции кубической параболы

  1. График кубической параболы определён на всём пространстве действительных чисел.
  2. Функция, задаваемая графиком кубической параболы, является нечётной, то есть:
    $f(-x) =(-x)^3= – x^3 = f(x)$.
  3. Из этого следует, что обратная функция кубической параболы, заданная уравнением $y = -x^3$ будет располагаться II и IV четвертях графика, тогда как для $y = x^3$ график располагается в I и III четвертях.
  4. График кубической параболы центрально-симметричен относительно начала координат или точки перегиба, если он сдвинут относительно начала координат. То есть форма кривой справа до точки перегиба полностью идентична форме кривой слева. График кубической параболы хотя бы 1 раз пересекает ось абсцисс.
  5. График кубической параболы возрастает на всей области определения.

Логотип baranka

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Анализ графика функции кубической параболы

  1. Найдя производную $f'(x)$ кубической функции первого порядка и приравняв полученное выражение к нулю, вы получите критические точки для кубической параболы, называемые также локальными минимумами и максимумами.
  2. Вторая производная $f”(x)$ параболы определяет точку перегиба функции.
  3. Области значения и определения кубической параболы – все действительные числа.

Пример 1

Найдите точку перегиба для кубической параболы, заданной уравнением $y = 2x^3 + 6x^2 – x +2$.

  1. Сначала найдём первую производную функции, она равна: $y’ = 6x^2 + 12x – 1$.
  2. Теперь найдём вторую производную, $y” = 12x + 12$. Чтобы найти значение по оси абсцисс точки перегиба, приравняем вторую производную к нулю и решим уравнение: $12x + 12 = 0$, $x = -1$.
  3. Найдём значение по оси ординат, для этого в исходную функцию подставим значение найденного $x$: $y = -2 + 6 + 1 +2 = 7$. Точка перегиба кубической параболы, заданной уравнением $y = 2x^3 + 6x^2 – x +2$ находится по координатам $(-1; 7)$.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 09.12.2022

Источник

Добавить комментарий