В этой статье вы узнаете как решить квадратное уравнение в Excel на конкретном примере. Подробно разберем решение несложно задачи с картинками.
Ход решения
Запустим программу Microsoft Office Excel. Я пользуюсь 2007 версией. Для начала объединим ячейки A1:A5 и запишем в них формулу квадратного уравнения в виде ax2+bx+c=0.Далее нам нужно возвести x в квадрат, для этого нужно сделать цифру 2 надстрочным интервалом. Выделим двойку и нажмем правой кнопкой мыши.
Получим формулу вида ax2 +bx+c=0
В ячейке A2 введем текстовое значение a= , в ячейке A3 b= и в ячейке A4 с= соответственно. Эти значения будут вводиться с клавиатуры в следующих ячейках (B2,B3,B4).
Введем текст для значений, которые будут считаться. В ячейке C2 d=, C3 x1= C4 x2=. Подстрочный интервал для xсделаем аналогично надстрочному интервалу в x2
Перейдем к вводу формул для решения
Дискриминант квадратного трехчлена равен b2-4ac
В ячейку D2 введем соответствующую формулу для возведения числа во вторую степень:
=B3^2-4*B2*B4
Квадратное уравнение имеет два корня, в случае если дискриминант больше нуля. В ячейку C3 введем формулу для x1
=ЕСЛИ(D2>0;(-B3+КОРЕНЬ(D2))/(2*B2);»Корней нет»)
Для расчета x2 введем похожую формулу, но со знаком плюс
=ЕСЛИ(D2>0;(-B3-КОРЕНЬ(D2))/(2*B2);»Корней нет»)
Соответственно при введенных значениях a,b,c сначала считается дискриминант, если его значения меньше нуля выводится сообщение «Корней нет», иначе получаем значения x1 и x2.
Защита листа в Excel
Нам нужно защитить лист, на котором мы производили расчеты. Без защиты нужно оставить ячейки, в которые можно вводить значения a,b,c, то есть ячейки B2 B3 B4. Для этого выделим данный диапазон и зайдем в формат ячеек, перейдем во вкладку Рецензирования, Защитить лист и уберем флажок с позиции Защищаемая ячейка. Нажмем кнопку OK, подтвердив внесенные изменения.
Этот диапазон ячеек будет не защищен при защите листа. Выполним защиту листа, для этого перейдем на вкладку Рецензирование пункт Защита листа. Пароль наберем 1234. Нажмем OK.
Теперь мы сможем изменять значения ячеек B2,B3,B4. При попытке изменения других ячеек мы получим сообщение следующего содержания: «Ячейка или диаграмма защищена от изменений. А так же совет по снятию защиты.
Так же вас может заинтересовать материал как закрепить область в Экселе.
A quadratic equation takes the following form:
ax2 + bx + c = y
Often you will be given the value for y and will be asked to solve for the value of x.
For example, suppose we have the following quadratic equation:
4x2 – 20x + 16 = -8
It turns out that setting x = 3 or x = 2 will solve this equation.
To solve quadratic equations in Excel, you can use the Goal Seek function.
The following step-by-step example shows how to use the Goal Seek function in practice.
Step 1: Enter the Equation
First, let’s enter some random value for x and the formula for the quadratic equation for y:
Step 2: Find the First X Value Using Goal Seek
Next, click the Data tab along the top ribbon, then click the What-If Analysis button, then Goal Seek:
In the new window that appears, specify that you’d like to set cell B2 equal to -8 by changing the value in cell A2:
Once we click OK, the Goal Seek function will automatically find the value for x that solves the equation:
Goal Seek finds that the value x=2 (assuming 1.9999 rounds to 2) solves the quadratic equation.
Step 3: Find the Second X Value Using Goal Seek
To find the second x value that solves the quadratic equation, set the initial x-value to a different number.
For example, we could choose to set the initial x-value to 4:
We can then run the Goal Seek function again and see that it finds a new solution of x=3:
Thus, the two x-values that can solve this quadratic equation are x=2 and x=3.
Additional Resources
The following tutorials explain how to perform other common tasks in Excel:
How to Solve a System of Equations in Excel
How to Plot an Equation in Excel
Для решения квадратного уравнения необходимо знать формулу и алгоритм нахождения квадратов уравнения
Шаг 1. Организация таблицы
На первом этапе мы организуем таблицу для ввода данных коэффициентов a,b и c.
- a называют первым или старшим коэффициентом,
- b называют вторым или коэффициентом при x,
- c называют свободным членом.
Шаг 2. Проверка равенства Дискриминанта.
Для того, чтобы вычислить корни уравнения второй степени, необходимо определить значение Дискриминанта.
Формула дискриминанта
D = b2 — 4ac
Вычисление корней уравнения второй степени происходит по формулам при условии величины Дискриминанта
| Условие | D > 0 | D = 0 | D < 0 |
| Число действительных корней | корней два | корень один | Нет решения |
| Формула | X1,2=(- b ±√ (b2 — 4 * a * c)) / (2 * a) | X1=X2=-b/(2*a) |
Шаг 3. Вычисляем корни уравнения.
После определения значения Дискриминанта используем выше приведенные формулы для нахождения корней.
Находим первый корень
Находим второй корень. Формула будет отличаться только в одном знаке.
Итог: с помощью Excel можем создать единожды таблицу и формулы для решения квадратного уравнения (уравнения второй степени) и быстро их решать.
людей нашли эту статью полезной. А Вы?
Приветствуем всех читателей и подписчиков канала! 👋
Сегодня в уроке рассмотрим как создать пользовательскую функцию, которая решает квадратные уравнения вида ax^2 + bx + c = 0 и возвращает решение в виде одного значения (если решение уравнения одно) или массива из двух значений (если решений уравнения два).
📢 Скачать исходник с примером вы можете в конце статьи 🔽
🔔 Представляем код, который является пользовательской функцией в Excel для решения квадратных уравнений вида ax^2 + bx + c = 0.
⏩ Алгоритм решения уравнения
– Если дискриминант равен нулю, то уравнение имеет один корень, который функция возвращает.
– Если дискриминант больше нуля, то уравнение имеет два корня, которые функция возвращает в виде массива.
⏩ Описание кода
- Первая строка объявляет функцию с названием QuadraticSolver и тремя аргументами (a, b, с), которые должны быть типа Double (вещественные числа).
- Объявляются 3 переменные типа Double: discriminant, х1 и х2.
- Выражение discriminant = b * b – 4 * a * c – вычисляет дискриминант квадратного уравнения (далее – D).
- Блок условий:
- Если D < 0, то решение не имеет действительных корней. В этом случае будет возвращена строка “Нет корней”: QuadraticSolver = “Нет корней”.
- Если D = 0, то решение имеет 1 действительный корень.
Мы вычисляем этот корень по формуле: x1 = -b / (2 * a) и возвращаем его в качестве результата функции: QuadraticSolver = x1
В последнем блоке, если D> 0, то решение имеет 2 действительных корня, вычисляемые по формулам:
- для 1-го: х1 = (-b + Sqr(discriminant)) / (2 * a)
- для 2-го: х2 = (-b – Sqr(discriminant)) / (2 * a)
Затем функция возвращает массив, содержащий 2 (два) решения, используя функцию Array(х1, х2): QuadraticSolver = Array(x1, x2)
5. Код функции заканчивается словом “End Function” указывающим на ее завершение.
🔲 Подводя итог:
Рассмотренная функция принимает 3 аргумента (a, b и c), являющиеся коэффициентами квадратного уравнения, возвращая 1 или 2 корня в зависимости от значения дискриминанта.
➡️ СКАЧАТЬ ПРИМЕР ФАЙЛА
В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.
Рассмотрим на примерах некоторые варианты решений.
Решение уравнений методом подбора параметров Excel
Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» – «Работа с данными» – «Анализ «что-если»» – «Подбор параметра».
Рассмотрим на примере решение квадратного уравнения х2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
- Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
- Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» – ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» – В1. Здесь должен отобразиться отобранный параметр.
- После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».
Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».
Как решить систему уравнений матричным методом в Excel
Дана система уравнений:
- Значения элементов введем в ячейки Excel в виде таблицы.
- Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
- Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
- Умножим обратную матрицу Ах-1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
- Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.
Получены корни уравнений.
Решение системы уравнений методом Крамера в Excel
Возьмем систему уравнений из предыдущего примера:
Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.
Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.
Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).
Определитель системы больше 0 – решение можно найти по формуле Крамера (Dx / |A|).
Для расчета Х1: =U2/$U$1, где U2 – D1. Для расчета Х2: =U3/$U$1. И т.д. Получим корни уравнений:
Решение систем уравнений методом Гаусса в Excel
Для примера возьмем простейшую систему уравнений:
3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9
Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.
Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.
- Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
- Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
- Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
- Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: {=B12:E12/D12}.
- В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки ({=(B11:E11-B16:E16*D11)/C11}). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты ({=(B10:E10-B15:E15*C10-B16:E16*D10)/B10}). В последнем столбце новой матрицы получаем корни уравнения.
Примеры решения уравнений методом итераций в Excel
Вычисления в книге должны быть настроены следующим образом:
Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:
Хn+1 = Xn– F (Xn) / M, n = 0, 1, 2, … .
M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:
f’ (1) = -2 * f’ (2) = -11.
Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х3 – 1. М = 11.
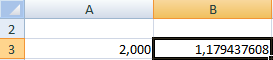
В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.
Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:
Скачать решения уравнений в Excel
Корень на заданном промежутке один.