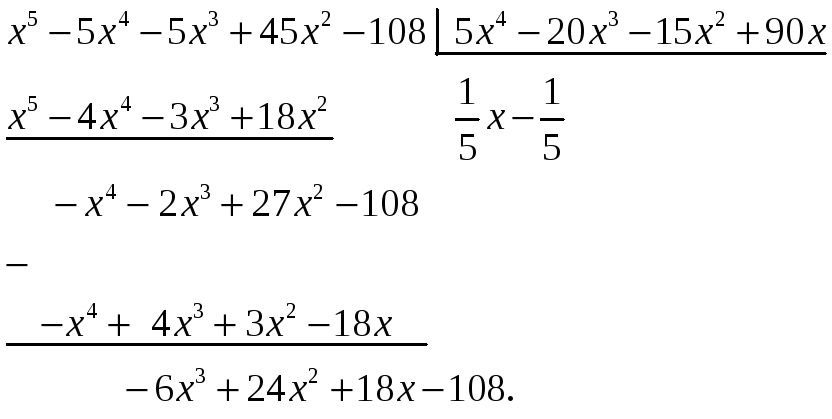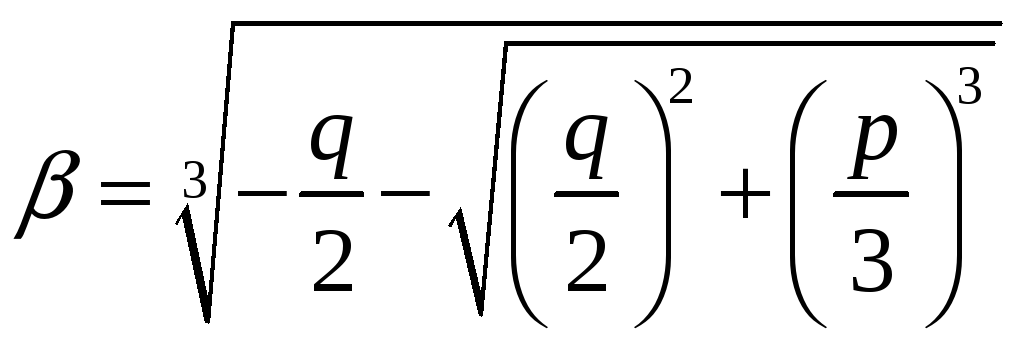Как найти корни любого многочлена

Корень многочлена (не равного тождественно нулю)

над полем  — это элемент (либо элемент расширения поля ) такой, что выполняются два следующих равносильных условия:

в тождество, то есть значение многочлена становится равным нулю.

Равносильность двух формулировок следует из теоремы Безу. В различных источниках любая одна из двух формулировок выбирается в качестве определения, а другая выводится в качестве теоремы.

Говорят, что корень имеет кратность , если рассматриваемый многочлен делится на и не делится на Например, многочлен имеет единственный корень, равный кратности . Выражение «кратный корень» означает, что кратность корня больше единицы.

Говорят, что многочлен имеет корней без учёта кратности, если каждый его корень учитывается при подсчёте один раз. Если же каждый корень учитывается количество раз, равное его кратности, то говорят, что подсчёт ведётся с учётом кратности.

Свойства[править | править код]

где  — (в общем случае комплексные) корни многочлена , возможно с повторениями, при этом если среди корней многочлена встречаются равные, то их общее значение называется кратным корнем, а количество — кратностью этого корня.

Нахождение корней[править | править код]

Способ нахождения корней линейных и квадратичных многочленов в общем виде, то есть способ решения линейных и квадратных уравнений, был известен ещё в древнем мире. Поиски формулы для точного решения общего уравнения третьей степени продолжались долгое время, пока не увенчались успехом в первой половине XVI века в трудах Сципиона дель Ферро, Никколо Тарталья и Джероламо Кардано. Формулы для корней квадратных и кубических уравнений позволили сравнительно легко получить формулы для корней уравнения четвертой степени.

То, что корни общего уравнения пятой степени и выше не выражаются при помощи рациональных функций и радикалов от коэффициентов (то есть то, что сами уравнения не являются разрешимыми в радикалах), было доказано норвежским математиком Нильсом Абелем в 1826 году^[1]. Это совсем не означает, что корни такого уравнения не могут быть найдены. Во-первых, при некоторых особых комбинациях коэффициентов корни уравнения всё же могут быть определены (см., например, возвратное уравнение). Во-вторых, существуют формулы для корней уравнений 5-й степени и выше, использующие специальные функции — эллиптические или гипергеометрические (см., например, корень Бринга).

В случае, если все коэффициенты многочлена рациональны, то нахождение его корней приводится к нахождению корней многочлена с целыми коэффициентами. Для рациональных корней таких многочленов существуют алгоритмы нахождения перебором кандидатов с использованием схемы Горнера, причем при нахождении целых корней перебор может быть существенно уменьшен приемом чистки корней. Также в этом случае можно использовать полиномиальный LLL -алгоритм.

Для приблизительного нахождения (с любой требуемой точностью) вещественных корней многочлена с вещественными коэффициентами используются итерационные методы, например, метод секущих, метод бисекции, метод Ньютона, Метод Лобачевского — Греффе. Количество вещественных корней многочлена на интервале может быть определено при помощи теоремы Штурма.

См. также[править | править код]

• Схема Горнера
• Метод Лиля — графический метод нахождения вещественных корней многочленов произвольной степени.
• Нуль функции

Примечания[править | править код]

Литература[править | править код]

• Винберг Э. Б. Алгебра многочленов. — М.: Просвещение, 1980. — 176 с.
• Прасолов В. В. Многочлены. — М.: МЦНМО, 2003. — 336 с. — ISBN 5-94057-077-1.

Разложение  многочлена на множители.  Теорема Безу и схема Горнера

При решении уравнений и неравенств нередко возникает необходимость разложить на множители многочлен, степень которого равна трем или выше. В этой статье мы рассмотрим,  каким образом это сделать проще всего.

Как обычно, обратимся за помощью к теории.

Теорема Безу утверждает, что остаток от деления многочлена    на  двучлен равен .

Но для нас важна не сама теорема, а следствие из нее:

Если число является корнем многочлена , то многочлен   делится без остатка на двучлен .

Перед нами стоит задача каким-то способом найти хотя бы один корень многочлена, потом разделить многочлен на , где – корень многочлена. В результате мы  получаем многочлен,    степень которого на единицу меньше, чем степень исходного. А потом при необходимости можно повторить процесс.

Эта задача распадается на две: как найти корень многочлена , и как разделить многочлен на двучлен.

Остановимся подробнее на этих моментах.

1. Как найти корень многочлена.

Сначала проверяем, являются ли числа 1 и -1 корнями многочлена.

Здесь нам помогут такие факты:

Если сумма всех коэффициентов многочлена равна нулю, то число является корнем многочлена.

Например, в многочлене сумма коэффициентов равна нулю: . Легко проверить, что является корнем многочлена.

Если сумма коэффициентов многочлена  при четных степенях равна сумме коэффициентов при нечетных степенях, то число является корнем многочлена. Свободный член считается коэффициентом при четной степени, поскольку , а – четное число.

Например, в многочлене  сумма коэффициентов при четных степенях :  , и сумма коэффициентов при нечетных степенях :   . Легко проверить, что является корнем многочлена.

Если ни 1, ни -1 не являются корнями многочлена, то двигаемся дальше.

Для приведенного многочлена степени (то есть многочлена, в котором старший коэффициент – коэффициент при – равен единице) справедлива формула Виета:

, где – корни многочлена .

Если многочлен не является приведенным, то его можно сделать таковым, разделив на старший коэффициент.

Есть ещё формул Виета, касающихся остальных коэффициентов многочлена, но нас интересует именно эта.

Из этой формулы Виета следует, что если корни приведенного многочлена целочисленные, то они являются делителями его свободного члена, который также является целым числом.

Исходя из этого, нам надо разложить свободный член многочлена на множители, и последовательно, от меньшего к большему, проверять, какой из множителей является корнем многочлена.

Рассмотрим, например, многочлен .

Для этого многочлена произведение корней равно

Делители числа : ; ;

Сумма всех коэффициентов многочлена равна , следовательно, число 1 не является корнем многочлена.

Сумма коэффициентов при четных степенях :  

Сумма коэффициентов при нечетных степенях :

, следовательно, число -1 также не является корнем многочлена.

Проверим, является ли число 2 корнем  многочлена: , следовательно, число 2  является корнем многочлена. Значит, по теореме Безу, многочлен делится без остатка на двучлен .

2. Как разделить многочлен на двучлен.

Многочлен можно разделить на двучлен столбиком.

Разделим многочлен  на двучлен столбиком:

Есть и другой способ деления многочлена на двучлен – схема Горнера.

Посмотрите это видео, чтобы понять, как делить многочлен на двучлен столбиком, и с помощью схемы Горнера.

Замечу, что если при делении столбиком какая-то степень неизвестного в исходном многочлене отсутствует, на её месте пишем 0 – так же, как при составлении таблицы для схемы Горнера.

Итак, если нам нужно разделить многочлен на двучлен и в результате деления мы получаем многочлен , то коэффициенты многочлена   мы можем найти по схеме Горнера:

Мы также можем использовать схему Горнера для того, чтобы проверить, является ли данное число корнем многочлена: если число является корнем многочлена , то остаток от деления многочлена на равен нулю, то есть в последнем столбце второй строки схемы Горнера мы получаем 0.

Используя схему Горнера, мы “убиваем двух зайцев”: одновременно проверяем, является ли число корнем многочлена и делим этот многочлен на двучлен .

Пример. Решить уравнение:

1. Выпишем делители свободного члена, и будем искать корни многочлена среди делителей свободного члена.

Делители числа 24:

2. Проверим, является ли число 1  корнем многочлена.

Сумма коэффициентов многочлена , следовательно, число 1 является корнем многочлена.

3. Разделим исходный многочлен на двучлен с помощью схемы Горнера.

А) Выпишем в первую строку таблицы коэффициенты исходного многочлена.

Так как член, содержащий отсутствует, в том столбце таблицы, в котором должен стоять коэффициент при пишем 0. Слева пишем найденный корень: число 1.

Б) Заполняем первую строку таблицы.

В последнем столбце, как и ожидалось, мы получили ноль, мы разделили исходный многочлен на двучлен без остатка. Коэффициенты многочлена, получившегося в результате деления изображены синим цветом во второй строке таблицы:

Будем делить дальше. Нам нужно найти корни многочлена . Корни также ищем среди делителей свободного члена, то есть теперь уже  числа -24.

Легко проверить, что числа 1 и -1 не являются корнями многочлена

В) Продолжим таблицу. Проверим, является ли число 2 корнем многочлена :

Так степень многочлена, который получается в результате деления на единицу меньше степени исходного многочлена, следовательно и количество коэффициентов и количество столбцов на единицу меньше.

В последнем столбце мы получили -40 – число, не равное нулю, следовательно, многочлен делится на двучлен  с остатком, и число 2 не является корнем многочлена.

Идем дальше.

В) Проверим, является ли число -2 корнем многочлена . Так как предыдущая попытка оказалась неудачной, чтобы не было путаницы с коэффициентами, я сотру строку, соответствующую этой попытке:

Отлично! В остатке мы получили ноль, следовательно, многочлен разделился на двучлен  без остатка, следовательно, число -2 является корнем многочлена. Коэффициенты многочлена, который получается в результате деления многочлена  на двучлен в таблице изображены зеленым цветом.

В результате деления мы получили квадратный трехчлен , корни которого легко находятся по теореме Виета:

Итак, корни исходного уравнения :

{}

Ответ: {}

И.В. Фельдман, репетитор по математике.

Если при значении

многочлен

принимает значение
,
то число

называется корнем этого многочлена.

Число

является корнем многочлена тогда и
только тогда, когда

делится на
,
т.е.
.
Если при этом

делится на
,
но уже не делится на
,
то

называется
-кратным
корнем многочлена
.
Корни кратности

называются простыми корнями многочлена.

Чтобы проверить, будет ли число

корнем многочлена

и какой кратности, можно воспользоваться
схемой Горнера. Сначала

делится на
,
затем, если остаток равен нулю, полученное
частное делится снова на

и т.д. до получения ненулевого остатка.

Пример 1. Проверить, является ли
число

корнем многочлена

и найти кратность.

Решение. Деление на

осуществляем по схеме Горнера

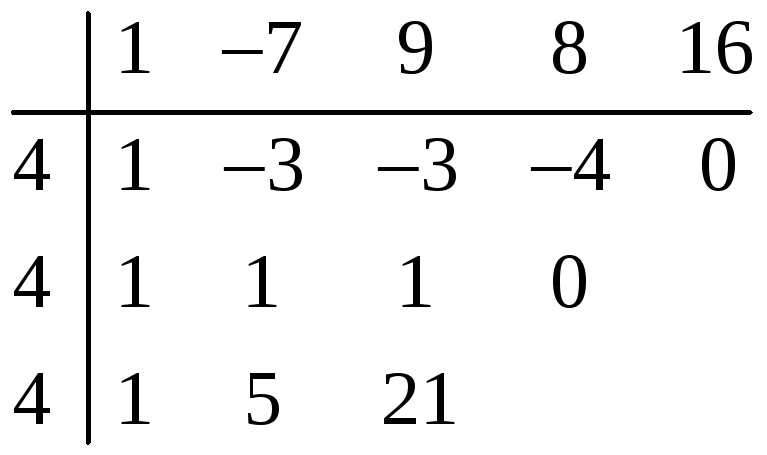
— корень кратности 2.

Пусть

— все различные корни многочлена

с кратностями, равными соответственно

— старший коэффициент
.
Тогда
.Корень
многочлена кратности

является корнем кратности

для его производной. Поэтому
,
где

— многочлен, уже не имеющий

своими корнями. Отсюда н.о.д. многочленов

и

равен
.

Следовательно, многочлен

имеет числа

простыми корнями.

Теперь для отыскания всех корней
многочлена

достаточно найти все корни многочлена
.
Это бывает сделать проще, так как степень

меньше степени
,
когда
.
Построение многочлена

называется отделением кратных корней
многочлена
.

Пример 2. Отделить кратные корни
многочлена
.

Решение.
.
Находим
.
Для этого делим с остатком

на
:

делится на остаток
.
Поэтому
.
Искомый многочлен, отделяющий кратные
корни
,
равен
.

Заметим, что в примере 2 все корни

легко вычислить.

Литература:
— § 22,
— § 9.4;

— № 555-559, 563-566, 569, 570, 585.

§ 3. Вычисление корней многочлена.

Задача вычисления корней некоторого
многочлена часто возникает в практике.
Согласно основной теореме алгебры, все
корни произвольного многочлена

с коэффициентами из числового поля

содержатся в поле комплексных чисел
.
Однако не существует какого-либо
универсального метода вычисления этих
корней. Метод решения этой задачи зависит
от степени многочлена и числового поля
.
Мы перечислим лишь самые основные методы
решения задачи вычисления корней
многочлена.

1. Корни многочленов 3-й и 4-й степени.

Если
,
то для отыскания всех корней многочлена

необходимо решить уравнение

(1)

Разделим обе части (1) на
.
В результате получим уравнение

(2)

имеющее те же корни, что и уравнение
(1). Сделаем теперь замену неизвестного
.
Эту замену проще всего осуществить,
представляя многочлен

по степеням

с помощью схемы Горнера (§
1) и делая затем замену
.
В результате замены получим уравнение

(3)

Корни уравнения (3) находятся по формуле
Кардано

где,
,

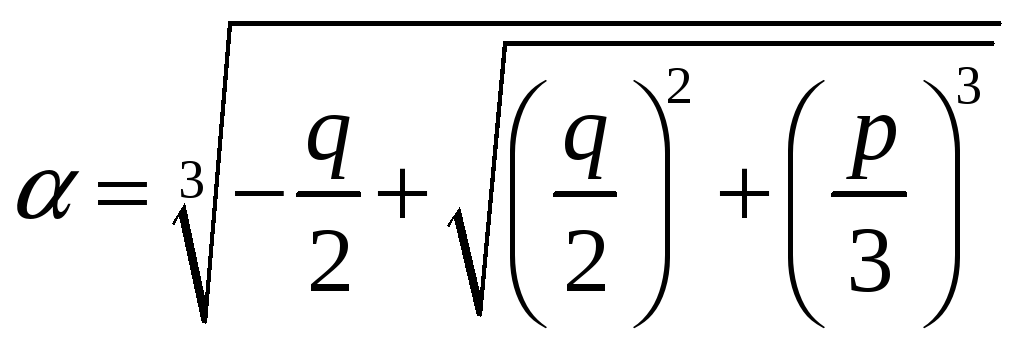
(корни извлекаются в поле комплексных
чисел
).
Применяя эту формулу, нужно для каждого
их трех значений

брать то значение
,
для которого выполняется условие

(такое значение всегда существует).

Если

— все корни уравнения (3), то

— все корни уравнения (1) и многочлена
.

Пример 1. Найти корни многочлена
.

Решение. Разложим многочлен

по степеням
.
Полагая
,
получим уравнение
.
Его корни находятся по формуле
,
где

или
.
Значениями корня

являются числа
.
Соответствующие им значения второго
корня

Отсюда
.
Корни многочлена
,
.

Если

— многочлен 4-й степени, то для вычисления
его корней достаточно иметь способ
вычисления всех корней уравнения вида

(4)

Способ Феррари решения уравнения (4)
состоит в следующем.

Левую часть (4) представляют в виде

, (5)

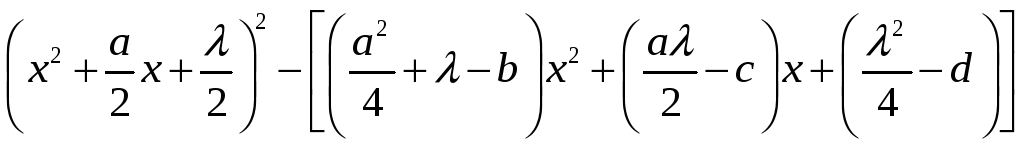
а затем подбирают

так, чтобы выражение в квадратных скобках
стало квадратом двучлена первой степени.
Для этого необходимо и достаточно
выполнение условия

, (6)

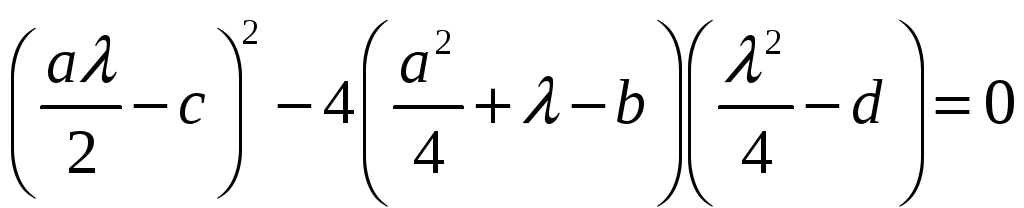
из которого следует, что

является корнем вспомогательного
кубического уравнения (6). Теперь находим
какой-нибудь один корень

и, подставляя его значение в (5), разлагаем
левую часть (4) как разность квадратов
на множители. Задача вычисления корней
сведена теперь к решению двух квадратных
уравнений.

Пример 2. Найти корни многочлена
.

Решение. Составим уравнение

(7)

Представим левую часть (7) в виде

(8)

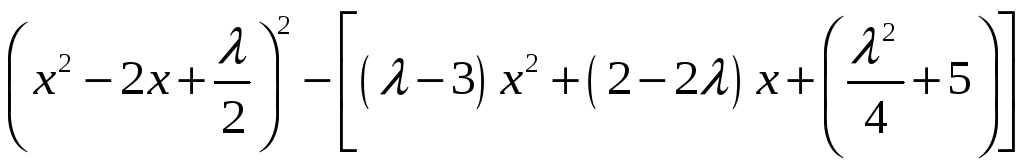
Подберем

так, чтобы дискриминант квадратного
трехчлена в квадратных скобках был
равен нулю:

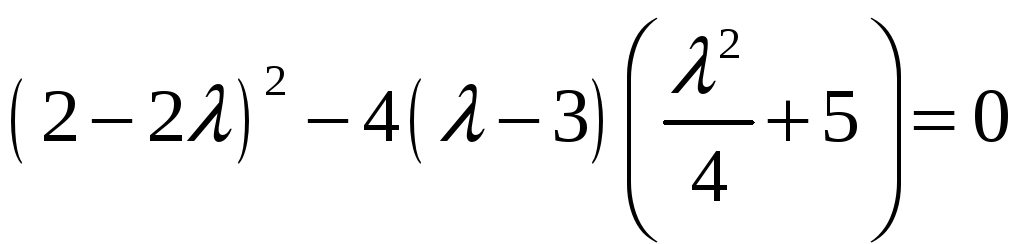
или

.

Можно заметить, что 4 — один из корней
этого уравнения. Тогда подставим

в (8) и уравнение (7) примет вид:

или

.

Отсюда, решая уравнения

и
,
получим корни нашего многочлена

Литература:

— § 38,

— № 167, 173, 174.

2. Рациональные корни
многочленов с рациональными коэффициентами.

Многочлен

имеет те же корни, что и многочлен

с целыми коэффициентами, полученный из

умножением на общее кратное знаменателей
всех коэффициентов
.

Если несократимая дробь

является корнем многочлена

с целыми коэффициентами, то выполняются
следующие условия:

1)

— делитель числа
;

2)

— делитель числа
;

3) для любого целого числа

число

является делителем числа
.

Поэтому все рациональные корни многочлена

(если они существуют) нужно искать среди
несократимых дробей, удовлетворяющих
условиям 1, 2, 3.

Если
,
то все рациональные корни

являются целыми числами.

Пример. Найти рациональные корни
многочлена

и определить их кратность.

Решение. Если

— несократимая дробь, является корнем
,
то

делит 12, а

делит 2. Все делители 12:
,
а делители 2: 1,2.

Зафиксируем
.
Тогда по (3) условию
.
В качестве

возьмем

и
.
Тогда

и
.
.
.
Числа 1 и -1 не являются корнями. Если
число

— корень, то

и
.
Такому условию удовлетворяют -2, 4. С
помощью схемы Горнера выясняем, что
число -2 является корнем кратности 2.

Далее, зафиксируем
.
Тогда

и

().
Проверять надо лишь

взаимно простые с
,
т.е.,
.
Среди этих чисел условию ()
удовлетворяют -1, 3. Проверяя по схеме
Горнера дроби

и

выясняем, что корнем является
.
Итак,

— простой корень,

— корень кратности 2.

Литература:

— § 57,

— § 11, 3,

— № 649-651.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Инфоурок

›

Другое

›Презентации›Способы нахождения корней многочленов

Способы нахождения корней многочленов

Теорема Безу и следствия из неё

19 июля 2022

Теорема Безу позволяет решать уравнения высших степеней, которые на первый взгляд не решаются, и раскладывать на множители многочлены, которые не раскладываются.:)

Формулировка теоремы довольно проста:

Терема Безу. Остаток от деления многочлена

[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]

на двучлен $x- color{red}{a}$ равен значению этого многочлена в точке $x= color{red}{a}$:

[r=Pleft( color{red}{a} right)]

На практике нас интересует не сама теорема Безу, а некоторые следствия из неё — именно они помогают решать уравнения и раскладывать многочлены на множители. В этом уроке мы рассмотрим все такие следствия и станем настоящими мастерами в работе с многочленами.

Содержание

1. Деление с остатком
2. Разложение на множители
3. Целые корни многочленов
4. Рациональные корни многочленов
5. Доказательства

В разных учебниках теорему Безу проходят то в 9-м классе, то в 10-м. Этот урок построен так, что вы поймёте его вне зависимости от школы, класса и учебника.

1. Деление с остатком

Итак, есть многочлен $Pleft( x right)$ и двучлен $x- color{red}{a}$. Разделим $Pleft( x right)$ на $x- color{red}{a}$ с остатком:

[Pleft( x right)=Qleft( x right)cdot left( x- color{red}{a} right)+r]

Теперь найдём значение многочлена $Pleft( x right)$ в точке $x= color{red}{a}$:

[Pleft( color{red}{a} right)=Qleft( color{red}{a} right)cdot left( color{red}{a}- color{red}{a} right)+r=r]

Собственно, мы только что доказали теорему Безу. А заодно подготовили основу для первого важного следствия.

Следствие 1. Деление на произвольный двучлен

Теорема Безу прекрасно работает не только для двучлена $x-color{red}{a}$, но и для любого линейного выражения вида $color{blue}{k}x+color{red}{b}$.

Следствие 1. Остаток от деления многочлена

[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]

на двучлен $color{blue}{k}x+color{red}{b}$ равен значению этого многочлена в точке $x=-color{red}{b}/ color{blue}{k};$:

[r=Pleft( -frac{color{red}{b}}{color{blue}{k}} right)]

На практике для большей надёжности рекомендуется приравнять двучлен $color{blue}{k}x+color{red}{b}$ к нулю:

[begin{align} color{blue}{k}x+color{red}{b} &=0 \ x &=-frac{color{red}{b}}{color{blue}{k}} \ end{align}]

Затем подставить найденное значение $x=-{color{red}{b}}/{color{blue}{k}};$ в многочлен $Pleft( x right)$ и таким образом найти $Pleft( -{color{red}{b}}/{color{blue}{k}}; right)$:

[r=Pleft( -frac{color{red}{b}}{color{blue}{k}} right)]

Пример 1. Стандартный многочлен

Не выполняя деления, найдите остаток от деления многочлена

[Pleft( x right)=4{{x}^{3}}-3{{x}^{2}}+5x-6]

на двучлен $Tleft( x right)=x-2$.

Решение. Это стандартный двучлен вида $x-color{red}{a}$, поэтому решаем по стандартной теореме Безу, согласно которой остаток от деления многочлена $Pleft( x right)$ на двучлен $x-color{red}{2}$ равен $Pleft( color{red}{2} right)$:

[begin{align}r &=Pleft( color{red}{2} right)= \ &=4cdot {color{red}{2}^{3}}-3cdot {color{red}{2}^{2}}+5cdotcolor{red}{2}-6 \ &=32-12+10-6=24 end{align}]

Ответ: 24.

Пример 2. Более сложный многочлен

Не выполняя деления, найдите остаток от деления многочлена

[Pleft( x right)={{left( {{x}^{3}}-2{{x}^{2}}+5 right)}^{3}}{{left( 2x+1 right)}^{5}}]

на двучлен $Tleft( x right)=x+1$.

Решение. Многочлен $Pleft( x right)$ представлен в виде произведения двух других многочленов, которые ещё и возведены в степени. Если раскрыть скобки и привести подобные слагаемые, получится обычный многочлен вида

[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]

По свойствам степеней найдём степень такого многочлена:

[deg Pleft( x right)=3cdot 3+1cdot 5=14]

Раскрывать скобки и приводить подобные в многочлене 14-й степени долго и трудно, а главное — в этом нет никакой необходимости. Ведь по теореме Безу остаток от деления $Pleft( x right)$ на двучлен $x-color{red}{a}$ всегда равен $Pleft( color{red}{a} right)$ — и не важно, как записан исходный многочлен $Pleft( x right)$.

Для надёжности, чтобы найти $color{red}{a}$, приравняем к нулю двучлен $Tleft( x right)=x+1$:

[begin{align}x+1 &=0 \ x &=color{red}{-1} \ end{align}]

Теперь подставим $x=color{red}{-1}$ в многочлен $Pleft( x right)$ и найдём остаток:

[begin{align}r &=Pleft( color{red}{-1} right)= \ &={{left( {{left( color{red}{-1} right)}^{3}}-2cdot {{left( color{red}{-1} right)}^{2}}+5 right)}^{3}}cdot {{left( 2cdot left( color{red}{-1} right)+1 right)}^{5}}= \ &={{left( -1-2+5 right)}^{3}}cdot {{left( -2+1 right)}^{5}}=-8 end{align}]

Ответ: −8.

Пример 3. Рациональные коэффициенты

Не выполняя деления, найдите остаток от деления многочлена

[Pleft( x right)=3{{x}^{20}}+{{x}^{19}}-7x+1]

на двучлен $Tleft( x right)=3x+1$.

Решение. Воспользуемся Следствием 1 из теоремы Безу. Для надёжности приравняем к нулю двучлен $Tleft( x right)$ и найдём $color{red}{a}$:

[begin{align}3x+1 &=0 \ x &=color{red}{-{1}/{3};} end{align}]

Подставим найденное $x=color{red}{-{1}/{3};}$ в многочлен $Pleft( x right)$ и найдём остаток:

[begin{align} Pleft( color{red}{-frac{1}{3}} right) &=3cdot {{left( color{red}{-frac{1}{3}} right)}^{20}}+{{left( color{red}{-frac{1}{3}} right)}^{19}}-7cdot left( color{red}{-frac{1}{3}} right)+1= \ &=frac{1}{{{3}^{19}}}-frac{1}{{{3}^{19}}}+frac{7}{3}+1=frac{10}{3} end{align}]

Ответ: ${10}/{3};$.

Пример 4. Иррациональные коэффициенты

Не выполняя деления, найдите остаток от деления многочлена

[Pleft( x right)={{x}^{6}}-12{{x}^{4}}+48{{x}^{2}}+64]

на двучлен $Tleft( x right)=left( 1-sqrt{3} right)x+2$.

Решение. Вновь воспользуемся Следствием 1 из теоремы Безу. Приравняем двучлен $Tleft( x right)$ к нулю и найдём $color{red}{a}$:

[left( 1-sqrt{3} right)x+2=0]

Это линейное уравнение с иррациональными коэффициентами. Такое уравнение решается стандартно (см. урок «Линейные уравнения»):

[x=-frac{2}{1-sqrt{3}}=frac{2}{sqrt{3}-1}]

Избавимся от иррациональности в знаменателе, домножив числитель и знаменатель на сопряжённое:

[x=frac{2color{blue}{left( sqrt{3}+1 right)}}{left( sqrt{3}-1 right) color{blue}{left( sqrt{3}+1 right)}}=frac{2left( sqrt{3}+1 right)}{2}= color{red}{sqrt{3}+1}]

Степень исходного многочлена: $deg Pleft( x right)=6$. Если подставить в такой многочлен иррациональное число, то это число придётся возводить в шестую степень. Это слишком долго и трудно, поэтому перепишем многочлен $Pleft( x right)$ так:

[begin{align} Pleft( x right) &=left( {{x}^{6}}-12{{x}^{4}}+48{{x}^{2}}-64 right)+128= \ &={{left( {{x}^{2}}-4 right)}^{3}}+128 end{align}]

Мы выделили точный куб разности — классическую формулу сокращённого умножения. Как это работает — см. уроки «Формулы сокращённого умножения» и «Куб суммы и разности».

В такую формулу намного проще подставить $x=color{red}{sqrt{3}+1}$:

[begin{align}Pleft( color{red}{sqrt{3}+1} right) &={{left( {{left( color{red}{sqrt{3}+1} right)}^{2}}-4 right)}^{3}}+128= \ &={{left( {{left( sqrt{3} right)}^{2}}+2sqrt{3}+{{1}^{2}}-4 right)}^{3}}+128= \ &={{left( 2sqrt{3} right)}^{3}}+128= \ &=24sqrt{3}+128 end{align}]

Ответ получился некрасивым, но это и есть искомый остаток от деления.

Ответ: $24sqrt{3}+128$.

2. Разложение на множители

Сейчас будет немного теории, которая может показаться непонятной, но далее на примерах всё встанет на свои места.

Рассмотрим ещё раз деление многочлена $Pleft( x right)$ на двучлен $x-color{red}{a}$ с остатком:

[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)+r]

По теореме Безу мы легко найдём остаток $r=Pleft( color{red}{a} right)$. В частности, при $Pleft( color{red}{a} right)=0$ многочлен примет вид

[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)]

А это значит, что многочлен $Pleft( x right)$ разделился на двучлен $x-color{red}{a}$ без остатка, и мы получили разложение на множители.

Кроме того, равенство $Pleft( color{red}{a} right)=0$ означает, что число $x=color{red}{a}$ — корень многочлена $Pleft( x right)$. И это ещё одно замечательное следствие теоремы Безу.

Следствие 2. Корни многочлена и деление

Следствие 2. Число $x=color{red}{a}$ является корнем многочлена $Pleft( x right)$ тогда и только тогда, когда $Pleft( x right)$ делится без остатка на $left( x-color{red}{a} right)$.

На практике это означает, что для разложения многочлена на множители мы просто перебираем разные числа $x=color{red}{a}$ до тех пор, пока не окажется, что $Pleft( color{red}{a} right)=0$. В этот момент многочлен перепишется в виде

[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)]

Такой перебор особенно эффективен в сочетании со схемой Горнера (см. урок «Схема Горнера»). Потому что параллельно с вычислением $Pleft( color{red}{a} right)$ мы получаем ещё и коэффициенты нового многочлена $Qleft( x right)$.

Пример 10. Обычный многочлен

Разложите на множители многочлен

[Pleft( x right)={{x}^{4}}+3{{x}^{3}}-3{{x}^{2}}-11x-6]

Решение. Для наглядности отметим синим цветом коэффициенты многочлена $Pleft( x right)$:

[Pleft( x right)= color{blue}{1}cdot {{x}^{4}}+color{blue}{3}cdot {{x}^{3}}+left( color{blue}{-3} right)cdot {{x}^{2}}+left( color{blue}{-11} right)cdot x+left( color{blue}{-6} right)]

Составим из них таблицу для схемы Горнера:

[begin{array}{r|r|r|r|r|r} {} & color{blue}{1} & color{blue}{3} & color{blue}{-3} & color{blue}{-11} & color{blue}{-6}\ hline{} & {} & {} & {} & {} & {}\ end{array}]

Все коэффициенты целые, поэтому логично проверять целые $x=color{red}{a}$, начиная с самых простых и маленьких чисел:

[x=pm 1; pm 2; pm 3; ldots ]

Проверим $x=color{red}{1}$ и $x=color{red}{-1}$:

[begin{array}{r|r|r|r|r|r}{} & color{blue}{1} & color{blue}{3} & color{blue}{-3} & color{blue}{-11} & color{blue}{-6}\ hline color{red}{1} & 1 & 4 & 1 & -10 & color{red}{-16}\ hline color{red}{-1} & 1 & 2 & -5 & -6 & color{green}{0}\ end{array}]

Проверка числа $x=color{red}{1}$ окончилась неудачей: остаток $r=color{red}{-16}$. Зато проверка $x=color{red}{-1}$ дала остаток $r=color{green}{0}$. Следовательно, $x=color{red}{-1}$ является корнем многочлена $Pleft( x right)$, и сам многочлен можно переписать так:

[begin{align}Pleft( x right) &=Qleft( x right)cdot left( x-left( color{red}{-1} right) right) \ &=left( {{x}^{3}}+2{{x}^{2}}-5x-6 right)left( x+1 right) end{align}]

Теперь разложим многочлен $Qleft( x right)$ по схеме Горнера. Проверим ещё раз число $x=color{red}{-1}$:

[begin{array}{r|r|r|r|r|r}{} & 1 & 3 & -3 & -11 & -6\ hline color{red}{-1} & color{blue}{1} & color{blue}{2} & color{blue}{-5} & color{blue}{-6} & color{green}{0}\ hline color{red}{-1} & 1 & 1 & -6 & color{green}{0} & {}\ end{array}]

И вновь получили $r=color{green}{0}$. Исходный многочлен примет вид

[Pleft( x right)=left( {{x}^{2}}+x-6 right){{left( x-1 right)}^{2}}]

В первой скобке стоит квадратный трёхчлен. Разложим его на множители по теореме Виета:

[{{x}^{2}}+x-6=left( x+3 right)left( x-2 right)]

Итого окончательное разложение многочлена $Pleft( x right)$:

[left( x+3 right)left( x-2 right){{left( x-1 right)}^{2}}]

Однако это было довольно простое задание: теорема Безу использовалась лишь в качестве обоснования, почему вместо $Pleft( x right)$ мы пишем $Qleft( x right)left( x-color{red}{a} right)$.

Следующее задание будет намного интереснее.:)

Пример 11. Многочлен с двумя переменными

Разложите на множители многочлен

[Pleft( x,y right)=y{{x}^{2}}+3yx+x-4y-1]

Решение. Это многочлен от двух переменных. Он квадратный относительно переменной $x$ и линейный относительно $y$. Чтобы разложить такой многочлен на множители, сгруппируем его слагаемые относительно переменной $x$:

[Pleft( x,y right)= color{blue}{y}cdot {{x}^{2}}+left( color{blue}{3y+1} right)cdot x+left( color{blue}{-4y-1} right)]

Составляем таблицу:

[begin{array}{c|c|c|c}{} & color{blue}{y} & color{blue}{3y+1} & color{blue}{-4y-1}\ hline {} & {} & {} & {}\ end{array}]

Чтобы воспользоваться теоремой Безу, нужно найти такое $x=color{red}{a}$, чтобы $r=Pleft( color{red}{a} right)= color{green}{0}$. Поскольку в роли коэффициентов выступают выражения, содержащие переменную $y$, вновь рассмотрим самые простые варианты, которые приходят в голову:

[x=pm 1; pm y]

Проверим, например, $x=color{red}{1}$:

[begin{array}{c|c|c|c}{} & color{blue}{y} & color{blue}{3y+1} & color{blue}{-4y-1}\ hline color{red}{1} & y & 4y+1 & color{green}{0}\ end{array}]

Первая же попытка привела к успеху: $r=color{green}{0}$, поэтому $x=color{red}{1}$ — крень многочлена $Pleft( x,y right)$. Разложим этот многочлен на множители согласно Следствию 2 теоремы Безу:

[Pleft( x,y right)=left( ycdot x+4y+1 right)cdot left( x-color{red}{1} right)]

В первой скобке стоит новый многочлен, линейный по $x$ и по $y$. Его уже нельзя разложить на множители, поэтому ответ окончательный:

[Pleft( x,y right)=left( xy+4y+1 right)left( x-1 right)]

Важное замечание. Строго говоря, линейность многочлена по каждой переменной ещё не означает, что его нельзя разложить на множители. Простой контрпример:

[xy-x+y-1=left( x+1 right)left( y-1 right)]

Однако в нашем случае дальнейшее применение теоремы Безу и проверки по схеме Горнера не даст никаких новых множителей.

3. Целые корни многочленов

До сих пор мы подставляли числа наугад. И если удавалось найти число $x=color{red}{a}$ такое, что $Pleft( color{red}{a} right)=0$, мы объявляли его корнем, а многочлен $Pleft( x right)$ переписывали в виде

[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)]

Однако с помощью теоремы Безу можно значительно ускорить отыскание корней, отбросив заведомо неподходящие варианты. В этом нам поможет следующее утверждение.

Следствие 3. Целочисленные корни

Пусть $Pleft( x right)$ — приведённый многочлен с целыми коэффициентами:

[Pleft( x right)={{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]

Тогда свободный член ${{a}_{0}}$ делится на любой целый корень многочлена $Pleft( x right)$.

Обратите внимание: старший коэффициент при ${{x}^{n}}$ равен единице. Именно поэтому многочлен $Pleft( x right)$ называется приведённым. Кроме того, все коэффициенты ${{a}_{n-1}},ldots ,{{a}_{0}}$ должны быть целыми числами.

И вот тогда целые корни следует искать среди делителей свободного члена ${{a}_{0}}$.

Пример 5. Простое уравнение

Решите уравнение

[{{x}^{3}}-2{{x}^{2}}-x+2=0]

Решение. Это приведённое кубическое уравнение с целыми коэффициентами. Рассмотрим многочлен

[Pleft( x right)= color{blue}{1}cdot {{x}^{3}}+left( color{blue}{-2} right)cdot {{x}^{2}}+left( color{blue}{-1} right)cdot x+color{blue}{2}]

Если у него есть целые корни, то по Следствию 3 теоремы Безу все они находятся среди делителей свободного члена ${{a}_{0}}=2$. Таких делителей всего четыре:

[x=pm 1; pm 2]

Подставим эти числа в схему Горнера:

[begin{array}{r|r|r|r|r}{} & color{blue}{1} & color{blue}{-2} & color{blue}{-1} & color{blue}{2}\ hline color{red}{1} & 1 & -1 & -2 & color{green}{0}\ hline color{red}{-1} & 1 & -2 & color{green}{0} & {}\ end{array}]

Уже на первом шаге мы получили $r=color{green}{0}$. Следовательно, $x=color{red}{1}$ — корень многочлена $Pleft( x right)$, и сам многочлен можно переписать так:

[Pleft( x right)=left( {{x}^{2}}-x-2 right)left( x-color{red}{1} right)]

Впрочем, если учесть третью строку таблицы, то можно вообще записать

[Pleft( x right)=left( x-2 right)left( x-left( color{red}{-1} right) right)left( x-color{red}{1} right)]

В любом случае, корни многочлена, как и корни уравнения — это числа 2, 1 и −1.

Ответ: $x=1$, $x=-1$, $x=2$.

Формула понижения степени

Итак, с помощью теоремы Безу мы можем:

1. Найти целый корень многочлена;
2. Разложить исходный многочлен на множители;
3. Далее искать корни многочлена степени на единицу меньше.

В самом деле, если $Pleft( color{red}{a} right)=0$, тогда по Следствию 2 теоремы Безу мы переписываем многочлен $Pleft( x right)$ в виде

[Pleft( x right)=Qleft( x right)left( x-color{red}{a} right)]

Далее мы ищем корни многочлена $Qleft( x right)$, степень которого на единицу меньше $Pleft( x right)$.

Этот приём называется понижением степени. Он помогает свести исходный многочлен к квадратному, корни которого легко считаются, например, через дискриминант.

Пример 6. Среднее уравнение

Решите уравнение

[{{x}^{3}}-3{{x}^{2}}-4x+12=0]

Решение. Это уравнение третьей степени. Достаточно найти один корень — далее останется решить квадратное уравнение. Заметим, что многочлен

[Pleft( x right)= color{blue}{1}cdot {{x}^{3}}+left( color{blue}{-3} right)cdot {{x}^{2}}+left( color{blue}{-4} right)cdot x+color{blue}{12}]

является приведённым с целочисленными коэффициентами. По Следствию 3 теоремы Безу все целые корни этого многочлена содержатся среди делителей свободного члена ${{a}_{0}}=12$. Таких делителей довольно много:

[x=pm 1; pm 2; pm 3; pm 4; pm 6; pm 12]

Впрочем, нам достаточно найти всего один корень. Воспользуемся схемой Горнера:

[begin{array}{r|r|r|r|r}{} & color{blue}{1} & color{blue}{-3} & color{blue}{-4} & color{blue}{12}\ hlinecolor{red}{1} & 1 & -2 & -7 & color{red}{5}\ hlinecolor{red}{-1} & 1 & -4 & 0 & color{red}{12}\ hlinecolor{red}{2} & 1 & -1 & -6 & color{green}{0}\ end{array}]

Проверка закончилась неудачей для $x=color{red}{1}$ и $x=color{red}{-1}$. Но для $x=color{red}{2}$ мы нашли то, что искали: остаток $r=color{green}{0}$. Следовательно, $x=color{red}{2}$ — корень многочлена $Pleft( x right)$.

Разложим многочлен на множители согласно теореме Безу:

[Pleft( x right)=left( {{x}^{2}}-x-6 right)left( x-color{red}{2} right)]

В первой скобке стоит квадратный трёхчлен. Его корни легко найти по теореме Виета:

[Pleft( x right)=left( x-3 right)left( x+2 right)left( x-2 right)]

Приравниваем полученное произведение к нулю и решаем уравнение: $x=3$, $x=-2$, $x=2$.

Ответ: $x=2$, $x=-2$, $x=3$.

Пример 7. Сложное уравнение

Решите уравнение

[{{x}^{4}}-{{x}^{3}}-5{{x}^{2}}+3x+2=0]

Решение. Слева приведённый многочлен с целочисленными коэффициентами, поэтому все целые корни находятся среди делителей свободного члена ${{a}_{0}}=2$:

[x=pm 1; pm 2]

Достаточно подобрать два корня — далее уравнение сведётся к квадратному. Воспользуемся схемой Горнера:

[begin{array}{r|r|r|r|r|r}{} & color{blue}{1} & color{blue}{-1} & color{blue}{-5} & color{blue}{3} & color{blue}{2}\ hlinecolor{red}{-1} & 1 & -2 & -3 & 6 & color{red}{-4}\ hlinecolor{red}{1} & 1 & 0 & -5 & -2 & color{green}{0}\ hlinecolor{red}{-2} & 1 & -2 & -1 & color{green}{0} & {}\ end{array}]

Получили корни $x=color{red}{1}$ и $x=color{red}{-2}$. Разложим многочлен на множители:

[left( {{x}^{2}}-2x-1 right)left( x-color{red}{1} right)left( x-left( color{red}{-2} right) right)=0]

Решим квадратного уравнение из первой скобки:

[{{x}^{2}}-2x-1=0]

Дискриминант положителен:

[begin{align} D &={{left( -2 right)}^{2}}-4cdot 1cdot left( -1 right)= \ &=4+4=8 end{align}]

Следовательно, уравнение имеет два корня:

[x=frac{2pm 2sqrt{2}}{2}=1pm sqrt{2}]

Ответ: $x=1$, $x=-2$, $x=1pm sqrt{2}$.

4. Рациональные корни

До сих пор мы работали лишь с приведёнными многочленами, где старший коэффициент равен единице. Однако теорема Безу прекрасно работает и для неприведённых многочленов — при условии что все коэффициенты остаются целыми.

Рассмотрим уравнение

[{{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}=0]

где ${{a}_{n}},ldots ,{{a}_{0}}$ — целые числа, причём ${{a}_{n}}ne 0$.

Следствие 4. Если рациональное число $x=color{red}{p}/color{blue}{q};$, где $color{red}{p}in mathbb{Z}$, $color{blue}{q}in mathbb{N}$ и дробь $color{red}{p}/color{blue}{q};$ несократима, является корнем уравнения

[{{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}=0]

то свободный член ${{a}_{0}}$ делится на $color{red}{p}$, а старший коэффициент ${{a}_{n}}$ делится на $color{blue}{q}$.

Это утверждение будет доказано в конце урока. Сейчас важен практический смысл, который состоит в том, что все рациональные корни уравнения

[{{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}=0]

имеют вид $x=color{red}{p}/color{blue}{q};$, где $color{red}{p}$ следует искать среди делителей ${{a}_{0}}$, а $color{blue}{q}$ — среди положительных делителей ${{a}_{n}}$.

Пример 8. Простой многочлен

Найдите рациональные корни многочлена

[Pleft( x right)=2{{x}^{5}}-{{x}^{4}}+4x-2]

Решение. Делители свободного члена ${{a}_{0}}=-2$:

[p=pm 1; pm 2]

Положительные делители старшего коэффициента ${{a}_{4}}=2$:

[q=1; 2]

Возможные рациональные корни многочлена $Pleft( x right)$ по Следствию 4 теоремы Безу:

[x=pm 1; pm 2; pm {1}/{2};]

Проверять числа $x=color{red}{pm 1}$ нет смысла, поскольку все коэффициенты многочлена $Pleft( x right)$, за исключением одного, чётные. Следовательно, при подстановке нечётных чисел многочлен принимает нечётные значения, которые точно не равны нулю.

Остальные числа проверим по схеме Горнера:

[begin{array}{r|r|r|r|r|r|r}{} & color{blue}{2} & color{blue}{-1} & color{blue}{0} & color{blue}{0} & color{blue}{4} & color{blue}{-2}\ hlinecolor{red}{2} & 2 & 3 & 6 & 12 & 28 & color{red}{54}\ hlinecolor{red}{-2} & 2 & -5 & 10 & -20 & 44 & color{red}{-90}\ hline color{red}{{1}/{2};} & 2 & 0 & 0 & 0 & 4 & color{green}{0}\ hline color{red}{-{1}/{2};} & 2 & -2 & 1 & -{1}/{2}; & {17}/{4}; & color{red}{-{33}/{8};}\ end{array}]

Подошло лишь одно число: $x=color{red}{{1}/{2};}$. Следовательно, многочлен имеет лишь один рациональный корень.

Ответ: $x={1}/{2};$.

Обратите внимание: проверку дробных чисел можно прекращать, как только в строке таблицы появилась дробь. Потому что дальше это число будет лишь умножаться на новые дроби и складываться с другими целыми числами. При таких обстоятельствах получить $r=color{green}{0}$ уже невозможно.

Пример 9. Сложный многочлен

Найдите рациональные корни многочлена

[Pleft( x right)=3{{x}^{7}}+2{{x}^{6}}-5{{x}^{5}}+3{{x}^{3}}-{{x}^{2}}-7x+5]

Решение. Это многочлен с целыми коэффициентами. Делители свободного члена ${{a}_{0}}=5$:

[p=pm 1; pm 5]

Положительные делители старшего коэффициента ${{a}_{7}}=3$:

[q=1; 3]

Кандидаты в корни согласно Следствию 4 теоремы Безу:

[x=pm 1; pm 5; pm {1}/{3};; pm {1}/{5};]

Всего восемь кандидатов. Проверим их все по схеме Горнера:

[begin{array}{r|r|r|r|r|c|c|c|c}{} & color{blue}{3} & color{blue}{2} & color{blue}{-5} & color{blue}{0} & color{blue}{3} & color{blue}{-1} & color{blue}{-7} & color{blue}{5}\ hlinecolor{red}{1} & 3 & 5 & 0 & 0 & 3 & 2 & -5 & color{green}{0}\ hlinecolor{red}{-1} & 3 & 2 & -2 & 2 & 1 & 1 & color{red}{-6} & {}\ hlinecolor{red}{5} & 3 & 20 & 100 & color{red}{500} & color{red}{-} & color{red}{-} & color{red}{-} & {}\ hlinecolor{red}{-5} & 3 & -10 & 50 & color{red}{-250} & color{red}{-} & color{red}{-} & color{red}{-} & {}\ hlinecolor{red}{{1}/{3};} & 3 & 6 & 2 & color{red}{{2}/{3};} & color{red}{-} & color{red}{-} & color{red}{-} & {}\ hlinecolor{red}{-{1}/{3};} & 3 & 4 & color{red}{-{4}/{3};} & color{red}{-} & color{red}{-} & color{red}{-} & color{red}{-} & {}\ hlinecolor{red}{{5}/{3};} & 3 & 10 & color{red}{{50}/{3};} & color{red}{-} & color{red}{-} & color{red}{-} & color{red}{-} & {}\ hlinecolor{red}{-{5}/{3};} & 3 & 0 & 0 & 0 & 3 & -3 & color{green}{0} & {}\ end{array}]

Обратите внимание: для чисел $x=color{red}{5}$ и $x=color{red}{-5}$ мы прекратили вычисления досрочно, поскольку получили явно неадекватные числа, которые дальше будут только расти.

При проверке $x=color{red}{{1}/{3};}$, $x=color{red}{-{1}/{3};}$ и $x=color{red}{{5}/{3};}$ мы в какой-то момент возникли дроби, после чего дальнейшие вычисления теряют смысл.

Итого найдены два рациональных корня: $x=color{red}{1}$ и $x=color{red}{-{5}/{3};}$. Пожалуй, это одно из самых утомительных заданий на применение теоремы Безу, которые я когда-либо решал.:)

5. Доказательства

Рассмотрим доказательства всех ключевых утверждений сегодняшнего урока.

5.1. Теорема Безу

Мы сформулировали эту теорему в самом начале урока:

Терема Безу. Остаток от деления многочлена

[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]

на двучлен $x-color{red}{a}$ равен значению этого многочлена в точке $x=color{red}{a}$:

[r=Pleft( color{red}{a} right)]

Доказательство. Разделим многочлен $Pleft( x right)$ на двучлен $x-color{red}{a}$ с остатком:

[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)+r]

Такое представление всегда однозначно (см. урок «Деление многочленов с остатком»). Здесь многочлен $Qleft( x right)$ — неполное частное, $r$ — остаток, причём

[begin{align}deg r lt deg left( x-color{red}{a} right) &=1 \ deg r &=0 \ end{align}]

Другими словами, остаток $r$ — это просто число.

Теперь найдём значение $Pleft( x right)$ в точке $x=color{red}{a}$:

[Pleft( color{red}{a} right)=Qleft( color{red}{a} right)cdot left( color{red}{a}-color{red}{a} right)+r=r]

Теорема Безу доказана. Однако её доказательство опирается на единственность деления с остатком.

5.2. Целочисленные корни

Целочисленные корни приведённого многочлена с целыми коэффициентами следует искать среди делителей свободного члена.

Следствие 3. Пусть $Pleft( x right)$ — приведённый многочлен с целыми коэффициентами:

[Pleft( x right)={{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]

Тогда свободный член ${{a}_{0}}$ делится на любой целый корень многочлена $Pleft( x right)$.

Доказательство. Пусть $color{red}{b}in mathbb{Z}$ — корень многочлена $Pleft( x right)$, т.е. $Pleft( color{red}{b} right)=0$. Подставим число $x=color{red}{b}$ в формулу многочлена и получим уравнение:

[{color{red}{b}^{n}}+{{a}_{n-1}}{color{red}{b}^{n-1}}+ldots +{{a}_{1}}color{red}{b}+{{a}_{0}}=0]

Перенесём последнее слагаемое вправо, а слева из оставшихся слагаемых вынесем множитель $color{red}{b}$ за скобку:

[color{red}{b}cdot left( {color{red}{b}^{n-1}}+{{a}_{n-1}}{color{red}{b}^{n-2}}+ldots +{{a}_{1}} right)=-{{a}_{0}}]

Поскольку $-{{a}_{0}}in mathbb{Z}$, а слева стоят два целочисленных множителя, получаем, что число $-{{a}_{0}}$ делится на $color{red}{b}$. Следовательно, свободный член ${{a}_{0}}$ тоже делится на $color{red}{b}$, что и требовалось доказать.

5.3. Рациональные корни

Рассмотрим уравнение

[{{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}=0]

где ${{a}_{n}},ldots ,{{a}_{0}}$ — целые числа, причём ${{a}_{n}}ne 0$.

Утверждение. Если рациональное число $x=color{red}{p}/color{blue}{q};$, где $color{red}{p}in mathbb{Z}$, $color{blue}{q}in mathbb{N}$ и дробь $color{red}{p}/color{blue}{q};$ несократима, является корнем уравнения $Pleft( x right)=0$, то свободный член ${{a}_{0}}$ делится на $color{red}{p}$, а старший коэффициент ${{a}_{n}}$ делится на $color{blue}{q}$.

Доказательство. Подставим число $x=color{red}{p}/color{blue}{q};$ в исходное уравнение. Поскольку $x=color{red}{p}/color{blue}{q};$ — корень, уравнение обратится в верное числовое равенство:

[{{a}_{n}}cdot {{left( frac{color{red}{p}}{color{blue}{q}} right)}^{n}}+{{a}_{n-1}}cdot {{left( frac{color{red}{p}}{color{blue}{q}} right)}^{n-1}}+ldots +{{a}_{1}}cdot frac{color{red}{p}}{color{blue}{q}}+{{a}_{0}}=0]

Домножим обе части на ${color{blue}{q}^{n}}$. Получим

[{{a}_{n}}{color{red}{p}^{n}}+{{a}_{n-1}}{color{red}{p}^{n-1}}color{blue}{q}+ldots +{{a}_{1}}color{red}{p}{color{blue}{q}^{n-1}}+{{a}_{0}}{color{blue}{q}^{n}}=0]

Перенесём последнее слагаемое ${{a}_{0}}{color{blue}{q}^{n}}$ вправо, а в левой части из оставшихся слагаемых вынесем множитель $color{red}{p}$ за скобку:

[color{red}{p}left( {{a}_{n}}{color{red}{p}^{n-1}}+{{a}_{n-1}}{color{red}{p}^{n-2}}color{blue}{q}+ldots +{{a}_{1}}{color{blue}{q}^{n-1}} right)=-{{a}_{0}}{color{blue}{q}^{n}}]

Слева и справа от знака равенства стоят целые числа, поскольку все слагаемые и множители являются целыми. Мы видим, что левая часть делится на $color{red}{p}$. Следовательно, правая часть тоже делится на $color{red}{p}$:

[-{{a}_{0}}{color{blue}{q}^{n}} vdots color{red}{p}]

По условию теоремы дробь $color{red}{p}/color{blue}{q};$ несократима. Следовательно, числа $color{blue}{q}$ и $color{red}{p}$ не имеют общих делителей, и единственный возможный вариант — это когда ${{a}_{0}}$ делится на $color{red}{p}$.

Аналогично доказывается, что старший коэффициент ${{a}_{n}}$ делится на $color{blue}{q}$. Теорема доказана.

Вот и всё.:)

Смотрите также:

1. Схема Горнера
2. Деление многочленов уголком
3. Теорема Виета
4. Задача B3 — работа с графиками
5. Метод коэффициентов, часть 2
6. Нестандартная задача B2: студенты, гонорары и налоги