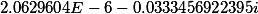Калькулятор ниже решает уравнение 4-й степени степени с одной неизвестной. В общем виде уравнение выглядит следующим образом: . В результате получается четыре комплексных или вещественных корня. Формулы, использующиеся для решения описаны сразу под калькулятором.
Уравнение 4-й степени
Точность вычисления
Знаков после запятой: 2
Первым шагом разделим все коэффициенты уравнения на a и получим эквивалентное уравнение следующего вида:
Далее решаем кубическое уравнение вида:
Это уравнение можно решить, например, способом описанным тут: Кубическое уравнение.
Один вещественный корень этого уравнения u1 мы будем использовать далее для вычисления корней квадратных уравнений. Если вещественных корней уравнения несколько, то нужно выбрать среди них один u1 таким образом, чтобы p и q в следующих выражениях были тоже вещественными:
Вычислив p1, p2,q1,q2, подставляем их в квадратные уравнения в правой части следующего выражения:
1
Четыре корня двух квадратных уравнений в правой части будут соответствовать корням исходного уравнения. Знаки в выражениях для pi и qi выбираются таким образом, чтобы выполнялись условия:
Фактически можно проверить только третье условие и если оно не выполняется — поменять q1 и q2 местами.
Решение можно проверить, получив значение полинома при помощи этого калькулятора: Вычисление значения полинома с комплексными числами.
Квадратные уравнения, уравнения третьей степени, уравнения четвертой степени – как это все не ново, но только жизнь такая штука, что стоит только покинуть стены родной школы, как все знания также покидают наши головы. Да и решение такого рода уравнений зачастую отнимает слишком много времени, которого в современном ритме жизни и так всегда не хватает.
Наш онлайн калькулятор поможет вам решить любое уравнение, особенно, он поможет тем, для кого ход решения не так важен как правильный ответ. Все что о вас может потребоваться это ввести искомые значения в уравнение и ровно через пару секунд вы получите значение всех неизвестных. Наш онлайн калькулятор это легко, просто и быстро!
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

| Коэффициенты полинома 4 степени |
| Исходный многочлен |
| Кубическая резольвента |
| Корни кубической резольвенты |
| Корни заданного многочлена 4 степени |
| Вспомогательные коэффициенты |
| F2= |
| F1= |
| T= |
Данный калькулятор позволяет высчитывать корни произвольного полинома четвертой степени. Коэффициенты могут быть как вещественными так и комплексными числами.
Использовалась определенная методика, которая нигде не описана и не разобрана.
Формулами Феррари не стал пользоваться – не интересно.
Несмотря на свой собственный путь, все равно утыкаешься в задачу решения вспомогательного уравнения третьей степени, так называемой кубической резольвенты.
И по всей видимости избежать её никак не получится.
Но дальше все идет по другому.
По любому значения корня резольвенты, мы высчитываем три вспомогательный параметра.
Зная эти три параметра, мы можем легко найти все четыре корня исходного уравнения.
Есть только один нюанс с которым сталкивались предшественники, мне тоже надо иногда каким то определять знак + или – для одного вспомогательного параметра.
Теперь в виде формул
Заменой 
Решение данного уравнения ищем в виде сумм двух функций
Три вспомогательных параметра связаны к коэффициентами приведенного полинома через следующие соотношения
Выражая любой из вспомогательных параметров мы получаем, в том или ином виде кубическую резольвенту
Например, если выразим F2
Это кубическое уравнение которое подстановкой 
Теперь о нюансе о котором говорил раньше. Какой же знак брать когда высчитываем корни?
Критерий оказывается очень простой. Берем любой корень резольвенты и сравниваем его
если это условие верное то ставится +(плюс), если условие неверное то -(минус)
Дальше все эти параметры подставляются в формулу
+F(T,F_2))
Еще хотелось бы поговорить про критерий. Вдумчивый читатель спросит: “А что если любой корень резольвенты является комплексным числом? Какой в этом случае критерий?”
Лучшим способом, я посчитал для подстановка корня в исходное уравнение. Для этого есть простой алогритический способ описанный в статье Значение производной многочлена по методу Горнера. Если выражение обращается в ноль, то есть является верным, то знак не меняется. Если иначе то знак ставим минус.
Решать комплексные уравнения 4 степени теперь можно достаточно легко и быстро. В онлайн сервисах Вы такого не найдете.
Попробуйте решить уравнение 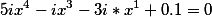
Один из корней равен
Кто считает что действительной частью можно принебречь и отбросить как “почти ноль” глубоко ошибается. Отбросив его у нас значение функции будет 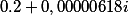
И только с учетом “такой маленькой” действительной части уравнение становиться тождественным.
Поэтому точность в вычислениях очень важны.
Если Вы вдруг заметили ошибку в расчетах ( а вдруг?) , просьба сообщить. Но я надеюсь, что такого не произойдет.
Несколько примеров:
| Исходный многочлен |
*x^3+(-9i)*x^2+(-4)*x^1+(-10i)) |
| Кубическая резольвента |
*x^2+(2620+2464i)*x^1+(-18432-34560i)) |
| Корни кубической резольвенты |
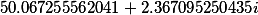 |
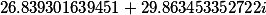 |
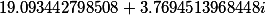 |
| Корни заданного многочлена 4 степени |
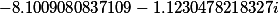 |
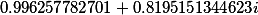 |
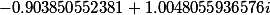 |
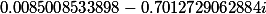 |
| Вспомогательные коэффициенты |
F2=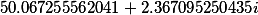 |
F1=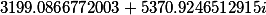 |
T=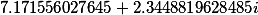 |
| Исходный многочлен |
*x^3+(-4)*x^2+(-20)*x^1+(-5)) |
| Кубическая резольвента |
*x^2+(272)*x^1+(-128)) |
| Корни кубической резольвенты |
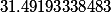 |
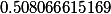 |
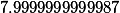 |
| Корни заданного многочлена 4 степени |
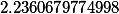 |
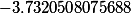 |
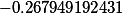 |
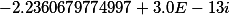 |
| Вспомогательные коэффициенты |
F2=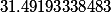 |
F1=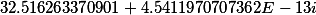 |
T=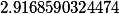 |
Главная >
Решение уравнений онлайн >
Решение уравнений четвертой степени онлайн
Рассчитать:
Уравнение четвертой степени – это уравнение, формула которого имеет вид:
ax4 + bx3 + cx2 + dx + e = 0 при этом “a” не равно нулю. Где a , b, c, d, e — известные действительные числа.
Примеры уравнений четвертой степени:
1) x4 -7x3 + 5x2 + 31x -30 = 0 (корни у этого уравнения: -2; 1; 3; 5
2) x4 -10x3 + 35x2 – 50x + 24 = 0 (корни у этого уравнения: 1; 2; 3; 4
Онлайн калькулятор найдет корни уравнения четвертой степени, для этого введите коэффициенты a , b, c, d и свободный член e:
Коэффициент a
Коэффициент b
Коэффициент c
Коэффициент d
Свободный член e
Уравнения четвертой степени имеет вид ах4; + bх3 + сх2 + ах + е = 0. Общее уравнение четвертой степени (также называемый биквадратным) является четвертой степени полиномиального уравнения. Бесплатный онлайн калькулятор расчета уравнения четвертой степени, используемый для нахождения корней уравнения.
Вычисление корней:
Например, Введите a=3, b=6, c=-123, d=-126 и e=1080
Формула уравнения четвертой степени:
ax4 + bx3 + cx2 + dx + e = 0
- Примечание : Допустим что p и q квадратные корни из 2 ненулевых корней.
- p = sqrt(y1)
- q = sqrt(y3)
- r = -g / (8pq)
- s = b / (4a)
- x1 = p + q + r — s
- x2 = p — q — r — s
- x3> = -p + q — r — s
- x4 = -p — q + r — s
Уравнением четвертой степени называется полиномиальное уравнение четвертого порядка вида, ax4+ bx3 + cx2 + dx + e = 0:
Формула уравнения четвертой степени:
ax4 + bx3+ cx2 + dx + e = 0
где,
- a = коэффициент для x4
- b = коэффициент для x3
- c = коэффициент для x2
- d = коэффициент для x
- e = константа.
Решение уравнения четвертой степени:
- x1 = p + q + r — s
- x2 = p — q — r — s
- x3 = -p + q — r — s
- x4 = -p — q + r — s
Пример 1:
Вычислить корни (x1, x2, x3, x4) уравнения четвертой степени, 3X4 + 6X3 — 123X2 — 126X + 1080 = 0
Шаг 1:
Из приведенного выше уравнения, значения a=3, b=6, c=-123, d=-126, e=1080.
Шаг 2:
Найдем x : Подставьте значения в приведенных ниже формул.
- f = c — ( 3b ² / 8 )
- g = d + ( b ³ / 8 ) — ( b x c / 2 )
- h = e — ( 3 x b4 / 256 ) + ( b ² x c / 16 ) — ( b x d / 4 )
Шаг 3:
Представим как уравнение третьей степени : y ³ + ( f / 2 ) y ² + (( f ² — 4 x h ) / 16 ) y — g ² / 64 = 0
где,
- a = коэффициент для y ³
- b = коэффициент для y²
- c = коэффициент для y
- d = константа
Шаг 4:
Из приведенного выше уравнения, значения:
- a = 1,
- b = f/2,
- c = (( f ² — 4 x h ) / 16 ),
- d = — g² / 64.
Шаг 5:
Найдем y: Подставьте значения в формулу, чтобы найти корни.
дискриминант (Δ) = q3 + r2
- q = (3c — b2) / 9
- r = -27d + b(9c — 2b2)
- s = r +√ (дискриминант)
- t = r — √(дискриминант)
- term1 = √(3.0) * ((-t + s) / 2)
- r13 = 2 * √(q)
- y1 = (- term1 + r13*cos(q3/3) )
- y2 = (- term1 + r13*cos(q3+(2∏)/3) )
- y3 = (- term1 + r13*cos(q3+(4∏)/3) )
Шаг 6:
Получим корни, y1 = 20.25 , y2 = 0 и y3 = 1.
Шаг 7:
После решения уравнения третьей степени решим уравнение четвертой степени.
Подставим y1, y2, y3 в p, q, r, s.
Примечание : Пусть p и q квадратные корни 2 ненулевых корней.
- p = sqrt(y1) = 4.5
- q = sqrt(y3) = 1
- r = -g / (8pq) = 0
- s = b / (4a) = 0.5
Шаг 8:
Мы получили корни, x1 = 5, x2 = 3, x3 = -4 и x4 = -6.
Практический пример решения уравнения четвертой степени.
людей нашли эту статью полезной. А Вы?
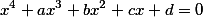
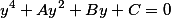
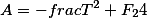
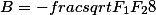
^2-frac{F_1}{2}}{64})
=8B^2)
)