Для нахождения корней полинома в MathCAD предназначена специальная функция polyroots (v). Она находит как действительные, так и комплексные корни полинома n-ой степени, коэффициенты которого хранятся в массиве v длиной n+1. Параметром данной функции является вектор-столбец коэффициентов полинома v.
Пример использования функции polyroots показан на рисунке 3.1.4. При решении задачи надо правильно формировать вектор-столбец коэффициентов полинома v, записывая в него значения коэффициентов, начиная коэффициентов при х в нулевой степени.
Решение систем уравнений
Системы уравнений в MathCAD решаются в следующем порядке:
1. Находится приближенное решение системы уравнений. Приближенное решение удобнее всего найти графически;
2. Записывается директива Given, и после нее записываются уравнения системы. Следует помнить, что вместо знака “равно” при записи уравнений используется знак “логическое равенство”, который набирается как + .
3. Записывается любое выражение, использующее функцию Find. Параметрами данной функции являются все переменные, входящие в систему. Функция возвращает вектор-столбец решений системы.
Рисунок 3.1.4 — Нахождение корней полинома при помощи функции
Пример 3.3 Найти решение системы уравнений
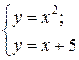
Процесс решения данной системы уравнений показан на рисунке 3.2.1
В результате функция Find вернула вектор-столбец 


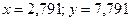
Символьное решение уравнений, неравенств и систем уравнений
Для символьного решения уравнений и неравенств надо выполнить следующее:
1. Вставить в рабочий лист структуру solve c панели инструментов Simbolic.
2. Ввести данные: слева – уравнение или неравенство, справа – переменную, относительно которой требуется его разрешить.
3. Щёлкнуть вне области решения, чтобы получить результат.
Рисунок 3.2.1 – Пример решения системы уравнений
При символьном решении уравнений и неравенств следует вводить знаки =, 
При символьном решении системы уравнений после Find надо ввести 
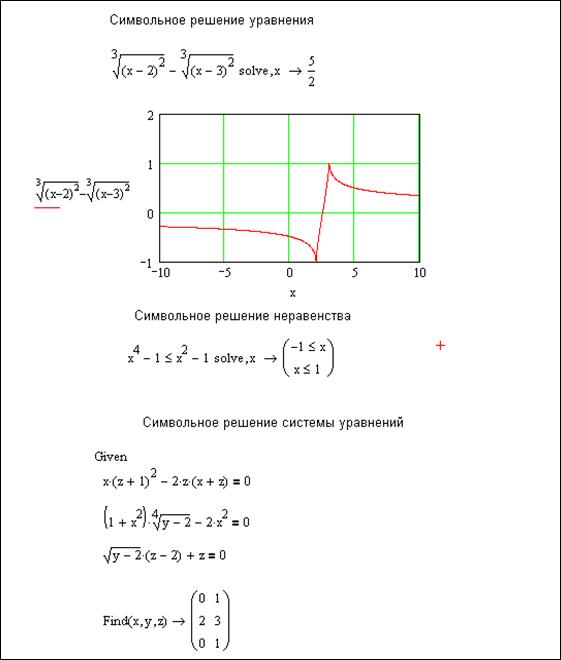
Пример символьного решения уравнений, неравенств и систем уравнений показан на рисунке 3.3.1
Рисунок 3.3.1 – пример символьного решения уравнения, неравенства
и системы уравнений
Некоторые возможности MathCAD
В этом разделе приводятся краткие сведения о возможностях MathCAD, которые могут быть полезны в процессе обучения.
Комплексные числа в MathCAD
MathCAD Воспринимает комплексные числа в форме a+bi, где a и b – вещественные числа. Комплексные числа можно вводить, или получать в результате вычислений. При вводе мнимые числа заканчиваются символом i или j. Нельзя использовать i или j сами по себе для обозначения мнимой единицы, во избежание смешения с именами переменных. Для ввода мнимой единицы следует напечатать 1i или 1j. При выходе из поля ввода единица не будет отображаться. Можно использовать j вместо i, если это удобнее. Чтобы MathCAD показывал нужный вам символ (i или j), выберите «Формат числа» из меню «Математика», нажмите на кнопку «Глобальный» и переключите «Мн.ед.» на i или j.
MathCAD содержит следующие операторы и функции для работы с комплексными числами:
Re(z) – вещественная часть z.
Im(z) – мнимая часть z.
arg(z) – угол в комплексной плоскости между вещественной осью и z. Результат заключён между π и –π.

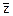
При использовании в комплексной области многие функции являются многозначными. Для многозначной функции MathCAD возвращает значение, составляющее на комплексной плоскости самый малый положительный угол с положительным направлением действительной оси, то есть главное значение.
Рисунок 3.4.1 – Комплексные числа в MathCAD
На рисунке 3.4.1 показан пример использования возможностей MathCADпри работе с комплексными числами.
Последнее изменение этой страницы: 2016-12-28; Нарушение авторского права страницы
Решение уравнений с помощью функции root(f(x),x)
Способы решения уравнений в MathCAD
Форматирование трехмерных графиков
Для форматирования графика необходимо дважды щелкнуть по области построения — появится окно форматирования с несколькими вкладками: Appearance,General,Axes,Lighting,Title,Backplanes,Special, Advanced, Quick Plot Data.
Назначение вкладки Quick Plot Data было рассмотрено выше.
Вкладка Appearance позволяет менять внешний вид графика. Поле Fill Options позволяет изменить параметры заливки, поле Line Option — параметры линий, Point Options — параметры точек.
Во вкладке General (общие) в группе View можно выбрать углы поворота изображенной поверхности вокруг всех трех осей; в группе Display asможно поменять тип графика.
Во вкладке Lighting (освещение) можно управлять освещением, установив флажок Enable Lighting (включить освещение) и переключатель On(включить). Одна из 6-ти возможных схем освещения выбирается в списке Lighting scheme(схема освещения).
В данном разделе мы узнаем, каким образом в системе MathCAD решаются простейшие уравнения вида F(x) = 0. Решить уравнение аналитически — значит найти все его корни, т.е. такие числа, при подстановке которых в исходное уравнение получим верное равенство. Решить уравнение графически — значит найти точки пересечения графика функции с осью ОХ.
Для решений уравнения с одним неизвестным вида F(x) = 0 существует специальная функция
root(f(x),x),
где f(x) — выражение, равное нулю;
Эта функция возвращает с заданной точностью значение переменной, при котором выражение f(x) равно 0.
Внимание. Если правая часть уравнения ¹0, то необходимо привести его к нормальному виду (перенести все в левую часть).
Перед использованием функции rootнеобходимо задать аргументу х начальное приближение. Если корней несколько, то для отыскания каждого корня необходимо задавать свое начальное приближение.
Внимание. Перед решением желательно построить график функции, чтобы проверить, есть ли корни (пересекает ли график ось Ох), и если есть, то сколько. Начальное приближение можно выбрать по графику поближе к точке пересечения.
Пример. Решение уравнения 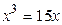
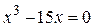
Рис. 3.1. Решение уравнения при помощи функции root
Для одновременного нахождения всех корней полинома используют функцию Polyroots(v),где v — вектор коэффициентов полинома, начиная со свободного члена.Нулевые коэффициенты опускать нельзя.В отличие от функции root функция Polyroots не требует начального приближения.
Пример. Решение уравнения 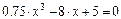
Рис. 3.2. Решение уравнения с помощью функции polyroots
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Как то на паре, один преподаватель сказал, когда лекция заканчивалась — это был конец пары: “Что-то тут концом пахнет”. 8526 — 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Для решения одного уравнения с одним неизвестным используется функция root. Аргументами этой функции являются выражение и переменная, входящая в выражение. Ищется значение переменной, при котором выражение обращается в ноль. Функция возвращает значение переменной, которое обращает выражение в ноль.
| root( f(z), z) | Возвращает значение z, при котором выражение или функция f(z) обращается в 0. Оба аргумента этой функции должны быть скалярами. Функция возвращает скаляр. |
Первый аргумент есть либо функция, определенная где-либо в рабочем документе, или выражение. Выражение должно возвращать скалярные значения.
Второй аргумент — имя переменной, которое используется в выражении. Это та переменная, варьируя которую Mathcad будет пытаться обратить выражение в ноль. Этой переменной перед использованием функции root необходимо присвоить числовое значение. Mathcad использует его как начальное приближение при поиске корня.
Рассмотрим пример, как найти a — решение уравнения e x = x 3 . Для этого выполните следующие шаги:
- Определите начальное значение переменной x. Введите x:3. Выбор начального приближения влияет на корень, возвращаемый Mathcad (если выражение имеет несколько корней).
- Определите выражение, которое должно быть обращено в ноль. Для этого перепишите уравнение e x = x 3 в виде x 3 — e x = 0. Левая часть этого выражения и является вторым аргументом функции root
- Определите переменную a как корень уравнения. Для этого введите a:root(x^3[Space]-e^x[Space],x).
- Напечатайте a=, чтобы увидеть значение корня.
При использовании функции root имейте в виду следующее:
- Удостоверьтесь, что переменной присвоено начальное значение до начала использования функции root.
- Для выражения с несколькими корнями, например x 2 — 1 = 0, начальное значение определяет корень, который будет найден Mathcad. На Рисунке 1 приведен пример, в котором функция root возвращает различные значения, каждое из которых зависит от начального приближения.
- Mathcad позволяет находить как комплексные, так и вещественные корни. Для поиска комплексного корня следует взять в качестве начального приближения комплексное число.
- Задача решения уравнения вида f(x) = g(x) эквивалентна задаче поиска корня выражения f(x) — g(x) =0. Для этого функция root может быть использована следующим образом:
Функция root предназначена для решения одного уравнения с одним неизвестным. Для решения систем уравнений используйте методику, описанную в следующем разделе “Системы уравнений”. Для символьного решения уравнений или нахождения точного численного решения уравнения в терминах элементарных функций выберите Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.
Рисунок 1: Использование графика и функции root для поиска корней уравнения.
Что делать, когда функция root не сходится
Mathcad в функции root использует для поиска корня метод секущей. Начальное значение, присвоенное переменной x, становится первым приближением к искомому корню. Когда значение выражения f(x) при очередном приближении становится меньше значения встроенной переменной TOL, корень считается найденным, и функция root возвращает результат.
Если после многих итераций Mathcad не может найти подходящего приближения, то появляется сообщение об ошибке “отсутствует сходимость”. Эта ошибка может быть вызвана следующими причинами:
- Уравнение не имеет корней.
- Корни уравнения расположены далеко от начального приближения.
- Выражение имеет локальные максимумы или минимумы между начальным приближением и корнями.
- Выражение имеет разрывы между начальным приближением и корнями.
- Выражение имеет комплексный корень, но начальное приближение было вещественным (или наоборот).
Чтобы установить причину ошибки, исследуйте график f(x). Он поможет выяснить наличие корней уравнения f(x)=0 и, если они есть, то определить приблизительно их значения. Чем точнее выбрано начальное приближение корня, тем быстрее функция root будет сходиться к точному значению. roots;using plots to find
Некоторые советы по использованию функции root
В этом разделе приведены несколько советов по использованию функции root:
- Для изменения точности, с которой функция root ищет корень, можно изменить значение встроенной переменной TOL. Если значение TOL увеличивается, функция root будет сходиться быстрее, но ответ будет менее точен. Если значение TOL уменьшается, функция root будет сходиться медленнее, но ответ будет более точен. Чтобы изменить значение TOL в определенной точке рабочего документа, используйте определение вида TOL := 0.01. Чтобы изменить значение TOL для всего рабочего документа, выберите из меню Математика команду Встроенные переменные и введите подходящее значение в поле TOL. Нажав “OK”, выберите из меню Математика команду Пересчитать всё, чтобы обновить все вычисления в рабочем документе с использованием нового значения переменной TOL.
- Если уравнение имеет несколько корней, пробуйте использовать различные начальные приближения, чтобы найти их. Использование графика функции полезно для нахождения числа корней выражения, их расположения и определения подходящих начальных приближений. Рисунок 1 показывает пример. Если два корня расположены близко друг от друга, можно уменьшить TOL, чтобы различить их.
- Если f(x) имеет малый наклон около искомого корня, функция может сходиться к значению r, отстоящему от корня достаточно далеко . В таких случаях для нахождения более точного значения корня необходимо уменьшить значение TOL. Другой вариант заключается в замене уравнения f(x)=0 на g(x)=0, где
Решение уравнений с параметром
Предположим, что нужно решать уравнение многократно при изменении одного из параметров этого уравнения. Например, пусть требуется решить уравнение для нескольких различных значений параметра a. Самый простой способ состоит в определении функции
Чтобы решить уравнение для конкретного значения параметра a, присвойте значение параметру a и начальное значение переменной x как аргументам этой функции. Затем найдите искомое значение корня, вводя выражение f(a,x)=.
Рисунок 2 показывает пример того, как такая функция может использоваться для нахождения корней исследуемого уравнения при различных значениях параметра. Обратите внимание, что, хотя начальное значение x непосредственно входит в определение функции, нет необходимости определять его в другом месте рабочего документа.
Рисунок 2: Определение функции пользователя с функцией root.
Нахождение корней полинома
Для нахождения корней выражения, имеющего вид
лучше использовать функцию polyroots, нежели root. В отличие от функции root, функция polyroots не требует начального приближения. Кроме того, функция polyroots возвращает сразу все корни, как вещественные, так и комплексные. На Рисунках 3 и 4 приведены примеры использования функции polyroots.
| polyroots(v) | Возвращает корни полинома степени . Коэффициенты полинома находятся в векторе v длины n+1. Возвращает вектор длины n, состоящий из корней полинома. |
Функция polyroots всегда возвращает значения корней полинома, найденные численно. Чтобы находить корни символьно, используйте команду Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.
Рисунок 3: Использование функции polyroots для решения задачи, изображенной на Рисунке 1.
Рисунок 4: Использование функции polyroots для поиска корней полинома.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Глава
5. Вычисление корней многочлена.
Многочлены (целые
рациональные функции) имеют совершенно
исключительное значение в математике,
поэтому вопрос о вычислении корней
(нулей) многочленов целесообразно
рассматривать отдельно.
В Mathcad
для вычисления корней многочленов
предусмотрены два способа: использование
встроенной функции polyroots,
работающей с числовым процессором и
применение оператора solve,
решающего широкий круг задач и работающего
с символьным процессором.
1. Функция
polyroots.
Аргументом функции
polyroots
является
вектор-столбец коэффициентов многочлена,
корни которого требуется вычислить
(начиная с коэффициента при нулевой
степени).
Пример
1.
Пусть
требуется вычислить корни многочлена:
Вектор-столбец
коэффициентов:
Для формирования
вектора коэффициентов удобно использовать
оператор coeffs
из палитры Symbolic.
Пример
2.
Пусть
требуется вычислить корни многочлена:
Сформируем
вектор-столбец его коэффициентов:
Подчеркнем, что
оператор coeffs
не нуждается в том, чтобы многочлен был
записан в канонической форме. Если
многочлен задан в форме сумм и произведений
(см. пример
3), то
оператор coeffs
сам преобразует его к канонической
форме и сформирует вектор коэффициентов.
Замечание.
Для того, чтобы представить многочлен
в канонической форме служит оператор
collect
из палитры Symbolic.
Пример
3.
Пусть
дан многочлен:
Построим
вектор-столбец его коэффициентов:
Теперь
представим многочлен q(x) в канонической
форме:
По умолчанию для
поиска корней полинома используется
метод ЛаГерра (LaGuerre),
но функция polyroots
может использовать также и метод
матриц-компаньонов. Чтобы выбрать именно
этот метод, поставьте курсор мыши на
функцию polyroots
и щелкните правой кнопкой мыши. Теперь
вам достаточно выбрать пункт Companion
Matrix из
всплывающего меню. Какой из двух численных
методов выбрать? Почему Mathcad
отдает предпочтение методу
LaGuerre,
а не Companion
Matrix? Теория
численных методов не дает однозначного
ответа на первый вопрос. В приведенных
ниже примерах метод Companion
Matrix
демонстрирует более высокую точность,
чем метод LaGuerre.
Но это ничего не доказывает. Можно только
отметить, что в силу ряда причин точность
метода LaGuerre
резко падает с возрастанием степени
многочлена. Что касается второго вопроса,
то, по-видимому, разработчики численного
процессора Mathcad
исходили из того, что метод LaGuerre
имеет репутацию исключительно надежного
метода счета. На наш взгляд, за исключением
очень простых случаев, целесообразно
вычислять корни двумя методами, а затем,
подставив полученные значения корней
в многочлен, оценить точность (см. пример
4).
Пример
4.
Пусть
дан многочлен:
Построим
вектор-столбец его коэффициентов:
Используем
вначале метод LaGuerre:
Теперь
воспользуемся методом Companion Matrix:
Заканчивая описание
функции polyroots,
отметим одно ее чрезвычайно важное
свойство. Функция polyroots
может вычислять корни многочленов с
комплексными коэффициентами (см. пример
5).
Пусть
дан многочлен:
Пример
5.
Построим
вектор-столбец его коэффициентов:
Используем
вначале метод LaGuerre:
Теперь
воспользуемся методом Companion Matrix:
2. Оператор solve.
Оператор solve
исключительно
прост в использовании. Не требуется
формировать вектор коэффициентов,
достаточно записать многочлен
(необязательно в канонической форме),
а затем ввести оператор
solve
из палитры
Symbolic.
Так как оператор
solve
работает с
символьным процессором, необходимо
учитывать, что, в зависимости от вида
операнда, задача будет решаться точно
или численным методом. Если вместе с
оператором
solve
используется оператор float,
символьный процессор использует
численный
метод.
Замечание.
Если символьный процессор, получив
инструкцию решить задачу точно, не смог
найти решение, он, не прибегая к помощи
численного процессора для поиска
приближенного решения, выдаст сообщение
“No
solution
found”
(решение не найдено).
Оператор solve
(если вместе с ним не используется
оператор float)
даст указание символьному
процессору найти корни уравнения точно,
если все числа в многочлене записаны
без десятичной точки. Кроме целых чисел
в записи многочлена могут содержаться
радикалы из целых положительных чисел,
а также символы π
и е.
Что понимает
символьный процессор под точным
определением корней?
Очевидно, что в том случае, когда все
корни уравнения рациональные числа, их
следует вычислить без погрешности. Но,
кроме этого, символьный процессор может
записать корни в форме радикалов, а если
это не удается, в форме тригонометрических
выражений (см. пример
6).
Пример
6.
Если коэффициенты
многочлена содержат десятичную точку,
то символьный процессор получит указание
найти численные значения корней и
записать их, используя двадцатиразрядные
числа.
Замечание.
В Mathcad
14.0 вы получите тот же результат, но в
показательной форме.
Какой численный
метод использует Mathcad
для нахождения корней? К сожалению,
фирма MathSoft
не сообщает этого пользователю. (Вообще,
«Руководство пользователя» и справочная
система Mathcad
ничего не сообщают о методах, используемых
в работе символьного процессора.)
В целом, корни
многочленов с действительными
коэффициентами символьный процессор
находит точнее, чем численный процессор.
Отметим одну
деталь. Иногда при вычислении кратных
корней символьный процессор сообщает
пользователю только об одном из них
(см. пример
7).
Пример
7.
Замечание.
В Mathcad
14.0 вы получите при решении того же
примера следующий результат:
Если многочлен
имеет комплексные коэффициенты, то
использование оператора solve
может не дать результата. До
14-той версии Mathcad
при вычислении корней многочлена с
комплексными коэффициентами
оператор solve
зачастую
выдает только один корень. Но
он может, вообще говоря, найти и все n
корней (если многочлен ему понравится).
(См. примеры
8 и
9).
Пример
8.
Ограничим
число разрядов в ответе:
Оператор float,
задающий число разрядов в получаемом
символьным процессором результате,
также как и оператор solve
берется из палитры Symbolic.
Замечание.
Mathcad
14.0 в этом случае найдет все пять корней
многочлена.
Пример
9.
Дан
многочлен:
Найдем
его корни с помощью оператора solve:
3. Проблемы при
вычислении корней многочлена.
При использовании
любого численного метода принципиально
возможны два дефекта:
-
низкая точность
вычисления корней; -
зацикливание,
когда вообще не удается получить
результат.
Сложность задачи
вычисления корней зависит от:
-
близости корней.
Чем меньше расстояние между корнями,
тем труднее задача. -
степени многочлена.
Чем выше степень, тем труднее получить
значения всех корней с высокой точностью.
Задача вычисления
корней многочлена очень чувствительна
к изменению значений коэффициентов.
Рассмотрим два
многочлена:
h1(z)
= (z
– 2)3 =
0 и h2(z)
= (z
– 2)3 –
10-6 =
0
Значения младших
коэффициентов многочленов h1(z)
и h2(z)
различаются
на 0.000001. А значения корней –на 0.01, причем
два корня стали комплексными!
|
h1(z) |
h2(z) |
|
z1 |
z1 |
|
z2 |
z2 |
|
z3 |
z3 |
Итоговые
упражнения.
-
Найти все
коэффициенты многочлена: (x-2)·(x-3.7)·(x-5)
и представить его в канонической форме. -
Найти все корни
многочлена: 1.7x6
+
3.8x4
–5.7x3
+
1.9x2
–
0.4x
+1.1 = 0. -
Найти все корни
многочлена: z5-1=0
различными
способами. -
Найти все корни
многочлена: z3+(3.2-1.4i)·z+1=0
79
Соседние файлы в папке методичка
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
|
0 / 0 / 0 Регистрация: 15.12.2021 Сообщений: 72 |
|
|
1 |
|
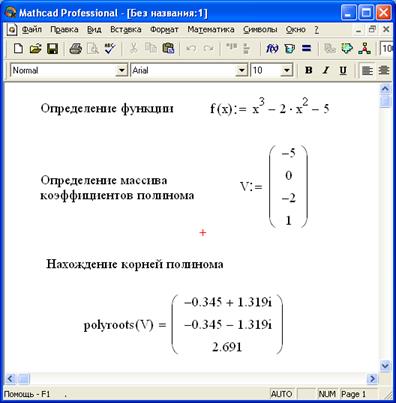
Найти все корни многочлена (полинома)25.04.2022, 21:38. Показов 2253. Ответов 13
Здравствуйте! Дана такая задача: Найти все корни многочлена (полинома). Построить график в области действительных корней. Помогите, пожалуйста!
0 |
|
8710 / 6313 / 3390 Регистрация: 14.01.2014 Сообщений: 14,491 |
|
|
25.04.2022, 22:05 |
3 |
|
РешениеВот так можно Миниатюры
1 |
|
0 / 0 / 0 Регистрация: 15.12.2021 Сообщений: 72 |
|
|
26.04.2022, 08:47 [ТС] |
4 |
|
mathmichel, попробовал, значения совпадают, но график другой. Что я сделал не так?
0 |
|
2132 / 1491 / 760 Регистрация: 25.12.2016 Сообщений: 4,242 |
|
|
26.04.2022, 08:50 |
5 |
|
Что я сделал не так? если приглядеться,то пределы по осям разные выставлены.
1 |
|
0 / 0 / 0 Регистрация: 15.12.2021 Сообщений: 72 |
|
|
26.04.2022, 08:55 [ТС] |
6 |
|
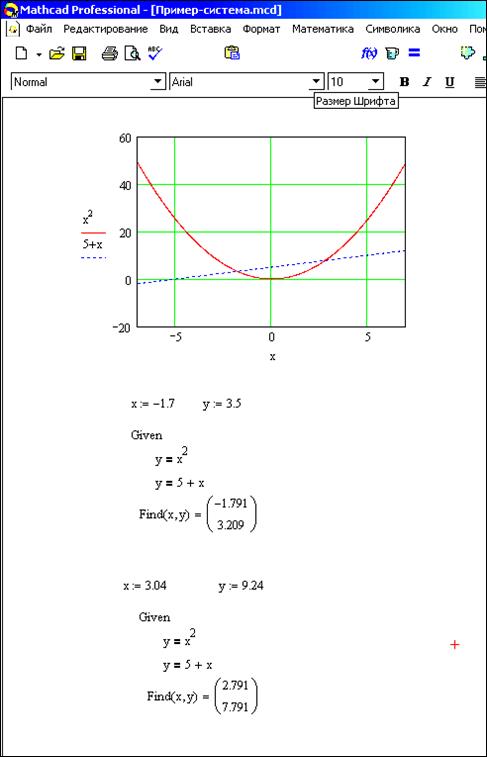
nick55782012, Спасибо! Исправил. А как ещё сделать, чтобы оси показывались, как у человека выше, а не значение вокруг, как у меня?
0 |
|
2132 / 1491 / 760 Регистрация: 25.12.2016 Сообщений: 4,242 |
|
|
26.04.2022, 09:01 |
7 |
|
переменную х выставить до графика в пределах от -3 до 1 с шагом,например 0,1
1 |
|
0 / 0 / 0 Регистрация: 15.12.2021 Сообщений: 72 |
|
|
26.04.2022, 11:04 [ТС] |
8 |
|
nick55782012, можете помочь, как осуществить проверку методом подстановки здесь?
0 |
|
2132 / 1491 / 760 Регистрация: 25.12.2016 Сообщений: 4,242 |
|
|
26.04.2022, 11:11 |
9 |
|
можно так. Миниатюры
1 |
|
0 / 0 / 0 Регистрация: 15.12.2021 Сообщений: 72 |
|
|
26.04.2022, 11:21 [ТС] |
10 |
|
nick55782012, у меня почему-то значения в f(xk) другие получаются
0 |
|
2132 / 1491 / 760 Регистрация: 25.12.2016 Сообщений: 4,242 |
|
|
26.04.2022, 11:23 |
11 |
|
в -10 и в -11 степени это практически ноль,округлите до трех значащих цифр после запятой.
1 |
|
0 / 0 / 0 Регистрация: 15.12.2021 Сообщений: 72 |
|
|
26.04.2022, 11:31 [ТС] |
12 |
|
nick55782012, у меня не так?
0 |
|
2132 / 1491 / 760 Регистрация: 25.12.2016 Сообщений: 4,242 |
|
|
26.04.2022, 11:32 |
13 |
|
выберите вторую строчку.
1 |
|
0 / 0 / 0 Регистрация: 15.12.2021 Сообщений: 72 |
|
|
26.04.2022, 11:33 [ТС] |
14 |
|
nick55782012, фух, спасибо! Получилось
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
26.04.2022, 11:33 |
|
Помогаю со студенческими работами здесь отобразить корни полинома на графике Линейные, нелинейные уравнения, упращение выражения, корни полинома Найти значения полинома в точках и найти корни полинома! Найти корни характеристического многочлена Найти корни характеристического уравнения EMBED… Как найти корни полинома нескольких переменных? Найти корни полинома и построить его график Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 14 |
































 Сообщение было отмечено sunheaZ как решение
Сообщение было отмечено sunheaZ как решение

