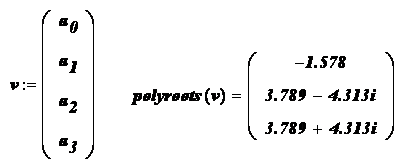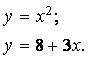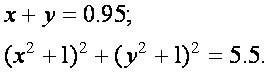Решение
нелинейных уравнений
Вычисление корней численными методами включает два основных
этапа:
· отделение корней;
· уточнение корней до заданной точности.
Рассмотрим
эти два этапа подробно.
Отделение
корней нелинейного уравнения
Учитывая легкость построения графиков функций в MathCAD,
в дальнейшем будет использоваться графический метод отделения корней.
Пример. Дано
алгебраическое уравнение
.
Определить интервалы локализации корней этого уравнения.
Пример. Дано
алгебраическое уравнение
.
Определить
интервалы локализации корней этого уравнения.
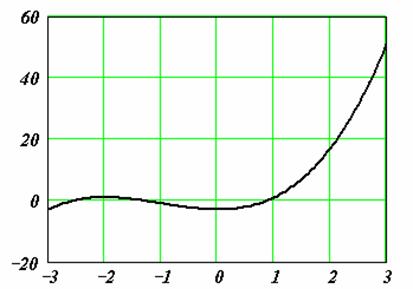
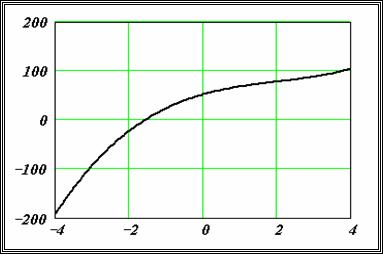
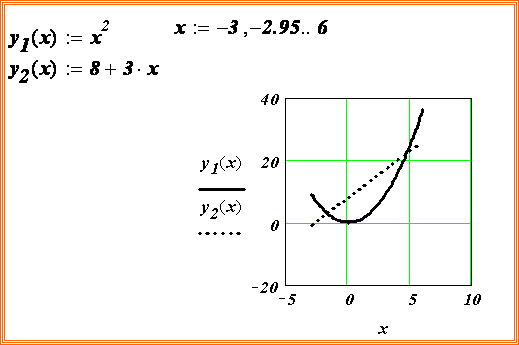
На рисунке приведен график
функции , построенный в MathCAD. Видно,
что в качестве интервала изоляции можно принять интервал . Однако уравнение имеет три корня.
Следовательно, можно сделать вывод о наличии еще двух комплексных корней. ¨
Уточнение
корней нелинейного уравнения
Для уточнения корня используются специальные вычислительные
методы такие, как метод деления отрезка пополам, метод хорд, метод касательных
(метод Ньютона) и многие другие.
Функция root. В MathCAD для уточнения корней любого нелинейного уравнения
(не обязательно только алгебраического) введена функция root, которая может иметь два или
четыре аргумента, т.е. или
, где
– имя функции или арифметическое выражение,
соответствующее решаемому нелинейному уравнению, – скалярная переменная, относительно которой
решается уравнение, –
границы интервала локализации корня.
Пример.
Используя функцию ,
найти все три корня уравнения , включая и два комплексных.
Заметим, что для вычисления всех трех корней
использовался прием понижения порядка алгебраического уравнения, рассмотренный в
п. 8.1.1. ¨
Функция root с двумя
аргументами требует задания (до обращения к функции) переменной начального значения корня из интервала
локализации.
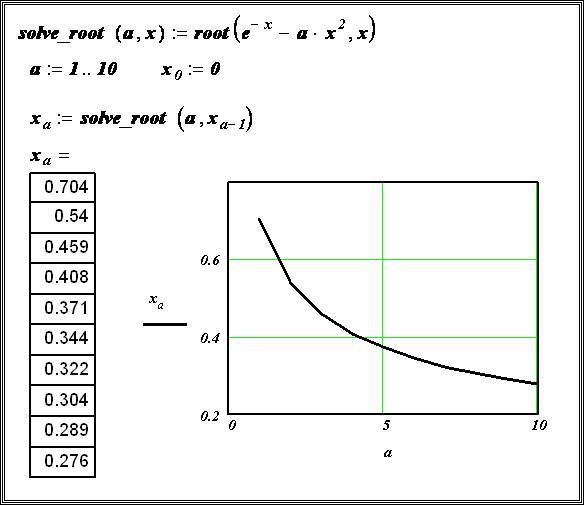
Пример 8.1.5.
Используя функцию root, вычислить
изменения корня нелинейного уравнения при изменении коэффициента а от 1 до
10 с шагом 1.
Функция polyroots.
Для вычисления всех корней алгебраического
уравнения порядка (не
выше 5) рекомендуется использовать функцию polyroots. Обращение к этой функции имеет
вид polyroots(v), где v – вектор, состоящий из n +1 проекций, равных коэффициентам
алгебраического уравнения, т.е. . Эта
функция не требует проведения процедуры локализации корней.
Пример.
Используя функцию polyroots, найти все три корня уравнения , включая и два комплексных
Блок Given. При уточнении корня нелинейного уравнения можно
использовать специальный вычислительный блок Given, имеющий
следующую структуру:
Решаемое уравнение задается в виде равенства, в котором
используется «жирный» знак равно, вводимый с палитры Логический.
Ограничения содержат равенства или неравенства, которым
должен удовлетворять искомый корень.
Функция Find
уточняет корень уравнения, вызов этой функции имеет вид Find(x), где x –
переменная, по которой уточняется корень. Если корня уравнения на
заданном интервале не существует, то следует вызвать функцию Minerr(x), которая
возвращает приближенное значение корня.
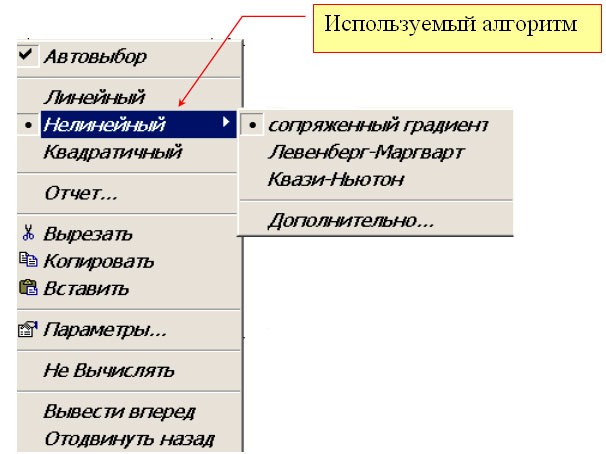
Для выбора алгоритма уточнения корня необходимо
щелкнуть правой кнопкой мыши на имени функции Find(x) и в появившемся контекстном меню (см. рисунок) выбрать
подходящий алгоритм.
Аналогично можно задать алгоритм решения и для функции
Minerr(x).
Использование численных методов в
функциях Find(x), Minerr(x)
требует перед блоком Given задать начальные
значения переменным, по которым осуществляется поиск корней уравнения.
Пример. Используя блок Given, вычислите корень уравнения в интервале отделения
.
Решение
систем уравнений
В зависимости от того, какие функции входят в систему
уравнений, можно выделить два класса систем:
· алгебраические системы уравнений;
· трансцендентные системы уравнений.
Среди алгебраических систем уравнений особое место
занимают системы линейных алгебраических уравнений (СЛАУ).
Системы
линейных алгебраических уравнений
Системой линейных алгебраических уравнений (СЛАУ) называется
система вида:
В матричном виде систему можно записать как
,
где
– матрица
размерности ,
– вектор с
проекциями.
Для вычисления решения СЛАУ следует использовать функцию
lsolve, обращение
к которой имеет вид: lsolve(А,b), где А – матрица системы, – вектор правой части.
Решение
систем нелинейных уравнений
MathCAD
дает возможность находить решение системы уравнений численными методами, при
этом максимальное число уравнений в MathCAD2001i
доведено до 200.
Для решения системы уравнений
необходимо выполнить следующие этапы.
Задание начального
приближения для
всех неизвестных, входящих в систему уравнений. При небольшом числе неизвестных
этот этап можно выполнить графически, как показано в примере.
Пример. Дана система уравнений:
Определить начальные
приближения для решений этой системы.
Видно, что система имеет
два решения: для первого решения в качестве начального приближения может быть
принята точка (-2, 2), а для второго решения – точка (5, 20). ¨
Вычисление решения
системы уравнений с заданной точностью. Для этого используется уже известный вычислительный
блок Given.
Функция
Find вычисляет решение системы уравнений с заданной точностью, и вызов этой
функции имеет вид Find(x), где x – список переменных, по которым ищется решение.
Начальные значения этим переменным задаются в блоке < Начальные условия
>. Число аргументов функции должно быть равно числу неизвестных.
Следующие выражения
недопустимы внутри блока решения:
·
ограничения со
знаком ¹;
·
дискретная
переменная или выражения, содержащие дискретную переменную в любой форме;
·
блоки решения
уравнений не могут быть вложены друг в друга, каждый блок может иметь только
одно ключевое слово Given и
имя функции Find (или Minerr).
Пример. Используя блок Given, вычислить все решения системы предыдущего примера.
Выполнить проверку найденных решений.
Пример. Используя
функцию , вычислите решение системы уравнений
Решение нелинейных уравнений и систем уравнений в пакете MathCAD
Решение нелинейных уравнений
Вычисление корней численными методами включает два основных этапа:
· уточнение корней до заданной точности.
Рассмотрим эти два этапа подробно.
Отделение корней нелинейного уравнения
Учитывая легкость построения графиков функций в MathCAD , в дальнейшем будет использоваться графический метод отделения корней.
Пример. Дано алгебраическое уравнение
.
Определить интервалы локализации корней этого уравнения.
Пример. Дано алгебраическое уравнение
.
Определить интервалы локализации корней этого уравнения.
На рисунке приведен график функции , построенный в MathCAD . Видно, что в качестве интервала изоляции можно принять интервал . Однако уравнение имеет три корня. Следовательно, можно сделать вывод о наличии еще двух комплексных корней. ¨
Уточнение корней нелинейного уравнения
Для уточнения корня используются специальные вычислительные методы такие, как метод деления отрезка пополам, метод хорд, метод касательных (метод Ньютона) и многие другие.
Функция root . В MathCAD для уточнения корней любого нелинейного уравнения (не обязательно только алгебраического) введена функция root , которая может иметь два или четыре аргумента, т.е. или , где – имя функции или арифметическое выражение, соответствующее решаемому нелинейному уравнению, – скалярная переменная, относительно которой решается уравнение, – границы интервала локализации корня.
Пример. Используя функцию , найти все три корня уравнения , включая и два комплексных.
Заметим, что для вычисления всех трех корней использовался прием понижения порядка алгебраического уравнения, рассмотренный в п. 8.1.1. ¨
Функция root с двумя аргументами требует задания (до обращения к функции) переменной начального значения корня из интервала локализации.
Пример 8.1.5. Используя функцию root , вычислить изменения корня нелинейного уравнения при изменении коэффициента а от 1 до 10 с шагом 1.
Функция polyroots . Для вычисления всех корней алгебраического уравнения порядка (не выше 5) рекомендуется использовать функцию polyroots . Обращение к этой функции имеет вид polyroots (v) , где v – вектор, состоящий из n +1 проекций, равных коэффициентам алгебраического уравнения, т.е. . Эта функция не требует проведения процедуры локализации корней.
Пример. Используя функцию polyroots , найти все три корня уравнения , включая и два комплексных
Блок Given . При уточнении корня нелинейного уравнения можно использовать специальный вычислительный блок Given , имеющий следующую структуру:
Решаемое уравнение задается в виде равенства, в котором используется «жирный» знак равно, вводимый с палитры Логический .
Ограничения содержат равенства или неравенства, которым должен удовлетворять искомый корень.
Функция Find уточняет корень уравнения, вызов этой функции имеет вид Find ( x ), где x – переменная, по которой уточняется корень. Если корня уравнения на заданном интервале не существует, то следует вызвать функцию Minerr ( x ), которая возвращает приближенное значение корня.
Для выбора алгоритма уточнения корня необходимо щелкнуть правой кнопкой мыши на имени функции Find ( x ) и в появившемся контекстном меню (см. рисунок) выбрать подходящий алгоритм.
Аналогично можно задать алгоритм решения и для функции Minerr ( x ).
Использование численных методов в функциях Find ( x ), Minerr ( x ) требует перед блоком Given задать начальные значения переменным, по которым осуществляется поиск корней уравнения.
Пример. Используя блок Given , вычислите корень уравнения в интервале отделения .
Решение систем уравнений
В зависимости от того, какие функции входят в систему уравнений, можно выделить два класса систем:
· алгебраические системы уравнений;
· трансцендентные системы уравнений.
Среди алгебраических систем уравнений особое место занимают системы линейных алгебраических уравнений (СЛАУ).
Системы линейных алгебраических уравнений
Системой линейных алгебраических уравнений (СЛАУ) называется система вида:
В матричном виде систему можно записать как
,
где – матрица размерности , – вектор с проекциями.
Для вычисления решения СЛАУ следует использовать функцию lsolve , обращение к которой имеет вид: lsolve (А, b ), где А – матрица системы, – вектор правой части.
Решение систем нелинейных уравнений
MathCAD дает возможность находить решение системы уравнений численными методами, при этом максимальное число уравнений в MathCAD 2001 i доведено до 200.
Для решения системы уравнений необходимо выполнить следующие этапы.
Задание начального приближения для всех неизвестных, входящих в систему уравнений. При небольшом числе неизвестных этот этап можно выполнить графически, как показано в примере.
Пример. Дана система уравнений:
Определить начальные приближения для решений этой системы.
Видно, что система имеет два решения: для первого решения в качестве начального приближения может быть принята точка (-2, 2), а для второго решения – точка (5, 20). ¨
Вычисление решения системы уравнений с заданной точностью . Для этого используется уже известный вычислительный блок Given .
Функция Find вычисляет решение системы уравнений с заданной точностью, и вызов этой функции имеет вид Find ( x ), где x – список переменных, по которым ищется решение. Начальные значения этим переменным задаются в блоке . Число аргументов функции должно быть равно числу неизвестных.
Следующие выражения недопустимы внутри блока решения:
· ограничения со знаком ¹ ;
· дискретная переменная или выражения, содержащие дискретную переменную в любой форме;
· блоки решения уравнений не могут быть вложены друг в друга, каждый блок может иметь только одно ключевое слово Given и имя функции Find (или Minerr ).
Пример. Используя блок Given , вычислить все решения системы предыдущего примера. Выполнить проверку найденных решений.
Пример. Используя функцию , вычислите решение системы уравнений
Решение нелинейных уравнений в Excel и Mathcad (стр. 1 )
 |
Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 |
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
Кафедра прикладной математики и вычислительной техники
Решение нелинейных уравнений в Excel и Mathcad
к выполнению лабораторных работ
по дисциплине «Вычислительная математика»
Решение нелинейных уравнений в Excel и Mathcad: Метод. указ. / Сост. , – Самара: СГАСУ, 20с.
Методические указания разработаны в соответствии с Государственным образовательным стандартом изучения дисциплины «Вычислительная математика».
Рассмотрена реализация численных методов при решении нелинейных уравнений и систем уравнений в Excel и MathCad. Приведены варианты заданий для индивидуального выполнения и вопросы для самоконтроля и тестирования.
Предназначены для студентов специальности 230201 – «Информационные системы и технологии» всех форм обучения.
Рецензент к. ф-м. н.
Ó , составление, 2012
1 Решение нелинейного уравнения
1.1 Общие сведения о решении нелинейного уравнения
1.2 Отделение корней
1.3 Уточнение корней стандартными средствами Excel и Mathcad
1.4 Метод деления отрезка пополам
1.6 Метод Ньютона (касательных)
1.7 Комбинированный метод
1.8 Метод итераций
2 Решение систем нелинейных уравнений
2.1 Общие сведения о решении систем нелинейных уравнений
2.2 Решение систем нелинейных уравнений методом Ньютона
2.3 Решение систем нелинейных уравнений методами итераций
3 Задания к лабораторным работам
Лабораторная № 1. Отделение корней и стандартные инструменты решения нелинейного уравнения
Лабораторная № 2. Сравнение методов уточнения корней нелинейного уравнения
Лабораторная № 3. Решение систем нелинейных уравнений
Лабораторная № 4. Программирование методов решения нелинейных уравнений и систем
4 Вопросы и тесты для самоконтроля
Список рекомендуемой литературы
1 Решение нелинейного уравнения
1.1 Общие сведения о решении нелинейного уравнения
Как правило, нелинейное уравнения общего вида f(х)=0 невозможно решить аналитически. Для практических задач достаточно найти приближенное значение x, в определенном смысле близкое к точному решению уравнения хточн.
В большинстве случаев поиск приближенного решения включает два этапа. На первом этапе отделяют корни, т. е. находят такие отрезки, внутри которых находится строго один корень. На втором этапе уточняют корень на одном из таких отрезков, т. е. находят его значение с требуемой точностью.
Достигнутая точность может оцениваться либо «по функции» (в найденной точке x, функция достаточно близка к 0, т. е. выполняется условие |f(x)|≤ ef, где ef требуемая точность по оси ординат), либо «по аргументу» (найден достаточно маленький отрезок [a,b], внутри которого находится корень, т. е. |b–a|≤ ex, где ex требуемая точность по оси абсцисс).
1.2 Отделение корней
Отделение корней может производиться сочетанием графического и аналитического исследования функции. Такое исследование опирается на теорему Вейерштрасса, в соответствии с которой для непрерывной на отрезке [a,b] функции f(х) и любого числа y, отвечающего условию f(a)≤y≤f(b), существует на этом отрезке точка x, в которой функция равна y. Следовательно, для непрерывной функции достаточно найти отрезок, на концах которого функция имеет разные знаки, и можно быть уверенным, что на этом отрезке есть корень уравнения f(х)=0.
Для ряда методов уточнения желательно, чтобы найденный на первом этапе отрезок содержал только один корень уравнения. Это условие выполняется, если функция на отрезке монотонна. Монотонность, можно проверить либо по графику функции, либо по знаку производной.
Пример Найти с точностью до целых все корни нелинейного уравнения y(x)=x3 ‑ 10x + 7=0 а) построив таблицу и б) построив график. Найти корень уравнения на выделенном отрезке, используя опции «Подбор параметра» и «Поиск решения».
Решение Создадим в Excel таблицу, содержащую аргументы и значения функции и по ней построим точечную диаграмму. На рисунке 1 приведен снимок решения.
На графике видно, что уравнение имеет три корня, принадлежащие отрезкам [-4, -3], [0, 1] и [2, 3]. Эти отрезки можно выявить и наблюдая за сменой знаков функции в таблице. По построенному графику можно сделать вывод, что на указанных отрезках функция f(x) монотонна и, следовательно, на каждом из них содержится только по одному корню.
Такой же анализ может быть выполнен и в пакете Mathcad. Для этого достаточно набрать определение функции f(x), используя оператор присваивания (:=) и естественные общепринятые обозначения математических операций и стандартных функций, задать цикл для изменения аргумента, например, а затем вывести на экран таблицу значений функции (расположенными в одной строке командами x= f(x)=) и график. Цикл можно задать, например, командой x:=-5,-4.5…5. Шаг цикла формируется путем задания начального и следующего за ним значений переменной, а перед конечным значением переменной ставится точка с запятой, которая будет визуально отображена на экране в виде многоточия.
Рисунок 1 – Таблица и график для отделения корней нелинейного уравнения
1.3 Уточнение корней стандартными средствами Excel и Mathcad
Во всех методах уточнения корней необходимо задать начальное приближение, которое затем и будет уточняться. Если уравнение имеет несколько корней, в зависимости от выбранного начального приближения будет найден один из них. При неудачно выбранном начальном приближении решение может и не быть найдено. Если в результате первого этапа расчетов уже выделен отрезок, содержащий единственный корень уравнения, в качестве начального приближения можно взять любую точку этого отрезка.
В Excel для уточнения значений корней можно использовать опции «Подбор параметра» и «Поиск решения». Пример оформления решения приведен на рисунках 2 и 3.
Рисунок 2 – Ввод значений для использования средств решения уравнения в Excel
Рисунок 3 – Результаты использования средств решения уравнения в Excel
В Mathcad для уточнения корней уравнения можно использовать функцию root(….) или блок решения. Пример использования функции root(…) приведен на рисунке 4, а блока решения на рисунке 5. Следует обратить внимание, что в блоке решения (после заголовка блока Given) между левой и правой частями уравнения должен стоять жирный знак равенства (тождества), который можно получить выбором из соответствующей палитры инструментов, либо нажатием одновременно клавиши Ctrl и =.

Рисунок 5 – Решение уравнения с использованием блока решения в Mathcad
Как видим, каждый стандартный инструмент находит решение уравнения с определенной точностью. Эта точность зависит от метода, используемого в пакете и, в определенной степени, настроек пакета. Управлять точностью результата здесь достаточно сложно, а часто и невозможно.
В то же время, очень просто построить собственную таблицу или написать программу, реализующие один из методов уточнения корней. Здесь можно использовать критерии точности расчета, задаваемые пользователем. При этом достигается и понимание процесса расчетов без опоры на принцип Митрофанушки: «Извозчик есть, довезет».
Далее рассмотрены несколько наиболее распространенных методов. Отметим очевидный момент: при прочих равных условиях тот метод уточнения корней будет более эффективен, в котором результат с той же погрешностью найден с меньшим числом вычислений функции f(x) (при этом достигается и максимальная точность при одинаковом числе вычислений функции).
1.4 Метод деления отрезка пополам
В этом методе на каждом шаге отрезок делится на две равные части. Затем сравнивают знаки функции на концах каждой из двух половинок (например, по знаку произведения значений функций на концах), определяют ту из них, в которой содержится решение (знаки функции на концах должны быть разные), и. сужают отрезок, перенося в найденную точку его границу (а или b). Условием окончания служит малость отрезка, где содержится корень («точность по x»), либо близость к 0 значения функции в средине отрезка («точность по y»). Решением уравнения считают середину отрезка, найденного на последнем шаге.
Пример. Построить таблицу для уточнения корня уравнения x3 –10x+7=0 на отрезке [-4, -3] методом деления отрезка пополам. Определить сколько шагов надо сделать методом деления отрезка пополам и какая при этом достигается точность по х, для достижения точности по y, равной 0,1; 0,01; 0, 001.
Решение Для решения можно использовать табличный процессор Excel, позволяющий автоматически продолжать строки. На первом шаге заносим в таблицу значения левого и правого концов выбранного начального отрезка и вычисляем значение середины отрезка с=(a+b)/2, а затем вводим формулу для вычисления функции в точке a (f(a)) и растягиваем (копируем) её для вычисления f(c) и f(b). В последнем столбца вычисляем выражение (b–a)/2, характеризующего степень точности вычислений. Все набранные формулы можно скопировать во вторую строку таблицы.
На втором шаге нужно автоматизировать процесс поиска той половины отрезка, где содержится корень. Для этого испльзуется логическая функция ЕСЛИ (Меню: Вставка

Вторую строку таблицы можно продолжить (скопировать) на необходимое число последующих строк.
Итерационный процесс завершается, когда очередное значение в последнем столбце становится меньшим, чем заданный показатель точности ex. При этом, значение середины отрезка в последнем приближении, принимается в качестве приближенного значения искомого корня нелинейного уравнения. На рисунке 6 приведен снимок решения. Для построения аналогичного процесса в Mathcad можно использовать бланк, подобный приведенному на рисунке 7. Число шагов N может варьироваться до достижения в таблице результатов требуемой точности. При этом таблица будет автоматически удлиняться или укорачиваться.
Итак, одним из трех корней нелинейного уравнения x3 – 10x + 7=0, найденным с точностью e=0,0001, является x= – 3,46686. Как мы видим, он действительно принадлежит отрезку [-4; -3].
Рисунок 6 – Уточнение корня методом деления отрезка пополам в Excel
Рисунок 7 – Уточнение корня методом деления отрезка пополам в Mathcad
1.5 Метод хорд
В этом методе нелинейная функция f(x) на отделенном интервале [а, b] заменяется линейной – уравнением хорды, т. е. прямой соединяющей граничные точки графика на отрезке. Условие применимости метода – монотонность функции на начальном отрезке, обеспечивающая единственность корня на этом отрезке. Расчет по методу хорд аналогичен расчету методом деления отрезка пополам, но теперь на каждом шаге новая точка x внутри отрезка [a,b] рассчитывается по любой из следующих формул:

1.6 Метод Ньютона (касательных)
Идея, на которой основан метод, аналогична той, которая реализована в методе хорд, только на каждом шаге кривая f(x) заменяется касательной к ней, проведенной в предыдущей найденной точке. В качестве начальной точки в зависимости от свойств функции берется или левая граница отрезка, содержащего корень – x0 = а (если f(а) f”(х) > 0), или правая его граница: x0 = b (если f(b) f”(х)>0). Расчет нового приближения на следующем шаге i+1 производится по формуле:

Алгоритм применим для монотонных функций, сохраняющих выпуклость или вогнутость в промежутке между начальным приближением и корнем уравнения (т. е. должен сохраняться знак первой и второй производных функции f(x)). работоспособен при выпуклых и монотонных функциях f(x). В расчетах нет необходимости отслеживать две границы отрезка, поэтому достаточно на каждом шаге вычислять значения x, f(x) и f′(x). При этом легко оценить «точность по y», по значению левой части уравнения на очередном шаге. Для оценки «точности по x» нужно отслеживать разницу приближений на предыдущем и последующих шагах, которая связана с разницей между найденным приближением и точным значением корня.
Следует обратить внимание на следующую особенность метода: последовательность x1, x2, x3,… приближается к корню с другой стороны, в отличие от использования метода хорд при прочих равных условиях.
Главным достоинством метода касательных является квадратичная скорость сходимости, что во многих случаях может привести к сокращению числа вычислений функции.
Уточнить корень уравнения tg (0,55x+0,1) – x2=0 на отрезке [0.6, 0.8] методом касательных до точности 0,001.
Точность вычислений можно оценить из соотношения
2 Решение систем нелинейных уравнений
2.1 Общие сведения о решении систем нелинейных уравнений
Систему n нелинейных уравнений с n неизвестными x1, x2, . xn записывают в виде:
где F1, F2,…, Fn – функции независимых переменных, среди которых есть нелинейные.
Как и в случае систем линейных уравнений, решением системы является такой вектор X*, который при подстановке обращает одновременно все уравнения системы в тождества.
Система уравнений может не иметь решений, иметь единственное решение, конечное или бесконечное количество решений. Вопрос о количестве решений должен решаться для каждой конкретной задачи отдельно.
Численные методы решения системы уравнений носят итерационный характер и требуют задания начального приближения X0.
Рассмотрим две группы таких методов: метод Ньютона с различными его модификациями и методы итераций (простых итераций и Зейделя).
2.2 Решение систем нелинейных уравнений методом Ньютона
Будем рассматривать этот метод на примере системы двух нелинейных уравнений с двумя неизвестными:
Начальные значения x0 и y0 определяются графически. Для нахождения каждого последующего приближения (xi+1, yi+1) используют вектор значений функций и матрицу значений их первых производных, рассчитанные в предыдущей точке (xi, yi).

Для расчета новых приближений на шаге i+1 используется матричная формула

Следует обратить внимание, что в последней формуле используется вычисление матрицы, обратной к матрице первых производных.
Расчет останавливают при выполнении одного (а иногда и обоих) из двух условий. Первое из них заключается в том, что на очередном шаге максимальное по модулю из изменений аргументов x и y становится меньше заданная погрешность по аргументам. В соответствии со вторым из условий, на очередном шаге максимальное по модулю значение левых частей уравнений должно отличаться от нуля меньше, чем заданная погрешность по функциям.
В упрощенном методе Ньютона матрица производных и матрица, обратная к ней вычисляются только один раз (в начальной точке) и для расчетов используется матричная формула

Приведенные формулы особенно легко записать в Mathcad, где имеются операторы для вычисления производных и действий с матрицами. Однако при правильном использовании матричных операций эти формулы достаточно просто записываются и в Excel. Правда, здесь придется заранее получить формулы для вычисления производных. Для аналитического вычисления производных также может быть использован Mathcad.
2.3 Решение систем нелинейных уравнений методами итераций
Для реализации этих методов исходную систему уравнений необходимо путем алгебраических преобразований явно выразить каждую переменную через остальные. Для случая двух уравнений с двумя неизвестными новая система будет иметь вид

Для решения такой системы задаются начальным приближением x0, y0. Уточненные решения получают по шагам, подставляя в правые части уравнений значения, найденные на предыдущем шаге. В методе простых итераций для уточнения решения используют формулы:

Если одно из решений системы и начальные значения x0 и y0 лежат в области D, задаваемой неравенствами: a ≤ x ≤ b, c ≤ y ≤ d, то расчет по методу простых итераций сходится при выполнении в области D соотношений:
Нелинейные уравнения в MathСad
Mathcad отменно справляется с обчислениями нелинейных уравнений благодаря специальным алгоритмам.
Изучая решения, предлагаемые программой, попробуем стартовать с примера с одной переменной. Поэтому пытаемся возвести график для наглядности. Далее нам предстоит рассмотреть систему уравнения.
Уравнения с одной переменной
Сейчас мы попробуем решить максимально простой пример.
Учтем, что это уравнение представляет собой пересекающиеся параболу и прямую линию. Нарисуем график из трёх прямых линий и смотрим на результаты.
Верхняя линия имеет два пересечения с параболой. Обратите внимание на верхнюю линию. Запускаем блок решения для того, чтобы перейти к развязке уравнения.
На данном этапе появляются три части для ведения записи.
В область ограничения уже записано актуальное уравнение. Слева задано его приблизительное значение. Решателем является функция find.
Очевидно, что 1.366. Оно представляет собой первую стычку параболы и прямой линии.
Пробуем поменять изначальное приближение к обозначению, более близкому к пересечению с левой стороны. Решение автоматически принимает показатель в -0.366.
Начальное приближен снова устанавливаем на 1.3. Пробуем поменять константу 0.5 на -0.25. посмотрите, что стало с решением.
Примерно такой же ответ станет окончательным для абсолютно любого обозначения изначального приближения.
Теперь переходим в последнее уравнение и ставим константу на -1. Кликните по полю за пределами блока. Программа автоматически выдаст информацию о наличии ошибки.
Решения не существует. Ставим константу снова на 0.5.
Вывод решения
Решения, находящиеся в рассматриваемом нами блоке, являются локальными. Соответственно, их нельзя использовать за пределами блока. Теперь переходим к уравнению, в котором мы установили приближенное значение на отметке в 1.3. Решение данного уравнения помогает отыскать максимально точное значение х=1.366. Если же попытаться внести значение х, у нас отобразится вектор, который оптимально определится нашим графиком.
Чтобы пользоваться полученными данными в дальнейшем, понадобится установить функцию решателя переменной.
Так мы сможем получить правильный результат.
Решение систем уравнений
Попытаемся разобраться с системой из трёх уравнений. Два из них линейные, одно – кубическое. Соответственно у нас есть сразу три неизвестных.
Полученные ответы оформляем как векторы.
Удаляем третье уравнение. Его отсутствие не помешает системе найти правильный ответ.
Обратите внимание, что полученное решение может оказаться не тем, что вы искали.
Также вам понадобится учесть ещё некоторые особенности данных исчислений. Блок решения отображает сразу два знака равнения. Также там можно увидеть знак присваивания и символ булева равенства. Данная разница имеет колоссальную значимость. Теперь нажмите дважды по опции “find”. Далее нам нужно открыть вкладку математики. В опции обозначения автоматически активировано “ключевое”. Более подробную информацию о таких функциях мы расскажем в остальных уроках.
Растворимость вещества
Теперь посвятим время изучению процесса растворения такого вещества, как DOH. Этот процесс производится двумя этапами. Сначала нужно растворить твердую фазу. После этого оставшуюся часть нужно диссоциировать на D и OH. Невысокий уровень растворимости можно увеличить, подмешав немного кислоты НА. После этого ионы водорода начинают взаимодействовать с гидроксильной группой.
В чем же проявляется зависимость растворимости D от количества кислоты? Давайте посчитаем концентрацию в моль/л. Формула данной реакции выглядит таким образом:
Уровень концентрации кислоты:
Константа равновесия реакции:
Начало блока решения стартует с трех неизвестных и их первоначальных приближений:
Полученная концентрация вещества:
А так будет выглядеть расчет, предназначенный для возведения графика.
График наглядно отображает концентрирование в виде функцию с учетом количества добавленной кислоты. Концентрация водорода оказалась значительно ниже, чем концентрация иных элементов. С учетом этого фактора, мы приняли решение снизить масштабирование в 1000000 раз и отобразить данный график в этих же осях.
Когда концентрирование кислоты чрезмерно низко, в решении будет отображена минимальная концентрация, диссоциируемая лишь частично. Увеличив концентрацию, можно просмотреть за тем, как диссоциируется все больше вещества.
Уважаемые пользователи, хотим Вас проинформировать о том, что некоторые антивирусные программы и браузеры ложно срабатывают на дистрибутив программы MediaGet, считая его зараженным. Данный софт не содержит никаких вредоносных программ и вирусов и многие из антивирусов просто Вас предупреждают, что это загрузчик (Downloader). Если хотите избежать подобных проблем, просто добавьте MediaGet в список доверенных программ Вашей антивирусной программы или браузера.
Выбрав нужную версию программы и кликнув ссылку, Вам на компьютер скачивается дистрибутив приложения MediaGet, который будет находиться в папке «Загрузки» для Вашего браузера. Находим этот файл с именем программы и запускаем его. И видим первый этап установки. Нажимаем унопку «Далее»
Далее Вам предлагается прочитать и одобрить лицензионное соглашение. Нажимаем кнопку «Принимаю»
В следующем окне Вам предлагается бесплатное полезное дополнительное программоное обеспечение, будь то антивирус или бразуер. Нажимаем кнопку «Принимаю». Также Вы можете отказаться от установки дополнительного ПО, нажав кнопку «Отклоняю»
Далее происходит процесс установки программы. Вам нужно выбрать папку, в которую будут скачиваться нужные Вам файлы.
Происходит завершение установки. Программа автоматически открывается и скачивает нужные Вам исходные файлы.
Обратите внимание, что предоставляемое программное обеспечение выкладывается исключительно для личного использования и ознакомления. Все файлы, доступные для скачивания, не содержат вирусов и вредоносных программ.
[spoiler title=”источники:”]
http://pandia.ru/text/78/157/38912.php
http://stylingsoft.com/sapr/mathcad/uroki-mathcad/1431-nelinejnye-uravneniya-v-mathsad
[/spoiler]
Методы решения нелинейных уравнений в MathCAD
Реализуем для некоторого уравнения 4 наиболее популярных численных метода для решения нелинейных уравнений. При этом мы стремимся именно запрограммировать методы, а не воспользоваться встроенным инструментом Given...Find или функциями root, polyroot. Об этих способах решения почитайте, например, здесь.
Определим функцию уравнения f(x)=0 как функцию пользователя, интервал поиска решения зададим переменными a и b. Найти этот интервал можно, например, табличным или графическим методом:
Уравнение и интервал поиска решения
Начальный интервал
[a,b]должен быть таким, чтобы значенияf(a)иf(b)имели противоположные знаки. Если искомый корень уравнения окажется единственным на интервале, то совсем хорошо 🙂
Логика метода дихотомии (возможно, более правильные названия – метод бисекции, метод половинного деления) довольно проста: если на концах выбранного интервала [a,b] знаки функции совпадают (произведение f(a)*f(b)>0), то вернуть результат “недопустимый интервал” (вернём в этом случае ответ “бесконечность”), в противном случае до тех пор, пока длина интервала не станет меньше заданной погрешности ε, будем находить середину текущего интервала c=(a+b)/2, считать в ней значение функции и проверять, какую из половин отрезка [a,c] или [c,b] нужно отбросить для выполнения следующего шага – а именно, ту, в которой знак f(c) совпадает со знаком функции на левой или правой границе интервала (в листинге – проверка f(a)*f(c)>0). Для большей точности вернём середину “последнего” интервала [a,b], меньшего ε:
Метод дихотомии в MathCAD
В методе простой итерации исходное уравнение f(x)=0 представляется в эквивалентном виде φ(x)=x (что, вообще говоря, можно сделать бесконечным числом способов), а затем шаг метода выполняется по формуле xk+1 = φ(xk), пока не будет достигнута заданная точность |xk+1-xk|<ε. Если выбрать φ(x)=x-c*f(x), то константу c целесообразнее всего искать методом релаксации, для которого c=2/(M+m), где M – максимальное из значений первой производной на концах отрезка или в находящихся на нём точках перегиба функции (точках, где f''(x)=0), а m – минимальное из таких значений. Вот соответствующий расчёт в MathCAD:
Метод простой итерации (релаксации) в MathCAD
Если заданной сходимости нет в течение 10000 шагов, в подпрограмме предусмотрен аварийный выход.
Численный метод Ньютона решения нелинейного уравнения основан на формуле вида xk+1 = xk-f(xk)/f'(xk), обеспечивающей наилучшую сходимость, но требующей дополнительного вычисления производной на каждом шаге. Так как производные для MathCAD – не проблема, можно всё сделать “в лоб”:
Метод Ньютона для решения нелинейного уравнения в MathCAD
Видно, что сходимость метода – на 2 порядка выше (погрешность найденного решения ~ 10-8).
Наконец, существует метод хорд, в котором кривая f(x) заменяется прямой линией (хордой), стягивающей точки (a, f(a)) и (b, f(b)). Формула этого метода зависит от знака выражения f(a)*f''(a), то есть, имеет два варианта:
Если f(a)*f''(a)>0, то x0=b, xk+1=a-(f(a)(xk-a))/(f(xk)-f(a))
Если f(a)*f''(a)<0, то x0=a, xk+1=xk-(f(xk)*(b-xk))/(f(b)-f(xk))
Вот примерная реализация на MathCAD, как и в предыдущих двух случаях, контролируется максимальное число итераций, равное 10000:
Метод хорд решения нелинейного уравнения в MathCAD
Видно, что сходимость метода оказалась в нашем случае не столь высока.
Подсчитать, сколько шагов какому методу потребовалось, можете сами, немного поменяв выдачу подпрограмм.
Скачать расчёты из статьи в архиве .zip с файлом .xmcd Mathcad 14/15 (34 Кб)
05.09.2013, 15:07 [106243 просмотра]
Подготовка
к работе
-
По указанной литературе изучить:
-
правила
локализации решения, -
решение
одного уравнения, -
решение
системы уравнений.
-
Разработать алгоритмы решения задач из варианта задания.
-
Составить программы решения задач.
Контрольные
вопросы
-
Задание
функции пользователя. -
Локализация
решений уравнения. -
Решение
нелинейного уравнения с использованием
функции root. -
Вывод
полученных решений уравнения. -
Использование
функции polyroot. -
Локализация
решений системы уравнений. -
Блок
Given
решения систем уравнений в Mathcad. -
Решение
системы нелинейных уравнений с
использованием функции Find. -
Решение
системы нелинейных уравнений с
использованием функции Minerr. -
Вывод
полученных решений системы уравнений.
Задание
к работе
Задача
1. Ввод данных
и текста.
-
Ввести текст, как заглавие программы.
-
Задать
функции, как функции пользователя. -
Задать
изменение аргументов.
Задача
2. Решение
нелинейного уравнения.
-
Ввести текст, как заглавие задачи.
-
Ввести
программу и вычислить значения функции
f1(x)
при изменении аргументов в заданных
пределах. -
Вывести
y(x)=f1(x)
в виде XY
графика. По нему определить приближенно
корни уравнения y(x)=0.
Если корни не просматриваются, то
изменить пределы изменения аргумента
и повторить операции. -
Для
каждого корня найти точное значение,
используя функцию root.
Задача
3. Решение
системы нелинейных уравнений.
-
Ввести текст, как заглавие задачи.
-
Ввести
программу и вычислить значения функций
f1(x)
и f2(x)
при изменении аргументов в заданных
пределах. Если корни не просматриваются,
то изменить пределы изменения аргумента
и повторить операции. -
Вывести
результаты в виде XY
графика. По нему определить приближенно
корни уравнения, как координаты точек
пересечения графиков f1(x)
и f2(x). -
Ввести
программу и вычислить при изменении
аргументов в заданных пределах, используя
функцию Find,
корни системы уравнений y=f1(x) y=f2(x). -
Для
одного из корней повторить решение,
используя функцию Minerr. -
Ввести текст о выводах по работе.
Методические
указания
1. Формирование задач
В работе предусмотрены
3 задачи:
-
ввод
исходных данных, -
решение
нелинейного уравнения, -
решение
системы из двух нелинейных уравнений.
При решении нелинейного
уравнения оно формируется из функций
задания, как f1(x)=0.
При решении системы
нелинейных уравнений она формируется
из функций задания, как два уравнения
y=f1(x)
и y=f2(x).
Рекомендуется
функции из задания определить, как
функции пользователя. Это упростит
обращения к ним при решении уравнений.
В качестве имен функций можно выбрать
f1 и f2.
2.
Локализация корней
Уравнение или система
уравнений может иметь несколько корней,
каждый из которых ищется отдельно. При
этом для каждого корня надо задать
начальное значение аргумента, близкое
к нему.
Начальное значение
ищется путем локализации корня. Для
этого надо просчитать значения функций
в заданном интервале и построить их
графики.
Начальное
значение для решения одного уравнения
– точка пересечения графиком функции
оси Х. Начальное значение для решения
системы двух уравнений – точка взаимного
пересечения графиков функций.
3.
Функция root
Используется для
нахождения корня нелинейного уравнения.
Формат этой функции:
root(выражение, имя
переменной).
В простейшем случае
выражение может быть именем функции.
Примеры использования:
х:= начальное значение
root(f1(x),x)=…
х:= начальное значение
x0:=root(f1(x),x)
х0=…
В первом случае
после знака равенства сразу выводится
значение корня, во втором сначала
переменной x0 присваивается значение
корня, и затем оно может быть выведено.
4.
Запись системы уравнений
Формат записи:
Начальные
значения аргументов
Given
Уравнение
1
Уравнение
2
………..
Ограничительные
условия
Выражения
с функциями Find
и/или Minerr
Проверка
при необходимости подстановкой
результата.
Для ввода знака
равенства используется комбинация
клавиш [Ctrl]+[=]. Выводится жирный знак
равенства. Его можно получить и из
палитры «Отношения».
5.
Функции Find и Minerr
Используются для
нахождения корней нелинейного уравнения.
В функции Find
реализован алгоритм поиска точного
значения корня, а в функции
Minerr –
приближенного
значения с минимальной среднеквадратичной
погрешностью. Формат функций:
Find(список переменных)
Minerr(список
переменных).
Примеры использования:
x:=
начальное значение y:=
начальное значение
Given
y=f1(x)
y=f2(x)
Ограничительные
условия
Find(x,y)=…
x:=
начальное значение y:=
начальное значение
Given
y=f1(x)
y=f2(x)
Ограничительные
условия
:=Find(x,y)
=…
В первом случае в
строке Find
после знака равенства сразу выводится
вектор со значениями переменных для
корня, во втором сначала вектору из x1 и
y1 присваиваются значение корня, и затем
вектор выводится.
Варианты
заданий
Таблица
3. Варианты заданий
|
№ |
f1(x)- полином 3-ей |
f2(x) |
|||
|
a3 |
a2 |
a1 |
a0 |
333 |
|
|
1 |
0 |
-1 |
4 |
-1 |
0.2exp(x)-20 |
|
2 |
0 |
2 |
-2 |
-15 |
40|cos(x)| |
|
3 |
0 |
1 |
4 |
-1 |
10ln(x+5.5) |
|
4 |
0 |
9 |
-8 |
-70 |
100|sin(x)| |
|
5 |
0 |
-4 |
4 |
50 |
70cos(x) |
|
6 |
.1 |
-5 |
4 |
40 |
60exp(|0.1*x|)-100 |
|
7 |
.2 |
-3 |
2 |
30 |
20sin(2x) |
|
8 |
.3 |
-6 |
1 |
50 |
exp(|x|)sin(2x) |
|
9 |
.4 |
-9 |
1 |
70 |
exp(|x|)cos(3x) |
|
10 |
.5 |
-7 |
5 |
60 |
-60|cos(x)| |
|
11 |
-.1 |
-4 |
9 |
60 |
15log(x+5.1) |
|
12 |
-.2 |
-6 |
-7 |
55 |
-50ln(x+5.1) |
|
13 |
-.3 |
-9 |
-8 |
75 |
-100|cos(x)| |
|
14 |
-.4 |
7 |
8 |
-75 |
100sin(x/2) |
|
15 |
-.5 |
1 |
4 |
-1 |
40cos(x/2) |
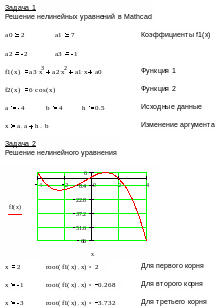
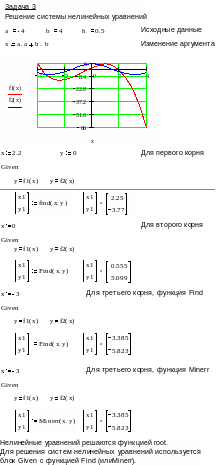
Пример программы
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
03.05.2019121.34 Кб1IP.doc
- #
- #
- #
- #
- #
- #
- #
Решение нелинейных уравнений в системе MathCAD.
1. Решение одного уравнения с одним неизвестным.
Для решения одного уравнения с одним неизвестным
используется функция root. Аргументами этой функции
являются выражение и переменная, входящая в выражение. Ищется значение
переменной, при котором выражение обращается в ноль.
Синтаксис: root(f(z),z) – возвращает значение z, при котором выражение
или функция f(z) обращается в ноль. Оба аргумента этой функции должны быть скалярами.
Функция root возвращает скаляр.
Первый аргумент есть либо функция, определенная где-либо в
рабочем документе, или выражение.
Второй аргумент – имя переменной, которое используется в
выражении. Это та переменная, варьируя которую Mathcad
будет пытаться обратить выражение в ноль. Этой переменной перед использованием
функции root необходимо присвоить числовое
значение. MathCad использует его как начальное приближение
при поиске корня.
Рассмотрим пример, в котором необходимо найти a – решение уравнения ex=x3. Для этого выполним следующие шаги:
·
Определим начальное значение переменной x (x := 3).
·
Определим выражение, которое должно быть обращено в
ноль. Для этого перепишем уравнение ex=x3 в виде ex–x3=0. Левая часть этого выражения и является вторым аргументом функции root.
·
Определим переменную a
как корень уравнения: a := root(ex‑x3, x).
·
Напечатаем a=, чтобы увидеть значения корня: a = 1.857.
Также существует второй способ записи функции root с четырьмя аргументами. Ее синтаксис следующий: root(f(z), z, a, b). В этом случае не требуется задавать начальное приближение, а MathCad самостоятельно будет пытаться найти корень уравнения f(z)=0 на отрезке [a; b]. Пример
использования такой записи будет показан далее (рисунок 1).
При использовании функции root
имейте в виду следующее:
·
Удостоверьтесь, что переменной присвоено начальное
значение до начала использования функции root (в
случае использования формы записи функции root с
двумя переменными).
·
Для выражения с несколькими корнями, начальное
значение определяет корень, который будет найден MathCad.
На рисунке 1 приведен пример, в котором функция root возвращает различные значения, каждое из которых зависит от начального
приближения.
·
MathCad позволяет находить как комплексные, так и
вещественные корни. Для поиска комплексного корня следует взять в качестве
начального приближения комплексное число.
·
Задача решения уравнения вида f(x)=g(x) эквивалентна задаче поиска корня выражения f(x)‑g(x)=0. Для этого функция root может быть использована следующим образом: root(f(x)‑g(x), x).
·
Функция root
предназначена только для решения одного уравнения с одним неизвестным.
Рисунок 1. Использование функции root
для нахождения корней уравнения.
Что делать, когда функция root
не сходится.
MathCad в функции root для
поиска корня использует метод секущей. Начальное приближение, присвоенное
переменной x, становится первым приближением к
искомому корню. Когда значение выражения f(x) при очередном приближении становится меньше
значения встроенной переменной TOL (по умолчанию TOL=10-3 – допускаемая погрешность для
различных алгоритмов аппроксимации, таких как интегрирование, решение уравнений
и т.д.), корень считается найденным, и функция root
возвращает результат.
Если после многих итераций MathCad не
может найти подходящего приближения, то появляется сообщение об ошибке «отсутствует
сходимость». Эта ошибка может быть вызвана следующими причинами:
·
Уравнение не имеет корней.
·
Корни уравнения расположены далеко от начального
приближения.
·
Выражение имеет локальные максимумы или минимумы между
начальным приближением и корнями.
·
Выражение имеет разрыв между начальным приближением
и корнями.
·
Выражение имеет комплексный корень, но начальное приближение
было вещественным (или наоборот).
Чтобы установить причину ошибки, исследуйте график f(x). Он поможет
выяснить наличие корней уравнения f(x)=0 и, если они есть, то определить
приблизительно их значения. Чем точнее выбрано начальное приближение, тем
быстрее функция root будет сходиться к точному значению.
Некоторые советы по использованию
функции root.
·
Для изменения точности, с которой функция root ищет корень, можно изменить значение встроенной переменной TOL. Если значение TOL увеличивается, функция root будет сходиться быстрее, но ответ будет менее точен. Если значение TOL уменьшается, функция root будет сходиться
медленнее, но ответ будет более точен. Чтобы изменить значение TOL в определенной точке рабочего документа, используется определение вида
TOL:=0.01. Чтобы изменить
значение TOL для всего рабочего документа, выберите
из меню Math команду Options (в русской версии из меню Математика команду Встроенные
переменные), и на вкладке Built–In Variables (Встроенные переменные) введите подходящее значение в
поле TOL. Нажав «ОК», выберите из меню Math команду Calculate Worksheet (в
русской версии из меню Математика команду Пересчитать всё), чтобы
обновить все вычисления в рабочем документе с использованием нового значения
переменной TOL.
·
Если уравнение имеет несколько корней, попробуйте
использовать различные начальные приближения, чтобы найти их. Использование
графика функции полезно для нахождения числа корней выражения, их расположения
и определения подходящих начальных приближений. Если два корня расположены
близко друг от друга, можно уменьшить значение переменной TOL, чтобы различить их.
·
Если f(x) имеет малый наклон около искомого корня,
функция root(f(x),x) может
сходиться к значению r, отстоящему от корня
достаточно далеко. В таких случаях для нахождения более точного значения корня
необходимо уменьшить значения TOL. Другой вариант
заключается в замене уравнения f(x)=0 эквивалентным ему уравнением g(x)=0, где
На этом пункте остановимся поподробнее и рассмотрим пример.
Пусть дана функция f(x)=0.000001×x2. Очевидно, что единственным кратным корнем
уравнения f(x)=0 является значение x0=0. Однако, если воспользоваться функцией root с начальным приближением, равным 3, то МathCad выдаст результат: root(f(x),x)=1.501. Как раз в этом примере функция f(x) имеет очень малый наклон вблизи искомого
корня. Теперь, если же воспользоваться заменой:
то
результат использования функции root будет
следующим: root(g(x),x)=4.445×10-13. Достаточно точное решение уравнения f(x)=0 также можно получить, установив значение TOL=10-10. При этом будет получен
следующий результат: root(f(x),x)=7.958×10-3.
·
Для выражения f(x) с известным корнем a нахождение дополнительных корней f(x) эквивалентно поиску корней уравнения h(x)=0, где h(x)=f(x)/(x–a). Подобный прием полезен для нахождения корней, расположенных близко
друг к другу. Часто бывает проще искать корень выражения h(x), определенного
выше, чем пробовать искать другой корень уравнения f(x)=0, выбирая
различные начальные приближения.
Решение уравнений с параметром.
Предположим, что нужно решить уравнение многократно при изменении
одного из параметров этого уравнения. Например, пусть требуется решить
уравнение ex=a×x2 для нескольких различных значений параметра a.
Самый простой способ состоит в определении функции
f(a,
x):=root(ex‑a×x2,
x)
Чтобы решить уравнение для конкретного параметра a, присвойте значение параметру a и начальное
значение переменной x, как аргументам этой функции.
Затем найдите искомое значение корня, вводя выражение f(a, x)=.
Рисунок 2 показывает пример того, как такая функция может
использоваться для нахождения корней исследуемого уравнения при различных значениях
параметра. Обратите внимание, что, хотя начальное значение x непосредственно входит в определение функции, нет необходимости
определять его в другом месте рабочего документа.
Рисунок
2. Решение уравнения с параметром.
2. Нахождение корней полинома.
Для нахождения выражения, имеющего вид:
vnxn+…+v2x2+v1x+v0
лучше
использовать функцию polyroots, нежели root. В отличие от функции root, функция polyroots
не требует начального приближения. Кроме того, функция polyroots
возвращает сразу все корни, как вещественные, так и
комплексные.
Синтаксис: polyroots(v) – возвращает корни полинома степени n. Коэффициенты полинома находятся в векторе v длины n+1. Возвращает
вектор длины n, состоящий из корней полинома.
Функция polyroots всегда возвращает
значение корней полинома, найденные численно. На рисунке 3 приведен пример
использования функции polyroots.
Рисунок 3. Пример использования функции polyroots.
3. Системы уравнений.
MathCad дает возможность решать также и системы уравнений.
Максимальное число уравнений и переменных равно пятидесяти. Результатом решения
системы уравнений будет численное значение искомого корня. Для решения системы
уравнений выполните следующее:
·
Задайте начальные приближения для всех неизвестных,
входящих в систему уравнений. MathCad решает уравнения при
помощи итерационных методов. На основе начального приближения строится
последовательность, сходящаяся к искомому решению.
·
Напечатайте ключевое слово Given. Оно указывает MathCad, что далее следует
система уравнений. При печати слова Given можно
использовать любой шрифт, прописные и строчные буквы. Убедитесь, что при этом
вы не находитесь в текстовой области или параграфе.
·
Введите уравнения и неравенства в любом порядке
ниже ключевого слова Given. Удостоверьтесь, что между
правыми и левыми частями уравнений стоит символ = (используйте [Ctrl]+= для печати этого символа). Между правыми и
левыми частями неравенств может стоять любой из символов <, >,
£ и ³.
·
Введите любое выражение, которое включает функцию Find. При печати слова Find можно использовать
шрифт любого размера, произвольный стиль, прописные и строчные буквы.
Синтаксис: Find(z1, z2, z3,…) – возвращает решение системы уравнений. Число аргументов должно быть
равно числу неизвестных.
Функция Find возвращает
найденное решение следующим образом:
·
Если функция Find имеет
только один аргумент, то она возвращает решение единственного уравнения,
расположенного между ключевым словом Given и
функцией Find.
·
Если функция Find имеет
более одного аргумента, то она возвращает ответ в виде вектора. Например, Find(z1, z2) возвращает вектор, содержащий значения z1 и z2, являющиеся решением
системы уравнений.
Ключевое слово Given, уравнения
и неравенства, которые следуют за ним, и какое-либо выражение, содержащее функцию
Find, называются блоком решения уравнения.
На рисунке 4 показан часть кода документа, которая содержит
блок решения уравнений для решения одного уравнения с одним неизвестным. Так
как имеется только одно уравнение, то только одно уравнение находится между
ключевым словом Given и формулой, включающей
функцию Find. Так как уравнение имеет одно
неизвестное, то функция Find имеет только один
аргумент.
Рисунок 4. Пример использования функции Find для решения одного уравнения.
Между ключевым словом Given и
функцией Find в блоке решения уравнений могут
появляться выражения строго определенного типа. Ниже приведен список всех
выражений, которые могут быть использованы в блоке решения уравнений.
Использование других выражений не допускается. Эти выражения часто называются
ограничениями. В таблице, приведенной ниже, через x и y обозначены вещественнозначные скалярные
выражения, а через z и w обозначены любые скалярные выражения.
|
Условие |
Как ввести |
Описание |
|
w=z |
[Ctrl]+= |
Булево равенство |
|
x>y |
> |
Больше чем. |
|
x<y |
< |
Меньше чем. |
|
x³y |
[Ctrl]+0 |
Больше либо равно |
|
x£y |
[Ctrl]+9 |
Меньше либо равно |
|
w¹y |
[Ctrl]+3 |
Не равно |
Следующие выражения недопустимы
внутри блока решения уравнений:
·
Дискретный аргумент или выражения, содержащий
дискретный аргумент в любой форме.
·
Неравенства вида a<b<c.
Блоки решения уравнений не могут быть вложены друг в друга.
Каждый блок решения уравнений может иметь только одно ключевое слово Given и имя функции Find. Можно, однако,
определить функцию f(x):=Find(x) в конце одного блока решения уравнений и затем использовать f(x) в другом
блоке.
Рисунок 5. Пример использования функции Find для решения двух уравнений с двумя неизвестными.
Как правило, нельзя использовать оператор присваивания
(выражения вида x:=1) внутри
блока решения уравнений. MathCad помечает операторы
присваивания, которые находятся внутри блока решения уравнений, сообщением об
ошибке.
На рисунке 5 показан блок решения уравнений, в котором
использованы некоторые виды ограничений на искомое решение. Решаются два
уравнения с двумя неизвестными. В результате функция Find содержит два аргумента, x и y, и возвращает ответ в виде вектора с двумя компонентами.
Как использовать найденное решение.
Функция Find, которая завершает
блок решения уравнений, может быть использована аналогично любой другой
функции. Можно произвести с этой функцией следующие три действия:
·
Можно вывести данное решение, напечатав выражение
вида Find(переменная)=.
Если решаются уравнения с несколькими неизвестными, то можно вывести вектор
результатов, введя выражение вида Find(переменная1,
переменная2,…)=.
·
Можно определить переменную с использованием этой
функции. Для этого в конце блока решения уравнений необходимо ввести выражение
типа a:=Find(x). Это удобно сделать, если требуется
использовать решение системы уравнений в другом месте рабочего документа. Как
только переменная a определена таким образом, она
сразу же принимает значение искомого корня. Пример, иллюстрирующий такую
возможность, был рассмотрен выше (рисунок 4). Если функция Find возвращает вектор значений, можно ввести выражение типа variable:=Find(переменная1, переменная2,…). После такого определения переменная становиться вектором (вместо
скаляра). Можно также определить переменные, как показано на рисунке 5.
·
Используя Find, можно
определить другую функцию. Для этого необходимо закончить блок решения
уравнений выражением типа f(a, b, c,…):=Find(x, y, z,…). Эта конструкция удобна при многократном
решении системы уравнений для различных значений некоторых параметров a, b, c,…, непосредственно входящих в систему уравнений.
Рисунок 6. Влияние выбора начального приближения на
найденное решение.
MathCad возвращает в блоке решения уравнений только одно
решение. Однако система уравнений может иметь несколько различных решений. Если
одно решение найдено, то для поиска других решений можно использовать различные
начальные приближения либо дополнительные ограничения в виде неравенств,
которым найденное решение не удовлетворяет. На рисунке 6 показано, как
начальное приближение влияет на найденное решение. На рисунке 7 показано, как
добавить ограничения в виде неравенства для поиска другого решения.
Рисунок 7. Добавление ограничений позволяет найти другое
решение.
Что делать, когда MathCad не может
найти решения.
Если в результате решения уравнений на каком-либо шаге
итераций не может быть найдено более приемлемое приближение к искомому решению
по сравнению с предыдущим шагом, то поиск решения прекращается, а функция Find помечается сообщением об ошибке.
Если при поиске решения встречаются трудности, то полезно
вывести те или иные графики, связанные с системой. Анализ графика может
облегчить поиск области, в которой находится искомое решение. Это поможет
выбрать подходящее начальное приближение.
На рисунке 8 приведена задача, для которой MathCad не смог найти решение. В этом конкретном случае ошибка заключается в
том, что в качестве начального приближения выбрано вещественное число, а решаемое
уравнение имеет только комплексные корни. Если в этом примере в качестве
начального приближения задать мнимую единицу (i), то MathCad выдаст ответ Find(x)=1.732i.
Рисунок 8. Пример задачи, решение которой не может быть найдено
в блоке решения уравнений.
Вообще, сообщение об ошибках «решение не найдено» («No
solution was found») при решении
уравнений появляется, когда различие между текущим приближением и приближением,
полученным на предыдущем шаге итераций, больше, чем значение встроенной
переменной TOL и выполнено одно из следующих
условий:
·
Достигнута точка, из которой не может быть получено
более точное приближение к решению.
·
Достигнута точка, из которой невозможно выбрать
подходящее направление спуска – направление вдоль которого ищется следующее
приближение. В связи с этим продолжать итерации невозможно.
·
Достигнут предел точности вычислений. Дальнейшие
вычисления не увеличивают точность найденного решения вследствие влияния ошибок
округления. Это часто случается, если значение переменной TOL установлено меньше, чем 10‑15.
Причиной сообщения об ошибке может быть следующее:
·
Поставленная задача может не иметь решения.
·
Для уравнения, которое не имеет вещественных
решений, в качестве начального приближения взято вещественное число. Этот
пример был рассмотрен ранее (рисунок 8).
·
В процессе поиска решения последовательность
приближений попала в точку локального минимума невязки. Метод поиска решения,
который используется в MathCad, не позволяет в этом случае
построить следующее приближение, которое бы уменьшало невязку. Для поиска
искомого решения попробуйте использовать различные начальные приближения или добавьте
ограничения на переменные в виде неравенств, чтобы обойти точку локального
минимума.
·
В процессе поиска решения получена точка, которая
не является точкой локального минимума, но из которой метод минимизации не
может определить дальнейшее направление движения. Метод преодоления этой
проблемы – такой же, как для точки локального минимума: измените начальное приближение
или добавьте ограничения в виде неравенств, чтобы миновать нежелательную точку
остановки.
·
Возможно, поставленная задача не может быть решена
с заданной точностью. Если значение встроенной переменной TOL слишком мало, то MathCad может достигнуть точки,
находящейся достаточно близко к решению задачи, но уравнения и ограничения при
этом не будут выполнены с точностью, задаваемой переменной TOL. Попробуйте увеличить значение TOL где-нибудь
выше блока решения уравнений.
Случай, когда число неизвестных больше
числа уравнений.
Если количество ограничений (уравнений) меньше, чем
количество переменных, MathCad вообще может не выполнить
блок решения уравнений. MathCad помечает в этом случае
функцию Find сообщением об ошибке «слишком мало
ограничений». Однако в этой ситуации MathCad может и
не выдать ошибки, а вывести на экран одно решение из их бесконечного числа.
Задача, аналогичная той, что приведена на рисунке 9,
называется неопределенной. Ограничений в ней меньше, чем переменных. Поэтому
ограничения не содержат достаточной информации для поиска решения. Вообще говоря,
такая задача обычно имеет бесконечное число решений.
В этом случае MathCad пытается решить
систему уравнения посредством подбора первых n переменных
(n – число уравнений в системе), а остальные
переменные MathCad приравнивает к нулю. В рассматриваемом
примере у нас имеется система из двух уравнений, поэтому MathCad варьирует только два первых аргумента функции Find, а именно, x и y. Остальные же аргументы (z, w, v) MathCad полагает
равными нулю.
Рисунок 9. Пример использования функции Find в случае, когда число неизвестных превышает число ограничений.
Многократное решение уравнений.
Методы, описанные до сих пор, эффективно позволяют решать
конкретную систему уравнений. Однако они имеют следующие два ограничения:
·
Как только используется функция Find, это означает, что блок решения уравнений завершен. Если употребить
эту функцию еще раз, появится сообщение об ошибке «нет соответствующего Given» («Only allowed inside a solve block. Try typing Given above»).
·
Если в системе уравнений нужно изменить значения
некоторых параметров или констант, чтобы изучить их влияние на решение системы,
необходимо вернуться обратно в блок решения уравнений, чтобы изменить их.
Оба эти ограничения могут быть преодолены, если прибегнуть
к возможности MathCad определять функции с использованием
блока решения уравнений.
Если определить функцию с использованием функции Find в правой части этого определения, то определенная таким образом
функция будет решать систему уравнений каждый раз, когда она вызывается. Таким
образом можно преодолеть первое ограничение.
Если эта функция имеет в качестве аргументов те параметры,
которые требуется изменять при решении уравнений, можно просто изменять
значения аргументов этой функции. Это преодолевает второе ограничение.
На рисунке 10 приведен конкретный пример. Коэффициент
трения трубки f зависит от диаметра трубки D, шероховатости e и числа Рейнольдса R. Было бы
неплохо экспериментировать с различными размерами трубки (D), сделанной из различных материалов с различной шероховатостью (e).
Уравнение на рисунке 14 показывает связь между этими
параметрами. Учитывая вид уравнения, можно отметить, что аналитически выразить
значение величины f от R, D, e нельзя.
Можно, однако, определить функцию с использованием блока
решения уравнений. Всякий раз, когда вычисляется функция FricFac(e, D, R), MathCad подставляет заданные конкретные
значения аргументов e, D и R в блок решения уравнений, решает уравнение относительно неизвестного f и возвращает найденное значение корня.
Рисунок 10. Определение функции с использованием блока
решения уравнений.
Предположим, что зафиксированы размер трубки и ее материал
(D и e,), и нужно
исследовать зависимость трения от значения числа Рейнольдса. Хотя функция FricFac на рисунке 10 была определена с использованием блока решения
уравнений, она обладает теми же самыми свойствами, что и любая другая функция.
Ее можно также использовать с дискретным аргументом.
На рисунке 11 показано, как решать задачу и построить
график зависимости коэффициента трения от числа Рейнольдса. Обратите внимание,
что, когда вместе с блоком решения уравнений используется дискретный аргумент, MathCad фактически решает систему уравнений для каждого значения дискретного
аргумента. В результате такой тип вычислений может потребовать значительное
количество машинного времени.
Рисунок 11. Построение графика функции FricFac при
фиксированных значениях D и e и переменном
значении числа Рейнольдса.
Предыдущий пример включает в себя только одно уравнение с
одним неизвестным. Также возможно многократно решать и систему уравнений при
различных значениях входящих в нее параметров. Однако в этом случае требуется
проявить аккуратность при выводе результата, чтобы избежать сообщения об
ошибке «нескалярная величина» («Not a scalar»).
Предположим, что ищется пересечение прямой и окружности переменного
радиуса R. Аналогично предыдущему примеру можно
определить функцию с использованием блока решения уравнений. В этом случае
функция может быть определена следующим образом: F(R):=Find(x, y). Эта
функция возвращает вектор значений, элементы которого – x и y – содержат координаты точки
пересечения.
Рисунок 12. Пример вывода трех решений, каждое из которых
является вектором.
Основное отличие от предыдущего примера состоит в том, что
определенная таким образом функция для каждого значения параметра R возвращает вектор, состоящий из двух элементов. Если попытаться вывести
найденный ответ, печатая F(R)=, то это будет попытка вывести таким
образом не таблицу чисел (скаляров), а таблицу, каждый элемент которой является
вектором , состоящим из двух элементов.
Решение этой проблемы состоит в раздельном отображении
таблиц для разных элементов вектора F(R)0 и F(R)1. Напечатав F(R)[0=, получаем
таблицу всех значений x – абсцисс точек
пересечения. Аналогично, напечатав F(R)[1=, получаем таблицу всех значений y – ординат точек пересечения прямой и окружности.
Приближенные решения.
MathCad содержит функцию, очень похожую на функцию Find. Она называется Minerr. Функция Minerr использует тот же самый алгоритм, что и функция Find. Различие состоит в следующем. Если в результате поиска решения не
может быть получено дальнейшее уточнение текущего приближения к решению, Minerr возвращает это приближение. Функция Find,
в отличие от функции Minerr, возвращает в этом
случае сообщение об ошибке «решение не найдено». Правила использования функции Minerr такте же, как и функции Find.
Синтаксис: Minerr(z1, z2, z3,…) – возвращает решение системы уравнений. Число аргументов равно числу
неизвестных.
На рисунках 13 и 14 приведен пример, в котором сравниваются
результаты решения уравнения, полученные с использованием функций Find
и Minerr.
Minner обычно возвращает ответ, который минимизирует
соответствующий функционал невязки, связанный с решаемой задачей. Однако Minerr не может проверить, реализует ли ответ абсолютный минимум для
функционала невязки. Если функция Minerr
используется в блоке решения уравнений, необходимо всегда включать дополнительную
проверку достоверности получаемых результатов. Встроенная переменная ERR дает величину невязки для приближенного решения. MathCad не имеет встроенной переменной для покомпонентного вывода вектора невязки
на найденном приближенном решении.
Рисунок 13. Сравнение работы функций Find и Minerr, в случае, когда функция Find не может вернуть решение уравнения. Величина ошибки при использовании
функции Minerr равна 56.904.
Рисунок 14. Сравнение работы функций Find и Minerr, в случае, когда функция Find возвращает решение уравнения. Результаты решения двумя способами
совпадают. Величина ошибки при использовании функции Minerr равна 1.082×10-6.