Как найти корни по тригонометрическому кругу

В этой статье и постараюсь объяснить 2 способа отбора корней в тригонометрическом уравнение: с помощью неравенств и с помощью тригонометрической окружности. Перейдем сразу к наглядному примеру и походу дела будем разбираться.

а) Решить уравнение sqrt(2)cos^2x=sin(Pi/2+x)
б) Найдите все корни этого уравнения, принадлежащие промежутку [-7Pi/2; -2Pi]

Решим пункт а.

Воспользуемся формулой приведения для синуса sin(Pi/2+x) = cos(x)

sqrt(2)cos^2x = cosx

sqrt(2)cos^2x – cosx = 0

cosx(sqrt(2)cosx – 1) = 0

cosx = 0

x1 = Pi/2 + Pin, n ∈ Z

sqrt(2)cosx – 1 = 0

cosx = 1/sqrt(2)

cosx = sqrt(2)/2

x2 = arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x3 = -arccos(sqrt(2)/2) + 2Pin, n ∈ Z

x2 = Pi/4 + 2Pin, n ∈ Z
x3 = -Pi/4 + 2Pin, n ∈ Z

Решим пункт б.

1) Отбор корней с помощью неравенств

Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [-7Pi/2; -2Pi], находим целые значения для n.

-7Pi/2 меньше или равно Pi/2 + Pin меньше или равно -2Pi

Сразу делим все на Pi

-7/2 меньше или равно 1/2 + n меньше или равно -2

-7/2 – 1/2 меньше или равно n меньше или равно -2 – 1/2

-4 меньше или равно n меньше или равно -5/2

Целые n в этом промежутку это -4 и -3. Значит корни принадлежащие этому промежутку буду Pi/2 + Pi(-4) = -7Pi/2, Pi/2 + Pi(-3) = -5Pi/2

Аналогично делаем еще два неравенства

-7Pi/2 меньше или равно Pi/4 + 2Pin меньше или равно -2Pi
-15/8 меньше или равно n меньше или равно -9/8

Целых n в этом промежутке нет

-7Pi/2 меньше или равно -Pi/4 + 2Pin меньше или равно -2Pi
-13/8 меньше или равно n меньше или равно -7/8

Одно целое n в этом промежутку это -1. Значит отобранный корень на этом промежутку -Pi/4 + 2Pi*(-1) = -9Pi/4.

Значит ответ в пункте б: -7Pi/2, -5Pi/2, -9Pi/4

2) Отбор корней с помощью тригонометрической окружности

Чтобы пользоваться этим способом надо понимать как работает эта окружность. Постараюсь простым языком объяснить как это понимаю я. Думаю в школах на уроках алгебры эта тема объяснялась много раз умными словами учителя, в учебниках сложные формулировки. Лично я понимаю это как окружность, которую можно обходить бесконечное число раз, объясняется это тем, что функции синус и косинус периодичны.

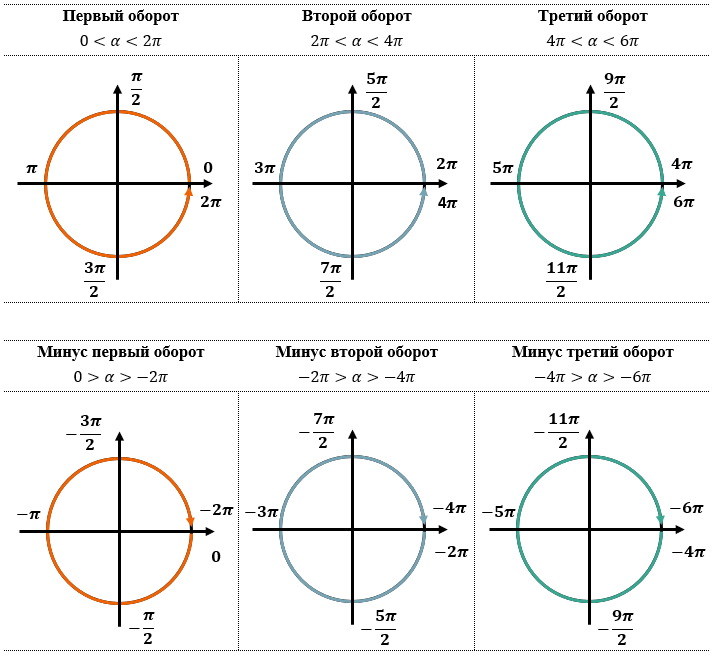
Обойдем раз против часовой стрелки

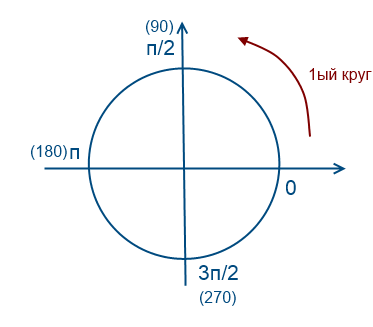
Обойдем 2 раза против часовой стрелки

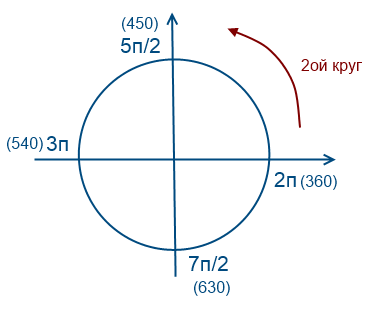
Обойдем 1 раз по часовой стрелки (значения будут отрицательные)

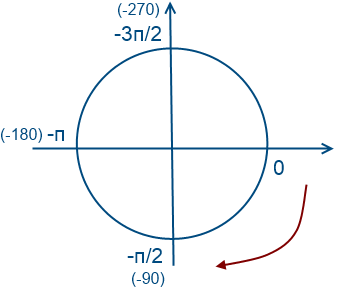
Вернемся к нашем вопросу, нам надо отобрать корни на промежутке [-7Pi/2; -2Pi]

Чтобы попасть к числам -7Pi/2 и -2Pi надо обойти окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.

Рассмотри x = Pi/2 + Pin. Какой приблизительно должен быть n, чтобы значение x было где-то в этом промежутке? Подставляем, допустим -2, получаем Pi/2 – 2Pi = -3Pi/2, очевидно это не входит в наш промежуток, значит берем меньше -3, Pi/2 – 3Pi = -5Pi/2, это подходит, попробуем еще -4, Pi/2 – 4Pi = -7Pi/2, также подходит.

Рассуждая аналогично для Pi/4 + 2Pin и -Pi/4 + 2Pin, находим еще один корень -9Pi/4.

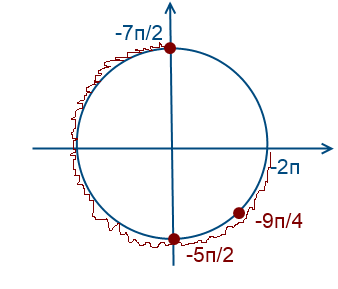
Сравнение двух методов.

Первый способ (с помощью неравенств) гораздо надежнее и намного проще для пониманию, но если действительно серьезно разобраться с тригонометрической окружностью и со вторым методом отбора, то отбор корней будет гораздо быстрее, можно сэкономить около 15 минут на экзамене.

Просмотры: 158005 |
Статью добавил: slava191 |
Категория: математика

Отбор корней с помощью тригонометрического круга

В заданиях, где требуется отобрать корни тригонометрического уравнения, принадлежащие определенному числовому промежутку, можно использовать тригокруг. Этот метод отбора корней является наиболее распространенным. Его плюсы заключаются в том, что это визуальный метод, т. е. отбор корней происходит наглядно, но у этого есть и свои недостатки – углов бесконечное множество, из которых только 360° можно визуализировать на тригокруге, поэтому может возникнуть путаница с количеством оборотов по нему.

«ОБОРОТЫ» ПО ТРИГОКРУГУ И СООТВЕТВЕТСТВУЮЩИЕ ИМ УГЛЫ:

АЛГОРИТМ ОТБОРА КОРНЕЙ С ПОМОЩЬЮ ТРИГОКРУГА

1. Отмечаем получившийся угол на тригокруге. Это будет серия ответов – бесконечное количество углов, визуально находящееся на тригокруге в одной точке.

2. Отмечаем нужную дугу, т. е. обозначаем указанный промежуток, в котором нужно отобрать корни.

3. Определяем корни, попадающие в эту дугу.

4. Находим искомые углы учитывая обороты – прибавляем соответствующее количество периодов к отмеченному на окружности углу.

Пример:

Даны корни уравнения:

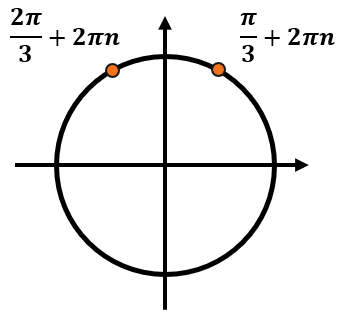
(x_{1} = frac{pi}{3} + 2pi n, nmathbb{in Z})

(x_{2} = frac{2pi}{3} + 2pi n, nmathbb{in Z})

Найдите корни, принадлежащие отрезку (leftlbrack – pi, frac{3pi}{2} rightrbrack).

1. Каждый из этих корней включает в себя бесконечное количество углов. Отметим эти серии ответов на тригокруге:

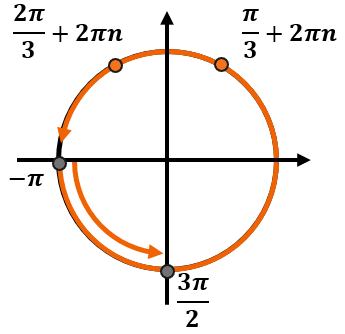
1. При этом мы знаем, что нужные корни должны находиться на промежутке (leftlbrack – pi, frac{3pi}{2} rightrbrack). Этот промежуток занимает больше, чем один оборот. Обозначим его так:

1. Так как промежуток занимает больше одного круга, каждая серия ответов так или иначе попадет в этот него.

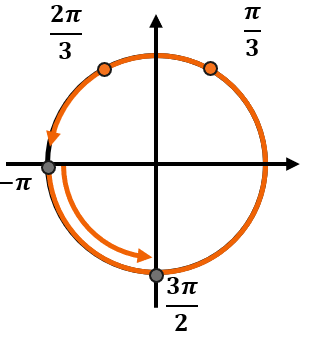
2. Теперь определим, на каком обороте серии ответов попадут именно в этот промежуток. Если мы будем идти по тригокругу от (- pi) до (frac{3pi}{2}), то попадем в точки с сериями ответов по одному разу – в первом обороте после нуля. Тогда получим следующие углы:

Запишем ответ.

Ответ: (frac{pi}{3});( frac{2pi}{3}).

Важно! Чтобы решение было обоснованным, очень важно отметить всё на круге: и точки, и углы, и промежуток.

Экспресс-тренинг

Подготовка к ЕГЭ-2023 по профильной математике в кратчайшие сроки!

До экзамена осталось совсем немного времени! Закрепите свои знания! Понятная теория и эффективные тренажеры с объяснением! Ваш ребенок успеет подготовиться к экзамену!

Всероссийский конкурс для школьных педагогов на лучшую образовательную статью «Просто о сложном»

Автор Лисицына Елена Федоровна.

учитель математики

МБОУ «Гимназия№11»

г. Бийска Алтайского кр.

Методы отбора корней в тригонометрических уравнениях

или

Ох уж эта тригонометрия!

Решение тригонометрических уравнений и отбор корней, принадлежащих заданному промежутку – это одна из сложнейших тем математики, которая выносится на Единый Государственный Экзамен в течение уже более 10лет. По результатам анкетирования многие учащиеся затрудняются или вообще не умеют решать тригонометрические уравнения и особенно затрудняются в отборе корней, принадлежащих промежутку. Необходимо также знать тригонометрические формулы, табличные значения тригонометрических функций для решения еще целого ряда заданий Единого Государственного Экзамена по математике. Постоянно работая в 10-11 классах, я регулярно сталкивалась с определенными проблемами при работе с вышеуказанным разделом тригонометрии: долго не могла установить баланс между доступностью изложения материала и достаточностью обоснований развернутого решения этой категории заданий. В моей практике были случаи, когда вполне успевающие по математике учащиеся начинали испытывать неуверенность и просто страх при решении тригонометрических уравнений с отбором корней, будь то принадлежность корней области допустимых значений переменной или указанному в задании промежутку. В результате целенаправленной многолетней работы в этом направлении у меня сложилась определенная методика работы с данным разделом, которая оказалась довольно успешной, что подтверждает следующая таблица результатов выполнения учащимися задания №13 профильного ЕГЭ по математике с 2015 по 2021 г.г. ( в % от общего количества учеников 11-х классов гимназии, сдающих профильный ЕГЭ по математике)

В тригонометрическом уравнении отбор корней можно осуществлять следующими способами: арифметическим, алгебраическим, геометрическим и функционально-графическим.

Арифметический способ отбора корней состоит в непосредственной подстановке полученных корней в уравнение, учитывая имеющиеся ограничения, при переборе значений целочисленного параметра.

Алгебраический способ предполагает составление неравенств, соответствующих дополнительным условиям, и их решение относительно целочисленного параметра.

Геометрический способ предполагает использование при отборе корней двух вариантов: тригонометрического круга или числовой прямой. Тригонометрический круг более удобен, когда речь идет об отборе корней на промежутке или в случае, когда значение обратных тригонометрических функций, входящих в решения, не являются табличными. Числовую прямую удобно использовать при отборе корней на промежутке, длина которого превосходит полный оборот или требуется найти наибольший отрицательный или наименьший положительный корень уравнения.

Функционально-графический способ предполагает отбор корней осуществлять с использование графиков тригонометрических функций. Чтобы использовать данный способ отбора корней, требуется умение схематичного построения графиков тригонометрических функций.

Моя практика показала, что чаще всего можно обойтись применением тригонометрического круга при отборе корней , а в случае, если промежуток превышает по длине полный оборот- алгебраическим способом. При этом, безусловно, следует познакомить учащихся и с остальными способами. Таким образом, работа над данным разделом разделилась у меня на следующие этапы:

1)Знакомство с устройством тригонометрического круга и отработка умений находить числа и промежутки на нем в ходе выполнения следующих упражнений:

2)Отработка навыков работы с тригонометрическим кругом при решении простейших тригонометрических уравнений с отбором корней , которая предполагает выполнение большого количества упражнений по типу приведенных ниже:

3)Отбор корней в одном и том же уравнении разными способами, чтобы учащиеся имели возможность выбора в соответствии со своими предпочтениями, например

Например,
а) Решить уравнение cos2x=sin(π/2+x).
б) Найдите все корни этого уравнения, принадлежащие промежутку [–7π/2; –2π].

Решим пункт а)Воспользуемся формулой приведения для синуса sin(π/2+x) = cos(x);cos2x = cosx ;
cos2x – cosx = 0; cosx(cosx – 1) = 0, т.е.

Решим пункт б).

I . Отбор корней с помощью неравенств

Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [–7π/2; –2π], находим целые значения для n.
–7π/2 ≤ π/2 + πn ≤ –2π;

Сразу делим все на π или умножаем на 1/ π
–7/2 ≤ 1/2 + n ≤ –2;
–7/2 – 1/2 ≤ n ≤ –2 – 1/2 ;
–4 ≤ n ≤ –5/2.
Целые n в этом промежутке это: n=–4 n= –3.

Значит, корни, принадлежащие этому промежутку, будут следующие:

х= π/2 + π(–4) = –7π/2; х=π/2 + π(–3) = –5π/2.
Аналогично решаем еще два неравенства:
–7π/2 ≤ π/4 + 2πk ≤ –2π;
–15/8 ≤ k ≤ –9/8.
Получили, что целых k в этом промежутке нет.
–7π/2 ≤ –π/4 + 2πm ≤ –2π;
–13/8 ≤ m ≤ –7/8.
Получили одно целое n в этом промежутке, m =–1. Значит, отобранный корень на этом промежутке имеет вид: х= –π/4 + 2π·(–1) = –9π/4.
Ответ: –7π/2, –5π/2, –9π/4.

II. Отбор корней с помощью тригонометрической окружности.

Чтобы использовать этот способ надо понимать, как работать с окружностью. Так как функции синус, косинус, тангенс и котангенс периодичны, то окружность, можно обходить бесконечное число раз.

«Обойдем» окружность один раз против часовой стрелки (положительное направление, т.е. значения будут положительные)

«Обойдем» окружность два раза против часовой стрелки (положительное направление т.е. значения будут положительные)

«Обойдем» 1 раз по часовой стрелки (отрицательное направление, т.е. значения будут отрицательные)

Вернемся к вопросу об отборе корней на промежутке

[–7π/2; –2π].
Чтобы попасть к числам –7π/2 и –2π надо «обойти» окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.

Рассмотри x = π/2 + πn. Какой приблизительно должен быть n, чтобы значение x было где–то в этом промежутке? Предположим n= –2, получаем х=π/2 – 2π = –3π/2, очевидно, это не входит в наш промежуток. Значит, берем меньше n=–3, то х= π/2 – 3π = –5π/2, это подходит. Попробуем еще n=–4, то х=π/2 – 4π = –7π/2, также подходит.
Рассуждая аналогично для х=π/4 + 2πk, k ∈ Z и х=–π/4 + 2πm, m ∈ Z находим еще один корень x=–9π/4.

После того, как отбор корней произвели разными способами, прошу проанализировать преимущества каждого из них, получились, в частности такие итоги: первый способ (с помощью неравенств) гораздо надежнее и намного проще для понимания, но нужно уметь решать простейшие неравенства. Если действительно серьезно разобраться с тригонометрической окружностью, то отбор корней по второму методу будет гораздо быстрее. Плюс экономия времени на экзамене.

4)Проведение смотра знаний по данной теме в форме математической игры «Своя игра»

(идея заимствована здесь https://kopilkaurokov.ru/matematika/uroki/okh-uzh-eta-trighonomietriia )

5)Рассмотрение реальных работ участников ЕГЭ прошлых лет, оцененных экспертами, с целью нахождения ошибок при выполнении отбора корней в тригонометрических уравнениях, например оценка эксперта-1 балл. Почему не засчитано решение п.б)?

Вывод: отбор корней нельзя назвать обоснованным, так как перебор остановлен на корне принадлежащем отрезку.

Вывод: при отборе корней отсутствует решение и ошибочно указано число, которое не является корнем тригонометрического уравнения.

В заключение отмечу, что поскольку задание № 13 (или №12 в модели профильного ЕГЭ 2022 года) является самым простым из заданий с развернутым решением, то целенаправленная работа над ним дает возможность большему числу выпускников успешно справиться с ним и получить высокий результат на экзамене.

Список используемых ресурсов:

1. Виленкин Н. Я. Алгебра и математический анализ 10 класс. Учебник для углубленного изучения математики в общеобразовательных учреждениях, Издательство Мнемозина, 13-е изд. стереотипное, 2006. – 336с.

2. Гельфанд И.М., Львовский С.М., Тоом А.Л. Тригонометрия, М. : МЦНМО, 2003.-7-16 с.

3. Захарова, И. Г. Информационные технологии в образовании: учебное пособие для студ. пед. учеб. заведений/ И. Г. Захарова,– М.: Издательский центр «Академия», 2003. – 192 с.

4. Звавич В.И., Пигарев Б.П. Тригонометрические уравнения (решение уравнений + варианты самостоятельных работ)//Математика в школе.№3, С.18-27.

5. А.Н. Колмагорова Алгебра и начала анализа. Учебник для 10-11 классов общеобразовательных учреждений, 17-е изд. – М. : Просвещение, 2008. – 384 с.

6. Королев С.В. Тригонометрия на экзамене по математике, изд. Экзамен, 2006. – 254 с.

7. Марасанов А.Н. О методологическом подходе в обучении тригонометрии/ Н.И. Попов, А.Н. Марасанов// Знание и понимание. Умение. -2008. – №4. – 139-141 с.

8. Марасанов А.Н. Тригонометрия: учебное пособие, 2-е изд., испр и доп. (Н.И. Попов, А.Н. Марасанов.-Йошкар-Ола; Мар. гос. Ун-т, 2009.-114с.)

9. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Тригонометрия. 10 класс, М. : Просвещение, 2008. – 61 с.

10. Мордкович А.Г. Алгебра и начала анализа.10-11 классы. Часть 1.Учебник для учащихся общеобразовательных учреждений(базовый уровень). – 10-е изд., стер. – М. : Мнемозина, 2009. – 399 с.:ил.

11. Мордкович А.Г. Алгебра и начала анализа.10-11 классы. Часть 2. Задачник для учащихся общеобразовательных учреждений(базовый уровень), – 10-е изд., стер. – М. : Мнемозина, 2009. – 399 с.:ил. 69

12. Мирошин В. Отбор корней в тригонометрических уравнениях.//Математика. Приложение к газете «Первое сентября» №17, 2006г.

13. Просветов Г.И. Тригонометрия. Задачи и решения, Альфа-Пресс, 2010. – 72 с.

14. Решетников Н.Н. Тригонометрия в школе: М. Педагогический университет «Первое сентября», 2006, лк 1.

15. Смоляков А.Н., Севрюков П.Ф. Приемы решения тригонометрических уравнений//Математика в школе. 2004. №1. С.24-26.

16. Шабашова О.В. Приемы отбора корней в тригонометрических уравнениях//Математика в школе. 2004. №1. С.20-24.

17. https://ppt-online.org/491236

18. Методические материалы для председателей и членов предметных комиссий субъектов Российской Федерации по проверке выполнения заданий с развёрнутым ответом экзаменационных работ ЕГЭ 2022 года. МАТЕМАТИКА. Федеральный институт педагогических измерений, 2022

19. https://kopilkaurokov.ru/matematika/uroki/okh-uzh-eta-trighonomietriia