Решение уравнений – навык, который необходим каждому нацеленному на успешную сдачу ЕГЭ и ОГЭ школьнику. Он поможет решить задания №4, 12 и 14 из профильного уровня математики.
Одна из их разновидностей уравнений – степенные уравнения, которые иногда также называют показательными. Основная отличительная особенность – наличие степеней и переменной (х) не в основании степени, а в самом показателе. Как это выглядит:
$$ a^{f(x)}=b^{g(x)}; $$
Где (a) и (b) – некоторые числа, а (f(x)) и (g(x)) – какие-то выражения, зависящие от (x). Не бойтесь – это самый общий вид показательных уравнений. Реальные примеры выглядят как-то так:
$$2^x=8;$$
$$ 2^x=2^{2x+1};$$
$$3^{x^2}=2^{x^2-2x+3};$$
Внимательно посмотрите на приведенные уравнения. В каждом из них присутствует, так называемая, показательная (степенная) функция. При решении необходимо помнить об основных свойствах степени, а также использовать особые правила, помогающие вычислить значение (х). Познакомиться с понятием степени и ее свойствами можно тут и тут.
И вам понадобится умение решать обыкновенные линейные и квадратные уравнения, те, что вы проходили в 7-8 классе. Вот такие:
$$ 7x+2=16;$$
$$x^2-4x+5=0;$$
И так, любое уравнение, в котором вы увидите показательную (степенную) функцию, называется показательным уравнением.
Ура! Теперь знаем, как выглядят показательные уравнения, но толку от этого не очень много. Было бы неплохо научиться их решать. Отличная новость – на наш взгляд показательные уравнения одни из самых простых типов уравнений, по сравнению с логарифмическими, тригонометрическими или иррациональными.
Простейшие показательные уравнения
Давайте начнем с самых простых типов уравнений и разберем сразу несколько примеров:
Пример 1
$$ 2^x=8;$$
Что такое решить уравнение? Это значит, что нужно найти такое число, которое при подстановке в исходное уравнение вместо (х) даст верное равенство. В нашем примере нужно найти такое число, в которое нужно возвести двойку, чтобы получить восемь. Ну это просто:
$$ 2^3=2*2*2=8; $$
Значит, если (х=3), то мы получим верное равенство, а значит мы решили уравнение.
Решим что-нибудь по-сложнее.
Пример 2
$$ 3^{4x-1}=frac{1}{9};$$
Такое уравнение выглядит сложнее. Попробуем преобразовать правую часть уравнения:
$$frac{1}{9}=frac{1}{3^2}=3^{-2};$$
Мы применили свойство отрицательной степени по формуле:
$$ a^{-n}=frac{1}{a^n};$$
Теперь наше уравнение будет выглядеть так:
$$ 3^{4x-1}=3^{-2};$$
Заметим, что слева и справа у нас стоят показательные функции, и там, и там основания одинаковые и равны (3), только вот степени разные – слева степень ((4х-1)), а справа ((-2)). Логично предположить, что если степени у такой конструкции будут равны, при условии, что основания одинаковые, то мы получим верное равенство. Так и поступим:
$$ 4x-1=-2;$$
Такое мы решать умеем, ведь это обыкновенное линейное уравнение.
$$4х=-2+1;$$
$$4x=-1;$$
$$x=-frac{1}{4}.$$
Поздравляю, мы нашли корень нашего показательного уравнения.
Пример 3
$$125^x=25;$$
Попробуем поступить так, как в предыдущем примере – преобразуем левую и правую часть, чтобы слева и справа была показательная функция с одинаковым основанием. Как это сделать? Обращаем внимание, что (125=5*5*5=5^3), а (25=5*5=5^2), подставим:
$$ (5^3)^x=5^2;$$
Воспользуемся одним из свойств степеней ((a^n)^m=a^{n*m}):
$$ 5^{3*x}=5^2;$$
И опять мы получили две показательные функции, у которых одинаковые основания и для того, чтобы равенство выполнялось, необходимо приравнять из степени:
$$ 3*x=2;$$
$$ x=frac{2}{3};$$
И еще один пример:
Пример 4
$$2^x=-4;$$
Те, кто хорошо знает свойства степеней, знают, что показательная функция не может быть отрицательной. Действительно, попробуйте возводить (2) в различную степень, вы никогда не сможете получить отрицательное число.
Внимание! Показательная функция не может быть отрицательной, поэтому, когда вы встречаете примеры на подобии примера 4, то знайте, что такого быть не может. Здесь корней нет, потому что показательная функция всегда положительна.
Теперь давайте разработаем общий метод решения показательных уравнений. И научимся решать более сложные примеры.
Общий метод решения показательных уравнений
Пусть у нас есть вот такой пример:
$$ a^x=b;$$
Где (a,b) какие-то положительные числа. ((a>0, ; b>0)).
Согласно разобранным выше примерам, логично предположить, что для того, чтобы решить данное уравнение, нужно его преобразовать к виду, где слева и справа стоят показательные функции с одинаковым основанием. Так и поступим.
Слева у нас уже стоит (a^x), с этим ничего делать не будем, а вот справа у нас стоит загадочное число (b), которое нужно попытаться представить в виде (b=a^m). Тогда уравнение принимает вид:
$$ a^x=a^m;$$
Раз основания одинаковые, то мы можем просто приравнять степени:
$$x=m.$$
Вот и весь алгоритм решения. Просто нужно преобразовать исходное уравнение таким образом, чтобы слева и справа стояли показательные функции с одинаковыми основаниями, тогда приравниваем степени и вуаля – сложное показательное уравнение решено. Осталось только разобраться, как так преобразовывать. Опять разберем на примерах:
Пример 5
$$2^x=16;$$
Замечаем, что (16=2*2*2*2=2^4) это степень двойки:
$$2^x=2^4$$
Основания одинаковые, значит можно приравнять степени:
$$x=4.$$
Пример 6
$$5^{-x}=125 Rightarrow 5^{-x}=5*5*5 Rightarrow 5^{-x}=5^3 Rightarrow –x=3 Rightarrow x=-3.$$
Пример 7
$$9^{4x}=81 Rightarrow (3*3)^{4x}=3*3*3*3 Rightarrow(3^2)^{4x}=3^4 Rightarrow 3^{8x}=3^4 Rightarrow 8x=4 Rightarrow x=frac{1}{2}.$$
Здесь мы заметили, что (9=3^2) и (81=3^4) являются степенями (3).
Все здорово, но проблема в том, что такая схема решения показательных уравнений работает не всегда. Что делать, если привести к одинаковому основанию не получается. Например:
Пример 8
$$ 3^x=2;$$
(3) и (2) привести к одинаковому основанию затруднительно. Но тем не менее мы должны это сделать. Воспользуемся следующей схемой преобразований: пусть есть некоторое положительное число (b>0), тогда его можно представить в виде степени любого, нужного вам, положительного числа не равного единице (a>0, ; a neq 1):
$$ b=a^{log_{a}(b)};$$
Эта очень важная формула, рекомендуем ее выучить. Вернемся к нашему примеру и по формуле представим (2) в виде (3) в какой-то степени, где (a=3), а (b=2):
$$ 2=3^{log_{3}(2)};$$
Подставим данное преобразование в наш пример:
$$3^x=3^{log_{3}(2)};$$
Получили равенство двух показательных функций с одинаковым основанием, значит можем приравнять их степени:
$$x=log_{3}(2).$$
Так в ответ и запишем. Никакой ошибки здесь нет, дело в том, что такие логарифмы можно посчитать только на калькуляторе, поэтому на ЕГЭ или в контрольной работе вы просто оставляете ответ в таком виде.
Кто забыл, что такое логарифм, можно посмотреть здесь.
Рассмотрим еще несколько аналогичных примеров.
Пример 9
$$ 7^{2x}=5;$$
$$ 7^{2x}=7^{log_{7}(5)};$$
$$2x=log_{7}(5);$$
$$x=frac{1}{2}*log_{7}(5).$$
Те, кто хорошо знает свойства логарифмов, могут поиграться с последней формулой и получить ответ в разном виде:
$$ x=frac{1}{2}*log_{7}(5)=log_{7}(5^{frac{1}{2}})=log_{7}(sqrt{5});$$
Все эти варианты ответа верные, их можно смело писать в ответ.
И так, мы с вами научились решать любые показательные уравнения вот такого вида: (a^x=b), где (a>0; ; b>0).
Но это еще далеко не все. Часто вы будете встречать показательные уравнения гораздо более сложного типа. В ЕГЭ по профильной математике это номер 15 из 2й части. Но бояться тут не нужно, все на первый взгляд сложные уравнения при помощи обычно не самых сложных преобразований сводятся к уравнениям типа (a^x=b), где (a>0; ; b>0). Рассмотрим типы сложных уравнений, которые могут попасться:
Решение показательных уравнений при помощи замены
Рассмотрим уравнение:
Пример 10
$$ 9^x-5*3^x+6=0;$$
Самое первое, что вы должны всегда делать, это пытаться привести все имеющиеся показательные функции к одинаковому основанию.
Здесь это сделать легко, замечаем, что (9=3^2), тогда (9^x=(3^2)^x=3^{2x}=(3^x)^2). Здесь мы воспользовались свойством степеней: ((a^n)^m=a^{n*m}). Подставим:
$$(3^x)^2-5*3^x+6=0;$$
Обратим внимание, что во всем уравнении все (х) «входят» в одинаковую функцию – (3^x). Сделаем замену (t=3^x, ; t>0), так как показательная функция всегда положительна.
$$t^2-5t+6=0;$$
Квадратное уравнение, которое решается через дискриминант:
$$D=5^2-4*6=25-24=1; Rightarrow t_{1}=frac{5+sqrt{1}}{2}=3; Rightarrow t_{2}=frac{5-sqrt{1}}{2}=2;$$
Оба корня больше нуля, значит оба нам подходят. Сделаем обратную замену и уравнение сводится к решению двух простых показательных уравнений:
$$ 3^x=3;$$
$$3^x=3^1;$$
$$x=1.$$
И второй корень:
$$ 3^x=2;$$
$$3^x=3^{log_{3}(2)};$$
$$x=log_{3}(2).$$
Ответ: (x_{1}=1; ; x_{2}=log_{3}(2).)
И еще один пример на замену:
Пример 11
$$3^{4x^2-6x+3}-10*3^{2x^2-3x+1}+3=0;$$
Воспользуемся нашим правилом, что все нужно приводить к одинаковому основанию – а стоп, тут и так у всех показательных функций основание (3). Давайте еще внимательно посмотрим на наш пример, очень похоже на то, что он тоже делается через замену. Но у нас тут нет одинаковых показательных функций, основания то одинаковые, а вот степени отличаются. Преобразуем первое слагаемое. Если быть внимательным, то можно заметить, что в первой степени можно разбить свободный член (3=2+1) и вынести общий множитель (2):
$$ 3^{4x^2-6x+3}=3^{4x^2-6x+2+1}=3^{2(2x^2-3x+1)+1}=3^{2*(2x^2-3x+1)}*3^1=3*(3^{2x^2-3x+1})^2;$$
Подставим в исходное уравнение:
$$3*(3^{2x^2-3x+1})^2-10*3^{2x^2-3x+1}+3=0;$$
Теперь показательные функции одинаковы и можно сделать замену:
$$t=3^{2x^2-3x+1}; ; t>0;$$
$$3*t^2-10t+3=0;$$
$$D=100-36=64; Rightarrow t_{1}=3; t_{2}=frac{1}{3};$$
Обратная замена, и наше уравнение сводится к простейшему:
$$ 3^{2x^2-3x+1}=3;$$
$$ 2x^2-3x+1=1;$$
$$x(2x-3)=0;$$
$$x=0; ; x=frac{3}{2}.$$
И второе значение (t):
$$3^{2x^2-3x+1}=frac{1}{3};$$
$$3^{2x^2-3x+1}=3^{-1};$$
$$2x^2-3x+1=-1;$$
$$2x^2-3x+2=0;$$
$$D=9-16=-7<0;$$
Раз дискриминант получился меньше нуля, то вторая ветка решений нам корней не дает.
Ответ: (x_{1}=0; ; x_{2}=frac{3}{2}.)
Однородные показательные уравнения
Иногда встречаются такие показательные уравнения, в которых не сразу видно, как сделать одинаковые функции, а именно одинаковые основания, чтобы произвести замену. Посмотрим на такой пример:
Пример 12
$$ 7^{x+1}+3*7^{x}=3^{x+2}+3^{x};$$
Тут у нас две показательные функции с основаниями (7) и (3), и как сделать из них одинаковые основания непонятно. Этот пример решается при помощи деления. Давайте поделим все наша уравнение на (3^x):
$$ 7^{x+1}+3*7^{x}=3^{x+2}+3^{x} ; ; :3^x$$
$$ frac{7^{x+1}}{3^x}+frac{3*7^{x}}{3^x}=frac{3^{x+2}}{3^x}+frac{3^{x}}{3^x};$$
Здесь нам придется воспользоваться свойствами степеней:
$$frac{a^n}{a^m}=a^{n-m};$$
$$ a^n*a^m=a^{n+m};$$
$$ frac{a^n}{b^n}=(frac{a}{b})^n;$$
Разберем каждое слагаемое:
$$ frac{7^{x+1}}{3^x}=frac{7*7^x}{3^x}=7*frac{7^x}{3^x}=7*(frac{7}{3})^x;$$
$$ frac{3*7^{x}}{3^x}=3*frac{7^x}{3^x}=3*(frac{7}{3})^x;$$
$$ frac{3^{x+2}}{3^x}=3^2*frac{3^x}{3^x}=3^2*1=9;$$
$$ frac{3^{x}}{3^x}=1;$$
Теперь подставим получившееся преобразования в исходное уравнение:
$$ 7*(frac{7}{3})^x+3*(frac{7}{3})^x=9+1;$$
Теперь видно, что в нашем уравнении есть одинаковая функция, которую можно убрать в замену (t=(frac{7}{3})^x):
$$7t+3t=10;$$
$$10t=10;$$
$$t=1;$$
Сделаем обратную замену:
$$(frac{7}{3})^x=1;$$
Вспоминаем, что (1=(frac{7}{3})^0):
$$(frac{7}{3})^x=(frac{7}{3})^0;$$
$$x=0.$$
Ответ: (x=0).
И последний пример на замену:
Пример 13
$$2^{x+2}+0,5^{-x-1}+4*2^{x+1}=28;$$
Первым делом нужно сделать так, чтобы все показательные функции были с одинаковым основанием и в идеале с одинаковой степенью. Для этого нам понадобятся формулы для степеней:
$$ a^n*a^m=a^{n+m};$$
$$a^{-n}=frac{1}{a^n};$$
$${(a^n)}^m=a^{n*m};$$
Разберем каждое слагаемое нашего уравнения:
$$2^{x+2}=2^x*2^2=4*2^x;$$
Все десятичные дроби всегда разумно представить в виде обыкновенных дробей. И будьте внимательны – отрицательная степень не имеет никакого отношения к знаку показательной функции!
$$0,5^{-x-1}=0,5^{-(x+1)}={(frac{1}{2})}^{-(x+1)}={(2^{-1})}^{-(x+1)}=2^{x+1}=2^x*2^1=2*2^x;$$
И последнее слагаемое со степенью:
$$ 4*2^{x+1}=4*2^x*2^1=8*2^x;$$
Подставим все наши преобразования в исходное уравнение:
$$4*2^x+2*2^x+8*2^x=28;$$
Теперь можно сделать замену (t=2^x) или можно обойтись без замены, просто приведя подобные слагаемые (вынести общий множитель (2^x)):
$$2^x*(4+2+8)=28;$$
$$14*2^x=28;$$
$$2^x=frac{28}{14}=2;$$
$$2^x=2^1;$$
$$x=1.$$
Ответ: (x=1.)
Особенно стоит подчеркнуть прием, который мы использовали при решении 13-го примера.
Всегда старайтесь избавляться от десятичных дробей. Переводите их в обыкновенные дроби.
И другой тип степенных уравнений, где обычно не нужно делать замену, а необходимо отлично знать все свойства степеней, некоторые из них мы уже обсудили выше. Все про свойства степеней можно посмотреть тут
Пример 14
$$2^{x+1}*5^x=10^{x+1}*5^{x+2};$$
Вот такое уравнение, в котором у нас, во-первых, показательных функции перемножаются, а еще хуже то, что у них у всех разные основания. Катастрофа, а не пример. Но ничего, все не так страшно, как кажется. Внимательно посмотрите на основания: у нас есть в основании (2), (5) и (10). Очевидно, что (10=2*5). Воспользуемся этим и подставим в наше уравнение:
$$2^{x+1}*5^x=(2*5)^{x+1}*5^{x+2};$$
Воспользуемся формулой ((a*b)^n=a^n*b^n):
$$ 2^{x+1}*5^x=2^{x+1}*5^{x+1}*5^{x+2};$$
И перекинем все показательные функции с основанием (2) влево, а с основанием (5) вправо:
$$frac{2^{x+1}}{2^{x+1}}=frac{5^{x+1}*5^{x+2}}{5^x};$$
Сокращаем и воспользуемся формулами (a^n*a^m=a^{n+m}) и (frac{a^n}{a^m}=a^{n-m}):
$$1=frac{5^{x+1+x+2}}{5^x};$$
$$1=frac{5^{2x+3}}{5^x};$$
$$1=5^{2x+3-x};$$
$$1=5^{x+3};$$
$$5^0=5^{x+3};$$
$$x+3=0;$$
$$x=-3.$$
Ответ: (x=-3).
Самая главная идея при решении показательных уравнений – это любыми доступными способами свести все имеющиеся степенные функции к одинаковому основанию. А еще лучше и к одинаковой степени. Вот почему необходимо знать все свойства степеней, без этого решить уравнения будет проблематично.
Как же понять, где какие преобразования использовать? Не бойтесь, это придет с опытом, чем больше примеров решите, тем увереннее будете себя чувствовать на контрольных в школе или на ЕГЭ по профильной математике. Сначала потренируйтесь на простых примерах и постепенно повышайте уровень сложности. Успехов в изучении математики!
Что такое показательные уравнения
Если ты забыл следующие темы, то для получения наилучшего результата, пожалуйста, повтори:
- Свойства степени и корня
- Решение линейных и квадратных уравнений
- Разложение на множители
Повторил? Замечательно!
Тогда тебе не составит труда заметить, что корнем уравнения ( 3x+5=2{x} -1) является число ( x=-6).
Ты точно понял, как я это сделал? Правда? Тогда продолжаем. Теперь ответь мне на вопрос, чему равно ( 5) в третьей степени? Ты абсолютно прав:
( {{5}^{3}}=5cdot 5cdot 5=125).
А восьмерка – это какая степень двойки? Правильно – третья! Потому что:
( 2cdot 2cdot 2={{2}^{3}}=8).
Ну вот, теперь давай попробуем решить следующую задачку: Пусть я ( x) раз умножаю само на себя число ( 2) и получаю в результате ( 16).
Спрашивается, сколько раз я умножил ( 2) само на себя? Ты, конечно, можешь проверить это непосредственно:
( begin{align} & 2=2 \ & 2cdot 2=4 \ & 2cdot 2cdot 2=8 \ & 2cdot 2cdot 2cdot 2=16 \ end{align} )
Тогда ты можешь сделать вывод, что ( 2) само на себя я умножал ( displaystyle 4) раза.
Как еще это можно проверить?
А вот как: непосредственно по определению степени: ( displaystyle {{2}^{4}}=16).
Но, согласись, если бы я спрашивал, сколько раз два нужно умножить само на себя, чтобы получить, скажем ( displaystyle 1024), ты бы сказал мне: я не буду морочить себе голову и умножать ( displaystyle 2) само на себя до посинения.
И был бы абсолютно прав. Потому как ты можешь записать все действия кратко (а краткость – сестра таланта)
( displaystyle {{2}^{x}}=1024),
где ( displaystyle x) – это и есть те самые «разы», когда ты умножаешь ( displaystyle 2) само на себя.
Я думаю, что ты знаешь ( а если не знаешь, срочно, очень срочно повторяй степени!), что ( displaystyle 1024={{2}^{10}}), тогда моя задачка запишется в виде:
( displaystyle {{2}^{x}}={{2}^{10}}), откуда ты можешь сделать вполне оправданный вывод, что:
( x=10).
Вот так вот незаметно я записал простейшее показательное уравнение:
( {{2}^{x}}={{2}^{10}})
И даже нашел его корень ( x=10). Тебе не кажется, что все совсем тривиально? Вот и я думаю именно так же.
Вот тебе еще один пример:
( {{1000}^{x}}=100).
Но что же делать?
Ведь ( 100) нельзя записать в виде степени (разумной) числа ( 1000).
Давай не будем отчаиваться и заметим, что оба этих числа прекрасно выражаются через степень одного и того же числа.
Какого?
Верно: ( 100={{10}^{2}},~1000={{10}^{3}}).
Тогда исходное уравнение преобразуется к виду:
( {{10}^{3x}}={{10}^{2}}),
откуда, как ты уже понял, ( 3x=2,~x=frac{2}{3}).
Давай более не будем тянуть и запишем определение:
Пример 1 (меркантильный)
Пусть у тебя есть ( displaystyle 1000000) рублей, а тебе хочется превратить его в ( displaystyle 1500000) рублей.
Банк предлагает тебе взять у тебя эти деньги под ( displaystyle 12%) годовых с ежемесячной капитализацией процентов (ежемесячным начислением).
Спрашивается, на сколько месяцев нужно открыть вклад, чтобы набрать нужную конечную сумму?
Вполне приземленная задача, не так ли?
Тем не менее ее решение связано с построением соответствующего показательного уравнения:
Пусть ( Sn) – начальная сумма, ( Sk) – конечная сумма, ( i) – процентная ставка за период, ( x) – количество периодов.
Тогда:
( Sk=Sn{{left( 1+frac{i}{100} right)}^{x}})
В нашем случае ( displaystyle Sn=1000000={{10}^{6}},~Sk=1500000=1.5cdot {{10}^{6}},~i=1) (если ставка ( 12%) годовых, то за месяц начисляют ( 1%)).
А почему ( i) делится на ( 100)? Если не знаешь ответ на этот вопрос, вспоминай тему «Проценты»!
Тогда мы получим вот такое уравнение:
( 1.5cdot {{10}^{6}}={{10}^{6}}{{left( 1+0.01 right)}^{x}})
( 1.5={{1.01}^{x}})
Данное показательное уравнение уже можно решить только при помощи калькулятора (его внешний вид на это намекает, причем для этого требуется знание логарифмов, с которыми мы познакомимся чуть позже), что я и сделаю: ( xtilde{ }40.7489)…
Таким образом, для получения ( 1.5) млн. нам потребуется сделать вклад на ( 41) месяц (не очень быстро, не правда ли?)
Пример 1. Метод простой замены
( {{4}^{x}}+{{2}^{x+1}}-3=0)
Решение:
Это уравнение решается при помощи «простой замены», как ее пренебрежительно называют математики.
В самом деле, замена здесь – самая очевидная. Стоит лишь увидеть, что
( {{4}^{x}}={{2}^{2x}}={{({{2}^{x}})}^{2}})
Тогда исходное уравнение превратится вот в такое:
( {{({{2}^{x}})}^{2}}+{{2}^{x+1}}-3=0)
Если же дополнительно представить ( {{2}^{x+1}}) как ( 2cdot {{2}^{x}}), то совершенно ясно, что надо заменять: конечно же, ( t={{2}^{x}}). Во что тогда превратится исходное уравнение? А вот во что:
( {{t}^{2}}+2t-3=0)
Ты без проблем самостоятельно отыщешь его корни: ( {{t}_{1}}=-3,~{{t}_{2}}=1).
Что нам делать теперь?
Пришло время возвращаться к исходной переменной ( displaystyle x).
А что я забыл указать? Именно: при замене некоторой степени на новую переменную (то есть при замене вида ( t={{a}^{x}})), меня будут интересовать только положительные корни!
Ты и сам без труда ответишь, почему.
Таким образом, ( {{t}_{1}}=-3) нас с тобой не интересует, а вот второй корень нам вполне подходит:
( {{t}_{2}}=1), тогда ( {{2}^{x}}=1), откуда ( x=0).
Ответ: ( x=0)
Как видишь, в предыдущем примере, замена так и просилась к нам в руки. К сожалению, так бывает далеко не всегда.
Однако давай не будем переходить сразу к грустному, а потренируемся еще на одном примере с достаточно простой заменой.
Пример 2. Метод простой замены
( {{3}^{3x+1}}-4cdot {{9}^{x}}=17cdot {{3}^{x}}-6)
Решение:
Ясно, что скорее всего заменять придется ( {{3}^{x}}) (это наименьшая из степеней, входящая в наше уравнение).
Однако прежде чем вводить замену, наше уравнение нужно к ней «подготовить», а именно:
( {{3}^{3x+1}}=3cdot {{left( {{3}^{x}} right)}^{3}}), ( {{9}^{x}}={{({{3}^{x}})}^{2}}).
Тогда можно заменять ( t={{3}^{x}}), в результате я получу следующее выражение:
( 3{{t}^{3}}-4{{t}^{2}}=17t-6)
( 3{{t}^{3}}-4{{t}^{2}}-17t+6=0)
О ужас: кубическое уравнение с совершенно жуткими формулами его решения (ну если говорить в общем виде). Но давай не будем сразу отчаиваться, а подумаем, что нам делать.
Я предложу смошенничать: мы знаем, что для получения «красивого» ответа, нам нужно получить ( t) в виде некоторой степени тройки (с чего бы это, а?).
А давай попробуем угадать хотя бы один корень нашего уравнения (я начну гадать со степеней тройки).
Первое предположение ( displaystyle t=1). Не является корнем. Увы и ах! Хорошо, а теперь возьмем…
Как видишь, отбор корней показательных уравнений требует достаточно глубокого знания свойств логарифмов, так что я советую тебе быть как можно внимательнее, когда решаешь показательные уравнения.
Как ты понимаешь, в математике все взаимосвязано! Как говорила моя учительница по математике, математику, как историю, за ночь не прочитаешь.
Как правило, всю сложность при решении задач повышенной сложности составляет именно отбор корней уравнения.
Еще один пример для тренировки
( {{9}^{x+1}}-2cdot {{3}^{x+2}}+5=0,~) при ( ~xin (lo{{g}_{3}}frac{3}{2};sqrt{5}))
Решение:
Ясно, что само уравнение решается довольно просто. Сделав замену ( t={{3}^{x}}) мы сведем наше исходное уравнение к следующему:
( {{t}^{2}}-18t+5=0)
( {{t}_{1}}=frac{1}{3},~{{t}_{2}}=frac{5~}{3})
Тогда ( {{x}_{1}}=-1,~{{x}_{2}}=mathbf{lo}{{mathbf{g}}_{3}}left( frac{5}{3} right)~~~)
Вначале давай рассмотрим первый корень.
Сравним ( -1) и ( lo{{g}_{3}}left( frac{3}{2} right)):
так как ( frac{3}{2}>1), то ( lo{{g}_{3}}left( frac{3}{2} right)>0). (свойство логарифмической функции ( y=lo{{g}_{a}}x) при ( a>1)).
Тогда ясно, что( lo{{g}_{3}}left( frac{3}{2} right)>-1) и первый корень не принадлежит нашему промежутку.
Теперь второй корень:
Пример уравнения с нестандартной заменой!
( displaystyle 4sqrt[x]{81}-12sqrt[x]{36}+9sqrt[x]{16}=0)
Решение:
Давай сразу начнем с того, что делать можно, а что – в принципе можно, но лучше не делать.
Можно – представить все через степени тройки, двойки и шестерки. К чему это приведет?
Да ни к чему и не приведет: мешанина степеней, причем от некоторых будет довольно сложно избавиться.
А что же тогда нужно?
Давай заметим, что ( 81={{9}^{2}},~16={{4}^{2}},~) а ( 36=4cdot 9.)
И что нам это даст? А то, что мы можем свести решение данного примера к решению достаточно простого показательного уравнения!
Вначале давай перепишем наше уравнение в виде:
( displaystyle 4cdot {{9}^{frac{2}{x}}}~-12cdot {{4}^{frac{1}{x}}}{{9}^{frac{1}{x}}}+9cdot {{4}^{frac{2}{x}}}=0)
Такие уравнения называются однородными (подробнее читай в теме «Однородные уравнения»).
Теперь разделим обе части получившегося уравнения на ( {{4}^{frac{2}{x}}}):
Например, уравнение вида:
( {{a}^{F(x)}}=b(x)), причем ( b(x)ne {{a}^{i}}), ( i)( in R/Q)
В общем случае можно решить только логарифмированием обеих частей (например по основанию ( a)), при котором исходное уравнение превратится в следующее:
( F(x)=lo{{g}_{a}}b(x))
Давай рассмотрим следующий пример:
( {{x}^{1+lgx}}=10x)
Ясно, что по ОДЗ логарифмической функции, нас интересуют только ( x>0). Однако, это следует не только из ОДЗ логарифма, а еще по одной причине. Я думаю, что тебе не будет трудно угадать, по какой же именно.
Давай прологарифмируем обе части нашего уравнения по основанию ( 10):
( lg({{x}^{1+lgx}})=lg(10x))
( (1+lg(x))cdot lg(x)=1+lg(x))
( (1+lg(x))(lg(x)-1)=0)
( lg(x)=1,~lg(x)=-1)
( {{x}_{1}}=10,~{{x}_{2}}=0,1)
Как видишь, логарифмирование нашего исходного уравнения достаточно быстро привело нас к правильному (и красивому!) ответу.
Давай потренируемся еще на одном примере:
( {{x}^{lo{{g}_{4}}x-2}}={{2}^{2(lo{{g}_{4}}x-1)}})
Здесь тоже нет ничего страшного: прологарифмируем обе стороны уравнения по основанию ( 4), тогда получим:
( lo{{g}_{4}}({{x}^{lo{{g}_{4}}x-2}})=lo{{g}_{4}}({{2}^{2(lo{{g}_{4}}x-1)}});)
( left( lo{{g}_{4}}x-2 right)text{lo}{{text{g}}_{4}}x=2left( text{lo}{{text{g}}_{4}}x-1 right)text{lo}{{text{g}}_{4}}2;)
( (lo{{g}_{4}}x-2)lo{{g}_{4}}x=(lo{{g}_{4}}x-1);)
Сделаем замену: ( t=lo{{g}_{4}}x)
( {{t}_{1}}=frac{3+sqrt{5}}{2},~{{t}_{2}}=frac{3-sqrt{5}}{2})
Тогда ( {{x}_{1}}=lo{{g}_{4}}left( frac{3+sqrt{5}}{2} right),~{{x}_{2}}=lo{{g}_{4}}left( frac{3-sqrt{5}}{2} right),~)
Однако мы кое-что упустили! Ты заметил, где я сделал промах?
Ведь ( frac{3-sqrt{5}}{2}<1,~) тогда:
( {{x}_{2}}=lo{{g}_{4}}left( frac{3-sqrt{5}}{2} right)<0,~~) что не удовлетворяет требованию ( x>0) (подумай откуда оно взялось!)
Ответ: ( lo{{g}_{4}}left( frac{3+sqrt{5}}{2} right))
Попробуй самостоятельно записать решение показательных уравнений, приведенных ниже
- ( {{x}^{2l{{g}^{3}}x-1.5lgx}}=sqrt{10})
- ( {{(x+5)}^{lo{{g}_{7}}(x+5)}}=7)
А теперь сверь свое решение с этим:
1. Логарифмируем обе части по основанию ( 10), учитывая, что ( x>0):
( lg left( {{x}^{2l{{g}^{3}}x-1.5lgx}} right)=lgsqrt{10})
( left( 2l{{g}^{3}}x-1.5lgx right)lgx=frac{1}{2},~), замена ( ~t=l{{g}^{2}}xge 0)
( 4{{t}^{2}}-3t-1=0)
( 4{{t}^{2}}-3t-1=0) (второй корень нам не подходит ввиду замены)
( l{{g}^{2}}x=1,~{{x}_{1}}=1,~{{x}_{2}}=0.1~)
2. Логарифмируем по основанию ( displaystyle 7):
( displaystyle lo{{g}_{7}}{{left( x+5 right)}^{lo{{g}_{7}}left( x+5 right)}}=lo{{g}_{7}}7)
Преобразуем полученное выражение к следующему виду:
( displaystyle left( lo{{g}_{7}}left( x+5 right)+1 right)left( lo{{g}_{7}}left( x+5 right)-1 right)=0)
( displaystyle {{x}_{1}}=2,~{{x}_{2}}=-frac{34}{7})
План урока:
Простейшие показательные уравнения ах = b
Уравнения вида аf(x) = ag(x)
Задачи, сводящиеся к показательным уравнениям
Уравнения с заменой переменных
Графическое решение показательных уравнений
Показательные неравенства
Простейшие показательные уравнения ах = b
Рассмотрим уравнение
2х = 8
Его называют показательным уравнением, ведь переменная находится в показателе степени. Для его решения представим правую часть как степень числа 2:
8 = 23
Тогда уравнение будет выглядеть так:
2х = 23
Теперь и справа, и слева стоят степени двойки. Очевидно, что число 3 будет являться его корнем:
23 = 23
Является ли этот корень единственным? Да, в этом можно убедиться, если построить в координатной плоскости одновременно графики у = 2х и у = 8. Второй график представляет собой горизонтальную линию.

Пересекаются эти графики только в одной точке, а потому найденное нами решение х = 3 является единственным.
Так как любая показательная функция является монотонной, то есть либо только возрастает (при основании, большем единицы), либо только убывает (при основании, меньшем единицы), то в общем случае ур-ние ах = b может иметь не более одного решения. Это является следствием известного свойства монотонных функций – горизонтальная линия пересекает их не более чем в одной точке.
Сразу отметим, что если в ур-нии вида ах = b число b не является положительным, то корней у ур-ния не будет вовсе. Это следует из того факта, что область значений показательной функции – промежуток (0; + ∞), ведь при возведении в степень любого положительного числа результат всё равно остается положительным. Можно проиллюстрировать это и графически:


Решая простейшее показательное уравнение
2х = 8
мы специально представляли правую часть как степень двойки:
2х = 23
После этого мы делали вывод, что если в обеих частях ур-ния стоят степени с равными основаниями (2 = 2), то у них должны быть равны и показатели. Это утверждение верно и в более общем случае. Если есть ур-ние вида
ах = ас
то его единственным решением является х = с.

Задание. Найдите решение показательного уравнения
8х = 8– 9
Решение. У обоих частей равны основания, значит, равны и показатели:
х = – 9
Ответ: – 9.
Задание. Найдите корень уравнения

Решение. Заметим, что число 625 = 54. Тогда ур-ние можно представить так:

Отсюда получаем, что х = 4.
Ответ: 4.
Видно, что основной метод решения показательных уравнений основан на его преобразовании, при котором и в правой, и в левой части стоят степени с совпадающими основаниями.
Задание. При каком х справедливо равенство

Решение. Преобразуем число справа:

Теперь ур-ние можно решить:

Ответ: – 3.
Задание. Решите ур-ние

Решение. Любое число при возведении в нулевую степень дает единицу, а потому можно записать, что 1 = 1270. Заменим с учетом этого правую часть равенства:

Ответ: 0.
Уравнения вида аf(x) = ag(x)
Рассмотрим чуть более сложное показательное ур-ние

Для его решения заменим показатели степеней другими величинами:

Теперь наше ур-ние принимает вид

Такие ур-ния мы решать умеем. Надо лишь приравнять показатели степеней:

При решении подобных ур-ний введение новых переменных опускают. Можно сразу приравнять показатели степеней, если равны их основания:

В общем случае использованное правило можно сформулировать так:

Задание. Найдите корень ур-ния

Решение. Представим правую часть как степень двойки:

Тогда ур-ние примет вид

Теперь мы имеем право приравнять показатели:

Ответ: – 1
Задание. Укажите значение х, для которого выполняется условие

Решение. Здесь удобнее преобразовать не правую, а левую часть. Заметим, что

С учетом этого можно записать

Основания у выражений слева и справа совпадают, а потому можно приравнять показатели:

Ответ: 12,5
Задание. Укажите корень показательного уравнения

Решение. Для перехода к одному основанию представим число 64 как квадрат восьми:

Тогда ур-ние примет вид:

Ответ: х = 3
Задание. Найдите корень ур-ния

Решение. Здесь ситуация чуть более сложная, ведь число 2 невозможно представить как степень пятерки, а пятерки не получится выразить как степень двойки. Однако у обеих степеней в ур-нии совпадают показатели. Напомним, что справедливы следующие правила работы со степенями:

С учетом этого поделим обе части ур-ния на выражения 53+х:

Ответ: – 2.
Задание. При каких х справедлива запись

Решение.
Можно сделать преобразования, после которых в ур-нии останется только показательная функция 5х. Для этого произведем следующие замены:

Перепишем исходное ур-ние с учетом этих замен:

Теперь множитель 5х можно вынести за скобки:

Ответ: 2
Рассмотрим чуть более сложное ур-ние, которое может встретиться на ЕГЭ в задании повышенной сложности №13.
Задание. Найдите решение уравнения

Решение. Преобразуем левое слагаемое:

Перепишем начальное ур-ние, используя это преобразование

Теперь мы можем спокойно вынести множитель за скобки:

Получили одинаковые основания слева и справа. Значит, можно приравнять и показатели:

Это квадратное уравнение, решение которого не должно вызывать у десятиклассника проблем:

Задачи, сводящиеся к показательным уравнениям
Рассмотрим одну прикладную задачу, встречающуюся в ЕГЭ по математике.
Задание. Из-за радиоактивного распада масса слитка из изотопа уменьшается, причем изменение его массы описывается зависимостью m(t) = m0 • 2–t/T, где m0 – исходная масса слитка, Т – период полураспада, t – время. В начальный момент времени изотоп, чей период полураспада составляет 10 минут, весит 40 миллиграмм. Сколько времени нужно подождать, чтобы масса слитка уменьшилась до 5 миллиграмм.
Решение. Подставим в заданную формулу значения из условия:
m0 = 40 миллиграмм;
T = 10 минут;
m(t) = 5 миллиграмм.
В результате мы получим ур-ние

из которого надо найти значение t. Поделим обе части на 40:

Ответ: 30 минут.
Далее решим чуть более сложную задачу, в которой фигурирует сразу 2 радиоактивных вещества.
Задание. На особо точных рычажных весах в лаборатории лежат два слитка из радиоактивных элементов. Первый из них весит в начале эксперимента 80 миллиграмм и имеет период полураспада, равный 10 минутам. Второй слиток весит 40 миллиграмм, и его период полураспада составляет 15 минут. Изначально весы наклонены в сторону более тяжелого слитка. Через сколько минут после начала эксперимента весы выровняются? Масса слитков меняется по закону m(t) = m0 • 2–t/T, где m0 и Т – это начальная масса слитка и период его полураспада соответственно.
Решение. Весы выровняются тогда, когда массы слитков будут равны. Если подставить в данную в задаче формулу условия, то получится, что масса первого слитка меняется по закону

а масса второго слитка описывается зависимостью

Приравняем обе формулы, чтобы найти момент времени, когда массы слитков совпадут (m1 = m2):

Делим обе части на 40:

Основания равны, а потому приравниваем показатели:

Ответ: 30 минут.
Уравнения с заменой переменных
В ряде случаев для решения показательного уравнения следует ввести новую переменную. В учебных заданиях такая замена чаще всего (но не всегда) приводит к квадратному ур-нию.
Задание. Решите уравнение методом замены переменной

Заметим, что в уравнении стоят степени тройки и девятки, но 32 = 9. Тогда введем новую переменную t = 3x. Если возвести ее в квадрат, то получим, что

C учетом этого изначальное ур-ние можно переписать:

Получили обычное квадратное ур-ние. Решим его:

Мы нашли два значения t. Далее необходимо вернуться к прежней переменной, то есть к х:

Первое ур-ние не имеет решений, ведь показательная функция может принимать лишь положительные значения. Поэтому остается рассмотреть только второе ур-ние:

Ответ: 2.
Задание. Найдите корни ур-ния

Решение. Здесь в одном ур-нии стоит сразу три показательных функции. Попытаемся упростить ситуацию и избавиться от одной из них. Для этого поделим ур-ние на выражение 44х+1:

Так как 14х+1 = 1, мы можем записать:

Обратим внимание, что делить ур-ние на выражение с переменной можно лишь в том случае, если мы уверены, что оно не обращается в ноль ни при каких значениях х. В данном случае мы действительно можем быть в этом уверены, ведь величина 44х+1 строго положительна при любом х.
Вернемся к ур-нию. В нем стоят величины (9/4)4х+1 и (3/2)4х+1. У них одинаковые показатели, но разные степени. Однако можно заметить, что
9/4 = (3/2)2, поэтому и (9/4)4х+1 = ((3/2)4х+1)2. Это значит, что перед нами уравнение с заменой переменных.
Произведем замену t = (3/2)4х+1, тогда (9/4)4х+1 = ((3/2)4х+1)2 = t2. Далее перепишем ур-ние с новой переменной t:

Снова получили квадратное ур-ние.

Возвращаемся к переменной х:

И снова первое ур-ние не имеет корней, так как при возведении положительного числа в степень не может получится отрицательное число. Остается решить второе ур-ние:

Ответ: – 0,25.
Графическое решение показательных уравнений
Не всякое показательное уравнение легко или вообще возможно решить аналитическим способом. В таких случаях выручает графическое решение уравнений.
Задание. Найдите графическим способом значение х, для которого справедливо равенство

Решение. Построим в одной системе координат графики у = 3х и у = 4 – х:

Видно, что графики пересекаются в одной точке с примерными координатами (1; 3). Так как графический метод не вполне точный, следует подставить х = 1 в ур-ние и убедиться, что это действительно корень ур-ния:

Получили верное равенство, значит, х = 1 – это действительно корень ур-ния.
Ответ: 1
Задание. Решите графически ур-ние

Решение. Перенесем вправо все слагаемые, кроме 2х:

Слева стоит показательная функция, а справа – квадратичная. Построим их графики и найдем точки пересечения:

Видно, что у графиков есть две общие точки – это (0;1) и (1; 2). На всякий случай проверим себя, подставив х = 0 и х = 1 в исходное ур-ние:

Ноль подходит. Проверяем единицу:

И единица тоже подошла. В итоге имеем два корня, 0 и 1.
Ответ: 0; 1.
Показательные неравенства
Рассмотрим координатную плоскость, в которой построен график некоторой показательной ф-ции у = ах, причем а > 0. Пусть на оси Ох отложены значения s и t, и t < s. То есть точка t располагается левее на оси Ох.

Ясно, что точкам t и s оси Ох соответствуют точки at и as на оси Оу. Так как
у = ах
является возрастающей функцией, то и величина at окажется меньше, чем as. Другими словами, точка at на оси Оу будет лежать ниже точки аs (это наглядно видно на рисунке). Получается, что из условия t < s следует неравенство at < as. Это значит, что эти два нер-ва являются равносильными.

С помощью этого правила можно решать некоторые простейшие показательные неравенства. Например, пусть дано нер-во

Представим восьмерку как степень двойки:

По только что сформулированному правилу можно заменить это нер-во на другое, которое ему равносильно:

Решением же этого линейного неравенства является промежуток (– ∞; 3).
Однако сформулированное нами правило работает тогда, когда основание показательной ф-ции больше единицы. А что же делать в том случае, если оно меньше единицы? Построим график такой ф-ции и снова отложим на оси Ох точки t и s, причем снова t будет меньше s, то есть эта точка будет лежать левее.

Так как показательная ф-ция у = ах при основании, меньшем единицы, является убывающей, то окажется, что на оси Оу точка as лежит ниже, чем at. То есть из условия t < s следует, что at > as. Получается, что эти нер-ва равносильны.

Например, пусть надо решить показательное неравенство

Выразим число слева как степень 0,5:

Тогда нер-во примет вид

По рассмотренному нами правилу его можно заменить на равносильное нер-во

В более привычном виде, когда выражение с переменной стоит слева, нер-во будет выглядеть так:

а его решением будет промежуток (3; + ∞).
В общем случае мы видим, что если в показательном нер-ве вида

основание a больше единицы, то его можно заменить равносильным нер-вом

Грубо говоря, мы просто убираем основание степеней, а знак нер-ва остается неизменным. Если же основание а меньше единицы, то знак неравенства необходимо поменять на противоположный:

Это правило остается верным и в том случае, когда вместо чисел или переменных t и s используются произвольные функции f(x) и g(x). Сформулируем это правило:

Таким образом, для решения показательных неравенств их следует преобразовать к тому виду, при котором и справа, и слева стоят показательные ф-ции с одинаковыми показателями, после чего этот показатель можно просто отбросить. Однако надо помнить, что при таком отбрасывании знак нер-ва изменится на противоположный, если показатель меньше единицы.
Задание. Решите простейшее неравенство

Решение.
Представим число 64 как степень двойки:

теперь и справа, и слева число 2 стоит в основании. Значит, его можно отбросить, причем знак нер-ва останется неизменным (ведь 2 > 1):

Задание. Найдите промежуток, на котором выполняется нер-во

Решение. Так как основание степеней, то есть число 0,345, меньше единицы, то при его «отбрасывании» знак нер-ва должен измениться на противоположный:

Это самое обычное квадратное неравенство. Для его решения нужно найти нули квадратичной функции, стоящей слева, после чего отметить их на числовой прямой и определить промежутки, на которых ф-ция будет положительна.

Нашли нули ф-ции. Далее отмечаем их на прямой, схематично показываем параболу и расставляем знаки промежутков:


Естественно, что в более сложных случаях могут использоваться всё те же методы решения нер-ва, которые применяются и в показательных ур-ниях. В частности, иногда приходится вводить новую переменную.
Задание. Найдите решение нер-ва

Решение. Для начала представим число 3х+1 как произведение:

Теперь перепишем с учетом этого исходное нер-во:

Получили дробь, в которой есть одна показательная ф-ция 3х. Заменим её новой переменной t = 3x:

Это дробно-рациональное неравенство, которое можно заменить равносильным ему целым нер-вом:

которое, в свою очередь, решается методом интервалов. Для этого найдем нули выражения, стоящего слева

Отмечаем найденные нули на прямой и расставляем знаки:

Итак, мы видим, что переменная t должна принадлежать промежутку (1/3; 9), то есть

Теперь произведем обратную замену t = 3x:

Так как основание 3 больше единицы, просто откидываем его:

Итак, мы узнали о показательных уравнениях и неравенствах и способах их решения. В большинстве случаев необходимо представить обе части равенства или неравенства в виде показательных степеней с одинаковыми основаниями. Данное действие иногда называют методом уравнивания показателей. Также в отдельных случаях может помочь графический способ решения ур-ний и замена переменной.
Что такое показательное уравнение и как его решать
20 декабря 2016
Этот урок предназначен для тех, кто только начинает изучать показательные уравнения. Как всегда, начнём с определения и простейших примеров.
Если вы читаете этот урок, то я подозреваю, что вы уже имеете хотя бы минимальное представление о простейших уравнениях — линейных и квадратных: $56x-11=0$; ${{x}^{2}}+5x+4=0$; ${{x}^{2}}-12x+32=0$ и т.д. Уметь решать такие конструкции совершенно необходимо для того, чтобы не «зависнуть» в той теме, о которой сейчас пойдёт речь.
Итак, показательные уравнения. Сразу приведу парочку примеров:
[{{2}^{x}}=4;quad {{5}^{2x-3}}=frac{1}{25};quad {{9}^{x}}=-3]
Какие-то из них могут показаться вам более сложными, какие-то — напротив, слишком простыми. Но всех их объединяет один важный признак: в их записи присутствует показательная функция $fleft( x right)={{a}^{x}}$. Таким образом, введём определение:
Показательное уравнение — это любое уравнение, содержащее в себе показательную функцию, т.е. выражение вида ${{a}^{x}}$. Помимо указанной функции подобные уравнения могут содержать в себе любые другие алгебраические конструкции — многочлены, корни, тригонометрию, логарифмы и т.д.
Ну хорошо. С определением разобрались. Теперь вопрос: как всю эту хрень решать? Ответ одновременно и прост, и сложен.
Начнём с хорошей новости: по своему опыту занятий с множеством учеников могу сказать, что большинству из них показательные уравнения даются намного легче, чем те же логарифмы и уж тем более тригонометрия.
Но есть и плохая новость: иногда составителей задач для всевозможных учебников и экзаменов посещает «вдохновение», и их воспалённый наркотиками мозг начинает выдавать такие зверские уравнения, что решить их становится проблематично не только ученикам — даже многие учителя на таких задачах залипают.
Впрочем, не будем о грустном. И вернёмся к тем трём уравнениям, которые были приведены в самом начале повествования. Попробуем решить каждое из них.
Первое уравнение: ${{2}^{x}}=4$. Ну и в какую степень надо возвести число 2, чтобы получить число 4? Наверное, во вторую? Ведь ${{2}^{2}}=2cdot 2=4$ — и мы получили верное числовое равенство, т.е. действительно $x=2$. Что ж, спасибо, кэп, но это уравнение было настолько простым, что его решил бы даже мой кот.:)
Посмотрим на следующее уравнение:
[{{5}^{2x-3}}=frac{1}{25}]
А вот тут уже чуть сложнее. Многие ученики знают, что ${{5}^{2}}=25$ — это таблица умножения. Некоторые также подозревают, что ${{5}^{-1}}=frac{1}{5}$ — это по сути определение отрицательных степеней (по аналогии с формулой ${{a}^{-n}}=frac{1}{{{a}^{n}}}$).
Наконец, лишь избранные догадываются, что эти факты можно совмещать и на выходе получить следующий результат:
[frac{1}{25}=frac{1}{{{5}^{2}}}={{5}^{-2}}]
Таким образом, наше исходное уравнение перепишется следующим образом:
[{{5}^{2x-3}}=frac{1}{25}Rightarrow {{5}^{2x-3}}={{5}^{-2}}]
А вот это уже вполне решаемо! Слева в уравнении стоит показательная функция, справа в уравнении стоит показательная функция, ничего кроме них нигде больше нет. Следовательно, можно «отбросить» основания и тупо приравнять показатели:
[2x-3=-2]
Получили простейшее линейное уравнение, которое любой ученик решит буквально в пару строчек. Ну ладно, в четыре строчки:
[begin{align}& 2x-3=-2 \& 2x=3-2 \& 2x=1 \& x=frac{1}{2} \end{align}]
Если вы не поняли, что сейчас происходило в последних четырёх строчках — обязательно вернитесь в тему «линейные уравнения» и повторите её. Потому что без чёткого усвоения этой темы вам рано браться за показательные уравнения.
Со всеми остальными мы идём дальше. На очереди третье уравнение:
[{{9}^{x}}=-3]
Ну и как такое решать? Первая мысль: $9=3cdot 3={{3}^{2}}$, поэтому исходное уравнение можно переписать так:
[{{left( {{3}^{2}} right)}^{x}}=-3]
Затем вспоминаем, что при возведении степени в степень показатели перемножаются:
[{{left( {{3}^{2}} right)}^{x}}={{3}^{2x}}Rightarrow {{3}^{2x}}=-{{3}^{1}}]
Ну а дальше вообще всё стандартно:
[begin{align}& 2x=-1 \& x=-frac{1}{2} \end{align}]
И вот за такое решение мы получим честно заслуженную двойку. Ибо мы с невозмутимостью покемона отправили знак «минус», стоящий перед тройкой, в степень этой самой тройки. А так делать нельзя. И вот почему. Взгляните на разные степени тройки:
[begin{matrix} {{3}^{1}}=3& {{3}^{-1}}=frac{1}{3}& {{3}^{frac{1}{2}}}=sqrt{3} \ {{3}^{2}}=9& {{3}^{-2}}=frac{1}{9}& {{3}^{frac{1}{3}}}=sqrt[3]{3} \ {{3}^{3}}=27& {{3}^{-3}}=frac{1}{27}& {{3}^{-frac{1}{2}}}=frac{1}{sqrt{3}} \end{matrix}]
Составляя эту табличку, я уж как только не извращался: и положительные степени рассмотрел, и отрицательные, и даже дробные… ну и где здесь хоть одно отрицательное число? Его нет! И не может быть, потому что показательная функция $y={{a}^{x}}$, во-первых, всегда принимает лишь положительные значения (сколько единицу не умножай или не дели на двойку — всё равно будет положительное число), а во-вторых, основание такой функции — число $a$ — по определению является положительным числом!
Ну и как тогда решать уравнение ${{9}^{x}}=-3$? А никак: корней нет. И в этом смысле показательные уравнения очень похожи на квадратные — там тоже может не быть корней. Но если в квадратных уравнениях число корней определяется дискриминантом (дискриминант положительный — 2 корня, отрицательный — нет корней), то в показательных всё зависит от того, что стоит справа от знака равенства.
Таким образом, сформулируем ключевой вывод: простейшее показательное уравнение вида ${{a}^{x}}=b$ имеет корень тогда и только тогда, когда $b gt 0$. Зная этот простой факт, вы без труда определите: есть у предложенного вам уравнения корни или нет. Т.е. стоит ли вообще его решать или сразу записать, что корней нет.
Это знание ещё неоднократно поможет нам, когда придётся решать более сложные задачи. А пока хватит лирики — пора изучить основной алгоритм решения показательных уравнений.
Как решать показательные уравнения
Итак, сформулируем задачу. Необходимо решить показательное уравнение:
[{{a}^{x}}=b,quad a,b gt 0]
Согласно «наивному» алгоритму, по которому мы действовали ранее, необходимо представить число $b$ как степень числа $a$:
[b={{a}^{m}}Rightarrow {{a}^{x}}={{a}^{m}}Rightarrow x=m]
Кроме того, если вместо переменной $x$ будет стоять какое-либо выражение, мы получим новое уравнение, которое уже вполне можно решить. Например:
[begin{align}& {{2}^{x}}=8Rightarrow {{2}^{x}}={{2}^{3}}Rightarrow x=3; \& {{3}^{-x}}=81Rightarrow {{3}^{-x}}={{3}^{4}}Rightarrow -x=4Rightarrow x=-4; \& {{5}^{2x}}=125Rightarrow {{5}^{2x}}={{5}^{3}}Rightarrow 2x=3Rightarrow x=frac{3}{2}. \end{align}]
И как ни странно, эта схема работает примерно в 90% случаев. А что тогда с остальными 10%? Остальные 10% — это немного «шизофреничные» показательные уравнения вида:
[{{2}^{x}}=3;quad {{5}^{x}}=15;quad {{4}^{2x}}=11]
Ну и в какую степень надо возвести 2, чтобы получить 3? В первую? А вот и нет: ${{2}^{1}}=2$ — маловато. Во вторую? Тоже нет: ${{2}^{2}}=4$ — многовато. А в какую тогда?
Знающие ученики уже наверняка догадались: в таких случаях, когда «красиво» решить не получается, к делу подключается «тяжёлая артиллерия» — логарифмы. Напомню, что с помощью логарифмов любое положительное число можно представить как степень любого другого положительного числа (за исключением единицы):
[a={{b}^{{{log }_{b}}a}},quad a gt 0,quad 1ne b gt 0]
Помните эту формулу? Когда я рассказываю своим ученикам про логарифмы, то всегда предупреждаю: эта формула (она же — основное логарифмическое тождество или, если угодно, определение логарифма) будет преследовать вас её очень долго и «всплывать» в самых неожиданных местах. Ну вот она и всплыла. Давайте посмотрим на наше уравнение и на эту формулу:
[begin{align}& {{2}^{x}}=3 \& a={{b}^{{{log }_{b}}a}} \end{align}]
Если допустить, что $a=3$ — наше исходное число, стоящее справа, а $b=2$ — то самое основание показательной функции, к которому мы так хотим привести правую часть, то получим следующее:
[begin{align}& a={{b}^{{{log }_{b}}a}}Rightarrow 3={{2}^{{{log }_{2}}3}}; \& {{2}^{x}}=3Rightarrow {{2}^{x}}={{2}^{{{log }_{2}}3}}Rightarrow x={{log }_{2}}3. \end{align}]
Получили немного странный ответ: $x={{log }_{2}}3$. В каком-нибудь другом задании многие при таком ответе засомневались бы и начали перепроверять своё решение: вдруг там где-то закралась ошибка? Спешу вас обрадовать: никакой ошибки здесь нет, и логарифмы в корнях показательных уравнений — вполне типичная ситуация. Так что привыкайте.:)
Теперь решим по аналогии оставшиеся два уравнения:
[begin{align}& {{5}^{x}}=15Rightarrow {{5}^{x}}={{5}^{{{log }_{5}}15}}Rightarrow x={{log }_{5}}15; \& {{4}^{2x}}=11Rightarrow {{4}^{2x}}={{4}^{{{log }_{4}}11}}Rightarrow 2x={{log }_{4}}11Rightarrow x=frac{1}{2}{{log }_{4}}11. \end{align}]
Вот и всё! Кстати, последний ответ можно записать иначе:
[x=frac{1}{2}{{log }_{4}}11={{log }_{4}}{{11}^{frac{1}{2}}}={{log }_{4}}sqrt{11}]
Это мы внесли множитель в аргумент логарифма. Но никто не мешает нам внести этот множитель в основание:
[x=frac{1}{2}{{log }_{4}}11={{log }_{{{4}^{2}}}}11={{log }_{16}}11]
При этом все три варианта являются правильными — это просто разные формы записи одного и того же числа. Какой из них выбрать и записать в настоящем решении — решать только вам.
Таким образом, мы научились решать любые показательные уравнения вида ${{a}^{x}}=b$, где числа $a$ и $b$ строго положительны. Однако суровая реальность нашего мира такова, что подобные простые задачи будут встречаться вам очень и очень редко. Куда чаще вам будет попадаться что-нибудь типа этого:
[begin{align}& {{4}^{x}}+{{4}^{x-1}}={{4}^{x+1}}-11; \& {{7}^{x+6}}cdot {{3}^{x+6}}={{21}^{3x}}; \& {{100}^{x-1}}cdot {{2,7}^{1-x}}=0,09. \end{align}]
Ну и как такое решать? Это вообще можно решить? И если да, то как?
Без паники. Все эти уравнения быстро и просто сводятся к тем простым формулам, которые мы уже рассмотрели. Нужно лишь знать вспомнить парочку приёмов из курса алгебры. Ну и конечно, здесь никуда без правил работы со степенями. Обо всём этом я сейчас расскажу.:)
Преобразование показательных уравнений
Первое, что нужно запомнить: любое показательное уравнение, каким бы сложным оно ни было, так или иначе должно сводиться к простейшим уравнениям — тем самым, которые мы уже рассмотрели и которые знаем как решать. Другими словами, схема решения любого показательного уравнения выглядит следующим образом:
- Записать исходное уравнение. Например: ${{4}^{x}}+{{4}^{x-1}}={{4}^{x+1}}-11$;
- Сделать какую-то непонятную хрень. Или даже несколько хреней, которые называются «преобразовать уравнение»;
- На выходе получить простейшие выражения вида ${{4}^{x}}=4$ или что-нибудь ещё в таком духе. Причём одно исходное уравнение может давать сразу несколько таких выражений.
С первым пунктом всё понятно — записать уравнение на листик сможет даже мой кот. С третьим пунктом тоже, вроде, более-менее ясно — мы такие уравнения уже целую пачку нарешали выше.
Но как быть со вторым пунктом? Что за преобразования? Что во что преобразовывать? И как?
Что ж, давайте разбираться. Прежде всего, отмечу следующее. Все показательные уравнения делятся на два типа:
- Уравнение составлено из показательных функций с одним и тем же основанием. Пример: ${{4}^{x}}+{{4}^{x-1}}={{4}^{x+1}}-11$;
- В формуле присутствуют показательные функции с разными основаниями. Примеры: ${{7}^{x+6}}cdot {{3}^{x+6}}={{21}^{3x}}$ и ${{100}^{x-1}}cdot {{2,7}^{1-x}}=0,09$.
Начнём с уравнений первого типа — они решаются проще всего. И в их решении нам поможет такой приём как выделение устойчивых выражений.
Выделение устойчивого выражения
Давайте ещё раз посмотрим на это уравнение:
[{{4}^{x}}+{{4}^{x-1}}={{4}^{x+1}}-11]
Что мы видим? Четвёрка возводится в разные степени. Но все эти степени — простые суммы переменной $x$ с другими числами. Поэтому необходимо вспомнить правила работы со степенями:
[begin{align}& {{a}^{x+y}}={{a}^{x}}cdot {{a}^{y}}; \& {{a}^{x-y}}={{a}^{x}}:{{a}^{y}}=frac{{{a}^{x}}}{{{a}^{y}}}. \end{align}]
Проще говоря, сложение показателей можно преобразовать в произведение степеней, а вычитание легко преобразуется в деление. Попробуем применить эти формулы к степеням из нашего уравнения:
[begin{align}& {{4}^{x-1}}=frac{{{4}^{x}}}{{{4}^{1}}}={{4}^{x}}cdot frac{1}{4}; \& {{4}^{x+1}}={{4}^{x}}cdot {{4}^{1}}={{4}^{x}}cdot 4. \end{align}]
Перепишем исходное уравнение с учётом этого факта, а затем соберём все слагаемые слева:
[begin{align}& {{4}^{x}}+{{4}^{x}}cdot frac{1}{4}={{4}^{x}}cdot 4-11; \& {{4}^{x}}+{{4}^{x}}cdot frac{1}{4}-{{4}^{x}}cdot 4+11=0. \end{align}]
В первых четырёх слагаемых присутствует элемент ${{4}^{x}}$ — вынесем его за скобку:
[begin{align}& {{4}^{x}}cdot left( 1+frac{1}{4}-4 right)+11=0; \& {{4}^{x}}cdot frac{4+1-16}{4}+11=0; \& {{4}^{x}}cdot left( -frac{11}{4} right)=-11. \end{align}]
Осталось разделить обе части уравнения на дробь $-frac{11}{4}$, т.е. по существу умножить на перевёрнутую дробь — $-frac{4}{11}$. Получим:
[begin{align}& {{4}^{x}}cdot left( -frac{11}{4} right)cdot left( -frac{4}{11} right)=-11cdot left( -frac{4}{11} right); \& {{4}^{x}}=4; \& {{4}^{x}}={{4}^{1}}; \& x=1. \end{align}]
Вот и всё! Мы свели исходное уравнение к простейшему и получили окончательный ответ.
При этом в процессе решения мы обнаружили (и даже вынесли за скобку) общий множитель ${{4}^{x}}$ — это и есть устойчивое выражение. Его можно обозначать за новую переменную, а можно просто аккуратно выразить и получить ответ. В любом случае, ключевой принцип решения следующий:
Найти в исходном уравнении устойчивое выражение, содержащее переменную, которое легко выделяется из всех показательных функций.
Хорошая новость состоит в том, что практически каждое показательное уравнение допускает выделение такого устойчивого выражения.
Но есть и плохая новость: подобные выражения могут оказаться весьма хитрыми, и выделить их бывает довольно сложно. Поэтому разберём ещё одну задачу:
[{{5}^{x+2}}+{{0,2}^{-x-1}}+4cdot {{5}^{x+1}}=2]
Возможно, у кого-то сейчас возникнет вопрос: «Паша, ты что, обкурился? Здесь же разные основания — 5 и 0,2». Но давайте попробуем преобразовать степень с основание 0,2. Например, избавимся от десятичной дроби, приведя её к обычной:
[{{0,2}^{-x-1}}={{0,2}^{-left( x+1 right)}}={{left( frac{2}{10} right)}^{-left( x+1 right)}}={{left( frac{1}{5} right)}^{-left( x+1 right)}}]
Как видите, число 5 всё-таки появилось, пускай и в знаменателе. Заодно переписали показатель в виде отрицательного. А теперь вспоминаем одно из важнейших правил работы со степенями:
[{{a}^{-n}}=frac{1}{{{a}^{n}}}Rightarrow {{left( frac{1}{5} right)}^{-left( x+1 right)}}={{left( frac{5}{1} right)}^{x+1}}={{5}^{x+1}}]
Тут я, конечно, немного слукавил. Потому что для полного понимания формулу избавления от отрицательных показателей надо было записать так:
[{{a}^{-n}}=frac{1}{{{a}^{n}}}={{left( frac{1}{a} right)}^{n}}Rightarrow {{left( frac{1}{5} right)}^{-left( x+1 right)}}={{left( frac{5}{1} right)}^{x+1}}={{5}^{x+1}}]
С другой стороны, ничто не мешало нам работать с одной лишь дробью:
[{{left( frac{1}{5} right)}^{-left( x+1 right)}}={{left( {{5}^{-1}} right)}^{-left( x+1 right)}}={{5}^{left( -1 right)cdot left( -left( x+1 right) right)}}={{5}^{x+1}}]
Но в этом случае нужно уметь возводить степень в другую степень (напомню: при этом показатели складываются). Зато не пришлось «переворачивать» дроби — возможно, для кого-то это будет проще.:)
В любом случае, исходное показательное уравнение будет переписано в виде:
[begin{align}& {{5}^{x+2}}+{{5}^{x+1}}+4cdot {{5}^{x+1}}=2; \& {{5}^{x+2}}+5cdot {{5}^{x+1}}=2; \& {{5}^{x+2}}+{{5}^{1}}cdot {{5}^{x+1}}=2; \& {{5}^{x+2}}+{{5}^{x+2}}=2; \& 2cdot {{5}^{x+2}}=2; \& {{5}^{x+2}}=1. \end{align}]
Вот и получается, что исходное уравнение решается даже проще, чем ранее рассмотренное: тут даже не надо выделять устойчивое выражение — всё само сократилось. Осталось лишь вспомнить, что $1={{5}^{0}}$, откуда получим:
[begin{align}& {{5}^{x+2}}={{5}^{0}}; \& x+2=0; \& x=-2. \end{align}]
Вот и всё решение! Мы получили окончательный ответ: $x=-2$. При этом хотелось бы отметить один приём, который значительно упростил нам все выкладки:
В показательных уравнениях обязательно избавляйтесь от десятичных дробей, переводите их в обычные. Это позволит увидеть одинаковые основания степеней и значительно упростит решение.
Перейдём теперь к более сложным уравнениям, в которых присутствуют разные основания, которые вообще не сводятся друг к другу с помощью степеней.
Использование свойства степеней
Напомню, что у нас есть ещё два особо суровых уравнения:
[begin{align}& {{7}^{x+6}}cdot {{3}^{x+6}}={{21}^{3x}}; \& {{100}^{x-1}}cdot {{2,7}^{1-x}}=0,09. \end{align}]
Основная сложность тут — непонятно, что и к какому основанию приводить. Где устойчивые выражения? Где одинаковые основания? Ничего этого нет.
Но попробуем пойти другим путём. Если нет готовых одинаковых оснований, их можно попробовать найти, раскладывая имеющиеся основания на множители.
Начнём с первого уравнения:
[begin{align}& {{7}^{x+6}}cdot {{3}^{x+6}}={{21}^{3x}}; \& 21=7cdot 3Rightarrow {{21}^{3x}}={{left( 7cdot 3 right)}^{3x}}={{7}^{3x}}cdot {{3}^{3x}}. \end{align}]
Но ведь можно поступить наоборот — составить из чисел 7 и 3 число 21. Особенно это просто сделать слева, поскольку показатели и обеих степеней одинаковые:
[begin{align}& {{7}^{x+6}}cdot {{3}^{x+6}}={{left( 7cdot 3 right)}^{x+6}}={{21}^{x+6}}; \& {{21}^{x+6}}={{21}^{3x}}; \& x+6=3x; \& 2x=6; \& x=3. \end{align}]
Вот и всё! Вы вынесли показатель степени за пределы произведения и сразу получили красивое уравнение, которое решается в пару строчек.
Теперь разберёмся со вторым уравнением. Тут всё намного сложнее:
[{{100}^{x-1}}cdot {{2,7}^{1-x}}=0,09]
Прежде всего, сделаем то, что я рекомендовал ещё в самом начале урока — избавимся от десятичной дроби:
[{{100}^{x-1}}cdot {{left( frac{27}{10} right)}^{1-x}}=frac{9}{100}]
В данном случае дроби получились несократимыми, но если бы что-то можно было сократить — обязательно сокращайте. Зачастую при этом появятся интересные основания, с которыми уже можно работать.
У нас же, к сожалению, ничего особо не появилось. Зато мы видим, что показатели степеней, стоящий в произведении слева, противоположны:
[1-x=-left( x-1 right)Rightarrow {{left( frac{27}{10} right)}^{1-x}}={{left( frac{27}{10} right)}^{-left( x-1 right)}}={{left( frac{10}{27} right)}^{x-1}}]
Напомню: чтобы избавиться от знака «минус» в показателе, достаточно просто «перевернуть» дробь. Что ж, перепишем исходное уравнение:
[begin{align}& {{100}^{x-1}}cdot {{left( frac{10}{27} right)}^{x-1}}=frac{9}{100}; \& {{left( 100cdot frac{10}{27} right)}^{x-1}}=frac{9}{100}; \& {{left( frac{1000}{27} right)}^{x-1}}=frac{9}{100}. \end{align}]
Во второй строчке мы просто вынесли общий показатель из произведения за скобку по правилу ${{a}^{x}}cdot {{b}^{x}}={{left( acdot b right)}^{x}}$, а в последней просто умножили число 100 на дробь.
Теперь заметим, что числа, стоящие слева (в основании) и справа, чем-то похожи. Чем? Да очевидно же: они являются степенями одного и того же числа! Имеем:
[begin{align}& frac{1000}{27}=frac{{{10}^{3}}}{{{3}^{3}}}={{left( frac{10}{3} right)}^{3}}; \& frac{9}{100}=frac{{{3}^{2}}}{{{10}^{3}}}={{left( frac{3}{10} right)}^{2}}. \end{align}]
Таким образом, наше уравнение перепишется следующим образом:
[{{left( {{left( frac{10}{3} right)}^{3}} right)}^{x-1}}={{left( frac{3}{10} right)}^{2}}]
Дальше всё просто. При возведении степени в степень показатели перемножаются:
[{{left( {{left( frac{10}{3} right)}^{3}} right)}^{x-1}}={{left( frac{10}{3} right)}^{3left( x-1 right)}}={{left( frac{10}{3} right)}^{3x-3}}]
При этом справа тоже можно получить степень с таким же основанием, для чего достаточно просто «перевернуть» дробь:
[{{left( frac{3}{10} right)}^{2}}={{left( frac{10}{3} right)}^{-2}}]
Окончательно наше уравнение примет вид:
[begin{align}& {{left( frac{10}{3} right)}^{3x-3}}={{left( frac{10}{3} right)}^{-2}}; \& 3x-3=-2; \& 3x=1; \& x=frac{1}{3}. \end{align}]
Вот и всё решение. Основная его идея сводится к тому, что даже при разных основаниях мы пытаемся любыми правдами и неправдами свести эти основания к одному и тому же. В этом нам помогают элементарные преобразования уравнений и правила работы со степенями.
Но какие правила и когда использовать? Как понять, что в одном уравнении нужно делить обе стороны на что-то, а в другом — раскладывать основание показательной функции на множители?
Ответ на этот вопрос придёт с опытом. Попробуйте свои силы сначала на простых уравнениях, а затем постепенно усложняйте задачи — и очень скоро ваших навыков будет достаточно, чтобы решить любое показательное уравнение из того же ЕГЭ или любой самостоятельной/контрольной работы.
А чтобы помочь вам в этом нелёгком деле, предлагаю скачать на моём сайте комплект уравнений для самостоятельного решения. Ко всем уравнениям есть ответы, поэтому вы всегда сможете себя проверить.
В общем, желаю удачной тренировки. И увидимся в следующем уроке — там мы будем разбирать действительно сложные показательные уравнения, где описанных выше способов уже недостаточно. И простой тренировки тоже будет недостаточно.:)
Смотрите также:
- Преобразование показательных уравнений

- Решение показательных неравенств

- Тест по теории вероятностей (1 вариант)

- Общая схема решения задач B15

- Задачи на проценты: считаем проценты с помощью пропорции

- Более сложные задачи на производительность

Содержание:
Рассмотрим уравнения, в которых переменная (неизвестное) находится в показателе степени. Например:

Уравнения такого вида принято называть показательными.
Решении показательных уравнений
При решении показательных уравнений нам будет полезно следствие из теоремы о свойствах показательной функции.
Следствие:
Пусть 
Каждому значению показательной функции  соответствует единственный показатель s.
соответствует единственный показатель s.
Пример:
Решить уравнение

Решение:
Согласно следствию из равенства двух степеней с одинаковым основанием 3 следует равенство их показателей. Таким образом, данное уравнение равносильно уравнению

откуда

Ответ: 2; 3.
Пример:
Решить уравнение:

Решение:
а) Данное уравнение равносильно (поясните почему) уравнению

Если степени с основанием 3 равны, то равны и их показатели:

Решив это уравнение, получим


Ответ: 
При решении каждого уравнения из примера 2 сначала обе части уравнения представили в виде степени с одним и тем же основанием, а затем записали равенство показателей этих степеней.
Пример:
Решить уравнение:

Решение:
а) Данное уравнение равносильно уравнению

Решая его, получаем:

Так как две степени с одинаковым основанием 2 равны, то равны и их показатели, т. е.  откуда находим
откуда находим 
б) Разделив обе части уравнения на  получим уравнение
получим уравнение  равносильное данному. Решив его, получим
равносильное данному. Решив его, получим 

Ответ: 
При решении примера 3 а) левую часть уравнения разложили на множители. Причем за скобку вынесли такой множитель, что в скобках осталось числовое выражение, не содержащее переменной.
Пример:
Решить уравнение 
Решение:
Обозначим  тогда
тогда 
Таким образом, из данного уравнения получаем

откуда находим: 
Итак, с учетом обозначения имеем:

Ответ: 1; 2.
При решении примера 4 был использован метод введения новой переменной, который позволил свести данное уравнение к квадратному относительно этой переменной.
Пример:
Решить уравнение 
Решение:
Можно заметить, что 2 — корень данного уравнения. Других корней уравнение не имеет, так как функция, стоящая в левой части уравнения, возрастающая, а функция, стоящая в правой части уравнения, убывающая. Поэтому уравнение имеет не более одного корня (см. теорему из п. 1.14).
Ответ: 2.
Пример:
Решить уравнение 
Решение:

Ответ: 3; 4.
Пример:
При каком значении а корнем уравнения  является число, равное 2?
является число, равное 2?
Решение:
Поскольку х = 2 — корень, то верно равенство

Решив это уравнение, найдем

Ответ: при 
Показательные уравнения и их системы
Показательным уравнением называется уравнение, в ко тором неизвестное входит в показатель степени. При решении показательных уравнений полезно использовать следующие тождества: 

Приведем методы решения некоторых типов показательных уравнений.
1 Приведение к одному основанию.
Метод основан на следующем свойстве степеней: если две степени равны и равны их основания, то равны и их показатели, т.е. уравнения надо попытаться привести к виду  . Отсюда
. Отсюда 
Пример №1
Решите уравнение 
Решение:
Заметим, что  и перепишем наше уравнение в виде
и перепишем наше уравнение в виде

Применив тождество (1), получим Зх – 7 = -7х + 3, х = 1.
Ответ: 1.
Пример №2
Решить уравнение 
Решение:
Переходя к основанию степени 2, получим:

Согласно тождеству (2), имеем 
Последнее уравнение равносильно уравнению 4х-19 = 2,5х. 
2 Введение новой переменной.
Пример №3
Решить уравнение 
Решение:
Применив тождество 2, перепишем уравнение как 
Введем новую переменную:  Получим уравнение
Получим уравнение 
которое имеет корни  Однако корень
Однако корень не удовлетворяет условию
не удовлетворяет условию  Значит,
Значит, 
Ответ: х=2.
Пример №4
Решить уравнение 
Решение:
Разделив обе части уравнения на  получим:
получим:

последнее уравнение запишется так: 
Решая уравнение, найдем 
Значение  не удовлетворяет условию
не удовлетворяет условию  Следовательно,
Следовательно,

Пример №5
Решить уравнение 
Решение:
Заметим что  Значит
Значит 
Перепишем уравнение в виде 
Обозначим  Получим
Получим 
Получим 
Корнями данного уравнения будут 
Следовательно, 
III Вынесение общего множителя за скобку.
Пример №6
Решить уравнение 
Решение:
После вынесения за скобку в левой части  , а в правой
, а в правой  , получим
, получим  Разделим обе части уравнения на
Разделим обе части уравнения на  получим
получим 

Системы простейших показательных уравнений
Пример №7
Решите систему уравнений: 
Решение:
По свойству степеней система уравнений равносильна следующей
системе : Отсюда получим систему
Отсюда получим систему 
Очевидно, что последняя система имеет решение 
Пример №8
Решите систему уравнений: 
Решение:
По свойству степеней система уравнений равносильна следующей системе:  Последняя система, в свою очередь, равносильна системе:
Последняя система, в свою очередь, равносильна системе: 
Умножив второе уравнение этой системы на (-2) и сложив с первым, получим уравнение —9х=-4. Отсюда, найдем  Подставив полученное значение во второе уравнение, получим
Подставив полученное значение во второе уравнение, получим 

Пример №9
Решите систему уравнений: 
Решение:
Сделаем замену:  Тогда наша система примет вид:
Тогда наша система примет вид: 
Очевидно, что эта система уравнений имеет решение 
Тогда получим уравнения 

Приближенное решение уравнений
Пусть многочлен f(х) на концах отрезка [a,b] принимает значения разных знаков, то есть  . Тогда внутри этого отрезка существует хотя бы одно решение уравнения Дх)=0. Это означает, что существует такое
. Тогда внутри этого отрезка существует хотя бы одно решение уравнения Дх)=0. Это означает, что существует такое  (читается как “кси”), что
(читается как “кси”), что 
Это утверждение проиллюстрировано на следующем чертеже.

Рассмотрим отрезок  содержащий лишь один корень уравнения .
содержащий лишь один корень уравнения .
Метод последовательного деления отрезка пополам заключается в последовательном разделении отрезка [a, b] пополам до тех пор, пока длина полученного отрезка не будет меньше заданной точности 
Для этого:
- вычисляется значение f(х) выражения

- отрезок делится пополам, то есть вычисляется значение

- вычисляется значение
 выражения f(х) в точке
выражения f(х) в точке 
- проверяется условие

- если это условие выполняется, то в качестве левого конца нового отрезка выбирается середина предыдущего отрезка, то есть полагается, что
 (левый конец отрезка переходит в середину);
(левый конец отрезка переходит в середину); - если это условие не выполняется, то правый конец нового отрезка переходит в середину, то есть полагается, что b=x;
- для нового отрезка проверяется условие

- если это условие выполняется , то вычисления заканчиваются. При этом в качестве приближенного решения выбирается последнее вычисленное значение х. Если это условие не выполняется, то, переходя к пункту 2 этого алгоритма, вычисления продолжаются.
Метод последовательного деления пополам проиллюстрирован на этом чертеже:

Для нахождения интервала, содержащего корень уравнения  вычисляются значения
вычисляются значения 
Оказывается, что для корня  данного уравнения выполнено неравенство. Значит, данное уравнение имеет хотя бы один корень, принадлежащий интервалу (-1 -А; 1+А). Для приближенного вычисления данного корня найдем целые
данного уравнения выполнено неравенство. Значит, данное уравнение имеет хотя бы один корень, принадлежащий интервалу (-1 -А; 1+А). Для приближенного вычисления данного корня найдем целые  и
и  удовлетворяющие неравенству
удовлетворяющие неравенству 
Пример №10
Найдите интервал, содержащий корень уравнения 
Решение:
Поделив обе части уравнения на 2 , получим, 
Так как, для нового уравнения 
Значит, в интервале,  уравнение имеет хотя бы один корень. В то же время уравнение при
уравнение имеет хотя бы один корень. В то же время уравнение при  не имеет ни одного корня, так как,
не имеет ни одного корня, так как,
 выполняется. Значит, корень уравнения лежит в (-2,5; 0). Для уточнения этого интервала положим
выполняется. Значит, корень уравнения лежит в (-2,5; 0). Для уточнения этого интервала положим  Для
Для  проверим выполнение условия
проверим выполнение условия


Значит, уравнение имеет корень, принадлежащий интервалу (-1; 0).
Нахождение приближенного корня с заданной точностью
Исходя из вышесказанного, заключаем, что если выполнено неравенство  корень уравнения принадлежит интервалу
корень уравнения принадлежит интервалу
 Пусть
Пусть Если
Если  приближенный
приближенный
корень уравнения с точностью  . Если
. Если  то корень лежит в интервале
то корень лежит в интервале  если
если то корень лежит в интервале
то корень лежит в интервале  . Продолжим процесс до нахождения приближенного значения корня с заданной точностью.
. Продолжим процесс до нахождения приближенного значения корня с заданной точностью.
Пример №11
Найдите приближенное значение корня уравнения  с заданной точностью
с заданной точностью
Решение:
Из предыдущего примера нам известно, что корень лежит в интервале
(-1; 0). Из того, что  заключаем, что корень лежит в интервале (-0,5; 0).
заключаем, что корень лежит в интервале (-0,5; 0).
Так как, |(-0,25)41,5(-0,25)2+2,5(-0,25)+0,5| = |-0,046| < 0,1, то х=-0,25 – приближенное значение корня с точностью 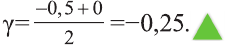
Решение показательных неравенств
Рассмотрим неравенства, в которых переменная (неизвестное) находится в показателе степени. Например, 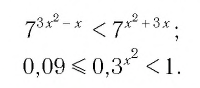
Неравенства такого вида принято называть показательными.
Из теоремы о свойствах показательной функции (п. 2.2, свойство 8) получаем следствие, которое постоянно используется при решении показательных неравенств.
Следствие:
Пусть а > 1. Если 
Пусть 
Изображения графиков показательной функции подсказывают это свойство. На рисунке 27 видно, что при а > 1 большему значению функции соответствует большее значение аргумента. А на рисунке 30 видно, что при 0 < а < 1 большему значению функции соответствует меньшее значение аргумента.
При решении показательных неравенств, так же как и при решении показательных уравнений, приходится использовать представление обеих частей неравенства в виде степеней с одним и тем же основанием, разложение одной из частей неравенства на множители, введение новой переменной.
Пример:
Решить неравенство 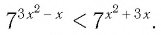
Решение:
Поскольку из двух степеней с основанием 7 больше та, показатель которой больше, то данное неравенство равносильно неравенству
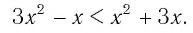
Решим его:
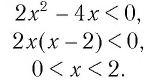
Ответ: (0; 2).
Пример:
Решить неравенство 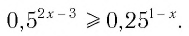
Решение:
Данное неравенство равносильно неравенству
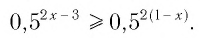
Поскольку из двух степеней с одинаковым основанием 0,5 больше та, показатель которой меньше, то имеем
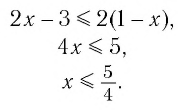
Ответ: 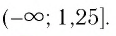
Пример:
Решить неравенство 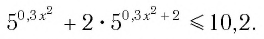
Решение:
Данное неравенство равносильно неравенству
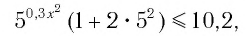
откуда
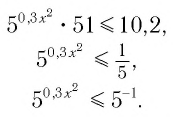
Поскольку из двух степеней с основанием 5 больше та, показатель которой больше, то данное неравенство равносильно неравенству
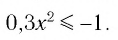
Решений нет, так как 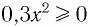 при любых значениях х.
при любых значениях х.
Ответ: нет решений.
Пример:
Решить неравенство
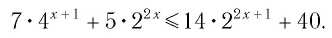
Решение:
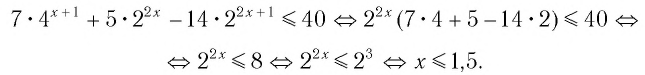
Ответ: 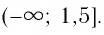
Пример:
Решить неравенство 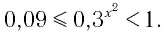
Решение:
Данное неравенство перепишем в виде 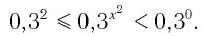
Поскольку из двух степеней с основанием 0,3 больше та, показатель которой меньше, то имеем:
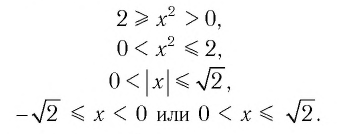
Ответ: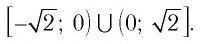
Пример:
Решить неравенство
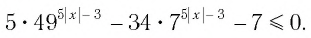
Решение:
Пусть 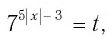 тогда
тогда 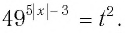 Использовав эти обозначения для данного неравенства, получим
Использовав эти обозначения для данного неравенства, получим 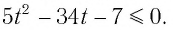
Решив это неравенство, получим: 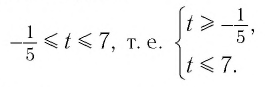 Поскольку
Поскольку 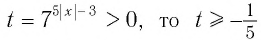 при любых значениях х.
при любых значениях х.
Остается решить второе неравенство системы:
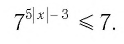
Получим:
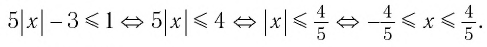
Ответ: 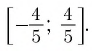
Пример:
При каких значениях m любое значение х из промежутка [9; 10] является решением неравенства
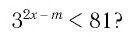
Решение:
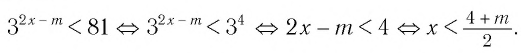 Чтобы решением неравенства
Чтобы решением неравенства 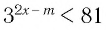 являлось любое значение х из промежутка
являлось любое значение х из промежутка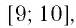 необходимо, чтобы промежуток
необходимо, чтобы промежуток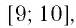 входил во множество решений данного неравенства, т. е. в промежуток
входил во множество решений данного неравенства, т. е. в промежуток 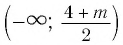 (рис.33).
(рис.33).
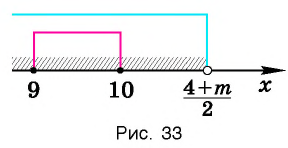
Итак, имеем:
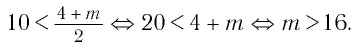
Ответ: при 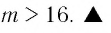
Показательные уравнения, неравенства и их системы
При решении показательных уравнений и неравенств, т. е. уравнений и неравенств, в которых переменная содержится в показателе степени, используются свойства показательной функции:
Пример №12
Решим уравнение:
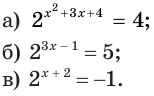
а) 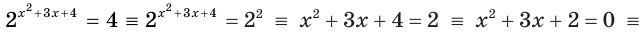
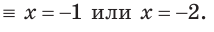
Ответ. -1; -2.
б) 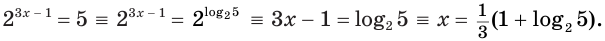
Ответ. 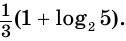
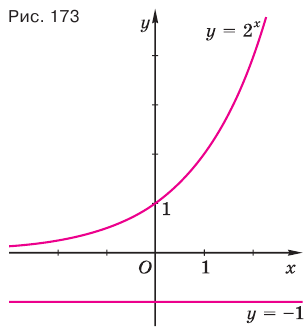
в) Поскольку число -1 не принадлежит области значений показательной функции 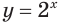 , то уравнение
, то уравнение 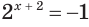 не имеет корней (рис. 173).
не имеет корней (рис. 173).
Ответ. Корней нет.
Пример №13
Решим неравенство:
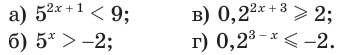
а) 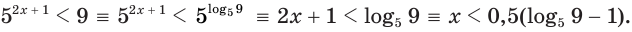
Ответ. 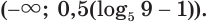
Здесь при переходе от неравенства 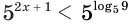 к неравенству
к неравенству 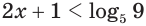 мы сохранили знак неравенства, так как основание степени больше единицы.
мы сохранили знак неравенства, так как основание степени больше единицы.
б) Поскольку значениями показательной функции 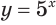 являются положительные числа, то условие
являются положительные числа, то условие 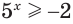 истинно при любом значении показателя, т. е. каждое действительное число является решением этого неравенства.
истинно при любом значении показателя, т. е. каждое действительное число является решением этого неравенства.
Ответ. 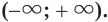
в) 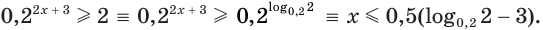
Ответ. 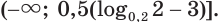
Здесь при переходе от неравенства 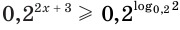 к неравенству
к неравенству 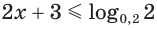 мы изменили знак неравенства на противоположный, так как основание степени меньше единицы.
мы изменили знак неравенства на противоположный, так как основание степени меньше единицы.
г) Поскольку при любом значении показателя 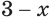 значением выражения
значением выражения 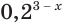 является положительное число, то неравенство
является положительное число, то неравенство 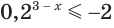 не может быть истинным ни при каком значении переменной
не может быть истинным ни при каком значении переменной 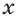 , т. е. оно не имеет решений (рис. 174).
, т. е. оно не имеет решений (рис. 174).
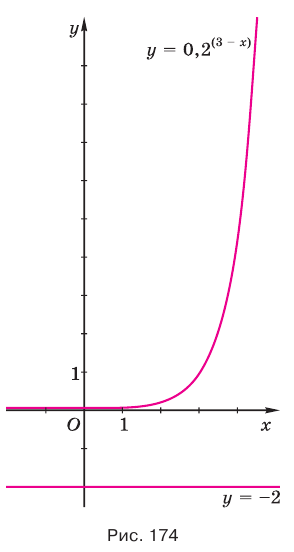
Для сведения показательного уравнения или неравенства к простейшим применяют общие приемы решения уравнений и неравенств: введение вспомогательной переменной, использование графических представлений, использование свойств функций, разложение на множители.
Пример №14
Решим уравнение:

а) Пусть 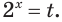 Тогда уравнение
Тогда уравнение 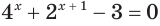 запишется в виде
запишется в виде 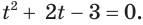 Числа 1 и -3 — его корни. Вернувшись к исходной переменной, получим уравнения
Числа 1 и -3 — его корни. Вернувшись к исходной переменной, получим уравнения 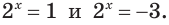 Корнем первого является число 0, а второе уравнение корней не имеет.
Корнем первого является число 0, а второе уравнение корней не имеет.
Ответ. 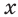 = 0.
= 0.
б) Перед введением вспомогательной переменной разделим обе части уравнения 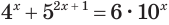 на выражение
на выражение 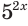 , которое положительно при любых значениях переменной. Будем иметь:
, которое положительно при любых значениях переменной. Будем иметь:
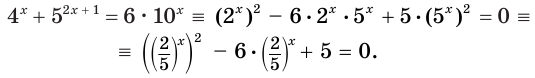
Пусть 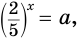 тогда получим уравнение
тогда получим уравнение 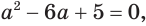 корнями которого являются числа 1 и 5. Значит,
корнями которого являются числа 1 и 5. Значит, 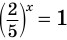 или
или 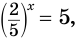 откуда
откуда 
Ответ. 
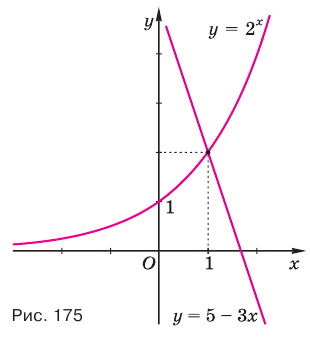
Пример №15
Решим неравенство 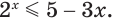
Построим графики функций 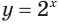 и
и 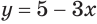 (рис. 175) и найдем, при каких значениях аргумента
(рис. 175) и найдем, при каких значениях аргумента  точка графика первой функции лежит ниже точки графика второй. Видим, что графики пересекаются в точке (1; 2). Если
точка графика первой функции лежит ниже точки графика второй. Видим, что графики пересекаются в точке (1; 2). Если 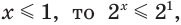 а
а 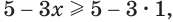 так как функция
так как функция 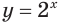 возрастает, а функция
возрастает, а функция 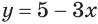 убывает. Значит, при
убывает. Значит, при 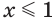 истинно неравенство
истинно неравенство 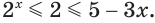 А если
А если 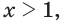 то
то 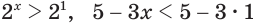 и потому истинно неравенство
и потому истинно неравенство 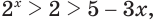 из которого следует, что ни одно число, большее 1, не является решением данного неравенства.
из которого следует, что ни одно число, большее 1, не является решением данного неравенства.
Ответ. 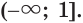
Пример №16
Решим неравенство 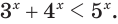
Функции, определяемые выражениями, записанными в левой и правой частях уравнения, возрастающие, но возрастают они с разной скоростью. Используем это. Разделим обе части неравенства на выражение 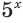 , которое всегда положительно. Получим равносильное неравенство
, которое всегда положительно. Получим равносильное неравенство 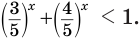 Функция
Функция 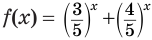 является убывающей как сумма убывающих функций. А поскольку
является убывающей как сумма убывающих функций. А поскольку 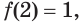 то решениями данного неравенства являются все числа, большие 2.
то решениями данного неравенства являются все числа, большие 2.
Ответ. 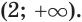
Пример №17
Решим уравнение 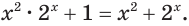
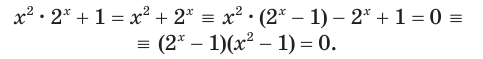
Остается решить уравнения 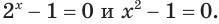 Их корни 0, -1 и 1 исчерпывают все корни исходного уравнения.
Их корни 0, -1 и 1 исчерпывают все корни исходного уравнения.
Ответ. 0; -1; 1.
Пример №18
Решим систему уравнений 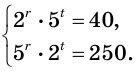
Перемножив уравнения системы, получим уравнение 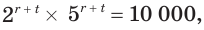 которое равносильно уравнению
которое равносильно уравнению 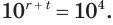 Значит,
Значит, 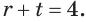
Разделив первое уравнение системы на второе, придем к уравнению 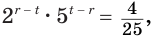 которое равносильно уравнению
которое равносильно уравнению 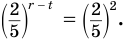 Потому
Потому 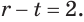
Таким образом, данная система равносильна системе 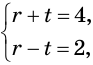 которая имеет решением пару (3; 1).
которая имеет решением пару (3; 1).
Ответ. (3; 1).
Пример №19
Решим систему 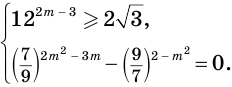
Решим уравнение системы:
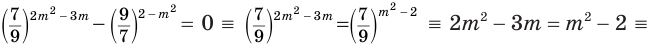
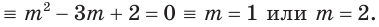
Из найденных чисел неравенству удовлетворяет только число 2.
Ответ. 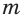 = 2.
= 2.
Пример №20
Решим уравнение 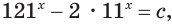 где
где 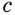 — некоторое число.
— некоторое число.
Данное уравнение равносильно уравнению 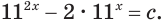 Оно заменой
Оно заменой 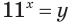 сводится к квадратному уравнению
сводится к квадратному уравнению 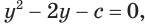 решение которого зависит от дискриминанта
решение которого зависит от дискриминанта 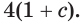
Пусть 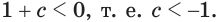 Тогда квадратное уравнение не имеет корней, а потому не имеет корней и исходное уравнение.
Тогда квадратное уравнение не имеет корней, а потому не имеет корней и исходное уравнение.
Пусть 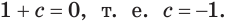 Тогда квадратное уравнение имеет один корень
Тогда квадратное уравнение имеет один корень 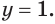 Учитывая замену
Учитывая замену 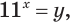 получим уравнение
получим уравнение 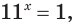 корнем которого является число
корнем которого является число  = 0.
= 0.
Пусть  Тогда квадратное уравнение имеет два корня:
Тогда квадратное уравнение имеет два корня: 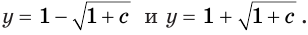 Возвращение к исходной переменной приводит к уравнениям:
Возвращение к исходной переменной приводит к уравнениям: 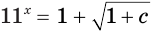 и
и 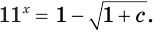 Корнем первого уравнения является число
Корнем первого уравнения является число 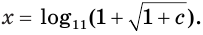 Второе уравнение имеет корнем число
Второе уравнение имеет корнем число 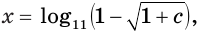 но при условии, что
но при условии, что  т. е. при
т. е. при 
Ответ. Если  то уравнение не имеет корней;
то уравнение не имеет корней;
если 
если 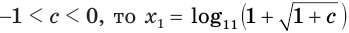
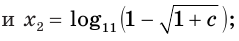
если 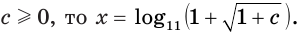
Степень с произвольным действительным показателем
Теперь мы выясним, что представляет собой степень положительного числа с действительным показателем.
Строгое определение степени с действительным показателем и доказательство ее свойств выходит за пределы школьного курса. Текст этого пункта содержит лишь общие пояснения того, как можно провести необходимые обоснования.
Начнем с частного случая. Выясним, что понимают под степенью числа 2 с показателем  .
.
Иррациональное число 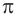 можно представить в виде бесконечной непериодической десятичной дроби:
можно представить в виде бесконечной непериодической десятичной дроби: 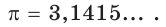
Рассмотрим последовательность рациональных чисел
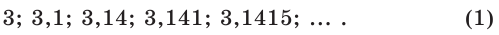
Понятно, что эта последовательность сходится к числу 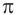 .
.
В соответствии с последовательностью  построим последовательность степеней с рациональными показателями:
построим последовательность степеней с рациональными показателями:
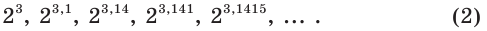
Можно показать, что члены последовательности  с увеличением номера стремятся к некоторому положительному числу. Это число и называют степенью числа 2 с показателем
с увеличением номера стремятся к некоторому положительному числу. Это число и называют степенью числа 2 с показателем 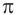 и обозначают 2
и обозначают 2 .
.
Аналогично можно действовать в общем случае, определяя смысл выражения 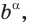 где
где  любое действительное число. Для числа
любое действительное число. Для числа  строят сходящуюся к нему последовательность рациональных чисел
строят сходящуюся к нему последовательность рациональных чисел  Далее рассматривают последовательность
Далее рассматривают последовательность 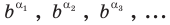 степеней с рациональными показателями (напомним, что степень положительного числа с рациональным показателем определена). Можно доказать, что эта последовательность сходится к положительному числу
степеней с рациональными показателями (напомним, что степень положительного числа с рациональным показателем определена). Можно доказать, что эта последовательность сходится к положительному числу  которое не зависит от выбора сходящейся к
которое не зависит от выбора сходящейся к  последовательности рациональных чисел
последовательности рациональных чисел 
 Число
Число  называют степенью положительного числа
называют степенью положительного числа  с действительным показателем
с действительным показателем  и обозначают
и обозначают 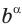 .
.
Если основание  равно единице, то
равно единице, то  для всех действительных
для всех действительных 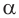 .
.
Если основание 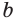 равно нулю, то степень
равно нулю, то степень 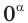 определяют только для
определяют только для 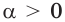 и считают, что
и считают, что 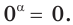 Например,
Например, 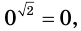
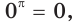 а выражение
а выражение 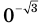 не имеет смысла.
не имеет смысла.
При 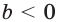 выражение
выражение 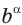 , где
, где 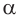 — иррациональное число, не имеет смысла.
— иррациональное число, не имеет смысла.
Степень с действительным показателем обладает теми же свойствами, что и степень с рациональным показателем.
В частности, для 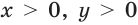 и любых действительных
и любых действительных  и
и 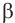 справедливы такие равенства:
справедливы такие равенства:
Докажем, например, свойство 1.
Пусть  и
и  — действительные числа, причем
— действительные числа, причем 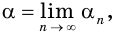
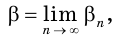
где  и
и  — последовательности рациональных чисел. Имеем:
— последовательности рациональных чисел. Имеем:
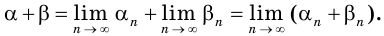
Для положительного числа 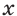 рассмотрим три последовательности:
рассмотрим три последовательности: 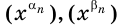 и
и 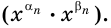
Имеем: 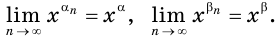
Так как для рациональных показателей 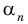 и
и 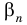 свойство 1 имеет место (мы узнали об этом при изучении свойств степени с рациональным показателем), то
свойство 1 имеет место (мы узнали об этом при изучении свойств степени с рациональным показателем), то 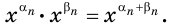
Последовательность рациональных чисел 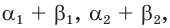
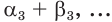 сходится к числу
сходится к числу 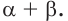 Поэтому можно записать, что
Поэтому можно записать, что 
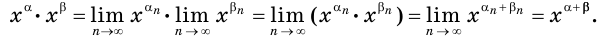
Пример №21
Упростите выражение 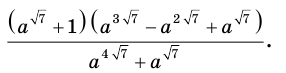
Решение:
Имеем:
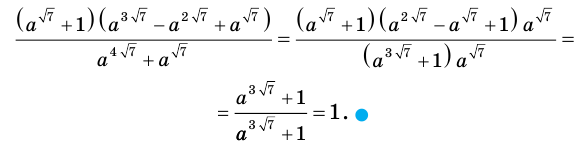
Выберем некоторое положительное число  отличное от 1. Каждому действительному числу
отличное от 1. Каждому действительному числу 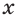 можно поставить в соответствие положительное число
можно поставить в соответствие положительное число 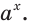 Тем самым задана функция
Тем самым задана функция 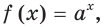 где
где 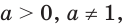 с областью определения
с областью определения 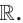 Эту функцию называют показательной функцией. Изучим некоторые свойства показательной функции. При
Эту функцию называют показательной функцией. Изучим некоторые свойства показательной функции. При 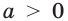 и любом
и любом 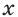 выполняется неравенство
выполняется неравенство 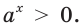 Поэтому область значений показательной функции состоит только из положительных чисел.
Поэтому область значений показательной функции состоит только из положительных чисел.
Можно показать, что для данного числа 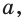 где
где 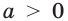 и
и 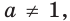 и для любого положительного числа
и для любого положительного числа 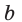 существует такое число
существует такое число 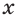 , что выполняется равенство
, что выполняется равенство 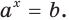
Сказанное означает, что областью значений показательной функции является множество 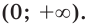
Показательная функция не имеет нулей, и промежуток 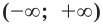 является ее промежутком знакопостоянства.
является ее промежутком знакопостоянства.
Показательная функция непрерывна.
Покажем, что при 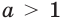 показательная функция является возрастающей. Для этого воспользуемся леммой.
показательная функция является возрастающей. Для этого воспользуемся леммой.
Лемма. Если 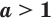 и
и 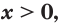 то
то 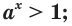 если
если  и
и 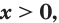 то
то 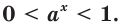
Например, 
Рассмотрим произвольные числа 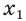 и
и 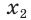 такие, что
такие, что 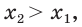 и функцию
и функцию 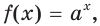 где
где 
Поскольку 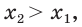 то
то 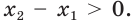 Тогда согласно лемме имеем:
Тогда согласно лемме имеем: 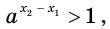 то есть
то есть 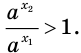 . Так как
. Так как 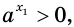 то
то 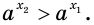
Отсюда 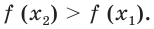
Мы показали, что из неравенства 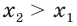 следует неравенство
следует неравенство 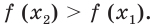 Это означает, что функция
Это означает, что функция 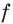 является возрастающей.
является возрастающей.
Аналогично можно показать, что при  показательная функция является убывающей. Поскольку показательная функция является либо возрастающей (при
показательная функция является убывающей. Поскольку показательная функция является либо возрастающей (при  ), либо убывающей (при
), либо убывающей (при 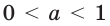 ), то она не имеет точек экстремума.
), то она не имеет точек экстремума.
Показательная функция является дифференцируемой. Подробнее о производной показательной функции вы узнаете в п. 23.
На рисунках 16.1 и 16.2 схематически изображен график показательной функции для случаев 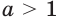 и
и 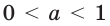 соответственно.
соответственно.
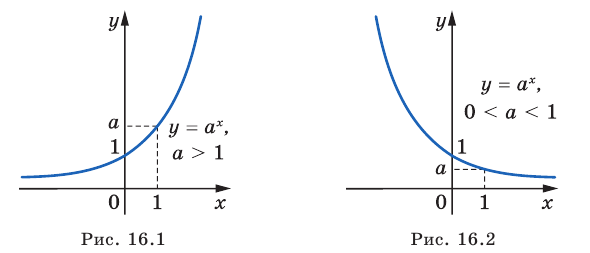
В частности, на рисунках 16.3 и 16.4 изображены графики функций 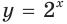 и
и 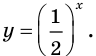
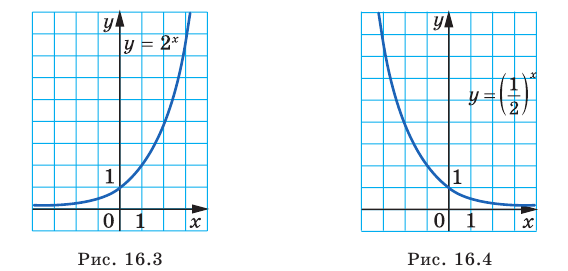
Заметим, что при  график показательной функции имеет горизонтальную асимптоту
график показательной функции имеет горизонтальную асимптоту 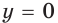 при
при 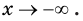 Аналогично при
Аналогично при 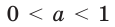 график показательной функции имеет горизонтальную асимптоту
график показательной функции имеет горизонтальную асимптоту 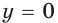 при
при 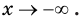
Показательная функция является математической моделью целого ряда процессов, происходящих в природе и в деятельности человека.
Например, биологам известно, что колония бактерий в определенных условиях за равные промежутки времени увеличивает свою массу в одно и то же количество раз.
Это означает, что если, например, в момент времени 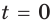 масса была равной 1, а в момент времени
масса была равной 1, а в момент времени 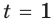 масса была равной
масса была равной 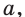 то в моменты времени
то в моменты времени  масса будет равной соответственно
масса будет равной соответственно 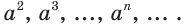 Поэтому естественно считать, что в любой момент времени
Поэтому естественно считать, что в любой момент времени 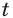 масса будет равной
масса будет равной 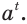 Можно проверить (сделайте это самостоятельно), что значения функции
Можно проверить (сделайте это самостоятельно), что значения функции 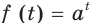 увеличиваются в одно и то же количество раз за равные промежутки времени.
увеличиваются в одно и то же количество раз за равные промежутки времени.
Таким образом, рассмотренный процесс описывают с помощью показательной функции 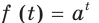 .
.
Из физики известно, что при радиоактивном распаде масса радиоактивного вещества за равные промежутки времени уменьшается в одно и то же количество раз.
Если поместить деньги в банк под определенный процент, то каждый год количество денег на счете будет увеличиваться в одно и то же количество раз.
Поэтому показательная функция описывает и эти процессы.
В таблице приведены свойства функции 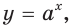 где
где 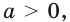
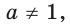 изученные в этом пункте.
изученные в этом пункте.
| Область определения | 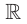 |
| Область значений | 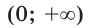 |
| Нули функции |  |
| Промежутки знакопостоянства | 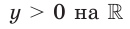 |
| Возрастание / убывание | Если 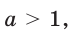 то функция возрастающая; если то функция возрастающая; если 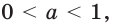 то функция убывающая то функция убывающая |
| Непрерывность | Непрерывная |
| Дифференцируемость | Дифференцируемая |
| Асимптоты | Если 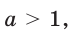 то график функции имеет горизонтальную асимптоту то график функции имеет горизонтальную асимптоту  при при  если если 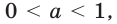 то график функции имеет горизонтальную асимптоту то график функции имеет горизонтальную асимптоту  при при  |
Пример №22
Найдите наименьшее и наибольшее значения функции 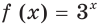 на отрезке
на отрезке 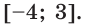
Решение:
Так как функция  возрастает на отрезке
возрастает на отрезке  то наименьшее значение она принимает при
то наименьшее значение она принимает при 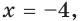 а наибольшее — при
а наибольшее — при 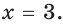
Следовательно,
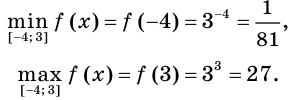
Ответ: 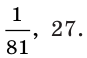
Пример №23
Решите уравнение 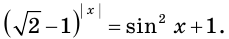
Решение:
Так как 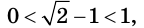 а
а 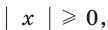 то
то 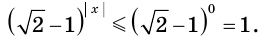 В то же время
В то же время 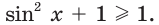 Таким образом, данное уравнение равносильно системе
Таким образом, данное уравнение равносильно системе
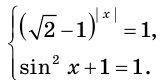
Отсюда 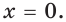
Ответ: 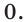
Вычисление показательных уравнений
Рассмотрим уравнения 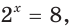
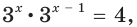
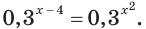
Во всех этих уравнениях переменная содержится только в показателе степени. Данные уравнения — примеры показательных уравнений.
Теорема 17.1. При 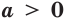 и
и 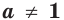 равенство
равенство 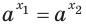 выполняется тогда и только тогда, когда
выполняется тогда и только тогда, когда 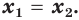
Доказательство. Очевидно, что если 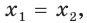 то
то 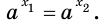
Докажем, что из равенства 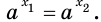 следует равенство
следует равенство 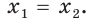 Предположим, что
Предположим, что 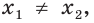 то есть
то есть 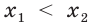 или
или 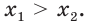 Пусть, например,
Пусть, например, 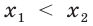 .
.
Рассмотрим показательную функцию 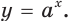 Она является либо возрастающей, либо убывающей. Тогда из неравенства
Она является либо возрастающей, либо убывающей. Тогда из неравенства 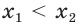 следует, что
следует, что 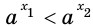 (при
(при 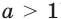 ) или
) или 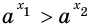 (при
(при 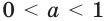 ). Однако по условию выполняется равенство
). Однако по условию выполняется равенство 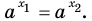 Получили противоречие.
Получили противоречие.
Аналогично рассматривают случай, когда 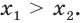
Следствие. Если 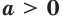 и
и 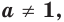 то уравнение
то уравнение

равносильно уравнению

Доказательство. Пусть 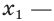 корень уравнения (1), то есть
корень уравнения (1), то есть 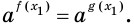 Тогда по теореме 17.1 получаем, что
Тогда по теореме 17.1 получаем, что 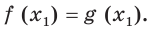 Следовательно,
Следовательно, 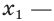 корень уравнения (2).
корень уравнения (2).
Пусть 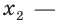 корень уравнения (2), то есть
корень уравнения (2), то есть 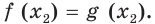 Отсюда
Отсюда 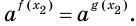
Мы показали, что каждый корень уравнения (1) является корнем уравнения (2) и наоборот, каждый корень уравнения (2) является корнем уравнения (1). Следовательно, уравнения (1) и (2) равносильны. А
Рассмотрим примеры решения показательных уравнений.
Пример №24
Решите уравнение 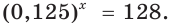
Решение:
Представим каждую из частей уравнения в виде степени с основанием 2. Имеем: 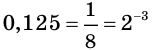 и
и 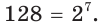 Запишем:
Запишем: 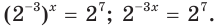 Это уравнение равносильно уравнению
Это уравнение равносильно уравнению
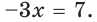
Отсюда 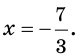 Ответ:
Ответ: 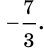
Пример №25
Решите уравнение 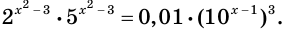
Решение:
Воспользовавшись свойствами степени, представим каждую из частей уравнения в виде степени с основанием 10. Имеем:
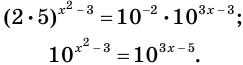
Переходим к равносильному уравнению:
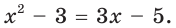
Отсюда 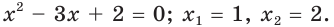
Ответ: 
Пример №26
Решите уравнение 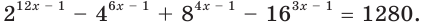
Решение:
Имеем:
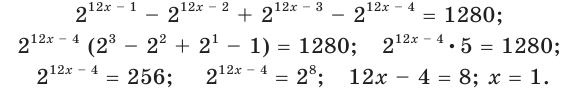
Ответ: 
Пример №27
Решите уравнение 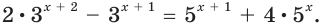
Решение:
Имеем:
Ответ: 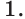
Пример №28
Решите уравнение 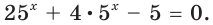
Решение:
Так как 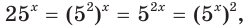 то данное уравнение удобно решать методом замены переменной.
то данное уравнение удобно решать методом замены переменной.
Пусть 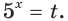 Тогда данное уравнение можно переписать так:
Тогда данное уравнение можно переписать так: 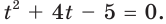 Отсюда
Отсюда 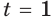 или
или 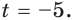 Если
Если 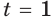 , то
, то 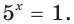 Отсюда
Отсюда 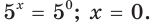 Если
Если 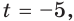 то
то 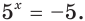 Так как
Так как 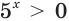 при любом
при любом 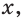 то уравнение
то уравнение 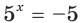 не имеет корней. Ответ:
не имеет корней. Ответ: 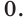
Пример №29
Решите уравнение 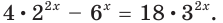
Решение:
Имеем: 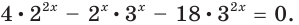
Так как 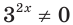 при любом
при любом 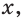 то, разделив обе части уравнения на
то, разделив обе части уравнения на 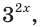 получим уравнение, равносильное данному:
получим уравнение, равносильное данному:
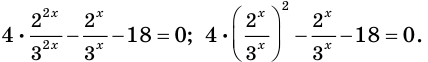
Пусть 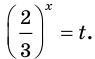 Тогда можно записать:
Тогда можно записать: 
Отсюда 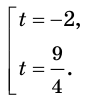 Имеем:
Имеем: 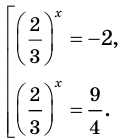
Так как 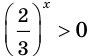 при любом
при любом 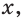 то первое уравнение совокупности решений не имеет. Второе уравнение совокупности перепишем так:
то первое уравнение совокупности решений не имеет. Второе уравнение совокупности перепишем так: 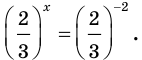
Отсюда 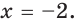
Ответ: 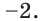
Пример №30
Решите уравнение 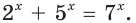
Решение:
Очевидно, что 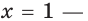 корень данного уравнения. Покажем, что этот корень — единственный.
корень данного уравнения. Покажем, что этот корень — единственный.
Разделив обе части исходного уравнения на 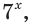 получим:
получим: 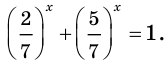
Рассмотрим функцию 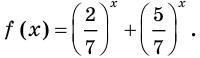 Так как функции
Так как функции 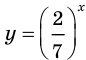 и
и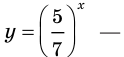 убывающие, то функция
убывающие, то функция  также является убывающей, а следовательно, каждое свое значение она принимает только один раз. Поэтому уравнение
также является убывающей, а следовательно, каждое свое значение она принимает только один раз. Поэтому уравнение  имеет единственный корень.
имеет единственный корень.
Ответ: 
Пример №31
При каких значениях параметра 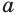 уравнение
уравнение
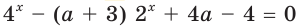 имеет единственный корень?
имеет единственный корень?
Решение:
Пусть 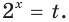 Имеем:
Имеем: 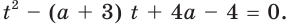
Отсюда 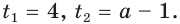 Следовательно, исходное уравнение равносильно совокупности:
Следовательно, исходное уравнение равносильно совокупности:
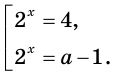
Первое уравнение совокупности имеет единственный корень 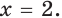 Второе уравнение совокупности при каждом значении параметра
Второе уравнение совокупности при каждом значении параметра 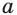 или имеет один корень, или вообще не имеет корней.
или имеет один корень, или вообще не имеет корней.
Для выполнения условия задачи второе уравнение совокупности либо должно не иметь корней, либо должно иметь единственный корень, равный 2.
Если 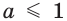 , то есть
, то есть 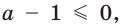 то уравнение
то уравнение 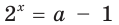 корней не имеет.
корней не имеет.
Число 2 является корнем второго уравнения совокупности, если 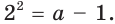 Отсюда
Отсюда 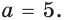
Ответ: 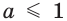 или
или 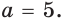
Вычисление показательных неравенств
Неравенства 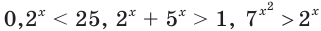 являются примерами показательных неравенств.
являются примерами показательных неравенств.
При решении многих показательных неравенств используют следующую теорему.
Теорема 18.1. При 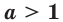 неравенство
неравенство 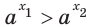 выполняется тогда и только тогда, когда
выполняется тогда и только тогда, когда 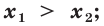 при
при 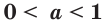 неравенство
неравенство 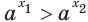 выполняется тогда и только тогда, когда
выполняется тогда и только тогда, когда 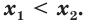
Справедливость этой теоремы следует из того, что при 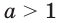 показательная функция
показательная функция 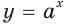 является возрастающей, а при
является возрастающей, а при 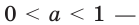 убывающей.
убывающей.
Следствие. Если 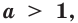 то неравенство
то неравенство 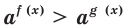 равносильно неравенству
равносильно неравенству 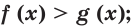 если
если 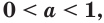 то неравенство
то неравенство 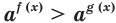 равносильно неравенству
равносильно неравенству 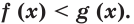
Воспользовавшись идеей доказательства следствия из теоремы 17.1, докажите это следствие самостоятельно.
Рассмотрим примеры решения показательных неравенств.
Пример №32
Решите неравенство 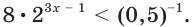
Решение:
Имеем: 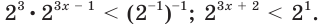
Так как основание степеней 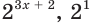 больше единицы, то последнее неравенство равносильно такому:
больше единицы, то последнее неравенство равносильно такому: 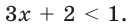
Отсюда 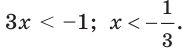
Ответ: 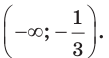
Пример №33
Решите неравенство 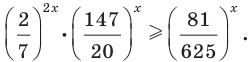
Решение:
Имеем: 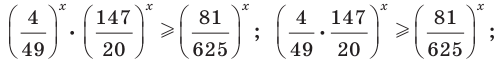
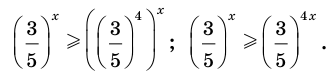
Так как 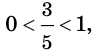 то последнее неравенство равносильно такому:
то последнее неравенство равносильно такому: 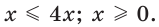
Ответ: 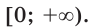
Пример №34
Решите неравенство 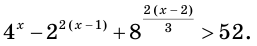
Решение:
Перепишем данное неравенство так: 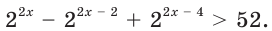
Отсюда
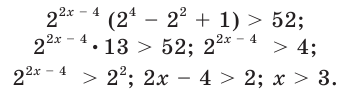
Ответ: 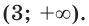
Пример №35
Решите неравенство 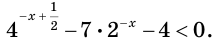
Решение.
Имеем:
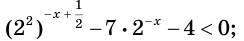
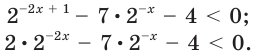
Пусть 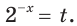 Тогда
Тогда 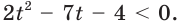
Решив это неравенство, получим 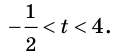 Отсюда
Отсюда 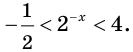
Так как 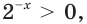 то
то 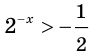 при всех
при всех 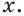 Поэтому достаточно решить неравенство
Поэтому достаточно решить неравенство 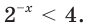
Имеем: 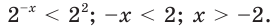
Ответ: 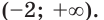
Пример №36
Решите неравенство 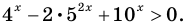
Решение:
Имеем: 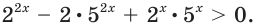 Так как
Так как 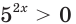 при любом
при любом 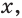 то, разделив обе части последнего неравенства на
то, разделив обе части последнего неравенства на 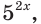 получаем равносильное неравенство
получаем равносильное неравенство 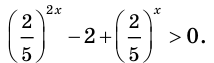
Пусть 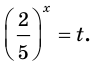 Тогда
Тогда 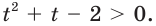 Решив это неравенство, получаем
Решив это неравенство, получаем 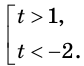
Отсюда: 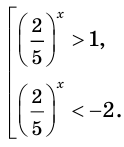
Из неравенства 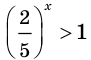 находим, что
находим, что 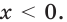 Неравенство
Неравенство 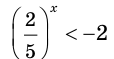 не имеет решений.
не имеет решений.
Ответ: 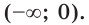
Пример №37
Решите неравенство 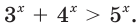
Решение:
Имеем: 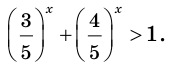
Рассмотрим функцию 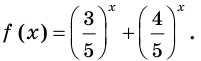 Заметим, что
Заметим, что 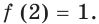 Так как функция
Так как функция  убывающая, то при
убывающая, то при 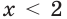 выполняется неравенство
выполняется неравенство 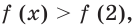 а при
а при 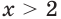 выполняется неравенство
выполняется неравенство 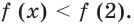 Следовательно, множеством решений неравенства
Следовательно, множеством решений неравенства  то есть неравенства
то есть неравенства 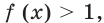 является промежуток
является промежуток 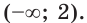
Свойство показательной функции
При условии, что 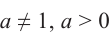
равенство 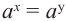 справедливо тогда и только тогда, если х = у. По данному свойству получаем:
справедливо тогда и только тогда, если х = у. По данному свойству получаем:
1)показательное уравнение 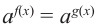 равносильно уравнению
равносильно уравнению 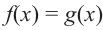 .
.
2)если в уравнении 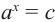 при
при 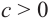 запишем
запишем 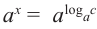 , то
, то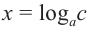 . Заданные показательные уравнения, при помощи определённых методов, приводятся к простейшим показательным уравнениям.
. Заданные показательные уравнения, при помощи определённых методов, приводятся к простейшим показательным уравнениям.
Применение свойств степени
Пример №38

Проверка.

Пример №39

Уравнения с разными основаниями можно решить разделив обе стороны на одну из степеней или логарифмированием обеих частей:
Примеры:

Введение новой переменной:
Пример:

Ответ: х = 2
Если уравнение состоит из членов, которые имеют одинаковую степень, а основания являются последовательными членами геометрической прогрессии, то обе части уравнения делится на один из крайних членов и вводится новая переменная.
Пример:

Зависимость между температурой и временем при охлаждении задаётся формулой Ньютона  где Т – температура в данный момент времени, То – температура в начальный момент времени, Тr – температура окружающей среды (средняя температура), r – скорость охлаждения ( скорость изменения за единицу времени),
где Т – температура в данный момент времени, То – температура в начальный момент времени, Тr – температура окружающей среды (средняя температура), r – скорость охлаждения ( скорость изменения за единицу времени),
t – время.
Решение показательных и логарифмических уравнений и неравенств
1. Конечная ОДЗ:
Если область допустимых значений (ОДЗ) уравнения (неравенства или системы) состоит из конечного числа значений, то для решения достаточно проверить все эти значения.
Пример №40
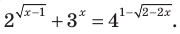
ОДЗ: 
Итак, ОДЗ: 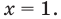
Проверка. 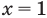 — корень
— корень 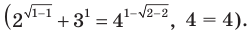 Других корней нет, поскольку в ОДЗ входит только одно число.
Других корней нет, поскольку в ОДЗ входит только одно число.
Ответ: 1.
2. Оценка значений левой и правой частей уравнения:
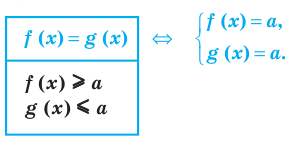
Если требуется решить уравнение вида 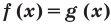 и выяснилось, что
и выяснилось, что 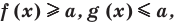 то равенство между левой и правой частями возможно тогда и только тогда, когда
то равенство между левой и правой частями возможно тогда и только тогда, когда  одновременно будут равны
одновременно будут равны 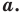
Пример №41
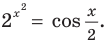
Оценим значения левой и правой частей данного уравнения: 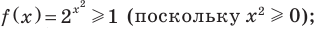 если
если 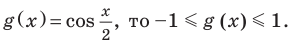 Итак,
Итак, 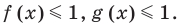 Тогда данное уравнение равносильно системе
Тогда данное уравнение равносильно системе 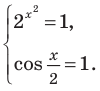
Из первого уравнения получаем 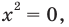 то есть
то есть 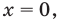 что удовлетворяет и второму уравнению.
что удовлетворяет и второму уравнению.
Ответ: 0.
3. Использование монотонности функций
1. Подбираем один или несколько корней уравнения.
2. Доказываем, что других корней это уравнение не имеет (используя теоремы о корнях уравнения или оценку значений левой и правой частей уравнения).
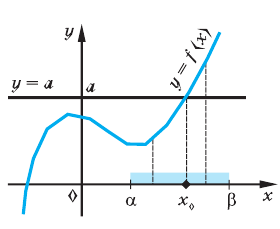
Теоремы о корнях уравнения:
1. Если в уравнении 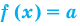 функция
функция 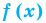 возрастает (убывает) на некотором промежутке, то это уравнение может иметь не более чем один корень на этом промежутке.
возрастает (убывает) на некотором промежутке, то это уравнение может иметь не более чем один корень на этом промежутке.
Пример №42
Уравнение 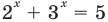 имеет единственный корень
имеет единственный корень 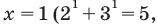 то есть
то есть 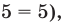 поскольку функция
поскольку функция 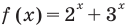 возрастает (на всей области определения
возрастает (на всей области определения 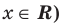 как сумма двух возрастающих функций.
как сумма двух возрастающих функций.
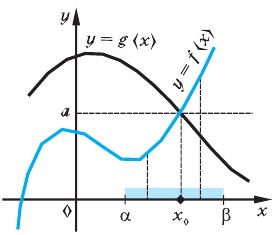
2. Если в уравнении 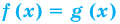 функция
функция 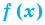 возрастает на некотором промежутке, а функция
возрастает на некотором промежутке, а функция  убывает на этом же промежутке (или наоборот), то это урав# нение может иметь не более чем один корень на этом промежутке.
убывает на этом же промежутке (или наоборот), то это урав# нение может иметь не более чем один корень на этом промежутке.
Пример:
Уравнение 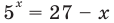 имеет единственный корень
имеет единственный корень 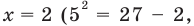 то есть
то есть 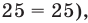 поскольку
поскольку 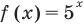 возрастает, а
возрастает, а 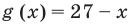 убывает (при всех
убывает (при всех 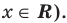
4. «Ищи квадратный трехчлен»
Попытайтесь рассмотреть заданное уравнение как квадратное относи# тельно некоторой переменной (или относительно некоторой функции).
Пример:
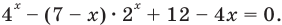
Запишем 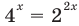 и введем замену
и введем замену 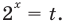
Получаем 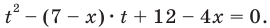 Рассмотрим это уравнение как квадратное относительно
Рассмотрим это уравнение как квадратное относительно 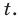 Его дискриминант
Его дискриминант 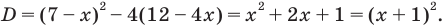 Тогда
Тогда 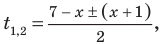 то есть
то есть 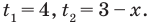 Обратная замена дает
Обратная замена дает 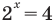 (отсюда
(отсюда 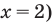 или
или 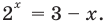 Последнее уравнение имеет единственный корень
Последнее уравнение имеет единственный корень 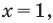 так как
так как 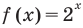 возрастает, а
возрастает, а 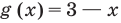 убывает (при всех
убывает (при всех 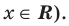
Ответ: 1; 2.
Пример №43
Решите уравнение 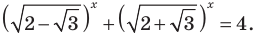
Решение:
Если 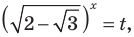 то
то 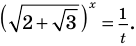 Получаем
Получаем 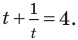 Отсюда
Отсюда 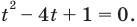 Тогда
Тогда 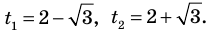 Обратная замена дает
Обратная замена дает 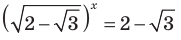 (отсюда
(отсюда 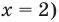 или
или 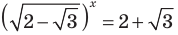 (отсюда
(отсюда 
Ответ: 
Комментарий:
Замечаем, что 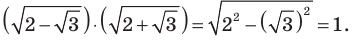 Таким образом, если
Таким образом, если 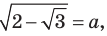 то
то 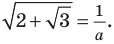 То есть данное уравнение имеет вид
То есть данное уравнение имеет вид 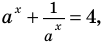 и его можно решить с помощью замены
и его можно решить с помощью замены 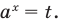 Но теперь эту замену можно непосредственно применить для данного уравнения, не вводя промежуточные обозначения. После обратной замены учитываем, что
Но теперь эту замену можно непосредственно применить для данного уравнения, не вводя промежуточные обозначения. После обратной замены учитываем, что
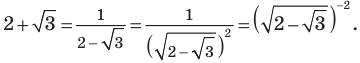
Пример №44
Решите уравнение 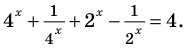
Комментарий:
Если привести все степени к одному основанию 2 и обозначить  то получим уравнение (1) (см. решение), в котором можно ввести замену
то получим уравнение (1) (см. решение), в котором можно ввести замену 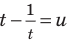 (тогда
(тогда 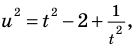 отсюда
отсюда 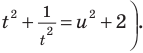 На ОДЗ данного уравнения
На ОДЗ данного уравнения  все замены и обратные замены являются равносильными преобразованиями этого уравнения. Таким образом, решив уравнения, полученные в результате замен, и выполнив обратные замены, мы получим корни данного уравнения.
все замены и обратные замены являются равносильными преобразованиями этого уравнения. Таким образом, решив уравнения, полученные в результате замен, и выполнив обратные замены, мы получим корни данного уравнения.
Решение:
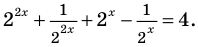
Замена  дает уравнение
дает уравнение
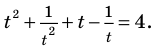
Обозначим 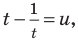 тогда
тогда 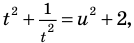 таким образом, из уравнения (1) получаем уравнение
таким образом, из уравнения (1) получаем уравнение 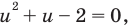 которое имеет корни:
которое имеет корни: 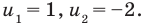
Обратная замена дает 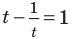 или
или 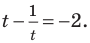
Тогда 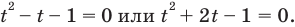
Получаем 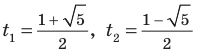 или
или 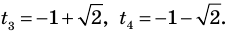 Тогда
Тогда 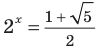 ( отсюда
( отсюда 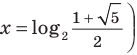 или
или 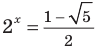 (корней нет, поскольку
(корней нет, поскольку 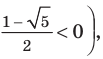 или
или 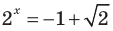 (отсюда
(отсюда 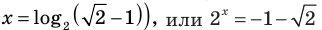 (корней нет, поскольку
(корней нет, поскольку 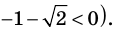
Ответ: 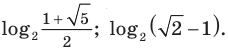
- Заказать решение задач по высшей математике
Пример №45
Решите уравнение 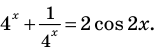
I способ
Комментарий:
Учитывая, что 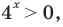 получаем, что в левой части уравнения стоит сумма двух взаимно обратных положительных чисел, которая всегда больше или равна 2. (Действительно, если
получаем, что в левой части уравнения стоит сумма двух взаимно обратных положительных чисел, которая всегда больше или равна 2. (Действительно, если 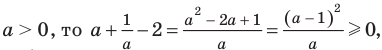 таким образом, при всех
таким образом, при всех 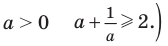
Для оценки значений правой части достаточно вспомнить, что областью значений функции 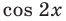 является промежуток
является промежуток 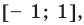 таким образом,
таким образом, 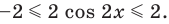
Решение:
Оценим значения левой и правой частей уравнения, 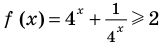 как сумма двух взаимно обратных положительных чисел. Если
как сумма двух взаимно обратных положительных чисел. Если 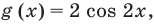 то
то 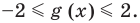 Таким образом,
Таким образом, 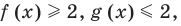 тогда данное уравнение равносильно системе
тогда данное уравнение равносильно системе 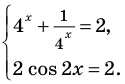
Из первого уравнения, используя замену  получаем
получаем
 то есть
то есть  Отсюда
Отсюда 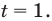
Тогда 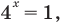 отсюда
отсюда 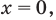 что удовлетворяет и второму уравнению.
что удовлетворяет и второму уравнению.
Ответ: 0.
II способ решения уравнения 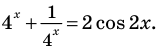
Комментарий:
Если обозначить 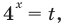 то данное уравнение приводится к уравнению (2) (см. решение), которое можно рассматривать как квадратное относительно переменной
то данное уравнение приводится к уравнению (2) (см. решение), которое можно рассматривать как квадратное относительно переменной 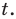 Заметим, что
Заметим, что 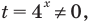 поэтому при таких значениях
поэтому при таких значениях 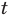 уравнения (1) и (2) являются равносильными. Далее используем условие существования корней квадратного уравнения.
уравнения (1) и (2) являются равносильными. Далее используем условие существования корней квадратного уравнения.
Решение:
После замены 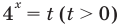 из данного уравнения получаем равносильное уравнение
из данного уравнения получаем равносильное уравнение 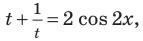 которое, в свою очередь, равносильно уравнению
которое, в свою очередь, равносильно уравнению 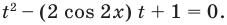
Рассмотрим уравнение (2) как квадратное относительно переменной 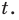 Тогда его дискриминант
Тогда его дискриминант 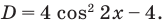
Уравнение (2) может иметь корни только тогда, когда 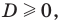 то есть когда
то есть когда 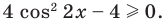 Отсюда
Отсюда 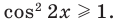
У этого неравенства знак «больше» не может выполняться 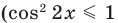 всегда), таким образом, неравенство (3) равносильно уравнению
всегда), таким образом, неравенство (3) равносильно уравнению 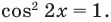 Тогда
Тогда 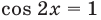 или
или 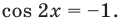 Подставляя эти значения в уравнение (2), получаем две системы:
Подставляя эти значения в уравнение (2), получаем две системы: 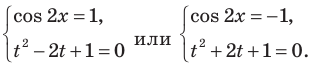 Во второй системе из второго уравнения имеем
Во второй системе из второго уравнения имеем 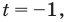 что не удовлетворяет условию
что не удовлетворяет условию 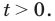 Таким образом, данное уравнение равносильно только первой системе. Из второго уравнения первой системы имеем
Таким образом, данное уравнение равносильно только первой системе. Из второго уравнения первой системы имеем 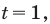 тогда
тогда 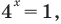 то есть
то есть 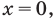 что удовлетворяет и первому уравнению этой системы.
что удовлетворяет и первому уравнению этой системы.
Ответ: 0.
Пример №46
Решите уравнение 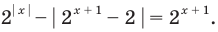
Комментарий:
Для решения уравнения с несколькими модулями можем применить общую схему (с. 240):
- найти ОДЗ;
- найти нули всех подмодульных функций;
- отметить нули на ОДЗ и разбить ОДЗ на промежутки;
- найти решения уравнения в каждом из промежутков.
Решение:
ОДЗ: 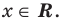
Нули подмодульных функций: 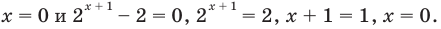
Этот нуль  разбивает ОДЗ на два промежутка, в каждом из которых каждая подмодульная функция имеет постоянный знак (см. рисунок).
разбивает ОДЗ на два промежутка, в каждом из которых каждая подмодульная функция имеет постоянный знак (см. рисунок).
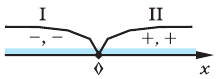
Промежуток I. При 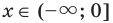 имеем уравнение
имеем уравнение 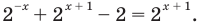 Тогда
Тогда
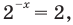 таким образом,
таким образом, 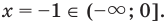
Промежуток II. При 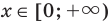 имеем уравнение
имеем уравнение 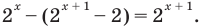 Тогда
Тогда
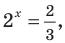 отсюда
отсюда 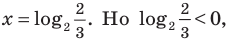 таким образом, во II промежутке данное уравнение корней не имеет.
таким образом, во II промежутке данное уравнение корней не имеет.
Ответ: -1.
Пример №47
Решите уравнение
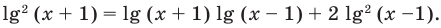
Решение:
ОДЗ 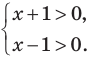 То есть
То есть 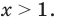
Поскольку 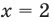 не является корнем данного уравнения, то при делении обеих частей уравнения на
не является корнем данного уравнения, то при делении обеих частей уравнения на 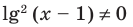 получаем равносильное (на ОДЗ) уравнение
получаем равносильное (на ОДЗ) уравнение
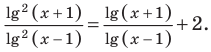
После замены 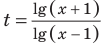 имеем уравнение
имеем уравнение 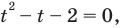 корни которого:
корни которого: 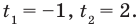 Выполнив обратную замену, получаем
Выполнив обратную замену, получаем
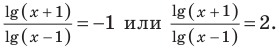
Тогда на ОДЗ имеем равносильные уравнения:
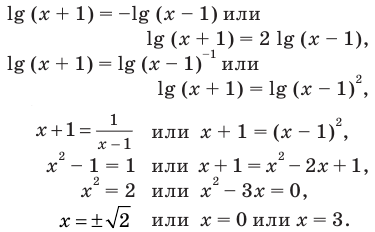
Учитывая ОДЗ, получаем
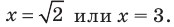
Ответ: 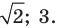
Комментарий:
Если выполнить замену 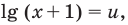
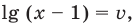 то получим уравнение
то получим уравнение 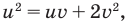 все члены которого имеют одинаковую суммарную степень — два. Напомним, что такое уравнение называется однородным и решается делением обеих частей на наибольшую степень одной из переменных. Разделим, например, обе части на
все члены которого имеют одинаковую суммарную степень — два. Напомним, что такое уравнение называется однородным и решается делением обеих частей на наибольшую степень одной из переменных. Разделим, например, обе части на 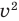 (то есть на
(то есть на 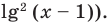
Чтобы не потерять корни уравнения при делении на выражение с переменной, необходимо те значения переменной, при которых это выражение равно нулю, рассмотреть отдельно. Значение 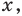 при котором
при котором 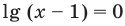 (тогда
(тогда 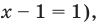 то есть
то есть 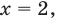 подставляем в данное уравнение.
подставляем в данное уравнение.
Для реализации полученного плана решения не обязательно вводить переменные  достаточно заметить, что данное уравнение однородное, разделить обе части на
достаточно заметить, что данное уравнение однородное, разделить обе части на 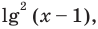 а затем ввести новую переменную
а затем ввести новую переменную 
В конце учитываем, что все преобразования были равносильными на ОДЗ, следовательно, необходимо выбирать только те из найденных корней, которые входят в ОДЗ.
Пример №48
Решите уравнение 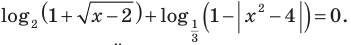
Комментарий:
Логарифмические функции, стоящие в левой части данного уравнения, принимают только неотрицательные значения.
Действительно, на всей области определения 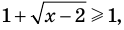 таким образом,
таким образом,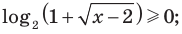 аналогично, поскольку
аналогично, поскольку 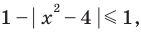 то на своей области определения
то на своей области определения 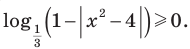 В этом случае сумма двух неотрицательных функций может равняться нулю тогда и только тогда, когда каждая из этих функций равна нулю.
В этом случае сумма двух неотрицательных функций может равняться нулю тогда и только тогда, когда каждая из этих функций равна нулю.
Заметим, что при переходе от данного уравнения к системе уравнений ОДЗ не изменяется, таким образом, ее можно не записывать в явном виде. При решении полученных простейших логарифмических уравнений ОДЗ также учитывается автоматически, поэтому ее можно вообще не записывать в решение.
Решение:
Поскольку на всей области определения 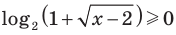 и
и 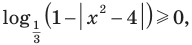 то данное уравнение равносильно системе
то данное уравнение равносильно системе
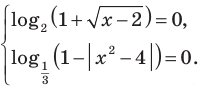
Из первого уравнения системы получаем 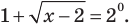 Тогда
Тогда 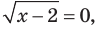 то есть
то есть 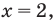 что удовлетворяет и второму уравнению системы.
что удовлетворяет и второму уравнению системы.
Ответ: 2.
Пример №49
При каких значениях параметра 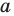 неравенство
неравенство 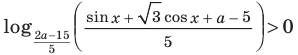 выполняется для любых значений
выполняется для любых значений 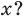
Комментарий:
Сначала воспользуемся формулой 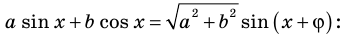
 Далее запишем правую часть неравенства как значение логарифмической функции и, переходя к аргументу, учтем, что в случае, когда основание этой функции больше 1, функция возрастает, а когда меньше 1 (но больше 0) — убывает.
Далее запишем правую часть неравенства как значение логарифмической функции и, переходя к аргументу, учтем, что в случае, когда основание этой функции больше 1, функция возрастает, а когда меньше 1 (но больше 0) — убывает.
При дальнейшем анализе полученных неравенств учитываем, что неравенство  выполняется для любых значений
выполняется для любых значений  тогда и только тогда, когда
тогда и только тогда, когда  а неравенство
а неравенство 
Решение:
Данное неравенство равносильно неравенству
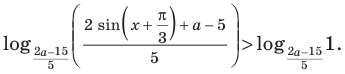
Эта неравенство равносильно совокупности систем
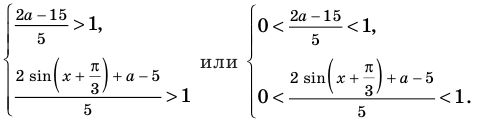 Тогда
Тогда 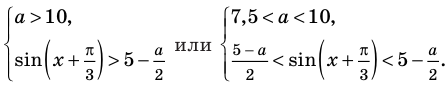
Неравенство с переменной 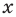 в последней совокупности систем будут выполняться для любых значений
в последней совокупности систем будут выполняться для любых значений 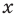 при условии:
при условии:
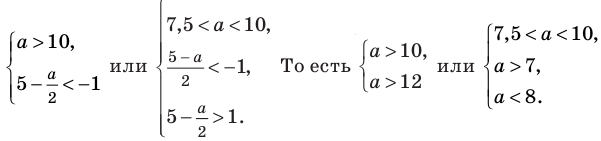
Тогда 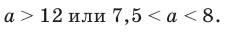
Ответ: при 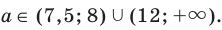
Пример №50
При каких значениях параметра а уравнение log2 (4′ имеет единственный корень?
Комментарий:
Выполняя равносильные преобразования данного уравнения, учитываем, что при использовании определения логарифма для решения этого простейшего логарифмического уравнения его ОДЗ учитывается автоматически.
При выполнении замены переменной в задании с параметром учитываем, что после замены требование задачи может измениться.
Исследуя расположение корней квадратного трехчлена 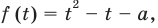 применим условия, приведенные на с. 225 в таблице 37 (для записи соответствующих условий используем обозначение:
применим условия, приведенные на с. 225 в таблице 37 (для записи соответствующих условий используем обозначение:  — дискриминант,
— дискриминант,  — абсцисса вершины параболы). Как известно, для того чтобы корни квадратного трехчлена
— абсцисса вершины параболы). Как известно, для того чтобы корни квадратного трехчлена  (с положительным коэффициентом при
(с положительным коэффициентом при 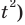 были расположены по разные стороны от числа
были расположены по разные стороны от числа 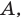 необходимо и достаточно, чтобы выполнялось условие
необходимо и достаточно, чтобы выполнялось условие 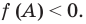
Решение:
Данное уравнение равносильно уравнению
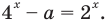
То есть 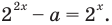 Замена
Замена 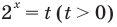 дает уравнение
дает уравнение
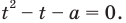
Требование задачи будет выполняться тогда и только тогда, когда уравнение (2) будет иметь единственный положительный корень. Это будет в одном из двух случаев:
- уравнение (2) имеет единственный корень, и он положительный;
- уравнение (2) имеет два корня, из которых только один положительный, а второй — отрицательный или нуль.
Для первого случая получаем 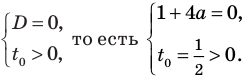
Таким образом, 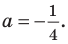
Для второго случая значение 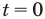 исследуем отдельно. При
исследуем отдельно. При 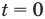 из уравнения (2) получаем
из уравнения (2) получаем 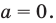 При
При 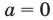 уравнение (2) имеет корни
уравнение (2) имеет корни 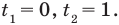 Таким образом, условие задачи при
Таким образом, условие задачи при 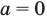 выполняется.
выполняется.
Остается еще один случай — корни уравнения (2) имеют разные знаки (расположены по разные стороны от нуля). Это будет тогда и только тогда, когда будет выполняться условие 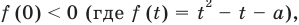 то есть условие
то есть условие 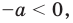 тогда
тогда 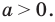 Объединяя все результаты, получаем ответ.
Объединяя все результаты, получаем ответ.
Ответ: при 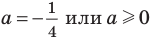 данное уравнение имеет единственный корень.
данное уравнение имеет единственный корень.
Справочный материал
Формулы сокращенного умножения. Разложение алгебраических выражений на множители
Основные приемы разложения многочлена на множители
Вынесение общего множителя за скобки 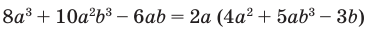
Способ группировки 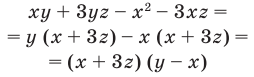
Применение формул сокращенного умножения 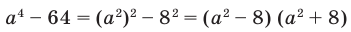
Разложение на множители квадратного трехчлена 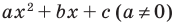
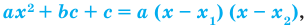
где 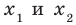 — корни квадратного трехчлена, то есть корни уравнения
— корни квадратного трехчлена, то есть корни уравнения 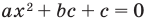
Поскольку 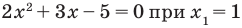 и
и 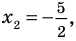 то
то 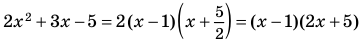
Обобщение некоторых формул сокращенного умножения
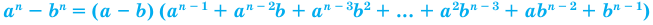
Примеры:
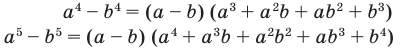
При 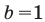
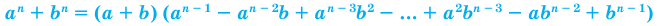
Примеры:
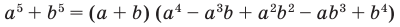
При 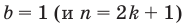
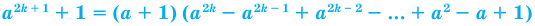
Системы уравнений
Если ставится задача найти все общие решения двух (или больше) уравнений с одной или несколькими переменными, то говорят, что требуется решить систему уравнений. Записывают систему уравнений, объединяя их фигурной скобкой. Решением системы называется такое значение переменной или такой упорядоченный набор значений переменных (если переменных несколько), которые удовлетворяют всем уравнениям системы. Решить систему уравнений — значит найти все ее решения или доказать, что решений нет. Если система не имеет решения, то ее называют несовместной.
Примеры:
1)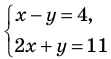 — система двух уравнений с двумя переменными. Пара чисел (5; 1), то есть
— система двух уравнений с двумя переменными. Пара чисел (5; 1), то есть 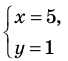 — решение системы.
— решение системы.
2) 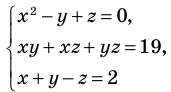 система трех уравнений с тремя переменными. Тройка
система трех уравнений с тремя переменными. Тройка 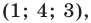 то есть
то есть 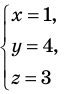 — одно из решений системы.
— одно из решений системы.
Равносильность систем уравнений:
Две системы уравнений называются равносильными на некотором множестве, если на этом множестве они имеют одинаковые решения (то есть каждое решение первой системы на этом множестве является решением второй и, наоборот, каждое решение второй системы является решением первой). Если изменить порядок уравнений заданной системы, то получим систему, равносильную заданной. Если одно из уравнений системы заменить на равносильное ему уравнение, то получим систему, равносильную заданной.
Областью допустимых значений (ОДЗ) системы называется общая область определения всех функций, входящих в запись этой системы. Все равносильные преобразования систем выполняются на ОДЗ исходной системы.
Основные способы решения систем уравнений
Способ подстановки:
Выражаем из одного уравнения системы одну переменную через другую (или через другие) и подставляем полученное выражение вместо соответствующей переменной во все другие уравнения системы (затем решаем полученное уравнение или систему и подставляем результат в выражение для первой переменной).
Пример №51
Решить систему 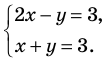
Решение:
Из первого уравнения системы 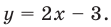 Подставляем во второе уравнение системы и получаем
Подставляем во второе уравнение системы и получаем 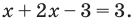 Отсюда
Отсюда 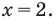 Тогда
Тогда 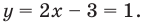
Ответ: (2; 1).
Способ сложения:
Если первое уравнение системы заменить суммой первого уравнения, умноженного на число  и второго уравнения, умноженного на число
и второго уравнения, умноженного на число  (а все остальные уравнения оставить без изменения), то получим систему, равносильную заданной.
(а все остальные уравнения оставить без изменения), то получим систему, равносильную заданной.
Пример №52
Решить систему 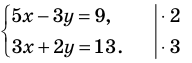
Решение:
Умножим обе части первого уравнения системы на 2, а второго — на 3 (чтобы получить как коэффициенты при переменной  противоположные числа) и почленно сложим полученные уравнения. Из полученного уравнения находим значение
противоположные числа) и почленно сложим полученные уравнения. Из полученного уравнения находим значение  подставляем результат в любое уравнение системы и находим значение
подставляем результат в любое уравнение системы и находим значение 
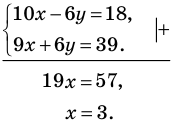
Тогда 
Ответ: (3; 2).
Основные способы решения систем уравнений
Способ подстановки:
Выполняем равносильные преобразования заданной системы так, чтобы удобно было строить графики всех уравнений, входящих в систему. Затем строим соответствующие графики и находим координаты точек пересечения построенных линий — эти координаты и являются решениями системы.
Пример №53
Решить графически систему 
Решение:
Заданная система равносильна системе 
Графиком каждого из уравнений системы является прямая. Для построения прямой достаточно построить две ее точки. Например, для
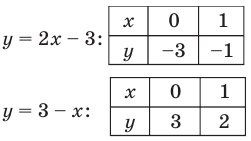
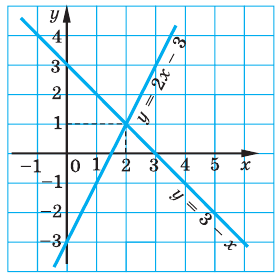
Графики пересекаются в единственной точке 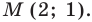 Итак, пара чисел (2; 1) — единственное решение заданной системы.
Итак, пара чисел (2; 1) — единственное решение заданной системы.
Ответ: (2; 1).
Пример №54
Решить графически систему 
Решение:
Заданная система равносильна системе 
График первого уравнения — окружность радиуса 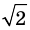 с центром в начале координат, а график второго — кубическая парабола
с центром в начале координат, а график второго — кубическая парабола 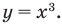 Эти два графика пересекаются в двух точках с координатами
Эти два графика пересекаются в двух точках с координатами 
Ответ:  — решение системы.
— решение системы.
Квадратные неравенства
Квадратным неравенством называется неравенство вида 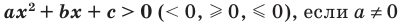
Для решения квадратного неравенства достаточно найти корни квадратного трехчлена 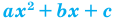 и построить эскиз его графика (параболу).
и построить эскиз его графика (параболу).
Как ответ записывают промежутки оси  для которых точки параболы расположены выше оси
для которых точки параболы расположены выше оси 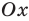 (для случая
(для случая 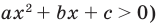 и ниже оси
и ниже оси 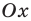 (для случая
(для случая 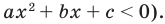
Если квадратный трехчлен имеет два разных корня 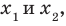 то для решения неравенства можно также использовать метод интервалов или равно% сильные преобразования неравенства.
то для решения неравенства можно также использовать метод интервалов или равно% сильные преобразования неравенства.
Разные случаи решения неравенства 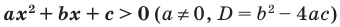
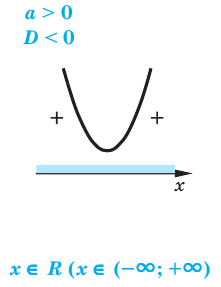
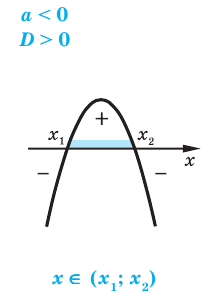
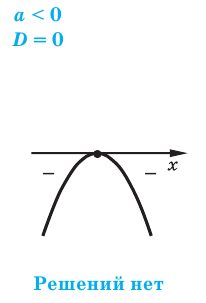
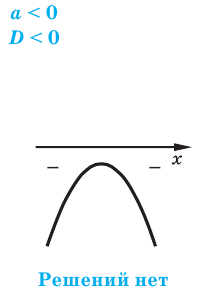
Пример №55
Решите неравенство 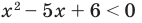
І способ
1. 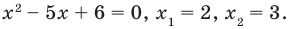
2. Строим эскиз графика функции 
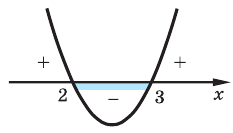
Ответ: (2 ; 3)
ІІ способ (метод интервалов)
Обозначим 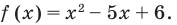
1. Область определения: 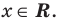
2. Нули функции: 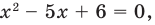
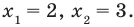
3. Отмечаем нули на области определения (на всей числовой прямой) и находим знак в каждом промежутке, на которые разбивается область определения (см. рисунок).
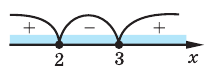
Для нахождения знаков функции 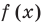 удобно разложить квадратный трехчлен на множители и записать заданное неравенство так:
удобно разложить квадратный трехчлен на множители и записать заданное неравенство так: 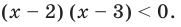
Ответ: (2; 3).
ІІІ способ (равносильные преобразования)
Поскольку 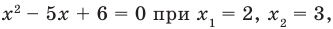 то заданное неравенство равносильно неравенству
то заданное неравенство равносильно неравенству 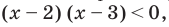 которое равносильно совокупности систем:
которое равносильно совокупности систем: 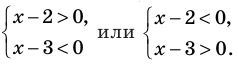
Тогда 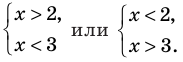
Из первой системы получаем 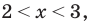 а вторая система не имеет решения.
а вторая система не имеет решения.
Ответ: (2; 3).
Нахождение области определения функции
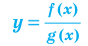
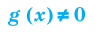 Знаменатель дроби не равен нулю
Знаменатель дроби не равен нулю
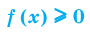 Под знаком корня четной степени может стоять только неотрицательное выражение
Под знаком корня четной степени может стоять только неотрицательное выражение
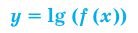
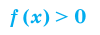 Под знаком логарифма может стоять только положительное выражение
Под знаком логарифма может стоять только положительное выражение
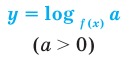
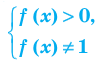 В основании логарифма может стоять только положительное выражение, не равное единице
В основании логарифма может стоять только положительное выражение, не равное единице
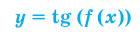
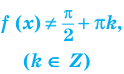 Под знаком тангенса может стоять только выражение, не равное
Под знаком тангенса может стоять только выражение, не равное 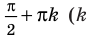 — целое)
— целое)
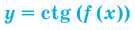
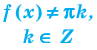 Под знаком котангенса может стоять только выражение, не равное
Под знаком котангенса может стоять только выражение, не равное 
 — целое)
— целое)

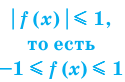 Под знаками арксинуса и арккосинуса может стоять только выражение, модуль которого меньше или равен единице
Под знаками арксинуса и арккосинуса может стоять только выражение, модуль которого меньше или равен единице

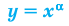
а) 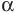 — натуральное
— натуральное  – любое число
– любое число
б)  — целое отрицательное или нуль
— целое отрицательное или нуль 
в) 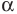 —нецелое положительное число
—нецелое положительное число 
г) 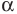 — нецелое отрицательное число
— нецелое отрицательное число 
Основные свойства числовых равенств и неравенств
Свойства числовых равенств:
1 Если 
2. Если  (транзитивность равенства)
(транзитивность равенства)
3. Если 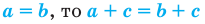
4. Если 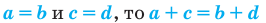
5. Если 
6. Если 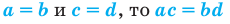
7. Если 
8. а) Если  то
то 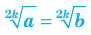
б) Если 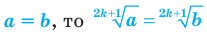
9. Если 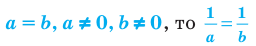
10. 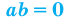 тогда и только тогда, когда
тогда и только тогда, когда 
11. 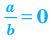 тогда и только тогда, когда
тогда и только тогда, когда 
Свойства числовых неравенств
1. Если 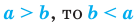
2. Если  (транзитивность неравенства)
(транзитивность неравенства)
3. Если 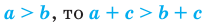
4. Если 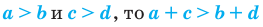
5. а) Если 
б) Если 
6. Если 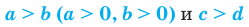
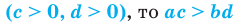
7. а) Если  то
то 
б) Если 
8. а) Если  то
то 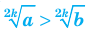
б) Если 
9. Если 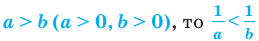
10.  тогда и только тогда, когда
тогда и только тогда, когда  или
или 
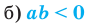 тогда и только тогда, когда
тогда и только тогда, когда  или
или 
11. а) 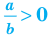 тогда и только тогда, когда
тогда и только тогда, когда  или
или 
б) 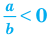 тогда и только тогда, когда
тогда и только тогда, когда  или
или 
Определение показательных уравнений и неравенств
Уравнение называется показательным, если его переменные входят только в показатели степеней.
Примеры:
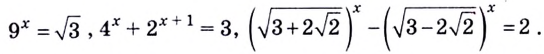
Существует много видов показательных уравнений и различных подходов к их решению. Основными методами решения показательных уравнений являются:
- Метод приведения обеих частей уравнения к степеням с одинаковыми основаниями.
- Метод введения новой переменной.
- Функционально-графический метод. Рассмотрим каждый из этих методов подробнее.
Метод приведения обеих частей уравнения к степеням с одинаковыми основаниями
Метод приведения обеих частей уравнения к степеням с одинаковыми основаниями применяется в двучленных уравнениях, которые можно свести к виду 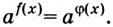 Такие уравнения решаются на основе монотонности показательной функции.
Такие уравнения решаются на основе монотонности показательной функции.
Если 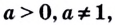 то уравнения
то уравнения 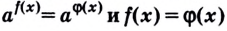 — равносильны.
— равносильны.
Пример №56
Решите уравнение: 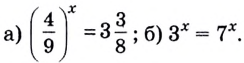
Решение:
а) Представим правую часть уравнения в виде неправильной дроби: 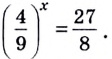
Запишем правую и левую части уравнения в виде степени с основанием 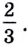 Получим:
Получим: 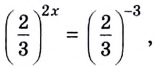 отсюда
отсюда 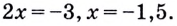
б) Поскольку 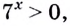 разделим обе части уравнения
разделим обе части уравнения 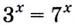 на
на  Получим
Получим 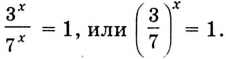 Запишем число 1 в виде степени с основанием
Запишем число 1 в виде степени с основанием 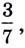 тогда
тогда 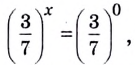 отсюда
отсюда 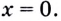
Существуют двучленные уравнения, члены которых вы пока не можете свести к степеням с одинаковыми основаниями. В общем виде их можно записать так: 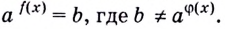
Если 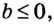 то уравнение решений не имеет, поскольку показательная функция принимает только положительные значения.
то уравнение решений не имеет, поскольку показательная функция принимает только положительные значения.
Если 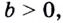 то уравнение имеет одно решение, поскольку прямая
то уравнение имеет одно решение, поскольку прямая 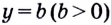 всегда пересекает график показательной функции. Как записать такое решение, например уравнения
всегда пересекает график показательной функции. Как записать такое решение, например уравнения 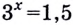 (рис. 26), вы узнаете позже.
(рис. 26), вы узнаете позже.
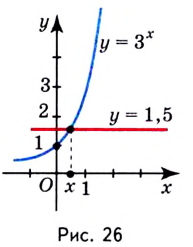
Методом введения новой переменной решаются многие виды уравнений
Рассмотрим решение некоторых из них на конкретных примерах.
Пример №57
Решите уравнение:
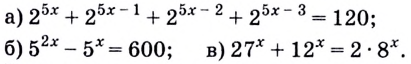
Решение:
В показателе каждой степени этого уравнения содержится одно и то же выражение  Обозначим наименьший показатель степени буквой
Обозначим наименьший показатель степени буквой  Тогда уравнение будет иметь вид:
Тогда уравнение будет иметь вид:
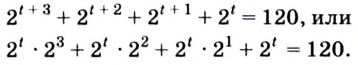
Вынесем общий множитель 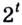 за скобки. Получим:
за скобки. Получим: 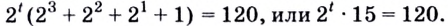 Отсюда
Отсюда 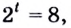 или
или 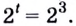 Следовательно,
Следовательно, 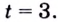 Поскольку
Поскольку 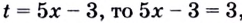 отсюда
отсюда 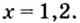
Решая такие уравнения, не обязательно вводить новую переменную, а можно сразу выносить общий множитель за скобки 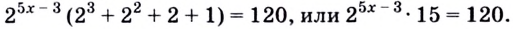 Отсюда
Отсюда 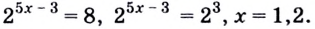
Именно поэтому этот способ называют способом вынесения общего множителя за скобки.
б) Пусть 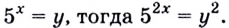 Подставим
Подставим 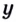 в данное уравнение. Имеем:
в данное уравнение. Имеем: 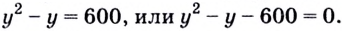 Корни последнего уравнения:
Корни последнего уравнения: 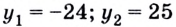 (проверьте).
(проверьте).
Поскольку 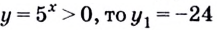 — посторонний корень. Если
— посторонний корень. Если 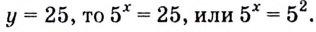
Следовательно, 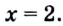
в) Запишем данное уравнение в виде 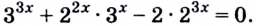
Разделим каждый член уравнения на 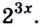 Получим:
Получим:
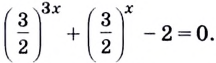 тогда
тогда 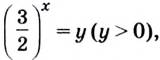 тогда
тогда 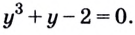
Поскольку 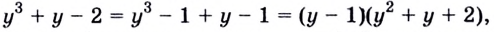 то уравнение
то уравнение 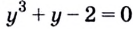 имеет один корень
имеет один корень 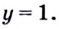 Следовательно,
Следовательно, 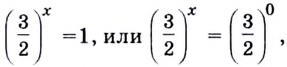 отсюда
отсюда 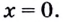
Функционально-графический метод
Функционально-графический метод состоит в следующем:
- с помощью построения графиков (или путём подбора) находят один корень уравнения;
- доказывают, что других корней уравнение не имеет.
Пример №58
Решите уравнение: 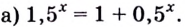
Решение:
Графически или методом проб убеждаемся, что 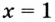 — корень уравнения. Поскольку
— корень уравнения. Поскольку 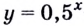 — возрастающая функция, так как
— возрастающая функция, так как 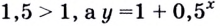 — убывающая
— убывающая 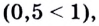 то других корней уравнение не имеет.
то других корней уравнение не имеет.
Если в показательном уравнении знак равенства изменить на знак неравенства, то получим показательное неравенство.
Неравенство называется показательным, если его переменные входят только в показатели степеней.
Для решения показательных неравенств используют те же методы, что и для решения показательных уравнений. А также правила решения простейших показательных неравенств, т.е. неравенств вида 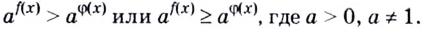
Решая простейшие показательные неравенства, используют монотонность (возрастание или убывание) показательной функции. А именно:
1. Если 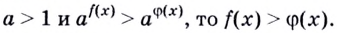
2. Если 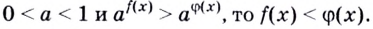
Пример №59
Решите неравенство:
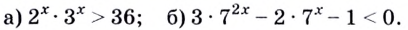
Решение:
а) Представим правую и левую части неравенства в виде степени с основанием 6:
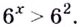
Поскольку 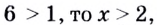 или
или 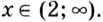
б) Пусть 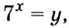 тогда
тогда 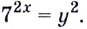 Подставим
Подставим 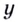 в данное неравенство. Получим:
в данное неравенство. Получим: 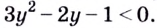 Поскольку квадратный трёхчлен
Поскольку квадратный трёхчлен 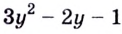 имеет корни
имеет корни 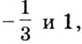 то множеством решений соответствующего неравенства будет:
то множеством решений соответствующего неравенства будет: 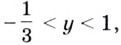 или
или 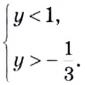
Поскольку 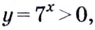 то условие
то условие 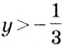 выполняется всегда. Если
выполняется всегда. Если 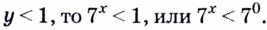 Следовательно,
Следовательно, 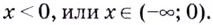 Показательные уравнения и неравенства — отдельный вид трансцендентных уравнений и неравенств. Вы уже знаете, что к трансцендентным относятся тригонометрические уравнения и неравенства. Трансцендентными считают также уравнения и неравенства, в которых сочетаются трансцендентные выражения с алгебраическими:
Показательные уравнения и неравенства — отдельный вид трансцендентных уравнений и неравенств. Вы уже знаете, что к трансцендентным относятся тригонометрические уравнения и неравенства. Трансцендентными считают также уравнения и неравенства, в которых сочетаются трансцендентные выражения с алгебраическими:
Только для некоторых из подобных уравнений можно указать точные решения. Их приближённые корни находят в основном графическим способом.
Уравнения вида 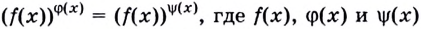 -функции переменной
-функции переменной 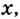 называются показательно-степенными.
называются показательно-степенными.
Их решают, проверяя, не будут ли решениями данного уравнения корни уравнений:
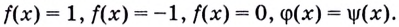
Полученные таким образом корни подлежат проверке.
Пример №60
Решите уравнение 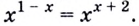
Решение:
1) Подставим 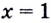 в данное уравнение. Имеем:
в данное уравнение. Имеем: 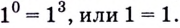 Следовательно,
Следовательно, 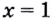 — корень данного уравнения.
— корень данного уравнения.
2) Если 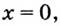 то имеем правильное равенство
то имеем правильное равенство 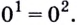 Следовательно,
Следовательно, 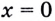 — корень данного уравнения.
— корень данного уравнения.
3) Если 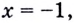 получим равенство
получим равенство 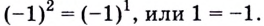 Равенство неправильное, следовательно,
Равенство неправильное, следовательно, 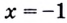 — посторонний корень.
— посторонний корень.
4) Решим уравнение 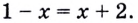
Его корень 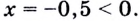 Это посторонний корень, так как
Это посторонний корень, так как 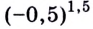 не существует.
не существует.
Ответ. 0; 1.
Пример №61
Решите уравнение 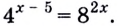
Решение:
Запишем правую и левую части как степени числа 2: 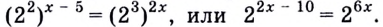 Отсюда
Отсюда 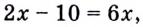
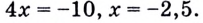
Пример №62
Решите неравенство 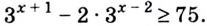
Решение:
Запишем неравенство в виде 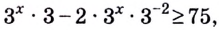 или
или 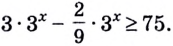 Вынесем
Вынесем 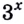 за скобки и упростим полученное неравенство
за скобки и упростим полученное неравенство 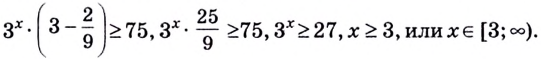
Пример №63
Решите уравнение 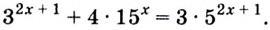
Решение:
Запишем уравнение в виде
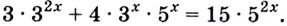
Разделим левую и правую части уравнения на 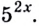 Имеем:
Имеем:
Если 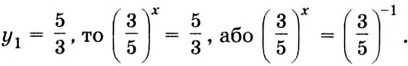 Следовательно,
Следовательно, 
Пример №64
Решите уравнение 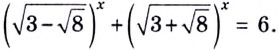
Решение:
Найдём произведение оснований степеней:
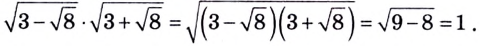
То есть 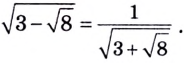
Обозначим 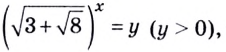 тогда
тогда 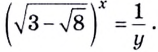
Перейдём к уравнению с переменной 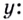
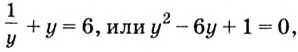 отсюда
отсюда 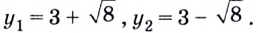
Получим:
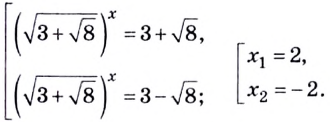
Пример №65
Решите графически неравенство 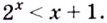
Решение:
Построим в одной системе координат графики функций 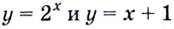 (рис. 27). Они пересекаются в точках
(рис. 27). Они пересекаются в точках 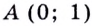 и
и 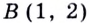 (проверьте подстановкой). Значения
(проверьте подстановкой). Значения 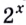 меньше соответствующих значений
меньше соответствующих значений 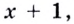 если
если 
Ответ. 
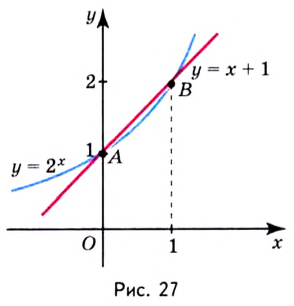
- Логарифмические уравнения и неравенства
- Степенная функция – определение и вычисление
- Степень с целым показателем
- Корень n-й степени
- Логарифмические выражения
- Показательная функция, её график и свойства
- Производные показательной и логарифмической функций
- Показательно-степенные уравнения и неравенства
