Как найти корни полинома в матлабе

Find All Roots of a Polynomial Function

Use vpasolve to find all the solutions to the function f(x)=6×7-2×6+3×3-8.

syms f(x)
f(x) = 6*x^7-2*x^6+3*x^3-8;
sol = vpasolve(f)

sol = 
(1.0240240759053702941448316563337-0.88080620051762149639205672298326+0.50434058840127584376331806592405 i-0.88080620051762149639205672298326-0.50434058840127584376331806592405 i-0.22974795226118163963098570610724+0.96774615576744031073999010695171 i-0.22974795226118163963098570610724-0.96774615576744031073999010695171 i0.7652087814927846556172932675903+0.83187331431049713218367239317121 i0.7652087814927846556172932675903-0.83187331431049713218367239317121 i)



  


                       
  

vpasolve returns seven roots of the function, as expected, because the function is a polynomial of degree seven.

Find Zeros of a Nonpolynomial Function Using Search Ranges and Starting Points

A plot of the function f(x)=e(x/7)cos(2x) reveals periodic zeros, with increasing slopes at the zero points as x increases.

syms x
h = fplot(exp(x/7)*cos(2*x),[-2 25]);
grid on

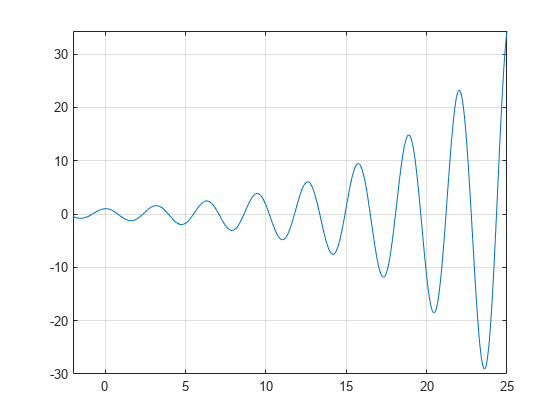
Use vpasolve to find a zero of the function f. Note that vpasolve returns only one solution of a nonpolynomial equation, even if multiple solutions exist. On repeated calls, vpasolve returns the same result.

f = exp(x/7)*cos(2*x);
for k = 1:3
  vpasolve(f,x)
end

ans = -7.0685834705770347865409476123789

ans = -7.0685834705770347865409476123789

ans = -7.0685834705770347865409476123789

To find multiple solutions, set the option 'Random' to true. This makes vpasolve choose starting points randomly. For information on the algorithm that chooses random starting points, see Algorithms on the vpasolve page.

for k = 1:3
  vpasolve(f,x,'Random',true)
end

ans = -226.98006922186256147892598444194

ans = 98.174770424681038701957605727484

ans = 52.621676947629036744249276669932

To find a zero close to x=10, set the starting point to 10.

ans = 10.210176124166828025003590995658

To find a zero close to x=1000, set the starting point to 1000.

ans = 999.8118620049516981407362567287

To find a zero in the range 15≤x≤25, set the search range to [15 25].

ans = 21.205750411731104359622842837137

To find multiple zeros in the range [15 25], you cannot call vpasolve repeatedly because it returns the same result on each call, as previously shown. Instead, set the search range and set 'Random' to true.

for k = 1:3
  vpasolve(f,x,[15 25],'Random',true)
end

ans = 21.205750411731104359622842837137

ans = 21.205750411731104359622842837137

ans = 16.493361431346414501928877762217

Because 'Random' selects starting points randomly, the same solution might be found on successive calls.

Find All Zeros in a Specified Search Range

Create a function findzeros to systematically find all zeros for f in a given search range, within a specified error tolerance. The function starts with the input search range and calls vpasolve to find a zero. Then, it splits the search range into two around the zero value and recursively calls itself with the new search ranges as inputs to find more zeros.

The function is explained section by section here.

Declare the function with the three inputs and one output. The first input is the function, the second input is the range, and the optional third input allows you to specify the error between a zero and the higher and lower bounds generated from it.

function sol = findzeros(f,range,err)

If you do not specify the optional argument for error tolerance, findzeros sets err to 0.001.

if nargin < 2
  err = 1e-3;
end

Find a zero in the search range using vpasolve.

If vpasolve does not find a zero, exit.

If vpasolve finds a zero, split the search range into two search ranges above and below the zero.

else
  lowLimit = sol-err;
  highLimit = sol+err;

Call findzeros with the lower search range. If findzeros returns zeros, copy the values into the solution array and sort them.

  temp = findzeros(f,[range(1) lowLimit],1);
  if ~isempty(temp)
    sol = sort([sol temp]);
  end

Call findzeros with the higher search range. If findzeros returns zeros, copy the values into the solution array and sort them.

  temp = findzeros(f,[highLimit range(2)],1);
  if ~isempty(temp)
    sol = sort([sol temp]);
  end
  return
end
end

The entire function findzeros is as follows. Save this function as findzeros.m in the current folder.

function sol = findzeros(f,range,err)
if nargin < 3
  err = 1e-3;
end
sol = vpasolve(f,range);
if(isempty(sol))
  return
else
  lowLimit = sol-err;
  highLimit = sol+err;
  temp = findzeros(f,[range(1) lowLimit],1);
  if ~isempty(temp)
    sol = sort([sol temp]);
  end
  temp = findzeros(f,[highLimit range(2)],1);
  if ~isempty(temp)
    sol = sort([sol temp]);
  end
  return
end
end

Call findzeros with search range [15 25] to find all zeros in that range for f(x) = exp(x/7)*cos(2*x), within the default error tolerance.

syms f(x)
f(x) = exp(x/7)*cos(2*x);
sol = findzeros(f,[15 25])'

sol = 
(16.49336143134641450192887776221718.06415775814131112116019945385719.63495408493620774039152114549721.20575041173110435962284283713722.77654673852600097885416452877624.347343065320897598085486220416)

Obtain Solutions to Arbitrary Precision

Use digits to set the precision of the solutions returned by vpasolve. By default, vpasolve returns solutions to a precision of 32 significant figures.

f = exp(x/7)*cos(2*x);
vpasolve(f)

ans = -7.0685834705770347865409476123789

Use digits to increase the precision to 64 significant figures. When modifying digits, ensure that you save its current value so that you can restore it.

digitsOld = digits;
digits(64)
vpasolve(f)

ans = -7.068583470577034786540947612378881489443631148593988097193625333

Next, change the precision of the solutions to 16 significant figures.

Solve Multivariate Equations Using Search Ranges

Consider the following system of equations.

z=10(cos(x)+cos(y))z=x+y2-0.1x2yx+y-2.7=0

A plot of the equations for 0≤x≤2.5 and 0≤x≤2.5 shows that the three surfaces intersect in two points. To better visualize the plot, use view. To scale the colormap values, use caxis.

syms x y z
eqn1 = z == 10*(cos(x) + cos(y));
eqn2 = z == x+y^2-0.1*x^2*y;
eqn3 = x+y-2.7 == 0;
equations = [eqn1 eqn2 eqn3];
fimplicit3(equations)
axis([0 2.5 0 2.5 -20 10])
title('System of Multivariate Equations')
view(69, 28)
caxis([-15 10])

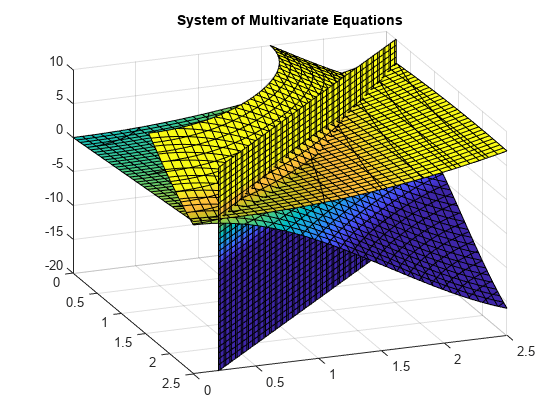
Use vpasolve to find a point where the surfaces intersect. The function vpasolve returns a structure. To access the x-, y-, and z-values of the solution, index into the structure.

sol = vpasolve(equations);
[sol.x sol.y sol.z]

ans = (2.3697477224547980.33025227754520212.293354376823228)

To search a region of the solution space, specify search ranges for the variables. If you specify the ranges 0≤x≤1.5 and 1.5≤y≤2.5, then vpasolve function searches the bounded area shown.

Use vpasolve to find a solution for this search range. To omit a search range for z, set the third search range to [NaN NaN].

vars = [x y z];
range = [0 1.5; 1.5 2.5; NaN NaN];
sol = vpasolve(equations, vars, range);
[sol.x sol.y sol.z]

ans = (0.91062661725633361.7893733827436663.964101572135625)

To find multiple solutions, set the 'Random' option to true. This makes vpasolve use random starting points on successive runs. The 'Random' option can be used in conjunction with search ranges to make vpasolve use random starting points within a search range. Because 'Random' selects starting points randomly, the same solution might be found on successive calls. Call vpasolve repeatedly to ensure you find both solutions.

clear sol
range = [0 3; 0 3; NaN NaN];
for k = 1:5
  temp = vpasolve(equations,vars,range,'Random',true);
  sol(k,1) = temp.x;
  sol(k,2) = temp.y;
  sol(k,3) = temp.z;
end
sol

sol = 
(2.3697477224547980.33025227754520212.2933543768232282.3697477224547980.33025227754520212.2933543768232282.3697477224547980.3302522775452022.2933543768232280.91062661725633361.7893733827436663.9641015721356250.91062661725633361.7893733827436663.964101572135625)

Plot the equations. Superimpose the solutions as a scatter plot of points with yellow X markers using scatter3. To better visualize the plot, make two of the surfaces transparent using alpha. Scale the colormap to the plot values using caxis, and change the perspective using view.

vpasolve finds solutions at the intersection of the surfaces formed by the equations as shown.

clf
ax = axes;
h = fimplicit3(equations);
h(2).FaceAlpha = 0;
h(3).FaceAlpha = 0;
axis([0 2.5 0 2.5 -20 10])
hold on
scatter3(sol(:,1),sol(:,2),sol(:,3),600,'yellow','X','LineWidth',2)
title('Randomly Found Solutions in Specified Search Range')
cz = ax.Children;
caxis([0 20])
view(69,28)
hold off

Lastly, restore the old value of digits for further calculations.