В этой статье и постараюсь объяснить 2 способа отбора корней в тригонометрическом уравнение: с помощью неравенств и с помощью тригонометрической окружности. Перейдем сразу к наглядному примеру и походу дела будем разбираться.
а) Решить уравнение sqrt(2)cos^2x=sin(Pi/2+x)
б) Найдите все корни этого уравнения, принадлежащие промежутку [-7Pi/2; -2Pi]
Решим пункт а.
Воспользуемся формулой приведения для синуса sin(Pi/2+x) = cos(x)
sqrt(2)cos^2x = cosx
sqrt(2)cos^2x – cosx = 0
cosx(sqrt(2)cosx – 1) = 0
cosx = 0
x1 = Pi/2 + Pin, n ∈ Z
sqrt(2)cosx – 1 = 0
cosx = 1/sqrt(2)
cosx = sqrt(2)/2
x2 = arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x3 = -arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x2 = Pi/4 + 2Pin, n ∈ Z
x3 = -Pi/4 + 2Pin, n ∈ Z
Решим пункт б.
1) Отбор корней с помощью неравенств
Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [-7Pi/2; -2Pi], находим целые значения для n.
-7Pi/2 меньше или равно Pi/2 + Pin меньше или равно -2Pi
Сразу делим все на Pi
-7/2 меньше или равно 1/2 + n меньше или равно -2
-7/2 – 1/2 меньше или равно n меньше или равно -2 – 1/2
-4 меньше или равно n меньше или равно -5/2
Целые n в этом промежутку это -4 и -3. Значит корни принадлежащие этому промежутку буду Pi/2 + Pi(-4) = -7Pi/2, Pi/2 + Pi(-3) = -5Pi/2
Аналогично делаем еще два неравенства
-7Pi/2 меньше или равно Pi/4 + 2Pin меньше или равно -2Pi
-15/8 меньше или равно n меньше или равно -9/8
Целых n в этом промежутке нет
-7Pi/2 меньше или равно -Pi/4 + 2Pin меньше или равно -2Pi
-13/8 меньше или равно n меньше или равно -7/8
Одно целое n в этом промежутку это -1. Значит отобранный корень на этом промежутку -Pi/4 + 2Pi*(-1) = -9Pi/4.
Значит ответ в пункте б: -7Pi/2, -5Pi/2, -9Pi/4
2) Отбор корней с помощью тригонометрической окружности
Чтобы пользоваться этим способом надо понимать как работает эта окружность. Постараюсь простым языком объяснить как это понимаю я. Думаю в школах на уроках алгебры эта тема объяснялась много раз умными словами учителя, в учебниках сложные формулировки. Лично я понимаю это как окружность, которую можно обходить бесконечное число раз, объясняется это тем, что функции синус и косинус периодичны.
Обойдем раз против часовой стрелки
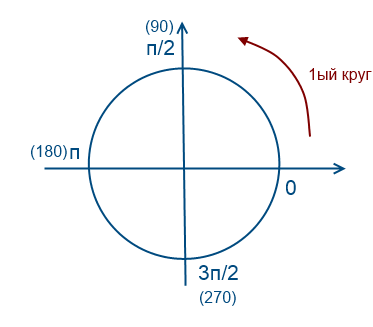
Обойдем 2 раза против часовой стрелки
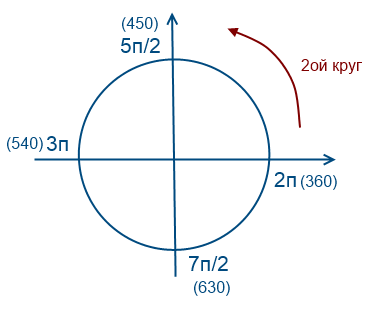
Обойдем 1 раз по часовой стрелки (значения будут отрицательные)
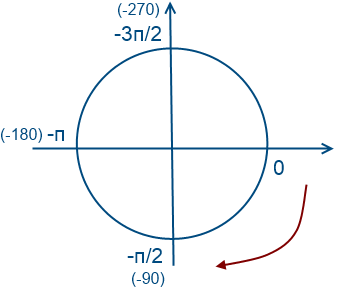
Вернемся к нашем вопросу, нам надо отобрать корни на промежутке [-7Pi/2; -2Pi]
Чтобы попасть к числам -7Pi/2 и -2Pi надо обойти окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.
Рассмотри x = Pi/2 + Pin. Какой приблизительно должен быть n, чтобы значение x было где-то в этом промежутке? Подставляем, допустим -2, получаем Pi/2 – 2Pi = -3Pi/2, очевидно это не входит в наш промежуток, значит берем меньше -3, Pi/2 – 3Pi = -5Pi/2, это подходит, попробуем еще -4, Pi/2 – 4Pi = -7Pi/2, также подходит.
Рассуждая аналогично для Pi/4 + 2Pin и -Pi/4 + 2Pin, находим еще один корень -9Pi/4.
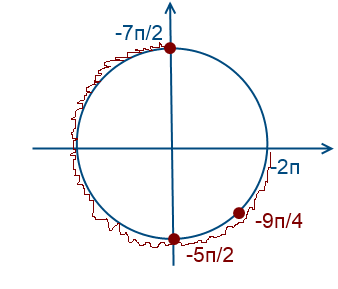
Сравнение двух методов.
Первый способ (с помощью неравенств) гораздо надежнее и намного проще для пониманию, но если действительно серьезно разобраться с тригонометрической окружностью и со вторым методом отбора, то отбор корней будет гораздо быстрее, можно сэкономить около 15 минут на экзамене.
Просмотры: 157052 |
Статью добавил: slava191 |
Категория: математика
Отбор корней в тригонометрическом уравнение
В этой статье и постараюсь объяснить 2 способа отбора корней в тригонометрическом уравнение: с помощью неравенств и с помощью тригонометрической окружности. Перейдем сразу к наглядному примеру и походу дела будем разбираться.
а) Решить уравнение sqrt(2)cos^2x=sin(Pi/2+x)
б) Найдите все корни этого уравнения, принадлежащие промежутку [-7Pi/2; -2Pi]
Решим пункт а.
Воспользуемся формулой приведения для синуса sin(Pi/2+x) = cos(x)
sqrt(2)cos^2x – cosx = 0
cosx(sqrt(2)cosx – 1) = 0
x1 = Pi/2 + Pin, n ∈ Z
sqrt(2)cosx – 1 = 0
x2 = arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x3 = -arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x2 = Pi/4 + 2Pin, n ∈ Z
x3 = -Pi/4 + 2Pin, n ∈ Z
Решим пункт б.
1) Отбор корней с помощью неравенств
Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [-7Pi/2; -2Pi], находим целые значения для n.
-7Pi/2 меньше или равно Pi/2 + Pin меньше или равно -2Pi
Сразу делим все на Pi
-7/2 меньше или равно 1/2 + n меньше или равно -2
-7/2 – 1/2 меньше или равно n меньше или равно -2 – 1/2
-4 меньше или равно n меньше или равно -5/2
Целые n в этом промежутку это -4 и -3. Значит корни принадлежащие этому промежутку буду Pi/2 + Pi(-4) = -7Pi/2, Pi/2 + Pi(-3) = -5Pi/2
Аналогично делаем еще два неравенства
-7Pi/2 меньше или равно Pi/4 + 2Pin меньше или равно -2Pi
-15/8 меньше или равно n меньше или равно -9/8
Целых n в этом промежутке нет
-7Pi/2 меньше или равно -Pi/4 + 2Pin меньше или равно -2Pi
-13/8 меньше или равно n меньше или равно -7/8
Одно целое n в этом промежутку это -1. Значит отобранный корень на этом промежутку -Pi/4 + 2Pi*(-1) = -9Pi/4.
Значит ответ в пункте б: -7Pi/2, -5Pi/2, -9Pi/4
2) Отбор корней с помощью тригонометрической окружности
Чтобы пользоваться этим способом надо понимать как работает эта окружность. Постараюсь простым языком объяснить как это понимаю я. Думаю в школах на уроках алгебры эта тема объяснялась много раз умными словами учителя, в учебниках сложные формулировки. Лично я понимаю это как окружность, которую можно обходить бесконечное число раз, объясняется это тем, что функции синус и косинус периодичны.
Обойдем раз против часовой стрелки
Обойдем 2 раза против часовой стрелки
Обойдем 1 раз по часовой стрелки (значения будут отрицательные)
Вернемся к нашем вопросу, нам надо отобрать корни на промежутке [-7Pi/2; -2Pi]
Чтобы попасть к числам -7Pi/2 и -2Pi надо обойти окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.
Рассмотри x = Pi/2 + Pin. Какой приблизительно должен быть n, чтобы значение x было где-то в этом промежутке? Подставляем, допустим -2, получаем Pi/2 – 2Pi = -3Pi/2, очевидно это не входит в наш промежуток, значит берем меньше -3, Pi/2 – 3Pi = -5Pi/2, это подходит, попробуем еще -4, Pi/2 – 4Pi = -7Pi/2, также подходит.
Рассуждая аналогично для Pi/4 + 2Pin и -Pi/4 + 2Pin, находим еще один корень -9Pi/4.
Сравнение двух методов.
Первый способ (с помощью неравенств) гораздо надежнее и намного проще для пониманию, но если действительно серьезно разобраться с тригонометрической окружностью и со вторым методом отбора, то отбор корней будет гораздо быстрее, можно сэкономить около 15 минут на экзамене.
Способы отбора корней в тригонометрических уравнениях
Класс: 10
Автор проекта:
Шелкова Полина,
Класс: 10
Руководитель:
Злобова Людмила Викторовна,
учитель математики
ВВЕДЕНИЕ
Слово «тригонометрия» греческое, оно переводится как «измерение треугольников» (τρίγονον – «тригон» – треугольник и μετρειν – «метрео» – измеряю).
Тригонометрия, как и всякая другая наука, выросла из практической деятельности человека. Потребности развивающегося мореплавания, для которого требовалось умение правильно определять курс корабля в открытом море по положению небесных светил, оказали большое влияние на развитие астрономии и тесно связанной с ней тригонометрией. Предполагают, что основополагающее значение для развития тригонометрии в эпоху ее зарождения, имели работы древнегреческого астронома Гиппарха Никейского (180-125 лет до н. э.) (прил. №3). Систематическое использование полной окружности в 360° установилось в основном благодаря Гиппарху и его таблице хорд (прил. №2). Т.е. таблицы, которые выражают длину хорды для различных центральных углов в круге постоянного радиуса, что является аналогом современных таблиц тригонометрических функций. Впрочем, до нас не дошли оригинальные таблицы Гиппарха, как и почти все, что им написано. И мы, можем составить себе о них представление главным образом по сочинению «Великое построение» или «Альмагесту» знаменитого астронома Клавдия Птолемея, жившего в середине II века н.э.
Несмотря на то, что в работах ученых древности нет «тригонометрии» в строгом смысле этого слова, но по существу они, пользуясь известными им средствами элементарной геометрии, решали те задачи, которыми занимается тригонометрия. Например, задачи на решение треугольников (определение всех сторон и углов треугольника по трем его известным элементам), теоремы Евклида и Архимеда представленные в геометрическом виде, эквивалентны специфическим тригонометрическим формулам. Главным достижением средневековой Индии стала замена хорд синусами. Это позволило вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии, как учению о тригонометрических величинах.
Учёные стран Ближнего и Среднего Востока с VIII века развили тригонометрию своих предшественников. Уже в середине IX века среднеазиатский учёный аль-Хорезми написал сочинение «Об индийском счёте». После того, как трактаты мусульманских ученых были переведены на латынь, многие идеи греческих, индийских и мусульманских математиков стали достоянием европейской, а затем и мировой науки. В дальнейшем потребности географии, геодезии, военного дела, способствовали развитию тригонометрии. Особенно усиленно шло ее развитие в средневековое время. Большая заслуга в формировании тригонометрии как отдельной науки принадлежит азербайджанскому ученому Насир ад-Дину ат-Туси (1201-1274), написавшему «Трактат о полном четырехстороннике». Творения ученых этого периода привели к выделению тригонометрии как нового самостоятельного раздела науки. Однако в их трудах еще не была введена необходимая символика. Современный вид тригонометрия получила в трудах Леонарда Эйлера (1707-1783). На основании трудов Эйлера были составлены учебники тригонометрии, излагавшие ее в строгой научной последовательности (прил. №4). Тригонометрические вычисления применяются во многих областях человеческой деятельности: в геометрии, в физике, в астрономии, в архитектуре, в геодезии, инженерном деле, в акустике, в электронике и т.д.
I РАЗДЕЛ (теоретический)
Тема проекта и её актуальность: почему я выбрала тему «Способы отбора корней в тригонометрических уравнениях»?
- Расширить и углубить свои знания, полученные в курсе геометрии 8-9 класса.
- Тригонометрические уравнения рассматриваются в курсе алгебры и начал математического анализа 10-11 класса.
- Тригонометрические уравнения включены в КИМы ЕГЭ по математике.
Решение тригонометрических уравнений и отбор корней, принадлежащих заданному промежутку – это одна из сложнейших тем математики, которая выносится на Единый Государственный Экзамен. По результатам анкетирования многие учащиеся затрудняются или вообще не умеют решать тригонометрические уравнения и особенно затрудняются в отборе корней, принадлежащих промежутку. Немаловажно также знать, тригонометрические формулы, табличные значения тригонометрических функций для решения целого ряда заданий Единого Государственного Экзамена по математике.
Цель проекта: изучить способы отбора корней в тригонометрических уравнениях и выбрать для себя наиболее рациональные подходы для качественной подготовки к ЕГЭ.
Задачи:
- познакомиться с историческими сведениями о возникновении тригонометрии, как науки;
- изучить соответствующую литературу;
- научиться решать тригонометрические уравнения;
- найти теоретический материал и изучить методы отбора корней в тригонометрических уравнениях;
- научиться отбирать корни в тригонометрических уравнениях, принадлежащим заданному промежутку;
- подготовиться к ЕГЭ по математике.
Приёмы отбора корней тригонометрического уравнения на заданном промежутке.
При решении тригонометрических уравнений предлагается провести отбор корней из множества значений неизвестного. В тригонометрическом уравнении отбор корней можно осуществлять следующими способами: арифметическим, алгебраическим, геометрическим и функционально-графическим.
Арифметический способ отбора корней состоит в непосредственной подстановке полученных корней в уравнение, учитывая имеющиеся ограничения, при переборе значений целочисленного параметра.
Алгебраический способ предполагает составление неравенств, соответствующих дополнительным условиям, и их решение относительно целочисленного параметра.
Геометрический способ предполагает использование при отборе корней двух вариантов: тригонометрической окружности или числовой прямой. Тригонометрическая окружность более удобна, когда речь идет об отборе корней на промежутке или в случае, когда значение обратных тригонометрических функций, входящих в решения, не являются табличными. В остальных случаях предпочтительнее модель числовой прямой. Числовую прямую удобно использовать при отборе корней на промежутке, длина которого не превосходит 2 или требуется найти наибольший отрицательный или наименьший положительный корень уравнения.
Функционально-графический способ предполагает отбор корней осуществлять с использование графиков тригонометрических функций. Чтобы использовать данный способ отбора корней, требуется умение схематичного построения графиков тригонометрических функций.
II РАЗДЕЛ (практический)
Покажу практически три наиболее эффективных и рациональных, с моей точки зрения, метода отбора корней на примере решения следующего тригонометрического уравнения:
sinx−cos2x=0; [применили формулу двойного угла: cos2x = cos 2 x−sin 2 x]
sinx−(cos 2 x−sin 2 x)=0;
sinx−(1−sin 2 x−sin 2 x)=0;
Введем новую переменную: sinx = t, -1 ≤ t ≤1, получим
Вернемся к замене:

б) Рассмотрим три способа отбора корней, попадающих в отрезок  .
.
1 способ: обратимся к единичной окружности. Отметим на ней дугу, соответствующую указанному отрезку, т.е. выполним отбор корней арифметическим способом и с помощью тригонометрической окружности:


2 способ: указанный отрезок соответствует неравенству: Подставим в него полученные корни: 

3 способ: разместим корни уравнения на числовой прямой. Сначала отметим корни, подставив вместо n, и нуль (0), а потом добавим к каждому корню периоды.

Нам останется только выбрать корни, которые попали в нужный нам отрезок.

ЗАКЛЮЧЕНИЕ
При работе над моим проектом я изучила методы решения тригонометрических уравнений и способы отбора корней тригонометрических уравнений. Выяснила для себя положительные и отрицательные моменты. При апробации этих подходов в отборе корней тригонометрического уравнения, понимаешь, что каждый из этих способов удобен по-своему в том или ином случае. Например, алгебраический способ (решение неравенством) наиболее эффективен, когда промежуток для отбора корней достаточно большой, в тоже время он дает практически стопроцентное нахождение целочисленного параметра для вычисления корней, а применение арифметического способа приводит к громоздким вычислениям. При отборе корней уравнения, удовлетворяющих дополнительным условиям, т.е. когда корни уравнения принадлежат заданному промежутку, мне проще и нагляднее получить корни с помощью тригонометрической окружности, а проверить себя можно арифметическим способом. Замечу, что при решении тригонометрических уравнений трудности, связанные с отбором корней, возрастают, если в уравнении приходится учитывать ОДЗ. Как показывает практика и анкетирование моих одноклассников, из четырёх возможных методов отбора корней тригонометрического уравнения по дополнительным условиям, наиболее предпочтительным является отбор корней по окружности. Анкетирование проходили 12 респондентов, изучающих тригонометрию (прил. №5). Большинство из них отвечали, что этот раздел математики достаточно сложный: большой объем информации, очень много формул, табличных значений, которые нужно знать и уметь применять на практике. Еще как одна из проблем – небольшое количество времени, отведенное на изучение этого сложного раздела математики. И я разделяю их мнение. При такой сложности, многие считают, что тригонометрия важный раздел математики, который находит применение в других науках и практической деятельности человека.
СПИСОК ЛИТЕРАТУРЫ
- Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс: учеб для общеобразоват. организаций: базовый и углубленный уровни/ [С.М.Никольский, М.К.Потапов, Н.Н.Решетников и др.]-3 -е изд.- М.: Просвещение, 2016.
- Алгебра и начала математического анализа: Учеб для 10-11 кл.общеобразоват. организаций / А.Н.Колмогоров, А.М.Абрамов, Ю.П.Дудницин и др. под редакцией А.Н.Колмогорова – М. Просвещение, 2017.
- С.В Кравцев и др. Методы решения задач по алгебре: от простых до самых сложных – М: Издательство: «Экзамен», 2005.
- Корянов А.Г., Прокофьев А.А. – Тригонометрические уравнения: методы решения и отбор корней. – М.: Математика ЕГЭ, 2012.
Тригонометрические уравнения
Решение простейших тригонометрических уравнений
Градусы и радианы
Знакомство с тригонометрической окружностью
Повороты на тригонометрической окружности
Как много боли связано со словом тригонометрия. Эта тема появляется в 9 классе и уже никуда не исчезает. Тяжело приходится тем, кто чего-то не понял сразу. Попробуем это исправить, чтобы осветить ваше лицо улыбкой при слове тригонометрия или хотя бы добиться «poker face».
Начнем с того, что как длину можно выразить в метрах или милях, так и угол можно выразить в радианах или градусах .
1 радиан = 180/π ≈ 57,3 градусов
Но проще запомнить целые числа: 3,14 радиан = 180 градусов. Это все одно и то же значение числа π.
Вспомним, что если нас просят развернуться, то нам нужно повернуться на 180 градусов, а теперь можно так же сказать: Повернись на π!
О графиках синуса, косинуса и тангеса поговорим в другой статье.
А сейчас начем с декартовой (прямоугольной) системы координат.
Раньше она помогала строить графики, а теперь поможет с синусом и косинусом.
На пересечении оси Х и оси Y построим единичную (радиус равен 1) окружность:
Тогда ось косинусов будет совпадать с х, ось синусов с y. Оси тангенсов и котангенсов также показаны на рисунке.
А теперь отметим основные значения градусов и радиан на окружности.
Давай договоримся с тобой, как взрослые люди: на окружности мы будем отмечать угол в радианах, то есть через Пи.
Достаточно запомнить, что π = 180° (тогда π/6 = 180/6 = 30°; π/3 = 180/3 = 60°; π/4 = 180/4 = 45°).
А теперь давай покрутимся на окружности! За начало отчета принято брать крайнюю правую точку окружности (где 0°):
От нее задаем дальнейший поворот. Вращаться можем как в положительную сторону (против часовой), так и в отрицательную сторону (по часовой стрелке).
Повернуться на 45° можно двумя спобами: через левое плечо на 45° в (+) сторону, либо через правое плечо на 315° в (-).
Главное — направление, куда мы будем смотреть, а не угол!
Нужно направить пунктир на 100 баллов, а сколько оборотов и в какую сторону вокруг себя мы сделаем — без разницы!
Получить 100 баллов можно поворотом на 135° или 360°+135°, или -225°, или -225°-360°.
А теперь у тебя есть два пути:
Выучить всю окружность (тригонометр). Неплохой вариант, если с памятью у тебя все отлично, и ничего не вылетит из головы в ответственный момент:
А можно запомнить несколько табличных углов и соответствующие им значения, а потом использовать их.
Находите равные углы (вертикальные, соответственные) на тригонометрической окружности. Попасть в любую точку можно с помощью суммы или разности двух табличных значений.
Сразу попробуем разобрать на примере:
1) Помним, что ось cos(x) — это горизонтальная ось. На ней отмечаем значение ½ и проводим перпендикулярную (фиолетовую) прямую до пересечений с окружностью.
2) Получили две точки пересечения с окружностью, значение этих углов и будет решением уравнения.
Дело за малым — найти эти углы.
Лучше обойтись «малой кровью» и выучить значение синуса и косинуса для углов от 30° до 60°.
Или запомнить такой прием:
Пронумеруй пальцы от 0 до 4 от мизинца до большого. Угол задается между мизинцем и любым другим пальцем (от 0 до 90).
Например, требуется найти sin(π/2) : π/2 — это большой палец, n = 4 подставляем в формулу для синуса: sin(π/2) = √4/2 = 1 => sin(π/2) = 1.
cos(π/4) – ? π/4 соответсвует среднему пальцу (n = 2) => cos(π/4) = √2/2.
При значении cos(x) = ½ из таблицы или с помощью мнемонического правила находим x = 60° (первая точка x = +π/3 из-за того, что поворот происходил против часовой стерелки (+), угол показан черной дугой).
Вторая же точка соответствует точно такому же углу, только поворот будет по часовой стрелке (−). x = −π/3 (угол показан нижней черной дугой).
И последнее, прежде чем тебе, наконец, откроются тайные знания тригонометрии:
Когда требуется попасть в «100 баллов», мы можем в них попасть с помощью поворота на . =-225°=135°=495°=.
То же самое и здесь! Разные углы могут отражать одно и то же направление.
Абсолютно точно можно сказать, что нужно повернуться на требуемый угол, а дальше можно поворачиваться на 360° = 2π (синим цветом) сколько угодно раз и в любом направлении.
Таким образом, попасть в первое направление 60° можно: . 60°-360°, 60°, 60°+360°.
И как записать остальные углы, не записывать же бесконечное количество точек? (Хотел бы я на это посмотреть☻)
Поэтому правильно записать ответ: x = 60 + 360n, где n — целое число (n∈Ζ) (поворачиваемся на 60 градусов, а после кружимся сколько угодно раз, главное, чтобы направление осталось тем же). Аналогично x = −60 + 360n.
Но мы же договорились, что на окружности все записывают через π, поэтому cos(x) = ½ при x = π/3 + 2πn, n∈Ζ и x = −π/3 + 2πk, k∈Ζ.
Ответ: x = π/3 + 2πn, x= − π/3 + 2πk, (n, k) ∈Ζ.
Пример №2. 2sinx = √2
Первое, что следует сделать, это перенести 2-ку вправо => sinx=√2/2
1) sin(x) совпадает с осью Y. На оси sin(x) отмечаем √2/2 и проводим ⊥ фиолетовую прямую до пересечений с окружностью.
2) Из таблицы sinx = √2/2 при х = π/4, а вторую точку будем искать с помощью поворота до π, а затем нужно вернуться обратно на π/4.
Поэтому вторая точка будет x = π − π/4 = 3π/4, в нее также можно попасть и с помощью красных стрелочек или как-то по-другому.
И еще не забудем добавить +2πn, n∈Ζ.
Ответ: 3π/4 + 2πn и π/4 + 2πk, k и n − любые целые числа.
Пример №3. tg(x + π/4) = √3
Вроде все верно, тангенс равняется числу, но смущает π/4 в тангенсе. Тогда сделаем замену: y = x + π/4.
tg(y) = √3 выглядит уже не так страшно. Вспомним, где ось тангенсов.
1) А теперь на оси тангенсов отметим значение √3, это выше чем 1.
2) Проведем фиолетовую прямую через значение √3 и начало координат. Опять на пересечении с окружностью получается 2 точки.
По мнемоническому правилу при тангенсе √3 первое значение — это π/3.
3) Чтобы попасть во вторую точку, можно к первой точке (π/3) прибавить π => y = π/3 + π = 4π/3.
4) Но мы нашли только y , вернемся к х. y = π/3 + 2πn и y = x + π/4, тогда x + π/4 = π/3 + 2πn => x = π/12 + 2πn, n∈Ζ.
Второй корень: y = 4π/3 + 2πk и y = x + π/4, тогда x + π/4 = 4π/3 + 2πk => x = 13π/12 + 2πk, k∈Ζ.
Теперь корни на окружности будут здесь:
Ответ: π/12 + 2πn и 13π/12 + 2πk, k и n — любые целые числа.
Конечно, эти два ответа можно объединить в один. От 0 поворот на π/12, а дальше каждый корень будет повторяться через каждый π (180°).
Ответ можно записать и так: π/12 + πn, n∈Ζ.
Пример №4: −10ctg(x) = 10
Перенесем (−10) в другую часть: ctg(x) = −1. Отметим значение -1 на оси котангенсов.
1) Проведем прямую через эту точку и начало координат.
2) Придется опять вспомнить, когда деление косинуса на синус даст еденицу (это получается при π/4). Но здесь −1, поэтому одна точка будет −π/4. А вторую найдем поворотом до π, а потом назад на π/4 (π − π/4).
Можно это сделать по-другому (красным цветом), но мой вам совет: всегда отсчитывайте от целых значений пи (π, 2π, 3π. ) так намного меньше шансов запутаться.
Не забываем добавить к каждой точке 2πk.
Ответ: 3π/4 + 2πn и −π/4 + 2πk, k и n — любые целые числа.
Алгоритм решения тригонометрических уравнений (на примере cos(x) = − √ 3/2) :
- Отмечаем значение (−√3/2) на оси тригонометрической функции (косинусов, это ось Х).
- Проводим перпендикулярную прямую оси (косинусов) до пересечений с окружностью.
- Точки пересечения с окружностью и будут являться корнями уравнения.
- Значение одной точки (без разницы, как в нее попадете) +2πk.
Азов достаточно, прежде чем идти дальше закрепите полученные знания.
[spoiler title=”источники:”]
http://urok.1sept.ru/articles/687140
http://ik-study.ru/ege_math/trighonomietrichieskiie_uravnieniia
[/spoiler]
Отбор корней с помощью тригонометрического круга
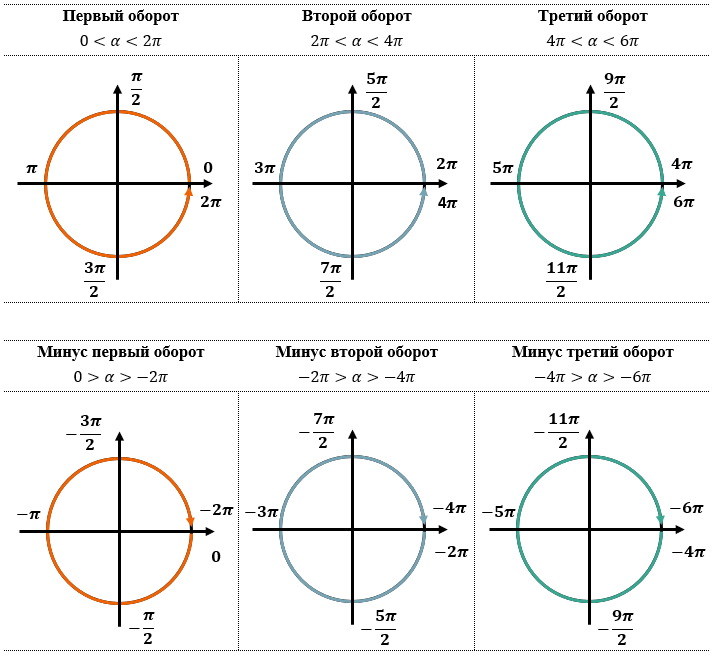
В заданиях, где требуется отобрать корни тригонометрического уравнения, принадлежащие определенному числовому промежутку, можно использовать тригокруг. Этот метод отбора корней является наиболее распространенным. Его плюсы заключаются в том, что это визуальный метод, т. е. отбор корней происходит наглядно, но у этого есть и свои недостатки – углов бесконечное множество, из которых только 360° можно визуализировать на тригокруге, поэтому может возникнуть путаница с количеством оборотов по нему.
«ОБОРОТЫ» ПО ТРИГОКРУГУ И СООТВЕТВЕТСТВУЮЩИЕ ИМ УГЛЫ:
АЛГОРИТМ ОТБОРА КОРНЕЙ С ПОМОЩЬЮ ТРИГОКРУГА
-
Отмечаем получившийся угол на тригокруге. Это будет серия ответов – бесконечное количество углов, визуально находящееся на тригокруге в одной точке.
-
Отмечаем нужную дугу, т. е. обозначаем указанный промежуток, в котором нужно отобрать корни.
-
Определяем корни, попадающие в эту дугу.
-
Находим искомые углы учитывая обороты – прибавляем соответствующее количество периодов к отмеченному на окружности углу.
Пример:
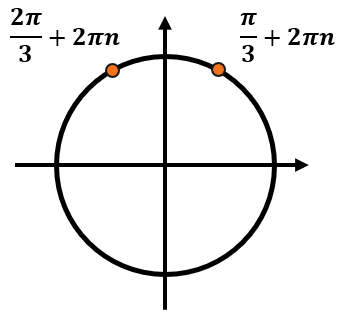
Даны корни уравнения:
(x_{1} = frac{pi}{3} + 2pi n, nmathbb{in Z})
(x_{2} = frac{2pi}{3} + 2pi n, nmathbb{in Z})
Найдите корни, принадлежащие отрезку (leftlbrack – pi, frac{3pi}{2} rightrbrack).
-
Каждый из этих корней включает в себя бесконечное количество углов. Отметим эти серии ответов на тригокруге:
-
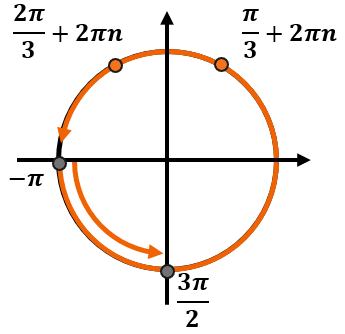
При этом мы знаем, что нужные корни должны находиться на промежутке (leftlbrack – pi, frac{3pi}{2} rightrbrack). Этот промежуток занимает больше, чем один оборот. Обозначим его так:
-
Так как промежуток занимает больше одного круга, каждая серия ответов так или иначе попадет в этот него.
-
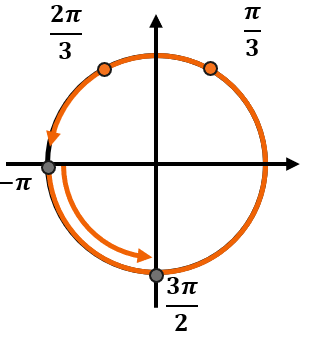
Теперь определим, на каком обороте серии ответов попадут именно в этот промежуток. Если мы будем идти по тригокругу от (- pi) до (frac{3pi}{2}), то попадем в точки с сериями ответов по одному разу – в первом обороте после нуля. Тогда получим следующие углы:
Запишем ответ.
Ответ: (frac{pi}{3});( frac{2pi}{3}).
Важно! Чтобы решение было обоснованным, очень важно отметить всё на круге: и точки, и углы, и промежуток.
Автор проекта:
Шелкова Полина,
Класс: 10Руководитель:
Злобова Людмила Викторовна,
учитель математики
ВВЕДЕНИЕ
Слово «тригонометрия» греческое, оно переводится как «измерение треугольников» (τρίγονον – «тригон» – треугольник и μετρειν – «метрео» – измеряю).
Тригонометрия, как и всякая другая наука, выросла из практической деятельности человека. Потребности развивающегося мореплавания, для которого требовалось умение правильно определять курс корабля в открытом море по положению небесных светил, оказали большое влияние на развитие астрономии и тесно связанной с ней тригонометрией. Предполагают, что основополагающее значение для развития тригонометрии в эпоху ее зарождения, имели работы древнегреческого астронома Гиппарха Никейского (180-125 лет до н. э.) (прил. №3). Систематическое использование полной окружности в 360° установилось в основном благодаря Гиппарху и его таблице хорд (прил. №2). Т.е. таблицы, которые выражают длину хорды для различных центральных углов в круге постоянного радиуса, что является аналогом современных таблиц тригонометрических функций. Впрочем, до нас не дошли оригинальные таблицы Гиппарха, как и почти все, что им написано. И мы, можем составить себе о них представление главным образом по сочинению «Великое построение» или «Альмагесту» знаменитого астронома Клавдия Птолемея, жившего в середине II века н.э.
Несмотря на то, что в работах ученых древности нет «тригонометрии» в строгом смысле этого слова, но по существу они, пользуясь известными им средствами элементарной геометрии, решали те задачи, которыми занимается тригонометрия. Например, задачи на решение треугольников (определение всех сторон и углов треугольника по трем его известным элементам), теоремы Евклида и Архимеда представленные в геометрическом виде, эквивалентны специфическим тригонометрическим формулам. Главным достижением средневековой Индии стала замена хорд синусами. Это позволило вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии, как учению о тригонометрических величинах.
Учёные стран Ближнего и Среднего Востока с VIII века развили тригонометрию своих предшественников. Уже в середине IX века среднеазиатский учёный аль-Хорезми написал сочинение «Об индийском счёте». После того, как трактаты мусульманских ученых были переведены на латынь, многие идеи греческих, индийских и мусульманских математиков стали достоянием европейской, а затем и мировой науки. В дальнейшем потребности географии, геодезии, военного дела, способствовали развитию тригонометрии. Особенно усиленно шло ее развитие в средневековое время. Большая заслуга в формировании тригонометрии как отдельной науки принадлежит азербайджанскому ученому Насир ад-Дину ат-Туси (1201-1274), написавшему «Трактат о полном четырехстороннике». Творения ученых этого периода привели к выделению тригонометрии как нового самостоятельного раздела науки. Однако в их трудах еще не была введена необходимая символика. Современный вид тригонометрия получила в трудах Леонарда Эйлера (1707-1783). На основании трудов Эйлера были составлены учебники тригонометрии, излагавшие ее в строгой научной последовательности (прил. №4). Тригонометрические вычисления применяются во многих областях человеческой деятельности: в геометрии, в физике, в астрономии, в архитектуре, в геодезии, инженерном деле, в акустике, в электронике и т.д.
I РАЗДЕЛ (теоретический)
Тема проекта и её актуальность: почему я выбрала тему «Способы отбора корней в тригонометрических уравнениях»?
- Расширить и углубить свои знания, полученные в курсе геометрии 8-9 класса.
- Тригонометрические уравнения рассматриваются в курсе алгебры и начал математического анализа 10-11 класса.
- Тригонометрические уравнения включены в КИМы ЕГЭ по математике.
Решение тригонометрических уравнений и отбор корней, принадлежащих заданному промежутку – это одна из сложнейших тем математики, которая выносится на Единый Государственный Экзамен. По результатам анкетирования многие учащиеся затрудняются или вообще не умеют решать тригонометрические уравнения и особенно затрудняются в отборе корней, принадлежащих промежутку. Немаловажно также знать, тригонометрические формулы, табличные значения тригонометрических функций для решения целого ряда заданий Единого Государственного Экзамена по математике.
Цель проекта: изучить способы отбора корней в тригонометрических уравнениях и выбрать для себя наиболее рациональные подходы для качественной подготовки к ЕГЭ.
Задачи:
- познакомиться с историческими сведениями о возникновении тригонометрии, как науки;
- изучить соответствующую литературу;
- научиться решать тригонометрические уравнения;
- найти теоретический материал и изучить методы отбора корней в тригонометрических уравнениях;
- научиться отбирать корни в тригонометрических уравнениях, принадлежащим заданному промежутку;
- подготовиться к ЕГЭ по математике.
Приёмы отбора корней тригонометрического уравнения на заданном промежутке.
При решении тригонометрических уравнений предлагается провести отбор корней из множества значений неизвестного. В тригонометрическом уравнении отбор корней можно осуществлять следующими способами: арифметическим, алгебраическим, геометрическим и функционально-графическим.
Арифметический способ отбора корней состоит в непосредственной подстановке полученных корней в уравнение, учитывая имеющиеся ограничения, при переборе значений целочисленного параметра.
Алгебраический способ предполагает составление неравенств, соответствующих дополнительным условиям, и их решение относительно целочисленного параметра.
Геометрический способ предполагает использование при отборе корней двух вариантов: тригонометрической окружности или числовой прямой. Тригонометрическая окружность более удобна, когда речь идет об отборе корней на промежутке или в случае, когда значение обратных тригонометрических функций, входящих в решения, не являются табличными. В остальных случаях предпочтительнее модель числовой прямой. Числовую прямую удобно использовать при отборе корней на промежутке, длина которого не превосходит 2 или требуется найти наибольший отрицательный или наименьший положительный корень уравнения.
Функционально-графический способ предполагает отбор корней осуществлять с использование графиков тригонометрических функций. Чтобы использовать данный способ отбора корней, требуется умение схематичного построения графиков тригонометрических функций.
II РАЗДЕЛ (практический)
Покажу практически три наиболее эффективных и рациональных, с моей точки зрения, метода отбора корней на примере решения следующего тригонометрического уравнения:
sinx=cos2x;
sinx−cos2x=0; [применили формулу двойного угла: cos2x = cos2x−sin2x]
sinx−(cos2x−sin2x)=0;
sinx−(1−sin2x−sin2x)=0;
sinx−(1−2sin2x)=0;
2sin2x+sinx−1=0.
Введем новую переменную: sinx = t, -1 ≤ t ≤1, получим
2t2+t-1=0
D=b2-4ac, т.е. D=9
t1 = -1, t2 = ½.
Вернемся к замене:
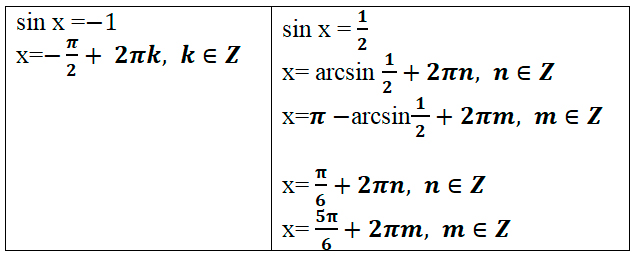
б) Рассмотрим три способа отбора корней, попадающих в отрезок 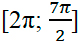 .
.
1 способ: обратимся к единичной окружности. Отметим на ней дугу, соответствующую указанному отрезку, т.е. выполним отбор корней арифметическим способом и с помощью тригонометрической окружности:
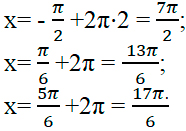
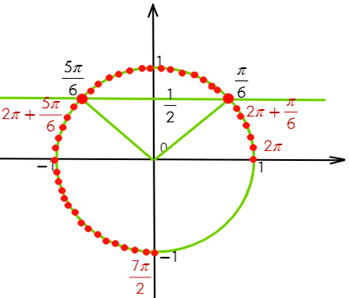
2 способ: указанный отрезок соответствует неравенству: Подставим в него полученные корни: 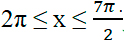

3 способ: разместим корни уравнения на числовой прямой. Сначала отметим корни, подставив вместо n, и нуль (0), а потом добавим к каждому корню периоды.
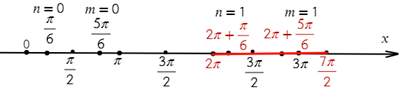
Нам останется только выбрать корни, которые попали в нужный нам отрезок.
Ответ:
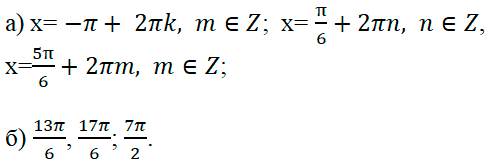
(Более подробный пример в приложении №1)
ЗАКЛЮЧЕНИЕ
При работе над моим проектом я изучила методы решения тригонометрических уравнений и способы отбора корней тригонометрических уравнений. Выяснила для себя положительные и отрицательные моменты. При апробации этих подходов в отборе корней тригонометрического уравнения, понимаешь, что каждый из этих способов удобен по-своему в том или ином случае. Например, алгебраический способ (решение неравенством) наиболее эффективен, когда промежуток для отбора корней достаточно большой, в тоже время он дает практически стопроцентное нахождение целочисленного параметра для вычисления корней, а применение арифметического способа приводит к громоздким вычислениям. При отборе корней уравнения, удовлетворяющих дополнительным условиям, т.е. когда корни уравнения принадлежат заданному промежутку, мне проще и нагляднее получить корни с помощью тригонометрической окружности, а проверить себя можно арифметическим способом. Замечу, что при решении тригонометрических уравнений трудности, связанные с отбором корней, возрастают, если в уравнении приходится учитывать ОДЗ. Как показывает практика и анкетирование моих одноклассников, из четырёх возможных методов отбора корней тригонометрического уравнения по дополнительным условиям, наиболее предпочтительным является отбор корней по окружности. Анкетирование проходили 12 респондентов, изучающих тригонометрию (прил. №5). Большинство из них отвечали, что этот раздел математики достаточно сложный: большой объем информации, очень много формул, табличных значений, которые нужно знать и уметь применять на практике. Еще как одна из проблем – небольшое количество времени, отведенное на изучение этого сложного раздела математики. И я разделяю их мнение. При такой сложности, многие считают, что тригонометрия важный раздел математики, который находит применение в других науках и практической деятельности человека.
СПИСОК ЛИТЕРАТУРЫ
- Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс: учеб для общеобразоват. организаций: базовый и углубленный уровни/ [С.М.Никольский, М.К.Потапов, Н.Н.Решетников и др.]-3 -е изд.- М.: Просвещение, 2016.
- Алгебра и начала математического анализа: Учеб для 10-11 кл.общеобразоват. организаций / А.Н.Колмогоров, А.М.Абрамов, Ю.П.Дудницин и др. под редакцией А.Н.Колмогорова – М. Просвещение, 2017.
- С.В Кравцев и др. Методы решения задач по алгебре: от простых до самых сложных – М: Издательство: «Экзамен», 2005.
- Корянов А.Г., Прокофьев А.А. – Тригонометрические уравнения: методы решения и отбор корней. – М.: Математика ЕГЭ, 2012.
Электронные ресурсы
- https://ru.wikipedia.org/wiki/Тригонометрия
- https://www.yaklass.ru/p/ege/matematika/podgotovka-k-ege-po-matematike-profilnyi-uroven-10744/trigonometricheskie-uravneniia-s-ogranicheniiami-zadacha-13-536475/re-a4b9cc95-fe96-40c2-b70c-f46548b726a0
- https://mat.1sept.ru/1999/no19.htm
- https://math-ege.sdamgia.ru/
- https://alexlarin.net/ege21.html
- https://www.academia.edu/10962821/МАТЕМАТИКА_ЕГЭ_2012_Тригонометрические_уравнения_методы_решений_и_отбор_корней_типовые_задания_С1
- http://teacher-andreeva.ru/wp-content/uploads/2016/03/тригоном-ур-я.pdf
- https://reshimvse.com/article.php?id=100
Тригонометрические уравнения
-
Замена переменной и сведение к квадратному уравнению
-
Разложение на множители
-
Однородные уравнения
-
Введение дополнительного угла
-
Универсальная подстановка
-
Учет ОДЗ уравнения
-
Метод оценки
-
Тригонометрические уравнения повышенной сложности.
Приемы решения
В данной статье мы расскажем об основных типах тригонометрических уравнений и методах их решения. Тригонометрические уравнения чаще всего встречаются в задаче 12 ЕГЭ.
В вариантах ЕГЭ задача, где нужно решить уравнение, состоит из двух пунктов. Первый пункт – решение самого уравнения. Второй – нахождение его корней на некотором отрезке.
Некоторые из методов (например, замена переменной или разложение на множители) являются универсальными, то есть применяются и в других разделах математики. Другие являются специфическими именно для тригонометрии.
Необходимых формул по тригонометрии не так уж и много. Учите наизусть!
Тригонометрические формулы.
Любой метод решения тригонометрических уравнений состоит в том, чтобы привести их к простейшим, то есть к уравнениям вида sin x = a, cos x = a, tg x = a, ctg x = a.
Если вы не помните, как решать простейшие тригонометрические уравнения, — читайте материал на нашем сайте: Простейшие тригонометрические уравнения, часть 1.
О том, что такое арксинус, арккосинус, арктангенс и арккотангенс, — еще одна статья на нашем сайте: Простейшие тригонометрические уравнения,часть 2.
Теперь — сами методы. Теория и примеры решения задач.
к оглавлению ▴
Замена переменной и сведение к квадратному уравнению
Это универсальный способ. Применяется в любых уравнениях — степенных, показательных, тригонометрических, логарифмических, каких угодно. Замена не всегда видна сразу, и уравнение нужно сначала преобразовать.
1. а) Решите уравнение:
б) Найдите корни уравнения, принадлежащие отрезку
Решение:
а) Рассмотрим уравнение
Преобразуем его, применив основное тригонометрическое тождество:
Заменяя sin x на t, приходим к квадратному уравнению:
Решая его, получим:
Теперь вспоминаем, что мы обозначили за t. Первый корень приводит нас к уравнению
Оно не имеет решений, поскольку
Второй корень даёт простейшее уравнение
Решаем его:
б) Найдем корни уравнения на отрезке с помощью двойного неравенства.
Разделим обе части неравенства на
Вычтем из обеих частей неравенства:
Разделим на 2 обе части неравенства:
Единственное целое решение – это n=0. Тогда — это единственный корень, который принадлежит отрезку
Ответ:
2. а) Решите уравнение:
б) Укажите корни этого уравнения, принадлежащие отрезку
Решение:
а)
Выразим косинус двойного угла по формуле
Получим:
Заменяя cosx на t, приходим к квадратному уравнению:
1)

2) нет решений, т. к.
Получим:
б) Отметим отрезок и найденные серии решений на единичной окружности.

Видим, что данному отрезку принадлежит только точка
Ответ: а)
б)
3. а) Решите уравнение:
б) Найдите все корни этого уравнения, принадлежащие отрезку
Решение:
а) Чтобы упростить уравнение применяем формулу приведения.
Так как получим:
Сделаем замену: Получим квадратное уравнение:
Сделаем обратную замену.
1) — нет решений, т. к.
2)
б) Найдем корни уравнения, принадлежащие отрезку , с помощью двойного неравенства.
Для серии решений получим:
Так как то
Для серии решений получим:
отсюда
У этого неравенства нет целых решенией, и значит, из второй серии ни одна точка в указанный отрезок не входит.
Ответ: а)
б)
к оглавлению ▴
Разложение на множители
Во многих случаях уравнение удаётся представить в таком виде, что в левой части стоит произведение двух или нескольких множителей, а в правой части — ноль. Произведение двух или нескольких множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю. Сложное уравнение, таким образом, распадается в совокупность более простых.
4. а) Решите уравнение:
б) Найдите все корни уравнения на отрезке
Решение:
а) Применяем формулу синуса двойного угла:
Ни в коем случае не сокращайте на косинус! Ведь может случиться, что cos x обратится в нуль, и мы потеряем целую серию решений. Переносим всё в одну часть, и общий множитель выносим за скобки:
Полученное уравнение равносильно совокупности двух уравнений: cosx = 0 и 2sinx – 1 = 0.
Получим:
Все эти три серии решений являются ответом в части (а).
б) Отметим отрезок и найденные серии решений на единичной окружности.

Видим, что данному отрезку принадлежат точки
Ответ: а)
б)
5. а) Решите уравнение:
б) Найдите все корни уравнения на отрезке
Решение:
Применим формулу суммы синусов:
Дальше действуем так же, как и в предыдущей задаче:
Решаем уравнение :
| (1) |
Решаем уравнение :
| (2) |
Ну что, перечисляем обе серии (1) и (2) в ответе через запятую? Нет! Серия (2) является в данном случае частью серии (1). Действительно, если в формуле (1) число n кратно 5, то мы получаем все решения серии (2).
Поэтому ответ в пункте (а):
б) Найдем корни уравнения, принадлежащие отрезку с помощью двойного неравенства:
Этот промежуток содержит 8 целых чисел: -2; -1; 0; 1; 2; 3; 4; 5.
Для каждого из этих n найдем x. Получим 8 решений на данном промежутке:
Ответ: а)
б)
6. В следующей задаче также применяется метод разложения на множители. Но это заметно не сразу.
а) Решите уравнение:
б) Найдите все корни уравнения на отрезке
Решение:
Используем формулу понижения степени:
Получаем:
Применяем формулу суммы косинусов:
Получаем:
Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом имеет смысл. Уравнение равносильно совокупности:
б) Найдем корни уравнения, принадлежащие отрезку с помощью двойного неравенства:
1)
Решив неравенство, получим:
Так как n ∈ Z, получим для n целые значения: 0, 1, 2.
Им соответствуют решения:
2) Из серии решений на указанном отрезке лежит только корень
Но он уже входит в первую серию решений.
Можно также заметить, что вся вторая серия решений является подмножеством первой.
Ответ: а)
б)
к оглавлению ▴
Однородные уравнения
7. а) Решите уравнение:
б) Найдите все корни уравнения на отрезке
Решение:
Такое уравнение называется однородным.
Степень каждого слагаемого в левой части равна двум. Точно так же, как в обычном многочлене степень каждого слагаемого равна двум. Мы помним, что степень одночлена — это сумма степеней входящих в него сомножителей.
Для однородных уравнений существует стандартный приём решения — деление обеих его частей на .
Возможность этого деления, однако, должна быть обоснована: а что, если косинус равен нулю?
Следующий абзац предлагаем выучить наизусть и всегда прописывать его при решении однородных уравнений.
Предположим, что cosx = 0. Тогда в силу уравнения и sinx = 0, что противоречит основному тригонометрическому тождеству. Следовательно, любое решение данного уравнения удовлетворяет условию cosx 0, и мы можем поделить обе его части на
.
В результате деления приходим к равносильному квадратному уравнению относительно тангенса:
Сделаем замену: получим:
б) Отметим отрезок и найденные серии решений на единичной окружности.
О том, как отметить на единичной окружности точки из первой серии решений, то есть арктангенс минус трех, читайте здесь: Простейшие тригонометрические уравнения, часть 2.

Видим, что данному отрезку принадлежат точки:
Ответ: а)
б)
8. а) Решите уравнение:
б) Найдите все корни уравнения на отрезке
Если бы в правой части стоял нуль, уравнение было бы однородным. Мы поправим ситуацию изящным приёмом: заменим число 3 на выражение
Получили однородное уравнение второй степени.
Так как не существует такой точки на единичной окружности, в которой одновременно синус и косинус равнялись бы нулю, мы разделим обе части уравнения на .
Получим:
Выполним замену: tgx = y, получим:
Обратная замена:
Ответом в пункте (а) являются две серии решений.
б) Найдем корни уравнения, принадлежащие отрезку с помощью единичной окружности. Для этого отметим на ней данный отрезок и найденные серии решений.

Видим, что данному отрезку принадлежит только точка
Ответ: а)
б)
к оглавлению ▴
Введение дополнительного угла
Этот метод применяется для уравнений вида acosx + bsinx=c. Он присутствует в школьных учебниках. Правда, в них рассматриваются только частные случаи — когда числа a и b являются значениями синуса и косинуса углов в 30°, 45° или 60°.
9. а) Решим уравнение:
б) Найдите все корни уравнения на отрезке
Решение:
Делим обе части на 2:
Замечаем, что
В левой части получили синус суммы:
отсюда
б) Отметим на единичной окружности отрезок и найденные серии решений.
Обратите внимание, что в этой задаче отрезок больше, чем полный круг. Как нам поступить? Один из способов – нарисовать рядом две окружности.

Видим, что данному отрезку принадлежат точки:
Ответ: а)
б)
Другой пример.
10. а) Решите уравнение:
б) Найдите все корни уравнения на отрезке
Решение:
Делим обе части на
Сделаем теперь для разнообразия в левой части косинус разности:
б) Найдем корни уравнения, принадлежащие отрезку с помощью единичной окружности. Отметим на ней данный отрезок и найденные серии решений.

Видим, что данному отрезку принадлежат точки 0 и
Ответ: а)
б)
Покажем, как применяется метод введения дополнительного угла в общем случае.
Рассмотрим уравнение
Делим обе части на
| (4) |
Для чего мы выполнили это деление? Всё дело в получившихся коэффициентах при косинусе и синусе. Легко видеть, что сумма их квадратов равна единице:
Это означает, что данные коэффициенты сами являются косинусом и синусом некоторого угла :
Соотношение (4) тогда приобретает вид:
или
Исходное уравнение сведено к простейшему. Теперь понятно, почему рассматриваемый метод называется введением дополнительного угла. Этим дополнительным углом как раз и является угол
к оглавлению ▴
Универсальная подстановка
Запомним две важные формулы:

Их ценность в том, что они позволяют выразить синус и косинус через одну и ту же функцию — тангенс половинного угла. Именно поэтому они получили название универсальной тригонометрической подстановки.
Единственная неприятность, о которой не надо забывать: правые части этих формул не определены при  . Поэтому если применение универсальной подстановки приводит к сужению ОДЗ, то данную серию нужно проверить непосредственно.
. Поэтому если применение универсальной подстановки приводит к сужению ОДЗ, то данную серию нужно проверить непосредственно.
11. а) Решите уравнение: 
б) Найдите все корни уравнения на отрезке
Решение:
Выражаем  , используя универсальную тригонометрическую подстановку:
, используя универсальную тригонометрическую подстановку:

Делаем замену  :
:

Получаем кубическое уравнение:


Оно имеет единственный корень  .
.
Стало быть,  , откуда
, откуда  .
.
Сужения ОДЗ в данном случае не было, так как уравнение с самого начала содержало  .
.
б) Найдем корни уравнения, принадлежащие отрезку с помощью двойного неравенства:
Получим, что
Ответ: а)
б)
Универсальная тригонометрическая подстановка может также пригодиться при решении задач по планиметрии из второй части ЕГЭ. Поэтому формулы лучше выучить.
к оглавлению ▴
Учет ОДЗ уравнения
12. а) Рассмотрим уравнение: 
б) Найдите все корни уравнения на отрезке
Решение:
Перепишем уравнение в виде, пригодном для возведения в квадрат:

Тогда наше уравнение равносильно системе:

Решаем уравнение системы:
 ,
,
 ,
,

Второе уравнение данной совокупности не имеет решений, а первое даёт две серии:

Теперь нужно произвести отбор решений в соответствии с неравенством  . Серия
. Серия  не удовлетворяет этому неравенству, а серия
не удовлетворяет этому неравенству, а серия  удовлетворяет ему. Следовательно, решением исходного уравнения служит только серия
удовлетворяет ему. Следовательно, решением исходного уравнения служит только серия  .
.
Ответ в пункте (а):  .
.
б) Найдем корни уравнения, принадлежащие отрезку с помощью двойного неравенства:
Неравенство имеет единственное целое решение
Тогда
Ответ: а)
б)
Мы рассмотрели основные методы решения тригонометрических уравнений, которые применяются в задаче 12 ЕГЭ.
Где же еще нам могут встретиться тригонометрические уравнения? Конечно, в задачах с параметрами. Или на олимпиадах по математике. Сейчас мы увидим еще несколько полезных приемов решения.
к оглавлению ▴
Метод оценки
В некоторых уравнениях на помощь приходят оценки  .
.
13. Рассмотрим уравнение: 
Так как оба синуса не превосходят единицы, данное равенство может быть выполнено лишь в том случае, когда они равны единице одновременно:

Таким образом, должны одновременно выполняться следующие равенства:

Обратите внимание, что сейчас речь идёт о пересечении множества решений (а не об их объединении, как это было в случае разложения на множители). Нам ещё предстоит понять, какие значения x удовлетворяют обоим равенствам. Имеем:

Умножаем обе части на 90 и сокращаем на π:
 ;
;
 ;
;

Правая часть, как видим, должна делиться на 5. Число n при делении на 5 может давать остатки от 0 до 4; иначе говоря, число n может иметь один из следующих пяти видов: 5n, 5m + 1, 5m + 2, 5m + 3 и 5m + 4, где . Для того, чтобы 9n+ 1 делилось на 5, годится лишь n = 5m + 1.
. Для того, чтобы 9n+ 1 делилось на 5, годится лишь n = 5m + 1.
Искать k, в принципе, уже не нужно. Сразу находим x:

Ответ: 
14. Рассмотрим уравнение: 
Ясно, что данное равенство может выполняться лишь в двух случаях: когда оба синуса одновременно равны 1 или −1. Действуя так, мы должны были бы поочерёдно рассмотреть две системы уравнений.
Лучше поступить по-другому: умножим обе части на 2 и преобразуем левую часть в разность косинусов:
 ;
;

Тем самым мы сокращаем работу вдвое, получая лишь одну систему:

Имеем:

Ищем пересечение:

Умножаем на 21 и сокращаем на π:

Данное равенство невозможно, так как в левой части стоит чётное число, а в правой — нечётное.
Ответ: решений нет.
Это был тренировочный пример. А в задачах ЕГЭ решения есть всегда.
Посмотрите, как применяется метод оценки в задачах с параметрами.
15. Страшное с виду уравнение  также решается методом оценок.
также решается методом оценок.
В самом деле, из неравенства  следует, что
следует, что  .
.
Следовательно,  , причём равенство возможно в том и только в том случае, когда
, причём равенство возможно в том и только в том случае, когда
Остаётся решить полученную систему. Это не сложно.
Перенесем в левую часть и вынесем общий множитель за скобки , получим:
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом имеет смысл.
Каждое уравнение равносильно совокупности:
Это значит, что синус угла х равен нулю, а его косинус равен 0, 1 или -1.
Или синус угла х равен 1, а косинус этого угла равен 0, 1 или -1.
Такие углы легко найти на тригонометрическом круге. Найденные серии решений запишем в ответ.
Ответ:
к оглавлению ▴
Тригонометрические уравнения повышенной сложности.
Приемы решения
16. Рассмотрим такое уравнение: 
Сделаем замену  .
.
Как выразить  через t? Имеем:
через t? Имеем:
 ,
,
откуда  . Получаем:
. Получаем:
Начнем со второго уравнения.
Так как и
то их сумма может быть равна 2, только оба слагаемых равны 1. Но на единичной окружности не существует точки, в которой одновременно синус и косинус равен единице. Значит, второе уравнение корней не имеет.
Решим первое уравнение методом введения дополнительного угла.
Для этого разделим обе части уравнения на и получим:
Ответ:
17. Помним формулы косинуса и синуса тройного угла:
 ,
,

Вот, например, уравнение:

Оно сводится к уравнению относительно  :
:
 ,
,
 ,
,

Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом имеет смысл. Уравнение равносильно совокупности:
Решим второе уравнение с помощью замены sinx = t.
Получим: или
Обратная замена:
А решением первого уравнения sinx = 0 являются числа вида
Ответ:
Интересно, что формулы синуса и косинуса тройного угла также могут пригодиться вам в решении задач по планиметрии из второй части ЕГЭ.
18. Как бороться с суммой четвёртых степеней синуса и косинуса?
Рассмотрим уравнение: 
Выделяем полный квадрат!
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;

19. А как быть с суммой шестых степеней?
Рассмотрим такое уравнение: 
Раскладываем левую часть на множители как сумму кубов:  .
.
Получим:
 ;
;

С суммой четвёртых степеней вы уже умеете обращаться.
Мы рассмотрели основные методы решения тригонометрических уравнений. Знать их нужно обязательно, это — необходимая база.
В более сложных и нестандартных задачах нужно ещё догадаться, как использовать те или иные методы. Это приходит только с опытом. Именно этому мы и учим на наших занятиях.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Тригонометрические уравнения» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023