Как найти корни уравнения четвертой степени

Уравнение четвёртой степени — в математике алгебраическое уравнение вида:

Четвёртая степень для алгебраических уравнений является наивысшей, при которой существует аналитическое решение в радикалах в общем виде (то есть при любых значениях коэффициентов).

Так как функция является многочленом чётной степени, она имеет один и тот же предел при стремлении к плюс и к минус бесконечности. Если , то функция возрастает до плюс бесконечности с обеих сторон, а значит, имеет глобальный минимум. Аналогично, если , то функция убывает до минус бесконечности с обеих сторон, а значит, имеет глобальный максимум.

Теорема Виета для уравнения четвёртой степени[править | править код]

Корни уравнения четвёртой степени связаны с коэффициентами следующим образом:

История[править | править код]

Уравнения четвёртой степени впервые были рассмотрены древнеиндийскими математиками между IV в. до н. э. и II в. н. э.

Лодовико Феррари приписывается получение решения уравнения четвёртой степени в 1540 году, но его работа опиралась на решение кубического уравнения, которого у него не было, поэтому сразу это решение не было опубликовано,^[1] а было опубликовано только в 1545 вместе с решением кубического уравнения наставника Феррари — Джероламо Кардано в книге «Великое искусство»^[2].

То, что это наибольшая степень уравнения, для которого можно указать общую формулу решения, было доказано в теореме Абеля — Руффини в 1824.
Записки, оставленные Галуа,
позже привели к элегантной теории корней многочленов, одним из результатов которой была эта теорема.^[3]

Решения[править | править код]

Решение через резольвенту[править | править код]

Решение уравнения четвёртой степени

сводится к решению кубической резольвенты

Корни резольвенты связаны с корнями исходного уравнения (которые и нужно найти) следующими соотношениями:

Корни резольвенты могут быть найдены по формуле Кардано.
Три формулы соотношений между и вместе с уравнением (соотношение Виета для коэффициента при )

дают систему из 4 алгебраических уравнений с 4 неизвестными, которая легко решается.

Решение Декарта — Эйлера[править | править код]

В уравнении четвёртой степени

сделаем подстановку , получим уравнение в следующем виде (оно называется «неполным»):

где

Корни такого уравнения равны одному из следующих выражений:

в которых сочетания знаков выбираются таким образом, чтобы выполнялось следующее соотношение:

причём  — это корни кубического уравнения

Решение Феррари[править | править код]

Решение уравнения четвёртой степени вида может быть найдено по методу Феррари.
Если  — произвольный корень кубического уравнения

(2)

(резольвенты основного уравнения), то четыре корня исходного уравнения находятся как корни двух квадратных уравнений

где подкоренное выражение в правой части является полным квадратом.

Биквадратное уравнение[править | править код]

Биквадратное уравнение^[4] — алгебраическое уравнение четвёртой степени вида , где  — заданные комплексные числа и . Иначе говоря, это уравнение четвёртой степени, у которого второй и четвёртый коэффициенты равны нулю. Подстановкой оно сводится к квадратному уравнению относительно .

Четыре его корня находятся по формуле

Возвратные уравнения четвёртой степени[править | править код]

Возвратное уравнение четвёртой степени является также относительно легко решаемым: для такого, что , решение находится приведением к виду:

,

После замены ищется решение квадратного уравнения , а затем — квадратного уравнения .

Примечания[править | править код]

Литература[править | править код]

• Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 2003. — 832 с. — 5000 экз. — ISBN 5-8114-0485-9.
• Лекция 4 в кн.: Табачников С. Л., Фукс Д. Б. Математический дивертисмент. — М.: МЦНМО, 2011. — 512 с. — 2000 экз. — ISBN 978-5-94057-731-7.

Ссылки[править | править код]

• Решение Феррари (англ.). Дата обращения: 27 сентября 2009. Архивировано 19 февраля 2012 года.
• Weisstein, Eric W. Quadratic Equation (англ.) на сайте Wolfram MathWorld.
• Weisstein, Eric W. Biquadratic Equation (англ.) на сайте Wolfram MathWorld.
• Biquadratic equation (англ.) на сайте PlanetMath.

Всем привет! 🖐🖐🖐

🎯 В этой статье мы разберемся как отличить и как решать уравнение 4 степени!
🎯 Задания из ЕГЭ, ОГЭ, ВПР, иногда из учебников

✅ Решения подробные, будет понятно 😎
✅ В конце задания для тренировки 💪
✅ В комментах отвечу на ваши вопросы 😊
✅ И без лишней воды ☔☔☔

Вот какие уравнения мы разберем сегодня:

📝 Как отличить и как решать уравнение 4 степени

Рассматриваем чем отличается уравнение 4 степени.

Способы решения:
◽ группировка и вынесение общего множителя
◽ деление столбиком многочлена на скобку (теорема Безу)
◽ формулы сокращенного умножения
◽ замена

Скрин:

📝 Уравнение 1

Как решить такие простые уравнения 4 степени? Избавляемся от 4 степени.

Скрины решения:

📝 Уравнение 2

Данное уравнение 4 степени является биквадратным. Делаем замену x²=t.

Скрины решения:

📝 Уравнение 3

Решаем:
◽ 1 способ – группировка и вынесение общего множителя за скобку
◽ 2 способ – деление столбиком многочлена на скобку

Скрины решения:

📝 Уравнение 4

Способы решения:
◽ 1 способ – группировка и вынесение общего множителя за скобку
◽ 2 способ – деление столбиком многочлена на скобку

Скрины решения:

📝 Уравнение 5

Решаем с помощью замены, сводим к квадратному уравнению.

Скрины решения:

📝 Уравнение 6

Решаем с помощью замены, в итоге сводим к квадратному уравнению.

Скрины решения:

А вот такую замену предложил сделать один мой зритель, очень удобно. Для замены на конце выражения выбирается +5, то есть число, которое находится посередине между +4 и +6. Этот способ замены дает возможность свернуть по формуле сокращенного умножения.

📝 Уравнение 7

Решаем это уравнение с учетом его особенности – в левой части стоит сумма квадратов.

Скрины решения:

📝 Уравнение 8

Способы решения:
◽ 1 способ – разложить на множители
◽ 2 способ – формула сокращенного умножения
◽ 3 способ – избавиться от квадратов

Скрины решения:

📝 Уравнение 9

Способы решения:
◽ 1 способ – формула сокращенного умножения
◽ 2 способ – понизить степень уравнения

Скрины решения:

📝 Уравнение 10

Сначала раскрываем скобки и после этого решаем как биквадратное.

Скрины решения:

📝 Задания для тренировки

Реши сам по аналогии и напиши свои ответы в комментариях! 😋😋😋

⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜

✅ Оглавление:

👉 Как решать любое уравнение (цикл занятий) здесь

✍ Занятие 0 Виды уравнений здесь
✍ Занятие 1 Линейное уравнение здесь
✍ Занятие 2 Часть 1 Полные квадратные уравнения здесь
✍ Занятие 2 Часть 2 Неполные квадратные уравнения здесь
✍ Занятие 2 Часть 3 Квадратные уравнения со скобками здесь
✍ Занятие 3 Часть 1 Стандартные кубические уравнения здесь
✍ Занятие 3 Часть 2 Кубические уравнения со скобками здесь
✍ Занятие 4 Уравнение 4 степени здесь
✍ Занятие 5 Уравнение со скобками (вида Произведение = 0) здесь
✍ Занятие 6 Уравнение со скобками (вида Произведение = выр) здесь
✍ Занятие 7 Дробное уравнение (вида Дробь = 0) здесь
✍ Занятие 8 Дробное уравнение (вида Дробь = выражению) здесь
✍ Занятие 9 Иррациональное уравнение (с корнями) здесь
✍ Занятие 10 Уравнение с модулем здесь
✍ Занятие 11 Часть 1 Простые показательные уравнения здесь
✍ Занятие 11 Часть 2 Сложные показательные уравнения здесь
✍ Занятие 12 Часть 1 Простые логарифмические уравнения здесь
✍ Занятие 12 Часть 2 Сложные логарифмические уравнения здесь
✍ Занятие 13 Тригонометрическое уравнение здесь
✍ Занятие 14 Уравнение смешанного типа здесь

🧭 Путеводитель по каналу Подслушано по Математике

здесь

Из школы известно, что уравнение второй степени a0x2+a1x+a2=0a_0x^2+a_1x+a_2=0 можно решить с помощью выделения полного квадрата. Есть и универсальная формула для корней, действительных или комплексных
x1,2=a1±a12−4a0a22a0x_{1,2}=frac{a_1pmsqrt{a_1^2-4a_0a_2}}{2a_0}.

В таком же стиле можно решить и уравнения, у которых в левой части многочлен не 2-й, а 3-й или 4-й степени — методы изложены ниже.
Надежды математиков, что и уравнения более высоких степеней могут быть решены с помощью 4 арифметических операций и извлечения корня, не оправдались. Абель в 1823 г. доказал, что уравнение 5-й степени x5+3x+1=0x^5+3x+1=0 неразрешимо в радикалах.

Здесь не ставятся целью готовые формулы, они будут довольно сильно «ветвящимися», напротив, подставьте вместо букв свои числа и все это проделайте, будет готовое полное решение уравнения 3-й или 4-й степени.

Метод Кардано

Пусть надо решить уравнение 3-й степени z3+a1z2+a2z+a3=0z^{3}+a_{1}z^{2}+a_{2}z+a_{3}=0.

Обнулим первый коэффициент заменой x=z+13a1x=z+frac{1}{3}a_{1}, получим уравнение относительно xx:

x3+px+q=0(1)x^{3}+px+q=0quadquad(1)

Будем искать в виде

x=y+zx=y+z

(y+z)3+p(y+z)+q=0(y+z)^{3}+p(y+z)+q=0
y3+z3+(3yz+p)(y+z)+q=0y^{3}+z^{3}+(3yz+p)(y+z)+q=0

Достаточно, чтобы выполнялась система

{3yz=−py3+z3=−q,{y3z3=(−p3)3y3+z3=−qbegin{cases}
begin{array}{cc}
3yz & =-p\
y^{3}+z^{3} & =-q
end{array}end{cases},begin{cases}
begin{array}{cc}
y^{3}z^{3} & =left(frac{-p}{3}right)^{3}\
y^{3}+z^{3} & =-q
end{array}end{cases}

По теореме Виета, y3y^{3} и z3z^{3} являются двумя корнями квадратного уравнения

t2+qt+(−p3)3=0t^{2}+qt+left(frac{-p}{3}right)^{3}=0
(y3,z3)=−q2±(q2)2+(p3)3(y^{3},z^{3})=-frac{q}{2}pmsqrt{left(frac{q}{2}right)^{2}+left(frac{p}{3}right)^{3}}

x=y+z=−q2+(q2)2+(p3)33+−q2−(q2)2+(p3)33x=y+z=sqrt[3]{-frac{q}{2}+sqrt{left(frac{q}{2}right)^{2}+left(frac{p}{3}right)^{3}}}+sqrt[3]{-frac{q}{2}-sqrt{left(frac{q}{2}right)^{2}+left(frac{p}{3}right)^{3}}}

Получили формулу Кардано для одного из корней. Однако если дискриминант использованного квадратного уравнения

D=(q2)2+(p3)3<0D=left(frac{q}{2}right)^{2}+left(frac{p}{3}right)^{3}<0,

то под кубическими корнями будут стоять комплексные числа. Если коэффициенты исходного кубического уравнения были действительны, мнимые части двух кубических корней будут взаимно противоположны, и корни получатся действительными, какие бы комплексные решения y,z исходной системы мы ни взяли. Но извлечение кубических корней из комплексных чисел — это еще большее искусство, чем решение исходного уравнения, поэтому сразу, как только у уравнения (1) оказалось D<0D<0, мы поступим иначе.

x3+px=−qx^{3}+px=-q

Чтобы уравнение стало еще больше похоже на формулу косинуса тройного угла, заменим

x=u−4p3x=usqrt{-frac{4p}{3}}
−4p3−4p3u3+pu−4p3=−qu3−34u=33/2q8(−p)3/2-frac{4p}{3}sqrt{-frac{4p}{3}}u^{3}+pusqrt{-frac{4p}{3}}=-qu^{3}-frac{3}{4}u=frac{3^{3/2}q}{8(-p)^{3/2}}
4u3−3u=q2(−p3)3/2=cos⁡3φ4u^{3}-3u=frac{q}{2(-frac{p}{3})^{3/2}}=cos3varphi

Благодаря условию D<0D<0 дробь меньше 11 по модулю, и найдется такое значение φ,  0<3φ<πvarphi,;0<3varphi<pi. Причем значения 3φ+2π3varphi+2pi, 3φ+4π3varphi+4pi приведут к другим значениям cos⁡φcosvarphi. Так по формуле косинуса тройного аргумента

u=cos⁡φ=cos⁡(13arccos⁡q2(−p3)3/2+2πk3),k=0,1,2u=cosvarphi=cosleft(frac{1}{3}arccosfrac{q}{2(-frac{p}{3})^{3/2}}+frac{2pi k}{3}right),quad k=0,1,2

найдется три решения u1,u2,u3u_{1},u_{2},u_{3}, и соответственно три решения x1,x2,x3x_{1},x_{2},x_{3} уравнения (1).

Метод Феррари

Решаем уравнение 4-й степени

z4+a1z3+a2z2+a3z+a4=0z^{4}+a_{1}z^{3}+a_{2}z^{2}+a_{3}z+a_{4}=0.

Обнулим первый коэффициент заменой x=z+14a1x=z+frac{1}{4}a_{1}, получим уравнение относительно xx:

x4+Ax2+Bx+C=0(2)x^{4}+Ax^{2}+Bx+C=0quadquad(2)

Это уравнение с действительными коэффициентами может иметь:

1. две пары комплексно-сопряженных корней,
2. пару комплексно-сопряженных корней и пару действительных корней,
3. четыре действительных корня, в том числе, может быть, совпадающие.

В любом случае левая часть разлагается в произведение двух квадратных трехчленов

x4+Ax2+Bx+C=(x2+ax+b)(x2−ax+c)=0x^{4}+Ax^{2}+Bx+C=(x^{2}+ax+b)(x^{2}-ax+c)=0

Например, x4+4=(x2+2x+2)(x2−2x+2)x^{4}+4=(x^{2}+2x+2)(x^{2}-2x+2)

Получаем систему условий:

{c+b−a2=Aa(c−b)=Bbc=C{c+b=A+a2c−b=Babc=Cbegin{cases}
begin{array}{cc}
c+b-a^{2} & =A\
a(c-b) & =B\
bc & =C
end{array}end{cases}begin{cases}
begin{array}{cc}
c+b & =A+a^{2}\
c-b & =frac{B}{a}\
bc & =C
end{array}end{cases}

Благодаря тождеству 4bc=(c+b)2−(c−b)24bc=(c+b)^{2}-(c-b)^{2} получаем уравнение на t=a2t=a^{2}

(A+a2)2=(Ba)2+4C(A+a^{2})^{2}=left(frac{B}{a}right)^{2} +4C
t3+2At2+(A2−4C)t−B2=0t^{3}+2At^{2}+({A^2}-4C)t-B^{2}=0

Это уравнение третьей степени, называемое резольвентным, и может быть решено методом Кардано, описанным выше. Находим любой один действительный положительный корень t1t_{1}. Он существует, так как левая часть отрицательна при t=0t=0, и стремится к бесконечности на +∞+infty. Из системы

{c+b=A+t1c−b=±Bt1=Babegin{cases}
begin{array}{cc}
c+b & =A+t_{1}\
c-b & =pmfrac{B}{sqrt{t_{1}}}=frac{B}{a}
end{array}end{cases}

находим однозначно, с точностью до замены (a,b)↔(−a,c)(a,b)leftrightarrow(-a,c)

{a=±t1c=12(A+t1±Bt1)b=12(A+t1∓Bt1)begin{cases}
begin{array}{cc}
a & =pmsqrt{t_{1}}\
c & =frac{1}{2}left(A+t_{1}pmfrac{B}{sqrt{t_{1}}}right)\
b & =frac{1}{2}left(A+t_{1}mpfrac{B}{sqrt{t_{1}}}right)
end{array}end{cases}

Значит, нашли разложение левой части уравнения (2) в произведение двух квадратных трехчленов. Остается решить два квадратных уравнения и найти 4 корня, действительных или комплексных.

Если резольвентное уравнение имеет один действительный корень t1t_{1}, то разложение в произведение двух квадратных трехчленов единственно, это происходит потому, что среди 4 корней есть два комплексно-сопряженных, и они обязательно должны быть объединены в пару. Если же все 4 корня уравнения (2), а значит и исходного, действительны, то их можно разбить на пары тремя различными способами, и возможны три разложения в произведение. Они соответствуют трем корням резольвентного уравнения. Но в итоге все 4 корня исходного уравнения получаются одни и те же, только по-разному упорядоченные.

Пример

Решить уравнение x4−x2+2x−1=0x^{4}-x^{2}+2x-1=0

A=−1,B=2,C=−1A=-1,B=2,C=-1.

По методу Феррари ищем разложение:

x4−x2+2x−1=(x2+ax+b)(x2−ax+c)x^{4}-x^{2}+2x-1=(x^{2}+ax+b)(x^{2}-ax+c)

{c+b=−1+a2c−b=2abc=−1begin{cases}
begin{array}{cc}
c+b & =-1+a^{2}\
c-b & =frac{2}{a}\
bc & =-1
end{array}end{cases}

Резольвентное уравнение на t=a2t=a^{2}

t3+2At2+(A2−4C)t−B2=t3−2t2+5t−4=0t^{3}+2At^{2}+(A^{2}-4C)t-B^{2}=t^{3}-2t^{2}+5t-4=0

Если не заниматься подбором его корня, а работать по методу Кардано:

X=t−23X=t-frac{2}{3}

(X+23)3−2(X+23)2+5(X+23)−4=0left(X+frac{2}{3}right)^{3}-2left(X+frac{2}{3}right)^{2}+5left(X+frac{2}{3}right)-4=0

X3+43X+827−83X−89+5X+103−4=0X^{3}+frac{4}{3}X+frac{8}{27}-frac{8}{3}X-frac{8}{9}+5X+frac{10}{3}-4=0

X3+113X−3427=0X^{3}+frac{11}{3}X-frac{34}{27}=0

p=113,  q=−3427p=frac{11}{3},;q=-frac{34}{27}

D=(119)3+(1727)3=1331729+289729=1620729=209D=left(frac{11}{9}right)^{3}+left(frac{17}{27}right)^{3}=frac{1331}{729}+frac{289}{729}=frac{1620}{729}=frac{20}{9}

По формуле Кардано

X=−q2+D3+−q2−D3=17+1853+17−18533=X=sqrt[3]{-frac{q}{2}+sqrt{D}}+sqrt[3]{-frac{q}{2}-sqrt{D}}=frac{sqrt[3]{17+18sqrt{5}}+sqrt[3]{17-18sqrt{5}}}{3}=

=1+95+135+13553+1−95+135−135536==frac{sqrt[3]{1+9sqrt{5}+135+135sqrt{5}}+sqrt[3]{1-9sqrt{5}+135-135sqrt{5}}}{6}=

=(1+35)33+(1−35)336=13=frac{sqrt[3]{left(1+3sqrt{5}right)^{3}}+sqrt[3]{left(1-3sqrt{5}right)^{3}}}{6}=frac{1}{3}

Это типичный исход применения формулы. При DD, не являющимся квадратом рационального числа, для рациональности ХХ не только достаточно, но и необходимо, чтобы выражения под кубическими корнями оказались точными кубами

(α±βD)3left(alphapmbetasqrt{D}right)^{3}
( α,βalpha ,beta рациональны), и тогда иррациональность Dsqrt{D} исчезнет в ответе. Но если X (и t) рациональны, их в резольвентном уравнении можно было найти и подбором.

Получили корень резольвентного уравнения

t=X+23=1t=X+frac{2}{3}=1
a=±t=±1,c=±1,b=∓1a=pmsqrt{t}=pm1,quad c=pm1,quad b=mp1

Получаем разложение

x4−x2+2x−1=(x2+x−1)(x2−x+1)=0x^{4}-x^{2}+2x-1=(x^{2}+x-1)(x^{2}-x+1)=0

Из этих квадратных уравнений

x1,2=−1±52,x3,4=1±i32x_{1,2}=frac{-1pmsqrt{5}}{2},quad x_{3,4}=frac{1pm isqrt{3}}{2}
-все корни данного уравнения.

Решение уравнений четвертой степени

Для уравнений четвертой степени применимы все те общие схемы решения уравнений высших степеней, что мы разбирали в предыдущем материале. Однако существует ряд нюансов в решении двучленных, биквадратных и возвратных уравнений, на которых мы хотели бы остановиться подробнее.

Также в статье мы разберем искусственный метод разложения многочлена на множители, решение в радикалах и метод Феррари, который используется для того, чтобы свести решение уравнения четвертой степени к кубическому уравнению.

Решение двучленного уравнения четвертой степени

Это простейший тип уравнений четвертой степени. Запись уравнения имеет вид A x 4 + B = 0 .

Для решения этого типа уравнений применяются формулы сокращенного умножения:

A x 4 + B = 0 x 4 + B A = 0 x 4 + 2 B A x 2 + B A – 2 B A x 2 = 0 x 2 + B A 2 – 2 B A x 2 = 0 x 2 – 2 B A 4 x + B A x 2 + 2 B A 4 x + B A = 0

Остается лишь найти корни квадратных трехчленов.

Решить уравнение четвертой степени 4 x 4 + 1 = 0 .

Решение

Для начала проведем разложение многочлена 4 x 4 + 1 на множители:

4 x 4 + 1 = 4 x 4 + 4 x 2 + 1 = ( 2 x 2 + 1 ) 2 – 4 x 2 = 2 x 2 – 2 x + 1 ( 2 x 2 + 2 x + 1 )

Теперь найдем корни квадратных трехчленов.

2 x 2 – 2 x + 1 = 0 D = ( – 2 ) 2 – 4 · 2 · 1 = – 4 x 1 = 2 + D 2 · 2 = 1 2 + i x 2 = 2 – D 2 · 2 = 1 2 – i

2 x 2 + 2 x + 1 = 0 D = 2 2 – 4 · 2 · 1 = – 4 x 3 = – 2 + D 2 · 2 = – 1 2 + i x 4 = – 2 – D 2 · 2 = – 1 2 – i

Мы получили четыре комплексных корня.

Ответ: x = 1 2 ± i и x = – 1 2 ± i .

Решение возвратного уравнения четвертой степени

Возвратные уравнения четвертого порядка имеют вид A x 4 + B x 3 + C x 2 + B x + A = 0

х = 0 не является корнем этого уравнения: A · 0 4 + B · 0 3 + C · 0 2 + B · 0 + A = A ≠ 0 . Поэтому на x 2 можно смело разделить обе части этого уравнения:

A x 4 + B x 3 + C x 2 + B x + A = 0 A x 2 + B x + C + B x + A x 2 = 0 A x 2 + A x 2 + B x + B x + C = 0 A x 2 + 1 x 2 + B x + 1 x + C = 0

Проведем замену переменных x + 1 x = y ⇒ x + 1 x 2 = y 2 ⇒ x 2 + 1 x 2 = y 2 – 2 :

A x 2 + 1 x 2 + B x + 1 x + C = 0 A ( y 2 – 2 ) + B y + C = 0 A y 2 + B y + C – 2 A = 0

Так мы проведи сведение возвратного уравнения четвертой степени к квадратному уравнению.

Найти все комплексные корни уравнения 2 x 4 + 2 3 + 2 x 3 + 4 + 6 x 2 + 2 3 + 2 x + 2 = 0 .

Решение

Симметрия коэффициентов подсказывает нам, что мы имеем дело с возвратным уравнением четвертой степени. Проведем деление обеих частей на x 2 :

2 x 2 + 2 3 + 2 x + 4 + 6 + 2 3 + 2 x + 2 x 2 = 0

2 x 2 + 2 x 2 + 2 3 + 2 x + 2 3 + 2 x + 4 + 6 + = 0 2 x 2 + 1 x 2 + 2 3 + 2 x + 1 x + 4 + 6 = 0

Проведем замену переменной x + 1 x = y ⇒ x + 1 x 2 = y 2 ⇒ x 2 + 1 x 2 = y 2 – 2

2 x 2 + 1 x 2 + 2 3 + 2 x + 1 x + 4 + 6 = 0 2 y 2 – 2 + 2 3 + 2 y + 4 + 6 = 0 2 y 2 + 2 3 + 2 y + 6 = 0

Решим полученное квадратное уравнение:

D = 2 3 + 2 2 – 4 · 2 · 6 = 12 + 4 6 + 2 – 8 6 = = 12 – 4 6 + 2 = 2 3 – 2 2 y 1 = – 2 3 – 2 + D 2 · 2 = – 2 3 – 2 + 2 3 – 2 4 = – 2 2 y 2 = – 2 3 – 2 – D 2 · 2 = – 2 3 – 2 – 2 3 + 2 4 = – 3

Вернемся к замене: x + 1 x = – 2 2 , x + 1 x = – 3 .

Решим первое уравнение:

x + 1 x = – 2 2 ⇒ 2 x 2 + 2 x + 2 = 0 D = 2 2 – 4 · 2 · 2 = – 14 x 1 = – 2 – D 2 · 2 = – 2 4 + i · 14 4 x 2 = – 2 – D 2 · 2 = – 2 4 – i · 14 4

Решим второе уравнение:

x + 1 x = – 3 ⇒ x 2 + 3 x + 1 = 0 D = 3 2 – 4 · 1 · 1 = – 1 x 3 = – 3 + D 2 = – 3 2 + i · 1 2 x 4 = – 3 – D 2 = – 3 2 – i · 1 2

Ответ: x = – 2 4 ± i · 14 4 и x = – 3 2 ± i · 1 2 .

Решение биквадратного уравнения

Биквадратные уравнения четвертой степени имеют вид A x 4 + B x 2 + C = 0 . Мы можем свести такое уравнение к квадратному A y 2 + B y + C = 0 путем замены y = x 2 . Это стандартный прием.

Решить биквадратное уравнение 2 x 4 + 5 x 2 – 3 = 0 .

Решение

Выполним замену переменной y = x 2 , что позволит нам свести исходное уравнение к квадратному:

2 y 2 + 5 y – 3 = 0 D = 5 2 – 4 · 2 · ( – 3 ) = 49 y 1 = – 5 + D 2 · 2 = – 5 + 7 4 = 1 2 y 2 = – 5 – D 2 · 2 = – 5 – 7 4 = – 3

Следовательно, x 2 = 1 2 или x 2 = – 3 .

Первое равенство позволяет нам получить корень x = ± 1 2 . Второе равенство не имеет действительных корней, зато имеет комплексно сопряженных корней x = ± i · 3 .

Ответ: x = ± 1 2 и x = ± i · 3 .

Найти все комплексные корни биквадратного уравнения 16 x 4 + 145 x 2 + 9 = 0 .

Решение

Используем метод замены y = x 2 для того, чтобы свести исходное биквадратное уравнение к квадратному:

16 y 2 + 145 y + 9 = 0 D = 145 2 – 4 · 16 · 9 = 20449 y 1 = – 145 + D 2 · 16 = – 145 + 143 32 = – 1 16 y 2 = – 145 – D 2 · 16 = – 145 – 143 32 = – 9

Поэтому, в силу замены переменной, x 2 = – 1 16 или x 2 = – 9 .

Ответ: x 1 , 2 = ± 1 4 · i , x 3 , 4 = ± 3 · i .

Решение уравнений четвертой степени с рациональными корнями

Алгоритм нахождения рациональных корней уравнения четвертой степени приведен в материале «Решение уравнений высших степеней».

Решение уравнений четвертой степени по методу Феррари

Уравнения четвертой степени вида x 4 + A x 3 + B x 2 + C x + D = 0 в общем случае можно решить с применением метода Феррари. Для этого необходимо найти y 0 . Это любой из корней кубического уравнения y 3 – B y 2 + A C – 4 D y – A 2 D + 4 B D – C 2 = 0 . После этого необходимо решить два квадратных уравнения x 2 + A 2 x + y 0 2 + A 2 4 – B + y 0 x 2 + A 2 y 0 – C x + y 0 2 4 – D = 0 , у которых подкоренное выражение является полным квадратом.

Корни, полученные в ходе вычислений, будут корнями исходного уравнения четвертой степени.

Найти корни уравнения x 4 + 3 x 3 + 3 x 2 – x – 6 = 0 .

Решение

Имеем А = 3 , В = 3 , С = – 1 , D = – 6 . Применим метод Феррари для решения данного уравнения.

Составим и решим кубическое уравнение:
y 3 – B y 2 + A C – 4 D y – A 2 D + 4 B D – C 2 = 0 y 3 – 3 y 2 + 21 y – 19 = 0

Одним из корней кубического уравнения будет y 0 = 1 , так как 1 3 – 3 · 1 2 + 21 · 1 – 19 = 0 .

Запишем два квадратных уравнения:
x 2 + A 2 x + y 0 2 ± A 2 4 – B + y 0 x 2 + A 2 y 0 – C x + y 0 2 4 – D = 0 x 2 + 3 2 x + 1 2 ± 1 4 x 2 + 5 2 x + 25 4 = 0 x 2 + 3 2 x + 1 2 ± 1 2 x + 5 2 2 = 0

x 2 + 3 2 x + 1 2 + 1 2 x + 5 2 = 0 или x 2 + 3 2 x + 1 2 – 1 2 x – 5 2 = 0

x 2 + 2 x + 3 = 0 или x 2 + x – 2 = 0

Корнями первого уравнения будут x = – 1 ± i · 2 , корнями второго х = 1 и х = – 2 .

Ответ: x 1 , 2 = – 1 ± i 2 , x 3 = 1 , x 4 = – 2 .

Формула решения уравнения 4 степени

Существует несколько методов нахождения корней полиномиального уравнения 4-ой степени.
Однако они не очень удобны при решении уравнений с коэффициентами, которые представляют собой выражения с параметрами.

1. Формула решения уравнения 4 степени

Рассмотрим уравнение 4-ой степени, сумма корней которого равна нулю. Коэффициенты могут быть вещественными или комплексными.

Произведение следующих двух квадратов тождественно рассматриваемому уравнению 4-ой степени.

Значение R является решением следующего кубического уравнения.

Почти такое же уравнение появляется при решении уравнения 4-ой степени путем разложения на разность полных квадратов. Будем называть данное кубическое уравнение вспомогательным.

Вычислим произведение двух квадратов new.

То же самое, но в форме коэффициентов при степенях x (в порядке убывания степеней).

Упростим выражения для коэффициентов при второй и первой степени x.

Приведенное выражение для первой степени x.

В итоге получаем k1.

Приведенное выражение для второй степени x.

Подставив выражение для R^3 получим

Итак, new тождественно уравнению 4-ой степени, сумма корней которого равна нулю.

Осталась проблема со вспомогательным кубическим уравнением.
Конечно можно использовать традиционные методы решения. Но тогда потребуется преобразовывать уравнение к каноническому виду и отдельно рассматривать три варианта решения в зависимости от значений коэффициентов. Для коэффициентов представляющих из себя выражения с параметрами это не всегда удобно.

2. Решение кубического уравнения методом преобразования Чирнгаузена

Рассмотрим решение кубического уравнения не очень широко распространенным методом преобразования Чирнгаузена.

Итак, решаем исходное уравнение

Суть метода заключается в следующих преобразованиях.

1. Вводится уравнение для y

2. Обе части равенства из п.1 умножаются на x

Затем выражение для x^3 заменяется на

В общем описанные в п.2 преобразования не являются тождественными. Но если считать интересными только значения x, которые являются корнями исходного уравнения, то данные преобразования можно считать квазитождественными. И тогда y представляется выражением, соответствующим корням исходного уравнения.

3. Для кубического уравнения операция в п.2 производится еще один раз. В итоге получается система из 3 уравнений по x, которая имеет три ненулевых решения, соответствующих корням исходного уравнения. Из коэффициентов x формируем матрицу

4. Находим определитель матрицы, который представляется кубическим выражением по y.
Вычисляем значения, обеспечивающие равенство определителя нулю.

5. В уравнении по y имеются два параметра P и Q. Вычислим их так, чтобы нулю равнялись коэффициенты при второй и первой степени y.

6. В итоге имеем уравнение c тремя кратными корнями для y

7. Остается решить квадратное уравнение с известными y, P, Q

Одно из решений будет решением исходного уравнения.

3. Параметры решения вспомогательного кубического уравнения

Для конкретных значений коэффициентов все выглядит не таким страшным образом.

Отметим, что для формулы решения уравнения 4-ой степени требуется только один корень R вспомогательного кубического уравнения.

Для конкретных коэффициентов вспомогательного уравнения имеем

При использовании формулы решения уравнения 4-ой степени необходимо ссылаться — «Метод ftvmetrics».

Интересные задачи присылайте в Direct Инстаграмм.

Решение уравнений 4-ой степени. Метод Феррари

Схема метода Феррари

Целью данного раздела является изложение метода Феррари , с помощью которого можно решать уравнения четвёртой степени

a0x 4 + a1x 3 + a2x 2 + + a3x + a4 = 0,

(1)

где a₀, a₁, a₂, a₃, a₄ – произвольные вещественные числа, причем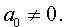

Метод Феррари состоит из двух этапов.

На первом этапе уравнения вида (1) приводятся к уравнениям четвертой степени, у которых отсутствует член с третьей степенью неизвестного.

На втором этапе полученные уравнения решаются при помощи разложения на множители, однако для того, чтобы найти требуемое разложение на множители, приходится решать кубические уравнения.

Приведение уравнений 4-ой степени

Разделим уравнение (1) на старший коэффициент a₀ . Тогда оно примет вид

x 4 + ax 3 + bx 2 + + cx + d = 0,

(2)

где a, b, c, d – произвольные вещественные числа.

Сделаем в уравнении (2) замену

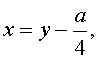(3)

где y – новая переменная.

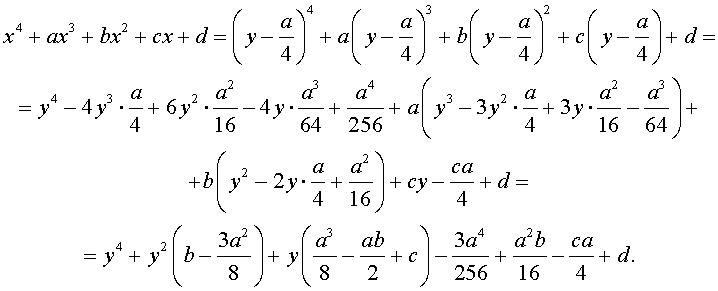
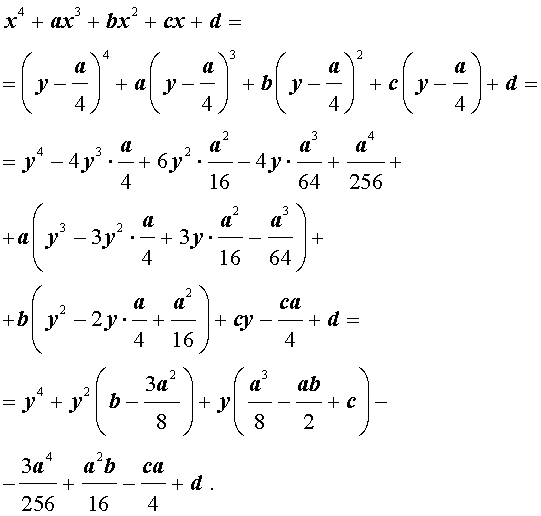
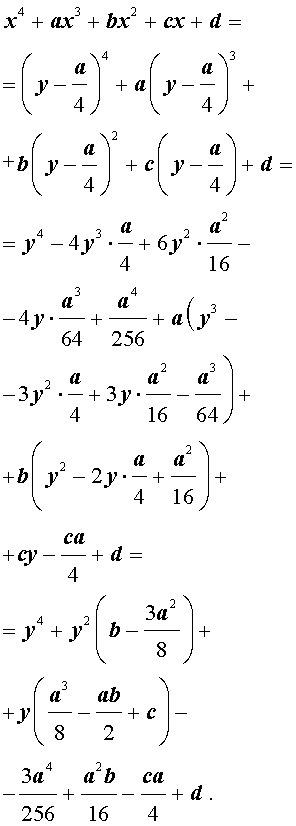
то уравнение (2) принимает вид

В результате уравнение (2) принимает вид

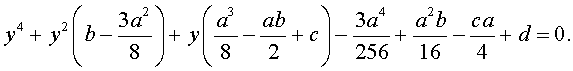
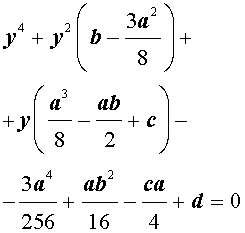
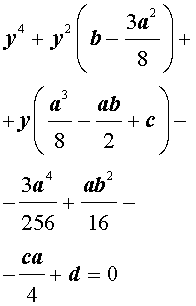
Если ввести обозначения

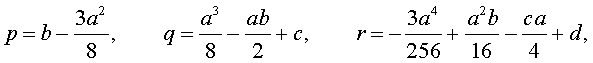
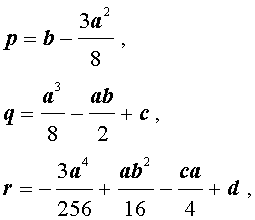
то уравнение (4) примет вид

y 4 + py 2 + qy + r = 0,

(5)

где p, q, r – вещественные числа.

Первый этап метода Феррари завершён.

Разложение на множители. Кубическая резольвента

Добавив и вычитая в левой части уравнения (5) выражение

где s – некоторое число, которое мы определим чуть позже, из (5) получим

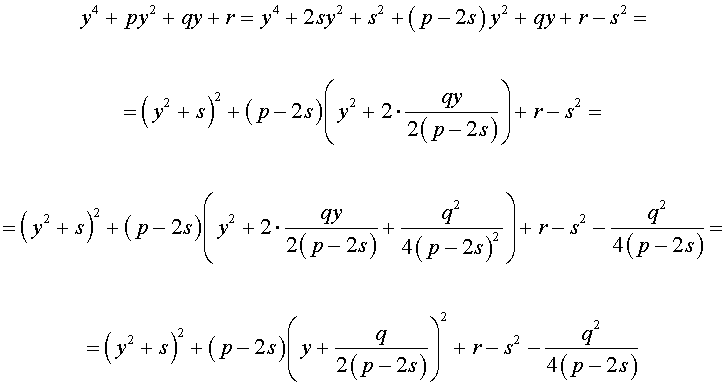
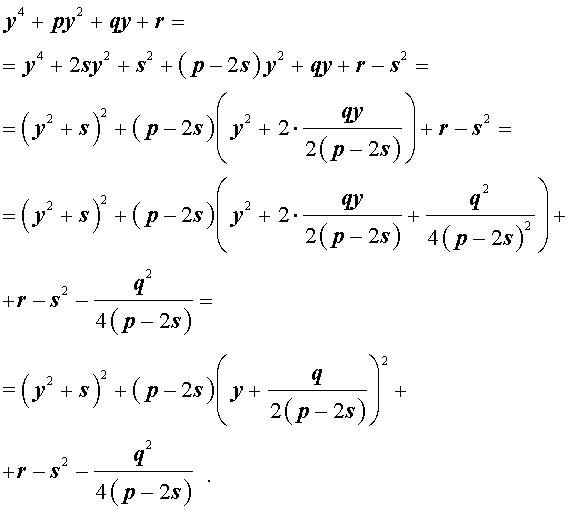
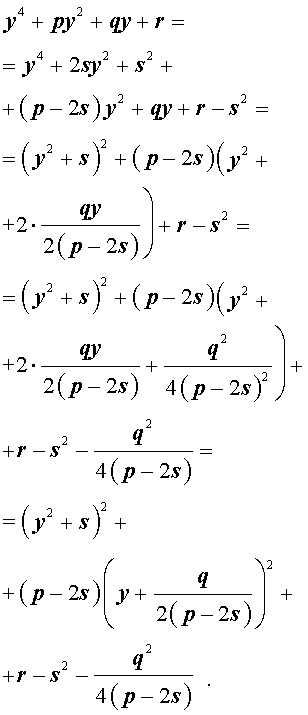
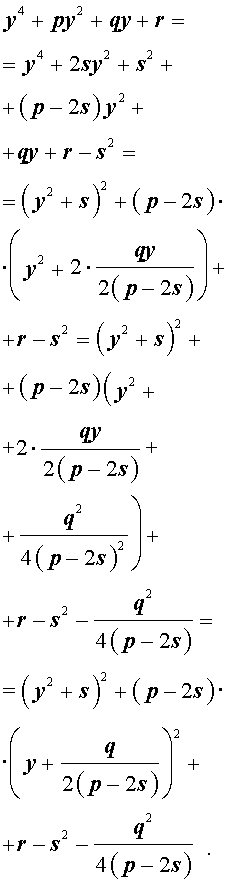
Следовательно, уравнение (5) принимает вид

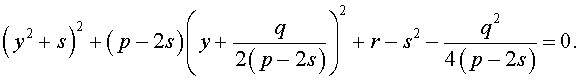
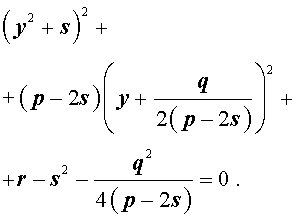
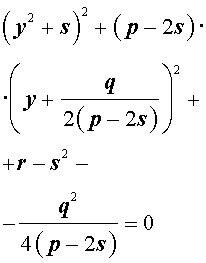
Если теперь выбрать число s так, чтобы оно являлось каким-нибудь решением уравнения

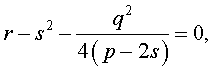
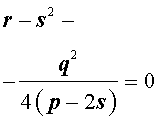
то уравнение (6) примет вид

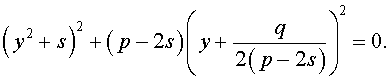
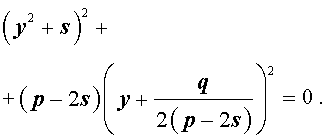
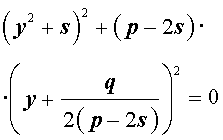
Избавляясь от знаменателя, уравнение (7) можно переписать в виде

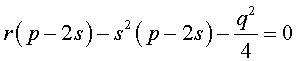
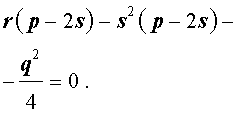
или, раскрыв скобки, – в виде

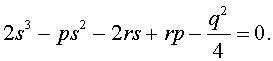
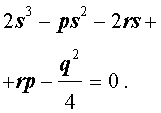
Полученное кубическое уравнение (9), эквивалентное уравнению (7), называют кубической резольвентой уравнения 4-ой степени (5).

Если какое-нибудь решение кубической резольвенты (9) найдено, то уравнение (8) можно решить, разложив его левую часть на множители с помощью формулы сокращенного умножения «Разность квадратов».

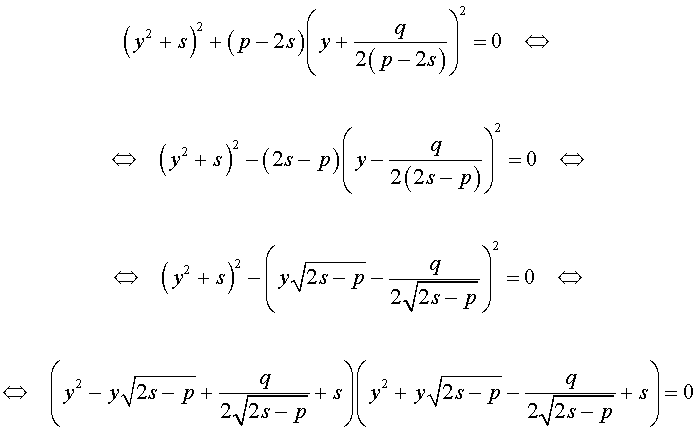
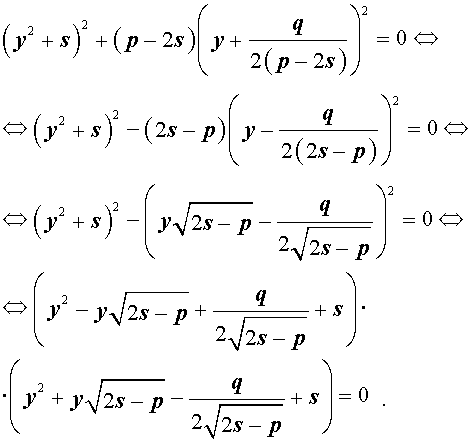
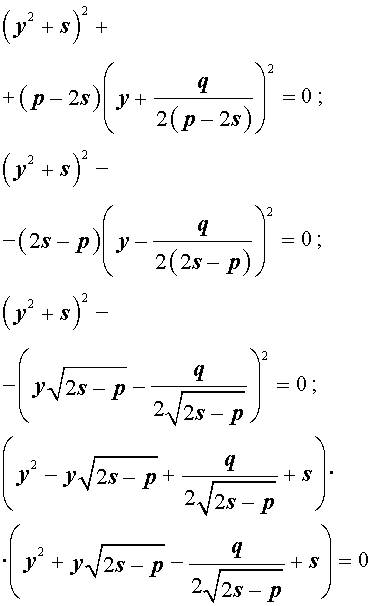
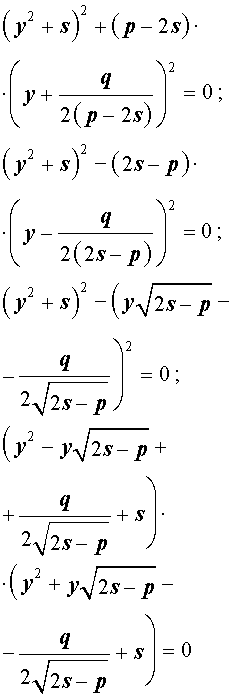
Таким образом, для решения уравнения (8) остаётся решить квадратное уравнение

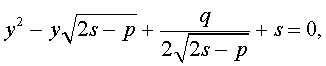
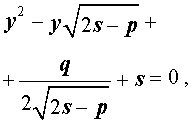
а также квадратное уравнение

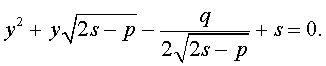
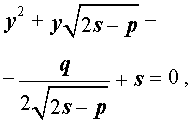
Вывод метода Феррари завершен.

Пример решения уравнения 4-ой степени

Пример . Решить уравнение

x 4 + 4x 3 – 4x 2 – – 20x – 5 = 0.

(12)

Решение . В соответствии с (3) сделаем в уравнении (12) замену

то в результате замены (13) уравнение (12) принимает вид

y 4 – 10y 2 – 4y + 8 = 0.

(14)

В соответствии с (5) для коэффициентов уравнения (14) справедливы равенства

p = – 10, q = – 4, r = 8.

(15)

В силу (9) и (15) кубической резольвентой для уравнения (14) служит уравнение

которое при сокращении на 2 принимает вид:

s 3 + 5s 2 – 8s – 42 = 0.

(16)

Подставляя значения (15) и (17) в формулу (10), получаем уравнение

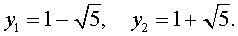
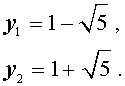
Подставляя значения (15) и (17) в формулу (11), получаем уравнение

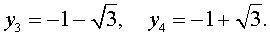
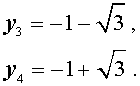
В завершение, воспользовавшись формулой (13), из (18) и (19) находим корни уравнения (12):

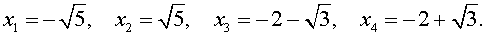
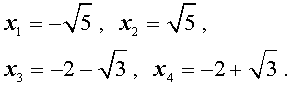
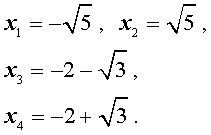
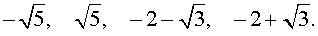
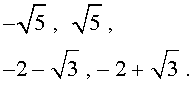
Замечание . При решении примера мы попутно получили разложение левой части уравнения (14) на множители:

y 4 – 10y 2 – 4y + 8 = = (y 2 – 2y – 4) (y 2 + + 2y – 2).

(20)

Предоставляем посетителю нашего сайта возможность убедиться в справедливости равенства (19) в качестве несложного упражнения.

[spoiler title=”источники:”]

http://habr.com/ru/post/537068/

http://www.resolventa.ru/spr/algebra/ferrary.htm

[/spoiler]

В общем случае решение уравнения четвёртой степени осуществляется с использованием методов решения уравнений для высших степеней, например, методом Феррари или с помощью схемы Горнера. Но некоторые уравнения 4-ой степени имеют более простое решение.

Существует несколько особых типов уравнений четвертой степени, со способами решения которых вы познакомитесь ниже:

• Биквадратное уравнения $ax^4+bx^2+c=0$;
• Возвратные уравнения вида $ax^4+bx^3+cx^2 +bx+ a=0$;
• Уравнения вида $ax^4+b=0$.

Решение биквадратных уравнений четвёртой степени

Биквадратные уравнения $ax^4+bx^2+c=0$ сводятся к квадратным путём замены переменной $x^2$ на новую, например, на $y$. После замены решается новое полученное уравнение, а затем значение найденной переменной подставляется в уравнение $x^2=y$. Результатом решения будут корни уравнения $x^2=y$.

Решение возвратных уравнений 4 степени

Эти уравнения вида $ax^4+bx^3+cx^2 +bx+ a=0$ повторяют своими коэффициентами при младших членах коэффициенты при многочленах со старшими степенями. Для решения такого уравнения сначала делят его на $x^2$:

$ax^4+bx^3+cx^2 +bx+ a=0|:x^2$

$ax^2+bx+c+frac{b}{x} + frac{a}{x^2}=0$

$a(x^2+frac{1}{x^2})+b(x+frac{1}{x}) + c=0$

Затем заменяют $(x+frac{1}{x})$ на новую переменную, тогда $(x^2+frac{1}{x^2})=y^2-2$, после подстановки получаем следующее квадратное уравнение:

«Решение уравнений четвертой степени» 👇

$a(y^2-2)+by+c=0$

После этого ищем корни уравнений $x+frac{1}{x}=y_1$ и $x+frac{1}{x}=y_2$.

Аналогичным методом решаются возвратные уравнения вида $ax^4+bx^3+cx^2 +kbx+ k^2a=0$.

Уравнения вида $ax^4+b=0$

Корни уравнения такой разновидности находятся с помощью применения формул сокращённого умножения.