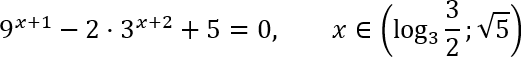В этой статье и постараюсь объяснить 2 способа отбора корней в тригонометрическом уравнение: с помощью неравенств и с помощью тригонометрической окружности. Перейдем сразу к наглядному примеру и походу дела будем разбираться.
а) Решить уравнение sqrt(2)cos^2x=sin(Pi/2+x)
б) Найдите все корни этого уравнения, принадлежащие промежутку [-7Pi/2; -2Pi]
Решим пункт а.
Воспользуемся формулой приведения для синуса sin(Pi/2+x) = cos(x)
sqrt(2)cos^2x = cosx
sqrt(2)cos^2x – cosx = 0
cosx(sqrt(2)cosx – 1) = 0
cosx = 0
x1 = Pi/2 + Pin, n ∈ Z
sqrt(2)cosx – 1 = 0
cosx = 1/sqrt(2)
cosx = sqrt(2)/2
x2 = arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x3 = -arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x2 = Pi/4 + 2Pin, n ∈ Z
x3 = -Pi/4 + 2Pin, n ∈ Z
Решим пункт б.
1) Отбор корней с помощью неравенств
Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [-7Pi/2; -2Pi], находим целые значения для n.
-7Pi/2 меньше или равно Pi/2 + Pin меньше или равно -2Pi
Сразу делим все на Pi
-7/2 меньше или равно 1/2 + n меньше или равно -2
-7/2 – 1/2 меньше или равно n меньше или равно -2 – 1/2
-4 меньше или равно n меньше или равно -5/2
Целые n в этом промежутку это -4 и -3. Значит корни принадлежащие этому промежутку буду Pi/2 + Pi(-4) = -7Pi/2, Pi/2 + Pi(-3) = -5Pi/2
Аналогично делаем еще два неравенства
-7Pi/2 меньше или равно Pi/4 + 2Pin меньше или равно -2Pi
-15/8 меньше или равно n меньше или равно -9/8
Целых n в этом промежутке нет
-7Pi/2 меньше или равно -Pi/4 + 2Pin меньше или равно -2Pi
-13/8 меньше или равно n меньше или равно -7/8
Одно целое n в этом промежутку это -1. Значит отобранный корень на этом промежутку -Pi/4 + 2Pi*(-1) = -9Pi/4.
Значит ответ в пункте б: -7Pi/2, -5Pi/2, -9Pi/4
2) Отбор корней с помощью тригонометрической окружности
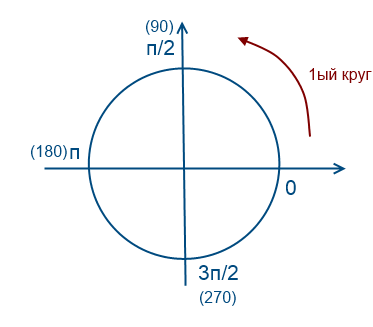
Чтобы пользоваться этим способом надо понимать как работает эта окружность. Постараюсь простым языком объяснить как это понимаю я. Думаю в школах на уроках алгебры эта тема объяснялась много раз умными словами учителя, в учебниках сложные формулировки. Лично я понимаю это как окружность, которую можно обходить бесконечное число раз, объясняется это тем, что функции синус и косинус периодичны.
Обойдем раз против часовой стрелки
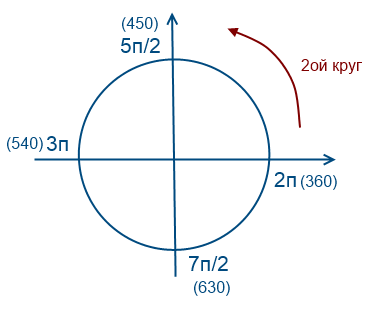
Обойдем 2 раза против часовой стрелки
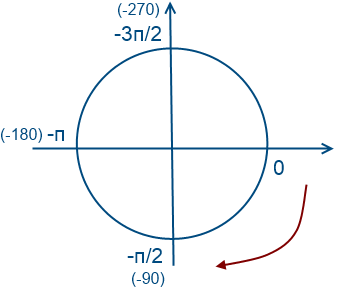
Обойдем 1 раз по часовой стрелки (значения будут отрицательные)
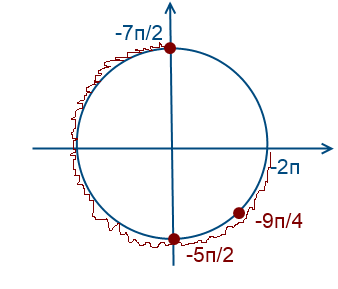
Вернемся к нашем вопросу, нам надо отобрать корни на промежутке [-7Pi/2; -2Pi]
Чтобы попасть к числам -7Pi/2 и -2Pi надо обойти окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.
Рассмотри x = Pi/2 + Pin. Какой приблизительно должен быть n, чтобы значение x было где-то в этом промежутке? Подставляем, допустим -2, получаем Pi/2 – 2Pi = -3Pi/2, очевидно это не входит в наш промежуток, значит берем меньше -3, Pi/2 – 3Pi = -5Pi/2, это подходит, попробуем еще -4, Pi/2 – 4Pi = -7Pi/2, также подходит.
Рассуждая аналогично для Pi/4 + 2Pin и -Pi/4 + 2Pin, находим еще один корень -9Pi/4.
Сравнение двух методов.
Первый способ (с помощью неравенств) гораздо надежнее и намного проще для пониманию, но если действительно серьезно разобраться с тригонометрической окружностью и со вторым методом отбора, то отбор корней будет гораздо быстрее, можно сэкономить около 15 минут на экзамене.
Просмотры: 157285 |
Статью добавил: slava191 |
Категория: математика
Отбор корней в тригонометрическом уравнение
В этой статье и постараюсь объяснить 2 способа отбора корней в тригонометрическом уравнение: с помощью неравенств и с помощью тригонометрической окружности. Перейдем сразу к наглядному примеру и походу дела будем разбираться.
а) Решить уравнение sqrt(2)cos^2x=sin(Pi/2+x)
б) Найдите все корни этого уравнения, принадлежащие промежутку [-7Pi/2; -2Pi]
Решим пункт а.
Воспользуемся формулой приведения для синуса sin(Pi/2+x) = cos(x)
sqrt(2)cos^2x — cosx = 0
cosx(sqrt(2)cosx — 1) = 0
x1 = Pi/2 + Pin, n ∈ Z
sqrt(2)cosx — 1 = 0
x2 = arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x3 = -arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x2 = Pi/4 + 2Pin, n ∈ Z
x3 = -Pi/4 + 2Pin, n ∈ Z
Решим пункт б.
1) Отбор корней с помощью неравенств
Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [-7Pi/2; -2Pi], находим целые значения для n.
-7Pi/2 меньше или равно Pi/2 + Pin меньше или равно -2Pi
Сразу делим все на Pi
-7/2 меньше или равно 1/2 + n меньше или равно -2
-7/2 — 1/2 меньше или равно n меньше или равно -2 — 1/2
-4 меньше или равно n меньше или равно -5/2
Целые n в этом промежутку это -4 и -3. Значит корни принадлежащие этому промежутку буду Pi/2 + Pi(-4) = -7Pi/2, Pi/2 + Pi(-3) = -5Pi/2
Аналогично делаем еще два неравенства
-7Pi/2 меньше или равно Pi/4 + 2Pin меньше или равно -2Pi
-15/8 меньше или равно n меньше или равно -9/8
Целых n в этом промежутке нет
-7Pi/2 меньше или равно -Pi/4 + 2Pin меньше или равно -2Pi
-13/8 меньше или равно n меньше или равно -7/8
Одно целое n в этом промежутку это -1. Значит отобранный корень на этом промежутку -Pi/4 + 2Pi*(-1) = -9Pi/4.
Значит ответ в пункте б: -7Pi/2, -5Pi/2, -9Pi/4
2) Отбор корней с помощью тригонометрической окружности
Чтобы пользоваться этим способом надо понимать как работает эта окружность. Постараюсь простым языком объяснить как это понимаю я. Думаю в школах на уроках алгебры эта тема объяснялась много раз умными словами учителя, в учебниках сложные формулировки. Лично я понимаю это как окружность, которую можно обходить бесконечное число раз, объясняется это тем, что функции синус и косинус периодичны.
Обойдем раз против часовой стрелки
Обойдем 2 раза против часовой стрелки
Обойдем 1 раз по часовой стрелки (значения будут отрицательные)
Вернемся к нашем вопросу, нам надо отобрать корни на промежутке [-7Pi/2; -2Pi]
Чтобы попасть к числам -7Pi/2 и -2Pi надо обойти окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.
Рассмотри x = Pi/2 + Pin. Какой приблизительно должен быть n, чтобы значение x было где-то в этом промежутке? Подставляем, допустим -2, получаем Pi/2 — 2Pi = -3Pi/2, очевидно это не входит в наш промежуток, значит берем меньше -3, Pi/2 — 3Pi = -5Pi/2, это подходит, попробуем еще -4, Pi/2 — 4Pi = -7Pi/2, также подходит.
Рассуждая аналогично для Pi/4 + 2Pin и -Pi/4 + 2Pin, находим еще один корень -9Pi/4.
Сравнение двух методов.
Первый способ (с помощью неравенств) гораздо надежнее и намного проще для пониманию, но если действительно серьезно разобраться с тригонометрической окружностью и со вторым методом отбора, то отбор корней будет гораздо быстрее, можно сэкономить около 15 минут на экзамене.
Решение тригонометрических уравнений на промежутке
Разделы: Математика
Цель урока:
а) закрепить умения решать простейшие тригонометрические уравнения;
б) научить выбирать корни тригонометрических уравнений из заданного промежутка
Ход урока.
1. Актуализация знаний.
а)Проверка домашнего задания: классу дано опережающее домашнее задание – решить уравнение и найти способ выбора корней из данного промежутка.
1)cos x = -0,5, где хI [- 

2) sin x = 


3)cos 2x = —

Ученики записывают решение на доске кто-то с помощью графика, кто-то методом подбора.
В это время класс работает устно.
Найдите значение выражения:
а) tg 



б) 2arccos 0 + 3 arccos 1. Ответ: ?
в) arcsin 


г) 5 arctg (-


– Проверим домашнее задание, откройте свои тетради с домашними работами.
Некоторые из вас нашли решение методом подбора, а некоторые с помощью графика.
2. Вывод о способах решения данных заданий и постановка проблемы, т. е. сообщение темы и цели урока.
– а) С помощью подбора решать сложно, если задан большой промежуток.
– б) Графический способ не даёт точных результатов, требует проверку, и занимает много времени.
– Поэтому должен быть ещё как минимум один способ, наиболее универсальный -попробуем его найти. Итак, чем мы будем заниматься сегодня на уроке? (Учиться выбирать корни тригонометрического уравнения на заданном промежутке.)
– Пример 1. (Ученик выходит к доске)
cos x = -0,5, где хI [- 
Вопрос: Отчего зависит ответ на данное задание? (От общего решения уравнения. Запишем решение в общем виде). Решение записывается на доске
х =


– Запишем это решение в виде совокупности:
– Как вы считаете, при какой записи решения удобно выбирать корни на промежутке? (из второй записи). Но это ведь опять способ подбора. Что нам необходимо знать, чтобы получить верный ответ? (Надо знать значения k).
(Составим математическую модель для нахождения k).
1 уровень: № 295 (а,б), № 317 (а,б)
2 уровень: № 307 (в), № 308 (б), № 326(б), № 327(б).
Задача C1: еще одно показательное уравнение
Будьте внимательны: само уравнение решается легко! Основные проблемы начинаются во время отбора корней.
Задача C1. Решите уравнение. Найдите все корни этого уравнения, принадлежащие промежутку.
Показательные уравнения в задачах C1 обычно сводятся к квадратным через замену переменной. Подобные уравнения вполне могут встретиться в реальном ЕГЭ по математике.
Обратите внимание на последний этап — отбор корней. Для строгого математического обоснования необходимо составить цепочку неравенств, которая убедительно покажет нам, что полученный корень действительно лежит на искомом интервале.
источники:
http://urok.1sept.ru/articles/419940
http://www.berdov.com/ege/equation-root/pokazatelnoe-uravnenie-ogranichenie-log/
Слайд 1
Методы отбора корней в тригонометрических уравнениях на заданном промежутке
Слайд 2
Баллы за задание №12 (С-1) 2015 2018 2020 2021 1 балл 90,7% 73, 7% 92,2% 100% 2 балла 69,4% 51,1% 83,5% 100%
Слайд 5
Обязательный минимум знаний sin x = a , -1 a 1 ( a 1) x = arcsin a + 2 n, n Z x = – arcsin a + 2 n, n Z sin x = 1 x = /2 + 2 k, k Z sin x = – 1 x = – /2 + 2 k, k Z sin x = 0 x = k, k Z y x y x x y
Слайд 6
Обязательный минимум знаний cos x = a , -1 a 1 ( a 1) x = arccos a + 2 n, n Z arccos (- a) = – arccos a cos x = 1 x = 2 k, k Z cos x = – 1 x = + 2 k, k Z cos x = 0 x = /2 + k, k Z y x y x y x
Слайд 7
Обязательный минимум знаний tg x = a , a R x = arctg a + n, n Z arctg (- a) = – arctg a ctg x = a , a R x = arcctg a + n, n Z arctg (- a) = – arctg a
Слайд 8
Рекомендации по решению тригонометрических уравнений Свести уравнение к простейшему Некоторые методы решения тригонометрических уравнений Применение тригонометрических формул Использование формул сокращённого умножения Разложение на множители Сведение к квадратному уравнению относительно sin x, cos x, tg x Введением вспомогательного аргумента Делением обеих частей однородного уравнения первой степени ( asin x +bcosx = 0 ) на cos x Делением обеих частей однородного уравнения второй степени (a sin 2 x +bsin x cos x+ c cos 2 x =0) на cos 2 x
Слайд 9
Различные способы отбора корней cos 2x = ½, x [- /2; 3 /2] 2x = ± arccos ½ + 2 n, n Z 2x = ± /3 + 2 n, n Z x = ± /6 + n, n Z Отберём корни с помощью тригонометрической окружности Ответ : – /6; /6; 5 /6; 7 /6 Найти корни уравнения, принадлежащие данному промежутку (с помощью тригонометрической окружности)
Слайд 10
Различные способы отбора корней Найти корни уравнения, принадлежащие данному промежутку (арифметический, метод перебора) sin 3x = √3/2, x [- /2; /2] 3x = ( – 1) k /3 + k, k Z x = ( – 1) k /9 + k/3, k Z Отберём корни с помощью перебора значений k: k = 0, x = /9 – принадлежит промежутку k = 1, x = – /9 + /3 = 2 /9 – принадлежит промежутку k = 2, x = /9 + 2 /3 = 7 /9 – не принадлежит промежутку k = – 1, x = – /9 – /3 = – 4 /9 – принадлежит промежутку k = – 2, x = /9 – 2 /3 = – 5 /9 – не принадлежит промежутку Ответ: -4 /9; /9; 2 /9
Слайд 11
Различные способы отбора корней tg 3x = – 1 , x (- /2; ) 3x = – /4 + n, n Z x = – /12 + n/3, n Z Отберём корни с помощью неравенства: Ответ: – 5 /12; – /12; /4; 7 /12; 11 /12 – /2 < – /12 + n/3 < , – 1/2 < – 1/12 + n/3 < 1, – 1/2 + 1/12 < n/3 < 1+ 1/12, – 5/12 < n/3 < 13/12, – 5/4 < n < 13/4, n Z, n = – 1; 0; 1; 2; 3 Найти корни уравнения, принадлежащие данному промежутку ( с помощью неравенства) n = – 1, x = – /12 – /3 = – 5 /12 n = 0, x = – /12 n = 1, x = – /12 + /3 = /4 n = 2, x = – /12 + 2 /3 = 7 /12 n = 3, x = – /12 + = 11 /12
Слайд 12
Различные способы отбора корней Найти корни уравнения, принадлежащие данному промежутку ( с помощью графика) cos x = – √2/2, x [ – 4; 5 /4] x = arccos (– √2/2) + 2 n, n Z x = 3 /4 + 2 n, n Z Отберём корни с помощью графика: Ответ: 5 /4; 3 /4 x = – /2 – /4 = – 3 /4; x = – – /4 = – 5 /4
Слайд 13
1. Решить уравнение 7 2cosx = 49 sin2x и указать его корни на отрезке [ ; 5 /2] 7 2cosx = 49 sin2x, 7 2cosx = 7 2sin2x, 2cos x = 2sin 2x, cos x – 2 sinx cosx = 0, cos x (1 – 2sinx) = 0, cos x = 0 , x = /2 + k, k Z или 1 – 2sinx = 0, sin x = ½, x = /6 + 2 k, k Z x = 5 /6 + 2 k, k Z Решим уравнение: Проведём отбор корней с помощью тригонометрической окружности: Ответ: а) /2 + k, k Z, x1 = /6 + 2 k, k Z; x2 = 5 /6 + 2 k, k Z б) 3 /2; 5 /2; 13 /6 x = 2 + /6 = 13 /6
Слайд 14
4cos 2 x + 8 cos (x – 3 /2) +1 = 0 4cos 2 x + 8 cos (3 /2 – x) +1 = 0, 4cos 2 x – 8 sin x +1 = 0, 4 – 4sin 2 x – 8 sin x +1 = 0, 4sin 2 x + 8sin x – 5 = 0, D/4 = 16 + 20 = 36, sin x = – 2,5 или sin x = ½ x1= /6 + 2 k, k Z x2 = 5 /6 + 2 k, k Z 2. Решить уравнение 4cos 2 x + 8 cos (x – 3 /2) +1 = 0 Найти его корни на отрезке [3 ; 9 2]
Слайд 15
Проведем отбор корней на отрезке [3 ; 9 2] (с помощью графиков) x = 4 + /6 = 25 /6 Ответ: а) x1 = /6 + 2 k, k Z x2 = 5 /6 + 2 k, k Z б) 25 /6 sin x = ½ Построим графики функций y = sin x и y = ½
Слайд 16
3. Решить уравнение 4 – cos 2 2x = 3 sin 2 2x + 2 sin 4x Найти его корни на отрезке [0; 1] 4 – cos 2 2x = 3 sin 2 2x + 2 sin 4x 4 (sin 2 2x + cos 2 2x ) – cos 2 2x = 3 sin 2 2x + 4 sin 2x cos 2x, sin 2 2x + 3 cos 2 2x – 4 sin 2x cos 2x = 0 Если cos 2 2x = 0, то sin 2 2x = 0, что невозможно, поэтому cos 2 2x 0 и обе части уравнения можно разделить на cos 2 2x. tg 2 2x + 3 – 4 tg 2x = 0, tg 2 2x – 4 tg 2x + 3= 0, tg 2x = 1, 2x = /4 + n, n Z x = /8 + n/2, n Z или tg 2x = 3, 2x = arctg 3 + k, k Z x = ½ arctg 3 + k/2, k Z
Слайд 17
Проведём отбор корней на отрезке [0; 1] 4 – cos 2 2x = 3 sin 2 2x + 2 sin 4x x = /8 + n/2, n Z или x = ½ arctg 3 + k/2, k Z Так как 0 < arctg 3< /2, 0 < ½ arctg 3< /4, то ½ arctg 3 является решением Так как 0 < /8 < /4 < 1,значит /8 также является решением Другие решения не попадут в промежуток [0; 1], так как они получаются из чисел ½ arctg 3 и /8 прибавлением чисел, кратных /2. Ответ: а) /8 + n/2, n Z ; ½ arctg 3 + k/2, k Z б) /8; ½ arctg 3
Слайд 18
4. Решить уравнение log 5 (cos x – sin 2x + 25) = 2 Найти его корни на отрезке [2 ; 7 /2] log 5 (cos x – sin 2x + 25) = 2 cos x – sin 2x + 25 > 0, cos x – sin 2x + 25 = 25, 25 > 0, cos x – 2sin x cos x = 0, cos x (1 – 2sin x) = 0, cos x = 0, x = /2 + n, n Z или 1 – 2sinx = 0, sin x = 1/2 x = /6 + 2 k, k Z x = 5 /6 + 2 k, k Z Решим уравнение:
Слайд 19
1) x = /2 + n, n Z 2 /2 + n 7 /2, n Z 2 1/2 + n 7/2, n Z 2 – ½ n 7/2 – ½, n Z 1,5 n 3, n Z n = 2; 3 x = /2 + 2 = 5 /2 x = /2 + 3 = 7 /2 x = 2 + /6 = 13 /6 x = 3 – /6 = 17 /6 Проведём отбор корней на отрезке [2 ; 7 /2]: Проведём отбор корней на отрезке 2) sin x = 1/2 Ответ: а) /2 + n, n Z; x1 = /6 + 2 k, k Z x2 = 5 /6 + 2 k, k Z б) 13 /6 ; 5 /2; 7 /2; 17 /6
Слайд 20
5. Решить уравнение 1/sin 2 x + 1/sin x = 2 Найти его корни на отрезке [-5 /2; -3 /2] 1/sin 2 x + 1/sin x = 2 x k Замена 1/sin x = t, t 2 + t = 2, t 2 + t – 2 = 0, t 1 = – 2, t 2 = 1 Решим уравнение: 1/sin x = – 2, sin x = – ½, x = – /6 + 2 n, n Z или x = – 5 /6 + 2 n, n Z 1/sin x = 1, sin x = 1, x = /2 + 2 n, n Z
Слайд 21
1) x = – /6 + 2 n, n Z -5 /2 – /6 + 2 n -3 /2, n Z -5/2 -1/6 + 2n -3/2, n Z -5/2 +1/6 2n -3/2 + 1/6, n Z – 7/3 2n -4/3, n Z -7/6 n -2/3, n Z n = -1 x = – /6 – 2 = -13 /6 Рассмотрим остальные серии корней и проведём отбор корней на отрезке алгебраическим методом [-5 /2; -3 /2] Продолжим отбор корней на отрезке Ответ: а) /2 + 2 n, n Z ; x1 = – /6 + 2 k, k Z x2 = – 5 /6 + 2 k, k Z б) -13 /6 ; -3 /2 2) x = /2 + 2 n, n Z -5 /2 /2 + 2 n -3 /2, n Z -5/2 1/2 + 2n -3/2, n Z -5/2 – 1/2 2n -3/2 – 1/2, n Z – 3 2n -2, n Z -1,5 n -1, n Z n = -1 x = /2 – 2 = -3 /2
Слайд 22
6. Решить уравнение |sin x|/sin x + 2 = 2cos x Найти его корни на отрезке [-1; 8] Решим уравнение |sin x|/sin x + 2 = 2cos x 1)Если sin x >0, то |sin x| =sin x Уравнение примет вид: 2 cos x=3, cos x =1,5 – не имеет корней 2) Если sin x <0, то |sin x| =-sin x и уравнение примет вид 2cos x=1, cos x = 1/2, x = ±π/3 +2πk, k Z Учитывая, что sin x < 0, то остаётся одна серия ответа x = – π/3 +2πk, k Z Произведём отбор корней на отрезке [-1; 8] k=0, x= – π/3 , – π < -3, – π/3 < -1, -π/3 не принадлежит данному отрезку k=1, x = – π/3 +2π = 5 π/3<8, 5 π/3 [-1; 8] k=2, x= – π/3 + 4π = 11 π/3 > 8, 11 π/3 не принадлежит данному отрезку. Ответ: а) – π/3 +2πk, k Z б) 5 π/3
Слайд 23
7. Решить уравнение 4sin 3 x=3cos(x- π/2) Найти его корни на промежутке [7 /2; 9 /2) Решим уравнение 4sin 3 x = 3cos(x- π/2) 4sin 3 x = 3cos(π/2-х), 4sin 3 x – 3cos(π/2-х) = 0, 4sin 3 x – 3sin x = 0, sin x (4sin 2 x – 3) = 0, sin x= 0 x= n, n Z или 4sin 2 x – 3=0, sin x=√3/2; sin x =-√3/2 sin x=√3/2, x1= /3 + 2 k, k Z, x2=4 /3 + 2 k, k Z. sin x =-√3/2, x1=- /3 + 2 k, k Z, x2= -4 /3 + 2 k, k Z.
Слайд 24
Объединим решения ( см. рисунок) Уравнение можно решить короче, зная формулу sin 3x = 3sinx – 4sin 3 x : 4sin 3 x – 3sin x =0, 3sin x – 4sin 3 x =0, s in 3x = 0, х = m/3, m Z или х = m/3, m Z
Слайд 25
Проведём отбор корней на промежутке [7 /2; 9 /2) х= m/3, m Z. 7 /2 ≤ m/3 < 9 /2, 21/2 ≤ m<27/2, m Z, 10,5 ≤ m < 13,5, m Z, m =10; 11; 12, x= 10 /3, x= 11 /3, x= 12 /3 Ответ : а) m/3, m Z; б) 10 /3; 11 /3; 12 /3
Слайд 26
8. Решить уравнение √1-sin 2 x= sin x Найти его корни на промежутке [5 /2; 4 ] Решим уравнение √1-sin 2 x= sin x. sin x ≥ 0, 1- sin 2 x = sin 2 x; sin x ≥ 0, sin x≥0, 2sin 2 x = 1; sin x =√2/2; sin x = – √2/2; sin x =√2/2 sin x =√2/2 x=(-1) k /4 + k, k Z
Слайд 27
Проведём отбор корней на отрезке [5 /2; 4 ] x=(-1) k /4 + k, k Z sin x =√2/2 у =sin x и у=√2/2 5 /2 + /4 = 11 /4 Ответ: а) (-1) k /4 + k, k Z ; б) 11 /4
Слайд 28
9. Решить уравнение (sin2x + 2 sin 2 x)/√-cos x =0 Найти его корни на промежутке [-5 ; -7 /2] Решим уравнение (sin2x + 2 sin 2 x)/√-cos x =0. 1) cos x <0 , /2 +2 n
Слайд 29
Отберём корни на заданном отрезке Отберём корни на заданном отрезке [-5 ; -7 /2] x= +2 n, n Z ; -5 ≤ +2 n ≤ -7 /2, -5-1 ≤ 2n ≤ -7/2-1, -3≤ n ≤ -9/4, n Z n = -3, x= -6 = -5 x= 3 /4 + 2 n, n Z -5 ≤ 3 /4 + 2 n ≤ -7 /2 -23/8 ≤ n ≤ -17/8, нет такого целого n. Ответ: а) +2 n, n Z ; 3 /4 + 2 n, n Z ; б) -5 .
Слайд 30
10. Решить уравнение 2sin2x =4cos x –sinx+1 Найти его корни на промежутке [ /2; 3 /2 ] Решим уравнение 2sin2x = 4cos x – sinx+1 2sin2x = 4cos x – sinx+1, 4 sinx∙cos x – 4cos x + sin x -1 = 0, 4cos x(sin x – 1) + (sin x – 1) = 0, (sin x – 1)(4cos x +1)=0, sin x – 1= 0, sin x = 1, x = /2+2 n, n Z или 4cos x +1= 0, cos x = -0,25 x = ± ( -arccos (0,25)) + 2 n, n Z Запишем корни этого уравнения иначе x = – arccos(0,25) + 2 n, x = -( – arccos(0,25)) + 2 n, n Z
Слайд 31
Отберём корни с помощью окружности x = /2+2 n, n Z, х = /2; x = -arccos(0,25)+2 n, х=-( -arccos(0,25)) +2 n, n Z, x = – arccos(0,25), x = + arccos(0,25) Ответ: а) /2+2 n, -arccos(0,25)+2 n, -( -arccos(0,25)) +2 n, n Z; б) /2; -arccos(0,25); +arccos(0,25)
Приветствую Вас!
Как мне кажется, самое простое в высшей математике – это тригонометрия. Если изначально ухватить ее за хвост, то и думать тут негде. Но, чтобы так было, ее нужно правильно преподнести. Долго разглагольствовать по этому поводу не буду. Просто приведу решение, которое в основном дается в школах, а потом свое.
Вот, к примеру, такое уравнение:
Кто дает эту дебильнейшую формулу? Как, бля, детям ее понять, и плюс найти корни на промежутке, еще и с периодом Пк/2, ничего не упустив? Господа-препода, вы что, бредите? Есть же легкие формулы по синусу. Их две, и они конкретные.
С помощью них и, решив простое неравенство, можно получить фактические корни, и ни в чем не сомневаться. Ведь математика – это точная наука!
Для кого-то я, безусловно, Америку не открою, и обращаюсь сейчас к тем ребятам, кто не знает этих формул, либо не владеет абсолютно точным методом определения корней на промежутке. Будем разбирать данное уравнение. Для начала формулы по синусу:
По-моему, здесь все предельно ясно. Где находятся корни, и куда их выставить на этом злополучном круге. Благо, что промежуток дан такой. Возможно понять, что отнимем 5П, да и попадем куда надо. А, если промежуток дан “кривой”, плюс период вышел из уравнения типо П/4. Что тогда? Гадать на кофейной гуще? Не, не надо. Можно точно все просчитать и ни в чем не сомневаться. Смотри:
Соответственно так же просчитываем остальные корни. В данном случае к= только -5, но бывает и так, что к= нескольким целым числам. Допустим:
И помни, этот “страшный” ноль является целым числом!
Много писанины, согласна. Зато, во-первых, это стопудово, а во-вторых, это экзамен, и ты ни в чем не должен сомневаться!
И еще одна рекомендация, которая так “не по вкусу”, а относится она к любому заданию:
НИЧЕГО не считай в “уме”. Только в СТОЛБИК. Расписывай абсолютно всё. Так ты избежишь “глупых” ошибок. Требуется в конце уравнения разделить на два, так запиши это, не пропускай эту строку.
2х=6,
х=6:2, (!)
х=3.
Желаю всем удачи и холодной головы!
Благодарю за внимание..
Чтобы успешно решать тригонометрические уравнения удобно пользоваться методом сведения к ранее решенным задачам. Давайте разберемся, в чем суть этого метода?
В любой предлагаемой задаче вам необходимо увидеть уже решенную ранее задачу, а затем с помощью последовательных равносильных преобразований попытаться свести данную вам задачу к более простой.
Так, при решении тригонометрических уравнений обычно составляют некоторую конечную последовательность равносильных уравнений, последним звеном которой является уравнение с очевидным решением. Только важно помнить, что если навыки решения простейших тригонометрических уравнений не сформированы, то решение более сложных уравнений будет затруднено и малоэффективно.
Кроме того, решая тригонометрические уравнения, никогда не стоит забывать о возможности существования нескольких способов решения.
Пример 1. Найти количество корней уравнения cos x = -1/2 на промежутке [0; 2π].
Решение:
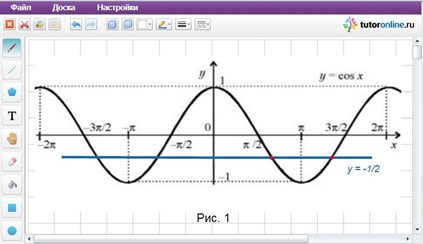
I способ. Изобразим графики функций y = cos x и y = -1/2 и найдем количество их общих точек на промежутке [0; 2π] (рис. 1).
Так как графики функций имеют две общие точки на промежутке [0; 2π], то уравнение содержит два корня на данном промежутке.
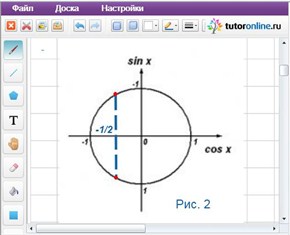
II способ. С помощью тригонометрического круга (рис. 2) выясним количество точек, принадлежащих промежутку [0; 2π], в которых cos x = -1/2. По рисунку видно, что уравнение имеет два корня.
III способ. Воспользовавшись формулой корней тригонометрического уравнения, решим уравнение cos x = -1/2.
cos x = -1/2;
x = ± arccos (-1/2) + 2πk, k – целое число (k € Z);
x = ± (π – arccos 1/2) + 2πk, k – целое число (k € Z);
x = ± (π – π/3) + 2πk, k – целое число (k € Z);
x = ± 2π/3 + 2πk, k – целое число (k € Z).
Промежутку [0; 2π] принадлежат корни 2π/3 и -2π/3 + 2π, k – целое число. Таким образом, уравнение имеет два корня на заданном промежутке.
Ответ: 2.
В дальнейшем тригонометрические уравнения будут решаться одним из предложенных способов, что во многих случаях не исключает применения и остальных способов.
Пример 2. Найти количество решений уравнения tg (x + π/4) = 1 на промежутке [-2π; 2π].
Решение:
Воспользовавшись формулой корней тригонометрического уравнения, получим:
x + π/4 = arctg 1 + πk, k – целое число (k € Z);
x + π/4 = π/4 + πk, k – целое число (k € Z);
x = πk, k – целое число (k € Z);
Промежутку [-2π; 2π] принадлежат числа -2π; -π; 0; π; 2π. Итак, уравнение имеет пять корней на заданном промежутке.
Ответ: 5.
Пример 3. Найти количество корней уравнения cos2 x + sin x · cos x = 1 на промежутке [-π; π].
Решение:
Так как 1 = sin2 x + cos2 x (основное тригонометрическое тождество), то исходное уравнение принимает вид:
cos2 x + sin x · cos x = sin2 x + cos2 x;
sin2 x – sin x · cos x = 0;
sin x(sin x – cos x) = 0. Произведение равно нулю, а значит хотя бы один из множителей должен быть равен нулю, поэтому:
sin x = 0 или sin x – cos x = 0.
Так как значение переменной, при которых cos x = 0, не являются корнями второго уравнения (синус и косинус одного и того же числа не могут одновременно быть равными нулю), то разделим обе части второго уравнения на cos x:
sin x = 0 или sin x / cos x – 1 = 0.
Во втором уравнении воспользуемся тем, что tg x = sin x / cos x, тогда:
sin x = 0 или tg x = 1. С помощью формул имеем:
x = πk или x = π/4 + πk, k – целое число (k € Z).
Из первой серии корней промежутку [-π; π] принадлежат числа -π; 0; π. Из второй серии: (π/4 – π) и π/4.
Таким образом, пять корней исходного уравнения принадлежат промежутку [-π; π].
Ответ: 5.
Пример 4. Найти сумму корней уравнения tg2 x + сtg2 x + 3tg x + 3сtgx + 4 = 0 на промежутке [-π; 1,1π].
Решение:
Перепишем уравнение в следующем виде:
tg2 x + сtg2 x + 3(tg x + сtgx) + 4 = 0 и сделаем замену.
Пусть tg x + сtgx = a. Обе части равенства возведем в квадрат:
(tg x + сtg x)2 = a2. Раскроем скобки:
tg2 x + 2tg x · сtgx + сtg2 x = a2.
Так как tg x · сtgx = 1, то tg2 x + 2 + сtg2 x = a2, а значит
tg2 x + сtg2 x = a2 – 2.
Теперь исходное уравнение имеет вид:
a2 – 2 + 3a + 4 = 0;
a2 + 3a + 2 = 0. С помощью теоремы Виета получаем, что a = -1 или a = -2.
Сделаем обратную замену, имеем:
tg x + сtgx = -1 или tg x + сtgx = -2. Решим полученные уравнения.
tg x + 1/tgx = -1 или tg x + 1/tgx = -2.
По свойству двух взаимно обратных чисел определяем, что первое уравнение не имеет корней, а из второго уравнения имеем:
tg x = -1, т.е. x = -π/4 + πk, k – целое число (k € Z).
Промежутку [-π; 1,1π] принадлежат корни: -π/4; -π/4 + π. Их сумма:
-π/4 + (-π/4 + π) = -π/2 + π = π/2.
Ответ: π/2.
Пример 5. Найти среднее арифметическое корней уравнения sin 3x + sin x = sin 2x на промежутке [-π; 0,5π].
Решение:
Воспользуемся формулой sin α + sin β = 2sin ((α + β)/2) · cos ((α – β)/2), тогда
sin 3x + sin x = 2sin ((3x + x)/2) · cos ((3x – x)/2) = 2sin 2x · cos x и уравнение принимает вид
2sin 2x · cos x = sin 2x;
2sin 2x · cos x – sin 2x = 0. Вынесем общий множитель sin 2x за скобки
sin 2x(2cos x – 1) = 0. Решим полученное уравнение:
sin 2x = 0 или 2cos x – 1 = 0;
sin 2x = 0 или cos x = 1/2;
2x = πk или x = ±π/3 + 2πk, k – целое число (k € Z).
Таким образом, имеем корни
x = πk/2, x = π/3 + 2πk, x = -π/3 + 2πk, k – целое число (k € Z).
Промежутку [-π; 0,5π] принадлежат корни -π; -π/2; 0; π/2 (из первой серии корней); π/3 (из второй серии); -π/3 (из третьей серии). Их среднее арифметическое равно:
(-π – π/2 + 0 + π/2 + π/3 – π/3)/6 = -π/6.
Ответ: -π/6.
Пример 6. Найти количество корней уравнения sin x + cos x = 0 на промежутке [-1,25π; 2π].
Решение:
Данное уравнение является однородным уравнением первой степени. Разделим обе его части на cosx (значение переменной, при которых cos x = 0, не являются корнями данного уравнения, так как синус и косинус одного и того же числа не могут одновременно быть равными нулю). Исходное уравнение имеет вид:
tg x + 1 = 0;
tg x = -1;
x = -π/4 + πk, k – целое число (k € Z).
Промежутку [-1,25π; 2π] принадлежат корни -π/4; (-π/4 + π); и (-π/4 + 2π).
Таким образом, заданному промежутку принадлежат три корня уравнения.
Ответ: 3.
Научитесь делать самое главное – четко представлять план решения задачи, и тогда любое тригонометрическое уравнение будет вам по плечу.
Остались вопросы? Не знаете, как решать тригонометрические уравнения?
Чтобы получить помощь репетитора – зарегистрируйтесь.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.