Применение производной для решения нелинейных уравнений и неравенств
- Количество корней кубического уравнения
- Количество корней произвольного уравнения
- Решение неравенств с построением графиков
п.1. Количество корней кубического уравнения
Кубическое уравнение $$ ax^3+bx^2+cx+d=0 $$ на множестве действительных чисел может иметь один, два или три корня.
С помощью производной можно быстро ответить на вопрос, сколько корней имеет данное уравнение. begin{gather*} f(x)=ax^3+bx^2+cx+d\ f'(x)=3ax^2+bx+c end{gather*} Если в уравнении (f'(x)=0) дискриминант (D=4b^2-12ac=4(b^2-3ac)gt 0), кубическая парабола имеет две точки экстремума: (x_{1,2}=frac{-2bpmsqrt{D}}{6a}). Если при этом значения функции в точках экстремума (f(x_1)cdot f(x_2)lt 0), т.е. расположены по разные стороны от оси OX, парабола имеет три точки пересечения с этой осью. Исходное уравнение имеет три корня.
Если две точки экстремума найдены, но (f(x_1)cdot f(x_2)=0), уравнение имеет два корня.
Во всех остальных случаях – у исходного уравнения 1 корень.
Уравнение (ax^3+bx^2+cx+d=0)
Имеет три корня, если ( begin{cases} b^2-3acgt 0\ f(x_1)cdot f(x_2)lt 0 end{cases} )
Имеет два корня, если ( begin{cases} b^2-3acgt 0\ f(x_1)cdot f(x_2)= 0 end{cases} )
В противном случае – один корень.
Пример 1. Сколько корней имеют уравнения:
п.2. Количество корней произвольного уравнения
Задачи на подсчет количества корней решаются с помощью построения графиков при полном или частичном исследовании функций.
Пример 2. а) Найдите число корней уравнения (frac 1x+frac{1}{x-1}+frac{1}{x-3})
б) Найдите число корней уравнения (frac 1x+frac{1}{x-1}+frac{1}{x-3}=k)
Построим график функции слева, а затем найдем для него количество точек пересечения с горизонталью (y=1). Это и будет ответом на вопрос задачи (а).
Исследуем функцию: $$ f(x)=frac1x+frac{1}{x-1}+frac{1}{x-3} $$ Алгоритм исследования и построения графика – см. §49 данного справочника.
1) ОДЗ: (xneleft{0;1;3right})
Все три точки – точки разрыва 2-го рода. begin{gather*} lim_{xrightarrow -0}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=-infty-1-frac13=-infty\ lim_{xrightarrow +0}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=+infty-1-frac13=+infty\ lim_{xrightarrow 1-0}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=1-infty-frac12=-infty\ lim_{xrightarrow 1+0}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=1+infty-frac12=+infty\ lim_{xrightarrow 3-0}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=frac13+frac12-infty=-infty\ lim_{xrightarrow 3+0}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=frac13+frac12+infty=+infty end{gather*} 2) Функция ни четная, ни нечетная.
Функция непериодическая.
3) Асимптоты
1. Вертикальные (x=0, x=1, x=3) – точки разрыва 2-го рода
2. Горизонтальные: begin{gather*} lim_{xrightarrow -infty}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=-0-0-0=-0\ lim_{xrightarrow +infty}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=+0+0+0=+0\ end{gather*} Горизонтальная асимптота (y=0)
На минус бесконечности функция стремится к 0 снизу, на плюс бесконечности – сверху.
3. Наклонные: (k=0), нет.
4) Первая производная $$ f'(x)=-frac{1}{x^2}-frac{1}{(x-1)^2}-frac{1}{(x-3)^2}lt 0 $$ Производная отрицательная на всей ОДЗ.
Функция убывает.
5) Вторую производную не исследуем, т.к. перегибы не влияют на количество точек пересечения с горизонталью.
6) Точки пересечения с OY – нет, т.к. (x=0) – асимптота
Точки пересечения с OX – две, (0lt x_1lt 1,1lt x_2lt 3)
7) График
Получаем ответ для задачи (а) 3 корня.
Решаем более общую задачу (б). Передвигаем горизонталь (y=k) снизу вверх и считаем количество точек пересечения с графиком функции. Последовательно, получаем:
При (klt 0) – три корня
При (k=0) – два корня
При (kgt 0) – три корня
Ответ: а) 3 корня; б) при (k=0) два корня, при (kne 0) три корня.
Пример 3. Найдите все значения параметра a, при каждом из которых уравнение $$ sqrt{x-1}+sqrt{10-2x}=a $$ имеет по крайней мере одно решение.
Исследуем функцию (f(x)=sqrt{x-1}+sqrt{10-2x})
ОДЗ: ( begin{cases} x-1geq 0\ 10-2xgeq 0 end{cases} Rightarrow begin{cases} xgeq 1\ xleq 5 end{cases} Rightarrow 1leq xleq 5 )
Функция определена на конечном интервале.
Поэтому используем сокращенный алгоритм для построения графика.
Значения функции на концах интервала: (f(1)=0+sqrt{8}=2sqrt{2}, f(5)=sqrt{4}+0=2)
Первая производная: begin{gather*} f'(x)=frac{1}{2sqrt{x-1}}+frac{-2}{2sqrt{10-2x}}=frac{1}{2sqrt{x-1}}-frac{1}{sqrt{10-2x}}\ f'(x)=0 text{при} 2sqrt{x-1}=sqrt{10-2x}Rightarrow 4(x-1)=10-2xRightarrow 6x=14Rightarrow x=frac73\ fleft(frac73right)=sqrt{frac73-1}+sqrt{10-2cdot frac73}=sqrt{frac43}+sqrt{frac{16}{3}}=frac{6}{sqrt{3}}=2sqrt{3} end{gather*} Промежутки монотонности:
| (x) | 1 | (1; 7/3) | 7/3 | (7/3; 5) | 5 |
| (f'(x)) | ∅ | + | 0 | – | ∅ |
| (f(x)) | (2sqrt{2}) | (nearrow ) | max (2sqrt{3}) |
(searrow ) | 2 |
Можем строить график:
(y=a) – горизонтальная прямая.
Количество точек пересечения (f(x)) и (y) равно количеству решений.
Получаем:
| $$ alt 2 $$ | нет решений |
| $$ 2leq alt 2sqrt{2} $$ | 1 решение |
| $$ 2sqrt{2}leq alt 2sqrt{3} $$ | 2 решения |
| $$ a=2sqrt{3} $$ | 1 решение |
| $$ agt 2sqrt{3} $$ | нет решений |
По крайней мере одно решение будет в интервале (2leq aleq 2sqrt{3}).
Ответ: (ainleft[2;2sqrt{3}right])
п.3. Решение неравенств с построением графиков
Пример 4. Решите неравенство (frac{2+log_3 x}{x-1}gt frac{6}{2x-1})
Разобьем неравенство на совокупность двух систем.
Если (xgt 1), то (x-1gt 0), на него можно умножить слева и справа и не менять знак.
Если (xlt 1), то (x-1lt 0), умножить также можно, только знак нужно поменять.
Сразу учтем требование ОДЗ для логарифма: (xgt 0)
Получаем совокупность: begin{gather*} left[ begin{array}{l} begin{cases} xgt 1\ 2+log_3 xgtfrac{6(x-1)}{2x-1} end{cases} \ begin{cases} 0lt xlt 1\ 2+log_3 xltfrac{6(x-1)}{2x-1} end{cases} end{array} right. \ 2+log_3 xgt frac{6(x-1)}{2x-1}Rightarrow log_3 xgt frac{6(x-1)-2(2x-1)}{2x-1}Rightarrow log_3 xgt frac{2x-4}{2x-1}\ left[ begin{array}{l} begin{cases} xgt 1\ log_3 xgtfrac{2x-4}{2x-1} end{cases} \ begin{cases} 0lt xlt 1\ log_3 xltfrac{2x-4}{2x-1} end{cases} end{array} right. end{gather*} Исследуем функцию (f(x)=frac{2x-4}{2x-1}=frac{2x-1-3}{2x-1}=1-frac{3}{2x-1})
Точка разрыва: (x=frac12) – вертикальная асимптота
Односторонние пределы: begin{gather*} lim_{xrightarrow frac12 -0}left(1-frac{3}{2x-1}right)=1-frac{3}{-0}=+infty\ lim_{xrightarrow frac12 +0}left(1-frac{3}{2x-1}right)=1-frac{3}{+0}=-infty end{gather*} Второе слагаемое стремится к 0 на бесконечности, и это дает горизонтальную асимптоту: (y=1) begin{gather*} lim_{xrightarrow -infty}left(1-frac{3}{2x-1}right)=1-frac{3}{-infty}=1+0\ lim_{xrightarrow +infty}left(1-frac{3}{2x-1}right)=1-frac{3}{+infty}=1-0 end{gather*} На минус бесконечности кривая стремится к (y=1) сверху, а на плюс бесконечности – снизу.
Первая производная: $$ f'(x)=left(1-frac{3}{2x-1}right)’=frac{3}{(2x-1)^2}gt 0 $$ Производная положительная на всей ОДЗ, функция возрастает.
Вторая производная: $$ f”(x)=-frac{6}{(2x-1)^3} $$ Одна критическая точка 2-го порядка (x=frac12)
| (x) | (left(0;frac12right)) | (frac12) | (left(frac12;+inftyright)) |
| (f”(x)) | >0 | ∅ | <0 |
| (f(x)) | (cup) | ∅ | (cap) |
Пересечения с осью OY: (f(0)=1-frac{3}{0-1}=4), точка (0;4)
Пересечение с осью OX: (1-frac{3}{2x-1}=0Rightarrow 2x-1=3 Rightarrow x=2), точка (2;0)
Строим графики (f(x)=frac{2x-4}{2x-1}) и (g(x)=log_3 x)
Первая система из совокупности ( begin{cases} xgt 1\ log_3 xgt frac{2x-4}{2x-1} end{cases} )
Логарифм при (xgt 1) все время выше, чем правая ветка гиперболы, т.е. система справедлива для всех (xgt 1).
Вторая система из совокупности ( begin{cases} 0lt xlt 1\ log_3 xlt frac{2x-4}{2x-1} end{cases} )
Логарифм попадает под левую ветку гиперболы на интервале (0lt xltfrac12), т.е. $$ begin{cases} 0lt xlt 1\ 0lt xltfrac12 end{cases} Rightarrow 0lt xltfrac12 $$ Решение совокупности – это объединение полученных решений систем: $$ 0lt xltfrac12cup xgt 1 $$ Ответ: (xinleft(0;frac12right)cup (1;+infty))
Решение квадратных уравнений через производные
Время на прочтение
3 мин
Количество просмотров 43K
Здравствуйте, уважаемые читатели. После прочтения статьи у вас, вероятно, возникнет закономерный вопрос: «А зачем, собственно, это надо?». В силу этого сперва считаю необходимым заблаговременно сообщить, что искомый метод решения квадратных уравнений представлен скорее с морально-эстетической стороны математики, нежели со стороны практического сухого применения. Также заранее извиняюсь перед теми читателями, которые посчитают мои дилетантские изречения неприемлемыми. Итак, начнем
забивать гвозди микроскопом
.
Имеем алгебраическое уравнение второй степени (оно же квадратное) в общем виде:
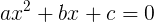
Перейдем от квадратного уравнения к квадратичной функции:
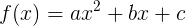
Где, очевидно, необходимо найти такие значения аргумента 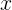 функции, в которых оная возвратила бы ноль.
функции, в которых оная возвратила бы ноль.
Кажется, нужно просто решить квадратное уравнение с помощью теоремы Виета или через дискриминант. Но мы ведь собрались здесь не для этого. Давайте-ка лучше возьмем производную!

Исходя из определения физического смысла производной первого порядка ясно, что подставляя аргумент 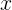 в получившуюся выше функцию мы (в частности) получим скорость изменения функции в заданной этим аргументом точке.
в получившуюся выше функцию мы (в частности) получим скорость изменения функции в заданной этим аргументом точке.
Что же дальше делать? Непонятно. А в любом непонятном случае нужно брать производную ещё раз:

На этот раз мы получили «скорость скорости» изменения функции (то бишь ускорение) в конкретной точке. Немного проанализировав полученное, можно сделать вывод, что «ускорением» является константа, которая не зависит от аргумента функции — запомним это.
Сейчас вспомним немного физику и равноускоренное движение (РУД). Что у нас есть в арсенале? Верно, имеется формула для определения координаты перемещения по оси  при искомом движении:
при искомом движении:
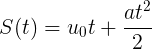
Где  — время,
— время, 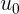 — начальная скорость,
— начальная скорость, 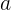 — ускорение.
— ускорение.
Нетрудно заметить, что наша изначальная функция как раз представляет из себя РУД.
Разве формула перемещения для РУД не является следствием решения квадратного уравнения?
Нет. Формула для РУД выше по факту есть результат взятия интеграла от формулы скорости при ПРУД. Или из графика  можно найти площадь фигуры. Там вылезет трапеция.
можно найти площадь фигуры. Там вылезет трапеция.
Формула перемещения при РУД не вытекает из решения каких-либо квадратных уравнений. Это очень важно, иначе не было бы смысла статьи.
Теперь осталось разобраться что есть что, и чего нам не хватает.
«Ускорение» 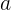 у нас уже есть — им является производная второго порядка
у нас уже есть — им является производная второго порядка 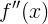 , выведенная выше. А вот чтобы получить начальную скорость
, выведенная выше. А вот чтобы получить начальную скорость 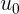 , нам нужно взять в общем-то любой
, нам нужно взять в общем-то любой 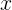 (обозначим его как
(обозначим его как 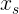 ) и подставить его в производную теперь уже первого порядка
) и подставить его в производную теперь уже первого порядка  — ибо она и будет искомым.
— ибо она и будет искомым.
В таком случае возникает вопрос, какой же 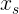 нужно взять? Очевидно, такой, чтобы начальная скорость
нужно взять? Очевидно, такой, чтобы начальная скорость 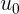 была равна нулю, чтобы формула «перемещения при РУД» стала иметь вид:
была равна нулю, чтобы формула «перемещения при РУД» стала иметь вид:

В таком случае составим уравнение для поиска 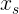 :
:
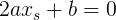 [подставили
[подставили 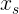 в производную первого порядка
в производную первого порядка  ]
]
Корнем такого уравнения относительно 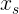 будет:
будет:

А значением исходной функции  при таком аргументе будет:
при таком аргументе будет:

Вспомним, какой целью мы задались в самом начале: «необходимо найти такие значения аргумента 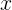 функции, в которых оная возвратила бы ноль». Иными словами, нам от положения
функции, в которых оная возвратила бы ноль». Иными словами, нам от положения  необходимо «дойти до нуля».
необходимо «дойти до нуля».
Так как теперь нам известна начальная скорость, ускорение и какой путь необходимо пройти, то настало время отметить следующее:
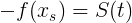 , также как и
, также как и 
Тогда, подставив все известные величины, получим:
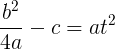
Поделим все на 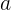 :
:

Теперь становится очевидно, что:

Соединим все «детали пазла» воедино:

Вот мы и получили окончательное решение поставленной задачи. Вообще Америку мы не открыли — мы просто пришли к формуле решения квадратного уравнения через дискриминант окольными путями. Практического смысла это не несет (примерно таким же образом можно решать уравнения первой/второй степени любого (не обязательно общего) вида).
Целью этой статьи является, в частности, подогрев интереса к анализу мат. функций и вообще к математике.
С вами был Петр, спасибо за внимание!
Применение производной для решения нелинейных уравнений и неравенств
п.1. Количество корней кубического уравнения
Кубическое уравнение $$ ax^3+bx^2+cx+d=0 $$ на множестве действительных чисел может иметь один, два или три корня.
С помощью производной можно быстро ответить на вопрос, сколько корней имеет данное уравнение. begin f(x)=ax^3+bx^2+cx+d\ f'(x)=3ax^2+bx+c end Если в уравнении (f'(x)=0) дискриминант (D=4b^2-12ac=4(b^2-3ac)gt 0), кубическая парабола имеет две точки экстремума: (x_<1,2>=frac<-2bpmsqrt><6a>). Если при этом значения функции в точках экстремума (f(x_1)cdot f(x_2)lt 0), т.е. расположены по разные стороны от оси OX, парабола имеет три точки пересечения с этой осью. Исходное уравнение имеет три корня.
Если две точки экстремума найдены, но (f(x_1)cdot f(x_2)=0), уравнение имеет два корня.
Во всех остальных случаях – у исходного уравнения 1 корень.
Пример 1. Сколько корней имеют уравнения:
п.2. Количество корней произвольного уравнения
Задачи на подсчет количества корней решаются с помощью построения графиков при полном или частичном исследовании функций.
Пример 2. а) Найдите число корней уравнения (frac 1x+frac<1>+frac<1>)
б) Найдите число корней уравнения (frac 1x+frac<1>+frac<1>=k)
Построим график функции слева, а затем найдем для него количество точек пересечения с горизонталью (y=1). Это и будет ответом на вопрос задачи (а).
Исследуем функцию: $$ f(x)=frac1x+frac<1>+frac<1> $$ Алгоритм исследования и построения графика – см. §49 данного справочника.
1) ОДЗ: (xneleft<0;1;3right>)
Все три точки – точки разрыва 2-го рода. begin lim_left(frac1x+frac<1>+frac<1>right)=-infty-1-frac13=-infty\ lim_left(frac1x+frac<1>+frac<1>right)=+infty-1-frac13=+infty\ lim_left(frac1x+frac<1>+frac<1>right)=1-infty-frac12=-infty\ lim_left(frac1x+frac<1>+frac<1>right)=1+infty-frac12=+infty\ lim_left(frac1x+frac<1>+frac<1>right)=frac13+frac12-infty=-infty\ lim_left(frac1x+frac<1>+frac<1>right)=frac13+frac12+infty=+infty end 2) Функция ни четная, ни нечетная.
Функция непериодическая.
3) Асимптоты
1. Вертикальные (x=0, x=1, x=3) – точки разрыва 2-го рода
2. Горизонтальные: begin lim_left(frac1x+frac<1>+frac<1>right)=-0-0-0=-0\ lim_left(frac1x+frac<1>+frac<1>right)=+0+0+0=+0\ end Горизонтальная асимптота (y=0)
На минус бесконечности функция стремится к 0 снизу, на плюс бесконечности – сверху.
3. Наклонные: (k=0), нет.
4) Первая производная $$ f'(x)=-frac<1>-frac<1><(x-1)^2>-frac<1><(x-3)^2>lt 0 $$ Производная отрицательная на всей ОДЗ.
Функция убывает.
5) Вторую производную не исследуем, т.к. перегибы не влияют на количество точек пересечения с горизонталью.
6) Точки пересечения с OY – нет, т.к. (x=0) – асимптота
Точки пересечения с OX – две, (0lt x_1lt 1,1lt x_2lt 3)
7) График
Получаем ответ для задачи (а) 3 корня.
Решаем более общую задачу (б). Передвигаем горизонталь (y=k) снизу вверх и считаем количество точек пересечения с графиком функции. Последовательно, получаем:
При (klt 0) – три корня
При (k=0) – два корня
При (kgt 0) – три корня
Ответ: а) 3 корня; б) при (k=0) два корня, при (kne 0) три корня.
Пример 3. Найдите все значения параметра a, при каждом из которых уравнение $$ sqrt+sqrt<10-2x>=a $$ имеет по крайней мере одно решение.
Исследуем функцию (f(x)=sqrt+sqrt<10-2x>)
ОДЗ: ( begin x-1geq 0\ 10-2xgeq 0 end Rightarrow begin xgeq 1\ xleq 5 end Rightarrow 1leq xleq 5 )
Функция определена на конечном интервале.
Поэтому используем сокращенный алгоритм для построения графика.
Значения функции на концах интервала: (f(1)=0+sqrt<8>=2sqrt<2>, f(5)=sqrt<4>+0=2)
Первая производная: begin f'(x)=frac<1><2sqrt>+frac<-2><2sqrt<10-2x>>=frac<1><2sqrt>-frac<1><sqrt<10-2x>>\ f'(x)=0 text<при> 2sqrt=sqrt<10-2x>Rightarrow 4(x-1)=10-2xRightarrow 6x=14Rightarrow x=frac73\ fleft(frac73right)=sqrt<frac73-1>+sqrt<10-2cdot frac73>=sqrt<frac43>+sqrt<frac<16><3>>=frac<6><sqrt<3>>=2sqrt <3>end Промежутки монотонности:
| (x) | 1 | (1; 7/3) | 7/3 | (7/3; 5) | 5 |
| (f'(x)) | ∅ | + | 0 | – | ∅ |
| (f(x)) | (2sqrt<2>) | (nearrow ) | max (2sqrt<3>) |
(searrow ) | 2 |
Можем строить график:
(y=a) – горизонтальная прямая.
Количество точек пересечения (f(x)) и (y) равно количеству решений.
Получаем:
| $$ alt 2 $$ | нет решений |
| $$ 2leq alt 2sqrt <2>$$ | 1 решение |
| $$ 2sqrt<2>leq alt 2sqrt <3>$$ | 2 решения |
| $$ a=2sqrt <3>$$ | 1 решение |
| $$ agt 2sqrt <3>$$ | нет решений |
По крайней мере одно решение будет в интервале (2leq aleq 2sqrt<3>).
п.3. Решение неравенств с построением графиков
Пример 4. Решите неравенство (frac<2+log_3 x>gt frac<6><2x-1>)
Разобьем неравенство на совокупность двух систем.
Если (xgt 1), то (x-1gt 0), на него можно умножить слева и справа и не менять знак.
Если (xlt 1), то (x-1lt 0), умножить также можно, только знак нужно поменять.
Сразу учтем требование ОДЗ для логарифма: (xgt 0)
Получаем совокупность: begin left[ begin begin xgt 1\ 2+log_3 xgtfrac<6(x-1)> <2x-1>end \ begin 0lt xlt 1\ 2+log_3 xltfrac<6(x-1)> <2x-1>end end right. \ 2+log_3 xgt frac<6(x-1)><2x-1>Rightarrow log_3 xgt frac<6(x-1)-2(2x-1)><2x-1>Rightarrow log_3 xgt frac<2x-4><2x-1>\ left[ begin begin xgt 1\ log_3 xgtfrac<2x-4> <2x-1>end \ begin 0lt xlt 1\ log_3 xltfrac<2x-4> <2x-1>end end right. end Исследуем функцию (f(x)=frac<2x-4><2x-1>=frac<2x-1-3><2x-1>=1-frac<3><2x-1>)
Точка разрыва: (x=frac12) – вертикальная асимптота
Односторонние пределы: begin lim_left(1-frac<3><2x-1>right)=1-frac<3><-0>=+infty\ lim_left(1-frac<3><2x-1>right)=1-frac<3><+0>=-infty end Второе слагаемое стремится к 0 на бесконечности, и это дает горизонтальную асимптоту: (y=1) begin lim_left(1-frac<3><2x-1>right)=1-frac<3><-infty>=1+0\ lim_left(1-frac<3><2x-1>right)=1-frac<3><+infty>=1-0 end На минус бесконечности кривая стремится к (y=1) сверху, а на плюс бесконечности – снизу.
Первая производная: $$ f'(x)=left(1-frac<3><2x-1>right)’=frac<3><(2x-1)^2>gt 0 $$ Производная положительная на всей ОДЗ, функция возрастает.
Вторая производная: $$ f”(x)=-frac<6> <(2x-1)^3>$$ Одна критическая точка 2-го порядка (x=frac12)
Решение уравнений с помощью производной
Определение 1. Пусть функция определена в некоторой окрестности точки . Придавая независимой переменной приращение х , невыводящее за пределы окрестности, получим новое значение + х , также принадлежащее окрестности . Тогда значение функции заменится новым значением , то есть получит приращение
Если существует предел отношения приращении функции у к вызвавшему его приращению независимой переменной х при стремлении х к 0, т.е. , то он называется производной функции в точке х и обозначается .
Операция вычисления производной называется операцией дифференцирования.
Образно говоря, равенство означает, что производная функции в точке х равна скорости изменения переменной у относительно переменой в указанной точке.
Определение 2. Функция , заданная в некоторой окрестности точки R называется дифференцируемой в этой точке, если ее приращение , представимо в этой окрестности в виде , где – постоянная, О( х) – бесконечно малая более высокого порядка, чем х.
Линейная функция (аргумента х ) называется дифференциалом функции в точке х и обозначается df(x или dy .
Таким образом, у = dy + О( х) , .
Можно доказать следующую теорему:
Теорема 1. Функция дифференцируема в некоторой точке в том и только том случае, когда в этой точке имеет конечную производную.
Учитывая определение 2 и утверждение теоремы, в качестве определения дифференцируемой функции может быть принято следующее:
Определение 3. Если функция у имеет производную в точке , то говорят, что при данном значении функция дифференцируема.
То есть существование производной функции в точке х равносильно ее дифференцируемости в этой точке.
Теорема 2 . Если функция дифференцируема в некоторой точке, то она непрерывна в этой точке.
Обратная теорема не верна: существуют функции, непрерывные в некоторой точке, но не дифференцируемые в этой точке.
Если функция определена в некоторой окрестности точки , принимает в этой точке наибольшее (наименьшее) в рассматриваемой окрестности значение и имеет в точке х производную, то эта производная равна нулю.
1) непрерывна на отрезке [ ]
2) имеет в каждой точке интервала конечную производную,
3) принимает равные значения на концах отрезка [ ], то есть f(a) = f(b) , то существует, по крайней мере, одна такая точка , что .
Если функция непрерывна на отрезке [ ] и в каждой точке интервала имеет конечную или определенного знака бесконечную производную, то существует такая точка , что f(b) – f(a) = f ( (b – a).
Используя теорему Лагранжа, можно доказать следующие теоремы:
Условие постоянства функции
Теорема 3. (Условие постоянства функции) Пусть функция определена и непрерывна на промежутке Х и во всех его внутренних точках имеет конечную производную . Для того, чтобы была на указанном отрезке постоянной, необходимое и достаточное условие внутри Х.
Если две функции и определены и непрерывны в промежутке Х и внутри него имеют конечные производные и , причем (внутри Х), то эти функции на всем промежутке Х отличаются лишь на постоянную: (C = const).
Теорема 4. (Признак монотонности функций)
Для того чтобы дифференцируемая на интервале функция возрастала (убывала) на этом интервале, необходимо и достаточно, чтобы ее производная была во всех точках интервала неотрицательна (неположительна).
Если производная функция во всех точках интервала положительна (отрицательна), то функция строго возрастает (строго убывает) на этом интервале.
Если функции и непрерывны на отрезке [ ] и в каждой точке интервала имеют конечные производные , , причем для , а f(а) g(а) , тогда для любой точки выполняется неравенство .
На основании утверждения теоремы 5 для того, чтобы доказать неравенство f(x) 0 при х 0 , достаточно доказать, что f(0) 0 и (х) 0 при х 0 . А для того, чтобы доказать неравенство при , можно воспользоваться второй производной и при и т.д.
С помощью производной можно также определить число корней того или иного уравнения. Один из возможных приемов основан на следующей теореме:
Если функция определена и непрерывна на отрезке и во всех его внутренних точках имеет конечную производную, то между любыми двумя корнями этой функции, расположенными на отрезке, имеется хотя бы 1 корень ее производной.
Рассмотренные теоретические положения используются при решении задач.
Задача 1. Докажите тождество 3 arcsin x – arccos( 3 4 ) = , если .
Решение. Рассмотрим функцию 3 arcsinx – arccos( 3 4 на отрезке [ ]. Докажем, что f(х) = с, с = const. Для этого достаточно доказать, что (т.3)
Если , то следовательно, и . Для определения значения вычислим значение функции в произвольной точке интервала . Пусть , тогда и .
Вычислим значение функции на концах заданного отрезка.
Таким образом, тождество верно при любом .
Задача 2. Найдите сумму .
Решение. Представив искомую сумму в виде , заметим, что .
Используя формулу суммы членов геометрической прогрессии, получим,
Итак, искомая сумма имеет вид .
Используя полученную формулу, можно, например, вычислить
Задача 3. Найдите сумму:
Решение. Используя результат, полученный в примере 2, заметим, что
Задача 4. Решите уравнение:
Решение. Очевидно, что – корень уравнения. Докажем, что уравнение других корней не имеет. Рассмотрим функцию
Для функции точка является точкой минимума, в которой функция принимает наименьшее значение. Значит, для всех , отличных от нуля, > .
Задача 5. Решите уравнение:
Преобразуем уравнение к виду:
Рассмотрим функции и при .
Сравним множества значений этих функций. Очевидно, что .
Найдем с использованием производной.
Функция непрерывна на промежутке и имеет на нем единственную критическую точку , в которой достигает своего наибольшего значения.
Следовательно, решение уравнения находим из решения системы:
Рассмотрим функцию , при .
Функция непрерывна на промежутке и является возрастающей, . – является точкой минимума функции , в которой функция принимает наименьшее значение, ровное нулю. Следовательно, для всех > .
Таким образом, исходное уравнение имеет единственный корень .
Задача 6. Докажите, что уравнение может иметь не более трех различных корней.
Решение. Рассмотрим функцию . Функция является дифференцируемой на R . Предположим, что функция имеет более трех различных корней, например, четыре. Тогда должна иметь не более трех различных корней (т.6), то есть обращается в нуль не менее трех раз.
Функция дифференцируема на R . Ее производная обращается в нуль не менее двух раз. Тогда имеет не менее двух нулей, а ее производная не менее одного нуля. Но функция нулей не имеет. Получили противоречие. Значит, сделанное предположение неверно, функция более трех различных корней иметь не может. Таким образом, заданное уравнение может иметь не более трех различных корней.
Производную можно использовать при доказательстве и решении неравенств.
Задача 7. Доказать, что при 0$”>.
Доказательство. Докажем справедливость следующих неравенств:
0. end –>
Для доказательства неравенства (2) рассмотрим функцию
“Решаем с помощью производной”
Разделы: Математика
Производная широко применяется при решении ряда задач элементарной математики. Из всего круга таких задач выделим те, при решении которых используется теорема Лагранжа и ее следствия. К ним относятся задачи на доказательство тождеств, неравенств, вывод формул тригонометрии, разложение алгебраических выражений на множители, решение уравнений, неравенств, систем уравнений, уравнений с параметрами. При этом можно указать общие методы решения и некоторые частные приемы.
Теорема Лагранжа. Пусть функция f непрерывна на отрезке [a;b] и дифференцируема во внутренних точках этого отрезка. Тогда существует внутренняя точка с этого отрезка, такая, что .
Следствие 1 (условие постоянства). Если функция f непрерывна на отрезке [a;b], а ее производная равна нулю внутри этого отрезка, то функция f постоянна на [a;b].
Следствие 2. Если функции  и
и  непрерывны на отрезке [a;b] и имеют одинаковые производные внутри этого отрезка, то они отличаются лишь постоянным слагаемым.
непрерывны на отрезке [a;b] и имеют одинаковые производные внутри этого отрезка, то они отличаются лишь постоянным слагаемым.
Условие монотонности функции также является следствием теоремы Лагранжа. В школьном учебнике оно устанавливается отдельно в виде теоремы.
Следствие 3 (условие монотонности). Если функция f непрерывна на промежутке I и ее производная положительна (соответственно отрицательна) во внутренних точках этого промежутка, то функция f возрастает (соответственно убывает) на I.
Теорему Лагранжа можно применять:
– при доказательстве неравенств, в частности – числовых неравенств;
– при исследовании вопроса о корнях многочлена или уравнения;
– при решении уравнений.
В процессе решения таких задач вводится в рассмотрение функция f(x) на отрезке [a;b], удовлетворяющая условиям теоремы Лагранжа, для нее записывается формула Лагранжа , c (a;b) и оценивается f’(c), а, следовательно, и выражение , что позволяет доказать рассматриваемое неравенство или решить вопрос о корнях многочлена, уравнения.
Пример 1. Доказать, что .
Решение. Функция f(x)=arccosx на отрезке [0,6;0,8] непрерывна и дифференцируема на интервале (0,6;0,8), . Следовательно, для функции f(x) на данном отрезке выполняются условия теоремы Лагранжа и , где 0,6 , т.е. . Оценим число . Так как 0,6 2 . Тогда и окончательно .
Пример 2. Доказать, что e x >=ex.
Решение. Неравенство справедливо при х=1. Рассмотрим функцию f(x)=e x -ex. Тогда для любого числа b (b>1) для данной функции выполняются условия теоремы Лагранжа на отрезке [1;b], а для b , т.е. . Так как c>1 при b>1, то e c >e и, следовательно, e c -e>0. Тогда , а значит e b -eb>0, т.е. e b >eb для любого b>1. Таким образом доказано, что e x >=ex при x>=1.
Если b , т.е. с c c -e , следует, что e b -eb>0, т.е. e b >eb.
Итак, доказано, что неравенство e x >=ex верно при любом действительном х. В частности, при x=c+1 получим e c+1 >=e(c+1), т.е. e c >=c+1, где с – любое действительное число.
Пример 3. Доказать, что уравнение не имеет действительных положительных корней.
Решение. Пусть b – любое положительное число. Рассмотрим функцию f(x)= , непрерывную на отрезке [a;b] и имеющую производную на интервале (0;b). По теореме Лагранжа имеем , 0 . А так как при любом с>0 e c >c+1 (доказано в примере 2), то e c -c>1 и, следовательно, . Отсюда получим , а значит для любого b>0. Таким образом, при x>0, т.е. , следовательно, равенство не выполняется ни при каком x>0. А, значит, уравнение не имеет действительных положительных корней.
Пример 4. Доказать, что на промежутке (0, 2) имеется не более двух различных действительных корней уравнения .
Решение. Предположим, что уравнение имеет не менее трех различных действительных корней х1, х2, х3, принадлежащих промежутку (0,2), и пусть x1 , т.е. f(x1)=f(x2)=f(x3)=0. На каждом из отрезков [x1;x2], [x2;x3] для функции f(x) выполняются условия теоремы Лагранжа, следовательно, существуют числа c1 и с2 из интервалов (х1;х2), (х2;х3) соответственно, такие, что и . А так как f(x1)=f(x2)=f(x3)=0, то f’(c1)=0 и f’(c2)=0, причем с1 с2.
с2.
Найдем производную f’(x):
. Так как для любых х, то уравнение f’(x)=0 имеет единственный корень x=, принадлежащий промежутку (0, 2). Пришли к противоречию, так как с1 и с2 (с1 с2) являются корнями уравнения f’(x)=0, тем самым доказано, что уравнение имеет на промежутке (0,2) не более двух различных действительных корней.
с2) являются корнями уравнения f’(x)=0, тем самым доказано, что уравнение имеет на промежутке (0,2) не более двух различных действительных корней.
Пример 5. Решить уравнение x 9 -9x 5 +63x-55=0.
Решение. Легко заметить, что число х1=1 является корнем данного уравнения. Предположим, что существует еще хотя бы один действительный корень х2, отличный от х1. Числа х1 и х2 являются нулями функции f(x)=x 9 -9x 5 +63x-55 и, следовательно, f(x1)=f(x2)=0. Применим терему Лагранжа к функции f(x) на отрезке [x1;x2], если x1 x2. Следовательно, найдется такая внутренняя точка с этого отрезка, что будет выполняться . Учитывая, что f(x1)=f(x2)=0, получим f’(с)=0, т.е. число с – корень уравнения f’(x)=0. Но производная f’(x)=9x 8 -45x 4 +63, т.е. f’(x)=9(x 4 -2,5) 2 +6,75 положительна для любых х, а значит уравнение f’(x)=0 не имеет корней. Полученное противоречие доказывает, что найденный корень х1=1 является единственным корнем уравнения x 9 -9x 5 +63x-55=0.
Определить число критических точек функции y=(x 2 -1)(x 2 -8х)(x-9).
Решение. Так как степень многочлена f(x)= (x 2 -1)(x 2 -8х)(x-9) равна 5, то его производная f’(x) является многочленом четвертой степени и имеет не более четырех действительных корней. Применим теорему Лагранжа к функции f(x)=(x+1)(x-1)х(x-8)(x-9) на отрезках [-1;0], [0;1], [1;8], [8;9] и при этом учтем, что f(-1)=f(0)=f(1)=f(8)=f(9)=0. На каждом таком отрезке найдутся внутренние точки х1, х2, х3, х4 соответственно, такие, что , , , , т.е. f’(x1)=0, f’(x2)=0, f’(x3)=0, f’(x4)=0. А учитывая, что x1, х2, х3, х4 – различные корни многочлена f’(x) четвертой степени, делаем вывод, что других корней, отличных от полученных, нет и, следовательно, функция y=(x 2 -1)(x 2 -8х)(x-9) имеет четыре критические точки.
Условие монотонности функции можно применять:
– при решении неравенств;
– при доказательстве неравенств с переменной;
– при доказательстве числовых неравенств;
– при исследовании вопроса о количестве корней уравнения;
– в некоторых случаях при решении уравнений, уравнений с параметрами, систем уравнений.
Решение задач с использованием условия монотонности основано на связи между возрастанием или убыванием функции и знаком ее производной на некотором промежутке. При этом, сравнивая различные значения аргумента из этого промежутка рассматриваемой монотонной функции, делается вывод о соответствующих значениях данной функции.
Пример 7. Доказать, что 3xcosx .
Решение. Докажем, что, если 0 , то sinx+sin2x-3xcosx>0, т.е. cosx(tgx+2sinx-3x)>0. Рассмотрим непрерывную на промежутке функцию f(x)=tgx-3x+2sinx. Ее производная при принимает положительные значения, следовательно, функция f(x) возрастает на промежутке и на нем f(x)>f(0).
Учитывая, что f(0)=0, будем иметь tgx-3x+2sinx>0. А так как на промежутке cosx>0, то и cosx(tgx+2sinx-3x)>0. Таким образом доказано, что sinx+sin2x-3xcosx>0, то есть, что 3xcosx .
Пример 8. Доказать, что
1) и , если 0 и , если e . Так как ее производная равна нулю при х=е, а при 0 0 и f’(x) e, то на промежутке (0;e] функция f(x) возрастает, а на промежутке [e;+) – убывает. Тогда для любых значений х1 и х2 таких, что 0 . Запишем его в виде , . Учитывая, что функция ln t возрастающая, получим . А если обе части неравенства умножить на произведение x1x2>0, то получим x2lnx1 , откуда и будем иметь .
Если же e f(x2), то есть , откуда и получим и .
Доказанными в примере 8 неравенствами можно воспользоваться при сравнении чисел и при доказательстве числовых неравенств.
Пример 9. Сравнить (сtg48°) tg48° и (сtg50°) tg50° .
Решение. Заметим, что сtg48°=сtg , tg48°=tg , ctg50°=ctg , tg50°=tg , а также, что . Взяв , и учитывая, что , если 0 , т.е. (сtg48°) tg48° > (сtg50°) tg50° .
Пример 10. Доказать, что 2006 2007 >2007 2006 .
Решение. Воспользуемся неравенством x1 x2 >x2 x1 , если e 2007 >2007 2006 .
Определить число действительных корней уравнения 2х 3 -24х-19=0.
Решение. Функция f(x)= 2х 3 -24х-19 непрерывна на всей числовой прямой и имеет производную f’(x)=6x 2 -24=6(x-2)(x+2).
При x 2 f’(x)>0, а при –2 0, f(2)=-51 0. Так как функция f(x) на концах отрезков [-3;-2], [-2;2], [2;5] принимает значения разных знаков, то на каждом из них имеется только один корень уравнения. Таким образом, уравнение 2х 3 -24х-19=0 имеет три действительных корня, которые находятся на промежутках (-3;-2), (-2;2), (2;5).
Остальные следствия теоремы Лагранжа можно применять:
– при доказательстве тождеств, в частности при выводе формул элементарной математики;
– при упрощении выражений;
– при разложении алгебраических выражений на множители.
При решении ряда таких задач на некотором промежутке рассматривается либо одна функция f(x), такая, что ее производная f’(x)=0 и, следовательно, функция постоянна, т.е. имеет вид f(x)=c, либо две функции f(x) и g(x), такие, что f’(x)=g’(x), и делается вывод, что f(x)=g(x)+c (c – постоянная). Эту постоянную находят, положив х равным некоторому значению х1.
Пример 12. Вывести формулу .
Решение. Функция f(x)= непрерывна на всей числовой прямой. Найдем производную этой функции f’(x)=2sinxcosx-sin2x=sin2x-sin2x. f’(x)=0 для любого действительного значения х, следовательно, на основании условия постоянства функции можно сделать вывод, что функция f(x) постоянна, т.е. f(x)=c. Для определения постоянной c положим х=0 и получим f(0)=c, т.е. sin 2 0-0,5+0,5cos0=c. Таким образом, с=0 и значит f(x)=0, откуда и получим =0, или .
Пример 13. Доказать, что arctgx=arcsin при x , тогда они непрерывны на любом отрезке [b;0]. Найдем производные этих функций.
, . Так как при x и тогда f’(x)=g’(x) внутри отрезка [b;0]. На основании следствия 2 имеем f(x)=g(x)+c, где с – постоянная. Для определения с положим, например, х=-1, что дает arctg(-1)=arcsin , то есть Итак, получим arctgx=arcsin при x
Решение. Заметим, что , для любого действительного х и функции , непрерывны на всей числовой прямой. Имеем ,
1) Рассмотрим функцию F(x)=f(x)+g(x), x (-;-1)  (0;1).
(0;1).
F(x)= , а F’(x)=f’(x)+g’(x)= . Если x (-;-1), то |х 2 -1|=х 2 -1, |х|=-х и F’(x)=0. Если x (0;1), то |х 2 -1|=-(х 2 -1), |х|=х и F’(x)=0. На основании условия постоянства функции F(x)=c, то есть . На каждом из рассматриваемых промежутков определим с, положив, например, х= и x= .
, cледовательно, с=.
, следовательно, с=0. Имеем: при x (-;-1), при x (0;1).
2) Рассмотрим функцию G(x)=f(x)-g(x), x (-1;0)  (1; +).
(1; +).
Если x (-1;0), то |х 2 -1|=-(х 2 -1), |x|=-x и G’(x)=0.
Если x (1; +), то |х 2 -1|=х 2 -1, |x|=x и G’(x)=0. Тогда на указанных промежутках функция G(x) постоянна, т.е. . Положим x= и x= , получим , следовательно, с=; , тогда с=0.
Имеем: при x (-1;0), при x (1;+ ).
3) Вычислим значения f(x) и g(x) при х=± 1 и х=0.
f(-1)=arccos(-1)=, g(-1)=arcsin0=0; следовательно, при х=-1 f(x)=+g(x), то есть . , , следовательно, при х=0 f(x)=-g(x), то есть . f(1)=arccos1=0, g(1)=arcsin0=0, следовательно, при х= 1 f(x)=g(x), то есть .
Таким образом, данное тождество доказано для всех действительных х.
Пример 15. Разложить на множители выражение
y 2 (x-z)+x 2 (z-y)+z 2 (y-x).
Решение. На данное выражение будем смотреть как на функцию от переменной х: f(x)=y 2 (x-z)+x 2 (z-y)+z 2 (y-x).
f’(x)=y 2 +2x(z-y)-z 2 =y 2 -z 2 -2x(y-z)=(y-z)(y+z)-2x(y-z)=(y-z)(y+z-2x).
Будем считать, что (y-z)(y+z-2x) есть производная некоторой другой функции g(x), при этом множитель (y-z) будем рассматривать как постоянную, вынесенную при дифференцировании за знак производной, т.е.
g’(x)=(y-z)((y+z)-2x). В качестве функции g(x) можно взять g(x)=(y-z)((y-z)x-x 2 ).
Так как функции f(x) и g(x) непрерывны и дифференцируемы на всей числовой прямой и f’(x)=g’(x), то по следствию 2 f(x)=g(x)+c, где с не зависит от х, но, возможно, зависит от y и z. Имеем y 2 (x-z)+x 2 (z-y)+z 2 (y-x)=(y-z)((y+z)x-x 2 )+c. Найдем с, полагая в этом равенстве, например, х=0. Имеем yz 2 -zy 2 =c. Тогда f(x)=g(x)+yz 2 -zy 2 , то есть
f(x)=(y-z)((y+z)x-x 2 )+yz 2 -zy 2 =(y-z)(xy+xz-x 2 )-yz(y-z)=(y-z)(xy-x 2 +xz-yz)=(y-z)(x(y-x)-z(y-x))=(y-z)(y-x)(x-z).
Итак, y 2 (x-z)+x 2 (z-y)+z 2 (y-x)=(y-z)(y-x)(x-z).
[spoiler title=”источники:”]
http://cito-web.yspu.org/link1/metod/met33/node2.html
http://urok.1sept.ru/articles/417890
[/spoiler]
Производная широко применяется при
решении ряда задач элементарной математики. Из
всего круга таких задач выделим те, при решении
которых используется теорема Лагранжа и ее
следствия. К ним относятся задачи на
доказательство тождеств, неравенств, вывод
формул тригонометрии, разложение алгебраических
выражений на множители, решение уравнений,
неравенств, систем уравнений, уравнений с
параметрами. При этом можно указать общие методы
решения и некоторые частные приемы.
Теорема Лагранжа. Пусть функция f
непрерывна на отрезке [a;b] и дифференцируема во
внутренних точках этого отрезка. Тогда
существует внутренняя точка с этого отрезка,
такая, что <Рисунок1>.
Следствие 1 (условие постоянства).
Если функция f непрерывна на отрезке [a;b], а ее
производная равна нулю внутри этого отрезка, то
функция f постоянна на [a;b].
Следствие 2. Если функции ![]() и
и ![]()
непрерывны на отрезке [a;b] и имеют одинаковые
производные внутри этого отрезка, то они
отличаются лишь постоянным слагаемым.
Условие монотонности функции также
является следствием теоремы Лагранжа. В школьном
учебнике оно устанавливается отдельно в виде
теоремы.
Следствие 3 (условие
монотонности). Если функция f непрерывна на
промежутке I и ее производная положительна
(соответственно отрицательна) во внутренних
точках этого промежутка, то функция f возрастает
(соответственно убывает) на I.
Теорему Лагранжа можно применять:
– при доказательстве неравенств, в
частности – числовых неравенств;
– при исследовании вопроса о корнях
многочлена или уравнения;
– при решении уравнений.
В процессе решения таких задач
вводится в рассмотрение функция f(x) на отрезке
[a;b], удовлетворяющая условиям теоремы Лагранжа,
для нее записывается формула Лагранжа
<Рисунок1>, c ![]()
(a;b) и оценивается f’(c), а, следовательно, и
выражение <Рисунок2>, что позволяет доказать
рассматриваемое неравенство или решить вопрос о
корнях многочлена, уравнения.
Пример 1. Доказать, что
<Рисунок3>.
Решение. Функция f(x)=arccosx на отрезке
[0,6;0,8] непрерывна и дифференцируема на интервале
(0,6;0,8), <Рисунок4>. Следовательно, для функции f(x)
на данном отрезке выполняются условия теоремы
Лагранжа и <Рисунок5>, где 0,6<c<0,8. Имеем
<Рисунок6>, т.е. <Рисунок7>. Оценим
число<Рисунок8>. Так как 0,6<c<0,8, то 0,36<1-c2<0,64
и 0,6<<Рисунок9><0,8, следовательно
<Рисунок10>. Тогда <Рисунок11> и окончательно
<Рисунок3>.
Пример 2. Доказать, что ex>=ex.
Решение. Неравенство справедливо
при х=1. Рассмотрим функцию f(x)=ex-ex. Тогда для
любого числа b (b>1) для данной функции
выполняются условия теоремы Лагранжа на отрезке
[1;b], а для b<1 – выполняется условие теоремы на
отрезке [b;1] и, следовательно, существует
внутренняя точка соответствующего отрезка,
такая, что <Рисунок12>, т.е. <Рисунок13>. Так
как c>1 при b>1, то ec>e и, следовательно, ec-e>0.
Тогда <Рисунок14>, а значит eb-eb>0, т.е. eb>eb
для любого b>1. Таким образом доказано, что ex>=ex
при x>=1.
Если b<1, то <Рисунок15>, т.е. с<1,
тогда ec<e и ec-e<0. Учитывая, что b-1<0,
из равенства <Рисунок13>, следует, что eb-eb>0,
т.е. eb>eb.
Итак, доказано, что неравенство ex>=ex
верно при любом действительном х. В частности,
при x=c+1 получим ec+1>=e(c+1), т.е. ec>=c+1,
где с – любое действительное число.
Пример 3. Доказать, что уравнение
<Рисунок16> не имеет действительных
положительных корней.
Решение. Пусть b – любое
положительное число. Рассмотрим функцию f(x)=
<Рисунок17>, непрерывную на отрезке [a;b] и
имеющую производную <Рисунок18> на интервале
(0;b). По теореме Лагранжа имеем <Рисунок19>,
0<c<b, т.е. <Рисунок20>. А так как при любом с>0 ec>c+1
(доказано в примере 2), то ec-c>1 и,
следовательно, <Рисунок21>. Отсюда получим
<Рисунок22>, а значит <Рисунок23> для любого
b>0. Таким образом, <Рисунок24> при x>0, т.е.
<Рисунок25>, следовательно, равенство
<Рисунок16> не выполняется ни при каком x>0. А,
значит, уравнение <Рисунок16> не имеет
действительных положительных корней.
Пример 4. Доказать, что на
промежутке (0, 2![]() ) имеется не более двух
) имеется не более двух
различных действительных корней уравнения
<Рисунок26>.
Решение. Предположим, что
уравнение имеет не менее трех различных
действительных корней х1, х2, х3,
принадлежащих промежутку (0,2![]() ), и пусть x1<x2<x3.
), и пусть x1<x2<x3.
Тогда они являются нулями функции <Рисунок27>,
т.е. f(x1)=f(x2)=f(x3)=0. На каждом из
отрезков [x1;x2], [x2;x3] для
функции f(x) выполняются условия теоремы Лагранжа,
следовательно, существуют числа c1 и с2
из интервалов (х1;х2), (х2;х3)
соответственно, такие, что <Рисунок28> и
<Рисунок29>. А так как f(x1)=f(x2)=f(x3)=0,
то f’(c1)=0 и f’(c2)=0, причем с1![]() с2.
с2.
Найдем производную f’(x):
<Рисунок30>. Так как <Рисунок31> для
любых х, то уравнение f’(x)=0 имеет единственный
корень x=![]() , принадлежащий промежутку (0, 2
, принадлежащий промежутку (0, 2![]() ).
).
Пришли к противоречию, так как с1 и с2
(с1![]() с2)
с2)
являются корнями уравнения f’(x)=0, тем самым
доказано, что уравнение <Рисунок26> имеет на
промежутке (0,2![]() ) не более двух различных
) не более двух различных
действительных корней.
Пример 5. Решить уравнение x9-9x5+63x-55=0.
Решение. Легко заметить, что число
х1=1 является корнем данного уравнения.
Предположим, что существует еще хотя бы один
действительный корень х2, отличный от х1.
Числа х1 и х2 являются нулями функции
f(x)=x9-9x5+63x-55 и, следовательно, f(x1)=f(x2)=0.
Применим терему Лагранжа к функции f(x) на отрезке
[x1;x2], если x1<x2 или на
отрезке [x2;x1], если x1>x2.
Следовательно, найдется такая внутренняя точка с
этого отрезка, что будет выполняться
<Рисунок32>. Учитывая, что f(x1)=f(x2)=0,
получим f’(с)=0, т.е. число с – корень уравнения
f’(x)=0. Но производная f’(x)=9x8-45x4+63, т.е.
f’(x)=9(x4-2,5)2+6,75 положительна для любых
х, а значит уравнение f’(x)=0 не имеет корней.
Полученное противоречие доказывает, что
найденный корень х1=1 является единственным
корнем уравнения x9-9x5+63x-55=0.
Пример 6.
Определить число критических точек
функции y=(x2-1)(x2-8х)(x-9).
Решение. Так как степень
многочлена f(x)= (x2-1)(x2-8х)(x-9) равна 5, то
его производная f’(x) является многочленом
четвертой степени и имеет не более четырех
действительных корней. Применим теорему
Лагранжа к функции f(x)=(x+1)(x-1)х(x-8)(x-9) на отрезках
[-1;0], [0;1], [1;8], [8;9] и при этом учтем, что
f(-1)=f(0)=f(1)=f(8)=f(9)=0. На каждом таком отрезке найдутся
внутренние точки х1, х2, х3, х4
соответственно, такие, что <Рисунок33>,
<Рисунок34>, <Рисунок35>, <Рисунок36>,
т.е. f’(x1)=0, f’(x2)=0, f’(x3)=0, f’(x4)=0.
А учитывая, что x1, х2, х3, х4
– различные корни многочлена f’(x) четвертой
степени, делаем вывод, что других корней,
отличных от полученных, нет и, следовательно,
функция y=(x2-1)(x2-8х)(x-9) имеет четыре
критические точки.
Условие монотонности функции можно
применять:
– при решении неравенств;
– при доказательстве неравенств с
переменной;
– при доказательстве числовых
неравенств;
– при исследовании вопроса о
количестве корней уравнения;
– в некоторых случаях при решении
уравнений, уравнений с параметрами, систем
уравнений.
Решение задач с использованием
условия монотонности основано на связи между
возрастанием или убыванием функции и знаком ее
производной на некотором промежутке. При этом,
сравнивая различные значения аргумента из этого
промежутка рассматриваемой монотонной функции,
делается вывод о соответствующих значениях
данной функции.
Пример 7. Доказать, что 3xcosx<sinx+sin2x,
если 0<x<<Рисунок37>.
Решение. Докажем, что, если
0<x<<Рисунок37>, то sinx+sin2x-3xcosx>0, т.е.
cosx(tgx+2sinx-3x)>0. Рассмотрим непрерывную на
промежутке <Рисунок38>функцию f(x)=tgx-3x+2sinx. Ее
производная <Рисунок39> при <Рисунок40>
принимает положительные значения,
следовательно, функция f(x) возрастает на
промежутке <Рисунок38>и на нем f(x)>f(0).
Учитывая, что f(0)=0, будем иметь
tgx-3x+2sinx>0. А так как на промежутке <Рисунок38>
cosx>0, то и cosx(tgx+2sinx-3x)>0. Таким образом доказано,
что sinx+sin2x-3xcosx>0, то есть, что 3xcosx<sinx+sin2x, если
0<x<<Рисунок37>.
Пример 8. Доказать, что
1) <Рисунок41> и <Рисунок42>, если
0<x1<x2<=e;
2) <Рисунок43>и <Рисунок44>, если
e<=x1<x2.
Решение. Рассмотрим непрерывную
на промежутке (0;+![]() ) функцию <Рисунок45>. Так как ее
) функцию <Рисунок45>. Так как ее
производная <Рисунок46> равна нулю при х=е, а
при 0<x<e f’(x)>0 и f’(x)<0 при x>e, то на
промежутке (0;e] функция f(x) возрастает, а на
промежутке [e;+![]() ) –
) –
убывает. Тогда для любых значений х1 и х2
таких, что 0<x1<x2<=e, будет
выполняться неравенство f(x1)<f(x2), то
есть <Рисунок47>. Запишем его в виде
<Рисунок48>, <Рисунок49>. Учитывая, что
функция ln t возрастающая, получим <Рисунок50>. А
если обе части неравенства <Рисунок47>
умножить на произведение x1x2>0, то
получим x2lnx1<x1lnx2, далее
<Рисунок51>, откуда и будем иметь <Рисунок52>.
Если же e<=x1<x2, то f(x1)>f(x2),
то есть <Рисунок47>, откуда и получим
<Рисунок53>и <Рисунок54>.
Доказанными в примере 8 неравенствами
можно воспользоваться при сравнении чисел и при
доказательстве числовых неравенств.
Пример 9. Сравнить (сtg48°)tg48° и
(сtg50°)tg50°.
Решение. Заметим, что сtg48°=сtg<Рисунок55>,
tg48°=tg<Рисунок55>, ctg50°=ctg<Рисунок55>, tg50°=tg<Рисунок55>,
а также, что <Рисунок57>. Взяв <Рисунок58>,
<Рисунок59> и учитывая, что <Рисунок53>, если
0<x1<x2<=e, получим <Рисунок60>, т.е.
(сtg48°)tg48° > (сtg50°)tg50°.
Пример 10. Доказать, что 2006 2007>2007
2006.
Решение. Воспользуемся
неравенством x1x2>x2x1,
если e<=x1<x2. Положив х1=2006 и х2=2007,
имеем e<2006<2007, следовательно, 2006 2007>2007 2006.
Пример 11.
Определить число действительных
корней уравнения 2х3-24х-19=0.
Решение. Функция f(x)= 2х3-24х-19
непрерывна на всей числовой прямой и имеет
производную f’(x)=6x2-24=6(x-2)(x+2).
При x<-2 и x>2 f’(x)>0, а при –2<x<2
f’(x)<0. Следовательно, на промежутках (-![]() :-2],[2;+
:-2],[2;+![]() ) функция возрастает, а на
) функция возрастает, а на
промежутке [-2;2] – убывает. Вычислим значения
функции в точках х=-3, х=-2, х=2, х=5. Имеем f(-3)=-1<0,
f(-2)=13>0, f(2)=-51<0, f(5)=111>0. Так как функция f(x) на
концах отрезков [-3;-2], [-2;2], [2;5] принимает значения
разных знаков, то на каждом из них имеется только
один корень уравнения. Таким образом, уравнение
2х3-24х-19=0 имеет три действительных корня,
которые находятся на промежутках (-3;-2), (-2;2),
(2;5).
Остальные следствия теоремы Лагранжа
можно применять:
– при доказательстве тождеств, в
частности при выводе формул элементарной
математики;
– при упрощении выражений;
– при разложении алгебраических
выражений на множители.
При решении ряда таких задач на
некотором промежутке рассматривается либо одна
функция f(x), такая, что ее производная f’(x)=0 и,
следовательно, функция постоянна, т.е. имеет вид
f(x)=c, либо две функции f(x) и g(x), такие, что f’(x)=g’(x),
и делается вывод, что f(x)=g(x)+c (c – постоянная). Эту
постоянную находят, положив х равным некоторому
значению х1.
Пример 12. Вывести формулу
<Рисунок61>.
Решение. Функция f(x)= <Рисунок62>
непрерывна на всей числовой прямой. Найдем
производную этой функции f’(x)=2sinxcosx-sin2x=sin2x-sin2x.
f’(x)=0 для любого действительного значения х,
следовательно, на основании условия постоянства
функции можно сделать вывод, что функция f(x)
постоянна, т.е. f(x)=c. Для определения постоянной c
положим х=0 и получим f(0)=c, т.е. sin20-0,5+0,5cos0=c.
Таким образом, с=0 и значит f(x)=0, откуда и получим
<Рисунок62>=0, или <Рисунок61>.
Пример 13. Доказать, что
arctgx=arcsin<Рисунок63> при x<0.
Решение. Рассмотрим две
непрерывные на промежутке (-![]() ;0] функции f(x)=arctgx и
;0] функции f(x)=arctgx и
g(x)=arcsin<Рисунок64>, тогда они непрерывны на
любом отрезке [b;0]. Найдем производные этих
функций.
<Рисунок65>, <Рисунок66>. Так как
при x<0 |x|=-x, то <Рисунок67> и тогда f’(x)=g’(x)
внутри отрезка [b;0]. На основании следствия 2 имеем
f(x)=g(x)+c, где с – постоянная. Для определения с
положим, например, х=-1, что дает
arctg(-1)=arcsin<Рисунок69>, то есть <Рисунок68> Итак,
получим arctgx=arcsin<Рисунок63> при x<0.
Пример 14. Доказать тождество
<Рисунок70>
Решение. Заметим, что
<Рисунок71>, <Рисунок72> для любого
действительного х и функции <Рисунок73>,
<Рисунок74> непрерывны на всей числовой прямой.
Имеем <Рисунок75>,
<Рисунок76>.
1) Рассмотрим функцию F(x)=f(x)+g(x), x ![]() (-
(-![]() ;-1)
;-1) ![]()
(0;1).
F(x)= <Рисунок77>, а F’(x)=f’(x)+g’(x)=
<Рисунок78>. Если x ![]() (-
(-![]() ;-1), то
;-1), то
|х2-1|=х2-1, |х|=-х и F’(x)=0. Если x ![]() (0;1), то |х2-1|=-(х2-1),
(0;1), то |х2-1|=-(х2-1),
|х|=х и F’(x)=0. На основании условия постоянства
функции F(x)=c, то есть <Рисунок79>. На каждом из
рассматриваемых промежутков определим с,
положив, например, х=<Рисунок80> и
x=<Рисунок81>.
<Рисунок82>, cледовательно, с=![]() .
.
<Рисунок83>, следовательно, с=0. Имеем:
<Рисунок84> при x ![]() (-
(-![]() ;-1),
;-1),
<Рисунок85> при x ![]() (0;1).
(0;1).
2) Рассмотрим функцию G(x)=f(x)-g(x), x ![]() (-1;0)
(-1;0) ![]() (1; +
(1; +![]() ).
).
<Рисунок86>, <Рисунок87>.
Если x ![]() (-1;0), то |х2-1|=-(х2-1), |x|=-x и G’(x)=0.
(-1;0), то |х2-1|=-(х2-1), |x|=-x и G’(x)=0.
Если x ![]() (1; +
(1; +![]() ), то
), то
|х2-1|=х2-1, |x|=x и G’(x)=0. Тогда на
указанных промежутках функция G(x) постоянна, т.е.
<Рисунок88>. Положим x=<Рисунок80> и
x=<Рисунок81>, получим <Рисунок89>,
следовательно, с=![]() ; <Рисунок90>, тогда с=0.
; <Рисунок90>, тогда с=0.
Имеем: <Рисунок91> при x ![]() (-1;0), <Рисунок92> при x
(-1;0), <Рисунок92> при x ![]() (1;+
(1;+ ![]() ).
).
3) Вычислим значения f(x) и g(x) при х=± 1 и
х=0.
f(-1)=arccos(-1)=![]() , g(-1)=arcsin0=0; следовательно, при х=-1 f(x)=
, g(-1)=arcsin0=0; следовательно, при х=-1 f(x)=![]() +g(x), то есть
+g(x), то есть
<Рисунок93>. <Рисунок94>, <Рисунок95>,
следовательно, при х=0 f(x)=-g(x), то есть
<Рисунок96>. f(1)=arccos1=0, g(1)=arcsin0=0, следовательно,
при х= 1 f(x)=g(x), то есть <Рисунок97>.
Таким образом, данное тождество
доказано для всех действительных х.
Пример 15. Разложить на множители
выражение
y2(x-z)+x2(z-y)+z2(y-x).
Решение. На данное выражение будем
смотреть как на функцию от переменной х: f(x)=y2(x-z)+x2(z-y)+z2(y-x).
Найдем f’(x).
f’(x)=y2+2x(z-y)-z2=y2-z2-2x(y-z)=(y-z)(y+z)-2x(y-z)=(y-z)(y+z-2x).
Будем считать, что (y-z)(y+z-2x) есть
производная некоторой другой функции g(x), при
этом множитель (y-z) будем рассматривать как
постоянную, вынесенную при дифференцировании за
знак производной, т.е.
g’(x)=(y-z)((y+z)-2x). В качестве функции g(x)
можно взять g(x)=(y-z)((y-z)x-x2).
Так как функции f(x) и g(x) непрерывны и
дифференцируемы на всей числовой прямой и
f’(x)=g’(x), то по следствию 2 f(x)=g(x)+c, где с не зависит
от х, но, возможно, зависит от y и z. Имеем y2(x-z)+x2(z-y)+z2(y-x)=(y-z)((y+z)x-x2)+c.
Найдем с, полагая в этом равенстве, например, х=0.
Имеем yz2-zy2=c. Тогда f(x)=g(x)+yz2-zy2,
то есть
f(x)=(y-z)((y+z)x-x2)+yz2-zy2=(y-z)(xy+xz-x2)-yz(y-z)=(y-z)(xy-x2+xz-yz)=(y-z)(x(y-x)-z(y-x))=(y-z)(y-x)(x-z).
Итак, y2(x-z)+x2(z-y)+z2(y-x)=(y-z)(y-x)(x-z).
Рисунки
Использование производной для
решения
уравнений и неравенств
Бирагова Л.Л.МБОУ лицей
г.Владикавказ
При решении
уравнения или неравенства часто бывает полезно доказать возрастание (убывание)
на некотором промежутке функций, в него входящих. При этом часто пользуются
производными.
Пример 1.
Решим уравнение
![]() .
.
(1)
Решение.
Рассмотрим функцию ![]() . Область существования этой функции есть
. Область существования этой функции есть
промежуток ![]() . Функция f(x) имеет внутри промежутка Х положительную производную
. Функция f(x) имеет внутри промежутка Х положительную производную ![]() .
.
Следовательно, функция f(x) возрастает на промежутке Х, и так как она непрерывна
на этом промежутке, то каждое свое значение она принимает ровно в одной
точке. А это означает, что уравнение (1) имеет не более одного корня. Легко
видеть, что число ![]() удовлетворяет уравнению (1).
удовлетворяет уравнению (1).
Следовательно, уравнение (1) имеет единственный корень ![]() .
.
Ответ: -1.
Пример 2.
Решим неравенство
![]()
(2)
Решение.
Рассмотрим функцию f(x)= ![]() . Поскольку эта функция на
. Поскольку эта функция на
интервале X=![]() имеет
имеет
производную ![]() , которая положительна на этом интервале,
, которая положительна на этом интервале,
то функция f(x) возрастает на интервале Х.
Так как функция f непрерывна на интервале Х,
то каждое свое значение она принимает ровно в одной точке. Следовательно,
уравнение f(x)=0 может иметь не более одного
корня. Легко видеть, что число ![]() является корнем
является корнем
уравнения f(x)=0. Поскольку функция f(x) непрерывна и возрастает на интервале Х, то f(x)<0 при x<0 и f(x)>0 при x>0. Поэтому решениями неравенства
(2) являются все х из промежутка ![]() .
.
Ответ: ![]() .
.
Пример 3.
Выяснить, сколько действительных
корней имеет уравнение:
![]() .
.
(1)
Решение.
Рассмотрим функцию ![]() . Она на интервале
. Она на интервале ![]() имеет производную
имеет производную ![]() .
.
Производная обращается в нуль точках:
![]() и
и ![]() . Так
. Так
как ![]() для любого х из интервалов
для любого х из интервалов ![]() и
и ![]() , то на
, то на
каждом из промежутков![]() и
и ![]() функция
функция
![]() возрастает. Так как
возрастает. Так как ![]() для любого х из промежутка
для любого х из промежутка ![]() , то на промежутке
, то на промежутке ![]()
![]() функция
функция ![]() убывает.
убывает.
Так как ![]() ,
, ![]() ,
, ![]() ,
, ![]() и функция
и функция ![]() непрерывна
непрерывна
на каждом из интервалов ![]() ,
, ![]() и
и ![]() , то на
, то на
каждом из них есть единственная точка, в которой эта функция обращается в нуль.
Следовательно, функция имеет три нуля, т.е. уравнение (1) имеет три
действительных корня.
Ответ: три действительных корня.
Пример 4.
Решить уравнение:
![]()
(1)
Решение.
Обе части уравнения (1) определены на
отрезке ![]() . Рассмотрим функцию
. Рассмотрим функцию
![]() .
.
Эта функция на интервале ![]() имеет производную
имеет производную
![]() ,
,
которая обращается в ноль в
единственной точке ![]() .Так как функция
.Так как функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , то она достигает на этом отрезке
, то она достигает на этом отрезке
наибольшего и наименьшего значений. Они находятся среди чисел ![]() ,
, ![]() ,
, ![]() .
.
Так как ![]() , то наибольшее значение 2 на отрезке
, то наибольшее значение 2 на отрезке ![]() функция достигает в единственной точке
функция достигает в единственной точке ![]() . Следовательно, уравнение (1) имеет
. Следовательно, уравнение (1) имеет
единственный корень ![]() .
.
Ответ: 3.
