В данном разделе будут представлены конкретные примеры и способы их решения в среде Scilab. Целью данного раздела является закрепление уже накопленных вами знаний, а также попутное изучение возможностей среды.
Практически для всех тривиальных задач в системе заготовлены стандартные функции. Перед тем, как мы начнем их разбирать, возьмите за правило:
Если в системе существует функция, которая реализует по крайней мере часть задачи, которую вы решаете, всегда используйте эту функцию и не прибегайте к программированию.
Дело в том, что все функции, входящие в стандартную комплектацию, тестируются разработчиками и оптимизированы под среду. В этом случае любой ваш программируемый алгоритм будет всегда менее эффективен по скорости, чем уже готовый. Хотя возможно это и не всегда так, но поверьте, что затраты времени на «придумывание велосипеда» в большинстве случаев не окупаются.
Простые выражения[править]
Для начала попробуем повычислять простые выражения.
Пример 1
Вычислить
Данное выражение является сложным и требует предварительного разбора. Конечно, можно ввести данное выражение одной строкой в командное окно, но в данном примере мы вычислим его по частям для лучшего понимания материала.
Для начала необходимо определиться с очередностью выполняемых действий. При несложном разборе очередность такова:
- Рассчитать числитель дроби функции синуса;
- Рассчитать знаменатель дроби функции синуса;
- Числитель поделить на знаменатель;
- Найти синус от результата 3;
- Рассчитать выражение степени;
- Возвести результат 4 в степень результата 5.
Описанный алгоритм отражает следующий листинг
-->5*6*sqrt(94-56)+6*sqrt(291+2); // Вычисляем числитель -->ans/(6*41.25^2*sqrt(25*26+1)); //Вычисляем знаменатель -->sin(ans); // Вычисляем синус -->ans^(log10(36.25)+log(34.25)) // Возводим в степень ans = 8.715D-16
Обратите внимание на то, что мы используем для хранения промежуточных результатов переменную ans. В этом примере исходный алгоритм немного облегчен, так, в 4 строке листинга мы объединили пункты 4 и 5.
В этом примере мы использовали две новые функции:
- log10() — вычисляет десятичный логарифм;
- log() — вычисляет натуральный логарифм.
В среде нет функции, которая реализует логарифм по произвольному основанию, но это не является проблемой. По свойству логарифма
тогда, например, логарифм 4 по основанию 2 можно вычислить так
-->log10(4)/log10(2) // через десятичный логарифм ans = 2. -->log(4)/log(2) // через натуральный логарифм ans = 2.
Стоит упомянуть, что в среде есть также встроенная функция для вычисления логарифмов по основанию 2 — log2().
Пример 2<br>
Вычислить<br>
В примере мы вновь возвращаемся к проблеме вычисления логарифма по произвольному основанию, однако применение свойства в данном случае напрямую серьезно усложнит само выражение. В данном случае рациональнее всего объявить собственную функцию, которая бы вычисляла логарифмы при любом основании.
Воспользуемся свойством логарифма и объявим функцию logn().
-->deff('out=logn(m,n)','out=log10(m)/log10(n)') // Имея теперь функцию, легко записать исходное выражение -->(logn(4,6)+logn(9,7))/(logn(32,4^-1)*logn(500,5)) ans = - 0.1971180
Алгебра[править]
В рамках данного раздела мы рассмотрим способы решения самых распространенных задач алгебры.
Решение алгебраических уравнений[править]
Найти корни уравнения
Ранее мы решали подобную задачу. Напомним, что для решения линейных уравнений в среде имеется функция roots(), которая принимает в качестве аргумента объект полином. Практически все действия выполняет за вас среда, необходимо только объявить полином. Напомним, что полином объявляется функцией poly(). В нашем случае полином составляется из коэффициентов, которые нужно переписать в обратном порядке.
-->p=poly([21 -7 -8 2],'x','c') p = 2 3 21 - 7x - 8x + 2x -->roots(p) ans = 4.2415355 - 1.6987739 1.4572384
Функция roots() имеет флаг, определеяющий используемый алгоритм:
- ‘f’ — расчет по алгоритму Дженкинса-Трауба (RPOLY-алгоритм); используется по умолчанию;
- ‘e’ — расчет через собственные вектора сопровождающих матриц.
RPOLY-алгоритм используется главным образом для поиска действительных и комплексных корней с порядком полинома, не превышающем 100. Второй алгоритм существует как альтернатива ему. В большинстве случаев RPOLY-алгоритма достаточно для решения многих задач, поэтому пользоваться флагом приходится редко.
Для примера, найдем корни следующего полинома по второму алгоритму
-->roots(poly([-1 0.6 0.4 1],'x','c'),'e') ans = - 0.5576818 + 1.0425361i - 0.5576818 - 1.0425361i 0.7153636
Решение систем уравнений[править]
Решение трансцендентных уравнений[править]
Трансцендентные уравнения решаются преимущественно численными методами. Обычно этот процесс заключается в выборе интервала, в который попадает по крайней мере один корень уравнения, а затем производится численное приближение к этому корню.
В Scilab определена всего одна функция для решения трансцендентных уравнений fsolve(). Если возможности этой функции по какой-либо причине не устраивают, то обычно пишут собственную функцию, реализующую некоторый численный метод.
Найти корни
// Объявляем функцию -->deff('y=f(x)','y=exp(x)/10-2*(x-1)^2-x^(2/3)') //Вызываем функцию -->fsolve(6,f) ans = 6.4401965
Для решения трансцендентных уравнений необходимо правильно выбирать приближение, для чего требуется представлять левую часть уравнения как функцию и строить график. Если начальное приближение очень далеко от корня, то нет гарантии, что функция fsolve() найдет решение.
Матричная алгебра[править]
Функциональный анализ[править]
Интегральное и дифференциальное исчисления[править]
Статистика[править]
Работа с текстовыми строками[править]
Основы работы с системой технических расчетов Scilab
Решение задач линейной алгебры
Функции для нахождения числовых характеристик матриц
Для определения количества строк и столбцов матрицы М используют функцию size, аргументом которой является имя массива:
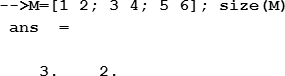
Если нужно определить количество только строк или только столбцов, то синтаксис функции модифицируется: добавляется второй аргумент, который имеет значение “1” или “r”, если следует определить количество строк, “2” или “с” – если столбцов. Например:
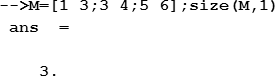
Общее количество элементов матрицы или длину вектора вычисляет функция length, аргументом которой является имя матрицы или вектора:

Для определения максимального значения элемента матрицы или вектора используется функция max, аргументом которой является имя матрицы или вектора. Если нужно определить максимальное значение для каждого из строк или столбцов матрицы, то синтаксис функции модифицируется: добавляется второй аргумент, который имеет значение “r”, если следует определить максимальное значение для каждой строки, или “c” – если для каждого столбца:
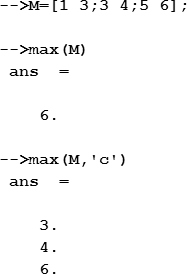
Аналогично используется функция min, предназначенная для определения минимального значения элемента матрицы или вектора.
Для вычисления определителя (детерминанта) квадратной матрицы используется функция det, аргументом которой является имя матрицы:
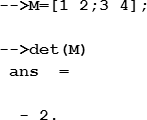
Для вычисления ранга матрицы используется функция rank, аргументом которой является имя матрицы:
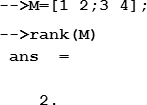
Функции, реализующие численные алгоритмы решения задач линейной алгебры
Вычисление матрицы, обратной М
Напомним, что обратной по отношению к матрице М называется такая матрица, которая при ее умножении на матрицу М дает единичную матрицу.

Как видим, обратная матрица А достаточно близка к единичной, но все же полностью ею не является, что является следствием погрешности численных вычислений.
Scilab позволяет решать системы линейных алгебраических уравнений вида Ax=b. В документе для значений A формируется матрица коэффициентов при неизвестных, каждая строка которой содержит коэффициенты одного уравнения, а для значений b формируется вектор-столбец из свободных коэффициентов.
После этого для решения системы используется функция linsolve, имеющая такой синтаксис:
где A – это матрица коэффициентов при неизвестных, b – вектор-столбец свободных коэффициентов.
Функция возвращает найденные значения неизвестных системы в виде вектора.
Таким образом, решение системы линейных уравнений 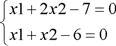 имеет вид:
имеет вид:
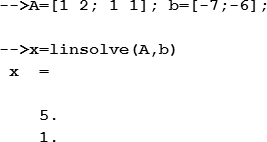
Искомые значения: х1=5, х2=1.
Если система не имеет решения, то об этом выдается сообщение “WARNING: Conflicting linear constraints!” (Конфликтующие условия для линейных уравнений). Например, такая ситуация возникнет при попытке решения системы линейных уравнений 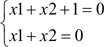 :
:

Система линейных алгебраических уравнений может иметь множество решений. В таком случае функция возвращает только одно. Ниже приведен пример такой ситуации при решении системы линейных уравнений 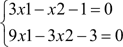 :
:
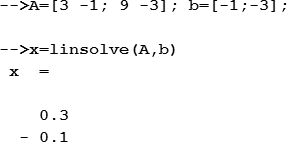
Работа с полиномами
Напомним, что полиномом или алгебраическим уравнением называется уравнение вида a0x n + a1x n-1 + . + an-1x + an.
Для создания полинома используется функция poly.
где р – это имя полинома (его можно и не задавать).
Аргументы функции: a – матрица или вещественное число, x – символьная переменная, “flag” – символьная переменная, которая определяет способ задания полинома и имеет значение “roots” (допускается сокращение “r”) или “coeff” (“c”). По умолчанию – “roots”. Если “roots” имеет значение “r”, то полином создается с параметрами ai для соответствующих символьных переменных xi. Если “flag” имеет значение “c”, то значения параметров ai воспринимаются как корни, для которых нужно рассчитать коэффициенты полинома.
Следующий пример демонстрирует использование функции poly для создания полиномов р1, который имеет корень “2” и р2 с коэффициентом “2”:
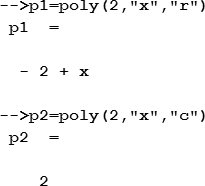
В следующих примерах создаются полиномы с соответствующими коэффициентами для кубического уравнения.
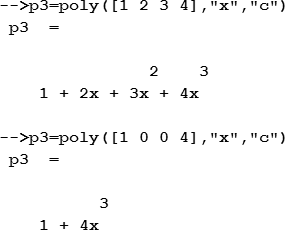
С полиномами можно производить действия умножения, создавать из них дроби (деление), складывать и вычитать.
Решение уравнения с одним неизвестным
Scilab может решать алгебраическое уравнение с одним неизвестным. Например, нужно найти корни уравнения x 2 = 1. Если – как в данном примере – уравнение не имеет вида полинома, то его следует предварительно преобразовать в полином: x 2 – 1 = 0. После этого используется функция roots, единственным аргументом которой является имя полинома. Функция возвращает найденные корни полинома.
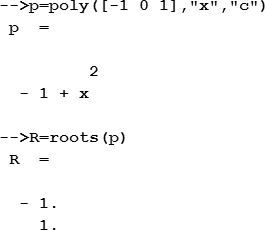
Если уравнение не имеет решения на множестве вещественных чисел (x 2 + 1 = 0), то Scilab ищет решение среди комплексных чисел:

Вычисление сумм элементов матрицы
Для вычисления суммы значений элементов матрицы используется функция sum.
Если следует вычислить отдельно сумму значений для каждого столбца, то вторым аргументом функции является число “1” или буква “с”, а если для строки, то – “2” или буква “r”.

Вычисление произведения элементов матрицы
Для вычисления произведения используется функция prod.
Если следует вычислить отдельно произведение значений каждого столбца, то вторым аргументом функции является число “1” или буква “с”, а если для строки, то – “2” или буква “r”.
Дифференциалы
Для нахождения дифференциалов в определенной точке используется функция numdiff, первый аргумент которой является именем функции, которую нужно продифференцировать, а второй – координата точки, в которой нужно вычислить производную.
Как найти корни уравнения в scilab
–>p2^(-1) //Возведение в отрицательную степень
Функция roots ( p ) предназначена для решения алгебраического уравнения.
Здесь p – это полином, созданный функцией poly и представляющий собой левую часть уравнения P(x) = 0.
Решим несколько алгебраических уравнений.
Задача 7.1 . Найти корни полинома 2x 4 − 8x 3 + 8x 2 − 1 = 0.
Для решения этой задачи необходимо задать полином p . Сделаем это при помощи функции poly, предварительно определив вектор коэффициентов V . В уравнении отсутствует переменная x в первой степени, это означает, что соответствующий коэффициент равен нулю:
Листинг 7.4 . Формирование полинома
1 + 8x 2 – 8x 3 + 2x 4
Теперь найдем корни полинома:
Листинг 7.5. Использование функции roots
Графическое решение задачи позволяет убедиться, что корни найдены верно.
Пересечение графиков функций F( x )= 1 + 8x 2 – 8x 3 + 2x 4 и g ( x )=0
Задача 7.2. Найти корни полинома x 3 + 0.4x 2 + 0.6x − 1 = 0.
Листинг 7.6. Решение задачи 7.2
Нетрудно заметить, что полином имеет один действительный и два комплексных корня.
Задача 7.3. Найти решение уравнения y(x) = 0, если y(x) = x 4 − 18x 2 + 6.
Листинг 7.7. Решение задачи 7.3
Приведите графическое решение данного уравнения.
Уравнение f(x) = 0, в котором неизвестное входит в аргумент трансцендентных функций, называется трансцендентным уравнением .
К трансцендентным уравнениям принадлежат показательные, логарифмические и тригонометрические.
В общем случае аналитическое решение уравнения f(x) = 0 можно найти только для узкого класса функций. Чаще всего приходится решать это уравнение численными методами.
Численное решение нелинейного уравнения проводят в два этапа.
- В начале отделяют корни уравнения, т.е. находят достаточно тесные промежутки, в которых содержится только один корень. Эти промежутки называют интервалами изоляции корня , определить их можно, изобразив график функции f(x) или любым другим методом.
- На втором этапе проводят уточнение отделенных корней, или, иначе говоря, находят корни с заданной точностью.
Для решения трансцендентных уравнений в Scilab применяют функцию
где x0 – начальное приближение, f – функция, описывающая левую часть уравнения y(x) = 0.
Рассмотрим применение этой функции на примерах.
Задача 7.4. Найти решение уравнения
Определим интервал изоляции корня заданного уравнения. Воспользуемся графическим методом отделения корней. Если выражение, стоящее в правой части уравнения, представить в виде разности двух функций f (x) − g(x) = 0 , то абсцисса точки пересечения линий f(x) и g(x) – корень данного уравнения. В нашем случае .
Корень данного уравнения лежит в интервале [0; 1].
Выберем ноль в качестве начального приближения, зададим функцию, описывающую уравнение и решим его:
Листинг 7.8. Решение задачи 7.4
Задача 7.5. Найти корни уравнения f(x) = e x /5 − 2(x − 1) 2 .
На рисунке видно, что график функции f(x) трижды пересекает ось абсцисс, т.е. уравнение имеет три корня.
Последовательно вызывая функцию fsolve с различными начальными приближениями, получим все решения заданного уравнения:
Листинг 7.9. Решение задачи 7.5
Кроме того, начальные приближения можно задать в виде вектора, и тогда функцию можно вызвать один раз:
Листинг 7.10. Решение задачи 7.5 (альтернативный способ)
Задача 7.6. Вычислить корни уравнения sin(x) − 0.4x = 0 в диапазоне [−5π; 5π].
Решение задачи представлено в листинге 7.11.
Листинг 7.11 . Решение задачи 7.6
–>X //Множество решений
X = !-16.11948 -12.154854 -9.8362948 -5.8716685 -3.5531095
0.4115168 2.7300758 6.6947022 9.0132611 12.977887 15.296446!
Задача 7.7. Найти решение уравнения y(x) = 0, если y(x) = x 5 − x 3 + 1.
Вычисление интегралов, решение уравнений и систем
Краткие теоретические сведения
В Scilab вычисление определенного интеграла методом трапеций реализовано функцией
где x –вектор значений аргумента подынтегральной функции на отрезке интегрирования, y –вектор значений, полученных при вычислении подынтегральной функции для элементов вектора x.
Например, для вычисления нужно выполнить следующий набор команд:
| Фрагмент программы x=2:0.01:5.3 y =2*x./(sin(x)+1.5) integral = inttrap(x,y)disp(integral) | Результат 30.436962 |
Для вычисления определенного интеграла с использованием алгоритма квадратурных формул предназначена функция
Integrate(fun, x, a, b, ,er1 ,er2),
где fun– подынтегральная функция в символьном виде, x – переменная интегрирования в символьном виде, a, b –пределы интегрирования, er1,er2 –абсолютная и относительная погрешности интегрирования (необязательные параметры).
Например, для вычисления нужно задать:
| Фрагмент программы z=integrate(‘2*x./(sin(x)+1.5)’, ‘x’, 2, 5.3)disp(z) | Результат 30.437056 |
Универсальная команда интегрирования:
[integral,err]=intg(a, b, name ,er1,er2),
где a, b –пределы интегрирования, name – имя подынтегральной функции (может быть задана с помощью внешней функции), er1,er2 –абсолютная и относительная погрешности интегрирования (необязательные параметры). Функция intgвозвращает значение интеграла (integral) и погрешность вычислений (err).
Внешнюю функцию можно задать командой
deff(‘переменная=имя функции(параметр)’, ‘символьное представление функции’) Например, deff(‘y=F(x)’, ‘y=2*x./(sin(x)+1.5)’).или
function переменная = имя функции(параметр-аргумент функции)
операторы, вычисляющие значение функции
endfunctionНапример, function y=f(t) y=t^2/sqrt(3+sin(t)) endfunctionилиfunction y=f(t),y=t^2/sqrt(3+sin(t)),endfunction
Ниже приводится пример вычисления интеграла .
| Фрагмент программы function y=f(x) y=2*x./(sin(x)+1.5)endfunctionz=intg(2,5.3,f), disp(z) | Результат 30.437056 |
Для решения нелинейных уравнений в Scilab используется функция
где x0 –начальное приближение корня, f– функция, описывающая левую часть уравнения f(x)=0.
Например, для решения уравнения для начального приближения нужно выполнить следующие команды:
| Фрагмент программы deff(‘y=F(x)’, ‘y=sin(2*x)-cos(3*x.^2)-sin(3*x)’)root=fsolve(7,F)disp(root) | Результат 6.9755674 |
Для решения полиномиальных уравнений вида используется функция
где а – вектор коэффициентов перед неизвестными полинома размерностью n+1(n – порядок полинома).
Результатом работы этой функции будет вектор корней полинома размерностью n.
Пример решения полиномиального уравнения приведен ниже.
| Фрагмент программы v=[3 1 -10 -8]R=roots(v)disp(R) | Результат 2. -1.3333333 — 1. |
Для уравнения два корня – комплексные.
| Фрагмент программы v=[3 1 -10 8]R=roots(v)disp(R) | Результат — 2.2935835 0.9801251 + 0.4494650i 0.9801251 — 0.4494650i |
Функция rootsможет также принимать в качестве параметра полином, созданный функциейpolyи представляющий собой левую часть уравнения :
где a –вектор коэффициентов полинома записанных в обратном порядке, x — символьная переменная, f1– символьная переменная, принимающая значения ‘c’ или ‘r’ (roots или coeff).
Например, чтобы создать полином , нужно использовать команду
| Фрагмент программы p=poly([3 -2 1 0 4],’x’,’c’)disp(p) | Результат |
Для решения уравнения можно выполнить следующие команды:
| Фрагмент программы p=poly([-8 -10 1 3],’x’,’c’)R=roots(p)disp(R) | Результат 2. — 1.3333333 — 1. |
Для решения систем линейных уравнений в Scilab есть следующие способы:
— применение операции левого матричного деления;
— использование обратной матрицы.
Если задана система линейных алгебраических уравнений вида:
где А – матрица коэффициентов перед неизвестными системы, В – вектор свободных членов, то решение системы может быть найдено в виде:
То же самое решение может быть получено с помощью обратной матрицы, например:
Например, решить систему уравнений
| Фрагмент программы A=[3 1;-3 5]; B=[-4 ;36]; X=inv(A)*B, disp(X)илиX1=AB , disp(X1) | Результат — 3.1111111 5.3333333 |
Для решения систем нелинейных уравнений можно использовать функцию
где x0 –вектор начальных приближений для неизвестных, f –функция, определяющая систему
Например, решение системы можно выполнить следующим образом:
| Фрагмент программы function [y]=fun(x) y(1)=2*x(1)+x(2)-6 y(2)=x(1)^2+x(2)^2-14endfunctionX0=[1;1]R=fsolve(X0,fun)disp(R) | Результат 1.2338096 3.5323808 |
Задание 1. Вычисление определенного интеграла
Постановка задачи. Вычислить числовое значение интеграла от этой функции в заданных пределах интегрирования методом трапеций, методом квадратурных формул и с помощью функции intg.
Шаг 1. Создадим вектор X, значения которого будут изменяться от 2,1 до 4,3 с шагом 0.01.
Шаг 2. Создадим вектор Y, каждое значение которого вычисляется по формуле .
Шаг 3. Применим команду inttrap(X, Y).
Шаг 4. Используем функцию integrate,задав подынтегральную функцию в символьном виде.
Шаг 5. Определим внешнюю функцию с помощью команды deffили конструкции function
Шаг 6. Выведем результаты, используя команду disp.
| Программа | Результат выполнения |
| X =2.1:0.01:4.3 Y =sin(X)/1.5 integral_1 = inttrap(X,Y)integral_2=integrate(‘sin(x)/1.5’, ‘x’, 2.1, 4.3)disp(integral_1)disp(integral_2) | — 0.0693640 — 0.0693646 |
| deff(‘y=F(x)’,’y=sin(x)/1.5′); integral_3=intg(2.1,4.3,F)function y=f(x) y=sin(x)/1.5endfunctionintegral_4=intg(2.1,4.3,f)disp(integral_3)disp(integral_4) | — 0.0693646 — 0.0693646 |
Индивидуальные задания приведены в таблице 3.4.
Задание 2. Поиск корней уравнения, графическая интерпретация
Постановка задачи. Найти корень уравнения для заданного начального приближения. Выполнить графическую интерпретацию результата.
Шаг 1. Определим внешнюю функцию с помощью команды deffили конструкции function
Шаг 2. Найдем корень уравнения с помощью функции fsolve,подставив в качестве первого параметра заданное начальное приближение.
Шаг 3. Выведем результат, используя команду disp.
Шаг 4. Выполним графическую интерпретацию результата. Для этого зададим аргумент функции из левой части уравнения таким образом, чтобы найденный корень попадал в диапазон между первым и последним элементом вектора. Построим график функции из левой части уравнения с помощью plot.Построим также линию y=0 и отметим точку с абсциссой, равной корню, и ординатой, равной значению функции для корня.
| Программа | Результат выполнения |
| deff(‘y=F(x)’, …’y=sin(x)-cos(x.^2)-sin(2*x)’)root=fsolve(1,F)disp(root)x=0.5:0.01:2.5plot(x,F(x),’-b’,root,F(root),’xr’,x,0,’-k’) | 1.1695683 |
Индивидуальные задания приведены в таблице 3.5
| Вариант | Уравнение | Начальноеприближение |
| 1. | ||
| 2. | ||
| 3. | ||
| 4. | ||
| 5. | ||
| 6. | ||
| 7. | ||
| 8. | ||
| 9. | ||
| 10. | ||
| 11. | ||
| 12. | ||
| 13. | ||
| 14. | ||
| 15. |
Задание 3. Поиск корней полиномиального уравнения, графическая интерпретация
Постановка задачи. Найти все корни полиномиального уравнения. Выполнить графическую интерпретацию для одного из найденных действительных корней.
Шаг 1. Создадим вектор коэффициентов полинома в левой части уравнения (или полином с помощью poly)
Шаг 2. Найдем корни уравнения с помощью функции roots.
Шаг 3. Выведем результат, используя команду disp.
Шаг 4. Выполним графическую интерпретацию результата. Для этого зададим аргумент функции из левой части уравнения таким образом, чтобы выбранный действительный корень попадал в диапазон между первым и последним элементом вектора. Построим график функции из левой части уравнения с помощью plot.Построим также линию y=0 и отметим точку с абсциссой, равной корню, и ординатой, равной значению функции для корня.
| Программа | Результат выполнения |
| v=[2 0 4 -6 -3]R=roots(v)disp(R)root=R(3)x=0.5:0.01:2y=2*x.^4+4*x.^2-6*x-3F_root=2*root^4+4*root^2-6*root-3plot(x,y,’-b’,root,F_root,’xr’,x,0,’-k’) | — 0.4129576 + 1.7282075i — 0.4129576 — 1.7282075i 1.2164706 — 0.3905555 |
Индивидуальные задания приведены в таблице 3.6.
| Вариант | Уравнение |
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. | |
| 6. | |
| 7. | |
| 8. | |
| 9. | |
| 10. | |
| 11. | |
| 12. | |
| 13. | |
| 14. | |
| 15. |
Задание 4. Решение системы линейных уравнений
Постановка задачи. Решить систему линейных уравнений.
Шаг 1. Создадим матрицу коэффициентов при неизвестных
Шаг 2. Создадим вектор свободных членов.
Шаг 3. Умножим матрицу, обратную к матрице коэффициентов, на вектор свободных членов (или применим операцию левого матричного деления).
Шаг 4. Выведем результат, используя команду disp.
| Программа | Результат выполнения |
| A=[3 1 1;-3 5 6;1 -4 -2]; B=[-4 ;36;-19]; X=inv(A)*B disp(X) | — 3. 3. 2. |
Индивидуальные задания приведены в таблице 3.7.
| № | Система уравнений | № | Система уравнений |
| 1. | 2. | ||
| 3. | 4. | ||
| 5. | 6. | ||
| 7. | 8. | ||
| 9. | 10. | ||
| 11. | 12. | ||
| 13. | 14. | ||
| 15. | 16. |
Статьи к прочтению:
Метод Крамера за 3 минуты. Решение системы линейных уравнений — bezbotvy
Похожие статьи:
Приближенное вычисление интегралов Приближённое вычисление определённого интеграла основано на геометрическом смысле интеграла и сводится к приближённому…
Задание: графически и численно решить систему нелинейных алгебраических уравнений, на примере поиска точек пересечения двух функций. Исходные данные:…
[spoiler title=”источники:”]
http://5fan.ru/wievjob.php?id=36869
http://csaa.ru/vychislenie-integralov-reshenie-uravnenij-i-sistem/
[/spoiler]

На рис. 10 приведен файл-сценарий построения графика рассматриваемой функции.
Рис. 10. Файл-сценарий построения графика рассматриваемой функции
3.2. РЕШЕНИЕ ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ
Уравнение f(x) = 0, в котором неизвестное входит в аргумент трансцендентных функций (показательных, логарифмических и тригонометрических), называется трансцендентным уравнением. В общем случае аналитическое решение нелинейного уравнения f(x) = 0 можно найти только для узкого класса функций. Чаще всего приходится решать такое уравнение численными методами.
Численное решение нелинейного уравнения проводят в два этапа:
1)В начале отделяют корни уравнения, т.е. находят достаточно тесные промежутки, в которых содержится только один корень. Эти промежутки называют интервалами изоляции корня, определить их можно, изобразив график функции f(х).
2)Затем проводят уточнение отделенных корней, или, иначе говоря, находят корни с заданной точностью.
Для решения трансцендентных уравнений в Scilab применяют функцию
fsolve(x0,f),
20

где х0 – начальное приближение;
f – функция, описывающая левую часть уравнения f(х) = 0.
Последовательно вызывая функцию fsolve с различными начальными приближениями, получают все решения заданного уравнения на заданном диапазоне.
Пример. Найти корни уравнения e x − 2(x − 1)2 = 0 . 5
Этап 1. Отделение корней. С помощью конструкции function … endfunction определяется вид функции, задается вектор диапазона значений аргумента x, вычисляется вектор значений функции y и строится график функции (рис. 11).
Рис. 11. Команды для задания вида функции и построения графика функции
Этап 2. По графику функции (рис. 12) определяются начальные приближения корней (0, 2, 5). Уточнить корни можно: либо последовательно вызывая функцию fsolve с различными начальными приближениями (рис. 13); либо задав вектор начальных приближений, тогда fsolve вызывается один раз (рис. 14).
21

Рис. 12. Графическое решение трансцендентного уравнения
Рис. 13. Последовательный вызов fsolve с различным начальным приближением
Рис. 14. Вызов fsolve при задании начальных приближений в виде вектора
На рис. 15 приведен файл-сценарий нахождения корней трансцендентного уравнения.
22
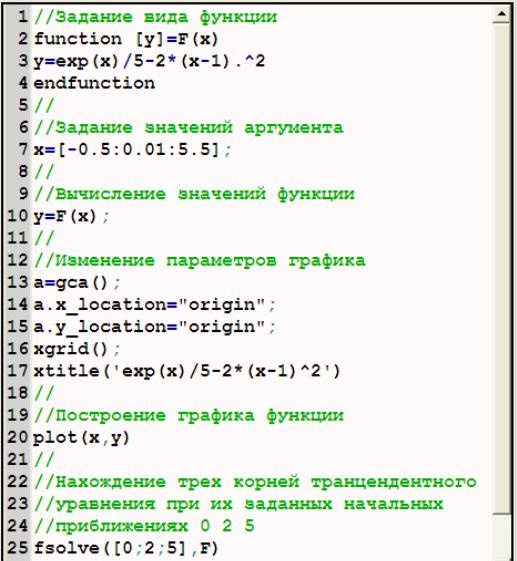
Рис. 15. Файл-сценарий построения графика трансцендентного уравнения
инахождения его корней
3.3.РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Любое уравнение Р(х) = 0, где Р(х) – это многочлен, отличный от нулевого, называется алгебраическим уравнением или полиномом. Всякое алгебраическое уравнение относительно х можно записать в виде
|
a |
0 |
x n + a x n −1 |
+ K + a |
n −1 |
x + a |
n |
= 0 , |
(1) |
|
1 |
где a0 ≠ 0, n ≥ 1 и ai – коэффициенты алгебраического уравнения n-й степени.
23

Например, линейное уравнение это алгебраическое уравнение первой степени, квадратное – второй, кубическое – третьей и так далее.
Решение алгебраического уравнения в Scilab состоит из двух этапов.
–задать полином Р(х) с помощью функции poly;
–найти его корни, применив функцию roots.
Определение полиномов в Scilab осуществляет функция
poly (a, ’x’, [’f1’]),
где а – это число или матрица чисел, х – символьная переменная, fl
– необязательная символьная переменная, определяющая способ задания полинома.
Символьная переменная fl может принимать только два значения – «roots» или «coeff» (соответственно «r» или «с»). Если f1 = с, то будет сформирован полином с коэффициентами, хранящимися в параметре а. Если же f1 = r, то значения параметра а воспринимаются функцией как корни, для которых необходимо найти коэффициенты соответствующего полинома. По умолчанию
fl = r.
Для решения алгебраического уравнения используется функция roots(p), где р – это полином, созданный функцией poly, и представляющий собой левую часть уравнения (1).
Пример. Найти корни полинома 2x 4 − 8x3 + 8x 2 − 1 = 0 . Предварительно необходимо задать вектор коэффициентов
полинома v, и сам полином p (рис. 16).
Рис. 16. Задание полинома
Затем необходимо найти корни заданного полинома (рис. 17).
24

Рис. 17. Нахождение корней полинома
Графическое решение задачи, показанное на рис. 18, позволяет убедиться, что корни найдены верно.
Рис. 18. Графическое решение полинома
На рис. 19 приведен файл-сценарий нахождения корней полинома и построения его графика.
25

Рис. 19. Файл-сценарий нахождения корней полинома
ипостроения его графика
3.4.РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ (СЛАУ)
СЛАУ можно записать в матричном виде
Ax = b ,
где А – матрица коэффициентов при неизвестных; х – вектор неизвестных;
b – вектор свободных членов.
При решении СЛАУ можно использовать метод обратной матрицы. Тогда решение можно найти по формуле
x = A−1 b .
26

Пример. Решить систему линейных алгебраических уравнений (СЛАУ)
|
6x |
− 2x |
+ x |
= |
4 |
|||
|
1 |
2 |
3 |
|||||
|
3x |
+ 2x3 |
= |
6 |
||||
|
6x |
− 2x2 |
+ 12x3 |
= 1 |
||||
Для решения СЛАУ методом обратной матрицы необходимо:
1.Задать матрицу коэффициентов при неизвестных A и вектор свободных членов b.
2.Проверить детерминант матрицы А.
3.Если детерминант не равен 0, найти обратную матрицу A-1.
4.Умножить обратную матрицу на вектор свободных членов.
Специальные матричные функции необходимые для решения СЛАУ методом обратной матрицы:
–Функция det(А) – вычисляет определитель квадратной матрицы А.
–Функция inv(A) вычисляет обратную матрицу к матрице А. Решение СЛАУ с помощью этого метода приведено на рис. 20.
Рис. 20. Решение СЛАУ с использованием обратной матрицы
27

Решить СЛАУ, заданную в виде уравнения Ax − b = 0 , можно, используя функцию linsolve(A, b) (рис. 21).
Рис. 21. Решение СЛАУ с использованием функции linsolve
3.5. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
Рассчитать значение определенного интеграла можно с помощью формулы Ньютона-Лейбница
|
b |
|
|
∫ f (x)dx = F (b) − F (a) , |
(2) |
a
где F(x) – первообразная подинтегральной функции.
Сложность заключается в том, что не всегда можно найти первообразную подинтегральной функции, или она оказывается слишком сложной. В этих случаях для вычисления интеграла используют различные численные методы.
В функциях интегрирования в Scilab реализованы различные численные алгоритмы. Наиболее универсальной командой интегрирования в Scilab является
[I, err] = intg(a, b, name [,erl [,er2]]),
где nаmе — имя функции, задающей подынтегральное выражение (функция может быть задана в виде набора дискретных точек, т.е. таблицей или с помощью внешней функции);
а и b – пределы интегрирования;
erl и еr2 — абсолютная и относительная точность вычислений (необязательные параметры).
28

|
5 |
||||
|
Пример. |
Вычислить значение интеграла ∫sin(x) cos(2x) . |
|||
|
2 |
||||
|
Первообразной |
подинтегральной функции является функция |
|||
|
F (x) = − |
cos(3x) |
+ |
cos(x) |
. |
|
6 |
2 |
Решение, полученное по формуле Ньютона-Лейбница, приведено на рис. 22.
Рис. 22. Вычисление интеграла по формуле Ньютона-Лейбница
При использовании функции intg необходимо вначале задать подинтегральную функцию как внешнюю. Это можно сделать с помощью конструкции function … endfunction.
Решение, полученное с помощью функции intg, приведено на рис. 23.
Рис. 23. Использование функции intg
На рис. 24 приведен файл-сценарий вычисления рассматриваемого интеграла.
29
Scilab предоставляет ряд средств для поиска корней уравнений, как с одной переменной, так и с несколькими.
Уравнения с одной переменной. Если речь идёт о полиноме, для поиска его корней используется функция roots(p). В общем же случае применяется функция fsolve(x0, func), которая находит решение (приближённое) трансцендентного уравнения func при начальном значении корня x0. Если корней несколько, можно задать вектор начальных приближений x0.

Системы уравнений. Если система уравнений линейная (Y=A*X+d), для её решения может быть использована функция linsolve(A,d), где A – матрица коэффициентов, d – вектор свободных коэффициентов.

В общем случае используется всё та же универсальная функция fsolve(X0, func), но на этот раз X0 – вектор начальных приближений, а func – система уравнений, заданная в виде функции.

В данном примере x = [x(1), x(2)] – вектор независимых переменных, y = [y(1), y(2)] – вектор значений, а fn1 определяет функциональную связь между ними.
fsolve
find a zero of a system of n nonlinear functions
Syntax
[x, v, info] = fsolve(x0, fct) [x, v, info] = fsolve(x0, fct, fjac) [x, v, info] = fsolve(x0, fct, fjac, tol) [x, v, info] = fsolve(x0, fct, tol)
Arguments
- x0
-
real vector (initial value of function argument).
- fct
-
external (i.e function or list or string).
- fjac
-
external (i.e function or list or string).
- tol
-
real scalar. precision tolerance: termination occurs when the
algorithm estimates that the relative error between x and the
solution is at most tol. (tol=1.d-10is the
default value). - x :
-
real vector (final value of function argument, estimated zero).
- v :
-
optional real vector: value of function at x.
- info
-
optional termination indicator:
0 improper input parameters. 1 algorithm estimates that the relative error between x
and the solution is at most tol.2 number of calls to fcn reached 3 tol is too small. No further improvement in the
approximate solution x is possible.4 iteration is not making good progress.
Description
find a zero of a system of n nonlinear functions in n variables by a
modification of the powell hybrid method. Jacobian may be provided.
fct is an “external”. This external returns
v=fct(x) given x.
The simplest syntax for fct is:
If fct is a character string, it refers to a C or
Fortran routine which must be linked to Scilab. Fortran calling sequence
must be
fct(n,x,v,iflag) integer n,iflag double precision x(n),v(n)
and C Syntax must be
Incremental link is possible (help link).
jac is an “external”. This external returns
v=d(fct)/dx (x) given x.
The simplest syntax for jac is:
If jac is a character string, it refers to a to a
C or Fortran routine which must be linked to Scilab calling sequences are
the same as those for fct. Note however that v must be a nxn array.
Examples
a=[1,7;2,8]; b=[10;11]; function y=fsol1(x) y=a*x+b endfunction function y=fsolj1(x) y=a endfunction [xres]=fsolve([100;100],fsol1); a*xres+b [xres]=fsolve([100;100],fsol1,fsolj1); a*xres+b [xres]=fsolve([100;100],'fsol1','fsolj1',1.e-7); a*xres+b
For some starting points and some equations system, the fsolve method can fail. The fsolve method is a local search method.
So, to have a good chance to find a solution to your equations system, you must ship, a good starting point to fsolve.
Here is an example on which fsolve can fail:
function F=feuler(x, r) F=x-r-dt*(x.^2-x.^3); endfunction function J=dFdx(x) J=1-dt*(2*x-3*x^2); endfunction r = 0.04257794928862307 ; dt = 10; [x,v,info]=fsolve(r,list(feuler,r),dFdx); disp(v); disp(info); [x,v,info]=fsolve(1,list(feuler,r),dFdx); disp(v); disp(info); clf(); x=linspace(0,1,1000); plot(x,feuler(x)) a=gca(); a.grid=[5 5];
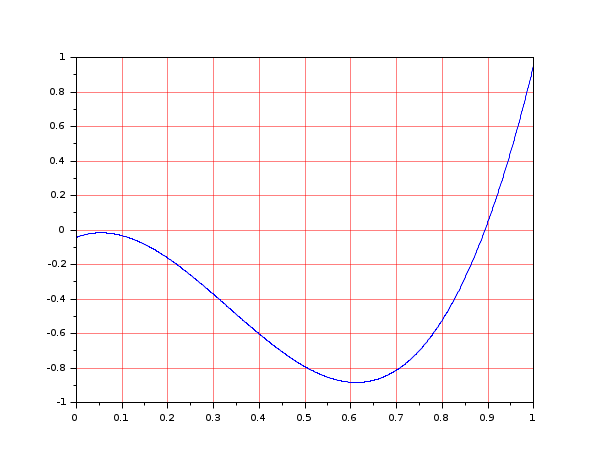
So, each time you use fsolve, be sure to check the termination indicator and the residual value to see if fsolve has converged.
See also
- external — Scilab Object, external function or routine
- qpsolve — linear quadratic programming solver
- optim — non-linear optimization routine





![{displaystyle e^{x}/10-2(x-1)^{2}-{sqrt[{3}]{x^{2}}}=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21d53619de1f6e3cd1bbe9e2fde69781e8e3f678)
