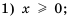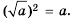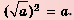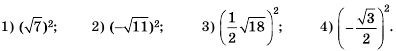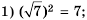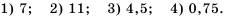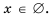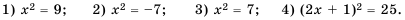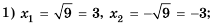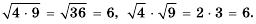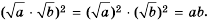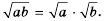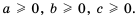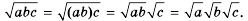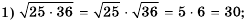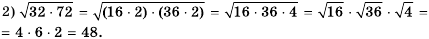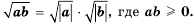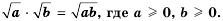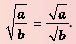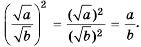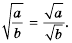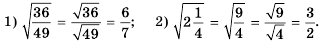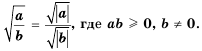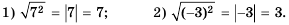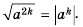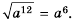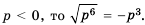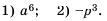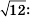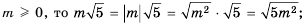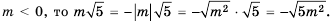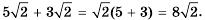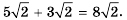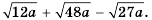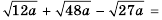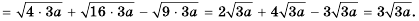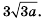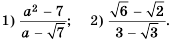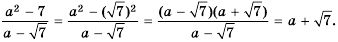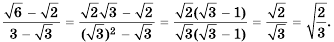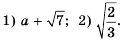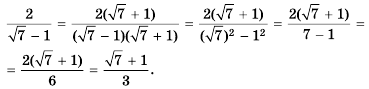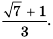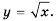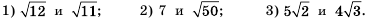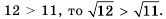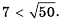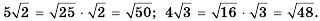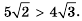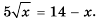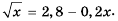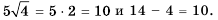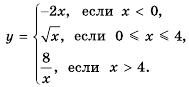Найти корень уравнения? Это просто!
В математике встречаются разнообразные уравнения. Их всегда нужно решать, то есть искать все числа, которые сделают его верным равенством. Пути поиска решений определяются первоначальным видом уравнения. От него же будет зависеть и количество верных значений переменной, которые обозначаются, как корень уравнения. Это число может варьироваться от нуля до бесконечности.
Что подразумевается под уравнением и его корнем?
Из названия понятно, что оно приравнивает две величины, которые могут быть представлены числовыми или буквенными выражениями. Кроме того, они содержат еще неизвестные величины. Самое простое уравнение имеет только одну.
Видов уравнений большое количество, но понятие корня для них всегда одно и то же. Корень уравнения — это такое значение неизвестного числа, при котором уравнение принимает становится верным равенством. Бывают ситуации, когда таких чисел несколько, тогда неизвестная называется переменной.
В алгебре при решении уравнений можно прийти к такой ситуации, что корней не будет совсем. Тогда говорят о том, что оно неразрешимо. А в ответе такого уравнения нужно записать, что решений нет.
Но иногда бывает и противоположное. То есть в процессе многочисленных преобразований появляются посторонние корни. Они не дадут верного равенства при подстановке. Поэтому числа всегда нужно проверять, чтобы избежать ситуации с лишними корнями в ответе. Иначе уравнение не будет считаться решенным.
О линейном уравнении
Оно всегда может быть преобразовано в запись следующего вида: а * х + в = 0. В нем «а» всегда не равно нулю. Чтобы понять сколько корней имеет уравнение, его потребуется решить в общем виде.
- перенести в правую часть равенства слагаемое «в», заменив его знак на противоположный;
- разделить обе части получившегося равенства на коэффициент «а».
х = -в/а.
Из него ясно, что ответом будет одно число. То есть всего один корень.
Квадратное уравнение
Его общий вид: а * х 2 + в * х + с = 0. Здесь коэффициенты являются любыми числами, кроме первого, «а», которое не может быть равным нулю. Ведь тогда оно автоматически превратится в линейное. Ответ на вопрос, сколько корней имеет уравнение, уже не будет столь однозначным, как это было в предыдущем случае.
Все будет зависеть от значения дискриминанта. Он вычисляется по формуле Д = в 2 – 4 а * с. После расчетов «Д» может получиться больше, меньше или равным нулю. В первом случае корней уравнения будет два, во втором ответом будет «корней нет», а третья ситуация даст только одно значение неизвестной.
Формулы, которые используют для нахождения корней квадратного уравнения, и содержащие дискриминант
В общем случае, когда «Д» положительное число, не равное нулю, нужно использовать такую формулу:
При равенстве «Д» нулю корень уравнения — это единственное число. Просто потому что квадратный корень из нуля равен нулю. А значит, прибавлять и вычитать нужно будет ноль. От этого число не изменится. Поэтому формулу корня уравнения можно записать без упоминания “Д”:
х = (-в) / (2 * а).
При отрицательном значении дискриминанта извлечь из него квадратный корень не представляется возможным. Поэтому корней у такого уравнения не будет.
Замечание. Это верно для курса школьной программы, в которой не изучаются комплексные числа. Когда они вводятся, то получается, что и в этой ситуации ответов будет два.
Формулы для расчета корней квадратного уравнения, не использующие дискриминант
Речь идет о теореме Виета. Она действительна в случае, когда квадратное уравнение записывается в несколько другом виде:
х 2 + в * х + с = 0.
Тогда формула корней квадратного уравнения сводится к тому, чтобы выполнить решение двух линейных:
Оно решается за счет того, что из первого выводится выражение для одного из корней. И это значение нужно подставить во второе. Так будет найден второй корень, а потом первый.
К этому варианту всегда можно прийти от общего вида квадратного уравнения.
Достаточно только разделить все коэффициенты на «а».
Как быть, если нужно узнать наименьшее значение корня?
Решать уравнение и находить все возможные числа, которые подойдут для ответа. А потом выбрать самое малое. Это и будет наименьший корень уравнения.
Чаще всего такие вопросы встречаются в заданиях, которые имеют степень большую, чем 2, или содержат тригонометрические функции. Примером, когда нужно найти наименьший корень, может служить такое равенство:
2 х 5 + 2 х 4 – 3 х 3 – 3 х 2 + х + 1 = 0.
Чтобы найти каждое значение, которое можно назвать “корень уравнения”, это равенство нужно преобразовать. Первое действие: сгруппировать его члены попарно: первый со вторым и так далее. Потом из каждой пары вынести общий множитель.
В каждой скобке останется (х + 1). Общим множителем в первой из пар будет 2 х 4 , во второй 3 х 2 . Теперь снова нужно выполнить вынесение общего множителя, которым будет являться одинаковая скобка.
После множителя (х + 1) будет стоять (2 х 4 – 3 х 2 + 1). Произведение двух множителей равняется нулю, только если один из них принимает значение, равное нулю.
Первая скобка равна нулю при х = -1. Это будет одним из корней уравнения.
Другие будут получены из уравнения, образованного второй скобкой, приравненной к нулю. Оно биквадратное. Для его решения нужно ввести обозначение: х 2 = у. Тогда уравнение существенно преобразится и примет привычный вид квадратного уравнения.
Его дискриминант равен Д = 1. Он больше нуля, значит корней будет два. Первый корень оказывается равным 1, второй будет 0,5. Но это значения для «у».
Нужно вернуться к введенному обозначению. х1,2 = ± 1, х3,4 = ± √0,5. Все корни уравнения: -1; 1; -√0,5; √0,5. Наименьший из них — -1. Это ответ.
В качестве заключения
Напоминание: все уравнения нужно проверять на то, подходит ли корень. Может быть, он посторонний? Стоит выполнить проверку предложенного примера.
Если подставить в изначально данное уравнение вместо “х” единицу, то получается, что 0 = 0. Этот корень верный.
Если х = -1, то получается такой же результат. Корень тоже подходящий.
Аналогично, при значениях “х” равных -√0,5 и √0,5 опять выходит верное равенство. Все корни подходят.
Этот пример не дал посторонних корней. Такое бывает не всегда. Вполне могло оказаться, что самое маленькое значение не подходило бы при проверке. Тогда пришлось бы выбирать из оставшихся.
Вывод: надо помнить о проверке и внимательно подходить к решению.
Решение простых линейных уравнений
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.
Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.
Решить уравнение значит найти все возможные корни или убедиться, что их нет.
Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Какие бывают виды уравнений
Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.
Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа.
Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Числовой коэффициент — число, которое стоит при неизвестной переменной.
Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:
Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.
Как решать простые уравнения
Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.
1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.
Для примера рассмотрим простейшее уравнение: x+3=5
Начнем с того, что в каждом уравнении есть левая и правая часть.
Перенесем 3 из левой части в правую и меняем знак на противоположный.
Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.
Решим еще один пример: 6x = 5x + 10.
Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.
Приведем подобные и завершим решение.
2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.
Применим правило при решении примера: 4x=8.
При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.
Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.
Разделим каждую часть на 4. Как это выглядит:
Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:
Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12
-
Разделим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.
−4x = 12 | : (−4)
x = −3
Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.
Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.
Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.
| Алгоритм решения простого линейного уравнения |
|---|
|
Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.
Примеры линейных уравнений
Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!
Пример 1. Как правильно решить уравнение: 6х + 1 = 19.
-
Перенести 1 из левой части в правую со знаком минус.
Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.
Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3 (х − 4) + 2х − 1.
5х − 15 + 2 = 3х − 12 + 2х − 1
Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.
5х − 3х − 2х = −12 − 1 + 15 − 2
Приведем подобные члены.
Ответ: х — любое число.
Пример 3. Решить: 4х = 1/8.
-
Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.
Пример 4. Решить: 4(х + 2) = 6 − 7х.
- 4х + 8 = 6 − 7х
- 4х + 7х = 6 − 8
- 11х = −2
- х = −2 : 11
- х = −2/11
Ответ: −2/11 или −(0,18). О десятичных дробях можно почитать в другой нашей статье.
Пример 5. Решить:
- 3(3х — 4) = 4 · 7х + 24
- 9х — 12 = 28х + 24
- 9х — 28х = 24 + 12
- -19х = 36
- х = 36 : (-19)
- х = – 36/19
Пример 6. Как решить линейное уравнение: х + 7 = х + 4.
5х — 15 + 2 = 3х — 2 + 2х — 1
Сгруппировать в левой части неизвестные члены, в правой — свободные члены:
Приведем подобные члены.
Ответ: нет решений.
Пример 7. Решить: 2(х + 3) = 5 − 7х.
Что такое уравнение и корни уравнения? Как решить уравнение?
Уравнения бывают разные. Вы изучите их многие виды в курсе математике, но все они решаются по одним правилам, эти правила мы сейчас рассмотрим подробно.
Что такое уравнение? Смысл и понятия.
Узнаем сначала все понятия, связанные с уравнением.
Определение:
Уравнение – это равенство, содержащее переменные и числовые значения.
Переменные (аргументы уравнения) или неизвестные уравнения – их обозначают в основном латинскими буквами (x, y, z, f и т.д.). При подстановки числового значения переменной в уравнение получаем верное равенство – это корень уравнения.
Решить уравнение – это значит найти все корни уравнения или доказать, что у данного уравнения нет корней.
Корни уравнения – это значение переменной при котором уравнение превращается в верное равенство.
Рассмотрим теперь, все термины на простом примере:
x+1=3
В данном случае x – переменная или неизвестное значение уравнения.
Можно устно решить данное уравнение. Какое надо число прибавить к 1, чтобы получить 3? Конечно, число 2. То есть наша переменная x =2. Корень уравнения равен 2. Проверим правильно ли мы решили уравнение? Чтобы проверить уравнение, нужно вместо переменной подставить полученный корень уравнения.
Получили верное равенство. Значит, правильно нашли корни уравнения.
Но бывают более сложные уравнения, которые устно не решить. Нужно прибегать к правилам решения уравнений. Рассмотрим правила решения уравнений ниже, которые объяснят нам как решать уравнения.
Правила уменьшения или увеличения уравнения на определенное число.
Чтобы понять правило рассмотрим подробно простой пример:
Решите уравнение x+2=7
Решение:
Чтобы решить данное уравнение нужно левую и правую часть уменьшить на 2. Это нужно сделать для того, чтобы переменная x осталась слева, а известные (т.е. числа) справа. Что значит уменьшить на 2? Это значит отнять от левой части двойку и одновременно от правой части отнять двойку. Если мы делаем какое-то действие, например, вычитание применяя его одновременно к левой части уравнения и к правой, то уравнение не меняет смысл.
Нужно остановиться на этом моменте подробно. Другими словами, мы +2 перенесли с левой части на правую и знак поменяли стало число -2.
Как проверить правильно ли вы нашли корень уравнения? Ведь не все уравнения будут простыми как данное. Чтобы проверить корень уравнения его значение нужно поставить в само уравнение.
Проверка:
Вместо переменной x подставим 5.
x+2=7
5+2=7
Получили верное равенство, значит уравнение решено верно.
Ответ: 5.
Разберем следующий пример:
Решите уравнение x-4=12.
Решение:
Чтобы решить данное уравнение нужно увеличить левую и правую часть уравнения на 4, чтобы переменная x осталось в левой стороне, а известные (т.е. числа) в правой стороне. Прибавим к левой и правой части число 4. Получим:
Другими словами, мы -4 перенесли из левой части уравнения в правую и получили +4. При переносе через равно знаки меняются на противоположные.
Теперь выполним проверку, вместо переменной x подставим в уравнение полученное число 16.
x-4=12
16-4=12
Ответ: 16
Очень важно понять правила переноса частей уравнения через знак равно. Не всегда нужно переносить числа, иногда нужно перенести переменные или даже целые выражения.
Рассмотрим пример:
Решите уравнение 4+3x=2x-5
Решение:
Чтобы решить уравнение необходимо неизвестные перенести в одну сторону, а известные в другую. То есть переменные с x будут в левой части, а числа в правой части.
Сначала перенесем 2x с правой стороны в левую сторону уравнения и получим -2x.
4+3x= 2x -5
4+3x -2x =-5
Далее 4 с левой стороны уравнения перенесем на правую сторону и получим -4
4 +3x-2x=-5
3x-2x=-5 -4
Теперь, когда все неизвестные в левой стороне, а все известные в правой стороне посчитаем их.
(3-2)x=-9
1x=-9 или x=-9
Сделаем проверку, правильно ли решено уравнение? Для этого вместо переменной x в уравнение подставим -9.
4+3x=2x-5
4+3⋅ (-9) =2⋅ (-9) -5
4-27=-18-5
-23=-23
Получилось верное равенство, уравнение решено верно.
Ответ: корень уравнения x=-9.
Правила уменьшения или увеличения уравнения в несколько раз.
Данное правило подходит тогда, когда вы уже посчитали все неизвестные и известные, но какой-то коэффициент остался перед переменной. Чтобы избавится от не нужного коэффициента мы применяем правило уменьшения или увеличения в несколько раз коэффициент уравнения.
Рассмотрим пример:
Решите уравнение 5x=20.
Решение:
В данном уравнение не нужно переносить переменные и числа, все компоненты уравнения стоят на месте. Но нам мешает коэффициент 5 который стоит перед переменной x. Мы не можем его просто взять и перенести в правую сторону уравнения, потому что между число 5 и переменно x стоит умножение 5⋅х. Если бы между переменной и числом стоял знак плюс или минус, мы могли бы 5 перенести вправо. Но мы так поступить не можем. За то мы можем все уравнение уменьшить в 5 раз или поделить на 5. Обязательно делим правую и левую сторону одновременно.
5x=20
5x :5 =20 :5
5:5x=4
1x=4 или x=4
Делаем проверку уравнения. Вместо переменной x подставляем 4.
5x=20
5⋅ 4 =20
20=20 получили верное равенство, корень уравнение найден правильно.
Ответ: x=4.
Рассмотрим следующий пример:
Найдите корни уравнения .
Решение:
Так как перед переменной x стоит коэффициент необходимо от него избавиться. Надо все уравнение увеличить в 3 раза или умножить на 3, обязательно умножаем левую часть уравнения и правую часть.
Сделаем проверку уравнения. Подставим вместо переменной x полученный корень уравнения 21.
7=7 получено верное равенство.
Ответ: корень уравнения равен x=21.
Следующий пример:
Найдите корни уравнения
Решение:
Сначала перенесем -1 в правую сторону уравнения относительно знака равно, а в левую сторону и знаки у них поменяются на противоположные.
Теперь нужно все уравнение умножить на 5, чтобы в коэффициенте перед переменной x убрать из знаменателя 5.
Далее делим все уравнение на 3.
3x :3 =45 :3
(3:3)x=15
Сделаем проверку. Подставим в уравнение найденный корень.
Как решать уравнения? Алгоритм действий.
Подведем итог разобранной теме уравнений, рассмотрим общие правила решения уравнений:
- Перенести неизвестные в одну сторону, а известные в другую сторону уравнения относительно равно.
- Преобразовать и посчитать подобные в уравнении, то есть переменные с переменными, а числа с числами.
- Избавиться от коэффициента при переменной если нужно.
- В итоге всех действий получаем корень уравнение. Выполняем проверку.
Эти правила действуют на любой вид уравнения (линейный, квадратный, логарифмический, тригонометрический, рациональные, иррациональные, показательные и другие виды). Поэтому важно понять эти простые правила и научиться ими пользоваться.
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/reshenie-prostyh-linejnyh-uravnenij
http://tutomath.ru/6-klass/chto-takoe-uravnenie-i-korni-uravneniya-kak-reshit-uravnenie.html
[/spoiler]
Содержание:
Квадратные корни
Уравнение х2 = 9 имеет два решения: 3 и -3. Говорят, что 3 и -3 — квадратные корни из числа 9.
Квадратным корнем из числа а называют число, I квадрат которого равен а.
Примеры:
Квадратными корнями из числа:
- а) 1600 являются 40 и – 40, поскольку 402 = 1600 и (-40)2 = 1600;
- б) 0,49 являются 0,7 и 0,7, поскольку 0,72 = 0,49 и (-0,7)2 = 0,49.
Среди известных вам чисел нет такого, квадрат которого был бы равен отрицательному числу, поэтому квадратного корня из отрицательного числа не существует.
Квадратный корень из числа 0 равен нулю. Квадратный корень из положительного числа имеет два значения: одно из них положительное, другое — противоположное ему отрицательное число.
Неотрицательное значение квадратного корня называют арифметическим значением этого корня.
Арифметическое значение квадратного корня из числа a обозначают символом
Примечание. Символом 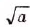
Вычисление арифметического значения квадратного корня называют извлечением квадратного корня.
Из небольших чисел, являющихся точными квадратами чисел, извлекать квадратные корни желательно устно.
| а | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | 144 |
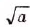 |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Квадратные корни из больших натуральных чисел можно находить, пользуясь таблицей квадратов.
Например, 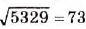
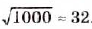
С помощью калькулятора можно извлекать квадратные корни с большей точностью. Например, чтобы извлечь квадратный корень из 1000, набираем это число, затем нажимаем клавишу 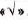
Следовательно, 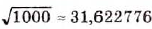
Если таким способом найти значение 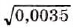
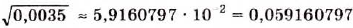
Хотите знать ещё больше?
Извлекать квадратные корни из натуральных чисел вавилонские учёные умели ещё 4 тыс. лет тому назад Они составили таблицу квадратов многих натуральных чисел и, пользуясь ею, находили квадратные корни. Если число m не было точным квадратом натурального числа, то они искали ближайшее приближённое значение а квадратного корня из m, представляли число m в виде m = а2 + b и применяли правило, которое сейчас можно записать в виде формулы 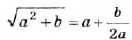
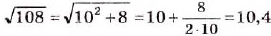
Проверка. 10,42 = 108,16.
Это правило извлечения квадратных корней было известно и учёным Древней Греции.
Известны и другие алгоритмы извлечения квадратных корней, но теперь это удобнее делать с помощью калькулятора.
Квадратный корень из произведения, дроби, степени
Арифметический корень из а — неотрицательное значение квадратного корня из неотрицательного числа а. Поэтому для любого неотрицательного числа а выполняется тождество 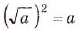
Примеры:
Верны и такие тождества:
— для неотрицательных значений а и b;
— для неотрицательного а и положительного b;
– для неотрицательного а и натурального к.
Докажем эти тождества:
1. Если а и b — произвольные неотрицательные числа, то числа 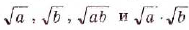
Следовательно, 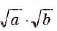
2. Если 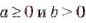
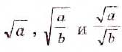
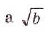
Следовательно, 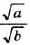
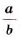
3. Если число а — неотрицательное, a k — натуральное, то числа 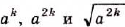
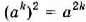
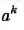
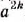
Доказанные три теоремы кратко можно сформулировать так.
- Корень из произведения двух неотрицательных чисел равен произведению корней из этих чисел (теорема о корне из произведения).
- Корень из дроби, числитель которой неотрицательный, а знаменатель положительный, равен корню из числителя, делённому на корень из знаменателя (теорема о корне из дроби).
- Корень из степени a , в котором числа а — неотрицательное и k — натуральное, равен ст (теорема о корне из степени)
Примечание. Здесь под «корнем» понимают только квадратный арифметический корень.
Теорему о корне из произведения можно распространить на три множителя и более. Действительно, если числа а, b и с — неотрицательные, то 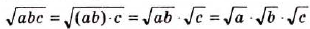
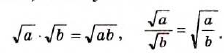
Из теоремы о корне из степени следует, что 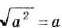
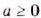
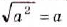
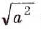
Равенство 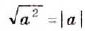
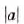
Примеры:
Хотите знать ещё больше?
В сформулированных выше теоремах представлены только простейшие случаи преобразования арифметических значений квадратных корней: если все числа под корнями положительные или неотрицательные Но бывают и такие выражения, в которых под знаком корня — произведение либо частное двух отрицательных чисел. В этом случае можно использовать определения квадратного корня, арифметического значения квадратного корня и т. д.
Например, 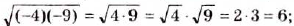
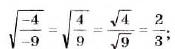
Из теоремы 3 несложно получить такое следствие.
Если натуральное число 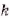
Ведь обе части этого равенства — числа неотрицательные, их квадраты – равны.
Выполним вместе!
Пример:
Найдите значение выражения: а) 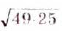
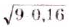
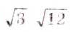
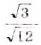
Решение:
О т в е т. а) 35; б) 1,2; в) 6; г)
Преобразование выражений с корнями
Выражения с квадратными корнями можно складывать, вычитать, умножать, возводить в степень и делить (на делитель, отличный от нуля).
Примеры:
Рассмотрим и другие преобразования выражений с корнями.
Подобное преобразование называют вынесением множителя за знак корня. В последнем примере за знак корня вынесен множитель 10.
Преобразование, обратное вынесению множителя за знак корня, называют внесением множителя под знак корня.
В атом примере под знак корня вносим множитель 0,3. Рассмотренные преобразования осуществляются на основании теоремы о корне из произведения.
Если знак корня находится в знаменателе дроби, то такую дробь можно заменить тождественной, знаменатель которой не имеет корней. Достаточно умножить члены дроби на соответствующее выражение. Например,
Такие преобразования называют освобождением дроби от иррациональности в знаменателе.
Эти преобразования можно выполнять также с выражениями, содержащими переменные. Например,
Примечание. При вынесении переменной за знак корня необходимо помнить, что равенство 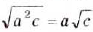
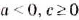
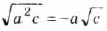
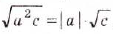
Пример:
Вынесите множитель за знак корня: a)
Решение:
а) 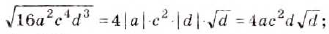
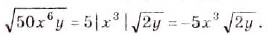
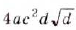
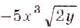
При внесении переменной под знак корня следует помнить, что под корень можно вносить лишь положительные числа.
Пример:
Внесите множитель под знак корня: а) 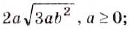
Решение:
а) 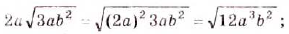
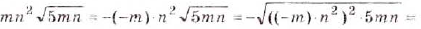
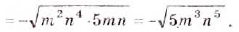
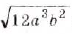
Используя словосочетание «выражения с корнями», в этой главе мы будем говорить только о «выражениях с арифметическими квадратными корнями». Но в математике выражения с корнями имеют более широкий смысл поскольку корни бывают не только квадратные, но и кубические четвёртой, пятой …. n-й степеней. Корни из числа а таких степеней обозначают символами:
Выражения, содержащие любые из таких корней, называют выражениями с корнями, или иррациональными выражениями. Выражения с арифметическими квадратными корнями – это только часть иррациональных выражений (рис 45) .
Рис. 45 Раньше знаки корней 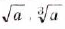
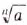
Выполним вместе!
Пример:
Упростите выражение: а) 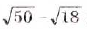
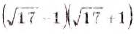
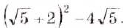
Решение:
a) 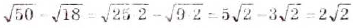
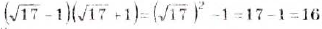
в) 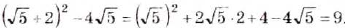
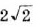
Пример:
Разложите на множители выражение: a) 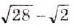
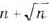
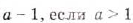
Решение:
а) 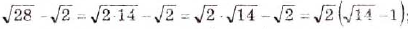
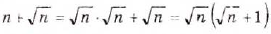
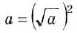
Ответ, a) 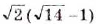
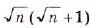
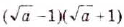
Пример:
Освободитесь от иррациональности в знаменателе дроби:
а) 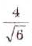
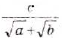
Решение:
а) 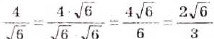
Ответ. а)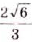
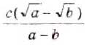
ИСТОРИЧЕСКИЕ СВЕДЕНИЯ
Квадратные корни из чисел вавилонские математики умели вычислять ещё 4 тыс. лет тому назад. Находили даже приближённые значения квадратных корней, пользуясь правилом, которое теперь можно записать (при небольших значениях с) в виде приближённого равенства:
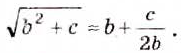
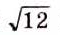
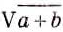
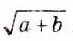
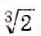
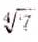
ОСНОВНОЕ В ГЛАВЕ
Квадратным корнем из числа а называют число, квадрат которого равен а. Например, число 16 имеет два квадратных корня: 4 и -4. Неотрицательное значение квадратного корня из числа а называют арифметическим значением корня я обозначают символом 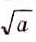
Для любого действительного 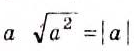
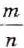
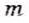
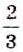
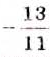
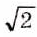
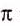
Квадратные корни. Арифметический квадратный корень
Рассмотрим квадрат, площадь которого равна 49 квадратным единицам. Пусть длина его стороны составляет 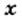
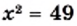
Корнями этого уравнения являются числа 7 и —7. Говорят, что числа 7 и —7 являются квадратными корнями из числа 49.
Определение: Квадратным корнем из числа 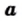
Приведем несколько примеров.
Квадратными корнями из числа 9 являются числа 3 и —3. Действительно,
Квадратными корнями из числа 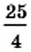
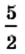
Действительно,
Квадратным корнем из числа 0 является только число 0. Действительно, существует лишь одно число, квадрат которого равен нулю, — это число 0.
Поскольку не существует числа, квадрат которого равен отрицательному числу, то квадратного корня из отрицательного числа не существует.
Положительный корень уравнения 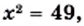
Определение: Арифметическим квадратным корнем из числа 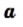
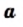
Арифметический квадратный корень из числа 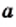
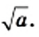
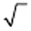
Запись 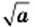
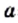
Выражение, стоящее под радикалом, называют подкоренным выражением. Например, в записи 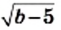
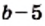
Действие нахождения арифметического квадратного корня из числа называют извлечением квадратного корня.
Рассмотрим несколько примеров:
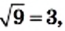
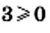
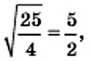
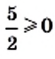
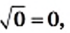
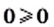
Вообще, равенство 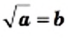

Этот вывод можно представить в другой форме: для любого неотрицательного числа 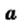
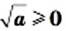
Например, 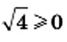
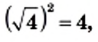
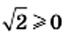
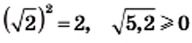
Подчеркнем, что к понятию квадратного корня мы пришли, решая уравнение вида 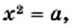
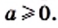
Поиск корней уравнения 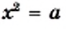
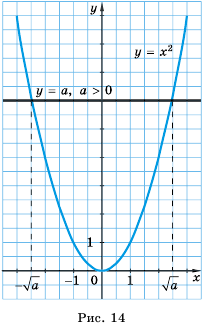
В одной системе координат построим графики функций 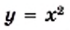
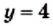
Уравнение 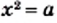
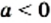
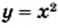
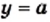
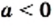
При 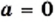
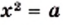
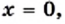
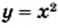
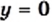
Графический метод также позволяет сделать следующий вывод: если 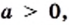
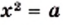
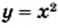
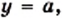
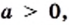
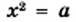
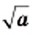
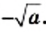
Например, уравнение 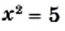
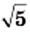
Пример:
Найдите значение выражения
Решение:
Применив правило возведения произведения в степень и тождество 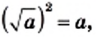
Пример:
Решите уравнение:
Решение:
1) Имеем: 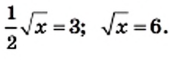
Ответ: 36.
2)
Ответ: 7.
Пример:
Решите уравнение
Решение:
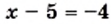
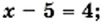
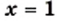
Ответ: 1; 9. ▲
Пример:
Решите уравнение
Решение:
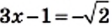
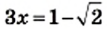
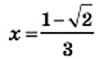
Ответ:
Пример:
При каких значениях 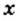
Решение:
1) Выражение 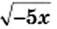
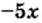
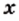
Ответ: при
2) Данное выражение имеет смысл, если выполняются два условия: имеет смысл выражение 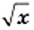
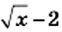
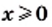
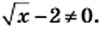
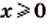
Ответ: при 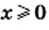
Пример:
Решите уравнение:
Решение:
1) Левая часть данного уравнения имеет смысл, если подкоренные выражения 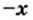
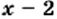
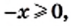

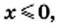
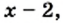
Ответ: корней нет.
2) Левая часть данного уравнения является суммой двух слагаемых, каждое из которых может принимать только неотрицательные значения. Тогда их сумма будет равна нулю, если каждое из слагаемых равно нулю. Следовательно, одновременно должны выполняться два условия: 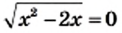
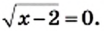
Имеем,
Решением последней системы, а значит, и исходного уравнения, является число 2.
Ответ: 2.
3) Используя условие равенства произведения нулю, получаем:
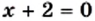
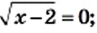
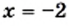
Однако при 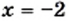
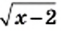
Ответ: 2.
Свойства арифметического квадратного корня
Легко проверить, что 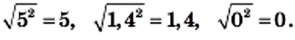
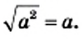
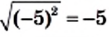
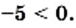
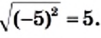
Вообще, справедлива следующая теорема.
Теорема: Для любого действительного числа а выполняется равенство
Доказательство: Для того чтобы доказать равенство 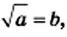
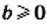
Имеем: 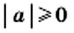
Также из определения модуля следует, что
Следующая теорема обобщает доказанный факт.
Теорема: (арифметический квадратный корень из степени). Для любого действительного числа 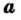
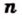
Доказательство этой теоремы аналогично доказательству теоремы 15.1. Проведите это доказательство самостоятельно.
Теорема: (арифметический квадратный корень из произведения). Для любых действительных чисел 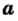
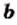
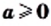
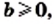
Доказательство: Имеем: 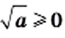
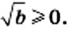
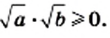
Следовательно, выражение 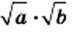
Эту теорему можно обобщить для произведения трех и более множителей. Например, если 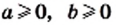
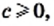
Теорема: (арифметический квадратный корень из дроби). Для любых действительных чисел 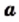
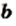
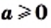
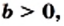
Доказательство этой теоремы аналогично доказательству теоремы 15.3. Проведите это доказательство самостоятельно.
Понятно, что из двух квадратов с площадями 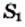
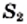
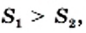
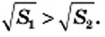
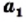
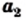
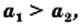
Пример:
Найдите значение выражения:
Решение:
Пример:
Найдите значение выражения:
Решение:
1) Заменив произведение корней корнем из произведения, получим:
2) Заменив частное корней корнем из частного (дроби), получим:
Пример:
Упростите выражение: 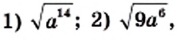
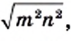
Решение:
1) По теореме об арифметическом квадратном корне из степени имеем:
2) Имеем: 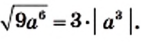
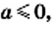
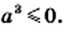
3) Имеем: 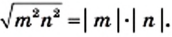
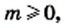
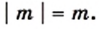
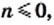
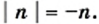
4) Имеем: 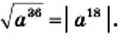
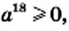
Пример:
Найдите значение выражения:
Решение:
1) Преобразовав подкоренное выражение по формуле разности квадратов, получаем:
Пример:
Постройте график функции
Решение:
Поскольку 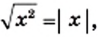
Если 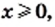
Если 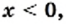
Следовательно,
График функции изображен на рисунке 28.
Тождественные преобразования выражений, содержащих квадратные корни
Пользуясь теоремой об арифметическом квадратном корне из произведения, преобразуем выражение 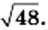
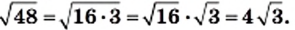
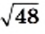
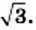
Такое преобразование называют внесением множителя под знак корня. В данном случае был внесен под знак корня множитель 4.
Пример:
Вынесите множитель из-под знака корня:
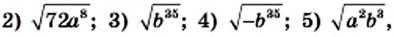
Решение:
1) Представим число, стоящее под знаком корня, в виде произведения двух чисел, одно из которых является квадратом рационального числа:
2)
3) Поскольку подкоренное выражение должно быть неотрицательным, то из условия следует, что 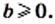
4) Из условия следует, что 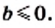
5) Из условия следует, что 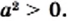
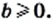
Пример:
Внесите множитель под знак корня:
Решение:
2) Если 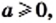
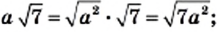
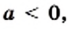
3) Из условия следует, что 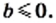
4) Из условия следует, что 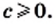
Пример:
Упростите выражение:
Решение:
1) Имеем:
2)
3) Применяя формулы сокращенного умножения (квадрат двучлена и произведение разности и суммы двух выражений), получим:
Пример:
Разложите на множители выражение:
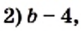
Решение:
1) Представив данное выражение в виде разности квадратов, получим:
2) Поскольку по условию 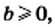
3) Применим формулу квадрата разности:
4) Имеем:
5)
6)
Пример:
Сократите дробь:
если
Решение:
1) Разложив числитель данной дроби на множители, получаем:
2)
3) Поскольку по условию 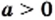
Освободиться от иррациональности в знаменателе дроби означает преобразовать дробь так, чтобы ее знаменатель не содержал квадратного корня.
Пример:
Освободитесь от иррациональности в знаменателе дроби:
Решение:
1) Умножив числитель и знаменатель данной дроби на 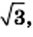
2) Умножив числитель и знаменатель данной дроби на выражение 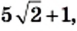
Пример:
Докажите тождество
Решение:
Пример:
Упростите выражение
Решение:
Представив подкоренное выражение в виде квадрата суммы, получаем:
Растут ли в огороде радикалы?
В Древней Греции действие извлечения корня отождествляли с поиском стороны квадрата по его площади, а сам квадратный корень называли «стороной».
В Древней Индии слово «мула» означало «начало», «основание», «корень дерева». Это же слово стали употреблять и по отношению к стороне квадрата, возможно, исходя из такой ассоциации: из стороны квадрата, как из корня, вырастает сам квадрат. Вероятно, поэтому в латинском языке понятия «сторона» и «корень» выражаются одним и тем же словом — radix. От этого слова произошел термин «радикал».
Слово radix можно также перевести как «редис», то есть корнеплод — часть растения — видоизмененный корень, который может являться съедобным.
В XIII-XV вв. европейские математики, сокращая слово radix, обозначали квадратный корень знаками 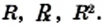
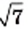
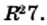
В XVI в. стали использовать знак 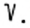
В XVII в. выдающийся французский математик Рене Декарт, соединив знак 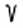
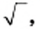
Множество и его элементы. Подмножество
Мы часто говорим: стадо баранов, букет цветов, коллекция марок, косяк рыб, стая птиц, рой пчел, собрание картин, набор ручек, компания друзей.
Если в этих парах перемешать первые слова, то может получиться смешно: букет баранов, косяк картин, стадо друзей. В то же время такие словосочетания, как коллекция рыб, коллекция птиц, коллекция картин, коллекция ручек и т. д., вполне приемлемы. Дело в том, что слово «коллекция» достаточно универсальное. Однако в математике есть термин, которым можно заменить любое из первых слов в данных парах. Это слово множество.
Приведем еще несколько примеров множеств:
Отдельным важнейшим множествам присвоены общепринятые названия и обозначения:
Как правило, множества обозначают прописными буквами латинского алфавита: 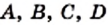
Объекты, составляющие данное множество, называют элементами этого множества. Обычно элементы обозначают строчными буквами латинского алфавита: 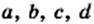
Если 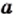
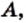
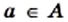
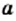
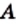
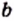
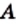
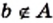
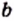
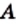
Если множество 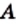
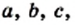
Если 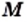
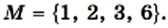
Задавать множество с помощью фигурных скобок, в которых указан список его элементов, удобно в тех случаях, когда множество состоит из небольшого количества элементов.
Определение: Два множества 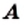
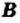
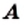
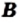
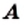
Если множества 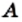
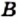
Из определения следует, что множество однозначно определяется своими элементами. Если множество записано с помощью фигурных скобок, то порядок, в котором выписаны его элементы, не имеет значения. Так, для множества, состоящего из трех элементов 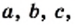
Поскольку из определения равных множеств следует, что, например, 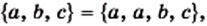
Заметим, что 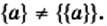
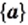
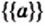
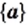
Чаще всего множество задают одним из следующих двух способов.
Первый способ состоит в том, что множество задают указанием (перечислением) всех его элементов. Мы уже использовали этот способ, записывая множество с помощью фигурных скобок, в которых указывали список его элементов. Ясно, что не всякое множество можно задать таким способом. Например, множество четных чисел так задать невозможно.
Второй способ состоит в том, что указывают характеристическое свойство элементов множества, то есть свойство, которым обладают все элементы данного множества и только они. Например, свойство «натуральное число при делении на 2 дает в остатке 1» задает множество нечетных чисел.
Если задавать множество характеристическим свойством его элементов, то может оказаться, что ни один объект этим свойством не обладает.
Обратимся к примерам.
Приведенные примеры указывают на то, что удобно к совокупности множеств отнести еще одно особенное множество, не содержащее ни одного элемента. Его называют пустым множеством и обозначают символом
Заметим, что множество 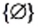
Рассмотрим множество цифр десятичной системы счисления: 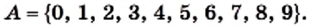
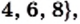
Определение: Множество 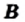
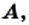
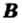
Это записывают так: 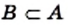
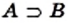
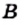
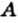
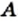
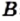
Рассмотрим примеры:
Для иллюстрации соотношений между множествами пользуются схемами, которые называют диаграммами Эйлера.
На рисунке 20 изображены множество 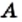
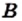
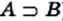
Из определений подмножества и равенства множеств следует, что если 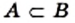
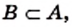
Если в множестве 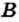
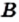
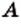
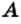
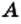
Любое множество 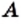
- Заказать решение задач по высшей математике
Пример:
Выпишите все подмножества множества
Решение:
Имеем:
Числовые множества
Натуральные числа — это первые числа, которыми начали пользоваться люди. С ними вы ознакомились в детстве, когда учились считать предметы. Все натуральные числа образуют множество натуральных чисел, которое обозначают буквой
Практические потребности людей привели к возникновению дробных чисел. Позже появилась необходимость рассматривать величины, для характеристики которых положительных чисел оказалось недостаточно. Так возникли отрицательные числа.
Все натуральные числа, противоположные им числа и число нуль образуют множество целых чисел, которое обозначают буквой
Например,
Множество натуральных чисел является подмножеством множества целых чисел, то есть
Целые и дробные (как положительные, так и отрицательные) числа образуют множество рациональных чисел, которое обозначают буквой 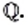
Понятно, что 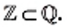
Каждое рациональное число можно представить в виде отношения 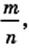
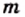
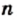
С возможностью такого представления связано название «рациональное число»: одним из значений латинского слова ratio является «отношение».
В 6 классе вы узнали, что каждое рациональное число можно представить в виде конечной десятичной дроби или в виде бесконечной периодической десятичной дроби. Для дроби 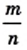
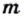
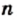
Например,
Число 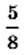
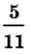
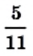
Заметим, что любую конечную десятичную дробь и любое целое число можно представить в виде бесконечной периодической десятичной дроби. Например,
Следовательно, каждое рациональное число можно представить в виде бесконечной периодической десятичной дроби.
Справедливо и такое утверждение: каждая бесконечная периодическая десятичная дробь является записью некоторого рационального числа.
В 9 классе вы научитесь записывать бесконечную периодическую десятичную дробь в виде обыкновенной дроби.
Сумма и произведение двух натуральных чисел являются натуральными числами. Однако разность натуральных чисел не всегда обладает таким свойством. Например,
Сумма, разность, произведение двух целых чисел являются целыми числами. Однако частное целых чисел не всегда обладает таким свойством. Например,
Сумма, разность, произведение и частное (кроме деления на нуль) двух рациональных чисел являются рациональными числами.
Итак, действие вычитания натуральных чисел может вывести результат за пределы множества 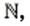
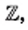
Вы ознакомились с новым действием — извлечением квадратного корня. Возникает естественный вопрос: всегда ли квадратный корень из неотрицательного рационального числа является рациональным числом? Иными словами, может ли действие извлечения квадратного корня из рационального числа вывести результат за пределы множества
Рассмотрим уравнение 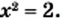
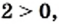
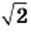
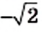
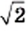
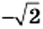
Следовательно, действие извлечения корня из рационального числа может вывести результат за пределы множества
Ни одно иррациональное число не может быть представлено в виде дроби 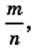
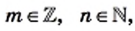
Иррациональные числа могут быть представлены в виде бесконечных непериодических десятичных дробей.
Например, с помощью специальной компьютерной программы можно установить, что
Числа 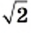
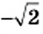
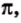
Иррациональные числа возникают не только в результате извлечения квадратных корней. Их можно конструировать, строя бесконечные непериодические десятичные дроби.
Например, число 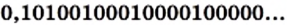
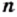
Вместе множества иррациональных и рациональных чисел образуют множество действительных чисел. Его обозначают буквой 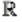
Теперь «цепочку» 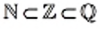
Связь между числовыми множествами, рассмотренными в этом пункте, иллюстрирует схема, изображенная на рисунке 23.
Длину любого отрезка можно выразить действительным числом. Eh-от факт позволяет установить связь между множеством 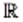
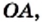
Над действительными числами можно выполнять четыре арифметических действия: сложение, вычитание, умножение, деление (кроме деления на ноль), в результате будем получать действительное число. Эти действия обладают известными вам свойствами:
Переместительное свойство сложения
Переместительное свойство умножения
Сочетательное свойство сложения
Сочетательное свойство умножения
Распределительное свойство умножения относительно сложения
Действительные числа можно сравнивать, используя правила сравнения десятичных дробей, то есть сравнивая цифры в соответствующих разрядах. Например,
Любое положительное действительное число больше нуля и любого отрицательного действительного числа. Любое отрицательное действительное число меньше нуля. Из двух отрицательных действительных чисел больше то, у которого модуль меньше.
Если отметить на координатной прямой два действительных числа, то меньшее из них будет расположено слева от большего.
Находя длину окружности и площадь круга, вы пользовались приближенным значением числа 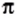
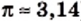
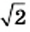
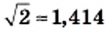
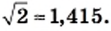
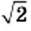
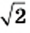
В заключение подчеркнем, что из любого неотрицательного действительного числа можно извлечь квадратный корень и в результате этого действия получить действительное число. Следовательно, действие извлечения квадратного корня из неотрицательного действительного числа не выводит результат за пределы множества
Открытие иррациональности
Решая графически уравнение 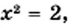
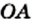
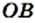
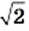
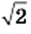
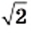
представить в виде несократимой дроби 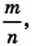
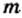
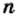
Тогда
Из последнего равенства следует, что число 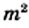
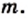
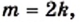
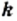
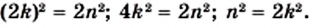
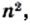
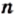
Таким образом, числитель и знаменатель дроби 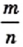
Приведенный пример показывает, что существуют отрезки (в нашем случае это отрезки 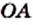
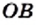
Этот факт был открыт в школе великого древнегреческого ученого Пифагора.
Сначала пифагорейцы считали, что для любых отрезков 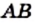
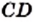
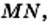
Например, на рисунке 25 имеем:
и 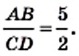
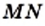
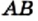
Если для отрезков существует общая мера, то их называют соизмеримыми. Например, отрезки 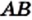
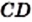
Итак, древнегреческие ученые считали, что любые два отрезка соизмеримы. А из этого следовало, что длину любого отрезка можно выразить рациональным числом.
Действительно, пусть некоторый отрезок 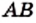
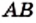
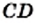
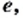
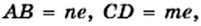
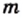
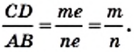
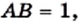
Однако сами же пифагорейцы сделали выдающееся открытие. Они доказали, что диагональ и сторона квадрата несоизмеримы, то есть если сторону квадрата принять за единицу, то длину диагонали квадрата выразить рациональным числом нельзя.
Для доказательства рассмотрим произвольный квадрат 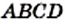
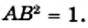
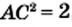
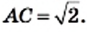
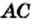
Это открытие изменило один из фундаментальных постулатов древнегреческих ученых, заключавшийся в том, что отношение любых двух величин выражается отношением целых чисел.
Существует легенда о том, что пифагорейцы держали открытие иррациональных чисел в строжайшей тайне, а человека, разгласившего этот факт, покарали боги: он погиб при кораблекрушении.
ГЛАВНОЕ В ПАРАГРАФЕ 2
Свойства функции
Область определения:
Область значений: множество неотрицательных чисел.
График: парабола.
Нуль функции:
Свойство графика: если точка 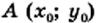
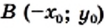
Квадратный корень
Квадратным корнем из числа 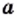
Арифметический квадратный корень
Арифметическим квадратным корнем из числа 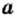
Равные множества
Два множества 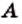
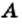
Подмножество
Множество 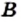
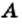
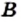
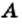
Обозначения числовых множеств
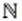
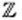
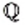
Связь между числовыми множествами
Свойства арифметического квадратного корня
Для любого действительного числа 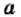
Для любого действительного числа 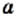
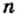
Для любых действительных чисел 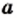
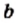
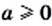
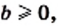
Для любых действительных чисел 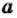
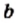

выполняется равенство
Для любых неотрицательных чисел 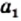
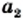
Свойства функции
Область определения: множество неотрицательных чисел.
Область значений: множество неотрицательных чисел.
График: ветвь параболы.
Нуль функции:
Большему значению аргумента соответствует большее значение функции.
———
Квадратные корни
Функция y=x2 её график и свойства
Функция 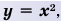
Пример №223
Пусть сторона квадрата равна 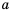
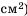
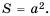
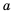
Если обозначить независимую переменную через 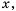
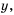
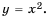
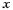
Составим таблицу значений функции 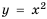
Отметим на координатной плоскости точки 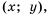
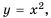
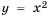
Сформулируем некоторые свойства функции
1. Область определения функции состоит из всех чисел.
2. Область значений функции состоит из всех неотрицательных чисел, то есть
Действительно, так как 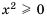
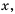
3. Графиком функции является парабола с вершиной в точке 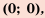
4. Противоположным значениям аргумента соответствует одно и то же значение функции.
Действительно, это следует из того, что 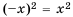
Пример №224
Решите графически уравнение
Решение:
График функции 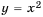
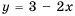
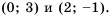
Убедимся, что числа 1 и -3 являются корнями уравнения:
1) для
2) для
Следовательно, 3 и -1 – корни уравнения
Ответ. -3; 1.
Пример №225
Между какими последовательными целыми числами лежит корень уравнения
Решение:
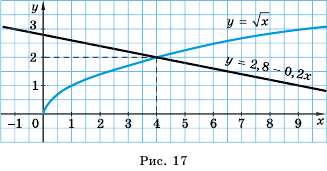
Решим уравнение графически, построив графики функций 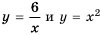
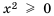
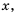
Откуда 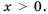
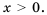
Графики пересекаются в одной точке, абсцисса которой является корнем уравнения и заключена между числами 1 и 2.
Таким образом, корень уравнения 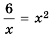
Ответ. Между числами 1 и 2.
Арифметический квадратный корень
Если известна сторона квадрата, можно легко найти его площадь. Но часто приходится решать и обратную задачу: по известной площади квадрата находить его сторону.
Пример №226
Площадь квадрата равна 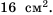
Решение:
Пусть длина стороны квадрата равна 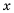
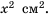
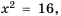
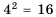
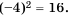
Корни уравнения 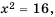
Квадратным корнем из числа 

Например, квадратными корнями из числа 100 являются числа 10 и -10, потому что 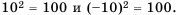
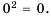
Число 4, являющееся неотрицательным корнем уравнения . 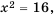
Арифметическим квадратным корнем из числа а называют неотрицательное число, квадрат которого равен
Арифметический квадратный корень из числа 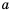
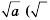
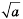
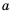
Пример №227
1) 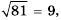
2) 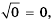
Вообще равенство 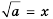
Так как 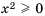
Выражение 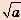
Например, не имеют смысла выражения
Действие нахождения значения арифметического квадратного корня называют извлечением квадратного корня. Из небольших чисел квадратный корень желательно извлекать устно. Извлекать квадратный корень из больших чисел поможет таблица квадратов двузначных натуральных чисел на форзаце или калькулятор.
Пример №228
Найдите значение корня
Решение:
По таблице квадратов двузначных натуральных чисел имеем: 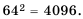
Пример №229
Вычислите
Решение:
Сначала нужно найти значение выражения 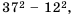
Ответ. 35.
Рассмотрим уравнение 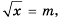
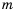
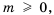
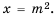
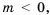
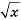
Систематизируем данные о решениях уравнения 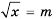
Пример №230
Решите уравнение:
Ответ. 1) 49; 2) решений нет; 3) 13.
Множество. Подмножество. Числовые множества. Рациональные числа. Иррациональные числа. Действительные числа
Понятие множества является одним из основных понятий математики. Под множеством будем понимать совокупность объектов, имеющих общую природу (или объединенных по общему признаку), сами объекты при этом будем называть элементами множества.
Как правило, множества обозначают большими латинскими буквами. Если, например, множество 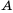
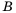
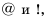
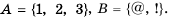
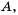
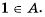
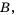
Множества, количество элементов которых можно выразить натуральным числом, называют конечными.
Множество, не содержащее ни одного элемента, называют пустым множеством. Его обозначают символом 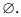
Множества, количество элементов которых нельзя выразить натуральным числом и которые не являются пустыми, называют бесконечными.
Если каждый элемент множества 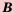
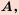
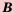
Записывают это следующим образом: 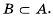
Пример №231
Пусть 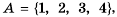
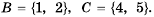
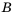
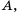
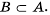
Считают, что пустое множество является подмножеством любого множества, то есть
Целые числа и дробные числа образуют множество рациональных чисел.
Множество натуральных чисел обозначают буквой 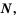
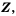
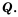
Можно утверждать, что
Любое рациональное число можно представить в виде 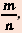
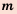
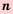
Например
Рациональное число можно также представить и в виде десятичной дроби. Для этого достаточно числитель дроби разделить на ее знаменатель. Например,
В последнем случае мы получили бесконечную десятичную периодическую дробь. Дроби 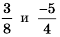
Таким образом, каждое рациональное число можно представить в виде бесконечной десятичной периодической дроби.
Справедливо и обратное утверждение:
Каждая бесконечная периодическая десятичная дробь является записью некоторого рационального числа.
Например,
В правильности этих равенств легко убедиться, выполнив соответствующее деление.
Но в математике существуют числа, которые нельзя записать в виде 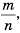
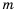
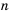
Числа, которые нельзя записать в виде 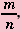
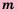
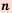
Префикс «иp» означает отрицание, иррациональные значит не рациональные.
Например, иррациональными являются числа 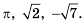
Каждое иррациональное число можно представить в виде бесконечной десятичной непериодической дроби.
Рациональные числа вместе с иррациональными числами образуют множество действительных чисел.
Множество действительных чисел обозначают буквой
Так как каждое натуральное число является целым числом, то множество 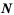
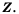
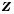
Действительные числа, записанные в виде бесконечных десятичных непериодических дробей, можно сравнивать по тем же правилам, что и конечные десятичные дроби. Например,
В задачах с практическим содержанием действительные числа (для выполнения арифметических действий) заменяют на их приближенные значения, округленные до определенного разряда.
Пример №232
Вычислите 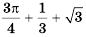
Решение:
Заметим, что при сложении, вычитании, умножении, делении и возведении в степень действительных чисел справедливы те же свойства и ограничения, что и при действиях с рациональными числами.
Понятие числа появилось очень давно.
А еще раньше Оно является одним из самых общих понятий математики. Потребность в измерениях и подсчетах обусловила появление положительных рациональных чисел. Именно тогда возникли и использовались натуральные числа и дробные числа, которые рассматривались как отношение натуральных чисел.
Следующим этапом развития понятия числа является введение в практику отрицательных чисел. В Древнем Китае эти числа появились во II в. до н. э. Там умели складывать и вычитать отрицательные числа. Отрицательные числа толковали как долг, а положительные – как имущество. В Индии в VII в. эти числа воспринимали так же, но еще и умели их умножать и делить.
Уже древние вавилоняне около 4 тыс. лет назад знали ответ на вопрос: «Какова должна быть длина стороны квадрата, чтобы его площадь равнялась 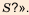
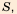
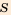
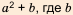
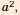
Например, с помощью этого метода:
Проверим точность результата:
Такой метод вычисления приближенного значения квадратного корня использовался и в Древней Греции. Его детально описал Герон Александрийский (I в. н. э.).
В эпоху Возрождения (XV – нач. XVII в.) европейские математики обозначали корень латинским словом Radix (корень), потом – сокращенно – буквой 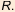


Тождество (√a)2=a, a⩾0 уравнение  x2=a
x2=a
Тождество  уравнение
уравнение 
Напомним, что для любых значений 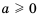
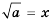
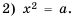
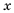
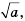
Для любого 
Пример №233
Вычислите:
Решение:
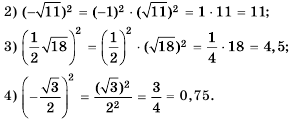
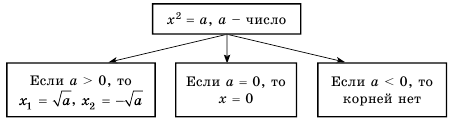
Рассмотрим уравнение 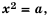
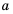
Так как квадрат числа не может быть отрицательным, то при 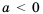
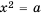
Если 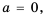
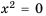
Если 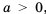
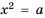
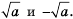
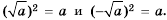
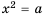
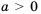
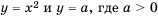
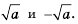
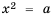
Пример №234
Решите уравнение:
Решение:
2) уравнение корней не имеет, то есть
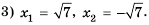
4) Имеем:
Таким образом, получим два корня:
Ответ.
Свойства арифметического квадратного корня
Сравним значения выражений
Имеем: 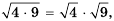
Теорема (о корне из произведения). Корень из произведения двух неотрицательных чисел равен произведению корней из этих чисел, то есть при 
Доказательство: Так как 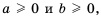
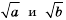
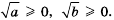
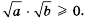
Имеем: 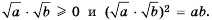
Доказанная теорема распространяется и на случай, когда множителей под знаком корня три и больше.
Следствие. Корень из произведения неотрицательных множителей равен произведению корней из этих множителей.
Доказательство: Докажем это следствие, например, для трех чисел
Имеем:
Пример №235
Замечание 1. Очевидно, что выражение 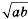
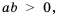
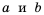
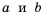
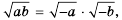
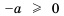
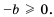
Если в равенстве 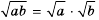
Произведение корней из неотрицательных чисел равно корню из произведения этих чисел.
Пример №236
Рассмотрим квадратный корень из дроби.
Теорема (о корне из дроби). Корень из дроби, числитель которой неотрицателен, а знаменатель -положителен, равен корню из числителя, деленному на корень из знаменателя, то есть при
Доказательство: Так как 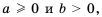
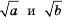
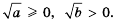
Кроме того,
Имеем: 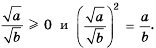
Пример №237
Замечание 2. По аналогии с замечанием 1, тождество, только что рассмотренное нами, можно записать и так:
Если в равенстве 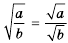
Частное, числитель которого является корнем из неотрицательного числа, а знаменатель — корнем из положительного числа, равно корню из частного этих чисел.
Пример №238
Рассмотрим, как извлечь квадратный корень из квадрата.
Теорема (о корне из квадрата). Для любого значения справедливо равенство
Доказательство: Так как 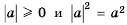
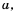
Пример №239
Рассмотрим квадратный корень из степени.
Теорема (о корне из степени). Для любого значения 
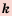
Доказательство: 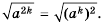
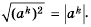
Пример №240
Вычислите:
Решение:
Пример №241
Упростите выражение:
Решение:
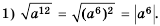
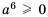
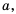
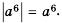
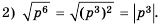
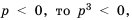
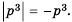
Ответ.
Тождественные преобразования выражений, содержащих квадратные корни
Рассмотрим тождественные преобразования выражений, содержащих квадратные корни.
Вынесение множителя из-под знака корня
Воспользуемся теоремой о корне из произведения для преобразования выражения
Говорят, что множитель вынесли из-под знака корня. В данном случае из-под знака корня вынесли множитель 2.
Пример №242
Вынесите множитель из-под знака корня в выражении
Решение:
Выражение 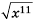
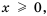
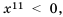
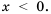
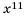
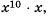
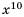
Так как 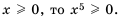
Следовательно,
Ответ.
Внесение множителя под знак корня
Рассмотрим тождественное преобразование, обратное к предыдущему. Воспользуемся правилом умножения корней:
Говорят, что множитель внесли под знак корня. В данном случае под знак корня внесли множитель 2.
Отметим, что под знак корня можно вносить только положительный множитель.
Пример №243
Внести множитель под знак корня:
Решение:
2) Множитель 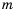
– если
– если
Ответ.
Сложение, вычитание, умножение, деление и возведение в степень выражений, содержащих квадратные корни
Используя свойства умножения и деления корней, можно выполнять арифметические действия с выражениями, содержащими квадратные корни.
Пример №244
Используя тождество 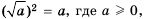
Пример №245
Рассмотрим примеры, где квадратные корни можно складывать.
Пример №246
Упростите выражение
Решение:
Слагаемые содержат общий множитель 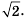
Обычно решение записывают короче:
Заметим, что выражения 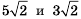
Пример №247
Упростите выражение
Решение:
В каждом из слагаемых можно вынести множитель из-под знака корня, в результате получим подобные радикалы и приведем их:
Ответ.
Пример №248
Упростите выражение:
Решение:
Применим формулы сокращенного умножения.
Ответ.
Сокращение дробей
Пример №249
Сократите дробь:
Решение:
1) Учитывая, что 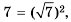
2) Учитывая, что 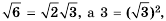
Ответ.
Избавление от иррациональности в знаменателе дроби
Пример №250
Преобразуйте дробь 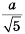
Решение:
Учитывая, что 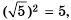
Ответ.
В таких случаях говорят, что избавились от иррациональности в знаменателе дроби.
Пример №251
Избавьтесь от иррациональности в знаменателе дроби
Решение:
Умножим числитель и знаменатель дроби на 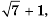
Ответ.
Заметим, что выражение 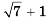
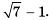
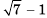
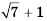
Взаимно сопряженными также являются выражения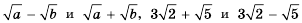
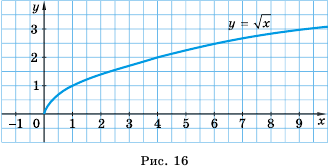
Функция y= √x её график и свойства
Функция 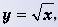
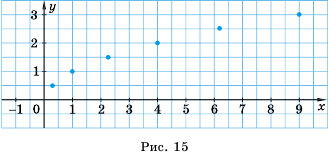
Пример №252
Пусть 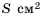
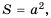
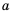
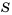
Рассмотрим функцию 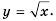
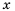
Составим таблицу значений функции 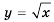
Отметим эти точки на координатной плоскости (рис. 15). Если бы мы отметили на этой плоскости больше точек, координаты которых удовлетворяют уравнению 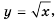
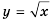
Графиком этой функции является ветвь параболы.
Обобщим свойства функции
1. Областью определения функции является множество всех неотрицательных чисел:
2. Областью значений функции является множество всех неотрицательных чисел:
3. График функции – ветвь параболы, выходящая из точки 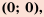
Большему значению аргумента соответствует большее значение функции
Последнее свойство дает возможность сравнивать значения выражении, содержащих корни.
Пример №253
Сравните числа:
Решение:
1) Так как
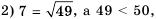
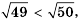
3) Внесем множитель в обоих выражениях под знак корня:
Так как 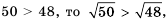
Пример №254
Решите графически уравнение
Решение:
Поскольку мы пока не умеем строить график функции 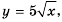
Построим графики функций 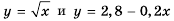
Ответ. 4.
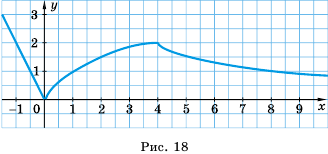
Пример №255
Постройте график функции
Ответ. График изображен на рисунке 18.
- Квадратные уравнения
- Неравенства
- Числовые последовательности
- Предел числовой последовательности
- Формулы сокращенного умножения
- Разложение многочленов на множители
- Системы линейных уравнений с двумя переменными
- Рациональные выражения
Поиск значений выражений — основное математическое действие. Им сопровождается каждый пример, задача. Поэтому чтобы вам было проще работать с различными математическими выражениями, подробно разберем способы и правила их решения в данной статье. Правила представлены в порядке увеличения сложности: от простейших выражений до выражений с функциями. Для лучшего понимания каждый пункт сопровождается подробным пояснением и расписанными примерами.
Поиск значения числовых выражений
Числовые выражения представляют собой математические задачи, состоящие, преимущественно, из чисел. Они подразделяются на несколько групп в зависимости от своей сложности: простейшие, со скобками, корнями, дробями и т.д. Каждый тип выражений подразумевает свои правила нахождения значения, порядок действий. Рассмотрим каждый случай подробнее.
Простейшие числовые выражения. К простейшим числовым выражениям относятся примеры, состоящие из двух элементов:
- Числа (целые, дробные и т.д.);
- Знаки: «+», «—», «•» и «÷».
Чтобы найти значение выражения в данном случае, необходимо выполнить все арифметические действия (которые подразумевают конкретные знаки). В случае отсутствия скобок решение примера производится слева направо. Первыми выполняются действия деления и умножения. Вторыми — сложение и вычитание.
Пример 1. Решение числового выражения
Задача. Решить:
20 — 2 • 10 ÷ 5 — 4 = ?
Решение. Чтобы решить выражение, нам необходимо выполнить все арифметические действия в соответствии с установленными правилами. Поиск значения начинается с решения деления и умножения. В первую очередь находим произведение цифр 2 и 10 (если рассматривать с левой стороны, данное действие является первым по значимости). Получаем 20. Теперь это число делим на 5. Итог — 4. Когда известно значение основных действий, можем подставить его в наш пример:
20 — 4 — 4 = ?
Упрощенный пример также решаем слева направо: 20 — 4 = 16. Второе действие: 16 — 4 = 12. Ответ 12.
Решение без пояснений. 20 — 2 • 10 ÷ 5 — 4 = 20 — (2 • 10 ÷ 5) — 4 = 20 — 4 — 4 = 12.
Ответ. 12
Пример 2. Решение числового выражения
Задача. Решить:
0,2 — 5 • (— 4) + 1/2 • 5 • 4 = ?
Решение. Начинаем решение с умножения и деления. Умножая 5 на (— 4) получаем (— 20), т.к. производное сохраняет знак множителя. Далее умножаем 1/2 на 5. Для этого преобразуем дробь: 1/2 = 5/10 = 0,5. 0,5 умножаем на 5. Ответ — 2,5. Далее умножаем полученное число на 4. 2,5 • 4 = 10. Получаем следующее выражение:
0,2 — (— 20) + 10
Теперь нам остается решить сложение и вычитание. В первую очередь раскрываем скобку и получаем:
0,2 + 20 + 10 = 30,2
Решение без пояснений. 0,2 — 5 • (— 4) + 1/2 • 5 • 4 = 0,2 — (— 20) + 10 = 0,2 + 20 + 10 = 30,2
Ответ. 30,2
Находим значение выражения со скобками
Скобки определяют порядок действий при решении примера. Выражения, находящиеся внутри скобок «()» имеют первостепенную значимость, независимо от того, какое математическое действие в них выполняется.
Пример 3. Значение числового выражения со скобками
Задача. Решить:
5 + (7 — 2 • 3) • (6 — 4) ÷ 2 = ?
Решение. Начинаем нахождение значения выражения с решения скобок. Порядок действий определяется слева направо. При этом не забываем, что после раскрытия скобок в первую очередь решаем умножение и деление и лишь потом — вычитание и сложение:
- 7 — 2 • 3 = 7 — 6 = 1
- 6 — 4 = 2
Когда скобки решены, подставляем полученные значения в наш пример:
5 + 1 • 2 ÷ 2
Снова решаем все по порядку, не забывая о том, что деление и умножение выполняется в первую очередь:
- 1 • 2 = 2
- 2 ÷ 2 = 1
Упрощенное выражение выглядит следующим образом:
5 + 1 = 6
Решение без пояснений. 5 + (7 — 2 • 3) • (6 — 4) ÷ 2 = 5 + (7 — 6) • 2 ÷ 2 = 5+ 1 • 2 ÷ 2 = 5 + 1 = 6
Ответ. 6
Значение числового выражения со скобками
Задача. Решить:
4 + (3 + 1 + 4 • (2+3)) = ?
Решение. Подобные примеры решаются поэтапно. Помним, что поиск выражения со скобками начинается с решения скобок. Поэтому в первую очередь решаем:
3 + 1 + 4 • (2+3)
В уже упрощенном примере снова встречаются скобки. Их будем решать в первую очередь:
2 + 3 = 5
Теперь можем подставить определенное значение в общую скобку:
3 + 1 + 4 • 5
Начинаем решение с умножения и далее слева направо:
- 4 • 5 = 20
- 3 + 1 = 4
- 4 + 20 = 24
Далее подставляем полученный ответ вместо большой скобки и получаем:
4 + 24 = 28
Решение без пояснений. 4 + (3 + 1 + 4 • (2+3)) = 4 + (3 + 1 + 4 • 5) = 4 + (3 + 1 + 20) = 4 + 24 = 28
Ответ. 28
Важно: Чтобы правильно определить значение числового выражения с множественными скобками, необходимо выполнять все действия постепенно. Скобки читаются слева направо. Приоритет в решении внутри скобок остается за делением и умножением.
Поиск значения выражения с корнями
Часто алгебраические задания основываются на нахождении значений из-под корня. И если определить √4 несложно (напомним, это будет 2), то с примерами, которые полностью расположены под корнем, возникает ряд вопросов. На самом деле в таких заданиях нет ничего сложного. В данном случае порядок действий следующий:
- Решаем все выражение, которое находится под корнем (не забываем о правильной последовательности: сперва скобки, деление и умножение, а лишь потом — сложение и вычитание);
- Извлекаем корень из числа, которое получили в результате решения обычного примера.
Если же и под корнем имеется корень (например: √ 4 + 8 — √4), то начинаем решение примера с его извлечения (в нашем примере это будет: √ 4 + 8 — 2). Если подкоренные числа возведены во вторую степень, то их квадратный корень будет равняться модулю подкоренного выражения.
Значение числового выражения с корнями
Задача. Решить:
√ 2² • 2² • 3² = ?
Решение. Все действия под корнем одинаковы — умножение. Это дает нам право разделить выражение на множители. Получаем:
√2² • √2² • √3² = ?
Т.к. под квадратным корнем у нас числа, возведенные во вторую степень, получаем:
2 • 2 • 3 = 12
Решение без пояснений. √ 2² • 2² • 3² = √2² • √2² • √3² = 2 • 2 • 3 = 12
Ответ. 12
Нет времени решать самому?
Наши эксперты помогут!
Находим значение числовых выражений со степенями
Следующий математический знак, который имеет приоритет в процессе решения, — степени. Они представляют собой результат многократного умножения числа на себя. Само число является основанием степени. А количество операций умножения — ее показателем. Причем выражен он может быть не только целым числом, но и дробью, полноценным числовым выражением.
Начинается решение выражения со степенями с вычисления самих степеней. Если они представляют собой полноценное выражение (например: [3^{3 cdot 4-10}]), то его необходимо решить в нашем примере это будет: [3^{12-10}=3^{2}=9].
Задача. Решите:
[
3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=?
]
Решение. Чтобы решить это выражение со степенями, воспользуемся равенством:
[(a cdot b)^{r}=a^{r} cdot b^{r}]
Рассматривая пример слева направо, видим, что у первых двух множителей одинаковые степени. Это позволяет нам упростить выражение:
[
(3 cdot 7)^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3} cdot 21^{2 / 3}
]
Зная, что при умножении степени с одинаковыми показателями складываются, получаем следующее выражение:
[
21^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3+2 / 3}=21^{1}=21
]
Решение без пояснений: [3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=(3 cdot 7)^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3+2 / 3}=21^{1}=21]
Ответ. 21
Интересно: Этот же пример можно решить и другим способом, преобразовав число 21 в степени ⅔ в два множителя. В данном случае решение будет выглядеть следующим образом:
[3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=3^{1 / 3} cdot 7^{1 / 3} cdot(3 cdot 7)^{2 / 3}=3^{1 / 3} cdot 7^{1 / 3} cdot 3^{2 / 3} cdot 7^{2 / 3}=3^{1 / 3+2 / 3} cdot 7^{1 / 3+2 / 3}=3^{1}+7^{1}=21]
Ответ. 21
Задача. Решить:
[
2^{-2 sqrt{5}} cdot 4^{sqrt{5}-1}+left((sqrt{3})^{1 / 3}right)^{6}
]
Решение. В данном случает получить точные числовые значения показателей степеней не удастся. Поэтому искать значение выражения с дробями в виде степени будем снова через упрощение:

Ответ. 3,25
Выражения с дробями
Поиск значения выражения дробей начинается с их приведения к общему виду. В большинстве случаев проще представить все значения в виде обыкновенной дроби с числителем и знаменателем. После преобразования всех чисел необходимо привести все дроби к общему знаменателю.
Важно: Прежде чем найти выражение дробей, необходимо провести вычисления в их знаменателе и числителе отдельно. В данном случае действуют стандартные правила решения.
Когда дроби приведены к единому знаменателю можно переходить к решению. Вычисление значений верхней строки (числителя) и нижней (знаменателя) производятся параллельно.
Задача. Решить:
[
6 frac{2}{13}+4 frac{1}{13}=?
]
Решение. Действуя по главному правилу, прежде чем найти значение числового выражения, преобразуем всего его части в простую дробь. Получаем:
[
frac{6 cdot 13+2}{13}+frac{4 cdot 13+1}{13}
]
Теперь выполняем вычисления в знаменателе и числителе и находим ответ:
[
frac{6 cdot 13+2}{13}+frac{4 cdot 13+1}{13}=frac{80}{13}+frac{53}{13}=frac{133}{13}=10 frac{3}{13}
]
Ответ. [10 frac{3}{13}]
Примеры(2):
Задача. Решить:
[
frac{2}{sqrt{5}-1}-frac{2 sqrt{5}-7}{4}-3=?
]
Решение. В данном примере мы не можем извлечь корень из пятерки. Но мы можем воспользоваться формулой разложения корней:
[
frac{2}{sqrt{5}-1}=frac{2(sqrt{5}+1)}{(sqrt{5}-1)(sqrt{5}+1)}=frac{2(sqrt{5}+1)}{5-1}=frac{2 sqrt{5}+2}{4}
]
Теперь можем придать нашему первоначальному выражению следующий вид:
[
frac{2 sqrt{5}+2}{4} frac{2 sqrt{5}-7}{4}-3=frac{2 sqrt{5}+2-2 sqrt{5}+7}{4}-3=frac{9}{4} 3=-frac{3}{4}
]
Ответ. [-frac{3}{4}].
Выражения с логарифмами
Как и степени, логарифмы (log), имеющиеся в выражении, вычисляются (если это возможно) в первую очередь. К примеру, зная, что [log _{2} 4=2] мы можем сразу упростить выражение [log _{2} 4+5 cdot 6] до простого и понятного 2 + 5*6 = 32.
Со степенями логарифмы объединяет и порядок выполнения действий. Прежде чем искать значение выражения логарифмов, необходимо вычислить его основание (если оно представлено математическим выражением).
В случаях, когда полное вычисление логарифма невозможно, производится упрощение примера.
Задача. Решить:
[log _{27} 81+log _{27} 9=?]
Решение. Чтобы найти логарифм выражения, воспользуемся свойствами логарифмов и представим значение логарифмов со степенями:
Это позволит нам решить пример следующим образом:
Ответ. 2
Решаем выражения с тригонометрической функцией
Часто в выражениях встречаются тригонометрические функции. Всего их в математике шесть:
- Синус;
- Косинус;
- Котангенс;
- Тангенс;
- Секанс;
- Косеканс.
Изучение тригонометрии начинается в 9-м классе, когда ученики уже подготовлены к сложным задачам. Большинство заданий представляются с sin и cos. Остальные функции встречаются значительно реже.
В математических примерах, которые содержат sin, cos, tg и др. функции, вычисление тригонометрической функции производится в первую очередь. Если это невозможно — осуществляется упрощение выражения до получения краткой формулы.
Задача. Решить:
[
frac{24}{sin ^{2} 127+1+sin ^{2} 217}
]
Решение. Разложим 217 на 90 и 127. Т.к. по формуле приведения sin(90 + a) = cosa, получаем:
sin217 — sin (90 + 127) = cos127
Теперь заменяем полученной формулой наше слагаемое в знаменателе дроби:
[
frac{24}{sin ^{2} 127+cos ^{2} 127+1}
]
Вспоминаем, что по тригонометрическому тождеству sin2a+ cos2 a= 1 (независимо от значения угла a). Поэтому одну часть слагаемого знаменателя (sin2127+ cos2127) преобразуем в единицу и получаем:
[
frac{24}{sin ^{2} 127+cos ^{2} 127+1}=frac{24}{1+1}=frac{24}{2}=2
]
Ответ. 2
Важно: Не стоит бояться буквенных тригонометрических значений. Большинство примеров построено таким образом, чтобы функции можно было заменить более удобной для вычисления формулой. Поэтому вместо того, чтобы пытаться сразу решить пример, стоит обратить внимание на особенности функций и возможность их приведения к подходящей формуле.
Задача. Решить:
[
sqrt{4} 8-sqrt{1} 92 sin ^{2} frac{19 pi}{12}=?
]
Решение. Начинаем решение с разбора второй дроби. Обращаем внимание, что 192 = 48 • 2. А значит, корень этого числа можно представить в виде 2√48. Зная это и используя формулу косинуса двойного угла, преобразим наше выражение:
Теперь по формуле приведения решаем наш пример:
[
sqrt{4} 8 cos left(3 pi+frac{pi}{6}right)=sqrt{4} 8left(-cos frac{pi}{6}right)=-sqrt{4} 8 cdot frac{sqrt{3}}{2}=-4 sqrt{3} cdot frac{sqrt{3}}{2}=-6
]
Ответ. — 6.
Общий случай: находим значения выражений с дробями, функциями, степенями и не только
Самым сложным считается поиск числовых выражений общих случаев. Они представляют собой тригонометрические примеры, которые могут содержать:
- Степени;
- Скобки;
- Корни;
- Функции и т.д.
Общие числовые выражения сложны только длительностью решения. В остальном же они ничуть не сложнее, чем решение каждого примера (со скобкой, степенями, функциями и т.д.) по отдельности.
Чтобы найти значение выражения с логарифмами, тригонометрическими функциями, скобками и/или другими действиями, необходимо помнить три основных правила:
- Упрощение. Прежде чем приступать к решению внимательно изучите выражение. Особенно — его степени, корни, логарифмы, функции. В большинстве случаев их можно сократить или заменить простым числовым значением еще до решения.
- Скобки. Независимо от типа выражения, действий, начинать решение всегда необходимо со скобок. Часто именно игнорирование этого правила приводит к получению неверного ответа или отсутствию решения в принципе.
- Общий вид. Старайтесь привести выражение к общему виду. Особенно это касается дробей. Смешанные и десятичные дроби преобразуйте в обычные.
- Последовательность. Действия в скобках и действия после их решения выполняются слева направо. В первую очередь необходимо совершать умножение и деление. Когда все произведения и частные найдены, можно переходить к сложению и вычитанию.
Для удобства решения и устранения возможных ошибок рекомендуем расставлять порядок действий непосредственно над математическими знаками.
Задача. Решить:
[
-frac{sqrt{2} sin left(frac{pi}{6}+2left(frac{2 pi}{5}+frac{3 pi}{5}right)right)+3}{operatorname{Ln} e^{2}}+left(1+3^{sqrt{9}}right)=?
]
Решение. Чтобы решить этот пример, сначала найдем значение выражения числителя дроби, а точнее — подкоренного выражения. Для этого необходимо вычислить значение sin и общего выражения. Начинаем с раскрытия скобок в числителе:
Полученное значение можем подставить в подкоренное выражение для вычисления числителя дроби:
[
sqrt{2} sin cdotleft(frac{pi}{6}+2left(frac{2 pi}{5}+frac{3 pi}{5}right)+3=sqrt{4}=2right.
]
Со знаменателем дела обстоят куда проще:
[
ln e^{2}=2
]
Числитель и знаменатель у нас одинаковые, что позволяет нам их сократить:
Теперь остается решить следующее выражение:
Ответ. 27
Как видите, при последовательном решении примеров с большим количеством действий нет ничего сложного. Главное — верно обозначить последовательность шагов и четко ей следовать.
Как найти значение выражения числителя дроби, подкорневого значения рационально?
Независимо от типа выражения решать его необходимо последовательно, руководствуясь стандартными правилами (описаны ранее). Но не стоит забывать, что во многих случаях поиск ответа может быть значительно упрощен за счет рационального подхода к решению. Основывается он на нескольких правилах.
Правило 1. Когда произведение равно нулю
Производное равно нулю в том случае, если хотя бы один из его сомножителей равен нулю. Если вы решаете пример из нескольких сомножителей, одним из которых является «0», то проводить многочисленные вычислительные действия не стоит.
Например, выражение [3 cdotleft(451+4+frac{18}{3}right)left(1-sin left(frac{3 pi}{4}right)right) cdot 0] будет равняться нулю.
Правило 2. Группировка и вынесение чисел
Ускорить процесс поиска ответа можно за счет группировки множителей, слагаемых или вынесения единого множителя за скобки. Также не стоит забывать о возможности сокращения дроби.
Например, выражение [frac{left(451+4+frac{18}{3}right)}{4left(451+4+frac{18}{3}right)}] решать не надо. Достаточно сократить скобки, чтобы получить ответ [=frac{1}{4}]
Решение примеров с переменными
Примеры с переменными отличаются от числовых только формой предоставления. В данном случае значения предоставляются дополнительно к выражению.
Пример задания: Найдите значение выражения 2x — y, если x = 2,5, а y = 2. В данном случае решение будет выглядеть следующим образом:
2x — y = 2 • 2,5 — 2 = 3
При этом в таких примерах сохраняются все описанные выше правила. Касается это и советов по рациональному решению примеров. Так, решать дробь [frac{sqrt{y}}{sqrt{y}}] бессмысленно, т.к. при любых значениях «y» ответ будет одинаковым — 1.
Выражения, записанные в форме
ab
, где
b≥0
, называются подобными, если их подкоренные выражения равны.
Выражения
35,135,5,−25
подобны.
Выражения
23
и
25
не подобны.
Подобные выражения можно складывать и вычитать. Действия производят с коэффициентами, стоящими перед знаками квадратных корней.
Пример:
упрости выражение:
57−117=5−117=−67
.
Обрати внимание!
Корни, подкоренные выражения которых не равны, также могут быть подобными. Чтобы в этом убедиться, необходимо вынести множители из-под знаков корней.
Пример:
упрости выражение:
125+280=25⋅5+216⋅5=55+2⋅45==55+85=5+85=135.
При упрощении выражений с корнями важно помнить, что:
a⋅b=a⋅b;еслиa≥0,a⋅a=aиa2=a.
Пример:
упрости выражение:
2−52
.
Используем формулу
a−b2=a2−2ab+b2
.
.
п.1. Определение уравнения и его корня
Уравнением с одной переменной x называют равенство f(x)=g(x), для которого поставлена задача найти все значения переменной x, которые обращают это равенство в истинное числовое равенство.
Значение переменной, при котором выражения f(x) и g(x) принимают равные числовые значения, называют корнем уравнения f(x)=g(x).
Например, для уравнения 15x+8=23 корнем является значение x=1.
В уравнении x(x + 5)(x – 3) = 0 три корня, $x_1 = 0,x_2 = -5,x_3 = 3$.
Уравнение $x^2 = -1$ действительных корней не имеет.
В уравнении 5(x + 3)=5x + 15 бесконечное количество корней, т.к. оно превращается в истинное равенство при любом $x in Bbb R$, т.е. является тождеством.
Решить уравнение означает найти все его корни или доказать, что их нет.
п.2. Примеры
Пример 1. Решите уравнение и выполните проверку x – (3 – 2x) = 9
Решение:
x-(3-2x)=9 $iff$ x-3+2x=9 $iff$ x+2x=9+3 $iff$ 3x=12 $iff$ x=4
Проверка:
$4 -(3 – 2 cdot 4)=9 implies 4 – 3 + 8 = 9 implies 9 equiv 9$
Ответ: x = 4
Пример 2. Решите уравнение и выполните проверку 7(x + 3) = 56
Решение:
7(x + 3)=56 |:7 $iff$ x + 3 = 8 $iff$ x = 8 – 3 $iff$ x=5
Проверка:
$7(5 + 3) = 56 implies 7 cdot 8 = 56 implies 56 equiv 56$
Ответ: x = 5
Пример 3. Решите уравнение и выполните проверку (3x + 4) : 2 = 14
Решение:
(3x + 4) : 2=14 |$times$2 $iff$ 3x + 4 = 28 $iff$ 3x = 28 – 4 $iff$ 3x = 24 $iff$ x=8
Проверка:
$(3 cdot 8 + 4) : 2 = 14 implies (24 + 4) : 2 = 14 implies 28 : 2 = 14 implies 14 equiv 14$
Ответ: x = 8
Пример 4. Решите уравнение $ frac{3x-7}{3} – frac {5x-11}{5} = 0$
Решение:
$frac {3x-7}{3} – frac {5x-11}{5} = 0 | times 15 iff5(3x-7)-3(5x-11)=0 iff$
$ iff 15x-35-15x+33=0 iff 0x=2 iff x in varnothing $
Решений нет.
Ответ: $x in varnothing $
Пример 5. Решите уравнение $frac {2x – 7}{2} = frac {3x+6}{3}$
Решение:
$frac {2x-7}{2}=frac {x+6}{3} | times 6 iff 3(2x-7)=2(x+6) iff 6x-21=2x+12 iff $
$iff 6x-2x=12+21 iff 4x=33 iff x= frac {33}{4} =8 frac 14$
Ответ: $8 frac 14$
Пример 6. Решите уравнение |x+1|=5
Решение:
$$|x+1|=5 iff left[ begin{array}{cc} {x+1=-5}\ {x+1=5} end{array} right. iff left[ begin{array}{cc} {x=-5-1}\ {x=5-1} end{array} right. iff left[ begin{array}{cc} {x_1=-6}\ {x_2=4} end{array} right. $$
Ответ: $ x_1=-6, x_2=4$
Пример 7*. Решите уравнение и выполните проверку |x + 1| = x + 3
Решение:
$$ |x + 1| = x + 3 iff left[ begin{array}{cc} {left{ begin{array}{c} x+1 ge 0 \ x+1=x+3 end{array} right.}\ {left{ begin{array}{c} x+1<0 \ -(x+1)=x+3 end{array} right.} end{array} right. iff left[ begin{array}{cc} {left{ begin{array}{c} x ge -1 \ 1=3 end{array} right.}\ {left{ begin{array}{c} x<-1 \ -x-1=x+3 end{array} right.} end{array} right. iff $$
$$ iff left[ begin{array}{cc} {emptyset}\ {left{ begin{array}{c} x<-1 \ -x-x=3+1 end{array} right.} end{array} right. iff left[ begin{array}{cc} {x<-1}\ {-2x=4} end{array} right. iff left[ begin{array}{cc} {x<-1}\ {x=-2} end{array} right. iff x=-2 $$
Проверка:
$$|-2+1|=-2+3 implies |-1|=1implies 1 equiv 1$$
Ответ: x = -2
Пример 8. При каком значении a уравнение 5ax + 18 = 3 будет иметь корень x = -3?
Решение:
Подставляем x=-3 в уравнение и решаем его относительно параметра a:
5a $cdot$ (-3) + 18 = 3 $iff$ -15a = 3 – 18 $iff$ -15a = -15 $iff$ a = -15:(-15)=1
a=1
Ответ: a = 1
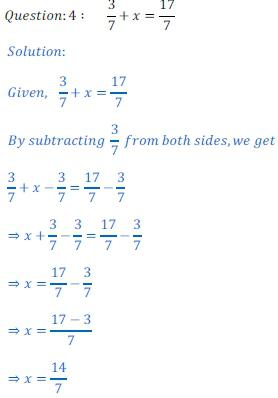
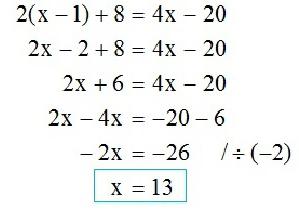
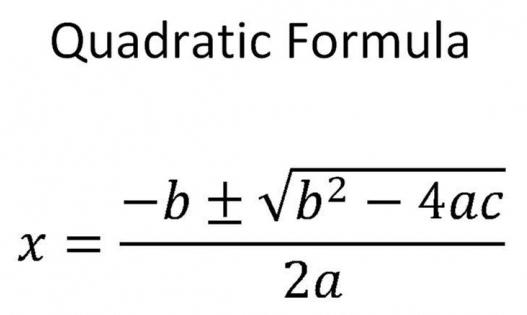
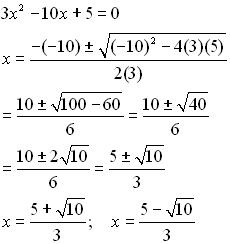




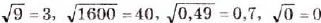
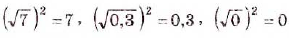
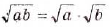 — для неотрицательных значений а и b;
— для неотрицательных значений а и b;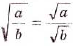 — для неотрицательного а и положительного b;
— для неотрицательного а и положительного b;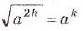 – для неотрицательного а и натурального к.
– для неотрицательного а и натурального к.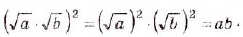
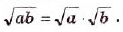
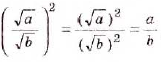
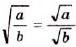
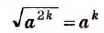
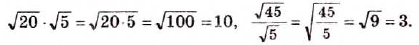
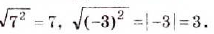
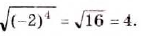
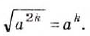
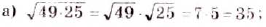
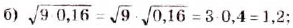
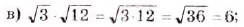
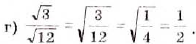
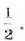
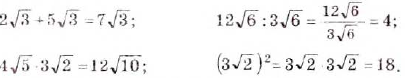
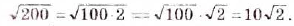
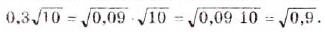
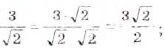
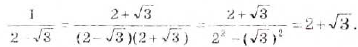
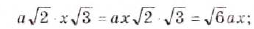
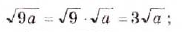
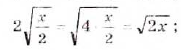
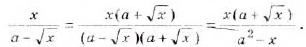
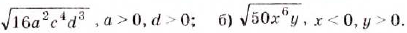
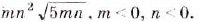
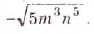
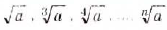

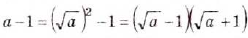
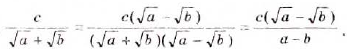
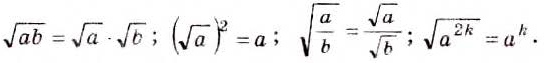
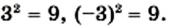
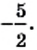
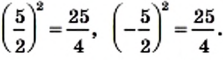
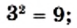
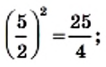
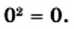
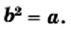
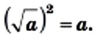
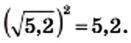
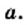
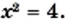
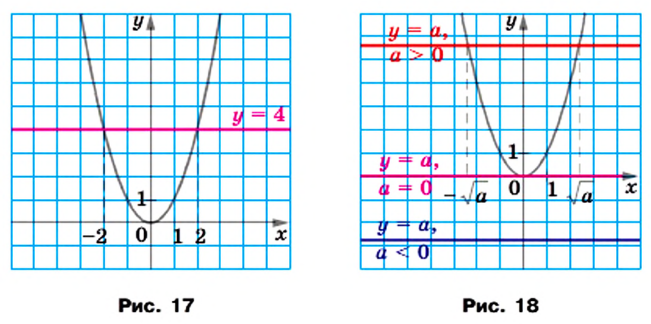
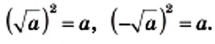
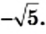
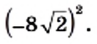
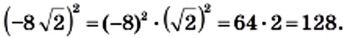
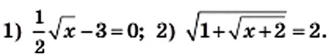
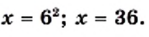
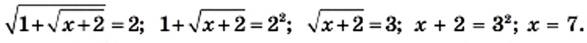
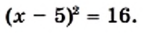
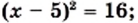
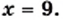
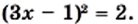
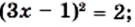
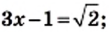
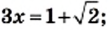
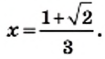
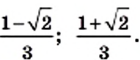
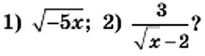
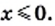
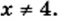
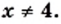
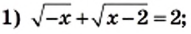
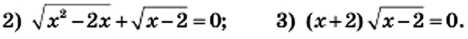
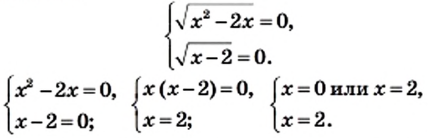
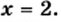
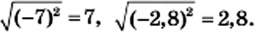
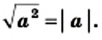
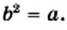
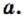
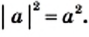
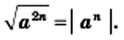
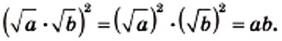
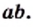
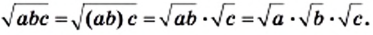
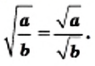
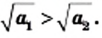
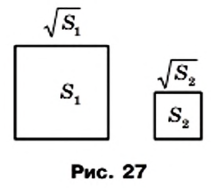
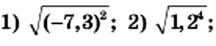
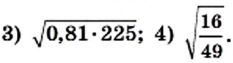
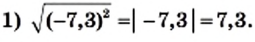
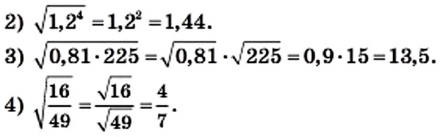
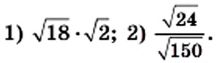
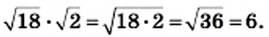
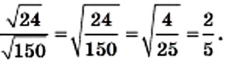
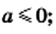
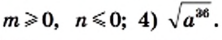
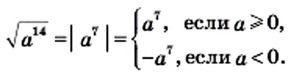
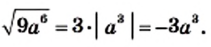
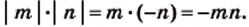
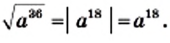
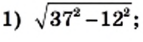
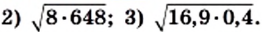
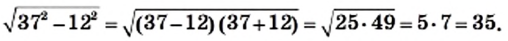
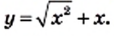
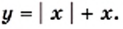
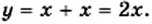
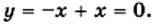
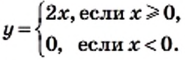
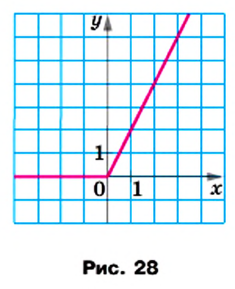
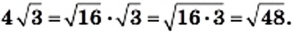
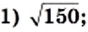
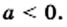
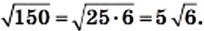
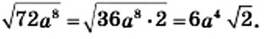
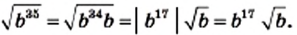
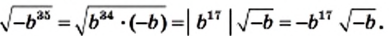
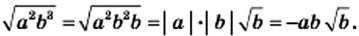
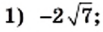
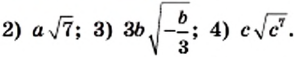
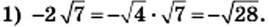
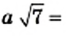
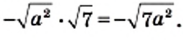
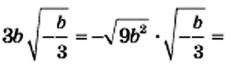
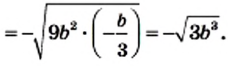
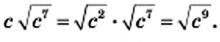
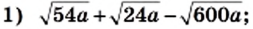
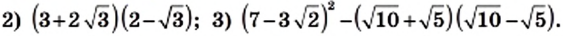
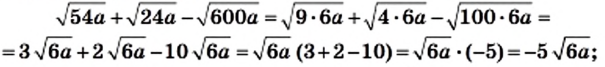
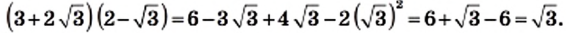
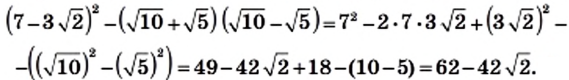
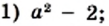
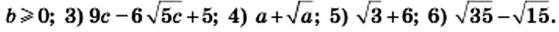
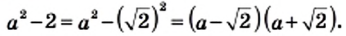
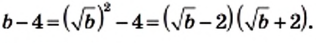
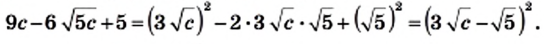
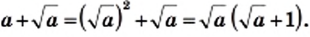
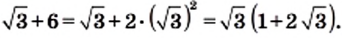
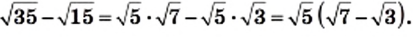
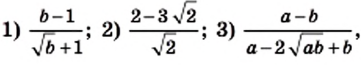
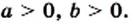
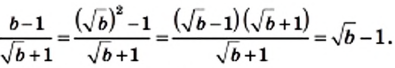
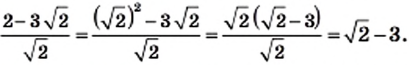
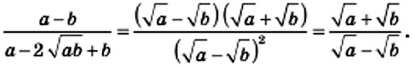
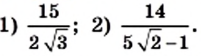
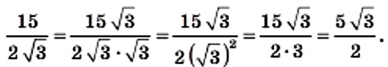
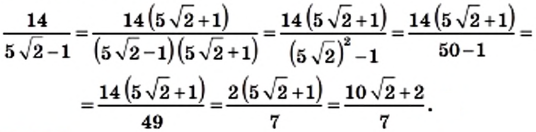
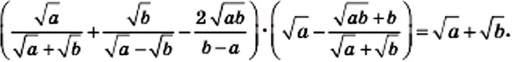
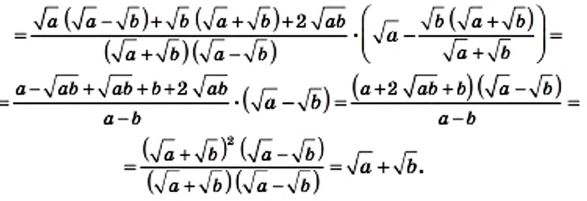
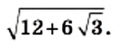
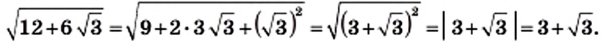
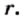
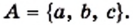
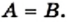
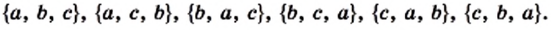
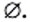
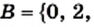
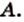
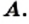
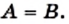
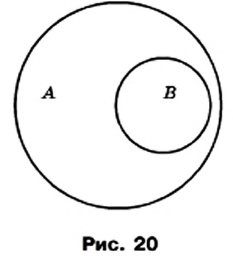
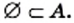
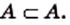
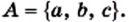
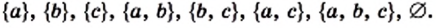
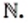
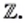
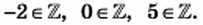
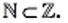
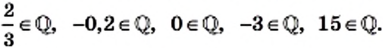
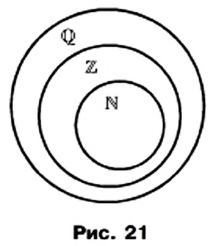
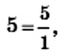
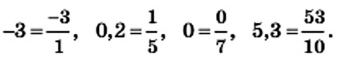
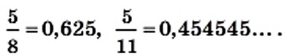
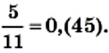
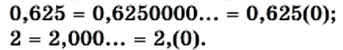
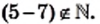
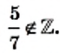
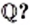
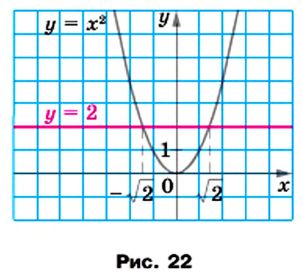
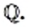
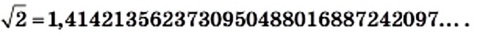
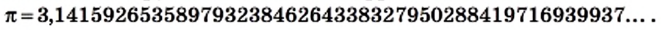
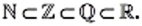
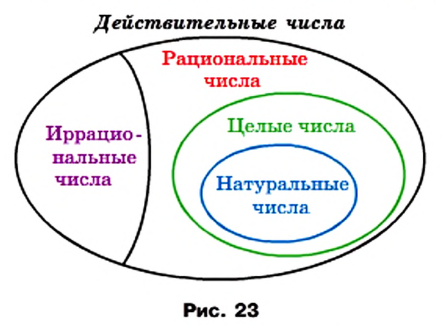
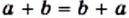 Переместительное свойство сложения
Переместительное свойство сложения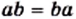 Переместительное свойство умножения
Переместительное свойство умножения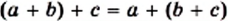 Сочетательное свойство сложения
Сочетательное свойство сложения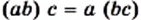 Сочетательное свойство умножения
Сочетательное свойство умножения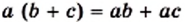 Распределительное свойство умножения относительно сложения
Распределительное свойство умножения относительно сложения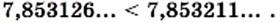
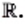
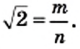
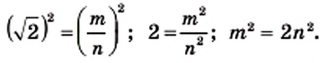
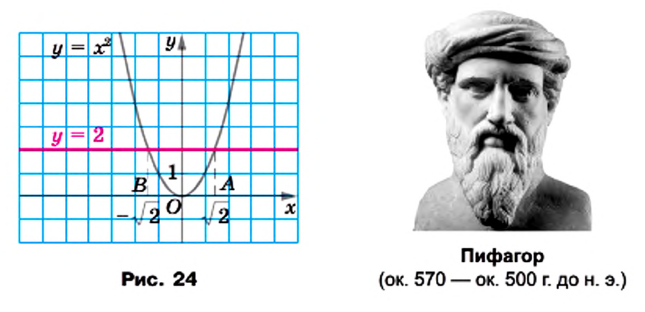
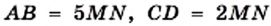
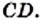
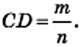
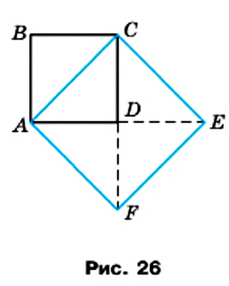
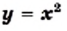
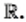
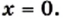
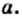
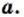
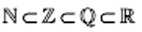
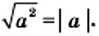
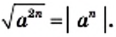
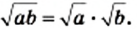
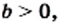
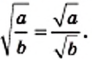
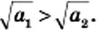
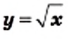
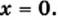
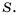

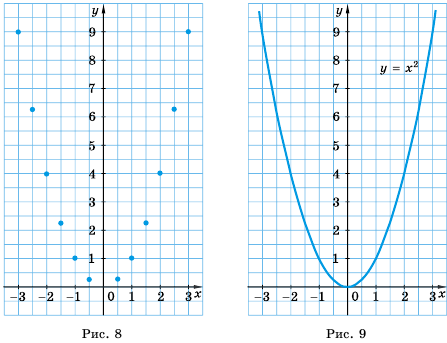
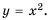

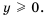
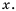
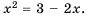
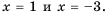
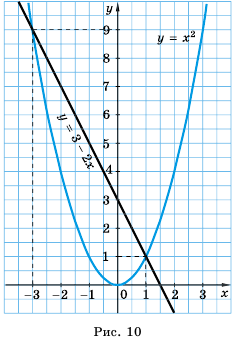
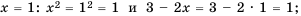
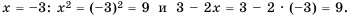
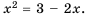
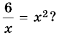
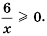
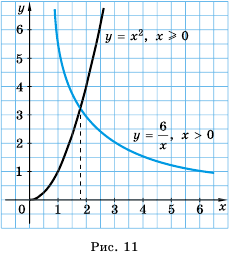
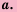
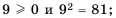
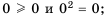
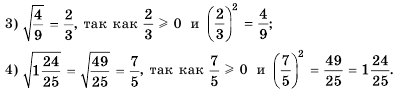
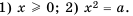
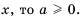

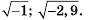
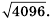
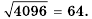
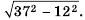
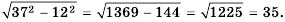
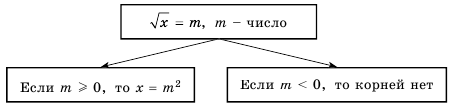
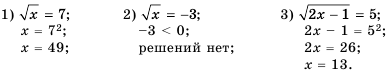
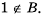
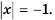
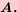
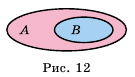
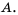
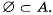
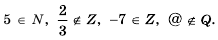
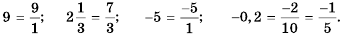
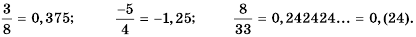

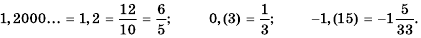
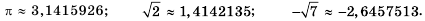
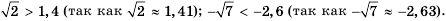
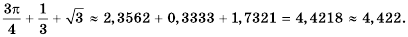
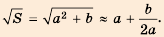
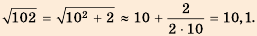
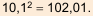
 x2=a
x2=a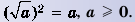 уравнение
уравнение