Как найти короткий путь графика - Сайт, где вы сможете решить свои вопросы

Базовые алгоритмы нахождения кратчайших путей во взвешенных графах

Время на прочтение
5 мин

Количество просмотров 240K

Наверняка многим из гейм-девелоперов (или просто людям, увлекающимися програмировагнием) будет интересно услышать эти четыре важнейших алгоритма, решающих задачи о кратчайших путях.

Сформулируем определения и задачу.
Графом будем называть несколько точек (вершин), некоторые пары которых соединены отрезками (рёбрами). Граф связный, если от каждой вершины можно дойти до любой другой по этим отрезкам. Циклом назовём какой-то путь по рёбрам графа, начинающегося и заканчивающегося в одной и той же вершине. И ещё граф называется взвешенным, если каждому ребру соответствует какое-то число (вес). Не может быть двух рёбер, соединяющих одни и те же вершины.
Каждый из алгоритмов будет решать какую-то задачу о кратчайших путях на взвешенном связном. Кратчайший путь из одной вершины в другую — это такой путь по рёбрам, что сумма весов рёбер, по которым мы прошли будет минимальна.
Для ясности приведу пример такой задачи в реальной жизни. Пусть, в стране есть несколько городов и дорог, соединяющих эти города. При этом у каждой дороги есть длина. Вы хотите попасть из одного города в другой, проехав как можно меньший путь.

Считаем, что в графе n вершин и m рёбер.
Пойдём от простого к сложному.

Алгоритм Флойда-Уоршелла

Находит расстояние от каждой вершины до каждой за количество операций порядка n^3. Веса могут быть отрицательными, но у нас не может быть циклов с отрицательной суммой весов рёбер (иначе мы можем ходить по нему сколько душе угодно и каждый раз уменьшать сумму, так не интересно).
В массиве d[0… n — 1][0… n — 1] на i-ой итерации будем хранить ответ на исходную задачу с ограничением на то, что в качестве «пересадочных» в пути мы будем использовать вершины с номером строго меньше i — 1 (вершины нумеруем с нуля). Пусть идёт i-ая итерация, и мы хотим обновить массив до i + 1-ой. Для этого для каждой пары вершин просто попытаемся взять в качестве пересадочной i — 1-ую вершину, и если это улучшает ответ, то так и оставим. Всего сделаем n + 1 итерацию, после её завершения в качестве «пересадочных» мы сможем использовать любую, и массив d будет являться ответом.
n итераций по n итераций по n итераций, итого порядка n^3 операций.
Псевдокод:

прочитать g // g[0 ... n - 1][0 ... n - 1] - массив, в котором хранятся веса рёбер, g[i][j] = 2000000000, если ребра между i и j нет
d = g
for i = 1 ... n + 1
     for j = 0 ... n - 1
          for k = 0 ... n - 1
              if d[j][k] > d[j][i - 1] + d[i - 1][k]
                  d[j][k] = d[j][i - 1] + d[i - 1][k]
вывести d

Алгоритм Форда-Беллмана

Находит расстояние от одной вершины (дадим ей номер 0) до всех остальных за количество операций порядка n * m. Аналогично предыдущему алгоритму, веса могут быть отрицательными, но у нас не может быть циклов с отрицательной суммой весов рёбер.
Заведём массив d[0… n — 1], в котором на i-ой итерации будем хранить ответ на исходную задачу с ограничением на то, что в путь должно входить строго меньше i рёбер. Если таких путей до вершины j нет, то d[j] = 2000000000 (это должна быть какая-то недостижимая константа, «бесконечность»). В самом начале d заполнен 2000000000. Чтобы обновлять на i-ой итерации массив, надо просто пройти по каждому ребру и попробовать улучшить расстояние до вершин, которые оно соединяет. Кратчайшие пути не содержат циклов, так как все циклы неотрицательны, и мы можем убрать цикл из путя, при этом длина пути не ухудшится (хочется также отметить, что именно так можно найти отрицательные циклы в графе: надо сделать ещё одну итерацию и посмотреть, не улучшилось ли расстояние до какой-нибудь вершины). Поэтому длина кратчайшего пути не больше n — 1, значит, после n-ой итерации d будет ответом на задачу.
n итераций по m итераций, итого порядка n * m операций.
Псевдокод:

прочитать e // e[0 ... m - 1] - массив, в котором хранятся рёбра и их веса (first, second - вершины, соединяемые ребром, value - вес ребра)
for i = 0 ... n - 1
    d[i] = 2000000000
d[0] = 0
for i = 1 ... n
    for j = 0 ... m - 1
        if d[e[j].second] > d[e[j].first] + e[j].value
            d[e[j].second] = d[e[j].first] + e[j].value
        if d[e[j].first] > d[e[j].second] + e[j].value
            d[e[j].first] = d[e[j].second] + e[j].value
вывести d

Алгоритм Дейкстры

Находит расстояние от одной вершины (дадим ей номер 0) до всех остальных за количество операций порядка n^2. Все веса неотрицательны.
На каждой итерации какие-то вершины будут помечены, а какие-то нет. Заведём два массива: mark[0… n — 1] — True, если вершина помечена, False иначе, d[0… n — 1] — для каждой вершины будет храниться длина кратчайшего пути, проходящего только по помеченным вершинам в качестве «пересадочных». Также поддерживается инвариант того, что для помеченных вершин длина, указанная в d, и есть ответ. Сначала помечена только вершина 0, а g[i] равно x, если 0 и i соединяет ребро весом x, равно 2000000000, если их не соединяет ребро, и равно 0, если i = 0.
На каждой итерации мы находим вершину, с наименьшим значением в d среди непомеченных, пусть это вершина v. Тогда значение d[v] является ответом для v. Докажем. Пусть, кратчайший путь до v из 0 проходит не только по помеченным вершинам в качестве «пересадочных», и при этом он короче d[v]. Возьмём первую встретившуюся непомеченную вершину на этом пути, назовём её u. Длина пройденной части пути (от 0 до u) — d[u]. len >= d[u], где len — длина кратчайшего пути из 0 до v (т. к. отрицательных рёбер нет), но по нашему предположению len меньше d[v]. Значит, d[v] > len >= d[u]. Но тогда v не подходит под своё описание — у неё не наименьшее значение d[v] среди непомеченных. Противоречие.
Теперь смело помечаем вершину v и пересчитываем d. Так делаем, пока все вершины не станут помеченными, и d не станет ответом на задачу.
n итераций по n итераций (на поиск вершины v), итого порядка n^2 операций.
Псевдокод:

прочитать g // g[0 ... n - 1][0 ... n - 1] - массив, в котором хранятся веса рёбер, g[i][j] = 2000000000, если ребра между i и j нет
d = g
d[0] = 0
mark[0] = True
for i = 1 ... n - 1
    mark[i] = False
for i = 1 ... n - 1
    v = -1
    for i = 0 ... n - 1
        if (not mark[i]) and ((v == -1) or (d[v] > d[i]))
            v = i
    mark[v] = True
    for i = 0 ... n - 1
        if d[i] > d[v] + g[v][i]
            d[i] = d[v] + g[v][i]
вывести d

Алгоритм Дейкстры для разреженных графов

Делает то же самое, что и алгоритм Дейкстры, но за количество операций порядка m * log(n). Следует заметить, что m может быть порядка n^2, то есть эта вариация алгоритма Дейкстры не всегда быстрее классической, а только при маленьких m.
Что нам нужно в алгоритме Дейкстры? Нам нужно уметь находить по значению d минимальную вершину и уметь обновлять значение d в какой-то вершине. В классической реализации мы пользуемся простым массивом, находить минимальную по d вершину мы можем за порядка n операций, а обновлять — за 1 операцию. Воспользуемся двоичной кучей (во многих объектно-ориентированных языках она встроена). Куча поддерживает операции: добавить в кучу элемент (за порядка log(n) операций), найти минимальный элемент (за 1 операцию), удалить минимальный элемент (за порядка log(n) операций), где n — количество элементов в куче.
Создадим массив d[0… n — 1] (его значение то же самое, что и раньше) и кучу q. В куче будем хранить пары из номера вершины v и d[v] (сравниваться пары должны по d[v]). Также в куче могут быть фиктивные элементы. Так происходит, потому что значение d[v] обновляется, но мы не можем изменить его в куче. Поэтому в куче могут быть несколько элементов с одинаковым номером вершины, но с разным значением d (но всего вершин в куче будет не более m, я гарантирую это). Когда мы берём минимальное значение в куче, надо проверить, является ли этот элемент фиктивным. Для этого достаточно сравнить значение d в куче и реальное его значение. А ещё для записи графа вместо двоичного массива используем массив списков.
m раз добавляем элемент в кучу, получаем порядка m * log(n) операций.
Псевдокод:

прочитать g // g[0 ... n - 1] - массив списков, в i-ом списке хранятся пары: first - вершина, соединённая с i-ой вершиной ребром, second - вес этого ребра
d[0] = 0
for i = 0 ... n - 1
    d[i] = 2000000000
for i in g[0] // python style
    d[i.first] = i.second
    q.add(pair(i.second, i.first))
for i = 1 ... n - 1
    v = -1
    while (v = -1) or (d[v] != val)
        v = q.top.second
        val = q.top.first
    q.removeTop
    mark[v] = true
    for i in g[v]
        if d[i.first] > d[v] + i.second
            d[i.first] = d[v] + i.second
            q.add(pair(d[i.first], i.first))
вывести d

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 августа 2021 года; проверки требуют 7 правок.

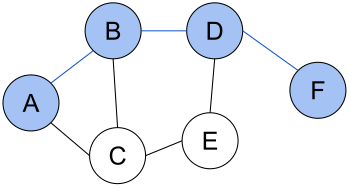
Кратчайший путь (A, B, D, F) между вершинами A и F в неориентированном графе без весов.

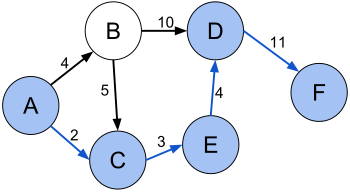
Кратчайший путь (A, C, E, D, F) между вершинами A и F во взвешенном ориентированном графе.

Зада́ча о кратча́йшем пути́ — задача поиска самого короткого пути (цепи) между двумя точками (вершинами) на графе, в которой минимизируется сумма весов рёбер, составляющих путь.

Задача о кратчайшем пути является одной из важнейших классических задач теории графов. Сегодня известно множество алгоритмов для её решения^[⇨].

У данной задачи существуют и другие названия: задача о минимальном пути или, в устаревшем варианте, задача о дилижансе.

Значимость данной задачи определяется её различными практическими применениями^[⇨]. Например, в GPS-навигаторах осуществляется поиск кратчайшего пути между точкой отправления и точкой назначения. В качестве вершин выступают перекрёстки, а дороги являются рёбрами, которые лежат между ними. Если сумма длин дорог между перекрёстками минимальна, тогда найденный путь самый короткий.

Определение[править | править код]

Задача поиска кратчайшего пути на графе может быть определена для неориентированного, ориентированного или смешанного графа. Далее будет рассмотрена постановка задачи в самом простом виде для неориентированного графа. Для смешанного и ориентированного графа дополнительно должны учитываться направления ребер.

Граф представляет собой совокупность непустого множества вершин и рёбер (наборов пар вершин). Две вершины на графе смежны, если они соединяются общим ребром. Путь в неориентированном графе представляет собой последовательность вершин $P=(v_{1},v_{2},ldots ,v_{n})in Vtimes Vtimes ldots times V$ , таких что $v_{i}$ смежна с $v_{{i+1}}$ для . Такой путь называется путём длиной из вершины $v_{1}$ в $v_{n}$ ( указывает на номер вершины пути и не имеет никакого отношения к нумерации вершин на графе).

Пусть $e_{{i,j}}$ — ребро соединяющее две вершины: $v_{i}$ и $v_{j}$ . Дана весовая функция , которая отображает ребра на их веса, значения которых выражаются действительными числами, и неориентированный граф . Тогда кратчайшим путём из вершины в вершину будет называться путь $P=(v_{1},v_{2},ldots ,v_{n})$ (где $v_{1}=v$ и $v_{n}=v'$ ), который имеет минимальное значение суммы $sum _{{i=1}}^{{n-1}}f(e_{{i,i+1}}).$ Если все ребра в графе имеют единичный вес, то задача сводится к определению наименьшего количества обходимых ребер.

Существуют различные постановки задачи о кратчайшем пути:

Задача о кратчайшем пути в заданный пункт назначения. Требуется найти кратчайший путь в заданную вершину назначения t, который начинается в каждой из вершин графа (кроме t). Поменяв направление каждого принадлежащего графу ребра, эту задачу можно свести к задаче о единой исходной вершине (в которой осуществляется поиск кратчайшего пути из заданной вершины во все остальные).
Задача о кратчайшем пути между заданной парой вершин. Требуется найти кратчайший путь из заданной вершины u в заданную вершину v.
Задача о кратчайшем пути между всеми парами вершин. Требуется найти кратчайший путь из каждой вершины u в каждую вершину v. Эту задачу тоже можно решить с помощью алгоритма, предназначенного для решения задачи об одной исходной вершине, однако обычно она решается быстрее.

В различных постановках задачи, роль длины ребра могут играть не только сами длины, но и время, стоимость, расходы, объём затрачиваемых ресурсов (материальных, финансовых, топливно-энергетических и т. п.) или другие характеристики, связанные с прохождением каждого ребра. Таким образом, задача находит практическое применение в большом количестве областей (информатика, экономика, география и др.).

Задача о кратчайшем пути с учётом дополнительных ограничений[править | править код]

Задача о кратчайшем пути очень часто встречается в ситуации, когда необходимо учитывать дополнительные ограничения. Наличие их может значительно повысить сложность задачи^[1]. Примеры таких задач:

Кратчайший путь, проходящий через заданное множество вершин. Можно рассматривать два ограничения: кратчайший путь должен проходить через выделенное множество вершин, и кратчайший путь должен содержать как можно меньше невыделенных вершин. Первое из них хорошо известна в теории исследования операций^[2].
Минимальное покрытие вершин ориентированного графа путями. Осуществляется поиск минимального по числу путей покрытия графа, а именно подмножества всех s-t путей, таких что, каждая вершина ориентированного графа принадлежит хотя бы одному такому пути^[3].
Задача о требуемых путях. Требуется найти минимальное по мощности множество s-t путей $P={p_{1},dots ,p_{m}}$ такое, что для любого $t_{i}in R$ найдется путь $p_{j}in P$ , накрывающий его. $R={t_{1},dots ,t_{k}}$ — множество некоторых путей в ориентированном графе G^[4].
Минимальное покрытие дуг ориентированного графа путями. Задача состоит в отыскании минимального по числу путей подмножества всех путей, такого, что каждая дуга принадлежит хотя бы одному такому пути. При этом возможно дополнительное требование о том, чтобы все пути исходили из одной вершины^[5].

Алгоритмы[править | править код]

В связи с тем, что существует множество различных постановок данной задачи, есть
наиболее популярные алгоритмы для решения задачи поиска кратчайшего пути на графе:

Алгоритм Дейкстры находит кратчайший путь от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса^[6].
Алгоритм Беллмана — Форда находит кратчайшие пути от одной вершины графа до всех остальных во взвешенном графе. Вес рёбер может быть отрицательным.
Алгоритм поиска A* находит маршрут с наименьшей стоимостью от одной вершины (начальной) к другой (целевой, конечной), используя алгоритм поиска по первому наилучшему совпадению на графе.
Алгоритм Флойда — Уоршелла находит кратчайшие пути между всеми вершинами взвешенного ориентированного графа^[6].
Алгоритм Джонсона находит кратчайшие пути между всеми парами вершин взвешенного ориентированного графа.
Алгоритм Ли (волновой алгоритм) основан на методе поиска в ширину. Находит путь между вершинами s и t графа (s не совпадает с t), содержащий минимальное количество промежуточных вершин (рёбер). Основное применение — трассировки электрических соединений на кристаллах микросхем и на печатных платах. Также используется для поиска кратчайшего расстояния на карте в стратегических играх.
Поиск кратчайшего пути на основе алгоритма Килдала^[7].

В работе (Черкасский и др., 1993)^[8] представлено ещё несколько алгоритмов для решения этой задачи.

Задача поиска кратчайшего пути из одной вершины во все остальные[править | править код]

В такой постановке задачи осуществляется поиск кратчайшего пути из вершины v во все остальные вершины на графе.

Невзвешенный ориентированный граф[править | править код]

Алгоритм	Сложность	Автор
Поиск в ширину	O(V+E)

Ориентированный граф с неотрицательными весами[править | править код]

Алгоритм	Сложность	Автор
–	O(V²EL)	Форд 1956
Алгоритм Беллмана — Форда	O(VE)	Беллман 1958^[9], Мур 1957^[10]
–	O(V² log V)	Данциг 1958, Данциг 1960, Minty (cf. Pollack&Wiebenson 1960), Whiting&Hillier 1960
Алгоритм Дейкстры со списком.	O(V²)	Leyzorek et al. 1957^[11], Дейкстра 1959^[12]
Алгоритм Дейкстры с модифицированной двоичной кучей	O((E + V) log V)	–
. . .	. . .	. . .
Алгоритм Дейкстры с использованием фибоначчиевой кучи	O(E + V log V)	Фридман&Тарьян 1984^[13], Фридман&Тарьян 1987^[14]
–	O(E log log L)	Джонсон 1982, Карлссон&Поблете 1983
Алгоритм Габова	O(E log_E/V L)	Габов 1983, Габов 1985
–	O(E + V√log L)	Ахуджа et al. 1990

Ориентированный граф с произвольными весами[править | править код]

Алгоритм	Сложность	Автор
Алгоритм Беллмана — Форда	O(VE)	Беллман^[9], Мур^[10]
Алгоритм Левита	O(VE)

Задача о кратчайшем пути между всеми парами вершин[править | править код]

Задача о кратчайшем пути между всеми парами вершин для невзвешенного ориентированного графа была поставлена Симбелом в 1953 году^[15], который обнаружил, что она может быть решена за линейное количество манипуляций (умножения) с матрицей. Сложность такого алгоритма O(V⁴).

Так же для решения данной задачи существуют другие более быстрые алгоритмы, такие как Алгоритм Флойда — Уоршелла со сложностью O(V³), и
Алгоритм Джонсона (является комбинацией алгоритмов Бэллмана-Форда и Дейкстры) со сложностью O(VE + V² log V).

Применение[править | править код]

Задача о поиске кратчайшего пути на графе может быть интерпретирована по-разному и применяться в различных областях. Далее приведены примеры различных применений задачи. Другие применения изучаются в дисциплине, которая занимается исследованием операций^[16].

Картографические сервисы[править | править код]

Алгоритмы нахождения кратчайшего пути на графе применяются для нахождения путей между физическими объектами на таких картографических сервисах, как карты Google или OpenStreetMap. В обучающем видео от Google можно узнать различные эффективные алгоритмы, которые применяются в данной сфере^[17].

Недетерминированная машина[править | править код]

Если представить недетерминированную абстрактную машину как граф, где вершины описывают состояния, а ребра определяют возможные переходы, тогда алгоритмы поиска кратчайшего пути могут быть применены для поиска оптимальной последовательности решений для достижения главной цели. Например, если вершинами являются состояния Кубика Рубика, а ребром представляет собой одно действие над кубиком, тогда алгоритм может быть применён для поиска решения с минимальным количеством ходов.

Сети дорог[править | править код]

Задача поиска кратчайшего пути на графе широко используется при определении наименьшего расстояния в сети дорог.

Сеть дорог можно представить в виде графа с положительными весами. Вершины являются дорожными развязками, а ребра дорогами, которые их соединяют. Веса рёбер могут соответствовать протяжённости данного участка, времени необходимому для его преодоления или стоимости путешествия по нему. Ориентированные ребра можно использовать для представления односторонних улиц. В таком графе можно ввести характеристику, которая указывает на то, что одни дороги важнее других для длительных путешествий (например автомагистрали). Она была формализована в понятии (идее) о магистралях^[18].

Для реализации подхода, где одни дороги важнее других, существует множество алгоритмов. Они решают задачу поиска кратчайшего пути намного быстрее, чем аналогичные на обычных графах.
Подобные алгоритмы состоят из двух этапов:

этап предобработки. Производится предварительная обработка графа без учёта начальной и конечной вершины (может длиться до нескольких дней, если работать с реальными данными). Обычно выполняется один раз и потом используются полученные данные.
этап запроса. Осуществляется запрос и поиск кратчайшего пути, при этом известны начальная и конечная вершина.

Самый быстрый алгоритм может решить данную задачу на дорогах Европы или Америки за доли микросекунды^[19].

Другие подходы (техники), которые применяются в данной сфере:

ALT
Arc Flags
Contraction hierarchies
Transit Node Routing
Reach based Pruning
Labeling

Постановка задачи линейного программирования[править | править код]

Пусть дан направленный граф (V, A), где V — множество вершин и A — множество рёбер, с начальной вершиной обхода s, конечной t и весами w_ij для каждого ребра (i, j) в A. Вес каждого ребра соответствует переменной программы x_ij.

Тогда задача ставится следующим образом: найти минимум функции $F=sum _{{ijin A}}w_{{ij}}x_{{ij}}$ , где $x_{{ij}}geq 0$ , при условии что для всех i и j выполняется следующее неравенство: $sum _{j}x_{{ij}}-sum _{j}x_{{ji}}={begin{cases}1,&{text{if }}i=s;\-1,&{text{if }}i=t;\0,&{text{ otherwise.}}end{cases}}$

См. также[править | править код]

IEEE 802.1aq
Транспортная сеть
Двунаправленный поиск

Примечания[править | править код]

↑ Применение теории графов в программировании, 1985.
↑ Применение теории графов в программировании, 1985, с. 138—139.
↑ Применение теории графов в программировании, 1985, с. 139—142.
↑ Применение теории графов в программировании, 1985, с. 144—145.
↑ Применение теории графов в программировании, 1985, с. 145—148.
↑ ¹ ² Дискретная математика. Комбинаторная оптимизация на графах, 2003.
↑ Применение теории графов в программировании, 1985, с. 130—131.
↑ Cherkassky, Goldberg, Radzik, 1996.
↑ ¹ ² Bellman Richard, 1958.
↑ ¹ ² Moore, 1957.
↑ M. Leyzorek, 1957.
↑ Dijkstra, 1959.
↑ Michael Fredman Lawrence, 1984.
↑ Fredman Michael, 1987.
↑ Shimbel, 1953.
↑ Developing algorithms and software for geometric path planning problems, 1996.
↑ Fast route planning.
↑ Highway Dimension, 2010.
↑ A Hub-Based Labeling Algorithm, 2011.
↑ Ladyzhensky Y., Popoff Y. Algorithm, 2006.

Литература[править | править код]

Евстигнеев В. А. Глава 3. Итеративные алгоритмы глобального анализа графов. Пути и покрытия // Применение теории графов в программировании / Под ред. А. П. Ершова. — Москва: Наука. Главная редакция физико-математической литературы, 1985. — С. 138—150. — 352 с.
Алексеев В.Е., Таланов В.А. Глава 3.4. Нахождения кратчайших путей в графе // Графы. Модели вычислений. Структуры данных. — Нижний Новгород: Издательство Нижегородского гос. университета, 2005. — С. 236—237. — 307 с. — ISBN 5–85747–810–8. Архивная копия от 13 декабря 2013 на Wayback Machine
Галкина В.А. Глава 4. Построение кратчайших путей в ориентированном графе // Дискретная математика. Комбинаторная оптимизация на графах. — Москва: Издательство “Гелиос АРВ”, 2003. — С. 75—94. — 232 с. — ISBN 5–85438–069–2.
Берж К. Глава 7. Задача о кратчайшем пути // Теория графов и её применения = Theorie des graphes et ses applications / Под ред. И. А. Вайнштейна. — Москва: Издательство иностранной литературы, 1962. — С. 75—81. — 320 с.
Ойстин Оре. Теория графов / Под ред. И. М. Овчинниковой. — Издательство наука, 1980. — 336 с. Архивная копия от 15 декабря 2013 на Wayback Machine
Виталий Осипов, Поиск кратчайших путей в дорожных сетях: от теории к реализации на YouTube.
Харари Ф. Глава 2. Графы // Теория графов / под ред. Г. П. Гаврилов — М.: Мир, 1973. — С. 27. — 301 с.
Cherkassky B. V., Goldberg A. V., Radzik T. Shortest paths algorithms: Theory and experimental evaluation (англ.) // Mathematical Programming — Springer Science+Business Media, 1996. — Vol. 73, Iss. 2. — P. 129–174. — ISSN 0025-5610; 1436-4646 — doi:10.1007/BF02592101
Ричард Беллман. On a routing problem // Quarterly of Applied Mathematics. — 1958. — Т. 16. — С. 87—90.
Dijkstra E. W. A note on two problems in connexion with graphs (англ.) // Numerische Mathematik / F. Brezzi — Springer Science+Business Media, 1959. — Vol. 1, 1, Iss. 1, 1. — P. 269—271, 269—271. — ISSN 0029-599X; 0945-3245 — doi:10.1007/BF01386390
Moore E. F. The shortest path through a maze (англ.) // Proceedings of an International Symposium on the Theory of Switching (Cambridge, Massachusetts, 2–5 April 1957) — Harvard University Press, 1959. — Vol. 2. — P. 285—292. — 345 p. — (Annals of the Computation Laboratory of Harvard University; Vol. 30) — ISSN 0073-0750
M. Leyzorek, R. S. Gray, A. A. Gray, W. C. Ladew, S. R. Meaker, R. M. Petry, R. N. Seitz. Investigation of Model Techniques — First Annual Report — 6 June 1956 — 1 July 1957 — A Study of Model Techniques for Communication Systems (англ.). — Cleveland, Ohio: Case Institute of Technology, 1957.
Michael Fredman Lawrence, Роберт Андре Тарьян. Fibonacci heaps and their uses in improved network optimization algorithms (англ.) : journal. — Институт инженеров электротехники и электроники, 1984. — P. 338—346. — ISBN 0-8186-0591-X. — doi:10.1109/SFCS.1984.715934. Архивировано 11 октября 2012 года.
Michael Fredman Lawrence, Роберт Андре Тарьян. Fibonacci heaps and their uses in improved network optimization algorithms (англ.) // Journal of the Association for Computing Machinery : journal. — 1987. — Vol. 34, no. 3. — P. 596—615. — doi:10.1145/28869.28874.
Shimbel, Alfonso. Structural parameters of communication networks // Bulletin of Mathematical Biophysics. — 1953. — Т. 15, № 4. — С. 501—507. — doi:10.1007/BF02476438.
Sanders, Peter. Fast route planning. — Google Tech Talk, 2009. — 23 марта.. — «Шаблон:Inconsistent citations».
Chen, Danny Z. Developing algorithms and software for geometric path planning problems (англ.) // ACM Computing Surveys (англ.) (рус. : journal. — 1996. — December (vol. 28, no. 4es). — P. 18. — doi:10.1145/242224.242246.
Abraham, Ittai; Fiat, Amos; Goldberg, Andrew V.; Werneck, Renato F. Highway Dimension, Shortest Paths, and Provably Efficient Algorithms (англ.) // ACM-SIAM Symposium on Discrete Algorithms : journal. — 2010. — P. 782—793.
Abraham, Ittai; Delling, Daniel; Goldberg, Andrew V.; Werneck, Renato F. A Hub-Based Labeling Algorithm for Shortest Paths on Road Networks. Symposium on Experimental Algorithms] (англ.) : journal. — 2011. — P. 230—241.
Kroger, Martin. Shortest multiple disconnected path for the analysis of entanglements in two- and three-dimensional polymeric systems (англ.) // Computer Physics Communications (англ.) (рус. : journal. — 2005. — Vol. 168, no. 168. — P. 209—232. — doi:10.1016/j.cpc.2005.01.020.
Ladyzhensky Y., Popoff Y. Algorithm to define the shortest paths between all nodes in a graph after compressing of two nodes. Proceedings of Donetsk national technical university, Computing and automation. Vol.107. Donetsk (англ.) : journal. — 2006. — P. 68—75..^{[источник не указан 924 дня]}

Источник

Given an unweighted graph, a source, and a destination, we need to find the shortest path from source to destination in the graph in the most optimal way.

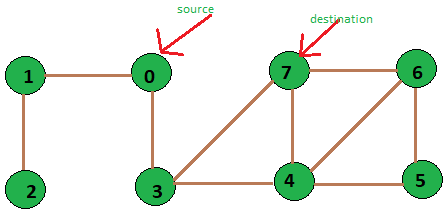
unweighted graph of 8 vertices

Input: source vertex = 0 and destination vertex is = 7.
Output: Shortest path length is:2
        Path is::
        0 3 7

Input: source vertex is = 2 and destination vertex is = 6.
Output: Shortest path length is:5
        Path is::
        2 1 0 3 4 6

One solution is to solve in O(VE) time using Bellman–Ford. If there are no negative weight cycles, then we can solve in O(E + VLogV) time using Dijkstra’s algorithm.
Since the graph is unweighted, we can solve this problem in O(V + E) time. The idea is to use a modified version of Breadth-first search in which we keep storing the predecessor of a given vertex while doing the breadth-first search.

We first initialize an array dist[0, 1, …., v-1] such that dist[i] stores the distance of vertex i from the source vertex and array pred[0, 1, ….., v-1] such that pred[i] represents the immediate predecessor of the vertex i in the breadth-first search starting from the source.

Now we get the length of the path from source to any other vertex in O(1) time from array d, and for printing the path from source to any vertex we can use array p and that will take O(V) time in worst case as V is the size of array P. So most of the time of the algorithm is spent in doing the Breadth-first search from a given source which we know takes O(V+E) time. Thus the time complexity of our algorithm is O(V+E).

Take the following unweighted graph as an example:

Following is the complete algorithm for finding the shortest path:

Implementation:

C++

#include <bits/stdc++.h>

using namespace std;

void add_edge(vector<int> adj[], int src, int dest)

{

adj[src].push_back(dest);

adj[dest].push_back(src);

}

bool BFS(vector<int> adj[], int src, int dest, int v,

int pred[], int dist[])

{

list<int> queue;

bool visited[v];

for (int i = 0; i < v; i++) {

visited[i] = false;

dist[i] = INT_MAX;

pred[i] = -1;

}

visited[src] = true;

dist[src] = 0;

queue.push_back(src);

while (!queue.empty()) {

int u = queue.front();

queue.pop_front();

for (int i = 0; i < adj[u].size(); i++) {

if (visited[adj[u][i]] == false) {

visited[adj[u][i]] = true;

dist[adj[u][i]] = dist[u] + 1;

pred[adj[u][i]] = u;

queue.push_back(adj[u][i]);

if (adj[u][i] == dest)

return true;

}

return false;

}

void printShortestDistance(vector<int> adj[], int s,

int dest, int v)

{

int pred[v], dist[v];

if (BFS(adj, s, dest, v, pred, dist) == false) {

cout << "Given source and destination"

<< " are not connected";

return;

}

vector<int> path;

int crawl = dest;

path.push_back(crawl);

while (pred[crawl] != -1) {

path.push_back(pred[crawl]);

crawl = pred[crawl];

}

cout << "Shortest path length is : "

<< dist[dest];

cout << "nPath is::n";

for (int i = path.size() - 1; i >= 0; i--)

cout << path[i] << " ";

}

int main()

{

int v = 8;

vector<int> adj[v];

add_edge(adj, 0, 1);

add_edge(adj, 0, 3);

add_edge(adj, 1, 2);

add_edge(adj, 3, 4);

add_edge(adj, 3, 7);

add_edge(adj, 4, 5);

add_edge(adj, 4, 6);

add_edge(adj, 4, 7);

add_edge(adj, 5, 6);

add_edge(adj, 6, 7);

int source = 0, dest = 7;

printShortestDistance(adj, source, dest, v);

return 0;

}

Java

import java.util.ArrayList;

import java.util.Iterator;

import java.util.LinkedList;

public class pathUnweighted {

public static void main(String args[])

{

int v = 8;

ArrayList<ArrayList<Integer>> adj =

new ArrayList<ArrayList<Integer>>(v);

for (int i = 0; i < v; i++) {

adj.add(new ArrayList<Integer>());

}

addEdge(adj, 0, 1);

addEdge(adj, 0, 3);

addEdge(adj, 1, 2);

addEdge(adj, 3, 4);

addEdge(adj, 3, 7);

addEdge(adj, 4, 5);

addEdge(adj, 4, 6);

addEdge(adj, 4, 7);

addEdge(adj, 5, 6);

addEdge(adj, 6, 7);

int source = 0, dest = 7;

printShortestDistance(adj, source, dest, v);

}

private static void addEdge(ArrayList<ArrayList<Integer>> adj, int i, int j)

{

adj.get(i).add(j);

adj.get(j).add(i);

}

private static void printShortestDistance(

ArrayList<ArrayList<Integer>> adj,

int s, int dest, int v)

{

int pred[] = new int[v];

int dist[] = new int[v];

if (BFS(adj, s, dest, v, pred, dist) == false) {

System.out.println("Given source and destination" +

"are not connected");

return;

}

LinkedList<Integer> path = new LinkedList<Integer>();

int crawl = dest;

path.add(crawl);

while (pred[crawl] != -1) {

path.add(pred[crawl]);

crawl = pred[crawl];

}

System.out.println("Shortest path length is: " + dist[dest]);

System.out.println("Path is ::");

for (int i = path.size() - 1; i >= 0; i--) {

System.out.print(path.get(i) + " ");

}

private static boolean BFS(ArrayList<ArrayList<Integer>> adj, int src,

int dest, int v, int pred[], int dist[])

{

LinkedList<Integer> queue = new LinkedList<Integer>();

boolean visited[] = new boolean[v];

for (int i = 0; i < v; i++) {

visited[i] = false;

dist[i] = Integer.MAX_VALUE;

pred[i] = -1;

}

visited[src] = true;

dist[src] = 0;

queue.add(src);

while (!queue.isEmpty()) {

int u = queue.remove();

for (int i = 0; i < adj.get(u).size(); i++) {

if (visited[adj.get(u).get(i)] == false) {

visited[adj.get(u).get(i)] = true;

dist[adj.get(u).get(i)] = dist[u] + 1;

pred[adj.get(u).get(i)] = u;

queue.add(adj.get(u).get(i));

if (adj.get(u).get(i) == dest)

return true;

}

return false;

}

Python3

def add_edge(adj, src, dest):

adj[src].append(dest);

adj[dest].append(src);

def BFS(adj, src, dest, v, pred, dist):

queue = []

visited = [False for i in range(v)];

for i in range(v):

dist[i] = 1000000

pred[i] = -1;

visited[src] = True;

dist[src] = 0;

queue.append(src);

while (len(queue) != 0):

u = queue[0];

queue.pop(0);

for i in range(len(adj[u])):

if (visited[adj[u][i]] == False):

visited[adj[u][i]] = True;

dist[adj[u][i]] = dist[u] + 1;

pred[adj[u][i]] = u;

queue.append(adj[u][i]);

if (adj[u][i] == dest):

return True;

return False;

def printShortestDistance(adj, s, dest, v):

pred=[0 for i in range(v)]

dist=[0 for i in range(v)];

if (BFS(adj, s, dest, v, pred, dist) == False):

print("Given source and destination are not connected")

path = []

crawl = dest;

path.append(crawl);

while (pred[crawl] != -1):

path.append(pred[crawl]);

crawl = pred[crawl];

print("Shortest path length is : " + str(dist[dest]), end = '')

print("nPath is : : ")

for i in range(len(path)-1, -1, -1):

print(path[i], end=' ')

if __name__=='__main__':

v = 8;

adj = [[] for i in range(v)];

add_edge(adj, 0, 1);

add_edge(adj, 0, 3);

add_edge(adj, 1, 2);

add_edge(adj, 3, 4);

add_edge(adj, 3, 7);

add_edge(adj, 4, 5);

add_edge(adj, 4, 6);

add_edge(adj, 4, 7);

add_edge(adj, 5, 6);

add_edge(adj, 6, 7);

source = 0

dest = 7;

printShortestDistance(adj, source, dest, v);

C#

using System;

using System.Collections.Generic;

class pathUnweighted{

public static void Main(String []args)

{

int v = 8;

List<List<int>> adj =

new List<List<int>>(v);

for (int i = 0; i < v; i++)

{

adj.Add(new List<int>());

}

addEdge(adj, 0, 1);

addEdge(adj, 0, 3);

addEdge(adj, 1, 2);

addEdge(adj, 3, 4);

addEdge(adj, 3, 7);

addEdge(adj, 4, 5);

addEdge(adj, 4, 6);

addEdge(adj, 4, 7);

addEdge(adj, 5, 6);

addEdge(adj, 6, 7);

int source = 0, dest = 7;

printShortestDistance(adj, source,

dest, v);

}

private static void addEdge(List<List<int>> adj,

int i, int j)

{

adj[i].Add(j);

adj[j].Add(i);

}

private static void printShortestDistance(List<List<int>> adj,

int s, int dest, int v)

{

int []pred = new int[v];

int []dist = new int[v];

if (BFS(adj, s, dest,

v, pred, dist) == false)

{

Console.WriteLine("Given source and destination" +

"are not connected");

return;

}

List<int> path = new List<int>();

int crawl = dest;

path.Add(crawl);

while (pred[crawl] != -1)

{

path.Add(pred[crawl]);

crawl = pred[crawl];

}

Console.WriteLine("Shortest path length is: " +

dist[dest]);

Console.WriteLine("Path is ::");

for (int i = path.Count - 1;

i >= 0; i--)

{

Console.Write(path[i] + " ");

}

private static bool BFS(List<List<int>> adj,

int src, int dest,

int v, int []pred,

int []dist)

{

List<int> queue = new List<int>();

bool []visited = new bool[v];

for (int i = 0; i < v; i++)

{

visited[i] = false;

dist[i] = int.MaxValue;

pred[i] = -1;

}

visited[src] = true;

dist[src] = 0;

queue.Add(src);

while (queue.Count != 0)

{

int u = queue[0];

queue.RemoveAt(0);

for (int i = 0;

i < adj[u].Count; i++)

{

if (visited[adj[u][i]] == false)

{

visited[adj[u][i]] = true;

dist[adj[u][i]] = dist[u] + 1;

pred[adj[u][i]] = u;

queue.Add(adj[u][i]);

if (adj[u][i] == dest)

return true;

}

return false;

}

Javascript

const max_value = 9007199254740992;

function add_edge(adj, src, dest){

adj[src].push(dest);

adj[dest].push(src);

}

function BFS(adj, src, dest, v, pred, dist)

{

let queue = [];

let visited = new Array(v);

for (let i = 0; i < v; i++) {

visited[i] = false;

dist[i] = max_value;

pred[i] = -1;

}

visited[src] = true;

dist[src] = 0;

queue.push(src);

while (queue.length > 0) {

let u = queue[0];

queue.shift();

for (let i = 0; i < adj[u].length; i++) {

if (visited[adj[u][i]] == false) {

visited[adj[u][i]] = true;

dist[adj[u][i]] = dist[u] + 1;

pred[adj[u][i]] = u;

queue.push(adj[u][i]);

if (adj[u][i] == dest)

return true;

}

return false;

}

function printShortestDistance(adj, s, dest, v)

{

let pred = new Array(v).fill(0);

let dist = new Array(v).fill(0);

if (BFS(adj, s, dest, v, pred, dist) == false) {

console.log("Given source and destination are not connected");

}

let path = new Array();

let crawl = dest;

path.push(crawl);

while (pred[crawl] != -1) {

path.push(pred[crawl]);

crawl = pred[crawl];

}

console.log("Shortest path length is : ", dist[dest]);

console.log("Path is::");

for (let i = path.length - 1; i >= 0; i--)

console.log(path[i]);

}

let v = 8;

let adj = new Array(v).fill(0);

for(let i = 0; i < v; i++){

adj[i] = new Array();

}

add_edge(adj, 0, 1);

add_edge(adj, 0, 3);

add_edge(adj, 1, 2);

add_edge(adj, 3, 4);

add_edge(adj, 3, 7);

add_edge(adj, 4, 5);

add_edge(adj, 4, 6);

add_edge(adj, 4, 7);

add_edge(adj, 5, 6);

add_edge(adj, 6, 7);

let source = 0;

let dest = 7;

printShortestDistance(adj, source, dest, v);

Output

Shortest path length is : 2
Path is::
0 3 7

Time Complexity : O(V + E)
Auxiliary Space: O(V)

Algorithm

Create a queue and add the starting vertex to it.

Create an array to keep track of the distances from the starting vertex to all other vertices. Initialize all distances to infinity except for the starting vertex, which should have a distance of 0.

While the queue is not empty, dequeue the next vertex.

For each neighbor of the dequeued vertex that has not been visited, set its distance to the distance of the dequeued vertex plus 1 and add it to the queue.

Repeat steps 3-4 until the queue is empty.

The distances array now contains the shortest path distances from the starting vertex to all other vertices.

Program

Python3

from collections import deque

def bfs_shortest_path(graph, start):

queue = deque([start])

distances = [float('inf')] * len(graph)

distances[start] = 0

visited = set()

while queue:

vertex = queue.popleft()

visited.add(vertex)

for neighbor in graph[vertex]:

if neighbor not in visited:

distances[neighbor] = distances[vertex] + 1

queue.append(neighbor)

return distances

graph = [[1, 2], [2, 3], [3], [4], []]

start_vertex = 0

distances = bfs_shortest_path(graph, start_vertex)

print(distances)

In the above example, the output [0, 1, 1, 2, 3] indicates that the shortest path from vertex 0 to vertex 1 is of length 1, the shortest path from vertex 0 to vertex 2 is also of length 1, and so on.

Time and Auxiliary space

The time complexity of the above BFS-based algorithm for finding the shortest path in an unweighted graph is O(V + E), where V is the number of vertices and E is the number of edges in the graph. This is because each vertex and edge is visited at most once during the BFS traversal.

The space complexity of the algorithm is also O(V + E), due to the use of the distances array to store the shortest distances from the starting vertex to all other vertices, and the visited set to keep track of visited vertices. The queue used for BFS traversal can also have a maximum size of O(V + E) in the worst case, which contributes to the space complexity.

Last Updated :
02 May, 2023

Like Article

Save Article

Источник

Графы. Нахождение кратчайшего расстояния между двумя вершинами с помощью алгоритма Дейкстры

Подробности: Категория: Сортировка и поиск

Алгоритм Дейкстры (англ. Dijkstra’s algorithm) — алгоритм на графах, изобретённый нидерландским учёным Эдсгером Дейкстрой в 1959 году. Находит кратчайшие пути от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса.

Лекция 2: Алгоритмы и методы сортировки. Алгоритмы нахождения кратчайшего пути в графе

Лекция 5: Поиск в графах и обход. Алгоритм Дейкстры

Алгоритмы и структуры данных, лекция 13

Рассмотрим выполнение алгоритма на примере графа, показанного на рисунке.

Пусть требуется найти кратчайшие расстояния от 1-й вершины до всех остальных.

Кружками обозначены вершины, линиями — пути между ними (рёбра графа). В кружках обозначены номера вершин, над рёбрами обозначена их «цена» — длина пути. Рядом с каждой вершиной красным обозначена метка — длина кратчайшего пути в эту вершину из вершины 1.

Первый шаг. Рассмотрим шаг алгоритма Дейкстры для нашего примера. Минимальную метку имеет вершина 1. Её соседями являются вершины 2, 3 и 6.

Первый по очереди сосед вершины 1 — вершина 2, потому что длина пути до неё минимальна. Длина пути в неё через вершину 1 равна сумме значения метки вершины 1 и длины ребра, идущего из 1-й в 2-ю, то есть 0 + 7 = 7. Это меньше текущей метки вершины 2, бесконечности, поэтому новая метка 2-й вершины равна 7.

Аналогичную операцию проделываем с двумя другими соседями 1-й вершины — 3-й и 6-й.

Все соседи вершины 1 проверены. Текущее минимальное расстояние до вершины 1 считается окончательным и пересмотру не подлежит (то, что это действительно так, впервые доказал Э. Дейкстра). Вычеркнем её из графа, чтобы отметить, что эта вершина посещена.

Второй шаг. Шаг алгоритма повторяется. Снова находим «ближайшую» из непосещённых вершин. Это вершина 2 с меткой 7.

Снова пытаемся уменьшить метки соседей выбранной вершины, пытаясь пройти в них через 2-ю вершину. Соседями вершины 2 являются вершины 1, 3 и 4.

Первый (по порядку) сосед вершины 2 — вершина 1. Но она уже посещена, поэтому с 1-й вершиной ничего не делаем.

Следующий сосед вершины 2 — вершина 3, так как имеет минимальную метку из вершин, отмеченных как не посещённые. Если идти в неё через 2, то длина такого пути будет равна 17 (7 + 10 = 17). Но текущая метка третьей вершины равна 9, а это меньше 17, поэтому метка не меняется.

Ещё один сосед вершины 2 — вершина 4. Если идти в неё через 2-ю, то длина такого пути будет равна сумме кратчайшего расстояния до 2-й вершины и расстояния между вершинами 2 и 4, то есть 22 (7 + 15 = 22). Поскольку 22< infty , устанавливаем метку вершины 4 равной 22.

Все соседи вершины 2 просмотрены, замораживаем расстояние до неё и помечаем её как посещённую.

Третий шаг. Повторяем шаг алгоритма, выбрав вершину 3. После её «обработки» получим такие результаты:

Дальнейшие шаги. Повторяем шаг алгоритма для оставшихся вершин. Это будут вершины 6, 4 и 5, соответственно порядку.

Завершение выполнения алгоритма. Алгоритм заканчивает работу, когда нельзя больше обработать ни одной вершины. В данном примере все вершины зачёркнуты, однако ошибочно полагать, что так будет в любом примере — некоторые вершины могут остаться незачёркнутыми, если до них нельзя добраться, т. е. если граф несвязный. Результат работы алгоритма виден на последнем рисунке: кратчайший путь от вершины 1 до 2-й составляет 7, до 3-й — 9, до 4-й — 20, до 5-й — 20, до 6-й — 11.

Реализация алгоритма на различных языках программирования :

C++

#include "stdafx.h"
#include <iostream>
using namespace std;
const int V=6;
//алгоритм Дейкстры
void Dijkstra(int GR[V][V], int st)
{
int distance[V], count, index, i, u, m=st+1;
bool visited[V];
for (i=0; i<V; i++)
{
distance[i]=INT_MAX; visited[i]=false;
}
distance[st]=0;
for (count=0; count<V-1; count++)
{
int min=INT_MAX;
for (i=0; i<V; i++)
if (!visited[i] && distance[i]<=min)
{
min=distance[i]; index=i;
}
u=index;
visited[u]=true;
for (i=0; i<V; i++)
if (!visited[i] && GR[u][i] && distance[u]!=INT_MAX &&
distance[u]+GR[u][i]<distance[i])
distance[i]=distance[u]+GR[u][i];
}
cout<<"Стоимость пути из начальной вершины до остальных:tn";
for (i=0; i<V; i++) if (distance[i]!=INT_MAX)
cout<<m<<" > "<<i+1<<" = "<<distance[i]<<endl;
else cout<<m<<" > "<<i+1<<" = "<<"маршрут недоступен"<<endl;
}
//главная функция
void main()
{
setlocale(LC_ALL, "Rus");
int start, GR[V][V]={
{0, 1, 4, 0, 2, 0},
{0, 0, 0, 9, 0, 0},
{4, 0, 0, 7, 0, 0},
{0, 9, 7, 0, 0, 2},
{0, 0, 0, 0, 0, 8},
{0, 0, 0, 0, 0, 0}};
cout<<"Начальная вершина >> "; cin>>start;
Dijkstra(GR, start-1);
system("pause>>void");
}

kvodo

Pascal

program DijkstraAlgorithm;
uses crt;
const V=6; inf=100000;
type vektor=array[1..V] of integer;
var start: integer;
const GR: array[1..V, 1..V] of integer=(
(0, 1, 4, 0, 2, 0),
(0, 0, 0, 9, 0, 0),
(4, 0, 0, 7, 0, 0),
(0, 9, 7, 0, 0, 2),
(0, 0, 0, 0, 0, 8),
(0, 0, 0, 0, 0, 0));
{алгоритм Дейкстры}
procedure Dijkstra(GR: array[1..V, 1..V] of integer; st: integer);
var count, index, i, u, m, min: integer;
distance: vektor;
visited: array[1..V] of boolean;
begin
m:=st;
for i:=1 to V do
begin
distance[i]:=inf; visited[i]:=false;
end;
distance[st]:=0;
for count:=1 to V-1 do
begin
min:=inf;
for i:=1 to V do
if (not visited[i]) and (distance[i]<=min) then
begin
min:=distance[i]; index:=i;
end;
u:=index;
visited[u]:=true;
for i:=1 to V do
if (not visited[i]) and (GR[u, i]<>0) and (distance[u]<>inf) and
(distance[u]+GR[u, i]<distance[i]) then
distance[i]:=distance[u]+GR[u, i];
end;
write('Стоимость пути из начальной вершины до остальных:'); writeln;
for i:=1 to V do
if distance[i]<>inf then
writeln(m,' > ', i,' = ', distance[i])
else writeln(m,' > ', i,' = ', 'маршрут недоступен');
end;
{основной блок программы}
begin
clrscr;
write('Начальная вершина >> '); read(start);
Dijkstra(GR, start);
end.

kvodo

Java

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.PrintWriter;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.StringTokenizer;

public class Solution {
   
    private static int INF = Integer.MAX_VALUE / 2;
   
    private int n; //количество вершин в орграфе
    private int m; //количествое дуг в орграфе
    private ArrayList<Integer> adj[]; //список смежности
    private ArrayList<Integer> weight[]; //вес ребра в орграфе
    private boolean used[]; //массив для хранения информации о пройденных и не пройденных вершинах
    private int dist[]; //массив для хранения расстояния от стартовой вершины
    //массив предков, необходимых для восстановления кратчайшего пути из стартовой вершины
    private int pred[];
    int start; //стартовая вершина, от которой ищется расстояние до всех других
   
    private BufferedReader cin;
    private PrintWriter cout;
    private StringTokenizer tokenizer;
   
    //процедура запуска алгоритма Дейкстры из стартовой вершины
    private void dejkstra(int s) {
        dist[s] = 0; //кратчайшее расстояние до стартовой вершины равно 0
        for (int iter = 0; iter < n; ++iter) {
            int v = -1;
            int distV = INF;
            //выбираем вершину, кратчайшее расстояние до которого еще не найдено
            for (int i = 0; i < n; ++i) {
                if (used[i]) {
                    continue;
                }
                if (distV < dist[i]) {
                    continue;
                }
                v = i;
                distV = dist[i];
            }
            //рассматриваем все дуги, исходящие из найденной вершины
            for (int i = 0; i < adj[v].size(); ++i) {
                int u = adj[v].get(i);
                int weightU = weight[v].get(i);
                //релаксация вершины
                if (dist[v] + weightU < dist[u]) {
                    dist[u] = dist[v] + weightU;
                    pred[u] = v;
                }
            }
            //помечаем вершину v просмотренной, до нее найдено кратчайшее расстояние
            used[v] = true;
        }
    }
   
    //процедура считывания входных данных с консоли
    private void readData() throws IOException {
        cin = new BufferedReader(new InputStreamReader(System.in));
        cout = new PrintWriter(System.out);
        tokenizer = new StringTokenizer(cin.readLine());
       
        n = Integer.parseInt(tokenizer.nextToken()); //считываем количество вершин графа
        m = Integer.parseInt(tokenizer.nextToken()); //считываем количество ребер графа
        start = Integer.parseInt(tokenizer.nextToken()) - 1;
       
        //инициализируем списка смежности графа размерности n
        adj = new ArrayList[n];
        for (int i = 0; i < n; ++i) {
            adj[i] = new ArrayList<Integer>();
        }
        //инициализация списка, в котором хранятся веса ребер
        weight = new ArrayList[n];
        for (int i = 0; i < n; ++i) {
            weight[i] = new ArrayList<Integer>();
        }
       
        //считываем граф, заданный списком ребер
        for (int i = 0; i < m; ++i) {
            tokenizer = new StringTokenizer(cin.readLine());
            int u = Integer.parseInt(tokenizer.nextToken());
            int v = Integer.parseInt(tokenizer.nextToken());
            int w = Integer.parseInt(tokenizer.nextToken());
            u--;
            v--;
            adj[u].add(v);
            weight[u].add(w);
        }
       
        used = new boolean[n];
        Arrays.fill(used, false);
       
        pred = new int[n];
        Arrays.fill(pred, -1);
       
        dist = new int[n];
        Arrays.fill(dist, INF);
       
    }

    //процедура восстановления кратчайшего пути по массиву предком
    void printWay(int v) {
        if (v == -1) {
            return;
        }
        printWay(pred[v]);
        cout.print((v + 1) + " ");
    }
   
    //процедура вывода данных в консоль
    private void printData() throws IOException {
        for (int v = 0; v < n; ++v) {
            if (dist[v] != INF) {
                cout.print(dist[v] + " ");
            } else {
                cout.print("-1 ");
            }
        }
        cout.println();
        for (int v = 0; v < n; ++v) {
            cout.print((v + 1) + ": ");
            if (dist[v] != INF) {
                printWay(v);
            }
            cout.println();
        }
               
        cin.close();
        cout.close();
    }
   
    private void run() throws IOException {
        readData();
        dejkstra(start);
        printData();
       
        cin.close();
        cout.close();
    }
   
    public static void main(String[] args) throws IOException {
        Solution solution = new Solution();
        solution.run();
    }
}

cybern.ru

Ещё один вариант:

 
import java.io.*;
import java.util.*;
 
public class Dijkstra {
   private static final Graph.Edge[] GRAPH = {
      new Graph.Edge("a", "b", 7),
      new Graph.Edge("a", "c", 9),
      new Graph.Edge("a", "f", 14),
      new Graph.Edge("b", "c", 10),
      new Graph.Edge("b", "d", 15),
      new Graph.Edge("c", "d", 11),
      new Graph.Edge("c", "f", 2),
      new Graph.Edge("d", "e", 6),
      new Graph.Edge("e", "f", 9),
   };
   private static final String START = "a";
   private static final String END = "e";
 
   public static void main(String[] args) {
      Graph g = new Graph(GRAPH);
      g.dijkstra(START);
      g.printPath(END);
      //g.printAllPaths();
   }
}
 
class Graph {
   private final Map<String, Vertex> graph; // mapping of vertex names to Vertex objects, built from a set of Edges
 
   /** One edge of the graph (only used by Graph constructor) */
   public static class Edge {
      public final String v1, v2;
      public final int dist;
      public Edge(String v1, String v2, int dist) {
         this.v1 = v1;
         this.v2 = v2;
         this.dist = dist;
      }
   }
 
   /** One vertex of the graph, complete with mappings to neighbouring vertices */
   public static class Vertex implements Comparable<Vertex> {
      public final String name;
      public int dist = Integer.MAX_VALUE; // MAX_VALUE assumed to be infinity
      public Vertex previous = null;
      public final Map<Vertex, Integer> neighbours = new HashMap<>();
 
      public Vertex(String name) {
         this.name = name;
      }
 
      private void printPath() {
         if (this == this.previous) {
            System.out.printf("%s", this.name);
         } else if (this.previous == null) {
            System.out.printf("%s(unreached)", this.name);
         } else {
            this.previous.printPath();
            System.out.printf(" -> %s(%d)", this.name, this.dist);
         }
      }
 
      public int compareTo(Vertex other) {
         return Integer.compare(dist, other.dist);
      }
   }
 
   /** Builds a graph from a set of edges */
   public Graph(Edge[] edges) {
      graph = new HashMap<>(edges.length);
 
      //one pass to find all vertices
      for (Edge e : edges) {
         if (!graph.containsKey(e.v1)) graph.put(e.v1, new Vertex(e.v1));
         if (!graph.containsKey(e.v2)) graph.put(e.v2, new Vertex(e.v2));
      }
 
      //another pass to set neighbouring vertices
      for (Edge e : edges) {
         graph.get(e.v1).neighbours.put(graph.get(e.v2), e.dist);
         //graph.get(e.v2).neighbours.put(graph.get(e.v1), e.dist); // also do this for an undirected graph
      }
   }
 
   /** Runs dijkstra using a specified source vertex */ 
   public void dijkstra(String startName) {
      if (!graph.containsKey(startName)) {
         System.err.printf("Graph doesn't contain start vertex "%s"n", startName);
         return;
      }
      final Vertex source = graph.get(startName);
      NavigableSet<Vertex> q = new TreeSet<>();
 
      // set-up vertices
      for (Vertex v : graph.values()) {
         v.previous = v == source ? source : null;
         v.dist = v == source ? 0 : Integer.MAX_VALUE;
         q.add(v);
      }
 
      dijkstra(q);
   }
 
   /** Implementation of dijkstra's algorithm using a binary heap. */
   private void dijkstra(final NavigableSet<Vertex> q) {      
      Vertex u, v;
      while (!q.isEmpty()) {
 
         u = q.pollFirst(); // vertex with shortest distance (first iteration will return source)
         if (u.dist == Integer.MAX_VALUE) break; // we can ignore u (and any other remaining vertices) since they are unreachable
 
         //look at distances to each neighbour
         for (Map.Entry<Vertex, Integer> a : u.neighbours.entrySet()) {
            v = a.getKey(); //the neighbour in this iteration
 
            final int alternateDist = u.dist + a.getValue();
            if (alternateDist < v.dist) { // shorter path to neighbour found
               q.remove(v);
               v.dist = alternateDist;
               v.previous = u;
               q.add(v);
            } 
         }
      }
   }
 
   /** Prints a path from the source to the specified vertex */
   public void printPath(String endName) {
      if (!graph.containsKey(endName)) {
         System.err.printf("Graph doesn't contain end vertex "%s"n", endName);
         return;
      }
 
      graph.get(endName).printPath();
      System.out.println();
   }
   /** Prints the path from the source to every vertex (output order is not guaranteed) */
   public void printAllPaths() {
      for (Vertex v : graph.values()) {
         v.printPath();
         System.out.println();
      }
   }
}

rosettacode.org

C

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
 
//#define BIG_EXAMPLE
 
typedef struct node_t node_t, *heap_t;
typedef struct edge_t edge_t;
struct edge_t {
	node_t *nd;	/* target of this edge */
	edge_t *sibling;/* for singly linked list */
	int len;	/* edge cost */
};
struct node_t {
	edge_t *edge;	/* singly linked list of edges */
	node_t *via;	/* where previous node is in shortest path */
	double dist;	/* distance from origining node */
	char name[8];	/* the, er, name */
	int heap_idx;	/* link to heap position for updating distance */
};
 
 
/* --- edge management --- */
#ifdef BIG_EXAMPLE
#	define BLOCK_SIZE (1024 * 32 - 1)
#else
#	define BLOCK_SIZE 15
#endif
edge_t *edge_root = 0, *e_next = 0;
 
/* Don't mind the memory management stuff, they are besides the point.
   Pretend e_next = malloc(sizeof(edge_t)) */
void add_edge(node_t *a, node_t *b, double d)
{
	if (e_next == edge_root) {
		edge_root = malloc(sizeof(edge_t) * (BLOCK_SIZE + 1));
		edge_root[BLOCK_SIZE].sibling = e_next;
		e_next = edge_root + BLOCK_SIZE;
	}
	--e_next;
 
	e_next->nd = b;
	e_next->len = d;
	e_next->sibling = a->edge;
	a->edge = e_next;
}
 
void free_edges()
{
	for (; edge_root; edge_root = e_next) {
		e_next = edge_root[BLOCK_SIZE].sibling;
		free(edge_root);
	}
}
 
/* --- priority queue stuff --- */
heap_t *heap;
int heap_len;
 
void set_dist(node_t *nd, node_t *via, double d)
{
	int i, j;
 
	/* already knew better path */
	if (nd->via && d >= nd->dist) return;
 
	/* find existing heap entry, or create a new one */
	nd->dist = d;
	nd->via = via;
 
	i = nd->heap_idx;
	if (!i) i = ++heap_len;
 
	/* upheap */
	for (; i > 1 && nd->dist < heap[j = i/2]->dist; i = j)
		(heap[i] = heap[j])->heap_idx = i;
 
	heap[i] = nd;
	nd->heap_idx = i;
}
 
node_t * pop_queue()
{
	node_t *nd, *tmp;
	int i, j;
 
	if (!heap_len) return 0;
 
	/* remove leading element, pull tail element there and downheap */
	nd = heap[1];
	tmp = heap[heap_len--];
 
	for (i = 1; i < heap_len && (j = i * 2) <= heap_len; i = j) {
		if (j < heap_len && heap[j]->dist > heap[j+1]->dist) j++;
 
		if (heap[j]->dist >= tmp->dist) break;
		(heap[i] = heap[j])->heap_idx = i;
	}
 
	heap[i] = tmp;
	tmp->heap_idx = i;
 
	return nd;
}
 
/* --- Dijkstra stuff; unreachable nodes will never make into the queue --- */
void calc_all(node_t *start)
{
	node_t *lead;
	edge_t *e;
 
	set_dist(start, start, 0);
	while ((lead = pop_queue()))
		for (e = lead->edge; e; e = e->sibling)
			set_dist(e->nd, lead, lead->dist + e->len);
}
 
void show_path(node_t *nd)
{
	if (nd->via == nd)
		printf("%s", nd->name);
	else if (!nd->via)
		printf("%s(unreached)", nd->name);
	else {
		show_path(nd->via);
		printf("-> %s(%g) ", nd->name, nd->dist);
	}
}
 
int main(void)
{
#ifndef BIG_EXAMPLE
	int i;
 
#	define N_NODES ('f' - 'a' + 1)
	node_t *nodes = calloc(sizeof(node_t), N_NODES);
 
	for (i = 0; i < N_NODES; i++)
		sprintf(nodes[i].name, "%c", 'a' + i);
 
#	define E(a, b, c) add_edge(nodes + (a - 'a'), nodes + (b - 'a'), c)
	E('a', 'b', 7);	E('a', 'c', 9); E('a', 'f', 14);
	E('b', 'c', 10);E('b', 'd', 15);E('c', 'd', 11);
	E('c', 'f', 2); E('d', 'e', 6);	E('e', 'f', 9);
#	undef E
 
#else /* BIG_EXAMPLE */
	int i, j, c;
 
#	define N_NODES 4000
	node_t *nodes = calloc(sizeof(node_t), N_NODES);
 
	for (i = 0; i < N_NODES; i++)
		sprintf(nodes[i].name, "%d", i + 1);
 
	/* given any pair of nodes, there's about 50% chance they are not
	   connected; if connected, the cost is randomly chosen between 0
	   and 49 (inclusive! see output for consequences) */
	for (i = 0; i < N_NODES; i++) {
		for (j = 0; j < N_NODES; j++) {
			/* majority of runtime is actually spent here */
			if (i == j) continue;
			c = rand() % 100;
			if (c < 50) continue;
			add_edge(nodes + i, nodes + j, c - 50);
		}
	}
 
#endif
	heap = calloc(sizeof(heap_t), N_NODES + 1);
	heap_len = 0;
 
	calc_all(nodes);
	for (i = 0; i < N_NODES; i++) {
		show_path(nodes + i);
		putchar('n');
	}
 
#if 0
	/* real programmers don't free memories (they use Fortran) */
	free_edges();
	free(heap);
	free(nodes);
#endif
	return 0;
}

rosettacode.org

PHP

<?php
function dijkstra($graph_array, $source, $target) {
    $vertices = array();
    $neighbours = array();
    foreach ($graph_array as $edge) {
        array_push($vertices, $edge[0], $edge[1]);
        $neighbours[$edge[0]][] = array("end" => $edge[1], "cost" => $edge[2]);
        $neighbours[$edge[1]][] = array("end" => $edge[0], "cost" => $edge[2]);
    }
    $vertices = array_unique($vertices);
 
    foreach ($vertices as $vertex) {
        $dist[$vertex] = INF;
        $previous[$vertex] = NULL;
    }
 
    $dist[$source] = 0;
    $Q = $vertices;
    while (count($Q) > 0) {
 
        // TODO - Find faster way to get minimum
        $min = INF;
        foreach ($Q as $vertex){
            if ($dist[$vertex] < $min) {
                $min = $dist[$vertex];
                $u = $vertex;
            }
        }
 
        $Q = array_diff($Q, array($u));
        if ($dist[$u] == INF or $u == $target) {
            break;
        }
 
        if (isset($neighbours[$u])) {
            foreach ($neighbours[$u] as $arr) {
                $alt = $dist[$u] + $arr["cost"];
                if ($alt < $dist[$arr["end"]]) {
                    $dist[$arr["end"]] = $alt;
                    $previous[$arr["end"]] = $u;
                }
            }
        }
    }
    $path = array();
    $u = $target;
    while (isset($previous[$u])) {
        array_unshift($path, $u);
        $u = $previous[$u];
    }
    array_unshift($path, $u);
    return $path;
}
 
$graph_array = array(
                    array("a", "b", 7),
                    array("a", "c", 9),
                    array("a", "f", 14),
                    array("b", "c", 10),
                    array("b", "d", 15),
                    array("c", "d", 11),
                    array("c", "f", 2),
                    array("d", "e", 6),
                    array("e", "f", 9)
               );
 
$path = dijkstra($graph_array, "a", "e");
 
echo "path is: ".implode(", ", $path)."n";

Output is:

path is: a, c, f, e

rosettacode.org

Python

from collections import namedtuple, queue
from pprint import pprint as pp
 
 
inf = float('inf')
Edge = namedtuple('Edge', 'start, end, cost')
 
class Graph():
    def __init__(self, edges):
        self.edges = edges2 = [Edge(*edge) for edge in edges]
        self.vertices = set(sum(([e.start, e.end] for e in edges2), []))
 
    def dijkstra(self, source, dest):
        assert source in self.vertices
        dist = {vertex: inf for vertex in self.vertices}
        previous = {vertex: None for vertex in self.vertices}
        dist[source] = 0
        q = self.vertices.copy()
        neighbours = {vertex: set() for vertex in self.vertices}
        for start, end, cost in self.edges:
            neighbours[start].add((end, cost))
        #pp(neighbours)
 
        while q:
            u = min(q, key=lambda vertex: dist[vertex])
            q.remove(u)
            if dist[u] == inf or u == dest:
                break
            for v, cost in neighbours[u]:
                alt = dist[u] + cost
                if alt < dist[v]:                                  # Relax (u,v,a)
                    dist[v] = alt
                    previous[v] = u
        #pp(previous)
        s, u = deque(), dest
        while previous[u]:
            s.pushleft(u)
            u = previous[u]
        s.pushleft(u)
        return s
 
 
graph = Graph([("a", "b", 7),  ("a", "c", 9),  ("a", "f", 14), ("b", "c", 10),
               ("b", "d", 15), ("c", "d", 11), ("c", "f", 2),  ("d", "e", 6),
               ("e", "f", 9)])
pp(graph.dijkstra("a", "e"))

Output:

['a', 'c', 'd', 'e']

rosettacode.org

Источник

Алгоритм Дейкстры – не единственный ваш выбор. Найдите самый простой алгоритм для каждой ситуации

Когда дело доходит до поиска кратчайшего пути на графе, большинство людей думают об алгоритме Дейкстры (также называемом алгоритмом Дейкстры сначала кратчайшим путем). Хотя алгоритм Дейкстры действительно очень полезен, существуют более простые подходы, которые можно использовать на основе свойств графа. Это может быть очень удобно в соревнованиях по программированию или собеседованиях по программированию, когда вас могут заставить вручную написать алгоритм кратчайшего пути. Вам нужен максимально простой подход, чтобы уменьшить вероятность ошибок в вашем коде.

Обратите внимание, что эта статья также доступна как интерактивный CodePled.

Если вы не знакомы с графиками или поиском в глубину (DFS) и поиском в ширину (BFS), я рекомендую прочитать эту статью.

Для следующих алгоритмов мы будем предполагать, что графы хранятся в списке смежности следующего вида:

Это HashMap HashSets, в которой хранятся соседние узлы для каждого узла.

Кроме того, каждый алгоритм будет возвращать кратчайшее расстояние между двумя узлами, а также карту, которую мы называем previous. Эта карта содержит предшественника каждого узла кратчайшего пути. С помощью этого сопоставления мы можем распечатать узлы на кратчайшем пути следующим образом:

1. Поиск в глубину (DFS)

Это, вероятно, самый простой алгоритм получения кратчайшего пути. Однако есть и недостатки. Ваш граф должен быть деревом или многодеревом. Если это условие выполнено, вы можете использовать слегка измененную DFS, чтобы найти кратчайший путь:

Если не существует пути между startNode и stopNode, кратчайший путь будет иметь длину -1. Мы инициализируем кратчайший путь этим значением и запускаем рекурсивную DFS. Этот рекурсивный DFS немного изменен в том смысле, что он будет отслеживать глубину поиска и останавливаться, как только он достигнет stopNode. Текущая глубина, когда она достигает stopNode, является нашей кратчайшей длиной пути.

Причина, по которой мы не можем использовать его для циклических графов, заключается в том, что всякий раз, когда мы находим путь, мы не можем быть уверены, что это кратчайший путь. DFS не дает такой гарантии.

Представление

Пусть n будет количеством узлов, а e будет количеством ребер в нашем графе. Тогда этот алгоритм имеет временную сложность O (n). Из-за своей рекурсивной природы он использует стек вызовов и, следовательно, имеет асимптотическое потребление памяти O (n).

Почему не O (n + e) ? Ну, это потому, что мы предположили, что наш график был ацикличным. Это означает, что e ≤ n-1 и, следовательно, O (n + e) = O (n).

2. Поиск в ширину (BFS)

Слегка модифицированный BFS – очень полезный алгоритм для поиска кратчайшего пути. Это просто и применимо к всем графам без весов ребер:

Это простая реализация BFS, которая отличается лишь несколькими деталями. С каждым узлом, который сохраняется в очереди, мы дополнительно сохраняем расстояние до startNode. Когда мы достигаем stopNode, мы просто возвращаем расстояние, которое было сохранено вместе с ним.

Это работает из-за природы BFS: к соседу не обращаются до тех пор, пока не будут посещены все прямые соседи. Как следствие, все узлы на расстоянии x от startNode посещаются после посещения всех узлов на расстоянии ‹x. BFS сначала посетит узлы с расстоянием 0, затем все узлы с расстоянием 1 и так далее. Это свойство является причиной того, что мы можем использовать BFS для поиска кратчайшего пути даже в циклических графах.

Представление

Пусть g описывает наибольшее количество смежных узлов для любого узла нашего графа. Кроме того, пусть d будет длиной кратчайшего пути между startNode и stopNode . Тогда этот алгоритм будет иметь временную сложность O (gᵈ).

Это почему? BFS ищет график на так называемых уровнях. Каждый узел уровня имеет одинаковое расстояние до начального узла. Требуется O (g) шагов, чтобы достичь уровня 1, O (g²) шагов, чтобы достичь уровня 2, и так далее. Следовательно, для достижения уровня d требуется O (gᵈ) шагов. Снова используя переменные n и e, время выполнения остается O (n + e) . Однако O (gᵈ) является более точным выражением при поиске кратчайшего пути.

В некоторых графах очередь может содержать все свои узлы. Следовательно, он также имеет пространственную сложность O (n).

Небольшое замечание: фактическое время выполнения вышеупомянутой реализации хуже, чем O (n + e) . Причина в том, что в качестве очереди используется массив JavaScript. Операция сдвига занимает O (с) времени, где с – размер очереди. Однако можно реализовать очередь в JavaScript, которая позволяет выполнять операции enqueue и dequeue в O (1), как описано в моей предыдущей части.

3. Двунаправленный поиск

Наш третий метод поиска кратчайшего пути – это двунаправленный поиск. Как и BFS, он применим к неориентированным графам без весов ребер. Для выполнения двунаправленного поиска мы в основном запускаем одну BFS с node1 и одну с node2 одновременно. Когда встречаются оба BFS, мы нашли кратчайший путь.

Это не самый короткий алгоритм, но его все же просто и легко написать с нуля, если вы знаете BFS. Но в чем преимущество простого BFS, который намного короче? Ответ – производительность. Если BFS позволяет нам найти путь длиной l за разумное время, двунаправленный поиск позволит нам найти путь длиной 2l.

Подробнее о производительности: двунаправленный поиск заканчивается после уровней d / 2, потому что это центр пути. Оба одновременных BFS посещают каждый узел g ^ (d / 2), что в сумме составляет 2g ^ (d / 2). Это приводит к O (g ^ (d / 2)) и, следовательно, делает двунаправленный поиск быстрее, чем BFS, в g ^ (d / 2 )!

4. Алгоритм Дейкстры.

Этот алгоритм может быть самым известным для поиска кратчайшего пути. Его преимущество перед DFS, BFS и двунаправленным поиском заключается в том, что вы можете использовать его во всех графах с положительными весами ребер. Не пытайтесь использовать его для графов с отрицательными весами ребер, потому что в этом случае завершение работы не гарантируется.

Ускоренный курс: приоритетные очереди

Чтобы понять алгоритм Дейкстры, важно понимать очереди с приоритетами. Очередь с приоритетом – это абстрактная структура данных, которая позволяет выполнять следующие операции:

isEmpty: проверяет, содержит ли очередь приоритетов какие-либо элементы
insert: вставляет элемент вместе со значением приоритета
extractHighestPriority: возвращает элемент с наивысшим приоритетом и удаляет его из очереди приоритетов

Что значит приоритет? Математически приоритет должен позволять определять частичный порядок элементов очереди приоритетов. В большинстве случаев это простое целое число p, а элемент с наивысшим приоритетом – это элемент с наименьшим (или наибольшим) значением для p. В нашем случае нам нужна приоритетная очередь для хранения всех узлов в графе вместе с их расстоянием до нашего начального узла. Таким образом, наша extractHighestPriority операция будет называться extractMin, , что является более описательным именем для получения узла с минимальным расстоянием до начального узла.

Как работает алгоритм Дейкстры?

Прежде чем мы рассмотрим код, позвольте мне вкратце описать алгоритм, чтобы вы поняли, как он работает.

Мы начинаем с инициализации кратчайшего пути от нашего начального узла до всех остальных узлов нашего графа. Первоначально это будет бесконечность для каждого узла, кроме самого начального. Начальный узел будет инициализирован значением 0, потому что это расстояние до него самого. Мы вставляем все узлы в нашу приоритетную очередь вместе с их ранее инициализированным расстоянием до нашего начального узла в качестве приоритета.

Теперь начинается собственно работа. Пока очередь приоритетов не станет пустой, мы извлекаем узел с текущим кратчайшим известным расстоянием до нашего начального узла. Назовем это currentNode. Затем мы перебираем в цикле всех соседей currentNode и для каждого из них проверяем, является ли достижение его через currentNode короче известного на данный момент кратчайшего пути к этому соседу. Если это так, мы обновляем кратчайшее расстояние до соседа и продолжаем. Но убедитесь сами:

Мы дали функцию обратного вызова приоритетной очереди, которая имеет доступ к нашей distances карте. Это используется в реализации приоритетной очереди для получения минимального расстояния. Однако реализация очереди с приоритетами не должна обсуждаться в этой статье.

Представление

Временная сложность этого алгоритма сильно зависит от реализации очереди приоритетов. Пусть n – количество узлов, а e – количество ребер в графе. Если он реализован с помощью простого массива, алгоритм Дейкстры будет работать за O (n²). Однако более распространенная реализация использует кучу Фибоначчи в качестве очереди с приоритетом. В этом случае время выполнения находится в пределах O (e + n log (n)).

5. Алгоритм Беллмана-Форда.

Последний алгоритм, который я представляю в этой истории, – это алгоритм Беллмана-Форда. В отличие от алгоритма Дейкстры, он может работать с отрицательными весами ребер. Есть только одно ограничение: график не должен содержать отрицательных циклов. Отрицательный цикл – это цикл, сумма граней которого равна отрицательному значению. Однако алгоритм способен обнаруживать отрицательные циклы и, следовательно, завершать работу, хотя и без кратчайшего пути.

Алгоритм очень похож на алгоритм Дейкстры, но не использует очередь с приоритетами. Вместо этого он многократно проходит по всем ребрам, обновляя расстояния до начального узла аналогично алгоритму Дейкстры. Пусть n снова будет количеством узлов в нашем графе. Алгоритм Беллмана-Форда проходит ровно n-1 раз по всем ребрам, потому что путь без циклов в графе никогда не может содержать больше ребер, чем n-1.

После многократного обхода всех ребер алгоритм снова перебирает все ребра. Если одно из расстояний все еще не оптимально, это означает, что на графике должен быть отрицательный цикл.

Представление

За способность справляться с отрицательными краевыми весами приходится расплачиваться. Сложность выполнения алгоритма Беллмана-Форда составляет O (n * e). Следовательно, вы должны использовать его только в том случае, если у вас действительно отрицательные веса ребер.

Заключение

Мы проверили некоторые из наиболее важных алгоритмов для получения кратчайшего пути в графе, а также их преимущества и недостатки. Давайте посмотрим на обзор, который поможет вам решить, какой алгоритм использовать в какой ситуации:

Как видите, какой алгоритм использовать, зависит от нескольких свойств графика, а также от времени выполнения алгоритма. Однако еще одним важным фактором является время реализации. Если вы участвуете в конкурсе или собеседовании по кодированию, скорость внедрения имеет значение. В этом случае вы можете захотеть найти компромисс между скоростью реализации и сложностью выполнения. Все эти наблюдения приводят к следующим вопросам:

Есть ли в графе отрицательные веса ребер?
Есть ли в графе положительные веса ребер ›1?
Есть ли в графе неориентированные циклы?
Скорость реализации важнее времени выполнения?

Основываясь на этих вопросах, вы можете определить правильный алгоритм для использования. Вот полезное дерево решений:

Обратите внимание, что эта часть не охватывает все существующие алгоритмы поиска кратчайшего пути на графе. Он дает обзор наиболее важных из них, а также рекомендации по лучшим из этих алгоритмов для вашей ситуации.

Я надеюсь, что смогу дать вам более глубокое понимание этого ландшафта, чтобы вы могли с умом выбрать алгоритм в следующий раз, когда он вам понадобится.

использованная литература

Структуры данных в JavaScript: графики
Дерево (теория графов)
Политри

Источник

Базовые алгоритмы нахождения кратчайших путей во взвешенных графах

Алгоритм Флойда-Уоршелла

Алгоритм Форда-Беллмана

Алгоритм Дейкстры

Алгоритм Дейкстры для разреженных графов

Определение[править | править код]

Задача о кратчайшем пути с учётом дополнительных ограничений[править | править код]

Алгоритмы[править | править код]

Задача поиска кратчайшего пути из одной вершины во все остальные[править | править код]

Невзвешенный ориентированный граф[править | править код]

Ориентированный граф с неотрицательными весами[править | править код]

Ориентированный граф с произвольными весами[править | править код]

Задача о кратчайшем пути между всеми парами вершин[править | править код]

Применение[править | править код]

Картографические сервисы[править | править код]

Недетерминированная машина[править | править код]

Сети дорог[править | править код]

Похожие задачи[править | править код]

Постановка задачи линейного программирования[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

C++

Java

Python3

C#

Javascript

Algorithm

Program

Python3

Time and Auxiliary space

Графы. Нахождение кратчайшего расстояния между двумя вершинами с помощью алгоритма Дейкстры

C++

Pascal

Java

C

PHP

Python

Алгоритм Дейкстры – не единственный ваш выбор. Найдите самый простой алгоритм для каждой ситуации

1. Поиск в глубину (DFS)

Представление

2. Поиск в ширину (BFS)

Представление

3. Двунаправленный поиск

4. Алгоритм Дейкстры.

Ускоренный курс: приоритетные очереди

Как работает алгоритм Дейкстры?

Представление

5. Алгоритм Беллмана-Форда.

Представление

Заключение

использованная литература

Вам также может понравиться

Индийские фильмы как найти фильм по описанию

Как найти свою сестру в роблоксе

Как найти аватарку на телефоне

Добавить комментарий Отменить ответ