Ковариационная и корреляционная матрицы случайного вектора
В случае многомерной случайной величины (случайного вектора) характеристикой разброса ее составляющих и связей между ними является ковариационная матрица.
Ковариационная матрица определяется как математическое ожидание произведения центрированного случайного вектора на тот же, но транспонированный вектор:
где
Ковариационная матрица имеет вид
где по диагонали стоят дисперсии координат случайного вектора on=DXi, o22=DX2, окк = DXk, а остальные элементы представляют собой ковариации между координатами
Ковариационная матрица является симметрической матрицей, т.е.
Для примера рассмотрим ковариационную матрицу двумерного вектора
Аналогично получается ковариационная матрица для любого /^-мерного вектора.
Дисперсии координат можно представить в виде
где Gi,C2. 0? — средние квадратичные отклонения координат случайного вектора.
Коэффициентом корреляции называется, как известно, отношение ковариации к произведению средних квадратичных отклонений:
После нормирования по последнему соотношению членов ковариационной матрицы получают корреляционную матрицу
которая является симметрической и неотрицательно определенной.
Многомерным аналогом дисперсии случайной величины является обобщенная дисперсия, под которой понимается величина определителя ковариационной матрицы
Другой общей характеристикой степени разброса многомерной случайной величины является след ковариационной матрицы
где т — вектор-столбец математических ожиданий;
|Х| — определитель ковариационной матрицы X;
? -1 — обратная ковариационная матрица.
Матрица X -1 , обратная к матрице X размерности пх п, может быть получена различными способами. Одним из них является метод Жордана—Гаусса. В этом случае составляется матричное уравнение
где х — вектор-столбец переменных, число которых равно я; b — я-мерный вектор-столбец правых частей.
Умножим слева уравнение (6.21) на обратную матрицу ХГ 1 :
Так как произведение обратной матрицы на данную дает единичную матрицу Е, то
Если вместо b взять единичный вектор
то произведение X -1 -ех дает первый столбец обратной матрицы. Если же взять второй единичный вектор
то произведение Е 1 е2 дает первый столбец обратной матрицы и т.д. Таким образом, последовательно решая уравнения
методом Жордана—Гаусса, получаем все столбцы обратной матрицы.
Другой метод получения матрицы, обратной к матрице Е, связан с вычислением алгебраических дополнений AtJ.= (/= 1, 2. п; j = 1, 2, . п) к элементам данной матрицы Е, подстановкой их вместо элементов матрицы Е и транспортированием такой матрицы:
Обратная матрица получается после деления элементов В на определитель матрицы Е:
Важной особенностью получения обратной матрицы в данном случае является то, что ковариационная матрица Е является слабо обусловленной. Это приводит к тому, что при обращении таких матриц могут возникать достаточно серьезные ошибки. Все это требует обеспечения необходимой точности вычислительного процесса или использования специальных методов при вычислении таких матриц.
Пример. Написать выражение плотности вероятности для нормально распределенной двумерной случайной величины v Х2)
при условии, что математические ожидания, дисперсии и ковариации этих величин имеют следующие значения:
Решение. Обратную ковариационную матрицу для матрицы (6.19) можно получить, используя следующее выражение обратной матрицы к матрице X:
где А — определитель матрицы X.
Аи, Л12, А21, А22 — алгебраические дополнения к соответствующим элементам матрицы X.
Тогда для матрицы ]г- ! получаем выражение
Так как а12 = 01О2Р и °2i =a 2 a iP> а a i2 a 2i = cyfст|р, то Значит,
Функция плотности вероятности запишется в виде
Подставив исходные данные, получим следующее выражение для функции плотности вероятности
Корреляция, ковариация и девиация (часть 3)
В первой части показано, как на основе матрицы расстояний между элементами получить матрицу Грина. Ее спектр образует собственную систему координат множества, центром которой является центроид набора. Во второй рассмотрены спектры простых геометрических наборов.
В данной статье покажем, что матрица Грина и матрица корреляции — суть одно и то же.
7. Векторизация и нормирование одномерных координат
Пусть значения некой характеристики элементов заданы рядом чисел . Для того, чтобы данный набор можно было сравнивать с другими характеристиками, необходимо его векторизовать и обезразмерить (нормировать).
Для векторизации находим центр (среднее) значений
и строим новый набор как разность между исходными числами и их центроидом (средним):
Получили вектор. Основной признак векторов состоит в том, что сумма их координат равна нулю. Далее нормируем вектор, — приведем сумму квадратов его координат к 1. Для выполнения данной операции нам нужно вычислить эту сумму (точнее среднее):
Теперь можно построить ССК исходного набора как совокупность собственного числа S и нормированных координат вектора:
Квадраты расстояний между точками исходного набора определяются как разности квадратов компонент собственного вектора, умноженные на собственное число. Обратим внимание на то, что собственное число S оказалось равно дисперсии исходного набора (7.3).
Итак, для любого набора чисел можно определить собственную систему координат, то есть выделить значение собственного числа (она же дисперсия) и рассчитать координаты собственного вектора путем векторизации и нормирования исходного набора чисел. Круто.
Упражнение для тех, кто любит «щупать руками». Построить ССК для набора <1, 2, 3, 4>.
8. Векторизация и ортонормирование многомерных координат
Что, если вместо набора чисел нам задан набор векторов — пар, троек и прочих размерностей чисел. То есть точка (узел) задается не одной координатой, а несколькими. Как в этом случае построить ССК? Стандартный путь следующий.
Введем обозначение характеристик (компонент) набора. Нам заданы точки (элементы) и каждой точке соответствует числовое значение характеристики . Обращаем внимание, что второй индекс — это номер характеристики (столбцы матрицы), а первый индекс — номер точки (элемента) набора (строки матрицы).
Далее векторизуем характеристики. То есть для каждой находим центроид (среднее значение) и вычитаем его из значения характеристики:
Получили матрицу координат векторов (МКВ) .
Следующим шагом как будто бы надо вычислить дисперсию для каждой характеристики и их нормировать. Но хотя таким образом мы действительно получим нормированные векторы, нам-то нужно, чтобы эти векторы были независимыми, то есть ортонормированными. Операция нормирования не поворачивает вектора (а лишь меняет их длину), а нам нужно развернуть векторы перпендикулярно друг другу. Как это сделать?
Правильный (но пока бесполезный) ответ — рассчитать собственные вектора и числа (спектр). Бесполезный потому, что мы не построили матрицу, для которой можно считать спектр. Наша матрица координат векторов (МКВ) не является квадратной — для нее собственные числа не рассчитаешь. Соответственно, надо на основе МКВ построить некую квадратную матрицу. Это можно сделать умножением МКВ на саму себя (возвести в квадрат).
Но тут — внимание! Неквадратную матрицу можно возвести в квадрат двумя способами — умножением исходной на транспонированную. И наоборот — умножением транспонированной на исходную. Размерность и смысл двух полученных матриц — разный.
Умножая МКВ на транспонированную, мы получаем матрицу корреляции:
Из данного определения (есть и другие) следует, что элементы матрицы корреляции являются скалярными произведениями векторов (грамиан на векторах). Значения главной диагонали отражают квадрат длины данных векторов. Значения матрицы не нормированы (обычно их нормируют, но для наших целей этого не нужно). Размерность матрицы корреляции совпадает с количеством исходных точек (векторов).
Теперь переставим перемножаемые в (8.1) матрицы местами и получим матрицу ковариации (опять же опускаем множитель 1/(1-n), которым обычно нормируют значения ковариации):
Здесь результат выражен в характеристиках. Соответственно, размерность матрицы ковариации равна количеству исходных характеристик (компонент). Для двух характеристик матрица ковариации имеет размерность 2×2, для трех — 3×3 и т.д.
Почему важна размерность матриц корреляции и ковариации? Фишка в том, что поскольку матрицы корреляции и ковариации происходят из произведения одного и того же набора векторов, то они имеют один и тот же набор собственных чисел, один и тот же ранг (количество независимых размерностей) матрицы. Как правило, количество векторов (точек) намного превышает количество компонент. Поэтому о ранге матриц судят по размерности матрицы ковариации.
Диагональные элементы ковариации отражают дисперсию компонент. Как мы видели выше, дисперсия и собственные числа тесно связаны. Поэтому можно сказать, что в первом приближении собственные числа матрицы ковариации (а значит, и корреляции) равны диагональным элементам (а если межкомпонентная дисперсия отсутствует, то равны в любом приближении).
Если стоит задача найти просто спектр матриц (собственные числа), то удобнее ее решать для матрицы ковариации, поскольку, как правило, их размерность небольшая. Но если нам необходимо найти еще и собственные вектора (определить собственную систему координат) для исходного набора, то необходимо работать с матрицей корреляции, поскольку именно она отражает скалярное произведение векторов.
Отметим, что метод главных компонент как раз и состоит в расчете спектра матрицы ковариации/корреляции для заданного набора векторных данных. Найденные компоненты спектра располагаются вдоль главных осей эллипсоида данных. Из нашего рассмотрения это вытекает потому, что главные оси — это и есть те оси, дисперсия (разброс) данных по которым максимален, а значит, и максимально значение спектра.
Правда, могут быть и отрицательные дисперсии, и тогда аналогия с эллипсоидом уже не очевидна.
9. Матрица Грина — это матрица корреляции векторов
Рассмотрим теперь ситуацию, когда нам известен не набор чисел, характеризующих точки (элементы), а набор расстояний между точками (причем между всеми). Достаточно ли данной информации для определения ССК (собственной системы координат) набора?
Ответ дан в первой части — да, вполне. Здесь же мы покажем, что построенная по формуле (1.3′) матрица Грина и определенная выше матрица корреляции векторов (8.1) — это одна и та же матрица.
Как такое получилось? Сами в шоке. Чтобы в этом убедиться, надо подставить выражение для элемента матрицы квадратов расстояний
в формулу преобразования девиации:
Отметим, что среднее значение матрицы квадратов расстояний отражает дисперсию исходного набора (при условии, что расстояния в наборе — это сумма квадратов компонент):
Подставляя (9.1) и (9.3) в (9.2), после несложных сокращений приходим к выражению для матрицы корреляции (8.1):
Итак, матрица Грина и матрица корреляции векторов — суть одно и то же. Ранг матрицы корреляции совпадает с рангом матрицы ковариации (количеством характеристик — размерностью пространства). Это обстоятельство позволяет строить спектр и собственную систему координат для исходных точек на основе матрицы расстояний.
Для произвольной матрицы расстояний потенциальный ранг (количество измерений) на единицу меньше количества исходных векторов. Расчет спектра (собственной системы координат) позволяет определить основные (главные) компоненты, влияющие на расстояния между точками (векторами).
Таким образом можно строить собственные координаты элементов либо на основании их характеристик, либо на основании расстояний между ними. Например, можно определить собственные координаты городов по матрице расстояний между ними.
Найти корреляционную матрицу вектора
6.5.1 лПЧБТЙБГЙС. лПЬЖЖЙГЙЕОФ ЛПТТЕМСГЙЙ
рХУФШ ЪБДБОП ЧЕТПСФОПУФОПЕ РТПУФТБОУФЧП ( W , F, P) Й ДЧЕ УМХЮБКОЩЕ ЧЕМЙЮЙОЩ ξ Й η ОБ ОЕН.
пртедемеойе 6.5.1.1
лпчбтйбгйек ДЧХИ УМХЮБКОЩИ ЧЕМЙЮЙО ξ Й η ОБЪЩЧБЕФУС ЮЙУМП, ПРТЕДЕМСЕНПЕ РП ЖПТНХМЕ: M((ξ – Mξ)(η – Mη)).
| пвпъобюеойе: cov(ξ, η) = M((ξ – Mξ)(η – Mη)) | (6.5.1.1) |
пЮЕЧЙДОП, ЮФП cov(ξ, η) НПЦОП ОБКФЙ ФПМШЛП Ч ФПН УМХЮБЕ, ЛПЗДБ УХЭЕУФЧХАФ УППФЧЕФУФЧХАЭЙЕ НБФЕНБФЙЮЕУЛЙЕ ПЦЙДБОЙС.
ъбнеюбойе. жПТНХМБ (6.5.1.1) Ч ТБУЮЕФБИ ЙУРПМШЪХЕФУС ТЕДЛП. пРЙТБСУШ ОБ УЧПКУФЧБ НБФЕНБФЙЮЕУЛПЗП ПЦЙДБОЙС Й ДЙУРЕТУЙЙ, НПЦОП РПМХЮЙФШ ВПМЕЕ ХДПВОЩЕ ДМС ТБУЮЕФПЧ ЖПТНХМЩ.
M((ξ – Mξ)(η – Mη)) = M(ξη – ηMξ – ξMη + MξMη) =
= M(ξη) – MξMη – MξMη + MξMη = M(ξη) – MξMη. уМЕДПЧБФЕМШОП,
D(ξ + η) = Dξ + Dη + 2M(ξη) – 2MξMη = Dξ + Dη + 2cov(ξ, η) (уНПФТЙ 6.2.2).
D(ξ – η) = D(ξ + (-η)) = Dξ + D(-η) – 2M(ξ(-η)) – MξM(-η) =
= Dξ + D(-η) – 2(M(ξη) – MξMη) = Dξ + Dη – 2cov(ξ, η).
фептенб 6.5.1.1 (уЧПКУФЧБ ЛПЧБТЙБГЙЙ ДЧХИ УМХЮБКОЩИ ЧЕМЙЮЙО)
1. еУМЙ ξ Й η – ОЕЪБЧЙУЙНЩЕ УМХЮБКОЩЕ ЧЕМЙЮЙОЩ, ФП cov(ξ, η) = 0.
2. cov(ξ, η) = cov(η, ξ).
3. cov(ξ, ξ) = Dξ.
4. cov(ξ, Cη) = Ccov(ξ, η),
cov(Cξ, η) = Ccov(ξ, η), ” C п R.
5. cov(ξ1 + ξ2, η) = cov(ξ1, η) + cov(ξ2, η);
cov(ξ, η1 + η2) = cov(ξ, η1) + cov(ξ, η2).
уРТБЧЕДМЙЧПУФШ ХФЧЕТЦДЕОЙК 2-3 УМЕДХЕФ ЙЪ ЖПТНХМЩ (6.5.1.2). дМС ДПЛБЪБФЕМШУФЧБ ПУФБМШОЩИ ЧПУРПМШЪХЕНУС УППФЧЕФУФЧХАЭЙНЙ УЧПКУФЧБНЙ НБФЕНБФЙЮЕУЛПЗП ПЦЙДБОЙС.
1) cov(ξ, η) = M(ξη) – MξMη = MξMη – MξMη = 0, ФБЛ ЛБЛ ДМС ОЕЪБЧЙУЙНЩИ η, ξ M(ξη) = MξMη.
4) cov(ξ, Cη) = M(ξCη) – MξM(Cη) = CM(ξη) – CMξMη = Ccov(ξ, η).
уРТБЧЕДМЙЧПУФШ ЧФПТПК ЖПТНХМЩ НПЦОП ДПЛБЪБФШ МЙВП БОБМПЗЙЮОП, МЙВП, ЙУРПМШЪХС УЧПКУФЧП 2.
уРТБЧЕДМЙЧПУФШ ЧФПТПК ЖПТНХМЩ НПЦОП ДПЛБЪБФШ МЙВП БОБМПЗЙЮОП, МЙВП ЙУРПМШЪХС УЧПКУФЧП 2.
умедуфчйе 6.5.1.1
1. cov(ξ, C) = cov(C, ξ) = 0, ” C п R.
2. cov(ξ, Aξ + B) = cov(Aξ+B, ξ) = ADξ, ” A, B п R.
1) рПУФПСООХА у НПЦОП ТБУУНБФТЙЧБФШ ЛБЛ УМХЮБКОХА ЧЕМЙЮЙОХ η, РТЙОЙНБАЭХА ПДОП ЪОБЮЕОЙЕ у У ЧЕТПСФОПУФША 1. пЮЕЧЙДОП, ЮФП Ч ЬФПН УМХЮБЕ УМХЮБКОЩЕ ЧЕМЙЮЙОЩ ξ Й η – ОЕЪБЧЙУЙНЩЕ УМХЮБКОЩЕ ЧЕМЙЮЙОЩ Й, УМЕДПЧБФЕМШОП, cov(ξ, η) = 0.
2) cov(ξ, Aξ + B) = cov(ξ, Aξ) + cov(ξ, B) = Acov(ξ, ξ) + 0 = ADξ.
ъбнеюбойе. уМЕДХЕФ РПНОЙФШ, ЮФП ЙЪ cov(ξ, η) = 0 ОЕ УМЕДХЕФ ОЕЪБЧЙУЙНПУФЙ УМХЮБКОЩИ ЧЕМЙЮЙО ξ, η.
оБРТЙНЕТ, РХУФШ ξ – УМХЮБКОБС ЧЕМЙЮЙОБ ДЙУЛТЕФОПЗП ФЙРБ, ЙНЕАЭБС УМЕДХАЭЙК ЪБЛПО ТБУРТЕДЕМЕОЙС:
| xk | -2 | -1 | 1 | 2 |
| pk | 1/4 | 1/4 | 1/4 | 1/4 |
Mξ = (1/4)ћ(-2) + (1/4)ћ(-1) + (1/4)ћ2 + (1/4)ћ1 = 0.
тБУУНПФТЙН η = ξ 2 (η Й ξ Ч ФБЛПН УМХЮБЕ ЪБЧЙУЙНЩЕ УМХЮБКОЩЕ ЧЕМЙЮЙОЩ!) ъБЛПО ТБУРТЕДЕМЕОЙС УМХЮБКОПК ЧЕМЙЮЙОЩ η ЙНЕЕФ ЧЙД:
Mη = (1/2)ћ1 + (1/2)ћ4 = 5/2.
cov(ξ, η) = M(ξη) – MξMη = M(ξћξ 2 ) – 0ћ(5/2) = M(ξ 3 ).
уМХЮБКОБС ЧЕМЙЮЙОБ ξ 3 ЙНЕЕФ ЪБЛПО ТБУРТЕДЕМЕОЙС:
| xk | -8 | -1 | 1 | 8 |
| pk | 1/4 | 1/4 | 1/4 | 1/4 |
Mξ 3 = (1/4)ћ(-8) + (1/4)ћ(-1) + (1/4)ћ1 + (1/4)ћ8 = 0. уМЕДПЧБФЕМШОП, cov (ξ, η) = 0, Б УМХЮБКОЩЕ ЧЕМЙЮЙОЩ СЧМСАФУС ЪБЧЙУЙНЩНЙ.
пртедемеойе 6.5.1.2
лПЬЖЖЙГЙЕОФПН лпттемсгйй ДЧХИ УМХЮБКОЩИ ЧЕМЙЮЙО ξ Й η ОБЪЩЧБЕФУС ЮЙУМП, ПРТЕДЕМСЕНПЕ РП ЖПТНХМЕ:
ъбнеюбойе. пЮЕЧЙДОП, ЮФП ЛПЬЖЖЙГЙЕОФ ЛПТТЕМСГЙЙ ДЧХИ УМХЮБКОЩИ ЧЕМЙЮЙО НПЦОП ПРТЕДЕМЙФШ МЙЫШ Ч ФПН УМХЮБЕ, ЛПЗДБ УХЭЕУФЧХАФ УППФЧЕФУФЧХАЭЙЕ НБФЕНБФЙЮЕУЛЙЕ ПЦЙДБОЙС Й Dξ 0, Dη 0.
пРЙТБСУШ ОБ УЧПКУФЧБ ЛПЧБТЙБГЙЙ Й ДЙУРЕТУЙЙ (6.2.2), НПЦОП РПМХЮЙФШ ЕЭЕ ФТЙ ДПРПМОЙФЕМШОЩЕ ЖПТНХМЩ ДМС ЧЩЮЙУМЕОЙС ЛПЬЖЖЙГЙЕОФБ ЛПТТЕМСГЙЙ.
(уНПФТЙ ЖПТНХМХ 6.5.1.3). уМЕДПЧБФЕМШОП,
уПЧЕТЫЕООП БОБМПЗЙЮОП, ПРЙТБСУШ ОБ ЖПТНХМХ 6.5.1.4, НПЦОП ДПЛБЪБФШ, ЮФП:
фептенб 6.5.1.2 (уЧПКУФЧБ ЛПЬЖЖЙГЙЕОФБ ЛПТТЕМСГЙЙ)
1. еУМЙ ξ Й η – ОЕЪБЧЙУЙНЩЕ УМХЮБКОЩЕ ЧЕМЙЮЙОЩ, ФП ρ(ξ, η) = 0.
2. ρ(ξ, η) = ρ(η, ξ).
3. ρ(Cξ, η) = ρ(ξ, Cη) = signC ρ(Cξ, η), ” C п R (C 0).
4. |ρ(ξ, η)| ≤ 1.
5. |ρ(ξ, η)| = 1 щ $ A, B п R (A 0): η = Aξ + B.
уЧПКУФЧБ 1-2 УМЕДХАФ ЙЪ УЧПКУФЧ ЛПЧБТЙБГЙЙ.
4) фБЛ ЛБЛ ДЙУРЕТУЙС МАВПК УМХЮБКОПК ЧЕМЙЮЙОЩ (ЕУМЙ ПОБ УХЭЕУФЧЕФ) – ЧЕМЙЮЙОБ ОЕПФТЙГБФЕМШОБС, ФП ЙЪ ЖПТНХМ (6.5.1.7 Й 6.5.1.8) УМЕДХЕФ:
5) ( а ) (ОЕПВИПДЙНПУФШ)
Б) ρ(ξ, η) = 1 а ЙЪ ЖПТНХМЩ 6.5.1.8 УМЕДХЕФ, ЮФП .
ч ФБЛПН УМХЮБЕ, $ C п R:
фБЛЙН ПВТБЪПН, η = Aξ + B, ЗДЕ
ъБНЕФЙН, ЮФП .
В) ρ(ξ, η) = -1. тБУУХЦДБС БОБМПЗЙЮОП Й ЙУРПМШЪХС ЖПТНХМХ 6.5.1.7, НПЦОП ДПЛБЪБФШ, ЮФП
( ш ) η = Aξ + B; A, B п R Й A 0. (дПУФБФПЮОПУФШ.)
умедуфчйе 6.5.1.2
ρ(ξ, ξ) = 1.
ъбнеюбойе. уМЕДХЕФ РПНОЙФШ, ЮФП ЙЪ ρ(ξ, η) = 0 ОЕ УМЕДХЕФ ОЕЪБЧЙУЙНПУФШ УМХЮБКОЩИ ЧЕМЙЮЙО ξ Й η. (фБЛ ЛБЛ ρ(ξ, η) = 0 щ cov(ξ,η)=0; Б ЙЪ cov(ξ,η)=0 ОЕ УМЕДХЕФ, ЮФП ξ Й η ОЕЪБЧЙУЙНЩЕ УМХЮБКОЩЕ ЧЕМЙЮЙОЩ).
пртедемеойе 6.5.1.3
еУМЙ ρ(ξ, η) = 0, ФП УМХЮБКОЩЕ ЧЕМЙЮЙОЩ ξ Й η ОБЪЩЧБАФУС оелпттемйтхенщнй.
ъбнеюбойе. еУМЙ ρ(ξ, η) 0, ФП УМХЮБКОЩЕ ЧЕМЙЮЙОЩ ξ Й η СЧМСАФУС ЪБЧЙУЙНЩНЙ (РТЙ ρ(ξ, η) = 0 ПОЙ НПЗХФ ВЩФШ ЛБЛ ЪБЧЙУЙНЩНЙ, ФБЛ Й ОЕЪБЧЙУЙНЩНЙ).
еУМЙ ρ(ξ, η) 1, ФП ОБЙМХЮЫЕЕ МЙОЕКОПЕ РТЙВМЙЦЕОЙЕ ДМС η ЙНЕЕФ ЧЙД:
ьФП РТЙВМЙЦЕОЙЕ СЧМСЕФУС ОБЙМХЮЫЕН Ч УНЩУМЕ:
рХУФШ ОБ ЧЕТПСФОПУФОПН РТПУФТБОУФЧЕ ( W , F, P) ЪБДБО УМХЮБКОЩК ЧЕЛФПТ (ξ1, ξ2, . , ξn).
фБЛ ЛБЛ kij = cov(ξi, ξj) = cov(ξj, ξi) = kji, ” i, j, ФП НБФТЙГБ K – УЙННЕФТЙЮОБС НБФТЙГБ (ПФОПУЙФЕМШОП ЗМБЧОПК ДЙБЗПОБМЙ); kii = Dξi, i= 1, . , n.
пртедемеойе 6.5.1.5
пРТЕДЕМЙФЕМШ ЛПЧБТЙБГЙПООПК НБФТЙГЩ ОБЪЩЧБЕФУС пвпвэеоопк дйуретуйек УМХЮБКОПЗП ЧЕЛФПТБ.
еУМЙ ξ1, ξ2, . , ξn РПРБТОП ОЕЪБЧЙУЙНЩ ЙМЙ cov(ξi, ξj) = 0, i j, ФП НБФТЙГБ K СЧМСЕФУС ДЙБЗПОБМШОПК::
фептенб 6.5.1.3
еУМЙ ЙЪЧЕУФОБ ЛПЧБТЙБГЙПООБС НБФТЙГБ л = (kij)n УМХЮБКОПЗП ЧЕЛФПТБ (ξ1, ξ2, . , ξn) Й ηi = ci1ξ1 + ci2ξ2 + . + cinξn, i = 1, . , n; ФП ЕУФШ
ФП ЛПЧБТЙБГЙПООБС НБФТЙГБ H = (hij), hij = cov(ηi, ηj) УМХЮБКОПЗП ЧЕЛФПТБ (η1, η2, . , ηn) НПЦЕФ ВЩФШ ОБКДЕОБ РП ЖПТНХМЕ:
H = CћKћC T .
уМЕДПЧБФЕМШОП, ЛПТТТЕМСГЙПООБС НБФТЙГБ R СЧМСЕФУС УЙННЕФТЙЮОПК.
еУМЙ УМХЮБКОЩЕ ЧЕМЙЮЙОЩ ξ1, ξ2, . , ξn РПРБТОП ОЕЪБЧЙУЙНЩ ЙМЙ ОЕЛПТТЕМЙТХЕНЩ, ФП ЛПТТЕМСГЙПООБС НБФТЙГБ R СЧМСЕФУС ЕДЙОЙЮОПК:
ъбнеюбойе. уМЕДХЕФ РПНОЙФШ, ЮФП ЮФП ЪОБС ЪБЛПО ТБУРТЕДЕМЕОЙС УМХЮБКОПЗП ЧЕЛФПТБ (ξ1, ξ2, . , ξn), НПЦОП ОБКФЙ ЮЙУМПЧЩЕ ИБТБЛФЕТЙУФЙЛЙ ЛПНРБОЕФ (ЕУМЙ ПОЙ УХЭЕУФЧХАФ).
оБРТЙНЕТ, ЕУМЙ ЧЕЛФПТ – УМХЮБКОБС ЧЕМЙЮЙОБ БВУПМАФОП ОЕРТЕТЧЩОПЗП ФЙРБ У РМПФОПУФША ТБУРТЕДЕМЕОЙС , ФП
ъБРЙЫЙФЕ УБНПУФПСФЕМШОП УППФЧЕФУФЧХАЭЙЕ ЖПТНХМЩ ДМС УМХЮБКОПЗП ЧЕЛФПТБ ДЙУЛТЕФОПЗП ФЙРБ.
ъбдбюб 6.5.1.1 йЪЧЕУФОП, ЮФП Mξ = 1, Dξ = 2; η = 5ξ + 7. оБКФЙ cov(ξ, η).
cov(ξ, η) = cov(ξ, 5ξ + 7) = 5Dξ = 10.
ъбдбюб 6.5.1.2 йЪЧЕУФОП, ЮФП Mξ = 3, Dξ = 8. оБКФЙ ρ(ξ, η), ЕУМЙ η = – 15ξ + 2.
ъбдбюб 6.5.1.3 дБО ЪБЛПО ТБУРТЕДЕМЕОЙС УМХЮБКОПЗП ЧЕЛФПТБ (ξ1, ξ2) ДЙУЛТЕФОПЗП ФЙРБ:
| 5 | 6 | 7 | |
|---|---|---|---|
| 0 | 0,2 | 0 | 0 |
| 0,1 | 0,1 | 0,15 | 0 |
| 0,2 | 0,05 | 0,15 | 0,1 |
| 0,3 | 0,05 | 0,1 | 0,1 |
оБКФЙ: ЛПЧБТЙБГЙПООХА Й ЛПТТЕМСГЙПООХА НБФТЙГЩ УМХЮБКОПЗП ЧЕЛФПТБ (ξ1, ξ2).
1) рТЕЦДЕ ЧУЕЗП ОБКДЕН ЪБЛПО ТБУРТЕДЕМЕОЙС ЛБЦДПК ЛПНРПОЕОФЩ (БМЗПТЙФН УНПФТЙ 4.4.2)
| ξ1 | 5 | 6 | 7 |
|---|---|---|---|
| 0,4 | 0,4 | 0,2 |
Mξ1 2 = 25ћ0,4 + 36ћ0,4 + 49ћ0,2 = 34,2;
| ξ2 | 0 | 0,1 | 0,2 | 0,3 |
|---|---|---|---|---|
| 0,2 | 0,25 | 0,3 | 0,25 |
Mξ2 = 0ћ0,2 + 0,1ћ0,25 + 0,2ћ0,3 + 0,3ћ0,25 = 0,16;
Mξ2 2 = 0ћ0,1 + 0,01ћ0,25 + 0,04ћ0,3 + 0,09ћ0,25 = 0,037;
ъБНЕФЙН, ЮФП УМХЮБКОБС ЧЕМЙЮЙОБ ξ1ћξ2 РТЙОЙНБЕФ УМЕДХАЭЙЕ ЪОБЮЕОЙС Ч ЪБЧЙУЙНПУФЙ ПФ ЪОБЮЕОЙК ЛПНРПОЕОФ:
| 5 | 6 | 7 | |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0,1 | 0,5 | 0,6 | 0,7 |
| 0,2 | 1 | 1,2 | 1,4 |
| 0,3 | 1,5 | 1,8 | 2,1 |
уМЕДПЧБФЕМШОП, ЪБЛПО ТБУРТЕДЕМЕОЙС УМХЮБКОПК ЧЕМЙЮЙОЩ ξ1ћξ2 ЙНЕЕФ УМЕДХАЭЙК ЧЙД:
| xk | 0 | 0,5 | 0,6 | 0,7 | 1 | 1,2 | 1,4 | 1,5 | 1,8 | 2,1 |
| pk | 0,2 | 0,1 | 0,15 | 0 | 0,05 | 0,15 | 0,1 | 0,05 | 0,1 | 0,1 |
M(ξ1ξ2) = 0ћ0,2 + 0,1ћ0,5 + 0,6ћ0,15 + 0,7ћ0 + 0,05ћ1 + 0,15ћ1,2 +
+ 1,4ћ0,1 + 1,5ћ0,05 + 0,1ћ1,8 + 0,1ћ2,1 = 0,975.
Dξ1Dξ2 = 0,56ћ0,0114 = 0,006384 а ρ12 = ρ21 = 0,588.
ъбдбюб 6.5.1.4 йЪЧЕУФЕО ЪБЛПО ТБУРТЕДЕМЕОЙС УМХЮБКОПЗП ЧЕЛФПТБ:
| 0 | 1 | |
|---|---|---|
| -1 | 0,1 | 0,2 |
| 0 | 0,2 | 0,3 |
| 1 | 0 | 0,2 |
оБКФЙ НБФЕНБФЙЮЕУЛПЕ ПЦЙДБОЙЕ Й ДЙУРЕТУЙА УМХЮБКОПК ЧЕМЙЮЙОЩ q = 2ξ1 + ξ 2 2.
уМЕДПЧБФЕМШОП, РТЕЦДЕ ЧУЕЗП ПРТЕДЕМЙН ЪБЛПОЩ ТБУРТЕДЕМЕОЙС ξ1 Й ξ2.
| ξ1 | xk | 0 | 1 |
|---|---|---|---|
| pk | 0,3 | 0,7 |
| ξ2 | xk | -1 | 0 | 1 |
|---|---|---|---|---|
| pk | 0,3 | 0,5 | 0,2 |
| ξ2 2 | xk | 0 | 1 |
|---|---|---|---|
| pk | 0,5 | 0,5 |
| ξ1ξ2 2 | xk | 0 | 1 |
|---|---|---|---|
| pk | 0,6 | 0,4 |
cov(ξ1, ξ2 2 ) = 0,4 – 0,7 ћ 0,5 = 0,05. фБЛЙН ПВТБЪПН,
M q = 2ћ0,7 + 0,5 = 1,9;
D q = 4ћ0,21 + 0,25 + 2ћ0,05 = 0,84 + 0,25 + 0,1 = 1,29.
ъбдбюб 6.5.1.5 йЪЧЕУФОБ РМПФОПУФШ ТБУРТЕДЕМЕОЙС УМХЮБКОПЗП ЧЕЛФПТБ (ξ, η):
оБКФЙ ЛПЧБТЙБГЙА УМХЮБКОЩИ ЧЕМЙЮЙО ξ, η.
Cov(ξ, η) = π/2 – 1 – π 2 /16.
(чУЕ ЧЩЮЙУМЕОЙС РТПЧЕТШФЕ!)
ъБДБЮЙ ДМС УБНПУФПСФЕМШОПЗП ТЕЫЕОЙС.
ъбдбюб 6.5.1.1(у) дБО ЪБЛПО ТБУРТЕДЕМЕОЙС УМХЮБКОПЗП ЧЕЛФПТБ (ξ1, ξ2):
| 0 | 2 | 5 | |
|---|---|---|---|
| 1 | 0,1 | 0 | 0,2 |
| 2 | 0 | 0,3 | 0 |
| 4 | 0,1 | 0,3 | 0 |
уПУФБЧЙФШ ЛПЧБТЙБГЙПООХА Й ЛПТТЕМСГЙПООХА НБФТЙГЩ.
ъбдбюб 6.5.1.2(у) ъБДБО УМХЮБКОЩК ЧЕЛФПТ (ξ, η). йЪЧЕУФОП, ЮФП Mξ = 0, Mη = 2, Dξ = 2, Dη = 1, ρ(ξ, η) = – . оБКФЙ НБФЕНБФЙЮЕУЛПЕ ПЦЙДБОЙЕ Й ДЙУРЕТУЙА УМХЮБКОПК ЧЕМЙЮЙОЩ q = 2ξ – 3η.
ъбдбюб 6.5.1.3(у) йЪЧЕУФОБ РМПФОПУФШ ТБУРТЕДЕМЕОЙС УМХЮБКОПЗП ЧЕЛФПТБ (ξ, η):
D – ФТЕХЗПМШОЙЛ, ПЗТБОЙЮЕООЩК РТСНЩНЙ x + y = 1, x = 0, y = 0. оБКФЙ ЛПЬЖЖЙГЙЕОФ ЛПТТЕМСГЙЙ.
© гЕОФТ ДЙУФБОГЙПООПЗП ПВТБЪПЧБОЙС пзх, 2000-2002
[spoiler title=”источники:”]
http://habr.com/ru/post/263907/
http://cde.osu.ru/courses2/course8/p_6_5_1.html
[/spoiler]
Макеты страниц
Совершенно так же, как в предыдущем параграфе было определено математическое ожидание функции двух случайных величин, можно определить математическое ожидание произвольной функции  случайных величин
случайных величин 

Очевидно, что формулу (10.3) можно рассматривать как сокращенную запись формулы (18.1), так как под  в (10.3) можно понимать
в (10.3) можно понимать  -мерные векторы с составляющими
-мерные векторы с составляющими  соответственно, а интеграл рассматривать как
соответственно, а интеграл рассматривать как  -кратный интеграл по переменным
-кратный интеграл по переменным 
Полагая в  , получим момент
, получим момент  -мерного случайного вектора
-мерного случайного вектора  порядка
порядка 

Центральный момент  -мерного случайного вектора
-мерного случайного вектора  порядка
порядка  определяется формулой
определяется формулой

где через  для краткости обозначено отклонение случайной величины
для краткости обозначено отклонение случайной величины  от ее математического ожидания
от ее математического ожидания

В дальнейшем мы везде будем отмечать нуликом вверху отклонения случайных величин от их математических ожиданий, т. е. центрированные случайные величины.
Полагая в формуле (18.2) по очереди один из индексов  равным единице, а остальные равными нулю, получим математические ожидания случайных величин,
равным единице, а остальные равными нулю, получим математические ожидания случайных величин,  Математические ожидания
Математические ожидания
 составляющих
составляющих  случайного вектора X определяют
случайного вектора X определяют  -мерный вектор
-мерный вектор  который естественно назвать математическим ожиданием случайного вектора
который естественно назвать математическим ожиданием случайного вектора  Полагая в (18.3) по очереди один из индексов
Полагая в (18.3) по очереди один из индексов  равным 2, а остальные равными нулю, получим дисперсии случайных величин
равным 2, а остальные равными нулю, получим дисперсии случайных величин  Наконец, полагая в (18.3) два из индексов
Наконец, полагая в (18.3) два из индексов  равными единице, а остальные равными нулю, получим корреляционные моменты случайных величин
равными единице, а остальные равными нулю, получим корреляционные моменты случайных величин 

При одинаковых индексах  эта формула дает дисперсии случайных величин
эта формула дает дисперсии случайных величин 

Очевидно, что корреляционный момент двух случайных величин не зависит от того, в каком порядке берутся эти случайные величины, т. е.

Совокупность дисперсий и корреляционных моментов составляющих случайного вектора образует корреляционную матрицу этого случайного вектора:

Формула (18.7) показывает, что корреляционная матрица случайного вектора симметрична, так как ее элементы, симметрично расположенные относительно главной диагонали, равны друг другу.
Если ограничиться численной характеристикой случайного вектора его моментами не выше второго порядка, то можно будет охарактеризовать случайный вектор X его математическим ожиданием и корреляционной матрицей. Во многих случаях практики такая характеристика случайного вектора оказывается исчерпывающей. Например, как мы увидим в § 23, математическое ожидание и корреляционная матрица нормально распределенного случайного вектора вполне определяют его плотность вероятности.
В рассмотренной в предыдущем параграфе механической интерпретации распределения вероятностей на плоскости и в трехмерном пространстве корреляционной матрице случайного вектора соответствует тензор инерции тела. Совершенно так же, как в механике тензору инерции соответствует геометрический образ — эллипс или эллипсоид инерции тела, при помощи корреляционной матрицы случайного вектора можно определить его эллипс или эллипсоид распределения. Мы не будем здесь на этом останавливаться (см., например, [49]).
Вместо корреляционной матрицы случайного вектора можно рассматривать его нормированную корреляционную матрицу, т. е. матрицу, составленную из коэффициентов корреляции составляющих  случайного вектора X:
случайного вектора X:

где  коэффициент корреляции случайных величин
коэффициент корреляции случайных величин 

Однако при этом для характеристики случайного вектора придется задать еще дисперсии  его составляющих.
его составляющих.
Если при определении моментов случайного вектора подставить в соответствующие формулы условную плотность вероятности этого случайного вектора относительно другого случайного вектора, то получим условные моменты рассматриваемого случайного вектора.
Сравнивая формулы (18.1) и (15.13), видим, что вероятность попадания конца случайного вектора X в данную область В равна математическому ожиданию характеристической функции области В. Таким образом, формула (10.16) справедлива и для случайных векторов.
На основании данного в § 14 определения вероятностной меры формулу (18.1) для математического ожидания функции случайного вектора можно представить в виде:

где интегрирование распространяется на все  -мерное пространство
-мерное пространство 
Формула (18.11) легко обобщается на произвольные случайные объекты. Пусть X — какой-нибудь случайный объект,  — множество всех его возможных значений. Предположим, что на множестве
— множество всех его возможных значений. Предположим, что на множестве  задана вероятностная мера
задана вероятностная мера  (т. е. для каждого подмножества А множества 9 определена вероятность того, что случайный объект X примет какое-нибудь значение из А). Если некоторая величина определяется значением, которое принимает в результате опыта объект X, то эта величина является функцией
(т. е. для каждого подмножества А множества 9 определена вероятность того, что случайный объект X примет какое-нибудь значение из А). Если некоторая величина определяется значением, которое принимает в результате опыта объект X, то эта величина является функцией  случайного объекта
случайного объекта  Математическое ожидание этой функции объекта X определяется формулой
Математическое ожидание этой функции объекта X определяется формулой

где интегрирование распространяется на все множество 
31

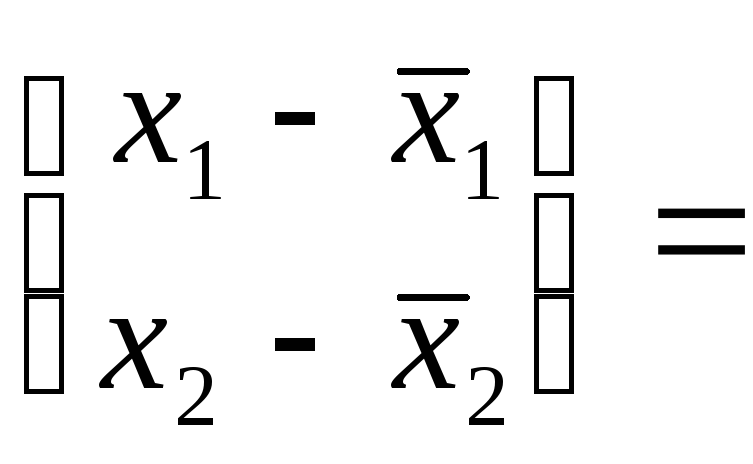
![]()
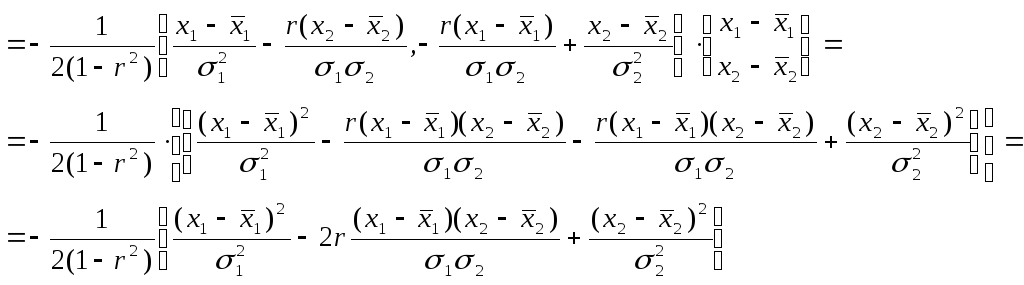
Тогда плотность
распределения имеет вид

выражения, в котором
коэффициент корреляции, матожидания и
дисперсии признаков
X1
и
X2
являются
основными числовыми характеристиками
распределения. Очевидно, что в случае
независимости данных признаков r12=r=
0 и выполнено
условие
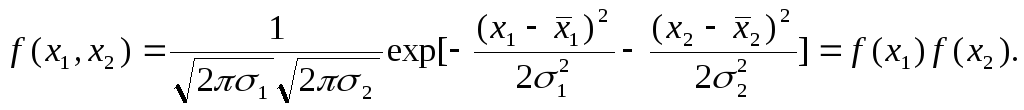
В случае линейной
зависимости данных признаков r12
= г
=
±1,
и распределение
f(x1,x2)
является вырожденным, так как
Det
=
0.
ОСНОВНЫЕ
СВОЙСТВА
При анализе связей
важное значение имеет структура
взаимосвязей между признаками. Как
известно, измерителем линейной связи
между признаками служит коэффициент
корреляции или, в более общем случае,
коэффициент ковариации. С другой стороны,
вектор средних и матрица ковариаций
являются исчерпывающими характеристиками
нормального закона распределения.
Поэтому остановимся более подробно на
свойствах корреляционной матрицы.
32
Корреляционная
матрица
R(n х n)
является симметричной, с единичной
главной диагональю,
положительно полуопределенной матрицей.
Напомним из линейной алгебры, что
квадратная матрица, не обязательно
симметричная,
называется
положительно полуопределенной, если
для любого вектора Y=(y1,…
yn)T
квадратичная форма
yTRy![]() 0
0
не отрицательна. Квадратная матрица
R положительно
определена, если для любых у квадратичная
форма yTRy
>
0 строго
положительна. В данном свойстве матрицы
R легко
убедиться:
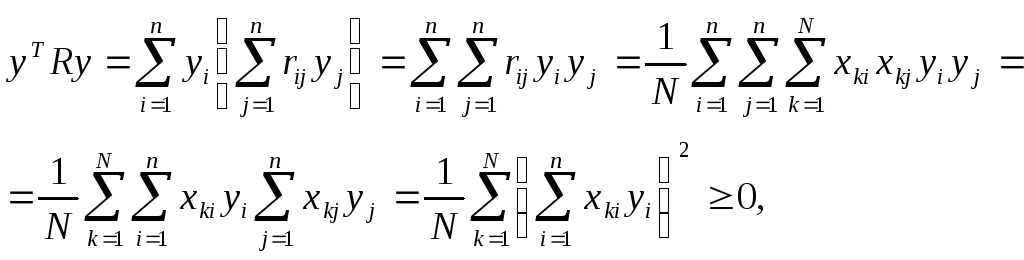
где ![]() –
–
коэффициент корреляции, вычисленный
как скалярное произведение признаков
Xi
и
X)i
в стандартной
матрице
X.
Заметим, что при
ненулевом векторе у квадратичная форма
yTRy
может обратиться в нуль, только если
признаки Xi
= (x1i,…
xNi
)T
, i=1,…n
линейно
зависимы
между
собой.
Действительно,
пусть все признаки
Xi
, линейно
зависимы между собой. Тогда матрица
R=(rij
=1),
i
= 1,… n,
j=
1,… n состоит
из единиц, если линейная связь, например,
положительна. Тогда для некоторого
вектора у получим
![]()
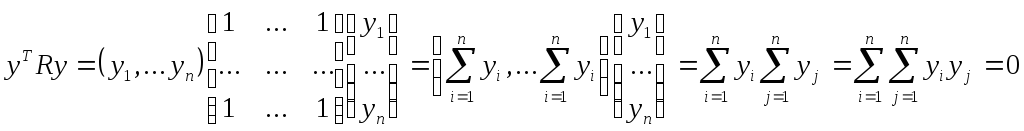
очевидно, что
данное число представляет собой сумму
всевозможных комбинаций попарных
произведений координат вектора у. Все
попарные произведения координат данного
вектора можно представить в виде
квадратной матрицы размером п
х п:
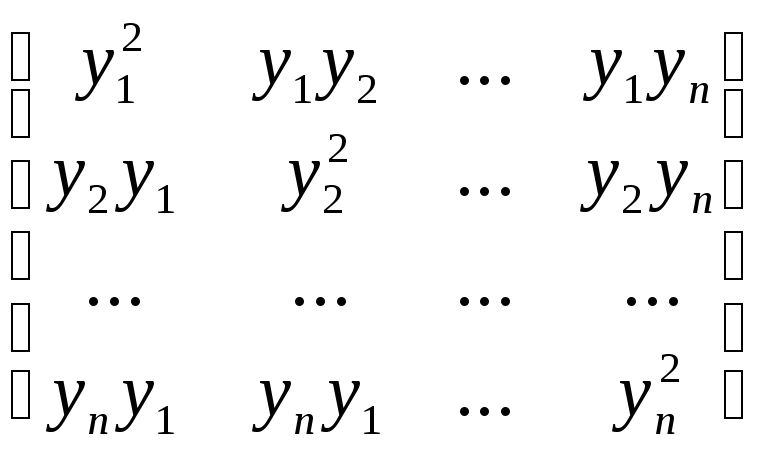 =yyT
=yyT
Матрица yyT
является симметричной, а сумма ее
диагональных элементов представляет
собой квадрат длины вектора у и всегда
положительна для ненулевого у.
Следовательно,
33
равенство yT
Ry
= 0 выполняется
только, когда сумма диагональных
элементов равна по модулю и противоположна
по знаку сумме недиагональных элементов
![]()
Для случая
n
=
2 получим:
![]()
Решив данное квадратное уравнение
относительно
y1,
получим, что уTRy
= 0 при
y1
= –
y2.
Но признаки
Xi
представляют собой результаты измерений,
где часто число объектов
N
много
больше числа признаков п.
Поэтому, в силу возможных ошибок и
неточностей измерений, не говоря уже
о случайных помехах, линейная зависимость
признаков
Xi
маловероятна. Поэтому, как правило,
данная квадратичная форма оказывается
строго положительной при любом ненулевом
векторе у.
Поэтому корреляционная
матрица
R на практике
считается положительно определенной.
В этом случае
detR всегда
ненулевой, а корреляционная матрица
всегда имеет обратную, то есть является
невырожденной.
2.4. Собственные векторы и собственные числа корреляционной матрицы
Собственным
вектором корреляционной матрицы
R,
соответствующим собственному числу
,
называется ненулевой вектор х
= (х1…
хn)T
,
удовлетворяющий уравнению
Rx =
х.
Как известно из
линейной алгебры, матрица
R
рассматривается в данном случае как
матрица линейного преобразования
вектора х в вектор х.
Это означает, что для данного линейного
преобразования
R в n-мерном
пространстве существует такое
направление, что преобразование
R только
растягивает вектор х в
раз, сохраняя его ориентацию.
Векторное уравнение
можно переписать в виде однородного
уравнения относительно х: (R
– Е)х
= 0. Данное
уравнение имеет ненулевое (нетривиальное)
решение только тогда, когда
определитель
det(R-Е)
равен нулю. Данный определитель
представляет собой уравнение относительно
Х и является полиномом n
степени вида
(-1)n
”
+ (-1)n-1
p1n-1+…+pn=0.
Данный полином называется
характеристическим полиномом
(многочленом), а уравнение det(R-Е)
= 0 –
характеристическим уравнением.
Характеристическое уравнение имеет
n,
вообще говоря, различных корней. При
этом его корни
являются собственными числами
преобразования
R. В качестве
собственных векторов хi
i= 1,… п
линейного преобразования
R,
соответствующих собственным числам
i,
i
=1,…n,
берутся векторы единичной длины
![]()
каждый
из которых удовлетворяет соответствующему
характеристическому уравнению
det(R-iE)=0.
Рассмотрим случай
п=1.
Тогда получим
34
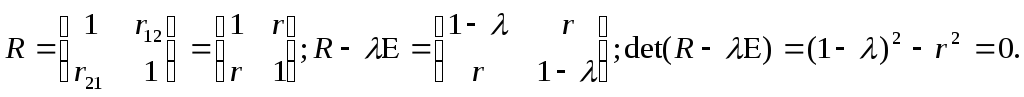
Решением квадратного
уравнения
-2r2=0
относительно
являются корни r
и =1-r.
Отметим следующие
свойства собственных чисел.
1)>>0.
Так как корреляционная матрица
R практически
положительно определена,
то при
произвольном п
все ее собственные числа являются
действительными и строго положительными
>>…>n>
0
.
2)
+=2.
Вычислим след матрицы
R как сумму
ее диагональных элементов trR
=r11+r22=1+1=2.
Следовательно,
trR=+,
то есть сумма собственных чисел
корреляционной матрицы равна ее следу.
При произвольном п
получим ![]()
= trR.
3)
=1-г2
. Определитель корреляционной матрицы
равен detR
в
1 – г2
.
Следовательно,
det R=.
При произвольном
n получим
![]()
Следовательно,
произведение собственных чисел равно
определителю корреляционной матрицы,
взятому со знаком плюс, так как все
собственные числа положительны.
Найдем собственные
векторы х1
и х2,
соответствующие собственным числам
и .
Из характеристического уравнения
следует, что первый вектор найдется из
уравнения

Согласно определению
![]()
=
1. Тогда
получим систему уравнений
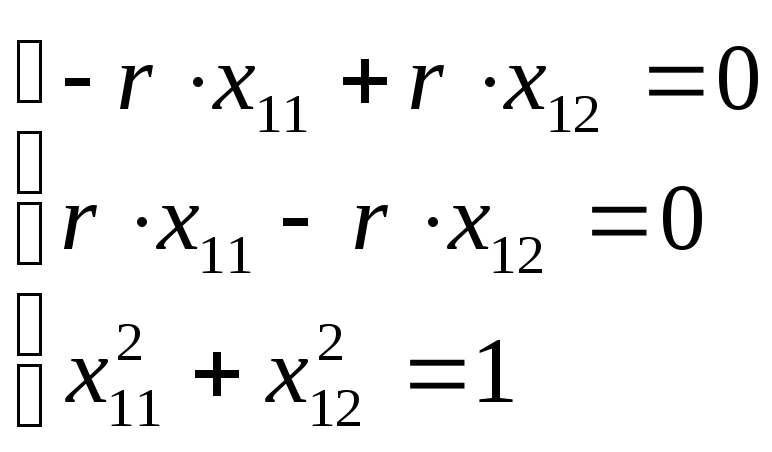
Из решения данной
системы следует, что x11
= x12
=
±![]() /2
/2
= ±0.707. Два
решения указывают на противоположные
направления вдоль диагонали первого
и третьего квадрантов плоскости
координат:

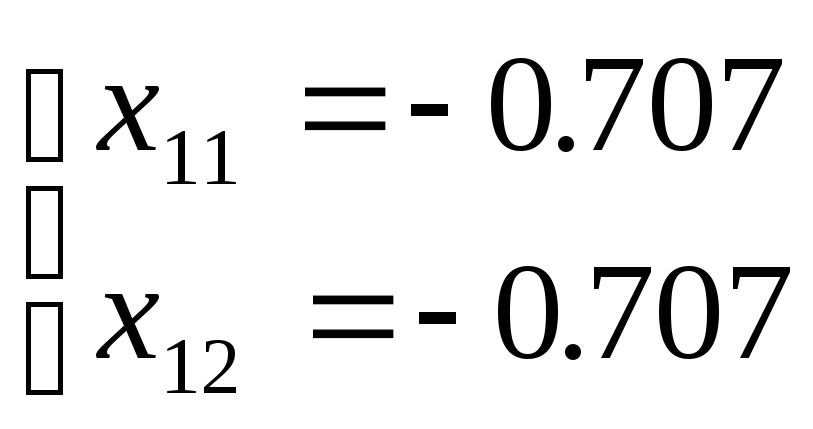
35
Второй вектор
найдется из уравнения:

В результате
получим два решения, указывающие на
противоположные направления вдоль
диагонали второго и четвертого квадрантов
плоскости координат:
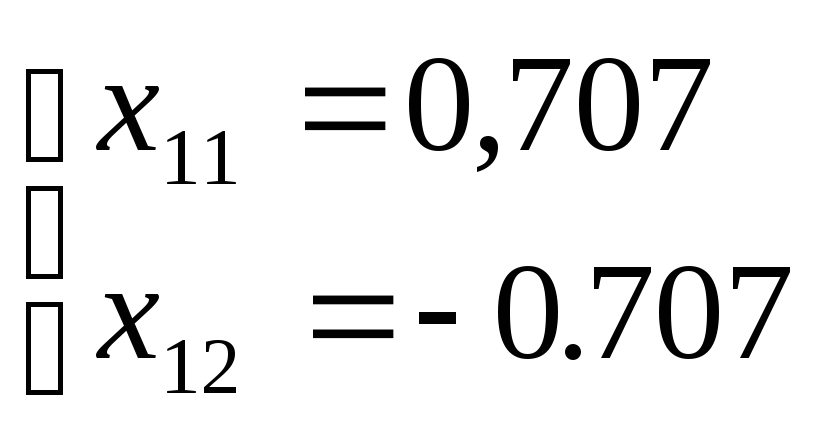

Как сразу нетрудно
заметить, собственные векторы матрицы
R, то есть
вещественной симметричной матрицы,
соответствующие различным собственным
числам, ортогональны между собой.
Покажем это для произвольного п.
Рассмотрим
уравнения
Rx1=x1
и Rx2=
x2,
где
Домножим каждое
из уравнений на собственный вектор
другого уравнения и получим
![]() и
и ![]()
Так как
![]()
то, вычтя одно
уравнение из другого, получим
![]()
Отсюда следует,
что
![]()
= 0.
Следовательно, собственные векторы
линейного преобразования
R образуют
ортонормированный базис в
n-мерном
пространстве. Такие векторы называются
главными компонентами корреляционной
матрицы.
Главные компоненты
корреляционной матрицы обладают весьма
важными свойствами, которые имеют
содержательный смысл в обработке данных
и поэтому широко используются. Ниже мы
покажем геометрический смысл главных
компонент на плоскости.
36
Соседние файлы в папке Основы обработки данных
- #
- #
- #
Время на прочтение
5 мин
Количество просмотров 42K
В первой части показано, как на основе матрицы расстояний между элементами получить матрицу Грина. Ее спектр образует собственную систему координат множества, центром которой является центроид набора. Во второй рассмотрены спектры простых геометрических наборов.
В данной статье покажем, что матрица Грина и матрица корреляции — суть одно и то же.
7. Векторизация и нормирование одномерных координат
Пусть значения некой характеристики элементов заданы рядом чисел . Для того, чтобы данный набор можно было сравнивать с другими характеристиками, необходимо его векторизовать и обезразмерить (нормировать).
Для векторизации находим центр (среднее) значений
и строим новый набор как разность между исходными числами и их центроидом (средним):
Получили вектор. Основной признак векторов состоит в том, что сумма их координат равна нулю. Далее нормируем вектор, — приведем сумму квадратов его координат к 1. Для выполнения данной операции нам нужно вычислить эту сумму (точнее среднее):
Теперь можно построить ССК исходного набора как совокупность собственного числа S и нормированных координат вектора:
Квадраты расстояний между точками исходного набора определяются как разности квадратов компонент собственного вектора, умноженные на собственное число. Обратим внимание на то, что собственное число S оказалось равно дисперсии исходного набора (7.3).
Итак, для любого набора чисел можно определить собственную систему координат, то есть выделить значение собственного числа (она же дисперсия) и рассчитать координаты собственного вектора путем векторизации и нормирования исходного набора чисел. Круто.
Упражнение для тех, кто любит «щупать руками». Построить ССК для набора {1, 2, 3, 4}.
Ответ.
Собственное число (дисперсия): 1.25.
Собственный вектор: {-1.342, -0.447, 0.447, 1.342}.
8. Векторизация и ортонормирование многомерных координат
Что, если вместо набора чисел нам задан набор векторов — пар, троек и прочих размерностей чисел. То есть точка (узел) задается не одной координатой, а несколькими. Как в этом случае построить ССК? Стандартный путь следующий.
Введем обозначение характеристик (компонент) набора. Нам заданы точки (элементы) и каждой точке соответствует числовое значение характеристики
. Обращаем внимание, что второй индекс
— это номер характеристики (столбцы матрицы), а первый индекс
— номер точки (элемента) набора (строки матрицы).
Далее векторизуем характеристики. То есть для каждой находим центроид (среднее значение) и вычитаем его из значения характеристики:
Получили матрицу координат векторов (МКВ) .
Следующим шагом как будто бы надо вычислить дисперсию для каждой характеристики и их нормировать. Но хотя таким образом мы действительно получим нормированные векторы, нам-то нужно, чтобы эти векторы были независимыми, то есть ортонормированными. Операция нормирования не поворачивает вектора (а лишь меняет их длину), а нам нужно развернуть векторы перпендикулярно друг другу. Как это сделать?
Правильный (но пока бесполезный) ответ — рассчитать собственные вектора и числа (спектр). Бесполезный потому, что мы не построили матрицу, для которой можно считать спектр. Наша матрица координат векторов (МКВ) не является квадратной — для нее собственные числа не рассчитаешь. Соответственно, надо на основе МКВ построить некую квадратную матрицу. Это можно сделать умножением МКВ на саму себя (возвести в квадрат).
Но тут — внимание! Неквадратную матрицу можно возвести в квадрат двумя способами — умножением исходной на транспонированную. И наоборот — умножением транспонированной на исходную. Размерность и смысл двух полученных матриц — разный.
Умножая МКВ на транспонированную, мы получаем матрицу корреляции:
Из данного определения (есть и другие) следует, что элементы матрицы корреляции являются скалярными произведениями векторов (грамиан на векторах). Значения главной диагонали отражают квадрат длины данных векторов. Значения матрицы не нормированы (обычно их нормируют, но для наших целей этого не нужно). Размерность матрицы корреляции совпадает с количеством исходных точек (векторов).
Теперь переставим перемножаемые в (8.1) матрицы местами и получим матрицу ковариации (опять же опускаем множитель 1/(1-n), которым обычно нормируют значения ковариации):
Здесь результат выражен в характеристиках. Соответственно, размерность матрицы ковариации равна количеству исходных характеристик (компонент). Для двух характеристик матрица ковариации имеет размерность 2×2, для трех — 3×3 и т.д.
Почему важна размерность матриц корреляции и ковариации? Фишка в том, что поскольку матрицы корреляции и ковариации происходят из произведения одного и того же набора векторов, то они имеют один и тот же набор собственных чисел, один и тот же ранг (количество независимых размерностей) матрицы. Как правило, количество векторов (точек) намного превышает количество компонент. Поэтому о ранге матриц судят по размерности матрицы ковариации.
Диагональные элементы ковариации отражают дисперсию компонент. Как мы видели выше, дисперсия и собственные числа тесно связаны. Поэтому можно сказать, что в первом приближении собственные числа матрицы ковариации (а значит, и корреляции) равны диагональным элементам (а если межкомпонентная дисперсия отсутствует, то равны в любом приближении).
Если стоит задача найти просто спектр матриц (собственные числа), то удобнее ее решать для матрицы ковариации, поскольку, как правило, их размерность небольшая. Но если нам необходимо найти еще и собственные вектора (определить собственную систему координат) для исходного набора, то необходимо работать с матрицей корреляции, поскольку именно она отражает скалярное произведение векторов.
Отметим, что метод главных компонент как раз и состоит в расчете спектра матрицы ковариации/корреляции для заданного набора векторных данных. Найденные компоненты спектра располагаются вдоль главных осей эллипсоида данных. Из нашего рассмотрения это вытекает потому, что главные оси — это и есть те оси, дисперсия (разброс) данных по которым максимален, а значит, и максимально значение спектра.
Правда, могут быть и отрицательные дисперсии, и тогда аналогия с эллипсоидом уже не очевидна.
9. Матрица Грина — это матрица корреляции векторов
Рассмотрим теперь ситуацию, когда нам известен не набор чисел, характеризующих точки (элементы), а набор расстояний между точками (причем между всеми). Достаточно ли данной информации для определения ССК (собственной системы координат) набора?
Ответ дан в первой части — да, вполне. Здесь же мы покажем, что построенная по формуле (1.3′) матрица Грина и определенная выше матрица корреляции векторов (8.1) — это одна и та же матрица.
Как такое получилось? Сами в шоке. Чтобы в этом убедиться, надо подставить выражение для элемента матрицы квадратов расстояний
в формулу преобразования девиации:
Отметим, что среднее значение матрицы квадратов расстояний отражает дисперсию исходного набора (при условии, что расстояния в наборе — это сумма квадратов компонент):
Подставляя (9.1) и (9.3) в (9.2), после несложных сокращений приходим к выражению для матрицы корреляции (8.1):
Итак, матрица Грина и матрица корреляции векторов — суть одно и то же. Ранг матрицы корреляции совпадает с рангом матрицы ковариации (количеством характеристик — размерностью пространства). Это обстоятельство позволяет строить спектр и собственную систему координат для исходных точек на основе матрицы расстояний.
Для произвольной матрицы расстояний потенциальный ранг (количество измерений) на единицу меньше количества исходных векторов. Расчет спектра (собственной системы координат) позволяет определить основные (главные) компоненты, влияющие на расстояния между точками (векторами).
Таким образом можно строить собственные координаты элементов либо на основании их характеристик, либо на основании расстояний между ними. Например, можно определить собственные координаты городов по матрице расстояний между ними.
From Wikipedia, the free encyclopedia
The cross-correlation matrix of two random vectors is a matrix containing as elements the cross-correlations of all pairs of elements of the random vectors. The cross-correlation matrix is used in various digital signal processing algorithms.
Definition[edit]
For two random vectors 



![{displaystyle operatorname {R} _{mathbf {X} mathbf {Y} }triangleq operatorname {E} [mathbf {X} mathbf {Y} ^{rm {T}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1337f507d7cb6918d742ae2f029e0554013f7a58)
and has dimensions 
The random vectors 

Example[edit]
For example, if 




![{displaystyle operatorname {E} [X_{i}Y_{j}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e511d6ea021c2d4b0579f621faec897ec52a1999)
Complex random vectors[edit]
If 



where 
[edit]
Two random vectors 

They are uncorrelated if and only if their cross-covariance matrix 
In the case of two complex random vectors 

and
Properties[edit]
Relation to the cross-covariance matrix[edit]
The cross-correlation is related to the cross-covariance matrix as follows:
- Respectively for complex random vectors:
See also[edit]
- Autocorrelation
- Correlation does not imply causation
- Covariance function
- Pearson product-moment correlation coefficient
- Correlation function (astronomy)
- Correlation function (statistical mechanics)
- Correlation function (quantum field theory)
- Mutual information
- Rate distortion theory
- Radial distribution function
References[edit]
- ^ Gubner, John A. (2006). Probability and Random Processes for Electrical and Computer Engineers. Cambridge University Press. ISBN 978-0-521-86470-1.
Further reading[edit]
- Hayes, Monson H., Statistical Digital Signal Processing and Modeling, John Wiley & Sons, Inc., 1996. ISBN 0-471-59431-8.
- Solomon W. Golomb, and Guang Gong. Signal design for good correlation: for wireless communication, cryptography, and radar. Cambridge University Press, 2005.
- M. Soltanalian. Signal Design for Active Sensing and Communications. Uppsala Dissertations from the Faculty of Science and Technology (printed by Elanders Sverige AB), 2014.
![{displaystyle operatorname {R} _{mathbf {X} mathbf {Y} }={begin{bmatrix}operatorname {E} [X_{1}Y_{1}]&operatorname {E} [X_{1}Y_{2}]&cdots &operatorname {E} [X_{1}Y_{n}]\\operatorname {E} [X_{2}Y_{1}]&operatorname {E} [X_{2}Y_{2}]&cdots &operatorname {E} [X_{2}Y_{n}]\\vdots &vdots &ddots &vdots \\operatorname {E} [X_{m}Y_{1}]&operatorname {E} [X_{m}Y_{2}]&cdots &operatorname {E} [X_{m}Y_{n}]\\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfaf0f3923eafd144f762732bbaa951102ed00bb)
![{displaystyle operatorname {R} _{mathbf {Z} mathbf {W} }triangleq operatorname {E} [mathbf {Z} mathbf {W} ^{rm {H}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b96a25804b6f71adb2dd4366a18cc65e96553d88)
![{displaystyle operatorname {E} [mathbf {X} mathbf {Y} ^{rm {T}}]=operatorname {E} [mathbf {X} ]operatorname {E} [mathbf {Y} ]^{rm {T}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a8bb45997c59ac08d38c6073ad03c832d11abf6)
![{displaystyle operatorname {E} [mathbf {Z} mathbf {W} ^{rm {H}}]=operatorname {E} [mathbf {Z} ]operatorname {E} [mathbf {W} ]^{rm {H}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e653a5949cb26600c65a6d23c16310eae1e9867f)
![{displaystyle operatorname {E} [mathbf {Z} mathbf {W} ^{rm {T}}]=operatorname {E} [mathbf {Z} ]operatorname {E} [mathbf {W} ]^{rm {T}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/500e14ec28154556c9b0aa741d1b036af7b7a67f)
![{displaystyle operatorname {K} _{mathbf {X} mathbf {Y} }=operatorname {E} [(mathbf {X} -operatorname {E} [mathbf {X} ])(mathbf {Y} -operatorname {E} [mathbf {Y} ])^{rm {T}}]=operatorname {R} _{mathbf {X} mathbf {Y} }-operatorname {E} [mathbf {X} ]operatorname {E} [mathbf {Y} ]^{rm {T}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d58fc3b03892e013a545da3322c2d4942d7314e)
![{displaystyle operatorname {K} _{mathbf {Z} mathbf {W} }=operatorname {E} [(mathbf {Z} -operatorname {E} [mathbf {Z} ])(mathbf {W} -operatorname {E} [mathbf {W} ])^{rm {H}}]=operatorname {R} _{mathbf {Z} mathbf {W} }-operatorname {E} [mathbf {Z} ]operatorname {E} [mathbf {W} ]^{rm {H}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3b852cac5898146e76309d2f9d00ac163d1d65a)
