Для описания системы двух случайных
величин, кроме математических ожиданий
и дисперсий составляющих пользуются и
другими характеристиками, к числу
которых относятся корреляционный
моментикоэффициент корреляции(кратко было упомянуто в конце Т.8.п.8.6).
Корреляционным моментом (иликовариацией, или моментом
связи) двух случайных величинX
иY называется
м. о. произведения отклонений этих
величин (см. равенство (5) п. 8.6):
(7)
.
Следствие 1. Для корреляционного
момента с.в. X иYтакже справедливы
равенства:
,
где
соответствующие централизованные с.в.X иY
(см. п.8.6.).
При
этом: если
–
двумерная д.с.в., то ковариация вычисляется
по формуле
(8)

если
–
двумерная н.с.в., то ковариация вычисляется
по формуле
(9)
Формулы (8) и (9) получены на основании
формул (6) п.12.1. Имеет место вычислительная
формула
(10)
которая
выводится из определения (9) и на основании
свойств м.о., действительно,
.
Следовательно, формул (36) и (37) можно
переписать в виде
(11)
;
Корреляционный момент служит для
характеристики связи между величинами
X иY.
Как
будет показано ниже, корреляционный
момент равен нулю, если XиY являются
независимыми;
Следовательно, если корреляционный
момент не равен нулю, то X
и Y – зависимые
случайные величины.
Теорема12.1. Корреляционный момент
двух независимых случайных величин X
иY равен нулю,
т.е. для независимых с.в. X
иY,
Доказательство.Так какX
иYнезависимые
случайные величины, то их отклонения
и
также независимы. Пользуясь свойствами
математического ожидания (математическое
ожидание произведения независимых с.
в. равно произведению математических
ожиданий сомножителей,
,
поэтому
.
Замечание. Из этой теоремы следует,
что если
то с.в. X иY
зависимы и в таких случаях с.в. X
иYназываюткоррелированными. Однако из того,
что
не следует независимость с.в.X
иY.
В этом случае (с.в.X иYназываютнекоррелированными, тем
самым из независимости вытекаетнекоррелированность; обратное
утверждение, вообще говоря, неверно
(см. далее пример 2.)
Рассмотрим основные свойства
корреляционного момента.
Cвойства ковариации:
1.Ковариация симметрична, т.е.
.
Непосредственно следует из формулы
(38).
2. Имеют место равенства:т.е.
дисперсия с.в. является ковариацией её
с самой собой.
Эти равенства прямо следуют из определения
дисперсии и равенство (38) соответственно
при
3. Справедливы равенства:
Эти
равенства выводятся из определения
дисперсии, ковариации с.в.и
,
свойств 2.
По определению дисперсии (с учётом
централизованности с.в.
)
мы имеем
теперь,
на основании (33) и свойств 2 и 3, получим
первое (со знаком плюс) свойство 3.
Аналогично, вторая часть свойства3,
выводится из равенство
.
4. Пустьпостоянные
числа,тогда справедливы равенства:
Обычно эти свойства называются свойствами
однородностью первого порядка и
периодичностью по аргументам.
Докажем
первое равенство, при этом будем
использовать свойства м.о.
.
.
Теорема 12.2. Абсолютное значение
корреляционного момента двух
произвольных случайных величин X
и Y не превышает
среднего геометрического их дисперсий:
т.е.
(12)
Доказательство. Заметим, что для
независимых с.в. неравенство выполняется
(с.м. теорему 12.1.). Итак, пусть с.в.X
и Y зависимые.
Рассмотрим стандартные с.в.и
и вычислим дисперсию с.в.
с учётом свойства 3, имеем: с одной
стороныС другой стороны
Следовательно,
с учётом того, что
и
–
нормированные (стандартизированные)
с.в., то для них м.о. равна нулю, а дисперсия
равна 1, поэтому, пользуясь свойством
м.о.получим
а
следовательно, на основании того, что
получим
Отсюда
следует, что
т.е.
=
Утверждение доказано.
Из определения и свойства ковариации
следует, что она характеризует и степень
зависимости с.в., и их рассеяния вокруг
точки
Размерность ковариации равна произведению
размерностей случайных величинXиY. Другими словами,
величина корреляционного момента
зависит от единиц измерения случайных
величин. По этой причине для одних и тех
же двух величинXиY,
величина корреляционного момента
будет иметь различные значения в
зависимости от того, в каких единицах
были измерены величины.
Пусть, например, X
и Y
были измерены в
сантиметрах и
;
если измерить XиY в миллиметрах,
тоЭта особенность корреляционного момента
и есть недостатком этой числовой
характеристики, так как сравнение
корреляционных моментов различных
систем случайных величин становится
затруднительным.
Для того чтобы устранить этот недостаток,
вводят новую числовую характеристику-
– «коэффициент корреляции».
Коэффициентом корреляции
случайных величин
и
называют отношение корреляционного
момента к произведению средних
квадратических отклонений этих величин:
(13)
.
Так как размерность
равна произведению размерностей величин
и
,
имеет размерность величины
σyимеет размерность величины
,
то
есть просто число (т.е. «безразмерная
величина»). Таким образом, величина
коэффициента корреляции не зависит от
выбора единиц измерения с.в., в этом
состоитпреимуществокоэффициента
корреляции перед корреляционным
моментом.
В Т.8. п.8.3 нами было введено понятие
нормированной с.в.,
формула (18), и доказана теорема о том,
чтои
(см.
там же теорема 8.2.). Здесь докажем следующее
утверждение.
Теорема 12.3. Длялюбых двух случайных
величин
и
справедливо
равенство.Другими словами, коэффициент корреляции
любых двух с.в.X
иYравно
корреляционному моменту их соответствующих
нормированныхс.в.и
.
Доказательство. По определению
нормированных случайных величини
и
.
Учитывая свойство математического
ожидания:
и равенство (40) получим
Утверждение
доказано.
Рассмотрим некоторые часто встречающие
свойства коэффициента корреляции.
Свойства коэффициента корреляции:
1. Коэффициент
корреляции по абсолютной величине
непревосходит 1, т.е.
Это
свойство прямо следует из формулы (41)
– определения коффициента корреляции
и теоремы 13.5. ( см. равенство (40)).
2. Если случайные величиныи
независимы,
токоэффициент корреляции
равен нулю, т.е.
.
Это свойство является прямым
следствием равенства (40) и теоремы 13.4.
Следующее свойство
сформулируем в виде отдельной теоремы.
Теорема 12.4.
Если
с.в.и
между
собой связаны линейной функциональной
зависимостью, т.е.то
при этом
и
наоборот, если
,то
с.в.и
между собой связаны линейной функциональной
зависимостью, т.е. существуют постоянныеи
такие, что имеет место равенство
Доказательство.
Пусть
тогда на основании
свойства 4 ковариации, имеем
и
поскольку,
,
поэтому
Следовательно,
.
Равенство в одну сторону получено. Пусть
далее,,
тогда
следует рассматривать два
случая:1)
и
2)Итак, рассмотрим первый случай. Тогда
по определениюи
следовательно из равенства,
где.
В нашем случае,
поэтому из равенства (см. доказательство
теоремы 13.5.)
=
,
получаем, что
,
значитпостоянна.
Так каки поскольку
,
тодействительно,
.
Следовательно,
.
Аналогично,
показывается, что для
имеет место (проверьте самостоятельно!)
,
.
Некоторые выводы:
1. Если
и
независимыес.в., то
2. Если с.в.и
между
собой связаны линейно, то.
3. В остальных случаях
:
В этом случае говорят, что с.в.и
связаны между собойположительной
корреляцией, еслив случаях же
отрицательной
корреляцией. Чем ближек единице, тем больше оснований считать,
чтос.в.и
связаны линейной зависимостью.
Отметим, что корреляционные моменты и
дисперсии системы с.в. обычно задаются
корреляционной матрицей:

Очевидно, что определитель
корреляционной матрицы удовлетворяет:
.
Как уже было отмечено, если две случайные
величины зависимы, то они могут быть
как коррелированными, так инекоррелированными.Другими словами,
корреляционный момент двух зависимых
величин может бытьне равен нулю,
но может иравняться нулю.
Пример 1. Закон распределения
дискретной с.в.задан таблицей
|
|
-1 |
0 |
1 |
|
0 |
|
|
|
|
1 |
|
|
|
Найти
коэффициент корреляции
Решение. Находим законы распределения
составляющихи
:
Теперь
вычислим м.о. составляющих:
.
Этих
величин можно было находить на основании
таблицы распределения с.в.
из
равенства (1) пункта 12.1. Например,
.
Аналогично,
находите
самостоятельно.
Вычислим
дисперсии составляющих при это будем
пользоваться вычислительной формулой:
Следовательно,Далее, на основании первой формулы
(6) имеем:
Составим
закон распределения
,
а затем найдём:
При
составлении таблицы закона распределения
следует выполнять действия:
1) оставить лишь различные значения
всевозможных произведений
.
2) для определения вероятности данного
значения
,
нужно
складывать все соответствующие
вероятности, находящиеся на пересечении
основной таблицы, благоприятствующие
наступлению данного значения.
В нашем примере с.в.принимает
всего три различных значения.
Здесь первое значение ()
соответствует произведениюиз второй строки и
из первого столбца, поэтому на их
пересечении находится вероятностное
числоаналогично
,
которое получено из суммы вероятностей,
находящихся на пересечениях соответственно
первой строки и первого столбца (0,15 ;
0,40; 0,05) и одно значение
,
которое находится на пересечении второй
строки и второго столбца, и наконец,,
которое находится на пересечении второй
строки и третьего столбца.
Из нашей таблицы находим:
Находим
корреляционный момент, используя формулу
(38):
Находим
коэффициент корреляции по формуле
(41)
Таким образом, отрицательная корреляция.
Упражнение.Закон
распределения дискретной с.в. задан
таблицей
|
|
-1 |
0,5 |
1 |
|
0,2 |
|
|
|
|
1 |
|
|
|
Найти коэффициент корреляции
Рассмотрим пример, где окажется две
зависимые случайные величинымогут
бытьнекоррелированными.
Пример 2. Двумерная случайная величина
)задана функцией плотностью
Докажем, что
и
зависимые,нонекоррелированные
случайные величины.
Решение.Воспользуемся ранее
вычисленными плотностями распределения
составляющихи
:
Так
как
,то
и
зависимые
величины. Для того, чтобы доказать
некоррелированность
и
,
достаточно убедиться в том, что
Найдем
корреляционный момент по формуле:
Поскольку дифференциальная
функция
симметрична относительно
оси OY,
то
аналогично
,
в силу симметрии
относительно оси OX.
Поэтому, вынося постоянный множитель
Внутренний интеграл равен
нулю (подынтегральная функция нечетна,
пределы интегрирования симметричны
относительно начала координат),
следовательно,
,
т.е. зависимые случайные величиныи
между собой некоррелируют.
Итак, из коррелированности двух
случайных величин следует их зависимость,
но из некоррелированности ещё нельзя
заключить о независимости этих величин.
Однако, для нормально
распределённых с.в. такой вывод является
исключением,
т.е. из некоррелированности
нормально распределенных
с.в. вытекает их независимость.
Этому вопросу посвящается
следующий пункт.
Для описания системы двух случайных величин, кроме математических ожиданий и дисперсий составляющих, используют и другие характеристики; к их числу относятся корреляционный момент и коэффициент корреляции.
Корреляционным моментом 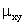
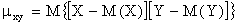
Для вычисления корреляционного момента дискретных величин используют формулу
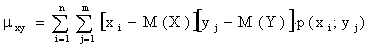
а для непрерывных величин – формулу 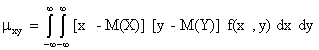
Корреляционный момент служит для характеристики связи между величинами X и Y . Как будет показано ниже, корреляционный момент равен нулю, если X и Y независимы; следовательно, если корреляционный момент не равен нулю, то X и Y – зависимые случайные величины.
Корреляционный момент можно записать в виде
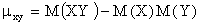
ТЕОРЕМА 13.1.18. Корреляционный момент двух независимых случайных величин X и Y равен нулю.
Доказательство. Так как X и Y – независимые случайные величины, то их отклонения X – M(X) и Y – M(Y) также независимы. Пользуясь свойствами математического ожидания (математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий сомножителей) и отклонения (математическое ожидание отклонения равно нулю), получим
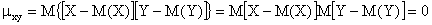
Из определения корреляционного момента следует, что он имеет размерность, равную произведению размерностей величин X и Y. Другими словами, величина корреляционного момента зависит от единиц измерения случайных величин. По этой причине для одних и тех же двух величин величина корреляционного момента имеет различные значения в зависимости от того, в каких единицах были измерены величины.
Пусть, например, X и Y были измерены в сантиметрах и 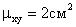
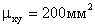
Коэффициентом корреляции 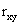
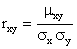
Так как размерность 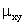
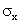
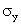
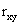
Очевидно, коэффициент корреляции независимых случайных величин равен нулю, так как 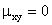
ТЕОРЕМА 13.1.19. Абсолютная величина корреляционного момента двух случайных величин X и Y не превышает среднего геометрического их дисперсий:
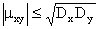
Доказательство. Введем в рассмотрение случайную величину
и найдем ее дисперсию 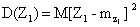
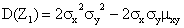
Любая дисперсия неотрицательна, поэтому 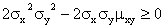
Отсюда 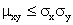
Введя случайную величину 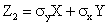
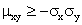
Объединим (1.51) и (1.52):
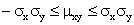
или 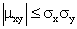
Итак,
.
ТЕОРЕМА 13.1.20. Абсолютная величина коэффициента корреляции не превышает единицы:
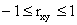
Доказательство. Разделим обе части двойного неравенства (13.1.53) на произведение положительных чисел 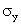
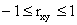
Итак, 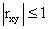
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 13 апреля 2022 года; проверки требуют 8 правок.
Ковариа́ция или корреляционный момент 
В теории вероятностей и статистике ковариация является мерой совместной изменчивости двух случайных величин. Если большие значения одной переменной в основном соответствуют большим значениям другой переменной, и то же самое верно для меньших значений (то есть переменные имеют тенденцию демонстрировать одинаковое поведение), ковариация положительна.В противоположном случае, когда большие значения одной переменной в основном соответствуют меньшим значениям другой (т. е. переменные имеют тенденцию показывать противоположное поведение), ковариация отрицательна. Таким образом, знак ковариации показывает тенденцию линейной зависимости между переменными. Величину ковариации нелегко интерпретировать, поскольку она не нормирована и, следовательно, зависит от величин переменных. Однако нормализованная версия ковариации, коэффициент корреляции, своей величиной показывает силу линейной зависимости.
Определение[править | править код]
Пусть 
,
где 

Предполагается, что все математические ожидания 
- Замечания
Выборочный коэффициент ковариации[править | править код]
Пусть 






где средние значения выборок (также называемые выборочными средними) определяют по формулам:
,
.
Если раскрыть скобки и воспользоваться формулой для выборочного среднего, то:

Свойства[править | править код]
- В частности, ковариация (в отличие от коэффициента корреляции) не инвариантна относительно смены масштаба, что не всегда удобно в приложениях.
Коэффициент корреляции[править | править код]
Коэффициент корреляции r или R- мера линейной зависимости между двумя случайными величинами. R лежит в пределах от -1 до 1. Если ковариация положительна, то с ростом значений одной случайной величины, значения второй имеют тенденцию возрастать, а если знак отрицательный — то убывать.
По абсолютному значению ковариации нельзя судить о том, насколько сильно величины взаимосвязаны, так как масштаб ковариации зависит от их дисперсий.
Значение ковариации можно нормировать, поделив её на произведение среднеквадратических отклонений (квадратных корней из дисперсий) случайных величин. Полученная величина называется коэффициентом корреляции Пирсона 
, где
— среднеквадратическое отклонение.
Соответственно,
[2].
Случайные величины, имеющие нулевую ковариацию, называются некоррелированными. Независимые случайные величины всегда некоррелированы. Обратное утверждение не всегда выполняется. Оно справедливо для нормально распределенных случайных величин.
См. также[править | править код]
- Ковариационная матрица — обобщение понятия ковариации для векторов из случайных величин
- Корреляция
- Дисперсия случайной величины
Примечания[править | править код]
- ↑ Мельников Р.М. Эконометрика. Учебное пособие
- ↑ Коэффициент корреляции. Дата обращения: 8 декабря 2011. Архивировано 17 декабря 2011 года.
Ссылки[править | править код]
- Weisstein, Eric W. Covariance (англ.) на сайте Wolfram MathWorld.
Пусть X и Y – любые две случайные величины (дискретные или непрерывные – неважно). Нас будет интересовать связь между ними. Относительно этой связи имеется, в принципе, три возможности.
1) Первая возможность: величины X и Y независимы друг от друга. Это значит, что каждая из этих величин принимает свои значения независимо от значений, принимаемых другой случайной величиной.
2) Вторая возможность – обратная первой: величины Х и Y связаны жесткой (функциональной) зависимостью, т. е. зависимостью вида Y=. В этом случае каждому возможному значению величины Y соответствуют вполне определенное значение Y=
величины Y. То есть возможные значения величины Y Жестко привязаны к возможным значениям величины X. Этому случаю был посвящен предыдущий параграф.
3) Третья возможность – промежуточная между первыми двумя: Х и Y в принципе связаны между собой (независимыми они не являются), но эта связь не жёсткая (размытая). Это значит, что каждому возможному значению Х величины Х могут соответствовать различные значения (У; у
; … ) величины Y, причём набор этих значений и (или) их вероятности меняются с изменением значения Х. Такого рода связь между случайными величинами называются Статистической (или Вероятностной) связью. Статистическая связь между случайными величинами X и Y означает, что изменение значения одной из них ведет к изменению Внешних условий Для реализации другой величины. Например, меняющаяся среднесуточная температура статистически влияет на плотность сельскохозяйственных вредителей на засеянном поле; объем денежной массы у покупателей статистически влияет на объем закупаемых ими товаров, и т. д.
Если при статистической связи между случайными величинами X и Y при изменении значения Х величины X еще и меняется Среднее значение величины Y, то говорят, что Y Корреляционно (в среднем) зависит от X. Аналогично понимается корреляционная зависимость X от Y. В частности, очевидно, что между температурой X воздуха и количеством Y вредителей имеет место не просто статистическая, а корреляционная зависимость, ибо с изменением температуры изменяется и среднее количество сельскохозяйственных вредителей. Аналогично между количеством X денег у покупателей и их тратами Y на покупку товаров тоже имеется, очевидно, корреляционная зависимость, ибо чем больше денег у покупателей, тем больше в среднем они покупают. Корреляционно (в среднем) связаны также урожайность различных культур с количеством внесенных под них удобрений, производительность труда рабочих с их квалификацией, и т. д.
Рассмотрим корреляционную связь между случайными величинами X и Y подробнее. Пусть – среднее значение тех значений У Величины Y, которые соответствуют данному значению X величины X. Оно же – условное математическое ожидание величины Y при X=X:
(6.1)
Так как каждому возможному значению X величины X будет соответствовать единственное значение , то это значение
является функцией от X:
(6.2)

меняется с изменением X, то есть если
, то между X и Y Имеется корреляционная связь – Y корреляционно (в среднем) зависит от X. А если
, то Y корреляционно от X не зависит. В последнем случае Y либо вообще не зависит от X, либо зависит, но лишь сугубо статистически.
Функциональная зависимость (6.2) называется Уравнением регрессии Y на X, А график этой зависимости – Линией регрессии Y на X (рис 2.22):
Линия регрессии Y на X наглядно показывает, как В среднем меняется случайная величинаY при изменении случайной величины X. Точки вокруг линии регрессии символизируют разброс возможных значений Y величины Y вокруг линии регрессии . Именно из этих значений Y для каждого X Должно быть найдено их среднее значение
.
Аналогично зависимость вида называется Уравнением регрессии X на Y, а ее график – Линией регрессии X на Y (рис 2.23)

Линия регрессии X на Y показывает, как В среднем меняется X при изменении Y.
Самой простой случай (и наиболее часто встречающийся на практике) – это когда функция или
линейна, то есть когда её график – прямая линия. В этом случае корреляционная зависимость Y от X и соответственно корреляционная зависимость X от Y Называется Линейной, в противном случае – Нелинейной.
В теории корреляции решаются Две основные задачи:
Первая задача теории корреляции – нахождение Уравнения регрессии, то есть нахождение зависимости между значениями одной случайной величины и соответствующими им средними значениями другой случайной величины.
Вторая задача теории корреляции – оценка Тесноты изучаемой корреляционной зависимости. В частности, теснота корреляционной зависимости Y от Х оценивается по степени рассеяния значений (У; у
; ….) величины Y (рис. 2.22) вокруг линии регрессии
. Большое рассеяние свидетельствует о слабой корреляционной зависимости Y от Х. Наоборот, малое рассеяние указывает на наличие достаточно сильной (тесной) корреляционной зависимости. Возможно даже, что Y зависит от Х функционально, то есть жёстко, но из-за второстепенных случайных факторов или просто из-за погрешностей измерений эта зависимость оказалась несколько размытой.
Те же задачи, естественно, стоят, если исследуется корреляционная зависимость X от Y.
Наиболее просто решаются обе эти задачи при наличии линейной корреляционной зависимости одной случайной величины от другой. И здесь важную роль играет так называемый Корреляционный момент Или, что одно и то же, Ковариация
случайных величин Х и Y, которые определяются как математическое ожидание произведения отклонений Х и Y От их математических ожиданий:
(6.4)
Их можно преобразовать к виду (проделайте это самостоятельно):
(6.5)
Как известно, у независимых случайных величин Х И Y, как у дискретных, так и у непрерывных, . А значит, для независимых случайных величин
(6.6)
Поэтому если , то это автоматически указывает на зависимость случайных величин Х и Y друг от друга.
Отметим, что обратное, вообще говоря, неверно: из того, что корреляционный момент , ещё нельзя сделать вывод, что Х И Y независимы. Они могут быть зависимы, причём даже функционально. Например, если распределение величины Х симметрично относительно точки Х=0,так что автоматически
и
, а
– функция от Х, то на основании (6.5) получаем:
И это несмотря на то, что Х и Y связаны функциональной зависимостью
Случайные величины, для которых , называются Линейно некоррелированными. Независимые величины всегда линейно некоррелированы. Но линейно некоррелированные величины могут быть, как мы только что видели, как зависимыми, так и независимыми. Линейно коррелированные же величины (для них
) всегда зависимы.
Кстати, если случайные величины X И Y распределены нормально, то можно доказать (на этом не останавливаемся), что Их линейная некоррелированность равнозначна их независимости. Для других же величин Х и Y это не обязательно одно и тоже.
Отметим, что корреляционный момент обладает одним существенным недостатком: он зависит от единиц измерения величин X И Y. Поэтому на практике вместо него часто используется безразмерная величина
(6.7)
Которая называется Коэффициентом линейной корреляции. Он играет, как мы увидим ниже, большую роль при решении обеих задач теории корреляции в случае линейной корреляционной зависимости между случайными величинами.
Корреляционный момент и коэффициент линейной корреляции
равны или не равны нулю одновременно. Поэтому линейную коррелированность и линейную некоррелированность случайных величин X и Y можно устанавливать и по равенству или неравенству нулю коэффициента линейной корреляции
.
Так как, согласно (6.5), , то и
=
(6.8)
Коэффициент линейной корреляции обладает еще одним важным свойством: он не изменится, если от X и Y перейти к безразмерным нормированным случайным величинам
(6.9)
То есть
=
(6.10)
Нормированными случайными величинами и
называются потому, что их математические ожидания равны нулю, а средние квадратические отклонения равны единице:
(
)=
(
)=
(6.11)
Равенства (6.11) легко доказываются с помощью свойств (3.17) – (3.23) математического ожидания и дисперсии, которые справедливы как для непрерывных, так и для дискретных случайных величин (проделайте это самостоятельно). Ну, а то, что=
, уже вытекает из (6.4), (6.5), (6.7), (6.9) и (6.11):
Для дальнейшего рассмотрения свойств коэффициента линейной корреляции случайных величин X и Y найдем дисперсию их суммы X+Y и разности X–Y. Если величина X и Y независимы, то такая формула уже получена (см. (3.22)):
(6.12)
Причем эта формула верна как для дискретных, так и для непрерывных случайных величин. А если X и Y зависимы (функционально или статистически), то соответствующая формула имеет вид:
(6.13)
Действительно:
В частности, для нормированных случайных величин формула (6.13) примет вид:
(6.14)
А так как, по смыслу дисперсии, , то из (6.14) получаем:
(6.15)
И так как, согласно (6.10), ) =
, то для любых случайных величин Х и Y получаем следующий вывод:
(6,16)
Если коэффициент линейной корреляции , то он характеризует не только Наличие зависимости (связи) между Х и Y. Своей величиной, как мы это сейчас увидим, он характеризует И тесноту этой связи. Однако не любой, а Лишь линейной корреляционной связи между Х и Y. Отсюда и его название – коэффициент Линейной корреляции. Максимальная теснота этой связи соответствует случаям, когда
=
. При этом между Х и Y имеет место жёсткая функциональная связь, причём связь непременно линейная:
.
Действительно, при =
и
)=
, а тогда из (6.14) вытекает, что имеет место одно из двух равенств: или
, или
. Но дисперсия случайной величины равна нулю, если только эта случайная величина является константой. То есть или
, или
. Заметим, что в обоих случаях константа
, ибо на основании (6.11) получаем:
Итак, при =
либо
, либо
. А отсюда уже, согласно связи (6.9)
с
, следует подтверждение того, что в обоих случаях величины Х и Y связаны линейной функциональной зависимостью вида
.
Верно и обратное: если случайные величины Х и Y связаны линейной функциональной зависимостью , то их коэффициент линейной корреляции
Равен либо 1, либо -1.
Докажем это. Действительно, если , то согласно (6.9) и свойств математического ожидания и дисперсии получаем:
;
=
=.
А тогда
Таким образом, коэффициент линейной корреляции есть показатель того, насколько зависимость между случайными величинами X и Y близка к строгой линейной зависимости
. Его малость (удаленность от
может означать одно из двух: или малую тесноту (большое рассеяние) линейной корреляционной связи между X и Y, или существенную нелинейность этой связи, которая, кстати, может быть весьма тесной.
Сформулируем это утверждение более определенно. Найдем такие числовые коэффициенты K и B, чтобы линейная функция КX+B случайной величины X наилучшим образом приближала случайную величину Y. Для этого представим Y в виде
Y=кX+B+Z (6.17) Случайную величину Z можно рассматривать как ошибку приближения величины Y линейной функцией Y=кX+B. Эту ошибку естественно считать минимальной, если потребовать, чтобы математическое ожидание и дисперсия
была минимальной. Первое из этих требований дает:
(6.18)
С учетом найденного значения B и (6.17) ошибка Z примет вид:
Теперь вычислим – дисперсию величины Z:
=
Первое из полученных слагаемых неотрицательно и не зависит от параметра K. Таким образом, дисперсия ошибки Z будет минимальной при том значении K, которое обеспечит обращение в нуль второго слагаемого. То есть при
(6.19)
При этом дисперсия (её минимальное значение) примет вид:
(6.20)
Итак, вывод: наилучшее приближение случайной величины Y линейной функцией КX+B случайной величины Х будет иметь место при значениях K и B, определяемых формулами (6.19) и (6.18). То есть такое приближение будет иметь вид:
(6.21)
Ошибка Z Этого линейного приближения величины Y имеет математическое ожидание (среднее значение), равное нулю. А дисперсия этой ошибки определяется формулой (6.20).
Если , то дисперсия ошибки
. А это, с учетом равенства
означает, что
. То есть при
в равенстве (6.21) ошибки нет и оно является точным. Но чем больше удален коэффициент линейной корреляции
От
, то есть чем ближе он к нулю, тем больше становится дисперсия
ошибки Z, а вместе с ней тем больше становится и сама ошибка Z приближения (6.21). При
Эта ошибка становится максимально возможной, а само приближение (6.21) принимает вид
и перестаёт, таким образом, зависеть от X. То есть при
=0 линейная зависимость Y от X отсутствует. Это значит, что или между случайными величинами X и Y вообще нет никакой связи, или они связаны, но какой-то нелинейной связью (функциональной или статистической).
Кстати, так как наилучшим приближением случайной величины Y при X=X является, очевидно, условная средняя , то из (6.21) сразу вытекает Наилучшее линейное приближение уравнения регрессии
величины Y на величину X. Для его получения нужно в (6.21) заменить X На X и Y на
. В итоге получим:
(6.22)
Здесь
(6.23)
Полученное простое линейное уравнение (6.22) используют на практике для приближенной замены истинного уравнения регрессии , если линия регрессии близка к прямой. Если же она сильно отличается от прямой (как на рис. 2.22), то его тоже можно использовать, только не на всем интервале (А; B) возможных значений величины X, а на коротких частях этого интервала, на которых линию регрессии можно приближенно считать прямой.
При приближенное линейное уравнение (6.22) становится точным. То есть становится истинным уравнением
регрессии Y на X. Более того, при этом
Превращается просто в Y – в единственное значение Y при X=X. Это происходит потому, что при
становится точным равенство (6.21). А это значит, что каждому значению X величины X будет соответствовать единственное значение Y величины Y. И, таким образом, будет
. Линия регрессии
(см. рис. 2.22) станет прямой, и никакого разброса вокруг неё точек, изображающих возможные значения величины Y, не будет – все они окажутся на этой прямой.
Но если , то по мере удаления его значения от
1 истинная линия регрессии или искривляется, или остается прямой, но вокруг нее появляется облако точек, причем тем более широкое, чем ближе
к нулю. Или одновременно и линия регрессии искривляется, и облако точек вокруг нее расширяется. При
близком к нулю или тем более равном нулю нельзя даже приближено считать величины X И Y Связанными линейной корреляционной зависимостью. Связь между этими линейно некоррелированными (или слабо линейно коррелированными) случайными величинами будет или отсутствовать вообще, или будет существенно нелинейной. То есть в этом случае полученные выше формулы (6.21) и (6.22) приближенного линейного выражения одной величины (Y) через другую величину (Х) применять нельзя – они могут давать слишком грубое приближение. Тут требуется дополнительное исследование характера связи между такого рода слабо линейно коррелированными случайными величинами X и Y, которое мы проведем ниже.
Перейдем к этому исследованию. То есть поставим вопрос об оценке тесноты Любой, А не только линейной, корреляционной связи между случайными величинами X и Y.
Итак, допустим, что корреляционная связь между случайными величинами X и Y есть, и эта связь заведомо нелинейная (квадратичная, экспоненциальная, логарифмическая, и т. д.). Это значит, что уравнение Регрессии Y на Х таково, что
и при этом
. То есть линия регрессии Y На Х – кривая линия (рис. 2.22). Для оценки тесноты такой криволинейной корреляционной связи между X и Y коэффициент линейной корреляции
, который будет близок к нулю, не годится. В этом случае указанною тесноту оценивают с помощью так называемого Корреляционного отношения.
Чтобы ввести это понятие, рассмотрим случайною величину , которая является функцией величины Х и которая при Х = х Принимает среднее значение
величины Y. Математическое ожидание
величины
Совпадает с математическим ожиданием (средним значением
) величины Y:
(6.24)
А дисперсия Величины
составляет лишь часть дисперсии
величины Y:
(6.25)
При доказательстве равенств (6.24) и (6.25) ограничимся случаем, когда X и Y – дискретные случайные величины.
Итак, пусть X и Y – зависимые дискретные случайные величины, а таблица (6.26) – закон их совместного распределения:
|
X Y |
Х |
Х |
………… |
Х |
Q |
(6.26) |
|
Y |
P |
P |
………… |
P |
Q |
|
|
Y |
P |
P |
………… |
P |
Q |
|
|
……. |
……. |
……. |
………… |
……. |
……. |
|
|
Y |
P |
P |
………… |
P |
Q |
|
|
Pi |
P |
P |
………… |
P |
1 |
Здесь (X, X
,… X
) и (Y
, Y
,…Y
) – возможные значения величин X и Y соответственно, а
– вероятности того, что в результате испытания парой случайных величин
Будет принята пара значений
. Кстати, сумма всех вероятностей
, как сумма вероятностей событий, составляющих полную группу событий, должна равняться единице:
(6.27)
Действительно, события, состоящие в том, что , являются несовместными. Причем одно из них обязательно произойдет. То есть эти события действительно образуют полную группу событий.
В последней строке таблицы (6.26) просуммированы вероятности по строкам (внутри каждого столбца). А в последнем столбце этой таблицы просуммированы вероятности
по столбцам (внутри каждой строки):
(6.28)
Вероятности – это, очевидно, вероятности значений
величины X, а вероятности
– это вероятности значений
величины Y. То есть на базе закона совместного распределения случайных величин X и Y можно записать и законы распределения каждой из этих величин в отдельности:
|
|
|
|
… |
|
|
|
|
… |
|
(6.29) |
|
|
|
|
|
… |
|
|
|
|
… |
|
Среднее значение Величины Y для каждого возможного значения
величины Y следует находить по формуле:

Действительно, согласно (6.1)
(6.31)
То есть – это условное математическое ожидание величины Y при X=
. А следовательно, оно должно быть найдено как сумма произведений значений
величины Y на соответствующее им вероятности этих значений при условии, что X=
. То есть
(6.32)
А условные вероятности можно найти из формулы вероятности произведения двух зависимых событий (формула (4.5) главы 1):

Из формул (6.32) и (6.33) и следует формула (6.30).
Подсчитав значения , можем составить и закон распределения случайной величины
:
|
|
|
|
… |
|
(6.34) |
|
|
|
|
… |
|
(вероятности значений величины
те же, что и вероятности значений
величины X).
Ну, а теперь можем перейти к доказательству равенств (6.24) и (6.25). Сначала докажем (6.24):
(6.35)
Равенство (6.24) доказано.
Для доказательства равенства (6.25) образует случайную величину и запишем закон её распределения:
Математическое ожидание этой случайной величины равно нулю – это следует из (6.24). Покажем ещё, что
(6.37)
Закон распределения случайной величины Имеет вид:
Отсюда следует:
=
= 
. (6.39)
А теперь, опираясь на доказанные равенства (6.24) и (6.37), можно доказать и равенство (6.25):
Равенство (6.25) доказано. Это равенство дает разложение общей дисперсии зависимой от X случайной величины Y на сумму двух слагаемых: дисперсии функции и среднего квадрата отклонения Y от этой функции. Иначе говоря, общий разброс значений У Величины Y Вокруг её среднего значения
складывается из разброса значений
величины
вокруг того же
, и разброса значений У вокруг
. То есть формула (6.25) раскладывает общий разброс всех возможных значений Y Величины Y вокруг её математического ожидания
на разброс вокруг
точек
Кривой регрессии, и на разброс значений У (облака точек, изображающих значения Y) вокруг кривой регрессии
Введем теперь отношение

Которое будет называть Корреляционным отношением Y к X. Очевидно, что всегда
(6.41)
Из определения следует, что
=0 при
, то есть при условии, что
=Const. Причем эта константа, естественно, равна
. Но тогда уравнение регрессии Y на X имеет вид
=
и, следовательно, случайная величина Y не зависит корреляционно (в среднем) от величины X. А если
, то в этом случае из (6.40) следует, что
=0, откуда вытекает, что
. То есть при
случайные величины X и Y связаны жесткой функциональной зависимостью
, причем
Const.
Из сказанного следует, что чем ближе корреляционное отношение к единице, тем ближе корреляционная зависимость Y от X к функциональной зависимости. А это значит, тем эта корреляционная зависимость теснее. Наоборот, чем ближе
к нулю, тем она слабее.
Таким образом, корреляционное отношение случайной величины Y К случайной величине X является мерой и наличия, и тесноты Любой (а не только линейной) корреляционной зависимости величины Y от величины X.
Естественно, можно ввести в рассмотрение и корреляционное отношение величины X к величине Y.

Которое оценивает наличие и тесноту корреляционной зависимости величины X от Y, где – уравнение регрессии X на Y.
Отметим, что в отличие от коэффициента линейной корреляции, которой симметричен относительно X и Y (), корреляционное отношение таким свойством, судя по (6.40) и (6.42), не обладает:
(6.43)
Можно еще доказать, что всегда
(6.44)
При этом в случае равенства
(6.45)
Имеет место Точная линейная корреляционная зависимость Y от X. Это значит, что при условии (6.45) приближенное уравнение регрессии (6.22) Y на X становится Точным.
Аналогично в случае
(6.46)
Становится точным соответствующее уравнение регрессии X на Y.
Пример. Дискретные случайные величины X и Y заданы следующим законом их совместного распределения:
|
Y |
0 |
1 |
2 |
|
|
0 |
0,10 |
0,16 |
0,18 |
0,44 |
|
1 |
0,06 |
0,20 |
0,30 |
0,56 |
|
|
0,16 |
0,36 |
0,48 |
1 |
Требуется:
1) Найти коэффициент линейной корреляции .
2) Найти корреляционное отношение .
3) Построить линию регрессии величины Y на величину X.
Решение. Запишем сначала законы распределения величин X и Y по отдельности:
|
X |
0 |
1 |
2 |
Y |
0 |
1 |
|
|
Р |
0,16 |
0,36 |
0,48 |
Р |
0,44 |
0,56 |
Отсюда, в частности, следует (получите это самостоятельно):
;
Теперь найдем . Для этого, согласно (6.7), предварительно нужно найти корреляционный момент
. Его найдем по формуле (6.5), используя совместный закон распределения (таблицу) величины Х и Y:
Тогда:
Величина . Таким образом, величины X и Y линейно коррелированы, а значит и зависимы. Вместе с тем величина
Невелика (она гораздо ближе к нулю, чем к 1 или к -1). Поэтому корреляционная зависимость Y от Х или слабая, или существенно нелинейная, или то и другое вместе.
Чтобы лучше выяснить этот вопрос, подсчитаем корреляционное отношение величины Y к величине Х. Для этого сначала для каждого значения Х величины Х подсчитаем среднее значение
величины Y. Используя формулы (6.30), получим:
Полученные данные позволяют записать таблицу вида (6.34) – закон распределения функции Случайной величины Х:
|
|
0,375 |
0,556 |
0,625 |
|
Р |
0,16 |
0,36 |
0,48 |
Из этой таблицы находим:
=
.
Величина оказалась большей, чем
– так и должно, согласно (6.44), быть. Однако и она невелика, что свидетельствует о малой тесноте корреляционной зависимости Y и X. А так как различие между
и
Незначительное, то корреляционная зависимость Y от X близка к линейной.
Этот вывод должна подтвердить линия регрессии . Ее следует строить по трем точкам:
|
|
0 |
1 |
2 |
|
|
0,375 |
0,556 |
0,625 |
Как легко убедиться, ломаная, соединяющая эти три точки, действительна близка к прямой линии.
| < Предыдущая | Следующая > |
|---|
Макеты страниц
При совместном изучении нескольких случайных величин приходится пользоваться, кроме моментов каждой из них в отдельности, еще смешанными моментами случайных величин. Прежде чем дать определение смешанных моментов случайных величин, дадим формулу для математического ожидания произвольной функции 





Легко видеть, что в частном случае, когда функция 




Полагая, в частности, 

Смешанным моментом порядка 



Очевидно, что при 


первого порядка 

Сметанным центральным моментом порядка 



Очевидно, что при 





Среди смешанных моментов случайных величин особую роль играет центральный смешанный момент второго порядка который обычно называется корреляционным моментом или просто смешанным моментом второго порядка случайных величин 



На основании общей формулы (17.1) формулу (17.5) можно переписать в виде:

Таким образом, при желании ограничиться численной характеристикой случайных величин при помощи их моментов не выше второго порядка при совместном изучении нескольких случайных величин необходимо учесть, кроме их математических ожиданий и дисперсий, еще корреляционные моменты, которые до известной степени характеризуют взаимосвязь между случайными величинами.
Совершенно так же, как в § 10 мы уподобили распределение вероятностей случайной величины распределению масс на прямой, распределение вероятностей двумерного или трехмерного случайного вектора можно рассматривать как распределение масс на плоскости 
необходимо знать его центр массы, центральные моменты инерции и произведения инерции, при совместном изучении нескольких случайных величин необходимо знать их математические ожидания, дисперсии и корреляционные моменты. Однако в отличие от динамики твердого тела в теории вероятностей численная характеристика случайных величин при помощи их математических ожиданий, дисперсий и корреляционных моментов не всегда бывает достаточной. Так, например, при вычислении вероятностей попадания случайной точки в заданные области плоскости или пространства необходимо знать соответствующие плотности вероятности случайного вектора.
Вместо корреляционного момента случайных величин часто пользуются так называемым коэффициентом корреляции. Коэффициентом корреляции случайных величин 

Легко видеть, что корреляционный момент и коэффициент корреляции независимых случайных величин равны нулю. В самом деле, подставляя в формулу (17.6) выражение (16.9) плотности вероятности независимых случайных величин 

Но каждый из двух последних интегралов равен нулю. Следовательно, и 



Случайные величины 

момент равен нулю. Согласно доказанному выше независимые величины всегда не коррелированы. Зависимые величины могут быть как коррелированными, так и некоррелированными. Случайные величины 


Пользуясь формулой бинома Ньютона, можно выразить все смешанные центральные моменты дгя двух случайных величин через их смешанные начальные моменты 
Если в формулы § 10 подставить вместо 



Математическое ожидание условного математического ожидания 


Действительно, на основании формул (16.7) и (17.1)

Формула (17.9) показывает, что при вычислении математического ожидания функции двух случайных величин вероятностное осреднение можно вести в два приема: сначала по всем возможным значениям одной случайной величины при фиксированном значении другой, а потом по всем возможным значениям другой случайной величины. Этим обстоятельством мы воспользуемся в главе 18.







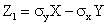
![{mathrm {cov}}(X,Y)={mathbb {M}}left[(X-{mathbb {M}}X)(Y-{mathbb {M}}Y)right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/484924339f3e4253c18c4f24d1be5125d1b4230e)













