Как найти корреляцию между двумя величинами - Сайт, где вы сможете решить свои вопросы

Download Article

Calculate correlation by hand, online, or with a graphing calculator

Download Article

By Hand

Online Calculators

Graphing Calculators

Reviewing the Fundamentals

The correlation coefficient, denoted as r or ρ, is the measure of linear correlation (the relationship, in terms of both strength and direction) between two variables. It ranges from -1 to +1, with plus and minus signs used to represent positive and negative correlation. If the correlation coefficient is exactly -1, then the relationship between the two variables is a perfect negative fit; if the correlation coefficient is exactly +1, then the relationship is a perfect positive fit. Otherwise, two variables may have a positive correlation, a negative correlation, or no correlation at all. You can calculate correlation by hand, by using some free correlation calculators available online, or by using the statistical functions of a good graphing calculator.

1
Assemble your data. To begin calculating a correlation efficient, first examine your data pairs. It is helpful to put them in a table, either vertically or horizontally. Label each row or column x and y.^[1]
- For example, suppose you have four data pairs for x and y. Your table may look like this:
  - x || y
  - 1 || 1
  - 2 || 3
  - 4 || 5
  - 5 || 7
2

Calculate the mean of x. In order to calculate the mean, you must add all the values of x, then divide by the number of values.^[2]

Advertisement
3

Find the mean of y. To find the mean of y, follow the same steps, adding all the values of y together, then dividing by the number of values.^[3]
4

Determine the standard deviation of x. Once you have your means, you can calculate standard deviation. To do so, use the formula:^[4]
5

Calculate the standard deviation of y. Using the same basic steps, find the standard deviation of y. You will use the same formula, using the y data points.^[5]
6
Review the basic formula for finding a correlation coefficient. The formula for calculating a correlation coefficient uses means, standard deviations, and the number of pairs in your data set (represented by n). The correlation coefficient itself is represented by the lower-case letter r or the lower-case Greek letter rho, ρ. For this article, you will use the formula known as the Pearson correlation coefficient, shown below:^[6]
- $rho =left({frac {1}{n-1}}right)Sigma left({frac {x-mu _{x}}{sigma _{x}}}right)*left({frac {y-mu _{y}}{sigma _{y}}}right)$
- You may notice slight variations in the formula, here or in other texts. For example, some will use the Greek notation with rho and sigma, while others will use r and s. Some texts may show slightly different formulas; but they will be mathematically equivalent to this one.
7

Find the correlation coefficient. You now have the means and standard deviations for your variables, so you can proceed to use the correlation coefficient formula. Remember that n represents the number of values you have. You have already worked out the other relevant information in the steps above.^[7]
8
Interpret your result. For this data set, the correlation coefficient is 0.988. This number tells you two things about the data. Look at the sign of the number and the size of the number.^[8]
- Because the correlation coefficient is positive, you can say there is a positive correlation between the x-data and the y-data. This means that as the x values increase, you expect the y values to increase also.
- Because the correlation coefficient is very close to +1, the x-data and y-data are very closely connected. If you were to graph these points, you would see that they form a very good approximation of a straight line.

1

Search the Internet for correlation calculators. Measuring correlation is a fairly standard calculation for statisticians. The calculation can become very tedious if done by hand for large data sets. As a result, many sources have made correlation calculators available online. Use any search engine and enter the search term “correlation calculator.”
2
Enter your data. Carefully review the instructions on the website so you will enter your data properly. It is important that your data pairs are kept in order, or you will generate an incorrect correlation result. Different websites use different formats to enter data.
- For example, at the website http://ncalculators.com/statistics/correlation-coefficient-calculator.htm, you will find one horizontal box for entering x-values and a second horizontal box for entering y-values. You enter your terms, separated only by commas. Thus, the x-data set that was calculated earlier in this article should be entered as 1,2,4,5. The y-data set should be 1,3,5,7.
- At another site, http://www.alcula.com/calculators/statistics/correlation-coefficient/, you can enter data either horizontally or vertically, as long as you keep the data points in order.
3

Calculate your results. These calculation sites are popular because, after you enter your data, you generally need only to click on the button that says “Calculate,” and the result will appear automatically.

1
Enter your data. Using a handheld graphing calculator, enter your calculator’s statistics function and then select the “Edit” command.^[9]
- Each calculator will have slightly different key commands. This article will give the specific instructions for the Texas Instruments TI-86.
- Enter the Stat function by pressing [2nd]-Stat (above the + key), then hit F2-Edit.
2
Clear any old stored data. Most calculators will keep statistical data until cleared. To make sure that you do not confuse old data with new data, you should first clear any previously stored information.^[10]
- Use the arrow keys to move the cursor to highlight the heading “xStat.” Then press Clear and Enter. This should clear all values in the xStat column.
- Use the arrow keys to highlight the yStat heading. Press Clear and Enter to empty the data from that column as well.
3
Enter your data values. Using the arrow keys, move the cursor to the first space under the xStat heading. Type in your first data value and then hit Enter. You should see the space at the bottom of the screen display “xStat(1)=__,” with your value filling the blank space. When you hit Enter, the data will fill the table, the cursor will move to the next line, and the line at the bottom of the screen should now read “xStat(2)=__.”^[11]
- Continue entering all the x-data values.
- When you complete the x-data, use the arrow keys to move to the yStat column and enter the y-data values.
- After all the data has been entered, hit Exit to clear the screen and leave the Stat menu.
4
Calculate the linear regression statistics. The correlation coefficient is a measure of how well the data approximates a straight line. A statistical graphing calculator can very quickly calculate the best-fit line and the correlation coefficient.^[12]
- Enter the Stat function and then hit the Calc button. On the TI-86, this is [2nd][Stat][F1].
- Choose the Linear Regression calculations. On the TI-86, this is [F3], which is labeled “LinR.” The graphic screen should then display the line “LinR _,” with a blinking cursor.
- You now need to enter the names of the two variables that you want to calculate. These are xStat and yStat.
  - On the TI-86, select the Names list by hitting [2nd][List][F3].
  - The bottom line of your screen should now show the available variables. Choose [xStat] (this is probably button F1 or F2), then enter a comma, then [yStat].
  - Hit Enter to calculate the data.
5

1
Understand the concept of correlation. Correlation refers to the statistical relationship between two quantities. The correlation coefficient is a single number that you can calculate for any two sets of data points. The number will always be something between -1 and +1, and it indicates how closely connected the two data sets tend to be.^[14]
- For example, if you were to measure the heights and ages of children up to the age of about 12, you would expect to find a strong positive correlation. As children get older, they tend to get taller.
- An example of negative correlation would be data comparing a person’s time spent practicing golf shots and that person’s golf score. As the practice increases, the score should decrease.
- Finally, you would expect very little correlation, either positive or negative, between a person’s shoe size, for example, and SAT scores.
2
Know how to find a mean. The arithmetic mean, or “average,” of a set of data is calculated by adding all of the values of the data together, then dividing by the number of values in the set. When you find the correlation coefficient for your data, you will need to calculate the mean of each set of data.^[15]
- The mean of a variable is denoted by the variable with a horizontal line above it. This is often referred to as “x-bar” or “y-bar” for the x and y data sets. Alternatively, the mean may be signified by the lower-case Greek letter mu, μ. To indicate the mean of x-data points, for example, you could write μ_x or μ(x).
- As an example, if you have a set of x-data points (1,2,5,6,9,10), then the mean of this data is calculated as follows:
  - $mu _{x}=(1+2+5+6+9+10)/6$
  - $mu _{x}=33/6$
  - $mu _{x}=5.5$
3
Note the importance of standard deviation. In statistics, standard deviation measures variation, showing how numbers are spread out in relationship to the mean. A group of numbers with a low standard deviation are fairly tightly collected. A group of numbers with a high standard deviation are widely scattered.^[16]
- Symbolically, standard deviation is expressed with either the lower-case letter s or the lower-case Greek letter sigma, σ. Thus, the standard deviation of the x-data is written as either s_x or σ_x.
4
Recognize summation notation. The summation operator is one of the most common operators in mathematics, indicating a sum of values. It is represented by the upper-case Greek letter, sigma, or ∑.^[17]
- As an example, if you have a set of x-data points (1,2,5,6,9,10), then ∑x means:
  - 1+2+5+6+9+10 = 33.

Add New Question

Question

You are given the following information about two variables x and y: Mean(x)= 315 and Mean(y)=1,103. Variance(x)=59 and Variance(y)=156. Covariance(x,y)= -54. Calculate the coefficient of correlation between X and Y. Calculate your answer to two decimal places.

This question raises a higher level of statistics than is addressed in this article. It is possible to calculate the correlation coefficient from the means, variance and covariance, without actually having the original data points to begin with. The relationship is Correlation Coefficient = Covariance / ((Std. Dev. (x) * (Std. Dev. (y)). The standard deviation is the square root of the variance. So, with your data, this simplifies to Corr.Coeff.=-54/sqrt(59)sqrt(156) = -0.56.

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Thanks for submitting a tip for review!

Video

Tips

In general, a correlation coefficient higher than 0.8 (either positive or negative) represents a strong correlation; a correlation coefficient lower than 0.5 (again, either positive or negative) represents a weak one.
The correlation coefficient is sometimes called the “Pearson product-moment correlation coefficient” in honor of its developer, Karl Pearson.

Warnings

Correlation shows that the two sets of data are connected in some way. However, be careful not to interpret this as causation. For example, if you compare people’s shoe sizes and their height, you will probably find a strong positive correlation. Taller people generally have larger feet. However, this does not mean that growing tall causes your feet to grow, or that large feet cause you to grow tall. They just happen together.

References

About This Article

Article SummaryX

To find the correlation coefficient by hand, first put your data pairs into a table with one row labeled “X” and the other “Y.” Then calculate the mean of X by adding all the X values and dividing by the number of values. Calculate the mean for Y in the same way. Next, use the formula for standard deviation to calculate it for both X and Y. Finally, use the means and standard deviations and the number of pairs in your data set as inputs to the correlation coefficient formula, and solve the resulting equation. To learn how to find the correlation coefficient with an online calculator or your own graphing calculator, read on!

Did this summary help you?

Thanks to all authors for creating a page that has been read 204,021 times.

Did this article help you?

Источник

Для графического представления корреляционной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая пара значений маркируется при помощи определённого символа. Такой график называется диаграммой рассеяния.

Корреля́ция (от лат. correlatio «соотношение»), или корреляцио́нная зави́симость — статистическая взаимосвязь двух или более случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми), при этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин^[1].

Математической мерой корреляции двух случайных величин служит корреляционное отношение ^[2] либо коэффициент корреляции (или )^[1]. В случае если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической^[3].

Впервые в научный оборот термин корреляция ввёл французский палеонтолог Жорж Кювье в XVIII веке. Он разработал «закон корреляции» частей и органов живых существ, с помощью которого можно восстановить облик ископаемого животного, имея в распоряжении лишь часть его останков. В статистике слово «корреляция» первым стал использовать английский биолог и статистик Фрэнсис Гальтон в конце XIX века^[4].

Корреляция и взаимосвязь величин[править | править код]

Значительная корреляция между двумя случайными величинами всегда является свидетельством существования некоторой статистической связи в данной выборке, но эта связь не обязательно должна наблюдаться для другой выборки и иметь причинно-следственный характер. Часто заманчивая простота корреляционного исследования подталкивает исследователя делать ложные интуитивные выводы о наличии причинно-следственной связи между парами признаков, в то время как коэффициенты корреляции устанавливают лишь статистические взаимосвязи. Например, рассматривая пожары в конкретном городе, можно выявить весьма высокую корреляцию между ущербом, который нанёс пожар, и количеством пожарных, участвовавших в ликвидации пожара, причём эта корреляция будет положительной. Из этого, однако, не следует вывод «увеличение количества пожарных приводит к увеличению причинённого ущерба», и тем более не будет успешной попытка минимизировать ущерб от пожаров путём ликвидации пожарных бригад^[5]. Корреляция двух величин может свидетельствовать о существовании общей причины, хотя сами явления напрямую не взаимодействуют. Например, обледенение становится причиной как роста травматизма из-за падений, так и увеличения аварийности среди автотранспорта. В этом случае две величины (травматизм из-за падений пешеходов и аварийность автотранспорта) будут коррелировать, хотя они не связаны причинно-следственно друг с другом, а лишь имеют стороннюю общую причину — гололедицу.

В то же время, отсутствие корреляции между двумя величинами ещё не значит, что между ними нет никакой связи. Например, зависимость может иметь сложный нелинейный характер, который корреляция не выявляет.

Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными. В первом случае предполагается, что мы можем определить только наличие или отсутствие связи, а во втором — также и её направление. Если предполагается, что на значениях переменных задано отношение строгого порядка, то отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой. При этом коэффициент корреляции будет отрицательным. Положительная корреляция в таких условиях — это такая связь, при которой увеличение одной переменной связано с увеличением другой переменной. Возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин.

Показатели корреляции[править | править код]

Метод вычисления коэффициента корреляции зависит от вида шкалы, к которой относятся переменные. Так, для измерения переменных с интервальной и количественной шкалами необходимо использовать коэффициент корреляции Пирсона (корреляция моментов произведений). Если по меньшей мере одна из двух переменных имеет порядковую шкалу, либо не является нормально распределённой, необходимо использовать ранговую корреляцию Спирмена или (тау) Кендалла. В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими — четырёхполевая корреляция. Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, когда связь между ними линейна (однонаправлена).

Параметрические показатели корреляции[править | править код]

Ковариация[править | править код]

Важной характеристикой совместного распределения двух случайных величин является ковариация (или корреляционный момент). Ковариация является совместным центральным моментом второго порядка^[6]. Ковариация определяется как математическое ожидание произведения отклонений случайных величин^[7]:

$mathrm {cov} _{XY}=mathbf {M} left[(X-mathbf {M} (X))(Y-mathbf {M} (Y))right]=mathbf {M} (XY)-mathbf {M} (X)mathbf {M} (Y)$ ,

где — математическое ожидание (в англоязычной литературе принято обозначение от expected value).

Свойства ковариации:

Доказательство

Введём в рассмотрение случайную величину $mathbf {Z} _{1}=mathbf {sigma } _{Y}mathbf {X} -mathbf {sigma } _{X}mathbf {Y}$ (где — среднеквадратическое отклонение) и найдём её дисперсию $mathbf {D} (Z_{1})=mathbf {M} [mathbf {Z} -m_{Z1}]^{2}$ . Выполнив выкладки получим:

$mathbf {D} (Z_{1})=2mathbf {sigma ^{2}} _{X}mathbf {sigma ^{2}} _{Y}-2mathbf {sigma } _{X}mathbf {sigma } _{Y}mathrm {cov} _{XY}.$

Любая дисперсия неотрицательна, поэтому

$2mathbf {sigma ^{2}} _{X}mathbf {sigma ^{2}} _{Y}-2mathbf {sigma } _{X}mathbf {sigma } _{Y}mathrm {cov} _{XY}geqslant 0$

Отсюда

$mathrm {cov} _{XY}leqslant mathrm {sigma } _{X}mathrm {sigma } _{Y}.$

Введя случайную величину $mathbf {Z} _{2}=mathbf {sigma } _{Y}mathbf {X} +mathbf {sigma } _{X}mathbf {Y}$ , аналогично

$mathrm {cov} _{XY}geqslant -mathrm {sigma } _{X}mathrm {sigma } _{Y}.$

Объединив полученные неравенства имеем

$-mathrm {sigma } _{X}mathrm {sigma } _{Y}leqslant mathrm {cov} _{XY}leqslant mathrm {sigma } _{X}mathrm {sigma } _{Y}.$

Или

$|mathrm {cov} _{XY}|leqslant mathrm {sigma } _{X}mathrm {sigma } _{Y}.$

Итак,

$|mathrm {cov} _{XY}|leqslant {sqrt {mathrm {D} _{X}mathrm {D} _{Y}}}.$

Ковариация имеет размерность, равную произведению размерности случайных величин, то есть величина ковариации зависит от единиц измерения независимых величин. Данная особенность ковариации затрудняет её использование в целях корреляционного анализа^[8].

Линейный коэффициент корреляции[править | править код]

Для устранения недостатка ковариации был введён линейный коэффициент корреляции (или коэффициент корреляции Пирсона), который разработали Карл Пирсон, Фрэнсис Эджуорт и Рафаэль Уэлдон в 90-х годах XIX века. Коэффициент корреляции рассчитывается по формуле^[10]^[8]:

$mathbf {r} _{XY}={frac {mathbf {cov} _{XY}}{mathbf {sigma } _{X}{sigma }_{Y}}}={frac {sum (X-{bar {X}})(Y-{bar {Y}})}{sqrt {sum (X-{bar {X}})^{2}sum (Y-{bar {Y}})^{2}}}}.$

где ${overline {X}}={frac {1}{n}}sum _{t=1}^{n}X_{t}$ , ${overline {Y}}={frac {1}{n}}sum _{t=1}^{n}Y_{t}$ — среднее значение выборок.

Коэффициент корреляции изменяется в пределах от минус единицы до плюс единицы^[11].

Доказательство

Разделив обе части двойного неравенства $-mathrm {sigma } _{X}mathrm {sigma } _{Y}leqslant mathrm {cov} _{XY}leqslant mathrm {sigma } _{X}mathrm {sigma } _{Y}$ на $mathbf {sigma } _{X}mathbf {sigma } _{Y}$ получим

$-1leqslant mathbf {r} _{XY}leqslant 1.$

Линейный коэффициент корреляции связан с коэффициентом регрессии в виде следующей зависимости: $mathbf {r} _{XY}=mathbf {a} _{i}{frac {{sigma }_{Xi}}{{sigma }_{Y}}},$ где $mathbf {a} _{i}$ — коэффициент регрессии, $mathbf {sigma } _{Xi}$ — среднеквадратическое отклонение соответствующего факторного признака^[12]. Отношение коэффициента регрессии к среднеквадратичному отклонению Y не зависит от единиц измерения Y. При линейной трансформации набора данных ${displaystyle x_{i}^{*}=a+bx_{i},;ain mathbb {R} ,bneq 0}$ и ${displaystyle y_{i}^{*}=c+dy_{i},;cin mathbb {R} ,dneq 0}$ линейный коэффициент корреляции будет равен ${displaystyle r_{X^{*}Y^{*}}={frac {bd}{left|bdright|}}r_{XY}}$ .

Непараметрические показатели корреляции[править | править код]

Коэффициент ранговой корреляции Кендалла[править | править код]

Применяется для выявления взаимосвязи между количественными или качественными показателями, если их можно ранжировать.
Значения показателя X выставляют в порядке возрастания и присваивают им ранги. Ранжируют значения показателя Y и рассчитывают коэффициент корреляции Кендалла:

${displaystyle tau ={frac {2S}{n(n-1)}}}$ ,

где
S=P-Q .

— суммарное число наблюдений, следующих за текущими наблюдениями с большим значением рангов Y.

— суммарное число наблюдений, следующих за текущими наблюдениями с меньшим значением рангов Y.
(равные ранги не учитываются!)

Если исследуемые данные повторяются (имеют одинаковые ранги), то в расчетах используется скорректированный коэффициент корреляции Кендалла:

${displaystyle tau ={frac {S}{{sqrt {[{frac {n(n-1)}{2}}-U_{x}][{frac {n(n-1)}{2}}-U_{y}}}]}}}$

$U_{x}={frac {sum {t(t-1)}}{2}}$

$U_{y}={frac {sum {t(t-1)}}{2}}$

— число связанных рангов в ряду X и Y соответственно.

Коэффициент ранговой корреляции Спирмена[править | править код]

Степень зависимости двух случайных величин (признаков) и может характеризоваться на основе анализа получаемых результатов ${displaystyle (X_{1},Y_{1}),ldots ,(X_{n},Y_{n})}$ . Каждому показателю и присваивается ранг. Ранги значений расположены в естественном порядке . Ранг записывается как R_i и соответствует рангу той пары , для которой ранг равен . На основе полученных рангов $X_{i}$ и $Y_{i}$ рассчитываются их разности $d_{i}$ и вычисляется коэффициент корреляции Спирмена:

${displaystyle rho =1-{frac {6sum d_{i}^{2}}{n(n^{2}-1)}}}$

Значение коэффициента меняется от −1 (последовательности рангов полностью противоположны) до +1 (последовательности рангов полностью совпадают). Нулевое значение показывает, что признаки независимы.

Коэффициент корреляции знаков Фехнера[править | править код]

Подсчитывается количество совпадений и несовпадений знаков отклонений значений показателей от их среднего значения.

$i={frac {C-H}{C+H}}$

C — число пар, у которых знаки отклонений значений от их средних совпадают.

H — число пар, у которых знаки отклонений значений от их средних не совпадают.

Множественный коэффициент корреляции[править | править код]

Коэффициент множественной ранговой корреляции (конкордации)[править | править код]

${displaystyle W={frac {12S}{m^{2}(n^{3}-n)}}}$

${displaystyle S=sum _{i=1}^{n}{(sum _{j=1}^{m}{R_{ij}})^{2}}-{frac {(sum _{i=1}^{n}{sum _{j=1}^{m}{R_{ij}}})^{2}}{n}}}$

— число групп, которые ранжируются.

— число переменных.

$R_{ij}$ — ранг -фактора у -единицы.

Значимость:

${displaystyle chi ^{2}=m(n-1)*W}$

${displaystyle {chi ^{2}}_{kp}=(alpha ;(n-1)(m-1))}$

${displaystyle chi ^{2}>{chi ^{2}}_{kp}}$ , то гипотеза об отсутствии связи отвергается.

В случае наличия связанных рангов:

${displaystyle W={frac {12S}{m^{2}(n^{3}-n)-msum _{j=1}^{m}{({t^{3}}_{j}-t_{j})}}}}$

${displaystyle chi ^{2}={frac {12S}{mn(n+1)-{frac {sum _{j=1}^{m}{({t^{3}}_{j}-t_{j})}}{n-1}}}}}$

Свойства коэффициента корреляции[править | править код]

Неравенство Коши — Буняковского:

если принять в качестве скалярного произведения двух случайных величин ковариацию

, то норма случайной величины будет равна

, и следствием неравенства Коши — Буняковского будет:

$-1leqslant mathbb {R} _{X,Y}leqslant 1$

$mathbb {R} _{X,Y}=pm 1Leftrightarrow Y=kX+b,kneq 0$

где

. Более того в этом случае знаки $mathbb {R} _{X,Y}$

совпадают:

$operatorname {sgn} mathbb {R} _{X,Y}=operatorname {sgn} k$

Доказательство

Рассмотрим случайные величины X и Y c нулевыми средними, и дисперсиями, равными, соответственно, ${overline {X^{2}}}=sigma _{X}^{2}$ и ${overline {Y^{2}}}=sigma _{Y}^{2}$ . Подсчитаем дисперсию случайной величины :

$sigma _{xi }^{2}={overline {(aX+bY)^{2}}}=a^{2}{overline {X^{2}}}+b^{2}{overline {Y^{2}}}+2ab{overline {XY}}.$

Если предположить, что коэффициент корреляции

$mathbb {R} _{X,Y}={frac {overline {XY}}{sigma _{X}sigma _{Y}}}=pm 1,$

то предыдущее выражение перепишется в виде

$sigma _{xi }^{2}=a^{2}sigma _{X}^{2}+b^{2}sigma _{Y}^{2}pm 2absigma _{X}sigma _{Y}=(asigma _{X}pm bsigma _{Y})^{2}.$

Поскольку всегда можно выбрать числа a и b так, чтобы $asigma _{X}pm bsigma _{Y}=0$ (например, если $sigma _{Y}neq 0$ , то берём произвольное a и $b=mp {frac {sigma _{X}}{sigma _{Y}}},a$ ), то при этих a и b дисперсия $sigma _{xi }^{2}=0$ , и значит почти наверное. Но это и означает линейную зависимость между X и Y. Доказательство очевидным образом обобщается на случай величин X и Y с ненулевыми средними, только в вышеприведённых выкладках надо будет X заменить на , и Y — на .

Корреляционный анализ[править | править код]

Корреляционный анализ — метод обработки статистических данных, с помощью которого измеряется теснота связи между двумя или более переменными. Корреляционный анализ тесно связан с регрессионным анализом (также часто встречается термин «корреляционно-регрессионный анализ», который является более общим статистическим понятием), с его помощью определяют необходимость включения тех или иных факторов в уравнение множественной регрессии, а также оценивают полученное уравнение регрессии на соответствие выявленным связям (используя коэффициент детерминации)^[1]^[2].

Ограничения корреляционного анализа[править | править код]

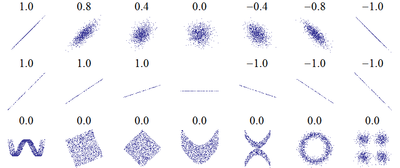
Множество корреляционных полей. Распределения значений (x,y) с соответствующими коэффициентами корреляций для каждого из них. Коэффициент корреляции отражает «зашумлённость» линейной зависимости (верхняя строка), но не описывает наклон линейной зависимости (средняя строка), и совсем не подходит для описания сложных, нелинейных зависимостей (нижняя строка). Для распределения, показанного в центре рисунка, коэффициент корреляции не определен, так как дисперсия y равна нулю.

Применение возможно при наличии достаточного количества наблюдений для изучения. На практике считается, что число наблюдений должно не менее чем в 5-6 раз превышать число факторов (также встречается рекомендация использовать пропорцию, не менее чем в 10 раз превышающую количество факторов). В случае если число наблюдений превышает количество факторов в десятки раз, в действие вступает закон больших чисел, который обеспечивает взаимопогашение случайных колебаний^[13].
Необходимо, чтобы совокупность значений всех факторных и результативного признаков подчинялась многомерному нормальному распределению. В случае если объём совокупности недостаточен для проведения формального тестирования на нормальность распределения, то закон распределения определяется визуально на основе корреляционного поля. Если в расположении точек на этом поле наблюдается линейная тенденция, то можно предположить, что совокупность исходных данных подчиняется нормальному закону распределения^[14].
Исходная совокупность значений должна быть качественно однородной^[13].
Сам по себе факт корреляционной зависимости не даёт основания утверждать, что одна из переменных предшествует или является причиной изменений, или то, что переменные вообще причинно связаны между собой, а не наблюдается действие третьего фактора^[5].

Область применения[править | править код]

Данный метод обработки статистических данных весьма популярен в экономике, астрофизике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие. В различных прикладных отраслях приняты разные границы интервалов для оценки тесноты и значимости связи.

Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.

См. также[править | править код]

Автокорреляционная функция
Взаимнокорреляционная функция
Ковариация
Коэффициент детерминации

Примечания[править | править код]

↑ ¹ ² ³ Шмойлова, 2002, с. 272.
↑ ¹ ² Елисеева, Юзбашев, 2002, с. 232.
↑ Елисеева, Юзбашев, 2002, с. 228.
↑ Елисеева, Юзбашев, 2002, с. 228—229.
↑ ¹ ² Елисеева, Юзбашев, 2002, с. 229.
↑ Суслов, Ибрагимов, Талышева, Цыплаков, 2005, с. 141.
↑ Гмурман, 2004, с. 176—177.
↑ ¹ ² ³ Гмурман, 2004, с. 177.
↑ Гмурман, 2004, с. 178—179.
↑ Шмойлова, 2002, с. 300.
↑ Гмурман, 2004, с. 179.
↑ Шмойлова, 2002, с. 301.
↑ ¹ ² Елисеева, Юзбашев, 2002, с. 230.
↑ Шмойлова, 2002, с. 275.

Литература[править | править код]

Гмурман В. Е.^ru_uk. Теория вероятностей и математическая статистика: Учебное пособие для вузов. — 10-е издание, стереотипное. — Москва: Высшая школа, 2004. — 479 с. — ISBN 5-06-004214-6.
Елисеева И. И., Юзбашев М. М. Общая теория статистики: Учебник / Под ред. И. И. Елисеевой. — 4-е издание, переработанное и дополненное. — Москва: Финансы и Статистика, 2002. — 480 с. — ISBN 5-279-01956-9.
Корреляционный анализ / А. В. Прохоров // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
Общая теория статистики: Учебник / Под ред. Р. А. Шмойловой. — 3-е издание, переработанное. — Москва: Финансы и Статистика, 2002. — 560 с. — ISBN 5-279-01951-8.
Суслов В. И., Ибрагимов Н. М., Талышева Л. П., Цыплаков А. А. Эконометрия. — Новосибирск: СО РАН, 2005. — 744 с. — ISBN 5-7692-0755-8.

Ссылки[править | править код]

Калькулятор для расчета коэффициента корреляции по Пирсону
Границы значений коэффициента корреляции
Иллюстрация: зависимые случайные величины с нулевой корреляцией
Корреляция между временными рядами: что может быть проще? // habr.com

Источник

Загрузить PDF

Коэффициент корреляции (или линейный коэффициент корреляции) обозначается как «r» (в редких случаях как «ρ») и характеризует линейную корреляцию (то есть взаимосвязь, которая задается некоторым значением и направлением) двух или более переменных. Значение коэффициента лежит между -1 и +1, то есть корреляция бывает как положительной, так и отрицательной. Если коэффициент корреляции равен -1, имеет место идеальная отрицательная корреляция; если коэффициент корреляции равен +1, имеет место идеальная положительная корреляция. В остальных случаях между двумя переменными наблюдается положительная корреляция, отрицательная корреляция или отсутствие корреляции. Коэффициент корреляции можно вычислить вручную, с помощью бесплатных онлайн-калькуляторов или с помощью хорошего графического калькулятора.

1
Соберите данные. Перед тем как приступить к вычислению коэффициента корреляции, изучите данные пары чисел. Лучше записать их в таблицу, которую можно расположить вертикально или горизонтально. Каждую строку или столбец обозначьте как «х» и «у».^[1]
- Например, даны четыре пары значений (чисел) переменных «х» и «у». Можно создать следующую таблицу:
  - x || y
  - 1 || 1
  - 2 || 3
  - 4 || 5
  - 5 || 7
2

Вычислите среднее арифметическое «х». Для этого сложите все значения «х», а затем полученный результат разделите на количество значений.^[2]
3

Найдите среднее арифметическое «у». Для этого выполните аналогичные действия, то есть сложите все значения «у», а затем сумму разделите на количество значений.^[3]
4

Вычислите стандартное отклонение «х». Вычислив средние значения «х» и «у», найдите стандартные отклонения этих переменных. Стандартное отклонение вычисляется по следующей формуле:^[4]
5

Вычислите стандартное отклонение «у». Выполните действия, которые описаны в предыдущем шаге. Воспользуйтесь той же формулой, но подставьте в нее значения «у».^[5]
6
Запишите основную формулу для вычисления коэффициента корреляции. В эту формулу входят средние значения, стандартные отклонения и количество (n) пар чисел обеих переменных. Коэффициент корреляции обозначается как «r» (в редких случаях как «ρ»). В этой статье используется формула для вычисления коэффициента корреляции Пирсона.^[6]
- $rho =left({frac {1}{n-1}}right)Sigma left({frac {x-mu _{x}}{sigma _{x}}}right)*left({frac {y-mu _{y}}{sigma _{y}}}right)$
- Здесь и в других источниках величины могут обозначаться по-разному. Например, в некоторых формулах присутствуют «ρ» и «σ», а в других «r» и «s». В некоторых учебниках приводятся другие формулы, но они являются математическими аналогами приведенной выше формулы.
7

Вычислите коэффициент корреляции. Вы вычислили средние значения и стандартные отклонения обеих переменных, поэтому можно воспользоваться формулой для вычисления коэффициента корреляции. Напомним, что «n» – это количество пар значений обеих переменных. Значение других величин были вычислены ранее.^[7]
8
Проанализируйте полученный результат. В нашем примере коэффициент корреляции равен 0,988. Это значение некоторым образом характеризует данный набор пар чисел. Обратите внимание на знак и величину значения.^[8]
- Так как значение коэффициента корреляции положительно, между переменными «х» и «у» имеет место положительная корреляция. То есть при увеличении значения «х», значение «у» тоже увеличивается.
- Так как значение коэффициента корреляции очень близко к +1, значения переменных «х» и «у» сильно взаимосвязаны. Если нанести точки на координатную плоскость, они расположатся близко к некоторой прямой.
Реклама

1

В интернете найдите калькулятор для вычисления коэффициента корреляции. Этот коэффициент довольно часто вычисляется в статистике. Если пар чисел много, вычислить коэффициент корреляции вручную практически невозможно. Поэтому существуют онлайн-калькуляторы для вычисления коэффициента корреляции. В поисковике введите «коэффициент корреляции калькулятор» (без кавычек).
2
Введите данные. Ознакомьтесь с инструкциями на сайте, чтобы правильно ввести данные (пары чисел). Крайне важно вводить соответствующие пары чисел; в противном случае вы получите неверный результат. Помните, что на разных веб-сайтах различные форматы ввода данных.
- Например, на сайте http://ncalculators.com/statistics/correlation-coefficient-calculator.htm значения переменных «х» и «у» вводятся в двух горизонтальных строках. Значения разделяются запятыми. То есть в нашем примере значения «х» вводятся так: 1,2,4,5, а значения «у» так: 1,3,5,7.
- На другом сайте, http://www.alcula.com/calculators/statistics/correlation-coefficient/, данные вводятся по вертикали; в этом случае не перепутайте соответствующие пары чисел.
3

Вычислите коэффициент корреляции. Введя данные, просто нажмите на кнопку «Calculate», «Вычислить» или аналогичную, чтобы получить результат.

Реклама

1
Введите данные. Возьмите графический калькулятор, перейдите в режим статистических вычислений и выберите команду «Edit» (Редактировать).^[9]
- На разных калькуляторах нужно нажимать различные клавиши. В этой статье рассматривается калькулятор Texas Instruments TI-86.
- Чтобы перейти в режим статистических вычислений, нажмите [2nd] – Stat (над клавишей «+»). Затем нажмите F2 – Edit (Редактировать).
2
Удалите предыдущие сохраненные данные. В большинстве калькуляторов введенные статистические данные хранятся до тех пор, пока вы не сотрете их. Чтобы не спутать старые данные с новыми, сначала удалите любую сохраненную информацию.^[10]
- С помощью клавиш со стрелками переместите курсор и выделите заголовок «xStat». Затем нажмите Clear (Очистить) и Enter (Ввести), чтобы удалить все значения, введенные в столбец xStat.
- С помощью клавиш со стрелками выделите заголовок «yStat». Затем нажмите Clear (Очистить) и Enter (Ввести), чтобы удалить все значения, введенные в столбец уStat.
3
Введите исходные данные. С помощью клавиш со стрелками переместите курсор в первую ячейку под заголовком «xStat». Введите первое значение и нажмите Enter. В нижней части экрана отобразится «xStat (1) = __», где вместо пробела будет стоять введенное значение. После того как вы нажмете Enter, введенное значение появится в таблице, а курсор переместится на следующую строку; при этом в нижней части экрана отобразится «xStat (2) = __».^[11]
- Введите все значения переменной «х».
- Введя все значения переменной «х», с помощью клавиш со стрелками перейдите в столбец yStat и введите значения переменной «у».
- После ввода всех пар чисел нажмите Exit (Выйти), чтобы очистить экран и выйти из режима статистических вычислений.
4
Вычислите коэффициент корреляции. Он характеризует, насколько близко данные расположены к некоторой прямой. Графический калькулятор может быстро определить подходящую прямую и вычислить коэффициент корреляции.^[12]
- Нажмите Stat (Статистика) – Calc (Вычисления). На TI-86 нужно нажать [2nd] – [Stat] – [F1].
- Выберите функцию «Linear Regression» (Линейная регрессия). На TI-86 нажмите [F3], которая обозначена как «LinR». На экране отобразится строка «LinR _» с мигающим курсором.
- Теперь введите имена двух переменных: xStat и yStat.
  - На TI-86 откройте список имен; для этого нажмите [2nd] – [List] – [F3].
  - В нижней строке экрана отобразятся доступные переменные. Выберите [xStat] (для этого, скорее всего, нужно нажать F1 или F2), введите запятую, а затем выберите [yStat].
  - Нажмите Enter, чтобы обработать введенные данные.
5

Реклама

1
Разберитесь с понятием корреляции. Корреляция – это статистическая взаимосвязь двух величин. Коэффициент корреляции – это числовое значение, которое можно вычислить для любых двух наборов данных. Значение коэффициента корреляции всегда лежит в диапазоне от -1 до +1 и характеризует степень взаимосвязи двух переменных.^[14]
- Например, даны рост и возраст детей (около 12 лет). Скорее всего, здесь будет наблюдаться сильная положительная корреляция, потому что с возрастом дети становятся выше.
- Пример отрицательной корреляции: штрафные секунды и время, проведенное на тренировках по биатлону, то есть чем больше спортсмен тренируется, тем меньше штрафных секунд будет начислено.
- Наконец, иногда имеет место очень слабая корреляция (положительная или отрицательная), например, между размером обуви и оценками по математике.
2

Запомните, как вычислить среднее арифметическое. Чтобы вычислить среднее арифметическое (или среднее значение), нужно найти сумму всех данных значений, а затем разделить ее на количество значений. Помните, что среднее арифметическое необходимо для вычисления коэффициента корреляции.^[15]
3
Обратите внимание на важность стандартного отклонения. В статистике стандартное отклонение характеризует степень разброса чисел по отношению к их среднему значению. Если стандартное отклонение мало, числа расположены близко к среднему значению; если стандартное отклонение велико, числа расположены далеко от среднего значения.^[16]
- Стандартное отклонение обозначается буквой «s» или греческой буквой «σ» (сигма). Таким образом, стандартное отклонение значений переменной «х» обозначается так: s_x или σ_x.
4
Запомните символ, обозначающий операцию суммирования. Символ суммирования является одним из наиболее распространенных символов в математике и указывает на сумму значений. Этот символ представляет собой греческую букву «Σ» (прописная сигма).^[17]
- Например, если даны следующие значения переменной «х»: 1,2,5,6,9,10, то Σx означает:
  - 1 + 2 + 5 + 6 + 9 + 10 = 33.
Реклама

Советы

Коэффициент корреляции иногда называют «коэффициентом корреляции Пирсона» в честь его разработчика Карла Пирсона.
В большинстве случаев, когда коэффициент корреляции больше 0,8 (положительный или отрицательный), имеет место сильная корреляция; если же коэффициент корреляции меньше 0,5 (положительный или отрицательный), наблюдается слабая корреляция.

Предупреждения

Корреляция характеризует взаимосвязь значений двух переменных. Но помните, что корреляция не имеет ничего общего с причинно-следственной связью. Например, если сравнить рост и размер обуви людей, вы, вероятно, обнаружите сильную положительную корреляцию. Как правило, чем выше человек, тем больше размер обуви. Но это не означает, что увеличение роста приводит к автоматическому увеличению размера обуви, или что большие ноги приведут к ускоренному росту. Эти величины просто взаимосвязаны.

Об этой статье

Эту страницу просматривали 79 031 раз.

Была ли эта статья полезной?

Источник

Для описания системы двух случайных
величин, кроме математических ожиданий
и дисперсий составляющих пользуются и
другими характеристиками, к числу
которых относятся корреляционный
моментикоэффициент корреляции(кратко было упомянуто в конце Т.8.п.8.6).

Корреляционным моментом (иликовариацией, или моментом
связи) двух случайных величинX
иY называется
м. о. произведения отклонений этих
величин (см. равенство (5) п. 8.6):

(7)
.

Следствие 1. Для корреляционного
момента с.в. X иYтакже справедливы
равенства:

где
соответствующие централизованные с.в.X иY
(см. п.8.6.).

При
этом: если
–
двумерная д.с.в., то ковариация вычисляется
по формуле

(8)
;

если
–
двумерная н.с.в., то ковариация вычисляется
по формуле

(9)

Формулы (8) и (9) получены на основании
формул (6) п.12.1. Имеет место вычислительная
формула

(10)

которая
выводится из определения (9) и на основании
свойств м.о., действительно,

Следовательно, формул (36) и (37) можно
переписать в виде

(11)
;

Корреляционный момент служит для
характеристики связи между величинами
X иY.

Как
будет показано ниже, корреляционный
момент равен нулю, если XиY являются
независимыми;

Следовательно, если корреляционный
момент не равен нулю, то X
и Y – зависимые
случайные величины.

Теорема12.1. Корреляционный момент
двух независимых случайных величин X
иY равен нулю,
т.е. для независимых с.в. X
иY,

Доказательство.Так какX
иYнезависимые
случайные величины, то их отклонения

также
независимы. Пользуясь свойствами
математического ожидания (математическое
ожидание произведения независимых с.
в. равно произведению математических
ожиданий сомножителей,,
поэтому

Замечание. Из этой теоремы следует,
что если
то с.в. X иY
зависимы и в таких случаях с.в. X
иYназываюткоррелированными. Однако из того,
что
не следует независимость с.в.X
иY.

В этом случае (с.в.X иYназываютнекоррелированными, тем
самым из

независимости
вытекает некоррелированность;
обратное утверждение, вообще говоря,
неверно (см. далее пример 2.)

Рассмотрим основные свойства
корреляционного момента.

Cвойства ковариации:

1.Ковариация симметрична, т.е.
.

Непосредственно следует из формулы
(38).

2. Имеют место равенства:т.е.
дисперсия с.в. является ковариацией её
с самой собой.

Эти равенства прямо следуют из определения
дисперсии и равенство (38) соотвеиственно
при

3. Справедливы равенства:

Эти
равенства выводятся из определения
дисперсии, ковариации с.в.и,
свойств 2.

По определению дисперсии (с учётом
централизованности с.в.
)
мы имеем

теперь,
на основании (33) и свойств 2 и 3, получим
первое (со знаком плюс) свойство 3.

Аналогично,
вторая часть свойства3, выводится из
равенство

4. Пустьпостоянные
числа,тогда справедливы равенства:

Обычно
эти свойства называются свойствами
однородностью первого порядка и
периодичностью по аргументам.

Докажем
первое равенство, при этом будем
использовать свойства м.о.
.

Теорема 12.2. Абсолютное значение
корреляционного момента двух
произвольных случайных величин X
и Y не превышает
среднего геометрического их дисперсий:
т.е.

(12)

Доказательство. Заметим, что для
независимых с.в. неравенство выполняется
(с.м. теорему 12.1.). Итак, пусть с.в.X
и Y зависимые.
Рассмотрим стандартные с.в.ии вычислим дисперсию с.в.с учётом свойства 3, имеем: с одной
стороныС другой стороны

Следовательно,
с учётом того, что
и–
нормированные (стандартизированные)
с.в., то для них м.о. равна нулю, а дисперсия
равна 1, поэтому, пользуясь свойством
м.о.получим

а
следовательно, на основании того, что

получим

Отсюда
следует, что
т.е.

Утверждение доказано.

Из определения и свойства ковариации
следует, что она характеризует и степень
зависимости с.в., и их рассеяния вокруг
точки
Размерность ковариации равна произведению
размерностей случайных величинXиY. Другими словами,
величина корреляционного момента
зависит от единиц измерения случайных
величин. По этой причине для одних и тех
же двух величинXиY,
величина корреляционного момента
будет иметь различные значения в
зависимости от того, в каких единицах
были измерены величины.

Пусть, например, X
и Y
были измерены в
сантиметрах и
;
если измерить XиY в миллиметрах,
тоЭта особенность корреляционного момента
и есть недостатком этой числовой
характеристики, так как сравнение
корреляционных моментов различных
систем случайных величин становится
затруднительным.

Для того чтобы устранить этот недостаток,
вводят новую числовую характеристику-
– «коэффициент корреляции».

Коэффициентом корреляции
случайных величин
иназывают отношение корреляционного
момента к произведению средних
квадратических отклонений этих величин:

(13)
.

Так как размерность
равна произведению размерностей величин
и,имеет размерность величиныσ_yимеет размерность величины,
то
есть просто число (т.е. «безразмерная
величина»). Таким образом, величина
коэффициента корреляции не зависит от
выбора единиц измерения с.в., в этом
состоитпреимуществокоэффициента
корреляции перед корреляционным
моментом.

В Т.8. п.8.3 нами было введено понятие
нормированной с.в.,
формула (18), и доказана теорема о том,
чтои(см.
там же теорема 8.2.). Здесь докажем следующее
утверждение.

Теорема 12.3. Длялюбых двух случайных
величин
и
справедливо
равенство.Другими словами, коэффициент корреляции
любых двух с.в.X
иYравно
корреляционному моменту их соответствующих
нормированныхс.в.и .

Доказательство. По определению
нормированных случайных величини

и.

Учитывая свойство математического
ожидания:
и равенство (40) получим

Утверждение
доказано.

Рассмотрим некоторые часто встречающие
свойства коэффициента корреляции.

Свойства коэффициента корреляции:

1. Коэффициент
корреляции по абсолютной величине
непревосходит 1, т.е.

Это
свойство прямо следует из формулы (41)
– определения коффициента корреляции
и теоремы 13.5. ( см. равенство (40)).

2. Если случайные величиныинезависимы,
токоэффициент корреляции
равен нулю, т.е.
.

Это свойство является прямым
следствием равенства (40) и теоремы 13.4.

Следующее свойство
сформулируем в виде отдельной теоремы.

Теорема 12.4.

Если
с.в.имежду
собой связаны линейной функциональной
зависимостью, т.е.то

при этом

и
наоборот, если
,то
с.в.и
между собой связаны линейной функциональной
зависимостью, т.е. существуют постоянныеи
такие, что имеет место равенство

Доказательство.
Пусть
тогда на основании
свойства 4 ковариации, имеем

и
поскольку,
,
поэтому

Следовательно,
.
Равенство в одну сторону получено. Пусть
далее,,
тогда

следует
рассматривать два случая:1)
и
2)Итак, рассмотрим первый случай. Тогда
по определениюи
следовательно из равенства,
где.
В нашем случае,
поэтому из равенства (см. доказательство
теоремы 13.5.)

получаем,
что
,
значитпостоянна.
Так каки поскольку,
тодействительно,

Следовательно,

Аналогично,
показывается, что для
имеет место (проверьте самостоятельно!)

Некоторые выводы:

1. Если
инезависимыес.в., то

2. Если с.в.имежду
собой связаны линейно, то.

3. В остальных случаях
:

В этом
случае говорят, что с.в.исвязаны между собойположительной
корреляцией, еслив случаях жеотрицательной
корреляцией. Чем ближек единице, тем больше оснований считать,
чтос.в.исвязаны линейной зависимостью.

Отметим, что корреляционные моменты и
дисперсии системы с.в. обычно задаются
корреляционной матрицей:

Очевидно, что определитель
корреляционной матрицы удовлетворяет:

Как уже было отмечено, если две случайные
величины зависимы, то они могут быть
как коррелированными, так инекоррелированными.Другими словами,
корреляционный момент двух зависимых
величин может бытьне равен нулю,
но может иравняться нулю.

Пример 1. Закон распределения
дискретной с.в.задан таблицей

-1

Найти
коэффициент корреляции

Решение. Находим законы распределения
составляющихи:

Теперь
вычислим м.о. составляющих:

Этих
величин можно было находить на основании
таблицы распределения с.в.

из
равенства (1) пункта 12.1. Например,

Аналогично,
находите
самостоятельно.

Вычислим
дисперсии составляющих при это будем
пользоваться вычислительной формулой:

Следовательно,Далее, на основании первой формулы

(6) имеем:

Составим
закон распределения
,
а затем найдём:

При
составлении таблицы закона распределения
следует выполнять действия:

1) оставить лишь различные значения
всевозможных произведений
.

2) для определения вероятности данного
значения
,
нужно

складывать все соответствующие
вероятности, находящиеся на пересечении
основной таблицы, благоприятствующие
наступлению данного значения.

В нашем примере с.в.принимает
всего три различных значения.
Здесь первое значение ()
соответствует произведениюиз второй строки ииз первого столбца, поэтому на их
пересечении находится вероятностное
числоаналогично

которое
получено из суммы вероятностей,
находящихся на пересечениях соответственно
первой строки и первого столбца (0,15 ;
0,40; 0,05) и одно значение
,
которое находится на пересечении второй
строки и второго столбца, и наконец,,
которое находится на пересечении второй
строки и третьего столбца.

Из нашей таблицы находим:

Находим
корреляционный момент, используя формулу
(38):

Находим
коэффициент корреляции по формуле
(41)

Таким образом, отрицательная корреляция.

Упражнение.Закон
распределения дискретной с.в. задан
таблицей

-1

0,5

0,2

Найти коэффициент корреляции

Рассмотрим
пример, где окажется две зависимые
случайные величинымогут бытьнекоррелированными.

Пример 2. Двумерная случайная величина
)задана функцией плотностью

Докажем, что
и
зависимые,нонекоррелированные
случайные величины.

Решение.Воспользуемся ранее
вычисленными плотностями распределения
составляющихи
:

Так
как
,то изависимые
величины. Для того, чтобы доказать
некоррелированность
и,
достаточно убедиться в том, что

Найдем
корреляционный момент по формуле:

Поскольку дифференциальная функция

симметрична относительно
оси OY,
то
аналогично,
в силу симметрии
относительно оси OX.
Поэтому,

вынося
постоянный множитель

Внутренний интеграл равен
нулю (подынтегральная функция нечетна,
пределы интегрирования симметричны
относительно начала координат),
следовательно,
,
т.е. зависимые случайные величиныи
между собой некоррелируют.

Итак, из коррелированности двух
случайных величин следует их зависимость,
но из некоррелированности ещё нельзя
заключить о независимости этих величин.

Однако, для нормально
распределённых с.в. такой вывод является
исключением,
т.е. из некоррелированности
нормально распределенных
с.в. вытекает их независимость.

Этому вопросу посвящается
следующий пункт.

Источник

Как рассчитать коэффициент корреляции Пирсона вручную

17 авг. 2022 г.
читать 2 мин

Коэффициент корреляции Пирсона измеряет линейную связь между двумя переменными.

Он всегда принимает значение от -1 до 1, где:

-1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными
0 указывает на отсутствие линейной корреляции между двумя переменными
1 указывает на совершенно положительную линейную корреляцию между двумя переменными.

Формула для расчета коэффициента корреляции Пирсона, обозначаемая r , выглядит следующим образом:

Источник: Википедия В этом руководстве представлен пошаговый пример того, как вручную рассчитать коэффициент корреляции Пирсона для следующего набора данных:

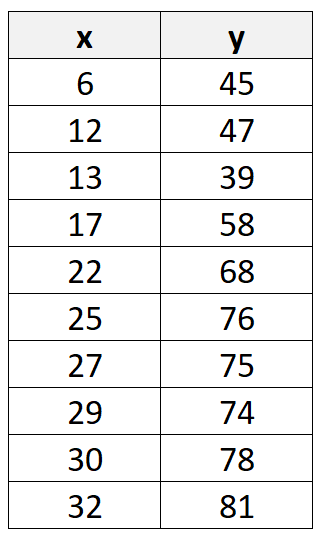
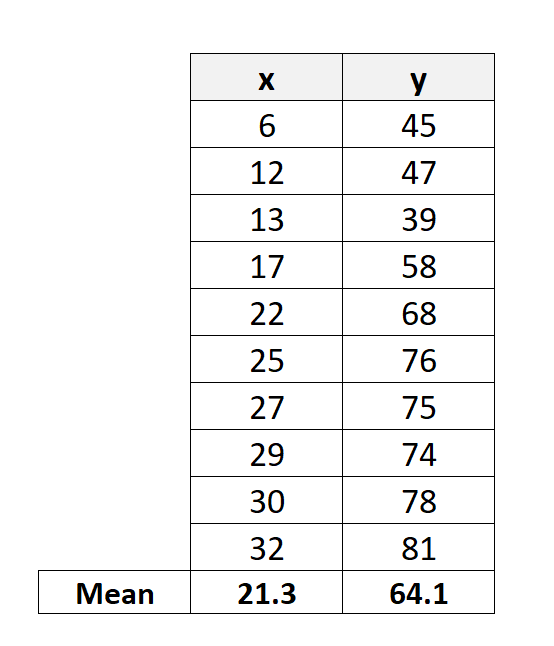
Шаг 1: вычислить среднее значение X и Y

Сначала мы вычислим среднее значение значений X и Y:

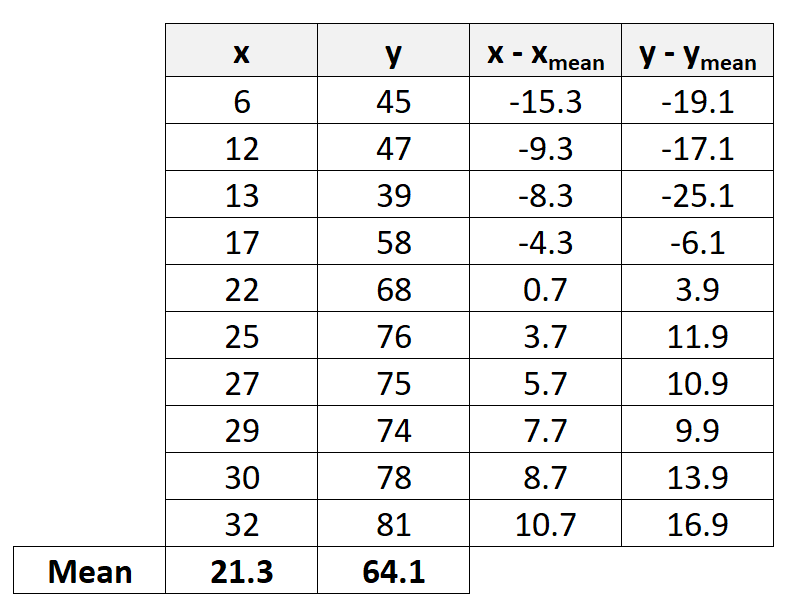
Шаг 2: Рассчитайте разницу между средними значениями

Далее мы рассчитаем разницу между каждым из отдельных значений X и Y и их соответствующими средними значениями:

Шаг 3: Рассчитайте оставшиеся значения

Далее мы рассчитаем оставшиеся значения, необходимые для завершения формулы коэффициента корреляции Пирсона:

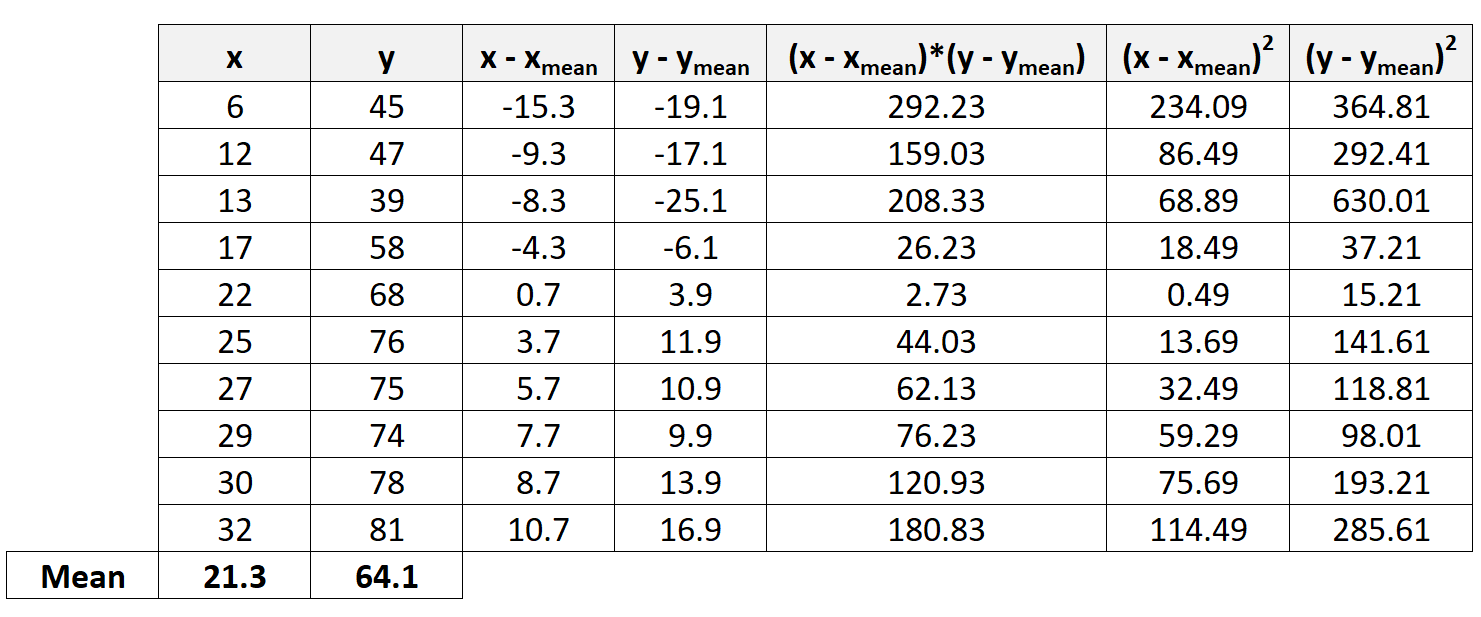
Шаг 4: Рассчитайте суммы

Далее мы вычислим суммы последних трех столбцов:

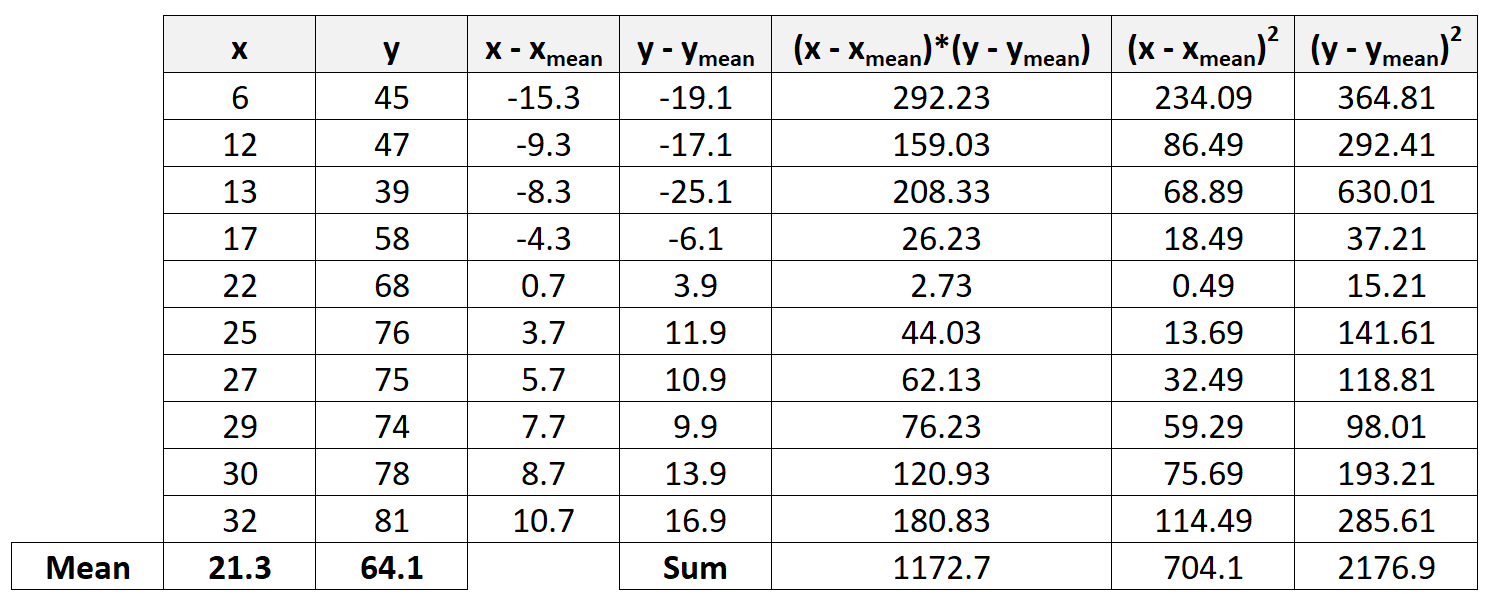
Шаг 5. Рассчитайте коэффициент корреляции Пирсона.

Теперь мы просто подставим суммы из предыдущего шага в формулу коэффициента корреляции Пирсона:

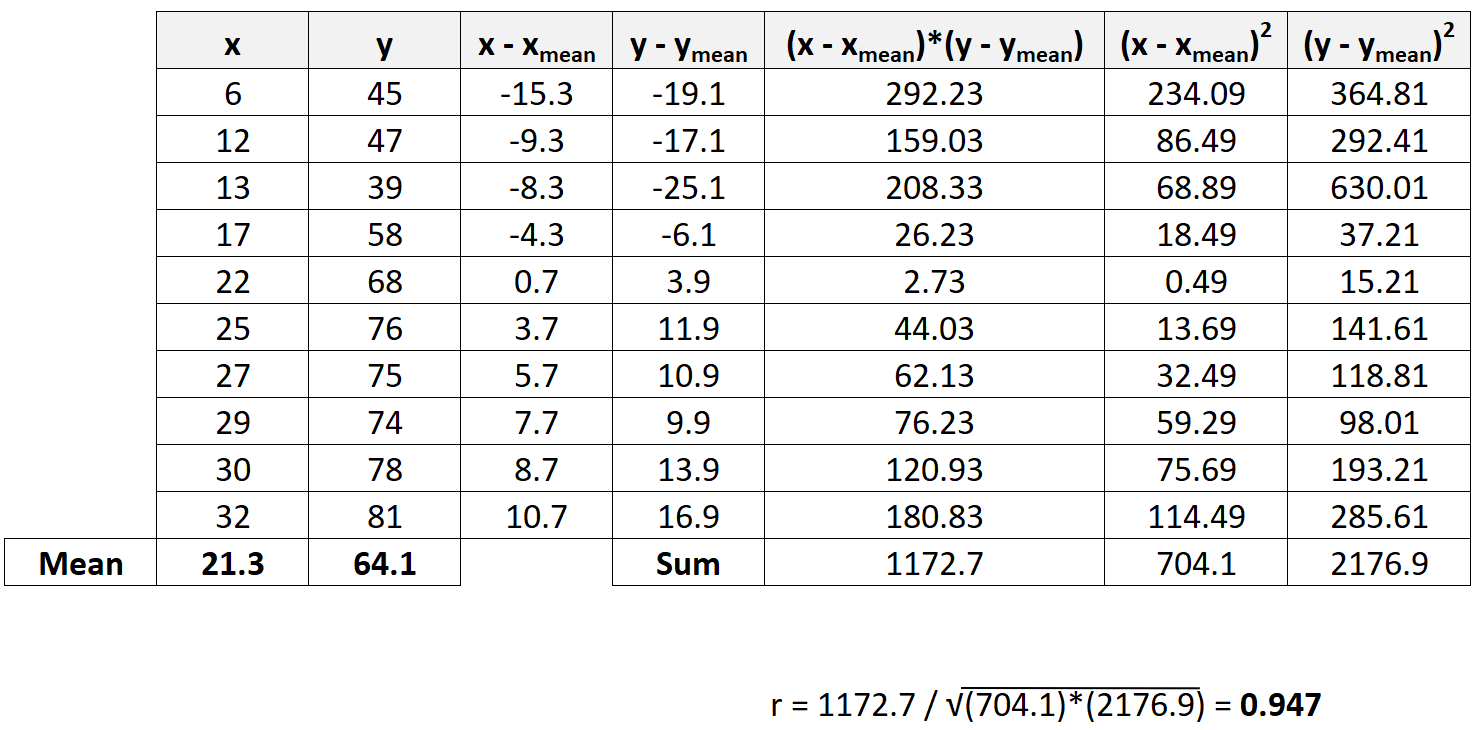
Коэффициент корреляции Пирсона оказывается равным 0,947 .

Поскольку это значение близко к 1, это свидетельствует о сильной положительной корреляции X и Y.

Другими словами, по мере увеличения значения X значение Y также увеличивается весьма предсказуемым образом.

Дополнительные ресурсы

Введение в коэффициент корреляции Пирсона
Как найти доверительный интервал для коэффициента корреляции

Написано

Замечательно! Вы успешно подписались.

Добро пожаловать обратно! Вы успешно вошли

Вы успешно подписались на кодкамп.

Срок действия вашей ссылки истек.

Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.

Успех! Ваша платежная информация обновлена.

Ваша платежная информация не была обновлена.

Источник

Video

Tips

Warnings

References

About This Article

Did this article help you?

Корреляция и взаимосвязь величин[править | править код]

Показатели корреляции[править | править код]

Параметрические показатели корреляции[править | править код]

Ковариация[править | править код]

Линейный коэффициент корреляции[править | править код]

Непараметрические показатели корреляции[править | править код]

Коэффициент ранговой корреляции Кендалла[править | править код]

Коэффициент ранговой корреляции Спирмена[править | править код]

Коэффициент корреляции знаков Фехнера[править | править код]

Множественный коэффициент корреляции[править | править код]

Коэффициент множественной ранговой корреляции (конкордации)[править | править код]

Свойства коэффициента корреляции[править | править код]

Корреляционный анализ[править | править код]

Ограничения корреляционного анализа[править | править код]

Область применения[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Советы

Предупреждения

Об этой статье

Была ли эта статья полезной?

Как рассчитать коэффициент корреляции Пирсона вручную

Шаг 1: вычислить среднее значение X и Y

Шаг 2: Рассчитайте разницу между средними значениями

Шаг 3: Рассчитайте оставшиеся значения

Шаг 4: Рассчитайте суммы

Шаг 5. Рассчитайте коэффициент корреляции Пирсона.

Дополнительные ресурсы

Вам также может понравиться

Как найти уравнение всех высот в треугольнике

Как найти что установлено на компьютере

Как найти косинус прямого угла в треугольнике

Добавить комментарий Отменить ответ