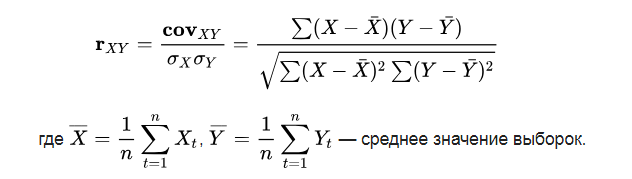Как найти корреляцию портфеля

Корреляция показывает, насколько активы схожи по поведению. Показатель описывает закономерности. Например, если при росте одного актива другой дешевеет и эта закономерность подтверждается историческими данными, говорят, что у активов обратная корреляция. Это относится как к отдельным ценным бумагам, так и к широким рынкам, классам активов и секторам экономики.

Коэффициент корреляции вычисляется на конкретном историческом отрезке. Он обозначается буквой r и принимает значения от −1 до +1. Если два актива движутся в связке, то коэффициент корреляции будет ближе к +1, а если в противоположных направлениях — ближе к −1. Но когда корреляция близка к нулю, взаимосвязи между ними нет. Это значит, что при росте или падении одного актива другой может вообще никак себя не проявлять. Например, корреляция акций и облигаций на рынке США в период с 1950 по 2012 год составила 0,11.

Расскажу, как можно использовать знание о корреляции при формировании портфеля.

Роль корреляции в управлении портфелем

Понимание корреляции между инструментами позволяет диверсифицировать портфель и снизить инвестиционные риски.

Например, если инвестор собрал портфель из 10 нефтегазовых компаний, он защитил себя только от специфических рисков, связанных с конкретным эмитентом. Волатильность портфеля по-прежнему будет высокой: если цены на нефть упадут, портфель также уйдет в красную зону из-за тесной корреляции акций.

Чтобы диверсификация работала, необходимо использовать инструменты с низкой или обратной корреляцией. Тогда движение цены одного актива будет компенсироваться движением другого. Так, государственные облигации — наиболее частный диверсификатор для акций, поскольку у этих активов исторически низкая взаимосвязь друг с другом.

Как изменяется корреляция со временем

Современная теория портфеля позволяет найти идеальную смесь активов, при которой у портфеля будет оптимальное соотношение доходности и риска. Но главный недостаток этой теории в том, что корреляции со временем могут меняться. Два актива могут начать двигаться синхронно, даже если в прошлом их взаимосвязь была низкой. И заметить это можно только постфактум — на исторических данных.

Если посмотреть на десятилетие перед кризисом 2008 года, то корреляция большинства инструментов по отношению к S&P 500 была ниже 0,5. Но после 2008 года она заметно выросла. Теперь только у высоконадежных облигаций по-прежнему слабая связь с акциями, хотя их корреляция сменилась с отрицательной на положительную: если раньше при падении S&P 500 они росли, то теперь тоже падают, пусть и не так сильно.

Корреляция различных классов активов с индексом S&P 500

	1998—2007	2008—2020
Глобальные акции	0,84	0,89
Недвижимость	0,32	0,74
Высокодоходные облигации	0,49	0,73
Товары	−0,01	0,59
Высоконадежные облигации	−0,21	0,01

Корреляция и волатильность

Между корреляцией и волатильностью существует взаимосвязь: когда рынки становятся волатильными, корреляции между инструментами возрастают. Поэтому рост корреляции со временем можно объяснить тем, что за последние десятилетия рынки стали более волатильными. Например, с 2000 по 2009 год было 95 торговых сессий, когда S&P 500 сдвинулся на 3% и больше. А за предшествующие 50 лет был всего 81 случай.

Количество дней в каждом десятилетии, когда S&P 500 сдвинулся на 3% и более

1950—1959	5
1960—1969	9
1970—1979	16
1980—1989	24
1990—1999	27
2000—2009	95
2010—2019	50

Особенно явно корреляции усиливаются во время фондовых обвалов. В панике инвесторы массово скидывают ценные бумаги широкого спектра, и в итоге все падает независимо от корреляции.

Но во время коронавирусного кризиса корреляции усилились. Все перечисленные выше активы стали взаимосвязаны. А облигации, которые традиционно считаются защитным инструментом, падали вместе с рисковыми активами.

Как посчитать корреляцию

Чтобы рассчитать корреляцию, можно воспользоваться онлайн-калькулятором, например от Portfolio Visualizer или более простым вариантом от Unicornbay.

Я использовал Portfolio Visualizer, чтобы проверить корреляции между такими классами активов:

1. Фонд TLT — долгосрочные казначейские облигации с дюрацией от 20 лет.
2. Фонд SHY — краткосрочные казначейские облигации с дюрацией от 1 до 3 месяцев.
3. Фонд SPY — компании из индекса S&P 500.
4. Фонд GLD — золото.
5. Фонд DBC — коммодити, или сырьевые товары.
6. Фонд VNQ — сектор недвижимости и фонды REIT.

Для этого я вбил через пробелы указанные тикеры, выбрал расчет корреляций на основе месячной доходности инструментов и рассчитал 36-месячную скользящую.

Я начал расчет с марта 2006 года, так как для фонда DBC более ранних данных нет.

Результаты расчетов представлены в таблице. Мы видим, что исторически у недвижимости, коммодити и S&P 500 слабая отрицательная корреляция по отношению к долгосрочным и коротким облигациям.

36-месячная скользящая корреляция разных классов активов

Название	Тикер	TLT	SHY	SPY	GLD	DBC	VNQ
iShares 20+ Year Treasury Bond ETF	TLT	—	0,54	−0,32	0,23	−0,37	−0,01
iShares 1-3 Year Treasury Bond ETF	SHY	0,54	—	−0,37	0,29	−0,21	−0,18
SPDR S&P 500 ETF Trust	SPY	−0,32	−0,37	—	0,05	0,54	0,72
SPDR Gold Shares	GLD	0,23	0,29	0,05	—	0,36	0,09
Invesco DB Commodity Tracking	DBC	−0,37	−0,21	0,54	0,36	—	0,34
Vanguard Real Estate ETF	VNQ	−0,01	−0,18	0,72	0,09	0,34	—

Как рассчитать корреляцию в «Экселе»

Скользящие корреляции также достаточно легко рассчитать в «Экселе». В этом помогает функция КОРРЕЛ() — или CORREL() в англоязычной версии.

После этого можно воспользоваться функцией КОРРЕЛ(), чтобы посчитать скользящие корреляции. Я приведу пример, как рассчитать скользящую трехмесячную, то есть значение за каждое предыдущее окно в три месяца.

Что в итоге

Корреляция показывает схожесть поведения активов. Понимание корреляций активов используется при диверсификации, а также оптимизации стратегии согласно современной теории портфеля.

Корреляция рассчитывается на конкретном временном отрезке, и она может меняться. Как показывают исторические данные, с течением времени корреляция растет.

Корреляция активов — это мера того, как различные активы движутся относительно друг друга. В финансовой и инвестиционной областях показатель отражает  степень изменения двух активов (индексы, ценные бумаги, деривативы и т.д.) по отношению друг к другу.

Самые простые примеры положительной корреляции: акции нефтяных компаний и стоимость нефти, ставки депозитов/кредитов и ключевая ставка, акции агропромышленных компаний и цены на фосфаты, акции металлургов и цены металлов на мировых рынках. По своей сути, результаты деятельности  любой добывающей компании, так или иначе коррелируют с ценами на сырье, которое оно добывает. Из-за этого часто динамика акций таких компаний может быть очень волатильной в краткосрочном периоде.

Корреляция является важной составляющей всего портфеля и каждого актива внутри него. В соответствии с современной портфельной теорией Марковица, диверсификация активов, в том числе инвестирование в комбинацию активов, которые не коррелируют друг с другом,  может снизить общий риск в портфеле и даже повысить его общую доходность. То есть при потенциальном падении одного актива, другой актив, имеющий отрицательную корреляцию, может показать рост и защитить портфель от падения. Другими словами, Вы владеете активами, которые не имеют тенденции двигаться одинаково в один период времени.

Например, трейдер может использовать прошлые данные корреляции, чтобы предсказать, будут ли акции компании расти или падать в ответ на изменение процентных ставок или цен на товары. Точно так же портфельный управляющий может снизить свой риск, следя за тем, чтобы отдельные активы в его портфеле не были чрезмерно коррелированы друг с другом.

В данной статье мы рассмотрим параметр «корреляции», его интерпретацию, способ расчета, а также рассмотрим возможности и примеры его использования в инвестиционных целях.

• Коэффициент корреляции активов.

• Корреляция активов в инвестиционном портфеле.

• Примеры работы с корреляцией активов в инвестировании.

• Ограничения корреляции.

Коэффициент корреляции активов

Перед погружением непосредственно в изучение параметра  корреляции активов на фондовом рынке мы разберем сам коэффициент корреляции, его интерпретацию и способ расчета.

Существует несколько типов коэффициентов корреляции, но наиболее распространенным считается коэффициент Пирсона, который измеряет силу и направление линейной зависимости между двумя переменными.

Рассчитывается данный показатель с помощью коэффициента корреляции – статистической меры силы связи между относительными движениями двух переменных. Измеряется в значении от -1 до +1, где:

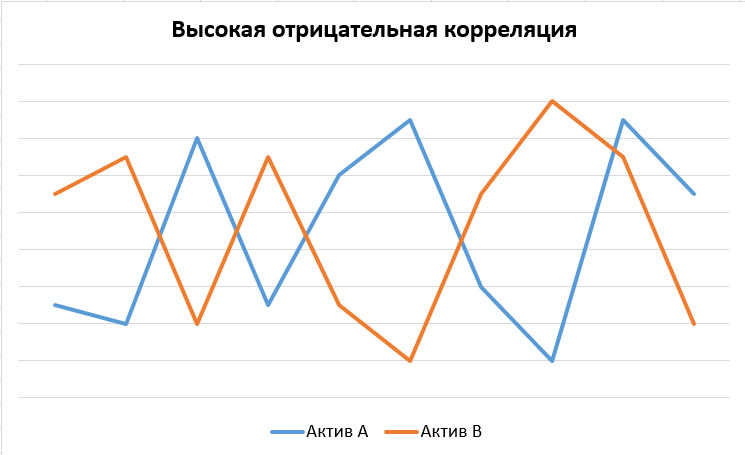
• -1 – это полностью отрицательная корреляция, при которой движение одной переменной вызывает полностью противоположное движение другой переменной.

  

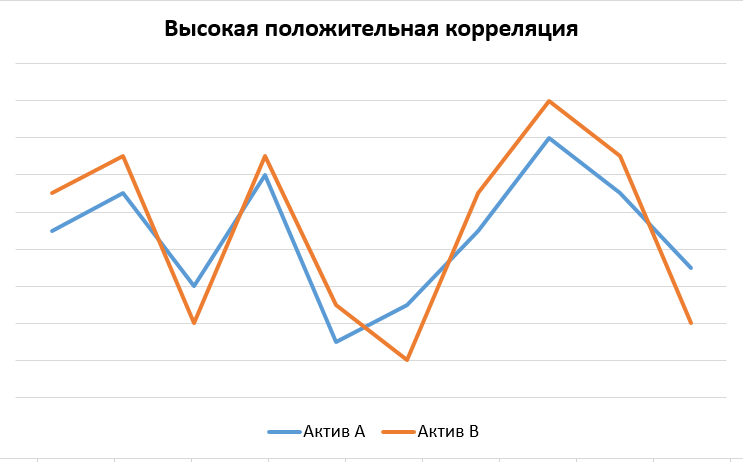
• +1 – это полностью положительная корреляция, при которой 2 переменные движутся в одинаковом направлении

  

• 0 – полное отсутствие зависимости между переменными.

  

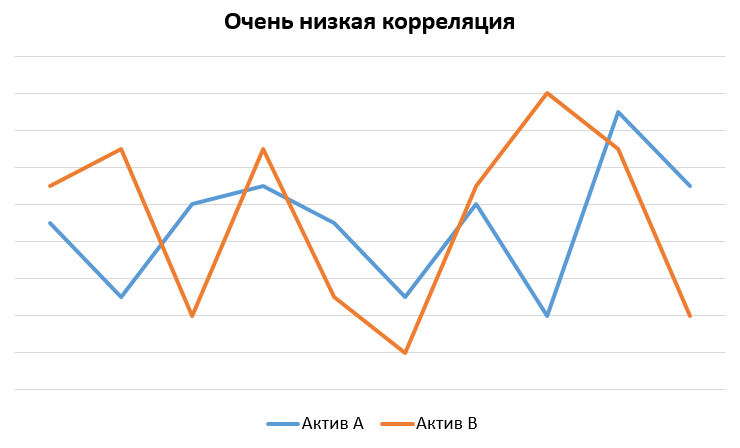
Степень связи варьируется в зависимости от значения коэффициента. Так, значение 0,3 показывает, что существует положительная корреляция между двумя переменными, но она довольно слабая и не имеет большого значения. При этом значение 0,8 и выше считается уже сильным и достаточным для более глубокого изучения. 0,9 и выше – крайне сильная связь между активами.

Формула корреляции Пирсона выглядит следующим образом:

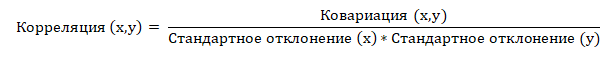
Сначала мы определяем ковариацию двух рассматриваемых переменных (зависимость двух величин друг от друга). Затем рассчитываем их стандартное отклонение (мера разброса данных от их среднего значения). И последним этапом определяется коэффициент корреляции путем деления ковариации на произведение стандартных отклонений двух переменных. Сама по себе ковариация также показывает меру изменчивости двух переменных вместе, но ее величина не ограничена, поэтому ее трудно интерпретировать.

Мы не будет вдаваться в подробное описание формулы расчета каждого показателя, так как их расчет уже давно автоматизирован – в программе Excel есть специальные формулы: «СТАНДОТКЛОН.Г» и «КОВАРИАЦИЯ.Г». С помощью данной программы и с использованием данных формул мы  и продемонстрируем пример расчетов, взяв за основу движение двух акций в течение года.

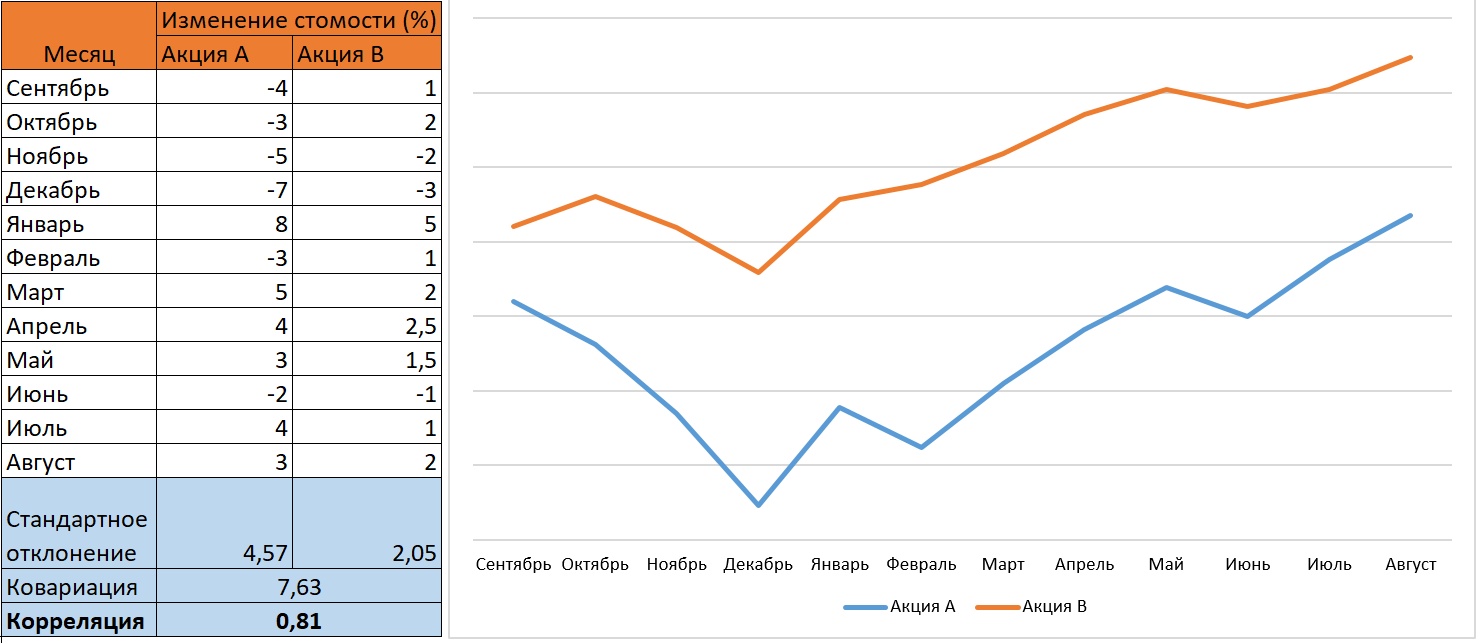
С помощью формулы «СТАНДОТКЛОН.Г»  вначале рассчитываем стандартное отклонение, по которому мы видим, что волатильность у акции А намного больше, чем у акции В. Далее вычисляем ковариацию, по которой мы уже можем видеть, что обе акции положительно коррелируют относительно друг друга, но пока непонятна сила их корреляции. Для этого мы и рассчитываем саму корреляцию, поделив ковариацию на произведение двух стандартных отклонений. В итоге получаем значение, довольно близкое к единице, – 0,81, что говорит об относительно сильной взаимосвязи активов друг с другом.

Также можно поступить проще и рассчитать корреляцию сразу с помощью соответствующей функции в Excel «КОРЕЛЛ». Значение получится идентичным.

Даже по таким цифрам без взгляда на сами компании мы уже можем определить, что перед нами, скорее всего, компании из одного сектора, но компания A является более молодой, тогда как компания B, вероятно, более стабильная и, вероятно, зрелая компания.

Теперь для примера возьмем реальные активы из одного сектора: Сбер и Тинькофф. Рассчитаем корреляцию их акций за последние 12 месяцев и получим 0,7, что также является относительно высоким значением и говорит об умеренной взаимосвязи в движении активов.

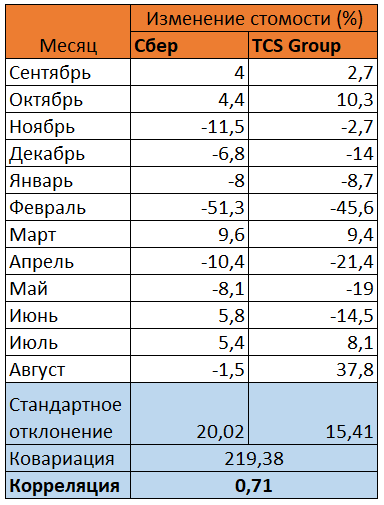
Это подтверждается и сравнением котировок напрямую:

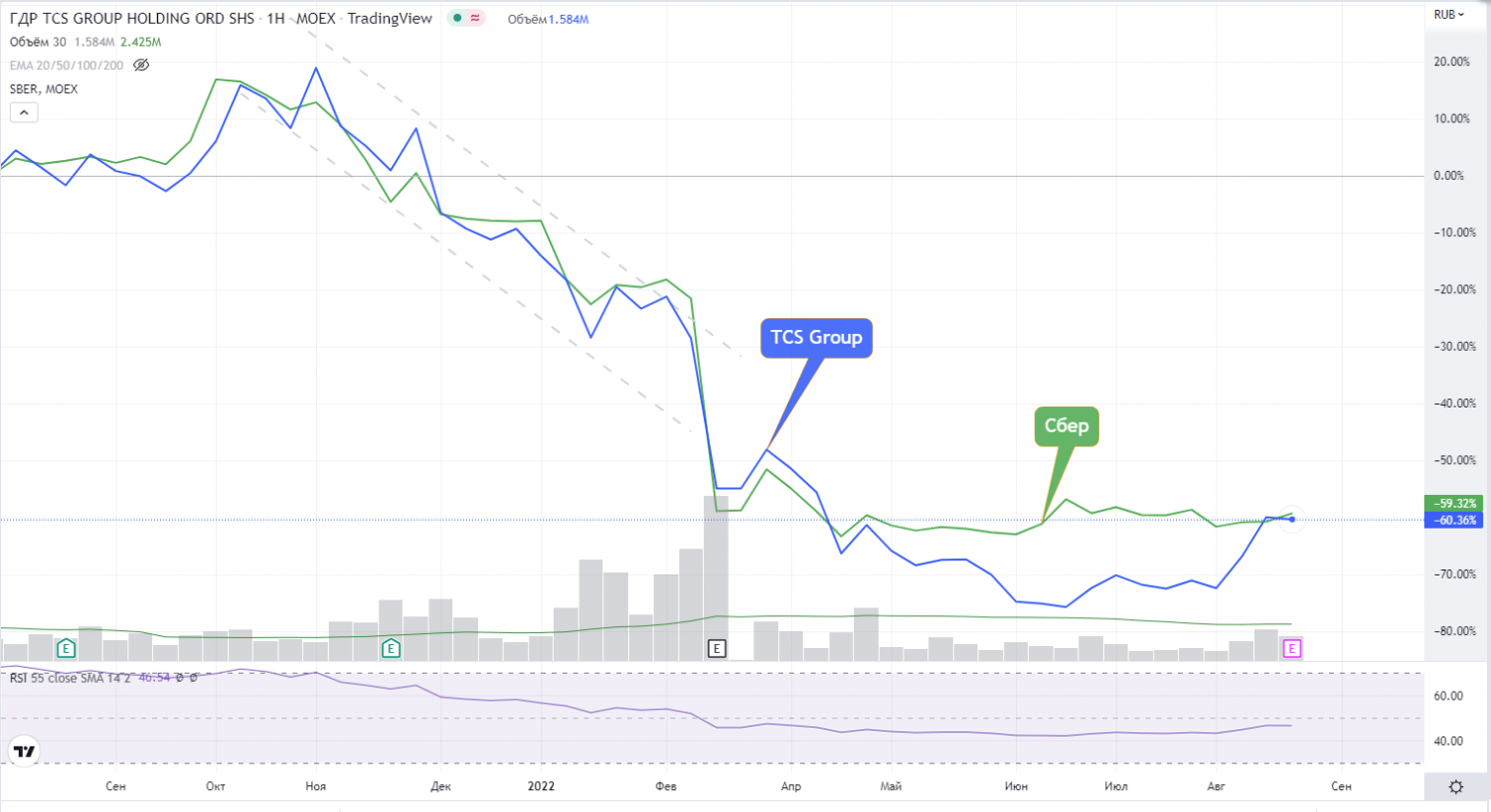
Такие расчеты можно повторять сколько угодно, но чаще всего идет сравнение портфеля и рынка (S&P 500 для США или IMOEX для РФ) либо акции и сектора.

Корреляция активов в инвестиционном портфеле

В инвестировании корреляция важна, в первую очередь, для помощи в создании правильно диверсифицированного портфеля. В классическом понимании диверсификация – это распределение капитала в разные активы. Но важно не просто купить как можно бОльшее количество акций и облигаций, а сделать это направленно. Например, инвестиционный портфель только из 15 или даже 30 акций компаний нефтегазового или металлургического секторов не будет защищен от отраслевых и секторальных рисков. Такие портфели будут подвержены рискам волатильности цен на сырьевых рынках (рынках энергоносителей и металлов). А вот при выборе акций компаний из разных отраслей с отрицательной корреляцией будут минимизированы риски как отраслевого, так и несистематического характера.

Также похожий подход часто используется при рассмотрении вопроса об инвестировании в разные классы активов. Акции, облигации, драгоценные металлы, недвижимость, криптовалюта, сырьевые товары и другие виды инвестиций имеют разную корреляцию друг к другу.  Разные инвесторы могут использовать такое свойство  по-своему в зависимости от индивидуального подхода к построению портфеля.

Инвесторы могут использовать ценные бумаги или другие активы с отрицательной корреляцией для хеджирования своих портфелей и снижения рыночного риска из-за волатильности или резких колебаний цен. Многие крупные инвесторы и фонды используют эту стратегию, хеджируя свои риски во время потенциального спада определенной отрасли или рынка в целом. Они покупают активы с отрицательной корреляцией, которые могут показать рост при падении их основных активов. Подробно этот процесс рассмотрен в статье «Как хеджировать инвестиционный портфель».

В качестве примера посмотрим на портфель одного из самых популярных инвесторов в мире Рея Далио и его фонда Bridgewater. Он состоит из активов разных отраслей, которые имеет отрицательную корреляцию между собой (подробнее об отраслях ниже), а в разные моменты времени увеличивается или уменьшается доля конкретного сектора. Так, в пандемийное время 2020 года доля активов сектора здравоохранения была увеличена с 5% до текущих 16,6%, тогда как доля финансового сектора значительно сократилась. 

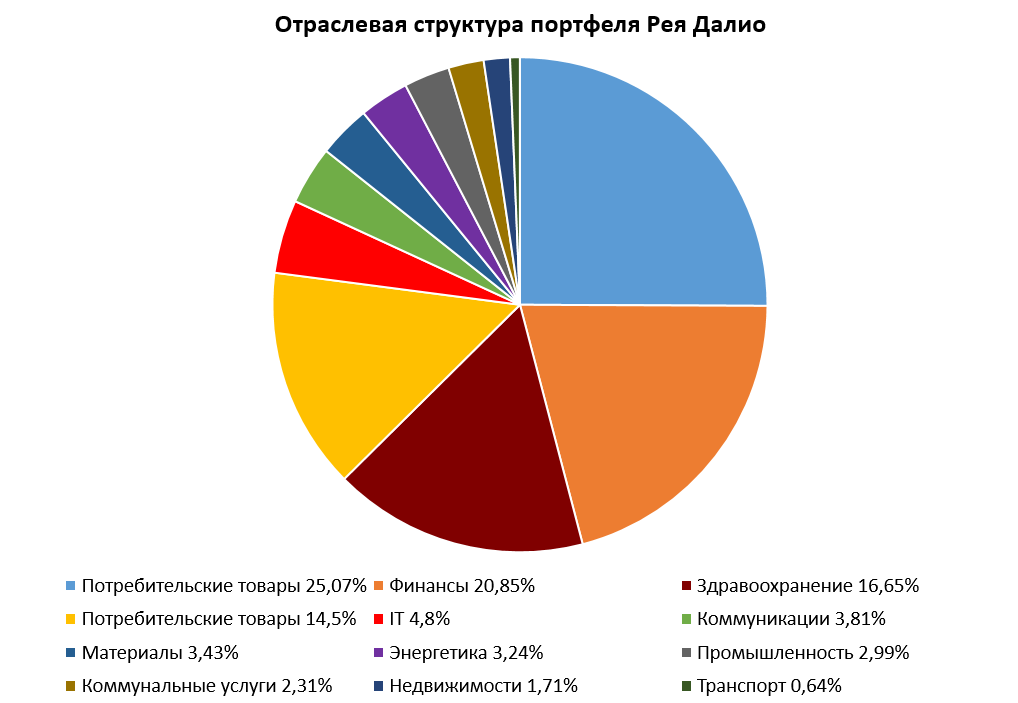
Стоит отметить, что в этом плане многие советуют добавлять золото в портфель в качестве защитного актива. Сейчас мы посмотрим на практике работоспособность  теории о защитных свойствах золота, сравним динамику цен на золото с динамикой S&P 500.

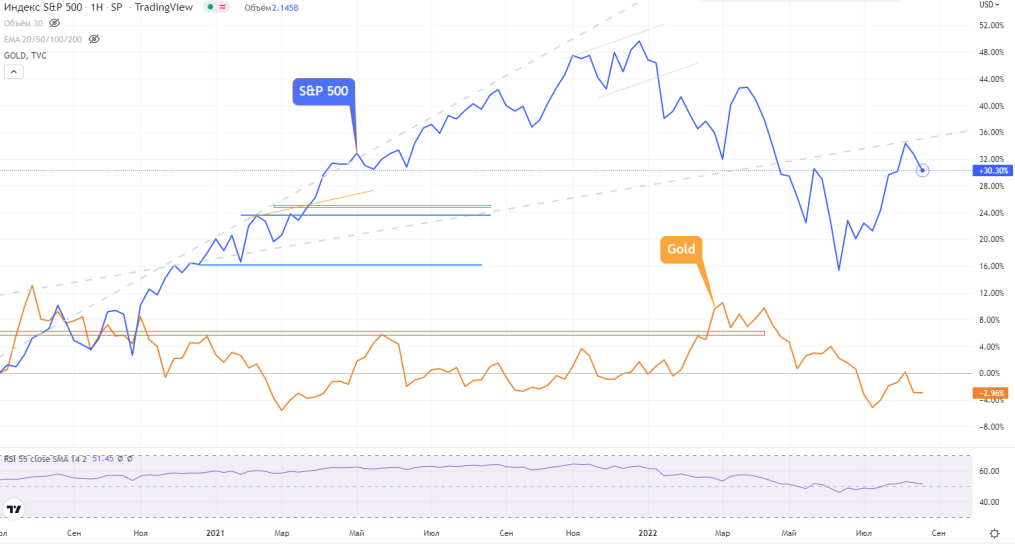
Произведем расчеты.

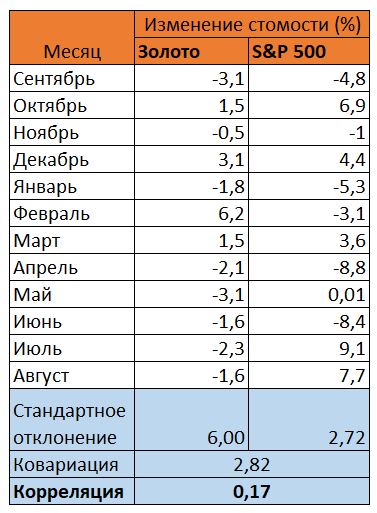
В итоге мы получаем корреляцию 0,17, что довольно близко к нулю и говорит о том, что как таковая связь практически отсутствует – падение или рост главного индекса США никак не влияет на динамику золота. О защите можно было бы утверждать при отрицательной корреляции, близкой к -1.

Также корреляцию интересно рассматривать более глобально с ее изменением в разные моменты времени. Например, с текущими непредсказуемыми рынками стало сложнее доказывать действительность корреляции из-за постоянной смены движения активов. Так, раньше облигации имели отрицательную корреляцию с акциями, тогда как сейчас эта корреляция больше положительная. Аналогичным образом, фондовый рынок США в настоящее время оказывает намного более сильное влияние на рынки других стран и международные акции, чем раньше, так как большинство компаний являются глобальными и не изолированы от одной конкретной страны или региона.

Примеры работы с корреляцией активов в инвестировании

Обычно, работая с корреляцией, для расчетов берут сразу несколько активов и наглядно их сравнивают в таблице. Для нашего примера мы возьмем 9 популярных компаний из разных отраслей индекса S&P 500 и рассчитаем, как они коррелируют между собой. В расчет попали акции Apple, Amazon, Advanced Micro Devices, Johnson & Johnson, Caterpillar,  Exxon Mobil, Alcoa Corporation, Walmart, Bank of America.

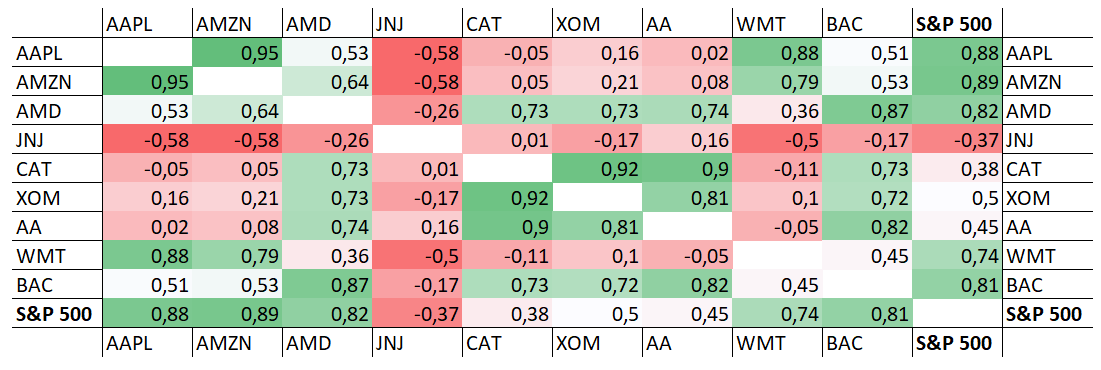
Можно заметить, что у большинства инструментов высокая корреляция как между собой, так и с индексом S&P 500. Выделяется лишь компания из сектора здравоохранения Johnson & Johnson c отрицательной корреляцией практически ко всем другим акциям. Высокая корреляция акций между собой – нормальное явление, даже несмотря на то, что они все из разных отраслей экономики. В целом, рынок акций почти всегда движется в одном направлении, о чем говорит высокая корреляция почти всех акций с S&P 500, различается только сила этого взаимного движения – у каких-то отраслей она больше, у каких-то меньше.

Для большей наглядности в отдельной таблице мы сравним между собой различные классы активов: золото, облигации, нефть, недвижимость, криптовалюта  и т.д.

Получились довольно любопытные результаты:

• Недвижимость имеет очень высокую корреляцию с рынком акций – как с общим, так и с отдельно перечисленными в таблице секторами.

• Китай отрицательно коррелирован практически со всеми другими активами.

• Криптовалюта в лице биткоина в целом «ходит» в одном направлении с другими активами, хотя корреляция довольно слабая.

• Нефть отрицательно коррелирована с рынком акций, но имеет неплохое совместное движение с золотом.

• Из всех результатов нет значения с отрицательной корреляцией меньше 0,65, что говорит о большой связи активов между собой.

Это лишь некоторые выводы.  Данную таблицу можно изучить подробнее и подстроить ее под свою стратегию инвестирования, улучшив общую диверсификацию портфеля.

Также стоит отметить ряд дополнительных коэффициентов, связанных с корреляцией:

• Бета – показывает силу движения актива или портфеля относительно всего рынка.

• Коэффициент Шарпа – показывает, насколько хорошо доходность актива компенсирует общий риск портфеля.

• Коэффициент Сортино – показывает, за счет чего по портфелю была получена сверхнормативная доходность.

• Коэффициент Трейнора – показывает, насколько хорошо доходность актива компенсирует принимаемый инвестором систематический риск портфеля

 Про каждый коэффициент у нас есть отдельная подробная статья. Здесь лишь скажем, что они помогают инвестору сравнивать эффективность и риски портфеля по сравнению с рынком в целом.

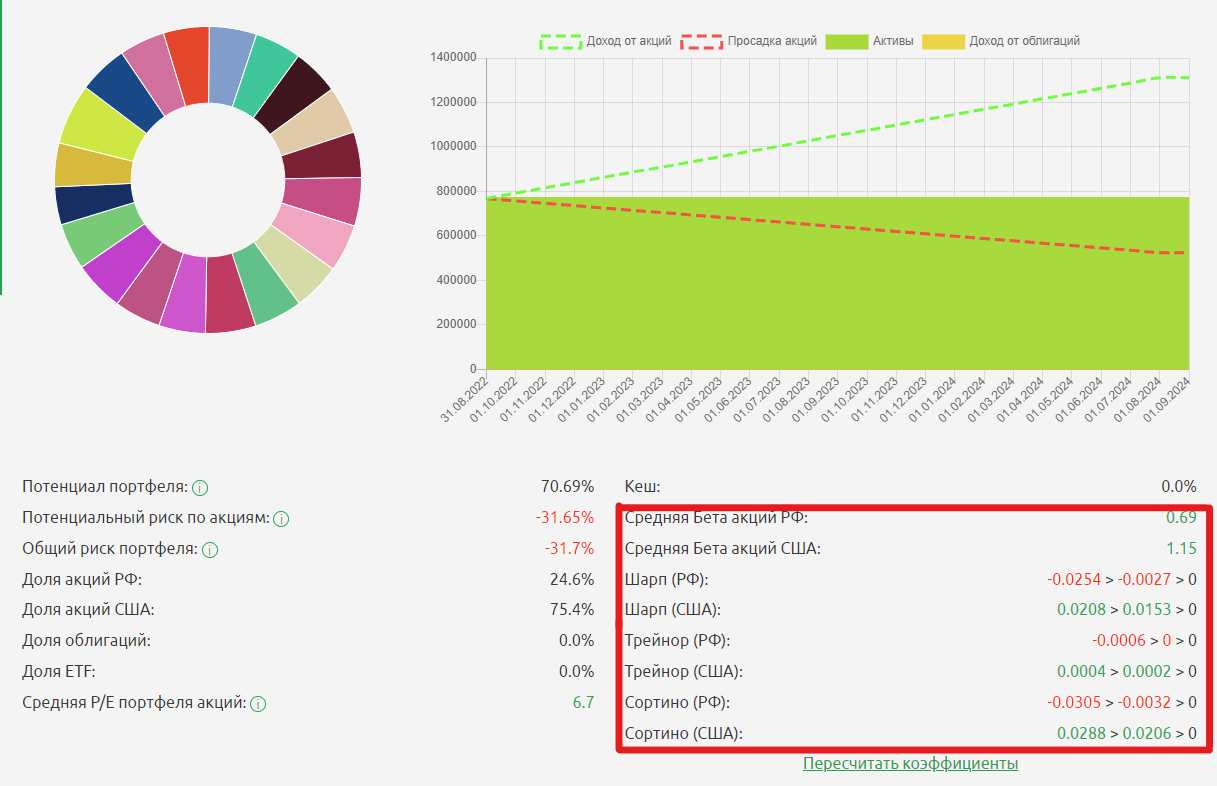
Для получения значений коэффициентов необходимо произвести многоступенчатый расчет с использованием большого массива данных. В профессиональном сервисе для инвесторов  Fin-plan Radar в разделе учета портфелей эти коэффициенты рассчитываются автоматически . Инвестор может по нажатию одной кнопки определить эффективность своего портфеля в сравнении с рынком: если левая часть значения  (портфель) окрашена в зеленый цвет, то портфель в теории имеет меньший риск и при потенциальной той же доходности, чем рынок (правая часть).

Ограничения корреляции

При расчете и дальнейшей работе с  параметром корреляции всегда стоит учитывать ряд нюансов, способных повлиять на итоговый результат и правильную трактовку его значения:

1. В первую очередь, корреляция – это инструмент статистического анализа. Следовательно, как и другие аспекты статистики, она может быть неверно истолкована. Небольшие размеры выборки могут давать ненадежные результаты, даже если кажется, что корреляция между двумя активами сильная. В ином случае наоборот – большой размер выборки может привести к некоррелированным результатам, когда две переменные фактически связаны. Собственно, определение, какая выборка является большой, а какая нет, также является спорным вопросом.

2. Корреляция часто искажается, когда присутствует какая-либо аномалия. Она только показывает, как одна переменная связана с другой и не может четко определить, как отдельный случай может повлиять на коэффициент корреляции. В текущих условиях такого рода аномалии происходят нередко – на котировки ценных бумаг, индексов, товаров и т.д. может повлиять любая новость. Причем она может быть отыграна относительно быстро, но на расчеты все равно повлияет, поэтому может потребоваться учитывать эту погрешность вручную.

3. Также корреляция может быть неверно истолкована, если связь между двумя переменными нелинейна. Гораздо проще определить два актива с понятной положительной или отрицательной корреляцией. Однако даже две переменные с нелинейным, на первый взгляд, движением могут быть коррелированы более сложной взаимосвязью.

Вывод

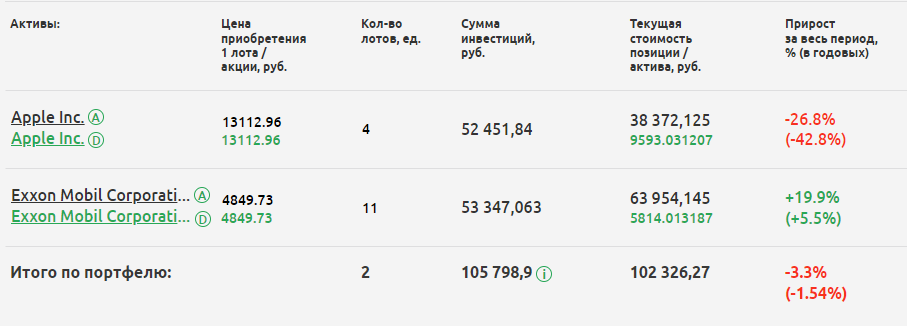
Контроль за корреляцией помогает добиться максимальной эффективности диверсификации инвестиционного портфеля, что, в свою очередь, может увеличить потенциальную доходность и уменьшить риски. Например, покупка в начале 2022 года только одной акции Apple, которая в данном случае символизирует весь технологический сектор, могла принести инвестору убыток в размере 26% (расчет на момент публикации статьи 06.09.2022). При этом добавление какой-либо акции сырьевого сектора, отрицательно коррелирующего с технологическим, например, Exxon Mobil, которая в текущем цикле чувствует себя лучше и растет с начала года на 20%, позволило бы инвестору избежать сильных убытков. Общий результат такого портфеля из двух акций на момент публикации статьи  составил бы -3%. Это довольно яркий пример работы диверсификации с использованием корреляции.

При этом важно следить  как за параметром корреляции отдельных активов, так и всего портфеля. Помочь в этом могут отдельные коэффициенты (Бета, Шарп, Сортино, Трейнор и др.).

Порой корреляцию можно определить из любопытства – она поможет понять устройство рынка, взаимосвязь разных классов активов и секторов экономики, а также развеять некоторые мифы – например, о защитных свойствах золота. Конечно, результатом таких расчетов и исследований является не просто удовлетворение любопытства, проверка работоспособности теорий разных инвестиционных гуру, а создание уникального всепогодного портфеля, который бы мог стабильно показывать положительный результат вне зависимости от ситуации в экономике и на фондовом рынке. Оценка активов по параметру корреляции – лишь один из этапов в решении данной задачи. Также важен точечный выбор надежных активов, минимально коррелированных между собой, следование принципам диверсификации, защиты инвестиционного портфеля. Как реализовать каждый этап данной задачи, в общих словах и с учетом множества нюансов, с примерами кейсов из реальной практики, мы рассказываем на наших открытых уроках для инвесторов. Записаться на наш бесплатный вебинар можно по ссылке.

Концепция портфельной теории

Девиз современной портфельной теории – “инвестиционный портфель должен быть с максимальной доходностью при допустимом риске”. Теория, придуманная Марковицем в 1950-ые, стала ядром пассивных инвестиций и по сей день так или иначе применяется в биржевых фондах.

Ключевая идея портфельной теории в диверсификации активов. “Диверсификацией” здесь называется формальная математическая модель, которая позволяет сделать риск портфеля в совокупности меньше, чем у каждого индивидуального актива.

Диверсификация использует активы, которые движутся независимо друг от друга. Тогда падение одного актива может компенсировать рост другого актива, и портфель будет изменяться более прогнозируемо.

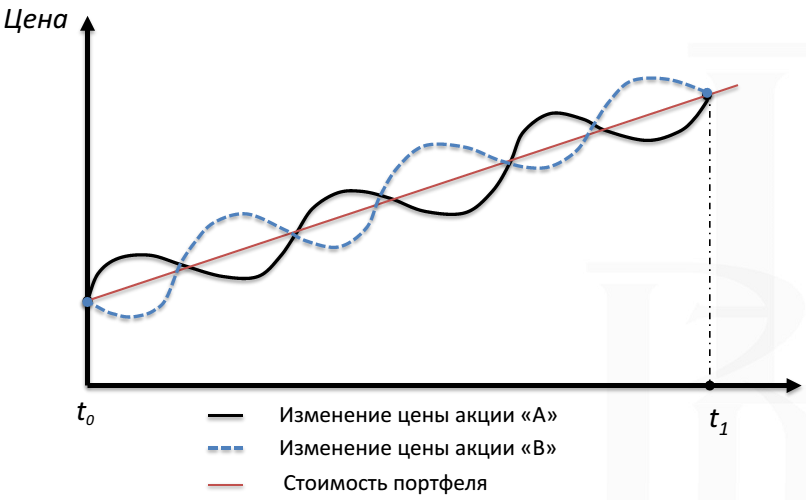
Если же в портфеле присутствуют активы, которые повторяют ценовую динамику друг друга, то падать они будут также одновременно, формируя огромные потери в деньгах.

Какие характеристики активов нужны в портфельной теории?

• Ожидаемая доходность активов
• Корреляция активов между собой

Вставка для математиков: доходность портфеля

Вставка для математиков: риск портфеля

Именно корреляция является тем самым формальным инструментом диверсификации, который позволяет усилить устойчивость портфеля. Но предупреждаем, у диверсификации есть свои пределы – она спасает от индивидуальных рисков компаний, но может оказаться бесполезной перед лицом всеобщей паники на рынке.

Что такое корреляция?

Все в нашем мире взаимосвязано. Причинно-следственные связи на рынке особенно сильны. Изменение цены одного финансового инструмента неизбежно влияет на цены остальных активов. Паника на нефтяном рынке может вызвать ослабления российской валюты, что неизбежно сказывается на всем рынке акций в целом.

Примеров зависимости на фондовом рынке множество:

1. Падение нефти приводит к увеличению курса доллара
2. Капитализация компаний прямопорциональна цене акций
3. Ключевая ставка цб влияет на проценты по депозитам, так как по ставке цб банки привлекают денежные средства в случае недостатка собственных средств

Корреляция показывает, насколько активы похожи по поведению цен. Корреляция может рассчитываться и к ценным бумагам, и к широким рынкам, и классам активов, и к секторам экономики. Все что имеет изменяющуюся во времени цену потенциально может обладать зависимостью с внешними факторами. Корреляция позволит ее найти.

Вставка для математиков: формула корреляций

Например, если при росте одного актива другой дешевеет и эта закономерность подтверждается историческими данными, говорят, что у активов обратная корреляция (близкая к -1).

Корреляция может принимать значения от −1 до +1. Если два актива движутся в связке, то коэффициент корреляции будет ближе к +1, а если в противоположных направлениях, то корреляция получится ближе к −1.

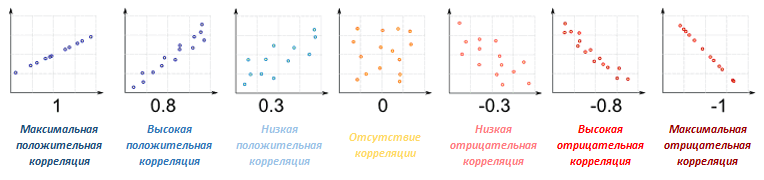
Предупреждаем, когда корреляция близка к нулю, то есть несколько вариантов, что на самом деле происходит. Наиболее вероятный сценарий: активы независимы и не влияют друг на друга. Но возможен и второй сценарий: зависимость между активами выражается сложной формулой и необходим более сильный алгоритм поиска зависимостей, чем корреляций.

Главный недостаток корреляций в том, что со временем значения корреляций могут меняться. Два актива могут начать двигаться синхронно, даже если в прошлом их взаимосвязь была низкой. И заметить это можно только постфактум — на исторических данных. Корреляции становятся высокими в моменты сильных распродаж на рынке. Рынок начинает двигаться одновременно, ломая привычные закономерности.

Вторым недостатком корреляций является сильная подверженность резким движениям активов. Если в спокойное время активы независимы друг от друга, но в момент кризиса они сдвинулись одновременно на большую величину, то корреляция может сильно сдвинуться к +1. Резкие сильные движения цен влияют на корреляцию сильнее, чем много маленьких движений.

Совет инвестору

Подбирая активы в свой портфель, убедитесь в независимости активов. Если у вас все активы зависят от S&P500, то любая просадка индекса будет приводить и к просадке Вашего портфеля.

Чтобы диверсификация работала, лучше собирать портфель из бумаг с низкой или обратной корреляцией. Тогда движение цены одного актива будет компенсироваться движением другого. К примеру, государственные облигации и золото — наиболее частный диверсификатор для акций, поскольку у этих активов исторически низкая взаимосвязь друг с другом.

Как считать корреляцию на RUSETFS

Для сбора портфеля на rusetfs.com у каждого фонда есть отдельная страница корреляций с другими фондами.

При расчете корреляций фонда используются недельные цены закрытия в заданной валюте. Используются недели, так как при оценке корреляции дневных цен закрытия возникает много шумов и оценка корреляции сильно занижается. Чем больше период сравнения, тем корреляция явнее выражена.

Для каждой пары фондов берется максимально возможный период – с последней даты из дат старта торгов двух фондов. В случае отсутствия торгов по какому-либо из ETF в один день, то этот день не учитывается для второго сравниваемого ETF и используется изменений цен за два периода.

Альтернативным и более простым измерителем зависимости являются “совпадения”. Совпадение – это % дней, в которых фонды двигаются в одну сторону. Так, если между RCMX (топ-15 компаний РФ) и SBMX (индекс IMOEX) количество совпадений 91%, то это значит, что каждые 9 из 10 дней эти фонды имеют схожую динамику.

Третий индикатор “Схожесть” помимо корреляций учитывает формальные признаки. Схожесть является суммой следующих переменных:

1. +50%*положительной корреляции (негативная корреляция принимается равной нулю)
2. +20%, если классы активов совпадают
3. +5%, если подклассы активов совпадают
4. +5%, если валюта активов совпадает
5. +10%, если совпадают рынки (развитые, развивающиеся)
6. +5%, если совпадают регионы
7. +10%, если совпадают страны
   Схожесть учитывает классификацию фонда и может помочь в случаях, если в ожидаемой закономерности двух активов были нарушения, и корреляция стала непоказательной.

Например, такие случаи были с ETF RUSE, когда необоснованная премия к цене фонда составляла более 40%. Так, у RUSE с похожим на него SBMX корреляция низкая и составляет всего 0,72, зато схожесть 86%.

Когда инвестор составляет свой портфель и подбирает ценные бумаги, он руководствуется несколькими основными правилами – постулатами. Один из этих постулатов звучит следующим образом: “активы в портфеле должны быть хорошо диверсифицированы”. Когда человек смотрит и видит, что у него приобретены, например, только акции нефтеперерабатывающих компаний, даже если часть эмитентов зарегистрирован в России, а часть в США, ясно дело, ни о какой диверсификации речь не идет. Но иногда инвестор смотри на свой портфель, не всегда можно легко понять диверсифицированы его активы или нет. Существует несколько простых и не очень простых способов оценить насколько портфель инвестора хорошо диверсифицирован.

Корреляция активов

Если говорить простыми словами, корреляция – это взаимосвязь двух случайных величин. Для измерения взаимосвязи котировок двух активов можно использовать коэффициент корреляции. Если коэффициент корреляции 1, значит активы полностью скоррелированы между собой, куда идет один график, туда пойдет и второй. Чем это плохо для инвестора? Тем, что если у него в портфеле много взаимосвязанных активов, которые например, завязаны на цену барреля нефти или металла. При падении цен на сырье, все активы, завязанные на них упадут. А просадка всего портфеля акций – это вдвойне обидно, хорошо когда хоть часть не просядет.

Если коэффициент корреляции составляет -1, значит есть обратная связь между котировками. Если один график идет вверх, второй вниз и наоборот.

Визуальный контроль по личному кабинету

Прежде чем переходить к сложным, более времязатратным методам анализа, необходимо сначала посмотреть визуальную статистику по портфелю. Многие брокеры показывают круговые диаграммы в различных разрезах на которых все очень наглядно видно. На круговых диаграммах видно из каких отраслей экономики эмитенты, на какие валюты куплены ценные бумаги и т.д..

Важно помнить:

1. В портфеле обязательно должны быть облигации или фонды облигация;
2. Эмитенты должны быть из разных секторов экономики;
3. Желательно чтобы хотя бы из некоторых секторов экономики было не менее 1 эмитента;
4. В идеальном портфеле должны быть активы приобретенные за разные валюты.

Выше я привела пример визуализации из своего личного кабинета. Это один из моих счетов, который я открыла ради участия в акции “акция в подарок”. Поэтому не судите меня за диверсификацию по этому скрину, это только один из моих счетов.

Визуальный контроль по графику

Даже когда эмитенты вроде бы относятся к разным отраслям экономики. Их котировки могут быть скоррелированы. Насколько котировки повторяют друг друга, проще всего понять по их графикам. В некотором программном обеспечении для работы с ценными бумагами есть функционал по сравнению котировок. Например, в Альфа Директе можно построить график под графиком. Этого уже достаточно для визуального сравнения. Есть другой вариант, на сайте https://investfunds.ru/ можно построить котировки 5ти активов на одном графике.

Когда графики перед глазами, уже сразу становится понятно, что они либо коррелирую либо нет. На графиках могут отличаться отдельные пики. Но если активы скоррелированы, это становится заметно невооруженным глазом. Например на графике выше видно, что обыкновенные акции Сбера ведут себя почти также как и привилегированные. ВТБ ведет себя немного по-другому, но он растет в цене почти на тех же промежутках, что и Сбер. Да и падают они синхронно.

Excel на друг и помощник

Один из не самых простых способов анализа корреляции портфеля – это excel. Это не самый простой способ, но он позволяет найти активы, чей коэффициент корреляции менее 0. Сделать это просто. Рассказываю алгоритм.

Шаг 1. С любого доступного сервиса копируем котировки в эксель. Например на сервисе https://investfunds.ru/ можно вытащить нужные цифры. Для этого, открываем котировки интересующего нас инструмента, и нажимаем на табличку.

Открывается таблица, которую можно скачать в эксель. Не забываем поменять даты, чтобы оценивать кореляцию не за неделю, а за более длительный срок.

Далее открываем второй инструмент, корреляцию с которым будем проверять и также сохраняем табличку в эксель. Я выбрала акции компании Ростелеком и ETF FinEx Gold.

Далее копируем табличку из одного экселя и вставляем в другой, чтобы котировки оказались в одном файле. Нажимаем Формула – Вставить функцию. Нам нужна функция КОРРЕЛ.

В качестве первого массива подаем “Цена Open” одного актива, в качестве второго “Цена Open” второго. Внизу сразу высвечивается коэффициент корреляции.

Получается, что между золотом и Ростелекомом обратная корреляция. А вот между Ростелекомом и Сбербанком коэффициент корреляции почти равен 0. Этот телеком никак не коррелирует со Сбером и их вполне можно брать в паре.

Корреляция активов – это очень важный параметр для оценки диверсификации долгосрочного инвестиционного портфеля. Оценить ее можно по-разному, начиная с примитивного осмотра статистики брокера, заканчивая точными расчетами в эксель.

В этой статье были ссылки на:

История моего участия в “акция в подарок”.

Современная теория инвестиционного портфеля часто использует идею о том, что инвестиционные возможности можно оценить с использованием ожидаемой доходности в качестве меры вознаграждения и дисперсии доходности в качестве меры риска.

Расчет и интерпретация ожидаемой доходности и дисперсии доходности портфеля являются фундаментальными навыками финансового аналитика. В этом разделе мы рассмотрим концепции ожидаемой доходности портфеля и дисперсии доходности.

Хотя в этом разделе мы коснемся ряда основных понятий, мы не будем разбирать портфельную теорию как таковую. Портфельная теория Марковица (англ. ‘mean-variance analysis’) будет рассматриваться в следующих чтениях.

Доходность портфеля определяется доходностью отдельных его составляющих. В результате расчет дисперсии портфеля как функция доходности отдельного актива является более сложным, чем расчет дисперсии, проиллюстрированный в предыдущем разделе.

---

Рассмотрим пример портфеля,

• 50% которого инвестируются в фонд индекса S&P 500,
• 25% – в фонд долгосрочных корпоративных облигаций США, и
• 25% – в фонд индекса MSCI EAFE (представляющий рынки акций в Европе, Австралии и на Дальнем Востоке).

Таблица 5 показывает это распределение.

Таблица 5. Портфельные веса.

Класс актива	Вес
S&P 500	0.50
Долгосрочные корпоративные облигации США	0.25
MSCI EAFE	0.25

Сначала рассмотрим расчет ожидаемой доходности портфеля. В предыдущем разделе мы определили ожидаемое значение случайной величины как средневзвешенную вероятность возможных результатов случайной величины.

Мы знаем, что доходность портфеля – это средневзвешенная доходность ценных бумаг в портфеле. Аналогично, ожидаемая доходность портфеля представляет собой средневзвешенную величину ожидаемой доходности ценных бумаг в портфеле с использованием точно таких же весов.

Когда мы оценили ожидаемую доходность отдельных ценных бумаг, мы сразу же получили ожидаемую доходность портфеля. Этот удобный факт вытекает из свойств ожидаемого значения.

Свойства ожидаемого значения.

Пусть ( w_i ) – любая постоянная величина (константа), а ( R_i ) – случайная величина.

1. Ожидаемое значение постоянной величины, умноженной на случайную величину, равно постоянной, умноженной на ожидаемое значение случайной величины.

( large E(w_iR_i) = w_i(R_i) )

2. Ожидаемое значение взвешенной суммы случайных величин равно взвешенной сумме ожидаемых значений с использованием тех же весов.

( large begin{aligned}
& E (w_1R_1 + w_2R_2 + ldots + w_nR_n) \
& w_1E (R_1) + w_2E(R_2) + … + w_nE(R_n)
end{aligned} ) (Формула 13)

Предположим, у нас есть случайная величина с заданным ожидаемым значением. Например, если мы умножим каждый результат на 2, ожидаемое значение случайной величины умножится также на 2. В этом смысл части 1.

Второе утверждение – это правило, которое напрямую приводит к выражению ожидаемой доходности портфеля.

Портфель с n ценными бумагами определяется весами его портфеля, ( w_1, w_2, ldots, w_n ), которые в сумме составляют 1. Таким образом, доходность портфеля, ( R_p ), равна ( R_p = w_1R_1 + w_2R_2 + ldots + w_nR_n ).

Теперь мы можем сформулировать следующий принцип:

Расчет ожидаемой доходности портфеля.

Для портфеля с n ценными бумагами ожидаемая доходность портфеля представляет собой средневзвешенную ожидаемую доходность по включенным в него ценным бумагам:

( large begin{aligned}
E(R_p) &= E(w_1R_1 + w_2R_2 + ldots + w_nR_n) \
&= w_1E(R_1) + w_2E(R_2) + ldots + w_nE (R_n)
end{aligned} )

Предположим, мы оценили ожидаемую доходность активов в портфеле, как показано в Таблице 6.

Таблица 6. Веса и ожидаемая доходность активов в портфеле.

Класс актива	Вес	Ожидаемая доходность (%)
S&P 500	0.50	13
Долгосрочные корпоративные облигации США	0.25	6
MSCI EAFE	0.25	15

Мы рассчитываем ожидаемую доходность портфеля как 11.75%:

( begin{aligned}
E(R_p) &= w_1E(R_1) + w_2E(R_2) + w_3E (R_3) \
&= 0.50(13%) + 0.25(6%) + 0.25(15%) = 11.75%
end{aligned} )

В предыдущем разделе мы изучали дисперсию как меру рассеивания результатов вокруг ожидаемого значения. Здесь нас интересует дисперсия доходности портфеля как мера инвестиционного риска.

Если ( R_p ) обозначает доходность портфеля, то дисперсия доходности портфеля составляет ( sigma^2(R_p) = E Big{ big[R_p – E(R_p)big]^2 Big} ) в соответствии с Формулой 8.

Как можно использовать это определение на практике?

В чтении о статистических концепциях и рыночной доходности мы узнали, как рассчитать историческую или выборочную дисперсию на основе выборки ставок доходности.

Теперь мы рассматриваем дисперсию в прогностическом смысле. Мы будем использовать информацию об отдельных активах в портфеле, чтобы получить доходность всего портфеля.

Чтобы избежать беспорядка в обозначениях, мы пишем ( ER_p ) вместо (E(R_p)). Нам нужна концепция ковариации.

Определение ковариации.

Для двух случайных величин (R_i) и (R_j) ковариация между (R_i) и (R_j) равна

( large
newcommand{Cov}{operatorname{Cov}}
Cov bigl(R_i, R_jbigr) = E big[(R_i – ER_i) (R_j – ER_j)big] ) (Формула 14)

Альтернативными обозначениями являются (sigma(R_i,R_j)) и (sigma_{ij}).

Формула 14 утверждает, что ковариация (англ. ‘covariance’) между двумя случайными переменными является средневзвешенной вероятностью для перекрестных произведений отклонения каждой случайной переменной от ее собственного ожидаемого значения.

Используя определением дисперсии, мы находим:

Итоговая формула следует из определений дисперсии и ковариации.

---

Полезные факты о дисперсии и ковариации включают в себя следующее:

1. Дисперсия постоянной величины (константы) умноженная на случайную величину равна квадрату константы умноженной на дисперсию случайной величины, или ( sigma^2(wR) = w^2sigma^2(R) );
2. Дисперсия константы плюс случайная величина равна дисперсии случайной величины, или ( sigma^2(w + R) = sigma 2(R)), поскольку константа имеет нулевую дисперсию;
3. Ковариация между константой и случайной величиной равна нулю.

Для выделенных курсивом ковариационных членов в Формуле 15 мы использовали тот факт, что порядок переменных в ковариации не имеет значения: например, (Cov(R_2,R_1) = Cov(R_1,R_2) ).

Как мы покажем далее, диагональные дисперсионные члены (sigma^2(R_1)), (sigma^2(R2)) и (sigma^2(R_3)) могут быть выражены как (Cov(R_1,R_1)), (Cov(R_2,R_2)) и (Cov(R_3,R_3)), соответственно.

Опираясь на этот факт, можно вывести наиболее компактный вид Формулы 15:

(sigma^2(R_p) = dsum_{i=1}^{3} dsum_{j=1}^{3}w_i w_j Cov(R_i,R_j) )

Знаки суммирования говорят: «Установите i = 1, и пусть j меняется от 1 до 3; затем установите i = 2 и пусть j меняется от 1 до 3; затем установите i = 3 и пусть j меняется от 1 до 3; наконец, добавьте девять членов”.

Эту формулу можно использовать для портфеля любого размера n:

(large sigma^2(R_p) = dsum_{i=1}^{3} dsum_{j=1}^{3}w_i w_j Cov(R_i,R_j) ) (Формула 16)

Из Формулы 15 видно, что отдельные отклонения доходности составляют часть, но не все отклонения портфеля. Три отклонения фактически превосходят по численности шесть ковариационных членов вне диагонали. Для трех активов это соотношение составляет 1 к 2 или 50 процентов.

Если имеется 20 активов, то есть 20 дисперсионных слагаемых и 20(20) – 20 = 380 недиагональных ковариационных слагаемых. Отношение слагаемых дисперсии к недиагональным слагаемым ковариации составляет менее 6 к 100, или 6%. Таким образом, первое наблюдение заключается в том, что с увеличением числа активов портфеля ковариация становится все более важной, в остальном все не меняется.

Когда значение ковариации как «недиагональной ковариации» очевидно, как здесь, мы опускаем уточняющие слова. Ковариация обычно используется в этом смысле.

Как именно влияет ковариация на дисперсию доходности портфеля?

Члены ковариации показывают, как совместное движение доходности отдельных активов влияет на дисперсию всего портфеля.

Например, рассмотрим две акции: одна имеет тенденцию к высокой доходности (относительно ее ожидаемой доходности), а другая имеет низкую доходность (относительно ее ожидаемой доходности).

Доходность одной акции имеет тенденцию компенсировать доходность другой акции, снижая изменчивость или дисперсию доходности портфеля.

Как и дисперсию, значения ковариации трудно интерпретировать, и мы вскоре представим более интуитивно понятную концепцию. Между тем, из определения ковариации мы можем установить два существенных примечания о ковариации.

---

1. Мы можем интерпретировать ковариацию следующим образом:

• Ковариация доходности отрицательна, когда доходность одного актива выше его ожидаемого значения, а доходность другого актива имеет тенденцию быть ниже его ожидаемого значения (средняя обратная зависимость между ставками доходности).
• Ковариация доходности равна 0, если доходность активов не связана.
• Ковариация доходности положительна, когда доходность обоих активов, как правило, находятся по одну сторону (выше или ниже) относительно ожидаемых значений в одно и то же время (средняя положительная зависимость между ставками доходности).

---

2. Ковариация случайной величины с самой собой (собственная ковариация) – это ее собственная дисперсия:

( begin{aligned}
Cov(R, R) &= E Big{ big[R – E (R) big] big[R – E (R) big] Big } \
&= E Big { big[R – E(R) big]^2 Big} = sigma^2(R)
end{aligned})

Полный список ковариаций составляет все статистические данные, необходимые для расчета дисперсии доходности портфеля. Ковариации часто представлены в табличном формате, который называется ковариационной матрицей (англ. ‘covariance matrix’).

В Таблице 7 показано, как вводятся расчетные значения в ковариационную матрицу для ожидаемой доходности и дисперсии доходности портфеля.

Таблица 7. Ожидаемая доходность и дисперсия портфеля – значения матрицы:

Актив	A	B	C
	E(RA)	E(RB)	E(RC)

Актив	A	B	C
A	(mathbf{Cov(R_A,R_A)})	(Cov(R_A,R_B))	(Cov(R_A,R_C))
B	(Cov(R_B,R_A))	(mathbf{Cov(R_B,R_B)})	(Cov(R_B,R_C))
C	(Cov(R_C,R_A))	(Cov(R_C,R_B))	(mathbf{Cov(R_C,R_C)})

Для трех активов ковариационная матрица имеет (3^2 = 3 times 3 = 9 ) ячеек, но значения ячеек по диагонали (дисперсия) обычно рассчитываются отдельно от недиагональных ячеек. Эти диагональные значения выделены жирным шрифтом в Таблице 7.

Это различие естественно, так как дисперсия акций – это концепция с одной переменной. Таким образом, есть 9 – 3 = 6 ковариаций, исключая дисперсии.

Но

( Cov(R_B,R_A) = Cov(R_А,R_В)), ( Cov(R_С,R_A) = Cov(R_B,R_A) )

и

( Cov(R_С,R_B) = Cov(R_B,R_C) )

Ковариационная матрица под диагональю является зеркальным отображением ковариационной матрицы над диагональю. В результате, есть только 6/2 = 3 различных ковариационных члена для оценки. В целом, для n ценных бумаг существует ( n(n – 1)/2 ) различных ковариаций для оценки и n дисперсий для оценки.

---

Предположим, у нас есть ковариационная матрица, показанная в Таблице 8.

Мы будем работать с доходностью, указанной в процентах, а записи в таблице будут выражены в процентах в квадрате (%²). Члены 38%² и 400%² равны 0.0038 и 0.0400 соответственно в десятичном виде; правильная работа в процентах и ​​десятичных дробях приводит к одинаковым ответам.

Таблица 8. Ковариационная матрица.

	S&P 500	Долгосрочные корпоративные облигации США	MSCI EAFE
S&P 500	400	45	189
Долгосрочные корпоративные облигации США	45	81	38
MSCI EAFE	189	38	441

Если взять Формулу 15 и сгруппировать дисперсионные члены, мы получим следующее:

(
small
begin{aligned}
sigma^2(R_p) &= (0.50)^2(400) + (0.25)^2(81) + (0.25)^2(441) \
&+ 2(0.50)(0.25)(45) + 2(0.50)(0.25)(189) \
&+ 2(0.25)(0.25)(38) \
&= 100 + 5.0625 + 27.5625 + 11.25 + 47.25 + 4.75 = 195.875
end{aligned} )

Разница составляет 195.875. Стандартное отклонение доходности составляет 195.875^1/2 = 14%. В итоге, ожидаемая годовая доходность портфеля составляет 11.75%, а стандартное отклонение доходности – 14%.

Давайте посмотрим на первые три члена в приведенном выше расчете. Их сумма, 100 + 5.0625 + 27.5625 = 132.625, является вкладом отдельных дисперсий активов в общую дисперсию портфеля. Если бы доходность по трем активам была независимой, ковариации были бы равны 0, а стандартное отклонение доходности портфеля составило бы 132.625^1/2 = 11.52% по сравнению с 14% ранее.

Портфель будет иметь меньший риск. Предположим, что члены ковариации были отрицательными. Тогда к 132.625 будет добавлено отрицательное число, поэтому дисперсия портфеля и риск будут еще меньше.

В то же время мы не изменили ожидаемую доходность. При той же ожидаемой доходности портфеля, портфель имеет меньший риск. Это снижение риска является преимуществом диверсификации, что означает снижение риска от владения портфелем активов.

Преимущество диверсификации увеличивается с уменьшением ковариации.

Это наблюдение является ключевым понятием современной теории портфеля. Это станет еще более интуитивно понятно, когда мы рассмотрим концепцию корреляции. Тогда мы сможем сказать, что до тех пор, пока ставки доходности акций портфеля не имеют абсолютно положительной корреляции, возможны преимущества диверсификации.

Кроме того, чем меньше корреляция между доходностью акций, тем выше стоимость отказа от диверсификации (с точки зрения упущенных выгод от снижения риска), при прочих равных условиях.

Определение корреляции.

Корреляция (англ. ‘correlation’) между двумя случайными величинами, (R_i) и (R_j), определяется как:

( large dst
rho(R_i,R_j) = {Cov(R_i, R_j) over sigma(R_i)sigma(R_j)} )

Альтернативными обозначениями корреляции являются (mathrm{Corr}(R_i,R_j) ) и ( rho_{ij}).

Ковариация часто представляется с использованием выражения:

( large Cov(R_i, R_j) = rho(R_i,R_j) sigma(R_i)sigma(R_j) )

Деление, указанное в определении, делает корреляцию чистым числом (т.е. без единицы измерения) и устанавливает границы для ее наибольшего и наименьшего возможных значений.

Используя приведенное выше определение, мы можем сформулировать корреляционную матрицу только на основе данных из ковариационной матрицы. В Таблице 9 показана матрица корреляции.

Таблица 9. Корреляционная матрица доходности.

	S&P 500	Долгосрочные корпоративные облигации США	MSCI EAFE
S&P 500	1.00	0.25	0.45
Долгосрочные корпоративные облигации США	0.25	1.00	0.20
MSCI EAFE	0.45	0.20	1.00

Например, ковариация между долгосрочными облигациями и MSCI EAFE составляет 38, как указано в Таблице 8. Стандартное отклонение доходности долгосрочных облигаций составляет 81^1/2 = 9%, а доходности MSCI EAFE – 441^1/2 = 21% (см. диагональные члены в Таблице 8).

Корреляция (rho)(Доходность долгосрочных облигаций, Доходность EAFE) составляет 38 / (9%) (21%) = 0.201, округленное до 0.20.

Корреляция доходности S&P 500 с самой собой равно 1: расчет представляет собой собственную ковариацию, деленную на квадрат стандартного отклонения.

Свойства корреляции.

1. Корреляция – это число от -1 до +1 для двух случайных величин, (X) и (Y):

( -1 leq rho(X,Y) leq + 1 )

2. Корреляция 0 (некоррелированные переменные) указывает на отсутствие какой-либо линейной (прямой) взаимосвязи между переменными.

Если корреляция равна 0, (R_1 = a + bR_2) + ошибка, при (b = 0).

Пример (12) расчета ожидаемой доходности и дисперсии доходности портфеля.

У вас есть портфель из двух взаимных инвестиционных фондов, A и B. 75% портфеля вложено в A, как показано в Таблице 10.

Таблица 10. Ожидаемая доходность, дисперсия и ковариация доходности взаимных фондов.

Фонд	A	B
	E(RA) = 20%	E(RB) = 12%
Ковариационная матрица
Фонд	A	B
A	625	120
B	120	196

1. Рассчитайте ожидаемую доходность портфеля.
2. Рассчитайте матрицу корреляции для этой задачи. Рассчитайте значения матрицы до двух десятичных знаков.
3. Рассчитайте стандартное отклонение доходности портфеля.

---

Решение для части 1:

( E(R_p) = w_AE(R_A) + (1 – w_A)E(R_B) )
= 0.75(20%) + 0.25(12%) = 18%.

Веса портфеля должны составлять в сумме 1: (W_B = 1 – W_A ).

 

Решение для части 2:

(sigma(R_A) = 625^{1/2} = 25%), (sigma(R_B) = 196^{1/2} = 14%).

Существует одна четкая ковариация и, следовательно, одна четкая корреляция:

( begin{aligned}
 rho(R_A,R_B) &= dst {Cov(R_A, R_B) over sigma(R_A)sigma(R_B)} \[1ex]
&= 120 / [25(14)] = 0.342857 text{  или  } 0.34
end{aligned} )

В Таблице 11 показана корреляционная матрица.

Таблица 11. Матрица корреляции.

	A	B
A	1.00	0.34
B	0.34	1.00

В корреляционной матрице диагональные члены всегда равны 1.

---

Решение для части 3:

Как оценивать ковариацию и корреляцию доходности?

Часто мы делаем прогнозы на основе исторической ковариации или используем другие методы, основанные на исторических данных о доходности, такие как регрессионная модель рынка.

Мы также можем рассчитать ковариацию, используя функцию совместной вероятности случайных величин, если ее можно оценить.

Функция совместной вероятности (англ. ‘joint probability function’) двух случайных величин (X) и (Y), обозначенная как (P(X, Y)), дает вероятность совместного появления значений (X) и (Y). Например, (P(3,2)) – это вероятность того, что (X) равен 3 и (Y) равен 2.

Предположим, что функция совместной вероятности доходности акций BankCorp(RA) и доходностей акций NewBank(RB) имеет простую структуру, приведенную в Таблице 12.

Таблица 12. Функция совместной вероятности доходности BankCorp и NewBank (записи в ячейках – совместные вероятности).

	RB = 20%	RB = 16%	RB = 10%
RA = 25%	0.20	0	0
RA = 12%	0	0.50	0
RA = 10%	0	0	0.30

Ожидаемая доходность акций BankCorp составляет:

0.20(25%) + 0.50(12%) + 0.30(10%) = 14%

Ожидаемая доходность акций NewBank составляет:

0.20(20%) + 0.50(16%) + 0.30(10%) = 15%

Функция совместной вероятности, приведенная выше, может отражать анализ, основанный на том, является ли состояние банковской отрасли хорошим, средним или плохим.

В Таблице 13 представлен расчет ковариации.

Таблица 13. Расчеты ковариации.

Состояние банковской индустрии	Отклоне- ния доход- ности BankCorp	Отклоне- ния доход- ности NewBank	Произ- ведение откло- нений	Вероят- ность состояния	Произ- ведение, взве- шенное по вероят- ности
Хорошее	25-14	20-15	55	0.20	11
Среднее	12-14	16-15	-2	0.50	-1
Плохое	10-14	10-15	20	0.30	6
					Cov(RA,RB) = 16

Примечание. Ожидаемая доходность для BankCorp составляет 14%, а для NewBank – 15%.

Первый и второй столбцы чисел показывают, соответственно, отклонения доходности BankCorp и NewBank от их среднего или ожидаемого значения.

В следующем столбце показано произведение отклонений. Например, для хорошего состояния отрасли (25–14)(20–15) = 11(5) = 55.

Затем 55 умножается на 0.20 или взвешивается на вероятность того, что условия банковской отрасли являются хорошими: 55(0.20) = 11.

Расчеты для средних и плохих банковских условий выполняются по той же схеме. Суммируя эти взвешенные по вероятности произведения, получим, что (Cov(R_A,R_B) ) = 16.

---

Формула для вычисления ковариации между случайными переменными (R_A) и (R_B) имеет вид:

Формула предписывает нам суммировать все возможные отклонения перекрестных произведений, взвешенных по соответствующей совместной вероятности.

В этом примере, как показано в Таблице 12, только три совместные вероятности отличны от нуля. Следовательно, при вычислении ковариации доходности в этом случае нам нужно учитывать только три перекрестных произведения:

(
small
begin{aligned}
Cov(R_A,R_B) &= P(25,20) big[(25-14) (20-15)big] \
&+ P(12,16) big[(12-14)(16-15) big] \ &+ P(10,10) big[(10-14)(10-15)big] \
&= 0,20(11)(5) + 0,50(-2)(1) + 0,30(-4)(- 5) \
&= 11 – 1 + 6 = 16
end{aligned} )

Одной из тем этого чтения была независимость событий. Две случайные переменные являются независимыми, когда каждая возможная пара событий (одно событие, соответствующее значению (X), и другое событие, соответствующее значению (Y)) – являются независимыми событиями. Когда две случайные величины независимы, их функция совместной вероятности упрощается.

Определение независимости для случайных величин.

Две случайные величины (X) и (Y) независимы тогда и только тогда, когда:

( P(X,Y) = P(X)P(Y) )

Например, учитывая независимость:

(P(3,2) = P(3)P(2))

Мы умножаем отдельные вероятности, чтобы получить совместные вероятности. Независимость является более сильным свойством, чем некоррелированность, потому что корреляция касается только линейных зависимостей.

Следующее правило распространяется на независимые случайные величины и, следовательно, также на некоррелированные случайные величины.

Правило умножения для ожидаемого значения произведения некоррелированных случайных величин.

Ожидаемое значение произведения некоррелированных случайных величин является произведением их ожидаемых значений.

Многие финансовые переменные, такие как выручка (цена, умноженная на количество), являются произведением случайных величин. Когда это применимо, приведенное выше правило упрощает расчет ожидаемого значения произведения случайных величин.

В противном случае расчет зависит от условного ожидаемого значения; расчет может быть выражен как:

( E(XY) = E (X) E(Y|X) )