Чем больше я узнаю людей, тем больше мне нравится моя собака.
—Марк Твен
В предыдущих сериях постов для начинающих из ремикса книги Генри Гарнера «Clojure для исследования данных» (Clojure for Data Science) на языке Python мы рассмотрели методы описания выборок с точки зрения сводных статистик и методов статистического вывода из них параметров популяции. Такой анализ сообщает нам нечто о популяции в целом и о выборке в частности, но он не позволяет нам делать очень точные утверждения об их отдельных элементах. Это связано с тем, что в результате сведения данных всего к двум статистикам – среднему значению и стандартному отклонению – теряется огромный объем информации.
Нам часто требуется пойти дальше и установить связь между двумя или несколькими переменными либо предсказать одну переменную при наличии другой. И это подводит нас к теме данной серии из 5 постов – исследованию корреляции и регрессии. Корреляция имеет дело с силой и направленностью связи между двумя или более переменными. Регрессия определяет природу этой связи и позволяет делать предсказания на ее основе.
В этой серии постов будет рассмотрена линейная регрессия. При наличии выборки данных наша модель усвоит линейное уравнение, позволяющее ей делать предсказания о новых, не встречавшихся ранее данных. Для этого мы снова обратимся к библиотеке pandas и изучим связь между ростом и весом спортсменов-олимпийцев. Мы введем понятие матриц и покажем способы управления ими с использованием библиотеки pandas.
О данных
В этой серии постов используются данные, любезно предоставленные компанией Guardian News and Media Ltd., о спортсменах, принимавших участие в Олимпийских Играх 2012 г. в Лондоне. Эти данные изначально были взяты из блога газеты Гардиан.
Обследование данных
Когда вы сталкиваетесь с новым набором данных, первая задача состоит в том, чтобы его обследовать с целью понять, что именно он содержит.
Файл all-london-2012-athletes.tsv достаточно небольшой. Мы можем обследовать данные при помощи pandas, как мы делали в первой серии постов «Python, исследование данных и выборы», воспользовавшись функцией read_csv:
def load_data():
return pd.read_csv('data/ch03/all-london-2012-athletes-ru.tsv', 't')
def ex_3_1():
'''Загрузка данных об участниках
олимпийских игр в Лондоне 2012 г.'''
return load_data()Если выполнить этот пример в консоли интерпретатора Python либо в блокноте Jupyter, то вы должны увидеть следующий ниже результат:
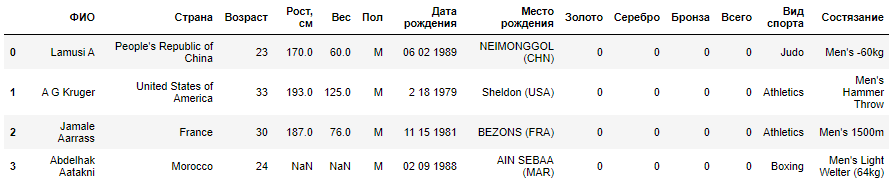
Столбцы данных (нам повезло, что они ясно озаглавлены) содержат следующую информацию:
-
ФИО атлета
-
страна, за которую он выступает
-
возраст, лет
-
рост, см.
-
вес, кг.
-
пол «М» или «Ж»
-
дата рождения в виде строки
-
место рождения в виде строки (со страной)
-
число выигранных золотых медалей
-
число выигранных серебряных медалей
-
число выигранных бронзовых медалей
-
всего выигранных золотых, серебряных и бронзовых медалей
-
вид спорта, в котором он соревновался
-
состязание в виде списка, разделенного запятыми
Даже с учетом того, что данные четко озаглавлены, очевидно присутствие пустых мест в столбцах с ростом, весом и местом рождения. При наличии таких данных следует проявлять осторожность, чтобы они не сбили с толку.
Визуализация данных
В первую очередь мы рассмотрим разброс роста спортсменов на Олимпийских играх 2012 г. в Лондоне. Изобразим эти значения роста в виде гистограммы, чтобы увидеть характер распределения данных, не забыв сначала отфильтровать пропущенные значения:
def ex_3_2():
'''Визуализация разброса значений
роста спортсменов на гистограмме'''
df = load_data()
df['Рост, см'].hist(bins=20)
plt.xlabel('Рост, см.')
plt.ylabel('Частота')
plt.show()Этот пример сгенерирует следующую ниже гистограмму:
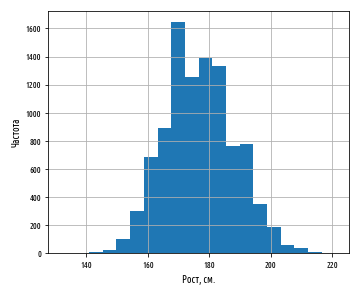
Как мы и ожидали, данные приближенно нормально распределены. Средний рост спортсменов составляет примерно 177 см. Теперь посмотрим на распределение веса олимпийских спортсменов:
def ex_3_3():
'''Визуализация разброса значений веса спортсменов'''
df = load_data()
df['Вес'].hist(bins=20)
plt.xlabel('Вес')
plt.ylabel('Частота')
plt.show()Приведенный выше пример сгенерирует следующую ниже гистограмму:
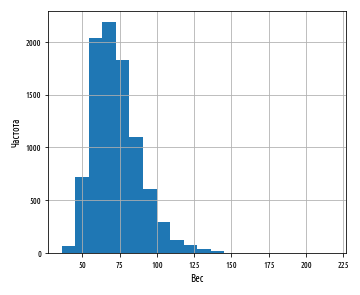
Данные показывают четко выраженную асимметрию. Хвост с правой стороны намного длиннее, чем с левой, и поэтому мы говорим, что асимметрия – положительная. Мы можем оценить асимметрию данных количественно при помощи функции библиотеки pandas skew:
def ex_3_4():
'''Вычисление асимметрии веса спортсменов'''
df = load_data()
swimmers = df[ df['Вид спорта'] == 'Swimming']
return swimmers['Вес'].skew()0.23441459903001483К счастью, эта асимметрия может быть эффективным образом смягчена путем взятия логарифма веса при помощи функции библиотеки numpy np.log:
def ex_3_5():
'''Визуализация разброса значений веса спортсменов на
полулогарифмической гистограмме с целью удаления
асимметрии'''
df = load_data()
df['Вес'].apply(np.log).hist(bins=20)
plt.xlabel('Логарифмический вес')
plt.ylabel('Частота')
plt.show()Этот пример сгенерирует следующую ниже гистограмму:
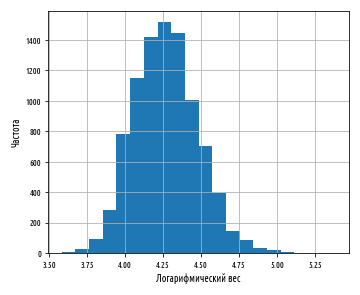
Теперь данные намного ближе к нормальному распределению. Из этого следует, что вес распределяется согласно логнормальному распределению.
Логнормальное распределение
Логнормальное распределение — это распределение набора значений, чей логарифм нормально распределен. Основание логарифма может быть любым положительным числом за исключением единицы. Как и нормальное распределение, логнормальное распределение играет важную роль для описания многих естественных явлений.
Логарифм показывает степень, в которую должно быть возведено фиксированное число (основание) для получения данного числа. Изобразив логарифмы на графике в виде гистограммы, мы показали, что эти степени приближенно нормально распределены. Логарифмы обычно берутся по основанию 10 или основанию e, трансцендентному числу, приближенно равному 2.718. В функции библиотеки numpy np.log и ее инверсии np.exp используется основание e. Выражение loge также называется натуральным логарифмом, или ln, из-за свойств, делающих его особенно удобным в исчислении.
Логнормальное распределение обычно имеет место в процессах роста, где темп роста не зависит от размера. Этот феномен известен как закон Джибрэта, который был cформулирован в 1931 г. Робертом Джибрэтом, заметившим, что он применим к росту фирм. Поскольку темп роста пропорционален размеру, более крупные фирмы демонстрируют тенденцию расти быстрее, чем фирмы меньшего размера.
Нормальное распределение случается в ситуациях, где много мелких колебаний, или вариаций, носит суммирующий эффект, тогда как логнормальное распределение происходит там, где много мелких вариаций имеет мультипликативный эффект.
С тех пор выяснилось, что закон Джибрэта применим к большому числу ситуаций, включая размеры городов и, согласно обширному математическому ресурсу Wolfram MathWorld, к количеству слов в предложениях шотландского писателя Джорджа Бернарда Шоу.
В остальной части этой серии постов мы будем использовать натуральный логарифм веса спортсменов, чтобы наши данные были приближенно нормально распределены. Мы выберем популяцию спортсменов примерно с одинаковыми типами телосложения, к примеру, олимпийских пловцов.
Визуализация корреляции
Один из самых быстрых и самых простых способов определить наличие корреляции между двумя переменными состоит в том, чтобы рассмотреть их на графике рассеяния. Мы отфильтруем данные, выбрав только пловцов, и затем построим график роста относительно веса спортсменов:
def swimmer_data():
'''Загрузка данных роста и веса только олимпийских пловцов'''
df = load_data()
return df[df['Вид спорта'] == 'Swimming'].dropna()
def ex_3_6():
'''Визуализация корреляции между ростом и весом'''
df = swimmer_data()
xs = df['Рост, см']
ys = df['Вес'].apply( np.log )
pd.DataFrame(np.array([xs,ys]).T).plot.scatter(0, 1, s=12, grid=True)
plt.xlabel('Рост, см.')
plt.ylabel('Логарифмический вес')
plt.show()Этот пример сгенерирует следующий ниже график:
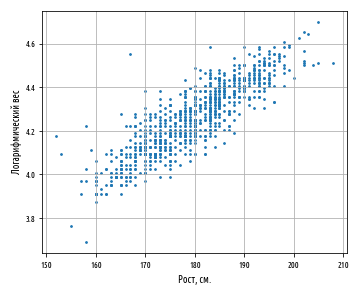
Результат ясно показывает, что между этими двумя переменными имеется связь. График имеет характерно смещенную эллиптическую форму двух коррелируемых, нормально распределенных переменных с центром вокруг среднего значения. Следующая ниже диаграмма сравнивает график рассеяния с распределениями вероятностей роста и логарифма веса:
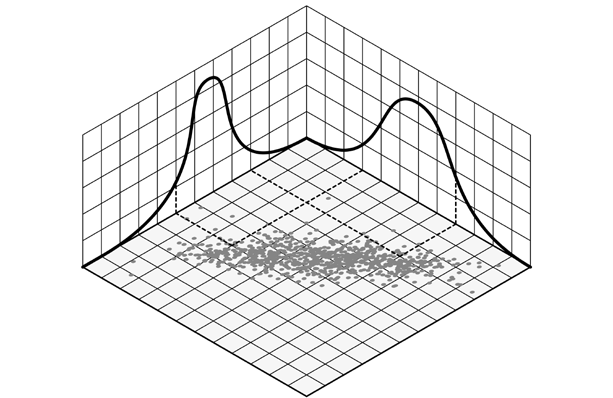
Точки, близко расположенные к хвосту одного распределения, также демонстрируют тенденцию близко располагаться к тому же хвосту другого распределения, и наоборот. Таким образом, между двумя распределениями существует связь, которую в ближайших нескольких разделах мы покажем, как определять количественно. Впрочем, если мы внимательно посмотрим на предыдущий график рассеяния, то увидим, что из-за округления измерений точки уложены в столбцы и строки (в см. и кг. соответственно для роста и веса). Там, где это происходит, иногда желательно внести в данные искажения, которые также называются сдвигом или джиттером с тем, чтобы яснее показать силу связи. Без генерирования джиттера (в виде случайных отклонений) может оказаться, что, то, что по внешнему виду составляет одну точку, фактически представляет много точек, которые обозначены одинаковой парой значений. Внесение нескольких случайных помех делает эту ситуацию вряд ли возможной.
Генерирование джиттера
Поскольку каждое значение округлено до ближайшего сантиметра или килограмма, то значение, записанное как 180 см, на самом деле может быть каким угодно между 179.5 и 180.5 см, тогда как значение 80 кг на самом деле может быть каким угодно между 79.5 и 80.5 кг. Для создания случайных искажений, мы можем добавить случайные помехи в каждую точку данных роста в диапазоне между -0.5 и 0.5 и в том же самом диапазоне проделать с точками данных веса (разумеется, это нужно cделать до того, как мы возьмем логарифм значений веса):
def jitter(limit):
'''Генератор джиттера (произвольного сдвига точек данных)'''
return lambda x: random.uniform(-limit, limit) + x
def ex_3_7():
'''Визуализация корреляции между ростом и весом с джиттером'''
df = swimmer_data()
xs = df['Рост, см'].apply(jitter(0.5))
ys = df['Вес'].apply(jitter(0.5)).apply(np.log)
pd.DataFrame(np.array([xs,ys]).T).plot.scatter(0, 1, s=12, grid=True)
plt.xlabel('Рост, см.')
plt.ylabel('Логарифмический вес')
plt.show()График с джиттером выглядит следующим образом:
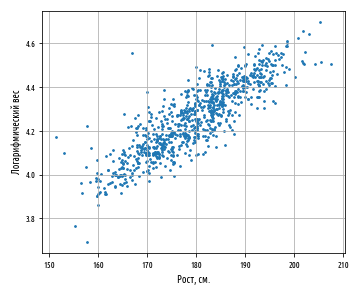
Как и в случае с внесением прозрачности в график рассеяния в первой серии постов об описательной статистике, генерирование джиттера — это механизм, который обеспечивает исключение несущественных факторов, таких как объем данных или артефакты округления, которые могут заслонить от нас возможность увидеть закономерности в данных.
Ковариация
Одним из способов количественного определения силы связи между двумя переменными является их ковариация. Она измеряет тенденцию двух переменных изменяться вместе.
Если у нас имеется два ряда чисел, X и Y, то их отклонения от среднего значения составляют:
Здесь xi — это значение X с индексом i, yi — значение Y с индексом i, x̅ — среднее значение X, и y̅ — среднее значение Y. Если X и Y проявляют тенденцию изменяться вместе, то их отклонения от среднего будет иметь одинаковый знак: отрицательный, если они — меньше среднего, положительный, если они больше среднего. Если мы их перемножим, то произведение будет положительным, когда у них одинаковый знак, и отрицательным, когда у них разные знаки. Сложение произведений дает меру тенденции этих двух переменных отклоняться от среднего значения в одинаковом направлении для каждой заданной выборки.
Ковариация определяется как среднее этих произведений:
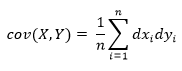
На чистом Python ковариация вычисляется следующим образом:
def covariance(xs, ys):
'''Вычисление ковариации (несмещенная, т.е. n-1)'''
dx = xs - xs.mean()
dy = ys - ys.mean()
return (dx * dy).sum() / (dx.count() - 1)В качестве альтернативы, мы можем воспользоваться функцией pandas cov:
df['Рост, см'].cov(df['Вес'])1.3559273321696459Ковариация роста и логарифма веса для наших олимпийских пловцов равна 1.356, однако это число сложно интерпретировать. Единицы измерения здесь представлены произведением единиц на входе.
По этой причине о ковариации редко сообщают как об отдельной сводной статистике. Сделать число более понятным можно, разделив отклонения на произведение стандартных отклонений. Это позволяет трансформировать единицы измерения в стандартные оценки и ограничить выход числом в диапазоне между -1 и +1. Этот результат называется корреляцией Пирсона.
Стандартная оценка, англ. standard score, также z-оценка — это относительное число стандартных отклонений, на которые значение переменной отстоит от среднего значения. Положительная оценка показывает, что переменная находится выше среднего, отрицательная — ниже среднего. Это безразмерная величина, получаемая при вычитании популяционного среднего из индивидуальных значений и деления разности на популяционное стандартное отклонение.
Корреляция Пирсона
Корреляция Пирсона часто обозначается переменной r и вычисляется следующим образом, где отклонения от среднего dxi и dyi вычисляются как и прежде:
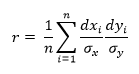
Поскольку для переменных X и Y стандартные отклонения являются константными, уравнение может быть упрощено до следующего, где σx и σy — это стандартные отклонения соответственно X и Y:
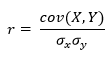
В таком виде формула иногда упоминается как коэффициент корреляции смешанных моментов Пирсона или попросту коэффициент корреляции и, как правило, обозначается буквой r.
Ранее мы уже написали функции для вычисления стандартного отклонения. В сочетании с нашей функцией с вычислением ковариации получится следующая ниже имплементация корреляции Пирсона:
def variance(xs):
'''Вычисление корреляции,
несмещенная дисперсия при n <= 30'''
x_hat = xs.mean()
n = xs.count()
n = n - 1 if n in range( 1, 30 ) else n
return sum((xs - x_hat) ** 2) / n
def standard_deviation(xs):
'''Вычисление стандартного отклонения'''
return np.sqrt(variance(xs))
def correlation(xs, ys):
'''Вычисление корреляции'''
return covariance(xs, ys) / (standard_deviation(xs) *
standard_deviation(ys))В качестве альтернативы мы можем воспользоваться функцией pandas corr:
df['Рост, см'].corr(df['Вес'])Поскольку стандартные оценки безразмерны, то и коэффициент корреляции r тоже безразмерен. Если r равен -1.0 либо 1.0, то переменные идеально антикоррелируют либо идеально коррелируют.
Правда, если r = 0, то с необходимостью вовсе не следует, что переменные не коррелируют. Корреляция Пирсона измеряет лишь линейные связи. Как продемонстрировано на следующих графиках, между переменными может существовать еще некая нелинейная связь, которую r не объясняет:
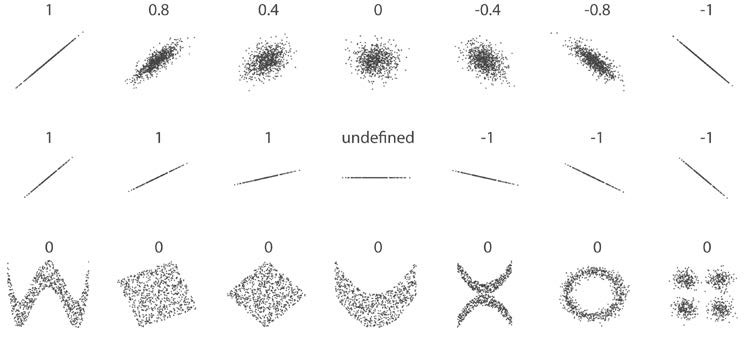
Отметим, что корреляция центрального примера не определена, потому что стандартное отклонение y = 0. Поскольку наше уравнение для r содержало бы деление ковариации на 0, то результат получается бессмысленным. В этом случае между переменными не может быть никакой корреляции; y всегда будет иметь среднее значение. Простое обследование стандартных отклонений это подтвердит.
Мы можем вычислить коэффициент корреляции для данных роста и логарифма веса наших пловцов следующим образом:
def ex_3_8():
'''Вычисление корреляции средствами pandas
на примере данных роста и веса'''
df = swimmer_data()
return df['Рост, см'].corr( df['Вес'].apply(np.log))0.86748249283924894В результате получим ответ 0.867, который количественно выражает сильную, положительную корреляцию, уже наблюдавшуюся нами на точечном графике.
Выборочный r и популяционный ρ
Аналогично среднему значению и стандартному отклонению, коэффициент корреляции является сводной статистикой. Он описывает выборку; в данном случае, выборку спаренных значений: роста и веса. Коэффициент корреляции известной выборки обозначается буквой r, тогда как коэффициент корреляции неизвестной популяции обозначается греческой буквой ρ (рхо).
Как мы убедились в предыдущей серии постов о тестировании гипотез, мы не должны исходить из того, что результаты, полученные в ходе измерения нашей выборки, применимы к популяции в целом. К примеру, наша популяция может состоять из всех пловцов всех недавних Олимпийских игр. И будет совершенно недопустимо обобщать, например, на другие олимпийские виды спорта, такие как тяжелая атлетика или фитнес-плавание.
Даже в допустимой популяции — такой как пловцы, выступавшие на недавних Олимпийских играх, — наша выборка коэффициента корреляции является всего лишь одной из многих потенциально возможных. То, насколько мы можем доверять нашему r, как оценке параметра ρ, зависит от двух факторов:
-
Размера выборки
-
Величины r
Безусловно, чем больше выборка, тем больше мы ей доверяем в том, что она представляет всю совокупность в целом. Возможно, не совсем интуитивно очевидно, но величина тоже оказывает влияние на степень нашей уверенности в том, что выборка представляет параметр . Это вызвано тем, что большие коэффициенты вряд ли возникли случайным образом или вследствие случайной ошибки при отборе.
Проверка статистических гипотез
В предыдущей серии постов мы познакомились с проверкой статистических гипотез, как средством количественной оценки вероятности, что конкретная гипотеза (как, например, что две выборки взяты из одной и той же популяции) истинная. Чтобы количественно оценить вероятность, что корреляция существует в более широкой популяции, мы воспользуемся той же самой процедурой.
В первую очередь, мы должны сформулировать две гипотезы, нулевую гипотезу и альтернативную:
H0 – это гипотеза, что корреляция в популяции нулевая. Другими словами, наше консервативное представление состоит в том, что измеренная корреляция целиком вызвана случайной ошибкой при отборе.
H1 – это альтернативная возможность, что корреляция в популяции не нулевая. Отметим, что мы не определяем направление корреляции, а только что она существует. Это означает, что мы выполняем двустороннюю проверку.
Стандартная ошибка коэффициента корреляции r по выборке задается следующей формулой:
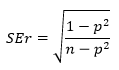
Эта формула точна, только когда r находится близко к нулю (напомним, что величина ρ влияет на нашу уверенность), но к счастью, это именно то, что мы допускаем согласно нашей нулевой гипотезы.
Мы можем снова воспользоваться t-распределением и вычислить t-статистику:
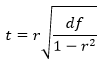
В приведенной формуле df — это степень свободы наших данных. Для проверки корреляции степень свободы равна n – 2, где n — это размер выборки. Подставив это значение в формулу, получим:
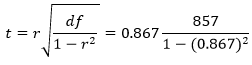
В итоге получим t-значение 102.21. В целях его преобразования в p-значение мы должны обратиться к t-распределению. Библиотека scipy предоставляет интегральную функцию распределения (ИФР) для t-распределения в виде функции stats.t.cdf, и комплементарной ей (1-cdf) функции выживания stats.t.sf. Значение функции выживания соответствует p-значению для односторонней проверки. Мы умножаем его на 2, потому что выполняем двустороннюю проверку:
def t_statistic(xs, ys):
'''Вычисление t-статистики'''
r = xs.corr(ys) # как вариант, correlation(xs, ys)
df = xs.count() - 2
return r * np.sqrt(df / 1 - r ** 2)
def ex_3_9():
'''Выполнение двухстороннего t-теста'''
df = swimmer_data()
xs = df['Рост, см']
ys = df['Вес'].apply(np.log)
t_value = t_statistic(xs, ys)
df = xs.count() - 2
p = 2 * stats.t.sf(t_value, df) # функция выживания
return {'t-значение':t_value, 'p-значение':p}{'p-значение': 1.8980236317815443e-106, 't-значение': 25.384018200627057}P-значение настолько мало, что в сущности равно 0, означая, что шанс, что нулевая гипотеза является истинной, фактически не существует. Мы вынуждены принять альтернативную гипотезу о существовании корреляции.
Интервалы уверенности
Установив, что в более широкой популяции, безусловно, существует корреляция, мы, возможно, захотим количественно выразить диапазон значений, внутри которого, как мы ожидаем, будет лежать параметр ρ, вычислив для этого интервал уверенности. Как и в случае со средним значением в предыдущей серии постов, интервал уверенности для r выражает вероятность (выраженную в %), что параметр ρ популяции находится между двумя конкретными значениями.
Однако при попытке вычислить стандартную ошибку коэффициента корреляции возникает сложность, которой не было в случае со средним значением. Поскольку абсолютное значение коэффициента корреляции r не может превышать 1, распределение возможных выборок коэффициентов корреляции r смещается по мере приближения r к пределу своего диапазона.
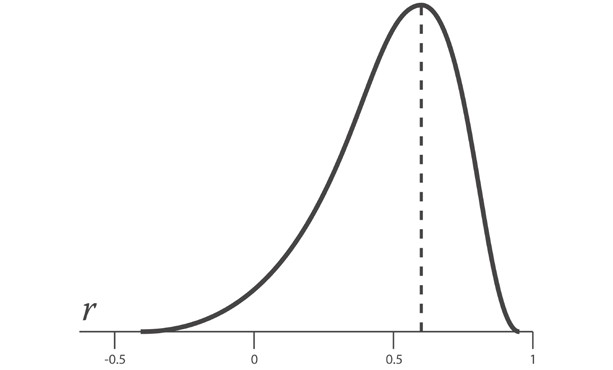
Приведенный выше график показывает отрицательно скошенное распределение r-выборок для параметра ρ, равного 0.6.
К счастью, трансформация под названием z-преобразование Фишера стабилизирует дисперсию r по своему диапазону. Она аналогична тому, как наши данные о весе спортсменов стали нормально распределенными, когда мы взяли их логарифм.
Уравнение для z-преобразования следующее:
![]()
Стандартная ошибка z равна:

Таким образом, процедура вычисления интервалов уверенности состоит в преобразовании r в z с использованием z-преобразования, вычислении интервала уверенности в терминах стандартной ошибки SEz и затем преобразовании интервала уверенности в r.
В целях вычисления интервала уверенности в терминах SEz, мы можем взять число стандартных отклонений от среднего, которое дает нам требуемый уровень доверия. Обычно используют число 1.96, так как оно является числом стандартных отклонений от среднего, которое содержит 95% площади под кривой. Другими словами, 1.96 стандартных ошибок от среднего значения выборочного r содержит истинную популяционную корреляцию ρ с 95%-ой определенностью.
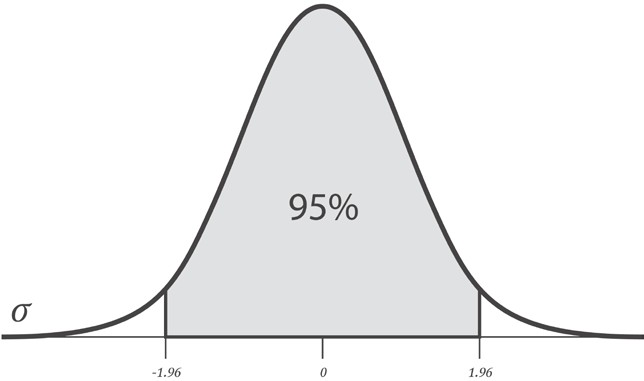
Мы можем убедиться в этом, воспользовавшись функцией scipy stats.norm.ppf. Она вернет стандартную оценку, связанную с заданной интегральной вероятностью в условиях односторонней проверки.
Однако, как показано на приведенном выше графике, мы хотели бы вычесть ту же самую величину, т.е. 2.5%, из каждого хвоста с тем, чтобы 95%-й интервал уверенности был центрирован на нуле. Для этого при выполнении двусторонней проверки нужно просто уменьшить разность наполовину и вычесть результат из 100%. Так что, требуемый уровень доверия в 95% означает, что мы обращаемся к критическому значению 97.5%:
def critical_value(confidence, ntails): # ДИ и число хвостов
'''Расчет критического значения путем
вычисления квантиля и получения
для него нормального значения'''
lookup = 1 - ((1 - confidence) / ntails)
return stats.norm.ppf(lookup, 0, 1) # mu=0, sigma=1
critical_value(0.95, 2)1.959963984540054Поэтому наш 95%-й интервал уверенности в z-пространстве для ρ задается следующей формулой:
![]()
Подставив в нашу формулу zr и SEz, получим:
![]()
Для r=0.867 и n=859 она даст нижнюю и верхнюю границу соответственно 1.137 и 1.722. В целях их преобразования из z-оценок в r-значения, мы используем следующее обратное уравнение z-преобразования:
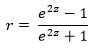
Преобразования и интервал уверенности можно вычислить при помощи следующего исходного кода:
def z_to_r(z):
'''Преобразование z-оценки обратно в r-значение'''
return (np.exp(z*2) - 1) / (np.exp(z*2) + 1)
def r_confidence_interval(crit, xs, ys):
'''Расчет интервала уверенности
для критического значения и данных'''
r = xs.corr(ys)
n = xs.count()
zr = 0.5 * np.log((1 + r) / (1 - r))
sez = 1 / np.sqrt(n - 3)
return (z_to_r(zr - (crit * sez))), (z_to_r(zr + (crit * sez)))
def ex_3_10():
'''Расчет интервала уверенности
на примере данных роста и веса'''
df = swimmer_data()
X = df['Рост, см']
y = df['Вес'].apply(np.log)
interval = r_confidence_interval(1.96, X, y)
print('Интервал уверенности (95%):', interval)Интервал уверенности (95%): (0.8499088588880347, 0.8831284878884087)В результате получаем 95%-й интервал уверенности для ρ, расположенный между 0.850 и 0.883. Мы можем быть абсолютно уверены в том, что в более широкой популяции олимпийских пловцов существует сильная положительная корреляция между ростом и весом.
Примеры исходного кода для этого поста находятся в моем репо на Github. Все исходные данные взяты в репозитории автора книги.
В следующем посте, посте №2, будет рассмотрена сама тема серии – регрессия и приемы оценивания ее качества.
Статистика
18 июля 2022 г.
читать 2 мин
Один из способов количественной оценки взаимосвязи между двумя переменными – использовать Коэффициент корреляции Пирсона, который является мерой линейной связи между двумя переменными.u00a0Он всегда принимает значение от -1 до 1, где:n
-1 указывает на совершенно отрицательную линейную корреляцию между двумя переменные
- 0 указывает на отсутствие линейной корреляции между двумя переменными
- 1 указывает на совершенно положительную линейную корреляцию между двумя переменными
Чем дальше коэффициент корреляции от нуля, тем сильнее Связь между двумя переменными.
В этом руководстве объясняется, как вычислить корреляцию между переменными в Python.
Как рассчитать корреляцию в Python
Чтобы вычислить корреляцию между двумя переменными в Python, мы можем использовать функцию Numpy corrcoef()
import numpy as np
np.random.seed(100)
#создать массив из 50 случайных целых чисел от 0 до 10
var1 = np.random.randint(0, 10, 50)
#создать положительно коррелированный массив с некоторым случайным шумом
var2 = var1 + np.random.normal(0, 10, 50)
#рассчитать корреляцию между двумя массивами
np.corrcoef(var1, var2)
# [[ 1. 0.335]
# [ 0.335 1. ]]Мы видим, что коэффициент корреляции между этими двумя переменными составляет 0,335, что является положительной корреляцией.
По умолчанию эта функция создает матрицу коэффициентов корреляции. Если бы мы только хотели вернуть коэффициент корреляции между двумя переменными, мы могли бы используйте следующий синтаксис:
np.corrcoef(var1, var2)[0,1]
#0.335Чтобы проверить, является ли эта корреляция статистически значимой, мы можем рассчитать p-значение, связанное с коэффициентом корреляции Пирсона, с помощью Scipy pearsonr(), которая возвращает коэффициент корреляции Пирсона вместе с двусторонним p-значением.
from scipy.stats.stats import pearsonr
pearsonr(var1, var2)
#(0.335, 0.017398)Коэффициент корреляции – 0,335, а двустороннее значение p – 0,017. Поскольку это значение p меньше 0,05, мы можем заключить, что существует статистически значимая корреляция между двумя переменными.
Если вас интересует вычисление корреляции между несколькими переменными в Pandas DataFrame, вы можете просто использовать функцию .corr()
import pandas as pd
data = pd.DataFrame(np.random.randint(0, 10, size=(5, 3)), columns=['A', 'B', 'C'])
data
# A B C
#0 8 0 9
#1 4 0 7
#2 9 6 8
#3 1 8 1
#4 8 0 8
#рассчитать коэффициенты корреляции для всех попарных комбинаций
data.corr()
# A B C
# A 1.000000 -0.775567 -0.493769
# B -0.775567 1.000000 0.000000
# C -0.493769 0.000000 1.000000И если вас интересует только расчет корреляции между двумя конкретными переменными в DataFrame, вы можете указать переменные:
data['A'].corr(data['B'])
#-0.775567Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в Python:
- Как создать корреляционную матрицу в Python
- Как рассчитать ранговую корреляцию Спирмена в Python
- Как рассчитать автокорреляцию в Python
Correlation coefficients quantify the association between variables or features of a dataset. These statistics are of high importance for science and technology, and Python has great tools that you can use to calculate them. SciPy, NumPy, and pandas correlation methods are fast, comprehensive, and well-documented.
In this tutorial, you’ll learn:
- What Pearson, Spearman, and Kendall correlation coefficients are
- How to use SciPy, NumPy, and pandas correlation functions
- How to visualize data, regression lines, and correlation matrices with Matplotlib
You’ll start with an explanation of correlation, then see three quick introductory examples, and finally dive into details of NumPy, SciPy and pandas correlation.
Correlation
Statistics and data science are often concerned about the relationships between two or more variables (or features) of a dataset. Each data point in the dataset is an observation, and the features are the properties or attributes of those observations.
Every dataset you work with uses variables and observations. For example, you might be interested in understanding the following:
- How the height of basketball players is correlated to their shooting accuracy
- Whether there’s a relationship between employee work experience and salary
- What mathematical dependence exists between the population density and the gross domestic product of different countries
In the examples above, the height, shooting accuracy, years of experience, salary, population density, and gross domestic product are the features or variables. The data related to each player, employee, and each country are the observations.
When data is represented in the form of a table, the rows of that table are usually the observations, while the columns are the features. Take a look at this employee table:
| Name | Years of Experience | Annual Salary |
|---|---|---|
| Ann | 30 | 120,000 |
| Rob | 21 | 105,000 |
| Tom | 19 | 90,000 |
| Ivy | 10 | 82,000 |
In this table, each row represents one observation, or the data about one employee (either Ann, Rob, Tom, or Ivy). Each column shows one property or feature (name, experience, or salary) for all the employees.
If you analyze any two features of a dataset, then you’ll find some type of correlation between those two features. Consider the following figures:
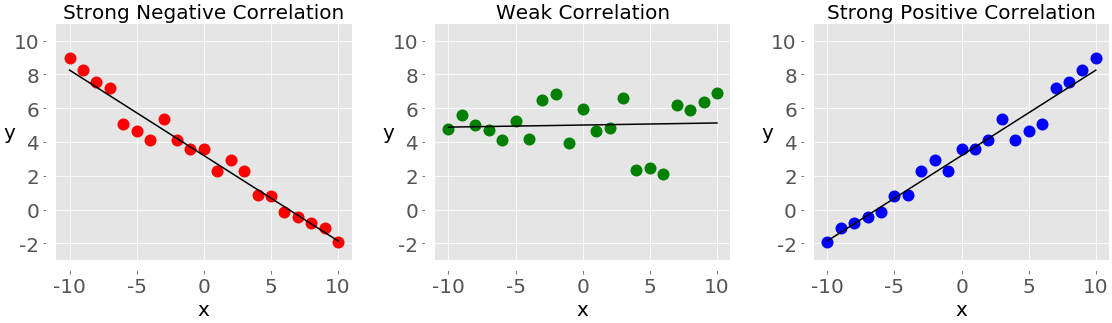
Each of these plots shows one of three different forms of correlation:
-
Negative correlation (red dots): In the plot on the left, the y values tend to decrease as the x values increase. This shows strong negative correlation, which occurs when large values of one feature correspond to small values of the other, and vice versa.
-
Weak or no correlation (green dots): The plot in the middle shows no obvious trend. This is a form of weak correlation, which occurs when an association between two features is not obvious or is hardly observable.
-
Positive correlation (blue dots): In the plot on the right, the y values tend to increase as the x values increase. This illustrates strong positive correlation, which occurs when large values of one feature correspond to large values of the other, and vice versa.
The next figure represents the data from the employee table above:

The correlation between experience and salary is positive because higher experience corresponds to a larger salary and vice versa.
Correlation is tightly connected to other statistical quantities like the mean, standard deviation, variance, and covariance. If you want to learn more about these quantities and how to calculate them with Python, then check out Descriptive Statistics with Python.
There are several statistics that you can use to quantify correlation. In this tutorial, you’ll learn about three correlation coefficients:
- Pearson’s r
- Spearman’s rho
- Kendall’s tau
Pearson’s coefficient measures linear correlation, while the Spearman and Kendall coefficients compare the ranks of data. There are several NumPy, SciPy, and pandas correlation functions and methods that you can use to calculate these coefficients. You can also use Matplotlib to conveniently illustrate the results.
Example: NumPy Correlation Calculation
NumPy has many statistics routines, including np.corrcoef(), that return a matrix of Pearson correlation coefficients. You can start by importing NumPy and defining two NumPy arrays. These are instances of the class ndarray. Call them x and y:
>>>
>>> import numpy as np
>>> x = np.arange(10, 20)
>>> x
array([10, 11, 12, 13, 14, 15, 16, 17, 18, 19])
>>> y = np.array([2, 1, 4, 5, 8, 12, 18, 25, 96, 48])
>>> y
array([ 2, 1, 4, 5, 8, 12, 18, 25, 96, 48])
Here, you use np.arange() to create an array x of integers between 10 (inclusive) and 20 (exclusive). Then you use np.array() to create a second array y containing arbitrary integers.
Once you have two arrays of the same length, you can call np.corrcoef() with both arrays as arguments:
>>>
>>> r = np.corrcoef(x, y)
>>> r
array([[1. , 0.75864029],
[0.75864029, 1. ]])
>>> r[0, 1]
0.7586402890911867
>>> r[1, 0]
0.7586402890911869
corrcoef() returns the correlation matrix, which is a two-dimensional array with the correlation coefficients. Here’s a simplified version of the correlation matrix you just created:
x y
x 1.00 0.76
y 0.76 1.00
The values on the main diagonal of the correlation matrix (upper left and lower right) are equal to 1. The upper left value corresponds to the correlation coefficient for x and x, while the lower right value is the correlation coefficient for y and y. They are always equal to 1.
However, what you usually need are the lower left and upper right values of the correlation matrix. These values are equal and both represent the Pearson correlation coefficient for x and y. In this case, it’s approximately 0.76.
This figure shows the data points and the correlation coefficients for the above example:

The red squares are the data points. As you can see, the figure also shows the values of the three correlation coefficients.
Example: SciPy Correlation Calculation
SciPy also has many statistics routines contained in scipy.stats. You can use the following methods to calculate the three correlation coefficients you saw earlier:
pearsonr()spearmanr()kendalltau()
Here’s how you would use these functions in Python:
>>>
>>> import numpy as np
>>> import scipy.stats
>>> x = np.arange(10, 20)
>>> y = np.array([2, 1, 4, 5, 8, 12, 18, 25, 96, 48])
>>> scipy.stats.pearsonr(x, y) # Pearson's r
(0.7586402890911869, 0.010964341301680832)
>>> scipy.stats.spearmanr(x, y) # Spearman's rho
SpearmanrResult(correlation=0.9757575757575757, pvalue=1.4675461874042197e-06)
>>> scipy.stats.kendalltau(x, y) # Kendall's tau
KendalltauResult(correlation=0.911111111111111, pvalue=2.9761904761904762e-05)
Note that these functions return objects that contain two values:
- The correlation coefficient
- The p-value
You use the p-value in statistical methods when you’re testing a hypothesis. The p-value is an important measure that requires in-depth knowledge of probability and statistics to interpret. To learn more about them, you can read about the basics or check out a data scientist’s explanation of p-values.
You can extract the p-values and the correlation coefficients with their indices, as the items of tuples:
>>>
>>> scipy.stats.pearsonr(x, y)[0] # Pearson's r
0.7586402890911869
>>> scipy.stats.spearmanr(x, y)[0] # Spearman's rho
0.9757575757575757
>>> scipy.stats.kendalltau(x, y)[0] # Kendall's tau
0.911111111111111
You could also use dot notation for the Spearman and Kendall coefficients:
>>>
>>> scipy.stats.spearmanr(x, y).correlation # Spearman's rho
0.9757575757575757
>>> scipy.stats.kendalltau(x, y).correlation # Kendall's tau
0.911111111111111
The dot notation is longer, but it’s also more readable and more self-explanatory.
If you want to get the Pearson correlation coefficient and p-value at the same time, then you can unpack the return value:
>>>
>>> r, p = scipy.stats.pearsonr(x, y)
>>> r
0.7586402890911869
>>> p
0.010964341301680829
This approach exploits Python unpacking and the fact that pearsonr() returns a tuple with these two statistics. You can also use this technique with spearmanr() and kendalltau(), as you’ll see later on.
Example: pandas Correlation Calculation
pandas is, in some cases, more convenient than NumPy and SciPy for calculating statistics. It offers statistical methods for Series and DataFrame instances. For example, given two Series objects with the same number of items, you can call .corr() on one of them with the other as the first argument:
>>>
>>> import pandas as pd
>>> x = pd.Series(range(10, 20))
>>> x
0 10
1 11
2 12
3 13
4 14
5 15
6 16
7 17
8 18
9 19
dtype: int64
>>> y = pd.Series([2, 1, 4, 5, 8, 12, 18, 25, 96, 48])
>>> y
0 2
1 1
2 4
3 5
4 8
5 12
6 18
7 25
8 96
9 48
dtype: int64
>>> x.corr(y) # Pearson's r
0.7586402890911867
>>> y.corr(x)
0.7586402890911869
>>> x.corr(y, method='spearman') # Spearman's rho
0.9757575757575757
>>> x.corr(y, method='kendall') # Kendall's tau
0.911111111111111
Here, you use .corr() to calculate all three correlation coefficients. You define the desired statistic with the parameter method, which can take on one of several values:
'pearson''spearman''kendall'- a callable
The callable can be any function, method, or object with .__call__() that accepts two one-dimensional arrays and returns a floating-point number.
Linear Correlation
Linear correlation measures the proximity of the mathematical relationship between variables or dataset features to a linear function. If the relationship between the two features is closer to some linear function, then their linear correlation is stronger and the absolute value of the correlation coefficient is higher.
Pearson Correlation Coefficient
Consider a dataset with two features: x and y. Each feature has n values, so x and y are n-tuples. Say that the first value x₁ from x corresponds to the first value y₁ from y, the second value x₂ from x to the second value y₂ from y, and so on. Then, there are n pairs of corresponding values: (x₁, y₁), (x₂, y₂), and so on. Each of these x-y pairs represents a single observation.
The Pearson (product-moment) correlation coefficient is a measure of the linear relationship between two features. It’s the ratio of the covariance of x and y to the product of their standard deviations. It’s often denoted with the letter r and called Pearson’s r. You can express this value mathematically with this equation:
r = Σᵢ((xᵢ − mean(x))(yᵢ − mean(y))) (√Σᵢ(xᵢ − mean(x))² √Σᵢ(yᵢ − mean(y))²)⁻¹
Here, i takes on the values 1, 2, …, n. The mean values of x and y are denoted with mean(x) and mean(y). This formula shows that if larger x values tend to correspond to larger y values and vice versa, then r is positive. On the other hand, if larger x values are mostly associated with smaller y values and vice versa, then r is negative.
Here are some important facts about the Pearson correlation coefficient:
-
The Pearson correlation coefficient can take on any real value in the range −1 ≤ r ≤ 1.
-
The maximum value r = 1 corresponds to the case in which there’s a perfect positive linear relationship between x and y. In other words, larger x values correspond to larger y values and vice versa.
-
The value r > 0 indicates positive correlation between x and y.
-
The value r = 0 corresponds to the case in which there’s no linear relationship between x and y.
-
The value r < 0 indicates negative correlation between x and y.
-
The minimal value r = −1 corresponds to the case when there’s a perfect negative linear relationship between x and y. In other words, larger x values correspond to smaller y values and vice versa.
The above facts can be summed up in the following table:
| Pearson’s r Value | Correlation Between x and y |
|---|---|
| equal to 1 | perfect positive linear relationship |
| greater than 0 | positive correlation |
| equal to 0 | no linear relationship |
| less than 0 | negative correlation |
| equal to -1 | perfect negative linear relationship |
In short, a larger absolute value of r indicates stronger correlation, closer to a linear function. A smaller absolute value of r indicates weaker correlation.
Linear Regression: SciPy Implementation
Linear regression is the process of finding the linear function that is as close as possible to the actual relationship between features. In other words, you determine the linear function that best describes the association between the features. This linear function is also called the regression line.
You can implement linear regression with SciPy. You’ll get the linear function that best approximates the relationship between two arrays, as well as the Pearson correlation coefficient. To get started, you first need to import the libraries and prepare some data to work with:
>>>
>>> import numpy as np
>>> import scipy.stats
>>> x = np.arange(10, 20)
>>> y = np.array([2, 1, 4, 5, 8, 12, 18, 25, 96, 48])
Here, you import numpy and scipy.stats and define the variables x and y.
You can use scipy.stats.linregress() to perform linear regression for two arrays of the same length. You should provide the arrays as the arguments and get the outputs by using dot notation:
>>>
>>> result = scipy.stats.linregress(x, y)
>>> result.slope
7.4363636363636365
>>> result.intercept
-85.92727272727274
>>> result.rvalue
0.7586402890911869
>>> result.pvalue
0.010964341301680825
>>> result.stderr
2.257878767543913
That’s it! You’ve completed the linear regression and gotten the following results:
.slope: the slope of the regression line.intercept: the intercept of the regression line.pvalue: the p-value.stderr: the standard error of the estimated gradient
You’ll learn how to visualize these results in a later section.
You can also provide a single argument to linregress(), but it must be a two-dimensional array with one dimension of length two:
>>>
>>> xy = np.array([[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
... [2, 1, 4, 5, 8, 12, 18, 25, 96, 48]])
>>> scipy.stats.linregress(xy)
LinregressResult(slope=7.4363636363636365, intercept=-85.92727272727274, rvalue=0.7586402890911869, pvalue=0.010964341301680825, stderr=2.257878767543913)
The result is exactly the same as the previous example because xy contains the same data as x and y together. linregress() took the first row of xy as one feature and the second row as the other feature.
linregress() will return the same result if you provide the transpose of xy, or a NumPy array with 10 rows and two columns. In NumPy, you can transpose a matrix in many ways:
transpose().transpose().T
Here’s how you might transpose xy:
>>>
>>> xy.T
array([[10, 2],
[11, 1],
[12, 4],
[13, 5],
[14, 8],
[15, 12],
[16, 18],
[17, 25],
[18, 96],
[19, 48]])
Now that you know how to get the transpose, you can pass one to linregress(). The first column will be one feature and the second column the other feature:
>>>
>>> scipy.stats.linregress(xy.T)
LinregressResult(slope=7.4363636363636365, intercept=-85.92727272727274, rvalue=0.7586402890911869, pvalue=0.010964341301680825, stderr=2.257878767543913)
Here, you use .T to get the transpose of xy. linregress() works the same way with xy and its transpose. It extracts the features by splitting the array along the dimension with length two.
You should also be careful to note whether or not your dataset contains missing values. In data science and machine learning, you’ll often find some missing or corrupted data. The usual way to represent it in Python, NumPy, SciPy, and pandas is by using NaN or Not a Number values. But if your data contains nan values, then you won’t get a useful result with linregress():
>>>
>>> scipy.stats.linregress(np.arange(3), np.array([2, np.nan, 5]))
LinregressResult(slope=nan, intercept=nan, rvalue=nan, pvalue=nan, stderr=nan)
In this case, your resulting object returns all nan values. In Python, nan is a special floating-point value that you can get by using any of the following:
float('nan')math.nannumpy.nan
You can also check whether a variable corresponds to nan with math.isnan() or numpy.isnan().
Pearson Correlation: NumPy and SciPy Implementation
You’ve already seen how to get the Pearson correlation coefficient with corrcoef() and pearsonr():
>>>
>>> r, p = scipy.stats.pearsonr(x, y)
>>> r
0.7586402890911869
>>> p
0.010964341301680829
>>> np.corrcoef(x, y)
array([[1. , 0.75864029],
[0.75864029, 1. ]])
Note that if you provide an array with a nan value to pearsonr(), you’ll get a ValueError.
There are few additional details worth considering. First, recall that np.corrcoef() can take two NumPy arrays as arguments. Instead, you can pass a single two-dimensional array with the same values as the argument:
>>>
>>> np.corrcoef(xy)
array([[1. , 0.75864029],
[0.75864029, 1. ]])
The results are the same in this and previous examples. Again, the first row of xy represents one feature, while the second row represents the other.
If you want to get the correlation coefficients for three features, then you just provide a numeric two-dimensional array with three rows as the argument:
>>>
>>> xyz = np.array([[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
... [2, 1, 4, 5, 8, 12, 18, 25, 96, 48],
... [5, 3, 2, 1, 0, -2, -8, -11, -15, -16]])
>>> np.corrcoef(xyz)
array([[ 1. , 0.75864029, -0.96807242],
[ 0.75864029, 1. , -0.83407922],
[-0.96807242, -0.83407922, 1. ]])
You’ll obtain the correlation matrix again, but this one will be larger than previous ones:
x y z
x 1.00 0.76 -0.97
y 0.76 1.00 -0.83
z -0.97 -0.83 1.00
This is because corrcoef() considers each row of xyz as one feature. The value 0.76 is the correlation coefficient for the first two features of xyz. This is the same as the coefficient for x and y in previous examples. -0.97 represents Pearson’s r for the first and third features, while -0.83 is Pearson’s r for the last two features.
Here’s an interesting example of what happens when you pass nan data to corrcoef():
>>>
>>> arr_with_nan = np.array([[0, 1, 2, 3],
... [2, 4, 1, 8],
... [2, 5, np.nan, 2]])
>>> np.corrcoef(arr_with_nan)
array([[1. , 0.62554324, nan],
[0.62554324, 1. , nan],
[ nan, nan, nan]])
In this example, the first two rows (or features) of arr_with_nan are okay, but the third row [2, 5, np.nan, 2] contains a nan value. Everything that doesn’t include the feature with nan is calculated well. The results that depend on the last row, however, are nan.
By default, numpy.corrcoef() considers the rows as features and the columns as observations. If you want the opposite behavior, which is widely used in machine learning, then use the argument rowvar=False:
>>>
>>> xyz.T
array([[ 10, 2, 5],
[ 11, 1, 3],
[ 12, 4, 2],
[ 13, 5, 1],
[ 14, 8, 0],
[ 15, 12, -2],
[ 16, 18, -8],
[ 17, 25, -11],
[ 18, 96, -15],
[ 19, 48, -16]])
>>> np.corrcoef(xyz.T, rowvar=False)
array([[ 1. , 0.75864029, -0.96807242],
[ 0.75864029, 1. , -0.83407922],
[-0.96807242, -0.83407922, 1. ]])
This array is identical to the one you saw earlier. Here, you apply a different convention, but the result is the same.
Pearson Correlation: pandas Implementation
So far, you’ve used Series and DataFrame object methods to calculate correlation coefficients. Let’s explore these methods in more detail. First, you need to import pandas and create some instances of Series and DataFrame:
>>>
>>> import pandas as pd
>>> x = pd.Series(range(10, 20))
>>> x
0 10
1 11
2 12
3 13
4 14
5 15
6 16
7 17
8 18
9 19
dtype: int64
>>> y = pd.Series([2, 1, 4, 5, 8, 12, 18, 25, 96, 48])
>>> y
0 2
1 1
2 4
3 5
4 8
5 12
6 18
7 25
8 96
9 48
dtype: int64
>>> z = pd.Series([5, 3, 2, 1, 0, -2, -8, -11, -15, -16])
>>> z
0 5
1 3
2 2
3 1
4 0
5 -2
6 -8
7 -11
8 -15
9 -16
dtype: int64
>>> xy = pd.DataFrame({'x-values': x, 'y-values': y})
>>> xy
x-values y-values
0 10 2
1 11 1
2 12 4
3 13 5
4 14 8
5 15 12
6 16 18
7 17 25
8 18 96
9 19 48
>>> xyz = pd.DataFrame({'x-values': x, 'y-values': y, 'z-values': z})
>>> xyz
x-values y-values z-values
0 10 2 5
1 11 1 3
2 12 4 2
3 13 5 1
4 14 8 0
5 15 12 -2
6 16 18 -8
7 17 25 -11
8 18 96 -15
9 19 48 -16
You now have three Series objects called x, y, and z. You also have two DataFrame objects, xy and xyz.
You’ve already learned how to use .corr() with Series objects to get the Pearson correlation coefficient:
>>>
>>> x.corr(y)
0.7586402890911867
Here, you call .corr() on one object and pass the other as the first argument.
If you provide a nan value, then .corr() will still work, but it will exclude observations that contain nan values:
>>>
>>> u, u_with_nan = pd.Series([1, 2, 3]), pd.Series([1, 2, np.nan, 3])
>>> v, w = pd.Series([1, 4, 8]), pd.Series([1, 4, 154, 8])
>>> u.corr(v)
0.9966158955401239
>>> u_with_nan.corr(w)
0.9966158955401239
You get the same value of the correlation coefficient in these two examples. That’s because .corr() ignores the pair of values (np.nan, 154) that has a missing value.
You can also use .corr() with DataFrame objects. You can use it to get the correlation matrix for their columns:
>>>
>>> corr_matrix = xy.corr()
>>> corr_matrix
x-values y-values
x-values 1.00000 0.75864
y-values 0.75864 1.00000
The resulting correlation matrix is a new instance of DataFrame and holds the correlation coefficients for the columns xy['x-values'] and xy['y-values']. Such labeled results are usually very convenient to work with because you can access them with either their labels or their integer position indices:
>>>
>>> corr_matrix.at['x-values', 'y-values']
0.7586402890911869
>>> corr_matrix.iat[0, 1]
0.7586402890911869
This example shows two ways of accessing values:
- Use
.at[]to access a single value by row and column labels. - Use
.iat[]to access a value by the positions of its row and column.
You can apply .corr() the same way with DataFrame objects that contain three or more columns:
>>>
>>> xyz.corr()
x-values y-values z-values
x-values 1.000000 0.758640 -0.968072
y-values 0.758640 1.000000 -0.834079
z-values -0.968072 -0.834079 1.000000
You’ll get a correlation matrix with the following correlation coefficients:
0.758640forx-valuesandy-values-0.968072forx-valuesandz-values-0.834079fory-valuesandz-values
Another useful method is .corrwith(), which allows you to calculate the correlation coefficients between the rows or columns of one DataFrame object and another Series or DataFrame object passed as the first argument:
>>>
>>> xy.corrwith(z)
x-values -0.968072
y-values -0.834079
dtype: float64
In this case, the result is a new Series object with the correlation coefficient for the column xy['x-values'] and the values of z, as well as the coefficient for xy['y-values'] and z.
.corrwith() has the optional parameter axis that specifies whether columns or rows represent the features. The default value of axis is 0, and it also defaults to columns representing features. There’s also a drop parameter, which indicates what to do with missing values.
Both .corr() and .corrwith() have the optional parameter method to specify the correlation coefficient that you want to calculate. The Pearson correlation coefficient is returned by default, so you don’t need to provide it in this case.
Rank Correlation
Rank correlation compares the ranks or the orderings of the data related to two variables or dataset features. If the orderings are similar, then the correlation is strong, positive, and high. However, if the orderings are close to reversed, then the correlation is strong, negative, and low. In other words, rank correlation is concerned only with the order of values, not with the particular values from the dataset.
To illustrate the difference between linear and rank correlation, consider the following figure:

The left plot has a perfect positive linear relationship between x and y, so r = 1. The central plot shows positive correlation and the right one shows negative correlation. However, neither of them is a linear function, so r is different than −1 or 1.
When you look only at the orderings or ranks, all three relationships are perfect! The left and central plots show the observations where larger x values always correspond to larger y values. This is perfect positive rank correlation. The right plot illustrates the opposite case, which is perfect negative rank correlation.
Spearman Correlation Coefficient
The Spearman correlation coefficient between two features is the Pearson correlation coefficient between their rank values. It’s calculated the same way as the Pearson correlation coefficient but takes into account their ranks instead of their values. It’s often denoted with the Greek letter rho (ρ) and called Spearman’s rho.
Say you have two n-tuples, x and y, where (x₁, y₁), (x₂, y₂), … are the observations as pairs of corresponding values. You can calculate the Spearman correlation coefficient ρ the same way as the Pearson coefficient. You’ll use the ranks instead of the actual values from x and y.
Here are some important facts about the Spearman correlation coefficient:
-
It can take a real value in the range −1 ≤ ρ ≤ 1.
-
Its maximum value ρ = 1 corresponds to the case when there’s a monotonically increasing function between x and y. In other words, larger x values correspond to larger y values and vice versa.
-
Its minimum value ρ = −1 corresponds to the case when there’s a monotonically decreasing function between x and y. In other words, larger x values correspond to smaller y values and vice versa.
You can calculate Spearman’s rho in Python in a very similar way as you would Pearson’s r.
Kendall Correlation Coefficient
Let’s start again by considering two n-tuples, x and y. Each of the x-y pairs (x₁, y₁), (x₂, y₂), … is a single observation. A pair of observations (xᵢ, yᵢ) and (xⱼ, yⱼ), where i < j, will be one of three things:
- concordant if either (xᵢ > xⱼ and yᵢ > yⱼ) or (xᵢ < xⱼ and yᵢ < yⱼ)
- discordant if either (xᵢ < xⱼ and yᵢ > yⱼ) or (xᵢ > xⱼ and yᵢ < yⱼ)
- neither if there’s a tie in x (xᵢ = xⱼ) or a tie in y (yᵢ = yⱼ)
The Kendall correlation coefficient compares the number of concordant and discordant pairs of data. This coefficient is based on the difference in the counts of concordant and discordant pairs relative to the number of x-y pairs. It’s often denoted with the Greek letter tau (τ) and called Kendall’s tau.
According to the scipy.stats official docs, the Kendall correlation coefficient is calculated as
τ = (n⁺ − n⁻) / √((n⁺ + n⁻ + nˣ)(n⁺ + n⁻ + nʸ)),
where:
- n⁺ is the number of concordant pairs
- n⁻ is the number of discordant pairs
- nˣ is the number of ties only in x
- nʸ is the number of ties only in y
If a tie occurs in both x and y, then it’s not included in either nˣ or nʸ.
The Wikipedia page on Kendall rank correlation coefficient gives the following expression:
τ = (2 / (n(n − 1))) Σᵢⱼ(sign(xᵢ − xⱼ) sign(yᵢ − yⱼ))
for i < j, where i = 1, 2, …, n − 1 and j = 2, 3, …, n.
The sign function sign(z) is −1 if z < 0, 0 if z = 0, and 1 if z > 0. n(n − 1) / 2 is the total number of x-y pairs.
Some important facts about the Kendall correlation coefficient are as follows:
-
It can take a real value in the range −1 ≤ τ ≤ 1.
-
Its maximum value τ = 1 corresponds to the case when the ranks of the corresponding values in x and y are the same. In other words, all pairs are concordant.
-
Its minimum value τ = −1 corresponds to the case when the rankings in x are the reverse of the rankings in y. In other words, all pairs are discordant.
You can calculate Kendall’s tau in Python similarly to how you would calculate Pearson’s r.
Rank: SciPy Implementation
You can use scipy.stats to determine the rank for each value in an array. First, you’ll import the libraries and create NumPy arrays:
>>>
>>> import numpy as np
>>> import scipy.stats
>>> x = np.arange(10, 20)
>>> y = np.array([2, 1, 4, 5, 8, 12, 18, 25, 96, 48])
>>> z = np.array([5, 3, 2, 1, 0, -2, -8, -11, -15, -16])
Now that you’ve prepared data, you can determine the rank of each value in a NumPy array with scipy.stats.rankdata():
>>>
>>> scipy.stats.rankdata(x)
array([ 1., 2., 3., 4., 5., 6., 7., 8., 9., 10.])
>>> scipy.stats.rankdata(y)
array([ 2., 1., 3., 4., 5., 6., 7., 8., 10., 9.])
>>> scipy.stats.rankdata(z)
array([10., 9., 8., 7., 6., 5., 4., 3., 2., 1.])
The arrays x and z are monotonic, so their ranks are monotonic as well. The smallest value in y is 1 and it corresponds to the rank 1. The second smallest is 2, which corresponds to the rank 2. The largest value is 96, which corresponds to the largest rank 10 since there are 10 items in the array.
rankdata() has the optional parameter method. This tells Python what to do if there are ties in the array (if two or more values are equal). By default, it assigns them the average of the ranks:
>>>
>>> scipy.stats.rankdata([8, 2, 0, 2])
array([4. , 2.5, 1. , 2.5])
There are two elements with a value of 2 and they have the ranks 2.0 and 3.0. The value 0 has rank 1.0 and the value 8 has rank 4.0. Then, both elements with the value 2 will get the same rank 2.5.
rankdata() treats nan values as if they were large:
>>>
>>> scipy.stats.rankdata([8, np.nan, 0, 2])
array([3., 4., 1., 2.])
In this case, the value np.nan corresponds to the largest rank 4.0. You can also get ranks with np.argsort():
>>>
>>> np.argsort(y) + 1
array([ 2, 1, 3, 4, 5, 6, 7, 8, 10, 9])
argsort() returns the indices that the array items would have in the sorted array. These indices are zero-based, so you’ll need to add 1 to all of them.
Rank Correlation: NumPy and SciPy Implementation
You can calculate the Spearman correlation coefficient with scipy.stats.spearmanr():
>>>
>>> result = scipy.stats.spearmanr(x, y)
>>> result
SpearmanrResult(correlation=0.9757575757575757, pvalue=1.4675461874042197e-06)
>>> result.correlation
0.9757575757575757
>>> result.pvalue
1.4675461874042197e-06
>>> rho, p = scipy.stats.spearmanr(x, y)
>>> rho
0.9757575757575757
>>> p
1.4675461874042197e-06
spearmanr() returns an object that contains the value of the Spearman correlation coefficient and p-value. As you can see, you can access particular values in two ways:
- Using dot notation (
result.correlationandresult.pvalue) - Using Python unpacking (
rho, p = scipy.stats.spearmanr(x, y))
You can get the same result if you provide the two-dimensional array xy that contains the same data as x and y to spearmanr():
>>>
>>> xy = np.array([[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
... [2, 1, 4, 5, 8, 12, 18, 25, 96, 48]])
>>> rho, p = scipy.stats.spearmanr(xy, axis=1)
>>> rho
0.9757575757575757
>>> p
1.4675461874042197e-06
The first row of xy is one feature, while the second row is the other feature. You can modify this. The optional parameter axis determines whether columns (axis=0) or rows (axis=1) represent the features. The default behavior is that the rows are observations and the columns are features.
Another optional parameter nan_policy defines how to handle nan values. It can take one of three values:
'propagate'returnsnanif there’s ananvalue among the inputs. This is the default behavior.'raise'raises aValueErrorif there’s ananvalue among the inputs.'omit'ignores the observations withnanvalues.
If you provide a two-dimensional array with more than two features, then you’ll get the correlation matrix and the matrix of the p-values:
>>>
>>> xyz = np.array([[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
... [2, 1, 4, 5, 8, 12, 18, 25, 96, 48],
... [5, 3, 2, 1, 0, -2, -8, -11, -15, -16]])
>>> corr_matrix, p_matrix = scipy.stats.spearmanr(xyz, axis=1)
>>> corr_matrix
array([[ 1. , 0.97575758, -1. ],
[ 0.97575758, 1. , -0.97575758],
[-1. , -0.97575758, 1. ]])
>>> p_matrix
array([[6.64689742e-64, 1.46754619e-06, 6.64689742e-64],
[1.46754619e-06, 6.64689742e-64, 1.46754619e-06],
[6.64689742e-64, 1.46754619e-06, 6.64689742e-64]])
The value -1 in the correlation matrix shows that the first and third features have a perfect negative rank correlation, that is that larger values in the first row always correspond to smaller values in the third.
You can obtain the Kendall correlation coefficient with kendalltau():
>>>
>>> result = scipy.stats.kendalltau(x, y)
>>> result
KendalltauResult(correlation=0.911111111111111, pvalue=2.9761904761904762e-05)
>>> result.correlation
0.911111111111111
>>> result.pvalue
2.9761904761904762e-05
>>> tau, p = scipy.stats.kendalltau(x, y)
>>> tau
0.911111111111111
>>> p
2.9761904761904762e-05
kendalltau() works much like spearmanr(). It takes two one-dimensional arrays, has the optional parameter nan_policy, and returns an object with the values of the correlation coefficient and p-value.
However, if you provide only one two-dimensional array as an argument, then kendalltau() will raise a TypeError. If you pass two multi-dimensional arrays of the same shape, then they’ll be flattened before the calculation.
Rank Correlation: pandas Implementation
You can calculate the Spearman and Kendall correlation coefficients with pandas. Just like before, you start by importing pandas and creating some Series and DataFrame instances:
>>>
>>> import pandas as pd
>>> x, y, z = pd.Series(x), pd.Series(y), pd.Series(z)
>>> xy = pd.DataFrame({'x-values': x, 'y-values': y})
>>> xyz = pd.DataFrame({'x-values': x, 'y-values': y, 'z-values': z})
Now that you have these pandas objects, you can use .corr() and .corrwith() just like you did when you calculated the Pearson correlation coefficient. You just need to specify the desired correlation coefficient with the optional parameter method, which defaults to 'pearson'.
To calculate Spearman’s rho, pass method=spearman:
>>>
>>> x.corr(y, method='spearman')
0.9757575757575757
>>> xy.corr(method='spearman')
x-values y-values
x-values 1.000000 0.975758
y-values 0.975758 1.000000
>>> xyz.corr(method='spearman')
x-values y-values z-values
x-values 1.000000 0.975758 -1.000000
y-values 0.975758 1.000000 -0.975758
z-values -1.000000 -0.975758 1.000000
>>> xy.corrwith(z, method='spearman')
x-values -1.000000
y-values -0.975758
dtype: float64
If you want Kendall’s tau, then you use method=kendall:
>>>
>>> x.corr(y, method='kendall')
0.911111111111111
>>> xy.corr(method='kendall')
x-values y-values
x-values 1.000000 0.911111
y-values 0.911111 1.000000
>>> xyz.corr(method='kendall')
x-values y-values z-values
x-values 1.000000 0.911111 -1.000000
y-values 0.911111 1.000000 -0.911111
z-values -1.000000 -0.911111 1.000000
>>> xy.corrwith(z, method='kendall')
x-values -1.000000
y-values -0.911111
dtype: float64
As you can see, unlike with SciPy, you can use a single two-dimensional data structure (a dataframe).
Visualization of Correlation
Data visualization is very important in statistics and data science. It can help you better understand your data and give you a better insight into the relationships between features. In this section, you’ll learn how to visually represent the relationship between two features with an x-y plot. You’ll also use heatmaps to visualize a correlation matrix.
You’ll learn how to prepare data and get certain visual representations, but you won’t cover many other explanations. To learn more about Matplotlib in-depth, check out Python Plotting With Matplotlib (Guide). You can also take a look at the official documentation and Anatomy of Matplotlib.
To get started, first import matplotlib.pyplot:
>>>
>>> import matplotlib.pyplot as plt
>>> plt.style.use('ggplot')
Here, you use plt.style.use('ggplot') to set the style of the plots. Feel free to skip this line if you want.
You’ll use the arrays x, y, z, and xyz from the previous sections. You can create them again to cut down on scrolling:
>>>
>>> import numpy as np
>>> import scipy.stats
>>> x = np.arange(10, 20)
>>> y = np.array([2, 1, 4, 5, 8, 12, 18, 25, 96, 48])
>>> z = np.array([5, 3, 2, 1, 0, -2, -8, -11, -15, -16])
>>> xyz = np.array([[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
... [2, 1, 4, 5, 8, 12, 18, 25, 96, 48],
... [5, 3, 2, 1, 0, -2, -8, -11, -15, -16]])
Now that you’ve got your data, you’re ready to plot.
X-Y Plots With a Regression Line
First, you’ll see how to create an x-y plot with the regression line, its equation, and the Pearson correlation coefficient. You can get the slope and the intercept of the regression line, as well as the correlation coefficient, with linregress():
>>>
>>> slope, intercept, r, p, stderr = scipy.stats.linregress(x, y)
Now you have all the values you need. You can also get the string with the equation of the regression line and the value of the correlation coefficient. f-strings are very convenient for this purpose:
>>>
>>> line = f'Regression line: y={intercept:.2f}+{slope:.2f}x, r={r:.2f}'
>>> line
'Regression line: y=-85.93+7.44x, r=0.76'
Now, create the x-y plot with .plot():
fig, ax = plt.subplots()
ax.plot(x, y, linewidth=0, marker='s', label='Data points')
ax.plot(x, intercept + slope * x, label=line)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.legend(facecolor='white')
plt.show()
Your output should look like this:

The red squares represent the observations, while the blue line is the regression line. Its equation is listed in the legend, together with the correlation coefficient.
Heatmaps of Correlation Matrices
The correlation matrix can become really big and confusing when you have a lot of features! Fortunately, you can present it visually as a heatmap where each field has the color that corresponds to its value. You’ll need the correlation matrix:
>>>
>>> corr_matrix = np.corrcoef(xyz).round(decimals=2)
>>> corr_matrix
array([[ 1. , 0.76, -0.97],
[ 0.76, 1. , -0.83],
[-0.97, -0.83, 1. ]])
It can be convenient for you to round the numbers in the correlation matrix with .round(), as they’re going to be shown be on the heatmap.
Finally, create your heatmap with .imshow() and the correlation matrix as its argument:
fig, ax = plt.subplots()
im = ax.imshow(corr_matrix)
im.set_clim(-1, 1)
ax.grid(False)
ax.xaxis.set(ticks=(0, 1, 2), ticklabels=('x', 'y', 'z'))
ax.yaxis.set(ticks=(0, 1, 2), ticklabels=('x', 'y', 'z'))
ax.set_ylim(2.5, -0.5)
for i in range(3):
for j in range(3):
ax.text(j, i, corr_matrix[i, j], ha='center', va='center',
color='r')
cbar = ax.figure.colorbar(im, ax=ax, format='% .2f')
plt.show()
Your output should look like this:
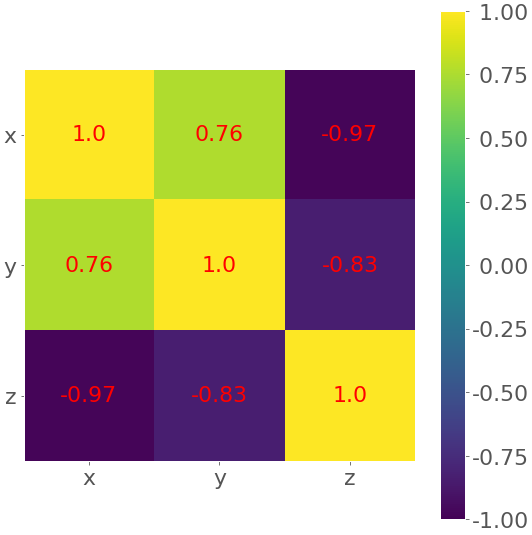
The result is a table with the coefficients. It sort of looks like the pandas output with colored backgrounds. The colors help you interpret the output. In this example, the yellow color represents the number 1, green corresponds to 0.76, and purple is used for the negative numbers.
Conclusion
You now know that correlation coefficients are statistics that measure the association between variables or features of datasets. They’re very important in data science and machine learning.
You can now use Python to calculate:
- Pearson’s product-moment correlation coefficient
- Spearman’s rank correlation coefficient
- Kendall’s rank correlation coefficient
Now you can use NumPy, SciPy, and pandas correlation functions and methods to effectively calculate these (and other) statistics, even when you work with large datasets. You also know how to visualize data, regression lines, and correlation matrices with Matplotlib plots and heatmaps.
If you have any questions or comments, please put them in the comments section below!
This article aims to give a better understanding of a very important technique of multivariate exploration. A correlation Matrix is basically a covariance matrix. Also known as the auto-covariance matrix, dispersion matrix, variance matrix, or variance-covariance matrix. It is a matrix in which the i-j position defines the correlation between the ith and jth parameter of the given data set. When the data points follow a roughly straight-line trend, the variables are said to have an approximately linear relationship. In some cases, the data points fall close to a straight line, but more often there is quite a bit of variability of the points around the straight-line trend. A summary measure called correlation describes the strength of the linear association.
Correlation in Python
Correlation summarizes the strength and direction of the linear (straight-line) association between two quantitative variables. Denoted by r, it takes values between -1 and +1. A positive value for r indicates a positive association, and a negative value for r indicates a negative association. The closer r is to 1 the closer the data points fall to a straight line, thus, the linear association is stronger. The closer r is to 0, making the linear association weaker.
Correlation
Correlation is the statistical measure that defines to which extent two variables are linearly related to each other. In statistics, correlation is defined by the Pearson Correlation formula :
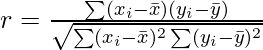
where,
Condition: The length of the dataset X and Y must be the same.
The Correlation value can be positive, negative, or zeros.
Correlation
Implementations with code:
Import the numpy library and define a custom dataset x and y of equal length:
Python3
import numpy as np
x = np.array([1,3,5,7,8,9, 10, 15])
y = np.array([10, 20, 30, 40, 50, 60, 70, 80])
Define the correlation by applying the above formula:
Python3
def Pearson_correlation(X,Y):
if len(X)==len(Y):
Sum_xy = sum((X-X.mean())*(Y-Y.mean()))
Sum_x_squared = sum((X-X.mean())**2)
Sum_y_squared = sum((Y-Y.mean())**2)
corr = Sum_xy / np.sqrt(Sum_x_squared * Sum_y_squared)
return corr
print(Pearson_correlation(x,y))
print(Pearson_correlation(x,x))
Output:
0.974894414261588 1.0
The above output shows that the relationship between x and y is 0.974894414261588 and x and x is 1.0
We can also find the correlation by using the numpy corrcoef function.
Python3
Output:
[[ 1. -0.97489441] [-0.97489441 1. ]]
The above output shows the correlations between x&x, x&y, y&x, and y&y.
Example
Import the necessary libraries
Python3
import pandas as pd
from sklearn.datasets import load_diabetes
import seaborn as sns
import matplotlib.pyplot as plt
Loading load_diabetes Data from sklearn.dataset
Python3
df = load_diabetes(as_frame=True)
df = df.frame
df.head()
Output:
| age | sex | bmi | bp | s1 | s2 | s3 | s4 | s5 | s6 | target |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.038076 | 0.050680 | 0.061696 | 0.021872 | -0.044223 | -0.034821 | -0.043401 | -0.002592 | 0.019907 | -0.017646 |
| 1 | -0.001882 | -0.044642 | -0.051474 | -0.026328 | -0.008449 | -0.019163 | 0.074412 | -0.039493 | -0.068332 | -0.092204 |
| 2 | 0.085299 | 0.050680 | 0.044451 | -0.005670 | -0.045599 | -0.034194 | -0.032356 | -0.002592 | 0.002861 | -0.025930 |
| 3 | -0.089063 | -0.044642 | -0.011595 | -0.036656 | 0.012191 | 0.024991 | -0.036038 | 0.034309 | 0.022688 | -0.009362 |
| 4 | 0.005383 | -0.044642 | -0.036385 | 0.021872 | 0.003935 | 0.015596 | 0.008142 | -0.002592 | -0.031988 | -0.046641 |
Find the Pearson correlations matrix by using the pandas command df.corr()
Syntax
df.corr(method, min_periods,numeric_only )
method : In method we can choose any one from {'pearson', 'kendall', 'spearman'} pearson is the standard correlation coefficient matrix i.e default
min_periods : int This is optional. Defines th eminimum number of observations required per pair.
numeric_only : Default is False, Defines we want to compare only numeric or categorical object also
Python3
corr = df.corr(method = 'pearson')
corr
Output:
| age | sex | bmi | bp | s1 | s2 | s3 | s4 | s5 | s6 | target | |
| age | 1.000000 | 0.173737 | 0.185085 | 0.335428 | 0.260061 | 0.219243 | -0.075181 | 0.203841 | 0.270774 | 0.301731 | 0.187889 |
| sex | 0.173737 | 1.000000 | 0.088161 | 0.241010 | 0.035277 | 0.142637 | -0.379090 | 0.332115 | 0.149916 | 0.208133 | 0.043062 |
| bmi | 0.185085 | 0.088161 | 1.000000 | 0.395411 | 0.249777 | 0.261170 | -0.366811 | 0.413807 | 0.446157 | 0.388680 | 0.586450 |
| bp | 0.335428 | 0.241010 | 0.395411 | 1.000000 | 0.242464 | 0.185548 | -0.178762 | 0.257650 | 0.393480 | 0.390430 | 0.441482 |
| s1 | 0.260061 | 0.035277 | 0.249777 | 0.242464 | 1.000000 | 0.896663 | 0.051519 | 0.542207 | 0.515503 | 0.325717 | 0.212022 |
| s2 | 0.219243 | 0.142637 | 0.261170 | 0.185548 | 0.896663 | 1.000000 | -0.196455 | 0.659817 | 0.318357 | 0.290600 | 0.174054 |
| s3 | -0.075181 | -0.379090 | -0.366811 | -0.178762 | 0.051519 | -0.196455 | 1.000000 | -0.738493 | -0.398577 | -0.273697 | -0.394789 |
| s4 | 0.203841 | 0.332115 | 0.413807 | 0.257650 | 0.542207 | 0.659817 | -0.738493 | 1.000000 | 0.617859 | 0.417212 | 0.430453 |
| s5 | 0.270774 | 0.149916 | 0.446157 | 0.393480 | 0.515503 | 0.318357 | -0.398577 | 0.617859 | 1.000000 | 0.464669 | 0.565883 |
| s6 | 0.301731 | 0.208133 | 0.388680 | 0.390430 | 0.325717 | 0.290600 | -0.273697 | 0.417212 | 0.464669 | 1.000000 | 0.382483 |
| target | 0.187889 | 0.043062 | 0.586450 | 0.441482 | 0.212022 | 0.174054 | -0.394789 | 0.430453 | 0.565883 | 0.382483 | 1.000000 |
The above table represents the correlations between each column of the data frame. The correlation between the self is 1.0, The negative correlation defined negative relationship means on increasing one column value second will decrease and vice-versa. The zeros correlation defines no relationship I.e neutral. and positive correlations define positive relationships meaning on increasing one column value second will also increase and vice-versa.
We can also find the correlations using numpy between two columns
Python3
c = np.corrcoef(df['age'],df['sex'])
print('Correlations between age and sexn',c)
Output:
Correlations between Age and Sex [[1. 0.1737371] [0.1737371 1. ]]
We can match from the above correlation matrix table, it is almost the same result.
Plot the correlation matrix with the seaborn heatmap
Python3
plt.figure(figsize=(10,8), dpi =500)
sns.heatmap(corr,annot=True,fmt=".2f", linewidth=.5)
plt.show()
Output:

Correlations Matrix
Last Updated :
16 Mar, 2023
Like Article
Save Article
В предыдущей части мы уже начали разбирать описательную статистику, а именно: центральные метрики и метрики оценки вариативности. В этой же части мы будем говорить той же описательной статистики, но уже разберем корреляции между парами данных. Корреляция – это статистическая взаимосвязь между двумя или более случайными величинами. И есть две статистические меры, которые характеризуют корреляцию между наборами данных — ковариация и коэффициент корреляции. Но прежде, чем нам начать с ними работать, необходимо установить и импортировать нужные библиотеки, а именно: math, statistics, numpy, scipy.stats, pandas и matplotlib.pyplot. После этого, мы формируем два списка Python, которые будем использовать для получения соответствующих массивов NumPy и серии Pandas:
x = list(range(-10, 11)) y = [0, 2, 2, 2, 2, 3, 3, 6, 7, 4, 7, 6, 6, 9, 4, 5, 5, 10, 11, 12, 14] x_, y_ = np.array(x), np.array(y) x__, y__ = pd.Series(x_), pd.Series(y_)
Теперь, когда у нас есть исходные данные, можно начать исследовать взаимосвязи между ними.
Ковариации
Выборочная ковариация — это мера, которая количественно определяет силу и направление взаимосвязи между парой переменных:
• Если корреляция положительная, то и ковариация тоже положительная. Более сильное отношение соответствует более высокой ценности ковариации.
• Если корреляция отрицательна, то и ковариация также отрицательна. Более сильное отношение соответствует более низкому (или более высокому абсолютному) значению ковариации.
• Если корреляция слабая, то ковариация близка к нулю.
Процесс расчета ковариации представлен ниже:
#Ковариация
#Расчет ковариации в чистом Python
mean_x, mean_y = sum(x) / n, sum(y) / n
cov_xy = (sum((x[k] - mean_x) * (y[k] - mean_y) for k in range(n))/ (n - 1))
print(f'Расчет ковариации в чистом Python: {cov_xy}')
#Расчет ковариации с помощью NumPy
cov_matrix = np.cov(x_, y_)
print(f'Расчет ковариационной матрицы с помощью NumPy функцией cov(): {cov_matrix}')
print(f'Проверка, что левый элемент ковариационной матрицы — это ковариация x и x или дисперсия x, '
f'а правый элемент — ковариация y и y или дисперсия y: {x_.var(ddof=1)} и {y_.var(ddof=1)}')
cov_xy = cov_matrix[0, 1]
cov_xy2 = cov_matrix[1, 0]
print(f'Проверка, что два других элемента ковариационной матрицы равны '
f'и представляют фактическую ковариацию между x и y: {cov_xy} и {cov_xy2}')
#Расчет ковариации с помощью Pandas
cov_xy = x__.cov(y__)
cov_xy3 = y__.cov(x__)
print(f'Расчет ковариации с помощью Pandas методом .cov(): {cov_xy} и {cov_xy3}')
Первым делом была найдена ковариация в чистом Python, где сначала необходимо найти среднее значение х и у, а затем применить математическую формулу. Но можно применить функцию cov() библиотеки NumPy, которая возвращает ковариационную матрицу, что и было сделано во втором примере. Обратите внимание, cov() имеет необязательные параметры bias (по умолчанию False) и ddof (по умолчанию None). Их значения по умолчанию подходят для получения образца ковариационной матрицы. Верхний левый элемент ковариационной матрицы — это ковариация x и x или дисперсия x. Точно так же нижний правый элемент — y и y или дисперсия y. А два других элемента ковариационной матрицы равны и представляют фактическую ковариацию между x и y. Как проверить и убедиться, что это правда, разобрано в примере. Использовав np.cov() мы получили то же значение ковариации, что и с чистым Python. Помимо этого, можно было использовать метод .cov() библиотеки Pandas, что и было сделано в третьем примере, где для одного объекта Series вызывается .cov() и передает другой объект в качестве первого аргумента.
Коэффициент корреляции
Коэффициент корреляции или коэффициент корреляции Пирсона — произведение, обозначается символом ??. Коэффициент является еще одним показателем корреляции между данными. К нему надо относиться как к стандартизированной ковариации. Вот несколько важных замечаний:
• ? > 0 указывает на положительную корреляцию.
• ? < 0 указывает на отрицательную корреляцию.
• r = 1 является максимально возможным значением ?. Это свидетельство полной линейной зависимости между переменными.
• r = −1 является минимально возможным значением ?. Это свидетельство полного отсутствия линейной зависимости между переменными.
• r ≈ 0 или когда around около нуля, означает, что корреляция между переменными отсутствует.
Процесс расчета коэффициента корреляции представлен ниже:
#Коэффициент корреляции
#Расчет коэффициента корреляции в чистом Python
var_x = sum((item - mean_x)**2 for item in x) / (n - 1)
var_y = sum((item - mean_y)**2 for item in y) / (n - 1)
std_x, std_y = var_x ** 0.5, var_y ** 0.5
r = cov_xy / (std_x * std_y)
print(f'Расчет коэффициента корреляции в чистом Python: {r}')
#Расчет коэффициента корреляции с помощью scipy.stats
r, p = scipy.stats.pearsonr(x_, y_)
print(f'Расчет коэффициента корреляции и p-value, используя функцию pearsonr() в scipy.stats: {r} и {p} ')
scipy.stats.linregress(x_, y_)
print(f'Расчет коэффициента корреляции с помощью scipy.stats.linregress(): {scipy.stats.linregress(x_, y_)}')
result = scipy.stats.linregress(x_, y_)
r = result.rvalue
print(f'Получение доступа к определенным значениям из результата linregress(), включая коэффициент корреляции, используя точечную запись: {r}')
#Расчет коэффициента корреляции с помощью Pandas
r = x__.corr(y__)
r1 = y__.corr(x__)
print(f'Расчет коэффициента корреляции методом .corr() библиотеки Pandas: {r} и {r1}')
В первом примере показано, как рассчитать это коэффициент в чистом Python. Для этого нам понадобятся средние значения (mean_x и mean_y) и стандартные отклонения (std_x, std_y) для наборов данных x и y, а также их ковариация cov_xy. Далее, этот коэффициент и значение p-value (значение, показывающее принимается или отклоняется гипотеза) были рассчитан с помощью функцию pearsonr() в scipy.stats. Первое значение – это коэффициент корреляции между x_ и x_. Второй элемент — это коэффициент корреляции между y_ и y_. Их значения равны 1,0. В третьем примере коэффициент корреляции был найдем с помощью scipy.stats.linregress(). linregress() принимает x_ и y_, вычисляет линейную регрессию и возвращает результаты — наклон и точка пересечения определяют уравнение прямой регрессии, а rvalue — коэффициент корреляции. Чтобы получить доступ к определенным значениям из результата linregress(), включая коэффициент корреляции, необходимо использовать точечную запись, что показано в примере. И в четвертом примере был использован метод .corr() библиотеки Pandas, который вызывается для одного объекта Series и передает другой объект в качестве первого аргумента.
Работа с 2D данными
Axis
В статистике очень часто работают с 2D данными. NumPy и SciPy предоставляют комплексные средства для работы с ними, а Pandas имеет специальный класс DataFrame для обработки 2D данных. И прежде, чем нам работать с ними, их необходимо создать:
#Работа с данными 2D (таблицы)
#Axis
#Создание 2D массива с помощью Numpy
a = np.array(2, 3, 1],[4, 9, 2], [8, 27, 4], [16, 1, 1], [2, 3, 1એ)
print(f'Вывод, созданного с помощью Numpy, 2D массива: {a}')
Теперь у нас есть набор 2D данных, который мы будем использовать в этом разделе. Можно применять к нему статистические функции и методы Python так же, как к данным 1D, используя или не используя при этом необязательный параметр axis, то есть ось. Ось может принимать любое из следующих значений:
• axis = None — расчет статистики по всем данным в массиве, как в приведенном выше примере. Такое поведение часто используется по умолчанию в NumPy.
• axis = 0 — расчет статистики для каждого столбца массива. Такое поведение часто используется по умолчанию для статистических функций SciPy.
• axis = 1 — расчет статистики для каждой строки массива.
Внизу представлен код, в котором я попробовал использовать к нашему 2D данным статистические функции и методы Python, как с параметром axis, так и без:
#Использование статистических функций и методов Python к 2d массиву с необязательным параметров axis
np.mean(a, axis=0)
a.mean(axis=1)
print(f'Вывод среднего значения 2D массива методом NumPy на оси = 0 и на оси = 1 соответствнно: {np.mean(a, axis=0)} и {a.mean(axis=1)}')
np.median(a, axis=0)
np.median(a, axis=1)
print(f'Вывод медианы 2D массива методом NumPy на оси = 0 и на оси = 1 соответствнно: {np.median(a, axis=0)} и {np.median(a, axis=1)}')
scipy.stats.gmean(a) # Default: axis=0
print(f'Вывод среднего геометрического значения 2D массива функцией SciPy на оси = 0 : {scipy.stats.gmean(a)}')
scipy.stats.gmean(a, axis=None)
print(f'Вывод среднего геометрического значения для всего 2D массива функцией SciPy: {scipy.stats.gmean(a, axis=None)}')
DataFrames
Класс DataFrame является одним из основных типов данных Pandas. С ним очень удобно работать, потому что в нем есть метки для строк и столбцов. Сам код представлен внизу:
#DataFrames
row_names = ['first', 'second', 'third', 'fourth', 'fifth']
col_names = ['A', 'B', 'C']
df = pd.DataFrame(a, index=row_names, columns=col_names)
print(f'Вывод класса DataFrame с ранее созданным 2d массивом: {df}')
df.mean()
df.var()
print(f'Вывод среднего значения и несмещенной дисперсии для всего класса DataFrame с ранее созданным 2d массивом: {df.mean()} и {df.var()}')
df.mean(axis=1)
print(f'Вывод среднего значения класса DataFrame с ранее созданным 2d массивом по оси = 1: {df.mean(axis=1)}')
df['A']
print(f'Пример изоляции класса DataFrame с ранее созданным 2d массивом по столбцу A: {df["A"]}')
df['A'].mean()
print(f'Пример расчета среднего значения класса DataFrame с ранее созданным 2d массивом по столбцу A: {df["A"].mean()}')
Первым делом был создан DataFrame использовав при этом массив a. На практике имена столбцов имеют значение и должны быть описательными. Имена строк иногда указываются автоматически как 0, 1 и т. Д. Вы можете указать их явно с помощью параметра index, хотя вы можете свободно опускать index, если хотите. Методы DataFrame очень похожи на методы Series, хотя их поведение отличается. Если вы вызываете методы статистики Python без аргументов, то DataFrame будет возвращать результаты для каждого столбца. Если же вы хотите получить результаты для каждой строки, просто укажите параметр axis = 1. Также можно изолировать каждый столбец DataFrame и применять к нему соответствующие методы. Процесс применения статистических методов и функций Python к DataFrame представлен в примере.
Визуализация данных
В дополнение к численному описанию, такому как среднее, медиана или дисперсия, можно использовать визуальные методы для представления, описания и обобщения данных. В этом разделе вы узнаете, как представить свои данные визуально, используя библиотеку matplotlib.pyplot, которая у нас уже установлена и импортирована. matplotlib.pyplot — очень удобная и широко используемая библиотека, хотя это не единственная библиотека Python, доступная для этой цели.
Box Plots
Ящик с усами является отличным инструментом для визуального представления описательной статистики данного набора данных. Он может показывать диапазон, межквартильный диапазон, медиану, моду, выбросы и все квартили. Сам код:
#Визуализация данных
#Box Plots
np.random.seed(seed=0)
x = np.random.randn(1000)
y = np.random.randn(100)
z = np.random.randn(10)
fig, ax = plt.subplots()
ax.boxplot((x, y, z), vert=False, showmeans=True, meanline=True,
labels=('x', 'y', 'z'), patch_artist=True,
medianprops={'linewidth': 2, 'color': 'purple'},
meanprops={'linewidth': 2, 'color': 'red'})
plt.show()
Первый оператор инициализирует генератора случайных чисел NumPy с помощью seed(). Поэтому при каждом запуске скрипта могут получаться одинаковые результаты. Не нужно устанавливать начальное значение и, если его не указывать, то каждый раз будут получаться разные результаты. Другие операторы создают три массива NumPy с нормально распределенными псевдослучайными числами. x относится к массиву с 1000 элементами, y имеет 100, а z содержит 10 элементов. Параметры .boxplot():
• х ваши данные.
• vert устанавливает горизонтальную ориентацию графика, когда False. Ориентация по умолчанию – вертикальная.
• showmeans показывает среднее значение ваших данных, когда True.
• meanline представляет среднее в виде линии, когда истина. Представлением по умолчанию является точка.
• labels: метки ваших данных.
• patch_artist определяет, как рисовать график.
• medianprops обозначает свойства линии, представляющей медиану.
• meanprops указывает свойства линии или точки, представляющей среднее значение.
Есть и другие параметры, но их анализ выходит за рамки данного руководства. Вы можете увидеть три сюжета. Каждый из них соответствует одному набору данных (x, y или z) и показывает следующее:
• Среднее значение — это красная пунктирная линия.
• Медиана — это фиолетовая линия.
• Первый квартиль — левый край синего прямоугольника.
• Третий квартиль — это правый край синего прямоугольника.
• Межквартильный диапазон — это длина синего прямоугольника.
• Диапазон — всё слева направо.
• Выбросы — точки слева и справа.
Сюжетная диаграмма может показывать столько информации на одном рисунке!
Результат:

Гистограммы
Гистограмма особенно полезна, когда в наборе данных содержится большое количество уникальных значений. Гистограмма делит значения из отсортированного набора данных на интервалы, также называемые ячейками. Часто все лотки имеют одинаковую ширину, но это не обязательно так. Значения нижней и верхней границ ячейки называются ребрами ячейки. Частота представляет собой одно значение, которое соответствует каждому бину. Это количество элементов набора данных со значениями между краями корзины. По договоренности, все корзины, кроме самой правой, наполовину открыты. Они включают значения, равные нижним границам, но исключают значения, равные верхним границам. Крайняя правая корзина закрыта, так как включает обе границы. Если вы разделите набор данных с ребрами 0, 5, 10 и 15, то есть три элемента:
• Первый и самый левый столбец содержит значения, большие или равные 0 и меньшие 5.
• Второй контейнер содержит значения, большие или равные 5 и меньшие 10.
• Третий и самый правый контейнер содержит значения, большие или равные 10 и меньшие или равные 15.
Сам код:
#Гистограммы
hist, bin_edges = np.histogram(x, bins=10)
fig, ax = plt.subplots()
ax.hist(x, bin_edges, cumulative=False)
ax.set_xlabel('x')
ax.set_ylabel('Frequency')
plt.show()
Функция np.histogram() — это удобный способ получить данные для гистограмм. Он берет массив с вашими данными и количеством (или ребрами) бинов и возвращает два массива NumPy:
• hist содержит частоту или количество элементов, соответствующих каждому бину.
• bin_edges содержит ребра или границы корзины.
Что рассчитывает histogram(), граф .hist() может показать графически. Первый аргумент .hist() — это последовательность с вашими данными. Второй аргумент определяет края бинов. Третий отключает возможность создания гистограммы с накопленными значениями. Результат представлен внизу:
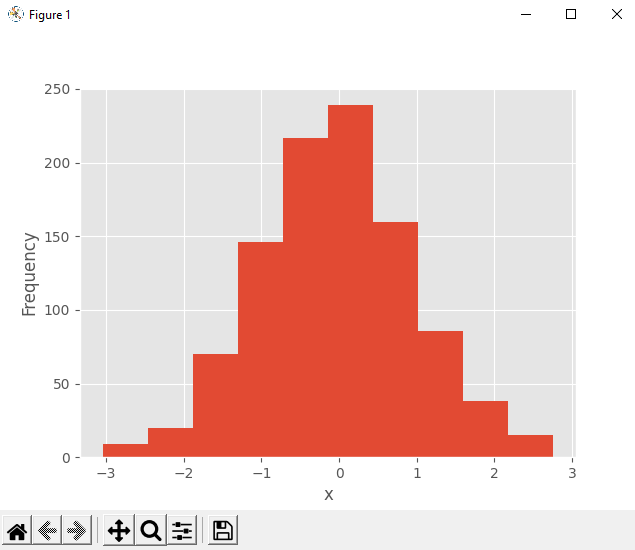
Вы можете видеть края корзины на горизонтальной оси и частоты на вертикальной оси.
При значении аргумента cumulative = True в .hist() можно получить гистограмму с совокупным количеством элементов:
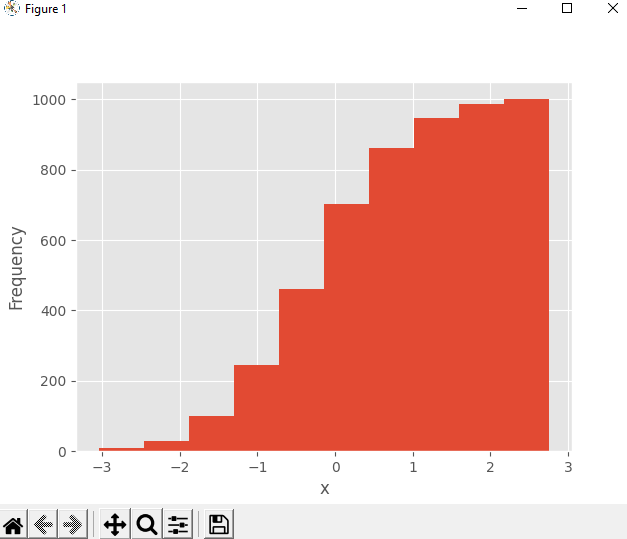
Частота первого и самого левого лотка — это количество элементов в этом лотке. Частота второго бина — это сумма количества элементов в первом и втором бинах. Другие контейнеры отрисовываются аналогично. Наконец, частота последнего и самого правого бина — это общее количество элементов в наборе данных (в данном случае 1000).
Pie Charts круговые диаграммы
Круговые диаграммы представляют данные с небольшим количеством меток и заданными относительными частотами. Они хорошо работают даже с ярлыками, которые нельзя заказать (например, номинальные данные). Круговая диаграмма представляет собой круг, разделенный на несколько частей. Каждый срез соответствует отдельной метке из набора данных и имеет площадь, пропорциональную относительной частоте, связанной с этой меткой. Сам код:
#Pie Charts круговые диаграммы
x, y, z = 128, 256, 1024
fig, ax = plt.subplots()
ax.pie((x, y, z), labels=('x', 'y', 'z'), autopct='%1.1f%%')
plt.show()
Первым делом мы определяем данные, связанные с тремя метками. Далее, Первый аргумент .pie() — данные, а второй — последовательность соответствующих меток. autopct определяет формат относительных частот, показанных на рисунке. Результат:
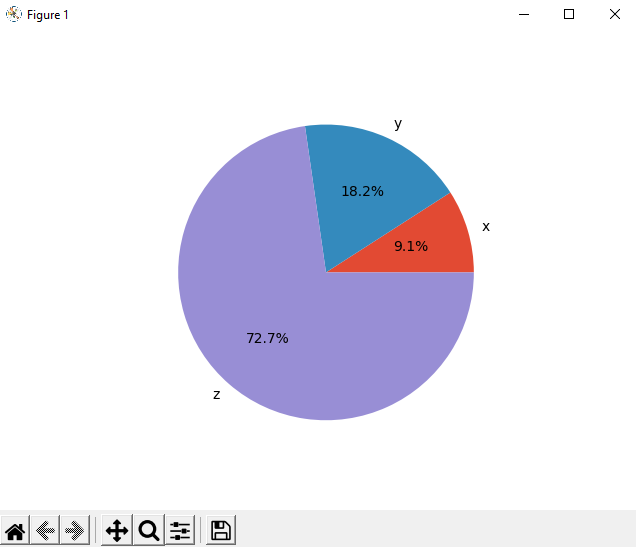
Круговая диаграмма показывает x как наименьшую часть круга, y как следующую наибольшую, а затем z как самую большую часть. Проценты обозначают относительный размер каждого значения по сравнению с их суммой.
Bar Charts
Гистограммы также иллюстрируют данные, которые соответствуют заданным меткам или дискретным числовым значениям. Они могут показывать пары данных из двух наборов данных. Элементы одного набора – это метки, а соответствующие элементы другого – их частоты. При желании они также могут отображать ошибки, связанные с частотами. Гистограмма показывает параллельные прямоугольники, называемые барами. Каждая полоса соответствует одной метке и имеет высоту, пропорциональную частоте или относительной частоте ее метки. Сам код:
#Bar Charts
x = np.arange(21)
y = np.random.randint(21, size=21)
err = np.random.randn(21)
fig, ax = plt.subplots()
ax.bar(x, y, yerr=err)
ax.set_xlabel('x')
ax.set_ylabel('y')
plt.show()
В данном коде мы использовали np.arange(), чтобы получить x или массив последовательных целых чисел от 0 до 20. Мы использовали это для представления меток. y — это массив равномерно распределенных случайных целых чисел, также от 0 до 20. Этот массив будет представлять частоты. err содержит нормально распределенные числа с плавающей точкой, которые являются ошибками. Эти значения не являются обязательными. Далее создаем гистограмму с помощью .bar(), если вам нужны вертикальные столбцы или .barh(), если вам нужны горизонтальные столбцы. Результат:
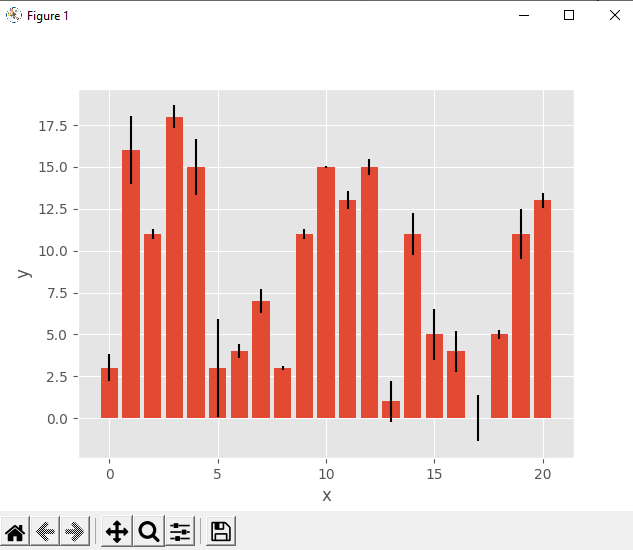
X-Y участки
Диаграмма x-y или диаграмма рассеяния представляет пары данных из двух наборов данных. Горизонтальная ось x показывает значения из набора x, а вертикальная ось y показывает соответствующие значения из набора y. При желании вы можете включить линию регрессии и коэффициент корреляции. Код построения представлен внизу:
#X-Y участки
x = np.arange(21)
y = 5 + 2 * x + 2 * np.random.randn(21)
slope, intercept, r, *__ = scipy.stats.linregress(x, y)
line = f'Regression line: y={intercept:.2f}+{slope:.2f}x, r={r:.2f}'
fig, ax = plt.subplots()
ax.plot(x, y, linewidth=0, marker='s', label='Data points')
ax.plot(x, intercept + slope * x, label=line)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.legend(facecolor='white')
plt.show()
Сначала мы генерируем два набора данных и выполняем линейную регрессию с помощью scipy.stats.linregress().Набор данных x снова является массивом с целыми числами от 0 до 20. y вычисляется как линейная функция x, искаженная некоторым случайным шумом. linregress возвращает несколько значений. Вам понадобится наклон и точка пересечения линии регрессии, а также коэффициент корреляции r. Затем применяем .plot(), чтобы получить график x-y. Результат:

Схемы Зоны активности
Тепловая карта может быть использована для визуального отображения матрицы. Цвета представляют числа или элементы матрицы. Тепловые карты особенно полезны для иллюстрации ковариационных и корреляционных матриц. Вы можете создать тепловую карту для ковариационной матрицы с помощью .imshow():
#Схемы Зоны активности
matrix = np.cov(x, y).round(decimals=2)
fig, ax = plt.subplots()
ax.imshow(matrix)
ax.grid(False)
ax.xaxis.set(ticks=(0, 1), ticklabels=('x', 'y'))
ax.yaxis.set(ticks=(0, 1), ticklabels=('x', 'y'))
ax.set_ylim(1.5, -0.5)
for i in range(2):
for j in range(2):
ax.text(j, i, matrix[i, j], ha='center', va='center', color='w')
plt.show()
Здесь тепловая карта содержит метки «x» и «y», а также числа из ковариационной матрицы. Результат:
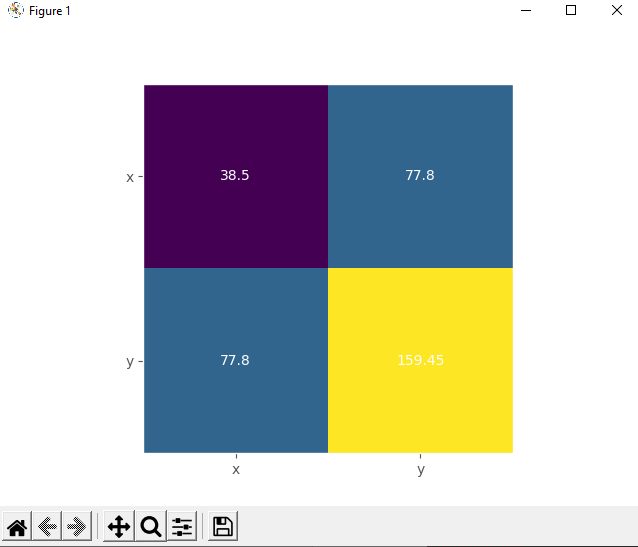
Желтое поле представляет самый большой элемент из матрицы 130.34, а фиолетовое соответствует наименьшему элементу 38.5. Синие квадраты между ними связаны со значением 77,8.
Вывод
Теперь, когда мы разобрали описательную статистику, вы можете смело применять ее на практике, причем реализовывая ее как на чистом Python, так и используя методы и функции библиотек, созданных специально для этих целей.

