Как найти корреляцию в спсс

---

Матрица корреляции — это квадратная таблица, которая показывает коэффициенты корреляции Пирсона между различными переменными в наборе данных.

Напомним, чтокоэффициент корреляции Пирсона — это мера линейной связи между двумя переменными . Он принимает значение от -1 до 1, где:

• -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными
• 0 указывает на отсутствие линейной корреляции между двумя переменными
• 1 указывает на совершенно положительную линейную корреляцию между двумя переменными.

Чем дальше коэффициент корреляции от нуля, тем сильнее связь между двумя переменными.

В этом руководстве объясняется, как создать и интерпретировать корреляционную матрицу в SPSS.

Пример: Как создать матрицу корреляции в SPSS

Используйте следующие шаги, чтобы создать матрицу корреляции для этого набора данных, которая показывает средние передачи, подборы и очки для восьми баскетболистов:

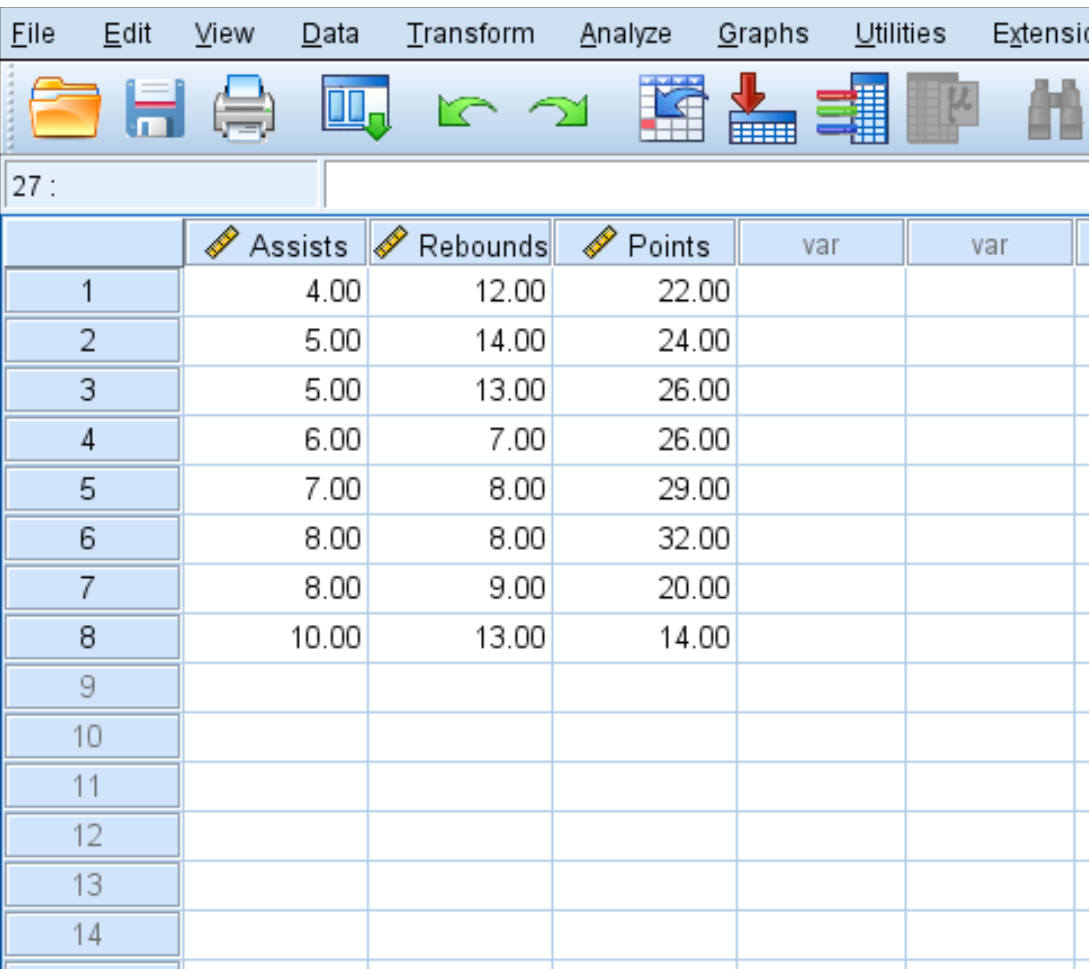
Шаг 1: Выберите двумерную корреляцию.

• Щелкните вкладку Анализ .
• Щелкните Сопоставить .
• Щелкните Двумерный .

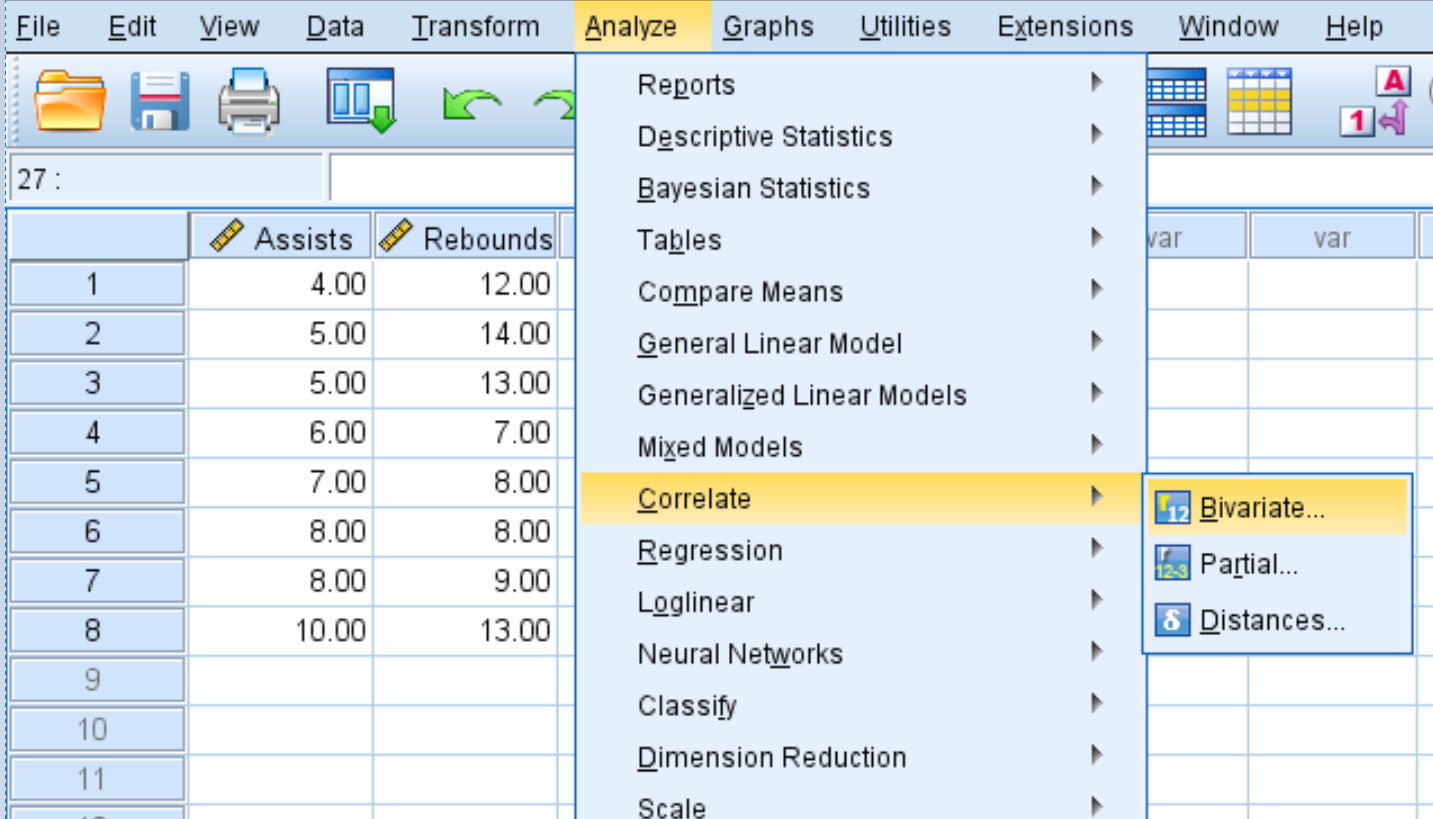
Шаг 2: Создайте матрицу корреляции.

Каждая переменная в наборе данных первоначально будет показана в поле слева:

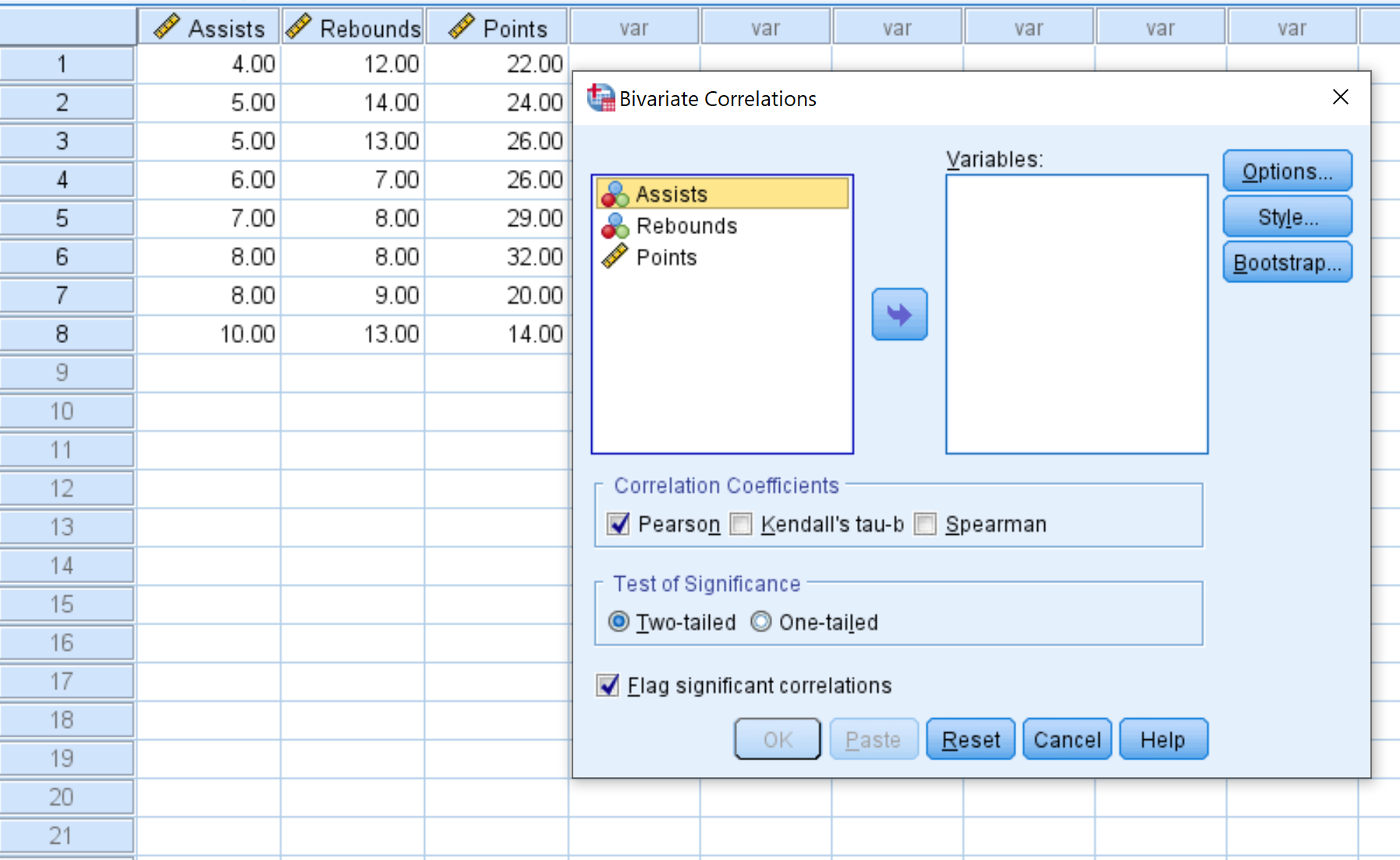
• Выберите каждую переменную, которую вы хотите включить в матрицу корреляции, и щелкните стрелку, чтобы перенести их в поле « Переменные ». В этом примере мы будем использовать все три переменные.
• В разделе Коэффициенты корреляции выберите, хотите ли вы использовать корреляцию Пирсона, тау Кендалла или Спирмена. Мы оставим его как Pearson для этого примера.
• В разделе Проверка значимости выберите, следует ли использовать двусторонний или односторонний тест, чтобы определить, имеют ли две переменные статистически значимую связь. Мы оставим его как Двухвостого.
• Установите флажок рядом с Отметить существенные корреляции , если вы хотите, чтобы SPSS помечал переменные со значительной корреляцией.
• Наконец, нажмите ОК .

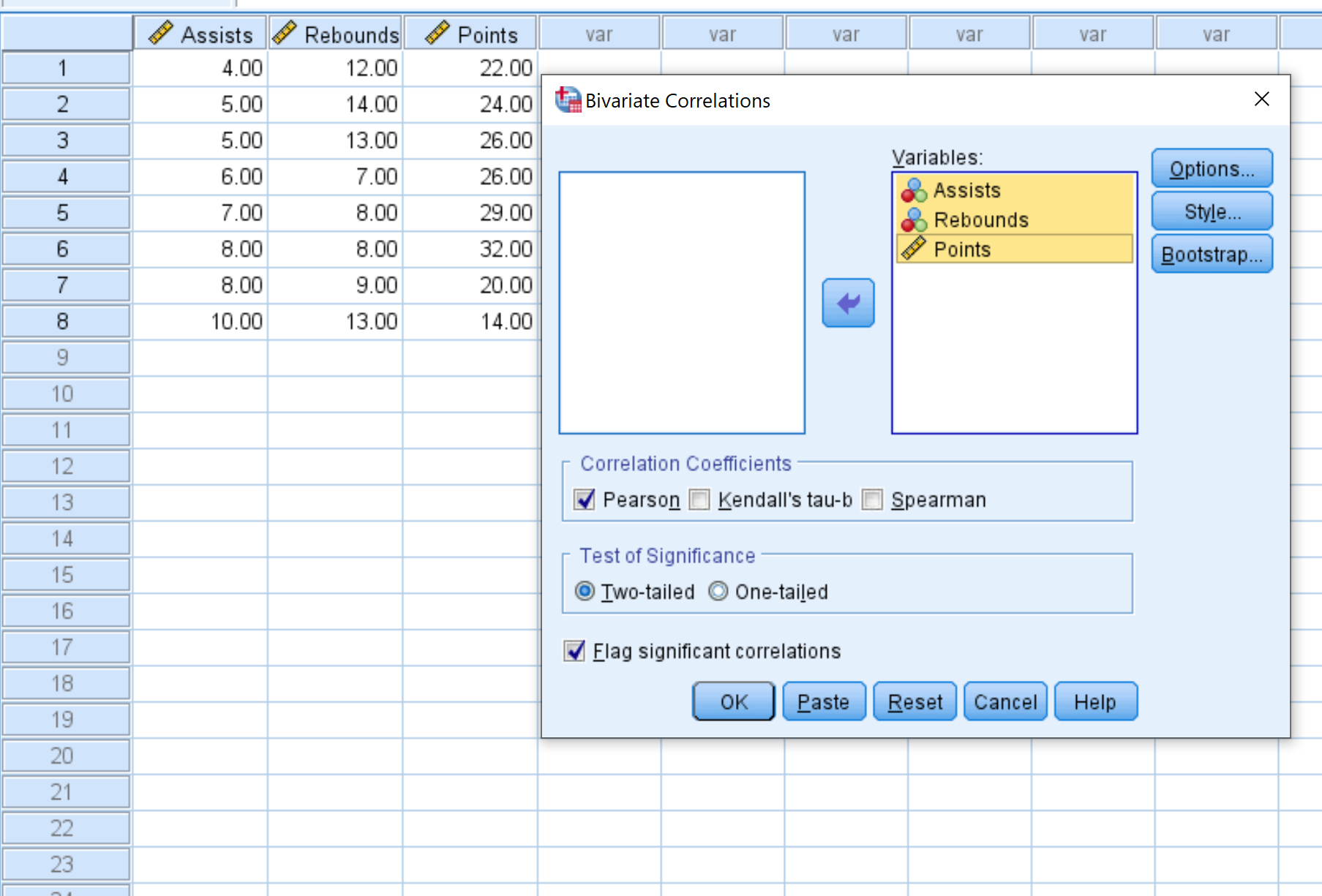
После того, как вы нажмете OK , появится следующая матрица корреляции:

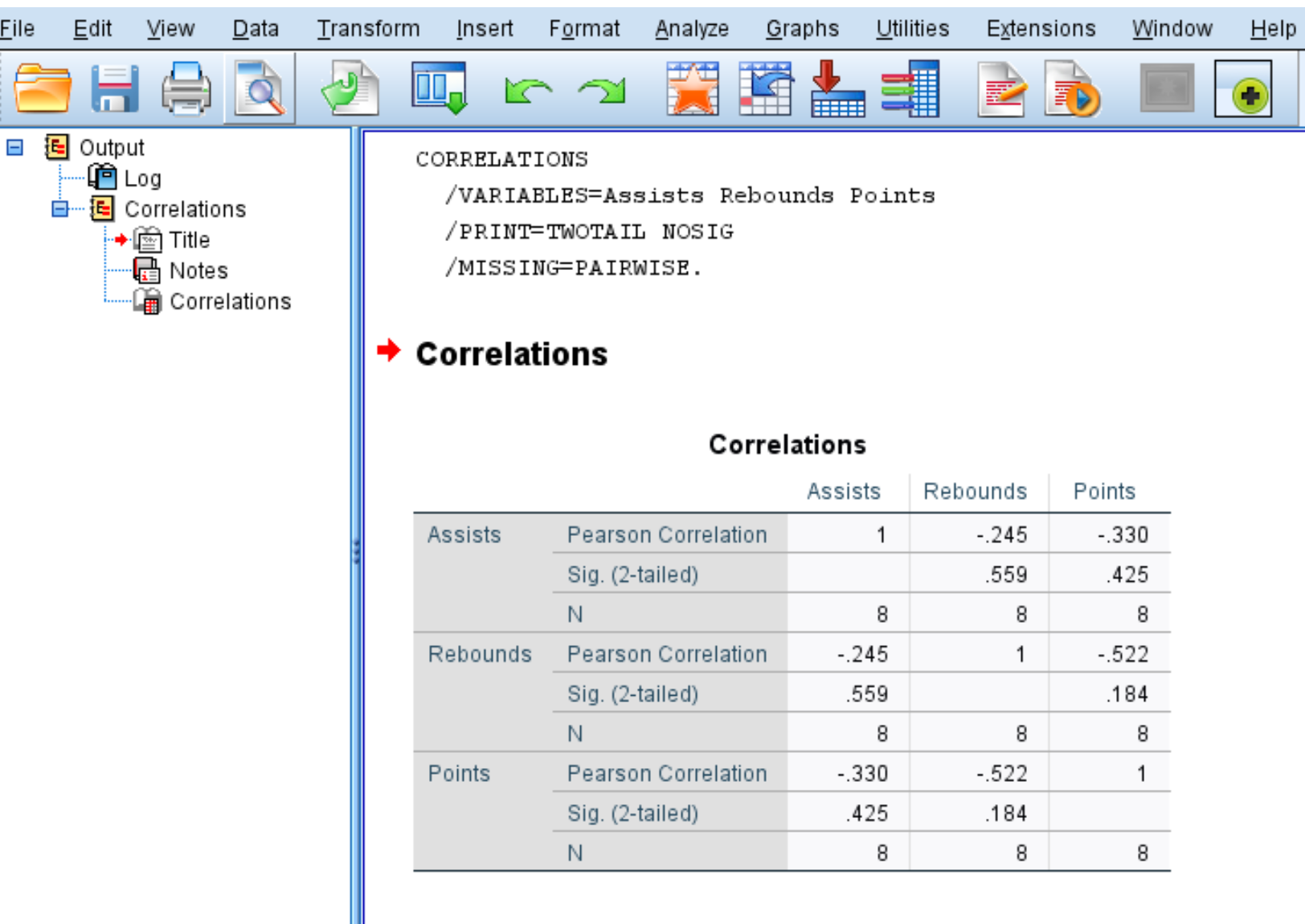
Шаг 3: Интерпретируйте матрицу корреляции.

Матрица корреляции отображает следующие три показателя для каждой переменной:

• Корреляция Пирсона: мера линейной связи между двумя переменными в диапазоне от -1 до 1.
• Сиг. (2-стороннее): двустороннее значение p, связанное с коэффициентом корреляции. Это говорит вам, имеют ли две переменные статистически значимую связь (например, если p < 0,05).
• N: количество пар, используемых для расчета коэффициента корреляции Пирсона.

Например, вот как интерпретировать вывод переменной Assists:

• Коэффициент корреляции Пирсона между передачами и подборами составляет -0,245.Поскольку это число отрицательное, это означает, что эти две переменные имеют отрицательную связь.
• Значение p, связанное с коэффициентом корреляции Пирсона для передач и подборов, составляет 0,559.Поскольку это значение не менее 0,05, две переменные не имеют статистически значимой связи.
• Количество пар, использованных для расчета коэффициента корреляции Пирсона, равнялось 8 (например, в этом расчете использовалось 8 пар игроков).

Шаг 4: Визуализируйте матрицу корреляции.

Вы также можете создать матрицу диаграммы рассеяния, чтобы визуализировать линейную зависимость между каждой из переменных.

• Щелкните вкладку Графики .
• Нажмите Построитель диаграмм .

• Чтобы выбрать тип диаграммы, щелкните Точечная/точечная .
• Щелкните изображение с надписью Матрица рассеяния .
• В поле « Переменные » в левом верхнем углу, удерживая Ctrl, щелкните все три имени переменных. Перетащите их в поле в нижней части диаграммы с надписью Scattermatrix .
• Наконец, нажмите ОК .

Автоматически появится следующая матрица диаграммы рассеяния:

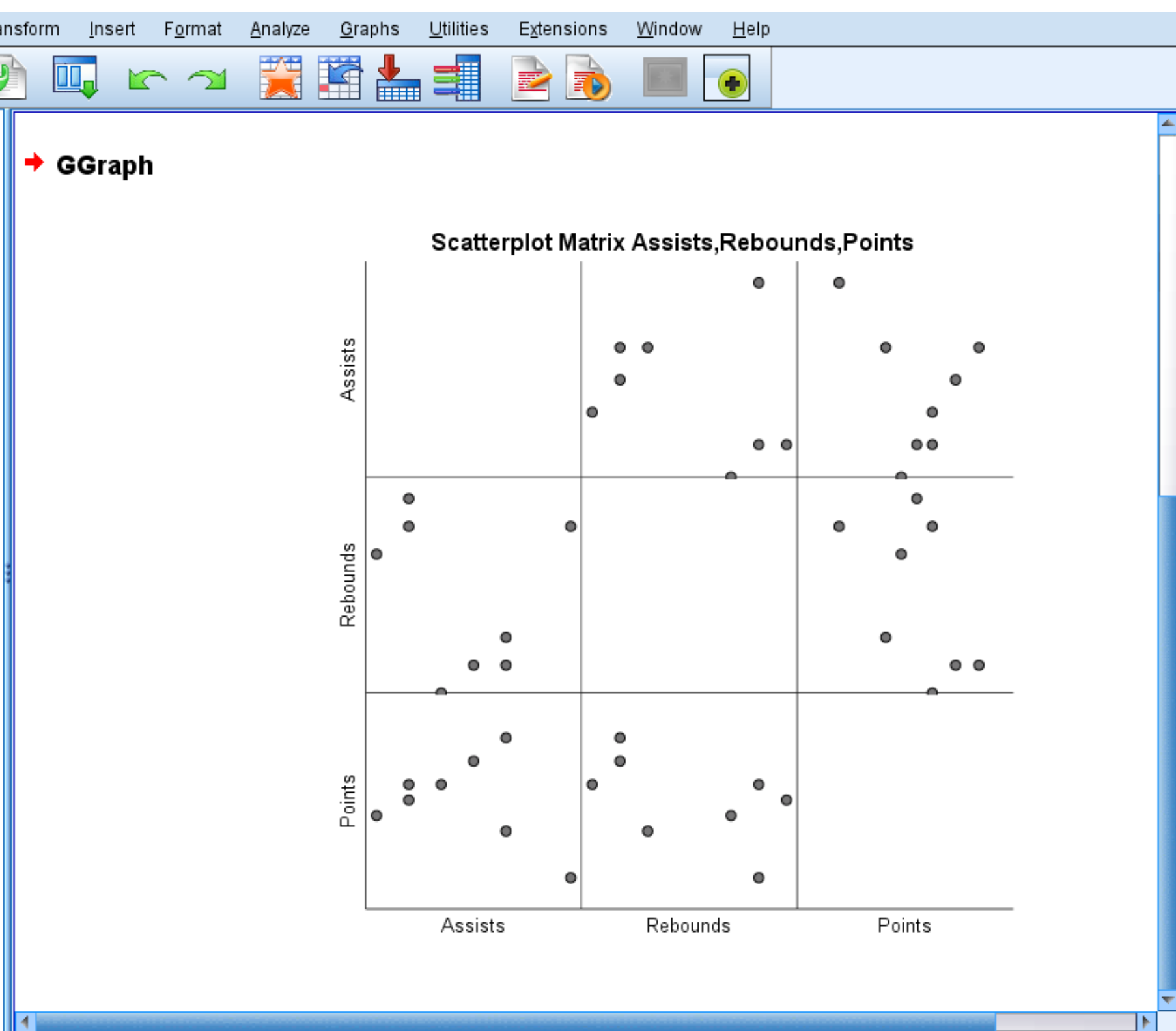
Каждая отдельная диаграмма рассеяния показывает попарные комбинации между двумя переменными. Например, диаграмма рассеяния в левом нижнем углу показывает попарные комбинации очков и передач для каждого из 8 игроков в наборе данных.

Матрица диаграммы рассеяния не является обязательной, но она предлагает хороший способ визуализировать взаимосвязь между каждой парной комбинацией переменных в наборе данных.

Глава 15. Корреляционный анализ

• 15.1. Коэффициент корреляции Пирсона
• 15.2. Ранговые коэффициенты корреляции по Спирману и Кендалу
• 15.3. Частная корреляция
• 15.4. Мера расстояния и мера сходства
• 15.5. Внутриклассовый коэффициент корреляции (Intraclass Correlation Coefficient (ICC))

Корреляция – связь между двумя переменными. Расчёты подобных двумерных критериев взаимосвязи основываются на формировании парных значений, которые образовываются из рассматриваемых зависимых выборок.

Если в качестве примера возьмём данные об уровне холестерина для первых двух моментов времени из исследования гипертонии (файл hyper.sav),
то в данном случае следует ожидать довольно сильную связь: большие значения в исходный момент времени являются веским поводом для ожидания больших значений и через 1 месяц.

Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным.
Каждая пара значений маркируется при помощи определенного символа. Такой график, называемый “диаграммой рассеяния” (Scatterplot) для двух зависимых переменных можно построить путём вызова меню
Graphs… (Графики) / Scatter plots… (Диаграммы рассеяния) (см. гл. 22.8).

Образовавшееся скопление точек показывает, что обследованные пациенты с высокими исходными показателями, как правило, имеют высокие значения холестерина и при повторном опросе через месяц.

Статистика говорит о корреляции между двумя переменными и указывает силу связи при помощи некоторого критерия взаимосвязи, который получил название коэффициента корреляции.
Этот коэффициент, всегда обозначаемый латинской буквой r, может принимать значения между -1 и +1, причём если значение находится ближе к 1, то это означает наличие сильной связи,
а если ближе к 0, то слабой.

Если коэффициент корреляции отрицательный, это означает наличие противоположной связи: чем выше значение одной переменной, тем ниже значение другой.
Сила связи характеризуется также и абсолютной величиной коэффициента корреляции. Для словесного описания величины коэффициента корреляции используются следуюшие градации:

Значение	Интерпретация
до 0,2	Очень слабая корреляция
до 0,5	Слабая корреляция
до 0,7	Средняя корреляция
до 0,9	Высокая корреляция
свыше 0,9	Очень высокая корреляция

Метод вычисления коэффициента корреляции зависит от вида шкалы, которой относятся переменные:

Типы шкал	Мера связи
Переменная X	Переменная Y
Интервальная (или отношений)	Интервальная (или отношений)	Коэффициент Пирсона
Ранговая, интервальная (или отношений)	Ранговая, интервальная (или отношений)	Коэффициент Спирмена
Ранговая	Ранговая	Коэффициент Кендалла
Дихотомическая	Дихотомическая	Коэффициент φ (фи), четырёхполевая корреляция
Дихотомическая	Ранговая	Рангово-бисериальный коэффициент

• Переменные с интервальной или с пропорциональной шкалой – коэффициент корреляции Пирсона.

• По меньшей мере, одна из двух переменных имеет порядковую шкалу, либо с интервальной шкалой, но не нормально распределённой – ранговая корреляция по Спирману или
  τ (тау-грого-соая) Кендала (реже).

• Одна из двух переменных является дихотомической – точечная двухрядная корреляция. Эта возможность в SPSS отсутствует. Вместо этого может быть применён расчёт ранговой корреляции по Спирману.

• Обе переменные являются дихотомическими – четырёхполевая корреляция. Данный вид корреляции рассчитываются в SPSS на основании определения мер расстояния и мер сходства (см. гл 15.4).

Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, кода связь между ними линейна (однонаправлена).
Если связь, к примеру, U-образная (неоднозначная), то коэффициент корреляции непригоден для использования в качестве меры силы связи: его значение стремится к нулю.
В следующих разделах будут рассмотрены корреляции по Пирсону, Спирману и Кендалу. Ешё один раздел специально посвящён частной корреляции.

Задание 2.4.

Произвести анализ
зависимости объема продаж товара от
затрат на рекламу данного товара. Данные
приведены в табл. 2.4.1.

Таблица 2.4.1

Затраты на рекламу, тыс. руб.	110	113	115	116	221	226	332	333	339	442
Объемы продаж, тыс. руб.	410	415	410	425	439	460	485	473	489	491

Выполнение.

В начале работы
создадим файл с данными как показано
на рис. 2.4.1.

Рис. 2.4.1. Фрагмент
файла данных

В пакете SPSS
для корреляционного анализа есть раздел
«Корреляция в меню. Анализ».

Для более наглядного
представления имеющихся данных построим
график зависимости «Затраты на рекламу
– объем продаж» в виде диаграммы
рассеяния.

• Выберем в меню
  Graphs
  (Визуализация) Scatter–Dot
  (Разброс/точка), откроется диалоговое
  окно Scatter–Dot
  (Разброс/точка) (рис. 2.4.2).

Рис. 2.4.2. Диалоговое
окно Scatter–Dot
(Разброс/точка)

• В диалоговом окне
  Scatter–Dot
  (Разброс/точка) щёлкнем на области
  Simple Scatter
  (Простой разброс).

• Щелчком по
  выключателю Define
  (Определить) откроем соответствующее
  диалоговое окно (рис. 2.4.3).

• Отобразим объем
  продаж в зависимости от затрат на
  рекламу, поэтому переменную объемы_продаж
  из списка исходных переменных перенесем
  в поле оси Y,
  а переменную затраты_на_рекламу
  – в поле оси X.
  И начнем построение диаграммы щелчком
  на ОК.

Результатом
выполнения вышеуказанных команд будет
следующий график (рис. 2.4.4).

Рис. 2.4.3. Вид окна
Simple Scatterplot
(Простой график рассеяния).

Рис. 2.4.4. Простой
график рассеивания

Теперь определим
основные корреляционные показатели.

Для этого в меню
Анализ выбираем Корреляция – Двумерный.

Далее появится
диалоговое окно (рис. 2.4.5).

Рис. 2.4.5. Диалоговое
окно «Двумерная корреляция»

Далее получаем
следующий вывод (рис.2.4.6).

Регрессионный
анализ служит для определения вида
связи между переменными и дает возможность
для прогнозирования значения одной
(зависимой) переменной отталкиваясь от
значения другой (независимой) переменной.

В пакете SPSS
для этой цели имеется раздел Regression
(Регрессия) (меню Analyze
(Анализ)), который предоставляет
пользователю широкий набор процедур
регрессионного анализа.

Каждая процедура
имеет модель регрессии, которая соотносит
зависимую переменную с независимой
переменной (или множеством независимых
переменных).

Простая линейная
регрессия лучше всего подходит для
того, чтобы продемонстрировать
основополагающие принципы регрессионного
анализа.

По виду получившейся
диаграммы рассеяния можно предположить
о наличии линейной зависимости между
исследуемыми показателями.

Описательные
статистики

	Среднее	Стд. отклонение	N
затраты_на_рекламу	24,7000	11,37297	10
объем_продаж	450,6000	32,63332	10

Корреляции(a)

		затраты_на_рекламу	объем_продаж
затраты_на_рекламу	Корреляция Пирсона	1	,983(**)
	Знч.(1–сторон)		,000
объем_продаж	Корреляция Пирсона	,983(**)	1
	Знч.(1–сторон)	,000

**
Корреляция значима на уровне 0.01
(1–сторон.).

a Искл. целиком
N=10

Корреляции(a)

		затраты_на_рекламу	объем_ продаж
тау–b Кендалла	затраты_на_рекламу	Коэффициент корреляции	1,000	,956(**)
		Знч. (1–сторон)	.	,000
	объем_продаж	Коэффициент корреляции	,956(**)	1,000
		Знч. (1–сторон)	,000	.
ро Спирмена	затраты_на_рекламу	Коэффициент корреляции	1,000	,988(**)
		Знч. (1–сторон)	.	,000
	объем_продаж	Коэффициент корреляции	,988(**)	1,000
		Знч. (1–сторон)	,000	.

**
Корреляция значима на уровне 0.01
(1–сторонняя).

a Искл. целиком N
= 10

Рис.
2.4.6. Вывод корреляций

Перейдем к построению
регрессионной зависимости между
показателями.

• Выберем в меню
  Analyze
  (Анализ) Regression
  (Регрессия) Linear
  (Линейная). Появится диалоговое окно
  Linear Regression
  (Линейная регрессия) (рис. 2.4.7).

Рис. 2.4.7. Вид
диалогового окна Linear
Regression
(Линейная регрессия)

• Перенесем переменную
  объемы_продаж
  в поле для зависимых переменных и
  присвоим переменной затраты_на_рекламу
  статус независимой переменной.

• Ничего больше не
  меняя, начните расчёт нажатием ОК.

Вывод основных
результатов выглядит следующим образом
(рис. 2.4.8).

Во второй таблице
дается заключение о соответствии модели
исходным данным, а именно приводится
коэффициент детерминации, который
характеризует качество получившейся
модели.

В третьей таблице
приведены величины, которые отражают
два источника дисперсии: дисперсию,
которая описывается уравнением регрессии
(сумма квадратов, обусловленная
регрессией) и дисперсию, которая не
учитывается при записи уравнения
(остаточная сумма квадратов). Также
приведено значение F–критерия
Фишера.

В последней таблице
выводятся коэффициент регрессии b
и смещение по оси ординат а
под именем «константа».

То есть, уравнение
регрессии выглядит следующим образом:

,

где
показатель «Объемы продаж»,показатель «Затраты на рекламу».

Включенные/исключенные
переменные(b)

Модель	Включенные переменные	Исключенные переменные	Метод
1	затраты_на_рекламу(a)	.	Принудительное включение

a Включены все
запрошенные переменные

b Зависимая
переменная: объем_продаж

Сводка для модели

Модель	R	R квадрат	Скорректированный R квадрат	Стд. ошибка оценки
1	,983(a)	,966	,962	6,39137

a Предикторы:
(константа) затраты_на_рекламу

Дисперсионный
анализ (b)

Модель		Сумма квадратов	ст.св.	Средний квадрат	F	Знч.
1	Регрессия	9257,603	1	9257,603	226,627	,000(a)
	Остаток	326,797	8	40,850
	Итого	9584,400	9

a Предикторы:
(константа) затраты_на_рекламу

b Зависимая
переменная: объем_продаж

Коэффициенты(a)

Модель	Нестандартизованные коэффициенты	Станд. коэфф.	t	Знч.
	B	Стд. ошибка	Бета
1	(Константа)	380,945	5,049		75,448	,000
	затраты_на_рекламу	2,820	,187	,983	15,054	,000

a Зависимая
переменная: объем_продаж

Рис. 2.4.8. Результат
выполнения процедуры Analyze
– Regression
– Linear

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Получена: 11 января 2017 / Принята: 2 февраля 2017 / Опубликована online: 28 февраля 2017 УДК 614.2 + 303.4

КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ДАННЫХ С ИСПОЛЬЗОВАНИЕМ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ

STATISTICA И SPSS

Андрей М. Гржибовский 1-4, http://orcid.org/0000-0002-5464-0498, Сергей В. Иванов 5, http://orcid.org/0000-0003-0254-3941 Мария А. Горбатова 2, http://orcid.org/0000-0002-6363-9595

1 Национальный Институт Общественного Здравоохранения, г. Осло, Норвегия;

2 Северный Государственный Медицинский Университет, г. Архангельск, Россия;

3 Международный Казахско-Турецкий Университет им. Х.А. Ясави, г. Туркестан, Казахстан;

4 Северо-Восточный Федеральный Университет, г. Якутск, Россия;

5 “Первый Санкт-Петербургский государственный медицинский университет им. акад. И.П. Павлова”, г. Санкт-Петербург, Россия.

Резюме

В настоящей работе представлены общие сведения о выполнении корреляционного анализа данных с использованием параметрических и непараметрических методов. Приведены алгоритмы расчета коэффициентов корреляции Пирсона, Спирмена и Кендалла с использованием программного обеспечения Statistica 10 и SPSS 20 и интерпретация полученных результатов анализа. Настоящая статья призвана дать общие сведения о корреляционном анализе, и не заменяет прочтения специализированной литературы по статистике и клинической эпидемиологии.

Ключевые слова: Statistica, SPSS, корреляционный анализ, коэффициент корреляции Пирсона, коэффициент корреляции Спирмена, коэффициент корреляции Кендалла.

Abstract

CORRELATION ANALYSIS OF DATA USING STATISTICA AND SPSS SOFTWARE

Andrej M. Grjibovski 1-4, http://orcid.org/0000-0002-5464-0498, Sergej V. Ivanov 5, http://orcid.org/0000-0003-0254-3941 Maria A. Gorbatova 2, http://orcid.org/0000-0002-6363-9595

1 Norwegian Institute of Public Health, Oslo, Norway;

2 Northern State Medical University, Arkhangelsk, Russia;

3 International Kazakh-Turkish University, Turkestan, Kazakhstan;

4 North-Eastern Federal University, Yakutsk, Russia;

5 Pavlov First Saint Petersburg State Medical University, St. Petersburg, Russia.

In this paper we present the main principles of correlation analysis using parametric and non-parametric methods. Algorithms for calculations of Pearson’s, Spearmen’s and Kendall’s coefficients using Statistica 10 and SPSS 20 software are presented. Special emphasis is given to interpretation of results of statistical analysis. The article complements, but does not substitute specialized literature on biostatistics and clinical epidemiology.

Keywords: Statistica, SPSS, correlation analysis, Pearson’s correlation coefficient, Spearmen’s correlation coefficient, Kendall’s correlation coefficient.

Туйшдеме

STATISTICA 10 ЖЭНЕ SPSS 20 БАГДАРЛАМАЛЫК КАМСЫНДАНДЫРУДЫ КОЛДАНУМЕН КОРРЕЛЯЦИЯЛЫК

МЭЛ1МЕТТЕРД1 ТАЛДАУ

Андрей М. Гржибовский 1-4, http://orcid.org/0000-0002-5464-0498, Сергей В. Иванов 5, http://orcid.org/0000-0003-0254-3941 Мария А. Горбатова 2, http://orcid.org/0000-0002-6363-9595

1 Когамдьщ Денсаулык сактау ¥лттык Институты, Осло к., Норвегия;

2 СолтYCтiк Мемлекетлк Медициналык Университетi, Архангельск к., Ресей;

3 Х.А. Ясави ат. Халыкаралык Казак – ТYрiк Университетi, Туркестан, Казакстан;

4 СолтYCтiк – Шыгыс Федералдык Университетi, Якутск к-, Ресей;

5 Академик И.П. Павлов атынд. бiрiншi Санкт-Петербург мемлекеттiк медициналык университетi, Санкт-Петербург к-, Ресей.

Осы жумыста nараметрлiк жэне параметрлiк емес эдiстердi колданумен корреляциялык; талдау мэлiметтерiн орындау туралы жалпы мэлiметтер усынылды.Statistica 10 жэне SPSS 20 багдарламалыккамсындандырудыколданумен Пирсонныц, Спирменныц жэне Кендаллдыц корреляциялары коэфициенттерш есептеу алгоритмдерi жэне алынган талдау нэтижелерi интерпретациясы келтiрiлген. Осы макала корреляциялык; мэлiметтердi талдау туралы жалпы мэлiметтер беруге талап етiлген жэне статистика жэне клиникалык; эпидемиология бойынша мамандандырылган эдебиеттi окудыц орнын толтырмайды.

Нег’]зг’] свздер: Statistica, SPSS, корреляциялык; талдау, Пирсонныц корреляциясы коэффициентi, Спирменныц корреляциясы коэффициентi, Кендаллдыц корреляциясы коэффициент

Библиографическая ссылка:

Гржибовский А.М., Иванов С.В., Горбатова М.А. Корреляционный анализ данных с использованием программного обеспечения Statistica и SPSS / / Наука и Здравоохранение. 2017. №1. С. 7-36.

Grjibovski A.M., Ivanov S.V., Gorbatova M.A. Correlation analysis of data using Statistica and SPSS software. Nauka i Zdravookhranenie [Science & Healthcare]. 2017, 1, pp. 7-36.

Гржибовский А.М., Иванов С.В., Горбатова М.А. Statistica жэне SPSS багдарламалы; камсындандыруды колданумен корреляциялык мэлiметтердi талдау / / Гылым жэне Денсаулык сактау. 2017. №1. Б. 7-36.

Настоящая статья продолжает серию публикаций, посвященных статистическому анализу данных биомедицинских исследований [9, 13, 14, 15, 16, 17].

Статистическая обработка данных является завершающим этапом исследования, но никакой статистический анализ не может «исправить» некорректно организованное исследование и неправильно собранные данные. Именно поэтому авторы настоящей статьи настоятельно рекомендуют читателю ознакомиться с литературой по эпидемиологии [32, 23, 35], а также с практическими аспектами организации и анализа результатов

различных типов научных исследований в здравоохранении (одномоментных, когортных, экологических, экспериментальных

исследований и «случай-контроль»), которые представлены в статьях, опубликованных в 2015 году в журнале «Наука и Здравоохранение» [10, 11, 12, 18, 19].

Высокое качество статистического анализа является обязательным условием востребованности результатов исследований международным научным сообществом [27, 1], поэтому задачами настоящей серии статей является формирование у начинающего исследователя базисных представлений о

статистической обработке данных, приобретение практического опыта работы с современными статистическими пакетами программ и предупреждение типичных ошибок, возникающих в процессе анализа результатов исследования.

Данная статья посвящена

корреляционному анализу данных с использованием программного обеспечения Statistica 10 и SPSS 20.

В процессе изучения различных явлений часто возникает необходимость оценить тесноту (силу) связи между ними. Цель корреляционного анализа – количественная оценка силы и направления взаимосвязи между явлениями.

Термин «корреляция» был впервые введен Ж.Кювье и 1806 году, и только в 1886 г. Ф. Гальтоном он впервые был применен к результатам биомедицинских исследований [24].

По направлению корреляционная связь может быть прямой (положительной), когда увеличение или уменьшение значения одного признака приводит, соответственно, к увеличению или уменьшению значения другого признака, или обратной (отрицательной), когда увеличение значения одного признака приводит к уменьшению значения другого и наоборот.

Например, между степенью бактериального загрязнения воды и количеством кишечных инфекций у проживающего на загрязненной территории может быть обнаружена прямая корреляционная связь, а между уровнем финансирования здравоохранения и смертностью населения от различных заболеваний – обратная корреляционная связь

По характеру связь может быть не только корреляционной, но и функциональной, когда каждому значению одного признака соответствует точное значение другого (например, функциональная связь между массой тела и индексом массы тела).

Исследователь должен ясно понимать, что в результате корреляционного анализа невозможно установить причинно-следственные связи между явлениями, поэтому выводы о влиянии одного явления на другое на основании одного лишь корреляционного анализа данных будут неправомерными. Не допускается подмена понятия причинно-следственной связи корреляционной связью. Юмористическим примером такого заблуждения служит обнаружение сильной положительной корреляционной взаимосвязи между количеством гнезд аистов и количеством новорожденных в Копенгагене в послевоенные годы, как доказательство того, что детей приносят аисты [35].

Для количественной оценки

корреляционной связи используются различные коэффициенты корреляции, имеющие разные способы расчета, однако наиболее популярными являются следующие три [7, 32, 5]:

1. Коэффициент корреляции Пирсона (Pearson) r – параметрический.

2. Коэффициент корреляции Спирмена (Spearman) rs – непараметрический.

3. Коэффициенты корреляции Кендалла (Kendall) Ta и ть – непараметрические.

Все коэффициенты корреляции могут принимать значение от 0 до 1 или от -1 до 0.

Оценка силы корреляционной связи проводится в соответствии с таблицей 1.

Количественные критерии оценки силы и направления корреляционной связи.

Таблица 1.

Сила связи Значения коэффициента корреляции

Прямая (+) Обратная (-)

Отсутствует 0,0 0,0

Слабая от 0,01 до 0,29 от -0,01 до -0,29

Средняя от 0,30 до 0,69 от -0,30 до -0,69

Сильная от 0,70 до 0,99 от -0,70 до -0,99

Полная (функциональная) 1,0 -1,0

Использование коэффициент корреляции обоснованно, поэтому следует указать Пирсона встречается в биомедицинских условия его применения [7, 32]: исследованиях наиболее широко, и не всегда

1. Обе переменные должны быть количественными и непрерывными.

2. Как минимум один из изучаемых признаков, а лучше оба, должны иметь распределение, близкое к нормальному.

3. Зависимость между переменными должна носить линейный характер.

4. Вариабельность одной переменной не должна зависеть от значения другой переменной, то есть разброс значений одной из переменных должен быть примерно одинаковым для всех значений другой переменной (так называемая «гомоскедастичность»).

5. Наблюдения должны быть независимы друг от друга.

6. Наблюдения должны быть парными (значение обоих анализируемых параметров

регистрируются одновременно у одного и того же объекта исследования).

7. Объем выборки должен составлять не менее 25 наблюдений [39].

Графически зависимость между переменными можно представить в виде скаттерограммы. Из представленных на рисунке 1 скаттерограмм коэффициент корреляции Пирсона можно рассчитать только для первого случая, когда наблюдается линейная зависимость между переменными и скаттерограмма гомоскедастична (для остальных двух случаев коэффициент корреляции Пирсона не может быть рассчитан вследствие несоблюдения условия гомоскедастичности и наличия нелинейной зависимости между переменными).

о . ■к-“0

Jjfc

/ЦйЩ&

Линейная зависимость (гомоскедастичность)

Линейная зависимость (гетероскедастичность)

Рис. 1. Примеры скаттерограмм.

Нелинейная зависимость

Коэффициент корреляции Пирсона для двух переменных (X и У) рассчитывается следующим образом:

1. Значения переменных X и Y располагают в ряд, в котором каждой величине X соответствует определенная величина Y.

2. Рассчитывают средние арифметические значения для каждой переменной Хф и Уф соответственно.

Sx = V(

3. Рассчитывают отклонения каждого значения X и Y от соответствующей средней величины.

4. Отклонения для X и Y перемножают между собой.

5. Рассчитывают стандартные отклонения для X и Y (Эх и Бу) по формулам:

(Xi – Хср)2 + (X2 – Хср)2

: + +

(X, – Хср)2

n – 1

Sy = V(

(Yi – Yep)2 + (Y2 – Yep)2 + … + (Y, – Yep)2 n – 1

)

6. Рассчитывают коэффициент корреляции Пирсона по формуле (п – количество наблюдений):

(Х1 – Хср) X – Уср) + (Х2 – Хср) X ^2 – Уср) + … + (X, – Хср) х (У, – Уср)

(п – 1) X Sx х Sy

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

)

7. Сравнивают полученное значение коэффициента Пирсона с критическим значением, взятым из специальных таблиц [30, 24, 5]. В случае, если расчетное значение г равно или превышает критическое значение для уровня статистической значимости, равного 0,05, то нулевую статистическую гипотезу отвергают и делают вывод о том, что коэффициент корреляции Пирсона статистически значимо отличается от нуля (р < 0,05).

Интерпретация коэффициента корреляции Пирсона включает следующие этапы:

1. Оценка статистической значимости коэффициента корреляции. Если р < 0,05, то коэффициента корреляции статистически значимо отличается от нуля. Если р > 0,05, то делается вывод об отсутствии корреляционной связи между анализируемыми признаками.

2. Оценка силы и направления корреляционной связи (таблица 1).

3. Оценка степени влияния одного признака на другой. Для понимания степени

100%

«тесноты» связи между признаками используется коэффициент детерминации, который рассчитывается как коэффициент корреляции, возведенный в квадрат (г2). Коэффициент детерминации показывает, какую долю вариабельности одного из признаков способно объяснить изменение другого признака. Зависимость значения детерминации коэффициента от коэффициента корреляции представлена на рисунке 2. Из представленного графика видно, что слабая корреляционная связь может объяснить не более 8,4% вариабельности признака, обусловленной влиянием другого признака, а связь средней силы – не более 47,6% вариабельности. Таким образом, коэффициент детерминации необходимо использовать для адекватного понимания фактической «тесноты» взаимосвязи между признаками, что особенно важно на этапе практических выводов по итогам анализа данных (например, при оценке клинической роли выявленной корреляционной связи).

X X

«и

I и к л

ю о

пГ

т о

а го с т о 5

1_ А

0 а. х с

1 £

О 1

л с; Ф ю го

а.

го ш

о: §

90%

70%

60%

40%

10%

0%

Сильная связь

Связь средней

силы

Слаба^связ!»^^

од 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 Значение коэффициента корреляции Пирсона

Рис. 2. Зависимость значения коэффициента детерминации от значения коэффициента корреляции.

Существует важное обстоятельство, интерпретации результатов корреляционного которое необходимо учитывать в процессе анализа: выявленные взаимосвязи между

двумя признаками могут быть обусловлены влиянием некоего третьего фактора. Например, известно, что вероятность рождения ребенка с синдромом Дауна тесно коррелирует с количеством родов у матери до момента настоящей беременности. Но это вовсе не значит, что количество предшествующих родов влияет на риск рождения больного ребенка, так как в данном случае имеется третий фактор, который связан с обеими переменными – возраст женщины. Поэтому между вероятностью рождения ребенка с синдромом Дауна имеется корреляционная, но ни в коем случае не причинно-следственная связь [7].

Следует отметить существенный недостаток коэффициента корреляции Пирсона – высокую чувствительность к наличию «выскакивающих» величин (выбросов). Даже небольшое количество

выбросов может значительно исказить значение коэффициента и буквально «уничтожить» зависимость между величинами, поэтому всегда следует анализировать выбросы и выяснять, не является ли они следствием ошибки регистрации данных.

Приведем для примера гипотетическое исследование, целью которого является оценка корреляционной связи между уровнем Ю респондента и временем, затраченным на решение типовой логической задачи (всего были протестированы 10 респондентов). Следует отметить, что для корреляционного анализа необходимо наличие не менее 25 наблюдений, но в данном примере приведены только 10 наблюдений для уменьшения трудоемкости расчетов вручную.

В таблице 2 представлены результаты наблюдений и расчет промежуточных значений, необходимых для вычисления значения г.

Таблица 2.

Продолжительность решения логической задачи респондентами с различным значением !0 и результаты промежуточных расчетов

№ X (уровень IQ, ед.) У (время на решение задачи, сек.) Для расчета г Для расчета Sx и Sy

Xi – Хср Yi – Yep (Xi – Хср) х (Yi – Yep) (X – Хср)2 (Yi – Yсp)2

1 140 235 16 -43,4 -694,4 256,0 1883,6

2 112 158 -12 33,6 -403,2 144,0 1129,0

3 124 185 0 6,6 0 0,0 43,6

4 130 219 6 -27,4 -164,4 36,0 750,8

5 128 215 4 -23,4 -93,6 16,0 547,6

6 121 176 -3 15,6 -46,8 9,0 243,4

7 115 167 -9 24,6 -221,4 81,0 605,2

8 127 209 3 -17,4 -52,2 9,0 302,8

9 117 165 -7 26,6 -186,2 49,0 707,6

10 126 187 2 4,6 9,2 4,0 21,2

Сумма -1853 604 6234,4

Согласно расчетам, Хср = 124,0 ед., Уср =191,6 сек., Эх = 8,2 ед., Бу = 26,3 сек.

Соответственно, рассчитываем значение г: -1853

r =

(10 – 1) х 8,2 х 26,3

– 0,95

Из таблицы критических значений критерия корреляции Пирсона для п = 10 и уровня статистической значимости 0,01 критическое значение г составляет 0,765 [30, 5, 24]. Так как расчетное значение больше критического, выявленная взаимосвязь между уровнем Ю и

длительностью решения типовой логической задачи является статистически значимой (р < 0,01).

В данном примере г = -0,95, что свидетельствует об обратной сильной зависимости: чем выше уровень Ю, тем меньше время, затрачиваемое на решение типовой логической задачи.

Значение коэффициента детерминации (г2 = 0,952 = 0,90) говорит о том, что 90%

вариабельности длительности решения типовой логической задачи обусловлены уровнем IQ (интеллектуального коэффициента) респондента (и 10% вариабельности обусловлены иными факторами).

Также следует рассчитать доверительный интервал (англ. CI – «confidence interval») для коэффициента корреляции Пирсона, так как

ZL = 0,5 • lnl

1 + г

1,96

—

1-r) Vn- 3

интервальная оценка любого генерального параметра всегда более информативна, чем точечная. Доверительные интервалы для коэффициента корреляции Пирсона можно рассчитать, с использованием z-преобразование Фишера. Нижняя (Zl) и верхняя (Zu) границы преобразованного 95% доверительного интервала для коэффициента корреляции Пирсона рассчитываются по формулам:

у 1 Г1 +r V 1,96 и Z^ = 0,5 • lnl-1+ -,

U – r) vn-з

где 1п обозначает натуральный логарифм, а п – объем выборки. Само же значение коэффициента корреляции для генеральной совокупности, рассчитанное по данным выборки, будет в 95% случаев находиться в интервале

от

где ехр(2г) рассчитывается как е22 (где е логарифма, оно примерно равно 2,72).

В нашем примере коэффициент корреляции Пирсона для взаимосвязи между Ю респондента и продолжительностью решения задачи был равен -0,95 и статистически значимо отличался от нуля (р < 0,01). Рассчитаем сначала ZL и Zu: ZL = -2,57, Zu = -1,09. Далее:

Ехр^) = 2,72 2 х (-257) = 0,0058 Ехр^и) = 2,72 2 х (-109) = 0,1128 Соответственно, ц = -0,99, ги = -0,80.

Таким образом, мы можем записать результаты корреляционного анализа, учитывающие доверительный интервал: г = -0,95 (95% С1 -0,99; -0,80), п = 10, р < 0,01.

Доверительный интервал для коэффициента корреляции Пирсона можно рассчитать и с помощью онлайн калькулятора расположенного по адресу:

http://faculty.vassar.edu/lowry/rho.html. Данный калькулятор использует те же формулы, которые были приведены выше, но требует использовать при внесении коэффициента корреляции в поле «г» не запятую, а точку (например, «-0.95» вместо «-0,95»).

В случае, если условия применения коэффициента корреляции Пирсона не выполняются, для корреляционного анализа следует использовать непараметрические

до

– число Эйлера, или основание натурального

коэффициенты корреляции Спирмена или Кендалла, расчет которых основан на использовании не исходных значений признаков, а их рангов [7, 2, 22]. Если в подобной ситуации применять коэффициент корреляции Пирсона, полученные результаты будут искаженными, а выводы -сомнительными.

Преимуществами непараметрических коэффициентов корреляции по сравнению с коэффициентом корреляции Пирсона является возможность оценки связи между порядковыми и количественными признаками (коэффициент корреляции Спирмена) или только между порядковыми признаками (коэффициент корреляции Кендалла).

Коэффициент корреляции Спирмена для переменных Х и У рассчитывается следующим образом:

1. Два ряда из парных сопоставляемых признаков составляются рядом, первый обозначается как Х, второй – как У.

2. Первый ряд признака ранжируется в убывающем или возрастающем порядке, а числовые значения второго ряда размещаются напротив того значения первого ряда, которым они соответствуют.

3. Значения первой и второй переменных заменяют порядковым номером (рангом) числовым значениям второго признака ранги

должны присваиваться в том же порядке, какой был принят при раздаче их величинам первого признака. При одинаковых величинах признака в ряду ранги следует определять как среднее число из суммы порядковых номеров этих величин.

4. Определяют разности рангов между ранговыми номерами Х| и

5. Проводят расчет коэффициента корреляции Спирмена по формуле (где п -число сравниваемых пар):

6 х (^2 + d22 + dз2 + … +

rs = 1

n3 – n

6. Для оценки статистической значимости выявленной взаимосвязи между переменными расчетное значение коэффициента Спирмена сравнивают с критическим значением, взятым из таблицы [30, 5, 24]. Если расчетное значение ^ равно или превышает критическое значение, равное 0,05, то нулевая гипотеза отвергается и делается вывод о том, что коэффициент корреляции статистически значимо отличается от нуля (р < 0,05).

7. Для коэффициента корреляции Спирмена также можно рассчитать

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

коэффициент детерминации (гб2), но он будет означать долю вариабельности рангов одной переменной, которую можно объяснить с помощью рангов другой переменной. Данная интерпретация достаточно громоздка и не совсем понятна, поэтому целесообразность использования коэффициента детерминации гб2 в приложении к практической интерпретации результатов корреляционного анализа сомнительна.

8. Приведем для примера гипотетическое исследование, целью которого является оценка корреляционной связи между функциональным классом (ФК) сердечной недостаточности (СН) пациента и количеством приступов стенокардии, возникающих у него в течение месяца. Всего были обследованы 11 пациентов, имеющих !-!У ФК СН.

9. ФК СН является ранговой переменной, а количество приступов стенокардии -дискретной количественной переменной.

10. В таблице 2 представлены результаты наблюдений и расчет промежуточных значений, необходимых для вычисления значения гб.

Количество приступов стенокардии у пациентов с различными ФК СН.

Таблица 3.

№ пациента ФК СН (переменная X) Количество приступов стенокардии в месяц (переменная У) Ранг X Ранг Y Разность рангов d2

1 3 2,5 2,5 0 0 1

1 3 2,5 2,5 0 0 1

1 4 2,5 8,5 6 36 1

1 4 2,5 8,5 6 36 1

2 4 6 8,5 2,5 6,25 2

2 3 6 2,5 -3,5 12,25 2

2 3 6 2,5 -3,5 12,25 2

3 4 9 8,5 -0,5 0,25 3

3 6 9 14 5 25 3

3 4 9 8,5 -0,5 0,25 3

4 4 12,5 8,5 -4 16 4

4 4 12,5 8,5 -4 16 4

4 5 12,5 13 0,5 0,25 4

Сумма: 176,5

Согласно формуле расчета коэффициента корреляции Спирмена

6 х 176,5

rs = 1 –

143 – 14

= 0,61

Из таблицы критических значений критерия корреляции Спирмена для п = 14 и уровня статистической значимости 0,05 критическое значение Гб составляет 0,532 [29, 5, 24]. Так как расчетное значение больше критического,

выявленная взаимосвязь между ФК СН и количеством приступов стенокардии в течение месяца является статистически значимой (р < 0,05).

Рассчитать доверительные интервалы для ^ можно с использованием уже известного

преобразования [37, 7]. Формулы для расчета ZL и Zu для 95% доверительного интервала для коэффициента корреляции Спирмена будут следующими:

(

ZL = 0,5 • ln

1_ + р)_ 1,96 •д/1 + 0,5 •р2

1 -р)

-Jn — з

Zy = 0,5 • ln

1+рУ 1,96 •J 1 + 0,5 •р2

1 -р)

-Jn — 3

где р – рассчитанное значение коэффициента корреляции Спирмена.

Далее полученные следует подставить в

от

значения Zl и Zu уже упоминавшуюся

exp(2zj – 1

exp(2zj + 1

rL =

Приведенная формула, по мнению D. Bonnett и T. Wright [36], является наиболее адекватной для расчета доверительного интервала для коэффициента корреляции Спирмена.

Рассчитаем значения для нижней и верхней границ 95% доверительного интервала коэффициента корреляции Спирмена, равного 0,61: Zl = 0,069, Zu = 1,349. Далее:

EXP(2Zl) = 2,72 2 * (0069) = 1,15 Exp(2Zu) = 2,72 2 * (1349) = 14,86 Соответственно, rsL = 0,07, rsu = 0,87. Таким образом, мы можем записать результаты корреляционного анализа, учитывающие доверительный интервал: rs = 0,61 (95% CI 0,07; 0,87), n = 14, р < 0,05. Следует обратить внимание на значительную ширину 95% доверительного интервала – от 0,07 (практически полное отсутствие связи) до 0,87 (сильная связь). Данный факт связан с небольшим количеством наблюдений в выборке. Например, если бы данное значение коэффициента корреляции Спирмена было бы получено на основании 28 наблюдений, то 95% доверительный интервал располагался бы в пределах от 0,28 до 0,81, а если бы расчеты проводились на основании 140 наблюдений, то границы сузились бы до значений от 0,48 до 0,71. В нашем примере большая широта доверительного интервала не позволяет делать каких-либо клинически значимых выводов о наличии корреляционной

ранее формулу для расчета верхней и нижней границ 95% доверительного интервала:

до ги

ехр(2ги) – 1 ехр(2ги) + 1

связи между ФК СН и количеством приступов стенокардии, и требует увеличения количества наблюдений в исследовании для того, чтобы выводы приобрели достаточную степень определенности.

Таким образом, приведенный пример наглядно продемонстрировал, как важно использовать интервальную, а не точечную оценку коэффициентов корреляции, так как точечная оценка «скрадывает» информацию, которая может оказаться крайне важной с клинической точки зрения.

Третьим рассматриваемым в настоящей статье коэффициентом корреляции является непараметрический коэффициент корреляции Кендалла. Существуют 3 его разновидности –

Та, Ть и Ть

Рассмотрим наиболее простой вариант коэффициента корреляции Кендалла – Та. Допустим, речь идет о двух участниках исследования i и j, у которых в ходе исследования изучаются признаки X и Y. Изучаемыми признаками могут, например, быть рост и масса тела, индекс массы тела и артериальное давление, и др. Пару наблюдений можно обозначить как X,, У, и X], У].

Если разности Х] – Х, и ^ – У, будут одинаковы по знаку (либо X] > X и Yj > Yi, либо X] < X и ^ < Yi), то пару называют конкордантной (например, и рост, и вес участника , больше, чем рост и вес участника ]). Количество конкордантных пар (или проверсий) обозначается как С.

Если разности X] – Х, и ^ – У, различаются по знаку (либо X] > Х, и ^ < У,, либо X] < Х, и ^

> У|), то такая пара называется дискордантной (например, рост участника I больше роста участника ], а вес участника I меньше роста участника ]). Количество дискордантных пар (или инверсий) обозначается как D. Если выборка состоит из п участников исследования, то возможно формирование п х (п – 1) / 2 пар, для которых 1 < i < j < п.

Коэффициент корреляции Кендалла Та рассчитывается по формуле [7, 40, 41]:

т =

2 ■ (C – D) n ■ (n -1)

Недостатком Та является то, что он не учитывает одинаковых (связанных, равных) рангов (англ. «ties»), которые возникают в тех случаях, когда у нескольких участников исследования изучаемый признак имеет одно и то же значение (например, одинаковый рост, или одинаковая стадия заболевания). Из формулы видно, что максимально возможное значение Та = 1 достигается только в том случае, если все пары являются конкордантными. Соотвественно, если все пары являются дискордантными, Та принимает минимально возможное значение -1. Если количество конкордантных и дискордантных пар равно, то Та = 0, что говорит об отсутствии взаимосвязи между изучаемыми признаками.

Если С представляет собой количество конкордантных пар из возможных в выборочной совокупности n х (n – 1) / 2 пар, то оценить вероятность того, что пара наблюдений будет конкордантной (п с), можно с помощью формулы:

2 ■ C

n ■ (n -1)

Аналогично, вероятность того, что пара наблюдений будет дискордантной (пс), можно оценить с помощью формулы:

2 • Б

n ■ (n -1)

Таким образом, для любой пары наблюдений, отобранных случайно, коэффициент корреляции Кендалла Та может интерпретироваться как разность между вероятностью того, что пара окажется конкордантной, и того, что она окажется дискордантной, то есть

Ta = КС -ЖА

Отрицательное значение Та будет говорить о том, что вероятность того, что любая случайно отобранная пара наблюдений с характеристиками (Х|, У| и X], У]) будет скорее дискордантной, чем конкордантной, и наоборот.

Кроме того, в генеральной совокупности, для которой коэффициент корреляции Кендалла равен Та, вероятность того, что любая случайно отобранная пара наблюдений с характеристиками (Х|, У| и X], У]) окажется конкордантной, будет в (1 + Та) / (1 – Та) раза выше, чем вероятность того, что эта пара будет дискордантной. Таким образом, если в исследовании с использованием случайно отобранной репрезентативной выборки был получен коэффициент корреляции Кендалла Та = 0,5, это означает, что вероятность того, что любая случайно отобранная из генеральной совокупности пара окажется конкордантной, в среднем в (1 + 0,5) / (1 – 0,5) = 3 раза выше, чем вероятность того, что эта пара будет дискордантной.

Коэффициент корреляции Кендалла Та отличается от ть тем, что учитывает связанные ранги. Появление связанных рангов, то есть, когда два или более наблюдений по любой из переменных имеют одинаковые ранги, неизбежно при изучении порядковых признаков, таких как, например, стадия заболевания, степень тяжести, уровень образования и других, имеющее ограниченное количество значений (например, использование 3-х степеней тяжести заболевания).

В целом, использование коэффициентов корреляции Кендалла предпочтительно при анализе корреляционной связи между порядковыми (ординальными) переменными. Например, коэффициент корреляции ть рекомендован для анализа связи между порядковыми признаками, которые проще всего представить в виде многопольных таблиц, у которых число рядов равно числу столбцов.

Коэффициент корреляции Кендалла Тс используется при расчете связи между порядковыми переменными, формирующими таблицу, в которой количество рядов и количество столбцов не равны (например, оценка корреляционной связи между порядковой переменной X, имеющей 5 наименований, и другой порядковой переменной У, имеющей 3 наименования).

=

=

В данной статье подробный алгоритм расчета коэффициентов корреляции Кендалла на примерах не приводится по причине трудоемкости их ручного вычисления.

Более подробно с различными коэффициентами корреляции Кендалла можно познакомиться в [7, 6].

В статистическом программном обеспечении в рамках корреляционного анализа как правило производится расчет коэффициента корреляции Кендалла Ть.

‘1+ И 1,96 -д/ 0,437

Большой практический интерес представляет расчет доверительного интервала для Ть, который также можно рассчитать с помощью преобразования Фишера, которое дает достаточно адекватную интервальную оценку коэффициента корреляции Кендалла для генеральной совокупности при объеме выборки не менее 10 наблюдений и значении Т не более 0,8. Отличие будет заключаться в расчете вспомогательных значений ZL и Zu:

^ = 0,5 – 1п|

— –

1 -г.

л/и – 4

^ = 0,5 – 1п|

1+ И 1,96 -д/ 0,437

1 -г.

+

л/и – 4

Значения ZL и Zu которые затем подставляют в уже известную формулу для расчета 95% доверительного интервала:

от

В завершении теоретической части настоящей статьи следует отметить, что корреляционный анализ встречается в русскоязычной научной периодике очень часто, поэтому целесообразно остановиться на основных ошибках его использования:

– Применение параметрического коэффициента корреляции Пирсона при несоблюдении необходимых условий его использования.

– Подмена понятия корреляционной связи понятием причинно-следственной связи.

– Беспорядочный расчет коэффициентов корреляции для всех пар переменных по принципу «сравнить все со всем».

– Смешивание понятий корреляционного и регрессионного анализа.

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

– Неполное представление результатов корреляционного анализа (значения коэффициента корреляции, объема выборки, значения уровня статистической значимости).

– Представление только точечной оценки (игнорирование доверительных интервалов).

– Отождествление статистически значимых коэффициентов корреляции с клинически важными.

– Отсутствие обсуждения, почему были получены те или иные коэффициенты корреляции (выяснение вопросов истинной или ложной является выявленная зависимость, возможность присутствия неких

до

переменных, тесно коррелирующих с обеими изучаемыми переменными).

– Однозначное заключение о полном отсутствии взаимосвязи между признаками при значении коэффициента корреляции близком к нулю (возможно, что взаимосвязь между переменными носит нелинейный характер, но исследователь этого не учел).

– Редкое применение скаттерограмм для графического представления зависимостей.

Для того, чтобы читатель приобрел практические навыки проведения корреляционного анализа, будет рассмотрен фрагмент данных, которые были собраны в ходе исследования, направленного на изучение метаболического синдрома и его детерминант в условиях неблагополучной социально-экологической ситуации в Южном Казахстане [20, 21, 25, 29].

В ходе данного исследования у 277 пациентов получены значения индекса массы тела (ИМТ), окружности талии, уровне креатинина и мочевины в крови (все четыре анализируемых признака являются непрерывными количественными переменными). Также были собраны данные об уровне образования пациентов (4 градации – высшее, незаконченное высшее, среднее и начальное).

На предварительном этапе обработки данных количественная шкала значений ИМТ была переведена в номинальную: были выделены 3 «рамки» значений ИМТ:

нормальная масса тела, избыточная масса тела и ожирение. Подобная группировка значений позволяет проводить сравнения между различными категориями пациентов и часто используется при анализе данных. Отметим, что получившаяся номинальная переменная, имеющая значения «нормальная масса тела», «избыточная масса тела» и «ожирение», является как номинальной, так и ординальной, поскольку все три значения могут быть ранжированы по возрастанию или убыванию.

Корреляционный анализ будет проведен с использованием программного обеспечения Statistica 10 [28, 3] и SPSS 20 [4], демонстрационные версии которого можно загрузить с официальных сайтов разработчиков (www.stаstsoft.com и www.ibm.com соответственно).

Представленные ниже алгоритмы действий являются не более чем инструментом анализа данных, в то время как корректная интерпретация полученных результатов требует наличия базисных знаний в области биомедицинской статистики, которые могут быть получены только путем изучения специализированной литературы [5, 26, 24, 34, 38].

Корреляционный анализ с использованием программы Statistica 10.

Для начала работы необходимо открыть файл 7_Correlation_STAT.sta, который потребуется загрузить с сайта журнала «Наука и Здравоохранение». В данном файле представлены следующие вариационные ряды:

1. ИМТ (переменная «BMI»): непрерывная количественная переменная.

2. Окружность талии (переменная «Waist_circum»): непрерывная количественная переменная.

3. Категория ИМТ (переменная «Category_BMI»): номинальная (или ординальная) переменная.

4. Уровень образования (переменная «Education»): номинальная (или ординальная) переменная.

5. Уровень креатинина крови (переменная «Creatinin»): непрерывная количественная переменная.

6. Уровень мочевины крови (переменная «Carbamide»): непрерывная количественная переменная.

В результате статистического анализа данных будет проведена оценка корреляционной связи между следующими переменными:

– ИМТ и окружностью талии.

– Уровнем креатинина и уровнем мочевины крови.

– Уровнем образования пациента и категорией ИМТ.

На начальном этапе обработки данных требуется построить скаттерограмму, чтобы визуально оценить степень связи между переменными.

Для этого войдем в меню «Graphs» в верхней части экрана и выберем раздел «Scatterplots…». В появившемся окне «2D Scatterplots» (рисунок 3) нажмем на кнопку «Variables» и выберем переменные, значения которых будут отложены по осям абсцисс и ординат, как это показано на рисунке 4. Выбор подтвердим нажатием на кнопку «ОК» и в снова открывшемся окне «2D Scatterplots» снова нажимаем на кнопку «ОК».

В результате наших действий программа сформирует скаттерограмму зависимости между переменными «BMI» и «Waist_circum» (рисунок 5). Видно, что скаттерограмма отражает линейную зависимость и в достаточной мере гомоскедастична: разброс значений одной переменной практически не зависит от разброса другой переменной, и разброс точек вокруг линии тренда примерно одинаков.

На следующем этапе обработки данных требуется определить тип распределения, чтобы понять, можно ли использовать параметрический метод (коэффициент корреляции Пирсона), или потребуется сравнивать группы с помощью непараметрического критерия Спирмена. Пошаговый алгоритм проверки распределения переменных на «нормальность» нескольких групп подробно описан в [13, 8, 31].

Проверка на «нормальность» распределения изучаемых количественных переменных показала, что обе переменные имеет близкое к нормальному распределение (читатель может

самостоятельно убедиться в этом, выполнив – «Basic Statistics/Tables» – «Descriptive проверку распределения переменных с statistics» – «Normality» – кнопка использованием разделов меню «Statistics» «Histograms» программы Statistica 10).

Рис. 3. Окно «2D Scatterplots» программы Statistica 10.

Рис. 4. Окно «Select Variables for Scatterplot» программы Statistica 10.

Рис. 5. Скаттерограмма зависимости между переменными «BMI» и «Waist circum»

(программа Statistica 10).

Для проведения корреляционного анализа с входим в раздел «Basic Statistics/Tables». В

использованием коэффициента корреляции появившемся окне выбираем раздел

Пирсона выбираем меню «Statistics» (в верхней «Correlation matrices», и подтверждаем выбор

части рабочего пространства программы) и нажатием на кнопку «ОК» (рисунок 6).

В открывшемся окне нажимаем на кнопку «One variable list» (рисунок 7) и в окне «Select the variables for the analysis» выбираем переменные «BMI» и «Waist_circum», как показано на рисунке 8, и подтверждаем выбор

кнопкой «OK» (для выбора обеих переменных необходимо левой кнопкой мыши выбрать одну переменную, после чего удерживая кнопку «Ctrl» также левой кнопкой мыши выбрать вторую переменную).

..¡¿¡И Product-Moment and Partial Correlations: Correlati… I. ^ J

Second list: none

SI Options »

Рис. 7. Окно «Product-Moment and Partial Correlations…» программы Statistica 10.

Рис. 8. Окно «Select the variables for the analysis» программы Statistica 10 (выбор переменных «BMI» и «Waist_circum»).

Программа вернется к окну «Product-Moment and Partial Correlations…», в котором нажмем на кнопку «Graphs» для формирования скаттерограммы (рисунок 9). Сформированная программой скаттерограмма соответствует представленной на рисунке 5, также по осям представляется гистограмма

распределения, для визуальной оценки соответствия распределения включенных в анализ переменных нормальному распределению. Выше графика в строке «Correlation: r = ,85705» представлено значение коэффициента корреляции Пирсона (r = 0,86).

Scatterplot: bmi vs. Waist_circum (Casewise MD deletion) Waist circum = 41,916 + 1,8662 *bmi Correlation: r = ,85705

100 50

0

140

130

120

110

О 100

90

1

80

70

60

50

-.—ТП

П

n—.

X: BMI N = 277

Mean = 29,740722 Std Dv. = 5,887103 Max. = 46,870000 Min = 17,720000

Y: Waist_circum N = 277

Mean = 97,418773 Std Dv = 12,819033 Max. = 127,000000 Min = 68.000000

3 – о о 0

О О 3, nftfelgO DO ° о о

ЧпоЖ SÄT” Чу ACT ° 8

о № сЙГЯж жГ?* JO

OJ ОЧ ä?<6Р9

о о

10

15

20

25

30

BMI

35

40

45

50 0

-inn

0,95 Conf.lnt.

Рис. 9. Результаты корреляционного анализа с использованием коэффициента корреляции Пирсона (скаттерограмма).

Далее нажмем на вкладку «Product-Moment…» в нижнем левом углу рабочего поля программы, чтобы вернуться к окну Product-Moment and Partial Correlations.», и нажмем на кнопку «Summary: Correlations». Программа представит таблицу (рисунок 10), в которой также приведено значение

коэффициента корреляции Пирсона, а выше таблицы программа указывает, что значение r является статистически значимым («Marked correlations are significant at p < ,05000»). В данном случае значение коэффициента статистически значим, поэтому в таблице программа выделяет его красным цветом.

Variable Correlations (Correlation_STAT) Marked correlations are significant at p < ,05000 N=277 (Casewise deletion of missing data)

Means Std. Dev. BMI Waist circum

BMI 29,74072 5 88710 1.000000 0 857052

Waist_circum 97.41877 12.81903 0 857052 1 000000

Рис. 10. Результаты корреляционного анализа с использованием коэффициента

корреляции Пирсона (таблица).

Таким образом, на основании проведенного корреляционного анализа установлено, что между ИМТ и окружностью живота существует сильная положительная корреляционная связь (г = 0,86, п = 277, p < 0,05). Соответственно, коэффициент детерминации равен г2 = 0,862 = 0,74, то есть вариабельность одной переменной способно объяснить 74% вариабельности второй переменной.

Далее рассмотрим корреляционный анализ переменных «Creatinin» и «Carbamide», имеющих распределение, отличное от нормального.

Для проведения корреляционного анализа с использованием коэффициента корреляции Спирмена выбираем меню «Statistics» (в верхней части рабочего пространства программы) и входим в раздел

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

«Nonparametrics». В появившемся окне выбираем раздел «Correlations (Spearman,

Kendall tau, gamma)» и подтверждаем выбор нажатием на кнопку «ОК» (рисунок 11).

Рис. 11. Окно «Nonparametric Statistics» программы Statistica 1

Программа откроет окно «Nonparametric Correlation» (рисунок 12), в котором нажмем на кнопку «Variables» для выбора переменных для анализа. В открывшемся окне выберем

переменные «Creatinin» и «Carbamide», после чего подтвердим выбор кнопкой «OK» (рисунок 13).

Рис. 12. Окно «Nonparametric Correlation» программы Statistica 10.

Программа вернется к окну «Nonparametric Correlation», в котором нажмем кнопку «Scatterplot matrix for all variables», которая сформирует представленную на рисунке 14 скаттерограмму и гистограммы распределения

переменных «Creatinin» и «Carbamide» (очевидно, что обе переменные имеют отличное от нормального, скошенное вправо распределение).

/V Select the variables for the analysis

S

1-BMI 2 – Waist_drcum 3 – Category_BMI 4 – Education

-.”^Я ♦ ^ – ,

Select All

Spread

Zoom

Select variables:

5-6

Sj/j Show appropriate variables only

OK

Cancel

[Bundles]…

Us« the “Show appropriate variables only-option to pre-screen variable lists and show catejorical ar-3 continuous variables Press F1 for more information.

Рис. 13. Окно «Select the variables for the analysis» программы Statistica 10 (выбор переменных «Creatinin» и «Carbamide»).

Рис. 14. Результаты корреляционного анализа с использованием коэффициента корреляции Спирмена (скаттерограмма).

Вернемся к окну анализа с помощью поля программы, и нажмем на кнопку нажатия на вкладку «Nonparametric «Spearman rank R» для запуска анализа correlations» в нижнем левом углу рабочего (рисунок 12).

В таблице, представленной на рисунке 15, программа демонстрирует значение коэффициента корреляции Спирмена (0,534125) и сообщает, что значение коэффициента статистически значимо

(«Marked correlations are significant at p < ,05000»). Как и при расчете коэффициента корреляции Пирсона, программа выделяет красным цветом значение статистически значимого коэффициента.

Variable Spearman Rank Order Correlations (Correlation_STAT) MD pairwise deleted Marked correlations are significant at p <.05000

Creatinin Carbamide

Creatinin 1.000000L 0 534125 1.000000

Carbamide

Рис. 15. Результаты корреляционного анализа с использованием коэффициента корреляции Спирмена (таблица).

Таким образом, между уровнем креатинина и мочевины сыворотки крови обнаружена положительная корреляционная связь средней силы: ^ = 0,53, п = 277, p < 0,05.

Далее на примере ординальных переменных «Category_BMI» и «Educatюn» рассмотрим алгоритм расчета коэффициента корреляции Кендалла ть.

Для этого снова входим в раздел «Nonparametrics». В появившемся окне выберем раздел «Correlations (Spearman, Kendall tau, gamma)» и подтвердим выбор нажатием на кнопку «ОК» (рисунок 11).

В окне «Nonparametric Correlation» (рисунок 12), нажмем на кнопку «Variables» и выберем переменные «Category_BMI» и «Education» после чего подтвердим выбор кнопкой «OK» (рисунок 16).

Рис. 16. Окно «Select the variables for the analysis» программы Statistica 10 (выбор переменных «Category_BMI» и «Education»).

Программа вернется к окну «Nonparametric Correlation» (рисунок 12), где нажмем на вкладку «Advanced», которая открывает

возможность расчета критерия Кендалла ть. Для запуска анализа нажмем на кнопку «Kendall Tau» (рисунок 17).

Рис. 17. Вкладка «Advanced» окна «Nonparametric Correlation» программы Statistica 10.

Результаты анализа программа «Marked correlations are significant at p <

представляет в виде таблицы (рисунок 18) где ,05000» сообщает о том, что значение

указано и выделено красным цветом значение коэффициента корреляции Кендалла ть

коэффициента корреляции (0,177778). Строка статистически значимо.

Рис. 18. Результаты корреляционного анализа с использованием коэффициента корреляции Кендалла ть.

Таким образом, между уровнем образования положительная корреляционная связь: ть = 0,18, и категорией ИМТ пациентов выявлена слабая п = 277, р < 0,05).

Корреляционный анализ с использованием программы SPSS 20.

Для начала работы необходимо открыть файл 7_Correlation_SPSS.sav, который потребуется загрузить с сайта журнала «Наука и Здравоохранение». В файле представлены те же вариационные ряды, что и в файле данных программы Statistica: ИМТ («BMI»), окружность талии («Waist_circum») категория ИМТ («Category_BMI»), уровень образования («Education»), уровень креатинина

(«Creatinin») и мочевины («Carbamide») крови пациентов.

На начальном этапе корреляционного анализа с использованием коэффициента корреляции Пирсона необходимо построить скаттерограмму.

Для этого войдем в меню «Graphs», раздел «Legacy Dialogs», подраздел «Scatter/Dot» (рисунок 14).

Correlation_SPSS.sav [DataSetl] – IBM SPSS Statistics Data Editor

File Edit View Data Transform Analyze Direct Marketing Graphs Utilities Add-ons Window Help

ЁЗ hi â Ш ^ If4 ‘ ^У t all Chart Builder… ¿И Graphboard Template Chooser .. 1 Jt¿á.%8

Legacy Dialogs S Ваг… И 3-D Ваг… И Line… @ Area… H Pie… H High-Low…

BMI Waist circum Category_BMI Ed ucation ureatinm ^aroamiae V

1 29.34 95.00 2.00 3.00 56,27 5.68

2 29,40 106,00 2.00 1.00 74,29 7,36

3 29,22 105.00 2.00 1.00 52,49 6.85

4 30,78 97.00 3.00 3.00 59,32 7.05

5 25,97 80,00 2.00 1.00 46,93 6.35

6 24,44 89.00 1.00 3,00 72.68 6,17 g Boxplot… CT Error Bar… f-1 Population Pyramid…

7 25,86 95.00 2.00 3,00 59.61 7,03

8 39.28 110,00 3.00 1.00 49.44 4,24

9 30.48 99.00 3.00 1.00 48.63 4.12

10 29.75 104.00 2.00 1.00 63,27 5.05 LI Scatter/Dot… Ц Histogram… 1 III

11 I 25,81 86.00 2.00 3,00 47.77 3.48

Рис. 14. Выбор подраздела «Scatter/Dot» меню «Graphs» программы SPSS 20.

|] в открывшемся окне «Scatter/Dot» выберем простую скаттерограмму «Simple Scatter» и нажмем на кнопку «Define» (рисунок 15).

В открывшемся окне «Simple Scatterplot» с помощью стрелок между полями перенесем переменную «BMI» в поле «X Axis», а переменную «Waist_circum» – в поле «Y Axis» и нажмем на кнопку «OK» (рисунок 16).

Рис. 16. Окно «Simple Scatterplot» программы SPSS 20.

В результате программа сформирует скаттерограмму, представленную на рисунке

17. Данный график полностью соответствует представленному на рисунке 5.

Рис. 17. Скаттерограмма зависимости между переменными «BMI» и «Waist_circum» (программа SpsS 20).

Для расчета коэффициента корреляции Пирсона в первую очередь необходимо проверить соответствие распределения имеющихся переменных закону нормального распределения. Алгоритм проверки

распределения с помощью программы SPSS подробно описан в [13, 8].

Непосредственно для проведения корреляционного анализа войдем в меню «Analyze», раздел «Correlate», подраздел «Bivariate» (рисунок 18).

Correlation_SPSS.sav [DataSetl] – IBM SPSS Statistics Data Editor

File Edit View Data Transform Analyze Direct Marketing Graphs Utilities Add-ons Window

muB)

iг

BMI

Waist cir<

29.34 29.40 29,22 30.78 25.97 24,44 25.86

Reports

Descriptive Statistics Tables

Compare Means

General Linear Model

Generalized Linear Models

Mixed Models

Correlate

Regression

Loglinear

Neural Networks

Creatinin Carbamide

1 56,27 5.68

1 74.29 7,36

1 52,49 6,85

£71 Bivariate.. Partial… £73 Distances… /.üb

6.35

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

6.17

7.03

k АП Л Л Л

Рис. 18. Выбор подраздела «Correlate» – «Bivariate» меню «Analyze» программы SPSS 20.

Откроется окно «Bivariate Correlations», в котором с помощью стрелки необходимо перенести переменные «BMI» и «Waist_circum»

в правое поле (рисунок 19). Оставим отмеченной галочкой позиции «Pearson» и «Two-tailed» и нажмем на кнопку «OK» для запуска анализа.

Рис. 19. Окно «Bivariate Correlations» программы SPSS 20 (выбор переменных «BMI» и «Waist_circum»).

Результаты расчета коэффициента корреляции Пирсона составляет 0,857 (строка корреляции Пирсона для переменных «BMI» и «Pearson Correlation»), а уровень «WaisLcircum»представлены в таблице 4. В статистической значимости менее 0,001 таблице указано, что значение коэффициента (строка «Sig. (2-tailed)»).

Таблица 4.

Результаты расчета коэффициента корреляции Пирсона для переменных «BMI» и «Waist_circum»

BMI Waist_circum

BMI Pearson Correlation 1 ,857**

Sig. (2-tailed) ,000

N 277 277

Waist circum Pearson Correlation ,857** 1

Sig. (2-tailed) ,000

N 277 277

Correlation is significant at the 0.01 level (2-tailed).

Для расчета коэффициента корреляции Спирмена для переменных «Creatinin» и «Carbamide» снова войдем в меню «Analyze», раздел «Correlate», подраздел «Bivariate» (рисунок 18). В окне «Bivariate Correlations»

перенесем в правое поле переменные «Creatinin» и «Carbamide» и отметим галочкой позицию «Spearman», после чего запустим анализ кнопкой «OK» (рисунок 20). Результаты расчетов представлены в таблице 5.

Рис. 20. Окно «Bivariate Correlations» программы SPSS 20 (выбор переменных «Creatinin» и «Carbamide»).

Таблица 5.

Результаты расчета коэффициента корреляции Спирмена для переменных «Creatinin» и «Carbamide».

Creatinin Carbamide

Spearman’s rho Creatinin Correlation Coefficient 1,000 ,534**

Sig. (2-tailed) ,000

N 277 277

Carbamide Correlation Coefficient ,534** 1,000

Sig. (2-tailed) ,000

N 277 277

*. Correlation is significant at the 0

01 level (2-tailed).

Для расчета коэффициента корреляции Кендалла ть для переменных «Creatinin» и «Carbamide» снова войдем в меню «Analyze», раздел «Correlate», подраздел «Bivariate» (рисунок 18), и в окне «Bivariate Correlations»

перенесем в правое поле переменные «Category_BMI» и «Education» и отметим галочкой позицию «Kendall’s tau-b», после чего запустим анализ кнопкой «OK» (рисунок 21). Результаты расчетов представлены в таблице 6.

Рис. 21. Окно «Bivariate Correlations» программы SPSS 20 (выбор переменных «Category_BMI» и «Education»).

Таблица 6.

Результаты расчета коэффициента корреляции Кендалла ть для переменных

Category_BMI Education

Kendall’s tau_b Category_BMI Correlation Coefficient 1,000 JS 8 7

Sig. (2-tailed) ,002

N 277 277

Education Correlation Coefficient ,178** 1,000

Sig. (2-tailed) ,002

N 277 277

Correlation is significant at the 0.01 level (2-tailed).

Следует отметить, что программа SPSS показывает точные значения достигнутого уровня статистической значимости для коэффициентов корреляции в отличие от Statistica 10, которая только указывает, выше или ниже критического уровня находится значение коэффициента корреляции.

В остальном результаты расчета критериев корреляции Пирсона, Спирмена и Кендалла с помощью программы SPSS 20 полностью соответствуют полученным при использовании программы Statistica 10 и не требуют дополнительных комментариев.

Литература:

1. Аканов А.А., Турдалиева Б.С., Изекенова А.К., Рамазанова М.А., Абдраимова Э.Т., Гржибовский А.М. Оценка использования статистических методов в научных статьях медицинских журналов Казахстана // Экология человека. 2013. №5. С. 61-64.

2. Банержи А. Медицинская статистика понятным языком: вводный курс. М. : Практическая медицина, 2007. 287 с.

3. Боровиков В. STATISTICA. Искусство анализа данных на компьютере: для профессионалов. СПб. : Питер, 2003. 688 с.

4. Бююль А., Цефель П. SPSS: искусство обработки информации. Анализ статистических данных и восстановление скрытых закономерностей. СПб. : ООО «ДиаСофтЮП», 2005. 608 с.

5. Гланц С. Медико-биологическая статистика. М. : Практика, 1998. 459 с.

6. Гржибовский А.М. Анализ порядковых данных // Экология человека. 2008. №8. С. 5662.

7. Гржибовский А.М. Корреляционный анализ // Экология человека. 2008. №9. С. 5060.

8. Гржибовский А.М. Типы данных, проверка распределения и описательная статистика // Экология человека. 2008. №1. С. 52-58.

9. Гржибовский А.М., Иванов С.В. Анализ номинальных и ранговых переменных данных с использованием программного обеспечения Statistica и SPSS // Наука и Здравоохранение. 2016. № 6. С. 5-39.

10. Гржибовский А.М., Иванов С.В. Исследования типа «случай-контроль» в здравоохранении // Наука и Здравоохранение. 2015. № 4. С. 5-17

11. Гржибовский А.М., Иванов С.В. Когортные исследования в здравоохранении/ / Наука и Здравоохранение. 2015. № 3. С. 5-16.

12. Гржибовский А.М., Иванов С.В. Поперечные (одномоментные) исследования в здравоохранении // Наука и Здравоохранение.

2015. № 2. С. 5-18.

13. Гржибовский А.М., Иванов С.В., Горбатова М.А. Описательная статистика с использованием пакетов статистических программ Statistica и SPSS: и проверка распределения // Наука и Здравоохранение.

2016. № 1. С. 7-23.

14. Гржибовский А.М., Иванов С.В., Горбатова М.А. Сравнение количественных данных двух независимых выборок с использованием программного обеспечения Statistica и SPSS: параметрические и непараметрические критерии // Наука и Здравоохранение. 2016. № 2. С. 5-28

15. Гржибовский А.М., Иванов С.В., Горбатова М.А. Сравнение количественных данных двух парных выборок с использованием программного обеспечения Statistica и SPSS: параметрические и

непараметрические критерии // Наука и Здравоохранение. 2016. № 3. С. 5-25.

16. Гржибовский А.М., Иванов С.В., Горбатова М.А. Сравнение количественных данных трех и более независимых выборок с использованием программного обеспечения Statistica и SPSS: параметрические и непараметрические критерии // Наука и Здравоохранение. 2016. № 4. С. 5-37.

17. Гржибовский А.М., Иванов С.В., Горбатова М.А. Сравнение количественных данных трех и более парных выборок с использованием программного обеспечения Statistica и SPSS: параметрические и непараметрические критерии // Наука и Здравоохранение. 2016. № 5. С. 5-29.

18. Гржибовский А.М., Иванов С.В. Экологические (корреляционные) исследования в здравоохранении // Наука и Здравоохранение. 2015. № 5. С. 5-18.

19. Гржибовский А.М., Иванов С.В. Экспериментальные исследования в здравоохранении // Наука и Здравоохранение. 2015. № 6. С. 5-17.

20. Жунисова М.Б., Шалхарова Ж.С., Шалхарова Ж.Н., Гржибовский А.М. Типы пищевого поведения и абдоминальное ожирение // Журн. Медицина. 2015. №4. С. 9295.

21. Жунисова М.Б., Шалхарова Ж.С., Шалхарова Ж.Н., Нускабаева Г.О., Садыкова К.Ж., Маденбай К.М., Гржибовский А.М. Психоэмоциональный стресс как предиктор типа пищевого поведения в Казахстане // Экология человека. 2015. №5. С. 36-45.

22. Зайцев В.М., Лифляндский В.Г., Маринкин В.И. Прикладная медицинская статистика. СПб. : Фолиант, 2003. 428 с.

23. Зуева Л.П., Яфаев Р.Х. Эпидемиология : учебник. СПб : ООО «Издательство Фолиант», 2008. 752 с.

24. Лакин Г.Ф. Биометрия. М. : Высшая школа, 1990. 351 с.

25. Маденбай К.М., Шалхарова Ж.С., Шалхарова Ж.Н., Жунисова М.Б., Садыкова К.Ж., Нускабаева Г.О., Гржибовский А.М. Оценка связи между площадью подкожной жировой ткани и показателями электронейромиографии // Экология человека. 2015. №7. С. 58-64.

26. Петри А., Сэбин К. Наглядная статистика в медицине. М. : ГЭОТАР-Мед, 2003. 140 с.

27. Рахыпбеков Т.К., Гржибовский А.М. К вопросу о необходимости повышения качества казахстанских научных публикаций для успешной интеграции в международное научное сообщество // Наука и Здравоохранение. 2015. №1. С. 5-11.

28. Реброва О.Ю. Статистический анализ медицинских данных. Применение пакета прикладных программ STATISTICA. М. :МедиаСфера, 2002. 312 с.

29. Садыкова К.Ж., Шалхарова Ж.С., Нускабаева Г.О., Садыкова А.Д., Жунисова М.Б., Маденбай К.М., Гржибовский А.М. Распространенность анемии, ее социально-демографические детерминанты и возможная связь с метаболическим синдромом в г. Туркестан, Южный Казахстан // Экология человека. 2015. №8. С. 58-64.

30. Статистический анализ эмпирических исследований [электронный ресурс]. URL:www.statexpert.org/articles/таблицы_крити ческих_значений_статистических_критериев (дата обращения 08.09.2015).

31. Субботина А.В., Гржибовский А.М. Описательная статистика и проверка нормальности распределения количественных данных // Экология человека. 2014. №2. С. 5157.

32. Унгуряну Т.Н., Гржибовский А.М. Корреляционный анализ с использованием пакета статистических программ STATA // Экология человека. 2014. №9. С. 60-64.

33. Флетчер Р. Клиническая эпидемиология. Основы доказательной медицины: пер. с англ. / Р. Флетчер, С. Флетчер, Э. Вагнер. М. : Медиа Сфера, 1998. 352 с.

34. Юнкеров В.И., Григорьев С.Г. Математико-статистическая обработка данных медицинских исследований. СПб :ВМедА, 2002. 266 с.

35. Anderson M. RSM simplified: optimizing processes using response surface methods for design of experiments / M. Anderson P., Whitcomb. – London : Taylor & Francis, 2005. P. 39-42.

36. Beaglehole R., Bonita R. Basic epidemiology. World Health Organization, Geneva, 1993.

37. Bonett D. Wright T. Sample size requirements for estimating Pearson, Kendall and Spearman correlations // Psychometrica. 2000. Vol. 65. P. 23-28.

38. Cleopas T.J. et al. Statistics Applied to Clinical Trials. 4th ed. Springer, 2009.

39. Davi’d F. Tables of the ordinates and probability integral of the distribution of the correlation coefficient in small samples. Cambridge : Cambridge University Press, 1938.

40. Kendall M. A new method of rank correlation // Biometrika. 1938. Vol. 30. P. 91-93.

41. Krnskal W. Ordinal measures of association // Journal of the American Statistical Association.1958. Vol. 53. P. 814-861.

References:

1. Akanov A.A., Turdalieva B.S., Izekenova A.K., Ramazanova M.A., Abdraimova, Grjibovski A.M. Otsenka ispolzovania statisticheskih metodov v nauchnih statyakh Kazakhstana [Assesment of use of statistical methods in scientific articles of the Kazakhstan’s medical journals]. Ekologiya cheloveka [Human Ecology]. 2013. No.5. PP. 61-64. [in Russian]

2. Banerzhi A. Meditsinskaya statistika ponyatnym yazykom : vvodnyy kurs [Medical statistics in plain language : an introductory course ]. M. : Prakticheskaya meditsina , 2007. P. 287. [in Russian].

3. Borovikov V. STATISTICA. Iskusstvo analiza dannikh na kompyutere: dlya professionalov [STATISTICA. The art of data analysis using computer: for professionals]. SPb. : Piter, 2003. P. 688.

4. Buhl A., Zofel P. SPSS: isskustvo obrabotki informatsii. Analiz statisticheskih daanikh i vosstanovlenie skritikh zakonomernostey [SPSS: the art of information analysis. Statistical data analysis and hidden regularities identification]. SPb. : OOO «DiaSoftUP», 2005. P. 608. [in Russian]

5. Glants S. Mediko-biologicheskaya statistika [The biomedical statistics]. M. : Praktika, 1998. PP. 459. [in Russian]

6. Grjibovski A.M. Analiz poryadkovikh dannikh [Analysis of ordinal data]. Ekologiya

cheloveka [Human Ecology]. 2008. No.1. PP. 5662. [in Russian].

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

7. Grjibovski A.M. Korrelatsionniy analiz [Correlation analysis]. Ekologiya cheloveka [Human Ecology]. 2008. No.9. PP. 50-60. [in Russian].

8. Grjibovski A.M. Tipy dannikh, proverka raspredeleniya I opisatelnaya statistika [Types of data, distribution estimation and descriptive statistics]. Ekologiya cheloveka [Human Ecology]. 2008. No.1. PP. 52-58. [in Russian].

9. Grjibovski A.M., Ivanov S.V. Analiz nominalnykh I rangovykh peremennykh dannykh s ispol’zovaniyem programmnogo obespecheniya Statistica i SPSS [Analysis of nominal and ordinal data using Statistica and SPSS software]. Nauka i Zdravoohranenie [Science & Healthcare]. 2016. № 6. pp. 5-39. [in Russian].

10. Grjibovski A.M., Ivanov S.V. Issledovaniya tipa sluchay-kontrol v zdravoohranenii [Case-control studies in health sciences]. Nauka i Zdravookhranenie [Science & Healthcare]. 2015, 4, pp. 5-17 [in Russian].

11. Grjibovski A.M., Ivanov S.V. Kogortnie issledovaniya v zdravoohranenii [Cohort studies in health sciences]. Nauka i Zdravookhranenie [Science & Healthcare]. 2015, 3, pp. 5-16. [in Russian]

12. Grjibovski A.M., Ivanov S.V. Poperechnye (odnomomentnye) issledovaniya v zdravookhranenii [Cross-sectional studies in health sciences]. Nauka i Zdravookhranenie [Science & Healthcare]. 2015, No2, pp. 5-18. [in Russian]

13. Grjibovski A.M., Ivanov S.V., Gorbatova M.A. Opisatel’naya statistika s ispol’zovaniyem paketov statisticheskikh programm Statistica i SPSS I proverka raspredeleniya [Descriptive statistics using Statistica and SPSS software]. Nauka i Zdravookhranenie [Science & Healthcare]. 2016, 1, pp. 7-23 [in Russian].

14. Grjibovski A.M., Ivanov S.V., Gorbatova M.A. Sravneniye kolichestvennykh dannykh dvukh nezavisimykh vyborok s ispol’zovaniyem programmnogo obespecheniya Statistica i SPSS : parametricheskiye i neparametricheskiye kriterii [Comparing the quantitative data of two independent groups using the software Statistica and SPSS: parametric and nonparametric tests]. Nauka i Zdravookhranenie [Science & Healthcare]. 2016, 2, pp.5-28 [in Russian].

15. Grjibovski A.M., Ivanov S.V., Gorbatova M.A. Sravneniye kolichestvennykh dannykh dvukh parnikh viborok s ispol’zovaniyem programmnogo obespecheniya Statistica i SPSS : parametricheskiye i neparametricheskiye kriterii [Comparing the quantitative data of two dependent variations using the software Statistica and SPSS: parametric and nonparametric tests]. Nauka i Zdravookhranenie [Science & Healthcare]. 2016, 3, pp. 5-25. [in Russian].

16. Grjibovski A.M., Ivanov S.V., Gorbatova M.A. Sravneniye kolichestvennykh dannykh trekh i boleye nezavisimykh vyborok s ispol’zovaniyem programmnogo obespecheniya Statistica i SPSS : parametricheskiye i neparametricheskiye kriterii [Comparing of the quantitative data of three or more independent samples using Statistica and SPSS software: parametric and nonparametric methods]. Nauka i Zdravoohranenie [Science & Healthcare]. 2016. 4. pp. 5-37. [in Russian].

17. Grjibovski A.M., Ivanov S.V., Gorbatova M.A. Sravneniye kolichestvennykh dannykh trekh i boleye parnikh vyborok s ispol’zovaniyem programmnogo obespecheniya Statistica i SPSS : parametricheskiye i neparametricheskiye kriterii [Comparing of the quantitative data of three or more dependent samples using Statistica and SPSS software: parametric and nonparametric methods]. Nauka i Zdravoohranenie [Science & Healthcare]. 2016. 5. C. 5-29 [in Russian].

18. Grjibovski A.M., Ivanov S.V. Ekologicheskiye (korrelyatsionnye) issledovaniya v zdravoohranenii. [Ecological (correlational) studies in health sciences]. Nauka i Zdravookhranenie [Science & Healthcare]. 2015,

5, pp. 5-18. [in Russian].

19. Grjibovski A.M., Ivanov S.V. Eksperimentalnye issledovaniya v zdravookhranenii [Experimental studies in health sciences]. Nauka i Zdravookhranenie [Science & Healthcare]. 2015,

6, pp. 5-17. [in Russian].

20. Zhunissova M.B., Shalkarova Zh.S., Shalkarova Zh. N., Nuskabayeva G.O., Sadykova K.Zh., Madenbay K.M., Grjibovski A.M. Tipy pischevogo povedeniya i abdominalnoe ozhirenie [Eating behavior types and abdominal obesity]. Meditsina [Medicine]. 2015. No.4. pp. 92-95. [in Russian].

21. Zhunissova M.B., Shalkarova Zh.S., Shalkarova Zh. N., Nuskabayeva G.O., Sadykova K. Zh., Madenbay K.M., Grjibovski A.M.

Psykhoemotsionalniy stress kak predictor tipa pischevogo povedeniya v Kazakhstane [Psychoemotional stress and eating behavior in Kazakhstan]. Ekologiya cheloveka [Human Ecology]. 2015. No.5. pp. 36-45. [in Russian]

22. Zaytsev V.M., Liflyandskiy V.G., Marinkin V.I. Prikladnaya meditsinskaya statistika [Applied medical statistics] . SPb . : Foliant , 2003. P. 428. [in russian]

23. Zueva L.P, Yafaev R.H. Epidemiologiya: uchebnik [Epidemiology: the textbook]. SPb : OOO «Izdatelstvo Foliant», 2008. P. 752. [in Russian].

24. Lakin G.F. Biometria [Biometrics]. M. : Vyscshaya shkola. 1990. P. 351. [in Russian]

25. Madenbay K.M., Shalkarova Zh.S., Shalkarova Zh. N., Zhunissova M.B., Sadykova K.Zh., Nuskabayeva G.O., Grjibovski A.M. Otsenka svyazi mezhdu ploshadyu podkojnoy jirovoy tkani I pokazatelyami electroneyromiografii [Assesment of the relationship between subcutaneous fat tissue an results of electromyoneurography]. Ekologiya cheloveka [Human Ecology]. 2015. No.7. pp. 58-64. [in Russian]

26. Petri A., Sebin K. Naglyadnaya statistika v meditsine [Demonstrative statistics in medicine]. M. : GEAOTAR-Med, 2003. p. 140. [in Russian]

27. Rakhypbekov T.K., Grjibovski A.M. K voprosu o neobhodimosti povysheniya kachestva kazakhstanskih nauchykh publikatsii dlya uspeshnoi integratsii v mezhdunarodnoe nauchnoe soobschestvo [The need for improvement of the quality of Kazakhstani publications for successful integration in the international research community]. Nauka i Zdravookhranenie [Science & Healthcare]. 2015. No.1. pp. 5-11. [in Russian]

28. Rebrova O. Yu. Statisticheskii analiz meditsinskikh danykh. Primenenie paketa prikladnikh program STATISTICA [Statistical analysis of medical data. Using of STATISTICA software]. M. : MediaSphera, 2002. P. 312.

29. Sadykova K.Zh., Shalkharova Zh.S., Shalkharova Zh.N. Nuskabaeva G.O., Sadykova A.D., Zhunissova M.B., Madenbay K.M., Grjibovski A.M. Rasprostranennost’ anemii, yeye sotsial’no – demograficheskiye determinanty i vozmozhnaya svyaz’ s metabolicheskim sindromom v g. Turkestan, Yuzhniy Kazakhstan [Prevalence of anemia, its socio-demographic

determinants and potential association with metabolic syndrome in residents of Turkestan, Southern Kazakhstan]. Ekologiya cheloveka [Human Ecology]. 2015. No.8. pp. 58-64. [in Russian]

30. Statistical analysis of empirical research [website] Available at: www.statexpeitorg/articles/Ta6™ qbi_Kp MTunecKM x_3HaHeHMM_CTaTMCTMHecKMx_KpMTepMeB

(Accesed 08 September 2015).

31. Subbotina A.V., Grjibovski A.M. Opisatelnaya statistika I proverka normal’nosti raspredeleniya kolichestvennyh dannykh [Descriptive statistics and normality testing for quantitative data]. Ekologiya cheloveka [Human Ecology]. 2014. No.2. pp. 51-57. [in Russian].

32. Unguryanu T.N., Grjibovski A.M. Korrelatsionnyi analiz s ispol’zovaniyem paketa statisticheskikh programm STATA [Correlation analysis using STATA] Ekologiya cheloveka [Human Ecology]. 2014. No.9. PP. 60-64. [in Russian].

33. Fletcher R. et al. Klinicheskaya epidemiologiya. Osnovy dokazatel’noi meditsiny [Clinical epidemiology. Basics of the evidence-based medicine] / R. Fletchtr, C. Fletcher, E. Vagner. M. : Media Sphere, 1998. 352 p. [in Russian].

34. Yunkerov V.I., Grigoryev S.G. Matematiko-statisticheskaya obrabotka dannykh meditsinskih issledovanii [Mathematical and statistical analysis of medical research data]. SPb : VMedA, 2002. P. 266. [in Russian]

35. Anderson M. RSM simplified: optimizing processes using response surface methods for design of experiments / M. Anderson P., Whitcomb. London: Taylor & Francis, 2005. P. 39-42.

36. Beaglehole R., Bonita R. Basic epidemiology. World Health Organization, Geneva, 1993.

37. Bonett D. Wright T. Sample size requirements for estimating Pearson, Kendall and Spearman correlations // Psychometrica. 2000. Vol. 65. P. 23-28.

38. Cleopas T.J. et al. Statistics Applied to Clinical Trials. 4th ed. Springer, 2009.

39. David F. Tables of the ordinates and probability integral of the distribution of the correlation coefficient in small samples. Cambridge : Cambridge University Press, 1938.

40. Kendall M. A new method of rank 41. Kruskal W. Ordinal measures of correlation // Biometrika. 1938. Vol. 30. P. 91-93. association // Journal of the American Statistical

Association.1958. Vol. 53. P. 814-861.

Контактная информация:

Гржибовский Андрей Мечиславович – доктор медицины, магистр международного общественного здравоохранения, Старший советник Национального Института Общественного Здравоохранения, г. Осло, Норвегия; Заведующий ЦНИЛ СГМУ, г. Архангельск, Россия; Профессор Северо-Восточного Федерального Университета, г. Якутск, Россия; Профессор, Почетный доктор Международного Казахско-Турецкого Университета им. Х.А. Ясяви, г, Туркестан, Казахстан; Почетный профессор ГМУ г. Семей, Казахстан.

Почтовый адрес: INFA, Nasjonalt folkehelseinstitutt, Postboks 4404 Nydalen, 0403 Oslo, Norway. Email: Andrej.Grjibovski@gmail.com

Телефон: +4745268913 (Норвегия), +79214717053 (Россия), +77471262965 (Казахстан).