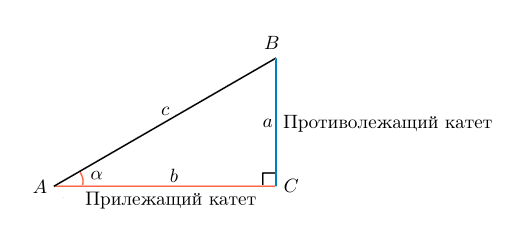
Косинусом угла в прямоугольном треугольнике называют отношение прилежащего катета к гипотенузе.
Для простоты запоминания можно дать такое определение: косинус угла — это отношение ближнего от рассматриваемого угла катета к гипотенузе.
В случае с рисунком, описанным выше: cosα=bccosalpha=frac{b}{c}
Гипотенуза прямоугольного треугольника равна 10 см10text{ см}. Один из катетов равен 6 см6text{ см}. Найдите косинус угла, прилежащего к наибольшему катету.
Решение
Пользуясь теоремой Пифагора вычислим длину неизвестного нам катета.
a2+b2=c2a^2+b^2=c^2
62+b2=1026^2+b^2=10^2
36+b2=10036+b^2=100
b2=64b^2=64
b=8b=8
Катет bb длиннее катета aa. Нам нужно найти косинус угла, прилежащего к наибольшему катету, то есть, к катету bb:
cosα=bc=810=0.8cosalpha=frac{b}{c}=frac{8}{10}=0.8
Ответ
0.8
Две стороны треугольника равны 4 см4text{ см} и 9 см9text{ см}. Периметр его равен 25 см25text{ см}.
Найдите косинус угла, прилежащего к неизвестной стороне и стороне с длиной 4 см4text{ см}.
Решение
Найдем третью сторону треугольника. Так как известен периметр, это будет легко сделать:
P=a+b+cP=a+b+c
25=9+4+c25=9+4+c
c=12c=12
При нахождении косинуса угла нам поможет следствие из теоремы косинусов, которое выглядит так:
cosα=b2+c2−a22⋅b⋅c=42+122−922⋅4⋅12=16+144−8196=7996≈0.82cosalpha=frac{b^2+c^2-a^2}{2cdot bcdot c}=frac{4^2+12^2-9^2}{2cdot 4cdot 12}=frac{16+144-81}{96}=frac{79}{96}approx0.82
Ответ
0.820.82
Решение задач по математике от экспертов сайта Студворк!
Тест по теме “Вычисление косинуса”
Примеры:
(cos{30^°}=)(frac{sqrt{3}}{2})
(cos)(frac{π}{3})(=)(frac{1}{2})
(cos2=-0,416…)
Содержание:
- Аргумент и значение
Коcинус острого угла
Косинус числа
Косинус любого угла
Знаки по четвертям
Связь с другими функциями
Функция
Аргумент и значение

Косинус острого угла
Косинус острого угла можно определить с помощью прямоугольного треугольника – он равен отношению прилежащего катета к гипотенузе.
Пример:
1) Пусть дан угол и нужно определить косинус этого угла.

2) Достроим на этом угле любой прямоугольный треугольник.

3) Измерив, нужные стороны, можем вычислить косинус.

Косинус острого угла больше (0) и меньше (1)
Если при решении задачи косинус острого угла получился больше 1 или отрицательным, то значит где-то в решении есть ошибка.
Косинус числа
Числовая окружность позволяет определить косинус любого числа, но обычно находят косинус чисел как-то связанных с Пи: (frac{π}{2}), (frac{3π}{4}), (-2π).
Например, для числа (frac{π}{6}) – косинус будет равен (frac{sqrt{3}}{2}). А для числа (-)(frac{3π}{4}) он будет равен (-)(frac{sqrt{2}}{2}) (приблизительно (-0,71)).

Косинус для других часто встречающихся в практике чисел смотри в тригонометрической таблице.
Значение косинуса всегда лежит в пределах от (-1) до (1). При этом вычислен косинус может быть для абсолютно любого угла и числа.
Косинус любого угла
Благодаря числовой окружности можно определять косинус не только острого угла, но и тупого, отрицательного, и даже большего, чем (360°) (полный оборот). Как это делать – проще один раз увидеть, чем (100) раз услышать, поэтому смотрите картинку.

Теперь пояснение: пусть нужно определить косинус угла КОА с градусной мерой в (150°). Совмещаем точку О с центром окружности, а сторону ОК – с осью (x). После этого откладываем (150°) против часовой стрелки. Тогда ордината точки А покажет нам косинус этого угла.
Если же нас интересует угол с градусной мерой, например, в (-60°) (угол КОВ), делаем также, но (60°) откладываем по часовой стрелке.

И, наконец, угол больше (360°) (угол КОС) – всё аналогично тупому, только пройдя по часовой стрелке полный оборот, отправляемся на второй круг и «добираем нехватку градусов». Конкретно в нашем случае угол (405°) отложен как (360° + 45°).

Несложно догадаться, что для откладывания угла, например, в (960°), надо сделать уже два оборота ((360°+360°+240°)), а для угла в (2640°) – целых семь.
Стоит запомнить, что:
Косинус прямого угла равен нулю. Косинус тупого угла – отрицателен.
Знаки косинуса по четвертям
С помощью оси косинусов (то есть, оси абсцисс, выделенной на рисунке красным цветом) легко определить знаки косинусов по четвертям числовой (тригонометрической) окружности:
– там, где значения на оси от (0) до (1), косинус будет иметь знак плюс (I и IV четверти – зеленая область),
– там, где значения на оси от (0) до (-1), косинус будет иметь знак минус (II и III четверти – фиолетовая область).

Пример. Определите знак (cos 1).
Решение: Найдем (1) на тригонометрическом круге. Будем отталкиваться от того, что (π=3,14). Значит единица, примерно, в три раза ближе к нулю (точке «старта»).

Если провести перпендикуляр к оси косинусов, то станет очевидно, что (cos1) – положителен.
Ответ: плюс.
Связь с другими тригонометрическими функциями:
– синусом того же угла (или числа): основным тригонометрическим тождеством (sin^2x+cos^2x=1)
– тангенсом того же угла (или числа): формулой (1+tg^2x=)(frac{1}{cos^2x})
– котангенсом и синусом того же угла (или числа): формулой (ctgx=)(frac{cos{x}}{sinx})
Другие наиболее часто применяемые формулы смотри здесь.
Функция (y=cos{x})
Если отложить по оси (x) углы в радианах, а по оси (y) – соответствующие этим углам значения косинуса, мы получим следующий график:

График данной функции называется косинусоида и обладает следующими свойствами:
– область определения – любое значение икса: (D(cos{x} )=R)
– область значений – от (-1) до (1) включительно: (E(cos{x} )=[-1;1])
– четная: (cos(-x)=cos{x})
– периодическая с периодом (2π): (cos(x+2π)=cos{x})
– точки пересечения с осями координат:
ось абсцисс: (()(frac{π}{2})(+πn),(;0)), где (n ϵ Z)
ось ординат: ((0;1))
– промежутки знакопостоянства:
функция положительна на интервалах: ((-)(frac{π}{2})(+2πn;) (frac{π}{2})(+2πn)), где (n ϵ Z)
функция отрицательна на интервалах: (()(frac{π}{2})(+2πn;)(frac{3π}{2})(+2πn)), где (n ϵ Z)
– промежутки возрастания и убывания:
функция возрастает на интервалах: ((π+2πn;2π+2πn)), где (n ϵ Z)
функция убывает на интервалах: ((2πn;π+2πn)), где (n ϵ Z)
– максимумы и минимумы функции:
функция имеет максимальное значение (y=1) в точках (x=2πn), где (n ϵ Z)
функция имеет минимальное значение (y=-1) в точках (x=π+2πn), где (n ϵ Z).
Смотрите также:
Синус
Тангенс
Котангенс
Решение уравнения (cosx=a)
|
Косинус угла cos(A) — есть отношение прилежащего катета b к гипотенузе c [ cos(A) = frac{b}{c} ] |
Косинус угла — cos(A), таблица
|
0° Косинус угла 0 градусов |
$ cos(0°) = cos(0) = 1 $ |
1.000 |
|
30° Косинус угла 30 градусов |
$ cos(30°) = cosBig(Largefrac{pi}{6}normalsizeBig) = Largefrac{sqrt{3}}{2}normalsize $ |
0.866 |
|
45° Косинус угла 45 градусов |
$ cos(45°) = cosBig(Largefrac{pi}{4}normalsizeBig) = Largefrac{sqrt{2}}{2}normalsize $ |
0.707 |
|
60° Косинус угла 60 градусов |
$ cos(60°) = cosBig(Largefrac{pi}{3}normalsizeBig) = Largefrac{1}{2}normalsize $ |
0.500 |
|
90° Косинус угла 90 градусов |
$ cos(90°) = cosBig(Largefrac{pi}{2}normalsizeBig) = 0 $ |
0.000 |
Вычислить, найти косинус угла cos(A) и угол, в прямоугольном треугольнике
Вычислить, найти косинус угла cos(A) по углу A в градусах
Вычислить, найти косинус угла cos(A) по углу A в радианах
Косинус угла — cos(A) |
стр. 218 |
|---|
Косинус угла. Таблица косинусов.
Косинус угла через градусы, минуты и секунды
Косинус угла через десятичную запись угла
Как найти угол зная косинус этого угла
У косинуса есть обратная тригонометрическая функция – arccos(y)=x
cos(arccos(y))=y
Пример cos(60°) = 1/2; arccos(1/2) = 60°
Рассчитать арккосинус
Определение косинуса
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
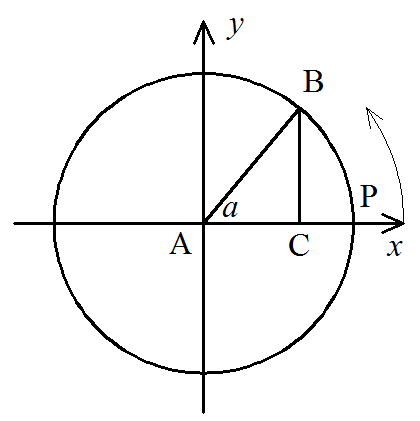
Косинусом угла α называется абсцисса точки B единичной окружности, полученной при повороте точки P(1;0) на угол α.
cos(α) = AC/AB
cos(-α) = cos(α)
cos(α ± 2π) = cos(α)
Таблица косинусов в радианах
cos(0°) = 1cos(π/12) = cos(15°) = 0.9659258263cos(π/6) = cos(30°) = 0.8660254038cos(π/4) = cos(45°) = 0.7071067812cos(π/3) = cos(60°) = 0.5cos(5π/12) = cos(75°) = 0.2588190451cos(π/2) = cos(90°) = 0cos(7π/12) = cos(105°) = -0.2588190451cos(2π/3) = cos(120°) = -0.5cos(3π/4) = cos(135°) = -0.7071067812cos(5π/6) = cos(150°) = -0.8660254038cos(11π/12) = cos(165°) = -0.9659258263cos(π) = cos(180°) = -1cos(13π/12) = cos(195°) = -0.9659258263cos(7π/6) = cos(210°) = -0.8660254038cos(5π/4) = cos(225°) = -0.7071067812cos(4π/3) = cos(240°) = -0.5cos(17π/12) = cos(255°) = -0.2588190451cos(3π/2) = cos(270°) = 0cos(19π/12) = cos(285°) = 0.2588190451cos(5π/3) = cos(300°) = 0.5cos(7π/4) = cos(315°) = 0.7071067812cos(11π/6) = cos(330°) = 0.8660254038cos(23π/12) = cos(345°) = 0.9659258263
Таблица Брадиса косинусы
| cos(0) = 1 | cos(120) = -0.5 | cos(240) = -0.5 |
| cos(1) = 0.9998476952 | cos(121) = -0.5150380749 | cos(241) = -0.4848096202 |
| cos(2) = 0.999390827 | cos(122) = -0.5299192642 | cos(242) = -0.4694715628 |
| cos(3) = 0.9986295348 | cos(123) = -0.544639035 | cos(243) = -0.4539904997 |
| cos(4) = 0.9975640503 | cos(124) = -0.5591929035 | cos(244) = -0.4383711468 |
| cos(5) = 0.9961946981 | cos(125) = -0.5735764364 | cos(245) = -0.4226182617 |
| cos(6) = 0.9945218954 | cos(126) = -0.5877852523 | cos(246) = -0.4067366431 |
| cos(7) = 0.9925461516 | cos(127) = -0.6018150232 | cos(247) = -0.3907311285 |
| cos(8) = 0.9902680687 | cos(128) = -0.6156614753 | cos(248) = -0.3746065934 |
| cos(9) = 0.9876883406 | cos(129) = -0.629320391 | cos(249) = -0.3583679495 |
| cos(10) = 0.984807753 | cos(130) = -0.6427876097 | cos(250) = -0.3420201433 |
| cos(11) = 0.9816271834 | cos(131) = -0.656059029 | cos(251) = -0.3255681545 |
| cos(12) = 0.9781476007 | cos(132) = -0.6691306064 | cos(252) = -0.3090169944 |
| cos(13) = 0.9743700648 | cos(133) = -0.6819983601 | cos(253) = -0.2923717047 |
| cos(14) = 0.9702957263 | cos(134) = -0.6946583705 | cos(254) = -0.2756373558 |
| cos(15) = 0.9659258263 | cos(135) = -0.7071067812 | cos(255) = -0.2588190451 |
| cos(16) = 0.9612616959 | cos(136) = -0.7193398003 | cos(256) = -0.2419218956 |
| cos(17) = 0.956304756 | cos(137) = -0.7313537016 | cos(257) = -0.2249510543 |
| cos(18) = 0.9510565163 | cos(138) = -0.7431448255 | cos(258) = -0.2079116908 |
| cos(19) = 0.9455185756 | cos(139) = -0.7547095802 | cos(259) = -0.1908089954 |
| cos(20) = 0.9396926208 | cos(140) = -0.7660444431 | cos(260) = -0.1736481777 |
| cos(21) = 0.9335804265 | cos(141) = -0.7771459615 | cos(261) = -0.156434465 |
| cos(22) = 0.9271838546 | cos(142) = -0.7880107536 | cos(262) = -0.139173101 |
| cos(23) = 0.9205048535 | cos(143) = -0.79863551 | cos(263) = -0.1218693434 |
| cos(24) = 0.9135454576 | cos(144) = -0.8090169944 | cos(264) = -0.1045284633 |
| cos(25) = 0.906307787 | cos(145) = -0.8191520443 | cos(265) = -0.08715574275 |
| cos(26) = 0.8987940463 | cos(146) = -0.8290375726 | cos(266) = -0.06975647374 |
| cos(27) = 0.8910065242 | cos(147) = -0.8386705679 | cos(267) = -0.05233595624 |
| cos(28) = 0.8829475929 | cos(148) = -0.8480480962 | cos(268) = -0.0348994967 |
| cos(29) = 0.8746197071 | cos(149) = -0.8571673007 | cos(269) = -0.01745240644 |
| cos(30) = 0.8660254038 | cos(150) = -0.8660254038 | cos(270) = 0 |
| cos(31) = 0.8571673007 | cos(151) = -0.8746197071 | cos(271) = 0.01745240644 |
| cos(32) = 0.8480480962 | cos(152) = -0.8829475929 | cos(272) = 0.0348994967 |
| cos(33) = 0.8386705679 | cos(153) = -0.8910065242 | cos(273) = 0.05233595624 |
| cos(34) = 0.8290375726 | cos(154) = -0.8987940463 | cos(274) = 0.06975647374 |
| cos(35) = 0.8191520443 | cos(155) = -0.906307787 | cos(275) = 0.08715574275 |
| cos(36) = 0.8090169944 | cos(156) = -0.9135454576 | cos(276) = 0.1045284633 |
| cos(37) = 0.79863551 | cos(157) = -0.9205048535 | cos(277) = 0.1218693434 |
| cos(38) = 0.7880107536 | cos(158) = -0.9271838546 | cos(278) = 0.139173101 |
| cos(39) = 0.7771459615 | cos(159) = -0.9335804265 | cos(279) = 0.156434465 |
| cos(40) = 0.7660444431 | cos(160) = -0.9396926208 | cos(280) = 0.1736481777 |
| cos(41) = 0.7547095802 | cos(161) = -0.9455185756 | cos(281) = 0.1908089954 |
| cos(42) = 0.7431448255 | cos(162) = -0.9510565163 | cos(282) = 0.2079116908 |
| cos(43) = 0.7313537016 | cos(163) = -0.956304756 | cos(283) = 0.2249510543 |
| cos(44) = 0.7193398003 | cos(164) = -0.9612616959 | cos(284) = 0.2419218956 |
| cos(45) = 0.7071067812 | cos(165) = -0.9659258263 | cos(285) = 0.2588190451 |
| cos(46) = 0.6946583705 | cos(166) = -0.9702957263 | cos(286) = 0.2756373558 |
| cos(47) = 0.6819983601 | cos(167) = -0.9743700648 | cos(287) = 0.2923717047 |
| cos(48) = 0.6691306064 | cos(168) = -0.9781476007 | cos(288) = 0.3090169944 |
| cos(49) = 0.656059029 | cos(169) = -0.9816271834 | cos(289) = 0.3255681545 |
| cos(50) = 0.6427876097 | cos(170) = -0.984807753 | cos(290) = 0.3420201433 |
| cos(51) = 0.629320391 | cos(171) = -0.9876883406 | cos(291) = 0.3583679495 |
| cos(52) = 0.6156614753 | cos(172) = -0.9902680687 | cos(292) = 0.3746065934 |
| cos(53) = 0.6018150232 | cos(173) = -0.9925461516 | cos(293) = 0.3907311285 |
| cos(54) = 0.5877852523 | cos(174) = -0.9945218954 | cos(294) = 0.4067366431 |
| cos(55) = 0.5735764364 | cos(175) = -0.9961946981 | cos(295) = 0.4226182617 |
| cos(56) = 0.5591929035 | cos(176) = -0.9975640503 | cos(296) = 0.4383711468 |
| cos(57) = 0.544639035 | cos(177) = -0.9986295348 | cos(297) = 0.4539904997 |
| cos(58) = 0.5299192642 | cos(178) = -0.999390827 | cos(298) = 0.4694715628 |
| cos(59) = 0.5150380749 | cos(179) = -0.9998476952 | cos(299) = 0.4848096202 |
| cos(60) = 0.5 | cos(180) = -1 | cos(300) = 0.5 |
| cos(61) = 0.4848096202 | cos(181) = -0.9998476952 | cos(301) = 0.5150380749 |
| cos(62) = 0.4694715628 | cos(182) = -0.999390827 | cos(302) = 0.5299192642 |
| cos(63) = 0.4539904997 | cos(183) = -0.9986295348 | cos(303) = 0.544639035 |
| cos(64) = 0.4383711468 | cos(184) = -0.9975640503 | cos(304) = 0.5591929035 |
| cos(65) = 0.4226182617 | cos(185) = -0.9961946981 | cos(305) = 0.5735764364 |
| cos(66) = 0.4067366431 | cos(186) = -0.9945218954 | cos(306) = 0.5877852523 |
| cos(67) = 0.3907311285 | cos(187) = -0.9925461516 | cos(307) = 0.6018150232 |
| cos(68) = 0.3746065934 | cos(188) = -0.9902680687 | cos(308) = 0.6156614753 |
| cos(69) = 0.3583679495 | cos(189) = -0.9876883406 | cos(309) = 0.629320391 |
| cos(70) = 0.3420201433 | cos(190) = -0.984807753 | cos(310) = 0.6427876097 |
| cos(71) = 0.3255681545 | cos(191) = -0.9816271834 | cos(311) = 0.656059029 |
| cos(72) = 0.3090169944 | cos(192) = -0.9781476007 | cos(312) = 0.6691306064 |
| cos(73) = 0.2923717047 | cos(193) = -0.9743700648 | cos(313) = 0.6819983601 |
| cos(74) = 0.2756373558 | cos(194) = -0.9702957263 | cos(314) = 0.6946583705 |
| cos(75) = 0.2588190451 | cos(195) = -0.9659258263 | cos(315) = 0.7071067812 |
| cos(76) = 0.2419218956 | cos(196) = -0.9612616959 | cos(316) = 0.7193398003 |
| cos(77) = 0.2249510543 | cos(197) = -0.956304756 | cos(317) = 0.7313537016 |
| cos(78) = 0.2079116908 | cos(198) = -0.9510565163 | cos(318) = 0.7431448255 |
| cos(79) = 0.1908089954 | cos(199) = -0.9455185756 | cos(319) = 0.7547095802 |
| cos(80) = 0.1736481777 | cos(200) = -0.9396926208 | cos(320) = 0.7660444431 |
| cos(81) = 0.156434465 | cos(201) = -0.9335804265 | cos(321) = 0.7771459615 |
| cos(82) = 0.139173101 | cos(202) = -0.9271838546 | cos(322) = 0.7880107536 |
| cos(83) = 0.1218693434 | cos(203) = -0.9205048535 | cos(323) = 0.79863551 |
| cos(84) = 0.1045284633 | cos(204) = -0.9135454576 | cos(324) = 0.8090169944 |
| cos(85) = 0.08715574275 | cos(205) = -0.906307787 | cos(325) = 0.8191520443 |
| cos(86) = 0.06975647374 | cos(206) = -0.8987940463 | cos(326) = 0.8290375726 |
| cos(87) = 0.05233595624 | cos(207) = -0.8910065242 | cos(327) = 0.8386705679 |
| cos(88) = 0.0348994967 | cos(208) = -0.8829475929 | cos(328) = 0.8480480962 |
| cos(89) = 0.01745240644 | cos(209) = -0.8746197071 | cos(329) = 0.8571673007 |
| cos(90) = 0 | cos(210) = -0.8660254038 | cos(330) = 0.8660254038 |
| cos(91) = -0.01745240644 | cos(211) = -0.8571673007 | cos(331) = 0.8746197071 |
| cos(92) = -0.0348994967 | cos(212) = -0.8480480962 | cos(332) = 0.8829475929 |
| cos(93) = -0.05233595624 | cos(213) = -0.8386705679 | cos(333) = 0.8910065242 |
| cos(94) = -0.06975647374 | cos(214) = -0.8290375726 | cos(334) = 0.8987940463 |
| cos(95) = -0.08715574275 | cos(215) = -0.8191520443 | cos(335) = 0.906307787 |
| cos(96) = -0.1045284633 | cos(216) = -0.8090169944 | cos(336) = 0.9135454576 |
| cos(97) = -0.1218693434 | cos(217) = -0.79863551 | cos(337) = 0.9205048535 |
| cos(98) = -0.139173101 | cos(218) = -0.7880107536 | cos(338) = 0.9271838546 |
| cos(99) = -0.156434465 | cos(219) = -0.7771459615 | cos(339) = 0.9335804265 |
| cos(100) = -0.1736481777 | cos(220) = -0.7660444431 | cos(340) = 0.9396926208 |
| cos(101) = -0.1908089954 | cos(221) = -0.7547095802 | cos(341) = 0.9455185756 |
| cos(102) = -0.2079116908 | cos(222) = -0.7431448255 | cos(342) = 0.9510565163 |
| cos(103) = -0.2249510543 | cos(223) = -0.7313537016 | cos(343) = 0.956304756 |
| cos(104) = -0.2419218956 | cos(224) = -0.7193398003 | cos(344) = 0.9612616959 |
| cos(105) = -0.2588190451 | cos(225) = -0.7071067812 | cos(345) = 0.9659258263 |
| cos(106) = -0.2756373558 | cos(226) = -0.6946583705 | cos(346) = 0.9702957263 |
| cos(107) = -0.2923717047 | cos(227) = -0.6819983601 | cos(347) = 0.9743700648 |
| cos(108) = -0.3090169944 | cos(228) = -0.6691306064 | cos(348) = 0.9781476007 |
| cos(109) = -0.3255681545 | cos(229) = -0.656059029 | cos(349) = 0.9816271834 |
| cos(110) = -0.3420201433 | cos(230) = -0.6427876097 | cos(350) = 0.984807753 |
| cos(111) = -0.3583679495 | cos(231) = -0.629320391 | cos(351) = 0.9876883406 |
| cos(112) = -0.3746065934 | cos(232) = -0.6156614753 | cos(352) = 0.9902680687 |
| cos(113) = -0.3907311285 | cos(233) = -0.6018150232 | cos(353) = 0.9925461516 |
| cos(114) = -0.4067366431 | cos(234) = -0.5877852523 | cos(354) = 0.9945218954 |
| cos(115) = -0.4226182617 | cos(235) = -0.5735764364 | cos(355) = 0.9961946981 |
| cos(116) = -0.4383711468 | cos(236) = -0.5591929035 | cos(356) = 0.9975640503 |
| cos(117) = -0.4539904997 | cos(237) = -0.544639035 | cos(357) = 0.9986295348 |
| cos(118) = -0.4694715628 | cos(238) = -0.5299192642 | cos(358) = 0.999390827 |
| cos(119) = -0.4848096202 | cos(239) = -0.5150380749 | cos(359) = 0.9998476952 |
Похожие калькуляторы
Для того, чтобы определить значение угла α, необходимо воспользоваться подходящей функции из тригонометрии. Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение.
В этой статье мы подробно поговорим о функциях из тригонометрии. Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая.
Рассмотрим подробно каждый случай.
Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.
Соотношения сторон и углов фигуры используются для того, чтобы определить значения для 30°, 45°, 60°. Если угол выходит за пределы 90°, то перед вычислением значения следует воспользоваться специальной формулой для того, чтобы привести угол к нужному виду.
Если известно значение синуса для α, можно быстро узнать значение косинуса для этого же угла. Это легко выполнить с помощью основных тождеств, которые представлены в геометрии.
В некоторых случаях для того, чтобы узнать sin или cos угла, можно использовать подходящую тригонометрическую формулу. Например, по известному значению синуса 45°, мы сможем определить значение синуса 30°, воспользовавшись правилом из тригонометрии.
Если для примера не подходит ни одно из приведенных выше решений, можно найти приближенное значение. В этом вам помогут таблицы основных тригонометрических функций, которые легко можно найти.
Если взять за основу определения, возможно определить значения для определенного угла α. Также можно вычислить значения тангенса и котангенса для определенного случая. Можно найти значений основных функций из тригонометрии для частных вариантов. Это углы 0°, 90°, 180°, 270°, 360°.
Разобьем эти углы на четыре группы: 360·z градусов (2π·z рад), 90+360·z градусов (π2+2π·z рад), 180+360·z градусов (π+2π·z рад) и 270+360·z градусов (3π2+2π·z рад), где z- любое целое число.
Изобразим данные формулы на рисунке:
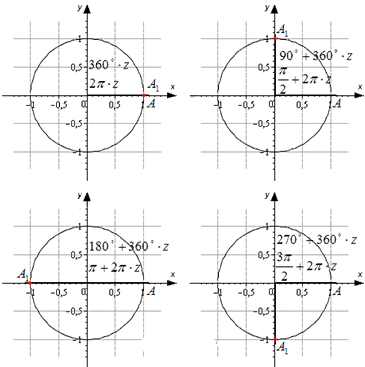
Для каждой группы соответствуют свои значения.
При повороте из точки A на 360·z°, она переходит в себя. А1(1, 0). Синус 0°, 360°, 720° равен 0, а косинус равен 1. Представим это в виде формулы: sin (360°·z)=0 и cos (360°·z)=1 .
Можно определить, что tg (360°·z)=01=0 , а котангенс не определен.
Если А(1, 0) повернуть на 90+360·z°, то она перейдет в А1 (0, 1). По определению: sin (90°+360°·z) =1 и cos (90°+360°·z) =0 . Мы не сможем определить значение тангенса, но котангенс рассчитывается по данной формуле: ctg (90°+360°·z) =01=0 .
Рассмотрим особенности для третьей группы углов. После поворота точки А(1, 0) на любой из углов 180+360·z°, она перейдет в A1(−1, 0). Мы находим значения функций кроме тангенса.
Рассмотрим правила для четвертой группы углов. При повороте точки на 270+360·z° мы попадем в A1(0, −1). Мы находим значения всех функций кроме тангенса.
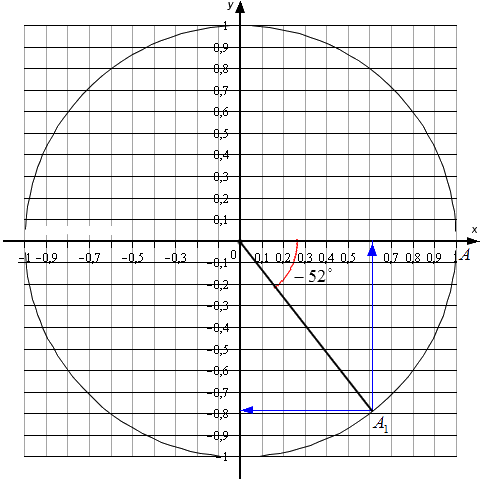
Для углов, которые не относятся к перечню от 0 °, 90 °, 180 °, 270 °, 360 °…, точных значений нет. Мы можем найти лишь приближенные значения. Рассмотрим пример. Условия – найти основные значения для угла −52 °. Выполним построения.
Согласно рисунку, абсцисса А1 ≈ 0,62, а ордината ≈ −0,78. Соответственно, sin(-52°)≈-0,78 и cos(-52°)≈0,62 . Осталось определиться с тангенсом и котангенсом.
Выполняем вычисления: tg(-52°)≈-0, 780, 62≈-1,26 и ctg(-52°)≈0,62-0,78≈-0,79.
Чем точнее выполняется чертеж, тем более точными будут значения для каждого индивидуального случая. Выполнять вычисления удобно только в теории, так как на практике довольно сложно и долго выполнять рисунки.
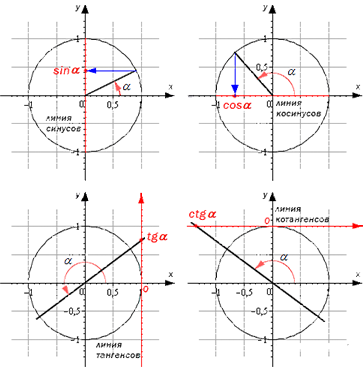
Линии тригонометрических функций
Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.
Рассмотрим их на подробном рисунке
Как найти sin α, cos α, tg α, ctg α
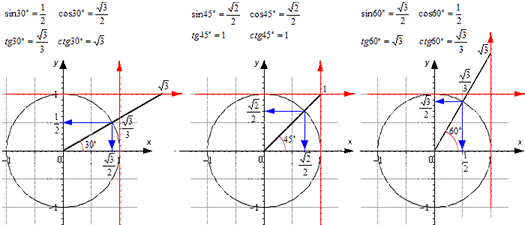
Для тридцати-, сорокопяти-, шестидесятиградусных углов мы имеем определенные значения. Чтобы найти их, можно воспользоваться правилами о прямоугольном треугольнике с острыми углами. Для этого используется теорема Пифагора.
Для того, чтобы узнать значения для углов тридцати- и шестидесятиградусных углов изображаем прямоугольный треугольник с углами данной величины. Длина гипотенузы должна быть равна 1. Согласно теореме Пифагора, катет, лежащий напротив тридцатиградусного угла, равен половине гипотенузы. Воспользуемся теоремой: 12-122=32 . Так как синус угла – это катет, деленный на гипотенузу, вычисляем, что sin 30°=121=12 и sin 60°=321=32 .
Косинус можно найти по формуле, которая предполагает деление прилежащего катета на гипотенузу. Вычисляем: cos 30°=321=32 и cos 60°=121=12 .
Тангенс можно найти по формуле, которая предполагает деление противолежащего катета на прилежащий. Котангенс находим по такой же схеме – делим прилежащий катет на противолежащий.
Вычисляем: tg 30°=1232=13=33 и tg 60°=3212=3 . Находим котангенс по подобной схеме: сtg 30°=3212=3 и сtg 60°=1232=13=33 . После этого приступаем к вычислению значений основных тригонометрических функций для сорока пятиградусного угла. Используем равнобедренный треугольник с углами 45° и гипотенузой, которая равна 1. Используем теорему Пифагора. Согласно формуле, длины катетов равны 22 . Т
Теперь мы сможем найти значения для основных тригонометрических функций. Используем формулу, которая предполагает деление длин соответствующих сторон рассматриваемого треугольника.
Выводим формулу: ctg 45°=2222=1 .
Полученные значения для тридцати-, сорокапяти-, шестидесятиградусных углов будут использоваться для решения различных задач. Запишите их – они часто будут использоваться. Для удобства можно использовать таблицу значений.
Проиллюстрируем значения для тридцати-, сорокапяти-, шестидесятиградусных углов с использованием окружности и линий.
Значения основных функций тригонометрии
Основные тождества из геометрии связывают с собой sin α, cos α, tg α, ctg α для определенного угла. С помощью одной функции вы легко сможете найти другую.
Для того, чтобы найти синус по известному косинусу, sin2α+cos2α=1 .
Тангенс по известному косинусу tg2α+1=1cos2α .
Котангенс по известному синусу или наоборот 1+ctg2α= 1sin2α .
Тангенс через котангенс или наоборот можно найти благодаря удобной формуле: tg α·ctg α=1 .
Для того, чтобы закрепить полученные знания, рассмотрим их на подробном примере
Необходимо найти значение синуса угла π8, если tg π8=2-1 .
Сначала найдем котангенс угла: ctgπ8=1tgπ8=12-1=2+1(2-1)·(2+1)= 2+1(2)2-12=2+1 Воспользуемся формулой 1+ctg2α=1sin2α . Благодаря этому мы вычисляем значение синуса. Имеем
sin2π8=11+ctg2π8=11+(2+1)2=14+22=12·(2+2)=2-22·(2+2)·(2-2)==2-22·(22-(2)2)=2-24
Для завершения необходимо определить значение синуса. Угол π8 является углом первой четверти, то синус является положительным. Чтобы точно определить знак, вы можете воспользоваться таблицей, в которой определены знаки по четвертям координатной плоскости. Таким образом, sin π8=sin2π8=2-24=2-22 . sin π8=2-22.
Сведение к углу
Удобнее всего находить значения для угла от 0 до 90 °. Сведение к углу из интервала от 0 до 90 °. Если угол не соответствует заданному интервалу, можно использовать законы и тождества, которые мы учили на уроках геометрии. Тогда мы сможем найти значение, которое будет равно для угла указанных пределах.
Задача заключается в том, чтобы найти синус 210°. Представим 210 как разность или сумму, разложив число на несколько. Воспользуемся соответствующей формулой для приведения. Используем формулу для нахождения значения синуса 30°: sin 210°=sin(180°+30°)=-sin 30°=-12 , или косинуса 60 ° sin 210°=sin(270°-60°)=-cos 60°=-12.
Для того, чтобы решать задачи было намного проще, при нахождении значений переходите к углам из интервала от 0 до 90° с помощью формул приведения, если угол не находится в этих пределах.
Использование формул
Раннее мы рассмотрели подробности, касающиеся нахождению значений основных функций с использованием формул тригонометрии. Для того, чтобы определить значение для определенного угла, используйте формулы и значения основных функций для известных углов.
Для примера вычислим значение тангенса π8, который был использован в предыдущем примере. Возьмем за основу основные формулы тригонометрии.
Найдите значение tgπ8 .
Используя формулу тангенса, преобразуем уравнение до следующего равенства tg2π8=1-cosπ41+cosπ4 . Значения косинуса угла π4 известны из предыдущего примера. Благодаря этому мы быстро найдем значения тангенса.
tg2π8=1-cosπ41+cosπ4=1-221+22=2-22+2==(2-2)2(2+2)·(2-2)=(2-2)222-(2)2=(2-2)22
Угол π8 является углом первой четверти. Согласно таблице основных тригонометрических функций по четвертям координатной плоскости, тангенс этого угла положителен. Продолжаем вычисления для дальнейшего решения: tgπ8=tg2π8=(2-2)22=2-22=2-1
tgπ8=2-1.
Частные случаи
Тригонометрия – довольно сложная наука. Далеко не всегда можно найти формулы, используемые для вычисления. Существует множество уравнений, которые не поддаются стандартным формулам. Некоторые значения очень сложно обозначить точной цифрой. Это не так просто, как может показаться.
Однако точные значения не всегда нужны. Хватает и тех, что не претендуют на высокую точность. Благодаря существующим таблицам, которые можно найти в математических учебниках, можно найти любое приближенное значение основных функций. Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.