Ответы Mail.ru
Образование
ВУЗы, Колледжи
Детские сады
Школы
Дополнительное образование
Образование за рубежом
Прочее образование
Вопросы – лидеры.
Особенности перевода в другой ВУЗ
1 ставка
Помогите решить задачи в Excel
1 ставка
Основные понятия и законы химии.
Билет №3
Помоги пожалуйста срочно!!!!!!!!!!!
1 ставка
Как построить третий вид чертежа по 2 данным?
1 ставка
Реставрационно-художественный колледж СПб
1 ставка
Лидеры категории
Лена-пена
Искусственный Интеллект
М.И.
Искусственный Интеллект
Y.Nine
Искусственный Интеллект
•••
Regin@
Ученик
(161),
закрыт
7 лет назад
Лучший ответ
Я
Ученик
(199)
14 лет назад
единица минус sin вадрат алфа
Остальные ответы
Andrey Kurgannikov
Мудрец
(12072)
14 лет назад
1-sin квадра альфа ))
ymka
Гуру
(3861)
14 лет назад
это выражение будет равно cos квадрат альфа
Похожие вопросы
Уравнения разложения тригонометрических функций:квадрат синус альфа, косинус альфа, тангенс альфа, котангенс альфа.
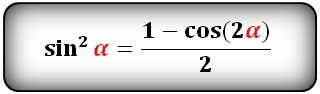
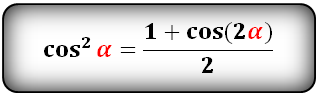
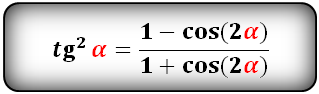
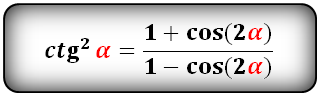
Формулы преобразования функций двойного угла (2α) в выражение через одинарный угол (α)
sin(2α)- через sin и cos:
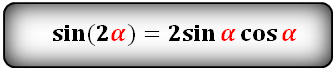
sin(2α)- через tg и ctg:
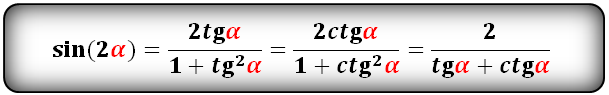
cos(2α)- через sin и cos:
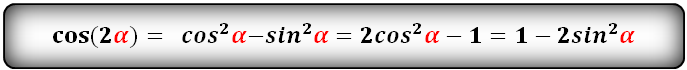
cos(2α)- через tg и ctg:
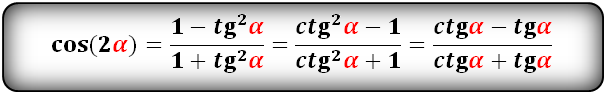
tg(2α) и сtg(2α):
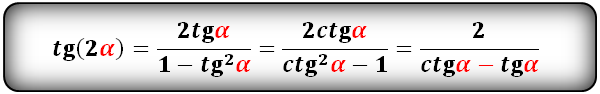
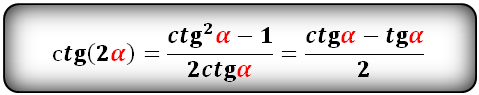
Формулы преобразования функций (синус, косинус, тангенс, котангенс), тройного угла (3α) в выражение через одинарный угол (α):


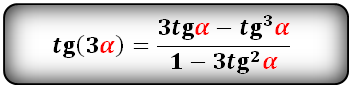
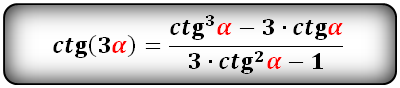
Тригонометрические формулы преобразования разности аргументов


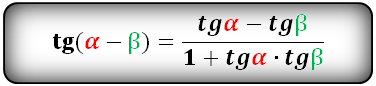
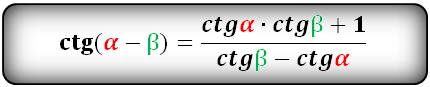
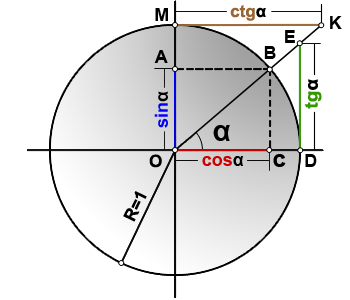
sin(α)=OA
cos(α)=OC
tg(α)=DE
ctg(α)=MK
R=OB=1
Значения функций для некоторых углов, α
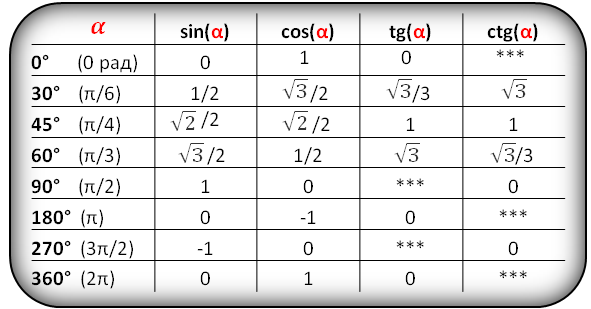
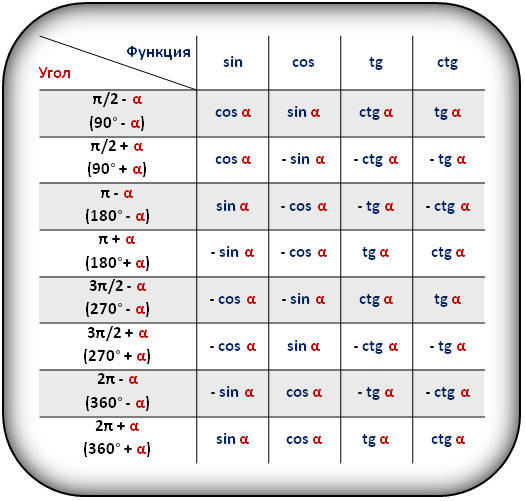
В таблице показаны формулы приведения для тригонометрических функций (sin, cos, tg, ctg).
Косинус в квадрате и синус в квадрате
Разбираемся с простыми понятиями: синус и косинус и вычисление косинуса в квадрате и синуса в квадрате.
Синус и косинус изучаются в тригонометрии (науке о треугольниках с прямым углом).
Поэтому для начала вспомним основные понятия прямоугольного треугольника:
Гипотенуза — сторона, которая всегда лежит напротив прямого угла (угла в 90 градусов). Гипотенуза — это самая длинная сторона треугольника с прямым углом.
Оставшиеся две стороны в прямоугольном треугольнике называются катетами.
Также следует помнить, что три угла в треугольнике всегда имеют сумму в 180°.

Теперь переходим к косинусу и синусу угла альфа (∠α) (так можно назвать любой непрямой угол в треугольнике или использовать в качестве обозначение икс — «x», что не меняет сути).
Синус угла альфа (sin ∠α) — это отношение противолежащего катета (сторона, лежащая напротив соответствующего угла) к гипотенузе. Если смотреть по рисунку, то sin ∠ABC = AC / BC
Косинус угла альфа (cos ∠α) — отношение прилежащего к углу катета к гипотенузе. Если снова смотреть по рисунку выше, то cos ∠ABC = AB / BC
И просто для напоминания: косинус и синус никогда не будут больше единицы, так как любой катит короче гипотенузы (а гипотенуза — это самая длинная сторона любого треугольника, ведь самая длинная сторона расположена напротив самого большого угла в треугольнике).
Косинус в квадрате, синус в квадрате
Теперь переходим к основным тригонометрическим формулам: вычисление косинуса в квадрате и синуса в квадрате.
Для их вычисления следует запомнить основное тригонометрическое тождество:
sin 2 α + cos 2 α = 1 (синус квадрат плюс косинус квадрат одного угла всегда равняются единице).
Из тригонометрического тождества делаем выводы о синусе:
sin 2 α = 1 — cos 2 α
или более сложный вариант формулы: синус квадрат альфа равен единице минус косинус двойного угла альфа и всё это делить на два.
sin 2 α = (1 – cos(2α)) / 2
Из тригонометрического тождества делаем выводы о косинусе:
cos 2 α = 1 — sin 2 α
или более сложный вариант формулы: косинус квадрат альфа равен единице плюс косинус двойного угла альфа и также делим всё на два.
cos 2 α = (1 + cos(2α)) / 2
Эти две более сложные формулы синуса в квадрате и косинуса в квадрате называют еще «понижение степени для квадратов тригонометрических функций». Т.е. была вторая степень, понизили до первой и вычисления стали удобнее.
Добавить интересную новость
Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников
user->isGuest) »]) . ‘ или ‘ . Html::a(‘зарегистрируйтесь’, [‘/user/registration/register’], [‘class’ => »]) . ‘ , чтобы получать деньги $$$ за каждый набранный балл!’); > else user->identity->profile->first_name) || !empty(Yii::$app->user->identity->profile->surname))user->identity->profile->first_name . ‘ ‘ . Yii::$app->user->identity->profile->surname; > else echo ‘Получайте деньги за каждый набранный балл!’; > ?>—>
Косинус в квадрате
Косинус (cos) — это тригонометрическая функция, геометрически представляющая отношение прилежащего катета к гипотенузе в прямоугольном треугольнике.
cos 2 (x)=cos(x)*cos(x)
Значение косинуса находится в диапазоне от -1 до +1.
Быстро выполнить эту простейшую математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор вычисления квадрата косинуса (косинуса в квадрате). С помощью этого калькулятора вы в один клик сможете вычислить квадрат косинус любого угла.
Квадрат синуса, косинуса, тангенса, котангенса (альфа)
квадрат синус альфа, косинус альфа, тангенс альфа, котангенс альфа.
sin в квадрате
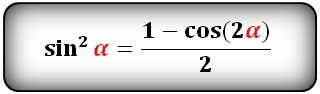
cos в квадрате
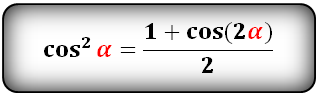
tg в квадрате
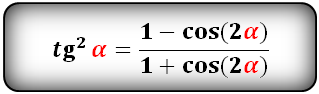
ctg в квадрате
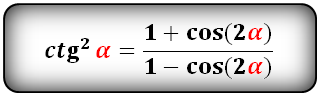
Подробности Автор: Administrator Опубликовано: 17 сентября 2011 Обновлено: 13 августа 2021
Чему равен косинус квадрат альфа?
Чему равен косинус квадрат альфа?
или более сложный вариант формулы: косинус квадрат альфа равен единице плюс косинус двойного угла альфа и также делим всё на два.
Чему равен синус в квадрате 60 градусов?
| значение угла α (градусов) | значение угла α в радианах | sin (синус) |
|---|---|---|
| 60 | π/3 | 0,8660 |
| 65 | 13π/36 | 0,9063 |
| 70 | 7π/18 | 0,9397 |
| 75 | 5π/12 | 0,9659 |
Что такое синус двойного угла?
Синус двойного угла равен удвоенному произведению синуса данного угла на косинус данного угла.
Какая из формул является формулой косинуса двойного угла?
Тригонометрические функции двойного угла
| Формула | Название формулы |
|---|---|
| sin 2α = 2 sin α cos α | Синус двойного угла |
| cos 2α = cos 2α – sin2α cos 2α = 2cos 2α – 1 cos 2α = 1 – 2sin 2α | Косинус двойного угла |
| Тангенс двойного угла |
Чему равен котангенс двойного угла?
Тригонометрические формулы
| (1) | Основное тригонометрическое тождество | sin2(α) + cos2(α) = 1 |
|---|---|---|
| (7) | Тангенс двойного угла | tg(2α) = 2tg(α) 1 – tg2(α) |
| (8) | Котангенс двойного угла | ctg(2α) = ctg2(α) – 1 2ctg(α) |
| (9) | Синус тройного угла | sin(3α) = 3sin(α)cos2(α) – sin3(α) |
| (10) | Косинус тройного угла | cos(3α) = cos3(α) – 3cos(α)sin2(α) |
Стоит почитать
- Что такое CH x?
- Чему равен синус п на 4?
- Как перевернуть страницу в ворде на альбомную?
- Что называется электрической ёмкостью конденсатора?
- Как поставить длинное тире на клавиатуре?
- Как в ворде набрать текст вертикально?
- Чему равен косинус 90 градусов?
- Что является качественной характеристикой физической величины?
- Как написать синус в квадрате в Excel?
- Как писать заявление на отгул за ранее отработанное время?
Похожие вопросы
- Что называется трапецией?
- Как найти высоту в произвольном треугольнике?
- Как убрать нумерацию страниц в ворде с первых страниц?
- Как найти диагональ квадрата если известна его площадь?
- Что значит косая черта?
- Как найти высоту прямоугольного треугольника зная катет и гипотенузу?
- Как написать дробь в тексте?
- Что такое равносильное неравенство?
- Как выровнять содержание?
- Как добавить страницу в ворде с помощью клавиатуры?
Ответ мой будет аналогичным ответу на похожий вопрос (см. здесь).
Из основного тригонометрического тождества:
выразим косинус в квадрате угла а:

Значит косинус угла равен либо корню квадратному из этого выражения, либо ему же, только со знаком -.
Знак перед корнем зависит от ограничения, которое накладывается для определенности в условии задачи.
Если дано положительное значение синуса,то угол находится в 1-й или во 2-й четверти. В первой четверти (0< a< 90) значение косинуса будет положительным. Здесь выбираем знак плюс. Во второй четверти (90< a< 180) значение косинуса будет отрицательным. Тогда перед корнем выбираем знак минус.
Если значение синуса отрицательное, то угол расположен в 3-й или 4-й четверти. В 3 четверти (180< a< 270) косинус угла будет меньше нуля.
В 4 четверти (270< a< 360) косинус угла будет больше нуля.
Примеры.
Пример 1. Найти косинус угла, если sina = -0,6. 180<a<270 (в градусах)
Решение. Находим разность 1 и квадрата значения sina, т.е. квадрата (-0,6).
-0,6 в квадрате находится так: (-0,6)*(-0,6) = 0,36. Подставим его в искомую разность:
1-0,36=0,64
Получили квадрат значения косинуса. Для нахождения значения самого косинуса, извлечем корень квадратный из 0,64 и возьмем его со знаком + или со знаком – . Получим 0,8 или -0,8.
Так как по условию угол находится в 3 четверти, то искомое значение косинуса будет также меньше нуля. Значит выбираем -0,8.
Ответ: cos a =-0,8.
Рассмотрим пример для случая, когда угол находится в 4 четверти:
Пример 2. Найти косинус угла, если sina = -0,6. 270<a<360 (в градусах)
Решение такое же (см. пример 1).
Перед выбором ответа рассуждаем так:
Т. к. по условию угол расположен в 4 четверти, то значение косинуса будет больше нуля. Значит выбираем 0,8.
Ответ: cos a =0,8.

